QUESTION:
ANSWER:
QUESTION:
ANSWER: γ-rays are being
detected, t he
photoelectron plows through the NaI crystal, ionizing and exciting atoms as
it goes. Ideally it gives up all its energy before escaping the crystal.
There are now a very large number of photons in visible or IR or UV the
number of which is proportional to the energy of the electron which is equal
to the energy of the incident
γ-ray. Because of reflective
coatings on the surface of the crystal, many of these photons reach the
photomultiplier tube as a pulse of
photons
and strike the photocathode which again cause the electron production via
the photoelectric effect; because low-energy photons do not cause
photoelectric effect, mainly the UV photons participate here. These
electrons are then multiplied by the many dynodes in the tube resulting in a
current pulse proportional the energy of the original
γ-ray. If charged particles are being
detected, the charged particle itself plays the role of the initial
photoelectron, ionizing and exciting atoms in the crystal.
QUESTION:
ANSWER: Ѕ) and
bosons (spin 1). The fermions are divided into two categories, quarks and
leptons. There are six quarks (purple in
the figure) (u, d, c, s, t, b), the components of hadrons which include neutrons and protons. All quarks have electric charge ±1/3 or ±2/3 so they feel the electromagnetic force. They also feel the strong force. They also feel the weak force since we know that β-decay changes a neutron/proton to a proton/neutron via the weak interaction. All are fermions.
There are six leptons (green in the figure) (electrons (e), muons (μ), and taus (τ), and three associated neutrinos). All feel the weak force. The neutrinos have no electric charge, so they do not feel the electromagnetic force; the charged leptons, of course, do. For each force there is a ‘field quantum’, that particle which communicates the force between particles which feel that force (the pink in figure 4.8—γ, g, Z0 , W± ); note that these are all bosons since they have spin 1. For the electromagnetic force, it is the photon. For the strong force, it is the gluon. For the weak force, it is the Z and the W bosons. Note that only the Z has electric charge. The electromagnetic and weak forces have been unified in theory, sometimes collectively called the electroweak force.
QUESTION:
ANSWER:
QUESTION:
ANSWER: … hold
the nucleus together …" .
Indeed, if you have a nucleus it takes energy to pull it apart. As an
example, t he
α -particle (
4 2 He)
has a binding energy of about 7 MeV per nucleon; a deuteron (2 1 H)
has a binding energy of about 1 MeV per nucleon. The α -particle has 2
neutrons and 2 protons and the deuteron has one neutron and one proton, so
fusing two deuterons should result in one α -particle. The energy
released in such a fusion would be (6 MeV/nucleon)x(4 nucleons)=24 MeV. The
rest mass energy of an α -particle is about 3700 MeV, so the fraction
of mass turned to energy is about 24/3700=0.0065=0.65%. This released energy
shows up as kinetic energy of the
α -particlesheat,
in other words.
QUESTION:
ANSWER:
No. There are two kinds of elementary particles, fermions and bosons, and
only fermions have antiparticles. For more detail, see this
link .
QUESTION:
ANSWER:
Half life is a statistical property—you need a large number for it to be
meaningful. I think you would agree that some radioactive atoms would be
more likely than others to decay. With that idea, it should make sense
to your that the rate R at which the number of radioactive atoms
in a large sample changes will be proportional to the number in the
sample, N . So you can write R=-λN where λ is the
proportionality constant (called the decay constant ) to make the
proportionality an equation; the negative sign is there because it is
conventional to make λ be positive and I know that if the number
is decreasing, the rate of change of N must be negative (getting
smaller). I do not know whether you have had calculus or not yet, but to
solve for the unknown N (t ) you really need it. I will
proceed assuming you know calculus: dN /dt =-λN and
so N =N 0 e-λt N 0
is the number of atoms when you started measuring (t =0). The half
life is defined to be the time when N=N 0 /2, so
solving, Ѕ=e-λt -λT Ѕ
or T Ѕ =0.693/λ. A graph of N (t ) for two values
of λ is shown to the right. Here N 0 =10,000 and
you can see that for λ= 1 that t≈ 0.7 when N =5000.
QUESTION:
ANSWER:
I think you are overreacting a little bit here! My opinion is that string
theory is not a theory because it makes no predictions and is therefore
not falsifiable or verifiable. However, it is a hypothesis which many
good scientists are struggling to develop. And who can predict that any
idea is not "possible"? And the math being "too complicated" does not
mean that there is no value in the ideas; Einstein found the math needed
for the theory of general relativity was "too complicated" for him and
he needed to get help from mathematicians.
QUESTION:
ANSWER:
Fission is fairly easy because all you have to do is "tickle" a heavy
nucleus and it will split in two; this is usually achieved by adding a slow
neutron to the nucleus which is easy to do because it has no electrical
charge and therefore does not feel any repulsive force from the nucleus.
Fusion, however, involves bringing two positively charged light nuclei
together. Since they repel each other, they can only get close together if
they are going very fast. Another way of saying the same thing is that the
fusing target material (generally isotopes of hydrogen) must be very hot.
Containing a hot enough gas (plasma, actually, since the high temperature
will cause the atoms to be ionized) has turned out to be an extraordinarily
difficult engineering problem. There is an old saying among physicists,
tongue in cheek, that "fusion is the energy of tomorrow and it always will
be!"
QUESTION:
ANSWER:
γ -decay of an excited
nuclear state. The nucleus certainly does not gain energy since the net
result (for the nucleus) is a loss of energy as it makes a transition to a
lower-energy state. The energy is carried of by the kinetic energy of an
atomic electron which is ejected in the process.
QUESTION:
ANSWER:
mass number (236) before and after this fission
reaction are the same. However, this does not mean that the total mass is
unchanged. If you look up all the atomic masses involved in this fission,
you will find that the mass is less after the fission. To understand why,
see an
earlier answer .
QUESTION:
ANSWER:
mc 2 ; if you just look at a single atom at rest in
its ground state, that is all the energy it has. But here is the interesting
part: If you take an atom, pull out all its electrons, protons, and neutrons
and weigh them, they will weigh more than the atom had before you pulled it
apart. So, if all these pieces are at rest and far apart, you have more
energy than the atom had. The reason is that you did work to pull it apart
and thereby added energy which showed up as mass energy. So your question
should really have been "where did atoms lose their energy?"
QUESTION:
ANSWER:
QUESTION:
ANSWER:
two photons ,
though. One well-known example is the interaction of a high-energy photon
with the electric field of a nucleus (and therefore a photon) to create an
electron-positron
pair .
QUESTION:
ANSWER:
QUESTION:
ANSWER:
12 C and
13 C. There is one unstable isotope of carbon which exists in nature
also, 14 C, sometimes referred to as radiocarbon. Radio carbon is
being constantly produced by cosmic rays interacting with 14 N in
the atmosphere. 14 C has a half life of about 5730 years, so if
cosmic rays suddenly stopped creating it there would be almost none left
after a few half lives. But, there is a balance between creation and decay
so that the amount of 14 C on earth is about constant at any time.
However, suppose you find a fossil which has only about half as much 14 C
as all the current living things on earth. Then you can conclude that the
fossil is about 5730 years old.
QUESTION:
ANSWER:
QUESTION:
ANSWER:
E=mc 2 ;
in order to pull a bound nucleon out of a nucleus you must do work, i.e.
add energy. Where does that energy go? It goes into the mass. In most
respects, nucleons in nuclei retain their identities. We know this from
nuclear spectroscopy, the energy levels we observe in nuclei. However, don't
forget that nucleons are composed of quarks and, to a small extent, the
nucleus can behave as a collection of quarks where nucleons may share and
exchange quarks. But this is a very small overall effect.
QUESTION:
ANSWER:
beam intensity is about 4x1018 protons per second and the mass of a proton is about
1.7x10-27 kg. So the mass per unit time would be about 7x10-9
kg/s=7x10-6 g/s=7 μg/s.
QUESTION:
ANSWER:
β - decay essentially changes a neutron into a
proton, so the quark composition becomes that of a proton instead of that of
a neutron. β + decay essentially changes a proton into a
neutron, so the quark composition becomes that of a neutron instead of that
of a proton.
QUESTION:
ANSWER:
Z atoms have
zero angular momentum in their ground states. There are countless ways you
can excite an atom, usually by just shooting something at it, and if you
excite it to a state which does not have zero angular momentum, you have
imparted angular momentum to it. However, the more angular momentum the atom
has, the bigger it is and, as far as I know, it never "flies" apart due to
some centrifugal effect; the way to make it fly apart is to give it a lot of
energy, not a lot of angular momentum. However, molecules have states which
are different from just the orbital motion of the electrons. Imagine a
diatomic molecule like O2 , for example. There are states which
are rotational states, that is the molecule rotates like a dumbbell. As you
give the rotating molecule more and more angular momentum it experiences
centrifugal stretching, just like you would expect. If you give it enought
angular momentum it will eventually break the molecular bond.
QUESTION:
ANSWER:
QUESTION:
ANSWER:
a=F/m and so any force will cause an infinite
acceleration. In fact the theory of special relativity requires that any
object with zero mass can move only at the speed of light in vacuum. So a
massless object at rest cannot exist.
QUESTION:
ANSWER:
etc . This peculiar labeling of angular
momentum quantum numbers is a historical artifact where the words sharp,
principal, diffuse, and fine were used to describe spectral lines.
QUESTION:
ANSWER:
QUESTION:
ANSWER:
112
—>2Mn56 . The binding energies of the tin and manganese are 953.5
MeV and 489.3 MeV respectively. So the energy released in the fission would
be 2x489.3-953.5=25.1 MeV. What I cannot tell you is what energy photon
would be required to cause the fission. This depends on the structure of the
Sn112
and how it interacts with the photon. Fission might be induced by a much
lower energy photon than 25 MeV. After all, uranium can fission with no
energy whatever added to it (spontaneous
fission ).
QUESTION:
ANSWER:
QUESTION:
ANSWER:
de
Broglie 's picture of the Bohr atom).
QUESTION:
ANSWER:
orbital angular momentum and its spinning on its axis is
called intrinsic angular momentum . Now think about an electron in an
orbit around a nucleus in an atom. It clearly has orbital angular momentum
because of its orbit. But it also has intrinsic angular momentum, that is,
it behaves in many ways as if it were spinning on its axis; this is usually
referred to simply as spin . This is a fine analogy, but it should be
emphasized that spin is not really such a simple classical concept. For
example, if you were able to exert a big enough torque on the earth you
could stop its spinning or make it spin faster. The spin of an electron is a
constant property and cannot be changed. You can change the direction
(clockwise or counterclockwise) but not the magnitude of spin. Also, if you
try to model the electron as a little spinning sphere to find out how fast
it is spinning, you get absurd, unphysical answers. So, you can only push
the electron/earth analogy so far. Finally, I should note that in
relativistic quantum mechanics (Dirac equation) the existence of electron
spin is predicted to be exactly what it is measured to be.
QUESTION:
ANSWER:
QUESTION:
Is it true that even an electron has its north and south poles; if it
is, then how?
ANSWER:
QUESTION:
At the LHC protons travel at .999999991 c, or about 3 metres per second slower than the speed of light. I the the proton is also spinning at above 3 metres per second in the direction of travel wouldnt at least part of the proton for a brief period of time exceed the speed of light.
I'm guessing the answer is no because all answers involving exceeding the speed of light are no, but i'm having trouble understanding why.
ANSWER:
QUESTION: f I'm not mistaken helium 3 is a very powerful energy source. But there is very little of it on earth.
There is lots of it on the moon. so what problems would we run into if we extracted it from the moon why haven't we already done it?
ANSWER:
3 He is a potential fuel for a nuclear fusion
reactor. The energy producing reaction is 3 He+2 H —>
4 He+1 H+energy; here 2 H is heavy hydrogen or deteurium
(proton plus neutron plus electron) and 1 H is normal hydrogen
(proton plus electron). There isn't necessarily more 3 He on the moon, it is just thought
to be more abundant relative to the much more abundant 4 He there.
The interesting thing about helium is that it does not form molecules
because it is inert; and, because it is so light, if it appears in the
atmosphere it moves so fast that it escapes right into space. The best
source of helium on earth is to separate it from natural gas with which it
has been trapped underground. The reason that we have not already gotten it
from the moon is that it is terribly expensive to send spacecraft to the
moon and we would also have to develop the technology to extract it from the
moon rocks in which it is embedded and transport it back to earth. Even if
that were not a problem, the simple fact is that, in spite of decades of
trying, we have been unable to build a nuclear fusion reactor which can
produce more energy than it consumes and we are still decades away from
having a commercial fusion reactor. There is a kind of funny saying about
nuclear fusion: "Nuclear fusion is the energy of the future and always will
be!"
QUESTION: s there a difference between a proton and photon, besides their difference in charge?
ANSWER:
protons are fermions (spin
Ѕ), photons are bosons (spin 1)
protons have mass, photons no
not
protons are composite
particles (quarks and gluons), photons are not
photons are the quanta of the
electromagnetic field, protons are baryons
protons have electric charge,
photons do not
photons have an "h", protons
have an "r"
QUESTION:
ANSWER:
M +2m e where m e
is the electron (or positron) rest mass. Your first thought might be that
the kinetic energy of the positrons would need to be Mc 2 .
But this would not work because the particles would have to be at rest which
would violate momentum conservation; so the energy would have to be
considerably larger. Proton antiproton interactions are considerably more
complicated because they have sufficient rest mass energies to create
massive particles even at rest and because they, unlike electrons and
positrons, are composite particles made up of quarks. They usually
annihilate into mesons which, being unstable, decay ultimately to some
combination of gamma rays, electrons, positrons, and neutrinos.
QUESTION:
ANSWER:
1 H) composed of only protons. On its
own, a neutron will beta-decay; quite simply, this is determined by
energetics—energy is released if a neutron decays into a proton, a neutrino,
and an electron. To find out what happens inside a nucleus, you again look
at energetics; if a neutron inside a stable nucleus were to decay, energy
would have to be added, so it does not happen.
QUESTION:
ANSWER:
QUESTION: E e /E p )c
and
b) the fractional energy transferred from the electron to the proton is (2E e /E p ), where
E e is the total incident energy of the electron and E p is the rest energy of the proton.
ANSWER:
here .
QUESTION:
Is there a speed or time measurement for how long it takes the nuclei of Uranium or Plutonium to transfer from Matter to Energy in nuclear fission after the neutron has split the atom?
ANSWER:
paper which
lists the "prompt energy release time" as in the range of 10-20 -10-7
s. This is the time between the scission and the end of prompt gamma rays
and neutrons. I presume this huge range is because of dependence on the
fissioning nucleus and the fission products.
QUESTION:
"Tritium is
produced in nuclear reactors by neutron activation of lithium-6" my question
would be; If lithium-7 (the product of the neutron capture) is a stable
isotope why does it split? And is this splitting α decay, or fission, that
just happens to result in an alpha particle & a tritium nucleus?
ANSWER:
7 Li does not get formed in its
ground state, rather it is highly excited. Or, you might want to look at it
as a nuclear reaction since it happens very quickly: 6 Li+n->4 He+3 H.
It is not surprising that this reaction goes because the alpha particle is
extraordinarily tightly bound; that is one of the reasons heavy nuclei often
undergo alpha decay—because it is such a tightly bound nucleus, there is a
reasonable probability that it will spontaneously form inside a nucleus.
QUESTION::
ANSWER:
mc 2 )
of a hydrogen atom is about 1 GeV. Therefore, since you have added energy by
ionizing the atom, the atom is lighter by about 100x13.6/109 %≈10-6
%. Any molecular binding energy will be of the same
order-of-magnitude. The energy we get from chemistry comes from mass and it
is extremely inefficient. So, although E=mc 2 is at the
heart of things, you usually do not have to worry about mass changes in
molecular chemistry because they are so tiny. To do detailed calculations of
chemical reactions usually requires that you do things quantum mechanically
which requires a potential energy function. These calculations can be very
complex and approximate models are used to simulate the potential energies
of the molecular systems. Once you get beyond the simplest atoms and
molecules, the calculations can only be done numerically and approximately
on computers. An example of a potential energy function, the Morse
potential, for a diatomic molecule is shown in the figure to the left. The
form of this potential is V Morse =D e [1-exp(-(r-r e ))]2 ;
note that, for one of the atoms in the molecule, the force (slope of the
potential energy function) is repulsive for r<r e and
attractive for r>r e . This is expected since the molecule
has a nonzero size because of repulsion but is bound because of attraction.
A first approximation often used for bound molecules is a harmonic
oscillator potential (masses attached to a spring).
QUESTION:
I know that neutrons is placed in a wax container to contain the neutrons, but why is this an effective way to contain the neutrons. I want to take in account the linear momentum and the energy, but I'm not sure how to begin or where to do the research?
ANSWER:
i.e . the paraffin slows the neutrons down. The reason that
paraffin is good is that it is a hydrocarbon and has lots of hydrogen in it.
Hydrogen is good to slow down neutrons because the best way to slow down a
fast moving object is to collide it with an object at rest which has about
the same mass (think of a head-on collision of two billiard balls); hydrogen
has about the same mass as a neutron.
QUESTION:
If a particle has a lifetime of say 100 years then what are the chances that that particle will decay in 1 year. How will one go about calculating particle decay probability?
ANSWER:
N (t )/dt =t /τ
where N (t ) is the number of particles at some time t
and τ is the mean lifetime. The solution of this differential
equation is N (t )=N 0 exp(-t /τ )
where N 0 =N (t= 0). So, when t =τ ,
N =0.37N 0 , there are 37% of the original particles
left. For your question, you might want to ask what is the situation when
t =1 if N 0 =1 and τ =100:
N =exp(-0.01)=0.99. If you want to interpret that as a 1% probablility
that the particle has decayed, I guess that that would be ok. But, of
course, there is no such thing as 99% of a particle. Keep in mind, though,
that this is not linear; for example, if t =50=τ /2,
N =exp(-0.5)=0.61, not 0.5.
QUESTION:
What happens to gamma rays when they are blocked by materials like lead, and how come they're not blocked by some other materials?
ANSWER:
QUESTION:
Two questions regarding radioactive halflife values.
ANSWER:
gravitational
time dilation ); and, certainly, the lifetime of any unstable system is a
clock. Your second question must refer to elementary particles since we do
not have antiatoms or antinuclei to study. (Actually,
antihydrogen has
been made in the lab in 2010, but I do not believe there have been any
detailed measurements on its properties.) The
CPT theorem requires
all particle-antiparticle pairs to have identical masses and
lifetimes . There has, to my knowledge, never been a case where this is
not correct; I am not sure to what extent extremely accurate measurement of
antiparticle halflives have been made to test this, but I suspect there is
no evidence to suspect CPT violation in this regard.
QUESTION:
In a beta particle emission, do the beta particle and the recoiling nucleus don't move along the same straight line? My friend tells me that. How can be that possible in view of the momentum conservation?
ANSWER:
QUESTION:
I was just thinking about the structure of atoms being made of protons, neutrons and electrons. Do you know why atoms even have neutrons if the neutrons are electrically neutral? what is the point of having neutrons?
Also, why do they say Pi is squared when it is so obviously round?
ANSWER:
1 H, which consists
only of protons. A simple way to look at it is that the nuclear force which
protons exert on each other is very strong but, because the protons are so
close to each other inside a nucleus, the Coulomb (electrostatic) repulsion
is also very strong; so you might think of the neutrons as "buffers" which
hold the protons far enough apart that the Coulomb force does not get too
big. During nucleosynthesis in a star, if a nucleus is formed which has one
or two too many protons, it will decay by transforming excess protons into
positrons (anti-electrons), neutrons, and neutrinos.
QUESTION:
Why is the probability of splitting an atom greater when sending slow neutrons rather than fast through the nucleus in fission reactors?
ANSWER:
QUESTION:
How many particles do the particle accelerators at most accelerate when they are running experiments? One, ten, hundreds or thousands?
ANSWER:
-19 C. So, suppose the beam
current is 16 nA=16x10-9 C/s; then the number current is [16x10-9
C/s]/[1.6x10-19 C/proton]=1011 protons/second, about
100 billion. At the LHC in Europe, the intensity is much larger, on the
order of 4x1018 protons/s which would correspond to an average
current of about 0.6 A. The high number intensities are vital because the
events physicists are looking for are extremely improbable. The LHC is a
pulsed machine, its beam is a series of very short pulses. So, the
instantaneous current during a pulse is much larger than the average
current.
QUESTION:
Is there something wrong with the theory that says, if there is enough dead matter from dying stars that comes together, gravity will take over and eventually produce a new star from this dead matter?
I am aware that stars form from hydrogen, but what if 999 trillion tons of the heaviest known elements got together all in one place? Most say a star would not form because there is no hydrogen, but…what then? It would appear that gravity, being indiscriminate, will continue crunching this big iron ball until critical mass is surpassed, regardless of what the result might end up being. What would that result be?
ANSWER:
nuclear fusion , fusing light nuclei to heavier nuclei. However, when you
reach iron on the periodic table you no longer gain energy by fusing nuclei
and therefore the energy production ceases. Before the whole star becomes
iron, though, other instabilities cause the star to, in one way or another,
end its life, the details depending on the mass of the particular star. The
most dramatic end is a supernova (of which there are several types, again
depending on details), a very dramatic explosion of the whole star; the
energy from such an event is what is generally thought to be responsible for
creation of heavier elements beyond iron. One possible end following a
supernova explosion is called a neutron star. The remnants of the star,
mostly heavy elements like you refer to, will undergo gravitational collapse
and, in essence, electrons will be pushed into protons such that the star is
made mostly of neutrons and is extraordinarily dense (it is essentially a
giant nucleus). With sufficient mass, that is what I believe would happen to
your collection of heavy elements. However, your number, about 1018
kg, is way too small for the requisite mass. Neutron stars have about
1.4-3.2 solar masses and the mass of the sun is about 2x1030 kg.
QUESTION:
From a physicist's point of view do you ever see us using antimatter as an energy source and are there any ways to even theoretically to create antimatter in adequate quantities? Is antimatter power really just a theoretical thing that won't get any practical use in your opinion?
ANSWER:
QUESTION:
if i put a half of Hollow tube insid the water(and the other half is in the
air) and drop to it a coin - it will sink.
now if i put from the top of the tube a coin that fit the Diameter of the
tube and water cant pass this coin what will happen?
ANSWER:
Mg down acting down on it, the atmospheric pressure force P A A
acting down on it (A is its area), and the atmospheric pressure force
P A A of the surface of the water acting up on it.
Hence the net force will be Mg down and it begins to sink. However,
after it has sunk to a depth D the pressure up from the water has
increased by an amount ρgD where ρ is the density of the
water. So now, Ma=-Mg -P A A+ (P A A+ρgDA ),
or a=-g+ρgDA /M . If the water caused no drag on the coin as it
fell (obviously not correct), the coin would oscillate about the equilibrium
depth D e =M /(ρA ) with simple harmonic
motion. In the real world, there would be some drag forces and the coin
would eventually come to rest at D e .
QUESTION:
I want to run a 7.5kw generator for eight hours. I do know it takes 15hp to run a 7.5kw generator.
But I want to use weight to do it. Like a grand father clock. How much weight would I need to use if the weight could drop 6ft. ? I would like the equation or equations so I could choose to use more distance or use more weight to make this work for my application.
ANSWER:
4 J/s. If a mass m in kg falls
with some constant speed v , the power generated will be P=mgv
where g =9.8 m/s2 is the acceleration due to gravity. Now,
you stipulate that the time must be 8 hr=2.88x104 s, so if it
falls h meters in 8 hr, the speed would be v=h /2.88x104 =3.47x10-5 h .
So, P=mh ∙9.8∙3.47x10-5 =1.12x104 =mh ∙3.4x10-4 ;
so, your sought equation is mh =3.29x107 kg∙m. So, for h =2
m (approximately 6 ft), m =1.65x107 kg≈16,000
tons. You might want to rethink your plan! If you want to include the time
as a variable (in other words, wind your "grandfather's clock" more
frequently), the equation would be mh /t =1,140 kg∙m/s. (You
will need some kind of governor to regulate the speed and some gearing
system to ensure that the translational speed of the mass creates the right
rpm for the generator design.) I am afraid that a falling weight is not a
very good choice of power source for this application.
QUESTION:
I am confused as to how an anti-particle and a particle can
collide. If the fundamental particles only exist at points and don't
have any volume, how exactly can two particles ever actually collide
with each other?
ANSWER:
QUESTION:
One of my friends (an oncologist, so no dummy) tells me that modern nuclear power plants have a safety switch that will automatically send all the rods into a graphite core in case of emergency which will then prevent a nuclear accident, such as Chernobyl or Fukushima, and will safely contain the fissionable material for.....essentially...ever. I can't find a reference to such a safety device on the internet, although I may be just looking in the wrong place. My understanding is that all nuclear power plants will fail at some point and breach the containment container if water is not constantly supplied. Which is correct?
ANSWER:
FOLLOWUP QUESTION:
Do nuclear power plants require a constant supply of water to remain safe? I'm not talking about the expended fuel rods, but about the core itself. Without water, will a power plant go critical at some point?
ANSWER:
irst
with the control rods all the way in, the reactor is subcritical which
means that any time a fission happens, fewer than one more occur. Each
fission is like a lighted match which goes out without starting a fire.
Now, start pulling the control rods out.
Eventually you reach the point where more than one fission happens after
each fission; this is called supercritical. So the rate of fission
increases and you have to be careful to keep it from "running away".
When it reaches the rate you want, maybe 1020
fissions per second, you have to stop the increasing rate by putting the
control rods back just far enough so that the reactor is critical—each
fission causes another so now energy is produced at a constant power of
P=E ∙1020 per second where E is the energy of a
single fission. This would be some number like P =1 gigawatt (GW).
Now, to the crux of your question. You are producing
energy, in the form of heat, of 1 GW which is one billion joules of energy
per second and that energy has to be carried away
somehow or else the whole reactor will heat up and melt (the dreaded
"meltdown"). The most common way to carry that energy away is with water and
the heated water is used to drive turbines to generate electricity. If you
do not do something to take the heat away, you have a disaster. (I just made
up 1020 . Don't quote me on that—it is just to illustrate.)
QUESTION:
Is it possible to accelerate neutrons?
ANSWER:
-15 m) away from the nucleus. So, although a
neutron can be accelerated in principle, I can conceive of no way to do it
in practice. So, I will go out on a limb and say that it is impossible to
build a workable neutron accelerator.
NOTE
ADDED:
QUESTION:
what is the difference between l and L in atomic theory?in one book L is given as energy shell and in one book L is represented as orbital angular momentum of electron...so i want to say that energy shell can also be represented as 1,2,3 but orbital angular momentum is always rep.as L so which one is right??
ANSWER:
n : n =1 is the
K shell, n =2 is the L shelln =3 is the M shell, etc .
The magnitude of the total orbital angular momentum of a quantum state is
almost always denoted by L . The value of L is determined by
the orbital angular momentum quantum number ℓ : L=ħ √[ℓ(ℓ+ 1)]
where ℓ =0,1,2,3… Also of importance is the projection (component) of
the angular momentum on to a z -axis, L z =mL ,
where m =-ℓ, -ℓ+ 1,-ℓ+ 2…0…ℓ -2,ℓ -1,ℓ .
(Note that it is usually conventional to use script ell (ℓ ) rather
than l .)
QUESTION:
I was wondering, since in quantum phisics observing a phenomenon can change the odds of this phenomenon to arise, how can a detector in a particle accelerator can be trusted? shouldn't it already vary the result simply by measuring them?
ANSWER:
that
particular particle to be 100% of what you measure. If, however, you
make many measurements then you can deduce the distribution of
probabilities. One measurement never gets you any useful information in
quantum mechanics. For example, suppose you want to measure the mass of a π0
meson. This particle decays into two photons, so, if you measure the enegies
of the two photons and add them, this is the rest-mass energy (E=mc 2 )
of the meson from which you can easily deduce the mass (m=E /c 2 ).
The graph to the right shows the results of many such measurements. Don't
worry about the units. The fact is that you might make one measurement which
gives you the mass and find that you get that m =0.026 units. You have
found that the meson you measured had that mass, but if you keep measuring
you will find that others have different masses; you have not caused all
mesons to have a mass of 0.026 units just because you determined one to have
that mass. You would be inclined to call the mass of the meson to be
approximately 0.020 units (the most probable value) with a distribution
determined by the rest of your data; the spread of these data, incidentally,
would tell you about how long this particle lives, on average, before
decaying into two photons. (Oh, by the way, any given meson has the whole
distribution of masses before you measure it; measuring it "puts it" at the
mass you measure. In other words, a particle does not have a definite mass
but a probability distribution of possible masses. Only if the particle is
stable (like an electron) does it have a definite mass.)
QUESTION:
While we were studying about atomic structure, our teacher taught us something (I don't remember precisely how was it) about the reason that electron can't be in the nucleus of an atom. She made some calculations and showed that if electron were in the nucleus, it would have to move with a velocity which is greater than that of light. But what about beta decay? Doesn't an electron originate from the nucleus during beta decay? Does it travel faster than light when it originates?
ANSWER:
confined in a nucleus, that is, the structure of an atom cannot
include electrons which spend most of their time inside the nucleus. There
is nothing forbidding an electron from ever being in there. In fact, the
wave function of any atomic electron has a nonzero value inside the nucleus
so it spends some (tiny amount of) time inside. I am not familiar with her
"faster than light" argument; usually the uncertainty principle is used
which shows that the energy uncertainty of an electron confined in a box the
size of a nucleus is too large to be consistent with measured atomic masses.
So, you see, your beta decay example does not violate what she taught you
since the electron does not remain inside the nucleus after its creation.
(Be sure to realize that the beta decay electron did not exist before the
decay happened, it was not hanging around waiting to pop out.)
QUESTION:
I am a high school physics teacher, and am troubled somewhat by inverse beta decay. From what I gather, it can occur when a proton absorbs an electron antineutrino and an up quark flips to a down quark. It then emits a positron and becomes a neutron. What troubles me is where the energy comes from. Flipping a proton to a neutron requires an input of energy, it seems, because of the mass difference. And then there is the mass and kinetic energy of the positron. Can the electron neutrino possibly supply all of this energy? It seems unlikely.
ANSWER:
QUESTION:
In simple artificial bombardment experiments with alpha particles, how do I determine the correct resulting isotope and if/which particles are emitted? For example, 27Al (a,N) 30P results in the release of a neutron. Some such alpha bombardments result in the release of a protons. How do I determine which will occur? Determining either the remaining particle or the resulting isotope is the issue.
ANSWER:
2 and a table of
atomic masses (a handy one is here ) which gives the atomic masses of
isotopes in AMU. I will do a some examples.
Your example: 27 13 Al(4 2 He,1 0 n)30 15 P;
M Al c 2 =26.981538578x931.494=25133.1413
MeV, M He c 2 =4.00260325413x931.494=3728.4009
MeV, M n =1.00866491600x931.494=939.5653
MeV, M P c 2 =29.978313753x931.494=27924.6194
MeV. So, Q=27924.6194+939.5653-25133.1413-3728.4009=2.6425 MeV. So, this
reaction can occur since there is an excess of of energy after the
reaction. There is an additional detail which I will discuss below.
Suppose instead we do the (α,p) reaction: 27 13 Al(4 2 He,1 1 H)30 14 Si;
M Si c 2 =29.973770136x931.494=27920.3870
MeV, M H c 2 =1.00794x931.494=938.8901
MeV. So, Q=27920.3870+938.8901-3728.4009-25133.1413=-2.2651 MeV. So, for
this reaction you must bring in an excess of at least 2.2651 MeV of
energy for it to proceed.
Finally, a reaction ((p,3n) which bombards with
protons and three neutrons come out) to illustrate my first point above
that the final product must be bound: 6 3 Li(1 1 H,31 0 n)4 4 Be.
4 4 Be would be a nucleus with 4 protons and 0
neutrons and, when you look up its mass you will not find it because it
does not exist; 4 protons will not bind together to make a nucleus,
6 4 Be is the lightest known berylium isotope.
Here is the additional detail mentioned above. The
first example, with a positive Q-value might seem to imply that you can just
have a bunch of Al and He nuclei at rest and they will react to give you a
bunch of neutrons and P nuclei plus a bunch of energy. But, both nuclei are
positively charged and they therefore repel each other. Therefore, you must
give the alpha particles at least enough energy so the two nuclei can
"touch" and interact. I calculate that energy to be roughly 10 MeV for
alphas on 27 Al, so your reaction will go for the kinetic energy
of the α-particles of greater than 10 MeV. For the (α,p) reaction, the
kinetic energy must be at least 12.27 MeV.
ADDED
DETAIL:
U of two point charges Z 1 e and Z 2 e
separated by a distance R is U =kZ 1 Z 2 e 2 /R
where k =9x109 J·m2 /C2 and e =1.6x10-19
C. The projectile, therefore, must start with its kinetic energy equal to
U in order to come from far away to R . I took the size of the
27 Al nucleus to be 1.2xA 1/3 x10-15
m=1.2x271/3 x10-15
m=3.6x10-15 m and treated the alpha as a point charge. So, for
Z 2 =13, Z 1 =2, U =26x9x109 x(1.6x10-19 )2 /3.6x10-15 =1.7x10-12
J=10.4 MeV. I have used 1 eV=1.6x10-19 J. This assumes that the
mass of the Al is infinite compared to the mass of the alpha-particle, but
this is just meant as an order-of-magnitude estimate.
QUESTION:
So I understand that protons and neutrons are made of quarks. A proton is made of two up quarks and one down quark and a neutron is made from two down quarks and one up quark. I know that much. But there are so many other particles in the standard model. Are there any other large particles we can (or cannot) observe besides protons and neutrons that are composed of quarks or bosons or whatever? I have been wondering this for a while.
ANSWER:
standard model .
QUESTION:
Why any atom having magic numbers(i.e 2,8,20,50 etc.) of nuclides has special stability?(sry for 2 in 1 but i am very curious). How can we determine magic numbers? Is there any specific method to calculate magic numbers?
ANSWER:
QUESTION:
ANSWER:
A , composed of N neutrons and
Z protons such that N+Z=A . Nuclei of a given A are
called isobars. So, N could be anything from 0 to A with
Z=A-N . In practice, nuclei which are bound at all must have both
protons and neutrons. Take a specific example: Plotted to the right is
the binding energy of the known isobars of A =73 plotted as a
function of Z . Binding energy is essentially the energy you would
have to supply to totally disassemble a nucleus and the more tightly
bound a nucleus is, the lower the energy state. So, if nature provides a
way to keep A constant but change Z and N , a
nucleus will take advantage of it. So, Zn and Ga have too few protons
(or too many neutrons, however you choose to look at it), and they will
decay by turning a neutron into a proton plus an electron plus a third
particle called a neutrino (which has practically no mass and no
charge). Because the energy of the nucleus decreases, the leftover
energy is used to shoot out the electron and neutrino. This is called β-
decay. But, when these two get down to Ge they will go no farther
because energy would have to be added to get to As and there would be
none left for the electron and neutrino. On the other side, As and Se
have too many protons (too few neutrons) compared to Ge and so they have
to hope that nature provides a way to turn protons into neutrons.
Indeed, a proton can decay into a neutron plus a positron (a positively
charged electron) plus a neutrino. This is called β+ decay.
Finally, there is a process which can compete with β+ decay
which is called electron capture which is what you refer to in your
question. There is a swarm of electrons around the nucleus and if a
proton could combine with one of them it would do so. Indeed, this is
allowed if a neutrino is ejected. The electrons do not have to suddenly
"crash into the nucleus", they are already there. The electrons in an
atom do not really run around in little circular orbits, they are
smeared everywhere, even inside the nucleus; there is a small but
nonzero probability of looking for an electron inside the nucleus and
finding it there. I think if you read through my answer carefully you
will find I answered all your questions. Nature is "smarter" than you
give her credit for!
QUESTION:
We've been learning about nuclear decay and radiation lately in AP Chemistry( I am junior in high school), and this question crossed my mind:
If protons can absorb electrons, what if a neutron absorbed a positron? I was imagining that if we had a neutron emitter pointed to the same place a positron emitter was pointed, positrons might merge into some neutrons and create protons. Then i wondered, now what if we were to isolate this new proton into a separate chamber of this weird apparatus I cannot fully explain, in which we emitted electrons, and thus making the proton into a neutron again, except it is now one electron and one positron heavier. Now what if we continued this cycle? Would the neutron become unstable as do heavy elements? Are current-day neutrons nothing but the development of the said process to the most stable form, as the amount of positrons and electrons must be just right? If we managed to force more positrons and electrons into the neutron than naturally allowed, would it be like nuclear fission, but make an explosion that is thousands of times greater than a hydrogen(fusion) bomb? Or will there be such a tiny mass defect when the neutron gets too large that it only explodes the apparatus and nothing more?
ANSWER:
mc 2 energies of the
particles) of all the participating particles before and after the
creation must be exactly the same. Electron (e-) capture by a proton is a common
nuclear decay mode, resulting in a neutron (np)
afterwards. One thing you miss, though, is that there is a third
participant, a neutrino (ν ), which exits afterwards in both cases. The
reason that electron capture is common is that the nucleus is surrounded
by a cloud of electrons available for capture; positrons are not
normally around unless you put them there and then they are much more
likely to annihilate with one of the many electrons before getting the
chance to interact with a neutron in the nucleus. So, let's talk about
the energetics of these reactions:
Rather than using
masses in kg, I will use rest mass energies Mc 2 in MeV
(million electron volts). [I assume that, since you are in an AP course
and talking about nuclear chemistry, you are familiar with the electron
volt as a measure of energy; if not, it is the energy an electron
acquires when accelerated across a potential difference of 1 volt.] The relevant masses are: M n c 2 =939.565378, M p c 2 =938.272046,
and M e- c 2 =M e+ c 2 =0.510999.
The neutrino has approximately zero mass. Although these are energies,
it is customary, if a bit sloppy, to refer to these numbers as masses
which I will do.
We will also need
sums of masses, M p c 2 +M e- c 2 =938.783045
and M n c 2 +M e+ c 2 =940.076377.
For electron
capture, p+e- ―> n+ν . Note that the sum of the mass on
the left is 938.783045 and on the right is 939.565378. That means that
if all masses are at rest before and after the capture, this is
impossible because there is not enough energy before to create a
neutron. The way this can happen is if the electron brings at least
0.782333 MeV of kinetic energy with it when it encounters the proton and
then any leftover energy will be shared by the kinetic energies of the
neutron and the neutrino. The energetics also tell us that the neutron
is not a stable particle because its mass is greater than the masses of
the particles it could decay to and a free neutron will decay, n―> p+e- +ν.
The half life of a free neutron is about 15 min. In a stable nucleus a
neutron does not decay.
For positron
capture, n+e+ ―> p+ν . Note that the sum of the mass on
the left is 940.076377 and on the right is 938.272046. There is adequate
mass to create the new mass and the excess energy is carried off by
the neutrino. It also tells you that the free proton is a stable particle
(at least against decaying into a neutron and positron) because where
would the extra energy come from?
So, a proton
(neutron) does not get a little heavier each time it combines with an
electron (positron) and then with a positron (electron), you end up with the
mass of the proton (neutron) again.
QUESTION:
1) is it possible to know the exact location of a single
atom? 2) If we use the most powerful microscope in the world and make it
1 million times more powerful would we be able to physically and
directly see what is happening at an atomic level? would we see the
atoms?
ANSWER: atomic force
microscope .
QUESTION:
Is the Proton Stable, or does it decay over time?
For instance I read it's Mean lifetime is: >1.9 x 10^29 years (stable)
it confused me because of the stable in the brackets, is it saying that it is stable and that the lifetime is actually hypothetical?
ANSWER: 35 years. A later more sensitive experiment might be
able to lower the limit to maybe 1030 years, and so on.
QUESTION:
what is the differences between the meaning of charge and matter densities of a nucleus?
ANSWER:
QUESTION:
Particle accelerators are said to reproduce the early conditions of the universe. At the same time the energies of these collision are said to be no greater than that of cosmic rays hitting the upper atmosphere. Can we say then that the early conditions of the universe are constantly reproduced in our own upper atmosphere? Do you think it would be feasible in the future to just build a detector in the upper atmosphere in the future? Can't we just point a very sensitive telescope toward our skies and learn from these collisions?
ANSWER:
QUESTION:
Conversion of mass to energy (fission) has been demonstrated many times in laboratory and field tests. Has conversion of energy to mass also been demonstrated in laboratories?
ANSWER:
A very energetic
photon (massless) can spontaneously turn into an electron-positron pair;
this is called pair production.
The mass of a nucleus is always less than the sum of all the constituent proton and neutron masses. Suppose you remove a neutron from a nucleus; it will take work because that neutron is bound in the nucleus. Hence, the final system of neutron and
the original nucleus minus one neutron has a greater mass if both objects are at rest. So let’s just say that the nucleus, having a mass smaller than the sum of its parts, is an example of converting energy into mass because there is more mass after you disassemble it by adding energy (doing work).
QUESTION:
Rutherford was able to determine the nature of alpha particles by recognizing that they have the same atomic spectrum as helium. However, if alpha particles are just the nuclei of helium atoms, then in the absence of electrons, what produced the spectra?
ANSWER:
QUESTION:
Why is radioactive decay dependent on the number of atoms or radioactive particles present in the sample? Does it have anything to do with the total energy of all the atoms in the sample?
ANSWER: For every radioactive nucleus there is a probability that it will decay
in a certain elapsed time. If you have a thousand of them, then you will see
them decay at a rate which depends on the probability tha any one will
decay. If you have a hundred thousand of them, the rate at which they will
decay will be 100 times the rate at which you observe the thousand to decay.
Given the fact that the likelihood of any given nucleus decaying is the same
as for all the others, then the number you actually see decay per unit time
is proportional to the number of nuclei present.
QUESTION:
I'm an English Ph.D. student writing about the figure of the microcosm in the modern novel, and am interested in the parallel with contemporary physics and the conception of the atom as a "little
solar system." My question is: how much did the evidence from the experiments done by Rutherford, et. al. make this theory necessary and how much was it just a convenient metaphor? Would other pictures of the atom have been equally plausible, or was this pretty much as accurate a representation as possible?
ANSWER:
earlier answers, the Borh model of the atom, electrons running around in
well-defined circular orbits like planets around the sun is, at best, a very
rough approximation of atomic structure. Historically, such a model was
ruled out because an electron moving in a circle radiates its energy away and
it would very quickly spiral into the center of the atom. However,
Rutherford's experiments showed unambiguously that nearly all the mass of an
atom and all its positive electric charge resided in a volume
extraordinarily tiny relative to the size of the atom. Putting the electrons
outside then became imperative and Bohr invented his model of the atom by
postulating certain rules for orbits which would be special in that
electrons in those orbits would not radiate away energy. His rules also had
to, and did, explain the spectrum of the hydrogen atom, those colors of
light which are emitted from hydrogen. But, this is clearly ad hoc in
many ways as new ideas often are. Within just a few years, though, partly
motivated by the success of this model, a new branch of physics, quantum
mechanics, was developed which provides an accurate picture of both how we
should think about atomic structure and why certain atomic states do not
radiate away their energy.
QUESTION:
I have been told that the strong force becomes repulsive at small distances. Is this the case and can you explain why or why not?
ANSWER:
QUESTION:
why does CO2 leak very quickly from a bicycle tube, while N2 (rather than pesky messy air) leaks very slowly?
I'm told "no easy answers", but maybe there is for the specific situation?
ANSWER: 2 is a much smaller
molecule than N2 .
FOLLOWUP QUESTION:
can you elaborate just a bit?
for this 7th grader mentality, it would seem that N2 & O2 should be about the same size - aren't all electrons are in the same orbital shells? and then the addition of a C to the O2 should make it bigger?
is it something to do with the double bonds on the CO2 that makes the molecule smaller?
ANSWER: i.e . A and B are more tightly
bound), then we can expect AB to be smaller than CD. I am not a chemist, but
maybe your double bond idea is a way of saying this. I am a nuclear
physicist and there is a similar effect in the following example: a
deuteron, consisting of a proton and a neutron has a radius of about 2.1x10-15
m and an alpha particle, consisting of two protons and two neutrons, has a
radius of about 1.6x10-15 m. The alpha particle is much more
tightly bound than the deuteron.
QUESTION:
What determines the number of neutrons in an atom?
ANSWER:
QUESTION:
I know a little about the bohr model of the atom and I am curious about
how the nuclear charge of an atom affects it's radii. If the nuclear
charge increases I would think that the radii would decrease but I'm not
sure of the math and if that model holds up.
ANSWER: Ze
instead of e (i.e . magnitude of the force on the electron is
k e Ze 2 /r 2 , you will
find that the radius is a 0 /Z where a 0
is the radius of the hydrogen orbit in the ground state.
QUESTION:
The P in PET scan stands for positron. Positrons are antimatter. How are the positrons transported and injected without destroying the instruments and how is the positron selecting the correct tissue to destroy?
ANSWER: PET .
QUESTION:
How do you make something radioactive? Can you simply hold it next to a radioactive item?
ANSWER: 60 Co, a radioactive isotope of
cobalt which is commonly used for cancer treatment. Stable cobalt which is
composed of 59 Co absorbs a neutron and becomes 60 Co
which has a half life of about five years.
QUESTION:
why don't electrons in an atom collide with the nucleus? Doesn't the nucleus of an atom have a positive charge? if so, then it should make sense that the electrons would be attracted to it, and not just go around it in orbitals. So yeah, I'd like to know why electrons don't fly into the nucleus, and stay in their orbitals. At the quantum level, I doubt gravity has any role in it, and even if it does, the mass of the nucleus would far succeed the mass of any individual electrons.
QUESTION:
What keeps an atom from getting smaller and smaller if an electron can lose energy and be attracted to the nucleus? What keeps electrons from moving closer and closer to the nucleus?
ANSWER:
QUESTION:
While reading " A brief history of
time by stephen Hawkings, i found that he explained something about spin
0,1,2. I wanna know that how is spin 0,1,2 different from Spin 1/2 and
how does pauli exclusion principle explains it?
ANSWER: s , then the intrinsic angular momentum of
that particle is S ={√[s (s +1)]}h /(2π ).
Intrinsic means that this is not due to some orbital motion, but is
associated with even a free particle. It is sort of like the earth whose
orbital motion around the sun and rotational motion about its axis are
different things; particle spin is sort of like the earth's rotational
motion about its axis. Particles with half odd-integer spin quantum numbers
(1/2, 3/2, etc .) are called fermions and obey the Pauli exclusion
principle; examples are electrons, protons, and neutrons (all with s =Ѕ).
Particles with integer spin quantum numbers are called bosons and do not
obey the Pauli exclusion principle; examples are the pi meson (s =0),
photon (s =1), and the graviton (if it exists, expected to have s =2).
QUESTION:
Do protons generate magnetic field around them ?
ANSWER:
QUESTION:
As I uderstand it, Carbon 14 is formed by neutrons comming from cosmic rays witch interract with Nitrogen(7 protons + 7 neutrons). Nitrogen lose a proton and win a neutron wich become carbon 14 (6 protons + 8 neutrons), right ?
Then, the part that I do not get is how Carbon 14 decay to Nitrogen. Wikipedia says that Carbon 14 loses eletrons and electrons antineutrinos to become Nitrogen again, but I don't understand because Nitrogen is 7 protons. Is Carbon gaining a proton ? Can you make this more clear for me ?
ANSWER: 14 C decay is what is called beta decay. Inside the
14 C nucleus one of the neutrons spontaneously turns into a
proton, an electron, and an antineutrino. The electron and the antineutrino
leave and the net effect has been to change 14 C to 14 N.
QUESTION:
How much energy does CERN use to smash 2 protons together to try & see the Higgs particle?
ie in laymans terms, would it be equal to lifting a chevy off the ground...or a train engine?
ANSWER:
link from CERN which fully discusses the energy content of the LHC
beams. The number they give for the beam at full intensity is 362 MJ. They
show that this is the energy of a 3200 kg Subaru going about 1000 mph. It is
the energy which could lift that car about 10,000 m, or about 30,000 feet.
But maybe you are asking about just the energy of the two protons? That is
much smaller, because the beam contains about 3x1014 protons and
so the energy of each proton would be about 10-6 J, not enough to
notice macroscopically.
QUESTION:
What would happen if
ANSWER: 235 U or 239 Pu),
but you could not make a reactor with radium as a fuel because it is not
fissile which means that it can be induced to fission by causing it to
absorb slow neutrons and to therefore sustain a chain reaction. The
energetics are such that if it were split into two fragments, energy would
certainly be released. You can tell your daughter that I had the pleasure of
working with Marie Curie's grandaughter Mme. Hйlиne Langevin-Joliot, also a
nuclear physicist, at Saclay National
Laboratory outside Paris in the 1990s.
QUESTION:
Is there any relationship between Lennard-Jones potential and Van der Waals force ?
ANSWER: r -12 )
and long range attraction (-r -6 ); the attraction part could be called Van
der Waals.
QUESTION:
what is the spin orbit force?
ANSWER: m in an orbit of radius r and speed v around the
nucleus, it has orbital angular momentum which classically is mvr and quantum mechanically is
ħ √[ℓ(ℓ +1)] where
ℓ is an integer. But, it also has a spin angular momentum of
ħ √[Ѕ(Ѕ+1)]. Now, if
there is some way these two separate angular momenta can interact with each
other, the result will be that the energy of the electron will depend on the
relative orientations of the angular momentum vectors, either parallel or
antiparallel. This is called spin-orbit splitting or fine structure in
atomic physics. In atomic physics it is pretty easy to understand why the
angular momenta couple. From the electron's point of view, it sees the
nucleus orbiting it and therefore sees a magnetic field due to that current;
the electron has an intrinsic magnetic moment (it looks like a tiny bar
magnet) antiparallel to its spin which wants to align with that field which
means that it takes work to move the electron to the unaligned orientation
meaning aligned is at a lower energy. The spin-orbit interaction is a very
much bigger effect in the structure of the nucleus but its origin is not as
easy to understand as for electons in atoms.
QUESTION:
A stable compound nucleus has a lower mass than the sum of its constituent protons and neutrons. I was told this is because the bound state has lower energy. A similar situation occurs in the atom: the stable bound state of an atom has a lower energy than its constituents, and thus the mass of the atom is slightly less than that of the electrons and protons that make it up. This leads me to believe that a bound system minimizes energy and hence mass. Why does this reasoning fail when thinking about the binding of quarks? The up and down quark masses are around 1-6 MeV, but the bound states of quarks, rather than being less than the sum of their constituents, are much larger (pion ~130 MeV, proton/neutron ~1 GeV). It seems that it is not necessary for a stable bound state to minimize energy. This seems strange to me. Do you see where my confusion is coming from?
ANSWER:
Any bound state is less massive than the sum of
its parts; this is easy to convince yourself of because it obviously
takes work to disassemble any bound state and therefore energy must be
added. This energy (which you put in) shows up as increased mass.
By definition, the ground state is the
"boundest" state of a system. Therefore the ground state is the least
massive.
Conversely, if a system binds, the resulting
object has less mass than what you started with and therefore energy is
released. For example, CO2 is less massive than C+O2
and that is where the energy comes from when you burn carbon—fossil
fuels, essentially.
Because of the
way quarks bind, there is no such thing as a free quark and therefore it
is difficult to talk about its rest mass. To zeroth approximation, it
takes infinite energy to unbind a quark so it would have infinite mass.
QUESTION:
if 50 billion neutrinos pass through your body every second .... I have
read this so many times .... why do only a few show up in the detectors
below ground. I thought that neutrinos could travel through anything.
ANSWER: —to
enhance the chance of "catching" one.
QUESTION:
I am having trouble comprehending the idea of a neutrino having no mass. Wouldn't that mean that it simply does not exist? How does something exist that does not exist? Do we just not have the technology to measure it's mass?
ANSWER:
QUESTION:
I was wondering. Just as one can record a video in 5000 fps, how many equivilant "fps" does the Atlas-detector at LHC record at? If that comparison is even possible?
ANSWER: 7 per second. Each bunch collision
results in about 25 potentially interesting proton-proton collisions per
second. So, the average event rate is about 109 per second.
The detector can store about 200 events/second, so very complex and
elaborate triggoring systems must be used to distinguish the interesting
from less interesting events.
QUESTION:
What's stopping entrepreneurs from using fission to turn mercury or
other elements into gold or silver? Do you think there will come a day
when we simply can create whatever elements we want? Any guesses as to
how far in the future that would be?
ANSWER: 24 . To get 1024
atoms would require a time of 1024 /106 =1018
s≈30 billion years.
QUESTION:
If my understanding is correct, Iodine-131 is a product of the fission reaction of uranium-235. If this is correct, then by the conservation of proton number, the other product has to be an isotope Yttrium. However this means the isotope has to have a crazy mass number or a very large number of neutrons are released.
So my dilemma comes down to understanding how to complete the equation:
U-235 + 1n ---> I-131 + ? + ?neutrons.
ANSWER: 235 U
splits into two nuclei which are extremely neutron rich. The two are so
neutron rich that they almost immediately eject some neutrons, typically
5-8 neutrons between them. But, after this, the remaining two nuclei are
still very neutron rich; therefore, they both undergo a series of
β decays where each decay results in a neutron turning into a proton
plus an ejected electron and neutrino. So, you can see, you cannot tell
what the initial decay products were just by looking at the final decay
products because the β decays result in a lot of negative electric
charge leaving the system.
QUESTION:
What about the structure of alpha particles makes them such a common form of radiation? Why aren't, for instance, lithium nuclei the common form of ionizing radiation?
ANSWER: 4 He, 2 protons and 2 neutrons) is the most tightly
bound of the light nuclei. The figure to the right shows the binding
energy per nucleon (the average energy it takes to remove a nucleon from
the nucleus, E /A , where E is the energy to totally
disassemble the nucleus and A is the atomic number) of stable
nuclei. So the alpha is tightly bound and has few particles and the
result is that it has a relatively high probability of spontaneously
forming inside the nucleus. The energetics are such that the total
energy of the original nucleus A XZ N s
greater than the energy of an alpha particle plus the daughter nucleus
A-4 WZ-2 N-2 and so, alpha particle decay
will happen if a mechanism for decay can be found. It gets a little
complicated, here because the alpha particle, if very close to the
daughter nucleus (which being inside certainly is) is strongly bound;
but if it could "figure out" a way to get to a distance a little outside
the surface of the daughter nucleus, the electrical repulsion would be
bigger than the nuclear attraction and it would shoot out. The mechanism
for getting away is called quantum tunneling and there is also a
probability that an alpha particle will tunnel out and escape. Heavier
nuclei (like Li) have a lower probability of formation and a lower
probability of tunneling out if they do form. Roughly speaking, the
probability of alpha decay is the product of the probabilities of
formation and tunneling. You could also think of alpha decay as a very
asymmetric fission of a heavy nucleus
QUESTION: I am a high school physics teacher and am having
some difficulty with part of the Compton Effect. I am trying to come to
grips with whether the collision between the x-ray and the electron is
elastic or inelastic? From what I have been able to find on the
subject, when the x-ray collides with the 'whole' atom it results in an
elastic collision and the x-ray leaves with the same frequency with
which it came in with. On the other hand, when the x-ray collides with
something closer to its own mass (an electron), it results in an
inelastic collision and the x-ray is ejected with a lower frequency and
energy. Any help you could provide would be greatly appreciated. I hate
to think that I am not teaching it correctly and sending my students
out into the world with misconceptions imparted to them by me.
ANSWER: The Compton effect is
elastic scattering of photons from some mass. Elastic does not mean
that the energy of the incoming particle remains constant, it means
that the sum of the energies of the incoming particle and the target
remain constant. Assuming the target is at rest before the collision,
after the collision it will recoil and carry away some of the energy
which the photon brought in and the only place it can get this energy
is from the photon. It is maybe easier to see this by thinking about
classical particles. If a BB (photon) hits a bowling ball (whole atom),
the bowling ball is almost at rest after being hit and therefore the BB
has approximately the same energy (and speed) after the collision. If
the BB (photon) hits a marble (electron), the marble will be moving
after the collision so the BB must have lost energy (and speed). Both
processes are elastic. An inelastic collision is one in which the total
energy before and after are not equal.
QUESTION: I’m having a problem determining the difference between
Nuclear Fusion and Nu clear Fission. Listed below are some
information that I’ve found. Could you clarify the major differences
between the two, especially when it comes to matter that is heavier or
lighter? Nuclear fusion - is the process by which multiple like-charged
atomic nuclei (two or more joined together) join together to form a
heavier nucleus. It is accompanied by the release or absorption of
energy, which allows matter to enter into a plasma state. Nuclear
fission - is a nuclear reaction in which the nucleus of an atom splits
into smaller parts, often producing free neutrons and lighter nuclei,
which may eventually produce photons (in the form of gamma rays).
ANSWER: The important concept here is that if you
find a reaction which results in less mass after the reaction than
before the reaction, you will release energy because E=mc 2
and energy is conserved in an isolated reaction. Hence, if you lose
mass, that energy must appear elsewhere. Where it usually appears is in
kinetic energy, that is thermal energy of the reaction products. Iron is
the most tightly bound nucleus, that is the mass of the average nucleon
(a nucleon is a generic term for neutron or proton) is smallest. As
shown in the figure, average nucleon mass steadily increases if you get
heavier or lighter than iron. Hence, splitting a nucleus twice the size
of iron or heavier results in mass loss and therefore energy gain; this
is called fission. Similarly, fusing two nuclei half the size of iron or
smaller results in mass loss and therefore energy gain; this is called
fusion. Fusion is the source of energy for stars and hydrogen bombs.
Fission is the source of energy for nuclear power plants and
conventional nuclear bombs.
QUESTION:
During Nuclear Fission, how does the atom actually split?
I understand that it becomes unstable with the absorption of a neutron but what I do not understand is how the atom can separate into two atoms.
Eg. U-235 + n > U-236 > various products My main concern is how an atom can split.
ANSWER:
235 U the resulting 236 U nucleus is very excited. By
this I mean that it is not just sitting there but vibrating wildly. So,
think of this egg-shaped fluid vibrating so that it gets more elongated,
in fact starts to develop a thinner "neck" in the middle, sort of like a
peanut. What happens is that the two halves of this peanut-shaped thing
break apart and, voilа ,
fission!
QUESTION:
Why does fusion stop at iron in a stars core? Is it temperature/pressure or something to do with the structure of iron?
ANSWER: It is because iron is the most tightly bound nucleus and so any further
fusion would require that energy be added. Heavier elements are made in
supernova explosions. See an earlier answer
for more detail.
QUESTION:
what evidence supports the contention that the strong nuclear interaction can dominate over the electrical interaction at short distances within the nucleus?
ANSWER: The fact that nuclei stay together?
QUESTION:
I have read that cosmic ray particles can pass completely through the Earth. if this is true, is it possible to measure fluctuations in how consistently or rapidly they do so?
The reason I ask is because, it seems that in the future we could produce a map of the Earth's substructure by reading such fluctuations like an x-ray machine. As the Earth rotated, I would imagine, it could be possible to triangulate on structures of varying densities, such as minerals, gas, or oil.
ANSWER: The only type of particle which will pass completely through the earth
is a neutrino and neutrinos are notoriously difficult to detect. They
interact with matter very, very weakly (otherwise, how could they go through
the whole earth). I can imagine no practical way they could be used like an
"x-ray machine".
QUESTION:
My doubt is if protons repel protons how is it possible for them to be in the nucleus?
if it is possible to separate a proton from a nucleus can we form new elements if done in large scale can we achieve creation of new elements?
ANSWER: This is how we know that there is another force present besides the
electrostatic repulsion. It is called the nuclear force or strong
interaction. This force is very short ranged. That is, if the protons are
not very close to each other, this force will will be very small and the
repulsion will win out; but if they are very close, the nuclear force wins
out and a nucleus may be held together. Neutrons also feel this force which
is why neutrons are in nuclei.
QUESTION:
Is there any natural antimatter in the universe? I mean by "natural" antimatter that was not created by humans. Does it exist naturally in our universe, or somewhere else. Also, how exactly do we, humans, obtain antimatter? Do we get it from another universe? I know that matter cannot be created by the Law of Conservation of Matter, so how do we do it?
ANSWER: Nuclei which have too many protons (or too few neutrons, depending on
how you look at it) undergo
β+ decay which turns a proton into a neutron, a neutrino, and
a positron (an antielectron). This is a naturally occuring process.
Antimatter can be created in an accelerator by colliding particles together;
for example, smashing a proton into a nucleus can cause a proton-antiproton
pair to be created. In fact, antiprotons are also naturally occuring in
cosmic rays in the same way—an energetic proton from outer space enters the
atmosphere and creates a proton-antiproton pair. There is no such thing as
the " Law of
Conservation of Matter"; matter can be created or destroyed.
QUESTION:
How did Chicago Pile 1 achieved a chain reaction? I know that they used purified graphite as a moderator and VERY pure uranium in the pile (reactor). The yellow cake was obtained from the Eldorado plant in Port Hope Ontario, which went through an ether process at the Mallinckrodt Chemical Works in St. Louis. Later some of the Mallinckrodt uranium was sent to the University of Iowa at Ames to be cast. Both the cast product and the Mallinckrodt product were used in the CP-1 matrix; the cast product, being purer, being placed closest to the center.
During the testing, building up to the pile, they used a beryllium/radium neutron source, both in New York City and, later, in Chicago, to test the graphite as a moderator (as well as initiators for the atomic bombs). That I understand.
However, when it came to the actual pile there is no mention of a beryllium/radium neutron source. It certainly appears that they relied on the uranium itself to initiate fission. But, how did they get the first neutron(s) to begin the chain reaction?
Does U-235 undergo spontaneous fission? If so, it must be at a VERY slow rate and with a good moderator (graphite or heavy water). I've heard about spontaneous fission and the Flerov-Petrzhak discovery of sontaneous fission in 1940. Fermi must have known about this.
So, did they use a radium/beryllium source or rely on spantaneous fission to start CP-1?
ANSWER:
source which explicitly said this (see page 23).
QUESTION:
When 64Co27 (where 64 is the mass number of cobalt and 27 is the proton number) undergoes gamma decay it produces 64Co27 and energy which is in the form of the gamma ray. I don't get why the binding energy per nucleon has increased?, there has been no change in mass number?
ANSWER: E , the
original nucleus has energy M*c 2 , and the final nucleus has energy
Mc 2 . Therefore, Mc 2 +E =M*c 2 .
This means that the final nucleus has less mass than the original nucleus,
M<M* , which means that the final nucleus is more tightly bound, which
means its binding energy per nucleon is greater. The binding energy per
nucleon is determined by the structure of the nucleus, not the number of
nucleons it has.
QUESTION: ;
Why do we always hear about critical mass in nuclear explosions. Shouldn't it really be critical density? It seems to me that the mass of fissionable material in a bomb is always there; it's when it gets compressed to some high density that the chain reaction occurs.
ANSWER: Critical mass is one of those unfortunate misnomers (because it
is not a mass) which has been passed down by common usage. (Another
example would be electromotive force which is not a force.) Your
suggestion that we call it critical density is not really very good
either. I would call it critical geometry. For example, a hemisphere of
uranium might not be a critical mass (that is, less than one neutron
from a fission causes another nucleus to fission); but, if you put two
such hemispheres together, they might be critical. When the material in
a bomb is "compressed", it is brought into proximity with more material,
it is not physically compressed to higher density.
QUESTION:
I'm a writer, working on a lyric essay about the space between things (kindof a lofty idea, I know... which is why it's a lyric essay). I've been trying to investigate what's in between the smallest particles, and I was hoping you could help me.
I understand basic atomic structure, so you don't have to start from there. I'm wondering more (and forgive me if this is obnoxiously unscientific in its phrasing), what exists between an atom's nucleus and its surrounding electron cloud? Is it just emptiness? Am I riddled with little pockets of nothing? How can that be?
Beyond that - what about the quanta? The quarks, up and down and so forth? Is there a space between these things (though, if I und
ANSWER:
QUESTION:
In addition to studying cosmic rays, can we use detectors placed in space that utilize these same cosmic rays to create high energy collisions in order to search for fundimental particles in the same way the LHC is searching for these particles (ie: an LHC in space, without the need of the huge magnetic ring)?
ANSWER:
QUESTION:
I am having a discussion with a colleague at the school where I teach. I believe that opposing beams are used in devices like the Large Hadron Collider because the collison of opposing beams (Beam A going clockwise and beam B going counterclockwise) have the additive energy of the the two beams, so the opposing beams give the apparent effect of approaching the speed of light without either particle having to be accelerated to such a great degree. My friend argues that if the two beams have the same energy it is no different than a single beam hitting a solid wall - beam A will be stopped dead in its tracks in either case - so there is no greater energy in either case. What is the real explanation?
ANSWER: M p c 2 .
So, you would just think you need to have the beam have an energy equal
to 2M p c 2 , right? Well, it turns out
that all the energy from a single beam is not available for making mass
because, in addition to energy being conserved in the collision, linear
momentum must also be conserved. Linear momentum is the mass times the
velocity of the particle and, in the case of a single beam and a
stationary target, there is a large linear momentum in the direction of
the incoming beam; this same amount of linear momentum must be present
after the collision. It turns out, if you conserve both energy and
momentum, the incoming beam needs about 6M p c 2 !
About 2 /3 of the energy you put into the beam is
"wasted" conserving momentum, just assuring that the system moves in the
direction of the beam after the collision. But now look at the situation
for a collider. Here, the linear momentum before the collision is zero
because the beams move in opposite directions. Therefore all the energy
of the beams is available to create particles. So a collider needs only
M p c 2 per beam to create a
proton-antiproton pair.
QUESTION:
Inspite of the fact that is generally beleived that like charges repels each other while unlike charges.why is it possible to que all the protons in the nucleus of the atom together.
ANSWER:
QUESTION:
Is it possible to find the exact a volume of a proton neutron or electron?
ANSWER: -15 m.)
QUESTION:
ANSWER: orbital angular momentum (like an
electron orbiting around the nucleus in an atom or like the earth orbiting
the sun) or it may have intrinsic angular momentum (like the earth
spinning on its own axis or like the spin angular momentum of the elementary
particle). When one goes to the microscopic level of elementary particles,
angular momentum is quantized, that is only discrete amounts of angular
momentum are allowed; for example, if the angular momentum quantum number of
a particle is L , its angular momentum is [h /(2π )]√ {L (L +1)}
where h is Planck's constant. For a spin
Ѕ particle, the intrinsic angular momentum quantum number is Ѕ and so
the particles intrinsic angular momentum is h √ 3/(4 π ).
Although it is sometimes described as spinning of the particle about its
own axis, this is a classical picture which is useful only as a rough means
of understanding what spin is. For example, it is impossible to do anything
to change the spin of the particle.
QUESTION: Can you please explain electron spin? It does not seem to
fit in with the model I have been taught of a cloud of electrons
'orbiting' a central nucleus.
ANSWER: orbital angular momentum. The earth
rotates about its own axis. Therefore the earth has an additional
angular momentum which we could call spin angular momuntum. The
spin angular momentum has nothing to do with the orbital angular
momentum.
An electron orbits around the nucleus (or, more sophiscatedly
has a wave function which contains the information about the electron
cloud). The electron has an angular momentum called orbital
angular momentum, the information about which is also contained in its
wave function. Like the earth, the electron has an additional intrinsic
angular momentum which we call spin angular momuntum. It is as
if the electron were spinning on its own axis (although that classical
idea has problems if taken too literally). The spin angular momentum
has nothing to do with the orbital angular momentum (or the electron
cloud).
QUESTION: Do electrons maintain a
standard orbit about the nucleus?
ANSWER: Actually, the idea of
electrons being in well-defined orbits in an atom is just a pictorial
way to qualitatively understand atomic structure. Originally Niels Bohr
solved the puzzle of how atoms are constructed but his ideas later
evolved into a much more complete theory of atomic structure. An atom
consists of "clouds" of electrons around the nucleus, that is the
electron does not maintain its identity as a point particle but becomes
"smeared" over the volume in a way which is determined by the
properties of the "orbital" it is in. This is quantum physics. However,
if you say that the shape of the cloud represents the orbit, then, yes,
electrons in one atom have the same distribution as in any other atom
of the same element.
QUESTION:
I recently heard about the clever creation of Hydrogen 4.1 and its use to study reaction kinetics. However, I cannot find an explanation in any of the reporting, or original Science paper on why the muon orbits so close to the nucleus beyond "it's 200x heavier than electron." Surely they did not apply gravity to a Bohr model of a muonized atom, so why does the muon orbit closer?
ANSWER:
QUESTION: Fusion of (ionized) hydrogen
molecules is done by increasing their temperature AND squeezing them
using powerful electromagnets.(right?). If so, is it possible to "FUSE"
them under normal room temperature just by indefinetly increasing the
electro-magnetic force?. If so possible, what about "FUSION" under
temperatures near 0 Kelvin ?
ANSWER: The magnetic fields are not
to "squeeze" them but to confine them. The high temperatures are
required so that the positive ions have enough energy (that is enough
speed) to overcome the electric repulsion from other positive ions.
They need to get close enough to feel the nuclear force for fusion to
occur and slow ions cannot do this. Furthermore, magnetic forces are
perpendicular to the direction of motion so this force cannot squeeze;
also, the magnetic force is proportional to the speed of the particle,
so the slower the particle is moving (cold) the smaller any magnetic
force is.
QUESTION: Is it possible the reason
why Electrons do not fall into the nucleus is; the closer an Electron
gets to the nucleus it's charge is diminished, or it begins to become
more positive and repelled? 2nd, the reason why it does not fly away
from the nucleus is; the farther away it gets from the nucleus, it
becomes more Negatively charged?
ANSWER: Your suggestions are not
possible. One of the most sacrosanct of all physical laws is
conservation of electric charge. The charge of an electron never
changes under any circumstances.
QUESTION: Why is heavy water (D2 O)
used in moderators of Nuclear Power Plants instead of normal water (H2 O)?
If heavy water (D2 O) absorbs and slows down the neutrons
emmited in fission what happens to it?
ANSWER: The purpose of a moderator is to slow
neutrons down so that they will be more probable to be absorbed by a
fuel nucleus (e.g. uranium) and cause a new fission. And each
new fission becomes the source of more neutrons, but they are fast and
the moderator slows them down. If you use something like lead as a
moderator, it would work poorly because the scattered neutrons would
have almost no loss in speed (think of bb's bouncing off bowling
balls). But, if you use something light, like hydrogen, then you are
bouncing neutrons off something about the same mass which will quickly
slow them down (think of a head-on collision between two billiard balls
where the cue ball stops dead). So, hydrogen gas or liquid would be the
best moderator, but hydrogen is very explosive, so we use something
rich in hydrogen, water. But the problem is that a single proton can
easily combine with a slow neutron (to create a deuteron) but that
removes the neutron which we want to use to cause more fissions. The
purpose of the moderator is not to remove neutrons, so we try
the next lightest atom, deuterium, which is chemically identical to
hydrogen but has a mass about twice as big. It is not quite such a good
moderator, but it has a very small probability of absorbing neutrons.
In the event that it does absorb a neutron, it becomes hydrogen with
one proton and two neutrons and is called tritium. Tritium is
radioactive and harmful to the environment.
QUESTION: what keeps electrons
energetically orbiting a nucleus?
ANSWER: What keeps a satellite orbiting the earth?
What keeps the moon going around the earth or the earth going around
the sun? In all cases, once you give an object the energy required for
a particular orbit, conservation of energy keeps it from changing. If
the earth were to suddenly stop moving and drop into the sun, it would
have far less energy; where did that energy go? To change the orbit you
need to add or subtract energy to/from the object. What is particularly
interesting about an electron in an atom is that an electric charge
running around in a circle radiates energy (that is what an antenna is)
and so the energy should radiate away and the electron fall into the
nucleus. However, it does not and this observation started the whole
branch of physics called quantum mechanics: one of the laws of nature
is that bound objects are allowed to exist only in specific (quantized)
energy states and therefore, if in such a state, a particle cannot
radiate its energy away except all at once by going to a lower energy
state. There is, however, a lowest state (called the ground state) and
if the atom is in that state, it must stay there.
QUESTION: If the half life period for
say Uranium is constant then it should be that every atom of particular
mass of Uranium degrade simultaneously and say after the half life for
one atom whole number of atoms in that mass should get degraded and
hence no more remians mass of Uranium but some thing else. Is it so?
ANSWER: What half life means is that at that time
half the number of original atoms will be converted into something
else. It is useful only for a very large number of atoms because
radioactive decay is a statistical process and you cannot know when any
given nucleus will decay, only what the probability for decay is. After
many half lives almost all the uranium will be gone.
QUESTION: Do photons have mass?
In one of your answers you say no. My penquin dictionary of science
says, no mass. However, in the September 2006 issue of ASTRONOMY, the
article, ASK ASTRO page 63. It is stated that the photon's mass is less
than 10(-50)kilograms. Or 14 orders of magnitude smaller than a
neutrino. Very low mass, yes, but there is mass. Is a photon massless?
ANSWER: When we say that photons have no mass, we
mean that every measurement we have ever made is consistent with their
having no mass. However, it is often of interest to test the limits of
our knowledge: how accurately do we know that the photon is massless?
Most likely the article you were reading put an upper limit on what the
mass of a photon could be based on experiments, 10-50 kg.
QUESTION: Could the comparison of an atom and a solar system exist
with the current understanding of nano science. I.e. do electrons orbit
the nucleus of an atom in relation with a nuclei's weight or mass? Do
the nucleus' of atoms emit light?
ANSWER: No. Gravity is not the force which holds the
electrons in their orbit. It is the electrostatic force (the attraction
between the negatively charged electrons and positively charged
nucleus) which does it. Gravitational forces in an atom are entirely
negligible compared to the electrostatic force. Mass, however, is not
irrelevant, however. The mass of an electron is very small compared to
the mass of the nucleus, so the nucleus, for all intents and purposes,
remains fixed as the electrons orbit. If the mass of an electron and a
proton in a hydrogen atom were equal, the two would orbit about a point
halfway between them, much like a binary star.
Regarding your second question,
yes a nucleus emits "light" but not light you could see. When an atom
emits light it is often within the visible spectrum. The
electromagnetic (called gamma rays) waves emitted from nuclei are much
more energetic and thus of a far shorter wavelength than your eye can
see.
QUESTION: What is the angular momentum of the spin axis of an atomic
nucleus? I have only heard about this in advanced physics. Is there any
way one could reverse the spin axis of the angular momentum of an atom?
ANSWER: i.e. 1/2, 3/2, 5/2...) If the nucleus has an even
number of protons and of neutrons, the ground state angular momentum is
always zero because it is energetically favorable for pairs to sum up
to zero angular momentum. Only nuclei with odd numbers of particles or
with an odd number of protons and neutrons have ground state angular
momenta. The total angular momentum of a nucleus is usually referred to
as its spin. To "reverse" the spin, you just need to flip the direction
of the spin vector. So you should think of taking a spinning object and
pointing its spin axis in the opposite direction, not stopping and
reversing it; the effect is the same.
QUESTION: When an alpha particle moves
through an atom it will leave the atom undeflected if it is far enough
away from the nucleus. What interactions are there with the electrons?
Why do the electrons not attract and therefore deflect the positive
alpha particle?
ANSWER: Most certainly the alpha
particle interacts with the electrons. But, the alpha particle has a
mass about 8000 times bigger than the electron so it is like throwing
bowling balls at bb's--the bowling ball is deflected only a miniscule
amount. However, this is the mechanism by which alpha particles lose
their energy going through matter; they have many collisions with
electrons giving each electron a tiny amount of energy but eventually
lose a large fraction (or all) of their energy. As you probably know,
alpha particles don't go very far in matter--even a piece of paper can
stop an alpha particle of a few thousand volts of energy.
QUESTION: ; can you please explain
nutrinos in basic terms?
ANSWER: Many radioactive nuclei
undergo a decay called beta decay. One kind of beta decay happens if a
nucleus has too many neutrons (which have no electric charge). Somehow
nature knows this and takes one neutron in the nucleus and turns it
into a proton; but electric charge must be conserved, so the appearance
of a positively charged proton necessitates the creation of a
negatively charged particle, so an electron is ejected from the
nucleus. It is this electron which is the "radioactivity". Back in the
1930s when beta decay was first discovered a most disturbing thing was
observed: the electrons which were ejected came out with a broad range
of energies. This was disturbing because each electron left behind the
same thing (that is a nucleus with a particular amount of energy), so
the range of electron energies implied that the energy was not
conserved by beta decay. This principle, energy conservation, is so
dearly held by us physicists that we invented a third particle, the
neutrino, which had no mass and no electric charge and carried off the
right amount of energy to insure that energy was conserved. A
remarkable fact is that, because it interacts so incredibly weakly with
matter, the neutrino was not experimentally observed until the late
1950s. So nearly 30 years elapsed before this hypothesized particle was
observed, yet no self-respecting physicist doubted its existence!
Neutrinos have been in the news
lately because of the so-called "solar neutrino problem". We believe
that we understand very well what goes on inside the sun and yet the
number of neutrinos which we observe on earth is considerably fewer
than the number predicted by our models of stars. This problem has
recently been solved by measurements which find that the neutrino is
not really massless but has an extremely small mass (much smaller than
the electron, the lightest of "everyday" particles). I will not attempt
to explain how this solves the puzzle, but it does!
QUESTION: Is there a way to
change/slow down the rate of radioactive decay...for example, Tc99m
half life is 6.01 hours. Is there a way to change that time, or slow it
down?
ANSWER: Not unless you slow down time itself, for
example if the radioactive nuclei had a very high speed in the
laboratory, they would live much longer because of time dilation.
QUESTION: in my gcse physics lesson
the teacher explained that an electron is given out by a nucleus when
it changes during beta decay and a nuetron changes into a proton. Why
is the electron made when the neutron changes?
also is there such a thing as anti elements for example the exact
opposite of hydrogen?
ANSWER: There is also a third,
chargeless particle, the neutrino, which is a product of neutron decay.
It is not simple to answer a question like why the electron is ejected;
that requires understanding the theory of beta decay (that is what this
is called). One easy way to believe that an electron might come off is
that the total electric charge of the universe must remain constant,
that is you cannot create or destroy electric charge. If a proton
appears, so does 1.6x10-19 Coulombs of charge; to keep the
total charge equal to zero, -1.6x10-19 Coulombs of charge
must appear which just happens to be the charge of an electron. And
yes, antihydrogen (consisting of an antiproton and a positron) has been
observed. Check out
this story from CERN.
QUESTION: I read that electrons at
SLAC are accelerated to speeds of 0.999 999 999 948c. What are the
specific products when electrons moving at this speed collide with
other particles? Could you list some of the reactions produced at this
speed? I would also like to know the applied EMF in volts needed for
achieving the above speed, so that I can determine the energy of the
accelerated electrons.
ANSWER: The huge number of possible reactions
depending on the target make it impossible to answer your first
question. However, you second question can be answered pretty easily.
However, you want to calculate the total energy E from the
speed from which you can infer the voltage which must have been
applied. The total energy is E=mc 2 /[1-v 2 /c 2 ]1/2 .
The arithmetic is a little tricky for v so close to c ,
but I find that E =4.9 GeV. This is the total energy, so to get
the kinetic energy you must subtract the rest mass energy; but the rest
mass of an electron is about 0.511 MeV=0.000511 GeV, so it is
negligible. Hence, the EMF you seek is about 4.9 x 109 volts.
QUESTION:
ANSWER: The decay of any individual nucleus is indeed a random event,
but it will occur with a probablilty. For example, one nucleus
may have a 50% probability of decaying in the next hour whereas another
may have a 50% probability of decaying in the next century. You
learn this by watching a bunch of them and counting the number of
decays you see in some time. Now if you have a very large number
of radioactive nuclei (a typical macroscopic sample, say the head of a
pin, would have something like 1023 atoms in it), you can
compare the rate of decays you see with the number of nuclei and
thereby deduce the probability that any nucleus will decay in some
particular time. The half life is the time it takes N
nuclei to decay away to N /2 and, if you think about it, you can
convince yourself that this is essentially a probability.
QUESTION: I am trying to find out approximately what the speed of an
electron around a hydrogen atom is? A teacher at my son's school said
that an electron around an atom moves close to the speed of light? I
found this difficult to swallow since according to my understanding of
relativity, the mass of the electron would become very large at that
speed and this would be the opposite of its known properties, ie small
mass. I've done some research on the web and according to Bohr's
theory, the speed of the electron should be approximately 1% that of
light. But since his theory is not the prevailing theory and the
Quantum Theory is, I was wondering if their is a probability
distribution for the speed of electrons around an atom. It seems to me
that if Quantum Theory can give us a probability of the location of
electrons around a nucleus, then it can give us a probability of its
speed around a nucleus.
ANSWER: The teacher who claims the speed to be comparable to the
speed of light is wrong; the Bohr theory gives the correct
approximation of the electron speed to be 2.2x106 m/s=0.7% c
(c is the speed of light). However, as you
note, the Bohr theory is not correct and quantum mechanics gives a
better picture of what is actually going on. However, the
essential details are the same--the most likely place the electron will
be is near the Bohr orbit and the most likely speed is still around 1% c .
Since the ground state of the H atom has a well defined energy, the sum
of the potential and kinetic energies of the electron must always be
the same. If the electron is at a smaller distance from the
nucleus than the most likely, the potential energy will be smaller
(more negative) so the kinetic energy will be larger (implying higher
speed); similarly, if the electron is further away it will be moving
more slowly. To give some perspective, if the electron were 1/100
of its most likely value (a very unlikely place to be found), its speed
would still be less than 10% c . Again, using
nonrelativistic quantum mechanics (Schrödinger equation) is not
exactly right because of the neglect of the (small) relativistic
effects, and the problem should be done relativistically.
QUESTION: I am confused by some questions concerned with the difference
among nuclear physics,particle physics,high energy physics etc.I'd love
to study nuclear physics in UGA.But is it true that the particle
physics and high energy physics are also related?
ANSWER: Well, all of physics is ultimately one science. That is
the beauty of physics--that the connections between all the various sub
areas are pretty well understood (with a few rare exceptions).
Nuclear physics, particle physics, and high energy physics are among
the most closely related branches of physics.
Particle
physics is the study of elementary particles, their properties, their
constituents, and the theories which describe them. High-energy
physics is sort of ill-defined because there is no clear line where
energy is high above it! Usually it refers to physics done at
particle accelerators around the world which have the highest
energies. In the 1950's 1 GeV (particles with energies equivalent
to accelerating an electron across a potential difference of a billion
volts) was high energy. Today it is more like a TeV (a thousand
GeV) for high energy. Usually high energy physics is synonymous
with particle physics but need not be. Sometimes high energy
accelerators are used to study solid state physics or nuclear physics. Nuclear
physics was traditionally separate from particle physics, but if you
think about it, that is kind of artificial, because what is a nucleus
made up of anyway? From the 1930's through the 1980's the study
of nuclear physics was just that--attempting to understand the
structure of the nucleus. The two main means of achieving this
are to look at the radioactive decay of nuclei and to look at particles
scattered from nuclei (particles which have been accelerated in an
accelerator).
By the
1980's and 1990's, great progress had been made in understanding
nuclear structure in terms of a collection of protons and neutrons
interacting via phenomenological forces. So much so that
traditional nuclear physics is now thought by many to be an essentially
solved problem. There are still lots of details and loose ends,
and these can be interesting problems, but that is not the real essence
of forefront science. Today, much of the field of nuclear physics
has merged with particle physics/high energy physics. Now nuclear
physicists are attempting to understand nuclear properties in terms of
the underlying constituents of the protons and neutrons--quarks and
gluons. In addition, inside the nucleus is being used as a place,
a "laboratory" if you like, to do particle physics. Nuclear
physics is still a vibrant and exciting branch of physics--it just
isn't what it was 20 years ago and that is good!
QUESTION: I understand that if negative and positive matter touch you
get E=0, m=0, or in other words: Nullification. But what happens just
before they touch? Since E=mc^2 can never be violated, and since
everything in the universe ultimately comes from one field or another,
when negative and positive matter 'almost' touch could local normal
space/time be modified, creating a new E, m, and c? Relativity would
still apply, but with a different c, which may be many times faster
than our 'regular' c.
ANSWER: When you refer to "negative and positive matter", I assume
you mean "matter and antimatter". Positive and negative are words
which usually refer to electric charge. "Nullification" is
certainly not what usually happens when a positive and negative charge
get together; for example, if you put an electron (negative) and proton
(positive) together you get a hydrogen atom. A particle and its
antiparticle usually have opposite electric charge (exceptions being
neutral particles which have neutral antiparticles). When a
particle and its antiparticle "touch", they annihilate, that is all
their mass disappears (m =0). However, where you are
incorrect is in saying that you get zero energy (E =0) because
energy is conserved. E =mc 2 doesn't have
to mean that if you have no mass then you have no energy. For
example, radio waves carry energy but no mass. What normally
happens when an electron and its antiparticle (a positron) annihilate
is that two "photons", quanta of electromagnetic energy, are created
which have all the energy which the electron and positron had before
the annihilation, but none of the mass.
QUESTION: Why does the neutron, a neutrally charged particle, have a
magnetic moment? Isn't the magnetic moment defined as the direction of
the magnetic field due to a rotational charge?
ANSWER: Magnetic fields (which are how you detect magnetic moments)
are caused by electric currents which are moving electric
charges. The source of the field need not have a net electric
charge to have a net electric current. The most obvious example
of this statement is a simple current-carrying wire: although its net
charge is zero, electrons move in the wire while the positively charged
remainder of the wire does not; there is a current but no charge and
there is a magnetic field. A neutron, as you know, has no net
charge but experiments have shown that it has a charge density.
Roughly speaking, the neutron has a positively charged core and a
negatively charged surface. So if the whole neutron were thought
of to be spinning as a rigid body (which is a naive but useful picture)
there would be a magnetic moment opposite the angular momentum of the
particle (in agreement with what is known about the neutron magnetic
moment). This is because there would be more negative current than
positive current since the negative charge is farther away from the
spin axis than the positive charge so it moves faster.
QUESTION: We know that during beta-decay, an neutron is converted to a
proton and an electron. The electron was emitted leaving the proton
inside the nucleus. So, it will increase the net charge of the atom by
1, changing it into an ion. As the decay goes on the net charge grows,
the attraction between the ions is reduced due to the net charge
produced. The radioactive material will explode eventually due to the
repulsion mentioned above. However, it does not agree with our common
experience that the material will not explode. How is it justified?
ANSWER: This is more a question of scale and number than anything
else. In order that the premise of your question be satisfied,
let us assume that the radioactive source is in a vacuum and that it is
thin enough that most of the electrons actually escape the
source. A quite "hot" radioactive source would have one Curie (C)
of radiation coming out and 1 C corresponds to 3.7x1010
decays per second. That sounds like a lot, but
consider how many atoms there are in the whole sample, something like 1023 ,
enormously larger than the number actually decaying over some
time. So, on the average, the ions which form will be far
separated from others. As time goes on, of course, the source
will acquire a net positive electrical charge, so its electric
potential relative to its surroundings will increase. Eventually,
there will be a large enough potential difference that perhaps a spark
will jump to neutralize the charge. Or, if the source is in the
air, a large enough potential would lead to corona discharge to the
surrounding air. In the real world it is pretty difficult to
maintain a large static charge on something, and a static charge large
enough to "explode" something just doesn't happen.
Oh, yes,
one more issue: You have to consider what happens to the charge once it
is created on one atom inside the volume of the source. If the
material of the source is a conducting material, then any net charge
must reside on the surface, so this puts the excess charge on the
surface where it is easier for it to be neutralized by the environment.
QUESTION: My question is, why do particles in a solid stick together?
Also, what happens on the atomic scale to make the solid "break" apart
when the substance is melted?
ANSWER: Think of an atom as a tiny positively charged nucleus
surrounded by a "cloud" of electrons. When these two atoms
approach each other there is, when they are farther apart than their
sizes, no force because each is electrically neutral. As the
clouds begin to overlap, there is a repulsion due to the force between
electrons, but there is also an attraction because the electrons in one
atom are attracted to the nucleus of the other. In most cases
there is a region, that is a range of separations, for which the
attractive force is larger than the repulsive force and the result is
that the two atoms may bind together. This is what causes
molecules to form and what causes solids to form. However, this
sticking together depends upon the kinetic energy of the individual
atoms; and, the average kinetic energy of the atoms is simply a measure
of the temperature of the collection of atoms. For example,
consider a hydrogen molecule H2 : think of the binding as a
tiny spring connecting the two atoms and, when the H2 gas is
heated up, some of the kinetic energy is taken by the oscillating pairs
of atoms such that the amplitude of oscillation may be large enough to
"break" the spring. This same thing happens in a solid where we
may think of all the atoms as being rigidly bound to their
neighbors. As the solid is heated up, the bonds break and the
solid is no longer a solid. At first it is a liquid where the
atoms or molecules move around in close proximity to their neighbors
with bonds being constantly in a flux of bonding and breaking
again. As more energy is added to the liquid, individual atoms or
molecules acquire enough kinetic energy to escape entirely forming a
gas.
QUESTION: We know that during beta-decay, an neutron is converted to a
proton and an electron. The electron was emitted leaving the proton
inside the nucleus. So, it will increase the net charge of the atom by
1, changing it into an ion. As the decay goes on the net charge grows,
the attraction between the ions is reduced due to the net charge
produced. The radioactive material will explode eventually due to the
repulsion mentioned above. However, it does not agree with our common
experience that the material will not explode. How is it justified?
ANSWER: This is more a question of scale and number than anything
else. In order that the premise of your question be satisfied,
let us assume that the radioactive source is in a vacuum and that it is
thin enough that most of the electrons actually escape the
source. A quite "hot" radioactive source would have one Curie (C)
of radiation coming out and 1 C corresponds to 3.7x1010
decays per second. That sounds like a lot, but
consider how many atoms there are in the whole sample, something like 1023 ,
enormously larger than the number actually decaying over some
time. So, on the average, the ions which form will be far
separated from others. As time goes on, of course, the source
will acquire a net positive electrical charge, so its electric
potential relative to its surroundings will increase. Eventually,
there will be a large enough potential difference that perhaps a spark
will jump to neutralize the charge. Or, if the source is in the
air, a large enough potential would lead to corona discharge to the
surrounding air. In the real world it is pretty difficult to
maintain a large static charge on something, and a static charge large
enough to "explode" something just doesn't happen.
Oh, yes,
one more issue: You have to consider what happens to the charge once it
is created on one atom inside the volume of the source. If the
material of the source is a conducting material, then any net charge
must reside on the surface, so this puts the excess charge on the
surface where it is easier for it to be neutralized by the environment.
![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER: ![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:![]() ANSWER:
ANSWER: ![]() QUESTION:
QUESTION: the straight parts a lot longer. So the particles would have time to realign in the center and all start going the same speed. My teacher said it is like a contained nuclear explosion. It would put out a lot more electricity than it takes to run it.
the straight parts a lot longer. So the particles would have time to realign in the center and all start going the same speed. My teacher said it is like a contained nuclear explosion. It would put out a lot more electricity than it takes to run it.
![]() ANSWER:
ANSWER: ![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER: ![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER: ![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER:
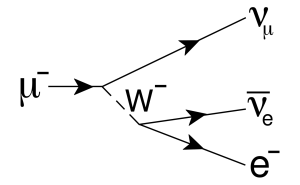
![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER:
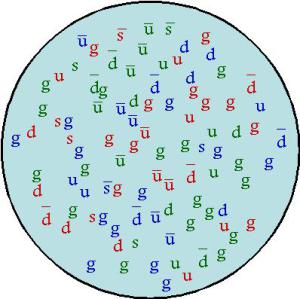
![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER:
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER:![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER: 
![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER: ![]() ADDED
NOTE:
ADDED
NOTE: 
![]() QUESTION:
QUESTION:
![]() ANSWER:
ANSWER: 