Ask the Physicist!

QUESTION: :
Is that true that a single atom can be in two places at once? If it's true, why?
ANSWER:
That depends by what you mean by "being in a place". Atoms must be described quantum mechanically where we talk about probability of being rather than being. An atom may have a probability of P1 of being in one volume and a probability of P2 of being in a different volume. In a practical sense, this means if you had a whole bunch of identical such atoms, half the time you observed one of them it would "be" in one place and half the time it would "be" in the other. Once you observe where it "is", it is no longer in two places.

QUESTION: :
is it possible for the internal energy of a system to be larger than the kentic energy of the molecules and the atoms making up the system?
ANSWER:
The internal energy is the sum of kinetic and potential energies. So, the internal energy certainly can be greater than the kinetic energy. This is not an issue for an ideal gas, but certainly is for a solid.

QUESTION: :
If a bird is packed in a box, and it's carried by a boy, then if a bird flies inside the box only will the weight less or more or equal?
ANSWER:
This

QUESTION: has been previously answered. Your

QUESTION: is a little different, though, since you do not specify that the bird is hovering. If the bird accelerates upward the box+bird will weigh more and if it accelerates down it they will weigh less. If you want to get much deeper into this, see another earlier answer.

QUESTION: :
When you fire a gun in space (say a rifle of some sort), what will happen? If I were to fire a projectile into space, what would be the net reaction? Would the bullet and rifle travel the same distance, just in opposite directions?
ANSWER:
The principle which governs this situation is conservation of momentum. The momentum of an object is its mass times its velocity. If a system is isolated (like your gun+bullet in space), its total momentum never changes. So, before you fire the gun, the momentum is zero. After you fire, the bullet emerges with a speed Vbullet and the gun recoils in the opposite direction with speed Vgun. If the masses are Mbullet and Mgun, we must have MbulletVbullet=MgunVgun since the total MV must be zero and they move in opposite directions. For example, a 40 gram bullet with a speed of 500 mph when fired from a 2 kg (2000 grams) gun: the speed of the gun recoil would be 5 mph. Of course, if you are holding the gun we would add your mass to the gun's. (Incidentally you refer to each as "travel[ing] the same distance" which implies you think they will stop. They will never stop but the bullet in my example will travel 100 times farther than the gun in a given time.)

QUESTION: :
what is the diffrence between following through a hit/kick/swing against a sports ball and stopping at impact
ANSWER:
Take a look at a recent answer and see if that addresses your

QUESTION: .

QUESTION: :
according to the law of universal gravitation, what would happen to earth if the sun were somehow replaced by a black hole of the same mass?
ANSWER:
Things would get very cold and dark! But the earth would go happily on its way in the same orbit. To see the effects of the black hole you need to be inside the Schwartzchild radius which, for the mass of the sun, would be 3 km.

QUESTION: :
As I can presume you would sympathize with the frustration one can feel at 'bad/inaccurate science' being used to move works of fiction along, I ask the following

QUESTION: s in order to avoid said pitfall. In the latest theories regarding controlled nuclear fusion for potential power purposes, is helium-3 a potential reactant, or is it more practical as we currently understand the science to use hydrogen isotopes? What kind of radiation hazards exist with nuclear fusion as a potential power source?
ANSWER:
You can learn a lot of what you seek in the Wikepedia article on fusion power. One possibility with 3He is the 3He+2H�>4He+1H. This has the advantage that neutrons are responsible for much of the radiation hazards in fusion and no neutrons are produced. However, since the 2H is abundantly present in the reaction, there will also be 2H+2H�>3He+n. A favored hydrogen-only process is 3H+2H�>4He+n, but again here we have copious neutrons, 3H itself is radioactive and rare.

QUESTION: :
I am currently taking a physics class in high school and we where discussing nuclear physics more specifically fusion and fission. My

QUESTION: s is a HBomb fuses hydrogen isotopes to create helium isotopes and large amounts of energy by means of using a traditional u238 atomic bomb for initial energy,could you create a device that creates hydrogen form helium exact opposite of nuclear fussion so basically fission of helium atoms to create hydrogen isotopes and take in a large amount of energy instead of burning and vaporizing every thing it would freeze or some thing similar( I'm not quite sure if something else could or would happen) my idea of how to get such a reaction to start would be a particle accelerator like the big one in sweden and just bash helium together at near the speed of light. So I was just wondering if such a thing could theoretically be possible.
ANSWER:
Whenever you split a light nucleus you must put energy in. For example, to cause one He4 nucleus to break into two H2 nuclei, you must add energy somehow. However, you will not be able to get it to happen on a big enough scale to see anything get cold.

QUESTION: :
Does the pound (lb) measure mass or force?
ANSWER:
In everyday life the pound is often used to represent either the weight (force) or mass of something; similarly, in non-US countries, the kilogram is often used to measure weight (force). In physics, a pound is unambiguously a measure of force and a kilogram is unambiguously a measure of mass.

QUESTION: :
We know that gravitational lensing is due to light being attracted by matter, as predicted by Einstein theory of special relativity. Has it been experimentally shown that Newton's third law applies here too? I.e., has anybody detected the light - matter attreaction, in the reverse direction? It seems that Heisenberg's uncertainty princile muddles this extremely small movements. So does Newton's third law also to be modified by the uncertainty equation?
ANSWER:
The first thing I would say is that just because nobody ever measured the recoil of the earth when I jump up into the air does not mean that Newton's third law is not true. Secondly, I would note that Newton's laws are not correct laws of physics in the theory of special relativity, and if anything is relativistic it is photons (light). Finally, Newton's third law is not always true for electromagnetism�the forces between two moving point charges are not always in opposite directions.

QUESTION: :
What is the difference between a "principle" and a "law" i n physics? Why do we have "Archimede's Principle" and "Newtow's Law"? I could never understand when one uses one or the other....
ANSWER:
Philosophy of physics may have very precise definitions of terms like these, but I think it can be ambiguous in physics. Here is my take on it. A physical law is a statement of an experimental measurement which is correct as accurately as you can measure it and for any condition under which it can be experimentally observed. Newton's second law is a very good example; it states that an object's acceleration is proportional to the net force on it and inversely proportional to its mass. The only way to find this out is to measure the acceleration while you vary the force and mass. Archimedes' principle, however, does not require that you go to a laboratory and measure the buoyant force, you can derive it using Newtonian mechanics. Sometimes, laws are misnamed from this perspective. Hooke's law, which states that the force a spring exerts on an object connected to it is proportional to its stretch (or compression) and opposite the stretch (or compression), is only approximately true and over only a limited range of stretches.

QUESTION: :
It is generally accepted in the firearms world that a longer barrel equals greater accuracy, but if repeatabilty and predictabilty are the hallmarks of accuracy then why wouldn't a short barrel be as accurate as long barrel. The short barrel has the same input or impact on the bullet shot to shot everyhing else being equal. I am not a student and hope this dose not fit into the "off the wall" catagory. I' m just and old man trying to decide on a project. It comes down to- If the imput is the same shot shot the results should be the same shot to shot, right?
ANSWER:
My brief research on the web reveals that there is considerable controversy over whether or not this is true. It will depend on other properties of the gun besides length, particularly the thickness of the wall of the barrel and the material from which it is made since these will determine the flexibility of the barrel. It appears that one important factor is that the firing will cause the barrel to vibrate like a reed; although this will be very small in amplitude, it may very well be large enough to make a significant difference in accuracy because of relatively large distances traveled by the projectile. One experimenter actually found that reducing the barrel length to 18" from 26" increased the accuracy of the rifle. Apparently one of the reasons for the belief that long is better is that if you rely only on mechanical sights on the barrel (as opposed to, say, a telescopic sight), it is the distance between the notch and the post which is responsible for the improved accuracy, not necessarily the effect of a long barrel on the projectile.

QUESTION: :
This

QUESTION: pertains to the penetration potential of two arrows having : -The same outside shaft diameter - different weights - traveling at different velocities - impacting into an identical target material. In effect, the arrows are identical in every regard with the exceptions noted as follows: Arrow "A" weighs 350 grains and leaves the bow at 212 feet/second; Arrow "B" weighs 650 grains and leaves the bow at 170 feet/second The arrows each travel 20 yards before impacting an identical target material. My

QUESTION: is, which arrow would penetrate deeper into the target; -The lighter (350 grain), faster travelling (212 feet/sec) arrow; or -The heavier (650 grain), slower travelling (170 feet/sec) arrow. In this "experiment" everything is the same except the weight and speed of the two arrows.
ANSWER:
I will make the following assumption: the forces on the two arrows are identical and constant as they stop. This may not be a good approximation since the forces are likely to be velocity dependent; still, it seems reasonable to me since the frictional force stopping the arrow is more like sliding friction (not velocity dependent) than air friction (velocity dependent). I have also assumed that the mass of the target is much larger than the the mass of the arrows. I will ignore the loss of speed due to air drag over that first 20 yd. Now, use Newton's second law in the form P/F=T where P is the magnitude of the change in momentum (mass times velocity), T is the time to stop, and F is the force the target exerts on the arrows. So the time to stop the heavier is TB=650x170/F=1.11x105/F and the time to stop the lighter one is TA=350x212/F=7.42x104/F. So, the time for the heavier arrow to stop is larger by a factor of TB/TA=1.5. Also, since the forces are equal, the accelerations will be in the inverse proportion to their masses, aA/aB=650/350=1.86, so the acceleration of the lighter arrow is of greater magnitude by about 86% (though both are negative since both are slowing down). Knowing the relative times and accelerations, it is straightforward to compute the relative distances using x=vT-�aT2. I find xB/xA=1.17�the heavier arrow will go about 17% deeper than the lighter one. I would say that, given the approximations made, there is not really a significant difference.

QUESTION: :
Why does gravity affect on the water when it is solid or liquid and does not affect it in its gaseous ?
ANSWER:
If gravity did not affect water vapor, it would escape into space. The reason the earth has an atmosphere is because it has gravity. On the moon, the gravity is not strong enough to hold gas molecules from escaping and hence has no atmosphere.

QUESTION: :
As time can be measured, what is the shortest duration of time? How many such periods would fill a second?
ANSWER:
See an earlier answer.

QUESTION: :
I've been reading about physicists that need to shield sensitive experiments (neutrino detection and the like) using "old" lead because the radiation from traces of lead-210 (half-life 22.2 years) in recently manufactured lead interferes with the detectors. My

QUESTION: : when and how is a metal "born"? I mean, any sample of lead-210 has been around for same length of time and so will be decayed to the same degree, surely? The implication is that when you create a new ingot of lead, it is virgin lead, and the radioactive isotope has yet to decay. Can you explain how that is so?
ANSWER:
210Pb is a naturally occuring isotope of lead. It is a decay product of 238U which has a half life of more than 4 billion years. Therefore, if there is any uranium in the ore from which lead is extracted, there will be 210Pb in the lead which is refined from the ore. Since the refining removes only lead, the 210Pb will eventually decay away.

QUESTION: :
If the rest mass of a photon is zero,then it should not be affected by gravity.But black hole shows that light is effected by gravity! how does it happen?
ANSWER:
See earlier answers.

QUESTION: :
Is it at all possible that just as photons are observable quantum particles (because of the huge quantity that are produced by things such as light bulbs and stars), there is some sort of observable quantum particle for gravity? It would make sense if these quantized particles were able to self-organize into different structures, causing different behaviors, when there are more or fewer of them around (maybe some kind of gravitational Lego block?).
ANSWER:
These quanta are called gravitons; they are hypothetical since they have never been observed and there is no successful theory of quantum gravity. See my earlier answers about gravitons. I do not see how their self-organizing would make sense. Do photons self organize? What they might or might not do needs to wait until a theory of quantum gravity is found.

QUESTION: :
why the sound not travel on moon whenever there is a surface of moon as a solid medium ?
ANSWER:
Sound will travel through the material of the moon, just not through the vacuum above it.

QUESTION: :
I was wondering, why do we say that electrons in an electric current move from positive to negative eventhough they move in the opposite direction? When physicists found out that electrons move from negative to positive, why wasn't the principal changed?
ANSWER:
Whether the electron is positively or negatively charged does not really matter. The charge was arbitrarily chosen to be negative (by Benjamin Franklin) before it was known that electrons are the charge carriers of most electric currents. Electric current is rate of charge passing through the wire, so that means positive current flows in the direction as positive charges would.

QUESTION: :
Sands drops on a conveyor belt from a stationary hopper. The belt was acted on by an external force to keep moving with a constant speed. I find out the power supply by the force is twice that of the gain in kinetic energy of the sands. I cannot figure out where the other half of the power is dissipated ?
ANSWER:
Friction between the sand and the belt must exist. Another way of saying it is that the collision between the belt and the conveyer is not elastic. The lost energy will show up as heat.

QUESTION: :
Can you point me in the direction of a formula that I can use to calculate the effective weight in pounds of 200 lbs dropped 1 meter? I want to understand (if I can) the relative load of doing a body weight squat (load equals body weight) vs the load of dropping down off a 1 meter high bench (load equals body weight x X).
ANSWER:
There is no way to determine this because the force which a falling object exerts on something depends on the time it takes it to stop. I do not know what a "body weight squat" is and do not have a picture of what you are trying to do.

QUESTION: :
I am a 8th grade physical science teacher and I want to be sure about my understanding of action/reaction forces before explaining it to my students. My students recently completed a �balloon rocket activity� where they calculated speed and identified and described the action/ reactions forces involved. Here are my two possible explanations. Which one is correct?
#1 action force-the air in the balloon exerts a force on the air in the room as it is released, reaction force-the air in the room pushes on the air coming out of the balloon causing motion
#2 action force-balloon pushes on the air in the balloon (forcing it out), reaction force-the air in the balloon pushes back on the balloon causing motion.
I do understand that action/reaction forces involve two objects and do not cancel. I tried to relate the balloon�s behavior to that of a rocket when launched to space.
ANSWER:
The balloon would work perfectly well in a vacuum. Hence, the room air has nothing to do with it. Your #2 is the correct view. The balloon pushes the air and the air pushes with an equal and opposite force on the balloon. When you say that they "do not cancel", that means that they do not cancel if you look at one body or another. But if you look at the two or more bodies as a whole, all the Newton's third law forces do cancel out. That is why when an artillery shell explodes the center of mass continues moving in a parabola even as the pieces fly apart. It is particularly important not to consider any pair of equal and opposite forces to be due to Newton's third law. For example, my weight is a force 200 lb down and the floor exerts a force up on me equal to 200 lb. These are due to Newton's first law, not the third; you seem to understand that when you say the forces "involve two objects". Any two forces on an object which are equal and opposite cannot be Newton's third law forces. For me on the floor, the floor exerts a force up on me and I exert an equal and opposite down on the floor�that is Newton's third law.

QUESTION: :
Can one gravitational field be made to reinforce another gravity field, like sound waves at the right frequency can reinforce each other?
ANSWER:
Interference of sound waves results from the wavelike properties; waves can interfere constructively or destructively. Gravity is not really analogous to this because a gravitational field is not a wave. If you have two gravitational fields, they just add like vectors. For example, if the moon is between the sun and the earth, it feels a smaller force than when the earth is between the sun and the moon. But, there is nothing analogous to interference.

QUESTION: :
If neutrons have only the attractive nuclear strong force to bind them together and no repulsive electromagnetic forces to push them apart, why isn't it possible to form large homogeneous "clumps" of neutron matter on earth? Or is it?
ANSWER:
The nuclear force is not just a simple attractive force as you suggest. It is much more complicated and, in fact, a bound system of neutrons has never been observed. A neutron star is a "clump" of neutron matter, but it is held together by gravity, not the strong interaction.

QUESTION: :
Why two protons stuck together have less mass than two single separate protons?
ANSWER:
First of all, two protons do not bind together�there is no such isotope as 2He. But, any bound system has less mass than the sum of its parts. Because E=mc2, if you do work on a system, you increase its mass. In order to pull a nucleus apart, you must do work and therefore add mass.

QUESTION: :
Is 2012 real?
ANSWER:
Yes, 2012 will come in a little more than a year. Prepare for the end! Seriously, read an earlier answer.

QUESTION: :
NASA Says "Gravity is a force of attraction that exists between any two masses" and relates this to why we don't fall off the earth. I am confused- as I am now watching NOVA, etc. on TV. As I understand it, gravity is the warping of the fabric of space-time. Please relate space-time to not falling off earth. Is it because the fabric of space-time of the earth is pushing on us, and the earth is equally pushing back on us? Does it have anything to do with the fact the earth is traveling at 67,0000 miles per hour around sun?
ANSWER:
Gravity is a force between objects with mass. But the origin of this force was a mystery for hundreds of years. Einstein's theory of general relativity is a theory which does an excellent job of solving this mystery: it views mass as warping the space around it such that the space becomes non-Euclidean, that is the shortest distance between two points is not a straight line. Hence, for example, light passing by a massive star is bent in its path because it is following a straight line which is curved if we project it onto our Euclidean space of everyday experience. None of this has anything to do with the motion of the earth. The easiest way to get a feeling for why we are attracted to the earth is to imagine a large mass sitting on a trampoline, warping it down. Then objects placed on the trampoline will be "attracted" to the large mass because of the warping of the "space". Be sure to note that this is not meant to be rigorous, just a simple cartoon to help us imagine the effects of warped space. You might want to read some of my earlier answers on general relativity and gravity.

QUESTION: :
Glockenspiel problem: From redistribution of lycopodium powder I have verified that there are 2 nodal lines which for a 790Hz G are about 14 cm apart. My understanding is that a standing wave has been set up in the bar with a wavelength of twice the nodal separation, and therefore the speed of the waves in the steel bar is 790 x 0.28 which gives about 220 m/s, 20 times too slow for steel. Indeed if you take the speed to be 6000 m/s the nodal lines should be 3.8 m apart! Can you help me work out what I've done wrong?
ANSWER:
Sound waves are longitudinal. But the bar is not vibrating longitudinally, it is vibrating transversely. Think of it like very heavy string vibrating; if you have a vibrating steel string, the speed of waves on the string have nothing to do with the speed of sound in steel.

QUESTION: :
I know there are nuclear processes that provide heat and energy, (the sun, power plants, etc...) but are there any nuclear process that mankind can harness that absorbs heat and energy and locks it away in matter.
ANSWER:
Certainly there are nuclear reactions in which the initial kinetic energy gets converted into mass. However, for a nuclear reaction to take place you need to get the nucleus of one atom close to another and that takes extremely hight energies. So if you are thinking of using such a thing as a way to deal with global warming, for example, forget it�hot air could never get involved in nuclear reactions.

QUESTION: :
If I were to roll a bowling ball off a 10ft-high ledge at 20mph, and another bowling ball from a 1000ft-high ledge at 20mph, would the bowling ball from the 1000ft ledge land farther away from the ledge than the other ball? In other words, since the height is the only difference, does that change the distance away from the ledge the ball will land?
ANSWER:
When the ball leaves the edge of the cliff, it has a horizontal component of its velocity of 20 mph and a vertical component of zero. As time goes on, the downward component of the velocity gets bigger and bigger but the horizontal component stays the same as 20 mph. Therefore, since it takes longer for the ball to fall from the high cliff, it will travel farther in the horizontal direction. (All this assumes that air drag on the ball is small.)

QUESTION: :
You stated in a previous answer, "The equivalence principle says that there is no experiment that you can perform which can distinguish whether you are in a gravitational field or an accelerating frame of reference." OK, what would happen if you were in an enclosed room away from any gravitational sources, and were accelarating at 1G? I understand that it would feel the same as being stationary on the earth. But, what if you stayed in this room for a very long time? At 1G accelaration, you would hit light speed in about a year (which, of course, is impossible). How could you remain in this room for many years, still feeling like you were in a 1-G field, and not exceed light speed?
ANSWER:
As I have emphasized in earlier answers, acceleration does not play the important role in relativity that it does in Newtonian physics. Acceleration is not an invariant quantity (i.e., unlike classical physics, all observers do not measure the same acceleration of an object). Newton's second law no longer may be written as F=ma but must be written in the form F=dp/dt. Anyhow, acceleration in the way you are thinking about it, such that you experience an apparent force equal to the earth's gravitational field, is not measured by an outside observer but is your acceleration relative to an inertial frame which has the same speed you do. An outside observer would see your acceleration get smaller and smaller as you approached the speed of light. I encourage you to read the earlier related answers.

QUESTION: :
First of all you are lucky, you're a physicist, I want to be one two :( but too bad I'm still 15 :( Anyway, I wanted to ask about E=MC2, I'm a big fan of the great Albert Einstein and his theory is the best, I'm trying to understand everything about it , Einstein said that M=E and E=M, but why did he have to put the speed of light2 in his theory I mean to me it's not strange that E can turn into M and M can turn into E but why did he have to say C2?
ANSWER:
Mass is a form of energy, that does not mean that you can have one kilogram of energy. In physics, all physical quantities must have the appropriate units. The appropriate unit we use for energy is kg-m2/s2 which is called a joule (J). Therefore, mass does not have the same units of energy. But since c has units of m/s, c2 has units of m2/s2 and so mc2 has the units of energy. Of course, that does not explain why E=mc2; that is a whole other kettle of fish. I expect you are not ready for the math, but I gave a brief derivation in an earlier answer.

QUESTION: :
My friend's brother was working on a science project, determining the angle which best optimises the distance traveled by a ping pong ball when launched from a catapult. He found 60 degrees above the horizontal to be the optimal distance, which really confused him because he was looking for 45 degrees. My friend and I explained to him that it was because of air resistance. Then we spent the last hour trying to get an equation for the distance a ping pong ball would travel in the x direction given the initial velocity and launch angle when considering air resistance. Basically, given Vo and theta, we are trying to solve for x, the distance the ping pong ball would travel in the x direction. How would you solve for this?
ANSWER:
This is a very difficult problem and one which can only be solved approximately. You can get an idea about how difficult this can be by reading some old answers involving air resistance. The textbook 450 is seldom appropriate for the real world. I would suggest that you keep this project restricted to an experimental one in which you determine the angle for maximum range. Here are a couple of suggestions to make it more interesting:
Change the initial velocity of the ball. For no air friction the maximum range is independent of initial speed, but if air friction is important it is not.
Maybe repeat for different balls. Perhaps a golf ball would be interesting because it has much more mass. The more massive ball would have a much smaller effect from air friction (although it experiences about the same force).
If possible, measure the terminal velocity of the ping pong ball (the speed it achieves after falling until it reaches a constant speed). There might be an interesting correlation between the results of #1.

QUESTION: :
In a chemistry class I took recently, my professor shared an interesting anecdote. He had taken a class in college where the final exam was a single

QUESTION: : how fast does a train measuring two miles long have to be traveling in order to fit entirely into a tunnel measuring one mile long? If I'm not mistaken, as an object approaches the speed of light, it will shrink (or shorten, I'm not sure of the terminology). I posted the

QUESTION: on Facebook, and some of my friends became interested. Unfortunately, none of us have the know-how to answer it. Could you please answer this

QUESTION: ? The idea that there is a single quantitative answer to this is extremely intriguing.
ANSWER:
One of the main results of the theory of special relativity is length contraction. An object actually becomes shorter in the direction of its velocity. It becomes a noticable effect only for speeds not small compared to the speed of light. The length shortens by a factor √(1-(v/c)2) where v is the speed and c is the speed of light. So, simply solve �=√(1-(v/c)2). I get v=0.87c=2.6x108 m/s=580,000,000 mph. Pretty fast!

QUESTION: :
What prevents a particle from being perfectly at rest?
ANSWER:
The uncertainty principle says that you cannot simultaneously know the momentum and the position of a particle to arbitrary accuracy. If you think about a particle being at rest at a particular position, this implies you know both its momentum and position simultaneously and exactly. If you know a particle is at rest, you know its momentum is zero exactly; thus, to avoid violating the uncertainty principle, you are completely ignorant of its position�it could be anywhere in the universe.

QUESTION: :
I work in the medical field and I do not understand how it is that the larger a syringe, the lower the pressure is on injection. If the diameter of each syringe opening is the same (which I would assume to be the case since they all fit into the same needles, etc.) and you use a different volume of fluid through the same diameter opening, wouldn't the pressure increase as the volume increases? I cannot understand why this is not so and am hoping that you can help me see the answer through math. Here is the info:http://tomfangrow.com/Syringe%20Pressure.html and they are listing the diameter of the of the syringe, not the diameter of the opening. So with a larger diameter syringe you have a larger volume of fluid.
ANSWER:
Basic fluid statics: If you increase the pressure at one point in a fluid by a certain amount, you increase the pressure everywhere by the same amount. If you have a syringe of radius R, its cross sectional area is πR2. If you now push with a force F on the plunger, you increase the pressure everywhere in that fluid by an amount ΔP=F/A=F/πR2. As R get bigger, ΔP gets smaller. If, as is probably the case, you are interested in the amount over atmospheric pressure you have caused the pressure to increase, ΔP is what you are interested in and is called the gauge pressure; gauge pressure is what you measure when you measure the pressure in your tires. ΔP is what is calculated in the little calculator on your website. The bottom line is that the big fat syringe will be less effective in pushing fluid through a particular needle than will a slender syringe pushed with the same force.

QUESTION: :
I understand that we have achieved temperatures in the lab of a few billionths of a degree kelvin (pK). Following E=mc^2 as the temperature (E) of the particles is reduced their mass should be reduced by deltaE/c^2. Does this mean that if the temperature of the particles could (hypothetically) be reduced to zero then they would have 0 mass and no weight in a gravitational field. How can matter have no mass and still be defined as matter?
ANSWER:
You misunderstand what E=mc2 means. When absolute temperature is approached, the kinetic energy of the atoms approaches zero, that is they stop moving. But, they still have their mass energy when they cease to move. (Actually, you know, absolute zero cannot be achieved and a particle cannot be perfectly at rest.)

QUESTION: :
If someone discovers a unique, undiscovered, physics principle do they have the right to name it... Like stars?
ANSWER:
In physics, there is no generally accepted way to name laws or principles. What normally happens is that if the finding is of sufficient importance to be referred to in the literature, it will come to have the name of its discover(s)�Newton's third law, Maxwell's equations, the Casimir effect, Čerenkov radiation, the Van Allen belt, etc. Sometimes there might be arguments over priority or some such. This sometimes happens for synthesis of new elements where two different labs might independently make a new element and each want to name it after their lab, for example.

QUESTION: :
So I understand the concept that based on the theory of relativity, the faster speed a traveler goes, the faster time occurs for that traveler. So, why can't we test this theory with some crazy fast planes? Or with a simple rocket with a clock and a radio? Or have we (that you know of)? I realize that this would require ridiculously fast speeds (ludicrous speed!) to give a significant result, but why couldn't we just measure with precision?
ANSWER:
Well, I guess you do not understand! Actually, moving clocks run slower, not faster. For the traveler himself, time progresses at a perfectly normal rate; you seem to imply that if I were going fast and looked at a clock I would see its hands spinning. Not so. Anyhow, time dilation, as this phenomenon is called, has been tested innumerable times. Scientists have taken extremely accurate atomic clocks on trips around the world and found the clocks to behave as relativity would have it. An everyday example is the GPS. Here the device is dependent on timing of signals from satellites which, of course, are moving. If corrections were not made for time dilation on the moving satellites, GPS systems would not work to an accuracy better than a few miles. To learn a little more about time dilation, read the following

QUESTION: .

QUESTION: :
do you know" why" time slows down if you are travelling near the speed of light? relative to someone who is not.
ANSWER:
It is not hard to show, mathematically, why moving clocks run slow. I have always found a simple example to be more instructive than a mathematical demonstration, though. An earlier answer describes the light clock which makes the fact plausible, I think.

QUESTION: :
When converting energy to usable energy, the portion of usable energy which is actually available after the conversion is less than energy used to create it. Does this hold true for nuclear fusion/fission?
ANSWER:
Actually, there is no such "law" that only part of energy can be usable. You are thinking of the second law of thermodynamics which states that no engine operating between two temperatures can be 100% efficient. But some machines are 100% efficient. For example, if I lift a stone I impart increased potential energy to the stone. If I then drop it, that energy is 100% converted to kinetic energy of the stone. In fission or fusion, mass is converted into kinetic energy of the reaction products, 100% efficiently. If you then try to build an engine to take that thermal energy and use it to, say, drive a turbine, only part of that energy can be thus used. This, however, is absolutely no different from trying to use the thermal energy from burning coal to drive the turbine.

QUESTION: :
Although theoretically impossible. if the Sun's mass suddenly ceased to exist how long before the lack of its gravity would be felt on earth and the solar system. We know light traveling at 186,000 miles per second would take seven minutes before we would notice its loss. Any hypothesis on a highly theoretical

QUESTION: ? Isn't it true that gravity is the least well understood of the four forces? Is there any connection with the speed of light?
ANSWER:
See an earlier answer. Regarding "least well understood," it all depends on what you mean by well understood. In some respects the theory of general relativity, the theory of gravity, is considered to be one of the most successful physics theories. On the other hand, nobody had been successful in devising a theory of quantum gravity.

QUESTION: :
what is the difference between an object at rest and the same or identical object in motion. Does the application of a force physically change the object or if the object itself is not changed then something else must be changed.
ANSWER:
The

QUESTION: s you ask are answered by Newton's first and second law. Newton's first law states that an object with no net force on it will remain at rest or continue moving in a straight line with constant speed. There is no difference between the two states of moving or rest, there is no meaning to absolute rest; whatever you see to be at rest may be seen as moving by another observer. Newton's second law says that if there is a net force on an object the result is that the object experiences an acceleration in the direction of the force and proportional to the force; so, what is changed by a force is the velocity.

QUESTION: :
Are there any effects on the body if traveling 30 miles per hour or more? My therapist says no and I say yes there has to be some effect. Who is right?
ANSWER:
Your therapist? Hmmm. The earth has a speed at its surface of about 1000 mph because of its rotation, a speed of about 67,000 mph due to its orbit. Do those have any effect on you? Speed is not what you feel, acceleration is what you feel. Accelerations greater than a few times larger than gravity can have bad effects on your body.

QUESTION: :
Why when we throw an object vertically upwards to reverse gravity and stops at a certain height, say that the speed of that object at that time equal to zero does not say that the weight of the object may become less or greater than the force of gravity ??
ANSWER:
The weight of an object is the force which the gravitational field exerts on it. Provided that the height is very small relative to the radius of the earth, the weight is totally independent of how the object is moving or where it is.

QUESTION: :
does the outside temperature change when a mass passes through the atmosphere. I imagine energy is released by the moving body creating a rise in the temperature......what happens in space , where there is no atmosphere?
ANSWER:
When an object moves through the air it experiences a drag force. This force does negative work on the object, that is it takes energy away from that object. What is happening, microscopically, is that the object is colliding air molecules which bounce off with more kinetic energy, that is the temperature of the air will increase. Hence we can say that energy lost to air drag is converted to thermal energy. Under normal circumstances, the increase in temperature is too small to notice.

QUESTION: :
is it true that while a rock is still rising its velocity and acceleration are both downward?
ANSWER:
No. A thrown rock always has its acceleration downward but its velocity on the way up is upward.

QUESTION: :
Equally massed negative electrons and positive positrons annihilate each other when they collide. What if positrons are replaced by heavier but singly charged positive protons in the experiment? Do they annihilate each other? If not and form a neutron or hydrogen, why that route? And come to think of it, why does not hydrogen collapse to form a neutron?
ANSWER:
No, an electron and proton do not annihilate each other because they are not each others' antiparticle. And a neutron is not simply a composite composed of an electron and a proton. When a neutron decays there is a third particle, a neutrino, which is emitted; this is called beta decay. An electron and proton may come together to form a hydrogen atom.

QUESTION: :
if you shoot a gun towards the back of the train and the bullet goes 2000 miles and hour in a train thats going 2000 miles does the bullet stop? what would happen?
ANSWER:
For

QUESTION: s like this I always start with "�you must specify the velocity relative to what�" You would see the bullet travel toward the back of the train with a speed of 2000 mph but somebody standing by the side of the tracks would see the bullet standing still.

QUESTION: :
What prevents something from getting colder than absolute zero? I have ideas, like "you can only lose so much heat", but nothing I can really put together. Nothing scientific.
ANSWER:
Temperature is a measure of the average kinetic energy per particle. At absolute zero all motion ceases. You can't get any "stoppeder" than stopped!

QUESTION: :
I'm working on a project involving gravitational fields, and I came across something interesting. If you calculate out the gravitational fields of the Sun and the Earth relative to the Moon, the Sun's field is much larger. So why is it that the Moon revolves around us instead of assuming a planetary orbit around the Sun?
ANSWER:
Interesting

QUESTION: . If you think about it for a minute, you will realize that the moon does orbit the sun also.

QUESTION: :
Why does crockery make such a loud sound when banged into another piece of crockery such as when stacking dinner plates?
ANSWER:
When two things collide, there is an apparent loss of energy (the kinetic energy before the collision). But, energy is never really lost, just sometimes converted into forms which we cannot get our hands on. The "energy loss" in a collision usually goes to two possible mechanisms, sound energy or thermal energy. If there is a possible way to produce sound, then sound may carry off some of the energy, and things like plates can vibrate like a cymbal and produce sound. In a collision between things which aren't so good as sound sources, say two blocks of foam rubber, most of the initial energy is converted to thermal energy�things get a little warmer. Usually this temperature increase is too small to be noticed, but if you fire a bullet into a block of wood the hole is pretty hot.

QUESTION: :
If your riding a motorcycle, going 55 miles per hour, and it is 75 degrees outside, what is the temperature of the air that you feel on your skin? I ride a motorcycle and I know that there is a formula but I just don't know what it is and I hope that you have the answer.
ANSWER:
You must be referring to the wind chill index which attempts to quantify how cold it feels at a certain temperature and wind speed. I find that it is not defined for the situation you want� 750F just never feels cold, I guess. It is only defined for temperatures between -450 and 450. Read all about it at NWS.

QUESTION: :
What happens if a spinning object is released from the axis of rotation? In what direction will it move?
ANSWER:
If it is spinning about an axis which passes through its center of mass (COM), nothing happens, it just continues spinning. If it is spinning about an axis not through its COM, its COM continues moving with a constant velocity equal to the velocity it had at the instant the object was released. It will also be spinning but about its center of mass now. (My answers assume there are no other forces or torques acting on the object.)

QUESTION: :
I am a biologist/teacher and I have a science

QUESTION: that came up as my son was doing a project that has me scratching my head. He was supposed describe how the work done my several natural events changed the environment by the work they did. One of the natural events was fire. Now, as a biologist...I can't lie...I am not great at physics. However, since work=force * distance, do fires do work? Fires may "travel", however, they do not have mass for forces to act upon (fire is energy, not matter).
ANSWER:
For starters, it is not true that fire is not matter; a flame consists of hot gas released by the chemical reactions going on in the burning. Certainly fires contain energy, so where is the work being done to create this energy? To understand this you have to look microscopically. There are chemical reactions going on and that is where the work is being done. Interestingly, the energy is really coming from E=mc2. The chemistry law which we all learn, that the sum of all the masses after a chemical reaction is the same as before is technically incorrect. For example, combining carbon and oxygen to form CO2, a simple form of "fire" releases energy and the mass of the CO2 would slightly smaller than the mass of C+O2; this difference is really tiny, too small to measure with any lab balance; what that means is that chemistry is really a crummy (by which I mean inefficient) source of energy if compared to nuclear energy which converts a much more significant fraction of the mass to energy. Thinking of work purely in terms of Fd is really a mechanical idea which does not give a bigger picture of energy. Of course, fire can do work because we can (and of course often do) use the energy it releases. If you want more details about the chemistry of fire, a good short article can be found on HowStuffWorks.

QUESTION: :
Why does the center of mass of a bomb follow a parabolic path if it explodes in the air?
ANSWER:
It is rather complicated to derive the equations which show that the center of mass is an important location for a body or collection of bodies. The basic idea is that, because of Newton's third law, all the forces on something (like the bomb) which originate inside the system cancel each other out if you observe the entire system. Also, Newton' second law says that the acceleration of the center of mass of a system is equal to the sum of the external forces on the system divided by the total mass of the system (this is what is complicated to prove). The bomb experiences only gravity as an external force; all the forces which caused it to explode are internal forces and sum to zero if you look at the whole system. If you really want, I can provide the derivation, but you probably do not really care!

QUESTION: :
barring gravitational forces, can a spacecraft, achieve the volicity of it's own thrust?
ANSWER:
Whenever you talk about velocity you need to specify with what it is relative to. If you are on the spacecraft, you will always see the exhaust coming out with some constant speed depending on how you create that exhaust there on the ship. If you are standing on earth, watching the spacecraft accelerate away from you, there is no reason why the ship could not be moving faster relative to the earth than the exhaust was moving relative to the spacecraft.

QUESTION: :
Does cooling a substance (e.g. a freezer pack) below its freezing point, take its temperature lower? or is the freezing temperature the lowest it can go?
ANSWER:
The only limit to how cold something can get is absolute zero, about -2730C=-4600F.

QUESTION: :
This maybe in quantum physics... couldn't find the answer(s) in previous ques/ans listing here. As an electron joins with an ion to complete an orbit/shell; does it impart any spin? Magnetic? does it impart any energy (Exo or Endo)? And the reverse Electron separating from an ion; spin... magnetic? energy (Exo/Endo) Is there any information concerning where a electron leaves an atom/ion? as an atom/ion has magnetic poles (North and South) Would this effect the spin/rotation?
ANSWER:
This

QUESTION: is really too unfocused. Let me simply say that any time you add or subtract something to a quantum mechanical system, the added particle brings with it all its properties�mass, magnetic moment, angular momentum, energy, etc. What happens in any particular case depends on that particular case.

QUESTION: :
We are studying momentum. We are taught that when delivering a karate chop to a board (in order to break it) one must pull back on the chop and not follow through. This delivers more force. Why, then, when you hit a baseball doesn't that same rule apply? Why are you taught to follow through?
ANSWER:
I guess I do not believe your basic tenet about "pulling back". Suppose that we simplify the situation and throw a ball at the board. If the ball sticks to the board it has transferred its momentum P to the board and if the collision lasts a time t then the force experienced by the board is P/t; but if the ball bounces back with the speed it came in with, the momentum transferred is 2P and the force is thus twice as great. But, here is my problem: your hand is not analogous because your arm is what is responsible for pulling back your hand, not the collision. Because of the addition of your arm to the equation, there is no guarantee that momentum will be conserved. I do not profess to know much about karate, but if this technique works it may be something like "letting" your hand bounce back, not "pulling" back, that is quit pushing when you collide. Then your hand would be more analogous to the bounced back ball. (What I am trying to say here is that the technique may be right, but the reason is not simple momentum conservation.) Regarding the baseball, the situation is very different because the baseball, unlike the board, is not at rest when the collision happens. If you looked at the ball-bat collision from the frame of reference of the incoming ball, the bat would bounce back.

QUESTION: :
I know that if two carts (same mass and velocity) stick together when they stop because the momentum is conserved. But, why, if they do not stick together, do they bounce off eachother? How come the momentum is not conserved then?
ANSWER:
Your

QUESTION: is incorrectly stated because what you describe happens if the carts have the same mass and opposite velocities. Momentum is a vector quantity and under the conditions you state, the momentum is zero before the collision and must also be zero afterwards. If the carts both stop, obviously the momentum is zero. But, if the carts have equal and opposite momenta after the collision they also have zero momentum.

QUESTION: :
do all electrons travel at the same speed? If they do what percentage of the speed of light do they move?
ANSWER:
No, all electrons do not move at the same speed. They can move at any speed less than the speed of light, just like anything else.

QUESTION: :
I am interested in blocking radiation for health reasons from cell phones, tv's, computers and surroundings in general. There is in the market different products you can carry around your body for this purpose. I would like to know your opinion on the most effective-cost effective method. One option is to carry a magnet but what kind and which side goes in which direction, does it need to touch the skin, and how much can it block? I would like an option that protects as much as possible of my entire body and also for my child who is 5. Please be as detail as possible, I want to do this right.
ANSWER:
You are setting yourself up to be preyed upon by people who take advantage of people's irrational fears. There is no credible scientific evidence that any of these devices is a health hazard. And one thing is really true: there is absolutely no way that a magnet will protect you from any of the radiations from any of these devices because the only radiation reaching you is electromagnetic waves (radio waves, light, maybe some x-rays) and all are totally unaffected by a magnet. If you are really worried about this, your only option is to get rid of them. Trust me, the dangers are minimal if not nonexistant.

QUESTION: :
My

QUESTION: is about the sound waves produced by a guitar. What happens to the sound when you touch the string of the guitar very lightly?
ANSWER:
A vibrating string does not just vibrate with the frequency which you "hear", the fundamental, but with all the harmonics of that frequency as well. If you were to touch the string in the center you would kill all vibrations of the fundamental and all even harmonics. If you touch it elsewhere, you kill all vibrations which do not have a node at that point. (A node is a point on the string which does not move at all as the string vibrates.) This is a technique used by violinists to excite higher frequencies than one normally can play on a violin.

QUESTION: :
I understand the equivalence between gravity and acceleraton. (Someone in a spaceship accelerating at just the right rate, would feel gravity as as he were on the earth). So then, if we feel gravity we must be accelerating but I don't understand what is accelerating. It can't be the earth so what is it?
ANSWER:
The equivalence principle says that there is no experiment that you can perform which can distinguish whether you are in a gravitational field or an accelerating frame of reference. It does not follow that if you are in a gravitational field, you are accelerating.

QUESTION: :
A� metre�rule measures 1 metre in its rest frame (surprise surprise). How fast would another observer need to travel past it in order to see it as a �12 inch� rule instead
ANSWER:
The formula for length contraction is L'=L√(1-(v/c)2). 1 ft=0.305 m. You figure it out!

QUESTION: :
If you're on a spaceship with rotating searchlight on top, traveling just a snail's pace slower than the speed of light, what happens to the light beam? When pointed forward, does it creep out at the snail's pace to make up the difference? And what about off the side or pointed behind?
ANSWER:
If you shine it forward, you see it receding at a speed of c. But an observer watching you go by will also see it going forward with a speed c. Amazing, huh? But true. At extremely high speeds things do not behave like you expect them to. If you shine the light out the side with speed c, you will see it going sideways with speed c. But, if somebody sees you going by, the light will come out of your ship sidways but also with a component forward in your direction. But the speed of this light will still be c.

QUESTION: :
recently i got an answer on why the speed of light 'c' has such high value. but from where did we calculate this speed? is there any mathematical calculations to find c = 3 x 10^8 m/s?
ANSWER:
See an earlier answer.

QUESTION: :
If I put a fly in a sealed container and place the container on an analytical balance, when the fly takes off and begins to hover in the container, will the reading on the analytical balance go down or stay the same?
ANSWER:
It will stay the same. The fly hovers because the air exerts a force up on him equal to his own weight. But, by Newton's third law, the fly exerts a force down on the air which is equal in magnitude to his weight; the scale registers this downward force. You might be interested in the answer to an earlier

QUESTION: similar to yours in which I go into much more detail.

QUESTION: :
If a hummingbird is hovering in a car, not in contact with any surface in the car, will it travel at whatever speed the car travels? And if so, what force is causing the hummingbird to travel forward in the car since it is not actually in contact with the car? Additionally, what happens to the hovering bird if the car is suddenly stopped? Will it lunge forward with the car or remain in place?
ANSWER:
The bird flies relative to the air in the car. An observer outside the car sees both that air and the bird moving with the same speed as the car itself. What makes you think that a force is necessary to move the bird forward? Newton's first law says that an object with no forces on it will move with constant velocity. Granted, the car requires a force to move with constant velocity but that is because there are frictional forces trying to slow it. The net force on the car is zero when traveling with constant velocity. If the car stops suddenly, the bird will do like you would if unrestrained�keep moving forward until he hits the windshield.

QUESTION: :
If it is impossible to reach the speed of light, and the nearest solar system is over 4 light years away, does this mean that the human race is pretty much stuck in our system?
ANSWER:
Well, if we could achieve speeds comparable to the speed of light (c), four years is not such a long time. And, at such high speeds, the clock of the travelers would show much less time, maybe only a few months. But the problems of attaining such speeds and the stresses large accelerations would put on the travelers would be such that, in my opinion, the only practicable way of traveling such distances would be to have a colony in a large craft with no intention of ever coming back. (Of course, that is not without its problems either!)

QUESTION: :
How did Chicago Pile 1 achieved a chain reaction? I know that they used purified graphite as a moderator and VERY pure uranium in the pile (reactor). The yellow cake was obtained from the Eldorado plant in Port Hope Ontario, which went through an ether process at the Mallinckrodt Chemical Works in St. Louis. Later some of the Mallinckrodt uranium was sent to the University of Iowa at Ames to be cast. Both the cast product and the Mallinckrodt product were used in the CP-1 matrix; the cast product, being purer, being placed closest to the center. During the testing, building up to the pile, they used a beryllium/radium neutron source, both in New York City and, later, in Chicago, to test the graphite as a moderator (as well as initiators for the atomic bombs). That I understand. However, when it came to the actual pile there is no mention of a beryllium/radium neutron source. It certainly appears that they relied on the uranium itself to initiate fission. But, how did they get the first neutron(s) to begin the chain reaction? Does U-235 undergo spontaneous fission? If so, it must be at a VERY slow rate and with a good moderator (graphite or heavy water). I've heard about spontaneous fission and the Flerov-Petrzhak discovery of sontaneous fission in 1940. Fermi must have known about this. So, did they use a radium/beryllium source or rely on spantaneous fission to start CP-1?
ANSWER:
It is indeed true that spontaneous fission is a rare event. On the other hand, there are one heck of a lot of atoms there and even very improbable events are quite possible at reasonable rates. Indeed, the first reactor, in Chicago, had no external neutron source but relied on spontaneous fission. Spontaneous fission can also be triggered by external radiation like cosmic rays. It took me a while to find a source which explicitly said this (see page 23).

QUESTION: :
we know that light is travelling at a very high speed. what makes the light (or photons) to travel at such speed. is there any force that is cating on these photons??????
ANSWER:
The most basic of physical laws, Newton's first law, states that an object upon which no force acts moves with constant speed in a straight line. Hence, nothing needs a force acting on it to continue at a constant velocity. The reason that light has the speed it does is because of the properties of electricity and magnetism of which it is composed. The speed of light in a vacuum is a fundamental physical constant.

QUESTION: :
What is power measured in kwh?
ANSWER:
kWh (kilowatt-hour) is not a measure of power, it is a measure of energy. Power, measured in watts (W), is the rate of energy consumption. One Watt-second is 1 Joule (J), a unit of energy. For example, a 100 W lightbulb consumes 100 J of energy per second. Since a kW is 1000 W, and one hour is 3600 s, 1 kWh=3,600,000 J.

QUESTION: :
Does the frame of reference concept carry over into the interaction between electrons and magnetic fields? Specifically, does a magnetic field only result from an electron moving relative to an observer? For example, would an observer not moving relative to an electron not see a magnetic field and an observer moving relative to an electron see a magnetic field?
ANSWER:
If the electron were a charge alone, it does not have a magnetic field if at rest. However, since the electron has a magnetic moment (i.e. it looks like a tiny bar magnet), it does have a magnetic field when at rest. If it is moving, there is an additional magnetic field due to the moving charge.

QUESTION: :
If there were two people on opposite ends of a metal rod that was one light-year long, and one person pushed their end of the rod one meter, how long would it take for the other end of the rod to move one meter?
ANSWER:
This

QUESTION: has been asked many times and has been answered. The bottom line is that it would take much more than one year.

QUESTION: :
Say you started moving straight upwards from the ground, how high could you go before the air becomes unbreathable?
ANSWER:
People climbing Mt. Everest, about 30,000 feet high, usually carry oxygen because the air becomes so thin at that altitude. It is not that the air becomes "unbreathable" but that there is not enough of it.

QUESTION: :
If the amount of gravity speeds/slows time, Then by that logic, would a person living on the moon age faster then a person who lives on the Earth?
ANSWER:
Yes, but the time rate would be so small as to be almost impossible to measure.

QUESTION: :
If you fired a gun in space, would the kickback send you flying in the opposite direction at the same speed as the bullet?
ANSWER:
No, you would fly off with the same momentum as the bullet. Momentum is mass times velocity, so if your mass is 1000 times larger than the bullet's, your speed would be 1000 times smaller.

QUESTION: :
I just watched a program on History last night about time travel. My Dad was really into it and I learn a lot from him. He told me back then that if you put a clock on a space ship and have a clock with the same time back on earth, and that ship travels close to the speed of light (actually he said "very fast") when the ship gets back to earth the clock on the ship will have run slower than the clock on the earth. They said that if we could hit warp, we could get to Alpha Centauri (sp?) in about 45 months. However, in actuality, it would take years. Here's the

QUESTION: : Does that not blow Star Trek and Warp Speed out of the water? Let's say that Kirk gets a distress call from a planet light years away. He hits warp. On his vessel it takes minutes. On the other planet it takes years for him to get there. By that time - well, it's all over.
ANSWER:
You are absolutely right with regard to what we currently believe to be possible for time travel. You may go to the future but you can never exceed the speed of light and you cannot go to the past. Star Trek is fanciful in that anything greater than warp 1 is greater than the speed of light. Warp 9, for example, is about 1500 times the speed of light; at that speed it would take 15 years to get to the center of our galaxy! (I mined these "facts" from Lawrence Krauss's fun book The Physics of Star Trek.) So Star Trek authors have to imagine another means of time travel than just going fast, things like worm holes which let you (in principle) burrow from one point in space-time to another. (Don't ask me about worm holes because I really do not know that much about them!)

QUESTION: :
In outer space, there isnt gravity to hold back and since space is a vacuum, there is almost nothing to cause drag or resistance or resistance on an object. If we kept applying a force on the object, wouldn't it keep accelerating? To and even past the speed of light? (provided we had a strong enough propulsion device)
ANSWER:
Gravity and drag are not the issue, the laws of physics are the issue. No object may go as fast as or faster than the speed of light. The simplest way to understand this is that the faster that an object go the greater its mass (its resistance to being accelerated) becomes such that if it reached the speed of light its mass would be infinite; so it would have required an infinite amount of energy to get there. Read an earlier answer for more detail

QUESTION: :
I understand that a moving charged particle creates a magnetic field. If you have two parallel wires with electrons moving the same direction, the magnetic fields cause the wires to attract. If the same two wires have electrons moving one way on one wire and the opposite way on the other wire, they repel. Now, what about the case where the electrons are traveling in a vacuum. When two electrons are moving opposite each other, they will repel. But what about when they are moving parallel to each other? Their velocity relative to each other is zero. Do they see a magnetic field and attract, or do they see only the electric charges and repel?
ANSWER:
The two situations (current in a wire and current in an electron beam) are very different as you seem to realize because there is no electric field in the case of the wires. There will still be magnetic forces in the beam cases, but the electric forces will be so much bigger that you would be hard-pressed to see any magnetic effect at all. If you try to look at two single electrons moving parallel, they will see no magnetic force in their own rest frames, but they will in the laboratory frame of reference. This is where releativity comes in and transformation of the electromagnetic field is probably beyond the scope of this site.

QUESTION: :
I just recently had an argument with an engineering friend of mine and was hoping you could help settle it as we tend to end up at an impasse when it comes to disagreements like this. The argument involves human body falling at terminal velocity and landing back first on various materials. He is of the opinion that landing on cement will ultimately cause less damage to the body than landing on soft loosely packed soil. He bases this on the idea that the speed of sound through something as dense as cement is faster than the speed of sound moving through something as dense as flesh and that this somehow imparts a greater ability to absorb an impact and therefore will do less damage to the body than loosely packed soil. I am of the opinion that the soil is able to shift its position under pressure and able to be compacted into a denser form than its current state and that this allows it to better absorb the impact (than concrete would) which reduces the damage done to the object hitting it. He argues that this is only the case in low speed impacts and that in a high speed impact at terminal velocity the concrete would be the better material to land on. So, which material would you expect to do the least amount of damage to an object with roughly the same density as water that hits it at terminal velocity and why?
ANSWER:
That is just about the craziest thing I ever heard! What hurts you when you stop is the force you feel. If you feel a large force, you are hurt; if the force you feel is small, you shrug it off. So the trick is to minimize the force. One way to write Newton's second law is that mΔv=Ft where m is the mass, Δv is the change in speed, F is the average force, and t is the time during which F acts. (The physics way to say this is that the change in momentum is equal to the impulse, mv being momentum and Ft being impulse.) So, letting your mass be about 100 kg and your terminal velocity be about 50 m/s, F=5000/t. Clearly, the bigger you make the collision time t, the smaller F will be. If you hit concrete you stop very quickly, say a hundreth of a second, so the force you feel is 500,000 Newtons, about 112,000 pounds. If you could make the collision last 1 second, for example by landing in a swimming pool full of shredded foam rubber, the force would be 5000 Newtons, about 1100 pounds, which you would probably survive.

QUESTION: :
Is there a formula which could be used to calculate the following scenario: How long would a single point on the floor be in contact with a disc brush having a surface area of 126 sq. in., rotating at 300 RPM, and traveling forward in a line at 2.5 mph?
ANSWER:
To answer your

QUESTION: , the rotational speed is not relevant�if it were not rotating at all the time would be the same if the machine were moving forward at 2.5 mph. It does not really sound like you want to see where the formula comes from, you just want the formula. First of all, the answer depends on where the point is relative to the center of the brush. A point which the center passes over will be in contact longer than a point which the edge passes over. Anyhow, the formula I get is t=[√(40-x2)]/22 seconds where x is the distance in inches from the line which the center travels. For example, if x=3 in, the point is in contact with the brush for 0.25 s, about a quarter of a second; a point in the center, x=0 in, is in contact for about 0.29 s. But, is this really what you want? It seems to me to be a much more complicated problem because the speed with which the brush is passing over the point depends on how far it is from the center.

QUESTION: :
I have a

QUESTION: about traveling around 99.9% the speed of light and communications at those speeds. If a ship were to travel away from Earth at 99.9% the speed of light would communications with Earth be possible? The second part is what effect would time dilation have on communications? Would it be possible to respond to a

QUESTION: that in relative time has not been asked yet?
ANSWER:
In an earlier answer I discussed how communications would sound, but communication is certainly possible. As I note in that earlier answer, you could not have a conversation type of communication because of the large distances and hence long travel times of signals. You certainly cannot respond to a

QUESTION: which you have not received.

QUESTION: :
Does the inverse square law apply to laser beams?
ANSWER:
No, because the inverse square law applies if the waves spread out in all directions uniformly. It does not apply to a flashlight either.

QUESTION: :
When you jump off a high building, your velocity changes drastically to zero as you hit the ground. Since your mass is constant, the impulse is also constant. How does a soft mat cushion the fall?
ANSWER:
The impulse is constant, not because the mass is constant but because the impulse is equal to the change of momentum. So, a 100 kg person hitting the ground at the speed of 20 m/s has a change of momentum of 2000 kg-m/s. The impulse is the average force times the time which it acts. If the time is short (as in hitting the hard ground), the force you experience is big�ouch! Putting a soft mat there increases the time to stop you, so the force decreases�ahhh!

QUESTION: :
in a current carrying wire ,is there a potential difference between any two points ,in between which there is neither active or passive elements
ANSWER:
All real-world wires have a nonzero resistance and so, if a current flows, a potential difference exists. (Superconducting wires will not have a potential difference.)

QUESTION: :
I am doing a report on breaking the sound barrier, achieved first by the United States Air Force (And Assistance with NASA!)! I was wondering how fast is the speed of sound in ranking? I know light would be the first, but would sound be the second fastest?
ANSWER:
Do you mean second fastest wave? Light, you must appreciate, is in a class by itself because, unlike all other waves, it can propogate through empty space. However, light propogating through a medium is somewhat slowed and therefore far faster than sound. Regarding sound: sound waves through a solid, like a steel rod, travel much faster than sound in air. There is really no point in trying to "rank" wave speeds because there are so many possibilities.

QUESTION: :
My daughter is working on a physics project that includes making a rollercoaster that must include 7 elements (loops,cork-screws,camelbacks) but the marble must complete the loop and stop at the original beginning. Is it possible, being pulled along by gravitiy and falling that it could be built to return to the original starting height? Without motors or mehanical propulsion?
ANSWER:
No, it is not possible. If she had a frictionless marble, she could do it but some energy will have to be lost to friction and the real therefore could not return to its original altitude without an external push somewhere.

QUESTION: :
why does a half empty bottle of sand (or half full lol) not roll?
ANSWER:
Whether or not it rolls depends on lots of things. If the sand is real dry and powdery, it will sort of behave like you have half filled it with a fluid and roll just fine. If it is real wet and sticky, it will behave as if you have half filled it with concrete; but this will still roll if you get it going fast enough, just in a jerky fashion. If it rolls too slowly, the fact that the center of gravity of the whole thing is not at the center of the bottle means that it will rock rather than roll. Think of the limiting case where the bottle has no mass, at least negligibly small compared to the sand. It will rock like a half cylinder.

QUESTION: :
I am looking for a physics answer to why it is bad to have too much positivity. That is, I am looking to describe - it in somewhat lay terms - how a basic structure of an atom has protons and neutrons... yada yada yada As you might have guessed, I am not a physicist but am looking for an answer that is indisputable and based in fact.
ANSWER:
It is not at all clear what you are asking. Since you mention protons and neutrons, maybe you mean the nucleus of the atom, not the atom (which also includes electrons, "negativity"?) There are two competing forces in a nucleus, the electrical force which tries to blow it apart because protons repel each other electrically, and the nuclear force by which nucleons (which is what we collectively call neutrons and protons) attract each other. If you try to make a nucleus with just protons, it will not be stable because the electrical force wins out. But, if you add some neutrons (which do not feel the electrical force) to the mix, you add some nuclear force without adding any electrical force, so the nucleus may become stable. This also has the effect of having the protons farther apart because there are more particles in the nucleus, and this means the electrical force is weaker. Atom heavier than around calcium tend to have more neutrons than protons in their nuclei.

QUESTION: :
An iron rod 1cm in diameter and 1 light year in length is located in outer space far from any astronomical body. Sufficient force is applied to one end (end A) of the rod the direction of its opposite end (end B) to move it one meter. An observer at end B will wait to observe the rod move one meter and then apply sufficient force on the end (end B) of the rod to move it one meter in the direction of end A. The final position of the iron rod along the axis of the forces applied from either end will be where it began. How long would an observer and end A wait between the initial force applied at end A and end A returning to it's original position?
ANSWER:
I have previously answered almost exactly the same

QUESTION: . The answer is that he would wait much much longer than two years.

QUESTION: :
Have tachyons been empirically proven to exist? If not, what evidence is there to suggest they might exist?
ANSWER:
Not to be flip, but the answers to your

QUESTION: s are "no" and "none". The Wikepedia entry on tachyons is pretty readable.

QUESTION: :
A friend says that changing electric and magnetic fields generate one another, and this gives rise to visible light when the frequency of change matches the frequencies of light.
ANSWER:
Your friend has it right. Electromagnetic waves are caused by radiating electric charges; charges which are accelerated radiate. An example of this is the broadcast antenna of a radio station which has electrons oscillating back and forth to create the radio waves. For visible light, atoms act like tiny antennas.

QUESTION: :
Why do balls bounce? Also because non-bouncy balls travel back up with less energy, does that mean more energy has been transferred to the surface upon which it was bounced (and a more bouncy ball has transferred less energy to the ground?) AND if that is true what would be the best way to measure the difference in energy transferred (throwing balls at scales, throwing them at Styrofoam and observing imprints, etc.)?
ANSWER:
Not all balls bounce. A ball of putty will not bounce. Essentially, a bouncing ball is a collision with an infinite mass (that is, the earth has totally negligible recoil). If a putty ball is dropped, where does the energy it had go to? Mainly it goes to thermal energy�the ball and the surface heat up a little; a little goes into the sound it makes. This is called a perfectly inelastic collision. The other extreme is a perfectly elastic collision where energy is conserved. So, the ball hits with velocity v down and recoils with velocity v up. Now, your

QUESTION: asking why balls bounce. During the time the ball is in contact with the floor, the floor exerts an upward force on the ball; the result of an upward force is an upward acceleration (that is Newton's second law) and therefore the ball reverses its direction. In the real world, a bouncing ball always loses some energy during the collision and the collision is somewhere between perfectly eleastic and perfectly inelastic. The easiest way to measure how much energy the ball has lost (which you should think of as lost, not "transferred to the ground") is to measure how high it bounces. If you drop it from a height h1 and it recoils to a height h2, it loses 100x(h1-h2)/h1% of its initial energy.

QUESTION: :
As I understand it, when a photon is created, say in a light bulb, it is instantaneously moving at light's speed. Its acceleration is therefore infinite. Since it's massless, perhaps that level of acceleration is acceptable, but the entire picture seems somewhat muddy to me. Is there a physical description of the event, or is it in reality no more than a mathematical result of equations those of us not in the field cannot grasp?
ANSWER:
Let's just stop thinking about photons for a second. Think about water waves; do you worry about their accelerating up to their speeds instantaneously? No, they just begin at the source and propogate out. Or sound waves? There is something beating against the air and the waves just move out. The same is true for electromagnetic waves. A radio antenna has electrons accelerating back and forth creating time varying electric and magnetic fields which result in electromagnetic waves. Acceleration is never an issue in these examples, waves are created going as fast as they go.

QUESTION: :
With my understanding of relativity an objects speed is determined by how fast it is moving in relation to another object. Also no object can pass the speed of light (C). So how would it be possible for an object to travel at 75% C in one direction while another object travels 75% C in the opposite direction?
ANSWER:
See earlier answer. The bottom line is that things do not behave like you expect if the velocities are not very small compared to the speed of light.

QUESTION: :
I came up with a thought experiment described below. I setup a potential difference of say V volts between two horizontal parallel plates kept fixeda certain distance apart.I have given the upper plate +q C charge & the lower plate -q C charge.This system of course has some energy that depends on the charge in the plates and the plates separation. Now what i do is I pass a negatively charges particle with some initial kinetic energy, say Ei and velocity component purely horizontal , halfway through the two plates . As the particle emerges out of the electric field, it has gained some velocity along the vertical direction and thus has a kinetic energy Ef, greater than Ei. The difference dE = Ef - Ei is obviously positive implying it has apparently absorbed some energy from the field in course of its passage through it. As far as I believe, this brings about no change in magnitude of charge in either of the plates and the separation between plates has been held constant. So in no way is there a change in the energy of the parallel plates system. It follows that by doing this I have managed my little particle to gain some energy without any other system having lost it!!
ANSWER:
Ah, the seemingly simplest

QUESTION: s are often the hardest for me to come to grips with! Here, as has happened before, we have a situation where we apply ideas about idealized simple situations and end up in trouble. We assume that the parallel plates were charged up in complete isolation from the rest of the universe. Further we assume that nothing will disturb these plates, their charge distributions or positions, no matter what we do. So, suppose that there is, in all the universe, only two plates, one point charge, and a battery. The battery charges the plates and the work it does is stored in the electric field which appears; then it is removed from the universe. When we calculate the energy necessary to charge the plates, we do it just the way our physics teachers told us to do it. But, wait a minute�our teachers never told us to worry about the field caused by our particle we are about to shoot through, but does that not make a difference? If there is some other field present the work to charge the plates will be different from the ideal case. In essence, the particle has a potential energy by virtue of its position vertically and this was imparted to it when the plates were charged by the battery. (A colleague pointed out to me that this problem is really no different from asking where the energy comes from when I drop a stone.) Also, when the particle passes through, the charges on the plates and the plates themselves will be pushed around. But, the energy which "magically appears" is normally infinetesmal compared to the total energy stored in the (not really) uniform and constant electric field. So, once again, the physics we learn in a physics class is only an excellent approximation to what goes on in the real world. My argument would be that the electron already had the energy it appears to acquire, but in the form of potential energy it acquired when the field was created.

QUESTION: :
I know that sub atomic particles are believed to have spin due to the internal angular momentum and magnetic field but i heard that if two sub atomic particles are created at the same time they both have to have opposite spins, but until the spins are observed they both have both spins.. how can this be? If it is true, how does this work to a pair of sub atomic particles where the twin of the particle is X number of light years away and we observed one and found it went clockwise tthis means the one x number of light years away instantly starts going anti clockwise which means the information travelled fast than the speed of light which ofcourse is impossible.
ANSWER:
What you are referring to is entanglement, often referred to as Einstein, Podolsky, Rosen or EPR paradox. And, you are not alone in finding this rather puzzling�Einstein himself was very uncomfortable with these kind of results which can happen in quantum mechanics. I will give you a bit of an overview. First, we do not "believe" elementary particles have spin, it is an experimentally well-established fact. In quantum mechanics a particle can exist only in certain discrete states. For example, if a direction is space is chosen as, say, a z-axis, than an electron's spin may point in either the +z direction or the -z direction, two states we usually refer to as spin up or spin down. Now here is the strange thing�an electron may be in a state which is a mixture of the two possible states, half up and half down. This does not mean sideways, it means partly up and partly down. Now, when you make a measurement, you must find it in either up or down and the customary interpretation is that the measurement "puts" the electron in the state you "find" it in. Now we get to the EPR experiment. Here we create a pair of electrons and the total spin of the whole system must be zero because of certain considerations I will not go into here and are not important. But they do not go into a state where one of them is up and the other is down, they go into a state where each is half up and half down. And they are flying apart, so if you wait a while they will be far apart. Now you observe one of them and find it in (that is, put it in) the up state. Since the spin of the whole system must be zero, you have effectively put the other electron in the down state, instantaneously. Preposterous you say? The fact is that experiments have been done to verify this! If it is of any comfort to you, you cannot use this to send a message instantaneously; you can just think of the entangled electrons as a really big quantum system which is constrained to have certain properties overall regardless of what you do to one little piece of it.

QUESTION: :
A physics teacher told me that velocity is the rate of change of displacement with respect to time. It seems to me that displacement is a vector, which is the difference between two vectors that describe a body's position relative to a fixed reference point. Velocity represents the change in these position vectors over a certain time period. So velocity is the rate of change of position with respect to time or it is the rate of displacement with respect to time. Either of these definitions is OK with me. But to say it is the rate of change of displacement with respect to time is very confusing to me. Is it actually correct to say that? If so, please explain how I am wrong.
ANSWER:
It is, I think, redundant to say rate of change with respect to time. "Rate of change" implies "with respect to time". Velocity is indeed the rate at which the displacement vector changes. The average velocity over a time interval is the change in displacement vector divided by the elapsed time. The instantaneous velocity is the average velocity over a vanishingly small time interval which, unless you have studied calculus, will likely not mean much to you.

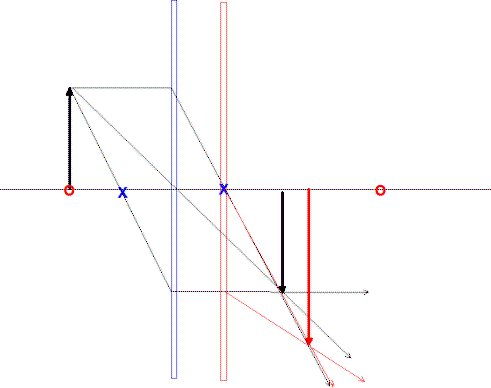QUESTION: :
In geometric optics, when we have two lenses in series, and we wish to calculate the position and size of an image of an object... we can take the image of the first lens as the object for the second lens. But it is not clear to me why we are allowed to do this in cases where the placement of the second lens prevents the image of the first from forming. For example, if we have a convex lens with on object to its left creating a real inverted image on the right... and now we place a concave/diverging lens between the convex lens and the real inverted image.... why are we allowed to use the hypothetical real image of the first lens, which doesn't exist now, as the object for the second lens? It doesn't seem obvious to me at all, that we should be allowed to do this. Can you explain this?
ANSWER:
In a case like you describe, if the object of the second lens never actually forms, then it is called a virtual object and the corresponding object distance must be entered as negative in the lens equation. I have chosen an example to show that it can be done both analytically and with ray tracing. There is a converging lens (blue) with focal length f1=1 cm, an object at an object distance p1=2 cm. The image distance is found using the lens equation, 1/f=1/p+1/q, so 1/1=1/2+1/q1, so q1=2; the magnification is m1=-q/p=-1 and the image is real since q1>0. Now, as you suggest, insert a diverging lens (red) with f2=-3 cm (f2<0) 1 cm to the right of the first lens so that the first image never actually forms. Take as the object distance p2=-1 cm so the lens equation is now 1/(-3)=1/(-1)+1/q2, so q2=1.5 cm, m2=-1.5/(-1)=+1.5; so the image is not inverted (compared with the object which is itself inverted on the ray diragram) and magnified by 1.5 and real. In my ray diagram I have only drawn two rays (in red) to locate the final image, the central ray and the ray coming in parallel to the axis; you could draw more but only need two to locate the image.

QUESTION: :
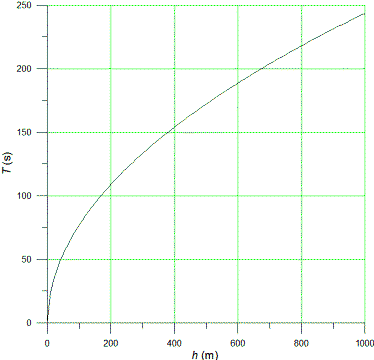
I am a artist currently studying in London! I was going to make some work about the Sun, more specifically the sunset. I did some calculations and tried to work out the difference in sunset times if you were on the ground and to each other floor in a building. Working with the measurement of one floor being 10ft I worked out the time, PER INCH, the sunsets are 0.05625 seconds in difference. I was wondering if you could confirm or replace this figure as correct.
ANSWER:
Here is the way I worked it out. Let R be the radius of the earth (R=6.4x106 m) and h be the height above the surface from which you observe the sunset. The sun will set over the horizon which is the point where you would draw a tangent from your observation point. Since the tangent to the surface is perpendicular to the radius drawn to that point, a right triangle is formed as shown in the picture to the right. For the angle A in that triangle we can write
cosA=R/(R+h)=(1+h/R)-1. If h is much less than R we can approximate (1+h/R)-1≈(1-h/R). Also, the angle A will be very small in which case you can approximate cosA≈1-(A2/2). Therefore, A≈√(2h/R); the angle A in these equations has to be expressed in radians. To find the time T associated with this angle, change A to revolutions by dividing it by 2π (e.g. if the angle is 900=π/2, this is � of a revolution); then divide the revolutions by 24 to get hours and that by 3600 to get seconds. If I do all this I get T≈7.7√h. So, for example, if you view the sunset from 100 m above the surface, it will occur 77 s later than if viewed from the surface, more than a minute. You cannot really specify the time difference per inch, as you do, because the time is not a linear function of the height. If you ask the average change per inch over the first 100 m, you get about 0.02 s/inch, in the same ballpark as your calculation. The graph shows a calculation of the time differences for heights up to 1000 m, the height of a modest mountain. I guess my calculations are really only right on the equator if the earth's axis were not tilted, but I don't think you want to worry about that kind of detail and neither do I!

QUESTION: :
If an object with mass greater than that of the earth (say 1.5X) was to be placed on the surface of the earth, would the earth remain stationary or would it travel on a new path? To develop on what I mean; because the gravitational field of the earth would of course act towards it's center, and the mass's weight would therefore be acting towards the center of the earth, would the object simply sit on the surface or invoke movement due to being of greater mass?
ANSWER:
For starters, the earth could not "remain stationary" because it is not stationary to start with. What would happen would depend on the size and shape of the object as well as its mass and how it was moving before it "attached"�its velocity and how it was rotating.

QUESTION: :
i just took up Table Tennis again after a long layoff and as you may know friction (imparting spin to the ball) is a large part of the game. I was surprised to read in one book that the amount of spin imparted to the ball from the paddle during the stroke was not a function of the SPEED at which the paddle "brushes" (almost tangentially) the ball, but of the ACCELLERATION while the paddle is in contact with the ball. They suggested approaching the ball slowly and accelerating through impact . I wrote to an "Ask the Coach" forum and the coach said he thought it was just a function of speed but asked if anybody knew the physics of the problem. I think i understand the difference between static and dynamic friction, but since the paddle isn't starting from rest, just going a constant high speed in one case vs. slow to fast in the other, i didn't think this would apply.
ANSWER:
Here is all I can think of. Because of inertia and limited frictional force, hitting the ball with a surface moving very rapidly may result mainly in slipping of the two surfaces which would not be so good for imparting spin. So, starting slow to allow the paddle to "grasp" the ball more effectively might result in more transfer of spin.

QUESTION: :
How do you explain Boyles Law in terms of molecules and atoms and what assumtions do you make?
ANSWER:
Boyle's law is just a special case of the ideal gas law (for constant temperature), PV=NRT. To derive the ideal gas law you assume the gas is in thermal equilibrium with the container and that the volume of all the molecules is small compared to the volume of the container.

QUESTION: :
What is the force called that makes items in a container go to the sides of the container when you spin the container around? Tony - 9yrs old
ANSWER:
Well, Tony, since you are only 9 years old I am tempted to just tell you that it is the centrifugal force. If you like, you can just stop there and have your answer. But, I do not like to mislead anybody, even a 9 year old, so I will give you a little tutorial about circular motion if you are interested. For anything to move in a circle there must be a force on it which points toward the center of the circle; this force is called the centripetal force. An example of a centripetal force is if you twirl a stone attached to a string around you, the string pulls on the stone with this force. What happens if the string breaks? The stone will fly off in the direction it was going just before the string broke (which is not straight out away from you). Although the stone is not moving straight away from you, it is moving farther away from you so it might look like there is a force pushing it away, but there isn't, it is just moving along in a straight path. The same kind of thing happens in a container. Imagine a stone sitting on the bottom of a barrel, and the barrel is spinning very slowly�the stone just spins along because the friction between it and the barrel bottom provides the centripetal force. But if the barrel spins real fast, there will not be enough friction and the stone will slide; it will eventually hit the outside side of the barrel and stay there, going around with the barrel. It looks like it was forced out there but it just drifted out there like that stone from the broken string going away from you.

QUESTION: :
Can you please break down Schrodingers equation for me? What each variable stands for and can you please explain to me the theory behind his equation. I'm just a curious English professor and I'm having a difficult time understanding the equation as well as Heisenberg's Uncertainty Principle equation. If you can put the breakdown in layman turns I will forever be grateful.
ANSWER:
Well, this is a tall order. I have attempted to do this, in spite of the fact that it really can't just be done concisely. It was a challenge! I have not done an explanation of the uncertainty principle because that does really cause the discussion to be too long and unfocused. Maybe we can deal with that later if my discussion of the Schr�dinger eqiation is what you had in mind. Link here.

QUESTION: :
When salt is poured on a table it couses a mound, why does gravity not couse the salt to spread out on a flat layer?
ANSWER:
Because of friction, the same reason a block will not necessarily slide down an incline if there is adequate friction. Actually the study of such phenomena (often called "sand pile physics") can be pretty complicated and is a serious study. The angle the pile makes with the ground is called the angle of repose; interestingly, the angle of repose for a particular material is independent of how high the pile is.

QUESTION: :
Doing an outside loop, why does the normal decrease with an increase in tangential speed?
ANSWER:
Think of a car with a speed v at the top of a hill with a radius R. Its acceleration must be a=v2/R, straight down. There are two forces, the normal force N up and the weight mg down; so, from Newton's second law, mg-N=ma=mv2/R. If you solve this for N, N=m(g-v2/R). You can see that as v gets larger, N gets smaller. Eventually, when v=√(gR), N=0 and all the centripetal acceleration is caused by the weight. If you go any faster the car will leave the road.

QUESTION: :
The more I read the more confused I get....I was asked What kind of light would be emitted by atoms if energy were not quantized?
ANSWER:
If an atom could be in any energy state and decay to a lower state, you would have a continuous spectrum of light. If you had lots of atoms being excited and the deexciting you would just get white light.

QUESTION: :
In a standard textbook example, a charged particle moving with a constant moderate velocity perpendicular to a constant magnetic field is deflected. If an uncharged observer is traveling parallel to the charged particle with the same velocity, it would see the charged particle as having zero velocity at first and then motion in the direction of the deflection observed by the stationary observer. If the magnetic field is "constant", how does the co-moving observer explain the force on the charged particle? I guess another way to ask the

QUESTION: is if charged particle motion in a magnetic field produces a force on the particle, and motion is relative (to the field), then is it possible to have "moving" field produce a force on a "stationary" particle? Or more fundamentally yet, if the field is constant, how does the particle "know" it's moving through the field?
ANSWER:
What a good

QUESTION: . The thing is that electric and magnetic fields are not really different fields like all elementary texts make it look. There is one field, the electromagnetic field and the "mixture" of how much of each is electric or magnetic depends on the frame of reference of the observer. If, in a particular frame of reference, there is a pure electric field, then if you view this field from a moving frame, a magnetic field will appear. Similarly, if, in a particular frame of reference, there is a pure magnetic field, then if you view this field from a moving frame, an electric field will appear. The situation you describe is the second and it is then the electric field which produces the force on the particle "at rest".

QUESTION: :
Lately, in physics class, I have been studying how some substances will heat up (less calories) faster than others. I have a

QUESTION: pertaining to this on the atomic level, rather than the molecular level as we have been learning. If some substances heat up faster than others, then wouldn't certain elements heat up faster than others when changing states (say from a liquid to gas)? For instance, if we take water, with both hydrogen and oxygen, why wouldn't one element separate from the other (assuming they have different boiling points, or require less calories for heat of fusion)? Why doesn't one element reach the boiling point and not separate from the other element?
ANSWER:
This is really chemistry, but chemistry is really physics! It all depends on the molecule you are working with. Some molecules will dissociate before the solid melts or the liquid boils and then you have a mixture of the constituent elements. But most often, particularly with common inorganic compounds, the molecules are sufficiently strongly bound that heating them does not supply the necessary energy to dissociate them and the properties are determined by the molecule, not its constituents. (Your particular example is one in which the atoms are too tightly bound to be broken apart by adding some heat. But, if they were not, when they separated you would already be well beyond the boiling points of either because both are gases at normal pressures and temperatures. The bottom line in answer to your

QUESTION: is that it takes energy to break a molecule apart and often supplying heat is insufficient to do that.

QUESTION: :
It's my understanding that as velocity increases, so does mass. Now, let's say we have two spaceships accelerating away from Earth at the same rate parallel to one another. To observer's on Earth, their velocities are increasing and therefore so is their mass. However, relative to one another, they are motionless and therefore their mass would not increase. Does this mean that the mass of a particle is relative to the observer? From Earth's perspective, the ships would need more and more energy to accelerate, but from the ships' perspective, they would not. What's the explanation for this apparent contradiction?
ANSWER:
Just as the case of your earlier

QUESTION: , the resolution of the apparent contradiction is length contraction. Think of there being a stick attached to the earth and pointing out to the spaceships' destination. As the spaceships go faster and faster this stick gets shorter and shorter so that each burn of fuel results in a smaller and smaller acceleration.

QUESTION: :
This is a pretty basic

QUESTION: , but what exactly is force? Newton's second law states that F=ma. Mass, distance, and time are easy, and velocity and acceleration are obvious to anyone who can ride a bike. Momentum is a little more difficult, but it has an intuitive definition (how hard it is to stop something, or how much it would hurt if you crash your bike at various speeds). I can't define force without using the terms "mass" or "acceleration." Given that F=ma is a law and not a definition, can you give me a definition of force? Or am I misunderstanding "law" and velocity=distance/time would also be a "law"?
ANSWER:
I will give you a brief rundown of how I present this when teaching. First, to start doing physics you need to have an intuitive idea of what three essentially underivable quantities are: two of these are length and time. Once you accept that length is what a stick measures and time is what a clock measures, you can do what we call kinematics which mathematically describes motion. So, velocity is time rate of change of position, acceleration is time rate of velocity, etc. No "laws" here, just definitions. Now, if we want to do dynamics, which is to determine what makes things move the way they do, we need a third fundamental concept; scientists generally start with mass. Technically mass is the inherent property an object has which causes it to resist being accelerated when we push or pull on it. This is what is called inertial mass. But, wait, I cannot really understand what mass is without introducing the language of force, viz. "push or pull". As you correctly point out in your

QUESTION: , mass and force are inextricably intertwined. So, why is mass the one we label as "fundamental", why not force? In fact, you could go either way, either operationally define what mass is (say 1 kg is the mass of some arbitrary chunk of stuff in a vault in Paris which is what we do) or operationally define what a unit of force is (say 1 lb is the force the earth exerts on a pint of water). The English system of units is the lb/ft/s (force/length/time) whereas the SI system used by scientists is kg/m/s (mass/length/time). Now, once we decide on mass, how do we find out how it relates to force? We do what all good scientists do�do experiments. Keep in mind that we do not have a defined unit of force, only a qualitative idea that it is a push or a pull. Imagine making a machine which will always deliver the same force when pushing on something; a simple example would be some spring which we attached to a mass and pulled such that it was always stretched by 1 cm. Now do a series of measurements keeping the force constant and varying the mass. You would find that the acceleration was inversely proportional to the mass�double the mass and you halve the acceleration. Now, do a series of experiment where you vary the force and keep the mass constant; you could do this by pulling with one spring, then two, then three, etc.). You would find that the acceleration was directly proportional to the force�double the force and you double the acceleration. So, you have now learned that the acceleration a is proportional to F/m. This is what I think of as Newton's second law. But, since F is not yet defined, I can now define it by choosing the proportionality constant to be 1. Hence, a=F/m or F=ma. One unit of force, which we call a Newton, is that force which will cause a 1 kg mass to have an accleration of 1 m/s2.

QUESTION: :
A rollerblader leans into a turn as he moves in a circle. The net torque about any point in the rollerblader must be zero if the rollerblader is not to fall over. If the torque is computed about his center of gravity, then the torque caused by the normal force of the ground up on his wheeels is balanced by the torque due to the centripetal force of static friction of the ground on his wheels. If these torques are computed about the contact point of the wheels on the ground, however, there seems to be a non-zero, net torque due to his weight since the normal and static friction forces act through the contact point and would not contribute to the torque about this point. The moment of inertia of the wheels negligable. How can there (seemingly) be a net torque about the contact point and none about the cg? P.S. I submitted this

QUESTION: to the "Mad Scientists Network" and the engineer who answered it said there was an outward, "righting" force that acts through the cg. He did not state the nature of this force but it sounded suspiciously like he was thinking of centrifugal force. This didn't seem right to me. I want to know how a physicist would explain this.
ANSWER:
Hey, guess what: the engineer got it right! He just didn't give you a complete enough explanation, and you deserve one! Ask the Physicist goes where other Q&A sites only dream to go! Enough silliness, here it is. Newton's laws are not valid in accelerating frames of reference and you are attempting to apply Newton's first law (N1) (the sum of all torques equal zero is the rotational equivalent of N1) to the skater who is accelerating because he is moving in a circle. If he were not accelerating, i.e. moving in a straight line and leaned over he would fall. The best way to deal with accelerating systems like this is to do a trick which inserts forces which do not exist to force Newton's laws to be true; these are called fictitious forces. In this case you must add a fictitious force which points away from the center of the circle, acts at the cg, and has a magnitude equal to the centripetal force; this is called the centrifugal (Latin root center fleeing, fugo is I flee) force. Then everything works out and he is in "equilibrium" in his accelerating frame.

QUESTION: :
what happens when a rubber ball is thrown in a square room in outer space?
ANSWER:
Every time it collides with the wall it will lose a little energy, but between collisions it will move in a straight line. So, if given an initial velocity parallel to one of the walls, it will bounce in a plane, going slower after each collision. If there is air in the room, it will also slow down as it goes on its path.

QUESTION: :
I have read that in the early formation of the universe photons collided to create electron. How can two massless particles (photons) create a particle with mass (electrons)? What is the process?
ANSWER:
Mass is not a problem, because photons have energy so it could be converted into mass, another form of energy. The real problem is electric charge. Photons have no charge and so charge would have to be created. I do not know where you read this, but I think you must have misunderstood.

QUESTION: :
I understand that nothing with mass can travel the speed of light because an infinite amount of energy would be required to accelerate the mass and there is not an infinite amount of energy in the universe. As a statement, it makes perfect sense. But I don't understand the math: ". . . The expression for the mass of an object m as a function of its velocity v is m=m0/√(1-(v2/c2)) where c is the speed of light and m0 is the mass when it is at rest. Note that as v approaches c, m approaches ∞ so it is impossible to push beyond c. Another way to look at it is from the perspective of energy. The energy of a particle is E=mc2=m0c2/√(1-(v2/c2)), so the energy required to accelerate the mass to the speed of light is infinite and there is not an inifinite amount of energy in the universe." Can you explain without math why an infinite amount of energy would be needed?
ANSWER:
No, you really cannot do it totally without math, but maybe I can make it more explicit. Let's calculate the quantity 1/√(1-b2) for various values of b. If b is the ratio of speed to light speed, then this factor is what determines how big the energy of the particle is. For example, if the speed is 50% the speed of light, b=0.5, b2=0.25, and 1/√(1-b2)=1/√(1-.25)=1.15. Go faster, say 80% the speed of light, then b=0.8, b2=0.64, and 1/√(1-b2)=1/√(1-.64)=1.67. Go faster, say 99% the speed of light, then b=0.99, b2=0.98, and 1/√(1-b2)=1/√(1-.98)=7.07. Go faster, say 99.999% the speed of light, then b=0.99999, b2=0.99998, and 1/√(1-b2)=1/√(1-.99998)=223.6. Go faster, say 99.99999% the speed of light, then b=0.9999999, b2=0.9999998, and 1/√(1-b2)=1/√(1-.99998)=2236. Can you see where this is going? When (never) we go 100% the speed of light, then b=1, b2=1, and 1/√(1-b2)=1/0=infinity.

QUESTION: :
Why is it necessary to orbit Earth and reach an escape velocity to fly away from the Earth? Why can't a spaceship, say destined for the Moon, just fly in a (generally) straight line from the ground to the Moon without orbiting Earth?
ANSWER:
It is not necessary. You could, in principle, go directly to the moon. Planetary probes do not go into earth orbit on their way out.

QUESTION: :
My inquiry is regarding a vertical ascent away from the Earth towards space. I was in a discussion with my father recently and we ran into a disagreement. His stance was that in order to leave the Earth vertically one needed to achieve Escape Velocity consistently through the ascent. My argument was that if there were a source of constant or, maybe consistent is a better word, propulsion an object could rise vertically at any speed.
ANSWER:
Escape velocity is the minimum speed you need to give to a projectile to go up and never come down. If you had a source of propulsion, you could escape the earth at 1 mph if you wanted to.

QUESTION: :
If you were in a helicopter hovering above a single point on earth's surface for a long period of time, would your helicopter need to have any horizontal velocity to keep up with the rotation of the earth? Would the answer to this

QUESTION: change with the distance you are from the surface of the earth (i.e., boundary layer effects)?
ANSWER:
Certainly not. The helicopter flies with respect to the air and the air moves (more or less) with the rotating earth. Any lateral velocity component the helecopter has would be to compensate for wind, not motion of the earth.

QUESTION: :
Someone told me that if one body revolving around another is always facing that body which it is revolving around, that it is also rotating about its own axis, I don't understand how a body can be rotating if it is always facing the body it is revolving around, can you explain how this can be so please?
ANSWER:
To determine whether you are rotating, look a distant objects. If the distant stars all do not move you are not rotating, if they do, you are. A good example is the moon, the same side of which always faces the earth. Over the course of one month, it sees all the stars rise and set.

QUESTION: :
I just have a basic

QUESTION: regarding relativity. It's my understanding that for an object traveling at 99% the speed of light, time will slow down by a factor of approximately 7 (from an observer's perspective). So, if I were to travel 4.37 light years to Alpha Centauri at 99% light speed, from the perspective of an observer on Earth I would get there in about 4.41 years, but time would have slowed down for me and I would only have aged 0.63 years. Thus, from my perspective, I just traveled 4.37 light years in a matter of only 0.63 years. So, from my perspective, did it seem like I was traveling faster than light or am I thinking about this in the wrong way?
ANSWER:
Here is what you are missing: you see the distance between the earth and the star as moving by you at 99% the speed of light. Not only do moving clocks run slow, moving lengths get shorter. The distance you see between the earth and the star is approximately 1/7 of 4.37 light years, so there are no inconsistencies.

QUESTION: :
Since the Earth is constantly spinning do you drive faster in one direction (east or west) than the other?
ANSWER:
You have to ask, faster relative to what? Relative to the ground, 60 is 60. Relative to a stationary point outside the earth, your velocity would be dependent on the direction of your velocity relative to the ground.

QUESTION: :
To my understanding, the binding energy is defined to be the energy that must be added to separate the nucleons. (i) The binding energy of Uranium-238 is positive, that is energy is required to separate the nucleons of U-238, then why is it still radioactive? (ii) Hydrogen-2 has an average binding energy per nucleon less than that of Uranium-238, but Hydrogen-2 is stable, why?
ANSWER:
Just because a system is bound, that does not mean that another configuration of that system cannot have a lower energy. Alpha decay often happens in very heavy nuclei because an alpha particle is very tightly bound. Energy is released in the fission of a heavy nucleus into two lighter products because of the systematics of binding energy. You should read my earlier answer on fission and fusion. I guess the bottom line is that bound is not synonymous with stable.

QUESTION: :
A person is rotating a string with a mass at the end of it above their head. Let's say the plane of rotation is formed by the x and y axes. While rotating, the string (and therefore, the tension force causing rotation) makes an angle A with the plane of rotation. If you are spinning the mass with a constant freqency, the mass has no vertical (z axis) movement. I assume this is due to the z-comp of tension force balancing Fg. As the tension force increases, the angle A decreases.

QUESTION: : Is it possible to have A = 0? Why can the mass never go above the plane of rotation?
ANSWER:
If A were zero, there would be no vertical component of the tension to hold up the weight unless the tension in the string were infiinite which is not going to happen. To move the mass above the horizontal plane where your hand is would require a net upward force and there is no source of such a force.

QUESTION: :
If you brought a flashlight into space and turned it on, would the light float away?
ANSWER:
The photons carry momentum, and so it would act like a little rocket to conserve the momentum; the flashlight would accelerate. However, the mass of the flashlight is so large that you might wait a long time to see anything happening. If there were an appreciable effect, you would feel the thrust when you held a flashlight.

QUESTION: :
The magnetic constant (permeability of vacuum) has an exact solution 4.pi/10000000 This solution is in SI units. I cannot find a comparable solution in imperial units. How could I convert to ft, lbs... the solution would be?
ANSWER:
The constant μ0 has units of N/A2. I presume you would like to retain the A2, so 4πx10-7 N/A2=1.26x10-6 (N/A2)x(1 lb/4.45 N)=2.83x10-7 lb/A2.

QUESTION: :
If Kinetic Energy is a product of mass and velocity does the massless photon in fact have kinetic energy?
ANSWER:
Well, I wouldn't say it is the "product of mass and velocity"; that sounds like linear momentum. Kinetic energy is a scalar quantity and equal to �mv2 classically, but photons are not classical particles, you have to use relativity. As I have noted many times before, kinetic energy K of any particle with mass m is K=E-mc2 where E is the total energy and mc2 is the rest energy. That is, kinetic energy is total energy minus rest mass energy. The mass of a photon is zero and so, all the energy of a photon is kinetic, it can never be at rest. So, what is the total energy of a particle? Relativity tells us that it is E=√(p2c2+m2c4) where p is linear momentum (but, not mv like classical physics, it must be redefined). So, you see, for a photon both the kinetic energy and the momentum are nonzero even though the mass is zero: K=E=pc. Incidentally, the energy of a photon is E=hf where h is Planck's constant and f is the frequency of the associated electromagnetic wave.

QUESTION: :
I had a

QUESTION: about Torque, Internal forces & external forces. Here are 2 examples helping me to state my

QUESTION: :
1) The earth is rounding the sun with respect to the Sun. The forces which are acting on the system are 2 gravitational forces that are action & re-action. The Force vector & the Position vector will be in opposite direction; so their cross product is Zero & then the Torque will be zero.
2) In a system of particles, two objects are attracting each other with respect to a point (Q), which is located outside of the system. With respect to (Q), We say these two forces cancel each other out & there will be no Torque on the system in view of (Q).
Why in case 2, we say these forces cancel each other; but in the first case, we don't consider the re-action of Sun's gravitational force?
ANSWER:
Both cases are the two-body system. Usually, when doing solar system calculations, we approximate the sun's mass to be infinite (because it is so large relative to any of the planets). In that case there is one and only one force, the gravitational force which the sun exerts on the earth. There is no "reaction" force which is pertinent. There is also no torque on the earth as you note, because rxF is zero, so the earth has a constant angular momentum. The whole problem is reduced to a one-body problem. If we treat the sun and earth as a two-body system (your case 2), we need to include both bodies. If we consider the system as isolated, the earth and sun exert equal and opposite forces on each other and so the net force is zero. Similarly, the net torque is still zero. Thus both linear momentum and angular momentum of the pair of bodies are constant. The two-body problem may be reduced to an equivalent one-body problem and solved for the motion. What you keep referring to as the "reaction" force does not make sense. If the sun exerts a force on the earth, the earth must exert an equal and opposite force on the earth; those are referred to as a Newton's third law pair. If the sun's mass is very large compared to the earth's mass, you ignore the force the earth exerts on the sun because it has negligible effect on the motion of the sun.

QUESTION: :
considering that two identical shaped objects of different masses hit the ground at the same time why if I add extra weight (as paperclips) to a paper spinner does it fall quicker when air resistance has not changed?
ANSWER:
The frictional force is approximately independent of mass. However, that is not the only force on the object�there is also the weight, mg. The frictional force is up and the weight is down, so, if you increase the mass, the net force down is larger. Another way to look at it is to estimate the terminal velocity. The air drag is approximately proportional to v2, F=Cv2, so when Cv2-mg=0 the object will fall with a constant speed v. Hence, v=√(mg/c), so you see it falls faster as m gets larger.

QUESTION: :
If you had a large rock's density but then smashed the rock into smaller pieces. How could the smaller piece's density compare to the larger rock's density...?
ANSWER:
It depends on whether the rock was homogeneous (all made of exactly the same stuff) or not. Density is mass divided by volume, and any particular stuff has the same ratio of mass to volume regardless of the volume. For example, if you had a 3 kg rock of pure quartz and broke into three pieces of equal volume, you could be sure that each piece had a mass of 1 kg. The density is determined by how heavy the individual atoms are and how they are put together and this is the same regardless of the size of the rock. [One proviso which you may not be interested in: if you break a material into small enough pieces, nanoparticles, a cluster of say 100 atoms might not have the same density as the bulk material. One of the things of interest to nanophysicists is how small a particle may be and still have the same properties as the bulk material.]

QUESTION: :
is it correct (or at all meaningful) to say that Planck's constant is the quantum of momentum?
ANSWER:
Planck's constant has the units of Joule-seconds, J s=kg m2/s; momentum has the units of mass times velocity, kg m/s. So it is not momentum. Instead, the units of Planck's constant are the same as the units for angular momentum which are also kg m2/s. However, it would be an oversimplification to say that "Planck's constant is the quantum of [angular] momentum"; it sort of minimizes the importance of h as a fundamental constant of nature. Planck's constant was first used by Niels Bohr in this context (a unit of angular momentum) in his model of the hydrogen atom. His model assumes that allowed orbits correspond to angular momenta Ln which are integral multiples of h/(2π), Ln=nh/(2π) where n is an integer greater than zero. It turns out that this, although it worked in some respects, is not quite correct. We now know that angular momentum is given by Ln={√[n(n+1)]}h/(2π) where n=0 is also allowed.

QUESTION: :
When discussing angular rotation, which is the correct phrase to use "the body is rotating about its axis" or "the body is spinning about its axis" or "the body is revolving about its axis"?
ANSWER:
This is really semantics, not physics. I will give some common usages which are by no means rules. Revolve usually means move around an orbit, not about an object's own axis; however, the dictionary lists this as one possible use of the word revolve. Rotate and spin are essentially synonymous. In atomic, nuclear, and particle physics spin is usually used as a noun meaning the intrinsic angular momentum a particle or system of particles has which is a lot like rotating about its own axis but not to be taken too literally because spin is a nonclassical quantity. Orbital motion in atomic, nuclear, and particle physics is usually referred to as orbital angular momentum rather than revolution. In astronomy, revolve normally refers to orbital motion and rotate normally refers to spinning on an axis.

QUESTION: :
If time is affected by both mass and speed (ie. the faster you go and the closer you are to a large mass the slower time goes realtive to others), does this mean that a planet that is smaller than ours and is orbiting its sun slower than ours experience time faster than us relativly? And thus if life is capable of existing on this planet could it have evolved quicker?
ANSWER:
First I need to note that gravitational time dilation in the vicinity of a mass the size of the earth is incredibly small; it is observable and used by GPS software, but really tiny. Similarly, the speed of earth in its orbit is very small with respect to the speed of light, so any time dilation due to that motion is also tiny. But the real crux is that time dilations are the rates of clocks as observed by observers other than in the clock's frame, the time for any observer in his own frame proceeds at the same rate as your clock. If you observe a clock at a lower altitude or one that is moving relative to you, it runs slow; to an observer riding with that clock, it runs perfectly normally.

QUESTION: :
My understanding of physics is that matter can neither be created no destroyed. Rather, it can only be changed. (ex. if a building is burnt down, all the matter would still exist, but just in different forms, such as smoke, dirt, etc.) If this is true, then where did the matter that was exploded in the 'Big Bang' come from? (i.e. it had to exist in some form BEFORE the Big Bang, since matter can neither be created nor distroyed)
ANSWER:
Your "understanding of physics" is wrong. Matter can be destroyed or created. Mass is a form of energy and it is energy which cannot be created or destroyed. We consider the total amount of energy in the universe to be constant. Your notion of the constancy of mass is from chemistry where, although mass is not really conserved in chemical reactions, it is so close to being constant that you can do chemistry assuming it is. So, where did the energy to create the universe come from? Nobody knows.

QUESTION: :
I saw a commercial for a new type of car tire designed to increase fuel efficiency by reducing the amount of friction between the tire and the pavement. This makes it easier to get the car moving which means the car is using less fuel to make the car move. All this I understand. My

QUESTION: is, if we reduce the friction that keeps us from moving, do we also reduce the friction which helps us stop moving? Is braking ability being sacrificed for the sake of a better fuel efficiency?
ANSWER:
The friction used to drive you forward or to brake is static friction, friction which keeps two objects which are in contact with each other (tire and road here) from slipping. Sometimes, it is kinetic friction (if you are "peeling out" or skidding). But there is also friction associated with the deformation of the tire; because the wheel slightly "squishes" when it rolls, energy is lost to this kind of friction. Also, there is something called rolling friction which is related to the tires sticking to the road so you are continually doing work "unsticking" the tires, thereby losing energy. The "improved tire" addresses, I presume, the latter two types of friction.

QUESTION: :
I am a volunteer in scouting. I was wondering (although I have my own theory) what may happen if an individual had a magnesium block on their person and was electrocuted or struck by lightning. What do you think would happen
ANSWER:
I don't think the electricity would have anything to do with what would happen, it would be the associated heat. Magnesium is easy to ignite in little flakes but hard to ignite in bulk. So it might or might not ignite under the circumstances. If it did, it would be very hard to put out. That would likely be the least of the victim's worries. What's your theory?

QUESTION: :
This relates to time dilation. I've learned that if a person is passing a motionless observer at the speed of light, he will be observed to be traveling faster (as far as measuring time) than he would observe himself to be moving. My

QUESTION: stems from this notion. If you're in space - is motion relative? Do you have grounds to say one person is traveling at the speed of light whereas another person is motionless verses the opposite? Who is to say - in a perfect, hypothetical environment - which person is moving? If so, would they both observer the other to be moving faster than they observe themselves to be moving?
ANSWER:
As I seem to have to say several times a day, no person (or any object with mass) can travel "at the speed of light". You can get close, but not at that speed. See an earlier answer. That said, the notion of absolute velocity has no meaning. If one space ship has a speed of 100,000 mph relative to another, the laws of physics are such that there is no difference if we consider the speed of the second ship to be 1000,000 mph relative to the first. See another earlier answer.

QUESTION: :
I'm watching the Empire Strikes Back right now and The Falcon's Hyper Drive is broken right now. Meaning it cannot go in to light speed. My

QUESTION: is, hypothetically of course, can a space ship enter hyper space with in the atmosphere of a planet?
ANSWER:
Physics of 2010 says no space ship can "go in to light speed".

QUESTION: :
http://en.m.wikipedia.org/wiki/File:Beta_Negative_Decay.svg
I found the above diagram while I was reading parts of the wikipedia article on a nutron. After a little thought am confused to how a down quark can decay in to an up quark, if quarks are elementary particles and by definition have no substructure.
ANSWER:
A particle with no substructure is not eternal. A simpler example, and electron and a positron, each with no substructure, can annihilate and create two photons. "Elementary" particles can participate in reactions.

QUESTION: :
When an acoustic wave travels through a medium of particular velocity, does it change its frequency? In other words, which is fundamental property for a sound wave, frequency or wavelength?
ANSWER:
Wavelength changes, frequency does not.

QUESTION: :
does a baseball and tennis ball have a different speed when thrown with the same force?
ANSWER:
Once again we have the

QUESTION: "how much speed does a force cause?" Read my earlier answer. The answer is that knowing the force is not enough. But, if you stipulate that you push on each with the same force for the same time, or that you push on each with the same force over the same distance, the tennis ball will have the larger speed because it has a smaller mass and will therefore have a larger acceleration.

QUESTION: :
how were physicists able to determine that vanishingly tiny particles have the property of spin? is it really possible that the spin of such small objects is observable or is "spin" simply a term used to denote some sort of mathematical abstraction? is it correct to think of an electron "spinning" the way a top or frisbee does?
ANSWER:
Nearly all experiments which detect spin are really detecting the magnetic moment of something. The first experiment was the Stern-Gerlach experiment which took a beam of silver atoms and passed them through an inhomogeneous (that is, not uniform) magnetic field. The idea is that a magnetic dipole (like a tiny bar magnet) will experience a net force in such a field. What was observed was that the beam split into two beams. This implied that the atomic dipoles were half in a N up, S down orientation and half in the other orientation. Any time you have a charge distribution which has an angular momentum (the more general physics term for spin), the result is a magnetic dipole moment. So, if you observe something about magnetic moments, you are likely observing something about angular momentum. In this case, the spin angular momentum of the electron in silver may be either up or down because the magnetic moment causes the beam to split in two, and from that it must follow that the spin angular momentum quantum number is �. Spin of elementary particles is very much like spin of macroscopic objects like tops, that is it is what we call intrinsic angular momentum, something which is intrinsic to the particle, not due to its motion (like in an orbit around the nucleus, which gives rise to a different kind of angular momentum called orbital angular momentum). On the other hand, there are distinct differences between micro- and macroscopic spin. In particular, you cannot explain it by using the standard classical models; for example, if you take the electron to be a solid sphere with its mass uniformly distributed and calculate the spin using a reasonable size, the surface will be moving faster than the speed of light. Also, unlike a top or frisbee, you cannot stop the spin or speed it up. The origin of spin can be understood using relativistic quantum mechanics where it appears naturally.

QUESTION: :
If time is affected by travel at the speed of light, (i.e. time travels more slowly for someone traveling at the speed of light). What would happen if you took two people (or clocks), and sent them in opposite directions on an elliptical course that will make them eventually pass by each other. What would the time difference be when they met in the middle? Say, subject A travels "west" and subject B travels "east" both leaving at the same time, traveling at the speed of light. Would both of their clocks be equally offset to normal time when they pass by each other going opposite directions? Does the direction you travel have anything to do with the time dilation?
ANSWER:
You must not say "at the speed of light" because nothing can go the speed of light. For relativistic effects to be important, the speed should be comparable to the speed of light, say 50% or more the speed of light. You do not need an "elliptical course" for your

QUESTION: , you just need to send the two in opposite directions and then bring them back. This was worked out in an earlier answer; the bottom line is that each ages the same as the other but less than if they had not made the trip.

QUESTION: :
Two pitches are thrown. Assuming all other variables remain constant such as batting power, wind, pitch, contact point, etc., which pitch would travel further? A 95 MPH pitch or a 85 MPH pitch.
ANSWER:
The important quantity is the impulse which is the average force times the time that force acts. I found that a typical impulse is about 13 Ns for a batted ball. The important thing is that the change in velocity is proportional to the impulse. So the ball which comes in with the smaller velocity will go out with the larger velocity. Equal impulses will project the 85 mph ball faster. If you are interested, the 13 Ns impulse will cause the 85 mph ball to end up with a speed of 116 and the 95 mph ball to end up with a speed of 106 mph.

QUESTION: :
With reference to energy transformation, why is a car's breaking distance greater down an incline rather than on a horizontal plane? I know that the main energy transfer would be of kinetic energy to heat energy [why heat energy?].
ANSWER:
Think in terms of forces doing work on the car. On level ground, the only force parallel to the car's motion is the friction of the brakes which takes energy away from the car. But when going down a hill there are two forces acting parallel to the car's motion�friction (opposite the motion) and the component of the car's weight parallel to the road (in the same direction as the motion). Therefore the net force stopping the car is smaller than the case of a level road so it goes farther. When friction takes energy away from a system, nearly all the energy ends up as thermal energy; for example, if you put your hands on your brakes just after stopping your car you will probalby burn your hands. Incidentally, the new hybrid cars are designed so that the energy from the brakes gets put into electrical energy and so this energy is used to charge the batteries.

QUESTION: :
What would happen to the volume of a basketball left outside on a sunny day? Which gas law applies to this phenomenon?.
ANSWER:
The ideal gas law will cover this

QUESTION: ; it combines all the other usual gas laws like Boyle's law, Charles' law, etc. It is PV=NRT wher P is pressure, V is volume, N is the amount of gas, R is a constant, and T is absolute temperature. In the case of your basketball, N is constant, so as the temperature increases the product PV has to increase. Basketballs I have seen are really not very stretchy, that is you can increase the pressure quite a bit without changing the volume very much, so mostly the volume would stay about the same and the pressure increase. If the ball starts out not fully inflated, then the volume would increase more.

QUESTION: :
how to compute the amount of power is needed to keep an object floating in the air. (For example how much power is needed to keep an electric helicopter floating)
ANSWER:
It is much more complicated than you think. At first blush, it would take no power because if just hovering there is a vertical force equal to the weight but it does no work. But in order to supply the necessary force you need a mechanism and energy must be put into that mechanism to supply the required force. For example, the force might be provided by a moving airfoil (the helicopter propeller blade) and, as you suggest, this might be driven by an electric motor. But the required energy input is determined primarily by the engineering design of this motor-propeller system, i.e. how efficient it is. So the bottom line is that there is no way to answer your

QUESTION: in general.

QUESTION: :
a weight lifter stands on a bathroom scale. she pumps a barbell up and down. what happens to the reading on the scale? SUPPOSE SHE IS STRONG ENOUGH TO ACTUALY throw the barbell upward. how does the reading on the scale vary now?
ANSWER:
When the barbell is accelerating up (which means going up and speeding up or coming down and slowing down) the scale reads more than the combined weights. When the barbell is accelerating down (which means going up and slowing down or coming down and speeding up) the scale reads less than the combined weights. If she throws the barbell up and it is not in contact with her, the scale will read her weight. (I assume that the scale can respond very quickly so it is really measuring the force her feet exert down on it at any instant.)

QUESTION: :
I was watching a documentary on Einstein, and contemplating his theory of relativity(and the recent debates on the speed of light being constant) and came up with a

QUESTION: , which while I am sure it is non-sense, still begs to be asked. Has/Can the speed of light in a vacuum, free of electromagnetic/gravitational anomalies ever been measured by two items that are truly at rest? This would seem, by its nature, to have to occur in space, with two items that are not moving with our solar system relative to the universe. It would also seem to need to occur between two man made items since all other objects in the universe are inherently in motion. Feel free to correct me if my assumptions on the requirement of the experiment are wrong. It would seem, though, that this would be the ultimate test of the speed of light being constant.
ANSWER:
Your whole idea does not hold water for one simple reason�there is no such thing as "truly at rest". (See earlier answer.) There is something called an inertial frame of reference where the laws of physics as we know them are true (things like Maxwell's equations, Newtonian mechanics, thermodynamics, etc.). Any other frame of reference which moves with constant velocity with respect to that one is also an inertial frame of reference, the laws of physics are exactly the same. There is therefore no experiment you can perform which distinguishes any of these as the "truly at rest" frame. The "ultimate test" of the constancy of the speed of light is that special relativity, for which that constancy is the cornerstone, works perfectly. Nobody feels any need to further test this; see FAQ page for more on why the speed of light must be the same to all observers.

QUESTION: :
I know about Einsteins theory of relativity and how nothing (even an affect like gravity) can travel faster then the speed of light. Does that mean, when I look up at a star at night, if i was able to instaneously travel to the star, it wouldn't actually be there because its light has taken us so long to reach us?
ANSWER:
No, it just means that it would not look like what you are seeing here on earth. Of course, there is no way to "instantaneously" travel anywhere.

QUESTION: :
A show about space stations were talking about a problem with communication with ground control because radio waves travel in a straight line. I wanted to know why do they travel in a straight line? I thought all EM waves spread spherically?
ANSWER:
How a radio wave is transmitted depends a lot on the design of the antenna. A point source (very small and more or less spherically symmetric) will send out waves that spread spherically, but since we generally do not wish to beam in all directions, an enormous amount of energy put into an antenna designed to look like a point source would be wasted. If instead we beam out in one direction by using a "dish" antenna (like the headlight of a car, for example), we can put our money where our mouth is (put our power where the receiver is, that is) and invest very little energy to send a signal. Another advantage is that the strength of the signal falls off very rapidly for spherical waves (like 1/r2) but maintains much more of its strength over large distances for a dish antenna. The disadvantage would be that you have to aim it at the receiver.

QUESTION: :
Will the coefficient of kinetic friction remain constant for a system, even if the mass and acceleration change?
ANSWER:
The whole idea of there being a coefficient of kinetic friction is an approximation. f=μkN is not a law of physics but an approximate and empirical statement that the frictional force is found experimentally to be approximately proportional to how hard the surfaces are pressed together and more or less independent of other variables (like the area of contact, the speed of sliding, etc. for example). But for normal conditions (in particular, N not too big) you may think of μk as being a constant.

QUESTION: :
I seem to have a paradox. Suppose we have 2 independent waves of amplitude A and energy E and in phase and travelling in the same direction coming from 2 lasers which are wired together. If we combine these 2 waves, by superposition, we will get a resultant wave with the same frequency and wavelength and amplitude 2A. Since the power of a wave is proportional to the amplitude squared and the frequency of all these waves are the same, the energy of the resultant wave should be 4E. However, by conservation of energy, the energy of the resultant wave should be 2E. Doesn't this violate the conservation of energy? Can't we get free energy?
ANSWER:
Well, this is the second time I have answered this

QUESTION: �I had to delete the first answer because it was flat-out wrong. Maybe I'll get it right this time. I have talked to a half dozen physicists, one of whom is an expert in laser spectroscopy and also does extensive computer simulations of electromagnetic wave phenomena. There are a few facets of the answer to the

QUESTION: , but the most important overview comment is that it turns out that the

QUESTION: technically violates my groundrule discouraging "

QUESTION: s based on unphysical assumptions". Of course, I am not criticizing the

QUESTION: er on this point inasmuch as it took me 3 weeks to decide that this was at the heart of why I was having so much trouble answering what seemed like such a straightforward

QUESTION: . I will try to address the facets of the answer with a bulleted list:
The

QUESTION: is posed as if we are looking at electromagnetic waves which are one-dimensional, like the idealized wave on a string. Physics texts do this all the time; so does Ask the Physicist�just look at an earlier answer where I even show a nice picture of such a wave.
Now, we need to make sure we know what is meant by "the power of a wave is proportional to the amplitude squared" as the

QUESTION: er states. This is almost right but it is the power flux, which is energy/time/area which is the integrated rate of energy flowing per square meter. Through zero area the power flux would be infinite because the area would be zero, so the whole amplitude squared thing would be of no physical consequence.
The bottom line, however, is that there is no such thing as a one-dimensional electromagnetic wave. Even if there were, we would not be able to satisfy the conditions of the

QUESTION: , putting two identical waves on top of each other, as I will argue below.
The light from a laser is, over the cross section of the beam, approximately a plane wave, that is the wave fronts are disks. This is a good approximation only away from the edges of the beam, so we will only use the center portion in our imagined experiment.
Now we come to the pi�ce de r�sistance. It is not possible to take the beams from two lasers, which are exactly alike in frequency and geometry, and put them together with their wave vectors parallel and perfectly in phase. (My laser expert agrees with this statement). You cannot shine the second laser through the first, for example. You might think you could do this with mirrors somehow, but those mirrors steering one beam will inevitably get in the way of the other beam. So the best you can do is have them almost the way you stipulate, coming together with the wave fronts almost parallel. Now there will indeed be places where the intensity over some small area is twice as large as the sum of the two laser intensities, but this does not violate energy conservation because there will be other places where there is zero intensity. If you integrate over the whole area which includes the intersection of the two beams, you get all the energy which came from the two lasers, no more, no less. In essence, you have the double-slit experiment.
Another word for energy/time/area is intensity and there is no such thing as conservation of intensity. A much more mundane example would be a lens: here we take a beam of light and focus it to a small spot hundreds of times more intense than the incident beam and do not worry about what that tells us about energy conservation.
One colleague advised me to tell you to just think of the two beams as being comprised of photons, each with a certain amount of energy and each indestructable, so energy has to be conserved. Of course, we both knew we wouldn't be getting any "free energy" anyway, didn't we?

QUESTION: :
Why does a superconductor have no resistance to a current. I mean what is the quantum state of a superconductor that allows it to have the properties that it has both with current and repultion of any magnetic field. Thanks for your time and hope to here from you soon.
ANSWER:
The basic idea is that, at low temperatures, electrons can pair up and these Cooper pairs become the current carriers. The theory of superconductivity is called BCS theory for its authors Bardeen, Cooper, and Schriefer; they won the Nobel prize in 1972. Although discovered in 1911, superconductivity was not understood until the 1950s. The mechanism for the more recently discovered high-TC superconductors is still not fully understood theoretically.

QUESTION: :
As an English major, you can imagine I've not done a whole lot of math. In movies and TV portrayals of mathematicians and physicists, we always see them working on blackboards with chalk or, more recently, on whiteboards using dry markers. These portrayal may well be stereotypes created by writers which have been emulated by subsequent writers. However, if these are true to life, why don't they use paper and pencil instead? I can think of a couple of likely reasons., but I'd like to know the real one.
ANSWER:
Sorry to disappoint you, but there is no "real one". Reasons to work at a board are that
science is often collaborative and this is a convenient way to show and share a train of thought;
it is easier to erase and revise than paper and pencil; and
some folks think better on their feet and while moving around.
Often the only contact with scientists that you humanities guys get is seeing us teach a class and we couldn't very well do that on paper and pencil. Finally, most scientists probably actually spend more time with paper and pencil or at a computer keyboard than at a blackboard.

QUESTION: :
I know that as an object moves though space it gains mass. Is there an equation to find the mass gained.
ANSWER:
If the mass of a particle at rest is m0, its mass m when traveling a speed v is given by m=m0/√(1-(v2/c2)) where c is the speed of light.

QUESTION: :
my

QUESTION: is about which equation properly governs the situation where an electron is approaching an electric field.
ANSWER:
I am not sure what you are after here. The force F felt by a charge q in an electric field E is given by F=qE and knowing the force you can calculate the motion of the electron. Since the charge of an electron is negative, the force it feels is opposite the direction of the field.

QUESTION: :
I am trying to calculate the force involved in one American football tackling another, assuming both are travelling at full speed and hitting head on, will it be the sum of the momentum of both players ?
ANSWER:
As I have explained many times before, there is no way to calculate the force from such information. It depends on the following:
What are the masses of each?
What are their speeds?
How long does the collision last?
What is the nature of the collision? Do they stick together? Or, if they bounce off, how much energy is lost?
FOLLOWUP

QUESTION: :
2 object collide, 1 weighing 210 lbs travels 6 metres at 9.52 metres per second with acceleration of 5.66 metres per second squared. It's force is equal to 1188.6 lbs per metres per seconds squared and it's momentum is 1999.2 lb metres per second the other object is 268 pounds, travels 4 metres at 8.49 metres per second with an acceleration of 4.51 metres per second. It's force is equal to 1208.68 lbs per metre per second squared and it's momentum is 2275.32 lb metres per second the collision last 1 second and is non elastic. What is the Impulse caused by the collision and how do i calculuate the force of generated during the collision ?

ANSWER:
Now, you have given me too much information! Since you give me masses and momenta and velocities, there is no need for the distances and the accelerations. Let me convert your weights to masses: 210 lb=95 kg and 268 lb=122 kg. Momenta:95x9.52=904 kg-m/s and -122x8.49=-1036 kg-m/s, so the momentum before the collision is -132 kg-m/s. Using momentum conservation for the collision and assuming a perfectly inelastic collision (stuck together), -132=(122+95)v so v=-0.61 m/s, that is in the direction the 268 pounder was going. So, the impulse delivered to the 268 pounder is equal to his change in momentum, J268=(122)(-.61-(-8.49))=961 Ns=FΔt where F is the average force during the time of collision Δt. Since you say the collision time is 1 s, the average force is F=961 N=216 lb. The other player feels the same force in the opposite direction.

QUESTION: :
Why do photons lack mass?
ANSWER:
Because, being the particle associated with electromagnetic waves which have no mass, they could not. Also, according to relativity, only a massless particle can go the speed of light.

QUESTION: :
Due to the length contraction, you notice that a passing train appears to be shorter than when it is stationary. What do the people in the train observe about you? If you are on a train that is going really fast, do the people on the ground look shorter, longer, or the same?
ANSWER:
Length contraction causes the lengths parallel to the direction of motion to be shortened. So, a fat man standing at the station would become a skinny man (side to side, but not front to back) but no shorter as measured by someone on the train. Similarly, as measured by someone on the platform, a fat lady standing on the train would become a skinny worman but no shorter. You will note that I did not say that these folks "look skinnier" because physicists normally do not care how something looks, they care about how something is. This is a very important distinction and one which even authors of physics books often fail to make. How something looks may be very different from how something is. Hence, your

QUESTION: is incorrectly stated ("appears to be shorter") although I believe I know what you meant.
I want to, in this answer, provide a very detailed discussion of how moving objects look (I will restrict this to one-dimensional objects like sticks moving along the direction of their lengths, directly toward or away from the observer). I will be able to refer to this answer when similar

QUESTION: s are asked in the future. When a physicist talks about the length of something, here is what he/she means: measure the positions of the two ends of the object at the same time; the difference of those positions is the length. When you look at a stick, you are not observing the stick ends where they were at one time but you are seeing the farther end as it was sometime earlier than when you see the closer end. Of course, this does not matter if the stick is at rest, but if it is moving it does matter. For everyday moving sticks, there is no perceptable change in the apparent length of sticks because speeds are much less than the speed of light. But what if the speed is really big, let's say 80% the speed of light? Then, as I will shortly show, the effect is really big. But before we go into how long the stick looks or appears, we better be sure we understand how long the moving stick is. The result from special relativity, using the definition of length I gave above, is that the moving stick is shorter by a factor of √(1-(v2/c2)), so if v=0.8c (i.e. 80% the speed of light), the length of the moving stick is only 60% its length when at rest. (This effect is called length contraction.) So now, the first picture shows the situation if the stick is coming toward you (you are on the right). Light (red arrow) leaves the far end of the stick and does not catch up with the near end of the stick until the stick has gone a long way (four stick lengths) and now light from the far (red arrow) and near (green arrow) ends move forward to your eye. So the stick looks to be 5 times longer than it actually is and 3 times longer than if it were at rest! Now, if the stick is moving away from you, the situation is very different. The moving stick is still 60% its at-rest length, but now the near end moves away to "meet" the light from the far end; the result is that the stick, as shown in the second figure, looks much shorter than it is. It now appears to be only 1/3 the rest length or 5/9 the actual (moving) length. Note that in neither case does the stick appear to be its actual length. (The scales of the two figures are different; note the different rest lengths. I had to do this so the "much-shorter" and "much-longer" figures would be about the same size.) So, maybe you can now understand why I often make a big deal about relativity being about how things are, not how things appear. The same kind of arguments may be made about time dilation: moving clocks run slower, they may or may not appear to run slower.

QUESTION: :
I am writing to you today to see if you can help me to understand the increase in velocity you are able to achieve by pumping a skateboard. I am not referring to pumping while inside of a pool or halfpipe, but instead pumping across a flat surface by carving back and forth left and right. How does this work?
ANSWER:
This is a bit involved, too much so for me to give a concise answer. The idea is much like roller skating, though, where you manipulate things so that the friction between the wheels and the ground is a force forward. There is lots of detail (including the physics) at silverfishlongboarding.com.

QUESTION: :
Re: The life cycle of matter. Does matter ever really disappear or does it simply change form? i.e - When something burns and produces heat, does the heat contain matter? Obviously heat dissipates but if it does contain matter, could that matter be reconstituted into something else later? Bottom line, is our universe a never ending cycle of matter into energy and energy into matter?
ANSWER:
The crucial idea is simply that mass is simply a form of energy and the total energy of an isolated system does not change. When something burns, the released energy is in kinetic energy of the reaction products (they move faster). This energy came from chemistry, specifically the binding energies of molecules. The root source of this energy is mass and a tiny amount of mass disappears when you burn something. It is very small because chemistry is really a poor source of energy. Nuclear reactions, fission and fusion, are a much better source of energy and there you can rather easily measure the loss of mass of a nuclear system which releases energy.

QUESTION: :
what percent of its hydrogen mass could the sun actually convert into helium?
ANSWER:
About 0.8%. That is how much mass is converted into energy in the fusion process.

QUESTION: :
does a single photon produce an interference effect or not?
ANSWER:
Yes. If you have a slit and a photon passes through it, the photon may end up being "deflected", that it will be diffracted. To see the single slit diffraction pattern, however, you need very many photons to "flesh it out", but you can send them through the slit one at a time so the interference is not with other photons. In essence, you must acknowledge the duality of the radiation, it is both a photon and a wave, and interference effects are manifestations of the "waveness".

QUESTION: :
Phobos, one of the moons of mars, orbits at a distance of 9378km from the center of the red planet. What is the orbital period of phobos? I would easily know how to do this if I was given the mass of mars, I am unsure if I am simply expected to look that up, or if there is a way to solve for this/ solve around this? T= 4pi2r3/GM
ANSWER:
Your equation is wrong, should be T2=4π2r3/GM; that is Kepler's third law. Yes, you do need the mass of Mars (6.42x1023 kg) to do this calculation.

QUESTION: :
This is quite possibly a fizzics

QUESTION: rather than a physics

QUESTION: , nonetheless, I ask you: Why don't sodas retaining their fizz like they used to? Is it the recipe, something to do with the planet, the atmosphere or what? How on earth can we get back our fizz?
ANSWER:
Funny, I have not noticed this at all. Maybe it is a case of misplaced nostalgia on your part? When I was a kid I thought Twinkies were delicious but when tried years later�well, yuk! How on earth can I get back my delicious Twinkies?

QUESTION: :
If I drop an object into a pool of water, is the wave generated proportional to the size of the object dropped? Example, if I drop a 1" and 4" ball bearings into a pool of water, will the the wave projected by the 4" ball bearing be 4X bigger than the wave generated by the 1" ball (keeping in mind that the 4" bearing is 4X heavier than the 1" bearing). Also, how does the height from which and the ball bearing is dropped affect the size of the wave?
ANSWER:
This is a problem which is very difficult to try to solve exactly because of the complicated way in which the dropped ball interacts with the water. If we assume that each ball were to give all its energy to the wave generated, we can make an estimate. First of all, your statement that "the 4" bearing is 4X heavier than the 1" bearing" is wrong. The weight will be proportional to the volume, not the radius (V=4πR3/3), so the 4" ball will be 64X heavier than the 1" ball. Therefore the energy that each ball brings to the water will be in the same proportion (64:1) if they are dropped from the same height. So the larger wave would have 64 times more energy. The energy of a wave is proportional to the square of the amplitude (the height of the wave); or, the height of the wave is proportional to the square root of the energy. Therefore, the 4" ball would make a wave 8 times bigger than the 1" ball but only if all the energies went into the waves which is certain not to be exactly the case. (Incidentally, if you were particularly interested in the relative wave heights for one ball 4 times heavier than another, it would be a factor of 2.)

QUESTION: :
I heard that you can die or pass out from an acceleration beyond 4 or 5 g's. Does this mean that if you are going, say 5 miles per hour, and you decelerate greater than 5 g's you could pass out?
ANSWER:
Your numbers are a bit low. Fighter pilots routinely experience around 10g in tight turns but they do wear special suits to help the blood being pushed from the brain causing loss of consciousness. Also, duration is an issue; you will not pass out immediately. Certainly the case you state will not cause you to pass out; the time to stop would be only about 0.05 seconds at an acceleration of 5g. Whatever was restraining you, though, might cause pain but you would not pass out from the acceleration. Finally, you will certainly never die from a 5g acceleration. You might read Wikepedia for more information on g-forces.

QUESTION: :
Why is kinetic energy a scalar even though it contains v in the formula which usually means a direction involved?
ANSWER:
Well, partly by construction; energy is defined in such a way that it is a scalar quantity. But the easiest way to answer the

QUESTION: is to note that the way v appears is as v2 and v2 is the scalar product of the vector v with itself, v�v=v2.

QUESTION: :
Why must a horizontally moving projectile have a large speed to become an Earth satellite?
ANSWER:
Because the harder you throw something horizontally, the farther it will go until eventually it will go all around the world. Newton realized this and discussed it in his famous book Principia. You might enjoy an applet which uses Newton's original sketch.

QUESTION: :
We are studying free-body diagrams. Say an object is tossed into the air and then reaches its highest point, does this mean that all the forces acting on the object are balanced?
ANSWER:
Absolutely not. You cannot tell whether an object is in equilibrium by knowing its velocity; its acceleration will tell you this. In this case, the object is at rest but an instant earlier it was not and an instant later it will not be. It is therefore accelerating and there must be an unbalanced force; this force is the object's own weight which does not disappear just because it stops for an instant.

QUESTION: :
Why does a bouncy ball bounce back up after it huts a surface?
ANSWER:
During the time the ball is in contact with the surface it is experiencing an upward force greater than its own weight. This force causes the ball to have an upward acceleration (Newton's second law) which causes it to acquire an upward velocity after the force has momentarily stopped it.

QUESTION: :
Does an electric arc generate an electromagnetic field??? Can a electric arc be be generated in complete vacum, for example in open space???
ANSWER:
Do three

QUESTION: marks make a

QUESTION: more pressing? Just kidding! Yes, an arc has electric charges in it and these charges are moving, so there will be fields generated. In fact, many of the electric charges have acceleration and so electromagetic waves are also generated. This is the origin of static on AM radio during thunderstorms. Also, Marconi, the discover of radio transmission, used spark gap transmitters to send his earliest radio signals. Since an arc is a plasma breakdown in the gas, it cannot happen in a vacuum. What can happen is corona discharge, where the electric field becomes sufficiently strong at the surface of a metal that electrons stream into the vacuum.

QUESTION: :
In two boys of unequal weights running towards each other with the same speed meet lead-on what is the result of the collision?
ANSWER:
It depends on how elastically they collide. For example, if they stick together after the collision, they will move in the direction of the heavier boy. In any case, the two will both move in the direction of the heavier boy after the collision.

QUESTION: :
"The laws of physics are the same for all observers in uniform motion relative to one another." But theoretically if one had a space shuttle that could travel at 2% the speed of light and on board it had a particle accelerator the could compensate for 99% the speed of light then relative to an observer out side the craft wouldn't the particle at times be moving at ~101% the speed of light. Why is this impossible?
ANSWER:
I have answered this

QUESTION: before. It is also linked to on the FAQ page.

QUESTION: :
Physics books and physics professors routinely explain gravity with the Einsteinian theory, that mass warps space. I have no evidence to dispute that and I have no reason to doubt it. My problem is with the model commonly used to illustrate it. A rubber sheet with a steel ball on it, hence gravity warped. If the universe were two dimensional then the analogy would make sense to me. Since the universe is at least three dimensional, then to be a valid model and become three dimensional, the warped rubber sheet has to be rotated through infinitely small arcs through 360 degrees at right angle to the plane of the rubber sheet before warping by the ball. When that is done the warping shape disappears. Remaining is possibly a model of density gradation but not of warping. If that is true then the model of the rubber sheet analogizes nothing, in my opinion. I would appreciate enlightenment if I am missing something.
ANSWER:
See an earlier answer.

QUESTION: :
A friend of mine and I have an argument over what is a faster sport tennis or badminton. The criteria is how fast it would take to serve a tennis ball/shuttlecock from one side of an olympic sized tennis/badminton court to the player waiting on the other side assuming that both are standing on the out of bounds line. We are assuming ideal conditions and that the players in both cases are equally strong and fast.
ANSWER:
You may not realize it, but your

QUESTION: is mostly about air drag on projectiles. I seem to get more

QUESTION: s about air drag than just about anything else except maybe variations of the twin paradox. Maybe that is because it is perhaps the most important phenomenon mostly swept under the rug in most elementary physics courses. There are several instances of earlier

QUESTION: s involving baseballs and lacrosse balls which are very similar to this one. For high speed projectiles, air drag is very important; e.g., a 100 mph baseball loses about 10 mph by the time it crosses the plate. Approximations have to be made to quantify the situation you are interested in, but I feel the results I will present are pretty close to what happens on the court. (The following is probably way more detail than you want, but I put it here for anybody who might be interested.)
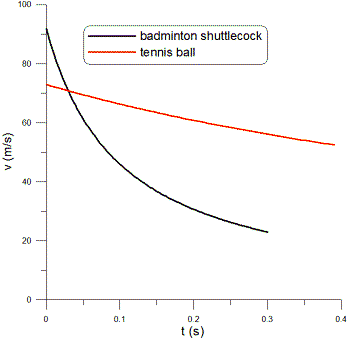
The approximations are:
I neglect gravity because the times involved are are sufficiently short that the ball/shuttlecock will not fall far or very much change its vertical speed.
I assume that the drag is proportional to the square of the speed�twice the speed, four times the force of drag. This is an excellent approximation for these speeds, these objects.
The form of the force I use is F≈�Av2 where A is the cross sectional area presented to the wind. Here A=πR2 where R is the radius of the ball or the outer circle of the feathers. This probably slightly overestimates the force for the tennis ball (whose "hairs" have the function of decreasing the drag) and underestimates it for the shuttlecock (whose "feathers" are designed to increase drag).
Data for tennis:
v0=73 m/s=163 mph
R=0.032 m=1.26 in
m=0.057 kg=2 oz
back line to back line distance: 24 m
Data for badminton:
v0=92 m/s=206 mph
R=0.025 m=1 in
m=0.005 kg=0.18 oz
back line to back line distance: 13.4 m
I used the fastest recorded serves for the velocity off the racquets, v0. If you integrate F=ma, you get the following solutions: v=v0/(1+kt) and x=(v0/k)ln(1+kt) where k=�Av0/m. Here are the results:
The tennis ball takes 0.39 s to travel the distance, arrives with a speed of 62 m/s (139 mph), a loss of 11 m/s (24 mph).
The badminton shuttlecock takes 0.30 s to travel the distance, arrives with a speed of 25 m/s (56 mph), a loss 67 m/s (150 mph).
I will leave it to you to argue about what these numbers tell you about which "is the fastest sport". The shuttlecock starts off the fastest because is has a smaller mass and can therefore have a larger acceleration from the force from the racquet. But it slows down very rapidly mainly because of its small mass. The graph shows the speeds as functions of time.

QUESTION: :
What is the origin of the word "magnet"? I have heard that there are two different explanations. I have found a lot of information referring to the ancient Greek city of Magnesia and a Shepard named Magnes. Is there any other possible explanation?
ANSWER:
From the Online Etymology Dictionary:
magnet
mid-15c. (earlier magnes, late 14c.), from L. magnetum (nom. magnes) "lodestone," from Gk. ho Magnes lithos "the Magnesian stone," from Magnesia, region in Thessaly where magnetized ore was obtained. Spread from Latin to most W. European languages (cf. Ger., Dan. magnet, Du. magneet, It., Sp., Port. magnete), but superseded in Fr. by aimant.

QUESTION: :
In a pendulum there is a force exerted on the mass by the string but why doesn't this force contribute to the energy of the pendulum? Is the force of the string simply counteracting the force of gravity?
ANSWER:
In order for a force to add or subtract energy it must do work. The tension in the string is always perpendicular to the motion of the mass and so it does no work.

QUESTION: :
The speed of wave works it way up the spectrum (i.e. sound, rf, microwave, light etc) The deeper the sound the slower and conversley the higher the sound the faster the wave. When measuring light speed, what "color" is used as the optimal for speed? I would have to assume InfraRed would be the fastest but that does not necessarily mean it is the benchmark used for determining the speed of light. Also is the variance in speed between ultraviolet and infrared a measured value? I know you can find the wavelength with a quick search, but are the differences in speed of the wavelengths a measured factor? (Yes, we often have some "off the wall" conversations at lunch)
ANSWER:
You start with a statement, not a

QUESTION: , which is wrong. First, sound is a completely different thing from the others you have listed. The speed of sound in air is independent of frequency; if this were not true you would not be able to listen to music because the different pitches would reach you at different times. In some media, there might be a slight difference but it is a very small effect. Electromagnetic radiation (all your other examples, rf etc.) is completely different from sound; sound is propogation of pressure variations in a medium like air whereas EM radiation is a traveling fluctuation of electric and magnetic fields. EM waves in a vacuum all travel with precisely the same speed, 3x108 m/s=186,000 miles per second. It does not matter if it is a radio wave from your local AM station, a microwave in your oven, the light you can see with your eye, or an x-ray to check your arthritis�all have the same speed. In a material, like glass or water, for example, light goes a bit slower and there is a slight difference for light with different colors; you stated that higher frequency waves have larger velocities, but actually it is the other way around. The slight difference in materials is called dispersion and it is the explanation for rainbows, prisms splitting white light, and pretty diamonds. To a very good approximation, though, the speed of light (and all other EM radiation) is independent of frequency; when the speed of light is referred to, it usually means the speed in a vacuum. Toss that all around at lunch!

QUESTION: :
At the Large Hadron Collider at CERN what is the mass of a proton at it's maximum speed, what kind of gravity is produced by that mass?
ANSWER:
The proton energy is about 7 TeV=7x1012 eV. The mass is given by m/√(1-(v2/c2)) and, for this energy (see answer below to see how to calculate this), 1/√(1-(v2/c2))≈7000, and so the mass is about 7000 times greater than the mass of a proton at rest. The gravity of such a mass is totally negligible. The mass is only about 10-22 kg, much heavier than a proton but much lighter than a speck of dust.

QUESTION: :
Will a car go faster if the body is 2" off the ground are 4" off the ground
ANSWER:
There is no way to answer this

QUESTION: .
FOLLOWUP

QUESTION: :
If a nascar car's front spoiler were raised 2 more inches in order to let more air pass underneth the car would they go faster?
ANSWER:
I guess I did not give enough detail in my first answer! The aerodynamics of a car can be very complicated and often not intuitive. This is a very difficult engineering problem and much computer time and wind tunnel time is usually consumed studying how best to design a vehicle to minimize drag. The various parts of the vehicle interact with each other and so messing with one part affects the way other parts contribute to drag.
Here is an anectdote which illustrates that your intuition is not always right regarding drag. Some years ago somebody called in to Car Talk on NPR and asked about these nets you can buy to replace the tailgate in a pickup truck to reduce air drag. Makes sense, right? The tailgate is like a wall in the wind and to get rid of it will reduce drag and increase your mileage. Click and Clack said that they thought these things were a great idea for reducing drag and increasing fuel efficiency. During the intervening week before the next show an engineer from GM called in and told them that removing the tailgate in fact greatly increases the overall drag on the truck. The reason is that the tailgate traps a bubble of air which rides along with the truck and the headwind slips over it. There was a lot of crow-eating that week at Car Talk Plaza!

QUESTION: :
Is the downward pressure of where a cars tire and the surface of the road meet the same when the car is moving 60 mph, or not moving at all? I had a friend tell me he drove across a frozen lake and could hear ice cracking while he drove 60 mph and made it to the other side. The lake was about 1 mile across and thinner ice toward the middle because of a creekbed that runs the lenght of the lake. everybody else just laughed in disbelief.
ANSWER:
The force the wheels exert down on the ice will be equal to the weight of the car regardless of whether the car is moving or not. If, indeed, the weight of the car was big enough to break the ice, then the explanation you seek is likely that it takes time. That is, if the car is placed on the ice at rest, small cracks will start to spread, get bigger until the ice fragments and the car falls through. If moving, the network of cracks likely would not have time to spread enough to sufficiently weaken the ice.

QUESTION: :
An electron accelerates through a potential difference V = 1000 keV. How do we find the speed of electron?
ANSWER:
When an electron, charge e=1.6x10-19 C, accelerates through a potential difference V, the kinetic energy acquired is K=eV. The energy acquired when accelerated through 1.0 V is 1.6x10-19 J and this amount of energy is also called 1.0 electron-volt (eV). You are asking to accelerate an electron across 1000 kV=1,000,000 V (you say keV, but you want to specify the voltage in kV, not the energy) which is 106 V, so K=1.6x10-13 J. It is now tempting to just set K=�mv2 and solve for v, but, if you do (m=9x10-31 kg), you will find that the speed is greater than c, the speed of light! The classical expression for kinetic energy is only true if the speed of the particle is much less than c. The correct relativistic expression for K is K=E-mc2=mc2[(1/√(1-v2/c2))-1] where E is the total energy and m is the mass of the particle at rest; it may not look like it, but this equation reduces to K≈�mv2 if v is much smaller than c. Before I finish your calculation, I will give you a handy-dandy way to determine whether you need to use relativity or not in this kind of calculation. If the kinetic energy is much less than the rest mass energy (mc2) of the particle, you may safely approximate K=�mv2. For your example, K=1 MeV and, for an electron, mc2=0.51 MeV (electron volts are a much more convenient unit of energy than joules for elementary particles); so, for your problem, the kinetic energy is twice the rest mass energy, so you have to use relativity to compute the speed. So, from our equation above, 1=0.51[(1/√(1-v2/c2))-1]; solving, v=0.94c=2.8x108 m/s, 94% the speed of light.

QUESTION: :
If you took an electron away from Iron would it still be Iron? I know if you took a proton away it would not be iron and if you took a neutron away it would still be iron,
ANSWER:
It is still iron but is now an iron positive ion, Fe+.

QUESTION: :
The scenario is three car collision. Car 1 is first in line in stopped traffic. Car 2 is stopped behind Car 1. Car 3 fails to stop and runs into Car 2, pushing Car 2 into the back of Car 1. Car 3 was the 100% cause of the accident, yet the driver of Car 1 says he felt "2 impacts." How is this possible?
ANSWER:
I am sure there could have been several ways this could have happened. Here is one that occurs to me. Car #3 is heavier than car #2 and their bumpers are sort of elastic; so car #2 rebounds forward but car #3 keeps going but with a reduced speed. Car #2 hits car #1 and both stop. Car #3 hits car #2 for the second time and then car #2 hits car #1 for the second time.

QUESTION: :
One of the most accurate clocks ever, I recently read, is accurate to one second in the next 3.7 billion years. Minutes before, I read an article about the discussion of whether time exists in the universe or not, and if so, how it exists in our world. My

QUESTION: is: Is it even possible to have a perfectly accurate clock? Furthermore, is it possible to keep that clock in a fixed point in space so it remains accurate?
ANSWER:
I am sure the article about whether time exists was interesting, at least philosophically. But if we are going to discuss clocks, I guess we need to assume that it does exist since a clock measures something. Our current understanding of time, based on the theories of special and general relativity, tells us that the rate that time ticks depends on two things, the speed of the clock relative to the observer and the gravitational field the clock is in (or, equivalently, if the clock is accelerating). If we construct a clock in a particular frame of reference such that it is at rest with respect to us, with a constant acceleration and/or gravitational field, the accuracy of the clock is ultimately determined by quantum mechanics. A time can not be measured with arbitrary accuracy because of the Heisenberg uncertainty principle, ∆E∆t≥h/(2π). Precision measurents of time always depend on having some precisely known energy, such as the energy of some atomic state, so the uncertainty in the energy is linked to the uncertainty of the time measurment. The clock will remain accurate to its design specifications in the frame where it started. Change the gravitational field (by changing its altitude, for example) or make it move, and it will not continue running at the rate it would have if left alone. One of the reasons we need such accurate clocks is that without them GPS would not work.

QUESTION: :
What are Alpha Particles, Beta Particles, and Gamma Rays? What is the differance between them?
ANSWER:
Alpha particles are the nuclei of 4He atoms, consisting of two protons and two neutrons. Beta particles are either energetic electrons or positrons. Gamma rays are energetic photons (electromagnetic radiation).

QUESTION: :
When we heat a metal, the positive kernels begins to vibrate.Will this vibrations produce electromagnetic waves ?
ANSWER:
All objects are continually radiating (and absorbing) electromagnetic radiation. Until they get very hot, however, they do not radiate in the visible range.

QUESTION: :
Imagine we are in a space craft which is moving with a constant velocity in empty space. If we are not influenced by any gravitational forces, and if we restart the engine, will it be accelerated ?
ANSWER:
Yes, of course. This is what classical physics is all about�an unbalanced force causes an acceleration.

QUESTION: :
Say there is a father and son. The father is the first astronaut to attempt to "time travel" into the future by flying his rocket around a black hole at extremely high velocities, so that for a given period of time (say an hour) it is a lot longer on earth (say 10 hours). My true

QUESTION: is, if the father could somehow communicate to his son in real time, what would this conversation sound like? Would the son hear his dad talking extremely fast? or would the distance between them make up the distance in "time travel". If it was the distance that is the factor, what if the dad was on a super train traveling at similar speeds on Earth?
ANSWER:
Below I have copied a figure from my earlier answer where I talk about the twin paradox, the situation you allude to in your

QUESTION: . Here there are specific numbers (given in the caption) to make it concrete. As explained in the earlier answer, the traveling twin (the father in your

QUESTION: ) takes 6 years to go each way while the stationary twin (son) has ten years elapse. Each (father and son in your case) sends out one light pulse each year and by looking at the spacing of those pulses you can deduce how a conversation would sound. Here is a summary of how each sounds to the other:
On the trip out, the father hears the son slowed down by a factor of 3 (2 yearly signals from home in 6 years).
On the trip home, the father hears the son speeded up by a factor of 3 (18 yearly signals from home in 6 years).
For the first 18 years, the son hears the father slowed down by a factor of 3 (6 yearly signals from dad in 18 years).
For the last 2 years, the son hears the father speeded up by a factor of 3 (6 yearly signals from dad in 2 years).
Of course, it cannot really be a conversation because of the long transit times of the signals; rather each is just speaking, reciting poetry or something. Higher speeds would lead to more extreme numbers but similar conclusions. Overall, note that the father has aged 12 years while the son has aged 20 years. I always like to emphasize that how time appears to elapse on a moving clock is not the same as the time which actually does elapse; for example, during the last two years for the son, the father's clock looks like it is running faster than the son's whereas it actually is running slower.

QUESTION: :
If I understand it correctly, Hubble stated that the further away a galaxy is from us the higher its red shift and therefore the faster it is moving away from us. My

QUESTION: is if the galaxy is 5 billion light years away the light we now receive is also 5 billion years old. To me that would indicate that the galaxy was moving away from us 5 billion years ago. How do we know if that galaxy is still moving away from us?
ANSWER:
We do not know what the galaxy is doing right now. Information cannot travel faster than the speed of light, and so there is no way to know what it is doing right now. We can make a very intelligent guess based on the systematics of many galaxies at different differences, but we cannot "know".

QUESTION: :
Is it possible that the earth and everything in the universe has mass just because they are moving?? How is it possible to know that a spacecraft in space is still or not if everything else in the universe is in motion??
Is it possible that the speed at which we (humans) perceive time depends on the intelligence of humans?? Could it differ based on individual IQ? And is it possible to disprove this??
ANSWER:
No, that is not possible because "moving" has no absolute meaning. This is one of the fundamental cornerstones of physics, both classical and relativistic. If you find the laws of physics (mechanics, electromagnetism, etc.) in one frame of reference, then any other frame of reference which moves with constant velocity relative to yours has exactly the same laws of physics. So there is nothing which defines what "still" means.
Regarding your second

QUESTION: (s), physicists have no interest in how time is "perceived". We define what we mean by a time interval; how it appears or is perceived is a subjective thing which has no quantitative value for a scientist. (Well, if a psychologist is a scientist, she might be interested!) A time interval is the difference between two time measurements at the same point in space; length is the difference between two position measurements made at the same time.

QUESTION: :
I recently read in the NY Times Science News section that a groundswell of physicists are challenging the law of gravity, saying what we are really observing is ENTROPY (disorder) when an object drops. What say you?
ANSWER:
I read that and it was interesting. Let me give you my overview, from the perspective of a nonspecialist in the field of gravity. For more than 200 years, gravity was thought to be understood, F=-GMm/r2, � la Isaac Newton. Then, in the early 20th century (ca. 1918), Albert Einstein published the theory of general relativity which gave us a much deeper understanding of gravity in terms of the warping of space time by mass. But, as the 20th century progressed, quantum mechanics was developed to great success; it seemed that all fields needed to be "quantized" at small distances, and so it was natural to seek a theory of quantum gravity. To this day, there is no successful theory of quantum gravity. Hence, gravity continues to be one of the hottest areas of physics and the thermodynamic view of gravity, very nice, is one of many attempts to better understand this rich field (the proponents can hardly be described as a "groundswell", however!) To further muddy the gravitational waters, the recent "discoveries" of dark matter and dark energy are still not understood. There are lots of ideas of what they are, but my own feeling is that, until somebody starts actually observing and measuring a new kind of dark matter particle, they are possible symptoms that we do not understand gravity as well as we think we do.

QUESTION: :
Why do charges reside on the surface of a conducting sphere? Why not inside it? Do charges gained by a conducting sphere not distribute equally all through the body?
ANSWER:
The definition of a conductor is that electric charge inside is free to move. For electrostatics, all charge at rest and in equilibrium, this implies that the electric field inside a conductor must be zero. Any charge inside a conductor will cause there to be an electric field; only by having charge on the surface can you find a solution where there is no field inside. You can have charge inside a conductor, but it cannot be static.

QUESTION: :
say we have a room that the length from wall to wall is the distance that light can travel in 2 seconds. on one side we have a flashlight. we flip it on for only a second would the light hit the farthest wall or would the light only reach the middle?
ANSWER:
Your room is 2 light seconds long. You create a pulse of light waves which is 1 light second long and which travels toward the other wall for 1 second and then illuminates it for 1 second.

QUESTION: :
I thought Specific weight = density x acceleration of gravity. Why do I keep seeing the same values for specific weight and density for water, i.e. 1000 kg/m3 or 62.4 ibs/ft3?
ANSWER:
Your definition is correct, it is weight/volume=mass density times g. So, wherever you see 1000 kg/m3 is wrong; this is a mass density. 62.4 lb/ft3 is correct since weight may be measured in pounds. Specific gravity is density/density of water, so specific gravity of water is 1.

QUESTION: :
I was watching the movie Open Range yesterday and there was a scene from the movie where a guy shot his gun at another man and the man who got shot went flying 10 feet back. My dad says the shooter should have also went flying 10 feet back according to Newton's Law because every actions has an equal and opposite reaction. Does size and weight of either man matter in how far either one would have flew back? Could the one being shot fly back further than the shooter if he was a smaller man?
ANSWER:
Just Hollywood drama! If the gunner did not jump back similarly, the gunned should not either. I did a quick calculation and found that the recoil should be about 0.04 m/s for a typical bullet hitting a 200 lb man. The recoil from a typical hand gun as well as the recoil of the victim is negligibly small.

QUESTION: :
what if you have a cart that is going up an inclined plane, and then it comes back down due to gravity; is the acceleration the same?
ANSWER:
Only in the ideal case of no friction. If there is friction, the frictional forces flip directions depending on up or down whereas other forces do not. So the net force along the incline will be different in the two cases leading to different accelerations.

QUESTION: :
Hi, I am a high school senior learning about the Biot-Savart Law. However, that law only applies for circuits but I was not taught any expression for permanent magnets. I have done some research on the Internet, but I have not found anything. I am curious to know if there is any formula for magnetic field strength in permanent ring magnets as a function of distance away from the center.
ANSWER:
Every permanent magnet may be represented by an equivalent distribution of currents, but that depends on how the magnet is magnetized. So, the answer to your

QUESTION: is that, no, there is no handy-dandy expression you can use to get the field. Qualitatively, what I mean by magnetization is the following. A permanent magnet may be thought of as a large number of aligned tiny (atomic size) bar magnets. So, one way you could magnetize a ring would be for all the north poles pointing away from the axis. Another way would be to have all the north/south poles pointing parallel to the axis with all the north poles pointing in the same direction. You can see, I am sure, how these two different magnetized rings would have very different fields. You need to check with the manufacturer to see what your particular ring magnet's field is like.

QUESTION: :
Does light produced by sun and that hits the surface of the earth, come from a specific section of the sun's surface. Or does the earth receive light from every area of the sun that faces the earth.
ANSWER:
You see light from the whole side of the sun facing us. If you did not receive light from a part of it, you would not see it at all. Each point on the surface acts like a point radiating light in all directions out.

QUESTION: :
Quantum Mechanics says that until we make a measurement of a particle (an electron, say), we really only know the probability of where it's located and, in addition, there is a non-zero, however small, probability of it being anywhere (although some locations will definitely have larger probabilities). Hope I'm making sense so far. Now, it occurred to me that when I see the trackings of a cloud chamber, don't we "know" then where the particle was over a period of time? Is the cloud chamber really, in some sense, taking a measure of the particle, thus collapsing the wave function? If so, since we see it over a course of time, is it making continuous measurements?
ANSWER:
"Collapsing a wave function" usually refers to putting a quantum system, originally in a superposition of many possible discrete states, into a single one of them. Position is not "a discrete state" since you cannot put the electron to a perfectly precise position because of the uncertainty principle. What you are doing with a cloud chamber is making succesive (not continuous) position measurements but even this is not what is happening because it takes some time for the condensation on the ion to occur so the electron will be long gone before you see a place where it was. At best, this just lets you visualize where (roughly) the electron was as it went through the chamber. If you put a magnetic field in the chamber and measure the curvature of the path, you can deduce the momentum of the electron. Rather than thinking of "collapsing" the wave function, I would think of "focusing" it. Before I made any measurements, I was totally ignorant of both the position and the momentum of the electron; after I watch its track in the cloud chamber, I now have a better idea of its position and momentum.

QUESTION: :
why does the golf ball whitch weighs about 18 times more then a ping pong ball fall at the same times or other words hit the ground at the same time if you drop them from the same distance
ANSWER:
Actually, a golf ball and and ping pong ball will likely hit the ground at noticeably different times if dropped from a height of more than a couple of feet. You have been told that the acceleration due to gravity is the same regardless of weight; see my earlier explanation why this is true. But, if there are other forces on the balls, they might have different accelerations. One force which is always present when an object moves through air is air drag. There is an earlier answer where I discuss the nature of air drag for balls. If you read that, you will see that when there is air drag, which gets bigger as the object goes faster, the ball will eventually stop speeding up and just drop with constant speed; that speed is called the terminal velocity and does depend on the mass. I did some rough calculations and found that the terminal velocity of a golf ball is about 20 m/s and the terminal velocity of a ping pong ball is about 5 m/s. It turns out that it only takes a freely falling (with negligible air drag) dropped object about a half second to reach 5 m/s and it does so after falling about 1 meter. So, dropping the two balls from more than a meter or so will result in the golf ball winning the race to the ground. Incidentally, the terminal velocity also depends on how large the object is and so you cannot simply assume that the more massive will win. A parachute, for example, will have a much bigger mass than a golf ball but will surely lose a race to the ground.

QUESTION: :
Do all particles decay? I understand that some, e.g., the proton, have very long expected lives. But are there any particles that are known (to the extent that theory can know these things) not ever to decay? What about quarks and photons? This site says that guage and higgs bosons are stable. Does that mean that they never decay? A related

QUESTION: is whether there are any particles that are indestructible, i.e., no matter how much energy is applied to them, they can not be forced to fragment into components or combine with something else and in doing so lose their identity?
ANSWER:
Electrons do not decay. Photons do not decay. Protons do not decay (although we are not really sure about that). I do not think positrons decay. Yes, stable means they never decay. Just because a particle is stable does not mean you cannot destroy it or make other particles from it. A simple example is bringing a positron and electron, both stable, together; you end up with two photons (usually).

QUESTION: :
Where is the proton? When using an accelerator to fire a proton into a target does the proton or just the energy of the proton get delivered and the actual proton stay in the accelerator.
ANSWER:
The proton and its energy are "in the same package". What happens to the proton itself depends on how it interacts. The proton can just scatter off something elastically, that is it just bounces off with most of its energy; the proton can interact with a nucleus and excite it and leave the scene with some of the energy it came in with; the proton (if sufficiently energetic) can create new particles and disappear itself (or not); the proton can get absorbed into some nucleus and just disappear; the proton can fly right on by and do nothing (this is what happens in the overwhelming majority of the time). In most accelerators, the beam is deflected out of the accelerator and focused on the target. None of these protons ever get back into the accelerator. In a collider accelerator, the particles which do nothing may be recirculated and come back later for another pass.

QUESTION: :
this is what it said about radio waves on wikpedia "although commercially important uses of radio use only a small part of this spectrum" what is the small part of that spectrum between 30kHz and 300 GHz that is most commonly used?
ANSWER:
Frequencies used is not really physics, it is just how the use is allocated by government agencies. Here is a chart which shows allocated frequencies.

QUESTION: :
My

QUESTION: is about gravity... In the depictions I have seen of the Einstein model of gravity, planets and stars are shown as depressing a plane of time space into a well like depression into which other objects tend to fall I am ok with this depiction However, it seems to make the assumption that space is a plane and has only two dimensions When I observe the universe, I see three dimensions It would seem to me that these "gravity wells" should exist in three dimensions not the two generally depicted In the two dimensional illustrations, these gravity wells seem logical and simple...the sun for example presses down to form a depression in the two dimensional plane and the earth falls in towards it in an orbit But space is not two dimensional These "wells" or depressions should exist in an infinite number of orientations in a three dimensional space Why are they only shown as if the fabric of space is like a sheet of paper, in two dimensions and not in an infinite number of orientations as would be the case in a three dimensional space?
ANSWER:
My stock answer to this kind of

QUESTION: is that the "trampoline illustration" of deformed space-time is meant to be a cartoon to illustrate the idea, not an accurate rigorous representation of the theory of general relativity. You must not take it too seriously or literally. It is also practically impossible to draw a picture of deformed three-dimensional space. To draw deformed 2-D space is easy because you use the third dimension to show the deformation; to draw a deformed 3-D space would require a fourth spacial dimension which cannot be drawn.

QUESTION: :
I have searched on the internet and can't seem to find an answer to what I thought would be simple aerodynamic

QUESTION: s. The first one is, unlike a regular airfoil surface, why does a spinning horizontal cylinder produce lift? I've seen several articles mentioning this effect, but without explanation of the dynamics. I understand that moving air produces a low pressure over an object, but since a cylinder is spinning and air is moving all around it on all sides, wouldn't the pressure differential be canceled out? If it is spinning clockwise, as the right side is turning downward, the left side is turning upward. I would think this would cancel any lifting effect. Also, would a sphere that is spinning, not top to bottom, but around like a top, produce lift or low air pressure at the top? Does the orientation of the spinning matter for lift effects, as long as the surface is moving?
ANSWER:
The cylinder must also be moving forward through the air. There is a nice NASA article about this "wing". Now that you know how it works, you see that a sphere spinning on a vertical axis would not work to give lift but, if moving through the air also, would result in a sideways force (a slider in baseball, I believe). Yet another example is if you put topspin on a tennis ball, it curves down.

QUESTION: :
I know that the electromagnetic field propels electrons around the nucleus and that the strong force binds the atomic nucleus together. BUT, are electromagnetic particles found INSIDE the nucleus?
ANSWER:
It is really not correct to say the electromagnetic force "propels" the electrons in the atom; but, let's not split hairs, the electrostatic force binds the atom together. The nucleus is composed of protons and neutrons, the protons having positive electric charge and both neutrons and protons having magnetic moments (they look like tiny magnets). Because the strong force is much stronger than the electromagnetic force, it holds nuclei together in spite of the fact that the repulsive electromagnetic force is trying to blow the protons apart.

QUESTION: :
Ok. This

QUESTION: has been bothering myself, my Dad and a couple of my friends for weeks now, and we just can't seem to come to a logical answer. So here goes: You are travelling in a car at 100mph. You have a gun which launches the bullet at 100mph. Firing the gun directly forward (the direction you are travelling) causes the bullet to move at 200mph (This bit we think we got right... please correct us if we are wrong). However. If you fire the gun directly behind you, whilst directly inline with an observer standing outside the car. To the observer... what happens to the bullet? We reached many conclusions, one being that to the observer, the bullet hangs in mid air until dropping to the ground as its acceleration finishes... This seemed logical... But wrong... which just confused us more...
ANSWER:
It may seem wrong, but the bullet fired backwards will drop straight to the ground as seen by a stationary observer. This is what is called Galilean velocity transformation. You can see more detail in my answer to another recent

QUESTION: nearly identical to yours.

QUESTION: :
What are the bases that scientists used to divide the electromagnetic spectrum into these bands ? I mean it is obvious that the visible light is the part of the spectrum that human eyes can perceive, but what made physicist define a boundary between ultraviolet rays and x-rays? or between x-rays and gamma rays ?
ANSWER:
There is nothing profound here. There are no hard boundaries between these classifications and they are mainly semantic and qualitative groupings. Historically, UV is just beyond (shorter wavelength) our vision and usually this radiation comes from dexications of atoms just like visible light normally does. When Roentgen discovered more energetic x-rays, which are still atomic deexcitations of atoms but involving the very innermost electrons, it was natural to give this region a new name. And, when it was discovered that γ-radiation from nuclei was just another higher-energy electromagnetic radiation, they were given a new classification. There is definitely overlap between categories; for example, some radiations called γ-rays by nuclear physicists have less energy than some radiations called x-rays by atomic physicists.

QUESTION: :
I have a

QUESTION: for a physicist about particle-wave duality of matter. If you fire one electron on at a time, does the electrons still exhibit their wave nature?
ANSWER:
Absolutely yes. Electrons, one at a time, just like photons one at a time, will exhibit wave properties if you look for them. For example, electron diffraction can be observed by sending in electrons one at a time, although you will have to wait a long time to see the pattern build up. In essence, the electron interferes with itself.

QUESTION: :
The office has a little on going arguement about force on a lever. Does it take more force to break a long stick or short stick. If a snowboarder hit a jump and came down on his tail that had 58cm between the end and his binding and another dude hit the same jump at the same height with the same weight and board and every thing is exactly the same, but the second guy come down on the tail that only has 38cm between the end and his binding; which board would break?
ANSWER:
One's first reaction is to say that the long tail will break more easily because we all know that it is easier to break a long stick than a short one. That is, the force required to bend a long stick far enough to exceed the strength of the material is less than for a short stick. I think back to breaking up sticks for a camp fire by wedging a long branch in the fork of a tree and pushing on it�it gets harder and harder as I break more and more off. But there is a lot more to this problem than that. When you state "every thing is exactly the same", it is easy to get deceived as to what that actually means. Until the time of impact, everything is the same, but then things get very different. What is going to happen when the tail hits the ground is that it will begin to bend, acting like a spring. But, the short-tail board will be very stiff, act like a stiff spring and the long-tail board will act like a "squishy" spring. What this means is that the short tail board will stop the downward motion in a shorter time than the long-tail board. Now, let's review Newton's second law: the force you experience is proportional to the acceleration you are subjected to. When you jump 20 feet to a concrete floor it hurts more than if you jump onto a matress; the reason is that the time it takes you to stop is much longer when hitting the mattress, your acceleration is smaller, so the force you experience is smaller. We can therefore conclude that, during impact, the short-tail board will experience a greater force during impact; it could therefore very well break more easily. From here it becomes a materials engineering problem�what is the board made of, what are the properties of that material, what is the snowboarder's weight, what is his velocity at the moment of impact, etc.�to determine which, if either, will break first.

QUESTION: :
Why is it important for you to have a �feel� for length, time, and mass?
ANSWER:
Sounds like you are a student in my class! The whole of physics is based on these three concepts. Everything we encounter in classical (Newtonian mechanics and Maxwellian electromagnetism) can be expressed in terms of the three fundamental quantities. It turns out that our intuitive "feeling" for these is wrong, they are interconnected and not universal; this is what we learn when we study the special theory of relativity. As long as speeds do not become comparable with the speed of light, though, you intuitive feelings for what these three quantities are is valid to a superb approximation.

QUESTION: :
I found this

QUESTION: in a chat forum in the "Games" section. Apparently, the answers are 200 mph and 0. 100 mph train motion + 100 mph throwing force of ball = 200. Ok, I can see that, but 0 for the second part? Why would a ball appear to be floating in one spot then drop to the ground to a bystander? Once I released the ball, why does it matter if I'm moving or standing still? Here is the

QUESTION: posted in the forum. I did a copy/paste so I wouldn't change the wording. "If you are on a train that is traveling at a speed of 100 miles per hour and at the front of the train you throw a ball. the ball is leaving your hand at a speed of 100 miles per hour going ahead of the train. to a man that is not on the train but standing by the way, what speed is that ball passing him? reverse the situation, the train is still going at 100 mph but this time you are at the back of the train and you throw the ball the opposite direction and it leaves your hand at 100 mph. to the man on the road what speed is that ball doing?"
ANSWER:
Maybe you would find this more plausible if you imagined the train moving at 5 mph and you walk backwards in the train with a speed, relative to the train, of 5 mph. If your friend were standing on the platform watching you he would see you stay right in front of him. Can you see this better? It is exactly the same idea.
FOLLOWUP

QUESTION: :
Actually no I can't see it better. Why would my friend see me right in front of him if Im walking backwards in a moving train? What is the math behind this?
ANSWER:
Try this: there is a conveyer belt traveling north 5 mph, so if you stood on it you would go north 5 mph. Now you start walking (on the conveyer belt) south with a speed 5 mph. If the conveyer belt were to stop you would travel south 5 mph because of your walking, but if the belt moves, you stand still relative to the ground.
[The math is as follows: vAB means the velocity of A with respect to (wrt) B. Then vAB=vAC+vCB; this is called the velocity addition formula. Here is your original specific case: A=ball, B=ground, C=train. Then the velocity of the train wrt the ground is vtrain,ground=100; if the ball is thrown in the same direction as the train is going, the velocity of the ball wrt the train is vball,train=100; so, the velocity of the ball wrt the ground is vball,ground=vball,train+vtrain,ground=100+100=200. If the ball is thrown in the opposite direction the train is going, the velocity of the ball wrt the train is vball,train=-100 because velocity is a vector quantity and we have chosen the direction the train is going as postive; so, the velocity of the ball wrt the ground is vball,ground=vball,train+vtrain,ground=100-100=0. You asked for it!]

QUESTION: :
According to Bohr's atomic model, each shell is associated with a definite amount of energy and the energy of an electron remains constant so long as it stays in the orbit. But how? How can the energy of moving electrons be constant? If the electrons are moving? Why not is energy continuously lost?
ANSWER:
Well, your

QUESTION: is a good one, but I am not sure about why you are asking it. You seem to imply that a moving object cannot have constant energy. How about the earth orbiting the sun? It has constant energy. So an electron in orbit should also, right? The difference is that the electron has an electric charge and electric charges radiate energy away if they accelerate (that is how transmitting antennas work). An object which moves in a circle is accelerating, even if its speed is constant, because its velocity is always changing direction. So the

QUESTION: is why does an electron in a Bohr orbit not radiate? But that is the triumph of the Bohr model�to conclude that certain special orbits simply do not radiate; it is just a postulate that orbits with particular angular momenta are stable. Subsequently, when models became more advanced, we were able to understand it in other ways. One of the best is using the deBroglie hypothesis which asserts that particles are waves. A Bohr orbit is stable is it is a standing wave, that is exactly an integral number of waves can fit in one circumference.

QUESTION: :
I am an avid runner and a sports medicine doc. Common "wisdom" is that you burn the same number of calories per mile walking or running. The explanation given is that since it takes longer to walk a mile, more time is spent burning calories. I intuitively disagree, and here is my reasoning based on physics: Calories are burned by the body as it performs Work--muscle contraction, respiration, cardiovascular output, etc. Work=ForcexDistance The distance is equal but it obviously takes more effort or Force to run the distance. Force=Mass x Acceleration. The body mass is the same but the acceleration of the heart, lungs, and skeletal muscles are much greater during running, therefore you should burn more calories for a given distance and time is not a factor. Am I correct?
ANSWER:
I will not argue that you are right or wrong in terms of the final conclusion. However, your reasoning is flawed for the following reason. In each case, work is being done at a different rate. But if the rate is low and the time is large, as for the walker, the net work done can be greater than or equal to the net work done by the runner where the rate is large but the time is short. Obviously, you need to know rates and times to make a sensible comparison. The assumption made in the "common wisdom" assertion is that the rate at which work is being done is proportional to the rate at which distance is being covered (also known as speed). I have no idea to what extent this is true, but it sounds like a pretty realistic first approximation to me. Applying physical principles to biological situations is often very tricky. An example is simply holding up a weight in an outstretched hand. Physics would say no work is being done because the force on the weight is not acting over a distance; you and I both know, however, that sugar is being burned to provide the energy necessary to hold this weight stationary. What is going on there, as I understand it, is that the muscle fibers in your arm are continually slipping and retensioning thereby doing lots of little parcels of work to hold your arm steady.

QUESTION: :
Why as you get farther from the Earth's equator does your weight not increase or if you stand on the Earth's rotational axis, why are you not crushed by the gravity. I would think one's centrifugal force or inertia to fly off the earth would decrease in proportion to the distance from the equator and aproach the axis but the gravitational pull would remain the same.
ANSWER:
There is an effect on your apparent weight due to the earth's rotation and your apparent weight decreases as you move away from the equator, just as you surmise. However, because the earth is so large and rotates so slowly, the effect is tiny, less than �%. So it would take a very careful measurement to see an apparent weight difference at the equator and the poles.

QUESTION: :
I recently read that if a spacecraft could travel very close to the speed of light for a period of 7 years approximatly 500 years will have passed on earth resulting in foward time travel. Doe's this mean that a craft sitting stationary in relation to the earth in space,(for a much longer time) would result in backward time travel since the earth's speed would slow relative time on earth?
ANSWER:
No, it does not mean that. Once the two are at rest with respect to each other their clocks run at identical rates. I suggest you read my earlier answer on the twin paradox and on the situation you describe, going out and stopping.

QUESTION: :
When different types of balls are launched, which will go the farthest
ANSWER:
The force of air drag can be very complicated as you can see from many of my earlier answers. However, if you want to compare balls of different sizes and masses moving through air near the ground and with speeds less than a few hundred miles per hour, there is a very useful approximation for the drag force: F≈�πR2v2 where R is the ball's radius in meters and v is its speed in meters/second. (Note that πR2 is just the ball's cross sectional area, so the force is proportional to the area times the square of the speed.) But, since what matters is the ball's acceleration (the rate at which its speed changes), we can use Newton's second law, F=ma where m is the mass in kilograms and a the acceleration in m/s2. Equating the two expressions for F, a=-�πR2v2/m. I have added a minus sign to make clear that the ball slows down as a result of this force, a is a "deceleration". So, for example, for two balls of roughly equal size but different masses (a baseball and a tennis ball, perhaps) launched with identical velocities, the baseball will go farther since it has a larger mass and hence a smaller deceleration. On the other hand, two balls of comparable mass but different sizes, when launched with equal velocities, would have the smaller ball go farther. It is important that the balls be launched with equal velocities; for example, if you threw a tennis ball and a baseball as hard as you could, the tennis ball would have a larger velocity to start with, an unfair advantage; it is hard to make comparisons if you do not control some of the variables. Still, common sense tells us the answer sometimes; for example, a basketball will go farther than a balloon of equal size regardless of how hard you threw the balloon. Of course, balls with both different sizes and different masses would have to be compared more quantatively. A bowling ball with a radius of 0.1 m and a mass of 7 kg going up against a golf ball with a radius 0.04 m and mass 0.05 kg: the deceleration of the bowling ball would be 0.0011 m/s2 and the deceleration of the golf ball would be 0.025 m/s2. The bowling ball would go farther because it slows down at a slower rate. (Note added: this would have to be a smooth golf ball; the dimples are designed to reduce drag and so our equation for drag would not be correct.)

QUESTION: :
if an object was sent in to the future instantaneously lets say one minute would we ever be able to catch up with it or would it always remain one minute ahead? If it takes us one minute to catch where it was sent then that object would've already been there for 1 minute as well, causing it to be 2 minutes ahead of its original time and constantly one minute ahead of the source.
ANSWER:
We can catch up with him but he cannot come back to our time. The only way we know how to time travel is to move at a high velocity and then stop. At the time we stop our clock will be behind a stationary clock we left behind, in other words we are in the future of the frame we left behind. If the clock we left behind now takes a trip identical to the one we took, when he stops he will be with us and our clocks will be again in agreement. You might understand this better by looking at an earlier answer. (By the way, you can't travel to the future instantaneously, but I do not think that is what you are most interested in here; rather you want to know, if somebody is in the future, whether we can get there too.)

QUESTION: :
My co-workers and I are having a discussion about age vs time. Some of us acknowlege time dialation, one however, does not. We use the example of two 10 year old twins. 1 twin goes off to outer space near the speed of light for 10 years. When he comes back to Earth the twin who went to outer space is 20 years old, however, the twin on Earth is say 90 years old. My

QUESTION: to you is time and age directly related? Will the 20 year old twin look like a 20 year old person or will he only be considered 20 years old while having the body of a 90 year old?
ANSWER:
Biological systems are just clocks, they are just not as accurate as mechanical clocks. Still, nobody lives past 120 so they are a clock of sorts. Also, nobody would argue that a body which aged, relative to a mechanical clock, 20 years could not be distinguished from a body which aged, relative to a mechanical clock, 90 years. If the traveling twin carried a mechanical clock with him and it went forward only 20 years, he would be a young man at the end of the trip. If his brother's mechanical clock went forward 90 years, he would surely be an old man. I recommend two of my earlier answers to be read by your doubting Thomas: the light clock and the twin paradox.

QUESTION: :
If a fly and a Train are travelling towards each other and collide head on. Does the train stop for an instant before continuing? At some point the fly must stop going forwards for the train to send it backwards!!! If you do this with a car, it must stop at some point before it changes direction!!
ANSWER:
The train definitely does not come to rest for an instant. The fly does because its velocity changes direction during the collision but the train does not. So, the fly experiences a large change in velocity in a short time which means a huge acceleration. Using Newton's second law, F=ma, a small mass times a big acceleration is a modest force, but likely big enough to destroy a fly; bye bye fly. The train experiences a tiny change in velocity in a short time but exactly the same force as the fly did. Because the train has a huge mass, it experiences virtually no acceleration.

QUESTION: :
what does it mean for a picture of the dead to fall to the floor?
ANSWER:
It means that the force of gravity on the picture was larger than the force which previously held the picture on the wall. I am not a psychic, by the way, I am a physicist.

QUESTION: :
I was watching a TV show on dark matter, and can't seem to wrap my head around it, if it is real shouldn't we be able to see it at the space station or measure it in deep mines? What if ,once you get to certain mass, space time does not just warp it creates a crater, with sharp drop offs? Sort like a hunting bow at first it is hard to pull but once get to a certain point it folds over. So when your in the creator, gravity behaves normal like our solar system , If a kid throws a paper airplane on a school bus that is traveling 55 mph; if you are out side the bus you can say the airplane is traveling 57 mph but if your inside the bus its only going 2 mph. Dark matter does not seem real, its like a god factor we create it to make since of the world around us. I don�t get it.
ANSWER:
Wow, your

QUESTION: is all over the place. Here is the thing about dark matter: it is very diffuse, that is, there is generally very little of it in a cubic meter of space, but it occurs all through the universe where there is almost no normal matter and ends up dominating the mass of the universe. Well, that is the party line anyway. I actually am not convinced that dark matter exists and feel that we do not understand gravity as well as we think we do. I am perfectly willing to change my mind when convincing direct experimental evidence for dark matter is found.

QUESTION: :
I'm currently having a discussion with someone regarding the spin of a bowling ball and how it effects it's degree of hook (neither of us are physics students nor have we taken a physics class). My

QUESTION: to you is as follows: It stands to reason that if you throw a bowling ball with complete backspin (no sidespin whatsoever) that it will travel down the land and depending on whether the lanes are oily it will either skid with that backspin until hitting the pins or it will, on dry lanes, stop spinning backward and develop a forward roll continuing to travel in a straight line from where you released the ball. If you impart some side spin to go along with the back spin, will the ball hook at all in the direction of the side spin? You don't have to be a physics expert to conclude that yes, the ball would move in the direction of the side spin. Now, my primary

QUESTION: is, if you threw a ball with a certain amount of revolutions (say 15 or so) and imparted a spin that was exactly between a full forward roll (no side spin) and a complete sideward spin, it will hook a certain amount in the direction of the side spin before it reaches the pins. **If you throw the ball with the same degree (amount;strength) of spin, but instead have it halfway between a full backspin and a full sidespin, will it hook further in the direction of the spin than it would in the previous 'forward-spin' example? I hope you understand what I'm trying to ask you, I doubt that I worded it very well.
ANSWER:
Let's first note that we need to specify the spin by an angular velocity, so many rpm (revolutions per minute) or revolutions per second or whatever. Next, we need to ask what each kind of spin does. A spin causes a force in some horizontal direction because the sliding of the ball on the lane results in a frictional force. A ball which has purely top spin (forward spin as you call it) will speed up in the direction in which it is moving. Similarly, back spin causes the ball to slow down, clockwise spin (from the bowler's perspective) causes the ball to curve right, and counterclockwise spin causes it to curve left. In all cases, if the alley were long enough, the ball would eventually stop slipping and simply roll in a straight line. If the ball starts with top spin and left spin it will curve less over the length of the alley than if it just had left spin because, since it speeds up, it would have less time to curve. You would get even more curve if you also had back spin on the ball. It is surely more complicated than this, but this is the basic physics. I am not sure that I answered your

QUESTION: .

QUESTION: :
I always thought that the energy of a photon was an intrinsic property of the photon, and represented some multiple of a quantum amount of energy (E = hf). But light from a receding star undergoes a red-shift, meaning that the frequency of a photon is a function of the speed of the observer. Two observers moving at different speeds with respect to a distant star see two different frequencies implying that the observed energy for a photon is different. So where did the energy go? If the light traveling around the universe isn't homogeneous, is the sum total of energy in the universe a function of where you are standing and your relative velocity with respect to some other object?
ANSWER:
Imagine a 2 kg ball moving past you with speed 1 m/s. This ball has a kinetic energy of �mv2=1 J. Now imagine running alongside the ball with a speed of 1 m/s. Where did the ball's energy go? The simple fact is that kinetic energy is not an invariant quantity, either classically or relativistically, that is, it depends on the observer. A photon's energy is purely kinetic since it has no mass. Yes, the energy of the universe does depend on your reference frame (assuming "the universe" means everything except you). However, physical laws like conservation of energy will still be true.

QUESTION: :
I was reading through the driver qualification handbook which all drivers need to read before they take on the driver qualification test. In the book it says: "Overtaking other vehicles is hazardous. If you misjudge the gap needed to overtake safely you could collide head-on with an on coming vehicle. Head-on crashes are usually very severe as the speed of your car combines with that of the other. For example, a head-on crash where both cars are travelling at only 50 km/h gives a collision speed of 100 km/h � equivalent to driving into a stationary object at 100 km/h!" Now, wouldn't the energy be divided and only be the equivalent of crashing into a non moving object at 50km/h?
ANSWER:
Here is the way to think about it. What matters is the force you feel. The force something experiences is proportional to its acceleration, the rate at which the speed changes. During the collision your speed goes from 50 km/hr (or 100 km/hr) to some constant speed. (Eventually you come to rest because of friction, but what matters is how fast you are going after the collision per se has finished, the cars mangled and stuck together.) What is your speed just after the collision? If the other car has about the same mass as yours and the opposite velocity, the two cars come to rest just after the time of the collision; but, if the other car is at rest, the two cars have a speed of half the speed you came in with. The time which the collision will last will be very short and roughly equal for the two situations. So your change in velocity (50 km/hr) for the head-on collision will be twice as great as for your change in velocity (25 km/hr) for the collision with the stationary car in roughly equal times. Hence the force will be twice as great. If you collide with a stationary car while going 100 km/hr, your speed right after the collision will be 50 km/hr so the change in velocity will be 50 km/hr, the same as the head-on collision. [To estimate the speed after the collision I have used momentum conservation, the product of the mass times the velocity does not change. In the head-on collision the total momentum is zero. In the other case, the mass after the collision is twice as big so the velocity is half as big.]

QUESTION: :
The potential midway between two charges of equal magnitude and opposite sign is zero. is it possible to bring a test charge from infinity to this midpoint in such a way that no work is done in any part of the displacement? if so, describe how it can be don. if it is not possible, explain why?
ANSWER:
It is possible. The plane which is the perpendicular bisector of the line connecting the two charges has electric field everywhere normal to it. It therefore takes zero work to move a charge around on that plane so it is an equipotential plane at zero potential extenting all the way to infinity.

QUESTION: :
I have been thinking about this for quite some time and have searched the internet for anything like it and have found nothing. If an orbit is perpetual, as i have read, why has it not been looked at as an energy source?
ANSWER:
An orbit is "perpetual" only if left alone. If you take energy away from an orbiting object, its orbit will decay and it will eventually drop out of orbit.

QUESTION: :
What would happen to the earth's orbit is the sun were to change it's mass? I understand what would happen to the period if the semi-major axis remained the same or what would happen to the semi-major axis if the period remained the same, but presumably changing the mass of the sun would affect both these things and create a completely new orbit. But how do you determine the effect it would have?
ANSWER:
Assume that the earth is in an approximately circular orbit. If the sun became more massive, the earth would be going too slow for a circular orbit so its orbit would become an elipse with the earth at the aphelion (furthest point to the sun); so the semimajor axis would be smaller and the period smaller. If the sun became less massive the earth would be going too fast for a circular orbit so its orbit would become an elipse with the earth at the perihelion (nearest point to the sun); so the semimajor axis would be larger and the period larger. In my reasoning I have used T=2π√(a3/GM) where a is the semimajor axis, T is the period, G is the universal gravitational constant, and M is the mass of the sun.

QUESTION: :
What is fire?does it have a mass?
ANSWER:
Fire is just hot gases undergoing chemical reactions. Yes, gas has mass.

QUESTION: :
Let's say that Bob is in a train travelling at relativistic speed. Then, Bob decides to make a cell phone call to his friend Jack, who is at home. Would there be any anomalous occurences during the phone conversation? Or would a cell phone conversation not even be possible at relativistic speeds?
ANSWER:
There are a couple of reasons a cell phone would not work. One is that there would be a big doppler shift so the signals you actually receive would not be the frequency your cell phone is designed to receive. Also, we would have to have cell towers stationed all along your route. But these would not be insurmountable obstacles and you could redesign the phones and infrastructure to work under these conditions. (Or maybe just communicate by radio which is essentially what a cell phone does anyway.) What would then happen would depend on whether you were going away from of moving toward the other phone; your

QUESTION: seems to imply you are going away. What both Bob and Jack would hear is the message from the other slowed way down, and by equal factors. Also, of course, a conversation would be very difficult because Bob would be very far away and therefore the transit times of the signals would be very long. To understand this in detail, study my earlier explanation of the twin paradox and focus only on the outward journey.

QUESTION: :
If your in a n elevator that is falling, you should jump in the air right before it hits the bottom to survive. Why or why not ?
ANSWER:
It will make practically no difference, you're dead either way. Suppose you fall from about 20 stories, about 100 m. The speed the elevator would hit the ground would be about 70 m/s (about 154 mph). How high can you jump? Maybe 1 m? The corresponding speed would be about 4 m/s. If you jumped an instant before rock bottom you would end up hitting the ground with a speed of only 66 m/s (about 150 mph).

QUESTION: :
If you made a hole through the centre of the earth large enough for a large round rock and threw that rock into to that hole what would happen when it reached the centre of the earth, I realize it would probable melt but supposing it didn't, an object can not fall up, so what would happen after the object had passed the centre because then it would be falling up?? or would it just stay in the middle??
ANSWER:
Neglecting air resistance, the stone speeds up until it gets to the center and then slows down until it gets to the other side of the world. You should read my earlier answers for more detail.

QUESTION: :
Air is thrown on a sail attached to a boat from an electric fan placed on the boat.but the boat will not move.acc. to answer when fan pushes the sail by air,air also pushes the fan in opposite direction.plz explain
ANSWER:
This is a complicated

QUESTION: because the boat and fan are not really an isolated system. But let's us assume they are. The fan pushes the air forward and the air pushes the fan backward. Now the air pushes the sail forward and the sail pushes the air backward. All told, the net force on fan+air+boat is zero. A simpler example which is easier to understand because there is not the complicating factor of the air is the following: you, standing on the deck, push the mast and the boat does not move forward because you are "part of the boat" and the mast pushes back on you with an equal and opposite force.

QUESTION: :
when a ball is thrown upwards,its momentum first decreases and then increases.is conservation of momentum violated? acc to answer momentum is conserved.how?
ANSWER:
Momentum is conserved only for systems where there are no external forces. The ball's momentum is not conserved because there is a force on it, its own weight (the gravity the earth exerts on it). The momentum of the ball plus the earth is conserved because, according to Newton's third law, they exert equal and opposite forces on each other, that is gravity is an internal force for the earth+ball system.

QUESTION: :
how can we make the antimatter.can it be made by moving matter in the velocity of light.has CERN prepared so?
ANSWER:
You cannot turn something into antimatter just by making it go fast. You can, however, create antimatter by colliding very energetic matter with other matter. You never make it by itself, though; usually it is produced in pairs with its normal matter counterpart, for example proton/antiproton pairs are created at accelerators like CERN. See an earlier answer.
FOLLOWUP

QUESTION: :
how fast should it travel?
ANSWER:
It depends on what you want to make and what the type of accelerator is. The incident particle(s) must have enough energy to create the new mass and to conserve energy and momentum. For example, to create an antiproton in a conventional accelerator requires the incident proton to have a speed of 99.4% the speed of light if it collides with a proton at rest; most of this energy is "wasted" conserving energy and momentum. For a proton collider, like the new machine in Switzerland, the momentum of the system is zero and so much less energy is wasted; that is why we build colliders. In a collider, each proton must have a speed of about 90% the speed of light to create an antiproton.

QUESTION: :
My

QUESTION: is related to gravity and I hope you will be able to answer it. On a documentary on television (I think it was called Invisible Worlds), I saw that the density of the earth�s crust may be the reason why a person�s weight will vary depending on where in the world he decides to weigh himself. This was apparently established by data received from two satellites following one another while orbiting earth. I immediately though of my bathroom scale and an effect I noticed once by chance. When I weighed myself on a carpet, I weighed more than when I weighed myself on a tiled floor. This now suddenly baffled me since I was always under the impression that a surface with higher density will have a stronger gravitational pull. I searched the internet and found an article by Ian Sample (http://www.newscientist.com/article/dn2462-people-weigh-less-on-a-hard-surface.html) where another physicist, David McKay at Cambridge, decided to get someone to investigate this phenomenon. One of McKay�s students, Jon Pendergast, found that on a hard surface, �the base of the scales bows. This makes the fulcrums at each corner of the scales tilt in slightly, shortening the distance between each fulcrum and the point at which the load pushes onto the lever. �Put the scales on a deep carpet, however, and the scales sink into it, so the carpet supports the base, which prevents it from bending. This increases the distance between each fulcrum and the point at which its lever is loaded, so for the same force the lever moves further. Even a small increase in this distance can add several kilograms to the weight registered on the display.� This explanation seemed logical enough, but I decided to test it anyway since I thought I saw another test that Mr Pendergast may have missed in the experiment. I found a solid board and placed it on two books, forming a bridge of sorts, to test the board�s strength. This board proved to be so solid, it did not even bend slightly under my weight. I then put the scale on it and weighed myself on a tile floor. I then moved the board, with the scale on it, onto a thick carpet and weighed myself again. To my surprise, I still weighed more on the carpet! I went to find a water level to make sure that the board was level and that it did not bend. I am thus sure that this has nothing to do with something from below supporting the base of the scale. In addition, the water level remained dead centre during my little experiment. My

QUESTION: : Is it possible that the lower density of the carpet compared to the higher density of a tiled floor may increase the gravitational pull?
ANSWER:
It has been known since long before satellites that local variations in the earth's density could affect the acceleration due to gravity and therefore one's weight. However, this is a very tiny effect because the earth is so massive (like 6x1024 kg) and close to spherical. The effect is so small that you could never hope to observe it with your bathroom scale. When you did your experiment, the rigid board was exactly the same as the tile floor, a hard flat surface. The mass of the board or of the floor is of no importance compared to the mass of the whole earth. Read the article you found more carefully: the fact that the scale reads more on the carpet is a purely mechanical effect having nothing whatever to do with gravity. You do not weigh more, the scale is simply making a measurement error.

QUESTION: :
when one moves forward he interacts with the earth. what is the momentum of recoil of the earth? why dont we feel it?
ANSWER:
Suppose you walk forward with a speed of 1 m/s and your mass is 100 kg. The earth has a mass of 6x1024 kg and so it would recoil with a speed of v=(1)(100)/6x1024≈2x10-23 m/s. At this speed it would take the earth about 3,000,000 years to move the diameter of one atom. No wonder we are not aware of the recoil! For all intents and purposes, the earth's mass is infinite compared to yours.

QUESTION: :
I understand that if someone were to fly a space ship at the speed of light for say 8 years (4 out 4 back) due to relativity they would be returning in 80 years our time(these numbers I believe they were given as an example, not as a precise calculation). If this is so, would some who flew jets often travel a few seconds in time every flight? Or more realistically at what speed does any change in time flow begin?
ANSWER:
First of all, you cannot fly the speed of light and the groundrules of the site say you cannot ask such

QUESTION: s. But I will answer your

QUESTION: since the focus is more "at what speed does it matter?" To get noticeable effects, the clock must be moving with an appreciable fraction (f) of the speed of light. How big is "appreciable"? The moving clock rate (T'), compared to a stationary clock (T), is given by T'=T/√(1-f2). So, what speed would you go to lose one second per hour? 3600/3500=1/√(1-f2), so f≈0.12, that is about 12% the speed of light. To put that number in perspective, the shuttle, about the fastest thing around (18,000 mph) has f≈0.00003 or about 0.003% the speed of light. For everyday life you are not likely to notice time dilation. But wait a minute�if corrections were not made for relativity, a GPS would not work at all. A GPS requires extremely accurate times and without corrections for special relativity and general relativity, would make very large errors (miles) in calculated positions. (To better understand time dilation, you might like to read my earlier answer on the twin paradox.)

QUESTION: :
Does the gravity that affects high tide affect how much how much we weigh?
ANSWER:
Tides are caused by the gravity of the moon (and, to a lesser extent, the sun). Your weight is the force which the gravity of the earth exerts on you.

QUESTION: :
When electric current flows in a wire, is the movement of electrons on the surface of the wire or is the entire wire (interior and exterior) involved?
ANSWER:
Under normal circumstances, current is distributed throughout the volume of the wire. Only with extremely high frequencies (greater than a few MHz) is the current pushed out to the surface.

QUESTION: :
An old type car antenna, often called whip aerial , moves back and forth when the car is moving but when you speed up it seem to oscillate in figure 8 motion. Why is that?
ANSWER:
Vibrating systems have different modes of vibration. The prettiest example I could find is some of the modes of a drum, shown above. A real drum will have all its infinite modes going on simultaneously but some will play a more important role than others depending on how the drum is excited. The leftmost one above is called the fundamental and would be the primary one if the drum were struck right in the center; the center of the drum in this case is called an antinode, a place which has maximum amplitude. The right-most one above is another higher mode which, you will note, has the center of the drum not moving; this is called a node and would probably not contribute much if the drum were struck in the center. Your antenna, when just going back and forth, is mainly in its fundamental mode. But when you go a different speed you are doing the equivalent of striking the drumhead somewhere other than its center and exciting a higher mode.
ANSWER ADDED LATER:
I found modes of a beam which should be analogous to your specific problem. Is the second mode similar to your "figure eight"?

QUESTION: :
Mine is but a simple

QUESTION: : what is the name of the theory or general principle relating to the rate of spin on a single axis? Specifically, I am rewriting a wikipedia stub-article describing a circus act called the "Iron Jaw". It is a performance in which a person hangs from a trapeze only by her mouth. The performer bites down on an attachment and spins, controlling her speed by alternately elongating and narrowing her body like a pencil to speed up, spreading out her arms and legs to slow down, or curling her body into a ball to both speed up and send her body off-axis as well. I'm sure it is something simple, covered in my 10th grade physics class, but I can not for the life of me remember what it is nor find the right word combination to google the answer.
ANSWER:
Mine is but a simple answer: conservation of angular momentum. The angular momentum is the product of angular velocity and moment of inertia. The moment of inertia depends on the mass distribution of the object, so when the person sticks out her arms, for example, her moment of inertia increases and she therefore slows down. Similar examples are seen in dancers, divers, and figure skaters.

QUESTION: :
You know the theory that as light has no mass, it is forced to go "the cosmic speed limit" i.e. the speed of light, can you consider these

QUESTION: s and give an answer if you can or if there is one?
Light travels slower through water, glass, diamond etc. than through a vacuum? To move from the higher speed to the lower speed, does it decelerate and over what time span? Does it lose energy in the process and gain it again on emergence back into a vacuum? Or does it just appear to? Is there a time dilation effect perhaps?
Light has no mass, so supposedly objects that have no mass cannot be attracted by other objects that have mass so how does light bend around a star as observed during a solar eclipse? Is it possible that gravity is providing a similar effect to a lens? i.e. does light travel slower through stronger gravity, this would explain the effect?
Blue light has more energy photon for photon than say red light? So does blue light travel faster than red light and does this explain why light splits when it goes through a prism? "Gravity waves" may have a large magnitude of wavelength different to say gamma waves so could this explain why these waves are seen to travel so fast? i.e. two massive objects approaching one other, the force of attraction between them increases faster than light propagates (earth orbiting the sun is a good example?)?
ANSWER:
The energy of the light is proportional to its frequency which does not change when it enters the optically dense medium. So no energy is lost when it slows down. This happens by the wavelength changing such that it satisfies v=fλ where v is speed, f is frequency, and λ is wavelength. The light travels with a slower speed because of complicated interactions with the medium, I would not think of there being a period of acceleration.
The reason it bends is that mass deforms the space around it so the space is no longer Euclidean. See earlier answers.
Dispersion, different wavelengths having different speeds in a medium, is not related to energy per photon but rather to the electronic structure of the medium. Gravity waves have never been directly observed let alone their speed of propogation measured; there is certainly no evidence that gravity (or anything) travels faster than the speed of light. Many things which work their way into public popularity (gravitons, worm holes, alternate universes, string theory, dark matter, etc.) are really nothing more than figments of our imagination until they are observed experimentally or are shown to describe nature in unique and correct ways.

QUESTION: :
I have tried to read a physics text book on this subject matter but was hoping to get a layman's term answer that i can understand. Is the downward (vertical) pressure of water on an object the same as the sideways (horizontal) pressure on an object at the same depth?
ANSWER:
Think of your ear drum as a pressure measuring device. Dive to the bottom of a 20 foot deep swimming pool. Your ear hurts no matter how you orient it, up, down, or sideways. Pressure pushes in all directions equally at a given depth.

QUESTION: :
I am studying the laws of free fall and air resistance and I came across a demonstration about a penny and a feather free-falling. Obviously, the penny hits first because of the air resistance of the feather, but in a vacuum, they accelerate at the same rate. So my

QUESTION: is, terminal velocity is achieved when an objects air resistance = the force of gravity, so, is the speed of free fall exponential and therefore unlimited in a vacuum? Could an object accelerate to light speed with a strong enough force of gravity and a large enough vacuum?
ANSWER:
As I showed in an earlier answer, speed does not increase exponentially; it increases linearly with time and like the square root of the distance fallen. In principle, if the acceleration were g for a long enough time, the speed could approach the speed of light (but, of course, not "to light speed"). It does get a little tricky, though, because at relativistic speeds acceleration is not a useful variable and you have to look at things differently; if you are interested in what happens at very high speeds, look at this earlier answer.

QUESTION: :
In attempting to determine "G" with a torsion balance, as Cavendish and more recently Gundlach and Merkowitz have done, is there any way of ruling out or guarding against an influence of van der Waals force between masses? After all, isn't it a van der Waals force that would lead two dust particles that might meet in space to cling together and continue to attract other dust particles until the result is what we would consider a sizable mass? Isn't the Earth, after all, just a giant dust-bunny?
ANSWER: (thanks to L. Magnani)
It depends on what size scales you are talking about, but certainly there is a stage where vdW produce clumping. But it's at small scales (smaller than pebbles). If you look at chondritic meteorites, they are a bunch of pebbles packed together by heat and pressure and chemical reactions (like rocks in concrete). Do a google search on chondritic meteorites and look at the images of what they look like. There has definitely been heat and chemical processing going on and they are the sizes of baseballs to ~ 1 km. After that, the planetesimals (1 km) collide, and again, heat and chemistry produces a loose aggregation of stuff. Once the object is 1000 km or greater, self gravity via gravitational potential energy is great enough to force the material to melt and reform into a sphere. So, there's no way the Earth is a giant dust bunny. I don't see how vdW forces have any measurable effect on big metal spheres.

QUESTION: :
while i was reading about newtons first law, a doubt arose. according to newton's first law, we say that a body will be in state of constant velocity or of rest if no force is exerted on it. suppose if i apply a force of 1 newton to a body of 1 kg on a frictionless surface, we can say that the body is moving with constant acceleration of 1 m/second squared . and if i apply a force of 2 newton, we can say that the body is moving with a constant acceleration of 2m/s squared.if i dont apply any force to body, then it does not accelerate. but the statement states that a body will be in state of constant velocity if i dont apply any force. how does a state of constant velocity exist now. if a body is in state of constant velocity, some force has acted on it initially and it has to accelerate. if i dont apply any force it will be in state of rest. now i have a doubt that there is no state of constant velocity itself. if it exists please tell me with what force should it be moved initially so as to be in constant velocity?
ANSWER:
Just because something has constant velocity does not mean it always had constant velocity. But if it does have constant velocity, the implication is that there is zero net force on it now; that does not mean it always had zero net force on it. Incidentally, being at rest is just a special case of constant velocity (v=0).

QUESTION: :
If you have runner who can run at any speed, under the speed of light, with no limitations from drag, friction, etc. is there a speed that the runner can go that he will break the bonds of gravity? Also if centripetal/centrifugal force can simulate gravity, can the runner traveling as fast as he was when he broke gravity's pull(?) or faster create any odd or interesting effects in his body, circle he is traveling in, or anywhere, -when, or -what you can think of.
ANSWER:
Anything which has a velocity greater than the local escape velocity can "break the bonds of gravity". And it is nowhere near the speed of light except for a black hole. Your second

QUESTION: has no meaning to me.

QUESTION: :
Can something be observed that looks like synchronous rotation, but is not synchronous rotation?
ANSWER:
I don't know what you are asking. A helicopter hovering over my house is rotating synchronously with me but is not in orbit. Is something like that what you mean?

QUESTION: :
The Shuttle orbits the Earth every 90 minutes or so, and from what I understand it's traveling at approx 18k/hr in order to maintain orbit and "fall" over the edge of Earth as gravity pulls on it.

QUESTION: is: How can a Geostationary satellite exist since it has to be traveling much slower to match Earth's rotation. How does it maintain orbit?
ANSWER:
The period of an orbit depends on its radius. If the orbital radius is about RE (radius of the earth), the period is about 1� hr and the speed about 18,000 mph. But, if you go out to an orbital radius of about 6.6 RE, the period is 24 hr and the speed about 6900 mph. And, if you go out to about 60 RE, the period is about 28 days and the speed about 2200 mph; must be the moon!

QUESTION: :
"In astronomy, of course, looking farther away means looking further back in time." This is related to the statement that everything gets older as you go farther away from us. But since there is not really any "center" of the universe, who is to say what farther away is. If i were on Pluto and I went towards earth that would be saying that earth is older since it is farther away than Saturn. If i went from Earth and towards Pluto we would be saying that Pluto is older because it is farther away than Saturn. I think that should make enough sense to get an answer but I was just kind of curious as to what astrophysicists define as "farther" away and where they measure it from.
ANSWER:
I think you are missing the point here. Since it takes time before we see something because the light needs to travel to us, whatever we see is what was when the light left it, so the farther away something is the more in the past we see it. Technically, when you see someone across the room you are not seeing them as they are but how they were when the light you are seeing left them. When you see the sun, you are seeing it as it was about 8 minutes ago; so if the sun were to go out, you would not know for about 8 minutes.

QUESTION: :
two monkeys of equal weight climb the rope from opposite ends,one of them climbing quickly than the other,relative to rope.rope is passing over pulley.which will reach the first?the answer given is both will reach at same time.but velocity=displacement/time.it means the monkey which has greater velocity should reach first.how both could reach at the same time.no doubt length of both segment is same.
ANSWER:
Each monkey has two forces on her: her own weight and the tension in the rope. But the weights are given to be equal and the tension on the rope is the same throughout the rope (assuming a massless rope and a massless, frictionless pulley). The forces on each monkey are identical. If one monkey jerks down on the rope so that the tension is greater than the weight, he accelerates up but the other monkey will experience the same net upward force and will accelerate up with precisely the same acceleration. Therefore, regardless of what the monkeys do they must always move identically because they have identical masses and forces on them at all times.

QUESTION: :
I teach 8th grade physical science, and we discussed the moon's gravity. One student wanted to know the lightest weight that would fall to the moon's surface. How do I calculate that? And is the low gravity the real reason that there could be no atmosphere on the moon?
ANSWER:
Motion of objects near the moon's surface is much easier to deal with than for the earth. The reason is the lack of atmosphere. On earth, very light objects like dust can be held aloft for years by the air; on the moon, dust will settle on the surface unimpeded. There is no limit to how light a particle could fall to the ground there. You are right that the low gravity is responsible for there being no atmosphere, but not simply because the molecules in the air are too light to fall. If you took one molecule of oxygen, it would drop to the ground on the moon. But when there is a gas, molecules are running around with a distribution of velocities (called the Maxwell-Boltzman distribution (MBD)). Some are very slow, some are very fast. On the moon, those going fast are going faster than the escape velocity (the speed necessary for anything to escape the gravity) and they leave. But now, the rest have to readjust to the MBD and the new fast ones escape; the process keeps repeating until all of the gas has "leaked" away from the moon. Interestingly, this is the reason that you find almost no hydrogen or helium in the earth's atmosphere; the lighter the molecule, the higher its average speed in the MBD at a given temperature. The figure shows the MBD for helium at two temperatures. The escape velocity on the moon is about 2400 m/s, so you can see that there are a significant number of atoms at 273 K (which is 00C); when those escape, slower atoms have to move in to take their place, and so on until all have escaped. At higher temperatures, you can see, the escape rate will be even faster.

QUESTION: :
If rising sea levels continue and begin to become a threat to humanity, what is the possibility of piping excess water into space? surely if a long enough hosepipe was created, the vacuum of space would suck water up the tube without need for a pump?
ANSWER:
The maximum height to which a vacuum can "suck" a column of water is 33 feet. Besides, this is a pretty wacky idea for solving this problem! Water is a precious commodity and, even if it seems like we have plenty right now, to throw away vast amounts of it just to save coastal cities would be short-sighted in my opinion.

QUESTION: :
My

QUESTION: is, I need to ask about the force of gravity, outr teachers say or we have studied that the gravity is constant i,e. 9.8 m/sec2, But gravity is basically the force of attraction because of the centre of earth then those countries or those places that are near to equator should have more force of attraction than those who are at poles? if it is like that then why do we say that the value of gravity is constant.?
ANSWER:
The earth is approximately a sphere, and so every point on earth is approximately equidistant from the center. In fact the earth is slightly oblate, that is it is a little "squashed" at the poles, making those points closer to the center and so having greater gravitational force. This, though, is a very small effect and local variations in g are due also to inhomogeneities in the earth's density and effects due to the rotation.

QUESTION: :
My

QUESTION: is about stationary waves. How these waves are formed? How the energy is limited within the region of production? where pressure variation is maximum and where pressure is maximum?
ANSWER:
We call these standing waves. A standing wave is actually two identical traveling waves traveling in opposite directions. An example is a guitar string. The way you create a standing wave in a guitar string is to pluck it. I do not understand your

QUESTION: about pressure.
FOLLOWUP

QUESTION: :
what are nodes and antinodes? how these are formed? how pressure variatuion occurs at nodes and antinodes?
ANSWER:
In a standing wave there are points where the medium is not moving at all, called nodes, and points where the medium has maximum motion, called antinodes. I guess you must be talking about standing sound waves (like in an organ pipe or other wind instrument) since you keep asking about pressure. At the nodes the pressure will simply be atmosperic pressure. At the antinodes the pressure will fluxuate (with the frequency of the waves) above and below atmospheric pressure.

QUESTION: :
A scoter speed on the earth is 100km/hr,friction also acts on between the scoter tyre and the earth.if this scoter is taken in the moon then what will b the speed of the scoter,would it change or not?why?
ANSWER:
It is actually the friction between the tires and the ground which drives the scooter forward. This force balances the friction in the bearings of the wheel, the air drag, friction in the motor, etc. to keep the scooter moving forward at a constant speed. As long as the tires did not slip on the moon, the scooter would move forward with a bit larger velocity because there is no air and so no air drag.

QUESTION: :
Considering space as the object between things, I am always curious as to what occupies the space between earth, and all other universal objects ? Is it actually empty space, or is it filled with atoms, protons, nutrons, and other particles that actually unify us with everything ?
ANSWER:
Space is certainly not empty. But, what there is and how much of it depends on where you are. Generally speaking, there is dust and gas but in amounts which are hugely below what you would find here on earth. There are some regions called molecular clouds with relatively higher numbers of atoms, but still what we would call very sparse compared to earth. And, of course, the universe has photons zipping through everywhere, and neutrinos, and who knows about more mysterious proposed dark matter? But, I wouldn't think of any of that stuff as "unifying us with everything".

QUESTION: :
I always hear that gravity is a weak force, typically demonstrated by using a magnet to overcome gravity to lift some object; yet gravity can bend light and a magnet doesn't, The earth is a huge magnet but it's gravity is felt by the moon. How is strength of the force defined for comparisons?
ANSWER:
I always think: "to be able to perceive the gravitational force I need an astronomical amount of mass, but I can easily perceive an electrostatic force with a very modest amount of charge." OK, this is a pretty qualitative and therefore unscientific argument. How about "when two protons interact, there is a region where the Coulomb repulsion dominates, a region where the attractive strong interaction dominates, but never a region where gravity makes the least amount of difference." Still not satisfied? The way physicists evaluate the strength of interactions is by defining coupling constants which are dimensionless numbers whose size indicates the strength of the force. Roughly they are 1 for the strong interaction; 1/137 for the electromagnetic interaction; 10-6 for the weak interaction; and 10-39 for the gravitational interaction. You can read where these come from at this link.

QUESTION: :
I have done a lot of readings about Kinetic Molecular Theory. I am quiet convinced that the theory says in an ideal gas(and I mean strictly ideal gas), the average kinetic energy of the gas particles is proportional to its absolute temperature. But the theory did not show this relation also applies to solid and liquid. Yet many authors seems to agree that that absolute temperature is proportional to the average kinetic energy for all three states. Were they wrong?
ANSWER:
Technically, it is the average energy per constituent rather than average kinetic energy. When the particles interact, such as in a solid, potential energy is part of the energy of an atom or molecule. Also be aware that kinetic energy need not be restricted to translational (�mv2) kinetic energy but may include other degrees of freedom like rotation and vibration.

QUESTION: :
When an electron absorbs a certain photon, and therefore jumps to a higher energy/shell level, how much time does the journey take? (I am making the assumption that there is an actual distance between lower and higher energy shells)
ANSWER:
It is all pretty complicated quantum mechanics, but the answer depends entirely upon what the initial and final state of the atom are. Incidentally, it is precisely the same problem as the excited electron dropping back down to the ground state. Such "decays" are always characterized by a half-life and that is essentially what you are asking me for; it varies with what the transition was.

QUESTION: :
I dont completely understand newton's third law of motion.. It says every action, there is an equal and opposite reaction, but when we apply force to a book, why doesnt the book apply the same force to us? And why are we able to push the book wherever we want, if, according to third law of motion, book should also have an equal reaction force?
ANSWER:
The book does exert an equal and opposite force on you. So, why does the book move and you do not? There are several reasons. First, you have much more mass than the book does and so your force on the book has a much bigger effect than its force on you (Newton's second law, a=F/m). Second, there is friction between you and the floor which can be much bigger than the force the book exerts on you, so you do not move; but the friction between the book and the table is normally less than the force you apply to it, so it does move. Imagine that the book is nailed to the table and you are standing on a floor which is very slippery ice. Now, when you push on the book, it will be you who moves. Or, if you and the book were in empty space and you threw it (by exerting a force on it), you would recoil (with a much slower speed) because of the book's force on you.

QUESTION: :
How can a planet like jupiter have enough gravity to cause tidal friction on one of its moons to cause volcanic activity. yet doesnt pull the moon crashing into it?
ANSWER:
It makes no difference how strong the gravity is, there will be a certain speed at a certain distance where a satellite can go into a stable orbit. So your second

QUESTION: has no relation to your first. The way tidal friction works is that the near side of the moon experiences a larger force than the far side because gravity falls off like 1/r2 as you go away from the source. This difference puts stress on the crust of the moon.

QUESTION: :
If you are in space between galaxy's, are you weightless inside your spacecraft or do you tend to stay near a bulkhead?
ANSWER:
You are, for all intents and purposes, weightless. If much of the mass of your spacecraft is concentrated in one locale, you would feel a net force toward it but the force would be so incredibly small that you would not notice it (maybe it would take ten million years for you to accelerate one cm toward it).

QUESTION: :
given ke=1/2 mv squared would it not be true that ke increases exponentially as an object falls in an accelerating gravitational pull like a rock falling to earth? in other words, the ke at any point in the fall increases exponentially with as it accelerates...
ANSWER:
You have asked an incomplete

QUESTION: because I need to know whether you want to know how it increases with time elapsed or with distance traveled. First, let us be clear what an exponential increase is: if kinetic energy may be expressed as a function of the form Cat or Cax where C and a are constants, and t and x are time and distance fallen, respectively, then it increases exponentially. So, let's see. I will assume I drop something from rest. Then the velocity is given by v=gt or v=√(2gx). So, KE=�mg2t2=mgx; KE increases quadratically with time and linearly with distance, not exponentially.

QUESTION: :
My girlfriend doesnt believe in the possibilty of traveling back in time because she doesnt believe theres anywhere to travel back too. In other words if you did travel back in time your not actually going back in time your going to an alternate universe so there would have to be an alternate universe for every second of the day because yesterday is gone. Is there some way or theory I could explain to her to help her understand in at least the possibility.
ANSWER:
She shouldn't say there is not "anywhere to travel back to", but rather not "anywhen to travel back to". As far as contemporary physics is concerned, she is right (not because the past does not exist somehow, but there is no known mechanism to get there). It is possible to time travel to the future, though. See my earlier discussion of the twin paradox. Alternate universes and worm holes are two speculative ideas which might supersede currently accepted physics, but they are hypothetical.

QUESTION: :
Considering that ether has been long debunked, how do we explain the wave part of the particle / wave duality, doesn't a wave mean a disturbance in some medium?
ANSWER:
Something has to be "waving" but it does not have to be a material medium. See my earlier discussion of electromagnetic waves.

QUESTION: :
If the earth is rotating on its axis at a speed of 1000 miles per hour, how come we dont experience the movement and only the change of light and darkness. Why would'nt vertigo be the norm? the earth appears to stand still.
ANSWER:
First, we do not experience movement because our whole environment is traveling with us, including the atmosphere. Note that if you are in an airplane going with a constant speed of 600 miles per hour you do not experience motion. The second thing to consider is the acceleration; anything going in a circle experiences an acceleration. Acceleration is what makes you queasy on an amusement park ride. But, since the radius of the earth is so large, the acceleration we experience because of our rotational motion is very small, in other words our path over a few minutes is just about a straight line and we experience no significant acceleration.

QUESTION: :
Why is it that spaceships need propulsion when there is nothing slowing them down. And if they reached a certain speed then continued untouched by gravity would they stay at that speed forever?
ANSWER:
If you are in truly empty space, no propulsion is needed to maintain your speed. This is approximately true for all space probes we send to other planets and beyond, approximately because they are usually far from massive objects and the space is almost free of gas. Of course, you need fuel if you ever want to change direction, slow down, correct for the gravitational effects which are small but not absent, etc. Most of the time, once the desired course has been set, no fuel is used.

QUESTION: :
I've recently been reading a book about physics, and, in one section, they describe how to calculate the exact position of a thrown object (such as a ball) on the y-axis. The mathematical formula that they present, though clear in some ways, is not clear in others. It is: y = vt - ( (1/2)g(t^2) ). I understand the (vt) part and the (g(t^2)) part because the velocity*time would give the distance travelled while the g, the earth's gravitational pull (9.8 m/s^2)*(time^2) would give the distance travelled caused by the force of gravity, but I do not understand why the (1/2) is there. I think (from the way I have understood what they have written) that they seem to have derived this equation from the equations describing the velocity of the ball, but they do not explain how they derived it. The first equation/statement that they have made is that the initial velocity in the x direction will remain constant over the course of the ball's movement (which adheres to Newton's first law), or v2x = v1x. The second equation is that the second velocity is equal to the first velocity minus earth's gravity*time, or v2y = v1y - gt. Can you help me understand what I am missing?
ANSWER:
What you are missing is just a little calculus to help you do the math to derive the equations from the basic assumptions. Velocity is rate of change of position, acceleration is rate of change of velocity; calculus deals with rates of change of things. What you have written is the position as a function of time if the acceleration is a constant, -g. What you write as v should be written as v0 which is the velocity at time t=0; by v we usually mean the velocity at time t and in a constant acceleration problem, v is always changing. I am going to tell you one piece of calculus. If you have a function of the form tn, where n is any integer, then the rate of change of that function is ntn-1. For example, the rate at which t3 changes is 3t2. OK, let's apply that to y=v0t-�gt2. What is the velocity? [Rate of change of position y]=v=v0∙1∙t0-�∙2∙gt1=v0-gt. This makes sense, because you can see that velocity is decreasing (becoming more negative) at the rate g, which is the acceleration due to gravity. The equation for velocity is easy to find the rate of change of because it is a linear equation whose slope is the rate of change. But, just to follow through on calculus I gave you, [rate of change of velocity v]=a=-g∙1∙t0=-g, in accordance with our expectations.

QUESTION: :
i am not a student. just interested in physics. this is a

QUESTION: just for the physicists. why do none of your theories have to be proved. take Schrodinger cat experiment for example. it does not make any sense and there is no logic to it. maybe Alastair Rae has it correct. is it real or just an illusion. Einstein spent most of his adult life trying to disprove theories that the person who came up with it could not prove and yet Albert could not disprove it either. some of these things make sense but others are nonsense and you have to sit back and wonder why. i know i will offend a lot of you but coming from a person who is not coledge educated and looks at things from a reality perspective you guys don't seem to have a clue. most of the basic theories make sense and do have validity. but when you get to the molecular level and start talking about things you cant both measure speed and position at the same time because just by observing it you alter it and thereby invalidate the measurement. well then you are getting a little ridiculous don't you think. your field of study is fascinating to me until you get to the useless stuff. well thats my rant , sorry if i pissed you off but sometimes common people have a better perspective on reality than those of you who are over educated and think too much.
ANSWER:
What makes you think that physicists do not need to "prove" theories. Making theories is only maybe 20% of our work, testing them is the other 80%. The first thing you do to betray your ignorance is to call Schr�dinger's cat a theory. It is what is called a gedanken, a thought experiment put forward to make a point. And, here is what is ironic, the point Schr�dinger was making was that which you evidently espouse, that quantum mechanics, at least the Copenhagen interpretation, is an incomplete theory. Even though Schr�dinger was one of the fathers of quantum mechanics, he was on Einstein's side on this point. In his original cat article Schr�dinger writes "One can even set up quite ridiculous cases." It makes no difference to me whether you are college-educated (or if you can spell it); lots of "common people" can think logically and analytically, keep an open mind to new ideas. A major part of your rant addresses "reality". You find the uncertainty principle (that you cannot measure position and speed to arbitrary accuracy simultaneously) untenable from a "reality perspective". Have you taken the trouble to find out how accurately you are able to measure them and at what point the uncertainty principle kicks in? Suppose that you could measure the position of a car to the diameter of one atom, about 10-10 m (even though you and I could never hope to make so accurate a measurement). How accurately could you measure the speed? For a 1000 kg car, I could measure the car's velocity to an accuracy of about 10-26 m/s=2.2x10-26 mi/hr. Have you ever thought about trying to make measurements to such accuracy? Your "reality" is not reality but intuition; your gut tells you that you can measure a car's speed and position at the same time just fine (just take a photo of the car driving past a meter stick with the speedometer visible in the photo, right?), so it must therefore be possible to do the same for an electron. But what you are doing is extrapolating your experience (with cars) into a region where you have zero experience; intuition is based on your experience, and it is not valid to apply your intuition where you have no experience. The real bottom line goes back to your claim that we have no need to prove our theories. The fact is that quantum mechanics has been shown innumerable times to describe the way the subatomic world is observed to behave; the "proof" is overwhelming.

QUESTION: s still exist and are vigorously debated concerning whether it is a complete theory, how to interpret the theory, what does a measurement or observation really mean, etc; this is how it should be�existing theories should always be held up for testing and contemplation. Your claim to be "interested in physics" but not "the useless stuff" really means you are interested only in physics more than 100 years old; 100 years ago most physicists assumed that, given how well Newtonian mechanics and Maxwell's electromagnetism worked, there was nothing left to understand, just keep making more accurate measurements of things that were already understood. In the end, I agree that theories need to be proven, but mainstream modern physics is at least shown to be in agreement with happens in nature and has been able to predict phenomena not previously known. That is why I am not a fan of string theory�it makes no predictions or descriptions of nature and therefore is not testable.

QUESTION: :
My

QUESTION: is in regard to special relativity. So according to this theory, we know that time changes based on how fast one is traveling or under different gravitational fields. I'm interested particularly with the time aspect of relativity--suppose one person is traveling fast enough or is under a strong gravitational field to result in some sort of time dilation effect and we compare this to an observer on earth. Using a simple mechanical clock, could we really observe a difference, and what is actually happening to the mechanical clock for this to happen?
ANSWER:
I know it is really hard to believe that clocks in moving systems really run slower. But if I could get you to agree that one particular clock is a perfectly good clock and all other clocks (mechanical, biological, etc.) would run in synchronicity with it, and I could make it believable that this clock runs slow when moving, then you would have to believe that time runs slower in moving systems, right?! The one thing you must believe is that all observers measure the speed of light in a vacuum to be the same. Now, read my earlier answer about the light clock.

QUESTION: :
Is it possible for physicists to know the half life of a radioactive substance just by the arrangement of the protons and neutrons or is it completely random and the only way to find out is by measurement of each of the different isotopes?
ANSWER:
The structure of nuclei is a pretty well developed theory. What that means is that we can often fairly accurately calculate the half lives of nuclear decays. But, if you want a really accurate value, you should measure it if possible.

QUESTION: :
Why does light travel so fast?
ANSWER:
Light is an electromagnetic wave, that is, it is a phenomenon involving electricity and magnetism. The physical laws which describe electric and magnetic effects are called Maxwell's equations (there are only 4 equations). It turns out that if you mess around with these equations you can actually calculate the speed of light. It is determined by only two quantities, one tells you how strong the electric force is and one tells you how strong the magnetic force is. So, the properties of electromagnetism fix the speed of light to what it is, 3x108 m/s.

QUESTION: :
If a car A, of mass 1,000 kg, and velocity 100 km/h, collides with a car B, of mass 1,750 kg, and of velocity 90 km/h, will the cars come to a stop when they collide, or will the overall forces push the cars in one direction or another? As in, will the greater mass of car B cause the cars to move in the direction that car B was travelling? I would assume this is so, because of the addition and subtraction of vectors, but I become confused when I try to account for the the law of action and reaction, and the elastic/inelastic nature of the cars.
ANSWER:
In a collision, the important quantity is linear momentum, mass times velocity; linear momentum in a collision does not change (this is called conservation of momentum). I presume that you are talking about a head-on collision. I will say that the 1750 kg is origninally going in the positive direction, that is its velocity is +90 km/hr and its momentum is 1750x90=157,500 kg-km/hr. The other car's momentum is 1000x(-100)=-100,000 kg-km/hr. So the net momentum before they collide is 57,500 kg-km/hr. Immediately after the collision let us assume that they stick together (called a perfectly inelastic collision); then the momentum after the collision of the 1000+1750 kg=2750 kg coupled cars is the same as just before. So, the speed of the two coupled cars is v=57,500/2750=20.9 km/hr (in the direction the 1750 kg car was originally going since it is positive). In the real world, the two will slide to a stop, but how far depends on local conditions (like is the road slipery, are the wheels locked, etc.) If they do not stick together, all sorts of possibilities exist, but it is quite unlikely that one of the cars will be at rest. Note that the 1750 kg car would not have "won" if it had been going much slower. You could figure the speed that the 1750 kg car would have if the two were to come to rest: 1750xv-100,000=0, so v=57 km/hr.

QUESTION: :
Why couldn't a scientist accelerate a metal object to near light speed by building a electromagnet around a long vacuum tube with a metal object (ball) within it. The way I imagined it.... the tube would be surrounded (the length of the tube) with electromagnets that would "fire" along the length the tube creating magnetic fields that pull (or push would work too I think?) the ball along.....In other words the steel ball in the tube would be at position "a" and then position "b" magnet would "fire" pulling the ball to position "b" and then the electromagnet at position "c" would fire and position "b" magnetic would shutoff pulling the already moving ball to position "c" at slightly increased speed and so on and so forth. Since its my understanding that electricity is conducted at virtually the speed of light, it seemed to me that proper engineering could accelerate the ball to virtually the speed at which electricity is conducted.
ANSWER:
The idea of using magnetism to accelerate a projectile has certainly been developed; it is called a railgun. However, just because the fields propagate at some speed does not mean the projectile will be easily accelerated to those speeds. No matter what, you have to somehow provide enough energy to your projectile and this has nothing to do with the speed of field propagation.

QUESTION: :
I understand that all forms of electromagnetic radiation travel at c in a vacuum. Do they travel at different speeds from one another in a medium such as water or glass?
ANSWER:
The speed with which an electromagnetic wave goes through a medium other than vacuum is very complicated to understand and depends on the structure of the material. However, it is certainly true that the speed of the wave depends on the wavelength of the wave. This is called dispersion and it is the reason that visible light passing through a prism (or raindrop) is spread into a rainbow of different colors.

QUESTION: :
If I have an observer A and B, and A is "at rest" while B is traveling .7c (or any big number smaller than c) in one direction, B would slow down in time, a la the effects of speed/mass and time dilation. This works in the reverse, since movement is relative. However, now A and B would perceive each other to be moving slower in time than the other, even though their "times" are slowed down equally. Why wouldn't they perceive one another to be traveling through time "normally"?
ANSWER:
I really do not know what you are asking. What does "normally" mean? And, time is not perceived to run slower for a moving clock, it really does run slower. The thing to grasp is that it is true that for both A and B, the other's clock is running slower. In order to compare their clocks they must get into the same frame (not moving relative to each other). You may be interested in the twin paradox and a recently asked related

QUESTION: .

QUESTION: :
If atoms, hence molecules,hence objects are predominately 'empty space', why do things not simply fall through the other e.g. a book does not fall through the table, we do not fall through the floor, etc
ANSWER:
This

QUESTION: has been often asked before and the answer is linked to from the FAQ page.

QUESTION: :
is it possible to conserve momemtum with a mousetrap? make the mousetrap continuously reload itself?
ANSWER:
I have no idea what you mean. Certainly a mousetrap cannot reload itself. It is really an energy thing, not a momentum thing. Before the trap trips, energy is stored in the spring. When tripped, that energy is converted into the kinetic energy of the "killer bar" and when it strikes the board, the energy is converted into thermal energy (the trap heats up a little) and sound energy. There is no way to use the thermal and sound energies to tension the spring back, i.e. the energy the spring originally had is essentially lost.

QUESTION: :
I am watching a tv show discussing the relationship between high velocity, gravity, and time. The show gave a hypothetical example: "Time travelers" or astronauts traveling at near the speed of light could experience 1 year of travel but find that 10 years had passed on earth while they were away. My

QUESTION: is: In the above scenario, what does physics say about those astronauts being able to send and receive a signal, say with a rover, or even to just receive a video signal, if the signal traveled at the speed of light while they traveled at "near" the speed of light? If they could receive a video signal of earth would they witness time slowed?
ANSWER:
If you were a frequent reader of this web site, you would see that one of my favorite points of view is that in special relativity, it is not how things look, it is how things are. A moving clock may appear (under some circumstances) to run faster, but it actually runs slower. There is nothing to prevent two observers from communicating with each other using light signals, but how those communications appear to each observer depends on their relative motion and does not reflect how fast their respective clocks are running. You should look at my earlier discussion of the twin paradox; if the moving twin is looking at a tv show (broadcast from earth) while on his way out, it is in super-slo-mo (he gets two years worth of signals every six years) but on the way home it is in fast-forward (he gets 18 years of signals in 6 years). As you will see, my whole explanation of the twin paradox hinges on the twins' communicating.

QUESTION: :
suppoose two blocks are placed such that one is belo and other is above ,,,,ionthe grond ....now below block have two rough surfaces....of ground and of other block......now if we apply ahorizontal force on bottom block such that it doesnot move ...... now it means both suface give static friction,,,,so by newtons third law...a staic fricion pair act on upper block $ hence it should move.,,,but it is never seen that ...below block is not moving but upper block is......where is my fault
ANSWER:
You are assuming that the upper block has a friction force on it, but that is incorrect. Suppose we apply Newton's law to the upper block: it is in equilibrium in the horizontal direction and therefore the sum of all horizontal forces on it must be zero. Now, the only possible horizontal force on it is static friction from the block below it. Therefore, that friction force must be zero. If you push on the upper block and nothing happens, there will be friction forces between it and the block below and between the block below and the floor.

QUESTION: :
I asked this

QUESTION: to many teachers of our country but couldnt get precise answer. It may sound a stupod

QUESTION: though. If two bodies having same volume but different mass(say 1 be 20 kg and another 30 kg) is dropped from equal significant height, which will fall on earth faster? And why?
ANSWER:
And, you will not get a precise answer because you are not asking a precise

QUESTION: . What does "significant height" mean? 5 m, 5000 m? What is the "same volume"? A marble size, a bowling ball size, a football stadium size? I am not being flip here, but the big

QUESTION: is how important is air drag? If air drag is not important, the two hit the same time. So, if you drop two bowling ball sized objects from a height of a few meters, they will hit the same time as long as their masses are not too different (like your 20 & 30 kg objects). You can find an explanation of why that happens on my FAQ. On the other hand, drop a balloon and a bowling ball, both the same size, and you and I know who wins that race. If there were no atmosphere, they would still tie, but you see that in the real world mass makes a difference. The air drag also depends on speed, in fact it is approximately proportional to the square of the speed for most objects, so the faster you go the more important drag becomes (in a hurry). That is why I stipulate from not too high. You can find exhaustive discussions of air resistance, free fall, and terminal velocity, also on my FAQ page.

QUESTION: :
I am having a little trouble understanding why certain differences exist in the densities between elements. For this

QUESTION: I'll use Uranium, and Osmium. Uranium has a density of 18.9 grams per cubic centimeter, Osmium has a density of 22.6, yes Uranium has an atomic mass of 238, whereas Uranium has 190. Since Uranium has more protons, electrons, and neutrons per atom than Osmium, I am afraid I am at a loss to explain to myself why a cubic centimeter of uranium is less dense than a cubic centimeter of osmium. Could it be that the volume of the uranium atoms is so much greater than the osmium atoms that fewer can occupy 1 cubic centimeter and thus account for the lower density?
ANSWER:
It all boils down to what is the size of an atom or, equivalently, how far apart to atoms of a particular element space themselves in the material. The size of an atom is determined not by what its atomic number or atomic weight is, rather it is the atomic structure. For example, the radius of potassium is much bigger than for lead. I have looked at a table of covalent radii in Wikipedia to get some numbers for this answer. In your case the radius of an osmium is about 130 compared with uranium which is about 175 (these are in pm, picometers, but that is not important because I will look at ratios). So if a solid were just a pile of atoms, the density would be m/V and the volumes are proportional to the radii cubed, so the ratios of the densities of uranium to osmium would be ρU/ρOs=(238/1753)/(190/1303)=0.51. In this simple model, uranium has only half the density of osmium. Of course, this is a really simple model and much depends on how the atoms bond in the bulk material.

QUESTION: :
I've been following the news about the LHC, and while it's very fascinating, I'm curious why it's any more imperative that we find a higgs boson than a graviton? I understand that we don't really have a very good understanding about how particles acquire mass (i.e. in the standard model), but there is also evidence that implies that our theory of gravitation might not be consistent under all circumstances (i.e. it isn't at singularities). Is it erroneous to think that finding the graviton is equally important to finding the higgs, or maybe even more so? It just really seems that finding the graviton would preclude finding the higgs, since it's responsible for one of the four forces in our physical universe.
ANSWER:
My perspective would be that the Higgs boson has been predicted by the standard model of particle physics, a very successful model in describing elementary particle physics; a graviton is predicted by no theory because there is no successful theory of quantum gravity. The graviton would be the quantum of the gravitational field if there were such a theory. For now, though, there is no particular reason to believe that gravitons actually exist. Also, we have no idea what to look for or how to look for it.

QUESTION: :
Is their a maximum tempeture or can heat be infinite. If their is an abslute cold why can't there be an absolute heat. If heat causes aomic particles to accelerate is it possible for heat to cause matter to go beyond e=mc^2.
ANSWER:
There is a speed limit for particles (the speed of light), but there is no energy limit. And, since the temperature is defined to be the average energy per particle in the object, there is no upper limit to temperature. Of course, as energy per particle increases, molecules and atoms disintegrate into nuclei and electrons (a plasma) and then nuclei start interacting with other and transmuting and so forth, so the identity of what it is you have may change, but there is no upper limit on the total energy of a system.

QUESTION: :
Doing a little target practice the other day I observed something that I am at a loss to explain. For this exercise I hung a large block of wood from a chain (I'd estimate the weight of the block at around 100 pounds) Then I shot it with a .30-06 springfield. The particular cartridge loads I was firing produce a muzzle energy of about 2600 foot-pounds. (I was about 50 feet away, more than close enough for the bullet to retain substantial energy) The bullet made it about 8 inches into the block, since the bullet failed to penetrate this tells me that the block took the full energy of the bullet. However when it was struck the block more or less wobbled on the chain. Now as I understand the term foot-pounds, this is the energy required to move 1 pound, 1 foot. So I am a bit of a loss to understand how all of the energy here was expressed. The energy of the bullet in foot pounds is exponentionally higher than the weight of the block yet it moved surprisingly litte. I am not sure I understand why. My first thought was that it had something to do with the law of equal and opposite reactions, as the bullet impacted and pushed the block, the block pushed back. It also occured to me the block is hanging from a chain, and when its center of gravity was disturbed gravity pulling it back toward that center could also have had an effect. So I was hoping you could explain for me why the block moved so little? Where did all of my bullet's energy go?
ANSWER:
First, what is a ft-lb? It is the energy needed to lift one pound one foot, not the energy necessary to move it one foot. So, your 2600 ft-lb could have, if transferred to a 100 lb block, lift it 26 feet. Wow, do you believe that? So your

QUESTION: "Where did all of my bullet's energy go?" really needs to be asked. The fact is that what you have is called a perfectly inelastic collision; that is where the projectile and target stick together after the collision. And, the energy is not "conserved" in an inelastic collision, that is, energy disappears during the collision. (It does not really disappear, we will get to that later.) Now, scientists do not really like to work with feet and pounds and stuff like that, we prefer meters and kilograms and Joules (for energy), so I am going to recast your problem to those units. 100 lb is about 45 kg, 2600 ft-lb is about 3500 J, the mass of the bullet (I get from Wikepedia) is about 0.01 kg (10 grams), and so the speed of the bullet is about 840 m/s (which is about 1900 mph). What is conserved in any collision is linear momentum which is the product of mass times velocity. The momentum of the bullet before it hits the block is 0.01x840=8.4 kg-m/s; this must be the momentum after the collision, so 45.01v=8.4, so v=0.19 m/s=0.6 ft/s. The energy after the collision (using �mv2 for kinetic energy) is only about 4.8 J=3.5 ft-lb. This is only enough to lift your block about half an inch! So, back to your

QUESTION: �where did the energy go? Don't stick your finger in the hole right afterwards, it will be hot. The energy goes into heat and you will find the bullet and block both hot. What "disappears" is kinetic energy (energy of motion), not total energy which is conserved.

QUESTION: :
If an electrically charged rod is brought near normal flow of water from a tap, the flow gets slightly diverted towards the rod. How does this happen ?
ANSWER:
The water, being in the electric field of the rod, becomes polarized, that is the water closer to the rod has a charge opposite the rod and the water on the other side of the stream has a charge the same. The opposite charge is pulled toward the rod and the like charge pushed away. But the opposite charge is closer and so the force it experiences is bigger, so the net force on the water is toward the rod.

QUESTION: :
Are not black holes, not holes at all but intensly hardened spherical objects?
ANSWER:
They are singularities, that is they are points but have mass. So, they have infinite density. But the reason they are called holes is that everything that comes within their range is captured and disappears. The reason they are called black is because light cannot escape them either. I would call that a hole.

QUESTION: :
if the earth is rotating and moving around the sun and the all while the milky way is rotating then why do we always see the same stars when we look up at night. i understand that the galaxy is full of stars and they move around the center and that we are on the outer reaches of an arm of the spiral but even so with the earth traveling around the sun and the solar system in motion and the earth rotation all at the same time it doesn't make sense why the sky is always filled with the same constilations. yes the are located in a different place over the night but they are always the same ones. help me to understand this phenominon please
ANSWER:
In fact, the sky is not the same all the time. It changes with both time of day and time of year. There are some constellations only visible at certain times of year. Regarding the galactic rotation, the period is 50-250 million years (depending on how you define it, it does not rotate like a rigid body) so wer are not likely to notice any drastic changes there.

QUESTION: :
I've been reading about dark matter and dark energy lately, and like most people, I'm very confused! I understand that dark energy is the energy of empty space, representing the cosmological constant. So is dark matter really just the matter that comprises empty space? This would make sense, given that 90% of the mass of a proton is empty space--we're living in a universe that is dominated by more dark matter than regular matter!
ANSWER:
The motion of many things in the universe cannot be understood if we apply known laws (gravitation) with observable mass (stars, planets, etc.). Therefore, it is postulated that there must be something, dubbed dark matter, which we cannot see which is causing things to move differently than we expect. I should note that all attempts to observe this stuff have failed, although the search goes on. My own take on dark matter is that it is just as likely that our "known laws" are not as good as we believe them to be; that is, we do not understand gravity as well as we think we do. Several years ago it was determined that the most distant objects were not just moving very fast, they are actually accelerating. This was totally unexpected because gravity is, as we know it, purely an attractive force and the speeding up would imply the existence of a repulsive force. The origin of this mysterious force is referred to as dark energy. Again, what it is is not well understood and one way to integrate it into general relativity (the theory of gravity) is, as you note, to reintroduce the cosmological constant rejected by Einstein early in the development of the theory. I have no idea what you mean by "90% of the mass of a proton is empty space", but if dark matter is the answer and it is found, the universe is dominated by it.

QUESTION: :
If a 60 kilogram human were to fall off the top floor of the Eiffel Tower (276.13 meters), how much would they accelerate before they hit the ground?
ANSWER:
First, the easy answer�ignore air friction. This is what an elementary physics book would tell you. In that case, 0=276-5t2 and v=-10t. The first equation tells us that he would fall for 7.4 seconds and then the second tells us that he would be going 74.2 m/s=166 mi/hr; the mass is irrelevalant. But the assumption that air resistance is negligible for this problem is surely wrong. Putting in the effects of drag is very complicated and I have written many answers related to this topic. If you are really interested, you can look at those answers.

QUESTION: :
I'm a high school student aspiring to study physics like a lot others students out there and I got a work related

QUESTION: : Do you get free leisure time for yourself and did you get to have fun and do your own things when in college? I'm not a party freak or something like that but I do like to paint, travel, reading, things like that, but a lot of people tell me that if I study physics I "won't have a life". I'm just curious as if this is a myth or is there some small truth behind it.
ANSWER:
Well, this isn't really a physics

QUESTION: , but I guess I can't resist saying a bit about this. Are there some scientists who are narrow, just do science, in short are nerds? Sure. But, there are just as many English professors who are narrow, only care about books and arcane criticism; and businessmen who spend 80 hours a week at work churning out money; and attorneys whose only interest in life is to just get that partnership; or physicians who have time for nothing but work and golf. In my experience, there are many more scientists who have appreciation for art, music, and literature than there are practitioners of the humanities who have any appreciation for science. Your life is what you make of it and science, although a demanding mistress, provides ample opportunities for those doing it to taste many flavors in life. Many of my fellow physicists, like myself, have collaborated with colleagues all over the world, traveled to spend time at other laboratories, done research around the world, attended conferences on many continents. I, myself, have done experiments in Paris, Tokyo, Vancouver, Los Alamos, and you can be sure I did not just go to the lab when at these places. Here is what matters�do what you love and have broad interests on top of that. You will have a happy life. Given the advice you have gotten, "a lot of people" are nuts. You can maybe get an idea of how a perfectly ordinary physicist can "have a life" from my personal web page. You might enjoy the book "The Life it Brings" by Jeremy Bernstein.

QUESTION: :
I can't get the actual concept of energy. In my text books it is given that energy is the capacity to do work. And work is the scalar product of force and displacement. But i can't understand anything from that definition. What is the need, or what is the physical significance of these two physical quantities?
ANSWER:
Here is my perspective. Sometimes the fundamental ideas of science can be expressed rather easily, take Newton's laws for example. But, there is often more than one way to skin a cat. Energy, at least at the level it appears in introductory textbooks, really is nothing more than Newton's laws expressed from a different point of view. Often in science we find that if we find clever new ways to express some idea, we gain insight and we make problem solving easier. No new fundamental physics is introduced but our whole understanding becomes clarified. That is what energy is, just a new way of looking at things. If we define something called work, it turns out that when we do work on a system we change its energy, and this energy stuff turns out to be very powerful (pun intended). One thing that comes from it is that if we have some system where no work is being done on it, its energy is conserved. And seemingly hard problems become easy. For example, if you have a car sliding down a smooth hill whose shape is unknown but whose height is known, it is trivially easy to find the car's speed at the bottom using energy concepts yet very subtle and tricky to do just using F=ma. The simplest example of work/energy is the isolated particle on which we do work; the thing you change about the particle is �mv2, the kinetic energy of the particle. If you look in your textbook, you will find that the derivation of this simple fact employs only Newton's second law and simple kinematics.

QUESTION: :
if gravity in space acts like a magnet is there a , if weak, a gravity in between planets?
ANSWER:
Gravity does not act like a magnet. A magnetic force is sometimes an attractive force, that is where the similarity ends. Gravity is throughout the universe, although the farther you are away from large masses, the weaker it is.

QUESTION: :
When we say that a large mass causes spacetime to be warped, what exactly does that mean? My understanding is that the idea that space is made up of some type of "ether" was long ago refuted (Morely-Michaelson?). Yet when photons travel near a massive body, their path is affected. This obviously can't be due to gravitational attraction since a photon has no mass.
ANSWER:
You will find these

QUESTION: s addressed in several earlier answers. Go to my FAQ page.

QUESTION: :
Is there a way to help nuclear decay happen more often than it happens naturally? Is there a way to pound nuclear waste into iron in a particle accelerator?
ANSWER:
You cannot change the half life of aome particular process. But you can force something to follow a different path and create something more benign. The ideas for transmutation of nuclear waste involve both accelerators and reactors. Although there has been lots of thought about how this might be done, it has not proven practical on a large scale as far as I know.

QUESTION: :
I was wondering what could happen if you could get energy from harnessing the ocean. for example could you create energy by filling a huge basin in the ocean with water, draining it through a turbine(s) and then repeat? I would assume you would have to drain the water to start the process again, which might be a problem because that would use energy? Is this a good idea or not plausible?
ANSWER:
It would take more energy to fill it (lift the water up) than you would get by letting it fall through turbines. However, the ocean is a vast source of energy via tides and waves.

QUESTION: :
Someone I know reckons the rotation observed when a ball on a string is going round in a circle is only a visual effect and not real, another person says its real and its called synchronous rotation. Can you tell me which of them is right and why?
ANSWER:
See an earlier answer.

QUESTION: :
If we spin a round object in a vaccum like in deep space will it rotate forever?
ANSWER:
In a classical sense, the answer is yes (although there is no such thing as a perfect vacuum). A second layer of this

QUESTION: is that a rotating mass will emit "gravity waves" the same way as a rotating charge distribution will emit electromagnetic waves, so its energy will eventually be radiated away. I should add the proviso, however, that gravity waves are hypothetical in the sense that they have never been observed directly.

QUESTION: :
Atoms are surrounded by electrons with a negative charge. What cohesive force keeps atoms together instead of being flung apart due to repulsion of negative charges?
ANSWER:
The easiest way to understand this is that the outermost electrons in an atom get shared shared with a neighbor. If one kind of atom has one "loosely bound" electron and another has a vacancy (hole) in its outermost shell, the two atoms will bind together to form a a molecule. This is sort of what chemistry is all about (valences). In a solid, the atoms are also bound by sharing electrons but, if there is too high a temperature, the atoms will separate (melting).

QUESTION: :
So quick

QUESTION: , was just curious as I was making iced coffee, I boiled it in a French press, then I stick the coffee in a mayonnaise jar, and put it in the freezer to cool it. (I usually put ice in it too, but I was out this time).. And I wondered 2 things at once: 1. I've heard that if water is hot when it's put in a freezer, it freezes faster. I know that a stopwatch and a well conducted experiment would allow me to answer this for myself, but truth be told, I'm lazy, and was wondering if maybe you could just ya or nay that

QUESTION: a lot faster, plus, it still wouldn't answer WHY that was the case, if it IS true, so hoping you can help there too. and 2. I was stopped for just a second by wondering if I should leave the lid on or off, or if it would make a difference at all.. If I left the lid off, seeing the steam come out of the jar as I put it in the freezer, I thought "well all that steam would get out and could thaw some of what I already have frozen in there.." (probably not true, but I thought it). Then on the heals of that I thought "well there would be a certain amount of heat energy inside that bottle that has to get out in some way, at some point, so the heat would transfer from the coffee, to the glass, then through the air in the freezer.. in other words, it's going to get out anyway, so what difference would it make whether the lid was on or off?"
ANSWER:
Read my earlier answer.

QUESTION: :
If coffee is placed on a coffee warmer that has a 110 degree F coil temperature, will the liquid gradually achieve a thermodynamic equilibrium by reaching and remaining at 110 degrees F? The coffee could begin either warmer or cooler?
ANSWER:
That depends on what else the cup is in thermal contact with. For example, if the room is real cold, the coffee will come into equilibrium at a temperature lower than 110.

QUESTION: :
Are movement (acceleration) and gravity linked? To clarify, I read that an object accelerating at 1g will be moving close to the speed of light within one lifetime. Why is it that here on earth we are not experiencing the effect of near light speed travel every 80 years, relative to an object that exists far away from our gravity well? also, is it that time passes more quickly for objects father out from a gravitational influence and this is the acceleration they 'feel' when they move against it? (the slowing of relative time is the 'force' of gravity)
ANSWER:
Certainly acceleration and gravitation are not related in the sense you suggest. Maybe you are thinking of the equivalence principle?

QUESTION: :
An object gains mass as it moves faster. So the inverse must also be true: An objects loses mass as it moves slower. If an object comes to a perfect (universal) stop, does it become massless? Time moves slower for an object, relative to other objects, as an object moves faster, relative to other objects. So the inverse must be true: Time moves faster relative as an object moves slower relative. If an object comes to a perfect stop, how fast is time, relatively speaking? Is there a similar function to "cannot reach or exceed lightspeed" as it relates to time, such that an object can never come to a perfect stop? (maybe because it becomes less massive than light, implying that light does, afterall, have some mass, which certainly is not our current understanding) Do we need an analogous term to "Lightspeed", called "Lighttime"? What's "Lighttime" and what are its limits? Maybe the analogous term would better be "Masstime"?
ANSWER:
The problem with your

QUESTION: is that the whole thing is based on a fallacious premise�that there exists something called "a perfect (universal) stop". That implies that there is some single preferred frame of reference in the universe and any other frame should be viewed as moving with respect to that one. In fact, there are an infinite number of frames where the laws of physics are those which we know and they all move with constant velocity with respect to all others. These are called inertial frames of reference. An object at rest in any inertial frame has a mass called its rest mass and, if it is moving with respect to some other frame, it has a larger mass as measured by an observer in that frame. Similarly, a clock at rest in any inertial frame runs at a rate called proper time and, if it is moving with respect to some other frame, it runs more slowly as measured by an observer in that frame. One thing you did not mention was length: an object at rest in any inertial frame has a length called its rest length and, if it is moving with respect to some other frame, it has a shorter length as measured by an observer in that frame. The only thing observers in all frames agree on is the speed of light�all observers measure the speed of a beam of light to be the same. So, the rest of your

QUESTION: does not really have any meaning. (Oh, by the way, light does not "afterall, have some mass".)

QUESTION: :
Can Gravity effect a Magnetic Feild? If there was a Magnatar (NutronStar) Orbiting a Black Hole would the Magnatar's electromagnetic feild be drawn toward the black holes gravity?
ANSWER:
There is no accepted relationship between gravity and electromagnetism. Einstein spent most of his life after relativity trying to find a relationship, to no avail. That is not to say there is no relationship, we just do not know it yet.

QUESTION: :
as photons have a momentum when they collide with objects (e.g a solar sail) and get reflected the solar sail gains a velocity and the reflected photon would have less energy and hence lower wavelength (by a very very small amount). I cant find any proof of this change in wavelength, is there any mechanism by which the energy of the photon is conserved or does the wavelength chance by an incredibly small amount.
ANSWER:
You can learn about photon elastic scattering by reading about the Compton effect, where x-rays scatter from electrons. This was one of the crucial observations and accompanying theory in paving the way for the new quantum mechanics early in the 20th century. So, let's look at the equation which, when energy and momentum are conserved, describes the change in wavelength as a result of the scattering: ∆λ=(h/(mc))(1-cosθ) where h=6.6x10-34 (Planck's constant), c=3x108 (speed of light), θ is the angle of scattering, and m is the mass (kg) of the electron or whatever else is doing the scattering (all in SI units). Let θ=1800 for bounce back reflection, then ∆λ=(2h/(mc))=8.8x10-42/m. Suppose that the wavelength is a visible photon, say λ=7x10-7 m and the mass of your solar sail is 1 kg. Then ∆λ=8.8x10-42 m. I think you would agree that, for all intents and purposes, the reflected photon has remained the same wavelength. On the other hand, if m=9x10-31 kg, electron mass, and λ=10-10 m (x-ray), ∆λ=10-11 m, a 10% effect.

QUESTION: :
is it true that matter cannot be produced just changed? what i mean is, does the matter that im made of come from the black hole and when i die, my matter simply changes but doesn't disapear?
ANSWER:
As I have said many times, there is no such thing as conservation of mass. Mass may be created or destroyed. The physical law is conservation of energy. The total energy of a system must remain constant. Mass is just a form of energy, E=mc2. Incidentally, you did not come from a black hole. The atoms from which you are made were manufactured in stars long since exploded and dead.

QUESTION: :
One man is inside a closed box in somewhere far in space with no force acting on this system and the container contains air. the man is holding onto a knob(which he can grab to stick to the wall) like thing in one side... and similar knob is on the other side of the box. At the begining, the momentum of the system is 0. He pusses himself against the knob with a force F and let go off the knob. he moves with a velocity V in one direction and the container moves in opposite direction with same velocity. After some time the man and the other side of the container meet. They collide and the man quickly holds the other knob. During his motion inside the box, he collided with millions of molecules moving in the random direction.for now, looking only in the direction of the motion, it may not be possible for equal no. of molecule to hit the man from both(towards and opposite)direction of motion( as the molecule are moving ranodmly) while moving through the air. So his final velocity(the velocity when he reaches the other end) may have increased or decreased as molecules randomly added their Vs to the man. But for the container the velocity has remained the same all the time. SO, there is difference in V during the final collision. AND as the man has held the knob again, he has in a way stuck to the wall making him part of the momentum of the box (which ultimately should have come to 0 when the man hit the opposite end of box.) BUT momentum of the both container and man donot cancel as the man has different V than it had when it separated from the box. THIS makes the system move in the one of the direction!!!! A object inside a Closed system affected the outer system( the whole container and the universe). This cannot not happen, as we know. so my

QUESTION: arises-- DID the air molecules acted in such a way that it was not random?? or equally distributed like a wave????????? to provide same Vs from both direction?
ANSWER:
Wow, what a rambling

QUESTION: ! Your

QUESTION: in essence boils down to: is linear momentum really conserved in an isolated system, regardless of how complicated the system is? First, you make a little error in saying that the box recoils with the same speed as the man; this happens only if the mass of the box happens to be the same as that of the man. In fact, when the man has latched on to the other side of the box and when everything has come into thermal equilibrium, the man and box will again be at rest. In order to understand what is going on, let's consider a more extreme situation: the box is filled with water. The mass of the box + water happens to be equal to the mass of the man. When he pushes off, the box + water recoils with the same velocity. Now, the man slows down, because of the water exerting a force on him (which is sometimes called viscous force, sometimes friction). As the man goes through the water he eventually stops. But, because of Newton's third law, the man exerts and equal and opposite force on the water + box, so they stop too. It is the same with the air as with the water, just less dramatic�any forces between the air and the man are equal and opposite so that the net momentum of the man and air has to stay the same. Momentum is always conserved in an isolated system. During the time of the man's flight, air molecules were not moving in their usual random way; those colliding with the leading wall slow down a little and those hitting the trailing wall speed up a little so that there is a net flow of air in the direction the box is moving. That is what you expect�the air has to move with the box. Those which you strike your front side slow you down but that speeds those molecules up in the opposite direction so that the net forward velocity of the air is a little less than the velocity of the box. At all times, the net momentum of everything is zero. A rambling

QUESTION: deserves a rambling answer!

QUESTION: :
does the volume of a liquid can be measure in litres or only in cubic meters? answer pleasse
ANSWER:
Volume can be measured in any units you like�l, m3, gal, qt, cc (i.e. cm3)� Of course, there may be some good reason to measure it in a particular way, like certain units are required in the answer of a homework problem or local conventions require a certain measure for people to understand.

QUESTION: :
Scholars teach that airplanes fly because the velocity of air on the top of the wing is higher than the velocity of air on the bottom of the wing, because the curve of the wing requires the air on top to travel a longer distance, the Venturi effect. A theory is that the Venturi effect is valid with liquids but is not the deciding factor with air planes, and that air plane lift is created predominantly by wing surface angles and opposing air forces, like a kite. Which is it and where is the proof? I envision an airfoil with the long curved surface above and the short curved surface below, both symetrical to the left and right, presenting it on the level to an airstream, and see if it flies. My bet is it won't fly and moreover it will dive. I'm trying to learn and any info will be greatly appreciated. Also I have a great deal of trouble understanding why the venturi effect works, with liquids or air. I can kind of see it with liquids, as the molecular attraction of passing liquid might pull inward the surface of the conduit, but find it difficult to imagine the same effect with gases of the magnitude required to lift an airplane. I guess my

QUESTION: is, how is the venturi effect described by physical equations?
ANSWER:
You are getting at a fact normally ignored in an introductory physics course�fluid dynamics is really a complex subject, not amenable to nice neat solutions on a blackboard. Nevertheless, we like to get real life applications of things like Bernoulli's equation which, although inexact and incomplete, provides much insight into fluid dynamics. I am not sure why you think that gases are less appropriate to apply fluid dynamics to than liquids. True, the notion that they are incompressible is much less applicable than for liquids, but the general ideas still hold. Your overall conclusion, that the "Venturi effect" is not the only important effect for airplane flight, is correct. You seem to want to assert that it has no effect, and that is certainly not true; the pressure being lower on the upper side of the wing plays an important role in providing lift. Your idea that the wing acts "like a kite" is not, I think, right either, since I think of a kite as being pushed up by a wind on the bottom which is not really what happens with a wing. I have had some flight instruction and one of the most important features in the theory of how planes fly is "angle of attack", the angle the surface of the wing makes with the oncoming airflow direction. Here is a brief explanation of how changing the angle of attack provides lift. When the wing is inclined, the air which comes off the trailing edge has a component downward. How did the air, originally moving horizontally, end up also moving down? It must have been that the wing exerted a downward force on the air. Finally, what does Newton's third law say about this situation? If the wing exerts a downward force on the air, the air exerts an equal upward force on the wing. Voil�! That, I believe, is the main reason airplanes fly (and also why curve balls curve and other phenomena which are normally attributed only to pressure difference in elementary physics classes). Keep this in mind, though: reread the first sentence of my answer�this is not simple stuff!

QUESTION: :
why do we need the wavelength of the light to be smaller than the object being viewed ?
ANSWER:
Because diffraction effects occur when the size of the object becomes comparable to the wavelength of the light. To form a good sharp image of something requires the wavelength to be much smaller than the size of the object.

QUESTION: :
Do light have mass? Why and how can light travel at the speed of 3 * 100000000 m/s? What is the accelerator of the light or due to which energy light so fast? Is the following statement proved or accepted without proof: Highest speed of any particle is 3 * 100000000 m/s. If it is proved then explain me how it is proved.
ANSWER:
Your statement about the highest speed of a particle being the speed of light is wrong; a particle with mass must have a velocity less than the speed of light. The answers to the rest of your

QUESTION: s may be found on the FAQ page.

QUESTION: :
In the Twin Paradox, someting I recently heard of, I have two

QUESTION: s.
Why is it that the closer you get to the speed of light, the less time affects you, in other words, what is it about extreme speed that makes your clock run slow?
The whole situation is just a though experiment, and if we assume the theory of speed affecting time (d=rt) then everything works out perfectly. Why is it a paradox?
ANSWER:
The reason that moving clocks run slow is that the speed of light is the same as seen by any observer. I know that this does not seem to follow, but that is the case. I believe the easiest way to see the connection is the "light clock" which I have described in an earlier answer. It is wrong to say that the faster you go, "the less time affects you". In your own frame of reference, time ticks on perfectly normally. Your second

QUESTION: makes no sense, but I assure you that the notion of moving clocks running slowly is not "just a thought experiment"; it is a well-verified fact. You might also be interested in reading my explanation of the twin paradox.

QUESTION: :
Do friction takes place in vacuum? If yes, then how and why? If no, then is fuel (force) required to continue the motion of spacecraft in vacuum (assume that it is moving with constant velocity)? I am confused because Galileo states that no force is required to continue the motion with constant velocity.
ANSWER:
In the context you are asking, no, there is no drag type friction in a vacuum. Hence, a spacecraft experiences no force and therefore moves with constant velocity without having to burn an engine. I should note that there is never a pure vacuum and so you are never really fully free of friction; this force is sufficiently tiny that you would probably go many millenia before there was any noticable loss of speed.

QUESTION: :
Is the graviton a particle like light is a particle, and if so, if you are moving away/toward it at high speed could it get 'red'/'blue' shifted, and you'd experience higher or lower gravitation?
ANSWER:
As I have said many times in my answers, there is no such thing as a graviton because there is no successful theory of quantum gravity. A graviton is the hypothetical quantum of the gravitational field in a quantized theory of the gravitational field (of which there is not one yet).

QUESTION: s about gravitons are also linked to on the FAQ page. Regarding your red/blue shift

QUESTION: : when photons are red/blue shifted, the electromagnetic force does not change strength.

QUESTION: :
Is the energy in our bodies (nervous system not nutrients) and the energy we power our devices with the same thing? i.e. are we electrical in the same way a television or stereo are? If so, can our electricity be measured in volts and amps and do we always transfer electricity when we touch?
ANSWER:
Electrophysiology is very complex and, in any reasonable detail, beyond the scope of this site. Nerve impulses are, indeed, electrical in nature. However, they are really very different from the electrical currents in your tv. Most appliances have currents carried by electrons in conductors whereas neural cells transmit currents using ions of certain salts. Currents are still measured in amperes and potential differences in volts.

QUESTION: :
why are the particles made to collide at a speed very near to the speed of light in the experiment carried out in the LHC at CERN?
ANSWER:
Because the things which they want to study take very large energies to create.

QUESTION: :
I recently was introduced to Hawking Radiation but somthing about it confused me how can particals with have Negitive Mass? I understand that photons dont have mass but how does Negitive Mass work all i can imagine when I think about it, is some sort of warped area of space that would curve inward relitive to the space around it???
ANSWER:
Hawking radiation is often pictured as a virtual particle/antiparticle pair being created near the the event horizon (called vacuum fluctuations) and one of the two (both with positive mass) escapes and the other is captured by the black hole. However, this creation is called "virtual" because it violates energy conservation (something from nothing) but that is ok, by the uncertainty principle, provided it only occurs for a very short time. However, because this particular pair does not get back together, energy must be conserved somehow and this is done by the particle which gets captured back having negative energy. Thus, the escaping particle carries away energy and the captured particle plus the black hole has net loss of energy. The final effect is for the black hole to lose energy which would be equivalent to saying we added negative mass to it.

QUESTION: :
Why torque is defined as cross product of r & F ?
ANSWER:
Torque represents the effectiveness of a given force to cause something to rotate about a given axis. Logically, it will depend on three things,
how far from the axis you apply the force,
the magnitude of the force, and
how much of the force is perpendicular to the moment arm (distance to the axis).
Taking the three together, torque should be proportional to rFsinθ where θ is the angle between the vectors r and F. Now, that just happens to be the magnitude of the vector product rxF! Finally, we want torque to be a vector because we want to distinguish between torques which make things want to go clockwise from those which make things want to go counterclockwise, so we very naturally define τ=rxF.

QUESTION: :
Is there any natural antimatter in the universe? I mean by "natural" antimatter that was not created by humans. Does it exist naturally in our universe, or somewhere else. Also, how exactly do we, humans, obtain antimatter? Do we get it from another universe? I know that matter cannot be created by the Law of Conservation of Matter, so how do we do it?
ANSWER:
Nuclei which have too many protons (or too few neutrons, depending on how you look at it) undergo β+ decay which turns a proton into a neutron, a neutrino, and a positron (an antielectron). This is a naturally occuring process. Antimatter can be created in an accelerator by colliding particles together; for example, smashing a proton into a nucleus can cause a proton-antiproton pair to be created. In fact, antiprotons are also naturally occuring in cosmic rays in the same way�an energetic proton from outer space enters the atmosphere and creates a proton-antiproton pair. There is no such thing as the "Law of Conservation of Matter"; matter can be created or destroyed.

QUESTION: :
How can a train moving without jerks between 2 stations be considered as a particle?
ANSWER:
To apply the ideas of physics to real-world problems, it is almost always necessary to make approximations. Just how to make the approximation depends on the particular problem you are addressing.
If you have a train which moves in a straight line with known acceleration and known initial velocity, you can do the kinematics telling you the position and velocity of, say, the front of the train at any time. This treats the train as a particle, makes no approximation, and is perfectly accurate.
If the train is moving at 50 m/s and has a mass of 108 kg, what is its kinetic energy? Treating it as a particle, we would say K=�mv2. Is that right? No, because not all of the energy is translational�the wheels are rotating and have energy in addition to their translational energy. But, is it a good approximation? Probably so because the rotational energy of the wheels is probably tiny compared to the total energy of the train.
How much work was done to accelerate the train to the speed given in the previous example? W=K, right? That would assume that there was no friction and so that would probably be a bad approximation.
The bottom line is that you have to make approximations to make the problem tractable, but not such severe approximations as to make the answer not approximately correct.

QUESTION: :
Is it possible for a universe to exist that is made up exclusively of subatomic particles that never combine to become atoms?
ANSWER:
I would not think so. Two of nature's most important forces, gravity and electromagnetic forces, are long range forces. Since protons and electrons each have charge, it seems inevitable that they will find each other and make hydrogen atoms. Now that we have large amounts of hydrogen atoms, it seems inevitable that they will attract each other and form stars. Now that we have stars, the atoms get really close to each other and the other forces of nature come into play and cause heavier atoms to form. Only if you change the laws of physics or create a universe with very extreme conditions like huge velocities per particle or all uncharged particles might there be no change in the microscopic structure.

QUESTION: :
If I had an electric jackhammer and used it to spin a turbine generator once I got the cyle running could I not just loop the generated electrical energy back into the jackhammer to make the device run forever by its self or atleast till the pound of the jackhammer broke what ever plate it was hitting to spin the turbine???
ANSWER:
One of the cold, hard facts of nature is that no engine, even if there were no friction (which there always is), can be 100% efficient. What this means is that the work you get out of a machine is always less than the energy you put into it. I think you can see the implication of this for your idea.

QUESTION: :
Is there any posibility that the speed of visible light could be slowed down? Basically what I am trying to ask is if the speed of light is a limit or a manditory constant?
ANSWER:
I assume we are talking about the speed of light in a vacuum. (Light goes more slowly through a material like glass, for example.) There is no possibility to slow it down�it is a mandatory constant. It is also a speed limit for everything else.

QUESTION: :
If an object is travelling at a velocity v, but has a constant acceleration a, why is it that I feel a force, mass x acceleration, rather than the momentum, mass x velocity? I suppose what I am asking is why, if the object hits me at its end point with an ending maximum velocity of vmax, do I measure the force I feel by the acceleration, the amount by which the velocity increased as a function of time, rather than by the end velocity of vmax? Even having read your answer to another

QUESTION: , that it is the force that causes the acceleration, I am still confused.
ANSWER:
Let's agree that what we feel is a force. We do not feel a mass x acceleration or a mass x velocity�we feel a force. We just need to understand why we feel a force when something hits us. And, you need to stop worring about what the velocity or acceleration of the mass is before it hits you�it is only what is going on when it is hitting you that matters. So, when a mass m hits you it stops and to stop it has to slow down, that is, it experiences an acceleration a. Newton's second law states that what causes a mass to accelerate is a force F=ma, so the object experiences a force F=ma. What is the source of that force? Why, you, of course! Finally, Newton's third law says that if you exert a force on an object, that object exerts an equal and opposite force on you; so you feel a force of magnitude F=ma. It is important to note that this is the a the object has while it is hitting you, not some acceleration it might have had before it hit you. An alternative way to view this, if you really want to express it in terms of the momentum, is the following. The acceleration is the time rate of change of velocity, a=dv/dt. But, since the mass remains constant, the force can be written as F=m(dv/dt)=d(mv)/dt=dp/dt; the force is the time rate of change of momentum (during the collision).

QUESTION: :
Does a ball on a string being whirled around in a circle also exhibit synchronous rotation like the moon?
ANSWER:
See an earlier answer.

QUESTION: :
Can water be change directly from a gas to a solid, without going through liquid form?
ANSWER:
Yes, it is called deposition and is the reverse of sublimation. This is how frost usually forms. See the phase diagram of water.

QUESTION: :
If a bullet is fired from a proper angle, can it skip across the water surface like a stone? Also what would be that angle?
ANSWER:
Yes, it is possible although, given its velocity, a single skip would probably be the result except at exceptionally small angles. My dad tells the story of a kid in his home town shooting a rifle into a lake and the bullet ricocheting into a home and killing someone. There is no way of telling what the angle is without knowing the geometry of the bullet, its velocity, its mass, etc. Even so, it would probably be just as well to do an experiment varying the angle and recording the effects (skip or not).

QUESTION: :
If the magnetic force of the Large Hadron Collider is 100,000 times that of the earth's magnetic fields, is there a chance that it could interfere with the earth's fields? If so, could it be causing a shift of the earth, which is then causing the weird occurences, earthquakes, tsunamis, etc. that are occuring?
ANSWER:
The field of the collider is very large compared to the field of the earth inside the collider. But, that field is essentially zero at the source of the earth's field in the core of the earth which is the only place you might have any effect on the field of the earth. The field inside the collider is huge compared to the field of a compass I have here in my pocket, but it has no effect on the compass because it is so far away. I suspect that, even if you could put the collider inside the core of the earth, there would be no important effect on the earth's fields because the electric currents in the core must be gigantic to cause the earth's field. Finally, even if the earth's field were to change dramatically (it is well known that it has changed direction many times in the past), it certainly would not cause the kind of castrophies you mention; the main effect would be that the field serves as a shield against cosmic radiation and if the field disappeared we would suffer health consequences of radiation.

QUESTION: :
My

QUESTION: is regarding the effects of mass on Universe. On Earth animals give birth. Fast forward a few hundred billion years and assuming all is well, there could be an enormous number of beings in Universe. Suppose they will inhabit and Terraform other planets, they will also multiply etc. My

QUESTION: is: Will this enormous number of beings (mass) in Universe alter the expansion rate at which Universe is expanding? In other words just by giving birth and multiplying are we adding mass to the system? (I know it takes a lot of imagination and if's but for the sake of discussion)
ANSWER:
But, birth is not the process of creating new mass. A new baby's mass came from the mother who got it from the food she ate and the air she breathed and the water she drank. And many processes in the universe result in a net loss of mass�stars, for example, are continually decreasing in mass as mass is converted into energy (you know, E=mc2).

QUESTION: :
My age is 20. I am wearing a wristwatch (which shows date and year also) and I am also carrying a mobile. Now assume that I travel at 99.99% speed of light (almost 3.8 * 108 m/s) for 100 years (100 years for the earth) and then I stop. My friends tell me that 100 years have passed. Now if I go through biological tests on the earth, will it show my age (a) 120 years or (b) 20 years and some days? If my age would be 20 years and some days then I would be of this age in 2110, yet I was born in 1990. In this case if I die at the age of 80, it will mean that I die in 2170. From given conditions is it right to say that a man born in 1990 died at the age of 80 in 2170. Now from the stated condition my second

QUESTION: is that in my journey if my friend call me on my mobile then what will happen? Will I be able to talk to him? What about the signal of the satellite due to phone? Please answer me briefly.
ANSWER:
Why should I be brief? You haven't been. First, the speed of light is 3x108 m/s (not 3.8). At your high speed, your clock, compared to an earth clock, runs slow. The elapsed time on your clock when the earth clock is 100 years is 100√(1-.99992)=0.014 year=5.2 days. Indeed, you will die in 2170 earth time but your clock is what matters to you�your clock will say 2070 when you die. (How can you undergo "biological tests on the earth" when you are 100 light years away from the earth?) You cannot talk to your friend on your mobile phone because he is dead; but the most important reason is the mobile phone signal travels at the speed of light so there is a long delay. For example, suppose he calls you after 50 years his time, a few years before he dies. You will receive it about 50 years after you arrive at your destination (which is 2060 your time but 2160 earth time) and, if you answer, your reply will not arrive on earth until after you and he have both been dead for many years (2160 your time, 2260 earth time). You make two serious mistakes: you seem to think earth time is special and that mobile phone messages are instantly transmitted.

QUESTION: :
Imagine a metal link chain of .5m in length with each link weighing 10 grams. Now rotate that chain about its centre point at 100 rpm. So, the very last link at either end of the chain is rotating at 2.60 m/s NOW, That very last link rotating at 2.60 m/s breaks off. Does it A) shoot off at a speed of 2.60 m/s and decelerate uniformly until it hits the floor. or B) experience a small degree of acceleration additional to its 2.60 m/s due to the centrifugal force that was acting upon its mass prior to it breaking off. I know the link was experienceing a centrifugal force (Fc=mv2/r), but I just cant work out if or how that affects the velocity of the link as it breaks free. Instinctively I think it would increase the initial velocity but I cant work out how. Any help would be greatly appreciated.
ANSWER:
First of all, the rotating link does not experience a centrifugal force, it experiences a centripetal force. The instant that the link leaves the chain, the chain is out of the picture entirely�the link leaves the chain moving 2.6 m/s in exactly the direction it was moving when it left. Thereafter it experiences two forces, gravity and air resistance. The gravity causes a uniform acceleration vertically down; the air resistance causes an acceleration which is opposite the direction of the velocity vector (that is it slows the link down). Whether the net effect as it falls to the floor is to speed up or slow down depends on the details of air resistance (can be very complicated), but in most cases like this air resistance may be neglected.

QUESTION: :
We have two clocks starting out in an the same inertial framework, and then accelerate one of them (Clock A) to some constant speed V, but the two clocks are also tethered by a rope. At some point, the accelerated Clock A will tug on the rope and begin accelerating the clock that is still at rest in the original framework (Clock B). Clock A will begin to decelerate and clock B will begin to accelerate until they are both traveling at the same speed V2. The

QUESTION: is, will they both show the same time (from the point of view of someone still at the initial framework)?
ANSWER:
I have been puzzzling over how to best explain this one! I believe that the problem, as stated, is equivalent to clock A moving away at constant speed for a while and then stopping. In both cases, clock A starts in the same inertial frame as B, then jumps out of that frame and stays there for a while, and then jumps back into B's frame. I recommend first reading my earlier explanation of the twin paradox to see what my paradigm is for the explanation illustrated by the graph at the right. The graph represents clock A traveling at 80% the speed of light to a point 8 light years from the earth; then clock A stops moving. The graph shows clock A's ticks (once a year) with black crosses, and clock B's ticks (once a year) with red crosses. Clock B measures 10 years for the trip [(8 light years)/(0.8 light years/year)]. But clock A measures only 6 years because of length contraction (the distance is only 4.8 light years for clock A). Thereafter, the clocks run at the same rate but clock A is 4 years behind clock B.

QUESTION: :
In my physics textbook, it says that electricity the movement of electric charge. This movement is MOSTLY carried by electrons. What other particles could possibly be used in electricity? Are electrons the fundamental part of electricity?
ANSWER:
In nearly all household electrical circuits (light bulbs, toasters, driers, motors, etc.) electrons flow through conductors to do the work. However, in some materials, as you note, the charge carriers are positive rather than negative. Here is how it works: the material has "holes" in atoms, places where electrons are missing and so the hole has an effective positive charge. When the voltage is applied across such a material, it is the holes which move (hop from atom to atom) rather than the electrons in a normal material. Such a material is called a p-type semiconductor.

QUESTION: :
In a previous answer, you said, "according to quantum mechanics, a change in one part of an entangled system immediately affects all other parts of the system." Is it possible for someone to force a change in one part of the system? And, if so, couldn't this be a form of communication (i.e., if I change the spin from up to down, it means I've done something), which would then violate light speed?
ANSWER:
If you make a measurement, that is equivalent to "forcing" a change; a measurement "puts" the particle into the state you observe (let's call it "up"). This instantly puts the other particle into the complementary state (let's call it "down"). But, if somebody observes the other particle and and finds it to be "down", he doesn't know whether this observation is the result of your having "put" it in that state or his having put it there, does he? Therefore, finding the second particle "down" conveys no information to him regarding what you did.

QUESTION: :
If a clock were moving at half the speed of light, how fast would it be going in m/s? Also, would the clock moving be showing half the time passed as the outside observer?
ANSWER:
The speed would be c/2=1.5x108 m/s where c is the speed of light. The change in clock speed is not proportional to the speed ratio β=v/c but rather to √(1-β2). So, the clock would show √(1-�2)=0.866 the time passed on a stationary observer's clock.

QUESTION: :
My doubt is if protons repel protons how is it possible for them to be in the nucleus? if it is possible to separate a proton from a nucleus can we form new elements if done in large scale can we achieve creation of new elements?
ANSWER:
This is how we know that there is another force present besides the electrostatic repulsion. It is called the nuclear force or strong interaction. This force is very short ranged. That is, if the protons are not very close to each other, this force will will be very small and the repulsion will win out; but if they are very close, the nuclear force wins out and a nucleus may be held together. Neutrons also feel this force which is why neutrons are in nuclei.

QUESTION: :
I have a problem in understanding Terminal Velocity. When we are handling the

QUESTION: s about drag force in college (1st Sem.), we consider the density completely constant. We have drag force in free falling. When we leave the object from a certain height, there is only W=mg applying on the objects. But, just as the object moves to the ground, it hits the molecules in its way, which causes in increasing of the drag force. After Drag force's magnitude becomes equal to the weight, the total acceleration will be Zero and we will reach the constant velocity which is the Terminal velocity. But after it reached the terminal velocity, it stills hit the molecules in the air, so the Drag force must become larger than the weight. Why it doesn't happen?
ANSWER:
The drag force is proportional to the velocity (or some power of the velocity). The reason the object speeds up at the beginning is that the downward force (its weight) is larger than the upward force (drag). But as it speeds up the drag gets bigger and so the acceleration (down) gets smaller. Eventually the drag force increases to the point where it is equal to the weight; now the forces are balanced and the object moves with constant speed. The air molecules are are still colliding with the object but their effect is no longer changing.

QUESTION: :
Does a light source from a torch or carlight (a light source that isn't spherical) obey the inverse square law or if you were to calculate the intensity differently?
ANSWER:
No. The inverse square law is for a point source (or spherically symmetric source). A beam of light is more like a plane wave which does not lose intensity as it travels. Of course, real world cases like a car headlight do eventually lose intensity due to imperfect optics and absorption of the light by the air.

QUESTION: :
If we are moving around in space at x speed and light is constant, then how do we know how fast light travels? If we shine light in the opposite direction we are traveling, won't it seem to travel faster (relative to us) than it truly is? What I mean to ask is, have physicists considered this variable for the speed of light
ANSWER:
Here is the basic rule of special relativity: the speed of light in vacuum is the same to all observers. Therefore, if there is a beam of light, you will measure its speed to be 3x108 m/s no matter what your own speed is. You should read my earlier discussion of this.

QUESTION: :
does an 40 lb object that is 12 inch X 12 inch X 2 inch have a greater downward force or pressure when starting from a resting position balanced atop a soda can if it is standing on its end or lying flat? does it have greater ability to crush the can in the two different positions? what if it were resting 12 inches above the ground and were in a free fall.
ANSWER:
First, model the can as a cylinder; the diameter of the can is about 3". However you place the object on the can, the force on the can will be 40 lb. However, standing on its end, this 40 lb will distributed over a smaller area (since the object will not cover the whole top when on end) so the pressure (force divided by the area over which it is applied) is larger and therefore more likely to crush the can. In reality, the top of the can is not flat but has a raised lip and so the pressure in both cases will be greatly increased (because of the greatly decreased area) but the on-end situation will still have the larger pressure. When dropped on the can, the block is more likely to crush the can. The reason is that, to stop the block, the can must exert an upward force on the object which is larger than the weight; by Newton's third law, the force the can exerts up on the object must be equal to the force the object exerts down on the can, so it is bigger than the weight.

QUESTION: :
A ray of light is moving towards a certain space station from 1 light year away. A rocket departs from the space station at exactly the same time, accelerating at a certain rate, directly towards the ray of light. (the exact rate of acceleration isn't necessary for the

QUESTION: ). Would I be right to assume that two observers, one on the rocket, and one on the space station, would each experience exactly one year passing before being reached by the ray of light, Even though the rocket may be a great distance away from the station now? As I understand it, light can never travel faster than c. So if the rocket is the body of reference, the light starts out 1 light year away, and travels towards it at c for the duration of 1 year. While if the space station is the body of reference, the same is true.
ANSWER:
No, less than one year will have elapsed for the rocket. Not only does it meet the light somewhere between the two points, the distance that it sees that it has to travel is contracted by length contraction (that is, the rocket sees the distance from the light source to the space station to be less than one light year.) If you just assume that the acceleration happens in a very short time so that he travels with constant speed, then you could calculate the time he travels before encountering the light. Here is an example: if the rocket has a speed of v=0.8c where c is the speed of light, the distance between the source and the station (measured by the rocket) is √(1-0.82) ly=0.6 ly. It is then a straightforward kinetmatics problem to show that the light and rocket will coincide at time 0.625 y (using the rocket's clock), so the place they coincide is 0.6x0.625=0.375 ly from the light source. The time for the light and rocket to coincide as measured by the station's clock would be 0.556 y, so the distance from the source would be 0.566 ly.

QUESTION: :
If nothing travels faster than the speed of light then how come 2 electrons can become entangled in such a way as to effect each other regardless of distance. ie light years apart. It seems to me that this would mean that they are breaking the speed limit to achieve this.
ANSWER:
No material object may travel at or faster than the speed of light. Information may not be transmitted faster than the speed of light. Since neither of these is violated, entanglement does not violate the speed of light limits. It may seem like information is being sent from one electron to the other, but you cannot use these two electrons to send information to somebody. I always find it easiest to think about the two electrons as a single system rather than as a pair of electrons talking to each other; according to quantum mechanics, a change in one part of an entangled system immediately affects all other parts of the system.

QUESTION: :
This might take a little time to explain. I know that the speed of light is such that when we look at stars, distant galaxies and other stellar phenomena, we are looking at them as they were (since it took light time to reach us). Here lies my problem. If physicists and cosmologists state that the universe is expanding due to the red-shifted light from galaxies, and the further away a glaxay is, the faster it is traveling, then that red-shifted light being observed took a long time to reach us. So, we are seeing a red-shift from, say, 1000 years ago. Could it be that now galaxies are moving towards us, just that the blue-shifted light has not reached us yet? What am I missing? Every text I read, every show I watch, everyone is certain the universe is expanding.
ANSWER:
First, your time scale is way off�we're talking billions of years, not thousands. You are right, it is certainly possible that distant objects could now be moving toward us and we won't find out for billions of years. But, we are able to see a huge range of distances into the cosmos and all systematics, near and far, indicate that everything is moving away. In recent years evidence has been found that the distant objects are actually speeding up (the source of which is called "dark energy"), providing even more evidence that we do not expect anything to be turning around.

QUESTION: :
Is a low or high current solar charger/battery system (same voltage) more efficient to charge small electrical devices (iphone etc) please?
ANSWER:
Well, since power is current times voltage, higher current is higher power�charges faster.

QUESTION: :
if electricity is made up of millions / billions of electrons and has a tiny amount of mass. Is it affected by G force when it goes from zero to the speed of light and back to zero, eg when its switch a light on and off?
ANSWER:
Indeed, electrons do not go at the speed of light in a wire. They go very slowly, maybe on the order of 1 mm/hour! In any case, the force of gravity on an electron is negligible under almost all possible conditions.

QUESTION: :
I am not wishing to make a weapon its purely scientific curiosity. If you had a laser beam and placed it behind a magnifying lens of some sort such as a telescope, you could magnify the lasers strength. Now my

QUESTION: is if you were to put another magnifying lens in place to magnify the current beam would it magnify it even stronger? What I am asking is if your laser is 1kW and by placing the magnifying lens or telescope makes your laser go to 2kW. Adding another lens or telescope would make it 4kW?
ANSWER:
You are confusing power with intensity. You can use a lens to increase the intensity (energy/second/square meter) but not the power (energy/second). Hence, you cannot take 1 kW and increase it, you can only decrease the area over which it hits.

QUESTION: :
If matter and anti-matter annihilate each other when they come into contact, how is Positron Emission Tomography possible ?
ANSWER:
Because PET detects the products of the annihilation (two 512 keV gamma rays).

QUESTION: :
How do you have Kinetic Energy at the top of a projectile? I thought the velocity in the y direction was 0, and even if we consider the x direction, wouldn't the kinetic energy at the top of the projectile equal the kinetic energy when the projectile initially set into motion?
ANSWER:
Anything which is moving has kinetic energy. Part of the the kinetic energy has been converted to potential energy, but not all of it. The energy conservation is expressed as �mvx2+�mvy2=mgh+�mvx2 at the top (y=h).

QUESTION: :
What l want to know is can you see something before the sound without it being faster than the speed of sound? For example, all my life l've noticed that l will hear the jet plane over here and see the jet plane there. l do hear and see it at the same moment in time but the sound and the sight are not in the same place. l hope what l just wrote makes sense, haha. The current argument raised is that this is not possible unless the thing is traveling faster than the speed of sound. However, the speed of sound is like 1000 miles an hour or something, right??? l'm not sure on that but l'm pretty sure it's faster than most commercial jets fly. So l have a sneaking suspicion that what's going on here is some kind of matter of semantics and/or we are both right and both wrong. Or we are talking about different things, l don't know.
ANSWER:
The answer is very simple: the speed of sound (about 330 m/s) is enormously smaller than the speed of light (300,000,000 m/s).

QUESTION: :
As the stars die, will the sun die too?
ANSWER:
All stars will eventually die because they will run out of energy. The sun may last a few billion more years but life on earth will be unsustainable in about one billion years because the sun will become too hot.

QUESTION: :
My

QUESTION: is: why does light bend when it slows down? I'm currently a physics student at UC Santa Barbara (2nd year) and so I know that light has a finite speed, and it slows down when it enters another medium, and if it enters another medium at an angle other than perpendicular it bends (refracts). I know about angle of incidence and all that, I just don't understand why light has to bend because it slows down? As I understand it light can be thought as a quanta of energy, an infinitesimal wave packet (maybe that's where I'm wrong?) So why does it need to bend just because it is slowing down in an angled medium? I've often heard the analogy of a car: if it hits glass angled downward from left to right then the upper left tire hits the glass first and slows down while the right wheel remains faster and therefore bends it "upwards". But light packets don't have a discernible "thickness" where one part hits before another (I don't think!) so that analogy breaks down for me! Sorry for rambling, I'm just confused.
ANSWER:
Refraction is geometric optics and thinking of photons is definitely not the way to best understand it. You should think in terms of waves�wave fronts and rays. I found a nice description (based on Huygen's principle) on the web. Refer to the picture on the right.
Wavefront 1 reaches A.
Wavefront from A starts to spread out.
When incident wavefront reaches B, secondary wavelet from A has travelled a shorter distance to reach D.
It gives a new wavefront 2.
As a result the wave path bends towards the normal.

QUESTION: :
What is the word for the amount of upward velocity necessary for an object to continue moving upward against gravity after it leaves your hand. I believe there is a word that distinguishes between simply applying the force necessary to move an object against gravity vs. accelerating that object so that it will continue moving against gravity on its own.
ANSWER:
I am not sure what you are asking because you have many misconceptions. You may be asking the term which describes the minimum velocity something must have to completely escape from the earth. This is called the escape velocity. Escape velocity from the surface of the earth is about 25,000 mi/hr. For comparison, the required speed to put a satellite in a low orbit (like the shuttle) is about 18,000 mi/hr.

QUESTION: :
What is the proper term for the opposite of antimatter? "Regular matter"? "Normal matter"? Just "matter"? Is anitmatter a form of matter, or are "regular matter" and antimatter both forms of a larger concept? And, if they are, what is that concept called? Is it also called "matter"?
ANSWER:
This is just semantics. As far as I know, there is no formal definition of the word matter but it very well could include antimatter. Here is what Wikipedia has to say: "�in practice there is no single correct scientific meaning; each field uses the term in different and often incompatible ways. A common way of defining matter is as anything that has mass and occupies volume."

QUESTION: :
What part of a U-235 or Pu-239 atom is converted into energy during nuclear fission? Proton? Neutron? or something else?
ANSWER:
The energy comes from mass, you know, E=mc2. When a heavy nucleus breaks into two pieces, the masses of the pieces are smaller than the mass of the original nucleus; that is mainly where the energy comes from. After the fission occurs, numerous neutrons are ejected from the smaller nuclei and these have kinetic energy which comes, again, from mass. The nuclei turn out to be unstable (they have too many neutrons) and so they beta decay, converting neutrons into electrons and protons in the nuclei; again, the energy released comes from the mass decreases which occur. In the end, if you measure the mass of everything that is left, it is less than everything you started with and that missing mass is where all the energy came from. You might like to learn a bit more at an earlier answer.

QUESTION: :
Do spirits have any mass ?
ANSWER:
The density of alcohol is 0.79 gm/mL.

QUESTION: :
I have another

QUESTION: for you sir. This is a simpler one, perhaps laughably simple to you, but I haven't taken physics in school yet. (It's next on the list). Anyway, why is the distance traveled by an object dropped from rest equal to half of the 9.8 m/s/s it's traveling at in the first second? Also, why does it's distance then increase four fold to match the velocity in the second second, and then why is the distance traveled by the object much larger than its velocity after the second second?
ANSWER:
This is very basic kinematics. 9.8 m/s/s is not the rate at which it is traveling, it is the rate at which it is changing its speed, its acceleration. At the end of one second after being dropped the speed is 9.8 m/s but, if you think about it, it started from rest and so its average speed over that first second must have been less than 9.8 m/s. It turns out (I will leave it to you to learn kinematics when your time for physics arrives or sooner if you want to dig it out for yourself) that the average speed is 4.9 m/s over that first second. In general, x=�gt2 where x is distance fallen from rest, g=9.8 m/s2, and t is the time fallen from rest. So you can see why the distance increases quadratically with time.

QUESTION: :
Are colors associated with sound? Specifically, do visible colors correlate with the musical scale... red=DO; orange=RA; yellow=MI; green=FA; blue=SO; indigo=LA; violet=TI
ANSWER:
Sound and light are two completely different kinds of physical phenomena and there is no intrinsic relation between any colors and pitches. You may define a corespondence but it has no meaning in physics. Your correlated pairs are at least both in the order of increasing frequencies, red and do are low frequencies and violet and ti are high frequencies.

QUESTION: :
I'm wondering about buoyant force. It seems to me that a particular liquid would exert a particular buoyant force, making the buoyant force a constant much the same way gravity is a constant force. An object's density would then determine the effect the buoyant force would have on the object. If an object is less dense than the liquid it will float - the buoyant force is having a great effect on the object. On the other hand, if the object is more dense than the liquid the buoyant force will have less of an effect. Am I thinking about this correctly? I would really appreciate an answer as soon as possible because I'm teaching a teacher workshop and I don't want to give teachers misconceptions.
ANSWER:
You are talking about a classic physics problem, perhaps the oldest known physics. The basic principle was discovered by Archimedes more than 2000 years ago. Simply stated, Archimedes' principle is that the buoyant force is equal to the weight of the fluid which the object displaces. So the buoyant force certainly depends on the density of the fluid. So your conclusions follow: an object whose weight is greater than the weight of the fluid it displaces will sink and the converse situation implies it will rise to the surface where it will settle to where it displaces a volume of fluid equal to its weight.

QUESTION: :
I am interested in building a device that might collect electrical energy from using a solenoid generator that would be push the magnet by being connected to the inside of the tire. The solenoid generator would be in-line on the rim where when the tire comes in contact with the road surface it would come toward the rim, then when the tire leaves thr road surface it would be returned with force to the original position. DOES THIS SOUND LIKE IT MIGHT COLLECT SOME USEFUL ENERGY IN=ORDER TO HELP RECHARGE A BATTERY IN A ELECTRIC VEHICLE ??
ANSWER:
It sounds to me like you want to replace the shock absorbers with electromagnetic dampers. What a shock absorber does is damp out the vertical motion of the wheels by converting the energy to heat. What you want to do is convert that energy instead into electrical energy. Although the idea is sound, I believe that the amount of energy you would harvest would be smaller than the energy you would lose by having to carry those heavy permanent magnets along. Already hybrid cars harvest the kinetic energy of the car by electromagnetic braking. Think about it: conventional brakes get very hot in use indicating that there is significant energy there to harvest whereas I suspect shock absorbers really do not heat up that much.

QUESTION: :
If I pointed an infrared-based remote control at a some mirror that are aligned so the beam can hit it several times before being recieved by a television or similar device, would the device be able to recognize the command sent to it, or would it think that nothing useful happened? Under what situations might these results be obtained?
ANSWER:
I have certainly bounced the signal from a remote to the TV. How many times you might bounce it around would depend on the nature of the reflecting surfaces and the power of the remote.

QUESTION: :
We know that the gratest persentage of an atom is vacuum. We also know that soundwaves do not travel through the vacuum. However sound travels through matter which, though, is mainly vacuum. How can this happen?
ANSWER:
Sound waves have wavelengths of a few centimeters to a few meters. Atoms are of a size roughly 10-10 meters and their structure is totally invisible to sound. Anyhow, the atom is not mostly a vacuum, but is filled up with electrons. The atom should not be thought of as tiny electrons orbiting the nucleus but as a "cloud" of electric charge surrounding the nucleus. You might think about the space between atoms in a gas as being "vacuum" but since the distance betweens atoms in a gas is on the order of 10-7 m, this too is invisible to sound waves.

QUESTION: :
I am reading a book "Power Hungry" by Robert Bryce. He takes a position that wind and solar energy are basically scams because they are unreliable. Society demands that power is availbale immediately, the moment it is needed. The nature of wind and solar is that it is unreliable - we cannot predict with 100 per cent certainty how hard the wind will blow or whether the sun will shine. More power may be generated from these sources when it is not needed and less energy may be generated when it is needed. Therefore, natural gas and coal-fired generators are still needed for backup and these generators must be constantly running because it takes time to bring them on line. Wind and solar are a waste because the gas and goal generators must run anyway. He gives other reasons but this is the main reason. My

QUESTION: is whether it is possible to store the energy generated from wind and solar. If we could build up reserves of this energy, it seems we could use it the same way as coal and gas is used - just switch it on when it is needed. Does this concept violate the laws of thermodynamics?
ANSWER:
The storage device is called a battery. This is already how home installations work, using wind or solar to charge a battery. And when the batteries are fully charged, send the excess onto the grid. Another storage possibility (less efficient, I suppose) is that energy may be used to pump water up to a reservoir and then let it fall back to drive turbines when power is needed. Yet another storage device is to use the heat from solar to melt salt; the molten salt is stored in insulated containers and used to later heat water to run steam turbines. To say that solar and wind are "scams" is idiotic. It is true that for a long time we will still need conventional power plants, not because of storage issues but because the amount of demand cannot be met overnight by alternative sources.

QUESTION: :
I was wondering, what are estimated or known deviations of the masses and radii for the 3 basic particles (protons, neutrons and electrons ) making up the atoms ? Can we expect atoms from one edge of the universe to match atoms plucked from the opposite reaches ? Is it possible that some atoms would be scaled up or down by multiple factors with respect to the lot we are familiar with ?
ANSWER:
Masses are extremely accurately known. Regarding the sizes, they are not simply well-defined particles like a marble or bowling ball, they have fuzzy edges. But you can define a size (for example, where charge density drops to � the maximum value). The size of an electron is unknown and maybe unmeasurable. The sizes of protons and neutrons are on the order of 10-15 m. There is no evidence whatever that atoms at the extreme edges of the known universe are different. Some physicists speculate that the fundamental constants of physics may change over time (hence distant regions would have different physics) but there is no good evidence for this being the case.

QUESTION: :
Can I move the Earth myself by jumping? Can a single atom move the Earth?
ANSWER:
When you jump, the earth exerts a force on you and you exert an equal and opposite force on the earth; that is Newton's third law. Hence the earth accelerates away from you and you accelerate away from the earth. But, your mass is small and the earths is huge, so your acceleration is modest and observable and the earth's is tiny and so small as to be unobservable. But, after you leave the ground you and the earth exert attractive forces on each other (gravity) and you fall back together so the net effect has been not to "move" the earth. Of course, a single atom would really have a negligible effect.

QUESTION: :
Electromagnetic physics asserts that when a charge is accelerated, in the medium of a copper wire (antenna), a disturbance in the electric field results (a "kink" in the E field lines develops), this "disturbance" is associated with propagating E and B fields. Does the summation of all photon energy comprise the energy of the E and B fields, and, if not, to what degree does photon energy comprise the energy found in either the E or B fields?
ANSWER:
There are electric and magnetic fields which are associated with the charge but are not radiation fields. Therefore, there is less energy in photons than in all the electric and magnetic fields.

QUESTION: :
I have read your ground rules, particularly the rule that bars asking about traveling faster than light. If the

QUESTION: I'm about to ask is in violation of this rule, please tell me. My

QUESTION: is this: If you could travel "at" the speed of light, and you shined a flashlight in front of you, what would happen to the beam? Would you be unable to see it, or would it behave normally?
ANSWER:
You have not violated the groundrules because I neglected to specify at the speed of light; I have fixed that now! As you can see from a previous answer, it is not possible for anything with mass to go as fast as the speed of light. However, if you happened to have a speed of 99.9999999999% the speed of light, you would observe the flashlight beam to be moving away from you at the speed of light. Again, see an earlier answer.

QUESTION: :
I was told in my electromagnetics class by my professor that a RF wave is a "photon." A photon appears to be defined as a quantity of measureable energy. I then read, that a microwave oven permits "photons" of light to pass through a metal mesh but not microwaves." Can you please distinguish between a light photon and a microwave (define)? How can a mesh be designed to block microwaves?
ANSWER:
Electromagnetic waves, it turns out, are both waves and streams of particles called photons. The photon is the smallest amount of energy possible for a wave of a given frequency. For most practical applications there is no need to talk about photons at all, just considering the wave properties is sufficient. There is no need to think about microwave photons when trying to understand why the waves do not penetrate the mesh enclosing the oven. Light waves have wavelengths typically hundreds of nanometers (very short). The wavelength of the microwaves is several inches. The holes are much bigger than the light wavelengths and much smaller than the microwaves.

QUESTION: :
I am perplexed at something a subsititute teacher in physics class told me. He said, rockets rely on Newton's Third Law (action/reaction) to leave Earth's gravitional force (they have to reach a speed called 'cosmic speed' I think). But I remember him saying rocket engines don't work in space. Is this true? Does that mean we rely on Inertia for space travel? Then, how would we avoid the gravity of other objects to stay on path? I remember you answering a

QUESTION: with 'influential gravity' to 'steer' through space; please explain this concept a little more. Back on rocket engines, how do we return from the moon then?
ANSWER:
It is scary how ignorant teachers can sometimes be. It is absolute nonsense to say rockets do not work in space.

QUESTION: :
Why do neutrons decay with a half-life of 10 minutes when free, but do not decay when they are attached to other protons in nuclei or when they occur in bulk in neutron stars? Does the presence of other particles have a stabilizing effect on the neutrons?
ANSWER:
Yes, the presence of other particles in nuclear matter does have a "stabilizing effect" on neutrons. But it is most easily understood in terms of energetics. A free neutron has a certain mass and has the "option" to decay into a proton, a neutrino, and an electron; the mass of a neutron is larger than the summed masses of its decay products, so energy is released and it can decay without any "help". A free proton, on the other hand, also has the "option" to decay into a neutron, a neutrino, and a positron; the mass of a proton, though, is smaller than the summed masses of its decay products, so energy must be added to it for it to "decay" and it is therefore stable. These processes are called beta decay. In a stable nucleus, the mass of the nucleus is smaller than the sum of all its part because it is bound. The net result is that the mass of a neutron is effectively reduced in nuclear matter, thereby rendering it stable.

QUESTION: :
I understand that the moon being tidally locked always presents the same face to the earth, and to do so must rotate about its axis in the same time as it takes to complete a single orbit. Now if you have a ball on a string which you spin around in a horizontal circle above your head, the ball presents the same face to the centre of the circle. I am certain that the ball also rotates about its axis to achieve this, but an associate says it isn't rotating about its axis otherwise it would wind up the string. Can you say which of us is right and explain why?
ANSWER:
You are right. The reason is that the string is also rotating with the same period around the axis about which the ball rotates. For example, imagine a very tall vertical pole sticking up from the earth; you wouldn't say the earth was not rotating on its axis just because the pole moved along with us.

QUESTION: :
obviously it isnt possible,but lets say for talking sake that it was... what would happen if something could travel faster than the speed of light? would there be a light version of the sonic boom?would the object pass you before you could actually see it?
ANSWER:
Although I normally refuse to answer "faster than light"

QUESTION: s, this one I will address because there are actually "sonic boom" (maybe we should call it optic boom) phenomena associated with superluminal speeds. What a particle cannot do is travel faster than the speed of light in a vacuum; but in a material medium (say glass or water) light travels more slowly and so a particle in water can go faster than the speed of light in water. When this happens a shock wave (which is what a sonic boom is) is created and the resulting effect is that there is a glow emanating from the water. This radiation is called Čerenkov radiation. For example, the water around some reactors has very fast neutrons traveling through it and glows blue.

QUESTION: :
How come we are able to see shadows of objects? Say there's a shadow on the wall, why can see the shadow of something, say an ornament when there is lack of light?
ANSWER:
Normally, a shadow blocks light from one source but there are other sources of light illuminating this place (where the shadow is) which are not blocked.

QUESTION: :
I know about most of the aspects of nuclear fusion (for example: Where it occurs, requirements), but what I do not understand is: Just because 2 light atomic nuclei fuse together to make a heavier atomic nuclei, why does this release a large amount of energy? I know with nuclear fission, you seperate the protons in the nucleus which releases energy due to the energy stored by keeping the protons attracted intially. But why does fusing nuclei release energy? Shouldn't it only store the energy?
ANSWER:
See an earlier answer.

QUESTION: :
what is rate of change of acceleration?
ANSWER:
It is called jerk.

QUESTION: :
Suppose a frictionless cube is placed at rest on a frictionless billiard table. If the cube is struck by a cue stick normal to one face of the cube, but not on a line that passes through the center of mass, in what direction will the cube move? Certainly the impulse J is normal to the face of the cube. But it can be decomposed into a component directed toward the cube's center of mass, and another component at right angles to that direction. Whether one uses this decomposition, or the original impulse, to calculate the angular momentum acquired by the cube, the answer obtained for that quantity is the same. But the motion of the cube's center of mass is not the same. So what's the answer?
ANSWER:
Let's assume the force is in the same horizontal plane as the center of mass of the cube; then you do not have to worry about tipping it over or similar rotations which might not be perpendicular to the table. You also must assume the impulse is delivered in a very short time so that the cube doesn't start rotating as you are pushing on it; I assume that is what you mean. Newton's second law still holds, the momentum after the collision must be in the direction of the impulse and have magnitude equal to the magnitude of the impulse�p=F∆t. The angular momentum acquired by the cube about its center of mass is L=Γ∆t where the torque is Γ=rxF and r is the vector from the center of mass to the point where the force is applied. I do not understand your statement that resolving the force into two components results in a different motion of the center of mass; calling any two components of the force F1 and F2, then p'=F2∆t+F2∆t=(F2+F2)∆t=F∆t=p, the same as before.

QUESTION: :
If photons have mass (E=mc^2) and a large mass curves its path, then 1) By newtons 3rd law will it attract the larger mass towards itself? 2) Does that mean that it can exert gravitational influence on mass and even on photons themselves? 3) If so,by using laser, can one create a black-hole by squeezing enough photons in a tiny space?
ANSWER:
Photons do not have mass. Because it has energy, it does warp space/time, but the "reaction force" on a large mass nearby would be unmeasurably small. I have no idea how your black hole laser is supposed to work.

QUESTION: :
I always thought of temperature as essentially a measure of how fast atoms were moving. I understand that when the volume of a gas is decreased, there is a coresponding rise in temperature. Why is this ? The atoms in a not moving through space any more quickly (momentum is not increased, is it ?). They are, however, bumping into each other more frequently. Is temprature the frequency of these interactions ? I so, does an isolated atom (thought experiment), which is not interacting, have a temprature ?
ANSWER:
Your first statement is correct for a gas. For a solid, it is more complicated since the average energy per atom includes potential energy as well as kinetic energy because the atoms interact with each other. You should read my earlier answer on heat and temperature. When you compress a gas you do work on it. If no heat leaks out or in, the energy you add (by doing work) ends up as increased kinetic energy of the gas molecules�they go faster. Think of compressing the gas by moving a piston. If the piston does not move, a molecule colliding with it rebounds with the same speed that it came in. If the piston is moving into the gas, the collisions with the piston cause the molecules to move faster after colliding (like when you hit a ball with a moving bat, speeding it up). The frequency of collisions among molecules is of little importance; an adequate model of a gas ignores collisions between molecules. Finally, temperature is a statistical concept and a single atom does not have a temperature.

QUESTION: :
If two objects are similiar in mass, will they move toward each other or not move at all?
ANSWER:
I do not really understand this

QUESTION: . What is true is that two objects with mass exert gravitational forces on each other. However, how they will move depends on what other forces they experience,where they are relative to each other, and what their masses are. In empty space, where there are no other significant forces, they will accelerate towards each other. Since you stipulate that their masses are similar, you can calculate the acceleration. Call the mass of each M; then the force each experiences is F=GM2/r2 where G=6.67x10-11 Nm2/kg2 and r is the distance between their centers. Since the acceleration of each will be a=F/M, a=6.67x10-11M/r2. Unless M/r2 is very large, the acceleration will be very small.

QUESTION: :
if i was traveling at 2000 ft per sec and shot an arrow the opposite direction also at 2000 ft per sec would the arrow travel or would it stay still?
ANSWER:
Relative to a stationary observer (who sees your speed as 200 fps), the arrow would be at rest.

QUESTION: :
Since atoms are mostly empty space, why dont we fall through a floor we stand on?
ANSWER:
It seems I have answered this

QUESTION: a hundred times. See FAQ page.

QUESTION: :
My

QUESTION: is simple.When Albert Einstein postulated that there was no gravity in the absolute sense but that the whole universe was made up of a 3 to 4 dimensional sheet called space time where when any sought of matter lied on it could warp the shape of the celestial sheet hence giving objects near it(the warped region) experience some form of force that in Newtonian physics was called gravity.However,I stand corrected but when Einstein was thinking of this he must have been thinking of it in reference to conditions on earth where the object smaller than the larger object on the sheet would roll toward the larger object due to a downward force,however this is not the case in space.I propose that in empty space time in non downward force pull region like space the smaller object would continual moving despite the warp in space time sheet. what do you think
ANSWER:
The picture of a warped rubber sheet is merely a "cartoon" to illustrate the qualitative idea of how mass deforms space-time in general relativity. It is not meant to be a rigorous and literal picture. You should read my earlier posts on general relativity linked to from the FAQ page.

QUESTION: :
could steam be below 100 degree Celsius.
ANSWER:
Yes, at pressures less than atmospheric pressure. See the phase diagram of water.

QUESTION: :
Why is the speed of light the speed that it is? What is stopping it from being even faster?
ANSWER:
See earlier answers.

QUESTION: :
I have read some things online about why ice and salt are mixed together to make ice cream. I'm not really understanding how a salt and ice mixture is colder than ice itself as is being said online. I understand the concept of how the freezing point of water and salt is lower than water itself. However, I do not see how adding salt to ice makes the solution colder. Ice freezes at 32 degrees, but ice in a freezer for example can reach a temperature as low as the freezer is set, correct? So, it seems to me that adding salt to this ice will make a brine because of the molecule interactions and the temperature will be very low (less than 32 degrees) because the ice in the beginning was much colder than 32 degrees, not because the salt/ice mixture is colder than ice alone.
ANSWER:
Yes, ice can be colder than 320; but, when put it in an ice cream maker it starts to melt and the melted water will be about 320. So, after a while, you have an ice-water mixture at about 320 and that is what the ice cream sees. Adding salt lowers the freezing point of the mixture (the brine) and hence the ice-brine mixture is below 320. You can lower the freezing point of the brine by as much as about 300.

QUESTION: :
If I shoot a laser at a hard drive platter on one side. Put a pin hole in the platter where it hits so the phtons can pass. Can I set up a Retroreflector at such a distance that the photon will return to the platter, when spun at 15,000 rpm, will pass back through the same hole except the hole has rotated 180 degrees? Or.... The photon having no time dimension or dimension in the direction of travel, always hits the platter 180 degrees from the start regardless of rotation? Or something I didn't thik of?
ANSWER:
The hole will let through a very short pulse of light. If the distance to the reflector is L, the pulse will take a time t=2L/c to return to the plane of the platter. If the hole is there, the pulse can pass back through. Hence, in the time t the platter must rotate through 3600, 7200, 10800, etc., some integer multiple of 3600.

QUESTION: :
If atoms, and hence the matter made up of attoms, are 99.9999999999999 percent empty space, why isn't everything invisible?
ANSWER:
Because there are many electrons with which the light (which is composed of electric and magnetic fields) interacts strongly. So, light is absorbed, reflected, and/or bent when it interacts with matter.

QUESTION: :
Can the radiation from CAT scans penetrate walls? I had my pocketbook in a room adjacent to the room where my CAT scan was performed. I had a metal water container in my pocketbook. Is it possible for the radiation to have penetrated the wall and permanently ruined my container/water bottle making it permanently radioactive?
ANSWER:
CT scans are nothing more than glorified x-rays. I am sure that the walls are probably shielded to keep the x-rays in the room where the scan is done. But that is beside the point because x-rays do not make anything radioactive, permanently or temporarily. If your purse and water bottle had been in the room with you they would not have become radioactive. The only reason for shielding is to protect people; excessive exposure to x-rays can cause damage to living tissue. That is why technicians leave the room when an x-ray machine is on. For the patient, who is there for a one-shot deal, it is no reason for concern, but for personnel around all day every day, it is.

QUESTION: :
I'm trying to settle an office debate. We are debating on how an electron travels through a conductor. Lets assume we are taking about DC current through a copper wire. I think that the electrons are passed from atom to atom on the last (4th) energy level. Can you tell me if this is accurate, if not can you explain to some detail how it works?
ANSWER:
In a good conductor, the conduction electrons (those which, in an isolated atom, would be called the valence electrons and are outermost) are almost perfectly free to move around. The atoms behave differently in the bulk than singly. In fact, a very good model of a conductor is simply that the electrons move around freely like gas in a box. Now, when a potential difference (voltage) is applied across the conductor, an electric field is established which causes the electrons to experience a force in the opposite direction from the field (since they are negative). If they were really free, they would simply accelerate from one end to the other. However, as soon as one electron starts speeding up along the field, it bumps into an atom and stops, then accelerates again, etc., etc. The net effect is for the conduction electrons to have, when all are averaged over, a net drift velocity in the direction opposite the field direction. For normal household currents this velocity is very small, smaller than 1 mm/s. It is really not accurate to say the electrons "jump" from atom to atom; rather the atoms and electrons suffer collisions.

QUESTION: :
I have played with special relativity and think I have a feel for it. But there is one example I find confounding. The thought experiment where a man in on a train and a man is on the platform of the station and lightening strikes far ends of the platform equal distance from both. It is easy to see how the man on the train if in relative motion (either he or platform moving) will not see the two lightning bolts as simultaneous. But wouldnt there be a doppler effect which would clue him that he is approaching one end and receding from the other? Thus he could calculate back and have the two bolts hitting at the same instant? I imagine a very large platform, like millions of light years in length, thus replicating the distances of galaxies. We say a relativistic doppler effect tells us about galaxies and their motion. If we can use this with galaxies couldnt the same be done with the lightning bolts?
ANSWER:
You are missing the point. Yes, he could use the doppler shift to determine that he was in motion with respect to the lightening bolts, but that does not alter the fact that they are simultaneous in one frame and not in another. You take the age-old stance that there is something special about one frame and that they just "appear" to not be simultaneous in other frames. In fact, even without doing any fancy doppler measurements, you could take any two events not simultaneous to you and find a frame of reference in which they were simultaneous. There is nothing special about the frame in which two events happen to be simultaneous. The thing you have to accept in relativity is that strange things are, they don't appear to be; moving clocks run slow, moving sticks are shorter, simultananeity is not absolute.

QUESTION: :
I live 3/4 of a mile from a motorway. Some days I can hear the traffic - other days I can't The wind only needs to be 5mph and it seems to "deflect" or "absorb" the noise vibrations Sound travels at 500+mph. How come a 5mph wind can "blow away" something that travels at 500mph?
ANSWER:
Wind will likely not be a big factor in sound suppression. More likely, a change in humidity can change the amount by which the air absorbs the sound wave energy. Another possibility is that there could be temperature gradients; if there were layers of different temperature air, this could cause the sound to be deflected, either down to the ground or up over your house. This is analogous to how mirages are formed except the deflected waves there are light.

QUESTION: :
Last week I set up a demonstration of Brownian Motion whiich worked fine and showed movement of the correct magnitude. It is a dilute suspension of 1 micrometer diameter polystyrene beads in distilled water. I came back to look at the suspension a day later with the same x400 microscope and found most of the beads had settled out but perhaps 1% were still doing the drunkard's walk. No surprise yet. What did strke me as odd was that a couple of beads wandered across rapidly spinning round each other. A bit too fast to count so perhaps around 3 revs per second. They did separate momentatrily by a few micrometers and slow down (at which time I wondered if I could see three beads) but were soon close together again and continued their frenzied dance until I lost them out of focus. I would have expected such spinning motion to be dissipated by viscous forces very quickly. There were other pairs of beads visible just being joggled around. How could this spinning be sustained?
ANSWER:
This is only a guess. I agree with you that if two or more were bound (maybe by electrostatics?), any orbital motion should quickly damp out. What I think you are seeing are vortices in which beads can become trapped. Vortices are much more common in nature than most people appreciate.

QUESTION: :
In physics class, we learnt that 'it is important for life on Earth that the Sun is in fact, a second generation star'. We were told it was important "because elements higher then helium on the periodic table would not be present in either the sun or any of the planets. These heavier elements are necessary for life on Earth". My

QUESTION: to my teacher was: Just because this elements are 'made' (correct term?) in the Sun, how does it relate to life on Earth? Were they 'transported' to Earth? I thought elements were already present on Earth after the Big Bang. My teacher actually requested me to ask you
ANSWER:
When the sun and solar system were formed, there was debris from earlier stars from which the planets were formed. Although the sun is continually forming heavier elements (up to iron), that is not where the planets' heavy elements came from. See earlier answers.

QUESTION: :
I've only had 1 class in physics, but that was about 5 years ago. I am trying to make cheese and I find that I need some physics information. My

QUESTION: is regarding force/pressure. How does pressure/force work when exerted over a certain area? In order to make some hard cheeses, you need to apply, say, 50 lbs of pressure to press it. Now, if the diameter of the cheese is, say, 5 inches, and you apply a direct downward force of 50 pounds per square inch on the press plate, would applying that same amount of pressure to a cheese with a diameter of 9 inches be the same amount of force needed to press the cheese? If you are using a 50 lb spring, compressing it the whole way would apply 50 pounds of pressure. Would it matter if this pressure is exerted on a 5 in diameter plate as opposed to a 9 in diameter plate? If the pressure is distributed evenly throughout the plate, does the size of the plate make any difference on how hard the cheese is being pressed? Here is a more specific example: the cheese weights 5 kilos and has a volume of 5 liters and the surface to be pressed is 23 cm in dimeter. Would compressing a 50 lb spring on this surface have the same effect as compressing the 50 lb spring on a cheese that weighs 2 kilos and has a top surface diameter of 12.7 cm? Sorry that this message is a little long, I'm having difficulty expressing my confusion. I guess what I am trying to ask is whether 50 pounds of pressure is always "50 pounds of pressure," irregardless of the surface area it is pressing? Are there formulas etc. that could help me solve this problem (because different cheeses have different volumes/diameters/etc.)? I'm sure this is an unusual

QUESTION: , but it is applicable to everyday life; I'm trying to figure out how to construct a press that will apply the right amount of pressure to different solids.
ANSWER:
You keep saying things like "50 lbs of pressure". This is the source of your confusion. Force is measured in pounds or newtons. Pressure is force per unit area, measured as pounds/inch2 (PSI) or newtons/m2. So, 50 lb loaded on a cheese with area 50 in2 results in a pressure of 1 psi. 50 lb loaded on a cheese with area 25 in2 results in a pressure of 2 psi. I do not know what you mean by a "50 lb spring". Springs are characterized by a spring constant k=F/x where F is the force necessary to cause a compression amount x. The spring constant is measured in pounds/inch or newtons/m. For example, a spring with spring constant 50 lb/in would exert a force of 50 lb on your cheese if compressed by 1 in, a force of 100 lb if compressed by 2 in, etc.

QUESTION: :
in a beam of sunlight entring a room.we can see sometimes dust particles moving in a zig-zag movement.what is the name given to this movement?what is the cause of this?
ANSWER:
Brownian motion caused by collisions between air molecules and dust particles.

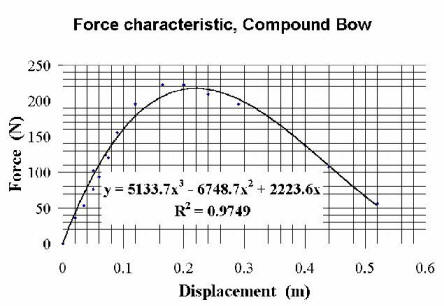QUESTION: :
Please settle an argument for me. I have tried to convince my wife that a compound bow cannot deliver more force to an arrow than one exerts upon it when pulling it back. My point is that regardless of the pulley system involved of the compound bow, the force imparted upon the arrow by the bow string cannot exceed the force imparted by the archer upon the bow string when pulling it back.
ANSWER:
My understanding is that the advantage of the compound bow is something called "let-off". The bow is designed in such a way that the force you must apply at a particular pull distance first increases and then decreases. (A conventional bow has force increasing the more the bow is pulled.) This allows you to be more relaxed and have longer time to aim. But, because the force applied in the middle was large, the energy stored in the bow can still be very large. The figure shows the force as a function of pull distance. You are correct, though, the force you exert on the string at each position will be the same as the force the string exerts on the arrow at each position after release.

QUESTION: :
I am pondering the classic equation E=MC2 in head and understand its straight definition (i.e. the correlation between mass at rest and energy). I also understand the equations implications for the relativity of the speed of light for observers as well as for nuclear fission and nuclear fusion. I was wondering where, in laments terms, the speed of light squared plays in the equation. I get how the math was worked out and that when mass is lost energy is produced, but does the speed of light squared mean that mass needs to travel this fast to produce energy? I am an amateur physicist and I have been trying to wrap my head around this for a few days.
ANSWER:
The only way that you can see where an equation comes from is to follow the derivation of that equation. The derivation is outlined in an earlier answer. And, why would the fact that c2 appears imply anything about the particle's speed?

QUESTION: :
I'm in 9th grade and so far none of my teachers, math or science, seem to be able to answer it; what keeps electrons from becoming attached to protons in an atom?
ANSWER:
I think the correct answer to your

QUESTION: is that the electrons do become attached to the protons. That is what an atom is�a bunch of protons (with neutrons) in a nucleus and a bunch of electrons "attached" to the nucleus. The attachment, though, is not a static attachment but more like little planets (electrons) orbiting a little sun (nucleus). The reason they do this instead of just sticking to the protons is that the laws of physics (quantum mechanics) forbid this system to have zero kinetic energy (being at rest). This whole picture is a little qualitative but probably good for a high school freshman.

QUESTION: :
Why does light travel at 186,000 mps rather than some other speed?
ANSWER:
Maxwell's equations, which are the equations describing electromagnetism, predict waves which travel with a velocity 1/√(ε0μ0) where the two constants are determined by the strengths of electric and magnetic forces. It just so happens that this velocity is 186,000 miles per second. See earlier answers.

QUESTION: :
I was wondering how a magnetic field is generated from a capable metal and why this happens for particular metals and nothing else?
ANSWER:
An electron is, in addition to being a tiny electric charge, a tiny magnet. In most materials the electrons north/south poles point in random directions and cancel each other out. In a few materials (called ferromagnetic) a large fraction of the electrons line up with each other making the whole object look like a magnet.

QUESTION: :
How many times does your heart beat during your lifetime?
ANSWER:
A healthy resting heart rate is about 60 beats per minute, or once per second. There are about 2.5 billion seconds in 80 years.

QUESTION: :
This is something I have thought about for a long time. I know it may seem off the wall, but here it goes. Thinking of distance, and the fact that anything can be divided in half, how is it we ever get anywhere (walking, driving etc.). Don't we always get halfway there first? Where do we "cross over" and actually make contact or get to where we are going?
ANSWER:
See my earlier answer on Zeno's paradox.

QUESTION: :
I read something recently about solar sails, whereby a spacecraft is given thrust by the momentum imparted by photons bouncing off a large reflective sail. My

QUESTION: : if a photon has imparted its momentum this way and has bounced off, it must presumably still be travelling at light speed, and rest mass by definition is still the same (zero) - so what has it lost to the sail? Presumably not kinetic energy? If this loss is represented by a lowered frequency or longer wavelength of the photon, what happens if the photon keeps bouncing off subsequent reflective surfaces? is there a lower limit to the frequency it can get to? Say a photon is introduced inside a hollow reflective sphere , does it continue to exist and bounce around forever but with frequency approaching zero?
ANSWER:
The photon has a momentum of p=E/c where E is the energy. When it reflects from the sail its momentum changes by an amount 2E/c. Hence, the sail gains an equal amount of momentum but in the opposite direction to conserve momentum. Technically, the photon will actually change its energy because of the recoil of the sail, but because the mass of the sail is large, this is a trivial correction and, for all intents and purposes, the reflected photon has unchanged energy (color). Your second

QUESTION: violates groundrules in that it requires a perfectly reflective surface; in practice, the photon would be absorbed in the blink of an eye even if the surface were 99.999% reflective.

QUESTION: :
I was wondering how the Heisenberg uncertainty principle applies to photons. As I understand the principle, it states we can either know the position, or the momentum of a particle with 100% certainty, but never both. With light though it's my understanding that it always travels at C. That this is one of the principles of relativity, the speed of light is always measured as the same no matter the speed of the observer or frame of reference. Therefore I'm puzzled about how this would reconcile with the uncertainty principle. If we had a photon in an eigenstate of position wouldn't we know that its momentum was C, and thus violate the principle?
ANSWER:
I do not know what you mean by "an eigenstate of position". The momentum of a photon is p=E/c where E is its energy. The uncertainty principle states that if the position of anything is known perfectly, its momentum is completely unknown. Hence, a photon whose position is known perfectly has an unknown momentum and, therefore, energy (color).

QUESTION: :
Which object more inertia a jet plane sitting still or a ping pong ball traveling at 100 mph?
ANSWER:
Inertia is just another word for mass, the resistance something has to being accelerated. The jet plane has more inertia than the ping pong ball regardless of their motion. The moving ping pong ball has more linear momentum than the stationary jet plane does.

QUESTION: :
Is their a equation that relates an object's real size, its distance from the viewer, and the size it appears to be?
ANSWER:
"�the size it appears to be" really has no meaning. We judge how large something appears to be by the angle it subtends. If the angle is small, the object looks small, if it is large, it looks large. The angle in radians is given by θ=D/R where D is the size of the object and R is the distance to it. Hence, if something is 10 times as far away it looks 10 times smaller.

QUESTION: :
I recently got a big magnet, and a small magnet. The big magnet is clearer stronger than the small magnet, yet when i use a magnetic field sensor to see how strong they are, it says they are the same strength. How can this be?
ANSWER:
Your measurement device presumably measures magnetic flux through a small area. Although the flux near the magnets are about the same, the larger magnet has a larger area overall and hence will result in a larger force on something iron.

QUESTION: :
Could you explain why the driver of a car must keep her foot on the accelerator to maintain a constant speed and therefore why energy is needed to maintain the cars speed??
ANSWER:
Wouldn't it be great if we could have a car which had no energy loss? Unfortunately, the world has forces which we cannot avoid which take energy away from something moving along. These fall into the category of frictional forces: a spinning wheel has friction in its bearings which will eventually cause it to stop; an object moving thought the air has air resistance which will eventually stop it as it moves along; the tires are not perfectly elastic and as they roll they are being continually deformed and undeformed and energy is lost. Without all these forces, we could accelerate up to speed and disengage the engine from the wheels and turn it off and just cruise. However, one can work hard to minimize these forces in the design of cars; making the cars aerodyamic, reducing the weight, and other tricks can minimize the energy we lose.

QUESTION: :
What force confines electrons to a negatively charged metal? I've read from many textbooks that a neutral metal confines its electrons because as soon as an electron escapes into the vacuum it leaves behind a positive charge that quickly attracts the electron back into the metal. Thus the electrons are imprisoned inside the metal forever, unless a high energy photon comes along to knock it out (or something of that nature)... Well, what about metals (say a metal sphere sitting in vacuum) that has a net negative charge?... It would seem to me that the metal "wants" the electron to leave... What I mean is, as soon as the electron leaves the metal it does not leave behind a positive charge anymore (because the metal is charged negatively). It leaves behind a negative charge that should push it away even further. What is the mysterious force that is counterbalancing this repulsive force and keeping the electron in?
ANSWER:
Imagine an electron very close to the surface of the sphere on the outside. Its field repels electrons inside the conductor leaving a net positive charge closer to the electron than the residual negative charge. Hence, the electron outside experiences an attractive force.

QUESTION: :
As you may or may not know, traditionally boats are moored through the use of a figure 8 knot on a cleat thats attached to the boat. In other words, the system is as follows Weight (usually about 400 lbs ) sitting at the bottom of the ocean, connected to a chain held up in the water by a buoy, which is attached to a thick rope connecting the buoy to the boat. Instead of using a figure 8 knot on the cleat, I want to use a climbing carabiner rated to a max load of 25 KN but that has no rating for a constant stress. My logic is that the only relevant force is the force of the current pulling the boat away from the buoy and weight set up which would come no where near (or even within any reasonable factor of safety) the 25KN rating. Is this valid? In other words, the fact that the boat weighs upwards of 6000 lbs is irrelevant, as the carabiner is not supporting its weight, the buoyancy of the boat is, correct? Also, is it safe to assume that the thick rope wouldn't even be able to match the 25KN stress rating meaning that if something were to break, it would be the rope before the carabiner? Please let me know if I'm overlooking some crucial force of if there's any reason this shouldn't work. Obviously I'm doing this project at my own risk and am just seeking a second opinion based more on theory than practical experience. As such, I understand you can't give me a 100% answer but under ideal circumstances, would you expect that I be ok?
ANSWER:
I do not want to get into all the numbers, but certainly 25 kN is much stronger than 400 lb. The only proviso I would add is that the mass (not weight) of the boat does matter but not because the weight needs to be held. Here is an example: assume, to make it clearer, that the boat is moored to a wall. Suppose the rope is slack and suddenly a strong wind starts the boat moving rapidly. When the rope becomes tight, the boat stops but it will not stop instantly. Rather the rope will stretch a bit so that the boat will stop in some short time t. So, during t, the boat will be accelerated by an amount a and the force F needed to provide this acceleration will be ma; F comes, of course, from the rope. If the required F>400 lb, the rope breaks. Probably a battleship will break the rope, a canoe will not. (How do you attach the rope to the carabiner?)

QUESTION: :
I was wondering how many times you'd have to double water's density to turn it into a solid (if that's possible).
ANSWER:
You make it sound like we could just squeeze the water and reduce its volume to half; this is really hard. It is very hard to answer your

QUESTION: quantitatively because the compressibility of water (how much it compresses for a given pressure increase) depends on the pressure and on the temperature and the details are not, as far as I have found, well known. We can make some rough estimates, though. The compressibility (I will call it C) is about C=0.46x10-9 Pa-1 at normal pressures and temperatures (say atmospheric pressure, about 100,000 Pa and room temperature). What this means is that the volume decreases by 0.46x10-7% if you increase the pressure by 1 Pa (1 N/m2). So, if compressibility were independent of pressure (a big if), you would have to increase the pressure by 1 GPa=109 N/m2≈1000 times atmospheric pressure to reduce the volume to 0.46 of its original value, about half. At around 2 GPa no liquid phase of water exists below temperatures of about 3000C and one of the exotic forms of ice would form.

QUESTION: :
Why does the glass of a wine glass vibrate when you rub your wet finger along the rim. i already know that it vibrates and has a natural frequency and what not but i want to know why it actually produces a sound?
ANSWER:
When you rub your finger here is what happens. Because of static friction, as you start to pull your finger it does not move but as you pull harder you eventually "break away" and your finger starts to move. If this were all that happens, the wine glass would not "sing" because your finger would just be moving around the rim; if you push down very gently while rubbing, it will just go smoothly sliding. But, if you push down a bit harder, the finger rubbing will start to "squeek". What is happening is that your finger sticks, then slides, then sticks, then slides, over and over and at very quick intervals. To make the glass sing, you usually have to mess around a little varying both the speed and push of your finger until you are exciting the glass with a frequency equal to its resonant frequency.

QUESTION: :
I don't quite understand Newton's Third Law of Motion. It makes sense when object A and object B are exerting the same force (thus, they do not move), but what if object A exerts more force on object B so that object B moves three inches in the direction that object A is pushing? What happens to the "equal and opposite" force that object B should be exerting?
ANSWER:
It makes no difference�if A exerts a force on B, B exerts and equal and opposite force on A. What you are forgetting, I think, is that how B moves does not just depend on what A does. For example, if A pushes on B and B does not move, then something else must be also pushing on B.

QUESTION: :
Photons are said to be carrier particles for the electromagnetic force but how do they do so. I have read that a force can be like two people passing a ball between them where one person throws the ball and recoils and when the second person catches the ball it pushes them away. And if photons cause a repulsive force between electrically charged bodies, what wavelengths do the photons have? If you can explain a repulsive force by exchange of particles (virtual or real) how can you explain an attractive force occurring in this way?
ANSWER:
See an earlier answer, particularly the note added at the end.

QUESTION: :
If it is given that light as no mass, how then, does it have the momentum to knock electrons out of there orbital shell? Wouldn't it be more reasonable to assume that light photons would just bounce off the electrons causing no change to them?
ANSWER:
In the real world, an object does not need mass to have momentum. The correct definition of momentum is not mv but p=√[(E/c)2-m2c2] where E is the energy and c is the speed of light. Hence, if m=0, p=E/c. For small velocities it may be shown that p≈mv.

QUESTION: :
does QED explain why magnets attract each other? If so, how do they?
ANSWER:
QED is simply classical E&M with the fields quantized. Classical E&M explains why magnets attract (or repel) each other, you do not need QED.

QUESTION: :
Can you please explain how the decay times of particles such as pi mesons are measured in accelerators to show they live longer than at rest?
ANSWER:
You set up detectors to look for the decay products, in the case of a pi meson they are a mu meson and a neutrino. You can trace the mu trajectory back to the path of the pi and hence determine where the decay occured. Knowing the speed of the pi and where it was created you can deduce the time from creation to decay.

QUESTION: :
On the myth busters, they took on a bullet versus gravity. They have a 45 caliber bullet being shot from a gun hitting the ground at the same time another bullet simply dropped from the same height hits the ground. My

QUESTION: is: Would changing caliber of weapon or height in which the gun is shot from change this outcome. A 22 caliber bullet will travel 2 miles approx. and leaves the chamber at 1200 ft. per sec.. I am not a gun person nor great at phsics. But I am curious enough to ask.
ANSWER:
The vertical and horizontal motions of a projectile are independent, so, since each bullet has the same initial conditions in the vertical direction (at the given height of the gun and at rest), they will hit the ground simultaneously regardless of the caliber or the height. If the gun is not aimed perfectly horizontally, it will not work.

QUESTION: :
how do you work out the average force of water in a swimming pool at one end of the pool?
ANSWER:
The force on an area of the bottom of a pool is equal to the weight of the water above it.

QUESTION: :
A person is sitting in a car that travels with constant velocity. He throws a ball verticall upwards. Why doe the ball fall in his hands when it returns?

QUESTION: :
why is it that when i drop a ball in a car that is going 60mph the ball doesnt fall in the place where i droped it relative to the highway?
ANSWER:
These are essentially the same

QUESTION: . When the ball is in motion in the car, the car passenger sees the ball having no accelerration in the horizontal direction (because, neglecting air friction there are no forces with horizontal components) and so, since it started out with no velocity in the horizontal direction it never acquires velocity in the horizontal direction. From the point of view of an observer on the road, though, the ball starts with some horizontal velocity component (the velocity of the car) and that never changes.

QUESTION: :
do alph,beta and gama comes from same element? why do we find all three in many radioactive substances?
ANSWER:
Gamma radiation can come from any nucleus; it is the electromagnetic radiation emitted when an excited nucleus deexcites (much like atoms emit visible light). Beta radiation is emitted from a nucleus which has either too many or too few neutrons to be stable and consists of a beta particle (either an electron or a positron) and a neutrino. Alpha radiation is a nucleus spitting out a helium nucleus (two neutrons and two protons) and is usually seen in very heavy unstable nuclei; it may be thought of as very asymmetric fission, the nucleus splitting into two nuclei. Some alpha emitters are also beta emitters.

QUESTION: :
I understand from Einstein, that a moving object experiences less time passing relative to a stationery object. Would this also happen to an object moving in a circle? More specifically, would a rotating object experience this effect at different rates across it's diameter?
ANSWER:
It is incorrect to say that the object "experiences" less time; the experience is that time just marches on like usual but his clock runs slow if viewed from another frame. The case you ask about is complicated because it is an accelerating frame of reference. Where the acceleration is larger (farther out on the rotating object), clocks run more slowly. This is called gravitational time dilation (because of the equivalence principle), it is not the usual time dilation you speak of.

QUESTION: :
I have been doing some calculations concerning interference/diffraction, and I saw that i could do some shortstepping and get a decent approximation using a little bit different equation than I was supplied with. I am talking about a laser beam in a Single-slit diffraction where the laser beam goes through a diffraction grating and is splitted into couple lines. Using the equation dsin(phi) = n*(gamma). I found that using an equation n*(gamma) * l / D = d (where gamma is wavelength, l = distance from the grating to the wall, D = distance from the center max to min/or between maxes and d = width of the grating)) Provided an excellent approximation, was easier and without the need to calculate the phi. My

QUESTION: is: Why is this a good approximation, and why cant I find it anywhere.. Is it because the original equation is simple enough.
ANSWER:
You seem to have discovered the small angle approximation. For very small angles you may write that sinφ≈tanφ≈φ. For your case, tanφ=(D/l)≈sinφ.

QUESTION: :
I put my cell phone in our microwave oven and closed the microwave oven's door. I then called that phone with another cell phone and it rang inside the microwave oven. Does this mean that since the calling signal was able to be picked up by the phone in the closed microwave oven, that microwaves could also be leaking out of the oven while it is being used in the cooking mode??
ANSWER:
The frequency used by your cell phone is not the same as the frequency used by the microwave. The oven is designed to shield the frequency of microwaves used in the oven. Of course, it is not a perfect shield and tiny amounts may get out.

QUESTION: :
How did scientists come to the 1st and 2nd law of thermodynamics and why are they so certain that they cannot be violated?
ANSWER:
The first law is simply conservation of energy. There is nothing mysterious there. The second law essentially forbids things which do not violate energy conservation but are never observed to happen. For example, when a hot body and a cold body are put in contact with other, we never see the hot body get hotter and the cold body get colder.

QUESTION: :
Is "Dark Matter" the proof for the existence of an ether? I have read articles stating that the Michealson-Morley experiment was flawed and that the existence of an "ether" was therefor not unproven.
ANSWER:
As far as I am concerned, dark matter does not exist until there is a definitive measurement of it. There is evidence that the majority of the mass in the universe is invisible. However, that evidence is based on the assumption that our current theory of gravity is correct. I am a member of a minority who believe that this evidence is likely a result of our not understanding gravity as well as we do. I have been heard to say that maybe dark matter is the 21st century's �ther; I know, that is heretical, but it is defensible that a hypothesized something does not exist if it is not observed. Also, the MM experiment is not as pivotal as many physics texts would have you believe. Einstein would have created special relativity with or without it. And relativity is such a successful theory that it is a moot point whether such a thing as the �ther exists. It certainly does not exist in the context that it is the medium with respect to which light travels. Finally, to answer your

QUESTION: , even if dark matter exists, it has nothing to do with the �ther.

QUESTION: :
why the tyers of a car moving with high speed looks to rotate with reverse direction of rotatio
ANSWER:
I assume you mean on a movie or TV. This

QUESTION: has been previously answered.

QUESTION: :
In Physic classes we are taught a stationary electron generates an electric field. Also a moving electron generates an magnetic field. Does a moving electron also generate an electric field (as well as the magnetic field)? For example if a stationary electron is placed near a wire carrying an electric current, does it experience an electric force pushing it away from the wire?
ANSWER:
The moving electrons do have an electric field. But the wire is overall neutral, that is there is a positive ion in that wire for every electron and so the net electric field is zero.

QUESTION: :
I am listening to Stephen Hawking say that heavy object slow down time, like a slow space in a river. Then using the pyramids as an example, he said that people looking out from the pyramid would see things traveling faster (time moving faster). Just to let you know I do know that this is just an example taken to the extreme and no one would really appear to be traveling faster. Ok here is my

QUESTION: , why isn't it called speed rather than time. Are speed and time the same in this case?
ANSWER:
In physics there are three fundamental concepts: length (L), time (T), and mass (M). All other physical concepts can be expressed in terms of these three fundamentals. For example, speed is L/T (e.g. miles per hour), force is ML/T2 (e.g. a kilogram meter/second squared is a Newton which is about a quarter pound), energy is ML2/T2 (e.g. a kilogram meter squared/second squared is a Joule, a million of which are about 3.6 kilowatt-hours). So we always talk about how M, L, and T are affected by the ideas of relativity and everything else, like speed, follows.

QUESTION: :
How is it that light, but nothing else, can travel at the speed of light? What allows it, and it alone, to travel at that speed?
ANSWER:
Actually, anything with zero mass will travel at (and only at) the speed of light. It just happens that light is the only massless particle we know of right now. Until recently we thought neutrinos were massless, but they have been shown to have mass. A particle called the graviton, hypothesized to be the quantum of gravity, might have no mass if ever found. Technically, the reason is that any particle with any mass would have to be given an inifinite amount of energy to accelerate it to the speed of light.

QUESTION: :
my class and i were discussing since light waves are part of the electromagnetic spectrum as are radio waves, then could light waves be converted to sound just as radio waves are? a concert with ROYGBIV?
ANSWER:
When you listen to music on the radio, you are not listening to the frequency of the radio waves. A trick called modulation allows one to use radio waves (whose frequencies are far too large to be heard by the ear) to carry a signal which has a frequency we can hear. The electronics in the radio passes the sound frequency to its amplifier and speakers. Sound waves which we can hear are in the range of about 20-20,000 cycles per second; radio waves are in the range of about 0.5-100 million cycles per second. The figure to the right shows an example of what is called amplitude modulation (AM). There is also something called frequency modulation (FM) which is similar but the modulating wave changes the frequency of the carrier instead of its amplitude; it's a little trickier to visualize. You can modulate light waves, but it is not as convenient and you could not use them for long-distance transmission. But then, you wouldn't be "hearing red", for example, but whatever you were modulating it with.

QUESTION: :
I am having a physics mental breakdown. My physics textbook (and experience studying physics) is contradicting popular belief and I would like to run this by an expert. When it comes to magnets, opposites attract. North poles are attracted to South poles and South poles are attracted to North poles. So when the North pole on my compass points towards the Geographical North Pole, that implies that the Geographical North Pole is really close to the Magnetic South Pole, correct? Similarly, the South pole on my compass pointing to the Earth's Geographical South Pole implies that the Geographical South Pole is really close to the Magnetic North Pole. Additionally, magnetic field lines are drawn from the North pole to the South pole, so on the Earth they are drawn from (near) the Geographical South Pole to (near) the Geographical North Pole. In summary, I have been researching a few educational websites and most are saying different (and contradicting) things. I believe that my physics book is correct, but other physics sites have labeled the Magnetic North Pole near the Geographical North Pole and the Magnetic South Pole near the Geographical South Pole. Which is correct?
ANSWER:
This is not really worth having a breakdown about! The north pole of a compass needle points in a generally northward direction. It is therefore pointing toward a magnetic south pole. The geographic pole near the point toward which a compass points is what everybody calls the north pole. Geographers tend to call this point the magnetic north pole but, if examined closely, magnetic field lines go into it, not out. It would be just too confusing to everybody to call it the magnetic south pole. See the picture at the right.

QUESTION: :
I have a

QUESTION: regarding the uncertainty principle. Whether expressed in the position-momentum form or the energy-time form, I have seen the right-hand side of the inequality given in two slightly different ways. The first is "greater than or approximately equal to h-bar" and the second is "greater than or approximately equal to h-bar over two". In the second case, that would of course be h over 4*pi instead of h over 2*pi. The two different forms differ by a factor of 2. Could you please shed some light on this?
ANSWER:
This

QUESTION: often comes up because, I believe, scientific statements are generally expected to be precise and unambiguous. But, this is a principle, not a law; it is not an equation, rather an inequality and an approximate one at that. The root of the problem is that the notion of "uncertainty" itself is a qualitative one. A precise quantative definition depends on the specific situation. For example, what is the shape of the wave packet which describes the position of a particular particle? Is it gaussian, square, maybe half a sine wave? And, establishing that, what is to be called uncertainty for that situation? Better, I think, to appreciate the principle as a philosophical idea�there are some things in nature that you simply cannot know with arbitrary precision. The statements you see give you an idea of the order-of-magnitude of how well some things can be known.

QUESTION: :
My

QUESTION: is about fluid dynamics. What is the relationship between the drag coeffient and the reynolds number? Based on my research I've been able to establish that for low reynolds numbers (which is what I'm interested in) the relationship is inversely proportional and defined as: Cd=24/Re
ANSWER:
This took some research on my part! The Reynold's number is Re=ρvL/μ where ρ is fluid density, v is speed of an object relative to the fluid, L is a length characteristic of the situation, and μ is the viscosity of the fluid. Drag coefficient is CD= 2FD/(ρv2A) where A is the area presented normal to the flow and FD is the drag force. To relate these, we must choose a specific example, typically a sphere at relatively low velocity for which the drag force may be written as FD=6πμRv and the characteristic length is the diameter, L=2R. Putting in that A=πR2, simple algebra leads to ReCD=24. I learned this all on Wikepedia!

QUESTION: :
Does (or can) light, or any EM radiation, interact with other EM radiation, of any wavelength? Simply asked: Can a beam of light hit another beam of light and if so, what happens?
ANSWER:
EM radiation is time varying electric and magnetic fields. If you add all the electric and magnetic fields at a point in space at a particular time you find the net effect of multiple beams of light. This is called the superposition principle.

QUESTION: :
From what I can gather, Einstein used the equivalence principle to formulate the idea that gravity and acceleration might be the same. This led to the idea that gravity is "simply" a depression in space-time caused by an objects mass. Could the same concept be used to explain the attraction between the proton and the electron? And maybe between opposite poles of a magnet? Perhaps these "attractions" are also due to depressions in space-time caused by an objects mass. Maybe in this concept lies the "unified field theory" that Einstein was searching for?
ANSWER:
There are at least two reasons I can think of, right off the top of my head, why "depressions in space time" are not the explanation of electrostatic (or magnetic) forces. First, mass and charge have nothing to do with each other; for example, a proton and a positron have identical charges and masses about a factor of 2000 different. Second, there are two kinds of charges and therefore both attractive and repulsive forces whereas there is only one kind of mass and only attractive gravitation. Einstein did, indeed, spend his entire life after about 1918 trying to incorporate electromagnetism into the theory of general relativity, to no avail.

QUESTION: :
I came across the fact that the average human being is made up of 7.0 x 10^27 atoms. In my effort to understand this number I calculated what this volume would look like if the atoms were the size of bb�s. I was astounded by the implications. If my calculations are correct, this quantity of bb�s would not only cover the contiguous United States, but they would be stacked 40,837 miles high. I�ve recalulated this numerous times and still can�t believe it. Looking for someone to check out my answer. Here are two givens: There are 6 bb�s per lineal inch. There are 3,119,884.69 square miles in the contiguous states
ANSWER:
It is good that you have been impressed by how big a number this is but be prepared to be shocked further because your numbers are way too small. I find, if I say it takes 36 BBs to cover one square inch, that it would take about 4.5x1017 to cover the US (using your number for area), about one ten billionth of the number of atoms in your body. I find that if I stacked up 7x1027 BBs, each 1/6 of an inch in diameter, the stack would be about 2x1022 miles high, way bigger than your number. Wait a minute! I now think you mean that you will stack many layers on top of the US covering layer. I figure that it would take about 7x1027/4.5x1017=1.6x1010 layers or 9.3x1010 inches or 1.5 million miles. So, your number is about 40 times too small. To see another example of how small atoms are, see an earlier answer.

QUESTION: :
is there any work done when we ignite a matchstick?
ANSWER:
Sure. You exert a force over a distance, pushing against friction. The match heats up as work is converted to thermal energy and this little bit of heat initiates a chemical reaction in the match where most of the subsequent energy comes from.

QUESTION: :
Why is it that air has the same index of refraction as empty space?
ANSWER:
It doesn't. Empty space has n=1.0 exactly, air is about n=1.0003. These are close enough that, for most purposes, one can approximate them to be the same. As to why they are so close, it is because air is already mostly empty space.

QUESTION: :
I have read that cosmic ray particles can pass completely through the Earth. if this is true, is it possible to measure fluctuations in how consistently or rapidly they do so? The reason I ask is because, it seems that in the future we could produce a map of the Earth's substructure by reading such fluctuations like an x-ray machine. As the Earth rotated, I would imagine, it could be possible to triangulate on structures of varying densities, such as minerals, gas, or oil.
ANSWER:
The only type of particle which will pass completely through the earth is a neutrino and neutrinos are notoriously difficult to detect. They interact with matter very, very weakly (otherwise, how could they go through the whole earth). I can imagine no practical way they could be used like an "x-ray machine".

QUESTION: :
Situation 1: A and B are moving on a paralell course, at similar velocities. Since the velocity differene between A and B is small (100M/sec) Situation 2: Particles A & B are Moving on the paralell course at similar velocities to each other, but particle C is moving at a significant fraction of the speed of light (say, .7c) relitive to A/B Does the mass of the particles change when the frame of reference changes to include particle C? A&B are still moving on the same course at the same velocity, only instead of viewing particle B from the frame of reference of particle A, we're viewing B from the frame of particle C, which has a velocity difference of .7c
ANSWER:
A and B will measure each other's masses as virtually unchanged. A and B will both measure C's mass to be significantly larger than its rest mass. C will measure A's and B's masses to be significantly larger than their rest masses.

QUESTION: :
Laminar flow and turbulent flow as in the two ends of the spectrum having to do with Reynolds #. What is actually happening to the liquid being forced through a pipe at a high Reynolds # >4000 compared to the liquid that is flowing laminar <2000? When turbulent does the water begin to spin like a bullet spins caused by rifling? What would happen if rifling grooves were implemented inside the pipe? Would a turbulet flow become less turbulent or stay the same?
ANSWER:
According to Wikepedia, when 2300<Re<4000, flow can be either laminar or turbulent, depending on the nature of the walls of the pipe. You are barking up the right tree with your rifling idea although I have no idea what rifling would do. My suspicion is that to keep it laminar you would want the walls very smooth. I think you will find the whole Wikepedia article very enlightening.

QUESTION: :
What keep a locomotive, with a load several times it's weight, from spinning when it starts off? How can it pull so many times it's weight?
ANSWER:
It is the friction between the wheels and the rails. As long as the force you require is not too great, the wheels will not slip. And, the amount of load which there is does not really matter because a small force can move a large mass, only with a small acceleration. If you try to accelerate too quickly, the wheel will slip; you often see this happen in old movies where the locomotive wheels will spin some when leaving the station. The exact same thing happens with a car: if you try to accelerate too quickly, the wheels will spin.

QUESTION: :
if you put an empty soda can on a skate board, set it in motion (with out knocking over the can) and then stop it suddenly.... compared to if you put a full 2 liter soda bottle on a skateboard, set it in motion at the same speed and stop it suddenly... would there be a difference in how far the can or bottle goes (because of inertia)?? Also would it make a difference if the same force were used to set it in motion (not the same speed) assuming it would take more force to move the 2 liter on the skate board.
ANSWER:
I am afraid you have designed an experiment which will not be very enlightening. The inertia part is that the object on the skateboard keeps going when the board stops. But how far each go will depend on the situation. Soda bottles are not good because they can tip over or roll. Let's consider a simpler situation: two cubes of the same size on the skateboard with different masses (to replace your empty and full bottles). Suppose that the boards are very slippery, frictionless. Then each cube will continue with the speed the board originally had, because of their inertia. To change the speed of something, a force must act on it. Now, suppose there is some friction. If there is, the force of friction is proportional to the mass, that is the frictional force on the heavier cube is larger. But, if there is ten times more mass, there will be ten times more friction. But, the acceleration of each cube will be the force on it divided by its mass (this is Newton's second law). Therefore, the accelerations will be the same! Each will go the same distance.

QUESTION: :
My physics teacher says if I were to wear a metal suit outside during a thunder storm and was struck by lightening, I would be safe. I think hes nuts. Is he right?
ANSWER:
He is right. Lightning kills because electric current if forced to flow through your body on its way to the ground. if you wore a metal suit, the current would flow through the suit, not you. However, the suit might get very hot and burn your skin, so you better wear something to protect you from that. My best advice is to not expose yourself to lightning in any way.

QUESTION: :
Prisms separate light into colors. The different colors refract differently. So Snell's Law says that they must have different speeds. I have always heard that electromagnetic radiation moves the same speed in the same medium. If blue light has a different speed in glass than red light, does that mean that radio waves have a different speed than say ultraviolet waves in air?
ANSWER:
The phenomenon you describe, velocity of electromagnetic waves being a function of wavelength, is called dispersion. All material media have some degree of dispersion; although air is a medium, it is so close to a vacuum in terms of the speed of light in it, that any dispersion would be all but unobservable.

QUESTION: :
I was recently participating in a Physical Test for a job. One of the tests was quantity of pushups, consecutively, without stopping or rest. Standard pushup postion, fully extending and locking out arms, coming down until chin touched the mat. I am in quite good shape so naturally I started at quite a rate of speed and was zooming through them when the Evaluator stopped me and said "You have to slow down, your cheating the number of pushups you can do by simply going off momentum." Does "momentum" even apply in this situation? There are 2 diffinitive start/stop postions and I can only go the distance of my arms.
ANSWER:
This is probably more physiology than physics. As far as physics is concerned, the same amount of work is done if you get up by exerting a large force for a short time or a smaller force for a longer time. However, different demands are placed on the muscles and, since I have been told that, when working out at the gym, all motions should be done slowly to get the maximum benefit, the evaluator probably had a point.

QUESTION: :
If a space craft like the Space Shuttle or the Millenium Falcon had fast spinning turbines beneath the floor, would that generate a gravitational field sufficient to keep things down?
ANSWER:
Why would you think that? It does not create any (at least any significant) gravity at all.

QUESTION: :
what evidence supports the contention that the strong nuclear interaction can dominate over the electrical interaction at short distances within the nucleus?
ANSWER:
The fact that nuclei stay together?

QUESTION: :
I was wondering if explosions are symmetrical. Or, more specifically, explosions in a vacuum.
ANSWER:
It depends entirely on how the bomb is designed. Probably very unlikely to be spherically symmetrical.

QUESTION: :
How dose a stainless steel tea pot generate the swirling, popping, and loud sound when applied to an electric radiant heat range top burner.
ANSWER:
Swirling sounds are, I presume, just the convection in the water as it heats and moves around. Popping is likely do to unequal expansions of various parts of the teapot.

QUESTION: :
if you are in free fall (having reached terminal velocity), will you still feel the air resistance on your body? on earth,you feel your weight because of the pushback of earth. will you feel some of your weight if you feel the pushback of air on you as you fall? i a trying to get at whether it is possible to truely feel weightless during free fall?
ANSWER:
Yes, because you are not in free fall, there is an upward force on you equal to your weight. You would feel like there was wind of about 120 mph in your face. Free fall means that there is no force on you other than your own weight. If you were in free fall in a vacuum, you would feel weightless. If you were in a freely falling elevator, you would feel weightless. If you were in an airplane which was following a particular parabolic path (Google vomit comet), you would feel weightless. If you were in a circular orbit around the earth, you would feel weightless. All the above are examples of free fall. I am pleased that you said "feel weightless" rather than "be weightless"; you are on the right track to understand.

QUESTION: :
I am researching on how it is possible for neutrinos to have mass, and I have come across flavour and mass eigenstates. I was wondering if you could enlighten me on what exactly an eigenstate is?
ANSWER:
If you have an equation of the form Ωfn(x)=Cnfn(x) where Ω is some mathematical operator, Cn is some constant, and fn is a function of x, it may have many possible solutions (which is what the n subscripts represent). The functions fn are called eigenfunctions and the constants Cn are called the eigenvalues. If a particular physical system is in a state described by one of the fn, it is said to be in an eigenstate. A physical system may also be in a superposition of eigenfunctions, for example g=af1+bf2; g is a possible state of the system, but it is not an eigenstate. One of the best known examples is the energy eigenvalue equation, Hψn=Enψn where H is called the Hamiltonian and En is the energy of the nth allowed state of the system described by the Hamiltonian H. The Wikepedia article on eigenfunctions is quite good (if you understand differrential equations).

QUESTION: :
if two cars are coming at each other at the speed of 50mph. Is it equal to one car heading at a concrete wall at 100mph?
ANSWER:
It depends a lot on the details of the collisions, but likely the car hitting the wall would be more damaged. Consider one possible case, a perfectly inelastic collision (one where the objects are stuck together after the collision). Also, let's assume the two cars have the same mass M. Further, let's assume that both collisions occur in the same time T (from when the car first contacts until it comes to rest). And, to generalize, let us let 50 mph=V so 100 mph=2V. When the car hits the wall, its momentum (mass times velocity) changes by 2MV; when the car hits the other car, its momentum changes by MV. Finally, what is the physics? One statement of Newton's second law is that rate of change of momentum equals force. So for hitting the wall, the force the car experiences is Fwall=2MV/T; for hitting the other car, the force is Fcar=MV/T. So, the force experienced by the car is twice as big when hitting the wall. (Don't forget the assumptions I have made in reaching this conclusion.)

QUESTION: :
Why does fusion stop at iron in a stars core? Is it temperature/pressure or something to do with the structure of iron?
ANSWER:
It is because iron is the most tightly bound nucleus and so any further fusion would require that energy be added. Heavier elements are made in supernova explosions. See an earlier answer for more detail.

QUESTION: :
Since mass is not conserved, gravitational field of the Sun for example is always changing. If its always changing, in this case decreasing, won't the potential energy of all objects around it decrease? Where does this energy go? If it is changed into energy according to special relativity, won't that transfer be a constant despite the position of such a body with changing mass in the universe? If so how do we prove that the energy is conserved despite the position of such an object in the universe.
ANSWER:
First of all, this is a very small effect. If all the hydrogen in the sun fused into helium, the total mass would decrease by less than 1%. Second, this energy is completely converted into forms we understand, namely the kinetic energy of the products and radiation (light and other electromagnetic waves). If the mass of the sun decreased, the orbits of the planets would change slightly, but that would not violate energy conservation. I am afraid the rest of your

QUESTION: does not make much sense to me.

QUESTION: :
I thumbed through as much of your old answers as I could but couldn't find what I was looking for. I understand that it is accepted the light travels at a constant and that nothing ( other then theoretical particals already doing so ) can travel faster then it.. But Why? I get the ideas behind the formula but it just seems arbirtary speculation. Why is it that light has been decided as an unbreakable barrier?
ANSWER:
So, do you know what FAQ stands for? Frequently Asked

QUESTION: s. You will find on the FAQ page an entry which links to my discussions of why c is a universal constant and another explaining why nothing material can go that fast.

QUESTION: :
a

QUESTION: regarding the situation where one twin stays on earth and the other travels on a space ship at close to the speed of light, only to return to earth younger than her sister who stayed behind. They're moving relative to one another. from the earth bound twin's perspective, her sister is moving away at a high velocity. but from the space ship sister's perspective, isn't it her sister on earth who's moving away at a high velocity? so why doesn't the earth bound sister age more slowly? is it the acceleration from a steady state that slows time? and if everything in the universe dissappeared except for the twins, how could we know which was accelerating away from the other? does the spaceship sister accelerate from a distinct point in the fabric of space?
ANSWER:
Well, that's why they call it the twin paradox! In fact, it is not a paradox at all and there is no

QUESTION: that the traveling twin is the one who ages less. See my earlier discussion of the twin paradox.

QUESTION: :
The other day I was thinking about energy...and this led to a little wonder! When we drop an object we hear a sound - this is generally considered as kinetic energy transforming into sound energy, correct? Well, what I was wondering was why does it become sound energy? What in the history of the universe/physics determined that kinetic energy will become sound energy when there is a collision? Why doesn't it become heat energy for example, or light energy?
ANSWER:
When two objects collide, kinetic energy is not conserved, that is, it does not remain constant. However, energy as a whole in an isolated system must be conserved, lost kinetic energy must show up somewhere. Where it shows up depends on the nature of the system but it can go to heat, sound (as you note), or, in rare cases, light. But, just because you hear it does not mean that sound is the only mechanism going on. In fact, even if the sound is very loud, the energy carried away by sound is usually a very small fraction of the total kinetic energy loss. In nearly all collisions of macroscopic objects, most of the energy is carried away as heat.

QUESTION: :
What is the phase of Earth one would see if viewing from the Moon during New Moon
ANSWER:
The moon and sun would be on the same side of the earth, so I guess you would, from the moon, see a "full earth".

QUESTION: :
If the history of the universe since the Big Bang could be condensed in one year (365 Earth days), when did humans evolve on our planet?
ANSWER:
Taking the age of the universe to be about 14 billion years and the age of "modern" humans to be about 2 million years, I find about an hour and a quarter.

QUESTION: :
in what ways can scientists test for the presence of each of the different components of the electromagnetic spetrum?
ANSWER:
This is a too broad

QUESTION: since there are so many types of electromagnetic waves to, in a brief answer, list all ways to detect them. For example you could detect visible light with your eyes but your eyes cannot see radio waves. You can detect radio waves with a radio but your radio cannot detect gamma rays. You can detect gamma rays with a scintillation detector, but a scintillation detector is not sensitive to microwaves. And on and on and on�!

QUESTION: :
Frictional force always acts opposite to the motion to the body then how come it provides the necessary centripetal force when car is moving in a circular road shouldn't it be acting opposite to the motion of the tier i.e. along the circumference or tangentially ?
ANSWER:
You have to be really careful with such a rule. In fact, friction does not have to act opposite the body. If an object is sliding, friction is always opposite the motion. But think of a box just sitting on an incline, it has no motion but friction acts up the incline. If you try to push it up the incline but do not succeed, it may be sitting still with the friction acting down the incline. So, static friction can act in any direction. This is what happens with a car rounding a corner�the wheels are not slipping and so it is static friction. So you see, you need to focus on the surfaces where the friction is acting, in this case the tires and the road, and here they are at rest with respect to each other. Another similar example is accelerating forward in your car; what is the force which propels you? It is, in fact, friction between the tires and the road which is a force that points forward in the direction the car is moving. But the direction the car is moving does not matter because friction is not between the car and the road, it is between the tires and the road.

QUESTION: :
I'm having trouble understanding the flow of AC current. If the current is generated by a rotating magnetic field, and switches direction each wave cycle, wouldn't that simply jiggle the electrons back and forth? I.e, push the electrons a tiny distance in one direction on the positive curve of the sine wave, and pull the electrons back the same distance in the opposite direction on the negative curve of the sine wave? Whence comes the directionality of the flow?
ANSWER:
Imagine a light bulb. Does it matter which way current flows through it? It works fine with DC current in either direction. The moving electrons interact with the filament and heat it up regardless of which way they are going. So, the fact that the electrons "jiggle" back and forth is irrelevant.

QUESTION: :
why do you use a ladder to go across a frozen lake?
ANSWER:
Because the ladder spreads out the force of your weight over a large area. What determines whether the ice will break is not just the force on it but over what area you exert it, that is, pressure (which is force per unit area) is what matters.

QUESTION: :
At what altitude does the moon's gravity over power the earth's? How far out in space do you have to be before you start falling to the moon and not the earth?
ANSWER:
You need to know that the gravitational force due to an object is proportional to its mass and inversely proportional to the square of the distance to it. Using this it is straightforward to show r=0.9R where R is the distance between the centers of the earth and the moon and r is the distance from the center of the earth to the point of zero gravity. R ranges over about 3.6-4.1x108 m over the course of a month.

QUESTION: :
Since the gravitational attraction between two objects varies with their mass at given distance per the Universal Gravitational Constant, why then do two objects with different masses fall at the same rate as described in the Pisa experiment? Or do they? Is not the combined gravitational force of the heavier object and the gravitational force of the Earth greater than the forces of the lighter object and the Earth? And if the force is greater why wouldn't the two objects both accelerate toward each other faster and come into contact quicker than the lighter object and the Earth?
ANSWER:
The acceleration is proportional to the force on the mass (weight) divided by the mass, and the force on the mass (weight) is proportional to mass. Therefore, the acceleration is independent of mass. See an earlier answer for more detail.

QUESTION: :
Does a heavier object go down a ramp faster than a lighter one? Assume all other variables stay the same.
ANSWER:
This link will link to several previous answers to this

QUESTION: .

QUESTION: :
If the sun was almost instantly coverted into pure energy, (e.g) the jet from a supermasive black hole the size of the sun was to hit the sun changing all the mass into energy in the time it takes for light to go from one side of the sun to the other. Would the time it took before the earth noticed there was no gravitational pull from the sun be almost instantaneous, or would it take ~ 9mins (Time light takes to reach the earth from the sun) (e.g) does gravity move faster than light speed.
ANSWER:
See earlier answser.

QUESTION: :
I've just seen some videos on youtube where people demonstrate how water, unlike other materials, actually expands when frozen. This fact is shown, for example, by keeping water inside a pipe with both ends tightly closed, and then freezing the water inside. The pipe, even if made of steel, explodes. I was wondering what would happen if you were to perform a hypothetical experiment where a really, really, really strong pipe (or some other container) is used. Would the expanding water still perform enough force to break the container, no matter how strong it is, or it would not freeze? Or maybe freeze but without expanding the usual ~9%?
ANSWER:
You can always make a container strong enough to perform the kind of experiment you propose. Normally, a phase diagram for a material (like water) is a picture of pressure as a function of temperature keeping volume constant. To the right is a phase diagram of water. Note that the line between liquid and solid has a very large negative slope so that as you cool the water, it just gets higher and higher pressure never actually solildifying. But this graph only goes up to a pressure of about 2 atmospheres; we cannot see what happens if we keep going colder just below zero. Water is very complicated at extremely high pressures, so I recommend that you look at this Wikepedia article to see what happens at very high pressures. It looks to me like when the pressure gets near 109 Pa (1 Pa=1 N/m2, and 1 atm≈105 Pa, so 109 Pa≈104 atm) liquid is no longer possible and one of the exotic forms of ice will form.

QUESTION: :
i am having trouble finding information on the compressibility of air. If i was to compress air under 100psi - in a 1 cubic inch container, how much distance would the air ultimately be compressed ? ...in other words, how much smaller than a cubic inch would the air become as it is squeezed ? ...also, i do not understand why tools that run on compressed air are rated for Cubic Feet per Minute, while air tanks are rated by Pounds per Square Inch, when square inch refers to surface area as opposed to the three dimensional quality of cubic inches. When the term PSI is used for air tanks, does it mean that is the pressure exerted on the surface area of the inside of the tank ? ...if so, is there a formula for converting the PSI of a tank into Pounds per Cubic Inch ? ...a 1-Gallon tank (1728 cubic inches) under 100psi = How many lbs. of pressure on each cubic inch of air in the tank ?
ANSWER:
PSI stands for pounds per square inch. It is a force per unit area, so when you ask "How many lbs. of pressure on each cubic inch�", it has no meaning, nor do your

QUESTION: s asking about "pounds per cubic inch". In a tank of gas, the pressure is (almost) the same everywhere; that is, if you move a tiny pressure gauge around inside, it will always read exactly the same. I say "almost" because the gas itself has weight and, technically, the pressure increases as you go lower in the tank; the effect is not nearly as important as for a liquid and, for what you seem to be interested in, of no importance. When a tank of gas has a certain pressure, say 100 PSI as you are interested in, this is normally the gauge pressure, the pressure above atmospheric pressure. If you open the valve of the tank to let gas escape, it will keep going out until the pressure inside is the same as the pressure outside�atmospheric pressure which is 14.7 PSI. So, 100 PSI means the pressure inside the tank is 114.7 PSI. Now, to ask about changes incurred by changing pressure, it is best to know the ideal gas law: PV=NRT; here, P is pressure, V is volume, T is temperature, R is just a constant depending on the units you are working with, and N is a measure of the amount of gas. It sounds like you are interested in situations where N and T are kept constant, in which case the product PV would be constant; if you double pressure, you must halve volume. In your specific case, starting with a 1.0 in3 container at 0 PSI gauge pressure (actually 14.7 PSI) and increasing the pressure to 100 PSI gauge pressure (actually 114.7 PSI), the compressed volume would be (14.7/114.7)x1.0 in3=0.128 in3. The cubic feet per minute part of your

QUESTION: would be relevant to the ability to maintain the pressure if gas were being removed. Again, look at the ideal gas law but now the volume and temperature stay constant but N is changing (gas is being removed), so P/N must remain constant. If you do nothing, just attach your tool to a tank, as you remove gas you must decrease pressure; if you remove half the gas, the pressure must go down by half also (use absolute, not gauge pressures here). So what the cubic feet per minute rating tells you is how fast you must replace the gas in the tank to maintain constant pressure, presumably done with a pump.

QUESTION: :
I was wondering how you can calculate the diameter of a drop of water which falls from an eye dropper.
ANSWER:
I did not know this, but there is a measure of volume called a drop whose volume is 0.06485 cm3. Knowing the volume of a sphere, 4πr3/3, you can show that r=0.25 cm, or d=0.5 cm. This actually sounds pretty big for a drop coming from an eyedropper, so here is another way: drop the drops into a teaspoon measure, counting them, until it is full. A teaspoon has a volume of about 4.93 cm3. So, if there are N drops in a teaspoon, the volume of a drop is (4.93/N) cm3, and from there you can calculate the diameter as I did above. Incidentally, there are about 76 official drops in a teaspoon.

QUESTION: :
why does water in canteen stay cooler if the cloth jacket surrounding the canteen is kept moist
ANSWER:
One of the most efficient means of cooling something is evaporative cooling. To evaporate water it takes a large amount of energy. So, the cover of the canteen extracts heat from its environment resulting in its becoming cool as the evaporated water carries away the heat. A simple experiment you can do is to wet a rag and then swing it around a few times briskly. You will find the rag gets quite cold, even on a hot day.

QUESTION: :
This

QUESTION: may sound trivial, but please bear with me. Assume a person is standing on Earth and is going to be hit by a very large object. Let's say there was a large object (with a large mass) and it started accelerating towards you from a foot away at a rate of about 1 foot/second. The mass of the object is such that the gravitational force between the person and the huge object is negligible compared to the gravitational force of Earth. If the acceleration is extremely small, will the huge mass of the object coming in contact with the person be enough to send the person flying?
ANSWER:
The acceleration is irrelevant, it is the speed at the instant it hits you that matters. "Send the person flying" is not a very quantitative statement. Let's just talk about your speed after the collision. Let your mass be 100 kg (about 220 lb) and you are hit by a freight train with a hugely bigger mass. Two extremes:
Perfectly inelastic, you "stick" to the locomotive so your speed is equal to the speed of the train, v. The collision will happen in a relatively short time, call it t. Your average acceleration is then v/t so the force you experience is mv/t. If v=0.1 m/s and the time of collision is 0.1 s, you would experience a force of about 100 N, about 22 lb. No big deal. But, as v gets bigger or t gets smaller the force gets bigger.
The other extreme is a perfectly elastic collision where you are moving on your own after the collision (and have done so conserving energy). In this case your final speed will be about twice the speed of the train, 2v. So the force over the collision time will be about twice as large.
The bottom line of my answer is that if you are hit by a big thing going very slowly you will probably not get hurt badly.

QUESTION: :
I've often read that an object falling toward a black hole or neutron star would be stretched along the direction of its path. I can see that gravity would attract the nearest parts of the object more strongly, but I don't see why that would stretch the object. It seems like a lot of unnecessary (and uncompensated) work.
ANSWER:
You have put your finger on the stretching aspect: since the force is so huge, the difference in force between two points separated by only a few centimeters is very large resulting in the tendency to stretch. This is called the tidal force.

QUESTION: :
For a while now I been trying to find out all that i could about the universal speed limit, the speed of light, and a recent metaphor has me slightly intrigued. say a train can travel extremely near to the speed of light, say 99.99999% close, but what would happen if there were another train, moving in the opposite direction, along a parallel track, wouldn't the relative speeds be breaking the speed of light?
ANSWER:
I have answered this

QUESTION: and others just like it many times before.

QUESTION: :
Would we weigh more if the earth's spin on its axis slowed down, due to a reduction in centrifugal force against a consistent graviational force?
ANSWER:
First, as I always insist on saying, your weight is the force the earth exerts on you and it does not change because of any motion you might have. That said, your apparent weight does depend on your motion. For example, we say an astronaut in orbit is "weightless", but this is wrong; the earth is still exerting the same force on her but that force is providing the centripetal acceleration holding her in orbit so she seems to be weightless. If the earth is spinning (as it, of course, is) your apparent weight is less; this effect is biggest at the equator and absent at the poles. It can be easily calculated that, at the equator, the reduction of your apparent weight about 0.3%, rather small.

QUESTION: :
A lottery machine uses blowing air to keep 2000 Ping-Pong balls bouncing around inside a 1.0m * 1.0m *1.0m box. The diameter of a Ping-Pong ball is 3.0 cm. What is the mean free path between collisions?
ANSWER:
For a nice discussion of how to calculate mean free path, see the Hyperphysics website. Using the equation derived there, 1/(πd2nV), I find about 18 cm.

QUESTION: :
Is gravitational force between the earth and sun, the same at all times of the year?
ANSWER:
No, the earth's orbit is not circular and so the distance is different at different times of year.

QUESTION: :
Do electromagnetic waves make magnetic fields?
ANSWER:
Electromagnetic waves are magnetic (and electric) fields. See my earlier discussion.

QUESTION: :
Can virtual particle pairs (such as electron-positron) annihilate each other on contact?
ANSWER:
They can and do. That is what they must do, in fact, to obey the laws of physics. When they come into existence, they violate conservation of energy because where there was nothing there is now something. According to the Heisenberg uncertainty principle, it is ok to violate energy conservation as long as it is done for a sufficiently short time, namely ΔEΔt≤ħ where ΔE is the amount by which energy conservation is violated (the mass energy of the particles, 2mc2 in this case), Δt is the time the pair exists before annihilating, and ħ is Planck's constant divided by 2π.

QUESTION: :
Current electricity is defined as the "flow" of electrons from one place to another. Would a "flow" of protons from one place to another have similar properties? I'm wondering, if I had a source of protons, could I construct a battery with them? I know that protons are not just floating around free like electrons. And I know that electrons are indivisible, while protons are composed of quarks, and electrons have very little mass compared to protons. But still... would moving positive charges along a conductor produce results similar to those we get when negative charges move along a conductor?
ANSWER:
Any moving charges constitute an electric current. The effects of a current of electrons in a wire could be reproduced precisely with a group of moving protons (in principle, since it would be very hard to do). It is just that it is so much easier to do with electrons since they exist naturally in conductors in an almost free state making them very easy to move around and manipulate.

QUESTION: :
How about a simple

QUESTION: about Dark matter? Since it is affected by gravity but doesn't interact with matter, wouldn't there be a bunch of it at the center of the earth?
ANSWER:
First, my usual refrain: as far as I am concerned, there is no such thing as dark matter until it is actually observed experimentally. I do not consider the anomalies suggesting too little observed mass in the universe to be "proof" of the existence of dark matter. My understanding is, again I am not an astrophysicist, that the workaround for the dark matter not accumulating around and in massive objects like the earth is that it is "hot", that is it is moving around very fast so it does not get bound.

QUESTION: :
how can it be that the resolution of the light being emitted from a object doesn't decrease with distance? ie if light is say 1mm2 in size and an object is emitting light particles and has a circumference of 360mm(thinking 2 Dimensionally) 1mm from it surface the resolution would be 1 light particle per 1mm2 of space, but between 1mm and 2 mm from the surface it would be 1 light particle per 2.(something)mm of space and so on. therefore by the time light particles being emitted from this object are lets say a billion lights years away....wouldn't it stand that the density of light particles being observed would be something very close to zero? ie; why do we see anything coming from a star on the other end of the known universe, or mayby this would explain why space appears mostly empty beyond what we observe, eventually we can't detect light particles coming from distant objects because the resolution (ie number of particles per given amount of space) becomes too low?
ANSWER:
It is not the resolution which is changed by distance. But you are right that the farther away you are the more difficult it is to form an image because of the loss of intensity over distance. Suppose that a particular object we wish to see has an intensity of only one photon per second per square meter at our distance. Obviously, if we wait ten seconds we will only get 10 photons into a telescope 1 m2 in area and a very grainy image will be seen. On the other hand, if we wait ten years we will get a perfectly good image. The other way to improve things is to collect more photons by having a bigger telescope; that is why the best research instruments are very big.

QUESTION: :
It's my understanding that gravity is the bending of space fabric. Earth weighs down the fabric, the moon falls in. What force or forces keeps the moon from sinking straight into Earth?
ANSWER:
Think of a big bowl. Take a marble and give it a push around near the rim of the bowl. It will, if given just the right amount of speed, roll around without falling to the bottom, right?

QUESTION: :
So splitting an atom causes an explosion. Would splitting other particles do the same thing? What's so unique about the atom? Is the energy in a nuclear explosion released from the atom, that is, how does splitting the atom cause all the observable chaos (mushroom cloud)?
ANSWER:
See my earlier answer on fission and fusion.

QUESTION: :
What would be the amount of energy needed to disable Earth's magnetic field?
ANSWER:
I don't find an estimate with a quick search and it would be extremely tedious to do because the field is not uniform. It would equal the energy stored in the field. The energy density near the surface is about 40 J/m3. So if you estimate the amount of energy over the whole earth up to an altitude of 1000 m, I find about 2x1019 J. This would probably be within a few orders magnitude of the total energy.

QUESTION: :
After constructing tables and graphs of E=mc^2, E/m=c^2 and (E/m)^1/2= c, I found that although E/m of course always gave the same value, it was not possible to destroy the whole mass whilst converting it to energy for the photon. Any rest mass value could be used, so long as it was very small ie in the magnitude of sub atomic mass, but destroying the whole mass caused the photon particle to accelerate to infinite speeds. The only way to resolve the problem was to assume that the rest mass was not destroyed in the transition from particle to photon, but that the mass just somehow gave up all of its energy without actually disappearing. This would imply that the mass was in a special degenerate state, ie very compact and at absolute zero temperature, I have not yet ascertained the magnitude of the mass, but hope to do so somehow after further and much more advanced physics study. I no that this seems to go against the accepted laws of physics and relativity, but it's the only way I can make sense of it at this point in time.

QUESTION: is: Am I way off the mark here, and have a made some bad assumptions.
ANSWER:
This

QUESTION: did not have a valid email, a violation of my rules, but I could not resist dealing with it because it is, as the

QUESTION: er suggests himself, "way off the mark." I completely do not understand the second, third, and fourth sentences of this

QUESTION: ; none of it makes physics sense. A complete explanation may be found in an earlier answer of mine, linked to on the FAQ page.

QUESTION: :
Why can't they make Power stations powered by their own electricity? You'd only need a device to start it and then it'd generate electricity with it's own power supply. I realise the Power station would need to be bigger than coal or hydro-electric power stations but couldn't it work?
ANSWER:
The first law of thermodynamics can be expressed as "you can't get something for nothing" and the second law can be expressed "you can't even break even". Think about it: the power station is providing energy to itself and to you; where does this energy come from? Maybe you could imagine the power station providing only energy to itself so that it uses exactly as much as it produces; that would not violate the first law which would say that energy being used was equal to energy produced. The second law forbids any machine which is 100% efficient, even if we were able to avoid mundane problems like friction, heat loss, etc.

QUESTION: :
I am curious about electromagnetic radiation and electric charge; do these two things have anything to do with each other? How are they linked and/or separable? I have done some searching and have yet to find a clear explanation of this issue.
ANSWER:
Electric charges cause electric fields. Electric charges in motion also cause magnetic fields. Electromagnetic radiation is a very special combination of electric and magnetic fields which propogates through space with a speed of 3x108 m/s. When I say "very special" I mean that not every combination of electric and magnetic fields is electromagnetic radiation; for example, imagine a charged particle moving with constant speed in a straight line�there is no radiation, just the associated electric and magnetic fields. However, if you make the charge accelerate the result is electromagnetic radiation. One simple example is to simply imagine a charge attatched to a spring and oscillating back and forth; it radiates electromagnetic waves. All electromagnetic waves have their source, in one way or another, in accelerating electric charges. Radio waves have their origin in antennas in which we make electric currents flow back and forth. Light has its origin in transitions in atoms where an electron moves from one orbit to another. You might want to look at my earlier discussion of electromagnetic waves.

QUESTION: :
If I'm driving on the freeway and a fly flies into my car through an open window, what happens to it? Does the rear window catch up to it or can the fly instantly marry with the new environment? (because the air trapped inside the vehicle can exert force on the fly, right?)
ANSWER:
Nothing in nature happens "instantly". I assume the fly flies straight in with a velocity (as seen by an outside observer) perpendicular to the car's velocity. From the fly's perspective, it enters a wind going the speed of the car and so he is accelerated in the direction of the car's velocity. From your perspective, he enters with a component of his velocity which is toward the rear window; but, you see that component decreasing steadily (he has acceleration toward the front of the car) and he may or may not hit the back window depending on how fast the car is going.

QUESTION: :
What is the difference between tangential and radial acceleration mathematically in a non uniform circular motion? Are they equal to dv/dt?
ANSWER:
Any vector can be resolved into components. For a particle moving in two dimensions on a curved path, it turns out to be particularly useful to choose the component directions to be perpendicular to (radial) and tangent to (tangential) the path of the particle at that instant. The radial component of acceleration is the rate of change of the direction of the velocity vector and the tangential component is the rate of change of speed. If the path is a circle, the radial is the centripetal component and the tangential is the "speeding up or slowing down" component. The acceleration is dv/dt (be sure to note that v is a vector) and dv/dt=r0v2/R+t0dv/dt. where r0 and t0 are unit vectors in the radial and tangential directions, respectively.

QUESTION: :
Various online postings about subatomic particles describe angular momentum as an intrinsic property of the particle rather than a force imposed on the particle or generated in the particle by rotating mass. In other words, the subatomic particles seem to possess properties of quantized angular momentum not due to axial quantized rotation of the particle, but by simply having that property independent of rotation, as is intuitively seen as necessary in classical conceptions of angular momentum. My

QUESTION: is, what empirical experiments, if any, rather than just theoretical considerations to avoid paradoxes, have actually proved beyond doubt that subatomic particles do not in fact have rotation inducing their angular momentum? It seems kind of like physicists are imposing an interpretation here rather than actually pointing to experiments that prove the impossibility of subatomic particle rotation, in order to arbitrarily preserve non-violation of relativity's dictum that nothing can go faster than the speed of light, since to produce the observed angular momentum, the quantized rotation would require the surface of the particle to exceed c. Is this conclusion an experimentally proven fact (if so, reference?), or, a convenient interpretation?
ANSWER:
There is no

QUESTION: that an isolated elementary particle has an intrinsic angular momentum (spin). The most common way to verify this experimentally (and how spin was discovered in the first place) is to observe the associated magnetic moment. If you think about a charge distribution which has intrinsic angular momentum, there must be associated current distributions which will make the particle look like a little magnet. For an electron, for example, which is known to have a spin angular momentum of �, it is found that the magnetic moment can point only up or down and therefore the spin must indeed be �. A much more thorough testing can be done through the study of atomic structure. The total angular momentum of an atom can be measured and hundreds of atoms and their excited states can only be understood if the spins of the electrons are included; for some very fine details, the spin of the nucleus must also be added in with the net angular momentum of the electrons. You should always be wary of, as you are trying to do, of imposing classical ideas on intrinsically quantum systems. Angular momentum need not be associated with rotating masses as you want to do. One final thing: when the Dirac equation is solved for an electron, it turns out that the orbital angular momentum L of the electron is not a constant of the motion, rather the appropriate quantity is L+�, that is spin automatically is incorporated in relativistic quantum mechanics.

QUESTION: :
For a planet of uniform density, how would the magnitude of the gravitational field halfway to the center compare with the field at the surface?
ANSWER:
For a spherically symmetric mass distribution like you describe, the only mass which exerts a force is that mass inside where you are measuring, so only the mass of the earth inside R/2 is effective, R being the radius of the earth. Since the mass of a sphere is proportional to R3, 1/8 of the mass of the earth is what is acting. The gravitational force is also inversely proportional to the distance squared, (R/2)2. Therefore, the field halfway is (1/8)/(1/4)=1/2 as strong as at the surface. In general the field is proportional to (r3/r2)=r, that is it increases linearly as you go out.

QUESTION: :
I was watching a recent sci trek episode that spoke of time travel as being true using the basic principle that time moves slower the faster you go. They proved this using an atomic clock. So my

QUESTION: is does that mean if I had fallen asleep on a jet liner going around the world, at the same time someone fell asleep in the city I left from, would I have had more sleep than the other person? I know off the wall but just poking around with some ideas.
ANSWER:
You are posing a

QUESTION: which is essentially a variation on the twin paradox. You should read my earlier answer on the twin paradox. So, when the two twins get together after the journey and compare clocks, less time has elapsed on the traveling twin's clock. Therefore, you would have slept less, not more. I hope you realize that the differences in time are trivially small unless your speed is comparable to the speed of light.

QUESTION: :
I want to give my students a relative understanding of the size of an atom. If a bowling ball were enlarged to the size of the entire earth, (and its atoms enlarged proportionately), how big would just one of its atoms be? the size of a house? a beach ball?
ANSWER:
The radius of a bowling ball is about 0.1 m and the radius of the earth is about 6x106 m. So the magnification is about 6x107. The radius of an atom is about 1 �=10-10 m, so the magnified atom would have a radius of about 6x107x10-10 m=6x10-3 m=6 mm, about a quarter of an inch. Now, take it a step farther: magnify the whole atom to the size of the earth, magnification now an additional 6x106/6x10-3=109. So the net magnification is now 6x107x109=6x1016. The radius of the atomic nucleus is about 5x10-15 m, so if the atom is the size of the earth, the nucleus has a radius of 6x1016x5x10-15 m=300 m. Atoms are small, nuclei are really small!

QUESTION: :
These

QUESTION: s are in relation to faster than light communications and travel, are in the form of hypothetical examples, and come from my childhood... Let's consider the seconds hand of a clock that moves from 12 to 3 in 15sec. If the hand is absurdly long, isn't it possible to reach and exceed the speed of light at some point along the hand towards the tip since it is covering an increasing distance in the same 15sec window of time? Let's consider a stick where if I push on one end, a button that lights a bulb is pressed on the other end. If the stick is, again, absurdly long, then isn't it possible for my signal to have exceeded the speed of light?
ANSWER:
This

QUESTION: is often asked in one form or another. You will see two similar

QUESTION: s not long before yours. You could find the answer on the FAQ page. The bottom line is that the "push" on a long rod travels with the speed of sound in the rod. And the long clock hand variation�the mass of the tip would become so huge that you would be unable to exert enough torque to accelerate it further, never mind that the effect of your push would not reach the end for millenia.

QUESTION: :
if E=MC2 where as you approach the speed of light mass increases as we approach it thereby having to increase the energy then why is it that photons travel at the speed of light but do not have infinite mass?
ANSWER:
Quite simply, because E=mc2 does not apply to photons. You could find this on the FAQ page (it is truly one of the most frequently asked

QUESTION: s).

QUESTION: :
A centrifuge simulates an intense gravity field as it rotates in a horizontal circle. That motion requires a centripetal acceleration directed towards the axis of rotation & hence, a force also directed toward to axis of rotation. I get the acceleration vector, but what is the source of the centripetal force? Is it the walls or bottom of the test tube? Is it the pressure gradient across a finite fluid element? The buoyant force? This is never mentioned in any literature I can find?
ANSWER:
The side walls exert an inward force on pieces of the fluid in contact with it (called normal force in elementary books); in addition, these small elements feel an outward force due to the fluid just inside them. I think of the vector sum of these two forces as being the centripetal force for small volume elements at the surface of the wall. But, what about parts of the fluid inside? Imagine a small volume inside somewhere. The forces on it are a force in by the adjacent element just outside where it is and a force out by the adjacent element just inside. The vector sum of these is the centripetal force. If this volume element is more dense than the fluid in general, it will "sink" toward the vessel wall, very analogous to what happens when something sinks in a fluid. Hence, the ability of a centrifuge to separate out heavier stuff.

QUESTION: :
I know our atmosphere is made up of infinitely small particles that compose gases, liquids, and solids; however is our atmosphere completely saturated with these molecules or is there residual.... "space"?
ANSWER:
These small particles (atoms or molecules) are not infinitely small, they are just very small (on the order of 10-10 m). In any gas only a small fraction of the volume is occupied by these particles, mostly it is empty space.

QUESTION: :
say in the future we are harvesting asteroids for their metal products and building things on earth. would adding so much new material to our planet have any effect on its rotation?
ANSWER:
I cannot imagine that the mass of such things would ever get anywhere close to the mass of the earth, totally negligible.

QUESTION: :
What types of sub atomic particles are photons made of? If not then of what?
ANSWER:
They are not "made of" anything, they are elementary. They are the quanta of the electromagnetic field.

QUESTION: :
Is empty space really empty? I can't imagine how it could be because in order for two things to be seperated there must be something in between to hold them apart.
ANSWER:
Why does there need to be something to hold them? Anyhow, physicists believe, not for your reason, that space or "the vacuum" is actually populated by a sea of particle-antiparticle pairs popping into and out of existence. This may sound like it violates energy conservation (where does the energy come from to create the mass of the pair?), but it turns out that energy need not be conserved over sufficiently small time intervals; hence, the popping back out of existence. The physical principle which allows this is the Heisenberg uncertainty principle.

QUESTION: :
If you drive 100 km/hr, at the end you have travelled 100 km in space and 1 hour forward in time. If you go 100 light years, haven't you travelled 1000 trillion km and 1 jullian year forward in time?
ANSWER:
100 light years is about 1018 m (so your 1000 trillion km is ok). At the rate of 100 km/hr it would take you about 60 million years. I do not know where you got that you could do it in one year.

QUESTION: :
My grade 9 science teacher believes for some reason that neutrinos are sub-subatomic particles because of beta decay. I`m certain that they are only subatomic, but she won`t listen. How can I scientifically prove to her that it is subatomic?
ANSWER:
Do not make the mistake that semantics is physics. There is no operational definition of what a subatomic particle is, it is a generic term. And, if your teacher insists on putting another sub- there, that is just fine because it has no important meaning. Perhaps she is trying to convey, using this terminology, that neutrinos do not exist in atoms until they come into existence in beta decay.

QUESTION: :
Assuming matter could be ramrod straight for a lightyear: If I have a one light year pole one inch away from a glass of water, and I push my end of the pole at the same instant I pointed a laser at the glass, would the beam or the pole reach first? I assume the pole. Does this void casulty? Ignoring practicality issues, would this mean that a morse code system could allow Faster than Light Communication?
ANSWER:
This

QUESTION: and ones like it are often asked. See the FAQ for an earlier answer.

QUESTION: :
My quandry is this: If e=mc2, how can a photon that has 0 mass, have any energy? Of course, I realize photons DO in fact have energy, since I can go outside on a sunny day and feel the warmth of the sunlight on my face. But when I plug "0" into the e=mc2 equation, I get a result of "0". Thanks for helping!
ANSWER:
I have answered this

QUESTION: many times before and it is among the

QUESTION: s on the FAQ page.

QUESTION: :
I have a

QUESTION: about how sweating cools the body. I understand that sweat is produced by our bodies and makes our outer body wet, and when the heat from our body comes into contact with the sweat, it turns the sweat into water vapour, which evaporates and carries away some of the heat energy from our body. However, I have two

QUESTION: s about this. 1) Since heat rises, wouldn't the heat just come off our body and naturally rise away from us, leaving us cool? 2) Why do our bodies feel cool after the sweat start carrying away the heat if more heat is still being produced by the body? I guess I'm just having trouble understanding the "cooling" effect. Can you please explain this to me in a more scientific way (without the use of kilojoules and Newtons and the like)?
ANSWER:
Evaporative cooling is very efficient because it takes quite a bit of energy to change the state of water from liquid to gas. Heat is not some fluid which will just rise up and away from you. It is not heat that rises, it is warm air that rises. Before that warm air can rise, it has to be warmed. Without evaporative cooling, the heat flow from your body can be via either conduction (your skin warming the air in contact with it) or radiation (actual electromagnetic radiation, mostly in the infrared). Both are very much slower than evaporative cooling. Even though your body continues to warm up, if you keep sweating you will attain an equilibrium situation where you the heat flows away as fast as you are warming up. You should also read my earlier answer regarding the meaning of heat.

QUESTION: :
Light-years. Is this a measurement of distance or is it also a measurement of time?
ANSWER:
A light year is the distance that light will travel in one year. It is a distance.

QUESTION: :
If a buss is going 100mph and I�m seating on the back seat, I am traveling 100mph within a moving object in this case a (school buss). It happens a fly lands on my �hand� That fly�s speed is as well 100mph, suddenly the fly takes of my hand and flies towards the buss driver within moving object (school buss) that is doing 100mph. What is the speed of the fly combined the 100mph? I don�t know if I�m making myself clear enough! But what I�m trying to find out is the length of the territory covered by a fly within motion object.
ANSWER:
Velocity is a relative thing. The velocity of the flying fly relative to the bus and you is however fast the fly is flying, let's say 1 mph. Then, relative to the bus, he will fly (1 mi/hr)x(1 hr/60 min)=1/60 miles in one minute. The velocity of this fly relative to the road is his velocity relative to the bus plus the velocity of the bus relative to the road, so it is 101 mph. So, relative to the road, he will fly 101/60 miles in one minute. Keep in mind that velocity is a vector, direction matters, so if the fly is flying from the driver back to you he is going 99 mph relative to the road.

QUESTION: :
I am trying to understand magnetic fields induced by electric fields. I can understand and calculate magnetic fields induced in small segments of wires, but I do not understand why the magnetic field at a point directly in the center of the center of a closed loop is not zero. Is there a difference between circles, squares, and other symmetrical polynomials?
ANSWER:
I think you must mean magnetic fields created by electric currents. An electric field does not induce a magnetic field unless the electric field is changing. The reason the magnetic field in the center of a loop is not zero is that the current from each piece of the loop has a magnetic field through the area defined by the loop pointing in the same direction as all the others, so they cannot add to zero.

QUESTION: :
If you could stretch a wire (A---------B) in space a distance of say... 1 light minute. Then you tugged end A, would you immediately notice the tug on end B or would it take a minute?
ANSWER:
It would take much longer than a minute; see my earlier answer.

QUESTION: :
Are theories testable. Or can a theory be based on speculalation?
ANSWER:
According to the Wikepedia entry on theory, "(t)heories are analytical tools for understanding, explaining, and making predictions about a given subject matter." In philosophy, "(t)heories whose subject matter consists not in empirical data, but rather in ideas are in the realm of philosophical theories as contrasted with scientific theories." I personally would endorse these semantics with regard to what a physical theory is. For example, the theory of general relativity, which is the current best theory of gravity, makes predictions which may be tested; string theory, on the other hand, makes no predictions about nature and must, in my opinion, be classed as a philosophical theory based on ideas.

QUESTION: :
Since energy cannot be created or destroyed, only converted from one form to another, what does a computer processor convert the electrical energy into? (if a processor which receives 50 watts, only converts 40% of that into heat, where does the rest go?)

ANSWER:
The way a processor works, essentially, is that many switches are being repeatedly turned on and off. Every time a switch is turned on or off it takes energy.

QUESTION: :
During a free fall ride at an amusement park, why do you not feel your seat when you're falling? You feel weightless, but you do not feel any force between your body and the seat of the car... why?
ANSWER:
During free fall (neglecting air resistance) the only force on you is your own weight and when an object falls with only its weight acting, its acceleration is g=9.8 m/s2. If the seat exerted an upward force on you, your acceleration would not be g and, therefore, by definition, you would not be in free fall because the net force on you (which is what determines acceleration) would differ from your weight. [In the real world, since air resistance does exist, the acceleration will be slightly smaller than g and so the seat will exert a small upward force on you, but much less than the magnitude of your weight which is "normal" when not accelerating.]

QUESTION: :
In the absence of air resistance, a ball thrown vertically upward with a certain initial kinetic energy will return to its original level with the same kinetic energy. When air resistance is a factor affecting the ball, will it return to its original level with the same, less, or more kinetic energy?
ANSWER:
Air resistance, a kind of friction, takes energy away both on the way up and on the way down.

QUESTION: :
I have been studying special relativity on and off for the past few years. I understand some of the concepts and find the ideas and theories fascinating. One problem i continue to have is with understanding gravity. When describing gravity, physicists often use a depiction of a well created in a fabric of space time. This does a great job of illustrating gravitation in a specific plane, but falls apart when one consideres space as a 3 dimentional void. Is this depiction the result of a dumbing down? Is there a better way of thinking of this concest of gravit? As it is, it seems incomplete.
ANSWER:
I recently answered a similar

QUESTION: .

QUESTION: :
Special Relativity Irregularity! A 100m train passes through a station at half the speed of light. Lightning strikes the front and back of the train simultaneously from the station's reference point. After solving the problem, I discovered that an observer in the station would see scorch marks 100m apart on the tracks and scorch marks 87m apart on the length contracted train. how is this difference possible when the observer supposedly saw two normal looking lightning bolts? According to the numbers, one lightning bolt must have been 13m in diameter!
ANSWER:
I believe you misunderstood the problem. If the lightening simultaneously struck two points 100 m apart in the station's frame, they would not strike the ends of an 87 m long train. There are different scenarios of this well-known thought experiment; I will give one which illustrates the point that simultaneaty is not absolute. A 100 m long train is moving with a high velocity on its track. It sees a bolt of lightning at each end simultaneously; it sees scorch at 100 m apart on the train and on the tracks. The observer at the station sees two flashes of lightning but not simultaneously; the first strikes the the rear of the train and, later, the second strikes the front just as it reaches a point 100 m from the first strike location. Hence, since the two events are not simultaneous in his frame, there is no paradox in having the marks 100 m apart on the track and 87 m apart on the train. I, personally, find a variation of this thought experiment to be easier to grasp. A flash of light occurs at the center of the train which strikes the ends simultaneously as seen on the train; the observer at the station sees the rear moving up to meet the flash and the front running away from the approaching flash, hence the rear of the train is struck by the flash first.

QUESTION: :
Let's say if a vaccuum cleaner standing on the floor turns through a small angle when the switched is on and then stops. Why does that happen?
ANSWER:
When the motor is speeding up there must be a torque exerted on it, exerted by the rest of the machine. So the rest of the machine experiences an equal and opposite torque which causes it to also have an angular acceleration, so it turns. When the motor reaches operating speed, torque is no longer necessary. Similar things happen when revving up the engine of a car or airplane.

QUESTION: :
How would you go about finding the change in magnitude of velocity in a system just containing the earth and sun, relative to the center of mass of the system, over a 6 month period? I found this in my book and am not sure about how to approach it or what it means by change in magnitude of velocity.
ANSWER:
First of all, the center of the sun is, for all intents and purposes, the center of mass; so we are talking about the earth. Since the earth's orbit is approximately circular, the magnitude of the velocity is approximately constant, so the change in magnitude of velocity is about zero. Maybe you meant the magnitude of the change in velocity; this would be twice the earth's speed.

QUESTION: :
what is the speed of a bullet?
ANSWER:
It depends on the gun. A rifle bullet can be anywhere from about 180 m/s to 1500 m/s; that's about 400-3300 mph. A passenger jet airplane goes around 500 mph, the shuttle goes about 18,000 mph.

QUESTION: :
I want to build a circular runway 2,000 ft in diameter for an aircraft that lands at 50 mph. How many degrees of inclination will be required to make the vertical acceleration forces perpendicular to the horizontal axis of the aircraft? Same

QUESTION: with a 1,000 and 3,000 ft diameter runway? Pls provide the formula.
ADDED:
As a retired Navy pilot landing on a circular runway would be a walk in the park - particularly because I'd never have to land in a crosswind and could not possibly run out of runway and wind up in the wait-a-minute bushes just off the end. If I got the inclination right landing forces would feel exactly as they would landing on a conventional runway (vertical acceleration forces perpendicular to the horizontal axis of the aircraft).
ANSWER:
This is the classic banked curve problem and the object is to find the angle such that a vehicle can negotiate the curve at a certain speed even on an icy (frictionless) road. So the idea is to make the the horizontal force the road exerts on the vehicle be the required centripetal force (mv2/R) and the vertical force the road exerts on the vehicle be equal to the weight (mg); here m is the mass of the vehicle, g the acceleration due to gravity, v the speed, and R the radius of the curve. The result is that tanθ=v2/(gR). For the numerical calculations it is good to use SI units, g=9.8 m/s2, v=50 mph=22.4 m/s, R=1000 ft=305 m; I find θ=9.50. You can test your prowess by doing the calculations for R=500 ft and R=1500 ft. A word of warning is that if you go too fast or too slow without enough friction you could slide off the runway (up or down, respectively) although it seems pretty unlikely, even at rest, that the plane would slide down a 9.50 incline. One thing that worries me a little is the moment of touchdown�will you try to be turning before you hit? Otherwise there will be that jolt of acceleration making the sudden transition from straight line to curved flight. But, hey, Navy pilots can land on a rolling carrier, right?

QUESTION: :
Our lecturer was showing us a demonstration whereby two cylindrical pieces of metal were allowed to free-fall down a hollow vertical tube made of copper.One of the pieces was a magnet and it took significantly longer to fall through the tube than the other. Can you explain why the fall times are different ?
ANSWER:
The one which is not a magnet just falls. The falling magnet causes there to be a time varying magnetic field through a section of the tube. This changing field causes an electric current to flow around the circumference of the tube (Faraday's law). This induced current itself has a magnetic field and that magnetic field exerts an upward force on the falling magnet.

QUESTION: :
When traveling in a car and you turn you are now accelerating. As long as your turning you are still accelerating. Is it possible to cancel out aceleration while in a turn by slowing down without coming to a full stop?
ANSWER:
There are two kinds of acceleration, one which changes direction (like when traveling on a curved path with constant speed) and one which changes speed (speeding up or slowing down). The first kind is always perpendicular to the direction of travel, the second always parallel. You cannot alter one component of a vector by altering another component perpendicular to the first. The answer to your

QUESTION: is no.

QUESTION: :
There are 3 people in a pitch-black room, spaced evenly apart, say maybe 5-6 meters each. The one in the middle has a laser pointer, turns it on and shines it straight ahead of himself perfectly parallel to the ground. Now, if the fact that we can see that light and the object(s) it illuminates is because the light is being reflected, how is it that all three people can see the laser pointer? The reason I don't understand this is that if light is composed of photons, and those photons reflect off of the object, I would think that only the person that is perpendicular to the laser pointer would be able to see the light because the photons would be reflected straight back at him. Sort of like if those same three people were bouncing a ball off the wall, the ball should only travel in one direction.
ANSWER:
Because the object is not perfectly flat, light is reflected in many directions. If the object were perfectly flat and perfectly reflective, only the first guy would see it. (Of course, there is no such thing.)

QUESTION: :
Are photons subatomic particles? And what type are they?
ANSWER:
Photons are particles, the quanta of the electromagnetic field. You may think of light as either a wave or a particle (photon). I don't know that there is a definition of subatomic particle, but let's say that it is smaller than an atom; in that case, some photons are and some aren't. Photons have no charge and no mass.

QUESTION: :
My curiosity combined with my lack of understanding of physics brings me to this strange

QUESTION: , which i can't seem to find the answer to on google. Basically I want to know: what is the 'weight' of music? In other words, when I copy music onto an iPod does it become heavier on any minute scale? Is there any number value, however small, that can be put to the 'weight' of the information that exists on the iPod/mp3 player?
ANSWER:
It takes energy to put a song into the memory of your iPod. Therefore, the mass of the memory will increase. However, this energy comes from the battery and so the mass of the battery would decrease by the same amount, keeping the mass of your ipod constant. That said, let's try to estimate the kind of mass changes we are talking about. I have no idea how much energy it takes to write a bit of data to memory, but it can't be much. Suppose that it takes 1 nJ=10-9 J of energy to write one song. Again, this is a guess but can't be more than a few orders of magnitude from the actual amount. The increase in mass would be about (10-9 J)/c2≈10-26 kg (E=mc2, you know). This is roughly the mass of an atom, really unmeasurably small. I don't think you have to worry about the extra weight you will be carrying in your backpack!

QUESTION: :
Because everything is in constant motion relative to some internal and external position, can everything be manipulated? Or better put, even though much of the universe appears immovable to human beings, is all of it actually moveable/changeable? For example, even though a table presents itself as permanently solid, is it concievable that a human hand could be able to go through a table in the event that its atoms/subatomic particles/etc. randomly rearrange themselves simply because of the impermanence that the movement of such atoms, etc. affords?
ANSWER:
I have no idea what you are asking in the first part of your

QUESTION: . Anything with mass can be "manipulated" by a force. The second part (table) seems to have nothing to do with the first part; however, your hand will never go through the table, I guarantee it.

QUESTION: :
Why can't humans exhibit wave-like behaviour when walking through the "single slit" of a doorway given that the de Broglie wavelength calculated is 6.1*10^-34m ?
ANSWER:
To see diffraction from a single slit, the wavelength must be comparable to the size of the slit. Notice that you do not see any diffraction of visible light through a door either.

QUESTION: :
How much anti-matter hydrogen would be required to destroy the earths atmosphere when relesed? I'm writing a book that I want to be realistic.
ANSWER:
The mass of the earth's atmosphere is about 5x1018 kg, so you would need that much antimatter to destroy it.

QUESTION: :
My

QUESTION: concerns the speed of light. My weak understanding is that nothing can travel faster than the speed of light. Matter becomes more dense and you would need an infinate amount of energy as you approach the speed of light. I've thought about this

QUESTION: a lot. I had a thought on the way to work this morning. What if I was big. Really big. Lets say I was big enough to hold a galaxy in my hand. Let's also say I had no problem with tempeture or pressure and I didn't have to breath air. I'm still human mind you. I'm just really really big. Big enough to hold a galaxy in one hand and another galaxy in the other. Now, I decide to move the galaxies closer together or a little further apart. As I move the galaxies together and apart, I don't see any issues with speed of light. From my point of view, it only takes seconds to do this. The galaxies would be moving at a tremendous speed for my wife who if still on earth calculating how fast the galaxies are moving back and forth. My

QUESTION: is: How does size figure in our perception of the speed of light?
ANSWER:
Nothing "figures in" to the perception of light speed. It is a universal constant and any measurement of it reaches the same result. With your long arms you could move them fast, but never as fast as the speed of light. And, if each was moving toward the other with speed greater than half the speed of light, they would still be moving relative to each other with a speed less than the speed of light (see earlier answer). Another issue with your experiment is that you cannot instantaneously start accelerating the galaxies in your hands since, once you decided to move them, the push which you initiated with your shoulders would not appear at the galaxies more quickly than the speed of light (millions of years given that galaxies are millions of light years apart); in fact, it would take much longer since the push would more likely travel at the speed of sound since your arm is a mechanical thing. Again, see an earlier answer.

QUESTION: :
After must time trying to learn about special reletivity I hit a brick wall. The faster you travel the more time would slow down, right? If you were to travel towards a light source and calculate the speed of light by your frame that light should be traveling faster. Similarly if you see a light source in the opposite direction and measure that speed you should see that light at the speed of light because at your slow-down frame (time-wise) it is. If this is not true then the inverse has to be true, and the light behind is slower your frame is sped up to make the oncoming light the approperiate speed, because nothing can travel faster than 186000m/s.
ANSWER:
You make the mistake to apply classical ideas about velocity addition to this problem, and these ideas are incorrect at high velocities or if light is involved. No matter what light you look at and no matter what your motion, the speed of light is always the same. Also, see my earlier answer on correct velocity addition relativistically.

QUESTION: :
If my severely limited understanding is correct, then the amount of matter in the universe is constant... never does anything pop in or out of existence; just changes form. If this is the case, then what does it mean when it is said that when matter and anti-matter come into contact they annihilate each other?
ANSWER:
Sorry, not correct. The amount of matter is not constant but the amount of energy is; mass is one form of energy. So when mass disappears, as in your example, energy must appear in some other form, in this case photons appear.

QUESTION: :
Why does it seem like almost everything in the universe in rotating or revolving? The earth rotates and revolves around the sun. The moon rotates and revolves around earth. The sun rotates and revolves around the milky way. Satelite galaxies rotate and revolve around larger galaxies etc. etc. And I know the theory is the universe is expanding but how do we know the universe is not on some grand rotation or revolution around other universes? Oh yea I forgot cause you are a physicist things of the very small rotate and revolve also (electrons around nuclei).
ANSWER:
Imagine a huge cloud of gas and dust, the one from which our sun and solar system formed. In the beginning there are many parts of the system very far away from the center of mass of the cloud moving in random motion. Think how unlikely it is that there is not some net flow around the center of mass. In physics terms, the cloud has angular momentum. Even if the motion of the particles is very slow, they are very far away from the center so they could have a very large angular momentum. Now, as this cloud collapses, it must obey the law of conservation of angular momentum since there is nothing nearby to exert torques on this cloud. So, what were originally very small rotational velocities become quite large. Think of a dancer or figure skater spinning with arms out and then pulling them in. Similar arguments can be made about larger or smaller systems. Atoms are not such a good example since the orbital model for electrons is really a quite poor description of what is happening; a hydrogen atom, for example, has no orbital angular momentum in its ground state. Elementary particles (like electrons) do have intrinsic angular momentum called spin.

QUESTION: :
I was watching a show on the Science network about super-massive black holes and was confused because they kept saying that they were proving the existence of super-massive black holes by the speed at which 'objects' rotate around the 'hole' before the event horizon (the bigger the black hole, the faster they spin - i think they were looking to obtain that equation, thereby linking a pattern between black holes based on mass and speed of rotation of the 'objects' rotating the black hole). This got me thinking about how they can measure speed in space. If v = d/t and time is relative (i.e. relativity theory), how can their measurements be accurate or at least not grossly biased based on our position in space/time? It was my understanding that they were looking at time lapsed photos and basically watching the 'objects' rotate, if that helps. I have been trying to research this and haven't found anything solid yet as an answer.
ANSWER:
If the sun were a massive black hole, the force on the earth would be much larger and so it would be necessary for it to have a much larger velocity to move in the nearly circular orbit it has now. The distance to the center of the galaxy where a supermassive black hole is believed to be is pretty well known, so, by geometry, if an object at that distance moves we can pretty accurately deduce the distance it moves.

QUESTION: :
Why does AM radio reception go haywire at sunset and through the night?
ANSWER:
Actually, AM transmission becomes better at night. The reason is that at night the radio waves can be reflected from the earth's ionosphere, something which is blocked during daylight hours because of the effects the sun has on the ionosphere. So, what happens is that distant stations with frequencies close to your favorite local station start to arrive at your antenna. Also, because of this, primarily local stations are required to turn down their power at night to keep from causing problems far away.

QUESTION: :
when were the atoms that comprise my body made?
ANSWER:
Hydrogen atoms may have come from the origin of the universe, about 14 billion years ago. Heavier atoms, up to around iron, likely came from stars which have burnt out. Heavier yet atoms are believed to have originated in supernovas, exploding stars. Of course, there is no way I can put a precise time, other than older than the age of our sun and solar system, when those events happened.

QUESTION: :
regarding microwave ovens it is desired to calculate the amount (key word amount) of microwaves that are produced per second during the operation of a microwave appliance. how may this be done? regarding "key word amount", it is not know in what units this "amount" or "quantity" of waves may be measured in. basically it is desired to know the quantity of microwaves produced by a magnetron due to a given power input. perhaps the quantity can be expressed in terms of energy, as energy would be dependent on the quantity. what constitutes "one" electromagnetic wave. one particle? one photon? so perhaps the quantity could be measured in terms of number of photons?
ANSWER:
The power rating tells the amount of energy per second consumed. So, assuming all the power goes into the microwaves, a 1000 watt oven will produce 1000 joules of energy per second. A common frequency used is f=2.5 GHz=2.5x109 s-1, and the energy of a photon is hf where h=6.6�10-34�m2�kg /s, so the typical energy per photon is 1.7x10-24 J. Therefore, there are on the order of 6x1026 photons of microwave energy per second if 1000 watts is the power rating.

QUESTION: :
I under stand the very nature of special relativity and am aware of the usual time dilation and length contraction experiments. I.e the moving spaceship and light beam theroretical experiment etc. A moving spaceship sees its light moving away at the speed of light because clocks in that frame of reference are slowed and length of the spaceship and all its rulers are contracted. However if a ship is moving in the opposite direction to the beam of light being fired, time must still be slowed as an observer (because it is moving) and the length contraction must remain, so in that case why doesnt the speed of light apear to be travelling faster then the speed of light (even when this is impossible)!?
ANSWER:
You make the mistake of trying to understand the constancy of the speed of light mechanically. Time dilation and length contraction are consequences of the fact that the speed of light is a universal constant, so it is circular reasoning to understand the fundamental by using the consequences. Rather, appreciate that the constancy of the speed of light is a postulate of the theory which is fully verified experimentally. Actually, as I have written before, this postulate is unnecessary if you accept the principle of relativity which states that the laws of physics must be the same in all inertial frames of reference, so in that sense it is straightforward to understand the constancy of the speed of light.

QUESTION: :
Why rotation or spin gives stability to objects, like a spinning top or a spinning football?
ANSWER:
A spinning object has angular momentum. It is a vector which points along the axis about which the object is spinning. It is one of the laws of physics that angular momentum stays the same unless there is a torque applied to it, and so if you keep the object isolated from external forces, the spin will always point in the same direction.

QUESTION: :
how is superconductivity used to produce strong magnetic fields?
ANSWER:
What determines the strength of the magnetic fields is the magnitude of the electric current. It is possible to have much larger currents in superconductors.

QUESTION: :
Since a gravitational force slows time, what happens to time when it is in the mid-point between two equal very massive objects (when the net gravitational force is 0)?
ANSWER:
If the clock is at rest and the gravitational field is zero, it runs at the same rate as if it were in empty space.

QUESTION: :
The atoms that constitute your body are mostly empty space, and structure such as the chair you're sitting are composed of atoms that are also mostly empty space. so why don't you fall through the chair?
ANSWER:
See the FAQ page.

QUESTION: :
According to the theory and the tests that have been made, time appears to pass slower the greater you accelerate. Time is measured with a clock, and anything accelerating will experience g-forces. By that rationale a mechanical clock should tick more slowly due to the g-forces acting upon its gears. A digital clock should operate more slowly because of the g-forces acting on the electrons flowing through its systems. How do we know that the time dilation we observe is not a direct result of the g-forces involved affecting our measuring devices? (An experiment where a cesium clock was flown from the US to Britain on a Concord to test the theory comes to mind.)
ANSWER:
Forget acceleration. A clock moving with a constant velocity, which experiences no "g-force", runs more slowly than the clock it is moving past. This is a fact of nature and has nothing to do with the actual design of the clock. You should read my earlier answers, and particularly the description of the light clock, to get a better feeling for this. If you are accelerating or in a gravitational field, time is also affected; these are effects in general relativity whereas the standard time dilation of moving clocks is special relativity. Experiments with atomic clocks take all effects into account. But the important thing is that time is not a universal constant, it depends on the motion of the clock, and this has nothing to do with clock design; if a clock does what you describe, it is an unacceptable clock because it is not measuring time.
FOLLOWUP

QUESTION: :
Per your suggestion I took a look at the "Light Clock" applet, and either I am mentally incapable of grasping this concept, or it seemed to support my thoughts on Time Dilation being a result of instrumentation limitations. In that applet the hypothetical clock is ticking slower because light is taking longer to bounce between mirrors. At least from what the applet suggests it is taking longer because light is having to travel a longer distance to reflect on trips between mirrors due to their motion and the diagonal path the light must travel. (Perhaps I am missing something because the applet does not demonstrate the 'stationary' clock being time-dilated relative to the one in motion)
I am also aware of experiments in particle accelerators concerning the lifetime of particles, which also bothers me given that there is the old law that one cannot observe without having an effect on what they are observing, and slowing or accelerating these particles removes them from their natural state.
ANSWER:
I will address your second

QUESTION: first: we do not do anything by observing a decaying particle which causes it to decay, we just sit and wait for it to decay. If there is a bomb with a 5 second fuse we might observe it to blow up after 8 seconds if it is speeding past; we did not do anything to cause the bomb to explode. And, you miss the whole point of relativity by saying that by moving with a large speed they are not in their "natural state". The principle of relativity states that the laws of physics are the same in all inertial frames of reference; there is nothing more natural about being at rest than moving with a speed of 99% the speed of light.
Regarding the light clock, the point is that the speed of light is the same in either moving or stationary frame. If this were instead a "sound clock", it would not be a good clock because, if there were a wind perpendicular to the distance to the reflector, the clock would run slow compared to other clocks you might have. (Think about it�it is like swimming across a flowing river which takes longer than across a still river.) But, with a light clock, there is nothing you could do in the rest frame of the clock which would cause it to not be synchronized with all other clocks in your frame because there is no medium through which light travels and so it cannot "flow". So, you have to admit, it seems to me, that if you are on the passing spaceship, all your clocks will run at the (normal) rate. But, the guy you are speeding past will see all clocks running at the same rate but slow because the light clock is demonstrably slow. Once you can accept the fact that the speed of light is the same for all observers, the rest of relativity just falls into place; read my earlier answer.
Again I need to emphasize that you should forget acceleration. You only need constant velocities to completely understand special relativity.

QUESTION: :
in a simple circuit (just a battery and bulb) electrons transfer their kinetic energy to the bulb by colliding with atoms in the filament, producing heat and light? [not sure how correct that is for a start]. If so, then wouldn't the electrons lose kinetic energy after the bulb causing the current after the bulb to be different than before the bulb? I know this is wrong as current is the same everywhere in a series circuit, but I am unsure where I am wrong,
ANSWER:
First, you are correct that the wire gets its energy by electrons colliding with the atoms in the wire. But the electrons are constantly colliding and then get going again because of the voltage across the ends of the filament which means that the electrons are always seeing a force so they speed back up as soon as they stop. See an earlier answer for more detail.

QUESTION: :
An electron is at rest in my reference frame. I see a proton move by the electron at rest. There is an electrical component force (opposites attract), but will there be a magnet force since there is initially only one current?
ANSWER:
There will be a magnetic field because you have a moving charge. However, there will be no magnetic force because the electron is at rest. If the electron is free to move in response to the electric field it experiences, it will then experience a magnetic force as well.

QUESTION: :
My 100 gram pepper drops at 9.8m per sec squared on Earth. According to my textbook we get this because The formula for the force of gravity is big G times big M times little m divided by distance squared I'm assuming that I can pick either the Earth of my little 100 gram pepper to be the big M or the little m. If I do that then the little g for the pepper is 1.64 x 10^-25. But isn't the Earth accelerating towards the pepper at the same rate that the pepper was accelerating towards the Earth when g = 9.8 m/sec squared?
ANSWER:
The accelerations of the earth and pepper are, most certainly, not the same. What is the same is the magnitude of the force each exerts on the other (Newton's third law). Because the pepper has a small mass, it experiences a large acceleration; because the earth has a huge mass, it experiences a tiny acceleration (the "little g" you erroneously calculated for the pepper). GMm/R2 (Newton's universal law of gravitation) gives the force, but the acceleration is Force over mass (Newton's second law). So g for the pepper is GM/R2 and g for the earth is Gm/r2.

QUESTION: :
I'm reading "Relativity" by Albert Einstein and in it he says that simulteneity is relative and uses the example of two lightning strikes at points "A" and "B" and an observer at the mid point between the two "M". Einstein states that an observer on a train moving from "A" to "B" observing the lightning strikes just as the observer reaches "M" will see that strike "B" occurs before "A" (as the train it moving toward the light from "B" and away from the light coming from "A"). Does this mean that an event only becomes real when the light from it reaches the observer? Or could one legitimately says "These two events happened simultaneously, but I saw the flash from "B" before I saw the flash from "A"?
ANSWER:
The relativity of simultaneaty is not "how it looks", it is how it is. In relativity you have to be careful how you define a time interval so that you correct for such things as the time it takes light to reach you. The converse is also true, a distant star is seen right now but as it was long ago. I always find the following example more convincing than the lightning at the ends of the train example. In the center of one of the cars there is a flashbulb which flashes. Light reaches the front and rear walls of the train at the same times. However, an observer on the side of the track watching the car go by sees the rear wall come forward to meet the oncoming light and the front wall running away from the light coming at it. Hence the event corresponding to the flash at the back wall occurs earlier for the observer at rest. (It is crucial to realize that both observers see all light moving with the same speed.)

QUESTION: :
i was trying to explain the quantum double slit experiment to my friend and he wasn't buying it so i wanted to tell him about quantum entanglement to help him better understand the "spooky action at a distance" (as Einstein called it). Seeing as i am 14 and have only the most basic of the basic understandings of physics i was flabbergasted when, while telling him about the experiment where 1 electron is taken to Chicago and another is taken to saaaay THE ANDROMEDA GALAXY but are both in a quantum state (spinning up and down at the same time i think) and are kept in a box (so we cant see them). If when you look at the one in Chicago, it spins down the one in the Andromeda galaxy spins the opposite of the one you look at WITHOUT EVEN LOOKING AT that one. After trying to explain that to him he asked "how do you know its spinning up and down at the same time when the second you look at it, its spinning up OR down and furthermore I cannot see an electron so how can we even detect whether it is spinning up or down in the first place". I tried and tried to figure it out in my head but to no avail so i ask, can you you tell me what piece of equipment, while doing the quantum double slit experiment, measures and therefore causes the spooky result and also solve my query about how the physicists know that an electron is spinning up and down at the same time when the second they measure (WITH WHAT) it, it chooses to change to only one.
ANSWER:
What makes your

QUESTION: difficult to answer is that the quantum double slit experiment is not an example of entanglement, rather an example of wave-particle duality; so you are trying to convince your friend of something by using an inappropriate example. I will briefly describe both:
In the double slit experiment, the intensity of the light is turned down so low that only one photon at a time passes through the slits. Lo and behold, a double slit pattern appears on the screen and it appears one photon at a time. In other words, the photon somehow passed through both slits, not one as you would expect if the photon were a particle. But it is still a single photon when you detect it, so how could it have gone through both slits? Only if it were a wave when you needed to be. You get what you look for. The pi�ce de r�sistance is that if you place a detector at one of the slits to try to determine through which slit the photon passed, you destroy the pattern on the screen!
In an entanglement experiment you create two electrons whose total spin is zero. However, it is a mixed quantum system; so it is not simply one electron has spin up and the other spin down, rather each has spin half up and half down. Now, if you take one of them and measure its spin, the effect is that you "put" this electron into the state you measure, say up; but, since the pair is a single system, the total spin still has to be zero and so if you put one into the up state, you are simultaneously putting the other into the down state. It will be true even, as you specify, one is 2.5 million light years away. You could have some alien measure the spin there and send you his results but you wouldn't find out for 2.5 million years! This experiment has actually been done here on earth where you can actually find out the results before you die!

QUESTION: :
I am having trouble with calculating how fast a stationary hydrogen atom would move after absorbing a photon. Logic tells me that if a hydrogen atom absorbed a photon that had exactly the same amount of energy as it has, i.e. 9.3899x10^8eV, it ought to move at half light speed. As a photon does not have mass its momentum cannot be calculated from momentum, p, = mv. I tried substituting for m from the equation E = mc^2 but this gave me an answer much higher than light speed. I know that momentum is supposed to change with speed in accordance with the equation E^2 = m^2c^4 = p^2c^2 but I do not understand why or how to use this equation. Also, the units of energy change when m is replaced by E/c^2 and physicists get around this by choosing a unit of length so that the speed of light is 1. This seems to be a bit of of a fiddle to me. So could you please show me how you would calculate the speed of a hydrogen atom after absorbing a photon of equal energy.
ANSWER:
The momentum of a photon is E/c. Take the rest mass of the atom to be M and the momentum of the recoiling excited atom P; the correct equation for P is P=Mv/√[1-(v2/c2)]. Then, energy conservation gives E+Mc2=√[(M*c2)2+(Pc)2] and momentum conservation gives E/c=P. Here, M* is the rest mass of the excited atom. You can expect that v<<c and so P≈Mv=E/c. That is the outline of what you need; if you want to be totally exact, just solve the two equations for the two unknowns (v and M*). I have assumed that the photon has a much smaller energy than the rest mass energy of the atom, whereas you have assumed otherwise, but a hydrogen atom is not capable of absorbing half its own rest energy because anything more than 13.6 eV will ionize the atom. You could go ahead, though, with the fiction that the atom did absorb a huge amount of energy and solve for the (physically unreasonable) velocity using the two conservation equations I give you above.
FOLLOWUP

QUESTION: :
I have been led to believe that the absorption of photons that excite an electron are those photons with very specific energies given by the equation 1/wavelength = R(1/n^2 - 1/m^2). These are usually photons below x-ray energies and the highest energy photon absorbs first to excites the electron and then a less energetic photon excites it further and so on until the electron is expelled. What happens to photons of other energies. Are you saying that these are not absorbed or does the atom just absorb the right amount of energy from one that has more than it needs? If other photons are not absorbed then where do atoms obtain their kinetic energy from? And what happens to gamma rays when they pass into a substance. Although these can pass through some distance they must eventually be absorbed. If they just ionise the atoms is this the way that atoms accumulate kinetic energy by expelling electrons to make them move fast and then reabsorbing them to make the whole atom move faster.
ANSWER:
For energies less than the binding energy, the photon will be absorbed only if it has just the right energy to excite the atom to one of its allowed states. Otherwise, the photon will scatter from the whole atom which will rebound in such a way to conserve energy and momentum but, for such low photon energies, it will look, for all intents and purposes, that the photon stays about the same except changing direction (like it had bounced off a mirror). (Incidentally, the energy of the incident photon must be very slightly larger than the energy of the excited state for absorption to occur because some of the final energy will be in the kinetic energy of the recoiling atom.) If the energy is larger than the binding energy, the photon will most likely scatter from the electron which will be ejected from the atom and you end up with three things, the photon, electron, and proton; the proton, being as massive as it is, can be ignored to an excellent approximation and the energy and momentum are shared between the photon and electron. This is called Compton scattering. It is also possible that the photon will scatter from the proton and the result is again that, approximately, the photon just changes direction (again like a mirror). The electron and proton will not get back together�the electron is moving so fast that it leaves the scene.

QUESTION: :
I have lots of

QUESTION: s regarding the nature of space-time...and especially gravity. I have yet to hear a satisfactory explanation of why mass causes a curvature (or is a curvature) in space-time and why that curvature results in an attractive force to all other objects. (the bowling ball example is flawed since the animation always shows the rolling ball pulled towered the depression that represents the curvature. So it seems to assume a gravitational force pulling the object toward the depression.
ANSWER:
General relativity is a very mathematical theory, so it is almost inevitable that explanations are going to be qualitative and not really rigorous. The bowling ball on the trampoline, for example, is just a qualitative example of how bending the space around something will make it look like other objects are attracted to it; also, it is meant to give an example of how mass can alter the space around it. I think that a more persuasive argument to convince yourself that space is warped by gravity is the equivalence principle which states that there is no experiment that you can do which can tell you whether you are in a gravitational field with an associated acceleration g or whether you are in empty space accelerating with acceleration g. This is the cornerstone of general relativity. So the experiment you think of is being in an accelerating spaceship and a beam of light, perpendicular to your direction of travel, enters from the side; you will then see the beam of light bend as it crosses the spaceship. Hence that beam of light will bend if passing by a massive object like a star. You should read my earlier answers on general relativity too.

QUESTION: :
It is understood that objects give off infrared radiation and can be imaged in this part of the electromagnetic spectrum. Further, photons are ejected by atoms as electrons move between energy states. So, I wonder if you had a single atom...in a 'dark, cold' space, would you be able to sense that the atom is there by viewing the infrared heat emissions? That's the basic

QUESTION: . But, beyond that... I can't find a good answer to, "Would the atom continue to emit photons forever? Or, would the atom eventually experience a sort of 'heat death'? (Where does it get the photon to begin with?)
ANSWER:
The mechanism by which objects emit infrared radiation is not the same mechanism by which atoms eject photons. An isolated atom will not radiate if in its ground state and, if it is excited, it will emit photons until it reaches its ground state and stop. It obviously cannot radiate forever because each photon carries energy and the atom does not have any source of energy once in its ground state. A macroscopic object radiates because of the thermal motion of all the atoms. This radiation differs from the deexcitation of atoms in that the spectrum is continuous and contains all wavelengths; individual atoms emit photons only of certain specific energies. The continuous radiation spectrum peaks at some wavelength and, for objects not too hot, is mainly in the infrared region. The object will continue to radiate until it comes to equilibrium with its environment at which point the rate of radiation will equal the rate of absorption of radiation from its environment.

QUESTION: :
I am constructing a machine/quasi-invention which involves a fairly large tank of compressed gas (air with high O2 concentration. I am trying to get a handle on how the internal surface area of the tank and the final PSI of the gas inside the tank will affect the stress on the various areas of the tank. Assume for now that it is a 7 ft. tall, 3 ft. diameter cylinder with compressed air at 2.0 atmospheres. Would I the tank's number of square inches of the tanks surface area (about 12,000), and then multiply that number by the extra 14.7 pounds per square inch I add to get up to the second atmosphere and conclude that every inch of the tank is under 180,000 lbs of inner pressure?
ANSWER:
You are confusing pressure and force. The pressure is the force per unit area (like PSI, pounds per square inch) and that is what is important for a tank. The total force on the inside of the tank is not important, how it is spread around is. In your situation, the total pressure over the surface of the tank is 1 atm (2 atm pushing out, 1 atm pushing in); this is normally called the guage pressure. The pressure inside is 2 atm.

QUESTION: :
I need to spin a low-friction disk without making a direct physical connection. I am using 2 neodymium magnetic cylinders, magnetized across their diameters. One is mounted in a wood dowel, chucked in a drill press. The other is pressed into a teflon bearing at the center of the disk. If the driving magnet is turned very slowly (maybe 10 or 20 rpm) the rotation is coupled as expected, and the disk turns. If the drill press rotates at 250 rpm, the disk simply vibrates, and does not rotate at all. I expected the rotating magnetic field to cause the disk to accelerate, even if slowly. It does not. Why?
ANSWER:
I suspect that the problem is the fact that the disk has inertia and will not start spinning instantly when it experiences a torque from the rotating magnet. So the magnet rotates 1800 and now the other pole tries to rotate it the other direction, and so forth. What you would need to do is to start it very slow and gradually increase up the speed you need.

QUESTION: :
I am running a Traveller gaming campaign (space sci-fi). I need a formula to quickly calclate transit time from point a to b within a star system. A space craft has to go from one point in space to another. Velocity to begin is zero they then accelerate at a constant 1g to arrive in orbit, assume ending velocity is also zero for simplicity. Assume at the half way point they begin decelerating also at a constant 1g. Assume 500,000 km is to be covered or at least a specific distance to be choosen. What is the time needed to complete this manuever?
ANSWER:
It is not technically possible to have a constant acceleration forever since eventually one approaches the speed of light which is as fast as you can go. If you are interested in these effects of relativity, see earlier answers. Let us assume that, for your conditions, relativity is not important. That is, I will use the classical kinematic equations for constant acceleration, x=�at2 and v=at (assuming the craft starts at rest at the origin). If my calculations result in a speed v which is not very small compared to the speed of light, then I will need to redo everything using relativity. So, the time t it takes to go halfway is found using 2.5x108 m=�(9.8 m/s2)t2; solving, I find t=7.1x103 s. This is about 2 hours. The speed would be v=9.8x7.1x103=7x104 m/s (about 160,000 mph). This is much less than the speed of light (3x108 m/s), so the answer to your

QUESTION: is that it takes about 14,200 s, about 4 hours, to make the 500,000 km (about 1.3 light seconds) trip.

QUESTION: :
Circular motion requires constant acceleration, I understand. Change in velocity in a straight line requires acceleration. So what is going on when there is a change in circular motion velocity?
ANSWER:
Your first statement is technically wrong because the acceleration of uniform circular motion is not constant although its magitude is; the acceleration, just like the velocity, is constantly changing direction which always points toward the center. If an object moves in a straight line with changing speed, it does have constant acceleration, and it has a direction along (if speeding up) or opposite (if slowing down) the velocity. If an object moves on a curved path (and therefore changing its direction) and is also changing its speed, its acceleration has two components, one parallel to the velocity and determined by the rate of change of speed (called the tangential component), and the other perpendicular to the velocity and determined by the rate of change of direction of velocity (called the radial component). If the curved path is a circle (your

QUESTION: ), the radial component is v2/R where v is the speed at a particular time.

QUESTION: :
please tell me about the physical interpretation of gradient divergence and curl

QUESTION: :
how does gradient, divergence and curl matter in physics?
ANSWER:
I guess you guys had the same assignment? These quantities play the role of the derivative in three dimensions. To answer your

QUESTION: s would require volumes. The derivative, you should know, is very important in elementary physics (it was invented by Newton to be able to sensibly talk about velocity and acceleration), so the importance in three dimensional physics should be pretty self evident. The gradient is a derivative-type operation which generates a vector function from a scalar function. The divergence converts a vector function to a scalar function. The curl converts a vector function to another vector function.

QUESTION: :
Okay, so nothing can travel faster then the speed of light, in theory, so what if you have a rope in space with two guys holding it, and the tension is at the max and the length, lets say, 5 light years. if one guy at the other end of the rope tugs it (remember its at maximum tension) would the guy 5 light years away from the rope feel it? would he feel it right away? if not when will he feel it, if he can feel it at all?
ANSWER:
This

QUESTION: has been answered before (that

QUESTION: was a pushed rod instead of a pulled rope, but the answer is the same). It is also so frequently asked that you could have found it on the FAQ page.

QUESTION: :
If light in a vacuum travels 300 million meters per second and it enters a pane of glass and slows to 200 million meters per second, then exits the glass into the vacuum again and speeds up to 300 million meters per second, what gives it the impetus to increase its speed? Where does the photon get the energy to accelerate?
ANSWER:
You are thinking of it classically where we accelerate something and it takes a force because the object has mass. However, even classically, if something has no mass it can change speed without there being any force on it; think about it�if you exert a force on a massless object, it would experience infinite acceleration. In the case of light, the light changes wavelength as it enters the medium but the frequency stays the same. Since the energy of a photon is proportional to the frequency, the energy inside is identical to the energy outside.

QUESTION: :
I have a quick

QUESTION: in regards to aerodynamics. I understand that Bernoulli's law demonstrates that velocity and pressure have an inverse relationship, and the air flowing on top of an airplane's wing is moving faster than the air flowing on the bottom, which means there is more pressure on the bottom, therefore creating lift. The only thing that I don't understand is why the air on top is arriving at the back of the wing at the same time as the air on the bottom. If the air on top has a longer distance to travel, why doesn't it just travel at normal speed and reach the back of the wing later than the air on the bottom?
ANSWER:
Maybe it would be easier to see thinking about the problem from the frame of reference of the air which is at rest. The wing moves through the air and pushes the air up above the wing and then it moves back down when the wing has passed. Viewed from the airplane, the air passing over the top takes the same time as the air passing under the bottom, hence moves faster.

QUESTION: :
Whilst checking out Kepler's laws on paper (as I often need to prove these things to myself) and attempting as an aside to apply them to the Bohr mode of the atom, I noticed a somewhat glaring problem with the latter. In the gravitational force balance the centripetal force (or whatever you want to call it) on the orbiting body is easily worked out as mv^2/(2r), equal to the gravitational force attracting the two bodies and Kepler & Newton are vindicated. However, applying the same equation to the electron/proton using the coulomb force, the centripetal term on the electron comes out about half what it should be. In other words, the centripetal force is taken to be mv^2/r, which is completely wrong as far as the maths is concerned. Also the Lorentzian energy of a relatavistic particle as (gamma)mv^2 is missing a factor of half. I cannot reasonably entertain the belief that physics has missed this completely for a hundred years, nor can I see how it is mathematically possible to just leave the half out for the sake of making it all add up. Where did it go and why?!
ANSWER:
I have no idea what you are talking about. Whether in the Kepler problem or the Bohr atom, centripetal force is mv2/r. This is set equal to GMm/r2 for the Kepler problem or ke2/r2 for the Bohr atom. And, relativistic energy is γmc2, not γmv2 as you have it, and there is no factor of � missing. It is pretty easy to show that, for v<<c, γmc2≈mc2+�mv2.

QUESTION: :
I understand that mass and weight are different, and that weight can change in your relation to Earth's gravity. Since we mass items on Earth, like in my science classroom, isn't the difference between weight and mass really more philosophical? As I place on item on the pan of a triple-beam balance, does gravity have an affect on the measurement, or does the nature of the instrument (a balance vs. a scale) render gravity inconsequential? Is there a demonstration I can set up, perhaps using a TBB and a spring or even bathroom scale, to show the difference? The terms weight and mass, as well as their units, get used so interchangably that it's been a very confusing concept for my students.
ANSWER:
Mass and weight are completely different things and the confusion has its roots in an amazing accident of nature. Contrary to your statement, you do not "mass" something when you use a balance, you weigh it because what you are doing is measuring the force which the earth exerts on it, called the weight. Only because the weight is proportional to the gravitational mass are you able to infer the mass, that is W=mGg. But, what is the first thing you teach your students about mass? If it doesn't involve the concept of inertia, then I suggest you rethink how you teach them about mass. What we usually mean when we talk about mass is that it is a quantity that measures how resistant something is to being accelerated when we push on it. This is what we call inertial mass and it is the mass of Newton's second law, F=mIa. One of these masses measures how strongly gravity affects something and the other measures how much resistance it has to having its speed changed. What on earth do these two concepts have to do with each other? That is the amazing accident of nature�they are exactly the same, mI=mG. Of course, it is not really an accident and its existence is what provided the opening for Einstein's theory of general relativity, the most modern and complete theory of gravity.
I have given a really long-winded answer because it is a subtle and important point. I have not really answered your

QUESTION: s. Neither your balance nor your scale would work without gravity, they both measure (indirectly, because you infer mass from weight) mass mG. You cannot measure mG without gravity because that is what it is all about. What might be fun is to devise an experiment where you measure the acceleration of an object (horizontally so that you get gravity out of the picture) by a known force; then you would be directly measuring mI and could compare it to mG you get from a balance.

QUESTION: :
Suppose I had an object at rest upon a frictionless table and gave it a push to make it move at vm/s. Let us say that according to the equation KE = 1/2mv^2 the object has acquired 10joules of kinetic energy. Now I give it a second push exactly the same as before and it accelerates to 2vm/s. According to the equation it now has 100joules of KE. Why is it that two identical forces can give 10 joules in the first occurrence and 90 joules in the second?
ANSWER:
First, there is an error in your premise. If the object with speed v has kinetic energy of 10 J, then if it has a speed 2v its energy will be 40 J. Your

QUESTION: , though, is still in tact�why does the same force give more energy. The simple reason is that you cannot tell from what the force is what energy it will impart. And, I think you could have easily figured that out if you had thought a little more about it. If you push something for an inch with a 50 N force will you impart the same energy as if you pushed it a mile? As I have said many times before, there is a tremendous misconception that if you know the speed of something you can determine what force caused that speed. You either must think of a force and the time it acts or a force and the distance over which it acts.
FOLLOWUP

QUESTION: :
With regard to my earlier

QUESTION: concerning pushing an object upon a frictionless table, you said that, I, like many others, have a serious misconception about force and speed. You must have misunderstood my

QUESTION: because I stated that if you gave an object a push with a certain force and for a certain time and found it moved that object at vm.per s. and then gave it another push with exactly the same force and for exactly the same time so that it now moved a 2m.per s., why does the first push impart 1 unit of kinetic energy to the object and the second push 4 units of kinetic energy? If you say that the second push is not the same as the first then what about an object subjected to a constant force such as gravity? After 1 s the speed has reached 10m.per s., 2s it reaches 20m.per s. etc. but the kinetic energy increases as the square of the speed. Where does the kinetic energy come from and if you say from potential energy, where does this come from, how and where is it stored in an object , how does gravity convert potential energy into kinetic energy and how does it do so at an ever increasing rate? After 100 s the kinetic energy being added is an astonishing 10,000 units per second.
ANSWER:
You did not say that the second push was for the same time, in fact you did not say anything about time. So, let's start all over again. You are correct, the speed will be v after the first push and 2v after the second push. Let us ask�why? The force times the time it acts is called impulse and impulse changes linear momentum, m(v2-v1)=Ft (true only for constant force in a straight line). But, just because the momentum changes by a certain amount does not mean the energy changes by the same amount because impulse is not what changes energy. Work changes energy and work is force times distance (again, for a constant force in a straight line). Now, think about your situation: the first push does a certain amount of work depending on how far you push during the (constant) time. The second push, however, finds the object moving, on average, much faster than the first push so it acts over a larger distance and hence does more work in the same time. That is why the second push imparts more kinetic energy than the first. An object freely falling is having work done on it by its own weight, that is, the earth is doing work on it. The amount of work the earth does is mgs where s is the distance it falls. It falls a short distance the first second, a larger distance the second second, and so forth such that as each second ticks by the rate of energy gain gets larger and larger. You do not need to introduce potential energy at all, it is just a clever bookkeeping device to keep track of the work the earth does. (One minor correction to your

QUESTION: : the second push imparts 3 units of energy if the first imparts 1 unit since energy went from 1 unit to 4 units.)

QUESTION: :
The static friction and the kinetic friction do not depend on the area of contact as long as the normal reaction R is the same.why?
ANSWER:
First, it is important to realize that friction f being proportional to normal force N only is not a law of nature, it is an approximate statement of experimental measurements. I think it is not too hard to realize why it might be true. Suppose that you have a 10 lb box on the floor and it experiences a kinetic friction when sliding of 20 lb; now, if you have a second identical box, it will also experience a 20 lb frictional force. Attach the two together and you get a total force of 40 lb and so we still have f proportional to N even though the area has doubled. However, there are definite exceptions, notably wide tires which reputedly give more traction. To read a discussion of that situation, see my earlier answer.

QUESTION: :
Why is it difficult to carry a load with the hands stretched out in front than carrying the same load with the hands lowered at the sides?
ANSWER:
Because of the design of your body. Look at the simple model of an arm to the right. The weight hangs from the outstreched arm and the arm is held horizontal by the biceps modeled here as a string from shoulder to elbow. The tension in the muscle must be very large to hold up the weight, much bigger than the weight itself. If the arm were straight down, the tension in the muscles holding it up would be equal to the weight.

QUESTION: :
If a circuit has 12V and a bulb is attached it will glow twice as bright as the same bulb with 6V. From ohms law it says that for the 12V circuit twice as much current will flow. My

QUESTION: . Does the voltage make the electrons have more kinetic energy? and is this kinetic energy then transferred to the light bulb? If so does this mean in both circuits there are the same number of electrons but in the 12V circuit they are just faster?
ANSWER:
I will assume that the resistance of the bulb stays constant. (It actually does not because as it gets hotter its resistance changes; we'll ignore that.) Your very first statement is false. If you double the voltage you will double the current. Since the power (to which brightness is proportional) is the product of voltage times current, the brightness will increase 4 fold. The number of electrons participating in current flow is mainly independent of the amount of current flowing, so, yes, more current means faster average electron velocity.
FOLLOWUP

QUESTION: :
You gave me an answer the other day about current and voltage which I really liked, and you showed me that the brightness of a bulb would increase 4 times (not 2) if voltage was doubled, thanks very much. I am working towards my theory papers for a 1st yr electrician and I just don't get how the energy from voltage is supplied to a load. Like, is it due to the kinetic energy of the electrons? Do the electrons always have the same charge (intrinsic electrical energy?) but are just moving quicker then release their energy in a collision with the load/resistance atoms, make heat/other energy? or do the electrons 'carry' extra charge? my teacher always talks about electrons as being like dump trucks. They have a little motor (the fundamental charge) then load up with extra energy and drop it off?
ANSWER:
A conducting material has approximately one electron per atom which is essentially free to move around. Even if there is no voltage, they are zipping around inside the material randomly; the first approximation of a model of a conductor is to just treat the electrons like a gas and it works pretty well. Now, when a voltage is applied, there is an electric field set up inside the material and the result is that each electron experiences a constant force from the field. Now, if the electrons were truly free, they would accelerate from the negative to the positive terminals. But they are, in fact, in a material and they just get going and they hit an atom. This collision essentially stops the electron and causes the atom to bounce back a little, in other words the electron's acquired kinetic energy is transferred to the atom. But, giving atoms in the material more energy means increasing the temperature of the material. That is how the load gets the energy from the current. Since you are studying to be an electrician, I should perhaps mention here what I hinted at last time�the light bulb changes its resistance as it heats up, that is it is not truly an ohmic device. If you double the voltage, the current will not double because the resistance does not stay the same as the bulb gets hotter but increases.

QUESTION: :
What is the effect of distance on the brightness of a light bulb?
ANSWER:
The intensity falls off like the square of the distance. For example, go 10 times farther away and the intensity is 1/100 as strong. (This assumes that the bulb looks like a point source which it will if you are far away compared to the size of the filament.)

QUESTION: :
Recently newspaper reported that at the Brookhaven National Laboratory, New York, the atom smasher was used to smash gold ions and the resulting quark-gluon plasma reached a temperature of four trillion degrees Celsius. How is such extra-ordinary high temperature measured?
ANSWER:
I do not know in detail but am sure it is something like estimating the average kinetic energy per particle which is essentially what temperature measures.

QUESTION: :
when a car is driving at a steady speed, is it "accelerating"?
ANSWER:
Acceleration is a vector concept (rate of change of velocity), speed is a scalar concept (magnitude of velocity). A car traveling in a circle with constant speed is accelerating because the (direction of) the velocity is changing. A car traveling in a straight line at constant speed is not accelerating.
ADDED NOTE:
More detail can be found here: http://physics.aps.org/articles/v3/28

QUESTION: :
My friend proposed the idea that there is no such thing as pull. He explained that when you pull something, you actually push it, for example, when you pull open a door by its knob, you actually reach around the knob and push it from behind with your fingers. I said "what about tug-of-war or what about when you drag a piece of paper across a table by pressing your finger on it and pull it toward you?" He answered "that's probably particles pushing particles". Anyway, I wanted your take on this. What is pull?
ANSWER:
"Push" and "pull" are qualitative ways of expressing force. I would say it is nonsense to say something like there is no such thing as a pull. In the simplest sense I would call any attractive force a pull and repulsive force a push. There are certainly plenty of attractive forces in nature.

QUESTION: :
Why do my TV and computer gather dust so fast?
ANSWER:
If they are cathode-ray tubes the acquire a net charge, probably negative. A nearby dust particle will become polarized with positive closer to the screen and be attracted to the negative screen.

QUESTION: :
How does gravity effect weight and density, and why is mass density more important than weight density?
ANSWER:
Weight is affected by gravity since weight is, by definition, the force something feels because of the gravitational field it is in. Mass is a property of the matter and therefore not dependent on gravity. It follows that weight density is affected by gravity and mass density is not. How important something is really subjective; I guess you could consider mass density more fundamental than weight density since it is independent of gravity.

QUESTION: :
As we know from our spectroscope lab, hydrogen and helium (Elements from which the sun is mostly composed of) emit specific frequencies of light, which one can measure and view via a spectroscope. We know that the reason is because of energy levels, and the traveling to and from a ground state to an excited state. If this is so, than the sun should not be a continuous spectrum of light, as it is. It should be, in fact, a very specific mix of both hydrogen and helium lines on our spectroscope. Why than is it a continuous spectrum?
ANSWER:
When something gets very hot it emits a continuum spectrum, not discrete lines. The reason is that the atoms in the material are violently vibrating around and so they look like a bunch of oscillators, and they have charge distributions which are oscillating. When electric charges are accelerated they emit electromagnetic radiation and this is different than the line spectra of atoms. The sun is mostly not hydrogen and helium atoms but hydrogen and helium ions with most of the electrons freed from the atoms�called a plasma. A hot plasma has this sea of positive and negative charges zipping around, colliding with other, and consequently radiating a continuum of radiation. If you look closely, it is not really a continuum but has dark lines in the spectrum. These are wavelengths which are just right to be absorbed by atoms mostly in the sun's outer region, called the absorbtion spectrum. So there are still some unionized atoms still around.

QUESTION: :
Why does visible light only travel through clear things? How come a proton can go thourgh the atoms of glass but not copper or silver? Or, why does a light wave move through my car window but not my roof, sound seems to make it in through both?
ANSWER:
Read an earlier answer. Sound is much easier to deal with because being simple pressure waves, it can easily travel through most continous media.

QUESTION: :
In an earlier

QUESTION: , a teacher asked about electromagnetic forces during an eggdrop in her science class. You told him/her that as the egg falls, the atoms in the egg are colliding with the atoms in the air, and the energy that's involved between those colliding atoms is electromagnetism. How exactly is electromagnetism involved here? Aren't the atoms just colliding because gravity is pulling the egg down and the air molecules are in the way of the egg?
ANSWER:
But, you must ask what colliding means. What it means is that two objects interact with each other via some force. An atom or molecule at very close range looks like a cloud of electrons which are negatively charged. So when one atom (in the air) and another (in the egg) come close to each other, they repel each other and the mechanism is the repulsion between like (negative) charges�electromagnetism.

QUESTION: :
Are there within the electromagnetic spectrum of visible light (say 380 - 750 nm) an infinite amount of different wavelengths? For example, are there wavelengths such as 380.1 nm, 380.11 nm, 380.111 nm, 380.1111 nm, etc?
ANSWER:
There are, indeed, an infinite number of possible wavelengths. It is, however, a moot point because the uncertainty principle forbids a light wave from having a wavelength precisely equal to 380.11 nm, for example, unless it is infinitely long which no wave, of course, is. All light waves are composed of a continuous distribution of different wavelengths; the distribution might be very narrowly peaked around a particular length, but never exactly one wavelength.

QUESTION: :
Sound waves are just vibrating fluid molecules, but isn�t energy responsible for those vibrations? Why aren�t sound waves a part of the Electromagnetic Spectrum, or am I misguided and the entire Electromagnetic Spectrum is actually responsible for sound?
ANSWER:
Sound and electromagnetic waves are totally different phenomena. The only thing they have in common is that both are waves. Sound waves get their energy from their source, a vibrating vocal cord, a running motor, an explosion, a violin,�

QUESTION: :
Minus any obstructions like smoke or dust to reflect the light into our eyes, why can't we perceive a light beam from a 90 degree angle, (standing perpendicular to the direction that the beam is traveling)? When light bounces off an object into our eyes, does this redirection at all result in a slight deceleration of the light?
ANSWER:
Because the way you see light is to get some of its energy and convert it to electrochemical energy. The energy in light is transported parallel to the direction the light moves. Light never leaving a medium certainly does not undergo a deceleration since the speed of light is constant; there may be a delay or phase shift depending on the nature of the reflection, but the speed of light through air depends only on the properties of the air. [This wasn't really a single

QUESTION: (see groundrules) was it?]

QUESTION: :
My girlfriend and I both have iPhones. My in protected by a rubber case and hers by a plastic case. I told here that when dropped, the plastic case is more likely to transfer the force of the impact to her phone, whereas the rubber surrounding my phone is more likely to absorb the force of impact thus reducing the rusk of damage to my phone. Who is right?
ANSWER:
Here is the main thing: the force needed to stop something depends on how long it takes to stop it. If you fall from 20 feet onto a thick slab of foam rubber, you are unhurt because, since the time it takes to stop you is relatively long, the force you experience is relatively small. On the other hand, if you fall onto a slab of concrete you get hurt because you stop very quickly and experience a very big force. The rubber of your case is likely to result in a longer time to stop than the plastic of your girlfriend's and that is why your phone is better protected. It is not really accurate to use the phrase "absorb the force of impact" because there is no such thing as a unique "force of impact", rather the force can be anything depending on the time as I explained above.

QUESTION: :
If gravity can bend light, does this imply that light therefore has mass?
ANSWER:
Certainly not. Light does not have mass. You should read an earlier answer. I am also often asked "if light has energy and E=mc2, why does it not have mass?" So just to complete your futile quest for mass of light, read another earlier answer!

QUESTION: :
if the hight of the tv tower is increased by 21% how much will its range increase?
ANSWER:
I presume you mean line-of-sight distance to the horizon. Well, it depends on how high the tower is. The distance L from the top of a tower of height h to the horizon is fairly easy shown to be L=√[h(h+2R)] where R is the radius of the earth.

QUESTION: :
I was wondering if you could explain how length contraction works. I've already done some background research and I understand the mathematical reasons my text book gives me, I was just wondering if you could give some kind of analogy that would enable me to picture the effects of length contraction, and better yet allow me to explain it to my friends in a way they can understand.
ANSWER:
I don't know a simple one-step way to intuitively understand length contraction. But, I know a good two-step way starting with intuitively understanding time dilation. Time dilation is pretty easy to understand in one simple example, the light clock. See my earlier answer about the light clock and be sure you understand that and have a good intuitive feeling for why moving clocks run slow. From that point, length contraction can be understood as a natural consequence of time dilation. Here is how it goes. Imagine a bomb which has a fuse of 1 s. That is a clock. If that bomb is moving by us with a speed of 99% the speed of light, the elapsed time before detonation will be 1/√[1-(0.99)2]=7.09 s. So, the distance it will travel is 0.99x3x108x7.09=2.1x109 m. But, the bomb will measure in his own frame that he should last 1 s and go 0.99x3x108x1=2.97x108 m, only about 1/7 the distance we measure. If you think about the distance we measure as a long stick of length 2.1x109 m, then the bomb sees this stick moving by him with speed 99% the speed of light, so to reconcile his results with ours he must measure that length to be 2.1x109x√[1-(0.99)2]=2.97x108 m.

QUESTION: :
Is it possible for a longitudinal (eg. sound) wave to interfere with a transverse (eg. water) wave? Can 2 such waves generate "negative interference" and mutually annihilate each other or cancel each other out ?
ANSWER:
There is no reason why both cannot both be present. Light and sound both go through air. And the superposition principle still applies, but the same thing has to be "waving" for them to add up. For example, light is waving electric and magnetic fields whereas sound is waving molecules, so those would not interfere. Some media can support both transverse and longitudinal waves of the same type. For example, water waves are a mixture of transverse and longitudinal. I do not know what "negative interference" is but the two waves would certainly interfere by virtue of the superposition principle. I can certainly not imagine a situation where they would "annihilate" each other.

QUESTION: :
place a card over the open top of a glass filled to the brim with water, and invert it. Why does the card stay in place? Try it sideways.
ANSWER:
The force of the atmospheric pressure pushing up on the card is greater than the force of the water pushing down (which is numerically equal to the weight of the water). It's hard to get it to work on its side because the force the water exerts on the card depends on the height and the card wants to slide under the influence of its own weight. Also, even the tiniest bubble of air will cause the seal to break.

QUESTION: :
During Nuclear Fission, how does the atom actually split? I understand that it becomes unstable with the absorption of a neutron but what I do not understand is how the atom can separate into two atoms. Eg. U-235 + n > U-236 > various products My main concern is how an atom can split.
ANSWER:
The atom does split, but the heart of the matter is the nucleus of the atom splitting. So, we usually do not call them atomic bombs anymore, we call them nuclear bombs (or, if you are George W. Bush, nuculer). Think of it like this: a nucleus is a very dense, very small object, often a sphere but sometimes more like a football, egg shaped. Uranium nuclei are more egg shaped. It also helps to think of the nucleus as a fluid. Now, if you add a neutron to 235U the resulting 236U nucleus is very excited. By this I mean that it is not just sitting there but vibrating wildly. So, think of this egg-shaped fluid vibrating so that it gets more elongated, in fact starts to develop a thinner "neck" in the middle, sort of like a peanut. What happens is that the two halves of this peanut-shaped thing break apart and, voil�, fission!

QUESTION: :
What is the maximum number of poles a magnet can have?
ANSWER:
There is no upper limit. However, the lower limit is 2 and the total number must be even. The reason is that there are no magnetic monopoles (which would be the magnetic analog of a point electric charge) in nature. Every electron is a tiny magnet, so any chunck of stuff may be thought of as having like ~1025 poles!

QUESTION: :
Hello, my

QUESTION: s is simple and you please explain the speed of light and the speed of electrons moving in a wire carrying a current?
ANSWER:
I do not really understand what you are asking. Maybe it has to do with the speed that information propogates through a wire and how fast the electrons move. When a potential difference (battery, for example) is connected across a wire, an electric field is established. This field is established essentially at the speed of light, so, for all intents and purposes, all the electrons in the wire start moving as soon as the potential difference is applied. The individual electrons, though, all move, on the average, with very small speeds because they keep bumping into atoms in the wire; so it is a start-stop-start-stop affair. Usually electrons move with average speeds of much less than one millimeter per second.

QUESTION: :
We always hear that it would be impossible to power a spaceship to the speed of light because as the ship neared the speed of light the mass would increase to near infinity and therefore require an infinite amount of fuel. Wouldn't the fuel, as it also increased in mass, produce more energy? I've always found this to be puzzling?
ANSWER:
The simple fact is that the amount of energy it takes to accelerate an object to the speed of light is infinite; there is not an infinite amount of energy in the universe. See an earlier answer for more detail.

QUESTION: :
Sports announcers and governing bodies of sports say that extra weight is a benefit in downhill speed events. For example, it is illegal to add extra weight to bobsleds and soapbox derby cars. Announcers often say that a heavier bicyclist has an and vantage going down hill. I can understand that perhaps on snow or ice the extra weight could help melt the snow or ice, but on a bike or other wheels this would make more surface area and friction. Obviously there is the belief that mass plus gravity = greater velocity. How does this reconcile with Galileo�s experiment with the two cannonballs?
ANSWER:
I have addressed this

QUESTION: numerous times before. You should read these discussions by linking here and following subsequent links. You will see that I never really came up with a satisfactory answer. This is a problem to which simple physics seems not very successful in describing�there are just too many variables and friction is a very difficult thing to deal with except in the simplest cases. However, do not let it get in the way of accepting that objects freely falling all have the same acceleration; this is a simpler experiment because it is easier to either eliminate air friction or calculate it relatively easily. If there were no friction, all cars would have the same acceleration on a ramp, I can guarantee that.

QUESTION: :
When we stretch a metal wire then energy is stored in it. My

QUESTION: is that when we lift the stretching forces and the wire unstretches then where does this energy go ?
ANSWER:
It goes into "helping" you lift the weight stretching the wire.

QUESTION: :
What would a 50 gallon plastic trash can full of water weigh on impact after falling 12 feet to the concrete? I assume the weight of the thrash can is approximately 400 pounds. Could you show me the formula you would use to calculate the problem.
ANSWER:
The weight is the weight is the weight! See an earlier answer.

QUESTION: :
Would a pin-ball machine with a higher spring constant result in its ball moving faster or slower than a regular pin-ball machine ball?
ANSWER:
Faster if the spring were compressed by the same amount to launch the ball.

QUESTION: :
how would you find the maximum number of interference maxima observed in a Young's experiment with two identical slits if you know the wavelength of the light and the spacing between the slits?
ANSWER:
This isn't homework is it? Starting with nλ=dsinθn, set θn=900 and solve for n.

QUESTION: :
is it possible to have a planet so dense that instead of that solar system being heliocentric, it becomes geocentric (basically would the sun then revolve around the planet instead of vice versa)
ANSWER:
Not in our universe! There is a certain mass a star must have to "ignite" and that is much larger than chunks of matter you might identify as a planet are likely to be. There are lots of binary star systems in the universe. Of course, you should realize that the planets do not move around the sun, the whole system moves around its center of mass. It is just that the sun is so much more massive than everything else that it looks like it is the center because the center of mass is always very close to the center of the sun.

QUESTION: :
Why is sonic boom audible and visible?
ANSWER:
A sonic boom is a shock wave which is a very intense pressure pulse. By definition, sound is variations of pressure transmitted through a medium, so it is to be expected to be audible. We do not expect to see variations of pressure (we do not see sound normally) but if the conditions are right (very rapid high-low pressure variation and ample humidity in the air), water vapor can condense to form droplets like a cloud to make it visible.

QUESTION: :
Dose weight affect the speed at which an object travels through a nonnewtonian liquid?
ANSWER:
If you mean the terminal velocity as it is falling through the fluid, then yes, the weight is important. For example, ketchup is a nonnewtonian fluid and a marble will certainly fall faster through ketchup than a grain of sand.

QUESTION: :
Does the moon spin on an axis? If so, why can't we see it spin? Since we are also spinning...
ANSWER:
The moon revolves around the earth (once every 28 days) and also rotates on its own axis (also once every 28 days). The moon appears to not be spinning on its own axis because it always presents the same side to us, but if it were not spinning we would see the other side of the moon 14 days from now because of its orbital motion.

QUESTION: :
I am preparing a test plan for a consumer electronics device. One of the test plans is to measure the microphonic distortion created when the device is impacted on any of its planes. The typical impact test can be as simple as dropping a deadweight (typical a sphere) from a short distance on to one of the surfaces of the device. I want to intelligently convey this in proper physics terms. It is my understanding that if I drop a mass of 350 gms from an elevation of slightly more than 20 cm as sea level, there will be an energy transfer of ~0.7 joules at impact (.35 kg * 9.81 m/sec^2 * .21 m). This leads me to the conclusion that I should state my subjective, witness microphonics test as follows: The device must not produce perceptible audio or video distortions when subjected to an impact energy transfer of 0.7 joules. For the record my co-worker believes that the test should be stated in terms of Newtons. I told him I can produce loads of Newtons merely by sitting on the device, but this would not produce any microphonic distortion.
ANSWER:
I don't know what "microphonic distortion" means, but in terms of measuring "impact" effects, you and your coworker are both wrong, it seems to me. Rather, you should talk about the rate at which energy is delivered to the device, power. For example, if you were to cover your device with foam rubber the falling ball would deliver just as much energy but over a much longer time and likely cause much less "microphonic distortion" (whatever that means!) Hence, you should talk about joules/second, watts (W). To take this a bit further, I would also guess that the area over which the impact was delivered would matter; e.g., energy delivered by a "pointy" object would likely cause more "microphonic distortion" than an object with a big flat surface. If so, you should quantify the impact with W/m2. W/m2 are the units used to measure the intensity of a wave, that is intensity is areal density of energy flow rate.

QUESTION: :
I have a

QUESTION: regarding electron density, wave function and radial distribution of electrons in electron shells. Sorry if its more related to chemistry, but I thought I'd try this site first. What are electron density, wave function and radial distribution defined as? I understand that they are all in one form or another describing the probability of finding an electron in a position in space, but i do not understand the difference between them, and how they are derived. More specifically, what really confused me is in a graph of electron density in a s orbital, it seems to suggest that there is infinite electron density at the nucleus, while the radial distribution graph contradicts that. If you could clear this up it would be greatly appreciated.
ANSWER:
The wave function is the solution to Schr�dinger's equation. The wave function, often a complex function, has no physical meaning on its own, but everything knowable can be extracted from it in one way or another. If you multiply the wave function by its complex conjugate (insuring a real number) you get what is called the probability density Ψ*Ψ=|Ψ|2. So, let's talk about density. If you have a mass density, it does not tell you what the mass is at a point, it tells you what the mass per unit volume is at a location in space. The mass at a point is zero since a point has zero volume. Therefore you have to be careful not to look at probability density as a picture of probability. Probability can only be really visualized for a particular volume; the probability, for example, of finding the electron inside some small volume dV is |Ψ|2dV. Atomic physics is usually done in spherical polar coordinates where, instead of the Cartesian (x,y,z), we use (r,θ,φ) where r is the distance from the origin (taken as the nucleus), θ is the polar angle (latitude) and φ is the azimuth angle (longitude). For your purposes, let's just stick to the 1s orbital of hydrogen. s orbitals are spherically symmetric, that is they depend only on r and not on the angles. The wave function for the 1s state is Ψ=Cexp[-r/a0] where C and a0 are constants. Therefore, |Ψ|2=C2exp[-2r/a0]. But this does not tell you what the probability of finding an electron looks like. |Ψ|2 is not infinite, as you seem to think, at the center of the atom but it is biggest there; this certainly is not where you most expect to find the electron. So, we need to multiply |Ψ|2 by dV. Here is the tricky part: dV=r2sin2θdθdφdr in spherical polar coordinates. If you don't know much or any calculus, this is probably all Greek to you. But, let's get rid of the angular part because the probability density for the 1s state does not depend on angle. In order to understand what the probability of finding an electron is, you can see that a factor of r2 must be multiplied in because it appears in the volume element dV. So the electron probability function, let's call it, is Kr2exp[-2r/a0] where K is a constant chosen so that the probability of finding the electron somewhere in all of space is 1 (called the normalization constant). Note that this is zero at the origin and zero very far away and has a maximum somewhere in between which you might call the radius of the "electron orbit". It turns out that a0, called the Bohr radius, is where it maximizes. (If you know a little calculus, you can prove this by differentiating the electron probability function and setting equal to zero and solving for r.) I am not familiar with the terminology "radial density". Likely it is the probability density with angular dependence taken out (which would render it the same as probability density for all s states). Higher orbitals (p, d, f, etc.) have wave functions which depend on (θ,φ). If you want to see the wave functions in more detail, go here.

QUESTION: :
I am in the 8th grade. I am doing a project for my science class on the physics of arm motion in swimming. Can you give me some information? I get extra credit if I get information from a professional.
ANSWER:
I do not quite know what you want. Here is something: what is it that pushes you forward? Is it your arm? No, it is the water that pushes you forward. Here is how it works. When you move your arm backwards under the water toward your feet, you are pushing on the water, pushing it backwards. Newton's third law says that if one object (hand) exerts a force on a second object (water), the second object (water) exerts an equal and opposite force on the first object (hand). Therefore, the water pushes you forward.

QUESTION: :
How much energy is required to remove the air of a container with a volume of one cubic meter to obtain a perfect vacuum?. Assume that the container is in a room at one atmosphere pressure and that the machine used to remove the air has an efficiency of 100%. I just made it up this problem from a talk with a friend in which we talked about if I can use the force produced for letting the air in to a vacuum container. I suppose it is the reverse process to the problem that I set and you will obtain (ideally) the same power that you used to extract the air.
ANSWER:
It would just be PV=(1x105 N/m2)x1.0 m3=105 J. This is the work necessary to start with a volume of zero and expand it to V. Imagine a piston in a cylinder of cross section A being pulled out from being completely inside the cylinder: the work would be ∫Fdx=∫PAdx=∫PdV=PV.

QUESTION: :
I was told that in free fall your mass is doubled every time you fall your length is this true if so can you explain?
ANSWER:
That is absolutely not true. Your mass is a constant (unless your speed becomes comparable to the speed of light). A recent

QUESTION: was similar to yours.

QUESTION: :
when sound travels a longer distance,a person standing at a very far place from origin of the sound, hears it very softly,but the person standing close to it hears it loud due to doppler effect.but, now in case that is with the ultrasonic sound (which is at the audible and ultrasonic limit)can this be also heard at a distance very far from its origin ?
ANSWER:
The loss of intensity with the distance from the source has nothing to do with the Doppler effect and almost nothing to do with the wavelength of the wave. It is because the sound waves spread out and so you get less and less of the wave front in your ear as you go farther away. The intensity falls off approximately quadratically for most sources, that is, if you are twice as far away you hear four times less loudness. The way you make the intensity fall off less is to focus the sound, much as a car headlight focuses light. That is how a megaphone works, or simply cupping your hands around your mouth.

QUESTION: :
i was just wondering...do satelites move randomly in space? or do they move in a defined path?
ANSWER:
Any object orbiting another much heavier object (in particular, satellites) move in a path which is an ellipse (an oval shape). A circle is a special case of an ellipse.

QUESTION: :
not sure how to explain this... what is the formula for calculating weight in motion? for example... If someone is hanging from a trapeze and weighs 60 kilos. how much weight does the rigging point need to be able to take if the trapeze is swinging 1 foot in each direction or 3 foot in each direction.
ANSWER:
I know what you are getting at, but allow me to correct a semantic point: weight is the force that the earth exerts on something and it has nothing to do with the motion of that object. However, something which is swinging from a rope may cause there to be a force on the rope rigging point which is greater than the weight. The force on the rigging point is applied by the rope which has a tension in it, so we might just as well ask what must the strength of the rope be? Suppose we have a 5 lb test fishing line (which means it will break if its tension exceeds 5 lb). Can we lift a 5 lb bass with this line? We can hang the fish from this line but we cannot lift it because, in order to lift it, we must exert an upward force greater than the weight to accelerate it upwards. In fact we could not even lift a 4 lb fish if we tried to do it too quickly, a fact which has left many fishermen feeling that their line was not as advertised. The same thing happens when an object is moving on a circular path, like your trapeze. The weight on the trapeze is accelerating because its velocity is changing direction as it moves along its path; the tension in the rope will be greatest when the rope is vertical. Unfortunately, you have framed the specifics of your

QUESTION: in a way that I cannot answer it because the 1 or 3 foot measure isn't enough information�you need to know the length of the rope too. If instead you specify the angle of the swing, then you do not need the length of the rope. The tension in the rope will be W(3-2cosθ) where W is the weight and θ is the angle. For example, if θ=200 then cosθ=0.94 and so the rigging point must support (3-2x0.94)=1.12 times the weight. Here is a table for angles a trapeze is likely to have.

θ (degrees)
cosθ
3-2cosθ
0
1.00
1.00
10
0.98
1.03
20
0.94
1.12
30
0.87
1.27
40
0.77
1.47
50
0.64
1.71
60
0.50
2.00

QUESTION: :
What feels the strongest pull of attraction toward the earth and why? A box containing 10 baseballs or a box containing 15 baseballs?
ANSWER:
The "pull of attraction toward the earth" is called the weight. The weight of something is proportional to its mass and so 15 baseballs has 50% more mass than 10 baseballs. Even though the "pull" is greater on the greater mass, both accelerate the same because the acceleration is inversely proportional to the mass. (I suspect from your

QUESTION: that maybe you are trying to make a case for the heavier box falling faster.)

QUESTION: :
Identical springs made of steel and aluminium are equally stretched.on which more works will have to be done?
ANSWER:
The work done to stretch a spring of spring constant k by an amount s is �ks2. If the springs are geometrically identical, then the one which has the larger Young's modulus has the larger spring constant. The Young's moduli for steel and aluminum are 200 and 69 GPa. The answer is steel.

QUESTION: :
If two objects, one of greater mass than the other, are dropped on the moon from the same height, wouldn't the object of greater mass hit the moon first (albeit to a negligible extent) due to the greater gravitational pull it exerts on the moon compared to the smaller object? Or, to put it another way, does my mass pull the earth towards me more strongly than, say, the mass of an ant would. Or to put it one last way, in the depths of space, would two very massive objects, independent of the gravitational pull of any other objects, accelerate towards each other more quickly than two less massive objects? no one's ever quite answered this one to my satisfaction.
ANSWER:
Yes, you are correct. You have to be careful that the center of each object begin at a certain height above the ground and that you take "hit the moon" to mean "fall a given distance". To see this for a specific example, consider two pairs of objects, each in empty space. The first two objects have equal masses, m. The second two objects have masses m and 2m. Both pairs are separated by the same distance. The force on each of the second pair is twice the force on each of the first pair. Therefore, since acceleration is force divided by mass, both objects of the first pair and the 2m mass of the second pair have the same accelerations; the mass m of the second pair, however, has twice the acceleration of all the others. Therefore, the second pair falls together faster.

QUESTION: :
Is it possible that no two independent events can begin at precisely the same moment? Or end at precisely the same moment?
ANSWER:
There is no reason why two events cannot be exactly simultaneous. What is important is that simultaneity, like time itself, is not an absolute thing and different observers may disagree regarding whether two events are simultaneous. Do not read this as appearing to be simultaneous; two events simultaneous for one observer may not be simultaneous to another.

QUESTION: :
How would one find where in an orbital an electron is? Is it even possible?
ANSWER:
It is not possible. The picture of a well-defined electron orbiting a nucleus is a very simplistic picture of an atom. Rather, you should think of a cloud surrounding the nucleus, the density at any particular place being proportional to the probability of finding the electron there if you made a measurement. The probability of finding an electron at a specific point in space is zero because the volume of a point is zero.

QUESTION: :
If you push for a half hour or a whole hour against a stationary wall how much work is done?
ANSWER:
Since the wall does not move and work is force time distance, no work is done on the wall. However, your

QUESTION: now verges on biology rather than physics if you are asking yourself "how can you say I am not doing work when I push on the wall when I know energy is required to do so?" That is, you will get tired pushing on the wall. The gist of the answer is that muscles exert a force by individual fibers of the muscle continually slipping and then recontracting, so for this special case the individual componenets of the total force are all contiually pulling over a distance and hence doing work. There is no physics way to quantify the amount of work; it would depend on, for example, how hard and long you pushed.

QUESTION: :
if a curling stone weighs 20 kilograms and is traveling at a speed of 0.5 meters/seconds3, with how much force did the curler throw it in N?
ANSWER:
Why the speed in m/s3? It should be m/s. Anyhow, it seems like I have answered

QUESTION: s like this a thousand times! You cannot determine the force needed to give a particular mass a particular speed. Just to make that plausible, suppose you push on the 20 kg stone with a force of 2 N for 1 s; surely it will have a different result than if you push on the 20 kg stone with a force of 2 N for 2 s. There are two (in the end, equivalent) ways you can think about this problem:
The impulse delivered by a force F in a time t is Ft. Linear momentum of an object with mass m and speed v is mv. The change in momentum is equal to the impulse and so, if the object starts at rest, Ft=mv. For example, in your case Ft=10 kg-m/s so you could push with a force of 10 N for 1 s.
The work done by a force F pushing over a distance s is Fs. Kinetic energy of an object with mass m and speed v is �mv2. The change in kinetic energy is equal to the work and so, if the object starts at rest, Fs=�mv2. For example, in your case Fs=2.5 kg-m2/s2 so you could push with a force of 10 N for a distance of 0.25 m.
In both cases, be sure to note that what the force is depends on how long or far it is applied.

QUESTION: :
The

QUESTION: I have is about relativity I would like to know why the speed of light is squared in E=MC squared, what is the significance of this number.
ANSWER:
For starters, it would not be dimensionally correct. Energy must have the dimensions of mass times (length/time) squared. For example, a kg-m2/s2 is called a joule. Your

QUESTION: is sort of like asking why is velocity not measured in kilograms. The derivation of the famous equation is a bit technical but may be seen in an earlier answer.

QUESTION: :
I recently did an egg drop lab with my students and when I asked "What forces were acting on the egg", most students identified gravity and air resistance. A few others also noted electromagnetic and nuclear forces. My

QUESTION: is: Were electromagnetic and nuclear forces acting on the egg?
ANSWER:
While it is falling, gravity and air resistance are indeed acting on the egg. You could ask: "what is the origin of the air resistance?" The atoms of the air are colliding with the atoms of the egg and the force between atoms (at these energies) is all electromagnetic. You could therefore replace air resistance by electromagnetic. There is another (which is very small for an egg) force�the buoyant force associated with the egg's being in a fluid (air); this is an upward force and, if the egg's weight were smaller than the weight of an equal volume of air, the egg would "fall" up! When the egg hits whatever it is falling onto, there is an upward force due to the contact force (often referred to as a normal force in physics texts); this force, like air resistance, has its microscopic origins in forces between atoms, electromagnetic forces. At no time do nuclear forces come into play because the energies involved are not great enough for nuclei to come into contact with each other.

QUESTION: :
A submarine rises to the ocean's surface to take on passengers and the sinks back underwater. How can I expain how this works to my 10 year old daughter.
ANSWER:
A submarine has balast tanks. They start out filled with air. Now, sea water is permitted to flow into the tanks and it is just like a boat springing a leak, so it sinks. However, the air which was in these tanks is not allowed to escape, rather it is pumped into small tanks under high pressure. When the submarine wants to come back up, the air is pumped back into the tanks pushing the water back out into the ocean.

QUESTION: :
I was wondering if you could help me understand something. Here is the scenario; I hit a golf ball with a golf club. the ball travels 6" and impacts a wall of equal hardness as the golf club that struck the ball. Does the ball take more force (newtons?) from the initial impact or the impact with the wall? If at all possible please describe why.
ANSWER:
It is not meaningful to ask how much force the collisions took because what matters is the impulse which is essentially the product of the average force times the time it acted. This should seem reasonable since you could stop a freight train with a modest force if you were willing to push for a long enough time. So, for the sake of argument, let us assume that the time that the golf club was in contact with the ball was the same as the time the ball was in contact with the wall. Then we can compare forces. The impulse delivered to the golf ball is proportional to its change in velocity. The golf club changed the ball's velocity by only half as much as the wall did (from 0 to v for the club, a change of v and from v to -v for the wall, a change of 2v). Therefore the wall exerts twice the force in an equal time as the club does. (I have assumed an elastic collision with the wall so the rebound speed is unchanged and that the club did not lose much of its speed when it struck the ball.)

QUESTION: :
how to know that if you double a car speed, the time it takes to stop is doubled, but the distance it takes to stop quadrupled. I understand that it is the distance, not the time, that determines what you will or will not hit or what will or will not get you into trouble. Please kindly guide me with this.
ANSWER:
The equations of kinematics for constant decceleration are v=v0-at and x=v0t-�at2 where t is the time, a is the magnitude of the acceleration, v is the speed at time t, v0 is the speed when t=0, and x is the position at time t; I have assumed that x=0 when t=0. The time t=0 is when you put on your brakes. So, if t is when you stop then v=0. Then, t=v0/a (t is proportional to v0) and, putting this t into the x equation, x=�v02/a (x is proportional to v02). All this assumes that the wheels are locked which results in nearly constant negative acceleration.

QUESTION: :
My son is doing a science fair project for 5th grade. His

QUESTION: is "does the distance from a starting point to a ramp, affect the distance of a jump?" He is using a remote controlled car...We've done the research having performed jumps at 5, 10, 15, 20, and 50 feet. We've determined that the greater the distance (ie, 50 ft). the greater the jump will be. I'm having trouble determining what scientific rule support this. [Clarification: Yes we have a starting line.Trying to figure out how the distance from the starting point to the ramp that goes up affects the distance that the remote controlled car (electric) will jump. We did it at various distances, 5, 10, 15, 20, and 50 feet away from the starting point. I mean the distance from the starting point until you reach the ramp. The ramp is about 10 inches tall and 3 feet long.]
ANSWER:
The only thing which will affect how far the car goes is how fast it is going when it becomes airborne. For your experiment the car starts at rest and accelerates as it goes. Of course, it won't keep accelerating forever, so it is surprising to me that there is any difference between 20' and 50' since I would have thought that the car would have acquired all the speed it was going to acquire after 20'. I would guess that your data would eventually level off and after some distance all greater distances would give the same result. One thing your son could do to is measure the distance and from that deduce the "launch" velocity. I estimate roughly for your geometry that if v (in m/s) is the speed and L (in m) the distance it goes before hitting the floor, then v≈1.1L√[20/(1+1.2L)]. (You might have to teach your 5th grader what a square root is!) For example, if L=1 m then v≈1.1√[20/(1+1.2)]=1.1√9.1=3.3 m/s. To convert m/s to mph, multiply by 2.2, so v would be about 7.2 mph. One additional tip would be to be sure the results are reproducable, that is each datum should be taken several times and the average value of L calculated; the spread of the data around the average value give you some idea of the accuracy of the measurement.

QUESTION: :
does the length of an object moving with high speed really shrink!
ANSWER:
Two of the most surprising results of the theory of special relativity are that moving sticks are shorter (along the direction of motion) and moving clocks run slower. These have been thoroughly verified experimentally. And it must be appreciated that moving sticks really are shorter, they don't just look that way; in fact they may very well appear longer. It is important to define what you mean by the length of something: length is the distance between the ends where the ends have been observed at the same time.

QUESTION: :
Does a rubberband lose it's potential energy the longer it is kept in the wound position? We are running a Cub Scout space derby and would like to wind the rockets ahead of time to help speed up the process but we do not want any issues with parents if the one rocket wound first would have a disadvantage because it lost some of it's potential energy.
ANSWER:
Yes, it certainly does. Rubber is a particularly unusual elastic material which exhibits strong hysteresis which means that when it is stretched it tends not to return all the way to its original shape. Under conditions of high temperatures or long times this hysteresis becomes more pronounced because the long molecules tend to relax when stretched if held there for a long time.

QUESTION: :
You're walking on the surface of a hollow planet. Imagine something like a pumpkin without the seeds and guts. The surface is thick enough to walk on and hold it's shape. The planet is also large enough to have an Earth-like gravity that attracts you to the surface. So you're walking along when you fall in a hole. The whole goes all the way to the hollow center. How far do you fall?
ANSWER:
During the time you are entering the hole, you accelerate because the part of you not yet inside feels a gravitational force toward the center. Once you are completely inside, you feel no graviational force and so you move with constant velocity across the cavity.

QUESTION: :
In a collision experiment, how would the conservation of momentum equation change if one metal sphere is replaced with a) rubber sphere; b) paper sphere; c) rock sphere of the same mass?
ANSWER:
Since momentum is always conserved in a collision (for an isolated system), the equations always look the same regardless of the material.

QUESTION: :
Why is there a percieved difference in time only a few miles above the earth? Ie, gps satelite daily time reset.
ANSWER:
Because general relativity has a result that the rate at which a clock runs depends on the gravitational field strength and the field gets weaker as you get farther from the center of the earth.

QUESTION: :
How planets orbit the sun without stopping? Wouldn't this be considered perpetual motion, which is, according to the conservation of energy, impossible?
ANSWER:
Perpetual motion is not forbidden by energy conservation. In fact, perpetual motion is perfect energy conservation. The reason satellites orbit (planets around the sun, moons around planets, etc.) is that they are in perpetual free fall. For example, see Newton's cannon.

QUESTION: :
Why do microwaves cause water molecules to heat up where as waves smaller and larger fail to do so? Why is it a person can be exposed to visible light which has a shorter wave length with no ill effects, and be exposed to longer radio waves with no damage as well? I can understand how waves smaller then visible light cause damage as they have more energy, but why is it a certain ban of IR and Microwaves cause heat? Is it sort of like a harmonic effect?
ANSWER:
It is basically a resonance thing. Electromagnetic waves with frequencies corresponding to microwaves are strongly absorbed by water, fat, and other organic molecules whereas other frequencies are not. See the Wikepedia article.

QUESTION: :
I would like to know how the size of a planet assuming the density is the same as the earth effects the graviy i.e if you double the mass do the gravity double and if the daimeter is doubled does the gravity go up 8 fold.
ANSWER:
I assume you want to know the strength of the gravitational force on the surface of the planet compared to on the surface of the earth. If the density remains constant, then doubling the mass means increasing the radius by a factor of 21/3=1.26. The force is proportional to the mass and inversely proportional to the square of the radius, and so F/FE=[2ME/(21/3RE)2]/[ME/RE2]=21/3. If you double the radius, you increase the mass by a factor of 8. The force is proportional to the mass and inversely proportional to the square of the radius, and so F/FE=[8ME/(2RE)2]/[ME/RE2]=2. ME and ME are the mass and radius, respectively, of the earth.

QUESTION: :
The potential (relative to a point at infinity) midway between two charges of equal magnitude and opposite sign is zero. Is it possible to bring a test charge from infinity to this mid point in such a way that no work is done in any part of the displacement?
ANSWER:
Imagine the plane perpendicular to the line and bisecting it. Moving a charge anywhere around this plane requires zero work.

QUESTION: :
As earth is moving around the sun and also rotates around itself is it possible that we can only lift the airplane without moving it towards ahead and we can reach to another place of the earth? If not then why?
ANSWER:
No, because an airplane flies relative to the air, not relative to the earth, and the air moves with the earth (more or less).

QUESTION: :
How does heat cause wind?
ANSWER:
The details are very complicated but the general ideas are simple. Adding heat to a gas causes changes in pressure, temperature, and volume. In a large volume of gas like the atmosphere, these changes cause movement of the air.

QUESTION: :
My chemistry teacher said that when electrons becomes exited in form of energy absorbed it releases a photon when it falls back to its original place. So, does this make the photon entangled with the electron?
ANSWER:
No. Both the photon and the electron are in definite states, not mixed with each other.

QUESTION: :
why is it necessaryto use two coeffeocient kinetic and static to describe the fritional force b/w two force how do u decide whoich cofficent to use when solving a problem
ANSWER:
Because they are two totally different things. For kinetic friction, the object must be sliding on a surface and the coefficient of kinetic friction tells you what the friction force is (coefficient times normal force). For static friction, you cannot use a formula to get the frictional force; it can be anything from zero up to the coefficient times normal force. The static is always larger than the kinetic coefficient since the object "pops away" when it starts to slide. Teflon is an example of a material with static and kinetic coefficients very nearly equal.

QUESTION: :
given Mars' gravitational field, would it be possible to catapult a vessel into space from the surface (of Mars)? And if it is possible, how much force would be required? Sorry, I know this is a rather vague

QUESTION: , I guess all I'm really asking is if it would be possible to launch a vessel into space via catapult at all... Don't worry, I'm not trying to build a space catapult or anything, I'm just wondering if it's even possible.
ANSWER:
The escape velocity from Mars is 5 km/2, about 11,000 mph. Whether you could do that with a catapult is an engineering

QUESTION: more than physics. I would not think this would be a practical way to launch a spacecraft since it would require a huge acceleration (because the size of the catapult means the speed would be acquired in a relatively short distance). A huge acceleration, of course, means a huge force so having people in the craft would certainly be out of the

QUESTION: .

QUESTION: :
a co-worker of mine was describing a time where he threw a box weighing about one hundred pounds out of a window on the eighth floor of a building. In an effort to dramatize the story a little, he wanted to express to us how forceful the impact was of the box on the ground below. he mentioned what I considered to be a rather dubious rule-of-thumb: an object's weight doubles for every foot it falls. At home in the evening I relayed the story to my roommates, and we discussed how unlikely it was that this was true--just for being such a simple, neat multiplier. Our subsequent research on the internet (involving many formulas, calculators and conversion charts) seemed to (roughly) confirm his statement. Being poor physicists, we are open to believing the calculations, but, perhaps as good scientists, we continue to doubt. Can you help? As a general rule-of-thumb, does his statement hold any water: does an object's "weight" double for every foot it falls?
ANSWER:
I must have written this a hundred times�the weight of something is the force that the earth pulls on it. The weight of the box is the same no matter where it is dropped from (unless the height is not small compared to the size of the earth). So, what might he be trying to say? Suppose we ask how much force would be needed to stop the box in a distance of, say, one foot. The work to stop an object with an energy of 500 ft-lb is equal to 500 ft-lb; so, to stop a 1 lb box which has an energy of 500 ft-lb, you would have to exert a 500 lb force to stop it in a distance of 1 ft (work is force times distance). To acquire this energy, it would have to be dropped from 500 ft up; the energy something has at the ground is proportional to how high you drop it from, so it has twice as much energy than if you had dropped it from 250 ft. Clearly, the energy does not double with every foot, so I don't know what he means about doubling every foot of fall. With every foot of fall a 1 lb box increases its energy by 1 ft-lb.

QUESTION: :
I keep pondering this scenario about centrefugal force, but there seems to be some principle I'm missing. If I rotate two balls connected by a rope here on earth, the centrefugal force will cause the rope to tighten as the balls move away from each other. Now I imagine I am watching the two balls in deep space, rotating, in relation to me perhaps, not in relation to anything else. If motion is relative, in what way are the two balls moving and is the rope taut? What am I missing? If I wasn't there to observe them, could the balls be rotating and the rope be taut?
ANSWER:
Imagine yourself in empty space with these two balls and rope. First find a frame of reference where the balls can be at rest with the rope totally slack. This is called an inertial frame of reference, defined as a frame in which Newton's first law is true. Now set the balls spinning. They now have an acceleration (relative to the inertial frame) and a force is required to maintain this acceleration�the tension in the rope. It makes no difference whether you are there or not, the rope must be taught to provide the acceleration. The idea that all "motion is relative" is often overstated: there is a big difference between inertial frames and all others. What you are suggesting is like saying that there would be no difference between how things are in a car moving with constant speed and a car having a very large acceleration (like hitting a brick wall).

QUESTION: :
I understand that gravity is thought to propagate at the speed of light. Consider two large bodies moving initially at the same high speed and parallel to one another, close enough to exert a gravitational attraction and far enough away from other bodies that they can be considered isolated. Now there will be a gravitational attraction between the two bodies drawing them together. But surely the direction of the vectors of attraction would lag slightly behind the actual position of the bodies. This would over a long period of time result in an overall slowing down of the bodies.
ANSWER:
This is really too technical a

QUESTION: . You are asking about what is often referred to as "retarded potentials" and, you may be sure, there is no force which will slow these particles down, only the force pulling them together. In the rest frame of the two masses they clearly have no acceleration other than toward each other.

QUESTION: :
I read that if electrical power is transmitted over long distances the resistance of the wires becomes significant. Why is this the case and which mode of transmission would result in less energy loss-- high current and low voltage or low current and high voltage?
ANSWER:
Power dissipated by a current I passing through a resistor R is I2R. A conducting wire has low resistance so this is not much of an issue in your house, say. However, R is proportional to the length of the wire and over many miles R, and therefore power loss, can become significant. Since R cannot be controlled, I is minimized. The way to do this is to use a very high voltage and low current.

QUESTION: :
What would happen if an object traveling at one half the speed of light passes through the earth's atmosphere?
ANSWER:
It depends entirely on the object. Cosmic rays go faster than half the speed of light and they hit the earth all the time; they tear up atoms as they go but mainly leave no significant trace. Something large would burn up and probably cause catastrophic damage.

QUESTION: :
Why does fusion reactions produce more energy than fission reactions, given that by Einstein's equation, energy is proportional to mass.
ANSWER:
Fusion reactions convert a higher percentage of mass to energy than fission. First you should look at an earlier answer about fusion and fission. You will see that the slope of the binding energy curve is much greater for light nuclei fusing than heavy nuclei fissioning. One uranium fission will give more energy than two hydrogens fusing but the ratio of mass converted to energy to mass of the fuel is much bigger for fusion.

QUESTION: :
does time move faster on the surface of the moon as opposed to on earth?
ANSWER:
Yes. Time moves more slowly as gravitational force gets larger. This is a consequence of the theory of general relativity.

QUESTION: :
Tie an object such as a pencil eraser to a string. Use the string to swing the object around your head at a constant speed. Can the object be swung so that the string is parallel to the horizontal, flat, and even floor on which you stand?
ANSWER:
No. The reason is that the object must in equilibrium in the vertical direction since it has no vertical component of its velocity (or acceleration), so the forces in the vertical direction must add to zero. One force in the vertical direction is the weight, straight down. There must be another force which points up and is equal in magnitude to the weight; this can only be the vertical component of the tension in the string and a horizontal string has no vertical component of its tension.

QUESTION: :
the time it takes for one heavenly body to make one complete revolution around another heavenly body is called what?
ANSWER:
The period.

QUESTION: :
why do physicists relate the four dimension to time more then just another physical dimention , much like the third dimension to flat-landers?
ANSWER:
Suppose that you have a two-dimensional coordinate system and the coordinates of some point are (x,y); now, if you rotate this coordinate system the new coordinates of the same point are (x',y') where x' depends on both x and y, and y' depends on both x and y. That is, the coordinates become mixed up with each other. Now suppose that one observer moves in the x direction of some coordinate system; this observer carries a clock which measures a time t' and measuring sticks which measure a distance x'. If (x',t') are compared with (x,t), analogous quantities measured by a second observer not moving in the coordinate system, it turns out that x' depends on both x and t, and t' depends on both x and t. This analogy tells you that it is fruitful to treat, mathematically at least, time on an equal footing with space, that is, special relativity can be developed using four-dimensional vectors. It is, however, a mistake to think of time as a fourth space dimension like a flatlander would think of the third dimension. Indeed, you should think of there being something which encompasses both space and time which we call space-time, not that space is now four dimensional.

QUESTION: :
Suppose that the mass holders in an experiment all have the same mass.May their masses be neglected in calculation of the acting force?
ANSWER:
Maybe for some particular experiment, but certainly not in general.

QUESTION: :
In my high school physics class, we have just finnished the section on electricity. The two equations my

QUESTION: relates to are: the relation between capacitance, voltage, and charge C=Q/V the force between two point charges (Q and q) as a function of distance F=(kQq)/d^2 My

QUESTION: , which none of my teachers can answer, is: Why don't these two eqations work when used together? I'm assuming they dont work because a capacitor of 100uF at 10v holds 1000uC and two charges of 500uC separated by 10cm should, according to those equations above, exert a force of roughly 225,000N. I've done the math many times and can't find any issues. Is it a calculation error or improper use of the equations?
ANSWER:
The reason is that the two equations are essentially unrelated. The force equation applies to two point charges separated by a distance d. The plates of a capacitor are not point charges. You also have some misceptions about capacitors. The capacitor carries a charge Q. This means that one plate of the capacitor carries a charge Q and the other a charge -Q such that the total charge is zero. The plates of a capacitor therefore exert an attractive force on each other. It is pretty easy to compute the force one of the plates of a parallel plate capacitor feels because the electric field between the plates is nearly uniform. The field is given E=4πkQ/A where A is the area of the plates, and the capacitance is C=A/(4πkd). The force felt by each plate is F=EQ/2. If I put in your numbers for Q=10-3 C, V=10 V, and d=0.1 m I find that F=0.5 N, a far more reasonable number!

QUESTION: :
Is a nuclear submarine called nuclear because it has nuclear weapons or because it is run with nuclear power?
ANSWER:
Because it is nuclear-powered.

QUESTION: :
I got in an argument with my friend about the weightless feeling in space. I say that if you're in a spaceship orbiting the earth, you'll feel weightless because you are technically in constant freefall. He says you'll feel weightless because theres no gravity. Who's correct?
ANSWER:
You are correct. If there were no gravity, what force would hold your spaceship in orbit? It is also insightful on your part to recognize that, when in orbit, you are actually in freefall.

QUESTION: :
Will a rock cool faster in deep space in sitting on a dinner plate at stp? (room temperature at my house) lets say it starts with a 300 degree F temp and cooling to 100 F
ANSWER:
I do not think you can say for sure. It would depend on the shape of the rock, the composition of the rock (in particular, how good a radiator the material is), the amount of contact of the rock with the plate, etc. The rock in deep space can cool only by radiation and would continue cooling below 1000F. The rock in your house would also cool by radiation but it would also absorb radiation being constantly emitted by the environment; if radiation were the only consideration, the rock in space would clearly win the race. But the rock in your house can also cool by conduction (via contact with the dinner plate) and convection (air moving over it carrying away heat). But the the rock in you house is tending toward room temperature, maybe 700F, so I would think that it would approach 1000F much more slowly than the space rock. So, my best guess is that the space rock will win the race, but careful tailoring of the conditions might reverse the situation.

QUESTION: :
I would like to ask a quick

QUESTION: regarding laser and color. I tried googling it but found no result. I'm trying to find some ways to detect the color of a material for a small project. I thought of two ways so far
1. through an optical lens that will capture the color and get it analyzed.
2. shoot a beam of laser at the material and analyze the wavelength that gets bounced back.
Obviously, the first example does not concern physics too much, but I was wondering if the second example is feasible in a relatively cheap manner.
ANSWER:
The laser will not work because laser light is of one color and that is the only color you could see reflected back. I do not see what you mean that "the first example does not concern physics". Optics is physics. But to "capture the color" is not the essence of what you want to do, it is determining the color that is the real task. For this you need a means of measuring the wavelength(s) of the light, e.g. using a prism or a grating as a spectrometer.

QUESTION: :
what makes people think that fundamental physical constants can be anything other than what they are? Is this a mistake akin to imagining a temperature of, say, −274.15�C (where −273.15�C is the number we use to say that atomic movement -- i.e. heat -- ceases). Just because we can change the numbers in our minds does that give us a basis for imagining what our universe would be like if the cosmological constant was anything other than it is? A recent article I read in SciAm seemed to treat it as a given that these constants are arbitrary and proceeded to hypothesise about multiple universes. Am I missing something, or is this baseless physics?
ANSWER:
For starters, absolute zero is not a fundamental constant. No matter what fundamental constants are, how units are operationally defined, absolute zero will always be that (unattainable) state of matter with zero kinetic energy. Examples of fundamental constants are the universal constant of gravitation, G, which quantifies the strength of gravity, and the permittivity of free space, ε0, which quantifies the strength of electrostatic interactions. And, you do not look at the numbers since those depend on the system of units; rather you look at the implications of the relative values for physics. The values of G and ε0 tell you that gravity is incredibly weak compared to electromagnetic forces. And we have no idea why they have the values they do. Amazingly, just relatively minor changes in the fundamental constants would make our universe as we know it impossible�stars would not form, atoms would not form, nuclei would not form, life could not exist, etc. One of the ideas advanced is that what the constants turn out to be is random but that there are many universes with many values of constants and few are anything like ours; whether this is "baseless" physics is open to debate, but there is certainly no physical evidence that it might be true.

QUESTION: :
if a water-filled container's weight with an object in it is equal to the container plus the buoyant force on the object if it has not sunk, Why then does the buoyant force point opposite to the direction of the weight of the container? Would you then not subtract the buoyant force from the weight of the container to get the total weight?
ANSWER:
Aha, you make the classic mistake made by thousands of physics students going before you�you are not focusing on one body at a time. Let me run through the various possible scenarios here and see if you understand.
Look at the object. What are the forces on it? Its weight w down and a force b which the water exerts on it, up. (We call b the buoyant force.) Newton's first law (N1) requires b-w=0, so b=w.
Look at the container and water. What are the forces on them? Their weight W down, a force N from the scale they are sitting on, up, and a force f which the object exerts on the water. Newton's third law tells us that f=b and points down. N1 now tells us N-W-f=0=N-W-w, and so N=W+w. There is the answer to your

QUESTION: �the scale reads the total weight. But let's look at another possibility.
Look at the container and water and object all together. The forces are the weight, W+w down, and the force of the scale N up. The buoyant force does not come into it at all because the forces the water and object exert on each other are internal forces and cancel out (or, b-f=0). So N1 tells you that N=W+w. Again, there is your answer�the scale reads the total weight.

QUESTION: :
In case one I accelerate an apple to one mph. It requires x amount of work to accelerate the apple by one mph. Next I accelerate the same apple by another one mph. This requires the same amount of energy as in the first example, ie the energy necessary to accelerate one kg by one mph. Thus I have expended twice as much energy to accelerate from one mph to two mph. But the apple now has 4 times as much energy. I would so much appreciate an explanation in laymen's terms. I must be really stupid. I just cannot see the logic.
ANSWER:
No, you're not stupid; it is a little subtle. Energy is not what we call an invariant quantity, that is the kinetic energy something has depends on the frame from which you observe it. What your thought experiment does is shift frames for the second acceleration; you have put yourself in a frame where the object starts at rest. When you do this, you move into a frame where the apple is at rest, that is has zero energy. Therefore, your second experiment is nothing more than a repeat of your first experiment. If you calculate the work you have to do in the original rest frame to accelerate the object from speed v to speed 2v you will find W=�m(3v2) which then leads to the correct total energy and work of �m(4v2).
FOLLOWUP

QUESTION: :
This is what I have trouble understanding. Assuming no friction or wind force, etc. it requires x amount of fuel to accelerate a car by 1 mph, and x amount of fuel for each additional 1 mph. Thus change in velocity is directly proportional to energy input. But change in kinetic energy is proportional to the square of change in velocity. Energy input should equal the change in kinetic energy of the car, but apparently does not. I know there is a basic flaw in that reasoning, but where is it?
ANSWER:
It does not take the same amount of fuel to accelerate the second 1 mph. It is a little tricky to talk about a car where it is actually the force of friction of the tires which push the car forward to accelerate it. That is were the work is done on the car, a forward force F which is constant if you are accelerating at a constant rate. Now, if the car starts at rest and increases its speed at a constant rate to speed v, how far, d, has it gone? Well, simple kinematics tell us that d=�(F/m)t2 and v=(F/m)t, so d=�(F/m)[mv/F]2=[�mv2]/F. Therefore, the work F does to bring it to v is W=Fd=�mv2. Now, let's calculate the work F must do to increase the speed from v to 2v. The new distance traveled, d', is d'=vt+�(F/m)t2 with 2v=v+(F/m)t => v=(F/m)t; note that the time the force acts is the same but the distance over which it pushes is larger, so more work is being done. If you do the algebra here (put t=mv/F into the d' equation), you will find d'=3d. It takes three times the energy to increase the speed by another 1 mph in your example. I suspect you are still bothered! And I think I can say why. If you burn fuel at a constant rate you will not accelerate at a constant rate; to accelerate at a constant rate you have to increase the rate at which you burn fuel as you go along. If you burn fuel at a constant rate, the time for the second 1 mph gain will be longer than for the first 1 mph; and guess how much�exactly 3 times longer! (I always go that extra mile for folks nice enough to make a donation!)

QUESTION: :
Gas particles travel at speeds really big like 400 or 500 meters per second. Why does it take so long for gas molecules to travel the length of a room? This came up in class and i couldn't figure it out.
ANSWER:
Because they collide with other molecules in the air and therefore have a zig-zag path. The mean free path, sort of an average distance between collisions, is around 10-7 m in air at STP.

QUESTION: :
I need to prove innocence in a car accident and need to find out the minimum speed a car would be travelling to push a stopped car forward about 2 metres. Scenario. 3 car crash where 2 front cars pulled up hard but were still a sufficient distance from each other eg 1.5-2.5 metres when the 3rd car rammed hard enough into the middle car to push it forward and bump the front car. Sealed road, dry conditons. the middle car weighs 1322KG and the 3rd car weighs 1703KG
ANSWER:
First of all, you are not going to "prove" anything. There are too many variables. The coefficient of sliding friction for rubber on dry asphalt is in the range 0.5-0.8. I will use 0.7. I will assume that the brakes of the middle car are engaged so so the tires slide, do not roll. It is crucial what car #3 does after the collision. One simple collision is called perfectly inelastic; in this case the two cars move together after the collision, essentially as one. At the other extreme, the collision can be perfectly elastic; in this case no energy is lost in the collision, sort of like two billiard balls colliding (almost elastic). I am not going to include all the details, just the results. First, I calculate the speed the middle car needs to have to slide 2 m and stop: 5.24 m/s=12 mph. If the collision is perfectly inelastic, the speed of car #3 at the instant of impact is about 9.31 m/s=21 mi/hr. If the collision is perfectly elastic, the speed of car #3 at the instant of impact is about 4.65 m/s=10 mph. I would guess that the collision would be more like the inelastic collision, that is, the speed would be closer to 20 mph. Of course, the speed of the middle car could have been greater than my minimum of 12 mph because it was probably moving when it hit the front car; so, to make a better estimate one needs to estimate the speed it had on the second impact. My final estimate based on limited data would be the speed of car #3 on impact was greater than 20 mph.
ADDED THOUGHT:
If you are the driver of car #3, it is my impression that you are at fault regardless of anything. It is the responsibility of all drivers to be able to stop to avoid hitting another car at rest.

QUESTION: :
If you are driving a car going 60 mph and you shine a beam of light from your car why isnt the light moving at a speed of the speed of light plus 60? The driver would measure the speed of the beam at the speed of light, but I'm pretty sure that to an observer the speed of that beam of light is moving 60mph faster than the speed of light. So technically, since the observer is at rest, isnt the beam traveling faster than the speed of light?
ANSWER:
See earlier answers.

QUESTION: :
A jet plane is traveling 1000 mph to the West, a gun mounted on the airplane facing East fires a bullet with a muzzle velocity of 1000 mph, does the bullet travel in either direction, East of West, or fall straight to the ground?
ANSWER:
To an observer on the airplane the bullet has a speed of 1000 mph east. To an observer on the ground, the bullet has zero velocity and, as you say, falls straight down.

QUESTION: :
the pressure at the bottom of earth's atmosphere is about 100,000 N/m squared. this means there is a force of 100,000N acting on every square meter of area! your body has about 1.5 square meters of surface.why arent you crushed by the atmosphere?
ANSWER:
Because we evolved in this environment and therefore there is a balancing pressure from inside. Every cell has an internal pressure of approximately one atmosphere. Think of a bottle which you have put a cork in�why doesn't it get crushed?

QUESTION: :
I noticed an answer of yours and you made a point that the fastest possible speed is the speed of light. Has this been proven? Or is it still a theory? Also isn't possible that there is some type of particle that we are unable to detect (as of now) that may actually move at a speed greater than the speed of light?
ANSWER:
This is the result of the special theory of relativity and the special theory of relativity has been shown to be correct in more experiments than you can imagine. The "speed limit" is clearly evident in our biggest accelerators where we push and push on the accelerated particles and they keep gaining energy but do not gain any significant speed once they get close to the speed of light; we can get them to 0.9999999 the speed of light, but never to it. There have been speculations about there being particles going faster than the speed of light (dubbed tachyons). But, "you can't get there from here", that is they have to have always been there because it takes an infinite amount of energy to accelerate something to the speed of light, let alone beyond.

QUESTION: :
I am not sure if this is a "highly technical

QUESTION: " or not. My

QUESTION: involves the relationship between a photon's energy, frequency, and wavelength. I am having trouble understanding what a photon's "wavelength" is exactly! I know that the energy of a photon is E = hc/lambda, where the frequency = c/lambda. When an electron falls from the conduction band back down to the valence band, a photon is emitted. If frequency = c/lambda, then what determines wavelength? Is it the distance that the electron falls between energy gaps? Is it wrong to view "frequency" as vibration or rotation of the photon in this case?
ANSWER:
This is the kind of conundrum you can get into when dealing with wave/particle duality. A photon of a given energy and momentum has a one to one correspondence with electromagnetic waves of a given wavelength and frequency. Energy and momentum of a photon are related as E=pc; frequency and wavelength of a wave are related as f=c/λ; the two are connected by E=hf. I think it is a mistake to try to visualize the frequency or wavelength of a photon.

QUESTION: :
I am an 8th-grade science teacher. We are teaching chemistry now and taught physics earlier this year. I did a small demonstration with dropping blue dye (food coloring) into water and watching the diffusion. We connect this back to physics by asking students to think about the dye molecules and what needs to happen for them to accelerate horizontally (there must be a force, Newton's 1st law) and then talk about where this force comes from -- the random motion of the water molecules. So we are using the physics the students know to introduce the basics of kinetic molecular theory. The blue dye also moves vertically and in cold water this motion is much faster than the horizontal diffusion. I don't think the density is substantially different and indeed the dye does not settle to the bottom, it diffuses throughout. So we talked about gravity as a force acting on the dye molecules. But one of my most astute students quite reasonably said, if gravity is an unbalanced force acting on the dye molecules and causing them to accelerate toward the bottom of the beaker, then why wouldn't there also be unbalanced force on the water molecules, which doesn't seem to be the case? So here is the

QUESTION: : Is it in fact gravity that immediately disperses dye vertically when dropped into water, or is it just the momentum of the falling drop? In general what are the forces on the molecules in a liquid that is "still" (not moving)? How do the forces from random molecular collisions relate to gravitational downward pull -- is one much stronger than the other, say for water at room temperature? Since the molecules are not accelerating downward, at least on average, then what force opposes gravity? Would you call it buoyant force when thinking about this at a molecular level? I would think not, the molecules aren't really floating. But it is not normal force either. Can you clarify?
ANSWER:
So, I tried this experiment myself. I believe that what happens is that in cold water the drop of dye keeps its integrity long enough to sink just like anything more dense than water would. As it falls, the influence of the moving water molecules causes this drop to "bloom" and, as it spreads out, its fall becomes less dramatic. In the hot water, this "blooming" just happens quicker before the drop can fall very far. Certainly, gravity acts on all the molecules, water included. However, water is essentially incompressible and so the molecules can't all fall to the bottom of the jar; the effect of gravity is that the pressure in the water gets larger as you go deeper. When I did my experiment, carefully letting the glass of cold water sit to still all currents, the dye did initially have a large fraction settle to the bottom. In the end, though, the molecular bombardment did redistribute it throughout the whole volume.

QUESTION: :
I need to know what is the mass of one milliliter of hydrogen protons! I need to know the answer in mass and show my work! I'm lost
ANSWER:
You can estimate the volume of a proton by assuming it is a sphere of radius 10-15 m. Then, looking up the mass of a proton you can get an estimate of its density, mass divided by volume. Now that you have the density, you can get the mass of any volume (like a milliliter).

QUESTION: :
I think I correctly understand the idea of the following but not the actual physics of it... If there's MORE light going out a window than there is going in, I will see a reflection of what's on my side and if there's LESS light going out the window than there is going in, I will see what's on the other side. Why is this?
ANSWER:
I do not know where you got this from, but it is wrong. Light striking the window from either side will be partly reflected and partly transmitted. If there is much more light coming in from outside than there is reflected inside, you will not notice the reflection but it is still there.

QUESTION: :
How can we find the initial velocity of a marble when we have the angle it's launched at, the final distance traveled, and the mass of the marble (special equations might be helpful) Please help us! We are trying to calculate the velocity of a marble with a different mass.
ANSWER:
The short answer is that, if air friction is negligible, it makes no difference what the mass is. Ignoring air friction, we can write the equations for the x and y positions of the marble as a function of time t (assuming that x=y=0 at t=0). Here, x is the horizontal position and y is the vertical position. These equations also include the angle θ the initital velocity v0 makes with the horizontal and the acceleration due to gravity g (9.8 m/s2 or 32 ft/s2).
x=v0tcosθ
y=v0tsinθ-�gt2
Now, if you put in y=0 (assuming the marble came back to the altitude it started) and x=d (distance traveled), you can eliminate t and solve for v0:
v0=√[gR/(2cosθsinθ)].
Note that this is all independent of mass. The reason that mass does not matter: as Galileo himself discovered, all objects have the same gravitational acceleration (neglecting air friction).

QUESTION: :
I am trying to help my 10 yr old son with a project. He is an avid hockey player, he wanted me to help him figure out the force (easiest explained in lbs or kg) of a hockey puck hitting a goalie at various speeds. I suggested we look at Newton's second Law, F=ma. I am having a problem with units, though for a 6 oz puck, my results suggest 10 mph = 3.75 lbs, 40 mph = 15 lbs, 80 mph= 30 lbs etc. Am I on the right track?
ANSWER:
I don't know how you got your answers, but it is impossible to get any answer by simply knowing the mass and the speed because the speed does not determine the acceleration (which is rate of change of speed). So you need to know or approximate the either the time it takes the puck to stop or the distance the puck moves before stopping. Then you can calculate the average force over that time or distance. This should be evident because if the goalie wears a thick foam chest protector (which causes the time or distance to be bigger than if he uses a hard shield), he will feel much less force. And, working in ounces and pounds is really hard�the English system just does not lend itself very well to doing this kind of calculation. So, let's do a simple calculation. The mass of the puck is 0.17 kg. Suppose that the puck stops after the chest protector has compressed by about an amount d=2 cm=0.02 m (a little less than an inch). A 20 mph puck has a speed of about 8.94 m/s. To calculate the acceleration a, use a=(v2/(2d))=8.942/0.04=2000 m/s2. Now that you have the acceleration and the mass you can calculate the force: F=ma=0.17x2000=340 N=76 lb. The time it took to stop was about t=v/a=8.94/2000=0.0045 s=4.5 microseconds. Keep in mind that I have just guessed at the distance to stop. Note that the acceleration is proportional to v2 so, assuming d stays the same (which it might not) the force at 80 mph would be 4 times bigger than that at 40 mph. (Incidentally, if you want to be able to easily convert back and forth between different units, I recommend a nice little free converter called, appropriately, Convert.)

QUESTION: :
What actually puts force on electrons to cause them to accelerate in a complete circuit?
ANSWER:
By causing there to be a potential difference across the ends of the circuit (by a battery, for example), an electric field is established in the conductor. This electric field causes electrons to experience a force in the opposite direction of the field (because they are negatively charged). This force wants to accelerate the electrons, but they accelerate only a short distance and then collide with one of the atoms in the conductor. Then this happens all over again, and again, and again, etc. The net result is, on average, a slow drift of electrons with constant speed opposite the direction of the field.

QUESTION: :
What happens if one section of a complete circuit is replaced with a good insulator? I know that in insulators, electrons are more tightly connected to individual atoms, so would the circuit slow down?
ANSWER:
What do you mean by "circuit slow down?" The total current in the circuit would get smaller because you have increased the resistance of the circuit by replacing a piece of conductor (low resistance) by a piece of insulator (high resistance).

QUESTION: :
I have a seemly simple

QUESTION: about conservation of energy (but I am confused). This

QUESTION: pertains to raising an object up and then letting it fall. I understand that it costs energy to raise an object to some height �h� which gives the object gravitational potential energy. Now let it be released and accelerated back toward the ground. The universe does work to accelerate the object back to z = 0. There is a force times a distance so work is done. So if a human does work to get the object up, and the universe does equal work to bring it back down, that should equal zero, where does all the energy come from to �smash� the object into the ground (assuming its broken into pieces which happens all the time). I�ve asked and they say, �no� is the kinetic energy which does the smashing. I�m not too worried what we call the energy, it took E to get it up, - E to get it down, then Es to do the smashing, which may get converted into heat, etc. It seems people ignore the energy the universe spent to bring the object back down considering that to be free. In the reverse direction it makes more sense. Drop and �bouncy ball� from some height �h,� and it can (in theory) bounce right back to height �h� having zero velocity. But the ball doesn�t just explode at the top which would violate conservation of energy.
ANSWER:
You are right, you do work E to get it up and, when you drop it, you get all that energy back just before it hits the ground. Energy is not conserved going up (you are adding it) but is conserved going down. What happens when it hits the ground? Let us take a simpler example first, where all it does is stop; maybe it is just a ball of putty. It has energy (kinetic) one moment and not the next. In the meantime there was another force doing work, the force the floor exerts on the ball. This force takes all the energy away from the ball (it must do negative work, right?). And, if the ball is putty, you cannot get the removed energy back. If, however, the ball is "bouncy", the compressed ball will uncompress and, as it does that, the lost kinetic energy is restored; the floor does positive work on the ball during this time. So, the energy to "smash" say a glass ball comes from the work which the floor does on it; this is evident because if you take away the floor, the ball will not smash (or squish or compress).

QUESTION: :
If an object is held stationary above the ground at a height of 10 cm, would work be done on it or not? I told my dad that work would be done because the object possesses gravitational potential energy but my father said that work would not be done since the object is stationary and work is force multiplied by displacement.
ANSWER:
Both and neither of you are correct. If the object is at rest, no work is being done on it. If it was previously at a different height, say the ground, work was done on it to raise it; that is where the potential energy came from.

QUESTION: :
Does the statement "a ball dropped from the top of a building increases in speed until it hits the ground" violate the law of conservation of energy?
ANSWER:
The law of conservation of energy is not a universal law, it is only true under certain situations. If you define a conservative system as one in which no external forces do work, then the total energy of that system remains constant. In the case of the ball, it is not a conservative system (the force the earth exerts on it, its weight, does work) and so you do not expect its energy to remain constant; hence its kinetic energy increases as it falls. If you are clever, though, in many cases like this you can introduce a potential energy function which is a trick to take a previously external force and internalize it. So, as the ball falls its kinetic energy increases but its potential energy decreases and the sum of the two remains constant. So, in this case the energy of the ball is either conserved or not, depending on how you define energy. But the case where it is not conserved is not an instance of "violation" or the law because the law ought not apply to that case.

QUESTION: :
When a body is being rotated in a circle by applying centripetal force, why doesn't it come towards the center of the circle since centripetal force acts towards the center of the circle?
ANSWER:
When a force acts on an object in a direction perpendicular to the object's direction of velocity, it causes the direction of the velocity to change but not its magnitude. In the case of a centripetal force, the result is that the object moves in a circle with constant speed, constantly changing its direction so that it is always moving tangent to the circle.

QUESTION: :
Just a quick

QUESTION: , Im a biologist and no virtually nothing of physics. There is currently a lot of debate here in the UK on the efficacy of homeopathic "medicines". According to homeopathists a 1M solution serially diluted 10^-50 (i.e. more than Avagadros constant) in water will somehow inprint a memory of the diluted molecule in the water. The pro homeopath lobby are trying to explain this with Quantum mechanics, is there any scientific basis for this? an example:
"From what I've read I think that Werner Heisenberg's theory of energy-time indeterminacy and Erwin Schr�dinger's thoughts on there being many indeterminate states possible until a conscious observation is made are the most fitting regarding homeopathic efficacy. These try to address the curious "tunneling" of electrons into unexpected areas of space, and the "wave function" of particles which are said to "collapse" into a specific state due to the act of being observed."
ANSWER:
In my opinion, this kind of statement is total nonsense. There is no basis in physics or chemistry to support the claims of homeopathy that somehow water molecules have a "memory" of previously dissolved chemicals. And, if it were so, what about all the other substances which must have been previously dissolved in the history of the water?

QUESTION: :
We were discussing in a biochemistry class about atoms, how is it if you have atoms in your hand, and a table has atoms, Why doesn't your hand go through the table?
ANSWER:
This is one of the FAQs.

QUESTION: :
Two balloons that have the same weight and volume are filled with equal amounts of helium. One is rigid and the other is free to expand as the pressure outside decreases. When released, which will rise higher? Why?
ANSWER:
On each balloon there are two forces�its weight (which makes it want to fall) and the buoyant force on it (which makes it want to rise). The weights are the same and never change. The buoyant force is proportional to the volume, so whichever has the greater volume has the greater buoyant force. The expanding balloon wins.

QUESTION: :
I recently found out that a bottle full of helium gas will weigh less than a bottle full of air. But would the helium bottle now weigh more or less than a bottle with the air pumped out of it?
ANSWER:
There is also the proviso that the pressures and temperatures of the two gasses must be the same; for example, you could have the helium bottle weigh more if you put enough helium in it. If you now evacuate the air bottle, it will weigh less.

QUESTION: :
Does the statement "a block sliding freely on level ice increases in speed until it hits a wall" violate the law of conservation of energy? Why or why not?
ANSWER:
It certainly does. If the ice is level and there are no external forces on the ball which do work, where does the increased kinetic energy come from?

QUESTION: :
I'v always thought of a light wave as coming towards me going up/down or left/right is it true that it is actually spinning in a circle as it goes along
ANSWER:
Any of those are possible. What you are talking about is called the polarization of the wave and, depending on the source or the preparation, several polarizations are possible. in all cases, the electric and magnetic fields are perpendicular to the direction of travel.

QUESTION: :
we were discussing time travel in class and learned that it is theoretically possible. We were thinking about this and wondered if it is possible to actually perform an experiment to prove this. Have there been any experiments that demonstrate this phenomena. Will traveling at great speeds actually cause a temporal shift? Also, does going back in time and "changing the past" affect present events or is it impossible to affect the present. We are aware of the "paradox of time travel" (going back and killing Mozart...would his music cease to exist?....or....going back and preventing your parents from uniting, would you cease to exist?)
ANSWER:
Here is what physics has to say about time travel: it is entirely possible to travel forward in time but impossible to travel back in time. In the theory of relativity, moving clocks run slow which is what allows forward time travel; see my earlier discussion of the twin paradox. Moving clocks running slow (called time dilation) has been verified experimentally in many ways. Since, as far as we know from physics, backward time travel is not possible, we do not need to worry about the kinds of paradoxes you ask about.

QUESTION: :
we were discussing rational and irrational numbers in math class one day. First of all, we were told that the numbers in an irrational number will never show a repeating pattern. We believe that eventually it will have to repeat. Our teacher told us that experiments were done with "pi" that showed no repeating pattern for a huge amount of decimal places. We are convinced though, that the digits will have to repeat at some point. What do you think?
ANSWER:
First, I think I am a physicist, not a mathematician! But let me opine that your "belief" is entirely unscientific. I suspect that there is a quite rigorous proof that there is no repeating pattern. You need to have a basis for making such statements other than "we believe".

QUESTION: :
We were wondering about the "Planck Distance." First of all, is it true that this is the shortest distance possible? Secondly, if that is true, wouldn't the reciprocal of the Planck Distance be the greatest distance possible?
ANSWER:
See an earlier answer. The flaw with your hypothesis about the reciprocal being the largest possible distance is that it would be dimensionally incorrect, that is its units would not be meters but rather meters-1.

QUESTION: :
Ok you are on the north end of a south bound plane going 300 miles an hour and you throw a baseball forward at 95 miles an hour. So at what speed is the baseball traveling????
ANSWER:
You must specify who is observing the baseball. The speed relative to you is 95 mph, relative to the ground is 395 mph.

QUESTION: :
Can you please tell me what if any visible changes to the structure and composition of wood will result when electro magnetic energy passes through it or near it?
ANSWER:
There is no single answer to this. For example, a powerful laser is em energy and it would burn the wood. But radio waves usually have no affect on the chemistry. Over long periods, visible light can bleach or fade the color of wood.

QUESTION: :
I dropped a bowling ball and ping pong ball from high above the floor. They hit the ground at the same time. A student asked about a balloon I also had. In that match, the ping pong ball easily bested the balloon (~8inch round). Why? Both are round, lightweight and filled with a gas. Is it aerodynamics/ air resistance? Smoothness of surface? I don't know what to tell them. Please Help!
ANSWER:
In the absence of air, all will fall together. But, air friction is clearly not negligible for a balloon. Air friction depends on the geometry (both are round, so that is not an important factor), cross sectional area (balloon has a bigger area), and weight (ping pong ball is heavier, probably). The area here is probably the main factor; if you were jumping out of an airplane, would you want a parachute of diameter 5 m or one of diameter 5 cm? To get a little more quantitative, the terminal velocity, the maximum speed v achieved by something falling through a fluid of density ρ, is v=[2mg/(ρACp)]� where mg is the weight, A the cross sectional area, and Cp a constant which is determined by the shape. You link to a bunch of other answers on air friction on the FAQ page.

QUESTION: :
A 100,000 N car is raised a distance of 5 m by an effort force of 500 N. (consider this an ideal frictionless situation) I have to solve for work output and work input, don't I need to know another force to do this? Out of school too long.
ANSWER:
The only way that you can lift a 100,000 N car with a 500 N force is on an incline. Determine the angle where the component of the weight along the incline is 500 N and then how far you would have to pull up the incline to lift it 5 m. I have no idea what is meant by "input" and "output" here. One would simply calculate the work done by the 500 N force, 500x(distance along incline). That is the concept. There is an easier way. Once the car is 5 m up it has an increased potential energy of mgy=500,000 J which must be the amount of work done on it. So, you see, not only do you not need another force, you do not need the 500 N force either!

QUESTION: :
why isotopes are same in chemical properties and different in physical properties ?
ANSWER:
Because the chemical properties are determined by the electron structure, not the nuclear structure. So, changing the number of neutrons in a nucleus has almost no effect on the electron structure which is determined by the charge of the nucleus, not its mass.

QUESTION: :
if the repulsion force between two protons in nucleus of iron atom is big value,the nucleus of iron is not destroyed?why?
ANSWER:
Because the Coulomb force is not the only force acting. The nuclear force, also called the strong interaction, is an attractive force which is much stronger than the repulsive Coulomb force at close distances.

QUESTION: :
Suppose an object tied to a string is being rotated. The string applies a centripetal force on the object. The object exerts a centrifugal force on the string as a reaction in accordance with Newton's third law.My

QUESTION: is that why we consider centrifugal force to be a fictitious force ?
ANSWER:
The object does indeed exert a force on the string. But this is not what is called a centrifugal force, it is what is called the force of the object on the string and exists because of Newton's third law. The thing referred to as a centrifugal force is a force which seems to be on the object but is not really there. See my earlier discussion of centrifugal forces.

QUESTION: :
Here's a relativity

QUESTION: I've been losing sleep over. If you're on an object that's traveling slightly slower than the speed of light and you fire a rifle, why does the bullet not exceed the speed of light?
ANSWER:
This has been discussed in several earlier answers; see this one for the most detail. In essence, it is that things just do not behave as they do in classical physics when traveling at very large speeds. Although you would see the bullet traveling with its usual muzzle velocity relative to you, an observer at rest would not see the speed of the bullet as the speed of you plus the muzzle velocity of the bullet. Try to get some sleep.

QUESTION: :
Hello, I was at a baseball game and my friend had a chance to catch a ball that came into the crowd. Being into Physics myself, I've always wondered to catch it safely, should you move your hands toward the ball, hold them still, or move them in the same direction as the moving ball?
ANSWER:
Move them in the same direction as the ball. This allows you to maximize the time during which you are stopping the ball thereby giving it as little acceleration (the rate of slowing down) as possible. Acceleration of the ball matters because of Newton's second law which says the force you must apply to stop the ball is proportional to the acceleration it has. Hence if you minimize the acceleration you minimize the force you exert on it; because of Newton's third law, if you exert a force on the ball, it exerts an equal and opposite force on you. So you will also minimize the force (which is what hurts) on you.

QUESTION: :
I know that to measure the half life of a radioactive element you just take a certain amount of it and count the rate at which the decay products change over time. But how do you measure the half life of neutrons where you do not have a pool of neutrons upon which to base your measurements as you cannot isolate a group of them?
ANSWER:
The difficulty of measuring you note is one of the reasons that the half life of the neutron has a larger uncertainty than some radioactive nucleus. There are, however, copious amounts of neutrons in reactors and that is where such measurements are made. Hence one must deal with beams of neutrons, not simply a box of them.

QUESTION: :
In a newton's cradle(which has usually 8 bobs or balls)if i let 5 balls bang on the other 3 balls then after collision 5 balls would move on the other side.Why 5 balls are moving and not three balls?
ANSWER:
Both energy (�Σmv2) and linear momentum (Σmv) must be conserved where Σm is the mass. Suppose that 5 come in and 3 go out. Then momentum conservation says 3m0u=5m0v (where v is the speed of the balls coming in, u is the speed of the 3 balls going out, and m0 is the mass of one ball). So, u=(5/3)v. So now, the energy of the incoming balls is �(5m)v2=2.5v2 and the energy of the outgoing balls is �(3m)u2=�(3m)((5/3)v)2=4.17v2; so energy would not be conserved. The only way to have both energy and momentum conserved is to have the same number of balls going out as went in.

QUESTION: :
Today in my physics class my teacher explained how a car being pulled by two ropes each having a force of 700 newtons could equal a magnitude of 1000 newtons, he said it had to do with mass and acceleration, i didn't quite understand this though, could you please explain this to me?
ANSWER:
Actually, it has nothing to do with mass and acceleration, it is just addition of vectors. Two guys pulling on two ropes attached to a car, one pulling south with 700 N and the other pulling north with 700 N: no net force, zero. Two guys pulling on two ropes attached to a car, both pulling south with 700 N: a net force of 1400 N south. Two guys pulling on two ropes attached to a car, one pulling southeast with 700 N and the other pulling southwest with 700 N: a net force of 990 N south. In fact, their net force can be anything between 0 and 1400 N.

QUESTION: :
An object is pulled at a constant F. KE0+PE0=0, so W=PE+KE. If there were no friction, the slope of a graph (KE+PE=Y-axis, W=X-axis) would be 1 and the y-intercept would be 0. What would the addition of friction do to the slope and y intercept (would the y intercept be more, less, or equal to 0 and the slope more, less, or equal to 1)
ANSWER:
The energy would still be equal to the work done assuming that the energy of the system is zero at the beginning of the experiment. So, even though the total work being done is both by F and the friction, the graph you describe would still have a slope 1 and an intercept 0.

QUESTION: :
If a charged particle passes close by me, I will experience a magnetic field because of the electric current that the moving charged particle represents. I will also experience a magnetic field because as the charged particle approaches me and then receeds away from me, the electric field stength will change in an inverse square of the distance between myself and the particle. So do I experience two magnetic fileds combined ? or is the magnetic field from the current the exact same thing as the magnetic field from the change in electric field, just by way of a different explanation ? What if the charge is stationary and it's me that's moving ?
ANSWER:
You experience an electromagnetic field. The sources of the magnetic field you experience are both the current density and the time varying electric field. Similarly, the electric field you experience is both from the charge and the time varying magnetic field.

QUESTION: :
According to the twins paradox [Relativity], one of the twins who goes on a space travel at a speed close to that of light, is much younger that his brother who stays back in Earth. Does that mean travelling at a speed close to that of light slows down biological processes also, as aging is a biological process? No virus found in this incoming message.
ANSWER:
All clocks, including biological clocks, slow down.

QUESTION: :
I have read about a theorized elementary particle called the graviton. As I understand, or think i understand, gravity is not a force at all but a result of the warping of spacetime. Am I wrong?
ANSWER:
This has been answered before. See FAQ

QUESTION: .

QUESTION: :
Can the size of a photon be measured and if so, is it bigger or smaller than the electron and positron it is said to be changed into under the proper conditions? Or is the electron emitted larger than the photon from whence it came?
ANSWER:
See an earlier answer.

QUESTION: :
a vertical conducting sheet is permitted to fall under the action of gravity between the poles of a powerful permanent magnet. is the motion of the sheet affected by the presence of the magnet? explain.

ANSWER:
Yes. Eddy currents are induced in the sheet which experience a force (as all currents do) from the magnet. This is used as a means of braking sometimes.

QUESTION: :
What will happen scientifically on 21 dec, 2012?

ANSWER:
See earlier answer.

QUESTION: :
I�m having a problem with the issue of gravity and force and with the issue of what laws of the universe in which I should use. When it comes to the issues of gravity and force, should Newtonian physics be used or should Einstein�s general theory of relativity be used? (Main

QUESTION: I Want Answered: Are the matter of which the inner planets, such as Earth, Venus, and Mercury made of pushed together by Einstein�s space-time curvature or are the matter of which the inner planets, such as Earth, Venus, and Mercury made of pulled together by gravity, which is described as weight or mass times gravity?)
ANSWER:
Newton's universal law of gravitation is what is called an empirical law: it is merely a statement of experimental facts, a mathematical expression of how nature works. What it says is that the force between two objects is proportional to the product of their masses and inversely proportional to the square of their separation. It says nothing about why this force exists or how it is caused. General relativity, the warping of space time by gravitational mass, addresses the why and how

QUESTION: s. For most practical applications like celestial mechanics (calculating how planets move, for example), classical mechanics is just fine. In fact, however, Newtonian gravity is not exactly correct; for example, it fails to predict that light is bent by gravity or that clocks run at different rates in different locations in a gravitational field. One can make corrections for general relativity, but they are usually very small.

QUESTION: :
According to my understanding of mass and gravity, two objects (in a frictionless environment) fall at the same speed regardless of their relative mass. For example, a basketball and a bowling ball dropped from the same height would hit the ground at the same time. My

QUESTION: to you is this: what if you held an object that had the same mass as the earth over the earth? Would that object hit the earth at the same duration as a basketball dropped from the same distance from the hearth? Or would the gravitational pull of the earth-size object pull the earth toward it and half the time they hit each other relative to the basketball?
ANSWER:
Let's talk about what happens. The earth exerts a force on the object which causes it to accelerate toward the earth; because of Newton's third law, the object exerts an equal and opposite force on the earth which causes it to accelerate toward the object. As long as we are talking about objects (like your bowling ball and basketball) which have a mass much smaller than the mass of the earth, the earth, for all intents and purposes, does not actually measurably accelerate toward the ball (because its mass m is big and the force F is small so the acceleratation, F/m, is exceedingly tiny). If you had an object the mass of the earth but the size of a basketball, the earth would accelerate up to meet it and they would meet halfway between. If, however, it was also the size of the earth, it would be a much more complicated problem because the acceleration due to gravity decreases as you go farther away; at a distance one earth radius above the earth's surface, the acceleration due to gravity would be only g/4.

QUESTION: :
Suppose two unlike charges are executing simple harmonic motion with no phase difference b/w them. Will there be a phase difference b/w the EM waves produced by the two charges?
ANSWER:
The electromagnetic waves created by each would be 1800 out of phase because the difference in the charges. Hence, if you were far away (far compared to the distance between them) from these two oscillating charges, you would see no EM waves at all.

QUESTION: :
My teacher says we are able to stand on the ground because of newton's third law i.e. the reaction from the ground balances our weight but we are unable to stand on water or a pool because there is less reaction to balance F=mg.But I don't agree with this.What newton law says is that there must be an equal and opposite force and hence even in the case of standing in water there must be an equal reaction and hence we must stand on water or a pool.But this is not the case.So I am confused with this.Please help me and tell me the reason why we are able to stand on the ground and not on the pool.
ANSWER:
I am sorry but your teacher is not right. The force that the ground exerts on you is not a "reaction force" to your weight. It is a reaction force to the force which your feet exert down on the floor. The reaction force to your weight is the force which you exert on the whole earth because your weight is the force which the whole earth exerts on you. Let us get clear what Newton's third law says: if body A exerts a force on body B, then body B exerts an equal and opposite force on body A. Newton's third law never refers to only forces on a single body, only to forces on two bodies. So, on you, there are only two forces, that which the earth exerts down on you and that which the floor exerts up on you. The reason that you are in equilibrium is because of Newton's first law: if you are at rest, the sum of the forces on you must be zero. Therefore, since you are at rest, the force from the floor must be equal and opposite to your weight. Now suppose that the floor were made of tissue paper. The floor would be incapable of exerting an upward force equal to your weight and so you would not remain in equilibrium. Now suppose that the floor is the surface of a lake. The surface of the lake is apparently incapable of exerting the requisite upward force.

QUESTION: :
We've learned in class that there are several ways in which one can experience weightlessness: during free fall, like jumping off a cliff, in orbit about a planet, going over a hill on a roller coaster or someplace deep in space where the force of gravity is very weak. There is one other place you can be and experience weightlessness. The hint was you don�t have to leave the Earth to find it, but it exists on other planets as well.
ANSWER:
As I always do, I should first remind you that your weight is the force exerted on you by the earth; therefore you are not really weightless during free fall, roller coaster, or in orbit, it just seems that way. Only the situation where you are free of gravitational forces are you actually weightless. I am not sure what your instructor is looking for, but if you could place yourself at the center of the earth you would be truly weightless because there would be no gravitational force on you.

QUESTION: :
why gravitational effects are ignored when considering motion of electrons in electric fields
ANSWER:
Because gravitational forces are insignificantly tiny compared to electric forces. Example: an electron a distance of any distance r from a proton. Gravitational force is Fg=MpMeG/r2 and electrostatic force is Fe=ke2/r2. Hence Fg/Fe=MpMeG/ke2=1.7x10-27x9x10-31x6.67x10-11/(9x109x(1.6x10-16)2)=4.4x10-46.

QUESTION: :
How fast is gravity communicated to the object it is pulling on? For example, I know that the light from the sun takes around 8 minutes to get to the earth. If the sun were to magically "blip" out of existence, would the earth start to fly out of orbit instantaneously, or would it take 8 minutes before it stops being affected by the sun's gravity? Or is there another answer?
ANSWER:
I have previously answered this

QUESTION: .

QUESTION: :
Suppose I had an airtight cylinder filled with water that extended to space. If I placed a bouyant object in the cylinder, would bouyant force propel the object to the top of the cylinder (into space)?
ANSWER:
I don't see why not.

QUESTION: :
Some years ago I have seen an experimental device like a bulb with a shaft in it. This shaft could rotate. When I sent a light beam onto the shaft, it started rotating. Can you explain this? What is the name and where I can find such a device?
ANSWER:
Maybe what you are talking about is a Crookes radiometer. There are lots of places you can buy one; just Google radiometer or physics toys.

QUESTION: :
Why does acceleration due to gravity always remain constant regardless of mass of object falling on earth ????
ANSWER:
See an earlier answer.

QUESTION: :
i know that nothing can travel at or faster than the speed of light. but, just simply why? what equations or whatever says no...
ANSWER:
Because the mass of an object, that is its inertia, increases as the velocity increases. Therefore it gets harder and harder to accelerate it as it goes faster and faster. The expression for the mass of an object m as a function of its velocity v is m=m0/√(1-(v2/c2)) where c is the speed of light and m0 is the mass when it is at rest. Note that as v approaches c, m approaches ∞ so it is impossible to push beyond c. Another way to look at it is from the perspective of energy. The energy of a particle is E=mc2=m0c2/√(1-(v2/c2)), so the energy required to accelerate the mass to the speed of light is infinite and there is not an inifinite amount of energy in the universe.

QUESTION: :
I know that energy is stored in Electric field b/w plates of a capacitor, Is there any energy stored in Electric field of an isolated charge? If yes then where does this energy comes from?
ANSWER:
There are sophisticated mathematical proofs which establish energy density, momentum density, etc. of electric and magnetic fields. But let us be a little less technical. Imagine two point charges on top of each other, one positive and one negative. There is a net charge of zero so there is zero electric field. Now, move them apart and an electric field appears. If you move the negative charge very far away you will eventually be left with the field of the positive point charge and, as you note, this field has energy. But you had to do work on the system in order to move the negative charge away and that work may be thought to now reside in the field. I just made that up, but the point is that it takes energy to create any electric field.

QUESTION: :
I am curious if the earths electro magnetic field has any impact on the moons rotation around earth. if so, what effect? I am under the impression that the earths magnetic field shifts frequently between polarities. if this is so, then would there be any effect on the orbit of the moon either immediately or long term? to summarize further, does the Em force effect G or vise versa? what about strong nuclear and weak nuclear forces? where do these forces come in contact with each other in such a scenario if at all?
ANSWER:
As far as we know, electromagnetism and gravity are independent and do not affect each other. There is no known effect of the earth's magnetic field on the moon.

QUESTION: :
With the theory that the universe started from a single point and thus expanded is there any thought as to where that single point came from it seems the so called 'answer to everything theory' starts just after the creation of the universe, for me if it is agreed the universe started from a singularity then where did it come from.
ANSWER:
This is answered on my FAQ page.

QUESTION: :
How are electrostatic fields set up in space? I believe I understand how to interpret such fields. What I am puzzled by is how they originate or establish themselves, and how they are maintained. Does the boundary of the field propagate at the speed of light? Assuming it does, what is propagated? A wave? Or is it a pulse, as in a 'nothing then something' pulse? Are there particles like photons associated with this propagation? For example, consider the field for a large charged flat sheet. It has the same strength at any distance (less than say the smallest dimension of the sheet), but it must set up some how? I'm puzzled by how. Then once established, what is established? Does a electrostatic field change a region of space for charges that find themselves in that region of space? Also, the presence of a single charge will impact any number of charges that enter the field (superposition), yet its effect on any one charge is not diluted by the presence of others.
ANSWER:
Think of a crack starting at one edge of a frozen lake and propogating across the lake. That is essentially what electric and magnetic fields do but they propogate at the speed of light. So, if you suddenly create an electric charge, the field takes time to establish itself; so, if you were 300 m from where the charge was created, you would not see a field from that charge for 3x102 m/3x108 m/s= 10-6 s=1 μs. To answer the "�once established, what is established"

QUESTION: , a field at some point in space will simply result in an electric charge Q being placed there experiencing a force QE in the direction of the vector E. Now, are they simple mathematical constructs to help us visualize forces or, as you ask, do they actually exist in the space where we visualize them? I believe that the view that they are just a construct is wrong because an electric field has an energy density, so energy resides where electric or magnetic fields reside.

QUESTION: :
Why does the mass of a particle increase as its speed approaches the speed of light? And how does this relate to the equation E=mc2?
ANSWER:
The reason that mass increases is discussed in an earlier answer. In a nutshell, it is because we need to redefine linear momentum (mass times velocity in classical physics) so that momentum is conserved for an isolated system. This results in mass increasing as speed increases but faster than the rate the speed is increasing. The mass may be written as m=m0/√(1-v2/c2). Since this quantity becomes infinite as v approaches c, the energy required to accelerate something to the speed of light is infinite, obviously impossible. The total energy of a particle with speed v is mc2 where m is as given above. See another earlier answer for more detail on E=mc2.

QUESTION: :
why does earth has magnetic poles? is it just a point or certain area? what caused it to occur?
ANSWER:
The origin of the earth's magnetic field is rather complicated. Essentially there is a portion of the earth's core which is molten iron which is ionized. The magnetic field is generated by convective motion of the electric charges in this ionized liquid and energy is supplied by various sources including radioactive decay of heavy elements. I recommend that you read the Wikepedia article on dynamo theory.
FOLLOWUP

QUESTION: :
well i know about dynamo convection theory... but dont know much about magnetic poles... how and why does the magnetic poles exist?
ANSWER:
Well, a magnetic pole is actually more or less a qualitative construct. If you have a region of space where magnetic field lines are coming out it is a north pole; if the field lines are going in it is called a south pole. Actually, the earth's north geographic pole is a south magnetic pole and vice versa. So, these two pictures show the poles of the earth and a bar magnet. The precise location of the earth's magnetic pole is determined by where the field lines come in (or go out) vertically. One important concept about magnetic poles is that they never exist alone, that is you will never find an isolated magnetic pole.

QUESTION: :
If heat causes most materials to expand, why do certain clothes shrink when put in the dryer?
ANSWER:
Obviously, shrinkage has nothing to do with thermal expansion since the clothes do not return to their original size when they cool down. So, we are really out of the realm of physics. What happens is that cotton contains quite a lot of cellulose and celluose is very good at soaking up water. But if the water is removed very quickly, the cellulose fibers become considerably shorter than they were, causing the whole garment to become smaller. It is usually possible, by rewetting the garment, stretching it, and drying it slowly, to reverse shrinkage.

QUESTION: :
I want to know what actually electricity is? Is it flow of electrons or just the electrons vibrate. If its of wave form then whats the need of free electrons , even electrons in shell may vibrate and pass the energy. And also what exactly is resistance, i thought resistance is obstacle which reduces amount of current as it passes throught it, but i find current remains constant, and instead it affects the circuit as a whole, How ?? And when current remains same then in what form energy is consumed by resistance like when it generates heat or any way ???
ANSWER:
In a conductor, some electrons are pretty easy to move (called conduction electrons). When a potential difference is applied across the ends of the conductor it causes an electric field in the conductor which, if the electrons were perfectly free, would cause them to accelerate from one end to the other; in that case, all the energy available from the power source would be converted into the kinetic energy of the electrons. However, each electron, when it starts to accelerate, quickly collides with one of the atoms in the material and loses the energy it just gained and the atom gets that energy. So the effect of the electric field on the electrons is start-stop-start-stop-start-stop. There is a net flow of electrons (that's the current) but on average there is no acceleration, just a slow drift of electrons opposite the direction of the field. Each collision gives an atom some added energy so the material heats up due to the motion of the electrons (that's ohmic heating, resistance).

QUESTION: :
Why is "back and forth" considered a different dimension than "side to side"? If you are on a sphere (i.e. Earth), aren't they really the same thing, depending on your perspective? If not, then why isn't "diagonal" considered a different dimension?
ANSWER:
There is no difference if you are on a sphere which is not rotating. However, if it rotates, you are in an accelerating frame of reference and Newton's laws do not work in accelerating frames. A rotating system is a particularly complicated system to analyze, but we usually do that by introducing "fictitious forces" which, when added, allow us to use Newton's laws; fictitious forces you may have heard of are centrifugal force and coriollis force. These "forces" depend on the direction of the angular velocity of the sphere and also on the direction of the velocity of the particle you are analyzing. I wouldn't say they are "differrent dimensions", rather that the dynamics depends on the direction something moves.

QUESTION: :
I have recently been pondering the potential benefits of quantum entanglement. Basically, after knowing just a little about the phenomenon, I thought that it might be possible to transfer classical information at faster-than-light speed (actually, maybe even at "immediate speed"). After doing a simple thought experiment I confused myself and now I am unclear as to whether or not it is actually possible. The way I had setup my thought experiment is this: 1. Entangle two pairs of particles. 2. Send 1 particle from each pair to Pluto (obviously, this part will take a long time). 3. If you want to communicate a "0" value for a classical bit, measure your two particles on Earth along some axis A. Else, you want to communicate a "1" value for a classical bit, so measure your two particles on Earth along some perpendicular axis B. 4. Now this is the part I am confused on -- is there some way to measure the two particles on Pluto in such a way that results in knowing whether or not a "0" or "1" was intended? I thought maybe you could measure one Pluto particle along axis A and the other Pluto particle along axis B.... In any case, I really just wanted to know if any kind of real faster-than-light communication can be achieved using quantum phenomena.
ANSWER:
Here is the problem with your scheme: Your measuring device must define a preferred axis. The usual discussion of entanglement assumes the first device makes a measurement and thus "puts" the first particle in either an up or a down state thereby putting the second particle into a down or up respectively state. The second observer, orienting his apparatus similarly to yours (which I will call "vertical" since I have called states up/down) can verify that this is true. But, suppose that the second observer orients his device horizontally instead of vertically. Then his measurement will either put the second particle in either the right or left state, each with 50% probability. If you think carefully about the logic of what I have said, you will see that it is not possible to determine the direction of the spin of the second particle even though you can verify its direction if you know the orientation of the first instrument. Thus, your scheme fails since you cannot tell which direction the second spin points, horizontally or vertically. Thanks to M. M. Duncan who helped me understand this situation.

QUESTION: :
While dealing with induced emf why do we always take the example of a coil ? Is no emf induced in a straight wire? why? Is self induction only the property of a coil and not a straight wire why?
ANSWER:
Any area through which a changing magnetic flux passes has an induced EMF around its edge. A long straight wire does not define an area and therefore cannot have any flux through it. If a straight wire moves through a magnetic field (with a component of its velocity perpendicular to the field) there will be an induced EMF between its ends because it "sweeps out flux". However, a changing current in a long straight wire can induce an EMF around an area through which the flux passes, for example an area in a plane which the wire is in. A long straight wire cannot have self inductance for the reason stated above: there is no defined area around through which a flux could pass.

QUESTION: :
I have been reading up on the photoelectric effect and I have a couple of

QUESTION: s: (1) I understand that the cutoff frequency of incident light (below which no photoelectrons are emitted) occurs because not enough energy can be imparted to electrons by low-frequency photons for the electron to overcome the work function of the metal. However, could a given electron absorb successive photons and in that way build up enough energy, or will the photon typically be re-emitted before the electron can absorb another? (2) Electrons bound in atoms can only absorb photons with appropriate energies (frequencies). Can free electrons (e.g. in a metal or plasma) absorb photons of any energy?
ANSWER:
(1) See an earlier answer about multiphoton ionization. (2) Bound electrons can also absorb photons with any energy above the ionization potential (the amount of energy necessary to remove the electron from the atom. Indeed, free electrons can absorb any energy. In a metal where the conduction electrons are essentially free, most if not all the photoelectrons are from conduction electrons.

QUESTION: :
what would happen if earth stopped rotating and if its axis were perpendicular to its orbit
ANSWER:
The length of a day would become one year, a half year of light and a half year of dark. This would play havoc with weather. If the earth were not rotating, then it would not have an axis.

QUESTION: :
why there is no effect of gravity in the motion of gas particles?
ANSWER:
There is. If not for gravity, there would be no atmosphere since all gas molecules would just zip off into space. See a recent answer to a related

QUESTION: .

QUESTION: :
I have a few

QUESTION: s relating to matter and antimatter. 1. I know that if matter comes into contact with antimatter, they are both annihilated. What if an antimatter element with a low mass such as hydrogen comes into contact with a matter element with a larger mass such as gold. Would the difference between the electrons and positrons, protons and antiprotons, and neutrons and antineutrons still remain or would the entire atom be annihilated? 2. If the above scenario can happen, what happens to the remaining particles? Will they annihilate with their opposites if they come into contact with an atom? 3. If combining matter and antimatter creates nothing, then could you create matter and antimatter from nothing?
ANSWER:
First of all, as far as I know hydrogen is the only antimatter atom which has been made; because of the predominance of matter, it is extraordinarily hard to manipulate antiprotons, antineutrons, and positrons. If you did have, say, an oxygen atom and an oxygen "anti-atom", positrons and electrons, neutrons and antineutrons, and protons and antiprotons would interact pairwise. (Other interactions besides "annihilation" occur leaving some residual particles and/or antiparticles; the possibilities are very many.) Regarding "annihilation" (which I take to mean the disappearance of the pair with no mass present after the interaction), you do not have "nothing" afterwards, but a pair of photons; energy must always be conserved and so the energy after the annihilation of each photon is the rest mass energy of an electron (for electron-positron annihilation).

QUESTION: :
My

QUESTION: involves the position of the stars in the night sky. Is there a way of working out the ACTUAL current position of very distant stars and galaxies? I'll explain what I mean: We are told that when we look at the most distant objects in the universe; right at "the edge of the observable universe" then we are seeing those objects as they were 13bn or so years ago. We are presumably seeing where they WERE 13bn years ago too, so where would they be today? In my thought experiments on this subject I imagine objects much further away than they appear and I would also expect them to be shifted in all 3 dimensions. IE if an object appears to be directly in front of me, then it's real position could well be many degrees up and to the right, or possibly even in the complete opposite direction, if it's moving fast enough. Ok, I understand that many of the stars we can see are no longer with us but it would still dramatically change a map of the skies if the 'current' positions of celestial bodies were mapped.
ANSWER:
There is no way to know where distant stars are "right now" because special relativity forbids information being transmitted at faster than the speed of light.

QUESTION: :
Ok, I understand "knowing exactly" but surely if you know where they were, roughly when it was, what direction they were travelling and how fast, it could be estimated quite accurately I would have thought...
ANSWER:
If you assume that you understand all the forces which act on those stars (including "dark matter" and "dark energy"), and if you assume you know all forces from its neighbors which you do understand, including those neighbors that you cannot see because they are too far away, you could do a calculation to predict where they would be "today". Don't forget that for the more distant objects you will have to know how to calculate all these forces over a time of billions of years.

QUESTION: :
Are all isotopes of iron magnetic or has nobody ever performed experiments upon the isolated isotopes to find out?
ANSWER:
Ferromagnetism is an atomic, not nuclear, effect and all isotopes of iron are ferromagnetic.

QUESTION: :
Does gravity effect a magnetic field?
ANSWER:
Not that we know of, but the relationship (if any) between gravity and electromagnetism is not well understood.

QUESTION: :
Can you settle an argument raging between physics teachers? When a capacitor is charged by a battery in a series R-C circuit, how much energy is 'lost' during the charging process? Some say 'always 50%', some say 'less' and some say 'none'.
ANSWER:
At the end of the charging process (technically infinite time, but for practical purposes much greater than RC), the voltage across the capacitor will equal V, the voltage of the battery, since no current is flowing. The energy stored in the capacitor is therefore �CV2. During the charging process, the current through the resistor is given by i=(V/R)e-(t/RC) so the instantaneous power loss in the resistor is i2R=(V2/R)e-(2t/RC). If you integrate the power from t=0 to ∞ you will find the energy lost to ohmic heating in the resistor is �CV2. So, exactly the same energy stored in the capacitor is dissipated in the resistor. Hence, since the battery is the only energy source, half the energy supplied is lost.

QUESTION: : ;
earth is a magnet in rotation if so by faradays laws it must induce current on all metallic objects on earth is this possible and deductable???
ANSWER:
But objects on earth rotate with it and so the field they see is constant.

QUESTION: :
Law of conservation of Linear Momentum states that the total Momentum of the system remains constant provided no external force acts on the system. Which forces can be regarded as external, is Friction an external force ?
ANSWER:
Friction between pieces of the system does not affect momentum conservation. But friction from an external agent would be external and cause momentum to be not conserved. One simple example: a 1 kg mass sliding on a floor with a speed of 1 m/s. Then the momentum right now is 1 kg m/s. But, if there is friction between the floor and the mass, it will be slowing down, that is losing momentum. Another example: a block of mass 1 kg sitting on a floor with friction is struck by a bullet of mass 1 gram going with a speed of 1000 m/s which lodges in the block. This is a

QUESTION: you often see in books and you are asked to find out how fast the block/bullet are going immediately after the collision using momentum conservation. However, momentum is not actually conserved because the bullet takes some short time to come to rest in the block and during that time the block is sliding (with friction). The reason it works (approximately) is that the time is very short and therefore the impulse (approximately the sliding friction force times the time of the collision) is very small.

QUESTION: :
I have internet WiFi set up in my house, because I have two different computers in different rooms. The wireless router and the wirelessly-connected computer both use dipole antennas, operating on a frequency range of 2.4210 Ghz to 2.4835 Ghz. This system is put together using common components from the local big box store. I�ve discovered a few web sites that show how to increase the range and signal strength by making and installing a parabolic trough reflector at one or more of the dipole antennas, constructed using cardboard and aluminum foil. In the case of parabolic dish reflectors (like the satellite TV dishes), there is apparently an optimum ratio of f/D, which is the focal distance divided by the diameter. This ratio, of course, defines the how "fat" or "thin" the parabola looks. In my application, is there an optimum shape of the trough parabola?
ANSWER:
The parabola has a focus but D is not a useful concept. The advantage of a parabola is that if a source is located at the focus the rays all come out parallel to each other. In essence, instead of spreading in all directions the waves come out in one direction. However, it will not be perfect and the main effect is probably to take waves which would have gone out away from the house and put them into the house. The equation of a parabola, y=ax2, tells you the "fat/thin" you want to know; the larger a, the "thinner" the parabola. You can't use a simple D because where you cut off the parabola is arbitrary. If the thing worked ideally (which it won't), the thinner the parabola, the narrower the output beam so you would have to "aim" very carefully at the other computer. Here is a great opportunity to experiment with different shapes to see which suits your purpose best. I would guess that the improvement, if any, would not be very dependent on the detailed shape and that a cylindrical reflector would work just as well in this application.

QUESTION: :
I recently read an article about new imaging of atoms and molecules using extremely brief pulses of electrons. This made me wonder where do these researchers get electrons, like what process? And then how is it possible to capture something so small as an electron and then control it?
ANSWER:
Electrons are very easy to get. If you have a wire and heat it up red hot in a vacuum, electrons will stream from it. This is how old-fashioned TV sets worked (cathode ray tubes) with a filament as a source of electrons. Once you get electrons, they are easy to manipulate with electric and magnetic fields.

QUESTION: :
Suppose a ball is spinning at a rate at which the surface is moving at the speed of light. Now what would happen if giant rod was attached to the surface of the ball. Would the end of the rod be moving faster than the speed of light since it would be covering more distance at the same time as the surface of the ball as the ball spins?
ANSWER:
First of all, groundrules forbid

QUESTION: s assuming something goes the speed of light. Trying to rotate a rod such that the end moves faster than the speed of light is futile. The rod could not be strong enough to compensate for the fact that the mass increases with velocity. Also, you could not get the information to the other end of the rod that you were trying to rotate it more quickly than at the speed of light (see earlier answer).

QUESTION: :
why two objects of different masses reach the ground at the same time? and what are the factors that affect their motion?
ANSWER:
The motion of a mass is determined by Newton's second law, F=ma where F is the net force on the mass, m is the mass, and a is the acceleration of the mass. A mass in free fall (no air friction) has only one force on it, its own weight which is the force with which the earth pulls on it. It turns out that the weight is proportional to the mass, that is W=mg where g is a proportionality constant called the acceleration due to gravity. So, if you have two masses, m and M you can calculate their accelerations, a and A respectively.Therefore A=W/M=g and a=W/m=g; since a=A the two fall identically. (You can see why g is called the acceleration due to gravity.)

QUESTION: :
I know that Kinetic energy and Momentum are related to each other. I have read that in every collision momentum is conserved but K.E may or may not be conserved.How is it possible ?
ANSWER:
While it is true that kinetic energy and linear momentum each depend on each mass and velocity, they are different quantities and one can change while the other does not. To determine whether momentum and/or energy are conserved, you must know the physical conditions for conservation: if there are no external forces on the system, linear momentum remains constant; if there are no external forces doing work on the system, energy remains constant. Also, techincally, if you know the kinetic energy you cannot calculate the linear momentum because energy is a scalar and momentum is a vector (although you can calculate the magnitude of the momentum).

QUESTION: :
When a radio signal is sent between two points, by what means is the actual energy conveyed? Are areas of electron density occurring between the points (matter waves?)? Radio is part of the electromagnetic spectrum, so might they be photons instead? I ask because I understand how signals are sent, but I just thought about it a day or two ago and realized that I actually don�t know the communicating force. Yipe!
ANSWER:
Read an earlier answer about electromagnetic waves. Since changing electric fields cause magnetic fields and changing magnetic fields cause electric fields (again, see an earlier answer), the wave is self sustaining, no "force" or medium is required for its transmission. And, yes, electromagnetic waves may always be thought of as photons.

QUESTION: :
How much does a gas compress under its own weight? For example, does a container 100m tall of xenon (a heavy gas) have a greater pressure/density at the bottom than a 100m tall container of helium ( a much lighter gas)? Thanks for your help.
ANSWER:
I do not want to get quantitative here by answering the "how much" part; that does not have much general interest. Certainly a gas is compressed because of the weight of the gas above it. That is why the atmospheric pressure gets smaller as we go up in altitude. And, a vessel of any height will have a higher pressure at the bottom than the top for this reason. The weight of the gas will certainly make a difference and if your xenon and helium have equal numbers of atoms in identical containers, the pressure at the bottom of the xenon container will be greater.

QUESTION: :
how do physicists come up with equations? i know that may sound vague, but i was watching a program on Einstein coming up with his equations, and the program said things like "he would sit and come up with equations". i know it sounds like a stupid

QUESTION: , but I am really interested in physics. I am currently a sophomore in college majoring in Biomedical/ Mechanical engineering, and am thinking about minoring in physics. I've been really interested in physics for a while, and I've noticed that I can think in terms of physics to do better in my mechanical lab/ design classes. So I guess what I'm asking is this: What books are there out there on how to come up with equations to model phenomena with math/ physics equations?
ANSWER:
A

QUESTION: of this kind essentially reveals that the

QUESTION: er does not understand what science is. Knowing equations is not what matters. What matters are basic fundamental ideas or principles from which equations emerge naturally. Here is a general example. Einstein most certainly did not one day, by some insight, say to himself "aha, E=mc2!" What he did was get the idea one day that the laws of physics must be the same for any observer in our universe and that the speed of light was the same for all observers. Starting with no more than these basic principles and a knowledge of classical physics, he was able to write all the equations of the theory of special relativity, including the biggie above, by just doing the basic mathematics and physics. Equations are the end, not the beginning, of a theory; you "come up with" principles, not equations.

QUESTION: :
Hydrogen is the most abundant element in the universe. A star, such as the sun in our solar system can produce all of the naturally occurring elements on the periodic table. Are all of the naturally occurring elements on the periodic table created by adding hydrogen atoms together under extreme temperatures and extreme pressures? (Ex: 1 hydrogen atom equals hydrogen, 2 hydrogen atoms added together equals helium, 3 hydrogen atoms added together equals lithium, and so on.)
ANSWER:
Starting with hydrogen, stars fuse nuclei together to get heavier elements, but not all heavier elements. The net effect is to make helium from two hydrogen, but the process is a little circuitous. Heavier elements are made by fusing lighter elements, but not three hydrogen for a lithium, rather something like a helium and a hydrogen; for example, see this link to see how carbon, oxygen, and nitrogen are made.. After iron, energy is lost when fusion to heavier nuclei occurs so it will not happen. The elements heavier than iron are made when the star explodes (supernova) and the energy from the explosion can be used to fuse heavier elements.

QUESTION: :
Is there a mechanism that create Hydrogen? It seems to me that over billions of yrs all of the H would be burned up in stars. Where does it get converted back to H after its been used up???
ANSWER:
This is the nature of our universe. When all the hydrogen is burnt up (that is, converted to heavier elements), that will be the end. After more than 14 billion years, there is still quite a bit left.

QUESTION: :
Can radioactive material such as Plutonium be used to generate electricity in the same fashion as electromagnetics? It just seems archaic to use nuclear material to heat water and so forth as is currently done in reactors.
ANSWER:
But, heat is mainly where the energy from fission ends up (kinetic energy of fission products), so it is perfectly reasonable to use it to heat water.

QUESTION: :
A geostationary orbit of any diameter above earth would have variable speeds but the time completed of any geostationary orbit would be relative to a 24 hour period on earth. Even if the orbit were 2 light years, the geostationary object would complete 2 light years in 24 hours time, the exact same as a 50 thousand mile geostationary orbit.. This seems to violate what I know about Time dilation. What am I missing? It seems impossible but all I would need is a long enough hypothetical pole and I could violate the laws of physics (as I know them). I'm sorry if this

QUESTION: is too elementary and I'm missing something very obvious but I have searched and searched for this answer and I just cannot understand enough physics vernacular to find a simple answer to this.
ANSWER:
There is only one geostationary orbit with a particular radius (about six and a half earth radii). See satellites here.

QUESTION: :
An astronaut steps away from the shuttle in orbit and activates a retro fuel source to begin re-entry. Before entering the atmosphere, a parachute is deployed.

QUESTION: is: as air molecules begin to inflate the shute, is it possible to realize a gentle re-entry into the atmosphere and to the Earth's surface?
ANSWER:
I don't really know. You have to realize that he is going at a tremendously fast speed (like 18,000 miles/hr) and the parachute would probably not slow him enough before the air density got big enough to burn him up. Perhaps with a well-designed parachute it could be accomplished.

QUESTION: :
one section in my ice cube tray formed a 'mountain' of ice. it stands 9mm above the surface of all the other cubes. in that there is no water source to this economy fridge and water [to my knowledge] does not flow uphill, how is this possible?
ANSWER:
I have previously answered this

QUESTION: .

QUESTION: :
I am studying circular motion, and I understand when something is swinging in a circle when attached to a string or rope that is above it, say attached to a ceiling. The gravitational force equals the y component of the tension, and you can set the equation for the centripetal force equal to the x component of the tension. Find both tension in the x and y directions, and you can solve for the vector tension. What is not so clear to me is when you are swinging something over head and the object is above the string or rope. I came across a problem in my text that has a ball being swung above your head such that the string made a 14 degree angle with the vertical. So instead of the string being hung from somewhere and the object attached to it being below it, the object is now above the string. I hope my description makes sense. Anyway, in the solution, it says that the tension in the y direction is equal to the force of gravity, mg. But wouldn't the tension in the y direction plus mg be equal to ma in the y direction?
ANSWER:
After pondering your

QUESTION: for a while, it just occurs to me that maybe you are talking about the conical pendulum where the string traces out a cone and the object moves in a horizontal plane. For your second part, you cannot have a conical pendulum with a string, it has to be a stick. Then the stick would have to exert a force on the object which has vertical component up and equal to the weight to keep it moving in a horizontal plane; a string, which can only pull along its own length, could not do this. For your first (below support) problem, there is a unique solution. For the second (above support) problem, you cannot find the speed and the "tension" because the force the stick exerts will not be along its own length. So, presumably, the second problem asks you to find the force the stick exerts on the object for a certain speed.

QUESTION: :
I understand that gravity slows down time. So this had me thinking. What would the speed of time be like in the absolute middle of dead space (no matter whatsoever) compared to time on Earth? Would it be so fast that it would almost be like it was infinite? (I don�t know if that makes sense�) Would that be an absolute reference point for time? I can�t seem to find any answers, so thanks for your website and in advance for the consideration of this

QUESTION: .
ANSWER:
The effect of gravity is very small, at least gravity in the vicinity of something of the size of the earth or the sun. So going to empty space (there is no such thing, of course) would have little effect on rate of time.

QUESTION: :
The force of gravity between two objects gets weaker as the distance between them increases. Why is it more correct to say the square of the distance?
ANSWER:
I wouldn't call it "more correct", I would call it more quantitative. The first statement is a qualitative statement which tells you it gets weaker. The second statement is a quantitative statement which tells you how much weaker it gets; e.g., if you double the distance you quarter the force.

QUESTION: :
I seem to remember a law of physics from high school about the collision of two objects with the same mass and density which says something along the lines that the one traveling at the higher velocity will break the other one. Do I have this right or even close? What is the name of the law?
ANSWER:
There cannot be any such law for more than one reason. First, the conditions for breaking depend on properties of the object other than its mass or its density; for instance, a glass ball would be more likely to break than a steel ball and not because of any density difference. Second, there is no physical difference whether ball A strikes ball B at rest or vice versa. All that matters is the relative velocity.

QUESTION: :
If a horse pulls on a calesa at rest, the calesa pulls back equally as much on the horsse. Will the calesa be set into motion?
ANSWER:
I learned a new word�calesa; never knew that word before. Anyhow, what determines how an object moves is the forces on it, not the forces by it. Therefore if there is not some other force in the horizontal direction (like maybe friction from brakes being set), the calesa will accelerate in the direction the horse is pulling. What the calesa does to the horse is irrelevant in the motion of the calesa.

QUESTION: :
A hammer falls off a rooftop and strikes the ground with a certain KE. If it fell from a roof that was four times higher how would its KE of impact compare?its speed of impact?
ANSWER:
Since gravitational potential energy is proportional to height, it would have four times the kinetic energy. However, since kinetic energy is proportional to the square of the speed, the speed would only be twice as great.

QUESTION: :
If you accelerate at a constant 1G, how long would your trip last ship time, for 100 years to pass on earth?
ANSWER:
As I explained in an earlier answer, constant acceleration is not possible in special relativity.

QUESTION: :
If all objects are attracted by the force of Gravity to the center of the earth, why aren't air moloculesd sucked down to the floor?
ANSWER:
They are, but they don't just go there and stay. Since the molecules are flying around with large velocities because of their temperature, they don't all just lie on the floor. However, there are more near the floor than there are near the ceiling. And, the higher you go, the fewer and fewer there are and eventually there are none�space. If there were no gravity at all, the air would all eventually leak out into space.

QUESTION: :
When you're riding in an elevator (or the space shuttle) you're accelerating away from the center of the earth. Gravity accelerates you toward the center of the earth. Acceleration is a vector quantity. So, why, when you're accelerating up at 9.8 m/s^2 do you feel 2g instead of 0g?
ANSWER:
The way we do this kind of problem is to use Newton's second law (N2). When you are in an elevator, what forces are there on you? Only two, your weight mg, straight down and some force F which the floor of the elevator exerts up on you. N2 says that the total force on you equals your mass m times your acceleration a, so F-mg=ma. If a=g, then F=2mg. Since F is how you judge your apparent weight, you feel twice as heavy as usual.

QUESTION: :
What causes the creation of plasma? Is it two or more nuclei being slammed together and heated to more than 200,000,000 degrees Fahrenheit or is it something else?
ANSWER:
If you have a solid and heat it, it eventually becomes liquid. If you have a liquid and heat it, it eventually becomes gas. If you have a gas and heat it, it eventually becomes a plasma; to create a plasma, the average kinetic energy per atom must be larger than the ionization energy of the atom so that an inelastic collision can result in the removal of an electron from the atom.

QUESTION: :
With all the hassle that has been lately around 2012 - the end of mankind, I'm intrigated by the subject. I'm quite curios what is your scientific opinion regarding this subject: Will it be 2012 the end of mankind ? If yes why ? If not why ?
ANSWER:
My scientific opinion is that it is astrological nonsense. See my earlier answer.

QUESTION: :
I�m having a problem determining the difference between Nuclear Fusion and Nuclear Fission. Listed below are some information that I�ve found. Could you clarify the major differences between the two, especially when it comes to matter that is heavier or lighter? Nuclear fusion - is the process by which multiple like-charged atomic nuclei (two or more joined together) join together to form a heavier nucleus. It is accompanied by the release or absorption of energy, which allows matter to enter into a plasma state. Nuclear fission - is a nuclear reaction in which the nucleus of an atom splits into smaller parts, often producing free neutrons and lighter nuclei, which may eventually produce photons (in the form of gamma rays).
ANSWER:
The important concept here is that if you find a reaction which results in less mass after the reaction than before the reaction, you will release energy because E=mc2 and energy is conserved in an isolated reaction. Hence, if you lose mass, that energy must appear elsewhere. Where it usually appears is in kinetic energy, that is thermal energy of the reaction products. Iron is the most tightly bound nucleus, that is the mass of the average nucleon (a nucleon is a generic term for neutron or proton) is smallest. As shown in the figure, average nucleon mass steadily increases if you get heavier or lighter than iron. Hence, splitting a nucleus twice the size of iron or heavier results in mass loss and therefore energy gain; this is called fission. Similarly, fusing two nuclei half the size of iron or smaller results in mass loss and therefore energy gain; this is called fusion. Fusion is the source of energy for stars and hydrogen bombs. Fission is the source of energy for nuclear power plants and conventional nuclear bombs.

QUESTION: :
Can you please explain how physics is used with character animation and animated films (disney, pixar, etc)? I am just wondering as I want to be an animator, but am struggling with physics.
ANSWER:
The object (one, anyway) of animations is to make the scenes look real, believable. So description of motion (kinematics) is important to understand, I would think. The way things move and respond to forces in the real world is determined by the laws of physics and therefore those same laws apply to a simulated real world (animation).

QUESTION: :
I read an answer of yours that ended with "Because water is essentially incompressible, the density of the water does not change as you go deeper and therefore there would be no depth at which a sinking object would stop sinking." I've never really thought about it, but now I'm wondering "If not from density, where does the increasing pressure (like what you feel in your ears) come from?"
ANSWER:
The pressure in a fluid is due to the weight of all the fluid above it. Atmospheric pressure in the air is due to the weight of all the air above it; because air is compressible, the higher the pressure, the higher the density. Similarly, deep under water the high pressure is due to the weight of all the water above you and the deeper you go the bigger it gets; however, since water is essentially incompressible, the increased pressure does not result in increased density.

QUESTION: :
Once an artificial satellite is placed in orbit above Mars it stays in orbit, why does this happen or does it simply follow the same principles that apply to it for staying in orbit above earth?
ANSWER:
The laws of physics are exactly the same in the vicinity of Mars as they are on earth. The mass of Mars is different and so the periods of stationary orbits will differ from what they would be around earth, but it is all determined by classical gravitation and classical mechanics. Mars has two natural moons as well, Phobos and Deimos.

QUESTION: :
I am a high school physics teacher and am having some difficulty with part of the Compton Effect. I am trying to come to grips with whether the collision between the x-ray and the electron is elastic or inelastic? From what I have been able to find on the subject, when the x-ray collides with the 'whole' atom it results in an elastic collision and the x-ray leaves with the same frequency with which it came in with. On the other hand, when the x-ray collides with something closer to its own mass (an electron), it results in an inelastic collision and the x-ray is ejected with a lower frequency and energy. Any help you could provide would be greatly appreciated. I hate to think that I am not teaching it correctly and sending my students out into the world with misconceptions imparted to them by me.
ANSWER:
The Compton effect is elastic scattering of photons from some mass. Elastic does not mean that the energy of the incoming particle remains constant, it means that the sum of the energies of the incoming particle and the target remain constant. Assuming the target is at rest before the collision, after the collision it will recoil and carry away some of the energy which the photon brought in and the only place it can get this energy is from the photon. It is maybe easier to see this by thinking about classical particles. If a BB (photon) hits a bowling ball (whole atom), the bowling ball is almost at rest after being hit and therefore the BB has approximately the same energy (and speed) after the collision. If the BB (photon) hits a marble (electron), the marble will be moving after the collision so the BB must have lost energy (and speed). Both processes are elastic. An inelastic collision is one in which the total energy before and after are not equal.

QUESTION: :
why do you hear your friends talking in he hallway even though you can't see them around a corner?
ANSWER:
Two reasons: reflection of sound from walls and diffraction of sound around the corner. See this link for more details.

QUESTION: :
I am curious about something that I just read in an earth science book about the shape of the Earth. Since the polar circumference is less than the equatorial circumference, the Earth is an oblate spheroid. The authors attribute this shape to centrifugal force caused by the Earth's acceleration. However, I thought that centrifugal force was not a real force, but was instead due to a mass's inertia resisting the acceleration. Am I misunderstanding the concept? Thanks for helping me resolve this conundrum.
ANSWER:
(This is sort of a long-winded answer, but I want to have an explanation of centrifugal and fictitious forces I can later refer to.) Centrifugal force is what we call a fictitious force. In an accelerating system, Newton's laws are not true. For example, if you are inside a big rotating drum you feel a force pushing you into the wall, right? Well, actually you do not; what you feel is the wall pushing you toward the axis of the drum. Your brain is trained mostly in nonaccelerating systems (moving with constant velocity) and so it wants to use Newton's first law which says that if an object is at rest the forces on it must add to zero; to make Newton's first law true (you are at rest in your system which is accelerating), your brain invents a force equal and opposite the centripetal force. This is called the centrifugal force and it does not really exist. A fictitious force is one we invent to force Newton's laws to be true in an accelerating system. Just because it does not exist does not mean that we cannot do physics with Newton's laws using it. If the accelerating system is a centrifuge, it works, doesn't it? The heaviest stuff is "pushed out" by the centrifugal force is true even if centrifugal force is just something we made up to make calculations easier. The rotating fluid earth is a little complicated, but I think that it is pretty intuitive: a ball of putty (or pizza dough) made to rotate faster and faster will stretch out into a pancake and you can say it is the centrifugal force which is causing it. A simpler case of "centrifugal stretching" is the following. A spring is attached to a nail at one end and a mass at the other. If you make it rotate about the nail, the spring will stretch out just the right amount so that the force of the spring will provide the necessary centripetal force. But if you make it go faster, a larger force will be required and so the spring will have to stretch more to do that. That example is easy to see without centrifugal force, but if you view it from the perspective of the rotating mass, you will say the centrifugal force pushes you out.

QUESTION: :
I would like to know if the protons and neutrons of metals such as nickel move about and vibrate relative to each other, or to they stay put (relative to each other)--while the atom vibrates and moves based on heat, chemical and magnetic affects, and other factors. If no one knows the answer to my

QUESTION: , if it's not known by the scientific community, then this is okay. Just say, "no one knows...the models we have today don't tell us."
ANSWER:
If you mean do the atomic nuclei (wherein reside all the protons and neutrons) move in response to the actions you note, then, yes, absolutely.

QUESTION: :
More quantum entanglement! The measurement of one side of the pair is said to "put" the other one into the same state (say spin up or spin down). But I don't see that the spin being indeterminate (prior to a measurement) prohibits the entangled pair from having "synchronized" spins, that occurred at the event that produced the entangled pair. How do we know that is not the case as opposed to the "put" action at a distance?
ANSWER:
I think you have the idea right. The use of the word "put" seems to be bothering you. The point is that the "entangled" particles are just that, what one "is" is determined by what the other "is"; call that "synchronized" if you wish. The pair is really a single system so making a measurement on one "collapses" the system to the required "synchronized" state.

QUESTION: :
I noted in some physics books that centrepital acceleration is inversely proportional to R (radius) while in others (and sometimes in the same text) that it is directly proportional to R. In the first case the book uses (a=v2/R) while in the second case the book refers to the formual (a=w2R). I feel something is wrong in this logic, as what relates a to v and R is basicaly a definition of the centrepital accelelration. Can you help?
ANSWER:
The "catch" here is that both velocity (v) and angular velocity (ω) depend on R, v=Rω. So the two equations you quote are the same: a=v2/R=(Rω)2/R=Rω2. It is incorrect, therefore, to say that the centripetal acceleration is proportional to R (or 1/R) unless ω (or v) is constant.

QUESTION: :
why is current a qualitative concept
ANSWER:
Do you mean electric current? It is not a qualitative concept. Electric current is the amount of electric charge per unit time. 1 Ampere=1 Coulomb/second.

QUESTION: :
My

QUESTION: is about Vacuum. it is the absence or air or any matter? there is a vacuum particule or something like that?
ANSWER:
Normally vacuum refers to a volume from which all gas has been removed. If there is a solid object inside this volume, we would still say there is a vacuum but the object would not be part of it. There is nothing called a vacuum particle. However, our modern understanding of a vacuum is that there are virtual particles (like particle-antiparticle pairs) popping into and out of existence, existing only for as short a time as allowed by the uncertainty principle; this is referred to as vacuum polarization. So, in some sense, there is really no such thing as a completely empty space. Maybe you have heard the old saying "nature abhors a vacuum".

QUESTION: :
I was standing at the bottom of the stairs in my house (which has a downstairs and upstairs heating zone) and felt cold air gently falling down from above (we have not yet turned on the upstairs heating zone). Then I thought of the phrase "hot air rises" and it did not ring true. Almost the opposite! Cold air "sinks". I was wondering if the answer really had to do with the idea of displacement instead of convection.
ANSWER:
This sounds more like an issue of semantics than of physics. Warm air rising displaces the colder air and forces it down, the only place it can go. So, does cold air sink? Sure, but it is doing so because it is displaced by rising warm air.

QUESTION: :
Can you tell me what sort of voltages can be achieved by a thermocouple when the temperature difference is only about 100� C ?
ANSWER:
Typically a few millivolts. Read the Wikepedia article on thermocouples.

QUESTION: :
If I run my computer with a 300W power supply, it will produce a lot of heat (as well as doing useful work). Will it be just as efficient at heating my house as running a 300W electric heater? Or will the 300W electric heater somehow produce more heat per unit of energy put into it? If the computer is less efficient, then where does the extra energy go?
ANSWER:
A 300 W power supply means that it can supply up to 300 W if called upon to do so, not that it is continuously consuming 300 W. Usually, it supplies much less than that. Not being 100% efficient, not all power it consumes is supplied at its output; rather some power is wasted in heating itself up. Therefore, if a 300 W power supply is running at full power, it is consuming more than 300 W of power from its source. In any case, it will certainly supply less heat than a 300 W electric heater which converts nearly all of its input power to heat.

QUESTION: :
Does a planet that is spinning on it's own axis exert more or less gravity (on its inhabitants) than a planet, of the same mass and distance from the sun, that is still ? What would happen to people and matter on earth if it stopped rotating on its own axis? Would we get heavier?
ANSWER:
As I have said repeatedly, the weight of something is the force the earth exerts on it and therefore independent of its motion. However, your apparent weight will be changed if the earth rotates on its axis. The apparent weight is the weight which would be registered by a scale you are standing on but it is not a measure of your true weight if you are accelerating (as you are in a rotating system). For example, if you were in an upward accelerating elevator you would appear to weigh more but would not. It depends on where on earth you are located; at the poles there would be no effect (true=apparent weight) and at the equator you would have maximum effect. For more details about how to calculate this see an earlier answer. As you will see there, if the earth stopped rotating you would appear to be about 0.35% heavier on the equator.

QUESTION: :
if you push on a tennis ball and a bowling ball with the same force which ball with roll faster? Why?
ANSWER:
Newton's second law states that if a force F is exerted on a mass m, its acceleration a will be given by a=F/m. Therefore, pushing with equal forces for equal times will result in a greater final speed for the less massive ball (the tennis ball) because it had larger acceleration.

QUESTION: :
Why is it more difficult to spin a metal cylinder around an axis perpendicular to its length than parallel to it?
ANSWER:
Why is a more massive object more difficult to get moving than a less massive object? Because of inertia. In translational physics (moving along a line) inertia depends only on mass. In rotational physics, inertia is determined not only by the mass but also by the geometry. The quantity that plays the role of mass (that is the quantity which quantifies resistance to rotation) is called moment of inertia. The farther the mass is from the axis around which you are trying to rotate it, the harder it is to rotate it. For an axis along the symmetry axis of the cylinder, most of the mass is close to the axis and so it is easy to rotate. For an axis through the center but perpendicular to the symmetry axis, much of the mass is much farther from the axis of rotation and so it is harder to rotate.

QUESTION: :
Why do objects appear black? A pure black object would absorb all light so could not be seen since no light would be reflected.
ANSWER:
If an object were truly black (absorbed all light striking it), you would not be able to see any detail on it. For example, if there were a lump on it, you would not be able to see it because your eyes would have to form an image of the light coming from the lump but there isn't any such light. However, you would be able to ascertain its shape because your eyes could image the light passing by its edges. Of course, there is no such thing as a perfect absorber and in the real world there is always come light coming from a "black" object.

QUESTION: :
Is there any way to visualize electromagnetic field lines similar to Faraday's experiment using iron shavings to visualize magnetic field lines? For example, is there a powerderized substance that could be tossed in the air that would expose the outline of an electromagnetic field?
ANSWER:
Grass seeds or semolina seeds in oil work for showing an electric field (I think you must mean electric, not electromagnetic). They become electrically polarized like iron filings become magnetically polarized and align with the electric field.

QUESTION: :
How do I figure out my weight when I am impact a hard surface at different speeds? Example If I am traveling at x mph, how much will I weigh when I hit the ground from h height?
ANSWER:
Weight is the force with which the earth pulls on you. It makes no difference how fast you are going or whether you are hitting the ground or anything else. Your weight is your weight.

QUESTION: :
It's very cold in my house, so I turn off the heat when I leave the house. When I come home, I turn the heat back on and it heats the house for a very long time. Is it more efficient to leave the heat on all day (so it must only heat the house a small amount each time the temperature drops below a certain point) or turn the heat off when I leave the house and let it heat the house for a very long time only after I get home?
ANSWER:
You should turn your heat down when you leave the house or off if there is no danger of freezing pipes, killing houseplants, etc. The physics behind this is simple: the rate at which heat moves from a warm space to a cold space is proportional to the temperature difference between the two. All the furnace does is replace lost heat and the less heat lost, the less energy will be consumed. The problem is, of course, that it might be unpleasant waiting for the house to get comfortable. I think the best thing to do is get a programmable thermostat so you can set it to come on an hour before you get home and an hour before you get up in the morning. Then just leave it off all day and all night when you are in bed under some good comforters.

QUESTION: :
Why are there two definitions of gravity?One states that gravity is an artifact of a change in direction of mass in the curves of spacetime.The other states that gravity is a force generated by the theoritical " graviton particle".At lectures I have seen physicist interchange these definitions,which confuses the audience,and become very angry when

QUESTION: ed about the inconsistencies between the two.I have never had a proper answer to this

QUESTION: and.in fact, have been called an idiot by lectures when I bring this

QUESTION: up.
ANSWER:
Really, called you an idiot? And for just asking for clarification? Such a speaker is an arrogant jerk, in my opinion. Anyhow, I would judge him as the idiot because there is no evidence that gravitons even exist and to put them on equal footing with the theory of general relativity is ludicrous. There is a serious problem in physics: we have been unable to reconcile gravitational theory (general relativity) with quantum mechanics, i.e. there is no successful theory of quantum gravity. If there were a theory of quantum gravity, there would be a quantum of the gravitational field, much like the photon is the quantum of the electromagnetic field, and this would be a graviton. A graviton has never been observed and there is no successful theory of physics which has a graviton as a component.

QUESTION: :
e=mc2.... why the speed of light? What is significant about the speed of light in determining the amount of energy in matter? How does multiplying mass by the speed of light squared give one an amount of energy? What does the speed of light have to to with energy? WHY THE SPEED OF LIGHT?
ANSWER:
This kind of

QUESTION: implies that some particular equation should stand alone and somehow be comprehensible on its own without anything else. In fact, the famous E=mc2 is just one small part of the theory of special relativity and must be derived within that theory. Starting with the postulates that the laws of physics must be the same in all inertial frames of reference and that the speed of light is the same for all observers, all of special relativity follows. (Actually, the second postulate is simply a special case of the first as I have discussed in earlier answers.) You may read a brief derivation in an earlier answer.

QUESTION: :
Could the accelerating expansion of the universe be due to electrostatic / magnetic repulsion? After all, gravity is the weakest of forces and the normal expansion (leading edge) of the universe makes the intergalatic / gravatic attraction weaker as time goes on. The weaker the gravatic attraction, the more the other effects become more noticeable. If true, this would not counter the proposed dark matter / forces, it would just be another aspect of what might be happening to accelerate the expansion.
ANSWER:
As my disclaimer says, I am no astrophysicist. However, I find it impossible to believe that electromagnetism could possibly be responsible for "dark energy", the term usually attached to this accelerating expansion. The reason is simply that the universe would have to have a huge net charge and there is no evidence to suggest that this might be. Keep in mind that even though gravity is the weakest force, it need not be the least influential if there is a huge amount of mass around, as there is. My own feeling is that we do not understand gravity as well as we think we do and that is the reason for the anamolous dark matter and dark energy.

QUESTION: :
Imagine two electrons, side by side, are moving along at a constant velocity. If these electrons were to fly past a person sitting on a chair, would that person see the electrons repel with a force of F=kqq/r^2 or would there be an additional magnetic force of attraction between the electrons? Would only the person in the chair experience the magnetic field generated by the moving charges?
ANSWER:
This is actually a pretty complicated, advanced problem. The fields of moving point charges are not as simple as you would guess from what you know about electric fields of stationary point charges and the magnetic fields of current-carrying wires. The answer to your

QUESTION: is that the electric force is not what you state because the electric field of a moving charge is not the same as that for a static charge. Also, there will be a magnetic field and therefore each moving charge will experience a force due to the magnetic field of the other. If you really care, here are the fields for a point charge moving in the x direction with speed v. Let E0 be the electric field in the rest frame of the point charge and E be the electric field in the lab frame. Then Ex=E0x, Ey=γE0y, Ez=γE0z where γ=1/√[1-(v2/c2)]. The magnetic field may be calculated from B=-(vxE)/c2. Notice that if v<<c, the force is approximately the force which you state, i.e. E is little changed and the magnetic force is very small compared to the electric force.

QUESTION: :
It is my understanding that quantum physics states that the existence of some subatomic particles is probabilistic (sometimes you can locate an individual particle sometimes you can't). The lack of ability to ascertain both the velocity and location of some subatomic particles has led some to assert further dimensions and even multiple universes. I am wondering if these theories (i.e. string and multiverse) could be challenged if we come up with equipment that can get both velocity and location of these particles. Do these theories work with or without such equipment? How?
ANSWER:
The problem is not that we don't have accurate enough equipment; the problem is that these quantities are actually unknowable no matter how carefully you measure. As you know if you read this site, I have little time for string theories and am unaware of their having come into being because of the uncertainty principle. However, there is nothing to "challenge" because these theories do not make any predictions.

QUESTION: :
Can sunlight be distilled- Passed through a prism where certain wavelengths would be directed to heat water, generate electricity, grow plants, etc. more efficiently?
ANSWER:
An interesting choice of words, "distilled". Yes, you certainly can do that. But I do not believe you would gain anything at all and certainly lose. Unless the light with less than ideal wavelengths for some task actually caused a negative effect, that is inhibited the task, you would lose their contributions. Much more important is to concentrate the light, to gather light from a big area to get more of it.

QUESTION: :
i noticed that if it takes light 1 second for it to reach about 300 million meters. this means that all we see around us is not present but the past? because when we see a supernova blow up and the news reached earth we are seeing it as it happened thousands of years ago. so, when i am seeing lets say a cabinet at 10 meter we are seeing it in the past? i am really confused...
ANSWER:
Yes, anything you see you are seeing in the past, technically. However, anything within a few thousand meters is being seen such a tiny time later that your eyes or brain could never process and observe such a time delay. For all practical purposes, everything you can see (excluding anything not on earth like stars, planets, the sun, even the moon) are happening simultaneously and right now. There is one interesting exception. For a GPS to work accurately times must be extraordianrily accurate; therefore corrections are made for times of transit and relativistic effects on time.

QUESTION: :
i don't have a teacher and i'm studying myself. It's because of that i can't go to a high-school in Islamic Republic. I wanted to know if you could help me please with my

QUESTION: s. Well, i have faced with a problem that says: We have a box with two light strings on two opposite sides of the box. We hang the box from ceiling by one of the strings. (It means that the system is vertical.) The problem says: if we pull the lower string suddenly, only the lower string will be cut from the box (system); but if we pull it calmly and continuum, the upper string will be cut from the the ceiling; so all of the system (except ceiling) will fall.
ANSWER:
The string has a maximum tension it can have without breaking. Before you do anything, the lower string has a tension of zero and the upper string has a tension equal to the weight of the box, W. If you pull down on the lower string with a force bigger than the maximum tension, it will break. If you pull down with a force F smaller than the maximum tension, the lower string will not break; but the tension in the upper string will be F+W and if this is bigger than the maximum tension, the upper string will break.

QUESTION: :
if an object say golf ball, fell from say a plane how long would it fall before it would stop getting faster or would it maintain its speed gain.
ANSWER:
Let's say it is a hovering helicopter because something dropped from an airplane already has a large forward velocity which complicates things. You will find a lengthy discussion about this problem at this link. I have lifted these two graphs from that website. The first graph shows that it takes about 10 s for terminal velocity (about 34 m/s down) to be (almost) reached. The second graph shows that the golf ball would have fallen about 250 m in 10 s.

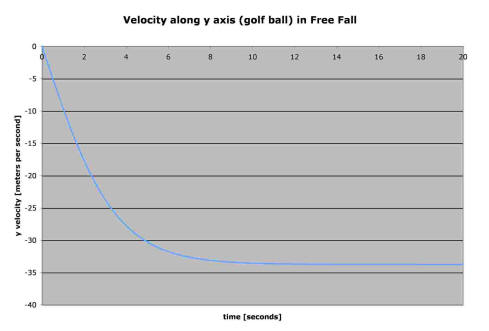
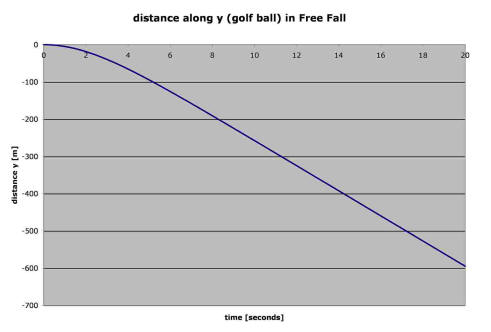
QUESTION: :
if you shoot a bullet out of a gun, straight down off a high building, will it get more speed or stay at the same speed?
ANSWER:
...or maybe slow down? If you drop a bullet (or anything) off a high place it experiences two forces, its weight (gravity) down and air resistance up. The air resistance gets bigger the faster it falls. Eventually the bullet will reach a speed where the weight and air resistance are equal and it stops speeding up. This speed is called the terminal velocity. If you shoot the bullet straight down with a speed larger than the terminal velocity, the upward force on it from air resistance will be bigger than the downward force of its weight and so it will slow down. The terminal velocity of a bullet is about 100 mph whereas the muzzle velocity is about 1000 mph (these are just rough numbers). So the bullet will slow down and, if the building is tall enough, it will slow down a lot.

QUESTION: :
I am doing a project for 8th grade technology. the objective is to stop an egg from braking upon impact. I have a list of what i can use and the budget i can spend. here is the Q: if i put paper towels folded up tightly around the egg, (not wrapped around it but just to keep it snug while laying down on the wood base) will this be enough to support the egg from cracking on impact? (30 degree angle from top of room to bottom) or should i have it so the egg hits one layer of paper towels and slides into another?
ANSWER:
It sounds like your idea is doomed to failure, particularly when you stipulate that your paper towel will be wrapped tightly. I will not tell you how to do it but will give you the general physical principal to think about. Suppose that you jump off the roof of your house and land on a cement driveway. It hurts a lot. The reason is that the driveway exerts a force up on you and that force is big. The reason it is big is because you stop very quickly and the force is inversely proportional to how long it takes you to stop, that is the force necessary to stop you in 1/10 second is ten times bigger than the force necessary to stop you in 1 second. So the trick is to make the stopping last as long as possible. So, if you put a big thick foam pad in the driveway you will not get hurt because the time to stop you becomes much longer. Your tightly wrapped egg will stop quickly and probably break.

QUESTION: :
What is the phase difference between applied and induced emf in an inductor ? If it is 180 then why don't they cancel each other
ANSWER:
Almost by definition, the phase in a perfect inductor (zero resistance) is 1800. They do not cancel because they are not of the same magnitude.

QUESTION: :
Am considering a formula for the "stop height" of a self rising object say a balloon, am of notion that a self rising balloon wouldn't do that for ever, i want to know what formula would be used to calculate the stop height given considerable parameters. Similarly, the formula for "stop depth" of a self sinking object in an ocean bed of water, am still of the notion that it stops sinking at a depth far down.
ANSWER:
I assume you are talking about a rigid object, something which does not change volume. Very high altitude balloons get much larger as they rise and this would be too complicated to answer without more information about the material from which they were made and other details of their design. For a rigid balloon of volume V and mass M the average density would be ρ=M/V. As you go higher in altitude, the density of the air gets smaller. When the density of the air becomes equal to ρ, the balloon stops rising. Because water is essentially incompressible, the density of the water does not change as you go deeper and therefore there would be no depth at which a sinking object would stop sinking.

QUESTION: :
How can I calculate the volume of air which would have to be introduced into the vacuum created at the trailing end of a cube moving through air in order to mitigate the turbulance? For example, a motor home travelling down the highway displaces the air in front and at the rear airnaturally wants to fill the vaccuum as quickly as possible. I want to assist that process.
ANSWER:
There is not a vacuum there, but likely a bubble of still (with respect to the RV) air. This bubble probably helps the vehicle be more aerodynamic. Here is an interesting ancecdote about a related issue: Several years ago the Car Talk guys were asked for their opinon of those nets sold to replace the tailgate in pickup trucks to reduce drag. They said they thought it was a great idea. The following week they issued a retraction; an engineer from GM had called them to say that the tailgate is an essential part of the design and causes there to be like a "box of still air" like an extension of the roof of the cab which facilitates flow of air over the truck. Removing the tailgate actually increases drag.

QUESTION: :
This

QUESTION: is regarding kinetic energy Lets say a man whose weight is hypothetically "1kg " travels down an airport travellator. The moment he steps onto the travellator, he accelerates from rest to 3m/s. Thus, to the observer X standing outside the travellator, his kinetic energy is 4.5 J On the travellator, he walks at an additional 2 m/s to the other end.Thus, to the observer Y on the travellator, he gains an additional 2 J.Since the kinetic energy of a stationary person on the travellator is 4.5J, the observer Y reasons that the man's total kinetic energy is 4.5J+2J = 6.5J However, Observer X sees the man's velocity is now at 5 m/s, thus, his kinetic energy should be 12.5J.
ANSWER:
Kinetic energy is not an invariant quantity. Different observers (as you have clearly found) do not observe the same kinetic energy of something. Nor do they measure the same speed. They do all measure the same acceleration, however.

QUESTION: :
I'd like to understand the concept of "north". How is "north" determined? Can it be determined without reference to some other position or circular reference (i.e. "north is the opposite of south, north is the "top", north's magnetic field points "downwards" - what is "down"). Is the definition of north Earth-centric, our solar system-centric, and will it work in other solar systems, including those that have more than one sun?
ANSWER:
It sounds like you are interested in geographic north as opposed to magnetic north. The earth rotates on its axis which is a line passing through the center of the earth. If you look at earth from one direction along the line of this axis, it goes clockwise; if you look from the other direction, it goes counterclockwise. Choose the case where it is going counterclockwise; the place where the axis pierces the earth is called the north pole. North is the direction along the surface of the earth pointing to that pole. Clearly, this refers to what north means on earth. A similar definition could be used for any body having a rotation about some axis. If viewed from far in space above the north pole of earth, nearly everything in our solar system has counterclockwise rotation (including the orbits of the planets).
If you are interested in the magnetic north pole, it is a little confusing. A bar magnet has a magnetic field (which it is too involved to talk about in detail here) which points out of the north pole and into the south pole of that magnet. The earth is also observed to have a magnetic field which looks like a giant bar magnet. Magnetic north is defined as the direction to which the north pole of a magnet points. However, north poles are attracted to south poles and repelled from north poles and so the magnetic north pole of the earth is actually a south pole. The magnetic and geographic north poles are not exactly at the same place on earth.

QUESTION: :
Hello, my

QUESTION: is about the photo-electric effect which was used as an early example of the particle nature of light/photons: The particle analogy is that the photon is like a billiard ball colliding with another, the electron, and knocking it loose. The photon has to contain enough energy to knock it loose. Even if you knocked it with a large number of photons of less energy (frequency), it won't work. In other words increased intensity of light will not work, as one might expect from the classical wave nature of light. I like this visualization to explain the particle nature of light. But what prevents a large number of low energy photons knocking into the electron at the same time, in other words why do we assume just one photon can try to knock out one electron?
ANSWER:
Essentially, probability prevents it. With sufficiently high intensity it is possible for two or more photons to participate in ionizing an atom. Until the advent of high intensity lasers, sufficiently high intensities were not available to have any observable multiphoton ionization of atoms.

QUESTION: :
Why is a body which falls freely in a weightless state???????
ANSWER:
It is not in a "weightless state". Its weight is still there since weight is just the force the earth exerts on the body and it does not disappear just because the body is falling. However, if you are falling along side the body it appears to be weightless. For example, if you are in a falling elevator you would feel weightless because you would no longer feel the floor pushing up on your feet, your muscles would no longer have to support your internal organs, etc. The same thing applies to a craft orbiting the earth which is just in a special kind of free fall. Weightlessness is a misnomer for these situations.

QUESTION: :
You mentioned the principle of equivalence in an earlier answer. Let's explore that principle this way: For the first case, assume you are in a room that has the necessary supplies to keep you alive for a long time. Now, assume that the room is on the earth � you could stay in that room for many years. Now, for the second case, assume that the room is being accelerated at 9.8 m/s away from a gravitational field. According to the principle of equivalence, you wouldn't know the difference between the two cases. However, if you are in the accelerating room for many years, you would eventually be going very fast. Disregarding relativistic effects (which, of course, cannot be ignored, but I'm doing so to make my point), after about a year at this acceleration, your speed would be approaching light speed. So, my

QUESTION: is, would you continue to feel the same effects as you would in a stationery room in a gravitational field, no matter how long you were in the accelerating room? Or, would the fact that you were approaching light speed have other relativistic effects which would make your experience different than if you were in the stationery room?
ANSWER:
As you point out, constant acceleration is problematic in special relativity. In fact, from a stationary observer's point of view it becomes impossible at higher speeds (see earlier answer). In the frame of the accelerating room, though, no relativity need be taken into account because everything seems normal here. You simply need to redefine acceleration in relativity to maintain the constant apparant gravity. See a nice essay by Baez; the constant acceleration is that measured by an inertial frame moving with your speed at a particular instant. To read several of my earlier answers relevant to your

QUESTION: , see the FAQ entry.

QUESTION: :
The magnetic force acting on a charged particle can never do work, because at every instant the force is perpendicular to the velocity. The torque exerted by a magnetic field can do work on a current loop when the loop rotates. Could you please explain how these seemingly contradictory statements can be reconciled?
ANSWER:
If you put a current carrying wire in a magnetic field, it will have a force exerted on it, right? So we do not need to get into torque doing work but can just talk about a current carrying wire which we can use a magnetic field to move (do work on) a wire. But here is what is really happening: the magnetic force on the electrons moving in the current causes them to migrate toward the edge of the wire. So there will be an electric polarization of the wire (called the Hall effect) and there will be an electric field inside the wire itself and this field will point towards the region of excess electrons. This electric field pulls the positively charged ions in the wire toward the excess electrons and it is this electric field which does the work.

QUESTION: :
Is there any particular object or system which doesn't abide by Newton's first law of motion?
ANSWER:
Newton's first law (N1), often called the law of inertia, is often used to define what is called an inertial frame of reference (IFOR). An IFOR is one in which N1 is true. So, suppose we can find a frame of reference in which N1 is true. Any other system which moves with constant velocity with respect to this one is also an IFOR. But, any frame which accelerates relative to the IFOR is not an IFOR and N1 will not be true. For example, if you are at rest in your car it is an IFOR and if you are moving down a straight road with constant speed it is an IFOR. But if you are are at rest and press the accelerator you feel like there is a force pushing you back in your seat but there is no such force; you just feel the seat pushing forward on you since it is the force which accelerates you. But, in your frame of reference, inside the car, you are at rest but there is one unbalanced force pushing you forward; N1 is not true.

QUESTION: :
If earth is escavated along its diameter (on any where) and an object is dropped in to it, what will happen? I thought that the object should stop at the centre of the earth, but i read somewhere that it will come back to the top in 85 minutes. If it is so, please tell me why and how?
ANSWER:
If you neglect air friction, it oscilates back in forth to the other side of the earth with a period about what you state. It will actually be going the fastest when you get to the center. To see a full discussion in several answers, link here. (You could have found this

QUESTION: on the FAQ page.)

QUESTION: :
When all the oil is used as fuel and burned off, will the Earth be lighter? And if so will there be consequences of a lighter Earth and no oil underground?
ANSWER:
Burning is chemistry and one of the tenets of chemistry is that the mass before (oil) equals the mass afterwards (CO, CO2, etc.).

QUESTION: :
our senses tell us that a table is solid but science tells that a table is made mainly of empty space.how can these two views be reconciled?
ANSWER:
Please see an earlier answer.

QUESTION: :
If you were to inflate one soccerball with air, and another with helium to the same presure, and hit them with exactly the same amount of forse, in an enclosed soccer field (so tempeture, weather, and air resistance will be the same with both balls) witch would travel further?
ANSWER:
It is not sufficient to specify equal forces, you must also specify that the force acts either over the same distance for both (equal work done) or over the same time interval for each (equal impulse). In either case, the lighter ball gains more speed and thus goes further. Helium.

QUESTION: :
Since perpetual motion machines are considered impossible because they defy the laws of physics, where does the electron get it's energy to move around within an atom. Is an atom not a perpetual motion machine?
ANSWER:
A machine is generally regarded as something which has energy output, can do work. An atom does not meet this criterion. Further, you should not think of an atom as an electron going around in a circular orbit; this is vastly oversimplified. The electron should be viewed as a cloud whose density at any point determines the probability of finding the electron there at some time. In fact, if the hydrogen atom is correctly done quantum mechanically, the average velocity of the electron is zero.

QUESTION: :
It is easier to catch a soft tennis ball than hard cricket ball moving with same velocity.why?
ANSWER:
The force you exert on a ball to stop it is equal to the mass of the ball times its acceleration. This is Newton's second law. A cricket ball has a larger mass than a tennis ball, so for equal accelerations it would be harder to stop. But the acceleration is important also. The tennis ball, being softer, compresses while being stopped and so the time to stop it is larger than for the hard cricket ball, thereby having a smaller acceleration, therefore needing a smaller force.

QUESTION: :
My

QUESTION: relates to how objects with differing mass (and thus, different gravity strength) affect each other when they are all simulatenously in each other's gravitational fields? My hypothetical example is as follows: You have an object with relatively small mass, a marble; an object with relatively larger mass, a bowling ball; and then an extremely massive object, like a planet. What happens if the marble and the bowling ball were both equidistant from the planet and also a measurable distance from each other? As the two objects "fell" towards the planet's stronger gravity, would they also be slightly attracted towards each other on the way "down"? Would the initial distance between the two objects gradually decrease, and if so, would the marble move a greater distance towards the bowling ball than the bowling ball would move towards the marble, due to the bowling ball's stronger gravity? Or does the presence of a superior gravity simply override any attraction between smaller objects?
ANSWER:
Any object with mass both causes and feels gravity. In your example, the earth feels a gravitational force from both the marble and the bowling ball, the bowling ball feels a force from both the earth and the marble, and the marble feels a force from both the earth and the bowling ball. However, the mass of the earth is so big that you would be hard pressed to observe any acceleration other than that toward the center of the earth. If you (roughly) work out what the accelerations are, you get:
Bowling ball and marble each have a component of their acceleration toward the center of the earth of about 10 m/s2.
Bowling ball has a component of its acceleration toward the marble of about 10-13 m/s2.
marble has a component of its acceleration toward the bowling ball of about 10-10 m/s2.
I assumed the marble and bowling ball were about 1 m apart.

QUESTION: :
What is the difference between saying "the sun revolves around the earth" and saying "the earth is the center of the universe"?
ANSWER:
Well, of course they are both wrong so they have that in common. Saying that the sun revolves around the earth simply says nothing about the rest of the universe. Maybe the sun goes around the earth but the earth goes around the center of the milky way galaxy and the rest of the universe is going around the Andromeda galaxy; in this scenario the sun goes around the earth but the earth is not the center of the universe, the Andromena galaxy is. Why did I spend time on this?!

QUESTION: :
Consider a baseball pitched with a spin around the vertical axis. To be precise, let the ball�s initial direction be Northward and the direction of its spin be clockwise when observed from above. Because of aerodynamic effects, the spinning ball will...
ANSWER:
...be deflected east. The general idea is shown in the figure to the right. The wake is deflected down in the picture for the ball moving to the right. The reason for the force is essentially Newton's third law. If the air is being deflected down, the ball must be exerting a force on it; if the ball exerts a force on the air, the air must exert an equal and opposite force on the ball. This force is called the Magnus force. There are also Bernoulli forces because the air goes faster over the top than the bottom and therefore there is lower pressure at the top, but I believe that this is much less important than the Magnus force (although most elementary physics texts say that this is the reason for the curve ball). (To apply this picture to your specifics, imagine you are looking from below and north is to the right; then east will be in the direction of the force.)

QUESTION: :
I have two very similar bikes, both almost perfectly balanced front to rear (with and without rider) with very similar geometry and parts, and one of them oversteers slightly, but for the life of me I can't figure out why the other one understeers, causing the front tire to wash out dangerously. The only way I can get the misbehaving bike to break traction more evenly is to hang my weight way over the back of the bike, but this is of course impractical and seems like a huge change considering how similar the bikes are. What makes a bike over/understeer and what can I do to the rebellious bike to make it safe to ride on fast trails (short of reducing rear tire and therefore overall traction)? Thanks in advance for significantly reducing my REM sleep (and likelihood of breaking a wrist/collarbone)!
ANSWER:
There is no way that I could figure this out; there are two many variables. Perhaps you can read up a bit on bicycle stability and apply it to your particular situation.

QUESTION: :
If we were to build a giant rail ultimately pointed skywards, we would be able to give the space shuttle a certain speed before it even ignited its rockets. This obtained speed would mean less rocket fuel would be necessary to achieve escape velocity. This reduction of mass would mean less required energy overall. Assuming that the apparatus used to speed up the shuttle has less mass then the saved fuel (a very bold and baseless assumption, no doubt), is there a physical explanation as to why we don't use this model?
ANSWER:
The total amount of energy necessary to put a particular payload in a particular orbit does not depend on where you get the energy. I guess you want to use some other device or method to get the shuttle moving along your rail, but that will take just as much energy as the way we do it now. And, such a "rail" would be pretty expensive to build, probably.

QUESTION: :
To travel in a circle at a constant angular velocity a body must be constantly accelerated. Yet its angular velocity and hence its kenetic energy does not increase. Where does the energy go?
ANSWER:
You actually told me the answer. If the energy does not change, it does not "go" anywhere. It is an example of energy conservation where, if no external forces do work on something, its energy remains constant. There is an external force here (whatever is keeping it moving in a circle, tension in a string, friction of tires for a car, etc.) but this force (called the centripetal force) always points toward the center of the circle. Since the particle always moves tangentially on the circle, the force and motion are perpendicular and no work is done. So, here is an important lesson: even if there are forces acting on something they do not necessarily change its energy.

QUESTION: :
A man on a skateboard is said to be travelling at constant motion until he hits a rock, his velocity goes from 12m/s to 2m/s what is the force that he hits the rock with? How do you work this

QUESTION: out?
ANSWER:
This sounds suspiciously like homework, but it can't be because you cannot find the answer. In order to calculate force you need to know the acceleration and you cannot calculate acceleration from the change in velocity; you need to know the elapsed time. If this took 1/10 of a second the force would be much bigger than if it took 10 seconds. Furthermore, to calculate the force you need the mass of the thing which is accelerating (you would probably want the mass of the skateboard + the man. If this was homework, your instructor played a nasty trick on you.

QUESTION: :
If a solid metal pole were made to be one lightyear long and it was pulled at one end, would it take over a year to feel the tug at the other end, or would the fact that it is a solid object cause the tug to be felt instantaneously at the other end?
ANSWER:
You could have found this answer on the FAQ page. The answer is here.

QUESTION: :
Suppose a ship is moving at 3/4 the speed of light. If an object aboard the ship were to be launched forward at 1/2 the speed of light relative to the ship, then would the object be moving faster than the speed of light or would the object for some reason never reach the speed of light?
ANSWER:
I have previously answered this

QUESTION: . The object, for your scenerario, would have a speed of about 91% the speed of light.

QUESTION: :
Is it possible to create artificial gravity? I know we have yet to figure out why we have gravity to begin with but if we get that answered it would seem logical that the next step would be to create it on our own. Also in your expertise, would you have any insight on how artificial gravity could potentially be utilized? Possibly for space travel?
ANSWER:
What do you mean that you "know we have yet to figure out why we have gravity"? If you mean we do not understand gravity, you are wrong; we have a very good theory of gravity called general relativity. One of the things that general relativity says is that there is really no difference between gravity and acceleration. For example, if you are in an elevator in empty space with an acceleration equal to the acceleration due to gravity, there is no experiment you can do which will have a different result from if you were sitting on earth. This is called the principle of equivalence. So one way to make "artificial gravity" is to simply be in an accelerating spaceship. However, it is not really practicable to have a spaceship always accelerating in a straight line because you would have to be continually burning fuel. On the other hand, something going in a circle is constantly accelerating so if you make a giant donut-shaped craft which is rotating, you could stand on the inside of the outer wall and have "artificial gravity". The acceleration depends on the radius of the circle, though, so it would have to be very large or else the gravity at your head would be much different from the gravity at your feet. Certainly if we ever have long distance space travel, a craft of this sort will be needed for a tolerable environment. I have little hope for space travel becoming a reality unless a colony of people is ok with leaving and never coming back. The distances are unimaginably big and very large speeds are difficult to achieve in reasonable times without crushing everybody on board. And, at very large speeds there would be a big problem with radiation shielding.
FOLLOWUP

QUESTION: :
I suppose I should have been more specific on my

QUESTION: . You were wondering what I meant by "When we figure out gravity". I was actually referring to what causes gravity and not so much how it works. I know we have a good understanding of it's mechanics but as to why there is gravity in the first place was my real

QUESTION: . To my knowledge we still dont know why gravity exists but I could be speaking out of ignorance.
ANSWER:
We do understand how it works. Mass bends spacetime and gravity is the result. The often used (instructive if not an exactly a true picture) is a bowling ball sitting on a trampoline; a marble will then roll toward it because it deforms the space it is in. General relativity is discussed in several previous answers. Although an extremely successful theory of gravity, it is probably not the last word because there is no quantum theory of gravity.

QUESTION: :
There is frequent mention in various publications that states that a spaceman's clock would run slower than that of an observer on earth. However, from the spaceman's perspective (assuming he was not accelerating) he would apparantly be at rest and whilst the earth was receding. This being the case, the earthbound clock would be running slower than his. The net result seems to be that when he eventually returns to earth, he will be the same age as his twin brother and not younger as is often suggested. Or am I missing something?
ANSWER:
What you are referring to is the twin paradox which is not really a paradox at all. The key to understanding is understanding the asymmetry between the two such that they can come back together to compare their clocks. See my earlier discussion of the twin paradox.

QUESTION: :
Apollo 13 the movie. 'We just put Isaac Newton in the driver's seat'. could you please justify this statement made by Jim Lovell
ANSWER:
When you go for a drive in your car, you burn fuel the whole way. In space travel, you coast most of the way. But in space, there is often very influential gravity you can use to pull you, push you, or steer you. I do not know the exact context of your quote, but Apollo 13 used gravity to swing it around the moon and then gravity to pull it back to earth and some stage of this is what is referred to by the quote because Isaac Newton is considered the first physicist to appreciate what gravity is.

QUESTION: :
Isn't space exploration a terrible waste of taxpayer dollars?
ANSWER:
I have a stock answer to this "waste of money"

QUESTION: which I have written earlier in reference to the CERN supercollider.

QUESTION: :
I want to be able to convince my father without a doubt that there is a valid way of finding the distance between earth and very distant stars or nebula. If you could explain in detail or perhaps in plain english, I would appreciate it. The next

QUESTION: is somewhat more complex. I was wondering if there was a rate at which gravity attracts. For instance, if the moon were to disappear suddenly. How long would it take the earth to be affected by the lack of the moons gravity? Instant? A a day? A minute? Would it be faster then light? Is that even possible?
ANSWER:
Please adhere to site grounrules for single, well-focused

QUESTION: s. I have previously answered your second

QUESTION: . Regarding your first

QUESTION: , there are three ways to measure the distance to the stars.
The first is parallax; this method works for fairly close stars (a few thousand light years). Hold your finger in front of your face and move your head back and forth. Your finger appears to move back and forth against the distant background. This is parallax and by doing careful measurements you could deduce the distance from your finger to your eyes. If you observe a star not too far away at two different times of year when the earth is at opposite ends of its orbit, it will appear to move against the background of much more distant stars.
The second is to use stars of known brightness and measure their apparent brightness. If a light bulb has a known brightness and you measure its light reaching you, you can deduce its distance. The bulb, for example, when viewed from one mile away will be four times as bright then when viewed from two miles away.
Finally, you can use red shift of light from the most distant objects. It is known that the farther something is away from us, the faster it is moving away. The principle is the doppler effect where the wavelength of waves (light in the case of stars) is longer. The every day example of this is a train whistle having a higher pitch when moving toward you and lower when moving away.
You can read about this in more detail here.

QUESTION: :
What's the physics behind ballpoint pen?
ANSWER:
Check out HowStuffWorks.

QUESTION: :
Based on the general fear that is going around about the world ending in 2012.... Is it really the end of time are we all going to die on 12/2012?
ANSWER:
Well, do you believe in astrology? I recommend, for a good balanced view of the evidence, a recent New York Times article.

QUESTION: :
If you are trying to calculate the rate at which atoms of a particular fission product are being produced. Are you looking for the activity of the fission product or the number of fissions per second?
ANSWER:
The overall fission rate would not give information about any particular fission product.

QUESTION: :
If electromagnetic energy in the form of visible light spectrum (photons) travels from the sun to the earth at the speed of light, it wouldn't have any mass? (i.e., photons are massless, therefore have no energy?, E=mc^2, m=0, then E=0. If a photon doesn't have any mass and therefore energy to begin with, how has the conservation of energy principle upheld? I ask this because clearly electromagnetic energy from photons of visible light are converted into chemical energy in plants thru photosynthesis so it would seem that photons do indeed have energy and therefore mass. But if they have mass, how can they travel at the speed of light?
ANSWER:
I have answered this

QUESTION: before.

QUESTION: :
A magnetic field can be created with a varying electric field. Hence, an electric field can be created with a varying magnetic field. In a betatron, where an electron is accelerated, the electric field remains constant while the magnetic field varies. Since, the electron is a charged particle, in motion, how does the electric field remain constant while the magnetic field fluctuates??
ANSWER:
Imagine a donut with a magnetic field passing through the hole. If the magnetic field is increasing there will be an electric field around the inside of the donut and it is this which exerts the force on the electron to accelerate it. If the magnetic field increases at a constant rate, the electric field will remain constant. If you are worrying about the electric field due to the electron itself, don't�a particle cannot exert a force on itself.

QUESTION: :
What happens to water molecules when water is heated from 90 degrees Celsius to 110 degrees Celcius?
ANSWER:
The same thing that would happen to any molecules�their average kinetic energy increases (they move around, on average, faster). Because you have specified particular temperatures it has a little more to it. If water is at 100 0C the molecules have acquired sufficient speed to escape from the liquid and become gas (boiling) and only molecules which escape the liquid can have temperatures above 100 0C.

QUESTION: :
Is there is a principle or theory that you cannot study an atom without changing the structure of said atom? And if there is, can you please tell me what that is?
ANSWER:
Maybe you are referring to the Heisenberg uncertainty principle, one incarnation of which can be that the act of measuring something disturbs that something. On the other hand, the "structure of an atom" refers to all its properties and, although you might change an atom from one state to another when studying it, you do not change the atom's essential properties; I would say you reveal those properties.

QUESTION: :
I know that materials are more likely to fail when energy is delivered over a short period of time for a given total energy load. Similary if an oil drum is pushed along by a bus at .5 miles per hour for several miles it is less likely to fail structuraly then if the bus hits the drum doing 75 miles per hour--even if the total energy displacement is less. Is there a simple characterization or formula to express this? Is there a general rule that applies to all materials. I have asked a shock physicists this

QUESTION: and could not get a straight answer.
ANSWER:
This is Newton's second and third law. There are a couple of problems with your example, one is the bus going with constant speed pushing the drum. If the drum slides smoothly or is on wheels, say, it will experience practically no force from the bus. Also, "total energy displacement" has no meaning in physics. Permit me to rephrase your

QUESTION: : Suppose I drop a hammer from 1 cm above your hand resting on the table; it doesn't hurt much. Suppose I slam the hammer down on your hand as hard as I can; it hurts a lot. Why? When the hammer hits your hand, it stops and so it experiences an acceleration. In order to stop the moving hammer, a force must be exerted on it and it is your hand which exerts this force. This is where Newton's second law comes in; the force F is given by F=ma where m is the mass of the hammer and a is the acceleration of the hammer. So, since the acceleration (the rate of change of speed) is much bigger for the fast hammer than the slow hammer, your hand must exert a much larger force on the fast hammer to stop it. Now, finally, this is where Newton's third law comes in; if your hand exerts a force up on the hammer, the hammer exerts an equal force down on your hand. I see on rereading your

QUESTION: that I have not quite yet answered it completely because I have assumed that your hand stopped the hammer in about the same amount of time for each blow because your hand was on the table. If your hand is not on the table and you are able to stop the fast hammer over some several feet, the acceleration is much smaller because the velocity change is over a much larger time; smaller acceleration again means smaller force.

QUESTION: :
An object on Earth accelerates at 9.8 m/s2. The object does this until it reaches "Terminal Velocity" which is when the object can accelerate no more because of the fluid friction with the air. If you put this object in a infinite complete vacuum with the gravity puling from one end. Will the vacuum make reaching Terminal Velocity impossible meaning that the object could reach the speed of light and beyond?
ANSWER:
Terminal velocity normally refers to the maximum speed of an object moving through a fluid like air. It can also mean the minimum speed if you start the projectile with a speed greater than the terminal velocity. If there is no fluid, then it will continue accelerating forever as long as the same force (its weight) acts on it. It cannot, however, exceed the speed of light, so you could say that its terminal velocity now is the speed of light. You may be interested in more details regarding acceleration in special relativity in an earlier answer.

QUESTION: :
I have a

QUESTION: about faster than light communication. If a string spanned a great distance through space and it were tugged on one end, wouldn't the other end move at the same time allowing for data to be transfered, perhaps through morse code? I believe this would require an extremely dense string that wouldn't expand, but is is possible?
ANSWER:
Your

QUESTION: has been asked before, so see an earlier answer. Your

QUESTION: is a little different since you are pulling instead of pushing, but the answer is essentially the same: no communication faster than the speed of light is possible and, for your proposal, it would be far smaller than the speed of light because the stretch in the string which would propogate the information about your tug would travel at the speed of sound.

QUESTION: :
1.What is the physical process of the conversion of mass into energy? 2.Is there a physical process by which energy can be transformed into mass?
ANSWER:
Your

QUESTION: is like "how can we convert an orange into fruit?" Mass is simply a form of energy. Can mass disappear and become another form of energy? Yes, it happens all the time. When you burn coal you are essentially turning carbon and oxygen into carbon dioxide; where does the heat energy come from? CO2 is slightly lighter than C+O2. The amount is so small that you could not hope to measure it. However, in nuclear physics it is easy to measure the mass difference: a nucleus with Z protons and N neutrons has a mass significantly less than the sum of the individual masses. For examples of converting non-mass energy to mass, see an earlier answer.

QUESTION: :
How magnet(magnetic field) acts on the PC monitor.What happends?
ANSWER:
I do not know if there is any effect on the modern LCD or LED screens. The older CRT screens are illuminated by an electron beam which sweeps across the screen. A magnet will deflect this beam. However, there is a thin screen with many tiny holes in it to assure that the electrons hit exactly on the spots intended. The metal of which this is fabricated can become magnetized if you hold a magnet near it and then this magnetic field will alter the path of the electron beam thereby messing up the picture. It is usually possible to demagnetize the screen with something called a degausser.

QUESTION: :
If there is no friction between two objects, and lets say object A is on top of object B and object B accelerates, will object A fall off and move to left? (assuming velocity is moving to the right in the X direction)
ANSWER:
If there is no friction, the block will not move at all and will drop straight to the table where it will remain at rest.

QUESTION: :
what exactly makes CO2 a greenhouse gas? As a 'blanket' there's no convection to outer space. Does it allow solar radiation in, but not allow earth's radiation out?
ANSWER:
To get a greenhouse effect, you need something which is transparent to visible light but absorbs infrared. Most objects (like the ground) absorb visible light and radiate infrared, so if there is an absorber of infrared blanketing the earth, that energy is trapped. CO2 is transparent to visible light and absorbs infrared.

QUESTION: :
Glow-in-the-dark, Radium painted, watch dials were popular in the 40's and 50's (until Radium use was discontinued). Today, sum fifty years later, these watch dials no longer glow, even if most of the original "paint" remains. My

QUESTION: is; if one were to move one of these old watch dials, close to an energetically active radiation source, such as a medial isotope or Uranium 235, would the watch dial glow again? -at least while it remained close to the radioactive material? I know X-rays are different than beta emitters, but would the old paint glow if you wore the watch while getting an X-ray?
ANSWER:
The phosphor is zinc sulfide. Its efficiency as a phosphor is complicated and is dependent on the impurities present. A little research on my part reveals that the reason that the dials no longer glow is not because the radium has decayed away (it has very long halflife), but rather because the alpha radiation had done sufficient damage to the crystal that the excited conduction electrons cannot efficiently get transported to the impurity sites. Therefore, nothing would make it glow; however, a "virgin" radioluminescent dial but without the radium could be made to glow with any external beta, x-ray or γ-ray source of sufficient energy. The definitive article on this seems to be here.

QUESTION: :
If a 400 lb man falls 3 feet to the ground and lands on one foot, How much force did the foot recive when it inpacted the ground.
ANSWER:
There is no way to answer this

QUESTION: because it depends on how long it takes the man to come to rest. Of course, that is why you should let your knees bend when you land, to lengthen the time of impact. Or, if you landed on a pile of foam there would be much less force than if you landed on a concrete floor.

QUESTION: :
Concerning newtons third law. Please explain which is receiving the reaction when a person is jumping on a trampoline. Is the spring the object receiving the opposite reaction or is it the trampoline fabric?
ANSWER:
Look at the person when he is in contact with the fabric: the forces on her are her own weight down and the force of the fabric up. No force on her from the springs because she is not in contact with the springs. Newton's third law says that if the fabric exerts a force up on her, she exerts an equal and opposite force down on the fabric.

QUESTION: :
If a fish tank containing only water weighs 50 pounds byt itself. You add a 5 pound fish, who swims around, but never touches the bottom. Does the fish tank increase in weight by 5 pounds?
ANSWER:
As I always say, you have to be really careful how you ask this kind of

QUESTION: . The weight of something is the force that the earth exerts on it and, the way you have asked the

QUESTION: , you can put a ten ton truck in the fish tank (assuming it would fit) and the tank would still have the same weight. But, what you are probably asking is: if the tank is sitting on a scale, will the scale still read 50 lb after I put in the 5 lb fish? No, it will not, it will read 55 lb. If you are worried that the fish is not resting on the bottom and should therefore not cause the scale to deflect, here is the appropriate argument. The fish is hovering and something must be holding him up�the water, of course. Therefore, the water exerts a 5 lb force up on the fish. But, Newton's third law tells us that the fish must therefore exert a 5 lb force down on the water. So the water pushes down on the bottom of the tank and therefore on the scale by 5 lb more than it normally would.

QUESTION: :
In my Science exam on Friday I was given a

QUESTION: that I was unsure about the answer to. I was hoping you would be able to assist me. The

QUESTION: was that if there was a balloon in a box with a needle attached to the top & another needle attached to the bottom, the balloon being secured with an elastic band what would happen if it was dropped from a heigh of 10m. Options were that it would be popped by top needle, bottom needle, or neither needle. I answered top needle based on Newton's law in relation to when a car accelerates fast after being at rest passengers are momentarily pushed forward but then pulled back into the seat, I figured the same would apply here. The balloon (when the box was dropped would fall towards the bottom needle but then due to the elastic band be pulled back up towards the top needle and popped. Can you advise me if this is right?
ANSWER:
You are right. The balloon must accelerate down and the only thing able to provide the required force are the rubber bands. But, for the rubber bands to have a component of their tension down, the balloon must move up (in the box).
CORRECTION:
I made an error in my answer. First of all, I had the wrong picture, namely I thought that there were two rubberbands stretched out to the walls of the box. But, more importantly, I failed to note the principle of equivalence which states that there is no experiment you can do to distinguish between being in an accelerating frame of reference or in a uniform gravitational field. In other words, as seen from inside the falling box, gravity can be ignored. As seen from outside the box, the balloon accelerates down because of its weight not as I said above "the only thing able to provide the required force are the rubber bands". Now, to answer the

QUESTION: correctly. The

QUESTION: is ambiguous about the elastic band and this is a problem. There are two possibilities: this is an air balloon and would drop to the floor if not secured by an elastic band to the ceiling; or this is a helium balloon which would rise to the ceiling if not secured to the floor by an elastic band. In either case, the elastic band will stretched before the box is dropped. When the box is dropped, gravity "disappears" for the balloon and it is pulled down if the band is attached to the floor or pulled up if it is attached to the ceiling. My thanks to the person in Portugal who spotted my error.

QUESTION: :
Why is it compulsory to make a photo diode reverse biased?
ANSWER:
It is not compulsory, it just works better that way. The photocurrent flows in the reverse direction and having a forward bias would have there be a steady current flowing in the direction opposite the photocurrent. Having a reverse bias greatly improves both response time and signal to noise ratio. See the Wikepedia article.

QUESTION: :
Is there a saturation point for energy(temperature gained by a body)??
ANSWER:
I really do not know what you mean by "saturation point for energy". If you mean is there a limit to how much energy you can add to something, then the answer is no. If you mean is there a limit to how much energy you can add to something without it "changing it", then the answer is yes. If you have a block of iron, you can keep adding energy until it melts; then keep adding energy until it vaporizes; then keep adding energy until it ionizes; etc. So, there are limits before phase changes occur.

QUESTION: :
If I was standing on Mars, would I be able to see the same constellations I see on Earth?
ANSWER:
Yes. The distance from Earth to Mars is very small compared to the distances to the stars and therefore there would be an insignificant change.

QUESTION: :
Where do radio waves end and light begin, if in physics, the term light sometimes refers to electromagnetic radiation of any wavelength, whether visible or not?In physics, if the term light sometimes refers to electromagnetic radiation of any wavelength, whether visible or not, would radio waves at very high frequencies be light?
ANSWER:
This is really semantics, not physics. Light usually refers to the visible part of the electromagnetic spectrum and sometimes also ultraviolet and infrared. Radio waves are usually not called light, nor are x-rays, gamma-rays, microwaves, etc. We often refer to the speed of light as the speed of any electromagnetic wave since all travel with the same speed in vacuum. There is no clear rule about where one type of electromagnetic wave ends and another begins.

QUESTION: :
My

QUESTION: regards finding the angular velocity. If you are given the radius of a cylindrical spool and the time it takes to pull something off it, how would you go about find the angular velocity of the spool?
ANSWER:
The first

QUESTION: you sent was too specific and likely homework. This is more general, so I will answer it. If you pull string off at a constant rate, say X m/s, that means that X m of circumference of the spool passes a point in a second. Therefore, the tangential velocity of the spool is X. But, that means that the spool has turned through an angle of X/R radians in one second or has a rate of X/R radians/s which is the angular velocity.

QUESTION: :
i am iraqi student.... i have a

QUESTION: about RESONANCE FREQUENCY i want to learn the fundamental explain of it..i want to learn more about RESONANCE FREQUENCY...
ANSWER:
Think of a physical system which wants to oscillate, vibrate. It has what is called a "natural frequency". For example, a particular pendulum will oscillate with a period of ten seconds. Now, suppose you push on that system. If you push with a period which is far from the natural frequency, the system will vibrate but only with a very small amplitude. If you push on it with a period near the natural frequency, it will vibrate with a large frequency. That is called resonance, the fact that a force with period close to the natural frequency will have a large response.

QUESTION: :
Why is it when I look in a mirror, my left and right sides are reversed, but I am not reversed upside-down? I was reading a book, Odd Perceptions by Richard L. Gregory who writes that that no one knows for sure. That was back in 1986. Is there an explanation in the 21st century? Just curious.
ANSWER:
It is ridiculous to say that "no one knows for sure". Goes to show you�don't believe everything you read. Read my earlier answer.

QUESTION: :
I often hear from prominent ecologists the statement that "All (sometimes adjusted to MOST) energy on earth comes from the sun." I do not believe this. Gravity produces energy when something falls (hydroelectricity). The movement of tides does the same. So, my

QUESTION: is, where does the energy on earth come from, and how much can be attributed to the sun vs. other forms?
ANSWER:
Most cases of "energy from gravity" would be erroneous because in order for something to fall it has to be raised up. So, hydroelectric energy comes from water falling, but how did it get up there? The water evaporated out of the sea (read sun) and then fell as rain in the mountains. Your tidal example is one where the sun is not responsible (although the sun does play a minor role in tides); the moon lifts the water and then it falls. Also, geothermal energy comes from the ambient heat in the earth. And, radioactivity and other nuclear energy comes not from our sun but from some other star where the elements were created (as did you). There is no quantitative way we can neatly separate solar from nonsolar energy here on earth. I think that what is most important is which forms of energy can we tap using current technology. I would agree that, by that criterion, solar or solar-orginated (like petro energy sources) are the pretty clear winner.

QUESTION: :
If you had two positive point-charges, seperated by a given distance, and you drew a graph of the potential on the line between them, would the graph look like a squashed Gaussian curve, with a maximum at the centre point?
ANSWER:
No, actually the potential would be minimized halfway between and would look like a "U" with the potential rising at the charges.

QUESTION: :
Why do you think Physics is such a difficult course for some students?
ANSWER:
From my many years teaching, I can tell you that there is no single reason. One important reason is that students entering a physics course have often been poorly taught in mathematics and are unprepared for applying mathematics to something real. I have often been astounded by how college students can be unable to do even simple arithmetic. Another thing, which is getting worse all the time as testing is becoming the focus of so much primary and secondary education, is that memorization of facts and equations is not the key to success in physics; it sounds corny, but your physics teacher is trying to teach you how to think, not how to do physics. Often the problem is a deep-seated psychological aversion to things quantitative; how often have you heard somebody say "I'm just not a math person"? Or, I get so sick of going to a party and, when asked what I do, have a response like "you must be sooooo smart".

QUESTION: :
Often dreaming of black holes connecting to some parallell uinverse was ok to reflect on however my daughter and I were observing a graphic of a quasar and how there is a polar emmision of energy. From what I understand we view black holes as a dense body swallowing all in it's orbit without a trace assuming all matter consumed goes somewhere or somewhen. My

QUESTION: is could the matter consumed by a black hole be expelled at it's poles the same way as a quasar in the form of dark energy thereby contributing to the expansion of the universe?
ANSWER:
As I explain on the home page, I am not an astrophysicist. But I do know that mass does not disappear when it goes into a black hole. As the black hole captures mass it becomes more massive. Regarding your

QUESTION: about whether a black hole might be a source of "dark energy", I can only tell you that both dark energy and dark matter are things which are not at all understood and your guess is as good as any, I guess!

QUESTION: :
In Einsteins Theiry of Relativity there is a part that explains time dialation. If you were on a space craft going near the speed of light could you mechanicaly adjust the clock on board the craft to display the time on Earth?
ANSWER:
Sure, you could design such a machine but it wouldn't really be a clock, would it? It is like asking if we could build a clock which showed one hour passing during each 10 hours.

QUESTION: :
How do we communicate with things like the hubble telescope/ satellites/ the mars rover (e.g. is it with radio waves)? Is this communication instantaneous? If the hubble telescope was really far away (say, 1 light year), how long would it take to tell it what to do/ receive an image from it?
ANSWER:
Communication is done with radio. It certainly is not instantaneous, no communication is; the fastest speed of communication is the speed of light. To get or receive any information from something one light year away takes one year.

QUESTION: :
Why are iron, nikkel or cobolt more likely to magnetize as opposed to copper or aluminum?
ANSWER:
Every electron is like a tiny magnet. In most materials in nature, all the electron magnets are pointing in random directions and the material has only very weak magnetic properties. In a very few materials, called ferromagnetic materials, the crystal structure of the material has a tendency for the outer electrons in one atom to align themselves with the electrons in neighboring atoms and so very large numbers of tiny magnets all line up with each other and the whole thing looks like a magnet. One additional subtlety is that a piece of iron may not be a very strong magnet because the alignment happens over small regions called domains (small like maybe grain-of-sand-small, not atom-small) and the domains all have random orientations. But when you expose the iron to a magnet, those aligned with the external magnet grow at the expense of those not aligned, so the iron becomes magnetized and attracted to the external magnet.
To see

QUESTION: s and answers from longer ago, link here.