![]() QUESTION:
QUESTION:
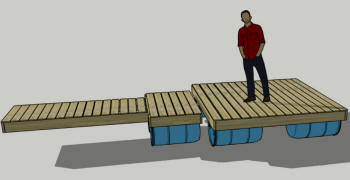
I am constructing a floating dock out of pressure-treated lumber and
55-gallon empty plastic barrels and want to ensure that I provide sufficient
buoyancy. Although the dock comprises a ramp and a platform, they will be
only loosely connected (with slack rope and eye bolts), and the buoyancy
calculations for the platform are easy; it's the ramp that is giving me
headaches. Specifically, one end of the ramp will be sitting on the shore
and the other end will be supported by the plastic barrels. The ramp is
T-shaped, with the lakeside end wider to accommodate the barrels. Please
give me some guidance as to how I might analyze a T-shaped structure with
the narrow end on shore and the wide end kept afloat by barrels, so that a
weight of w placed at any point on the ramp will not submerge the barrels
more than 45% (because, although I think I did a good job sealing off the
barrel caps, I'd rather not have to find out). Although I've meant for this
question to be somewhat general to allow for design modifications, I will
mention that I've built part of the ramp already, with the walkway being 3'
wide and 8' long, and the cross of the T being 5' wide and 3' long and
covering two empty barrels; I'm willing to add another section with more
barrels if needed. Any help in analyzing buoyancy of a T-shaped ramp with
the narrow end resting on land would be greatly appreciated!
![]() ANSWER:
ANSWER:
I will not be able to do any quantitative calculations without knowing the
weights of the ramp and dock. Also, will the level of the water remain
fairly constant?
![]() FOLLOWUP:
FOLLOWUP:
-
I must mention that I modified the design to make the walkway eight feet longer, so that it is now 16 feet long. Also, I had another empty 55-gallon barrel on hand, and placed it lengthwise under the walkway at the end where the walkway joins the cross of the tee. The salient data for the components are as follows:
-
T-shaped ramp (total weight 648 lb)
-
Walkway (463 lb) is 3 feet wide and 16 feet long; a 55-gallon drum is placed under the walkway on the lake end.
-
Cross of tee (185 lb): 5 feet wide and 3 feet long, covering two 55-gallon drums.
-
The dock platform weighs 515 lb and is 8'x8'. Four 55-gallon drums support it.
-
-
My dock will be located in a tributary of the Potomac River. As such, the water is tidal, varying in depth between 2 and 5 feet. (This is the reason I did not join the ramp and the platform rigidly, as I anticipate that the angle of surface of the ramp relative to that of the platform will fluctuate, given that one end of the ramp rests on the shore.)
-
In order to help visualize the situation, I am attaching three JPG images which I created in Sketchup. Please note that these images do not include the latest modification, whereby I lengthened the walkway and placed a barrel under its far end. Also, I recognize that you will probably make certain simplifications in order to expedite the analysis. That is fine with me; I only wish to obtain a rough idea of the limits of motion of the ramp and dock as I walk upon them.
-
At high tide the walkway and platform are approximately horizontal. At low tide the water level is about 2-5 feet down.
![]() ANSWER:
ANSWER:
Some preliminaries:
-
The volume of each barrel is 55 gallons=7.35 ft3;
-
the density of water is 64.2 lb/ft3;
-
each barrel is 45% submerged, so each barrel provides a buoyant force of 7.35x64.2x0.45=212 lb;
-
each barrel has a weight of 21.5 lb;
I will first do the platform which is easiest if you assume that the load is at the center.
-
The weight of the platform is 515 lb;
-
the weight of the four barrels is 21.5x4=86 lb;
-
the weight of the load will be denoted as W;
-
the buoyant force of the four barrels will be 4x212=848 lb.
Therefore, W=848-515-86=247 lb.
If
the load is not in the center, the total buoyant force will still have to be
848 lb but the platform will tilt so that two of the barrels will be
submerged more than 45% and the other two less than 45%. I made an estimate
of how much the platform would tilt if the load were moved over to 1 ft from
one side edge. Without going into details, the heavy side would go down by
about 2.8 inches and the other side would go up by the same distance; the
corresponding tilt would be about θ=4.50. This would make two of
the barrels 65% submerged, beyond your desired limit.
Next I will look at the walkway.
-
the weight of the tee and two barrels under it as well as the net buoyant force of those barrels act at 17.5 ft from the shore;
-
the weight and buoyant force of the third barrel act at 14.5 ft from the shore
-
the maximum weight W acts at a distance x from the shore;
-
there is a force F exerted up by the shore which we will not need to know;
-
I have assumed that the ramp has no interaction with the platform, since reference is made to "slack ropes".
All this is shown in my diagram. If one now sums the torques about the point of shore contact and sets that sum equal to zero, the product Wx can be solved for.
0=212x14.5+424X17.5-228x17.5-21.5x14.5-Wx-463x8=2488-Wx.
Wx=2488 ft⋅lb. So, for x=19
ft, the end of the ramp, W=131 lb. I am guessing that this result
does not make you happy!
I am not sure how rigidly coupled the platform and walkway are ("slack ropes"), but suppose that they are coupled as if, when horizontal, they were rigidly attached. So now the summed torque equation is 0=212x14.5+424X17.5-228x17.5-21.5x14.5-Wx-463x8+848x23-601x23=8169-Wx. So W=8169/x. So, for x=19, W=430 lb and for x=27, W=303 lb. It would seem that it is important that the coupling be designed such that the platform can help hold up the walkway. I figure that the walkway will only go down a maximum of about 150 at low tide; this should not significantly alter the estimates I made for the horizontal situation. So you should allow a fairly rigid coupling like some kind of hinge.
![]() QUESTION:
QUESTION:
The question relates to a medical procedure. If you fill a balloon to a
set pressure to use in a semirigid tube to dilate it, will the radial force
exerted on the tube by the balloon be different if the balloon is filled
with water as opposed to air? In otherwords, does the density of the medium
filling the balloon change the radial force exerted on the walls of a hollow
tube if pressure is kept constant? Is there a known law that describes this?
![]() ANSWER:
ANSWER:
I am afraid that your question is very ambiguous. I do not get the picture
at all. What is the idea, to use the balloon to pressurize the tube or vice
versa? When you say "to use in a semirigid tube to dilate it" what does "it"
refer to? Can you give me a description of what this device does and how it
is used? Would the tube be filled with water also? Is the patient horizontal
or vertical? Is the balloon above or below the tube?
![]() FOLLOWUP:
FOLLOWUP:
The tube is a hollow tube with muscular walls. The patient is laying
flat. The balloon is within the tube at an area along the tube that is
narrowed compared with the rest of the tube.
![]() ANSWER:
ANSWER:
Ah, one picture is worth a thousand words! Water has a density about
1000 times the density of air. Therefore, although you can ignore the
pressure differences between places at different heights for air, you can
possibly not for water. That is, the pressure will be higher at the bottom
of the balloon than at the top by an amount ρgd where
ρ is the density of the fluid, g≈10 m/s2 is the
acceleration due to gravity, and d is the diameter of your inflated
cylindrical balloon. For example, if d=1 cm=0.01 m the pressure on
the back side is 0.1 N/m2=1.5x10-5 psi larger at the
front for compared to 100 N/m2=0.015 psi for water. In other
words, the back side of the esophagus (I assume that is what this is) must
support the weight of the water creating a larger push by the balloon on the
back than the front. The density of the fluid does make a significant
difference; I have no way of judging whether the difference is enough to
make a difference in the efficacy of your device.

![]() QUESTION:
QUESTION:
But for my work, I need to figure out one parameter. Usual passenger
vehicle. We know door velocity (for instance driver door) and I need to
convert it to Joule. I am suppose that also need a mass (27 kg trim
assembled door), distance from hinge to outside handle (approximately 1000
mm) What also? Please share a proper equation.
![]() ANSWER:
ANSWER:
Joules measure energy. This would be kinetic energy of rotation. You do not
tell me what you mean by "door velocity"; I assume it is rotating about the
hinges with some angular velocity ω radians/second. Since it will
be rotating about the hinges, you need to know its moment of inertial I
about that axis; if you model the door as a uniform rectangle, I=ML2/3=27x12/3=9
kg m2. If it had an angular velocity of ω=1 rev/s=2π
s-1 then its rotation kinetic energy is K=˝Iω2=178
J.
![]() FOLLOWUP
QUESTION:
FOLLOWUP
QUESTION:
I am working in vehicle assembly plant and at the
end of a final line we measure all doors speed of closing (velocity). For
this check, DURR 5000 is used. It devise install at the edge of the rear
door when the front door is measured and at the rear body panel when rear
door is measured. For this measurement, we have upper limit borders: for
front/rear own. As I know, velocity 1.62 m/s it is about 5 J and 1.49 m/s is
4 J for our C-class model, at least I found these data in my documents. I am
puzzled that the result 178 J it is not appropriate equation (after my poor
explanation). Can you please figure out in Joules or provide equation then
is known: door mass = 27 kg, hinge to handle distance = 1000 mm, velocity =
1.1 m/s.
![]() ANSWER:
ANSWER:
Everything I did above was correct, but since you did not give me a velocity
in your original question, I had to make up a speed of 1 revolution per
second for the angular velocity; now that you gave me some velocities, I can
see that my guess was way too big. If the door is closing, then it is
rotating about the hinges. So specifying a velocity (1.1 m/s) does not tell
me anything because the speed depends on how far from the rotation axis you
are measuring. For example, if this is the speed of the center of the door,
the outer edge has a speed 2.2 m/s and the hinge edge has a speed of 0 m/s.
If I take the outer edge (1 m) as where the speed is measured, I find that
ω=v/R=(1.1 m/s)/(1 m)=1.1 s-1 and
therefore, K=˝Iω2=˝x(9 kg m2)x(1.1 s-1)2=5.45
J. The equation you want is K=˝Iω2=˝(ML2/3)(v/R)2
=M(vL/R)2/6 where L is the
distance from the hinge to the outer edge of the door and R is the
distance from the hinge to the point where v is measured. If
L=R, then K=Mv2/6. (Keep in mind that this
(I=ML2/3) assumes that the door's mass is uniformly
distributed in the radial direction which will certainly not be exactly
true. It would be most accurate if you could get a good measurement of the
moment of inertia about its hinges.)
![]() ADDED
THOUGHT:
ADDED
THOUGHT:
I looked up the use of this Durr 5000 device and saw it also
applied to sliding doors in addition to the hinged doors I have considered
in my answer. In the case of a sliding door the energy is K=˝Mv2.
![]() QUESTION:
QUESTION:
I apologize if this question seems a bit simple. I'm setting up a small
malthouse, and I have a plastic holding tank (not insulated) that holds the
water for the malting process. I'm trying to determine if I need to heat the
tank in the winter or not. The tank holds 18928 liters. The water comes into
the tank at 9 degrees C, and the ambient temperature around the tank is 17
degrees C. My question is, how long will it take the water in the tank to
reach equilibrium with the ambient temperature.
![]() ANSWER:
ANSWER:
To answer this question it is necessary to know the material from which the
tank is fabricated and its thickness and its geometry (mainly the area
exposed to the ambient temp).
![]() FOLLOWUP:
FOLLOWUP:
Okay, the tank is a cylinder with 102" diameter, and 154" high. The
walls are 1/4 thick, high density polyethylene.
![]() ANSWER:
ANSWER:
The equation for heat transfer through a conducting barrier is
dQ/dt=(kA/s)(Thigh-T)=3.17x103(290-T)
where k=0.47 W/(mˇK) is the thermal conductivity of high density polyethylene, s=0.25"=0.00635 m is the thickness of the barrier, A=43.15 m2 is the area of this tank, T is the temperature of the water as it warms, and Thigh=290 K. dQ/dt is the rate at which energy (heat) enters the tank.
The equation involving the rate of increase of the temperature of water to which heat is being added at a rate dQ/dt is
dQ/dt=mC(dT/dt)=8.51x107(dT/dt)
where m=20.5x103 kg is the mass of the water and C=4.19x103 J/(kgˇK) is the specific heat of water.
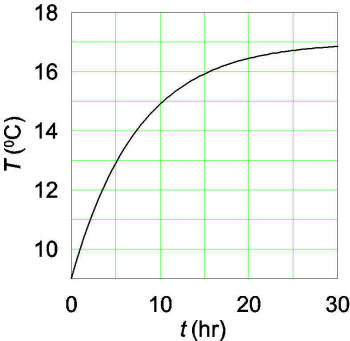
Combining the two equations, I find [dT/(290-T)]=3.73x10-5dt . Integrating and solving for T I find T=290-8ˇexp(-3.73x10-5t)=290-8ˇexp(-0.134t); the first expression is for t in seconds, the second for t in hours, and the temperature is in K. The final result is shown in the graph converting the Kelvin temperatures to 0C. Note that the temperature never (theoretically) reaches 170C, but a day to a day and a half would probably be fine for your purposes. (By the way, the volume which I calculated and used was 20.5 m3, a tad larger than the volume you quoted, 18.9 m3.)
![]() FOLLOWUP
(DIFFERENT QUESTIONER):
FOLLOWUP
(DIFFERENT QUESTIONER):
You recently worked out a heat
transfer/tank problem where you came up with: the equation "Integrating and
solving for T, I find T=290-8ˇexp(-3.73x10-5t)=290-8ˇexp(-0.134t)". Is this
e raised to (values), or is it 290-8^(-3.73x10-5 t). It's not clear about
the intermediate steps? Using Wolfram on-line integration, I get:
-log(290-T) + constant = 3.73x10^-5t. Just looking for clarity.
![]() ANSWER:
ANSWER:
exp(x) is standard alternative notation for ex.
The reason that an exponential function appears in the answer is that
Wolfram's log(x) is the natural log, ln(x) in more common
notation, and x=eln(x). So, if you have an
equation of the form ln(x)=y and you want to solve for
x, x=ey. Also, the integrator you used is
for indefinite integrals and you need to do an integration here from 282 to
T. You also need to remember the properties of logarithms, viz.,
ln(a)-ln(b)=ln(a/b) and ln(a)=-ln(1/a).

![]() QUESTION:
QUESTION:
Me and my brother are having a debate about running on a treadmill vs
running on a track. Not counting mental stuff like learning how to pace i
feel that the only real difference is wind resistance. He seems to think
inertia comes into play differently for each. I feel like once you are on
the treadmill and it starts moving that the treadmill track is your inertial
frame of reference so any change in inertia would require just as much
energy as it would on an outdoor track. He seems to think that since you
don't let the treadmill ever move you actually that you never have to work
against inertia of rest while you're accelerating or decelerating on a
treadmill. I mean if the treadmill was already moving at 10mph and then you
just jumped on it i could see his point but not if you start off standing on
the treadmill while its at rest and accelerate along with it.
![]() ANSWER:
ANSWER:
In terms of simple introductory physics, you are correct. However, there are
often subtle differences between simple physics and the real world when
applied to very complicated systems like the human body. Your brother is
also wrong because he is just trying to explain any differences in terms of
simple physics also. In fact, there are many differences between running on
a track and running on a treadmill due to biomechanics. A good article to
read is a post on the
RunnersConnect blog. Or just google treadmill vs. track.
![]() QUESTION:
QUESTION:
Is there a formula for calculating the side-ways deflection wind has on
a lawn bowl(over and above the bias deflection ) running at 12 s, the time a
bowl takes from delivery to stop over a 26 m distance over bowling green
grass?
![]() ANSWER:
ANSWER:
Once again, doing Ask the Physicist has led me to learn something new. I
never really knew anything about lawn bowls other than it is done on grass
and rolling balls are involved. For the benefit of others who are ignorant
of the game, let me summarize by describing the ball. (A good article on the
physics of lawn bowls balls can be found
here.) The ball is not a sphere but rather an oblate spheroid which
makes it sort of like a door knob but not so extremely flattened; but it is
slightly more flattened on one side of the ball than on the other which
results in a center of gravity being displaced to one side of the equatorial
plane as shown in figure (a). This results in a tendency for the ball to
curve left if it is rolling the angular velocity shown in the figures; this
motion is the "bias" referred to by the questioner which I am to ignore.
When rolling in the x direction (figure (b)), there is a frictional
drag force called, rolling friction D, which
opposes the motion (v) and eventually brings the rolling to a halt.
If there is a wind, there is a force W due to the
wind which tries to make the ball roll to the right (figure (a)) but if it
does roll, there will also be rolling friction trying to keep it from
rolling. In order for the wind to have any effect at all, it is clear that
we must have W>D; if this is not the case, there will only be
static friction in the y direction which will be equal and opposite
to W. A lawn bowls ball has a mass of about m=1.5
kg and a radius of about R=6 cm=0.06 m.
To get the equations of motion for the x and y motions, we first need expressions for D and W. The rolling friction may be expressed as D=-μmg where μ is the coefficient of rolling friction and mg is the weight of the ball. The force due to the wind may be approximated as W≈źAV2 where A=πR2 is the cross sectional area of the ball and V is the speed of the wind; this approximation is only correct if SI units are used. The equations of motion in the x-direction are
-
D=-μmg=max ⇒ ax=-μg
-
vx=v0-μgt
-
x=v0t-˝μgt2.
Here t is the time and v0 is the speed of the ball at t=0. If the ball is rolling in the y-direction because of the wind, the equations of motion are:
-
W=źAV2-μmg ⇒ ay=(źAV2/m)-μg
-
vy=[(źAV2/m)-μg]t
-
y=˝[(źAV2/m)-μg]t2.
It should be noted that if (źAV2/m)<μg, these equations imply that the ball will accelerate opposite the direction of the wind, obviously not correct; hence the wind will have no effect on the ball if V<√(4μmg/A). In that case, ay=vy=y=0.
So, having found the general solutions, let us now apply the solutions to the specific case from the questioner. We are told that when t=12 s, vx=0 and x=26 m. With that information you can solve the x-equations to get v0=4.32 m/s and μ=0.037, reasonable values compared to numbers in the article I read. The area is 3.14x0.062=0.0113 m2. The first question we should ask is what is the minimum speed of the wind to have any effect at all: Vmin=√(4x0.037x1.5x9.8/0.0113)=13.9 m/s=31 mph=50 km/hr; this is a pretty stiff wind, so the wind probably has no effect on bowling under normal conditions. So, just to complete the problem, consider V=15 m/s=34 mph=54 km/hr.
-
vx=4.32-0.363t vy=0.0612t
-
x=4.32t-0.182t2 y=0.0306t2
The trajectory during the 12 seconds is shown in the graph below; after 12 seconds the ball will continue accelerating in the y direction.
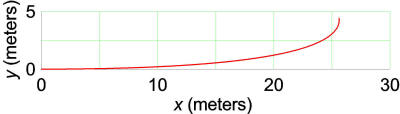
So the bottom line is that unless you are playing in a gale-force wind, the wind has no effect on the ball if the wind has no component along the original direction of the ball (which I have called the x-axis). You can tell if wind makes a difference by simply setting the ball on the groundunless the wind blows the ball away, you need not worry about its effect. If the wind is blowing in the +x or -x direction, that is a whole different thing, but the questioner asked for the sideways deflection.
![]() ADDED
THOUGHTS:
ADDED
THOUGHTS:
This question continues to intrigue me and I have carried
my investigation further. The question originally stipulated "over and above
the bias deflection" so my whole discussion totally ignored the fact that
the ball, owing to its off-center center of mass, will curve. At the very
end of my answer I noted that if the wind is not perpendicular to the path
of the ball, it would be a different story; indeed for a spherically
symmetric ball I showed that, except for very strong winds, a wind
perpendicular to the path has no effect at all. However, for an actual lawn
bowls ball, the path curves to where a wind in the y-direction
might have a significant component along the path. I have calculated
(graphed below) the x and y positions of a realistic path
with no wind using equations (10) and (11) of the
article referred to above. To do these I used all the numbers used above
(R, m, A, v0,
μ); I used the moment of inertia for a solid sphere ( I0=Icm+mR2=(7/5mR2))
and chose the COM off-center distance to be d=1 mm. As you can see,
the curving is substantial, carrying the ball about 4 m from its original
direction. You can see that now a wind of any magnitude can have an effect
on the trajectory. The angle φ which the tangent to the
trajectory is given in the article as φ=(2/p)ln(v0/(v0-μgt))
where p is a constant also given in the article. As can be seen,
once the trajectory leaves the x-axis the wind contributes with the
component of its force along the trajectory; this has the effect of reducing
the effect of the frictional force causing the ball to slow down less
rapidly. However, this is now like having a time dependent force of friction
which, I believe, will lead to equations of motion which will not have an
analytical solution but would have to be solved numerically.

![]() QUESTION:
QUESTION:
For a snow plow that is very heavy, is there an advantage to having the
connection point of the winch line up high so that there is less weight to
pull or is there no difference? I can send a picture for clarification.
![]() ANSWER:
ANSWER:
Yes send me a picture. You are talking about a winch which is used for what?
Pulling a stuck vehicle? Lifting and lowering the plow? What?
.png)
.jpg)
.jpg)
![]() FOLLOWUP
QUESTION:
FOLLOWUP
QUESTION:
Yes, lowering and lifting a plow. The problem is
that the plow is out very far out and that my winch is mounted pretty low on
my machine. So instead of the winch simply lifting the plow up, right now it
is mostly pulling backwards and then that is making the plow come up. I
attached a picture of what the manufacturer recommends but I haven't had too
good of luck with them in the past. The last two pictures are of my machine.
You can see how far out the plow is and how low my winch is. Would that
pulley and cable system helped at all?
![]() ANSWER:
ANSWER:
You may not want to get the full physics explanation here, so I will first
give you a qualitative explanation. The tension T
in the strap is what is lifting plow and any part of it which is horizontal
(TH) is wasted. Your gut feeling is right, "
it is
mostly pulling backwards
" Anything which you can do to increase the
vertical part (TV) will make the lift easier, and moving
the winch up is a good way to do this but it might be easier to have a
pulley higher up which then brings the strap back down to the winch.
The figure shows all the forces on the plow assembly: the weight W which acts at the center of gravity (yellow X), the tension T in the strap (where I have shown vertical (TV) and horizontal pieces (TH)), and the force the truck exerts on the support which I have represented as its vertical and horizontal parts, V and H respectively. (Note that the various forces are not drawn to scale since T has to be much larger than W to lift the plow.) Suppose T is just right that the plow is just about to lift. Then the sum of all the forces must add to zero, or V+TV-W=0 and H-TH=0. The sum or torques must also add to zero; summing torques about the point of attachment to the truck (light blue X), WD+THs-TVd=0. Note that the TV is trying to lift the plow but TH is trying to push it down. Now, in order to get a final answer for the unknowns (which are T, V, and H) we note that TV=Tsinθ and TH=Tcosθ where θ is the angle which the strap to the winch makes with the horizontal. The final answers I get are:
-
T=DW/(dsinθ-scosθ)
-
V=W-Tsinθ
-
H=Tcosθ
I put in some reasonable numbers just to get an idea of the answers, W=500 lb, θ=200, D=2m, d=1.8 m, and s=0.1 m. Then T=1920 lb, H=1800 lb, and V=-157 lb. The negative value for V means that V is down, not up. In this scenario, the pulling force has to be nearly four times greater than than the weight being lifted.
Now
we need to look at whether the manufacturer's suggestion will be better than
a straight shot to the winch. Now there are two forces pulling up, the
tension T from the pull point to the winch and the
tension P from the pull point to some anchor
higher up. Of course the magnitudes of these two tensions are the same,
P=T. The picture shows only the pulling forces, the rest are the same
as in the picture above. There are still three unknowns, T, V,
and H. I will call the angle that P makes
with the horizontal φ. I will not show the details, just give the
final results:
-
T=DW/[d(sinθ+sinφ)-s(cosθ+cosφ)]
-
H=T(cosθ+cosφ)
-
V=W-T(sinθ+sinφ)
As a numerical example, I will use the same numbers as above and add φ=400. Then T=624 lb, H=1070 lb, and V=-115 lb. It is definitely advantageous to use the manufacturer's suggestion here which, in my numerical example, reduced the force the winch needed to exert by a factor of about 3.
![]() QUESTION:
QUESTION:
What would a chart of an 8g impact look like for an 8g impact with a 100
ms duration? I can send a jpg of what I am told fits the requirement. But I
seriously doubt that it does fit the requirement. But then again I am barely
understanding the test. I see spikes to 20-30g. I am having a hard time
finding anyone that can answer this question. (I asked for more
information.)
![]() FOLLOWUP
QUESTION:
FOLLOWUP
QUESTION:
These are the charts provide by the AF to me when they
tested a pallet that we built.
The requirement is: Ultimate load. When uniformly loaded to 10,000 pounds,
the load being restrained to the pallet by chains, the pallet installed
between restraining rails locked to the rails by 2 locks through each rail
and engaging 2 lock notches on each side of the pallet, and resting on 4
rows of conveyor as specified (see 3.4.5.1), the loaded pallet shall
withstand a dynamic load of 3 times the force of gravity (g's) for a period
of 0.1 second. The pallet shall be serviceable after undergoing the test. In
addition, the pallet shall withstand a dynamic load of 8 g's for a period
not less than 0.1 second. The pallet need not be serviceable after
undergoing such a load; however, the pallet shall remain in one piece.
These are the result of those tests. These charts just do not look right to
me in their conclusions. I am not a math major, but I do understand some
stuff and this does not look correct. ie. "Area under the curve." or correct
averaging. If you can set me straight or put me on another path it would be
greatly appreciated.
![]() ANSWER:
ANSWER:
So, I must admit that I do not understand all the details of the
requirements (locks, chains, notches, etc.) What I can do, though,
is estimate the area under the curve which seems to be one of your main
concerns. I drew in a rough fit (green) to the data (red) and calculated the
area under the green curves (keeping in mind that the area of the triangular
segment below the axis is negative). As you can see, the area I got as a
rough estimate is 0.37 compared to the actual area of 0.35. The average
would simply be the area/time=3.5. My guess is that your pallets did not
fulfil the requirements since the precipitous drop before the 0.1 s had
passed would seem to indicate a collapse of the pallet. Both tests show this
behavior, with the 8g test having the "collapse" occur earlier as would be
expected. However, since I do not understand the details of the test well
enough, I would not take my guess as gospel.

![]() QUESTION:
QUESTION:
I teach middle school science, however I've spent more time advancing my
understanding in several of the other science disciplines I teach so my
ability to work through this problem is above my current skill set. However
I would really like to be able to walk my students through this scenario, in
part because I'm not good with subtlety. I would like to know what other
variables I need to measure/know in order to calculate the force a
hypothetical student's head would experience at the moment it hit the floor
after they tipped their chair back too far (despite numerous warnings not
to). I imagine I'll need the Mass of the hypothetical student + the mass of
the chair. The Time from when the hypothetical student's center of gravity
passes over the point of rotation for the chair, the Height of the
hypothetical student's head is above the floor. With Gravity being constant,
I "should" have all the necessary information to calculate this (no chance
at all will I let my students try to measure the force in real life) but I
still have the niggling sense that I'm missing some variable.
![]() ANSWER:
ANSWER:
Let's first do the simplest estimate: imagine dropping the head from
about h=1 m above the floor. The speed the head would hit the floor
could be found from energy conservation, ˝mv2=mgh
or v=√(2gh)=√(2x9.8x1)=4.4 m/s. Now, you either need to
know the distance the head stops in or the time it takes to stop. There is
not much give in either the head or the floor, so let's just guess that the
distance it takes to stop is 3 mm. If you do the kinematics, the
acceleration of something moving 4.4 m/s and stopping in 3 mm is about 3000
m/s2, about 300 gs! If you take the mass of the head to be about
4.5 kg, the force is about F=ma=13,500 N=3000 lb. The time over
which this force acts is very short, about 4.4/3000=0.0015 s.
To be fancier, you would have to do the rotational problem. The student plus the chair have a certain moment of inertia I and when they rotate about the rear chair legs they acquire a rotational velocity ω when the center of mass has fallen a distance h. In that case ˝Iω2=mgh and so ω=√(2mgh/I); now you can get the speed the head hits the ground by writing v=Lω where L is the distance of the head from the rear legs of the chair. But to calculate the moment of inertia of the student/chair would be very complicated and, in the end, the speed of the head would not be all that different from the simple calculation above. And you still have to make approximations over how far it would travel to stop. Just use the simple head dropping calculation to convince the students that the order of magnitude of the force would be a few thousand pounds.
![]() QUESTION:
QUESTION:
I am working on a science fiction book and have a bombardment of a
planet happening. I would like to get an idea of the force of impact of 2
kinetic kill vehicles
1 is a 10 pound Depleted Uranium ball.
2 is a
100 pound Depleted Uranium dart.
They are traveling at 1/10th light
speed.
They impact an Earth like planet.
I only need a ballpark
value. If either or both are some how destroyed interacting with the
atmosphere or cause some other effect, that would be good to know too.
![]() ANSWER:
ANSWER:
I am not sure what the material being depleted uranium has to do
with anything. Also, "force of impact" cannot be calculated unless you know
the details of the collision, in particular how long the collision lasted.
You could estimate the kinetic energy classically for your projectiles
because the speed is much less than the speed of light. 1 lb is about 4.5
kg, so K≈˝mv2=˝x4.5x(3x107)2=2x1015
J=2000 TJ (terajoules); the Hiroshima bomb had an energy of about 63 TJ.
If the collision lasted 10 s, this would correspond to a power of 200 TW
(terawatts). To give you a feeling for the magnitude of this power, the
total output of all power sources on earth is about 15 TW. The 100 lb
projectiles would have 10 times the energy and power as the 10 lb
projectiles. So those things would have quite a punch. Here is the problem
that most sci-fi writers never think about, though. Whoever is firing these
projectiles has to give them this energywhere are you going to get 200 TW
in the middle of empty space?
Now, the second part of your question. These things have a speed (3x104 km/s) which is much faster than the fastest meteor (72 km/s) and you know what happens to themthey burn up and break up. The recent (2013) Chelyabinsk meteor exploded at an altitude of about 20 mi and most of its energy (about 1500 TJ) was absorbed by the atmosphere. It had a much smaller speed than your projectiles (about 20 km/s compared to about 30,000 km/s) but a much larger mass (about 107 kg compared to 4.5 kg), so the energies were quite comparable (1500 TJ compared to 2000 TJ). So I would guess that your projectiles would not do much damage to the objects on the surface of the planet.
![]() QUESTION:
QUESTION:
i'm traveling at the speed of sound and a gunshot is fired at the exact
moment I am passing the gun, what is the resulting sound that I hear and for
how long?
![]() ANSWER:
ANSWER:
The figure shows the plane at three times:
-
just after the gun has been shot;
-
at the time when the sound reaches where the plane had been at time 1;
-
at a time twice as long as 2.
Also shown are the corresponding spherical wave fronts of the sound from the shot. As you can see, the wave fronts never catch up with the plane. You will never hear the gun.

![]() QUESTION:
QUESTION:
I am a nurse at a long term care facility. My back hurts every time I
get finished pushing a medication cart for the 8 hour shift. My question
is...If the medication cart weighs 220 pounds when assembled, how much
weight am I pushing given the fact it is on wheels?
![]() ANSWER:
ANSWER:
You may assume that the wheels almost remove the frictional force of
moving forward; in other words, it takes very little force to keep it moving
once it is up to speed. The times you need to exert a significant force on
the cart would be when it speeds up or slows down. The more quickly you
bring it up to speed or bring it to rest, the larger force you need to
exert. So plan ahead and speed it up or slow it down gradually. Here is an
example: if you sped the cart up to a speed of about 6 ft/s in 1 s, you
would need to exert a force of about 40 lb, whereas if you took 2 s, the
needed force would be about 20 lb. Also, when you turn a corner, go slowly
since it takes a force to turn the cart also and the faster you take the
corner, the greater the required force.
![]() QUESTION:
QUESTION:
I have a small (15' diameter) swimming pool. I have a round leaf netk,
about 17' in diameter, which I suspend over the pool as follows: I took 5
10' lenghts of 1" PVC electrical conduit, and joined them end-end to form a
hoop/circle ca. 16' in diameter. The round leaf net has a drawstring, so I
placed the 17' diameter leaf net on the ground, then placed the 16' diameter
on top of the net. Then I folded the excess leaf net up above the conduit
hoop and tightned the drawstring. So far so good -- net below hoop, edges
wrap around hoop, drawstring holds the net on the hoop. I suspend this
hoop-supported net from a single point in the middle of the circle formed by
the hoop/net. From this central point, I have 10 "spokes" of cord (parachute
cord) going to 10 points along the hoop. The pieces of cord forming these
"spokes" were measured carefully to all be the same length. Here's my
question: When I suspend this hoop/net from this central point and the 10
lengths of cord (spokes), the hoop/net does not want to stay in a plane.
Instead, 2 opposite sides (e.g. at 12 and 6 on a clock face) lift
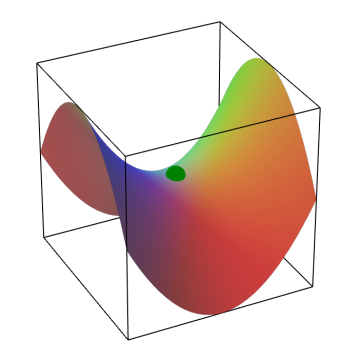 up,
and the other opposite sides (e.g. at 3 and 9 in the clock face) drop down.
I know in German, when a bycicle wheel gets stressed too much and deforms,
this is referred to as an "eight" -- I suppose because from the edge it may
resemble an eight. I suspect there is something similar going on with my
hoop/net, but don't really understand enough to know for sure. As a followup
question, I would be grateful for any thoughts as to how I might get this
hoop/net to remain in a plane. Many people suggest just tightening up
(shortening) some of the "spokes" but I have tried this and it does not
help.
up,
and the other opposite sides (e.g. at 3 and 9 in the clock face) drop down.
I know in German, when a bycicle wheel gets stressed too much and deforms,
this is referred to as an "eight" -- I suppose because from the edge it may
resemble an eight. I suspect there is something similar going on with my
hoop/net, but don't really understand enough to know for sure. As a followup
question, I would be grateful for any thoughts as to how I might get this
hoop/net to remain in a plane. Many people suggest just tightening up
(shortening) some of the "spokes" but I have tried this and it does not
help.
![]() ANSWER:
ANSWER:
The surface defined by your deformed loop is called a saddle point.
Because the pvc is pretty flexible (you were able to easily bend it into a
hoop), unless the weight is distributed very symmetrically, it is quite
possible for this kind of warping to take place. To minimize this uneven
distribution of weight, your spokes should be connected to the points where
you have used straight through connectors to connect the pvc pipes and the
points opposite as shown in blue in my drawing. But I suspect that there
will still be an asymmetric distribution of mass and the circle will deform
again. If so, then you will need to add crossbars as shown in red; this
should keep the hoop pretty resistant to deformation. You will probably only
need 3 spokes now and if it does not hang so the plane of the hoop is
horizontal, you can just adjust the lengths. It would also be good to have a
cord coming straight up from the center, maybe another piece of pvc to which
the spokes could be attached or just another cord. You could get some idea
of the balance by just hanging it from the center.

![]() QUESTION:
QUESTION:
I was fishing and the water was rough. Waves crashing all over. Then I
look over and see a perfect about 20M circle of calm water while the whole
lake is thrashing about. It lasted for about 5mins. The water was about
20feet deep and there was not large rock anything different where the circle
appeared. The calm circle did not appear to be like a vortex or whatever of
water. It was calm and not rotating. Can you explain the physics behind this
or at least give me a guess of what you think caused this. (It almost looked
like an object that was not visible to the naked eye caused it but I know
thats not true)
![]() ANSWER:
ANSWER:
I was just about to reply that I have no idea but just googled
calm water in a storm. It turns out that there is an old sailor's trick
to calm water in choppy conditions: just pour a little oil on the surface.
There seems also to be
physics
understanding of this phenomenon. For a good overview, see the
discussion on
Physics Stack Exchange. Perhaps there was some oil in your calm
area.

![]() QUESTION:
QUESTION:
How could I measure the viscosity of pizza sauce (and other materials)
using "at home" equipment? I want to determine the viscosity of a sauce,
then take the pizza sauce and place it on a turntable whose speed can be
controlled and see what speed is required to make the sauce flow from the
center to the edge.
Then, I want to alter the sauce and make it more and/or less watery (changing its viscosity) and measure that new sauces viscosity.
Then, I'll take the new sauce and re-measure the turntable speed necessary to make the new sauce flow from the center to the edge.
Last, I want to replicate the tests enough times so I can create an equation that would allow me know what turntable speed would be necessary to correctly flow the sauce based upon the viscosity of the substance.
![]() ANSWER:
ANSWER:
Why not just experiment with sauces until you find the right
thickness to achieve what you want? Measuring the viscosity (not an easy
task) is just an unnecessary step in the process.
![]() FOLLOWUP
QUESTION:
FOLLOWUP
QUESTION:
The reason is that I want to be able to alter the
sauce, test the viscosity, then know how much to alter the speed of the
rotating table consistently. Knowing, for example, a 1% increase in
viscosity requires a 5% increase in rotation speed allows me to continuously
alter the sauces and know with certainty the speed the table must rotate.
![]() ANSWER:
ANSWER:
This must be a science fair project or something because it will
certainly not be of any help in making pizzas in the real world. In a pizza
you want to spread the sauce uniformly over the whole area, right? What
causes the sauce to move out on the rotating turntable? There is a
(fictitious) force F, the centrifugal force, which pushes the sauce
out, F=mv2/R for a mass m with speed
v when at a distance R from the center. But, the speed
depends on the distance from the center, v=Rω where
ω is the angular velocity; so F=mRω2 and an
ounce of sauce experiences a bigger force as it moves out. In other words
the sauce will tend to all be pushed out the the rim of the pizza regardless
of its viscosity. If the viscosity of the sauce too large, the centrifugal
force might be too small to move the sauce at all, so there would be the
tendency for the sauce to stay in the center. In any case, I cannot imagine
that it is possible to use rotation to get a uniform spread of sauce.
If you still want to pursue this, I found the description of a straightforward experiment to measure viscosity μ. You get a tall cylindrical container and fill to a depth d with the fluid (density ρf). Drop a sphere (density ρs radius R) into the fluid and measure the time t it takes to reach the bottom; then the velocity of the falling sphere was v=d/t. The viscosity is then μ=(4R2g( ρs-ρf))/(9v). It will be a little tricky since the sauce is not transparent. Also, it is important that the sauce be homogeneous, no chuncks in it.

![]() QUESTION:
QUESTION:
What happens to the atmosphere inside a cupping vessel when a flame is
introduced and causes a partial vacuum (negative pressure) - which allows
the therapeutic vessel to adhere to the skin surface? What are the physics
that explain this happening?
![]() ANSWER:
ANSWER:
Cupping vessels have been in use for thousands of years. Ancient
Greek and Roman physicians used them to assist in
blood letting.
Chinese medicine uses them to
treat a variety
of maladies; cupping therapy is generally considered pseudoscience by modern
medicine. The idea is to provide suction on the surface of the skin and is
achieved by first heating the cup and air inside and then placing it on the
skin. As the air inside cools, the pressure decreases. The physics of this
pressure decrease can be understood by examining the ideal gas equation
which relates pressure P, temperature T, volume V,
and amount of gas N: PV=NRT where R is a constant
which depends on the units you use. So, as you can see, keeping the volume
and amount of gas constant, if the temperature decreases the pressure must
decrease. The fact that P∝T is sometimes called
Gay-Lussac's law.
A similar thing happens when canning food in glass jars. The canning is done with the contents very hot and a lid which is slightly domed is affixed. As the contents cool, the pressure decreases causing the dome to pop inward toward the contents, signaling that a good seal has been achieved.
![]() QUESTION:
QUESTION:
I am a hot air balloon pilot. I am trying to develop a mathematical
formula, for calculating where my Scoring baggy will land, when I
participate in a Ballooning event. I am given a location in a Pilots
briefing, as to where the Scoring X's are located. I attempt to fly to that
particular location, drop my Scoring Baggy on the X, and earn points
depending on how close I am to the center of the X. (Each Leg of the X is
approximately 100' to 300' long, depending on the Ballooning event.)
-
The Scoring Baggy (6 ounces) has a constant weight.
-
My Balloon's Speed, as I approach the Target, is a variable. the Scoring Baggy will share that speed once I release it, Correct ?
-
And, the height I release the Scoring Baggy from, at the time I release it, is also a variable, correct ?
My question is, is there a Mathematical formula that will calculate, how many feet from where I release the Scoring Baggy, it will land ? And how long it will take ?
![]() ANSWER:
ANSWER:
This is not a simple question. Although it would be simple if air
drag were neglected, I suspect that it is not negligible for the bag
weighing only 6 oz. I will do the calculation without air drag here. I will
not include the details, just the final results. The time t in
seconds it takes for the bag to hit the ground is t=√(2h/g)=ź√h
where h is the height in feet from which you drop it and g=32
ft/s2 is the acceleration due to gravity. For example if you drop
it from h=144 ft, t=3 s. The distance x in feet
it will travel horizontally in this time is x=vt where vx
is the horizontal speed of the balloon in ft/s when you drop it; so if vx=20
ft/s (about 13.6 mph) and you drop it from 144 ft, x=60 ft. The
equation for x can be written as x=źvx√h
which is handy if you do not care about the time. Note that the weight
of the bag does not come into this at all.
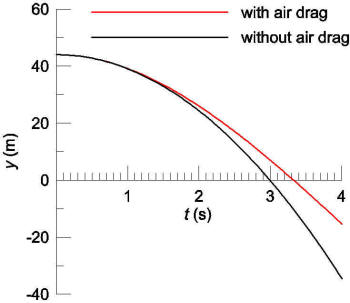 Warning:
this is pretty mathematical and probably not a computation you would want to
do in the heat of a competition! For my own interest, I want to estimate how
much error is introduced by neglecting air drag. It is much more complicated
if you include air drag. For this case, I need to do the calculation in SI
units rather than English units. The reason I need to use SI units is that I
will estimate the air drag force as Fd≈ź(vy2/A)
where vy is the vertical velocity of the bag and A
is the area it presents to the onrushing air; this estimate is correct only
for SI units because it has things like the density of the air at sea level
built into it. Now, it is my understanding that the speed of a hot air
balloon moving horizontally is the same as the speed of the wind; in other
words, from the perspective of a person riding in the balloon, he is in
perfectly still air. This greatly simplifies the problem because the bag
will drop straight down as seen from the balloon, i.e. it should
strike the ground directly below the balloon. So, the bag sees two forces,
its own weight mg down and air drag up; Newton's second law becomes
may=m(dvy/dt)=-mg+ź(vy2/A).
This is a first-order differential equation has a solution vy=-[√(g/c)]tanh([√(gc)]t)
where c=A/(4m). This solution is also a differential
equation since vy=dy/dt where y
is the distance above the ground; solving this differential equation, y=h-(1/c)ln(cosh([√(gc)]t).
A graph of this function compared to the case above for dropping from 144 ft
(note that 144 ft=44 m) is shown. (I approximated the area of the bag to be
0.01 m2≈16 in2=4x4 inches.) The time for the bag to
hit the ground is now 3.33 s rather than 3 s, approximately 10% longer
meaning that you should drop it when you are 66 ft from the target rather
than 60 ft. If you are lower the correction is smaller, if you are higher
the correction is larger. Given the circumstances under which you must act,
I would expect the inclusion of air drag to be unnecessary unless you are at
a very high altitude and that you should just drop it when you are about
x=źvx√h from the target.
Warning:
this is pretty mathematical and probably not a computation you would want to
do in the heat of a competition! For my own interest, I want to estimate how
much error is introduced by neglecting air drag. It is much more complicated
if you include air drag. For this case, I need to do the calculation in SI
units rather than English units. The reason I need to use SI units is that I
will estimate the air drag force as Fd≈ź(vy2/A)
where vy is the vertical velocity of the bag and A
is the area it presents to the onrushing air; this estimate is correct only
for SI units because it has things like the density of the air at sea level
built into it. Now, it is my understanding that the speed of a hot air
balloon moving horizontally is the same as the speed of the wind; in other
words, from the perspective of a person riding in the balloon, he is in
perfectly still air. This greatly simplifies the problem because the bag
will drop straight down as seen from the balloon, i.e. it should
strike the ground directly below the balloon. So, the bag sees two forces,
its own weight mg down and air drag up; Newton's second law becomes
may=m(dvy/dt)=-mg+ź(vy2/A).
This is a first-order differential equation has a solution vy=-[√(g/c)]tanh([√(gc)]t)
where c=A/(4m). This solution is also a differential
equation since vy=dy/dt where y
is the distance above the ground; solving this differential equation, y=h-(1/c)ln(cosh([√(gc)]t).
A graph of this function compared to the case above for dropping from 144 ft
(note that 144 ft=44 m) is shown. (I approximated the area of the bag to be
0.01 m2≈16 in2=4x4 inches.) The time for the bag to
hit the ground is now 3.33 s rather than 3 s, approximately 10% longer
meaning that you should drop it when you are 66 ft from the target rather
than 60 ft. If you are lower the correction is smaller, if you are higher
the correction is larger. Given the circumstances under which you must act,
I would expect the inclusion of air drag to be unnecessary unless you are at
a very high altitude and that you should just drop it when you are about
x=źvx√h from the target.
![]() ADDED
COMMENT:
ADDED
COMMENT:
It occurs to me that I have assumed that the wind speed and
direction are the same at all altitudes. This will not be true in the real
world and I am told that taking advantage of this is how hot air balloons
can get some control over direction of travel. Obviously, trying to do a
calculation including this would be impossible other than for a particular
set of wind velocities as a function of altitude.
![]() QUESTION:
QUESTION:
The ideal gas law says that pv=nrt. If I have a balloon filled with an
inert gas and put heat into the balloon while holding the volume constant
the pressure will increase on the left side of the equation and the
temperature will increase on the right side of the equation. If I remove the
heat source and allow the balloon to expand the volume will increase and due
to the gas laws the pressure will decrease by the inverse of the volume
keeping the value for pv constant. However, on the right side of the
equation with a constant number of molecules the temperature will decrease.
How can pv remain equal to nrt with the temperature decreasing and pv
remaining a constant value?
![]() ANSWER:
ANSWER:
What makes you think that PV will remain constant? This is
called an adiabatic expansion, a process where no heat enters or leaves the
system. What remains constant is PVγ
where γ is a constant which depends on the gas. For example, for a
monotonic gas γ=5/3 and for a diatomic gas γ=7/5. Once you
know what the new P and V are you can get the new T:
T=PV/NR.
![]() QUESTION:
QUESTION:
So while I was a little kid due to numerous headaches I had, I was
scanned in an MRI machine. I was feeling a little anxious when the machine
was put on and my mom came to me to ease my anxiety. She had her wallet with
her and pretty much all her cards went dead. What exactly causes magnetism
to destroy payment/membership cards?

![]() ANSWER:
ANSWER:
The magnetic strip is just like magnetic recording tape. There is a
layer of very fine particles which are magnetizable. Data is written on the
tape by using an electromagnet called the recording head; when the magnet is
turned on the particles become magnetized. So the data is written in stripes
in a code, sort of like the UBS labels used to scan products at the cash
register. In a magnetic strip, the card moves by a tiny coil in which a
current is caused to flow when the magnetic stripe goes past it. Since
magnetic fields are used to create the magnetized particles, magnetic fields
can be used to destroy them. Even a relatively weak field, if present for a
long enough time, can mess up the data on a magnetic strip. An MRI machine
has a huge field and it would easily demagnetize the strip.
![]() QUESTION:
QUESTION:
I would like to perform a calculation of a man descending a tower using
cords and subjected to the action of the winds. I have been trying to find
some equations but it is somewhat difficult due to the drag force. My main
objective is to calculate the maximum horizontal distance x that the man
could reach due to the wind action against the technician descending the
tower using cords.
Tower height: 78 m (please consider up tower as a
zero reference).
wind speed: 20 m/s
Mass of man: 70 kg
Man
descending with constant speed and slowly.
So, please what is the
maximum distance when the man is at 66 m from the top of the tower ?
![]() ANSWER:
ANSWER:
As shown in the figure, there are three forces on the man, his
weight mg, the tension in the cords T,
and the force of the wind F. The equations of
equilibrium are F-Tsinθ=0 and mg-Tcosθ=0.
Solving, tanθ=x/y=F/(mg), so
x=ytanθ=Fy/(mg). Now, how can we get F?
There is a very good approximation to the drag force by air at sea level
moving with speed v: F≈źAv2 where
A is the area of the object presents to the onrushing air (and which
works only for SI units). Finally, x=Av2y/(4mg).
If I approximate g≈10 m/s2 and A≈1 m2
and use your numbers, x≈9 m.
![]() ADDED
COMMENTS:
ADDED
COMMENTS:
I should have emphasized that air drag calculations are
only rough calculations, probably accurate to maybe ą20%. Also, for
your situation, the general approximation for x as a function of
y is x≈y/7. Also, if the horizontal displacement seems too
large, keep in mind that 20 m/s is a very strong wind, about 45 mph which is
gale force.
![]() QUESTION:
QUESTION:
Please explain me that why if a thin layer of water is spilled on a
rough surface like plastered floor and we place our finger in it then why
water move away from the point of contact of our finger on that surface and
it appear to be dried around.
![]() ANSWER:
ANSWER:
This is probably akin to the similar phenomenon of a foot pressing
down on wet sand and the area close to the foot is visibly dried. I found an
explanation on
Physics Forums which seems to be correct: "The phenomenon being
described is called 'Dilatancy' and was discovered by Reynolds about 100
years ago. It works only when you have well compacted sand that contains
just enough water to cover all the individual grains. When you stand on the
sand you create a stress / force which causes the sand to move. In order for
the sand to move / flow individual grains have to be able to move past one
another. Imagine a bunch of oranges stacked as you might see them at a
grocers. The first layer has them all tightly arranged and then the second
layer sits down into the gaps between the oranges on the first and third
layer. Now imagine trying to move one of the oranges in the second layer. In
order to move it the oranges on the first and third layer mut move down and
up respectively to enable the orange to move. Effectively the volume of the
pile of oranges or grains of sand increases with bigger gaps in between. So
when you put your foot down on the sand it shoves sand out the way but in
doing so the volume in between grains has to increase temporarily to allow
the grains to move relative to one another. Consequently all the fluid at
the surface is sucked by surface tension into the extra gaps made by the
rearrangement of the sand. Since there is no longer any fluid at the surface
the grains of sand are now dry." If you go to the original Physics
Forums question, ignore all the early answers which are wrong.
![]() QUESTION:
QUESTION:
Say I fill an airtight barrel with water and have a valve at the bottom
and a feeder hose at the top. If this barrel is uphill and I have the feeder
hose down lower say in a pond will the draining of the barrel through the
lower valve create enough vacuum to pull the water uphill creating a siphon?
![]() ANSWER:
ANSWER:
First of all, I would call what you are proposing a pump, not a
siphon. You are trying to "suck" water uphill using a vacuum. The first
thing that comes to mind is that there will be a limit on how high the hill
is above the water level below. Even if you have a perfect vacuum, the
highest you can lift water this way is 10.3 m=33.9 ft. But you start off
with a hose full of air, so you will never get a vacuum, so you will be
limited further in the height to which you can pull the water from below.
For example, if the volume of the air in the hose were 1/10 of the volume of
the barrel, you could only lift the water 9.3 m. Or, if the volume of the
air in the hose were equal to the volume of the barrel, you could only lift
the water 5.1 m. So there is no simple answer to your question, but this is
probably not a very workable way to lift water.
![]() QUESTION:
QUESTION:
How much heat would it take to heat 1 gallon of water to 600 deg F in a
pressurized system, from 70 deg F to 600 F in 1 hour. Not counting the ss
vessel. Also since the water is not allowed to change states are the
calculations just the Sensible heat cals or are there special calculations
needed. This is part of a R&D Application.
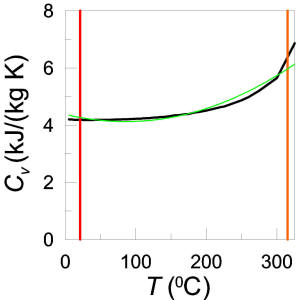
![]() ANSWER:
ANSWER:
For my approximation to be fairly accurate, the water must remain
liquid at a constant volume. I will work in SI units so 700F=210C
and 6000F=3150C; I will convert back to Imperial units
for the final answer. I looked up
data for the specific heat of water which turns out to have a
significant temperature dependence as shown in the figure (black). I did a
quadratic fit (green) to these data and integrated over the temperature
range to get E=1356 kJ/kg. The mass of a gallon of water is about
3.8 kg so the total heat is Q=1356x3.8=5.2x103 kJ=1.44
kW⋅hr=1240 kilocalories. Keep in mind that the pressure will be very large
at 6000F, about 1800 psi.
![]() QUESTION:
QUESTION:
How much "work" (physics definition) is actually accomplished in a gym
workout? I'm currently using F x D x reps = actual work done. The upward
lift ("D") x the amount of weight lifted ("F") x the number or
repetitions... to get actual work done. Am I in making some mistake, here?
Thanks, in advance, for your help.
![]() ANSWER:
ANSWER:
By "upward lift" I assume you mean the distance lifted. So, lifting
a weight F over a distance D you would do W=FD
units of work on the weight. For example, the weight of a 2 kg mass is about
19.6 N and the work to lift it 1 m is 19.6 J. But, and here is the catch,
you use more energy than 19.6 J to lift that weight because your body is not
a simple machine like a lever or a pulley. To understand why, see the
faq page. In a nutshell,
the reason is that to just hold up a 2 kg mass, not move it up at all,
requires input of energyyou get tired trying to hold up a weight at arm's
length, right? And, what about lowering the weight back down? The work done
on the weight is negative which implies that energy is being put back into
you but know that it also takes energy for you to lower the weight at a
constant speed. A biological system is considerably more complex than
systems we talk about in elementary physics classes. I think that it is of
little use to try to analyze a workout in terms of elementary physics.
![]() QUESTION:
QUESTION:
If the earth is curved how is it you can get a laser to hit a target at same height at sea level more then 8 km away?
How is it that it's bent around the earth?
![]() ANSWER:
ANSWER:
First of all, light is not bent around the earth; it travels in
a perfectly straight line and therefore, because the earth is curved,
there is a maximum distance away for a target at the same altitude. What
that distance is depends on the altitude of the laser. You say that the
laser is exactly at sea level by which I presume you mean the surface of
the earth; at this altitude you could not hit any target also at sea
level. In the figure I have drawn the earth, radius R, a point
a distance h above the earth's surface (laser location), and
another point a distance h above the earth's surface (target
location). The distance between them is 2d. Focus your
attention on one of the triangles with hypotenuse (R+h).
From the Pythagorean theorem, d=√[(R+h)2-R2]=√[2Rh+h2];
if h<<R, d≈√(2Rh). For example, if
h=10 km, about the height a commercial jet flies, 2d≈714 km is the most distant target at the same altitude which you could hit.

![]() QUESTION:
QUESTION:
I have always wondered how much energy do you do with if you let a kettle at 1800 W be running for two minutes? What is the approximate cost for this?
this is not a homework question.. just a question i wonder =)
![]() ANSWER:
ANSWER:
A
Watt is one Joule per second, 1 W=1 J/s. Energy consumed by an 1800 W
kettle in 2 min is 1800x120=216,000 J. But, we are more used to
measuring electrical energy in kilowatt hours, (1 kW·hr)(1000
W/1 kW)(3600 s/1 hr)=360,000 J. So the energy used by the kettle is
(216,000 J)/(360,000 J/kW·hr)=0.6 kW·hr. A kW·hr
costs on the order of 5¢-15¢, so the cost would be between 3¢
and 9¢.
![]() QUESTION:
QUESTION:
This is odd, but My family has just moved into a huge house with little outdoor space. We live in a climate that is cold in the winter, and I want my children to get some exercise on a daily basis. We own a trampoline, and have space for it indoors on the Second floor of our house. The ceilings are 12 feet high, so there would be no problem with the kids hitting their heads on the ceiling. My question is whether or not the house would stand up to the force generated by the trampoline. The walls of the house are made of concrete (you can't nail into it.) I am assuming the floors are quite solid as well, as they must support the weight of the house. They are concrete as well.
My Youngest child is quite large (6 ft, 260 lbs)--he is only twelve. We need the activity.
![]() ANSWER:
ANSWER:
First, a disclaimer: I can give you an idea of how much force the floor
will experience. I cannot predict whether this will cause your floor to
fail because I have no information about your floor other than that it
might be concrete. I have watched some videos and it seems that the
jumper never goes as high as h=2 m and the trampoline never
goes down as far as s=1 m. So I will just do my calculations
with those to get an upper limit on what force might be expected. Your
son's mass is about m=120 kg. An object falling from h=2
m will hit the trampoline with a speed of about v=√(2gh)≈√(2x10x2)=6.3
m/s. I will treat the trampoline as a simple spring so that I can write ½mv2=½ks2-mgs
where k is the spring constant. Putting in m,
v, and s and solving for k I find k=7200
N/m; since the force exerted by a spring is F=ks,
the largest force the trampoline exerts on your son is about 7200 N=1600 lb;
Newton's third law tells you that this is also the force your son exerts
down on the trampoline. Therefore, the trampoline exerts a force down on
the floor of 1600+W where W is the weight of the
trampoline. This is a little more than the weight of a grand piano.Keep
in mind that this is the greatest force and just for an instant; the
average force over the collision time would be half this. This is a
little more than the weight of a grand piano.
![]() QUESTION:
QUESTION:
hi, can and are earthquakes be caused by celestial alignments ie planets?
![]() ANSWER:
ANSWER:
Let's take a simple example. As seen from earth, Mars and Jupiter are
aligned. I estimated the force on a 1 kg object which is sitting, let's
say, on the San Andreas fault: F=3x10-11 N; the
weight of that 1 kg object is about 10 N. I would say that putting a 1
kg object on the ground is a great deal more likely to cause an
earthquake than those planets, wouldn't you?
![]() QUESTION:
QUESTION:
So there's a powerline outside my bedroom window, and I thought, huh. Turns out I'm sleeping with my head in a 6mG AC magnetic field (according to two meters). Help me use physics to stop caring.
How do I estimate/calculate which puts more force on the charged particles (calcium, potassium, sodium) in my brain: a) An aqueous solution at 98.6 degrees Fahrenheit or b) a magnetic field acting on charged particles moving at some estimated speed in said aqueous solution.
My hope here is that the force of (b) is like an order of magnitude or two, or something, below the "noise floor" of (a) and then I can stop caring forever.
![]() ANSWER:
ANSWER:
How about this: the earth's magnetic field is about 0.6 G, two orders of
magnitude bigger than the field due to the power line, and you are
exposed to it 24 hours a day. It is also possible that there is some
other source of field closer by than the power line which, though a much
smaller current, would produce a much bigger field. For example, if
there were a wire in the wall carrying a typical household current of 1
A, the field 2 m away would be 1 mG. There is no good scientific
evidence that any magnetic fields you are likely to encounter have any
effect, good or bad, on the functioning of your body.
![]() QUESTION:
QUESTION:
Several years ago, I was caught in a massive windstorm in a skyscraper. I was on the 54th floor (approx. 756 feet from street level, full building height is 909 feet) , pulling cable, and I stopped for a break. I left a cable pulling string hanging from the ceiling (48 inches free hanging length) in the office, with a 1/4 lb weight attached, and when the storm hit, the weight began swinging like a pendulum. The arc was 16 inches (eyeballing it), and traversing the length of the arc took about 1 second. How can I calculate how far (full arc) the skyscraper was moving by observing what the pendulum in the building was doing?
![]() ANSWER:
ANSWER:
A 48" pendulum has a period of about 2.2 s, the time to swing over the
arc and back. Since you were estimating, the pendulum was swinging with
about the period it would if the building were not moving at all. I
would conclude that either the pendulum got swinging somehow and the
building was not perceptibly moving or that the period of the building's
motion was about the same. If the building was swinging with a period
significantly different from 2 s, the pendulum would be swinging with
that same period; that is called a driven oscillator.

![]() QUESTION:
QUESTION:
How strong is 0.01 newton meters of
torque? I want to build a motorized
camera slider that will pull a Canon 5d mk 2 up a 45 degree slope. It weighs
1.5 kg. How much torque do I need?
This
is the motor I am thinking of buying:
Rated speed:20 rpm
Rated torque:0.01 N·m
![]() ANSWER:
ANSWER:
I will work it out in general and then we will see if this motor can do
the job. There are some things you have not told me, in particular the
speed v you want the camera to move on the slope and the nature
of how the camera moves on the surface (in particular coefficient of
friction μ). But the general solution will have those
in there and you can calculate with them. You will want to attach a
spool of some sort the the drive shaft of the motor to act as a reel to
pull up the string attached to the camera, say its radius is R.
The angular velocity of this motor is ω=20 rpmx(2π
rad/1 rev)x(1 min/60 s)=2.1 s-1. The weight of the camera is
mg=(1.5 kg)x(9.8 m/s2)=14.7 N. The angle of the
incline is stipulated to be 450. The force necessary to pull
the camera up the ramp with constant speed may be shown to be F=mg(1+μ)/√2;
since the torque τ is the
known quantity, FR=τ=mgR(1+μ)/√2.
In order for the camera to move at speed v, the radius of the
spool should be R=v/ω.
If the speed of the camera is v and the force is F, the
power being generated in the motor is P=Fv=mgv(1+μ)/√2.
Let's do an example. Suppose you want the camera to move with a speed of
v=1 cm/s=0.01 m/s and the friction is negligible, μ≈0.
Then the spool has a radius R=0.01/2.1=0.0048 m=0.48 cm; the
required torque would be
τ=0.0048x14.7/√2=0.05
N·m; the required power would be P=14.7x0.01/√2=0.1
W. I am afraid that your proposed motor is inadequate.
![]() QUESTION:
QUESTION:
Unlike a submarine traveling in a horizontal line at 5 fathoms compared to 50 fathoms (the pressure in the vertical direction would be the same....) But in a vertical line I imagine from 50 fathoms it would rise slower in the first 5 fathoms than it would in its final 5 fathoms.... I.e in its first 5 fathoms of accent it had the external pressure of 50 fathoms descending (dropping to 49 fathoms pressure then 48 etc) compared to 5 fathoms pressure descending to 0 fathoms pressure as it ascends.
Is this correct....
![]() ANSWER:
ANSWER:
As long as the water is considered incompressible (which it is for all
intents and purposes), the net force on the submarine due to water
pressure (called the buoyant force) is the same at every depth. Even
though the pressure in the water is enormously bigger at great depths,
the pressure difference between bottom and top of the submarine is the
same. Therefore, if drag forces are neglected there will be a net force
up on the submarine which is constant and equal to the buoyant force
minus the weight of the submarine. However, the drag force is not
negligible and is approximately proportional to the speed. So as the
rising submarine speeds up the drag force down becomes bigger and bigger
until it is eventually equal to the buoyant force minus the weight;
hence the net force is zero and from that depth up to the surface the
speed is constant. You might also be interested in a related
earlier question about
submarines.
![]() QUESTION:
QUESTION:
If you took two 1000 mile long metal bars, laid one horizontally on the
ground and stood the other vertically, would they weight the same and if
not, why?
![]() ANSWER:
ANSWER:
By weight we mean the force of attraction between the earth and the
object. Therefore, they would not weigh the same because the vertical
bar has most of its mass farther from the center of the earth than the
horizontal rod does. The weight of a point mass on the surface of the
earth is W1=mMG/R2
where M is the mass of the earth, R is the radius of
the earth, G is the universal gravitational constant, and m
is the mass of the point mass. This is usually written as W1=mg.
But, if the point mass is a distance H above the surface,
its weight is smaller, W2=mMG/(R+H)2=mg/(1+(H/R))2.
If you know integral calculus it is not hard to show that the weight of
a vertical uniform bar of length L and mass m is W3=mg/(1+(L/R)).
In your example L=1000 mi is not small compared to R≈4000
mi, so
W3=mg/(1.25)=0.8W1.
But, because L is so large, your horizontal bar does not have a
weight of mg either unless it bends to conform with the curved
surface of the earth. But, you can see from the figure that the
distances from the center of the earth are much smaller than for the
vertical bar, so it will surely have a larger weight, just not quite as
big as mg.
![]() ADDED
THOUGHT:
ADDED
THOUGHT:
Actually, even if the bar conformed to the
surface of the earth, it would weigh less than mg because the
components along the length of the bar of the forces on each piece of
the rod would all cancel out. I think I will not calculate the exact
answer for the horizontal bar, just say that is slightly smaller than
mg.
![]() QUESTION:
QUESTION:
according to the formula of variation of g above the surface of earth
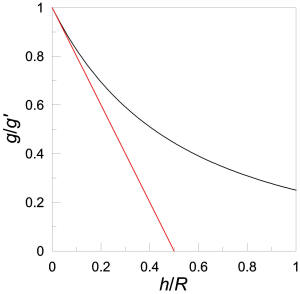
g' = g(1+2h/R) and the radius of earth is 6400 km .If we put R/2=3200 in the previous formula,did it mean that after 3200 km space start ?
![]() ANSWER:
ANSWER:
First, let's see where your "formula" comes from. The acceleration due
to gravity g may be written as g=MG/R2
where M is the mass of the earth, G is the
gravitational constant, and R is the radius of the earth. For
some height h above the earth, g'=MG/(R+h)2.
Therefore g'/g=R2/(R+h)2=(1+(h/R))-2.
This is an exact expression and you can see that g' never
becomes exactly zero but continues decreasing forever as h gets
larger. (Note that your "formula" cannot be correct because g'
gets bigger as h increases.) However, for many applications you
want to know what g' is if h/R is very small;
one can do a binomial expansion of g'/g, g'/g=(1+(h/R))-2≈1+(-2)(h/R)+…=1-2h/R.
So your formula was almost right, just need to change the + to -. But
this is only an approximation and will fail when h gets too
big. The graph above compares the exact (black) and approximate
solutions (red); as you can see, the approximation only works up to
about 0.1R. The fact that the approximation goes to zero at
h=R/2 has no meaning.
![]() QUESTION:
QUESTION:
Is a board suspended between two points and evenly weighted across it's
length (by books, for instance), less likely to bend if the ends are clamped
or nailed so they don't move? This is in contrast to if the ends simply
rest on end supports.
![]() ANSWER:
ANSWER:
Yes. Keep in mind, though, that the board will be exerting a horizontal force
on the support. Be sure the end supports are strongly attached to
the walls.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
If the end points are dado slots (the boards are shelves for media storage), and the shelves and dados are cut so that the shelves fit the dado slots very precisely on all three sides, then horizontal travel and twisting could be eliminated, which would obviate the need to attach to the wall. Correct?
![]() ANSWER:
ANSWER:
For the board to bend, the ends are pulled toward the center and lifted
up (see figure). I would anchor the ends.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
One more question though, and a more challenging one I hope.
If one wanted to screw a square block of wood to a wall, where would the optimal places be to put the screws? Assume that the block of wood is 12" on a side, two edges are parallel to the floor and only two screws are used. The wood will be weight-bearing and the weight will be evenly distributed along the top edge of the block. Also, assume that the thickness of the wood is small relative to the other dimensions and that the screws can find equal purchase in the wall in back of the block of wood being fastened.
My gut tells me that (a) the screws both should be put along a horizontal line parallel to the floor, and, (b) it doesn't matter where that line is, high or low, since the weight is evenly distributed. What I can't intuit, is if it's better to have the screws be 3" or 4" or some other distance from a vertical side, as long as they are symmetrically placed.
In the general case, if N randomly placed screws are used, what is the math that tells me what percentage of the weight each screw bears according to its geometric placement?
![]() ANSWER:
ANSWER:
I really do not think it is worth worrying about. The reason is that it,
paradoxically, is likely not the screws which keep the block from
falling, it is the static friction between the wall and the block; the
function of the screws is more to press the block against the wall than
to hold up the weight. Therefore, regardless of where you put the
screws, tighten them as tight as you can get them since the amount of
frictional force you can get depends on the normal force, the force
pressing the wall and block together.
![]() QUESTION:
QUESTION:
 I have measured the thickness of steel pipes with a thickness meter (pocketmike) with a sound velocity of 5813 m/s.
No I need to change my thickness values with a sound velocity of 5920 m/s.
This because this value is more accurate for this steel pipes I measured...
Which formula I need to use?
I have measured the thickness of steel pipes with a thickness meter (pocketmike) with a sound velocity of 5813 m/s.
No I need to change my thickness values with a sound velocity of 5920 m/s.
This because this value is more accurate for this steel pipes I measured...
Which formula I need to use?
![]() ANSWER:
ANSWER:
I would assume that the device measures a time. In that case, the
thickness T would be proportional to the product of the
velocity v and the time t, T=cvt where c is
some constant. So, if you change v to v' but keep
t (measured) constant, the corrected thickness T' will be
T'=cv't. Take the ratio of the two equations and solve for the
thickness: T'=T(v/v')=(5813/5920)T=0.982T.
![]() QUESTION:
QUESTION:
What ideas are the basis of the special theory of relativity and what conservation laws does it preserve?
This isn't from homework, but a class discussion that I didnt understand
![]() ANSWER:
ANSWER:
This could be called an unfocused question, but the answer is pretty
brief so I will carry on. Most textbooks will tell you that you need to
postulate that the laws of physics are the same in all inertial frames
of reference and accept that the speed of light (electromagnetic
radiation) is independent of the motion of the observer or of the
source. My take on this is that only the first postulate is needed
because Maxwell's equations are laws of physics and they predict that
the speed of light depends only on two physical constants, not on the
motion of the source or observer. All important conservation laws—energy,
linear momentum, angular momentum—are preserved but only if
changes to the definition of these quantities are changed. E.g.,
kinetic energy is no longer ½mv2 and linear
momentum is no longer mv; the new quantities, however, are
approximately their classical values if the velocity is very small
compared to the speed of light.
![]() QUESTION:
QUESTION:
This came up in a discussion about the use electro-magnetic rails guns whose power is contained in the speed of a given mass when it slams into a stationary object as there is no explosive material involved, the energy produces is converting the kinetic energy of the projectile into heat on impact.
-
How much energy is contained in every stationary object on earth due to the rotation speed of the earth? I understand this this is only Potential energy and would require the object to be shielded from the earth's gravitational pull in order to release it but if a steel block weighing 100 kg were to no longer be held by gravity how much potential energy would it contain as it was flung from the earth rotational spin.
-
Also, once released from the earth's gravitational attraction, would you also need to factor in the speed of the earth's rotation around the sun to the calculations? The mass was travelling in two different directions (planetary rotational and orbital rotational) at extremely high speeds before the gravitational ties were cut?
-
And as a final factor, while trying to calculate this someone pointed out that the starting 100 kg piece of mass would instantly become a 0.KG piece of mass once it was no longer had any weight with respect to the Earth.
-
At that point, we pretty much tossed in the towel. But, still feel that because we started with a 100 kg item that became weightless, that would not remove the potential energy it contained before gravity released it. If afterward it were to crash into the moon or some other object in its path, wouldn't the amount of destruction still be equal to the energy it contained when it was "fired from the planet" much as a bullet fired from a gun?
![]() ANSWER:
ANSWER:
You have many misconceptions, so I have edited your question(s) by
itemizing the parts of your question. I will answer by parts.
-
The most important misconception should be dealt with first. Energy is something which depends on your frame of reference. If a mass is on the surface of the earth it has zero kinetic energy if you are also on the surface of the earth. If you view that same mass from a frame moving along with the earth in its orbit but not rotating like the earth is, it has the kinetic energy you envision, that due to the earth's rotation. Kinetic energy is given by K=½mv2 where m is the mass and v is the velocity you see it to have. The speed v of an object on the earth's surface depends on the latitude λ, v=Rωcos(λ) where R=6.4x106 m/s and ω=7.3x10-5 s-1 is the angular velocity of the earth. Let's just look at the equator where v is largest, v=Rω=6.4x106x7.3x10-5=470 m/s=1050 mph; you should note that this is not really that large. The kinetic energy of 100 kg flung into space with this speed is K=½x100x4702=1.1x107 J.
-
By now you should appreciate that it depends on who is looking at your projectile. Someone who is at rest relative to the sun would need to calculate the speed and therefore add in the velocity of the earth around the sun, call it V. But, this would get complicated because it would depend on time of day the projectile was launched. If you are standing right on the orbit and the earth is coming toward you, the speed would be V+v an noon and V-v at midnight; at other times it would be somewhere between these two extremes.
-
You have this all wrong. Weight is the gravitational force which the earth exerts on the mass; the weight does not "instantly" become zero when it is launched, it gradually decreases as it gets farther away from earth. But, that is beside the point because the kinetic energy depends on the mass, not the weight, and the mass stays the same regardless of whether there is any gravity or not.
-
Whenever the projectile stikes something, like the moon in your question, all that matters is what its velocity is with respect to the moon.
![]() QUESTION:
QUESTION:
Due to the ideal gas law/approximation the speed of sound does not change with altitude or barometric pressure. Yet ask any long range shooter and they will tell you, from practical experience, that the lower the barometric pressure or the higher the altitude, the less drag there is on the bullet and therefore the bullet takes longer to slow resulting in less time for gravity to affect the bullet leading to less "drop" for the bullet over long ranges. Why then doesn't the ideal gas law apply to bullet trajectory?
![]() ANSWER:
ANSWER:
I do not know about the speed of sound, but I would certainly not assume
that anything about sound could be applied to bullets. The drag force
Fd of a bullet of speed v in air is well
represented by Fd=½Cρv2
where ρ is the density of the air and C is a
constant determined only by the geometry of the bullet. As the density
of the air gets smaller, the drag on a bullet gets smaller, in accord
with your experience. There is really no need to invoke the ideal gas
law at all, but if you want to connect density to the ideal gas law,
PV=NRT, note that the density will be proportional to N/V,
so ρ∝P/T. For
constant temperature, density is proportional to pressure—the
lower the pressure, the lower the drag.
![]() QUESTION:
QUESTION:
Would it be possible for an 'average' human to throw a 500 g weight 40 ft but
with only a 2 ft high corridor of travel without the projectile touching any
of the corridor's sides? This isn't homework, it's a really ridiculous question that we can't physically try at work! We work in a theatre that has two people positioned 40 ft apart and roughly 30 ft up in the air near the ceiling. Ages ago someone said that they could throw a spanner from one person to the other person. Some people agreed, some said that it wasn't possible due to the arc needed. This question comes up every few months and I just wondered if you might have an answer.
![]() ANSWER:
ANSWER:
So the problem is, with what speed would you need to throw the spanner
in order that it reach a maximum height of 2 ft above its starting
height when it has gone 20 ft? This is a straightforward kinematics
problem. You are probably not interested in the details, so I will just
give you the final result. The necessary speed would be 57.7 ft/s=39.4
mph. A major league baseball pitcher can throw a fastball with a speed
of around 100 mph, so there is probably somebody in your theater company
who could throw the spanner with the necessary speed, but I would not
want a 1.1 lb wrench coming at me with a speed of nearly 40 mph!
![]() QUESTION:
QUESTION:
In some of the more realistic space combat science fiction there is a concept called a 'BFR' (Big Fast Rock) which, mined from a dead world or asteroid, melted to molten and then reformed to a near-perfect density distribution with collars of ferrous metal impressed in it, is shot at some fraction of light speed from a large EML cannon running down the long axis of mile long ships. I would like to know how to calculate the impact force release for a 2,000 lb BFR moving at .10, .15 and .30 C. I'm assuming it's going to be in the high Megaton range and I don't know what the translative math per ton equivalence in TNT.
![]() ANSWER:
ANSWER:
What you want is the energy your projectile has when it hits. The energy
in Joules is E=mγc2 where γ=√(1-(v/c)2).
In your case, 2000 lb=907 kg, c=3x108 m/s,
γ=1.005, 1.011, and 1.048. The energies in Joules are
E=8.204x1019, 8.253x1019, and 8.555x1019
J. There are about 4x109 J per ton of TNT, so the energies
are 20.51, 20.63, and 21.39 Megatons of TNT. I might add that this is
not actually very "realistic". Where are you going to get that much
energy (you have to supply it somehow) in the middle of empty space? Or,
look at it this way: I figure that for a mile-long gun the time to
accelerate the BFR to 0.1c is about t=10-4
s. During that time the required power is about 8x1019/10-4=8x1023
W=8x1014 GW; the largest power plant on the earth is about 6
GW! Also, don't forget about the recoil of the ship which would likely
destroy it.

![]() QUESTION:
QUESTION:
I have a question related to determining the force at impact.
Here's the question in two parts:
-
If a firefighter adds 45 pounds of gear to his overall weight, does it increase the impact force if he has no choice but to jump out a window and if so to what degree?
-
What is the effect on impact force of jumping out a second floor window vs. 3rd floor and above?
This actually isn't homework. I'm 54 years old and advising a charitable organization that provides safety systems to firefighters. One of the challenges they face is fire departments who don't have high rise buildings and feel they don't need the bailout systems. So I'm trying to figure out what the impact is for a firefighter forced to jump out a second story or third story window. This will help inform how they talk to prospective donors. If you could help me with that (understanding/identifying the increase in impact force from 1st to 2nd to 3rd floors and then up) it would be greatly appreciated. I've done a lot of googling around calculating impact and g forces, but its not making sense to me (I'm not being lazy, just not understanding).
![]() ANSWER:
ANSWER:
The "force at impact" depends, essentially, on the time to stop. If she
has a speed v, a mass m, and stops in a time t,
the average force F during the stopping time is given by
F=m(g+v/t) where g=32 ft/s2 is the acceleration due to
gravity. So, yes, if you increase the mass you increase the force
proportionally; I guess I would toss that extra 45 lb over before I
jumped! Regarding your second question, call the height of one floor
h. Jumping from the second floor would result in a speed of v2=√(2gh);
jumping from the third floor would result in a
speed of v3=2√(gh) which is
about 1.4 times larger than v2. In general, jumping
from the nth floor would result in a speed vn=√[2(n-1)gh].
Maybe some numerical examples would be useful to you. You prefer Imperial units, which makes things a little complicated. The quantity mg is the weight. I will take mg=160 lb and h=12 ft for my numerical calculations, so when I need the mass I will use 160 lb/32 ft/s2=5 lb·s2/ft. (The unit of mass in Imperial units is called the slug, 1 slug=1 lb·s2/ft.) The speeds from second and third floors will then be v2=27.7 ft/s=18.9 mph and v3=39.2 ft/s=26.7 mph; these speeds are independent of the mass. Finally we must approximate the times to stop. If she lands feet first, she could extend, as parachutists do, her stopping time by bending her knees into a squat; I will estimate the distance s she will travel while stopping as s=3 ft. The time may be shown to be t=2s/v so t2=2x3/27.7=0.22 s and t3=2x3/39.2=0.15 s. Finally, the average forces during impact are F2=160+5x27.7/0.22=790 lb and F3=160+5x39.2/0.15=1467 lb. These are approximately 5 and 9 times her weight (g-forces of about 5g and 9g).
![]() QUESTION:
QUESTION:
I want to ask about the Mandela effect theory. I do not want detailed answers concerning blackholes and cosmology,instead i want to know if it's real. I personally do not believe in time travel and all the "clues" people have been providing don't seem credible enough. So please if it is true what is the exact physics background that proves it? And how can i have further information and dig deeper into this theory?
![]() ANSWER:
ANSWER:
I never heard of the
Mandela effect. For readers who, like me, are similarly ignorant it
is a special case of a psychiatric phenomenon called
confabulation,
defined as "the production of fabricated, distorted or misinterpreted memories about oneself or the world, without the conscious intention to deceive";
in other words, a "false memory". The Mandela effect is a confabulation
where a large number of people have the same same false memory; it is
apparently so called because there are many people who "remember" that
Nelson Mandela died in 1980, not 2013. So, where is the physics in all
this? A "paranormal consultant" named
Fiona Broome
suggested that such cases could be explained as "bleed through" from
parallel universes. She is not a physicist and her speculation, maybe
amusing, has no real basis in physics and there is no way to test it one
way or another; therefore it should not be labeled as a "theory" since
it is neither testable nor falsifiable.
Snopes.com has a long article on the Mandela effect which you can
read if you want to learn more.
![]() QUESTION:
QUESTION:
As surface tension means force acting on surface then why not its unit if force per unit area i.e N/m2.
If it is N/m then which length will we have to take here.
![]() ANSWER:
ANSWER:
Think of the surface as an elastic sheet. What you want to call the
surface tension is how hard you need to pull on this sheet in order to
make it rip. The way this is usually measured is to create a film which
is actually a very thin volume with surfaces on both sides; a simple
device to do this is shown in the figure. Now, pull on the sliding side
to stretch the film. When the film breaks, measure F. It is
found, by doing many experiments, that F depends on L,
but that the ratio F/L is always the same.
Furthermore, it makes no difference what the shape of the film to the
left of the slider is. We therefore define the surface tension for this
fluid to be γ=F/(2L) as determined by
this experiment, the factor of ½ because there are two surfaces
we are stretching.
![]() QUESTION:
QUESTION:
I just came across an ad saying that
the earth's magnetic field keeps us healthy and strong, and saying that if we live in the world with no magnetic field, all life on earth will end (assume that sunlight / water / oxygen exist / and for some weird reason gravity still works)
So my question is, is this valid? If there is no magnetic field, even though we have sunlight, water and air, we would perish?
![]() ANSWER:
ANSWER:
The
magnetic field has no direct effect on you. There are many magnetic
products touted as having miraculous beneficial effects on your health;
do not buy them, they are a scam. There are important indirect effects
of the magnetic field which help provide a healthy environment at the
surface of the earth, though. Probably the most important is that the
field extends far into space and protects the earth from the solar wind
which is a stream of charged particles (mainly electrons and protons)
which are deflected around the earth by the field. If there were no
field, the effect of this "wind" would be to strip the upper atmosphere,
including the ozone layer which protects you from intense ultraviolet
radiation from the sun. But I do not think that buying a magnetic
matress pad, for example, would help that issue! Lack of a magnetic
field cannot result in our perishing, though, since it is well known
that the field reverses direction periodically; the reversal would not
be instaneous which would mean there would have been a period at least
hundreds of years long when the field was negligibly small. The most
recent reversal was about 780 million years ago when humans existed and
we survived somehow. One thing about your question is strange: "…for
some weird reason gravity still works…" The earth's
gravity has nothing to do with its magnetic field.
![]() QUESTION:
QUESTION:
If you tow a boat from a tow path which is the best point to tie the rope onto the boat?
![]() ANSWER:
ANSWER:
The rope will exert a force on the boat, obviously. This force will tend
to do three things: exert a torque which will tend to rotate the boat
about a vertical axis through the center of gravity (you don't want
this), have a component along the bank which will pull it along the
canal (that is what you want), and have a component which will pull the
boat toward the shore (you don't want this). To minimize the tendency of
the boat to turn, attach the rope close to the center of gravity of the
boat. To minimize the tendency to drift (not turn) to the bank, make the
rope as long as possible so that most of its force will be exerted along
the bank. Some tiller will be needed to make small corrections, but
those should be minimal.
![]() QUESTION:
QUESTION:
Does water slow down gradually as it rises vertically out of a fountain? It would seem that it should, but that would mean the water behind would catch up and create a constantly wider jet. However it seems that the jet stays relatively consistent in width (subject to some splashing) until it reaches the top. At which point it splays and falls. This would suggest it is at a consistent speed all the way up until it suddenly decelerates and falls.
![]() ANSWER:
ANSWER:
Any "piece" of the water has a downward acceleration (slows down on the
way up, speeds up on the way down) at all times; ignoring friction
effects, each drop of the water follows the same trajectory as a thrown
ball would follow. So, if one piece is slowing down, why doesn't the
piece behind it catch up? Because it is slowing down too at exactly the
same rate. If you threw two balls up, one right after the other, the
second would never catch up. Of course, if the stream of water were
going vertically up, the water falling from the top would collide with
the water rising and, as you say, splay out.

![]() QUESTION:
QUESTION:
It's a question about R value, and directed to you partly because it appears you are in New Zealand. I'm looking at a video from an inventor in New Zealand who is recycling plastics into building blocks. I cannot find him on the net to ask what is the R value of these blocks. I know it is a long shot to ask you, but I wondered if there is a way to calculate R value, based on assumptions about physical properties of plastics such as milk jugs, trapped air and density in these blocks.
![]() ANSWER:
ANSWER:
There are
tables where the R-value per inch of thickness is tabulated for
various materials. But, these blocks are fabricated from a random mix of
all classes of recyclable plastics. Furthermore, it is not clear how
much air is trapped in them. Plastics seem to have R-values in the range
of 3-5 ft2·°F·h/BTU/in, so you could
certainly take this range to estimate the value for a block of known
thickness. If you are interested in the details of the physics of the
R-value, you might be interested in an
earlier answer.
![]() QUESTION:
QUESTION:
Heavy water is Deuterium oxide. Water is H2O. So is Deuterium oxide water with one Protium and one deuterium atom, or water with two deuterium atoms. If both hydrogens in water are actually deuterium, how did that come to be?
![]() ANSWER:
ANSWER:
Deuterium (D) is a naturally occuring isotope of hydrogen; approximately
0.015% of hydrogen atoms are deuterium, which is about 1:6,670.
Therefore about 1:3,330 molecules of water would be HDO and
approximately 1:44,400,000 (6,6702)would be D2O.
The term "heavy water" refers to D2O and DHO is sometimes
referred to as semiheavy water. You would think it would be a hopeless
task to extract such a tiny fraction of D20 from natural
water. I was very interested to learn that there is a much more clever
way to get nearly pure heavy water. There are relatively many DHO
molecules so it is much more practicable to use standard isotope
separation techniques to get enriched DHO. So, for example, suppose that
you enrich the water such that the hydrogen atoms present are 50%
deuterium. Then it turns out that the water is 50% HDO, 25% H20,
and 25% D2O. Where did all that D2O come from? It
turns out that in water the hydrogen atoms (both isotopes) do not stay
attached to the same oxygen atom, rather they move more or less freely
around. By repeating whatever you did to get this far, you can get a
higher and higher percentage of deuterium. Enrichments of 99.75% D2O
are routinely achieved.
![]() QUESTION:
QUESTION:
Is it possible for a skydiver to not be strapped in to a parachute, just holding onto it,
or even wrapping his arm into the straps. When he pops the schute, is it possible to hold on to it? Would his arm withstand the sudden deceleration or could it be torn from the shoulder socket?
![]() ANSWER:
ANSWER:
There is, of course, no simple answer to this question. It depends on
how fast he is falling and the parachute design. It also depends on
"luck" as the graph shows since the two graphs are for identical
parachutes, weights, and speeds. The drag force (the force the parachute
exerts up on him) as a function of time is shown in gs. One
g would correspond to the weight of the parachutist. Both graphs
end up after about 7 s at gforce=1 which means that
the force up on him would be equal to his weight. For the "soft"
deployment, about 3g is the maximum, so you would have to be
able to hang from your hands from a stationary bar with three times your
weight attached to you; you could probably do this briefly and it would
certainly not tear the arm from its socket. For the "hard" deployment,
almost 6g is the maximum, so you would have to be able to hang
from your hands from a stationary bar with six times your weight
attached to you. You could probably not do this but it still would
probably not tear the arm from its socket. In any case, I would never
depend on being able to hang on with my hands!
![]() QUESTION:
QUESTION:
If I have a .25 inch airtube in
a 2 ft deep fish tank, how can I calculate the force necessary to expel the first bubble of air at the bottom of the tank if the other end of the tube is at the surface?
![]() ANSWER:
ANSWER:
The weight density of water is ρ=62.4 lb/ft3=0.0361
lb/in3. Therefore the
gauge pressure 2 ft down is P=ρh=62.4x24=0.867 lb/in2
(psi). That pressure will just keep the tube filled with air all
the way to the bottom. Any pressure greater than this will expel air
into the water. This is probably the number you want; the force over the
area of the tube is F=0.867·π·(0.25/2)2=0.0426
lb=0.68 oz.
![]() QUESTION:
QUESTION:
I am an avid sports fan and I have often wondered if the experts may be wrong about the myth of the rising fastball in the game of baseball. I played baseball for over 20 years and I can tell you that the ball does appear to rise when certain pitchers throw hard put a heavy backspin on the ball. I have been told that experts say it is nothing more than a visual trick your eyes play on you because a rising fastball is considered to be physically impossible. I can tell you first hand that a softball pitcher I know can throw a ball that rises after being thrown on a straight trajectory. I suspect the Magnus effect may have something to do with the anit-gravitational behavior of the ball. Do you think this could be what causes the ball to appear to rise as it travels, or is it just our perception?
![]() ANSWER:
ANSWER:
There is such a thing as a rising fastball, but it does not actually
rise; it simply falls more slowly than a nonspinning ball does. An
experienced hitter knows intuitively what a normal fastball does and
when presented with a rising fastball he will swear that it rose because
it actually fell less. Incidentally, by rise or fall, I am talking about
the direction of the acceleration. So a ball which is thrown at an angle
above the horizontal is obviously rising but it rises at a
 decreasing
rate of rise until it reaches the peak of its trajectory and then begins
back down; the rising fastball will actually rise farther. Then why do
we say it is a myth? It is easiest to understand by looking at a ball
thrown purely horizontally. Can spin cause the ball to actually go
upwards? To answer this, you need to think about all the forces on a
pitched ball. There is the weight, FG, which points
vertically down and causes the ball to accelerate downward (a
horizontally thrown 90 mph fastball falls about 4 feet on the way to the
plate); there is the drag FD which points opposite
the direction of flight and tends to slow the ball down (a
90 mph fastball
loses about 10 mph on the way to the plate); and there is the magnus
force FM which, for a ball with backspin ω
about a horizontal axis points perpendicular to the velocity and upward.
If the ball is moving horizontally the only way it could rise is for the
Magnus force to be larger than the weight. Measurements have been done
in wind tunnels and it is found that if the rotation is 1800 rpm, about
the most a pitcher could possibly put on it, the ball would have to be
going over 130 mph for the Magnus force to be equal to the weight. When
you say "thrown on a straight trajectory", you cannot mean it left his
hand horizontally because it would hit the ground before it got to the
plate; a fast pitch like that is impossible to accurately judge the
initial angle of the trajectory.
decreasing
rate of rise until it reaches the peak of its trajectory and then begins
back down; the rising fastball will actually rise farther. Then why do
we say it is a myth? It is easiest to understand by looking at a ball
thrown purely horizontally. Can spin cause the ball to actually go
upwards? To answer this, you need to think about all the forces on a
pitched ball. There is the weight, FG, which points
vertically down and causes the ball to accelerate downward (a
horizontally thrown 90 mph fastball falls about 4 feet on the way to the
plate); there is the drag FD which points opposite
the direction of flight and tends to slow the ball down (a
90 mph fastball
loses about 10 mph on the way to the plate); and there is the magnus
force FM which, for a ball with backspin ω
about a horizontal axis points perpendicular to the velocity and upward.
If the ball is moving horizontally the only way it could rise is for the
Magnus force to be larger than the weight. Measurements have been done
in wind tunnels and it is found that if the rotation is 1800 rpm, about
the most a pitcher could possibly put on it, the ball would have to be
going over 130 mph for the Magnus force to be equal to the weight. When
you say "thrown on a straight trajectory", you cannot mean it left his
hand horizontally because it would hit the ground before it got to the
plate; a fast pitch like that is impossible to accurately judge the
initial angle of the trajectory.
![]() QUESTION:
QUESTION:
I'm learning about ideal gases in class and learning about the ideal gas law, but we also (very briefly) mentioned that at low temperatures and high pressures the ideal gas law no longer holds very well. We didn't go much pass that but I did a bit of research and an explanation included another set of constants calculated experimentally, but again only really explained very briefly that the size of the molecules become much greater and the inter molecular force between the molecules is no longer insignificant (as is a factor of the kinetic molecular theory of gases). I guess my question is, what is so substantial to the aspects of low temperatures and high pressures of ideal gases that causes them to follow a different set of parameters?
![]() ANSWER:
ANSWER:
V=NkT/P is the ideal gas law (IGL). I write it like this to
emphasize what happens if T decreases and/or P
increases while N stays the same—V decreases.
(You may write it as V=nRT/P where n is the number of
moles and R is the universal gas constant. For reasons of
clarity in my answer, N is the number of molecules and k
is Boltzmann's constant.) The IGL assumes that the volume occupied by
the molecules is insignificant and that the molecules do not interact
with each other. But, when the volume decreases the molecules get closer
together so that their interactions start to matter and the total
fraction of the volume which the molecules occupy is no longer a
negligible fraction of the volume of the container. (You are incorrect
when you say that "…the size of the molecules become much greater…";
the size stays the same but now occupies a larger fraction of the whole
volume.) The first thing to do to correct the IGL is to replace V
by V-Nv where v is the volume of a single molecule:
P(V-Nv)=NkT. Although this improves the
accuracy of the IGL, it still overestimates the pressure observed
experimentally. The reason is that the effects of the intermolecular
forces have not been included. It turns out by doing measurements that
the pressure is proportional to the square of the number density, P∝(N/V)2;
this makes some sense because the molecules interact by pairs and there
are N(N-1)/2≈N2/2
pairs because N is very large. So, finally,
(P-c(N/V)2(V-Nv)=NkT
where c is a proportionality constant which depends on what the
particular gas is. This is sometimes called the van der Waal equation.
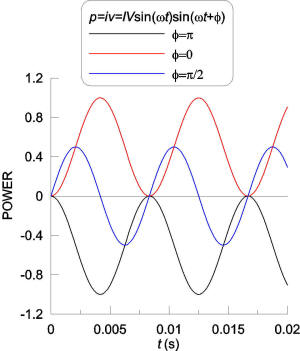
![]() QUESTION:
QUESTION:
When I had solar panels installed on my house the old fashioned meter ran backwards when the Sun was bright. They have now fitted a digital meter which can sense when energy is being sent into the grid. I can see how this could be done with DC, but how does it work with AC? In AC the current is switching direction at 50 Hz. How can the meter sense the 'direction' of the energy flow?
![]() ANSWER:
ANSWER:
You are right, the average current is zero. However, the current is not
the power—the power is the product of the current and the
voltage. Both current and voltage are sinusoidal functions of time,
i(t)=Isin(ωt) and v(t)=Vsin(ωt+φ),
so p(t)=IVsin(ωt)sin(ωt+φ).
The graph above shows three choices for the phase φ between
i and v. For φ=π/2 the time average of
the power is zero, no energy flow; for φ=π and φ=0
the time average of the power is negative and positive, respectively.
The motor in a mechanical meter turns in opposite directions for
different signs of the average power; in a digital meter the average
power is determined by an electronic circuit.
![]() FOLLOWUP
QUESTION:
FOLLOWUP
QUESTION:
Thank you for your reply to my question about the power direction with energy generated by solar panels. I now understand that phase angles are crucial.
The inverter in the loft takes DC from the panels and converts it into AC. To feed energy back into the grid does the inverter have to deliberately adjust the phase or does this occur naturally when there is an excess of energy?
![]() ANSWER:
ANSWER:
All that matters is what the phase is at the meter. If energy is flowing
into your house the phase will be one way, if flowing out it will be the
other.
![]() QUESTION:
QUESTION:
Why don't liquid pipelines that run downhill rupture from the weight of the liquid in them? For instance, a 14 mile long section of 10" ID pipe carrying crude oil that runs at a 22.5 degree angle has about 301,592.89 gallons of crude in it. That Crude weighs 91,328,360.39 pounds. I calculate that the static weight at the bottom of that run should be about 22,832,090.10 pounds of oil. That exceeds the tensile strength of the pipe wall by a factor of 50 to 100. At first I thought it was because a closed pipe would have sort of a vacuum at the top, but then I realized that would make the pipe crush from atmospheric pressure. I'm missing something simple I am sure, but darned if I can figure out what it is...
![]() ANSWER:
ANSWER:
There is something seriously wrong with your numbers. They imply that
the weight of one gallon of crude is about 9x107/3x105=300
lb, and 14 miles at 22.5° would take you to 14sin22.5°=5.4
miles, higher than Mount Everest! Also, since we are working with a
fluid, pressure would be a more appropriate quantity to look at than
force. I will start from scratch with new
numbers: the density of crude oil is about ρ=900 kg/m3
and I will take a distance of about y=1000 m between the
top and the bottom, about the height of a small mountain; you need only
the drop, as we shall see below. Like you, I will assume that the oil in
the pipe is static which simplifies things. A good approximate way to
solve this kind of problem is to use Bernoulli's equation, P+ρgy+½ρv2=constant;
P is the pressure, g=9.8 m/s2 is the
acceleration due to gravity, and v (=0 for us) is the speed. At
the top, Ptop=PA and ytop=1000
m and at the bottom Pbottom=P+PA
and ybottom=0; here, PA is the
atmospheric pressure. Therefore, PA+900x9.8x1000=P+PA+0.
So the gauge pressure is P≈107 N/m2≈100
atm=1450 PSI. The brief research I have done indicates that this pressure
is at the extreme upper limit of specifications for pipelines. To make
the oil move, you need to add a lot more pressure. My use of Bernoulli's
equation is a very crude approximation because it assumes a fluid with
no viscosity and no frictional forces with the walls, obviously not a
very good approximation.
![]() QUESTION:
QUESTION:
Suppose I have a 10 tons weight hanging 5 meters up in the air. I want to get electricity by lowering the weight against a dynamo (for example).
How much energy do I get?
A 100 W light bulb needs 100 W of power when it's ON. So, if it stays on for 10 hours it will consume 1 KW, am I right?...
Ok, so my question is... How many 100 W light bulbs can I have ON at the same time with the energy coming from that falling weight? -- while the weight is falling, obviously.
-
if the weight falls for 1 hour
-
if the weight falls for 2 hours.
What's the formula?
Somebody asked the same question on some forum on the web. His weight was 200 tons falling 100 meters for 1 hour, and someone said that the solution is:
dU=Fdy =
200,000kg * 9.81m/s2 * 100m
=
196.2MJ =
196.2MW/3600 = 54,500KW/h
Is the formula right? If yes, how do I apply it? Because I get extremely small numbers if I change his 200,000 with my 10,000, and his 100 meters with my 5 meters.
Plus, I don't know what KW/h means. All I'm interested is knowing how many Watts are available at any given moment while the weight is falling.
![]() ANSWER:
ANSWER:
The first thing we need to get straight is what a watt is. The unit of
energy in SI units is the Joule (J); 1 J is 1 N·m where a Newton
(N) is the unit of force and the meter (m) is the unit length. A Joule
is the kinetic energy which a 2 kg mass moving with a speed of 1 m/s
has; or, it is the work you need to do to lift a 1 kg mass to a height
of 1/9.81 m. A Watt (W) is the rate at which energy is delivered or
consumed, 1 W=1 J/s. Therefore, your 100 W bulb consumes 100 J of energy
every second. Incidentally, if you look at your electricity bill, you
will be billed for how many kW·hr you have consumed; a
kW·hr is a unit of energy, 1
kW·hr=1000x3600 J=3,600,000 J.
The example stated is correct but the units are not. It is fine up to the point where the potential energy of the mass is 196.2 MJ (mega=M=106). Now, if you let this mass drop over 3600 s, it is losing its energy at the rate of (196.2x106 J)/(3600 s)=5.45x104 J/s=54.5 kW (not kW/hr). For your case, your mass has a potential energy of 104x9.81x5=4.9x105 J. If you deliver this energy over an hour, the power is 4.9x105/3600=136 W; You could power one light bulb over this hour and have some energy left over at the end (about ¼ of what you started with). Clearly, the power delivered over two hours would only be half as much, not enough to power even one 100 W bulb.
![]() QUESTION:
QUESTION:
If there's less gravity on the moon, then why do astronauts move slower? Why don't they have more spring if gravity's pull is weaker? I'm thinking that this should be a matter of resistance, but obviously there's a factor I'm not accounting for.
![]() ANSWER:
ANSWER:
Sure, with less gravity (about 1/6 of earth) an astronaut can jump much
higher, but it will take longer to get to the top and back down than on
earth; that would look like slow motion, right? Or, just think about
taking a step. Your center of gravity is forward of your trailing foot
and so you rotate about that foot. The rate of rotational acceleration
is only 1/6 that on earth, again like slow motion.

![]() QUESTION:
QUESTION:
Engineers in the Bay of Fundy are trying to harness tidal power to generate electricity. It's claimed that they can generate enough electricity to power the entire Atlantic Provinces of Canada.
This got me to thinking, if that much power can be harnessed, where has that energy been going? I'm assuming it goes to heat and warms the water. If that's the case, would harnessing the power therefore cool the water and potentially harm aquatic ecosystems?
![]() ANSWER:
ANSWER:
My research shows that all the power projects on the Bay of Fundy will
generate about 20 MW. These will be powered by underwater turbines. I
did a very rough estimate of the total power available by the falling
water: The average rise in sea level is 15 m, area of the bay is 13,000
km2,
density of water is 1000 kg/m3. I find that the total volume
to fall is about 2x1011 m3, the mass is 2x1014
kg, and the potential energy of this mass is about 3x1016 J. If
you deliver that much energy over the course of a day, the average power
is about 350 GW. So, the power plants will only reduce the energy of the
tidal flow by less than 0.01%, a truly negligible amount.
![]() QUESTION:
QUESTION:
i was studying something on the internet where i need to know one question i.e If an object Travelling at about 2500 km per hour or may be higher collides with other object in the ocean around 90 meters below the ocean level is it possible that the debris of that object will go around 2 km approx ahead in the water itself?
![]() ANSWER:
ANSWER:
Extremely unlikely. Let me show you a very rough calculation which will
demonstrate this for an extreme case. If one object collides elastically
with another mass whose mass is very small compared to the incident
mass, the collided-with mass will recoil with a speed twice the incident
speed, in your case that would be 2x2500 km/hr=5000 km/hr≈1400
m/s. The drag force on an object with speed v in water may be
approximated as Fdrag=½CρAv2;
here I will choose C≈1 (order of magnitude for most
shapes) is the drag coefficient which depends only on the shape, ρ≈1000
kg/m3 is the density of water, and A≈1 cm2≈10-4
m2 is the cross sectional area of the object. I want this
object to go as far as possible, so I have chosen A to be
relatively small; an object this small will have a relatively small
mass, certainly no larger than m≈100 gm=0.1 kg. Knowing
all this, one can calculate the velocity v and position x
as functions of time t, v=v0/(1+kt)
and x=(v0/k)ln(1+kt)
where k=½CρAv0/m≈7000
s-1 and v0=1400 m/s is the
starting velocity. I find that at t=½ s, v≈0.4
m/s and x≈1.6 m; the object will have lost nearly all its
speed after having traveled only about a meter and a half. I can think
of no earthly way that any debris could propogate 2 km!
![]() QUESTION:
QUESTION:
Would my weight be the same on the surface of earth and one mile underground? How about one mile in the atmosphere?
![]() ANSWER:
ANSWER:
Above the surface of the earth the gravitational force falls off like 1/r2
where r is the distance from the center of the earth. If R=6.4x106
m is the radius of the earth, W is your weight at the surface,
and W+ is your weight 1 mile=1.6x103 m above the
surface, then W+/W=R2/r2=0.9995;
your weight would be about 0.05% smaller. If you assume that the mass of
the earth is uniformly distributed throughout its entire volume, the
gravitational force falls off like r as you go toward the
center. Then W-/W=r/R=0.99975;
your weight would be about 0.025% smaller. Given other factors like
local variations in the density of the surrounding earth, these would be
unmeasurably small; one mile (about 1600 m) is, after all, extremely
tiny realtive to the size of the earth. I should also note that
approximating the earth's density as uniform is a very poor
approximation; see an
earlier answer. If you had asked your weight 100 miles below the
surface the answer would be that your weight is nearly the same as at
the surface.
![]() QUESTION:
QUESTION:
Helium. Where do we get it from if it is lighter than air and doesn't react with any other elements in the normal human tolerant environment?
![]() ANSWER:
ANSWER:
Good question. Even though it is the second most abundant
element in the known universe, there is virtually none in the atmosphere
(because it is so light that its average speed is greater than escape
velocity and it shoots off into space) and is not tied up in rocks,
water, or other chemicals (because it is inert) like hydrogen is, for
example. This element was not even discovered until 1868 as a spectral
line in the sun (where untold zillions of tons are being produced every
second from nuclear fusion) and not found on earth until 1895 when trace
amounts were found coming from uranium ore; the source was as a nuclear
decay product in α-decay. The first large amounts were
discovered in 1903 as a byproduct mixed with the methane in natural gas
wells; today large scale amounts come only from helium trapped
underground.
![]() QUESTION:
QUESTION:
I am curious about a topic. In golf, if I hit a ball very hard and then I hit one very softly, is the one
hit very softly more likely to move or sway in its straight path?
![]() ANSWER:
ANSWER:
You refer to "its straight path". No golf ball goes in a
straight path, so I presume you mean that it does not curve left or
right; such a ball, if not curving, would have a projected path on the
ground (like the path of its shadow) which is straight. For a
right-handed golfer, a ball which curves right is called a slice
and one which curves to the left is called a hook; these have
opposite spins. Neglecting the possibility of wind, the reason that a
ball curves is because it has spin. But now it gets complicated because:
-
the hard-hit ball is in the air much longer than the softly-hit ball;
-
the lateral force causing the curve depends on both the rate of spin and the speed of the ball, so the hard-hit ball will experience more lateral force than the softly-hit one if they have the same spin;
-
even if the slow ball has a bigger lateral force, the fast ball is likely to be deflected a greater distance because of its longer flight time;
-
a lateral wind will exert the same force on both, but the fast ball will be deflected farther because of the longer time.
So, you see, there is no simple answer. To avoid curving, learn to hit the ball without imparting significant spin!

![]() QUESTION:
QUESTION:
We had a phenomenon happen recently about 8:30 PM that is inexplicable to us, but there must be some explanation. My wife and I were in separate rooms when we both heard an extremely loud noise from the living room! The noise sounded like a large glass that just hit a hard tile floor, but loudness was magnified. As it turned out we came into the living room to find a glass platter that we had sitting on the coffee table for about a year just shattered. âIt broke completely by itself as there was no one in the room.
Do you know how this may have shattered/blew apart all by itself?We used the platter to put 3 little oil lamps on.
Inside our house the next morning at 6 AM we heard thunder outside so thought it might have had something to do with the barometric pressure.Very low barometric pressure and the type of glass it was made up combined just right to explode it like that? The temperature was a constant 68 degrees as it was for the months that was on the table.
If you have any idea about this, we would appreciate it.
![]() ANSWER:
ANSWER:
Glass, as you know, is manufactured at very high temperatures.
It has a quite large coefficient of theremal expansion (a large change
in size for a small change in temperature) and is a poor conductor of
heat. This means that as it cools it does not all cool at the same time.
This can result in very large stresses being "frozen in" at some
locations. What causes it to spontaneously break is usually difficult to
determine; most likely it had recently been bumped or your oil lamps
might have caused hot spots on the glass. Such things could have caused
a tiny fracture to begin and the final shattering could easily come at
some unpredictable later time. Unusual but not unexpected.

![]() QUESTION:
QUESTION:
On a skate board going down a .5 mile hill at 45 degrees slopes if I weigh
187 lbs how many mph would I be going by the bottom of the slope.
![]() FOLLOWUP
QUESTION:
FOLLOWUP
QUESTION:
This isn't homework I'm a 35 year old heavy equipment operator and my son had a accident on skate board and we are curious how fast he was going when he wiped out.
I just wasn't sure how accurate I was when I said about 30-35mph. Please if you don't know just tell me so I can find someone who does—we got bets on it now amongst the family.
![]() ANSWER:
ANSWER:
Wow, 45º is pretty darn steep! A half mile would
correspond to his having dropped by about 0.35 miles≈560 m. If
there were no friction at all his speed would have been v=√(2gh)=√(2x9.8x560)=105
m/s=235 mph! Back to the drawing board! There is some friction due to
the wheels and bearings and I estimate that this is probably not more
than about 15 lb; this would only slow him down to about 99 m/s=220 mph.
Back to the drawing board! Finally, since the speed is going to get
pretty big, we need to take air drag into consideration because the drag
force is proportional to the square of the speed. A rough estimate would
be that the force is about Fdrag≈¼Av2
where A is the area his body presents to the onrushing wind. When Fdrag
is equal the net force down the incline (component of weight minus
friction, which I estimate to be about 117 lb=520 N), he will stop
accelerating. Taking his area to be about 2 m2, you can then solve ¼Av2=520 to get
v=32 m/s=70 mph. This is all very rough but should give you an
order-of-magnitude estimate. (I still find it hard to believe that he
went down a half mile, 45º slope without braking at all!)
![]() QUESTION:
QUESTION:
I am curious about generating power in space. Why do they always use solar instead of the windmill type of generation?
A coil/magnet rotating. It seems to me, once the rotation is started, it would continue forever? Thus if you used a rocket to start the rotating part of the generator, and it kept spinning, could you use the magnetic field to protect say, an astronaut inside the generator? If it was big enough. Would you get perpetual energy if you used the electricity created in say, a microwave rocket engine or electromagnet. Or does the magnetic force alone cause the spin to lose momentum?
![]() ANSWER:
ANSWER:
So, you start something rotating in a vacuum and it never stops
because there is no air drag. You could even imagine making extremely
low-friction bearings so you could mount this on the side of your
spacecraft and it would at least spin for a very long time before
slowing down. But, the minute you hook it up to a generator you are
asking it for energy so it immediately begins to slow down, giving its
kinetic energy to you to power a light bulb, maybe. There is no free
lunch in this universe, and if you want energy you need something to
give it to you and the sun is the most convenient source in our
neighborhood.
![]() QUESTION:
QUESTION:
If the planet earth was perfectly smooth and spherical will the water cease to flow?
![]() ANSWER:
ANSWER:
Not if everything else stayed the same. If the earth were
completely isolated, not rotating, and without atmosphere, water would
flow until it formed a uniform layer over the earth; eventually any
currents would damp out due to the viscosity of the water. The fact that
the earth is rotating and heated by the sun and has an atmosphere would
mean that the water would try to distribute itself mostly uniformly but
with an equatorial bulge; however heating and cooling of the atmosphere
would cause weather patterns and the resulting winds would move the
water around just like what happens today. Also, the moon causes tides
which are, by definition, motions of the water. You probably could think
of many more reasons the water would not become totally static.
![]() QUESTION:
QUESTION:
We're trying to design a vessel for working in the vacuum of space. We have a vacuum chamber that can pull a 0.01 atm partial vacuum, so the question is : How does the force difference compare on the walls of a vessel, with 14 psi inside to outside chamber or space, i.e. force comparison between 0.01 atm in the chamber and the 10-14 in space?
My guess is that we are capturing 99% of the effective force differential using the chamber, so not much more to expect from the vacuum of space.
![]() ANSWER:
ANSWER:
Ok, the 14 psi inside your chamber is about 0.953 atm and the
pressure outside is 0.01 atm making the net pressure difference 0.943
atm. The pressure outside in space is, for all intents and purposes,
zero, so the net pressure difference would be 0.953 atm. So, the percent
difference is 100x(0.953-0.943)/0.953=1.05%, about what you guessed. In
other words, the force on any part of the walls of your chamber is
about 1% smaller than it would be in space.
![]() QUESTION:
QUESTION:
Not sure if this is physics or not but how can you record silent sound ? I found the patent for it on google it's
5159703
and I wanna know how you can record it because a regular microphone doesn't pick it up.
![]() ANSWER:
ANSWER:
The idea here is essentially the same as AM radio where the
high-frequency radio wave is modulated by the audible message. For this
invention the radio wave is replaced with sound of a frequency larger
than is audible but modulated by an audible signal. You could certainly
make a detector (call it a microphone if you like) to detect these
high-frequency sound waves; ultrasound imaging in medicine does just
that. Then you would need some electronics to extract the audible signal
from the carrier, just like you need a radio receiver to extract the
audible signal from the AM radio carrier.

![]() QUESTION:
QUESTION:
Imagine if you wrapped a rope tightly around the earth. How much longer would you have to make the rope if you wanted
it to be exactly one foot above the surface all the way around?![]() ANSWER:
ANSWER:
I hope you don't think that the rope would spontaneously rise up if
it were longer than the circumference of the earth; you would have a
slightly slack rope laying on the ground. You are specifying the difference
in radii between one circle with a circumference C and another of
circumference C+
![]() QUESTION:
QUESTION:
What will happen if we fill water in the tyres of our cars instead of air?Does it have any effect?.
![]() ANSWER:
ANSWER:
Three important issues I can think of. First, it would add a lot
of weight to the vehicle which would hurt your gas economy. Second, the
moment of inertial of a wheel would be larger requiring a larger torque
having to be exerted for either acceleration or braking. Third, air is
compressible and water is not and so the wheel would not have a
cushioning effect on the ride.
![]() QUESTION:
QUESTION:
I just saw a
music video in which a group of performers appear to be in an aeroplane cabin in free-fall for 2 minutes and 40 seconds. The choreography is spectacular, and it appears to have been done in ONE take!
How far would the plane have had to descend to maintain zero gravity conditions for 160 seconds?
![]() ANSWER:
ANSWER:
This video was shot in Russia in a reduced-gravity jet provided
by S7 Airlines. Weightlessness is not achieved by falling but by
following the parabolic path which a projectile would follow. Imagine
that someone shot you from a cannon with a speed of 500 mph (the typical
speed of a commercial jet). If there were no air drag, you would follow
a parabolic path. The plane which contains you now follows that exact
path and that is how you appear to be weightless. An alternative way
would be for the plane to simply go straight down with an acceleration
of 9.8 m/s2, but I think you can see that this would not be a
very safe situation. Anyhow, back to you question, I could not find
reference to any such parabolic flight lasting longer than 30 s, so the
video must have been shot in more than one take. Because this is such an
unfamiliar environment, I cannot believe that, even with a lot of
practice, it could be done in a single take without errors. And, if the
plane were simply falling for 160 s, it would have to have started at an
altitude of about 80 mi (far higher than a plane can actually fly) and
would end with a speed of about 3600 mph (far faster than the plane
could fly without disintegrating).
![]() QUESTION:
QUESTION:
Have scientists done experiment on what is the value of gravity below the earth surface as depth increases? if done pl. provide chart g vs depth.
![]() ANSWER:
ANSWER:
The
deepest hole ever drilled is only about 12 km deep. I could
not find any reference to attempts to measure g at various depths
down
this hole. Since the radius is about 6.4x103 km, you would
only expect about a 0.2% variation over that distance. There are models
of the density of the earth, though, which have been determined by
observing waves transmitted through the earth during earthquakes or
nuclear bomb tests; these are believed to be a pretty good
representation of the radial density and can be used to calculate g.
The two figures above show the deduced density distribution and the
calculated g.
Usually in introductory physics
classes we talk about the earth as having constant density, but as you
can see, that is far from true—the core is much more dense than
the mantles and crust. If it were true, g would decrease
linearly to zero inside the earth. Instead, it increases slightly first
to around 10 m/s2 and remains nearly constant until you are
at a depth of around 2000 km. There is little likelihood that g will
ever actually be measured deep inside the earth because the temperature
increases greatly as you go deeper, already to near 200ºC at 12 km.
However, if you have detailed information on density distribution, there
is really no need to measure g.
A little should be said about the other end,
launching the slug in the first place. In this case, unless the cannon
has a 10 km barrel, the recoil force on the ship will be huge. You would
be interested in similar
Q&As
along the same line as yours.
![]() QUESTION:
QUESTION:
Many Science Fiction ships have for protection a shield that stops projectiles and saves the ship from a lethal impact. Such an example would be the energy shields possessed by the faction known as Covenant from Halo.
So given the laws of Newton and the third law about there always being an equal force countering the force that was exerted first, wouldn't this just mean that whenever the energy shield takes a hit by a projectile, the force would ''travel'' from the shield to whatever generator generates the shield.
Like the UNSC Frigates shoot a 600 ton slug at 30km/s. They're 30ft long and around 7ft wide. So they have a lot of force and momentum behind them.
So wouldn't an impact like this just cause the shield generator to be violently thrown off its attachments and ''fly off'' through the compartments of the ship destroying a lot of the ship?
![]() ANSWER:
ANSWER:
"So they have a lot of force and momentum behind them." Yes, these
projectiles have a lot of momentum, but saying that "…there is a
lot of force…behind them…"
has no meaning. The momentum a slug has is p=mv=(6x105
kg)(3x104 m/s)=1.8x1010 kg m/s. When this hits
something, it will certainly exert a force, but the magnitude of that
force will depend on how long it took to stop. I have no idea how big it
is, but suppose it has a radius of 10 km from the ship; I will think of
it as very flexible and suppose that it stretches inward just stopping
before it hits the ship. I also will assume that the ship is much more
massive than the slug; (elsewise how could a comparably-sized ship carry
a bunch of them and fire them without huge recoil?) If it stops in 10
km=104 m with uniform acceleration, I can apply simple
kinematics, -3x104=at and 104=3x104+½at2,
and find that t=1.5 s, the time for the slug to stop. The
average force felt by the slug is (Newton's second law) the rate of
change of the momentum, F=1.8x1010/1.5=1.2x1010
N. You are certainly right, this very large force will be felt by the
ship because of Newton's third law. But suppose that the ship is 100,000
times more massive than the slug, 6x1010 kg; in that case,
the final velocity of the ship after being hit will be found from F=mv/t=6x1010v/1.5=1.2x1010
N, so v=0.3 m/s, not so bad! If the shield were very rigid, it
would be catastrophe for the ship. I have never played these games but I
expect the shield is shown as stopping the slug almost instantly.
![]() QUESTION:
QUESTION:
I am writing a blog and had my friends to ask of what they would want to talk about.. I get this one. I have no clue with physics, so, I am asking. Explain why a photon particle- which is a very small bundle of energy and travels at the speed of light- seems to defy the laws of physics by never losing speed or velocity?
![]() ANSWER:
ANSWER:
There is no law of physics which says an object naturally loses velocity. To
change the velocity of something you have to apply a force to it, it must
interact with something. If you had a bowling ball which had no forces on it
it would continue going with a constant speed in a straight line forever.
This is just Newton's first law. However, Newtonian mechanics is not valid
for a photon, but it behaves like any other particle when it experiences no
interactions which would change it. There is one important difference—regardless
of how it interacts with something else, it never speeds up nor slows down;
the speed of light in a vacuum is a constant of nature. If you look on my
faq page you will find links to discussions regarding
why the speed is constant and why it has the value it does. When you throw a
ball up in the air, it slows down; you throw it down from a tall building,
it speeds up. Photons don't do that but they do change their energies by
changing to a longer, redder (shorter, bluer) wavelength when going up
(down) in a gravitational field.
![]() QUESTION:
QUESTION:
Gasoline contains 40 megajoules of energy per kilogram and gasoline trucks have around a hundred tons of it. So how does a gasoline truck exploding not produce an explosion similar to a small nuke?
![]() ANSWER:
ANSWER:
Since it is always a little ambigous what is meant by a ton, I did my own
calculation using the volume of a tanker truck of about 10,000 gallons and
the density of gasoline of about 2.7 kg/gallon. I got the total energy
content of about 1012 J. The energy of the Nagasaki bomb, a small
bomb by today's standards, was about 1014 J, 100 times bigger.
Two things to consider are:
-
The bomb number represents total energy delivered whereas I would guess that likely less than half the energy content of the gasoline would actually be delivered.
-
The time over which the energy is delivered is likely much longer for the gasoline explosion than the nuclear explosion. As an example, just to illustrate the importance, suppose the bomb exploded in 1 ms=10-3 s and the tank in 1 s. Then the power delivered by each is 108 GW for the bomb and 103 GW for the tank. As a result the destructive power of the bomb would be much bigger.
![]() QUESTION:
QUESTION:
If a man could travel with a near speed of light, what would happen to him if he'd run though an elephant. Would that man be demolished or could he survive that impact?
![]() ANSWER:
ANSWER:
Are you kidding? A man going 200 mph, far below the speed of light, would be
instantly killed in this scenario. A 100 kg man going at 80% the speed of
light would bring in about 5x1018 J of energy to the collision
which is equivalent to about 10,000 Nagasaki atomic bombs. Not only would
the man and elephant be obliterated, also anything within miles would be.
![]() QUESTION:
QUESTION:
Bodies of water bend with the curvature of the planet. How large would a body of water have to be in order to measure a difference of 1 inch from one end to the other.
![]() ANSWER:
ANSWER:
I
often get questions like this. I have used this figure many times before.
Here R=6.4x106 m is the radius of the earth, d=1
in=0.024 m is your 1 inch, θ is the angle which
subtends the arc length, call it s, you seek.
From the triangle you can write cosθ=R/(R+d)=[1+(d/R)]-1≈1-(d/R)+…
where I have done a binomial expansion of [1+(d/R)]-1
because (d/R) is extremely small. Now, because
θ is also very small, I can represent cosθ by
the expansion cosθ≈1-½θ2+…
so (d/R)≈½θ2.
Finally we can write that θ=s/R. If you now solve
for s you will find s≈554 m.
![]() QUESTION:
QUESTION:
I'm a science geek and an IT person who just found out that there are sixteen types of water ice. I've been googling the phenomena, and can only find discussions of the physical make-up at the atomic level. Can you help me with some discussion of the various forms of ice at a macro level? Like, what does it look like, how does it act, etc. Everything I've found is in science speak, which I really can't envision myself.
![]() ANSWER:
ANSWER:
Refer to the figure above which came from the Wikepedia article on
ice. You can get a clearer
picture there. The thing to notice is that all the ices except for ice I and
ice XI occur at extremely high pressures—1000 atmospheres or
higher. So, you cannot really "look" at them and say what they look like
since they are formed in a containment vessel of some sort. Ice XI occurs at
atmospheric pressure but only at very low temperatures. If you look at the
Phases section of the
article, you will find links to separate articles for all 16 forms of ice
where you can get information about their properties. Although the
terminology for the crystal structure is pretty "science speak" as you say,
you will find usually pretty comprehensible pictures of these crystal
structures. I think you would find these articles about as understandable as
you will find.
![]() QUESTION:
QUESTION:
If atoms at room temperature move around at roughly the speed of a jet airplane, how fast do atoms that make up a jet airplane move when said airplane is moving (at room temperature)?
![]() ANSWER:
ANSWER:
I assume you are talking about molecules in a gas. It is much more
complicated to talk about molecular speeds in solids. So let's talk about
the air in the airplane cabin. The speeds are distributed from very low to
very high, but the most probable speed would be around 1000 mph, about twice
the speed of a commercial jet. But, that does not mean that the most
probable speed of molecules in a jet flying by would be around 1500 mph
because the molecules measured inside the airplane would be moving in all
directions so the result of adding 500 mph to all the molecules going 1000
mph would yield anything from 500 mph to 1500 mph. Measured inside the
airplane, the average velocity of all the molecules would be zero because
for every molecule going in one direction with some speed v there
is always another going in the opposite direction with speed v. The
average velocity of the air in the airplane as measured by an observer on
the ground would be 500 mph. It could be thought of as like a wind in which
there is a net flow of air in the direction the wind is blowing.
![]() QUESTION:
QUESTION:
In what medium would sound travel the fastest?
![]() ANSWER:
ANSWER:
I have not done an exhaustive search, but the largest I found was beryllium
with a speed of 12,890 m/s. Diamond is a close second with a speed of 12,000
m/s.

![]() QUESTION:
QUESTION:
if a cat fell from 100 feet how fast was the cat in mph falling when it hit the ground
![]() ANSWER:
ANSWER:
The terminal velocity of a cat is about 60 mph and that speed is achieved
after falling about 50 ft. Therefore falling from 100 ft the speed would be
about 60 mph. See earlier answers (1
and 2) for more
details. Keep in mind that all cats are not the same size, weight, or
fuzziness, so this can only be an approximate answer. It is interesting that
about 10% of cats falling from 5 stories are killed but fewer from higher
stories because, once reaching terminal velocity, they can relax, spread out
(to slow down) and get ready to hit.
![]() QUESTION:
QUESTION:
When I was very young, I used a hand-held fish scale to try and measure my
own weight by attaching the hook (normally placed in the gills of the fish
just caught) to my belt and then pulled up on it. I'm interested in the
physics behind my folly and, expanding it further, if the scale was attached
to a light (not heavy) bar (that would support more than my weight) and the
scale could measure a fish weighing more than me, and I was strong enough to
lift more than my weight above my head, how close could I expect to get to
seeing my weight on the scale (attached to the bar I'm pushing up, and a
belt-device around my waist)?
![]() ANSWER:
ANSWER:
The way you always solve a statics problem like this is to first choose a
body, then apply Newton's first law which states that the sum of all forces
on the body must equal zero; I choose the scale as the body.
What are the forces on the scale itself? Your hand pulls up with a force
Fhand, your belt pulls down with a force Fbelt,
and the earth pulls down on the scale (its weight) with a force Wscale.
These three have to add to zero which means that Fhand=Fbelt+Wscale.
Now, the scale is calibrated so that it reads zero when Fbelt=0,
so the scale will read whatever force your hand exerts up. Note that when
you do this analysis, the desired quantity, your weight, never
appears; everything would be just the same if you weighed 1000 lb. Regarding
your second question, it is really no different from the first question:
simply replace 'belt' by 'bar' everywhere. In either case you would observe the scale reading your weight when you pulled up with a force equal
to your own weight.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Thank you! So it sounds like it wasn't a folly after all (except for the fact that the scale I used wouldn't support my weight at that age).
![]() ANSWER:
ANSWER:
Of course it was folly, total folly! Doing this experiment gives
you absolutely no information about your weight. Only if you already knew
your weight and were able to pull with a force that hard would the scale
read your weight.
![]() QUESTION:
QUESTION:
Hi, I was wondering what are the chances of survival from falling from the ninth floor of a building, going over the science of that how does surface affect the fall, body weight and trajectory. What is the difference from falling from a third story window as opposed to a higher up one?
![]() ANSWER:
ANSWER:
Someone else also asked this question; apparently it refers to a recent actual
incident of a student falling out a dorm room window about 85 ft≈26
m high; the student survived without serious injury. The second person also
wanted to know if I could estimate the force experienced on impact. First I
will calculate the speed he would hit the ground if there were no air drag.
The appropriate equations of motion are y(t)=26-½gt2. and
v(t)=gt where y(t) is the height above the ground
at time t, and g is
acceleration due to gravity which I will take to be g≈10
m/s2. The time when the ground (y=0) is reached is found
from the y equation, 0=26-5t2 or t=√(26/5)=2.3
s. Therefore v=10x2.3=23 m/s (about 51 mph). The terminal velocity of a falling
human is approximately 55 m/s, more than double the speed here, so the
effects of air drag are small and can be neglected for our purposes of
estimating. (If there is air drag, terminal velocity is the speed
which will eventually be reached when the drag becomes equal to the weight.)
Estimating the force this guy experienced when he hit the ground is a bit trickier, because what really matters is how quickly he stopped. Keep in mind that this is only a rough estimate because I do not know the exact nature of how the ground behaved when he hit it. The main principle is Newton's second law which may be stated as F=mΔv/Δt where m is the mass, Δt is the time to stop, Δv=23 m/s is the change in speed over that time, and F is the average force experienced over Δt. You can see that the shorter the time, the greater the force; he will be hurt a lot more falling on concrete than on a pile of mattresses. I was told that his weight was 156 lb which is m=71 kg and he fell onto about 2" of pine straw; that was probably over relatively soft earth which would have compressed a couple of more inches. So let's say he stopped over a distance of about 4"≈0.1 m. We can estimate the stopping time from the stopping distance by assuming that the decceleration is constant; without going into details, this results in the approximate time Δt≈0.01 s. Putting all that into the equation above for F, F≈71x23/0.01=163,000 N≈37,000 lb. This is a very large force, but keep in mind that if he hits flat it is spread out over his whole body, so we should really think about pressure; estimating his total area to be about 2 m2, I find that this results in a pressure of about 82,000 N/m2=12 lb/in2. That is still a pretty big force but you could certainly endure a force of 12 lb exerted over one square inch of your body pretty easily.
Another possibility is that the victim employed some variation of the technique parachuters use when hitting the ground, going feet first and using bending of the knees to lengthen the time of collision. Supposing that he has about 0.8 m of leg and body bending to apply, his stopping distance is about eight times as large which would result in in an eight times smaller average force, about 5,000 lb.
Falling from a third story window (about 32 feet, say) would result in a speed of about 14 m/s (31 mph) so the force would be reduced by a factor of a little less than a half.
![]() ADDED NOTE:
ADDED NOTE:
A rough estimate including air drag would have his speed at the ground be
about 21 m/s rather than 23 m/s as above. Given the rough estimates in all
these calculations, this 10% difference is indeed negligible.
![]() QUESTION:
QUESTION:
When in the early universe did life become possible? I'm assuming it would have had to have been at some point when the temperature had cooled down enough so that the protons and neutrons of basic elements of life like carbon and oxygen could bond and come together. Also, what do you believe is the purpose for intelligent life in the Universe?
![]() ANSWER:
ANSWER:
I usually do not answer questions about astronomy/astrophysics/cosmology as
stated on the site. I can give you a little information here, though. The
universe just after the big bang was almost exclusively hydrogen. No
elements which could be used to form planets where life might develop or the
material for life itself. The first stars started forming about 100 million
years after the big bang, basically pure hydrogen stars. These had to be
much larger than the sun (perhaps 300-1,000 times heavier) because of the
lack of heavier elements and consequently their lifetimes were too short (a
few million years) for life to evolve (it has taken about 5 billion years to
reach our stage of evolution, about half the sun's lifetime). Inside these
stars nuclear fusion caused heavier and heavier elements up to about iron to
form; then when those stars used up all the fuel, they exploded (super
novae) scattering the heavier elements to eventually be part of clouds of
dust and hydrogen which subsequently formed new stars with the possibility
of planets. (As you can see, it is not "cooling down" which is responsible
for heavier elements which are created in stars which are super hot.) So, we
are now at least several billion years into the age of the universe. More
detail on early stars can be read in a
Scientific American article. The "purpose" for anything is not within
the purview of physics.
![]() QUESTION:
QUESTION:
What is the purpose of utilizing a percentage of body weight to determine how much weight to bench press/push/whatever? I know this seems like a fitness question and not a physics question, but what I am interested in is WHY weight would be used to determine how much one could (or should be able to) lift/push?
For example: A gym teacher wants to grade his students on their strength. He decides to use abililty to push a weighted sled across the floor as the measure. He wants to make the task equally difficult for every student in order to make the grading fair. So, he decides that each student will push 2x his/her body weight for 5 minutes and the grade will be based on how FAR the student is able to push.
So, Student A weighs 170 pounds and pushes 340 pounds (including the weight of the sled) for a total of 160 yards. Student B weighs 240 pounds and pushes 480 pounds (again, including the weight of the sled) for 80 yards. Student A pushed farther and gets a better grade, but Student B complains that he had to push much more weight so he should not get a worse grade.
Does Student B have a legitimate complaint or does his heavier weight contribute somehow to his ability to push that doesn't have anything to do with his strength? As in, does his weight help push the sled in some way?
Sorry, I don't know enough about physics to ask this question using proper physics terms like force, mass, etc. I hope you will still answer my question!
![]() ANSWER:
ANSWER:
I cannot comment on the rationale for correlating weight to strength. I can
certainly comment on the physics of your particular example of sled pushing.
I would first of all comment that this example is certainly not one solely
of strength because, since it is a timed activity, endurance as much as
strength is being tested; if one student, for example, were a heavy smoker,
he would likely become exhausted more easily. As a physicist, I would equate
"strength" with force. The specific example you give, though, seems to me to
be more related to energy (work done by the student) or power (rate of
energy delivered) than strength; purely in terms of strength, the heavier
student exerts more force. The force F which each student must exert
depends on the weight w he is pushing and the coefficient of friction
#956;
between the sled and the ground, F= μw.
The work W done in
pushing the sled a distance d is W=Fd= μwd.
The power generated if W
is delivered in a time t is P=W/t=μwd/t .
Both students have the same
μ
and
t , so WA/WB=PA/PB=dAwA/dBw
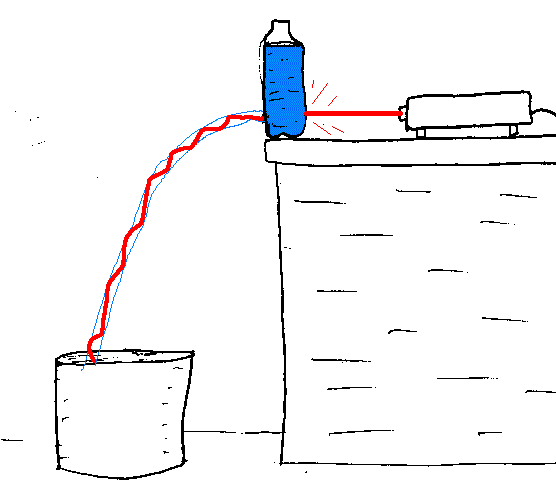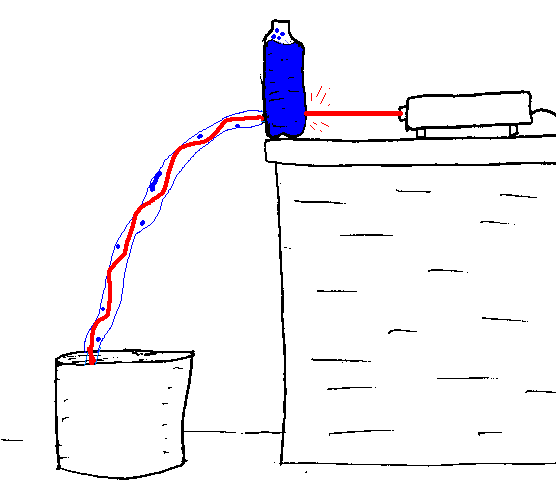
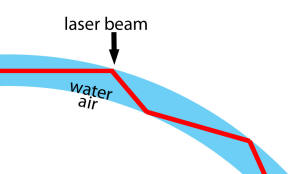
![]() QUESTION:
QUESTION:
The demonstration wherein one pours water from a clear vessel and one shines a laser pointer (a red laser pointer in my case) through the water and it appears the laser beam bends with the water pouring out of the clear vessel;
What causes the beam to bend with the water? Would this same type of effect work with other fluids than water, such as air or glass?
![]() ANSWER:
ANSWER:
It is caused by
total
internal reflection. If the angle which the light hits the surface
between the water and the air is glancing enough, the light will be
reflected back into the water rather than be refracted into the air. Total
internal reflection can happen whenever light strikes the interface with a
material of smaller index of refraction; the minimum angle for which it can
occur depends on the relative indices of refraction.
![]() QUESTION:
QUESTION:
Why simple harmonic motion is called simple?
![]() ANSWER:
ANSWER:
Take a look at the figure above. The red curves are all pure sine waves, just
having different frequencies. These are all called simple harmonic motion
because they may be expressed as a single sine wave. Now, take all four of
these and add them together. The result is the black curve. This curve is
still harmonic (which means that it is periodic, it repeats itself after
some time, called the period, has elapsed) but it is not "simple" because to
describe it you must use four different sine waves.
![]() QUESTION:
QUESTION:
Hi ...here is a link to Felix Baumgartner's freefall jump from space -
https://www.youtube.com/watch?v=vvbN-cWe0A0
135,890 feet - or, 41.42 km (25.74 mi)
In the video you see speed at which he is supposedly travelling, 729 mph (1173km/hr), 46 seconds after he jumped. The footage is cut then seconds later speed strangely falls to 629 mph...anyway after 4 mins and 18 seconds of free falling he releases parachute. My questions are What speed would he be going at a 4 mins and 18 seconds into freefall? Also how do you explain the deacceleration when it was at 729 mph then down to 629 mph?
![]() ANSWER:
ANSWER:
(You might be interested in an
earlier answer.) There is a better video at
https://www.youtube.com/watch?v=raiFrxbHxV0; this video shows data
acquired by instruments on Baumgartner. Here some clips from that video:
The first three are the times also showing speeds; these are roughly the speeds you refer to in your question. The second three show speeds and altitudes. The third graph shows the whole history of altitude, speed, and mach speed. The speeds are all larger than indicated in your video. The speed at 4:20, 113 mph, answers your first question. The speed at 0:50 is about the maximum, 847 mph or mach1.25. The speed at 1:01 has dropped to 732 (about the same change as your video); I suspect this deceleration is due to two factors: there is getting to be much more air resulting in higher drag and, probably after he broke the record he oriented his body to increase drag and slow down. The official maximum speed after everything was calibrated was 843.6 mph.
![]() QUESTION:
QUESTION:
Will the drag coefficient be the same in air and water?
![]() ANSWER:
ANSWER:
There is no simple answer to this question. The drag coefficient CD
is a constant characterized by the geometry of an object used to
calculate the drag force FD if it is proportional to the
square of the velocity v: FD= CD ρAv 2
where A is the area
the object presents to the fluid flow and
ρ
is the density of the fluid.
Whether or not this equation is true depends on a quantity called the
Reynolds number Re=Lρv/η
where L is a length along the direction of flow and
η
is the viscosity of the fluid. It turns out that only if Re>1000 is
the velocity dependence approximately quadratic. If Re<1 the drag
force is approximately proportional to v. Anywhere between these
extremes the drag force is a combination,
FD≈CD ρAv 2+kv.
CD ≈constant
only for the case Re>1000; the drag coefficient would then be the
same for identically shaped objects. It is interesting, though, to get a
feeling for what the relative speeds in air and water corresponding to Re=1000
are. The necessary data at room
temperature are ρ air≈1 kg/m3, ρ water ≈1000 kg/m3, η air≈1.8x10-5 Pa·s, and η water≈1.0x10-3 Pa·s. Then vwater/vair≈(1.0x10-3/1000)/(1.8x10-5/1)=0.056 (which is true for any Re). Taking a sphere of diameter 0.1 m as a specific example for the critical Re=1000, CD=0.47, A=7.9x10-3 m2, L=0.1 m, vair=1000x1.8x10-5/(0.1x1)=0.18 m/s and vwater=1000x1.0x10-3/(0.1x1000)=0.01 m/s. Since the speeds are relatively low, you can conclude that for many cases of interest the quadratic drag equation holds for both water and air. Therefore, for many situations you can approximate that the drag coefficient in air and water are about the same. For a specific case you should check the Reynolds numbers to be sure that they are >1000. The bottom line is that if the drag force depends quadratically on velocity, the drag coefficient approximately depends only on geometry, not the properties of the fluid. Keep in mind that all calculations of fluid drag are only approximations.
![]() ADDED
COMMENT:
ADDED
COMMENT:
As I said above, for 1<Re<1000, FD ≈av+bv2
where a and b depend on Re; e.g., a≈0 for
Re>1000 and b≈0 for Re<1. So, for Re<1, a
is just a constant and FD≈av≡½CD ρAv 2
so CD=2a/( ρAv )=2aL/(A ηRe )≡c/Re
where c is a constant. If FD is proportional to
v, CD is inversely proportional to Re; this is
called Stokes' law. As we saw above, Re>1000 leads to CD=constant.
Ferguson and Church have derived an analytical expression which very
neatly reproduces data for the transition from Stokes' law (1/Re) to
constant CD. Calculations for a golf ball are shown at the
left (constant CD, the green line, is called turbulent in
the legend). Note, as we have stated, that the transition occurs in the
region
1<Re<1000. Note the sudden drop in the data around Re=500,000.
I believe that this must be due to the
dimples on the golf ball which
reduce drag.

![]() QUESTION:
QUESTION:
What is the true shape of the Sun?
![]() ANSWER:
ANSWER:
I was surprised to learn that the sun is almost a
perfect sphere.
![]() QUESTION:
QUESTION:
I have something I have been wondering about.maybe you can answer. I recently drank a glass bottle of rootbeer and then set the empty bottle on the hood of my car that was slanted slightly (1980's model). Within seconds the empty bottle started to vibrate slightly and then"walked" down the hood of my car. The engine was turned off. I was trying to tell my girlfriend that it was from heat convection, but she disagreed. How can this happen? I did it a second time and the empty bottle did it again. Not my imagination.
![]() ANSWER:
ANSWER:
Here is what I think: The bottle probably had condensation (water) which was
fairly cool and the hood of your car was warm or even hot. The viscosity of
water depends quite sensitively on its temperature. If the water is heated
from 250C to 500C, for example, the
viscosity
decreases from about 890 to 547
μPa¡s which will result in a
much slipperier contact. (Think of a very heavy oil and a very light oil to
get an intuitive feeling for how viscosity would affect the frictional
force. Or, think of the old expression "âŚas slow as molasses in JanuaryâŚ".)
![]() QUESTION:
QUESTION:
Why in the michelson and morley experiment that air does not have any effect on the experiment. To me air would be the current medium that the light is using to propagate and would yield a null result. The main key to this line of thought is that light travels slower through air then in a vacuum. The same as the speed of sound through different medium.
![]() ANSWER:
ANSWER:
The Michelson-Morley experiment does not attempt to measure the absolute
speed of light. Rather, the idea is to find the difference in speeds between
two different directions of travel. That measurement would not depend on the
presence of air.
![]() QUESTION:
QUESTION:
Why does stirring a liquid makes it cool faster? Shouldn't the reverse happen, as the kinetic energy imparted to liquid in stirring should also change eventually to heat?
![]() ANSWER:
ANSWER:
The liquid in the cup loses energy to its environment (cools) by conduction
and radiation from its surfaces. The energy inside the surfaces is
transmitted to the surfaces (to continue cooling) by convection. Convection
is a relatively slow process for transmitting heat. Stirring more
effectively moves hot liquid to the surface. Energy you add by stirring is
trivially small compared to the increased cooling rate.
![]() QUESTION:
QUESTION:
What is the true shape of the earth?
![]() ANSWER:
ANSWER:
There is no "true shape" of the earth because the earth is geologically
active, constantly changing due to volcanism and plate tectonics. To a very
good approximation, though, the earth is a sphere. Closer inspection shows
that the earth is slightly oblate, that is, it is slightly pushed out at the
equator and scrunched in at the poles; still, it is small, the equatorial
diameter being about 42 km larger than the polar diameter. This is referred
to mathematically as a negative quadrupole moment, an oblate spheroid of
revolution. I remember learning back in the early 60s when satellites were
first being launched, that their orbits also indicated an octupole moment of
the earth, sort of pear-shaped with the fatter part of the pear in the
southern hemisphere. I believe, though that there is still a lot of
controversy about such higher moments because similar effects on orbits can
be caused by uneven mass distribution of the earth which certainly does
occur. You can read more detail in
Wikepedia.
![]() QUESTION:
QUESTION:
Why isn't nitrogen forced upwards by the much heavier oxygen and co2?
![]() ANSWER:
ANSWER:
The details are very complicated. I found an
article where you can read
about it. The key finding of interest to you is in the abstract of this article: "Turbulent mixing keeps the relative concentrations of gases nearly constant in the lowest 100 km. At higher altitudes, molecular diffusion controls the concentrations, with the lighter gases becoming relatively more abundant with increasing altitude."
![]() QUESTION:
QUESTION:
Iâm a middle school teacher and I had a bright student show to me the following: If the mean radius of the earth is 3959 miles (taken from space.com) and we assume the earth to be spherical, then we could use the Pythagorean thereom to show the difference between the hypotenuse from the radius over 10 miles to be 66.883 feet. We get after squaring the 3959 and adding 100 for 10 squared, and finding the square root, and finding the difference between the hypotenuse and the radius = 66.883â. The National Geodetic Survey shows only 7.874 inches of variation across the Bonneville Salt Flats. In other words the 10 mile stretch of the Bonneville Speed Track should dip down below the horizon from the start 66+â because of the curvature of the earth, but in fact, does not. Iâd appreciate any help you can give me to explain to the student why the curvature of the earth does not seem to show itself on the salt flats.
![]() ANSWER:
ANSWER:
I am sorry, but I do not understand your calculation. I cannot figure out
what you mean by hypotenuse. Let me give you a calculation where I will
define clearly what I mean by the amount of variance over 10 miles. Maybe it
is not what you want, but at least there is a picture where you can tell me
where your hypotenuse is. In my drawing on the left there is an arc of
length s (10 miles in your case) which subtends an angle
θ from the earth's
center. The arc is a distance d above the corresponding chord at its
center (the 5 mile mark in your case). The distance along the radius
bisecting the angle to the chord is Rcos(θ/2). Noting that
Rcos(θ/2)+d=R, you can solve for d=R(1-cos(θ/2)).
The angle in radians is θ=s/R=10/3959=0.002526=0.1450.
It turns out that d=16.67'.
Now I see what you did. The figure on the right adds a tangent. Now (the newly defined) d is given by d=R[(1/cosθ)-1]=66.68' essentially your answer (I think you must have misread your calculator since I get my answer if I do it your way.)
Now, what does it mean? If you had a vertical tower at the end of the track and aimed a transit on the ground horizontally you would see about 67' up on the tower if the earth were a perfectly uniform sphere. But, on a scale as small as 10 miles, there is no reason to expect the terrain to be perfectly spherical, certainly it is not. What if the surface were truly flat? My first calculation shows that the center would only be about 17' lower than the ends, a very small variation over 10 miles (52,800'). I do not know what the 7.874" number means, but it could be a mean variation from truly flat.
![]() QUESTION:
QUESTION:
I am hoping you can help me solve a question. I am trying to figure out how much a given volume of air expands per degree increase in temperature. (volumetric thermal expansion)I have looked online but I seem to be finding several equations but the formulas seem to have unclear factors and definitions. Here is the exact variables in this problem:
If I had 1 cubic inch of air @ 80 degrees Fahrenheit (standard atmospheric pressure and standard air like what we breath)and heated it to 350 degrees Fahrenheit, how much would the volume increase?
![]() ANSWER:
ANSWER:
The ideal gas law is what you need, PV/(NT)=constant where
P is pressure, V is volume, T is temperature, and N
is some measure of the amount of gas. For your case, N and P
do not change, so V/T is unchanged as you heat the air, so
V1/T1=V2/T
First of all, any drop at all of part of the mass of the object (even 2-3
inches) will result in a drop of the center of mass of the object.
However, usually the drop is substantially more than just the distance
from the top to the bottom of the handlebars because the cyclist also
bends his arms at the elbows as shown in the figures above. Of course
there is also the reduced air drag when in the lower position.
Both 1 and 2 play an important role. This is basic Newtonian physics.
Newton's second law can be written as F=mΔv/Δt
where F is the average force felt by a mass m which
changes its speed by an amount Δv over a time interval Δt.
So, as your #1 suggests, the shorter the time of the acceleration, the
larger the force, everything else being the same. Similarly, the larger
the mass, the larger the force, everything else being the same, as per
your #2. (Also, of course, the larger the change in speed, the larger
the force, everything else being the same.) Clearly, the bigger the
force on the bullet, the bigger the force on your shoulder; that should
be adequate to demonstrate that your arguments are valid. Quantifying
that is tricky because it depends on how you define recoil. To see an
exhaustive discussion of recoil, see an
earlier answer.
Well, this turned out to be a real tour de force, particularly since
thermodynamics has never been my strong suit! First, let me explain
carefully how I did it; I think it matters when and how things happen. I
first imagined igniting and letting all the water be formed holding the
initial volume fixed and found the new temperature and pressure; next I
let the volume expand adibatically (no flow of heat into or out of the
volume) until the pressure was 1 atm inside and calculated the new
volume and temperature. Data I needed:
The internal energy of a gas may be written U=CVnRT.
I find that U(O2)=3.285x107 J and U(H2)=1.013x109
J before the ignition, so the initial internal energy of the system is
U1=1.046x109 J. When ignition is complete,
the energy added to the system is Q=44x286x103=1.258x107
J and so U2=U1+Q=1.059x109
J. But, from the internal energy of the water vapor, the temperature may
be calculated, T2=2900 K, and then from the ideal gas
law (PV=nRT), P2=7.06x105 N/m2.
Finally, the adiabatic expansion. In an adiabatic expansion from P2,V2
to P3,V3, PVγ=constant,
where γ=CP/CV. The work W
done by the gas in the expansion is W=P2V2γ(V31-γ-V21-γ)/(1-γ).
At this stage we do not know V3, so we do not know
W. But W is also known from the first law of thermodynamics
as being equal to the change in internal energy U3-U2=W
(provided no heat flows in or out). Now, we also know that U3=CVnRT3
and T3=T2[(P3V3)/(P2V2)].
Those equations then lead to the transcendental equation 146V3-1059=3.747V30.322-4.268
which I solved graphically (see figure to right) to obtain V3=7.27
m3 and T3=1991 K.
I often get this kind of question. Just because some quantity appears in an
equation in some form other than just itself, why would that imply that
that quantity was no longer that quantity. For example, suppose you want
to know the volume V of a cube of side L, V=L3
and L=2 m. Would that mean that as soon as you write the equation
that L was now 23=8 meters long? Of course not, 8 does not even have
the dimensions of length, it has the dimensions of length cubed. Just
because c appears in Einstein's equation squared does not mean
that light now can travel that fast; c2 does not even
have the dimensions of a speed which would be length/time. In fact the
quantity mc would not have the dimensions of energy. And nobody
ever said that the number c is the biggest possible number, it is
just the biggest possible speed anything can have.
There are ways that light pressure may be detected. See earlier answers
about a
"singing cymbal",
light pressure, and Crooke's radiometer.
The force for normal light intensities and normal size of target is very
small, though, so it is certainly impossible that you could measure the
force on a projector due to the light it projects. I will do a very
rough estimate of the force felt by the projector to convince you. From
the
"singing cymbal" answer, you will find an expression for force,
F=2Nhf/c where N is the number of photons per
second, h=6.6x10-34 J∙s is Planck's constant, c
is the speed of light, and f is the frequency of the light. This
equation has a factor of 2 because in that question the photons were
being reflected from the target, but in your case they are simply being
emitted, so the factor of 2 should be omitted. Also, note that the
wavelength of the light is λ=c/f. So, in your case we may
write that F=Nh/λ. I showed in a recent answer that an estimate of the intensity of of visible
photons from the sun at the earth's surface is about 4.4x1017
photons/s/m2; this should be a reasonable of the intensity of
a bright projector. Estimating the lens to have about a 1 cm radius, the
area which the light exits is about 3x10-4 m2, so
N=4.4x1017x3x10-4=1.3x1014
photons/s, and therefore F=1.3x1014x6.6x10-34/550x10-9=1.6x10-13
N. I have taken λ=550 nm, yellow, the peak intensity of the sun's
visible light.
It occurs to me that with a force this small, how could the singing cymbal
possibly work? I believe that the answer lies in the fact that I have
approached this from the perspective of visible light and this is only a
very small fraction of the total radiated power. Suppose we reframe the
problem by assuming the projector has a color temperature of 5500 K (the
same as the sun) and calculating power flux Φ using the
Stefan-Boltzman law assuming black body radiation, Φ=σT4
where σ=5.7x10-8 W/m2/K4;
then Φ=5.2x107 W/m2. The
radiation pressure for this flux is P=Φ/c where
c=3x108 m/s, so P=0.17 N/m2.
Estimating, as above, that the area of the exiting radiation is 3x10-4
m2,
the force turns out to be about F=5.2x10-5 N. I
suppose that a carefully designed experiment could detect a force this
small. For example, if the projector had a mass of 1 kg and were on a
frictionless surface, it would move a distance of about 2 m in a day due
to the acceleration caused by such a force.
It turns out that the wave pattern of a wake in deep water is well
understood. It is called a
Kelvin wave pattern. The mathematics is somewhat daunting. To the
right are a calculated pattern and a figure showing some of the
terminology. To the left is a photograph of a boat and its wake. For
years I taught that the wake of a boat was just a shock wave because the
boat is going faster than the speed of waves in the water (analogy of a
shock wave for an airplane going faster than the speed of sound) but
apparently that was wrong. The angle of the wave, from the research I
did, seems to depend on the depth of the water, not on the speed of the
boat. (Once again, Ask the Physicist learns something new!) The
"diverging wave crests" which seem to bend forward are what you refer to
in your question, I assume.
Well, your question seems a little muddled regarding what "power source"
means. What would a power source 200 years ago have meant? You might have
said human muscles and domesticated animals' muscles. But that would not
be the source, rather the food you and they ate. But that would not have
been the source because the sun provided the energy to make that food. Or you might have
said water (grist mills) and wind (wind mills and sailing ships). But
that would not be the source, rather the sun's heating of the atmosphere
causes the wind and causes water to evaporate and then fall at high
altitudes so that it can fall down and run your mill. Or you might have
said fire which you would used to heat your home or cook your food. But
that had its source in the fuel you used, wood or coal or peat. But,
those are all from the sun just like the food you eat is. So, you would
conclude that the sun was the "ultimate source" of energy 200 years ago.
Now, looking at today, you say that electricity is the power source we use.
But that, again is not the ultimate "source". And, it is certainly not the
only end of the "energy chains" which power our world. Petro fuels makes
most cars, trains, boats, and airplanes do their thing. Muscles still are
used to move us around and do lots of work. Also, we are still using wind
and hydro power, but those are still ultimately from the sun. But now, these
days, we new have sources, some of which are not from the sun. Geothermal taps
the thermal energy deep inside the earth which is not the result of the
sun's heating. Nuclear power
utilizes the energy released in the splitting of very heavy atoms. The
source of heavy atoms was not the sun but some long dead star. Solar cells
directly convert the sun's light into electrical power. So, electricity is
not the culprit at all. It is a very clean and efficient way to use energy
which we reap from the sun and other sources. And I fail to see the link
between electricity and wealth distribution. What we should be worrying
about is what energy consumption does to the environment. The continued
overuse of energy sources which put large amounts of CO2 into the
atmosphere will ultimately mean disaster for all nations regardless of their
wealth.
It would make more sense for your question to ask about either force, as
the original question did, or power, the rate
of delivering energy. If the mass is 104 metric tons, the
weight would be about F=108 N; that would be the force
you would need to exert to lift the submarine. If you were lifting at
the rate of v=10 m/s, the power P required would be about
P=F∙v=109 W=1 GW. A gigawatt is a typical
output for a nuclear power plant.
I think you are overreacting a little bit here! My opinion is that string
theory is not a theory because it makes no predictions and is therefore
not falsifiable or verifiable. However, it is a hypothesis which many
good scientists are struggling to develop. And who can predict that any
idea is not "possible"? And the math being "too complicated" does not
mean that there is no value in the ideas; Einstein found the math needed
for the theory of general relativity was "too complicated" for him and
he needed to get help from mathematicians.

![]() QUESTION:
QUESTION:
This is a classic point of contention for pilots, and has recently come up again. I'd like to know your take on this. It seems more often than not, that the answer is the plane will take off. However, no one from that side of the argument addresses the force of the conveyer in the opposite direction canceling forward force from the engine thrust. I don't see how the aircraft could accelerate from a starting velocity of 0kts.
This question has grown men lobbing profanity-laced insults back and forth. The answers are generally not backed by aerodynamics or physics equations.
I am graduating from Embry-Riddle in August with a major in Aeronautics. I'm well past my aerodynamics class, so this is certainly not homework for me, but it is most interesting nonetheless. Without further delay, here is the question:
Imagine a 747 is sitting on a conveyor belt, as wide and long as a runway. The conveyor belt is designed to exactly match the speed of the wheels, moving in the opposite direction. Can the plane take off?
![]() ANSWER:
ANSWER:
My goodness, this is pretty basic physics and should not be a puzzle at a
school which has aviation as its main focus. In order for an airplane to
fly, lift must be generated. During takeoff, lift is almost entirely the
result of air passing over the wings and if the airplane is not moving
relative to the air, there is no lift. The engines, if you could point them
vertically, could provide lift and cause the airplane to "take off" if their
thrust were greater than the weight of the airplane. I looked up the maximum
thrust for a 747 and it is only a little greater than
Ń the weight. This is no
different than an airplane revving up its engines with the brakes locked. It
will certainly not be able to take off. Vertical takeoff planes like the
Harrier (pictured above) can do this, not conventional ones. A final
thought: if you had your 747 on the conveyer belt pointed into a very high
wind, it could take off, but since the takeoff speed of a 747 is around 180
mph, there are no such winds even in a hurricane.
![]() QUESTION:
QUESTION:
Which main part of the electromagnetic spectrum emitted from the sun, is reflected by mirrors on to a water boiler. For generating renewable energy?
![]() ANSWER:
ANSWER:
It depends on two things, the spectrum emitted by the sun and the
reflectivity of the mirror itself. The sun has the most energy emitted at
wavelengths in the visible region but a significant amount is also in the
infrared region. If the reflectivity is fairly flat over this region for the
metal you choose as a mirror, the spectrum reflected will be similar to the
spectrum of the sun. Both aluminum and silver are at about 90% reflectivity
over th range of most of the spectrum and therefore the energy reflected
will be very similar to the energy which strikes the mirror. The other thing
to consider is that whatever absorbs the reflected radiation should absorb
as much of the incident radiation on it as possible, i.e. be "black".
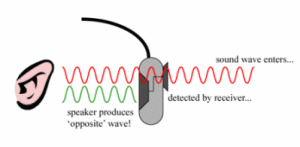
![]() QUESTION:
QUESTION:
Is it possible to reduce a sound with a sound? To clarify, if sound waves come from point A to p. B, is it possible to reduce that sound pollution by channeling another sound from point B to A? is there any possibility of it with different waves?
![]() ANSWER:
ANSWER:
The way you can do this at some point is not to send some other sound back
to the source but to cause another sound identical to but out of phase with
the first to the same point. This is called interference. This is why some
auditoriums have "dead spots" where reflected sound arrives at that point
out of phase with the direct sound. It is also the idea behind noise
canceling headphones which sample sound coming from the outside and add to
it an identical sound but upside down.
![]() QUESTION:
QUESTION:
Why charge is not considered as a 'Fundamental' physical quantity?
We say that 'mass' originated from energy then from where did 'charge' originate?
![]() ANSWER:
ANSWER:
The international system of units have agreed to use electric current as the
fundamental quantity because it is easier to do an experiment (the force
between two current-carrying wires) as an
operational definition of the ampere. Since the ampere is charge per unit time, a coulomb is one ampere¡second,
the amount of charge a one ampere current delivers in one second. I would
not say that mass "originated from energy", rather that mass is one form of
energy.
![]() QUESTION:
QUESTION:
Say I toss a coin into the air. From the moment it leaves my hand, are the cumulative effects of quantum uncertainty in the whole system enough to cause a 50/50 chance of heads/tails? Or is it all, in theory, predictable, provided we knew the initial conditions as defined in classical physics?
![]() ANSWER:
ANSWER:
I believe that if you had a very good determination of the initial
conditions that this would be deterministic. Corrections for
air drag would be necessary which might entail doing computer calculations,
but provided the air was still or moved in a known way during the time of
the flip, you could reliably predict the outcome (no longer a 50-50 chance)
of a particular throwâthe
uncertainty principle would play no role for this macroscopic experiment.
A further complication would be the interaction with whatever the coin
landed on, but you could start off making that surface sticky and add that
complication later.


![]() QUESTION:
QUESTION:
I have a question about the CoM on a rider and a bicycle.
The popular narrative or meme is that while riding a bike, with your hands on top of the bars, if you then move your hands to the 'drops' on road bike handlebars, that this lowers the CoM.
Personally, I do not believe it because we are talking about the riders shoulders and hands moving downward about 2-3".
![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:
Firearms have always been a hobby (and sometimes a profession for me). A question I am often asked is why shotguns have such high recoil. (Totally subjective as I have shot many rifles with far more recoil than a shotgun.) However there is some validity in the question.
Shotguns usually have more felt recoil (that is the recoil forces perceived by the shooter) than many rifles, even when the kinetic energy of those rifles is higher. Now discounting factors such as the weight of the gun, recoil-suppressing equipment such as muzzle brake, etc I have always attributed this to two factors.
1) Shotguns utilize very fast-burning powders, which means the reaction takes place over a shorter period of time resulting in less time for the body to absorb the recoil forces, thus making it feel sharper and more jarring to the shooter.
2) Shotgun payloads, be they shot or slugs tend to be considerably heavier than rifle projectiles. These heavier projectiles by virtue of being more massive have greater resistance to a change in their motion than do lighter projectiles resulting in heavier recoil per unit of acceleration applied to the projectile.
I am mostly inquiring about Number-2. I was recently challenged on this by an argumentative individual. (One of those who just likes to argue even if he knows nothing about the subject.) So I did not engage, but it occurred to me that I might seek the knowledge of a physicist should it come up in conversation with someone who does merit a discussion. Is my science correct on Number-2?
![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:
I have an expandable container with 1 m3 hydrogen and 1/2 m3 oxygen at stp. If I ignite this what would the final volume be if there is no heat loss? The pressure outside the container is 1 atm. I have asked this question on a number of web sites and no one seems to be able to answer this. Most want to answer only if there is heat disapation or ignited in open air. I hope you would answer this. it has plagued me for weeks! Could you show the equations so I can understand how to figure similar problems?
![]() ANSWER:
ANSWER:
Initial temperature T1=273 K,
Initial volume V1=1.5 m3,
Initial pressure P1=105 N/m2,
Specific heats at constant volume and pressure:
CV(O2)=0.659x103 J/(kg∙K)
CV(H2)=10.16x103 J/(kg∙K)
CV(H2O)=1.46x103 J/(kg∙K)
CP(H2O)=1.93x103 J/(kg∙K)
Universal gas constant R=8.3 J/mol∙K
Combustion energy per mole for water 286x103 J/mol
Taking the molecular weights of H2, O2, and H2O
to be 2, 32, and 18, respectively, I find that the container contains 22
moles of O2, 44 moles of H2, and 44 moles of H2O.
![]() QUESTION:
QUESTION:
Why would Einstein square light in his formula E = mc2, since light will only travel 186,290 miles/second? If 186,290 mi/sec is the peak, doesn't squaring it make the peak; the sum of the speed of light times itself, hugely faster than 186,290?
![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:
I heard that when light strikes a target, there is a measurable force that pushes the target a certain amount. So light can exert some "presure", right? My question is, if a light projector is emitting light towards this target, is there any measurable "recoil" on that projector or any force that pushes the projector in the opposite direction the light is traveling?
![]() ANSWER:
ANSWER:![]() ADDED
THOUGHTS:
ADDED
THOUGHTS:


![]() QUESTION:
QUESTION:
The wake of a model boat traveling at constant speed seems to bend so that
the 'older' part (furthest from the boat) appears to be catching up to the
boat. I have read that water waves don't accelerate - though they do spread
out before they disappear. Is that fact the waves spread causing this effect
or something else because they do appear to accelerate?
![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:
I recently started taking a sociology course, our main focus of study is global inequality and the distribution of wealth. How the current climate of wealthy and poor nations came to be. What's struck me is that it's mostly due to the era of colonialism and the mad dash for resources. Which got me to thinking about how we power our world. Coal, hydroelectric, nuclear, solar, and geothermal. It all boils down to electricity. And I couldn't help but wonder if there isn't anything else? Why is electricity the only energy source we can exploit? The universe is a large and varied place, you'd think that there would be some other power source we could use. So in a nutshell, is electricity all there is? Are we looking into alternatives?
![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:
I just saw the question in your page about super powered people telekinetically lifting objects and how Newton's laws have something to say about that.
So that rose me a question about the thing. Lifting the submarine should require enormous amounts of energy, and this would naturally mean that a super powered individual who uses his or hers powers to lift an object such as a submarine would need to have some borderline magical energy production methods far surpassing anything biology gives to any creature.
So if we assume that the sub marine weighs ten thousand tons, how much energy would Magneto need to lift it at the speed of let's say ten meters per second? And how does that relate to energy consumption of a normal human, and would even a nuclear reactor be enough to produce the necessary energy for lifting the submarine?
![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:
I just wanted to ask you about your opinion on string theory outrageous claims, things appearing out of nothing, really string theory. String theory math is all too complicated and with no experimental
evidence besides the equations. And the hope of putting all that into a"one
inch equation" noble but is it possible? I would love to hear your opinion.
![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:
I understand that, with a roughly spherical object, like the earth, the gravitational force tends to act on objects towards the centre of the sphere.
What would the direction of the force be with an object shaped like a cylinder? Also would the gravitational pull be greater on each end of the cylinder than at some point in the middle? (In which case I would guess that, in nature, any massive cylinder would collapse to form a sphere?)
![]() ANSWER:
ANSWER:
The gravitational field of a cylinder is pretty easy to calculate on its axis and very difficult to calculate elsewhere. At the center of each end of a cylinder of length L and radius R, the field g can be shown to be gend=[GM/(RL)][(2L/R)+Đ -Đ √(R2+L2)/R]. Let me first provide a qualitative argument that the field at the "poles" will be larger than at the "equator". At the equator, the contribution to the field from each piece of mass in one half will have a corresponding piece on the other side and their axial components will cancel out, leaving only the radial components. As long as L>R, there will be much less cancellation for fields at the "poles"; therefore, if the cylinder is not rigid, it will collapse to a sphere axially (from the poles). If L<R, this argument will work in the opposite way and you would expect the collapse to be radially in from the equator. Next, here is an approximate analytical solution for the case L>>R. The end fields can be approximated as gend≈3GM/(2R2). At the equator, Gauss's law may be used to show that gequator≈2GM/(LR). So gend/gequator≈3L/(2R)>>1. So, your expectation was right, but only if R<L. On the other hand, if R>>L, the field at the pole approaches the field at the center of a uniform disk which is zero by symmetry. So, whatever the field is at the equator, the force tends to collapse the cylinder radially (inward from the equator). The details of the calculations here are given in a separate page where I have also shown a rough sketch of the field for the L>R case.
![]() QUESTION:
QUESTION:
Is there a way for water in a static position upwards to create a waterfall effect without the use of any machine or human involvement?
Strictly just the water powering itself?
![]() ANSWER:
ANSWER:
It is not clear what you mean by "waterfall effect". Ancient Rome had fountains without machines. The trick is to have a reservoir of water higher up than the fountain. And, the water is not "powering itself", it is being powered by gravity.
![]() QUESTION:
QUESTION:
Approximately how many photons of sun light are in a square inch over one second? Assuming the sun is directly over head, clear day, standard earth atmosphere at sea level.
How many photons in one square inch over one second from a one foot candle source at one foot and would it then be a simple matter of multiplication if I doubled the intensity of the source?
The light is coming from a 575 w, 120 v, 3600 kelvin halogen lamp for the
second question. I teach the art of lighting design for theater and dance.
![]() COMMENT:
COMMENT:
Reading below, you will see that there is an error in the questioner's units since the ft-candle is a measure of intensity, not of power. The source would be characterized by its power, namely a candle or a lumen (which is a fraction of a candle). So I have changed "foot candle" above to just candle.
![]() ANSWER:
ANSWER:
I have come to appreciate how convoluted measurement of light is! Furthermore, since the questioner asked for photons/in2/s, one runs into the problem that photons of different color (frequency or wavelength) have different energies. The energy e per photon of a particular wavelength λ is e=hc/λ where c=3x108 m/s is the speed of light and h=6.6x10-34 J∙s is Planck's constant. The Joule (J) is the SI unit for energy and is most familiar to nonphysicists as the amount of energy delivered per second by a power source of 1 W. So 100 photons of red light delivers much less energy than 100 photons of blue light because blue has a much shorter wavelength. Light intensity is energy/second/area, so equal photons are not equal intensities. Almost any source of light will contain a whole spectrum of light. The spectra of both the sun and the lamp in the second part of the question are well-approximated as black bodies. The curve to the left labelled 5000 K is what the radiation from the sun looks like as a function of wavelength. It peaks at about about λ=555 nm (0.555 μm), yellow. One can find the maximum intensity wavelength (in meters) for any absolute temperature T black-body spectrum using Wien's law, λmax=2.9x10-3/T. So the peak for the halogen lamp in the second part of the question is λmax=2.9x10-3/3600=810 nm, in the infrared. The problem is that all the "photometric" units (the candle and everything derived from it) are defined in a way which incorporates the sensitivity of the human eye; "radiometric" units are more what a physicist would prefer, the raw data as it were. It is very difficult to unfold one to the other. I will do my best!
To estimate the photon flux I will assume that all the sun's light is at
550 nm. Now, I found that the average intensity of the sun at the
distance the earth is from the sun is about I=1367 W/m2.
Using the expression above, the energy of a yellow photon is e=3.6x10-19
J/photon. Therefore the flux of photons is Φ=I/e=3.8x1021
(photons/s/m2)(1 m2/1550 in2)=2.45x1018
photons/s/in2). To get a more accurate estimate of the photon
flux would involve very complicated mathematics to get the net flux from
the continuum of wavelengths, but this calculation certainly gives a
reasonable order-of-magnitude estimate.
Another way to approach this is to express the intensity in lux, I=110,000 lux for bright sunlight. Using an online converter to SI units, I=0.16 W/m2. Why is this so different from the value of 1367 W/m2 above? I believe it is because the lux includes only the visible light which is a very tiny slice of the whole spectrum. So this is probably a much more useful way for the questioner to approach this problem. The photon flux then (maybe we should call it "visible photon flux") is approximated as Φvisible=I/e=4.4x1017 (photons/s/m2)(1 m2/1550 in2)=2.9x1014 photons/s/in2.
The second part of the question is trickier because of the units used. The "candle" is a unit measuring power (like a Watt), energy/s. It was historically based on the brightness of a single candle. However, as you get farther away from a source, its brightness gets smaller, so we introduce a quantity usually called intensity or flux which is indicative of energy at some distance passing through some area in one second. The usual unit is the lumen (lm), 1 lm=1 candle∙1 ft2/(4πr2) where r is the distance from the source to where the intensity is measured. Knowing that 4πr2 is the area of the sphere with the source at the center, a lumen is seen to be the fraction of the total rate at which energy passes through the 1 ft2 at the distance R. [This can be more elegantly expressed by defining a sterradian (sr), the three dimensional analogue of angle called a solid angle, Ω=A/r2 (see picture at the right). So you can write 1 lm=1 candle∙Ω/(4π).] So the lumen is also a measure of power but only a well-defined fraction of the total power. The foot-candle is defined as 1 ft-candle=1 lm/ft2; the metric equivalent is the lux, 1 lux=1 lm/m2. The ft-candle and lux are both measures of intensity, power/area.
Now to the second part of the question. For a distance of one foot from a 1 candle source, the intensity is 1 ft-candle=10.76 lux. Now, as above, convert this to Watts/m2 using the online calculator, I=1.6x10-6 W/m2. And so, Φvisible=I/e=4.4x1012 (photons/s/m2)(1 m2/1550 in2)=2.9x109 photons/s/in2. In this case, I have again used the 555 nm conversion which might not be appropriate for an 810 nm max lamp, but I suspect it may be ok for you since you are interested in visible light.
Regarding your question about doubling intensity, if you double the intensity of the entire spectrum uniformly, then there would be just a doubling of the number of photons. If, for example, you change intensity by increasing the temperature of the lamp, the distrubution would change so that all bets are off.
This may be a long, rambling answer, but I had to learn a lot as I went along. Keep in mind that the photon fluxes are order-of-magnitude, not exact.
![]() QUESTION:
QUESTION:
Why kinetic theory claims that free atoms do not have a rotational kinetic energy component while macroscopic spheres obviously have? Is it because a rotational component does not transmit during elastic collisions and hence is not distributed?
![]() ANSWER:
ANSWER:
Single atoms do not have rotational degrees of freedom; the reason is that they are quantum mechanical objects which are spherically symmetric. In that regard, they are not well modeled as rigid spheres. Molecules, however, being not spherically symmetric, do have rotational (and vibrational) degrees of freedom which must be included in kinetic theory of gases to get correctly describe the thermodynamic properties.

![]() QUESTION:
QUESTION:
Built my kid a marshmallow shooter for a science project. Simple design. Main air chamber is 2" pvc
with a total length (including bend) of 32". It is then directed into a 3/4" inch
pvc pipe with 2 valves. The first valve (1) is the main shut off valve and inch or two from the 2" chamber. Then there is another
21" of 3/4" pvc into the 2nd valve (2). The barrel is 1/2" pvc and 24" long. We can fill the gun with 40 psi with both valves closed. We then open valve 1.
Pressure should drop a little, but not much. We then close 1 to preserve pressure and shoot marshmallows with almost 40 psi. They will go 40'. When we fill the tank with 40 psi with valve 1 open and valve 2 closed and shoot it, it'll shoot the marshmallow 100' or more. My question is:
why is releasing all the air at once shooting the marshmallows further? It's
driving me nuts. Is it the volume of gasses? How can I mathematically solve
this mystery?
![]() ANSWER:
ANSWER:
It is pretty easy to understand this qualitatively. As the
marshmallow moves down the barrel, the volume of the gas behind it increases
so the pressure decreases. Your first case (valve 1 closed) there is a
pretty big fractional increase in volume so, since PV is constant, a
pretty big decrease in the final pressure; in the second case (valve 1
open) there is a much smaller fractional increase in volume so there will be
a much smaller decrease in the final pressure. The average force felt by the
marshmallow over the length of the barrel will be bigger for the second
case.
Now, let's do it analytically. I will ignore the couple of inches between the main chamber and the first valve. The operative principle is that if temperature and amount of gas are unchanged, the product of the pressure and volume is a constant or, equivalently, Vinitial/Vfinal=Pfinal/Pinitial. An important thing to keep in mind is that 40 psi is the gauge pressure, the pressure above atmospheric pressure which is about 15 psi; so Pinitial=55 psi. The volume of each section is π(d/2)2L where d is the inner diameter of the pipe (a 3/4" pipe, e.g., specifies the diameter). So Vbarrel=4.7 in3, Vprimary=100 in3, Vsecondary=9.3 in3. In the first case Vinitial=Vsecondary=9.3 in3 and Vfinal=Vsecondary+Vbarrel=14 in3. Therefore Vinitial/Vfinal=0.66=Pfinal/Pinitial and, taking Pinitial=55 psi, Pfinal=36 psi and the corresponding gauge pressure is 21 psi; so the average gauge pressure during firing was (40+21)/2=30 psi. In the second case, Vfinal=Vsecondary+Vbarrel+Vprimary=114 in3 and Vinitial=Vsecondary+Vprimary=109.2 in3. Going through the same procedure as the first case, Pfinal=53 psi and the corresponding gauge pressure is 38 psi; so the average gauge pressure during firing was (38+40)/2=39 psi. This means the average force on the marshmallow was 81% greater for the second case; this means that the speed of the marshmallow is almost twice as great, so it is roughly in agreement with your measurements of a distance of 100' compared to 40'. I have not considered air drag during the flight after leaving the gun which will be fairly important for a marshmallow. Also, I have ignored friction between the marshmallow and the barrel; because of this and neglect of air drag, don't expect real good quantitative predictions of range.
![]() ADDED
NOTE:
ADDED
NOTE:
In the first case where you pressurize to 40 psi and then open
valve 1, the pressure will drop more than just a little as you expect. Vinitial/Vfinal=100/109.2=0.92,
so Pfinal=55x0.92=51 psi, so the final gauge pressure will
be about 36 psi, about a 10% drop.
![]() QUESTION:
QUESTION:
In a theoretical universe, only two hydrogen atoms exist. At time=0, they are 100 light years apart from one another. How much time will elapse before they are physically "aware" of each other?
![]() ANSWER:
ANSWER:
I guess you mean that they have just "popped into existence".
They each have mass, so they can interact gravitationally.
It is believed that a gravitational field propagates at the speed of
light, so it would be 100 years before they were "aware". A hydrogen atom is
electrically neutral and is spherically symmetric, so they will not interact
electromagnetically at such a distance.
![]() QUESTION:
QUESTION:
2 glasses of water - same volume, same temp, same container characteristics - one placed in 31.5 degree temp and one in 0 degree temp. Does one of them freeze more quickly than the other and if so, why.
![]() ANSWER:
ANSWER:
I am assuming you mean the whole volume freezes. Most of the
heat lost by the water will occur as conduction through the glass. The rate
of heat transfer through some barrier is proportional to the temperature
difference across the barrier. Therefore the water in the 00 F
environment would freeze first.

![]() QUESTION:
QUESTION:
When a gas is pressurized (in favorable conditions) it turns into liquid.
Further pressurizing it turns into solid. Now I exert larger pressure on
a uniform solid (form all directions). What will happen?
Also what will happen if I subject a fundamental particle to very large
pressure?
![]() ANSWER:
ANSWER:
Very large pressures can change the properties of the material
and new phases may occur (like water and ice are two different phases of H2O).
A particularly good example is water itself as shown in the figure to the
right; pressures up to about 10,000,000 atmospheres are shown in the graph
and numerous phases beyond ice/water/steam are seen at high pressures or
very low temperatures. For higher yet pressures, you need to look to stars.
If a star is massive enough it will, after going through a supernova stage,
collapse under the pressure of its own gravity to where electrons are pushed
into the protons and the whole star becomes a neutron star, essentially a
gigantic nucleus. If heavy enough, it will continue collapsing into a black
hole. What individual particles do depends on the pressure and they
essentially will retain their identities or undergo reactions with other
particles (as in the neutron star formation) or lose their identities (in a
black hole).
![]() QUESTION:
QUESTION:
I want to know is there any expression for relativistic force as we have for momentum?
![]() ANSWER:
ANSWER:
In classical mechanics, force F only only has meaning in
terms of the acceleration a it causes some mass m to have, F=ma.
This can be more generally stated as the force is the time rate of change of
linear momentum, F=dp/dt. Using the relativistic
expression for p, this defines force in special relativity. Usually,
though, it is much more useful, both in classical mechanics and relativistic
mechanics, to solve problems using the potential energy V(r)
associated with a force, V(r)=-∫F∙dr.
![]() QUESTION:
QUESTION:
This link is a video of anti gravity and
I want to know on how it really works?
![]() ANSWER:
ANSWER:
This one is pretty easy to debunk, I believe. The guy and all
the apparatus are upside down; the camera taking the video is also upside
down.

![]() QUESTION:
QUESTION:
I am building a customizable "cat highway" of wooden shelves in my living room. The issue I am having is figuring out how much holding force I need, rather than how much weight the actual shelf can support. I know the shelves are plenty strong enough. Now I need to have them fastened strongly enough to the wall. It would be easy, if all I had to consider was the maximum weight a shelf has to take, if all three cats were to lie on it at once. However, I also need to how much weight I have to budget for for impact force - both from a descending and an ascending cat.
As there isn't room for multiple cats to jump up or come down at one time, so only the weight of the heaviest cat (3.26587 kg) needs to be used for the calculations. Also, there will not be a height of more than 0.5 m from one shelf to another, nor a distance of more than 0.5 m between one shelf and another. I can't guarantee that they won't skip a shelf, so it might be safer to double the maximum distances just to be safe.
![]() ANSWER:
ANSWER:
Normally I answer such questions by "you cannot tell how much
force results if an object with some velocity drops onto something". The
reason is that the force depends on how quickly the object stops; that is
why it hurts more to drop on the floor than to drop on a mattress. In your
case, however, we can estimate the time the cat takes to stop because we can
estimate the length of its legs which is the distance over which it will
stop. You are probably not interested in the details, so I will give you the
final answer: assuming constant acceleration during the stopping period, the
force F necessary to stop a cat of mass m, falling from a
height h, and having legs of length ℓ may be approximated as F=mg(1+(h/ℓ)).
E.g., if h≈0.5 m and ℓ≈0.1 m, F≈6mg, six times
the weight of the cat.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Thank you for your answer!
I thought you might want to know that, unlike a lot of people, I AM actually interested in the details.
![]() ANSWER:
ANSWER:
OK, here goes: I will use a coordinate system with increasing
y vertically upward and y=0 at the landing shelf. The cat will
have acquired some velocity -v when his feet hit the shelf. Assuming
he stops after going a distance ℓ and accelerates uniformly, we have the two
kinematic equations 0=ℓ-vt+Đ
at2 and 0=-v+at.
From the second equation t=v/a; so, from the first equation,
0=ℓ-v(v/a)+Đ
a(v/a)2=ℓ-Đ
v2/a
so a=Đ
v2/ℓ. Now, as the cat is landing there are
two forces on him, his own weight mg down and the force F of
the shelf up, -mg+F and this must be equal, by Newton's second law,
to ma, so F=m(g+Đ
v2/ℓ). This, by
Newton's third law, is the force which the cat exerts down on the shelf.
Finally, the speed if dropped from a height h is v=√(2gh),
so F=mg(1+(h/ℓ)).

![]() QUESTION:
QUESTION:
In light of the recent deflated football scandal, is there a way to mathematically calculate the change in pressure as the temperature inside the ball changes? Would you assume the volume of the bladder inside the ball to change very little?
![]() ANSWER:
ANSWER:
Yes, the ideal gas law, PV/(NT)=constant where
P is pressure (not gauge pressure), V is the volume,
N is the amount of gas, and T is the absolute temperature.
Assuming that V and N remain constant, P/T=constant.
Let's do an example. Suppose that the ball is filled to a gauge pressure of
13 psi when the temperature is 700F. The absolute pressure is 13
plus atmospheric pressure 14.7 psi, P1=13+14.7=27.7 psi.
The temperature in kelvins (absolute) is 700F=294 K. Now suppose
we cool the football to 100F=261 K. Then, 27.7/294=P2/261,
P2=24.6 psi, and the resulting gauge pressure is
24.6-14.7=9.9 psi. I guess it is important to fill the ball at the
temperature at which it will be played.
![]() ADDED
NOTE:
ADDED
NOTE:
An article in the January 30
New York Times came to essentially the same conclusion as I did here. My
answer was posted on January 26. I was astounded to read in that article,
though, that initial calculations by physicists had applied the ideal
gas law using gauge pressure rather than absolute pressure! Shame on them!
![]() QUESTION:
QUESTION:
How is Relativity Theory explain the different measure of time?
for example: the Sun rotate around itself in 25 days ( depend on the stars observing ) But here on Earth we observe it about 27 days.
and some of other lifetime of particles is like this, have a different time in space and in Earth.
![]() ANSWER:
ANSWER:
This has nothing to do with relativity theory nor with different
rates of time. The reason we observe the sun to rotate with a longer period
is that we are in an orbit revolving around the sun and that orbit is the
same direction the sun is rotating about its axis. Think of it this way: if
the sun rotated on its axis once every 365 days, we would observe it to not
rotate at all. The different lifetimes of particles is a different
phenomenon and results from their moving at speeds close to the speed of
light; that is relativity.
![]() QUESTION:
QUESTION:
If aluminium and copper pipes are of same length and diameter ... same magnet is dropped through them ...in copper it takes more time to come out of other end, i myself have done this... please answer why is it so?
![]() ANSWER:
ANSWER:
Aluminum has an electrical conductivity of about 3.5x108
Ω-1m-1 and copper has a value of about 6x108
Ω-1m-1. Therefore, at any speed, the magnet will
induce a larger current in the pipe for the more conductive copper.
![]() QUESTION:
QUESTION:
I was at a training and learned that the Andromeda Galaxy revolves around a black hole. Is that true of all galaxies?
![]() ANSWER:
ANSWER:
Astrophysicists believe that nearly all large galaxies have a
supermassive black hole at their centers.
![]() QUESTION:
QUESTION:
I'm doing an assignment on helicopter flight, and I'm a little confused about the Bernoulli principle. He said that if a pipe is bigger at the beginning and smaller at the end, the fluid traveling through the end of the pipe would have a lower pressure.
This seems counter-intuitive. I would have thought that there would be more pressure on the fluid that's "squeezed in together". I don't think I fully understand the concept of pressure.
![]() ANSWER:
ANSWER:
Let's first write Bernoulli's equation, P+Đ
ρv2+ρgy=constant.
At any point in the fluid P is the pressure, ρ is the density,
v is the speed, g is acceleration due to gravity, and y
is the distance relative to some chosen reference point (above, y>0,
below y<0). Maybe it would help you to accept this if I tell you
that Bernoulli's equation is simply conservation of energy. Since To answer your question we can ignore the y part,
it is a horizontal pipe, P+Đ
ρv2=constant. You
should also understand that this equation is exactly true only under
idealized conditions:
-
An incompressible fluid (water is a very good approximation)
-
Laminar flow which means flowing smoothly, no turbulence
-
Irrotational which means there is never any local circulation like whirlpools.
-
There must be no viscosity or other kind or friction
What goes on around a helicopter blade satisfies none of these conditions! Nevertheless, Bernoulli's equation can be a very useful approximation to understand what is going on even if it is not exactly correct. The most important one for aerodynamics is that which you cite, that when v increases, P increases. I have struggled to come up with a way you could understand this intuitively, but don't seem to find a simple explanation. You should convince yourself that your intuition is wrong by doing some experiments. For example, notice that inside a moving car the smoke from a smoker is drawn through a cracked-open window because of the lower pressure outside where the velocity is higher. Or, do the old blowing on the piece of paper demonstration.

![]() QUESTION:
QUESTION:
I am looking to find out at what speed an object (object 1) was traveling while hitting an other object (object 2) and pushing it straight ahead.
Object 1 was traveling straight, rubber wheels on asphalt (no skid marks), had a weight of 4500 lbs, and hit the object 2 with a weight of 3000 lbs at a 90 degree angle (side impact, rubber
sliding on dry asphalt). Object 2 was pushed 50 feet. I am looking for the formula to calculate
the speed of object 1 at impact. I know there are several factors involved and I do not need a exact number,
just an approximate but fairly close value.
![]() QUERY:
QUERY:
I take it that car 2 was at rest initially and that the two
remained in contact the whole time (since you said "pushed"). Also, that car 1 did not apply brakes.
![]() REPLY:
REPLY:
Yes that is correct - object 2 was at rest and object 1 did not apply
brakes.
![]() ANSWER:
ANSWER:
I prefer to work in SI units, so I will transform back to mph in
the end. The masses of the cars are about m1=4500 lb≈2040 kg and
m2=3000 lb≈1360 kg. The coefficient of kinetic friction for rubber
on dry asphalt is in the range 0.5-0.8, so I used μ=0.65. The
acceleration due to gravity is g=9.8 m/s2. The distance
pushed is d=50 ft≈15
m. The frictional force F acting on the two cars as they slide is due
only to the friction between the wheels of car 2 sliding on the
asphalt is F=μm2g=0.65x1360x9.8=8660 N. The work
done by this friction was W=-Fd=-8660x15=-130,000 J. This took away
the kinetic energy K the two vehicles had just after the collision,
so K=Đ
(m1+m2)v2,12=1700v2,12=130,000,
so v2,1=8.7 m/s≈20 mph; this is the speed the two cars had
immediately after impact. Finally, use momentum conservation to get the
speed of car 1 before the collision: m1v1=(m1+m2)v2,1=2040v1=3400x8.7=29,600
k∙m/s, and so v1=14.5 m/s≈32 mph.
![]() QUESTION:
QUESTION:
I purchased a visco elastic (memory foam) mattress topper for my queen sized bed. The advertised dimensions of the topper are 76 inches x 56 inches x 4 inches, and the advertised foam density is 4 pounds per cubic foot. I calculated that the topper should weigh 38 pounds. The delivered topper weighs about 5 pounds. The delivered topper is in a very compressed state constrained by its plastic packaging. The delivered topper has a cylindrical shape with the cylinder being approximately 15 inches tall and 12 inches in diameter. Would the compressed state account for the weight discrepancy? ie if the topper was released from its packaging and allowed to expand to its full size on top of the bed, would the expanded topper weigh 38 pounds. I don't think so. I can't release the topper from its packaging and then return it. I can't put that genie back in the bottle. It is very important to me. The topper was very expensive. Your wisdom would be greatly appreciated.
![]() ANSWER:
ANSWER:
The volume of the topper is 76x56x4/123=9.85 ft3
and would have a weight of 39.4 lb if its density were 4 lb/ft3.
The volume of the compressed topper is about π62x15/123=0.982
ft3 and since the compressed topper weighs about 5 lb, its
density is about 5.09 lb/ft3. Clearly the density number must
refer to the material with all air removed from it. That is also the
impression I get from looking at advertisements for these products. If you
think about it, there is no way that a 4 inch thick foam matress topper for
a queen bed whose volume is clearly mainly air would weigh almost 40 lbs. I
think that what you got was not falsly advertised.
![]() QUESTION:
QUESTION:
What is radiocarbon?
![]() ANSWER:
ANSWER:
I suspect you are asking about radiocarbon dating of organic
materials. There are two stable isotopes of carbon, 12C and
13C. There is one unstable isotope of carbon which exists in nature
also, 14C, sometimes referred to as radiocarbon. Radio carbon is
being constantly produced by cosmic rays interacting with 14N in
the atmosphere. 14C has a half life of about 5730 years, so if
cosmic rays suddenly stopped creating it there would be almost none left
after a few half lives. But, there is a balance between creation and decay
so that the amount of 14C on earth is about constant at any time.
However, suppose you find a fossil which has only about half as much 14C
as all the current living things on earth. Then you can conclude that the
fossil is about 5730 years old.
![]() QUESTION:
QUESTION:
What happens when you compress gas (for example carbondioxide) into a gas cylinder? I am thinking that as pressure increases, so does temperature (because of the increased kinetic energy of the gas molecules). But the 0th law of thermodynamics say that heat energy goes from an object of high temperature to an object of low temperature - so I am thinking that after a while the temperature of the gas will be the same as the room temperature?! Since pressure is constant in the cylinder, isn't the kinetic energy of the molecules? What happens with the gas as energy is transferred to the room? Am i misunderstanding something? I just can't seem to Get my head around this, so I am really hoping you can help med understand!
![]() ANSWER:
ANSWER:
When you say "âŚcompress gasâŚinto a gas cylinderâŚ" I assume you
mean that you are adding gas to a cylinder with constant volume. All you
really need to know is the ideal gas law, PV=NRT where P is
pressure, V is volume, N is some measure of how much gas you
have, T is the absolute temperature, and R is just a constant
of proportionality. You need to make some approximations for a real-world
situation. If you add the gas really slowly and/or the cylinder has very
thin conductive walls, T will remain constant for the reason you
stateâbecause the whole system will keep in thermal equilibrium with its
environment; this is called an isothermal process and as N increases,
P increases. The other extreme is that you take care to insulate the
cylinder and/or add the gas very quickly so no heat enters or leaves. In
this case, increasing N will increase the ratio P/T;
however, you do not have enough information to determine how P and
T independently change. If you are using some sort of pump, you will be
doing work on the system which will increase its temperature and therefore
the pressure has to increase also to keep P/T from decreasing.
Another way to add gas to the tank is to take another tank with much more
gas in it and connect the two of them together. Since the volume of the two
tanks and the total amount of gas in them is constant, the temperature of
the whole system will decrease. Again, pressure in your tank must change in
such a way that P/T increases and that could mean that P
would increase, decrease, or stay the same, depending on initial situations.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Thanks for the quick reply! I am still wondering though, is it possible for a compressed gas in a cylinder to have higher temperature than the room it is stored in over time? I am thinking comparing to coffee in a thermos after some hours will be the same temperature as its surroundings. Is the gas cylinder any different due to pressure inside the tank?
![]() ANSWER:
ANSWER:
Eventually the cylinder, room, and gas will all be at the same
temperature. If (see above) the temperature right after filling were higher
than the room temperature, it would cool down and the pressure would
decrease because now both V and N would be constant while the
gas cooled. Here is a numerical example: suppose that the room temperature
is 200C=293 K and the gas temperature is 400C=333 K
and the hot gas has a pressure of 4.0 Atm. Then, P/T=constant=4/333=Pfinal/293
or Pfinal=3.5
Atm.
![]() QUESTION:
QUESTION:
How does a GPS station work? I just learned about them and my teacher was a little unclear so I'm depending on you to hopefully give me a direct answer.
![]() ANSWER:
ANSWER:
Suppose that you were on a line and you wanted to know where you
were. If there were some point on that line and you knew where you were
relative to that point, then you would know where you are. Now suppose that
you were on a flat plane. Now you would need two other points the positions
of which you knew to figure out where you were relative to these points
(this is often called triangulation). Now suppose that you are just
somewhere in a three dimensional volume; it would follow that you would need
three points whose positions you knew to find out where you were in that
space. So, if you want to know where you are if you are at rest, you would
need to know the positions three points of reference at rest relative to you
and simple geometry would tell you where you were. The GPS system is a bunch
of satellites which are zooming around in their orbits and therefore,
because both they and possibly you also are moving, you also need to
synchronize all the clocks on the satellites with your clock; this
synchronization means that you need one more point because you now have four
unknowns you need to solve for, your three spacial positions and the data
necessary to find the exact time. The GPS receiver in your iphone or
whatever receives the data beamed from the four satellites and computes your
position to remarkably good accuracy.
![]() QUESTION:
QUESTION:
According to Newton's law of gravitation, gravitational force is inversely proportional to the distance between the center of mass of the bodies. So if i place my hands together, the distance between them is very less so the gravitational force should be very high but it is easier to separate them. How?
![]() ANSWER:
ANSWER:
First of all, the force is inversely proportional to the
square of the distance between the centers of mass. Because gravity is
nature's weakest force, it is tiny unless there is a very large amount of
mass. Let's estimate that the center of mass of your hands are separated by
1 cm=0.01 m and that the mass of each hand is about 0.25 kg (about Đ
lb).
The force each hand feels can be approximated as F=Gm1m2/r2=6.67x10-11x0.25x0.25/0.12=4.2x10-10
N≈10-10 lb. As a comparison, the gravitational force on each hand
by the earth (whose center is much farther away) is about 2.5 N.
![]() QUESTION:
QUESTION:
Is dark matter and dark energy controlled by the brain? Does dark energy and dark matter have a brain?
![]() ANSWER:
ANSWER:
Well, my gut tells me to say no and no. However, since neither has ever
been directly observed and we have no idea what they are, maybe I should say
maybe and maybe!
![]() QUESTION:
QUESTION:
Suppose an object is at rest. Its momentum is zero. According to Heisenberg uncertainty principle, the uncertainty in its position should be infinite, so that the product of the uncertainties of the momentum and position equals a non zero value. But what does this infinite uncertainty in the position mean? I mean the object is there, at rest, so don't we know its position exactly? Or is the uncertainty principle valid only for moving bodies?
![]() ANSWER:
ANSWER:
The lesson to be learned here is that you cannot have an object
(perfectly) at rest. Infinite uncertainty means you have absolutely no idea
where it is. If you make a measurement to determine its position, any place
in the universe is equally probable to be where you find it. And since the
universe is not infinitely large, you cannot have exactly zero momentum.

![]() QUESTION:
QUESTION:
I'm writing a fantasy novel and I just want to check my science.
In it there's a tower which is so tall that it is higher than the troposphere. There is a scene where someone smashes a window. My question is would the air all rush out due to unequal air pressure and when the air pressure settles would everyone feel the effects of explosive decompression or at least find it hard to breathe?
![]() ANSWER:
ANSWER:
Presumably, all your windows are sealed such that the inside is at
atmospheric pressure. "Higher than the troposphere" would imply the
stratosphere which is where commercial jets fly. As you doubtless know, the
pressure there is very low. The figure to the right shows that just above
the troposphere the pressure is only about 200 millibars, about 1/5 of
atmospheric pressure. There is not enough air there to keep you alive. You
may recall the crash of the private jet in 1999 which killed golfer Payne
Stewart. The plane lost pressure at an altitude of 11.9 km and everyone lost
consciousness; it flew on autopilot until it ran out of fuel and crashed.
Most certainly the air would be drawn (violently) out of your broken window.
Another thing you should think about is that you cannot simply pressurize
your entire tower to atmospheric pressure; you have to pressurize in layers
of a few hundred meters and isolated from each other. Otherwise you will
have the same strong pressure gradient with altitude as the atmosphere has!
![]() QUESTION:
QUESTION:
Can you tell me in an everyday comparison how much energy is in 200 Mev?
![]() ANSWER:
ANSWER:
200 MeV=200 MeV[1.6x10-13 J/MeV]=3.2x10-11
J. Suppose that I doled out 1000 200 MeV packages each second. Then the rate
of energy being delivered would be 3.2x10-8 J/s=3.2x10-8
W, 32 nanowatts, pretty small! To power a 100 W light bulb, you would have
to deliver 3.1x1012 200 MeV packages each second, 3.1 trillion.
Here is another way to envision it: taking the acceleration due to gravity
to be g≈10 m/s2 and the potential energy for an object of
mass m lifted to a height h to be U=mgh or h=U/(mg),
you could lift a 1 gm=10-3 kg mass to a height h=3.2x10-11/10-2=32x10-10
m, about 30 times the size of an atom, with 200 MeV of energy.
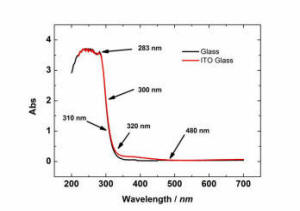
![]() QUESTION:
QUESTION:
Why can't UV-B and UV-C rays pass through glass but UV-A rays can?
![]() ANSWER:
ANSWER:
I am sure that this will not be a very satisfying answer to
you, but that is just the way it is. Every material has a characteristic
absorption spectrum where small numbers mean mostly not absorbed and large
numbers mean mostly absorbed. What determines the wavelengths which are
absorbed and those which are not is determined by the molecular structure of
the material, how it interacts with electromagnetic radiation. This is not
simple to calculate, even for the simplest assumptions and the simplest
materials. The absorption spectra for two different kinds of glass are shown
to the left. Since UVA is nominally defined as about 315-400 nm wavelength
and UVB and UVC nominally span 100-315 nm, you can see that glass is mainly
transparent to UVA and much less so to UVB and UVC.
![]() QUESTION:
QUESTION:
I have been attempting to teach myself chaos theory, however I have had trouble understanding it and how it is involved with different levels of quantum physics as well as relativity. I am also having trouble understanding the "three body problem", which seems to occur in many different physical systems.
I was hoping that you could help me to understand at least some of Chaos theory and how it connects to both quantum physics and relativity, and what exactly the "three body problem" is.
![]() ANSWER:
ANSWER:
I am sorry, but your question is too technical and too unfocused for the
purposes of this site. I can tell you something about the 3-body problem, though. If two bodies interact only with each other, for example the earth and the moon, you can write the orbits in simple analytic closed form. However, if there are three interacting bodies there is, in general, no closed-form solution. There are special cases where the 3-body problem can be solved, for example if one of the bodies is held fixed, but not in general.
If you google "three body problem" you will find more information. A
particularly interesting (and newsworthy) discussion may be read in
AAAS Science News. All these special cases are not chaotic because
they repeat in a periodic way. More general cases are not periodic and are
extraordinarily sensitive to initial conditions.

![]() QUESTION:
QUESTION:
Does Einstein's theory of relativity account for light having properties of a solid? I remember from high school the simple experiment of putting a twirlers in a vacuum, placing it in sunlight and it twirling. The current relativity theory states as an object approaches the speed of light, its mass is increasing exponentially and time is slowing. But if light has properties of a solid, how is that factored into Einstein's equations? Is it true all rays do not have this distinct characteristic of acting on an object as a solid as demonstrated in the simple h.s. experiment?
![]() ANSWER:
ANSWER:
I think you must mean that light behaves like a particle, not a
solid; indeed Einstein, not in relativity but in explaining the
photoelectric
effect, showed that electromagnetic radiation was quantized, that is it
consists of photons which have energy E=hf where h is Planck's
constant and f is the frequency of the light. A photon also has a
linear momentum p=hf/c (that does come from the theory of relativity)
where c is the speed of light. The fact that photon's have momentum
means that they can exert a force and this is the usual explanation for
Crooke's
radiometer which is the experiment I believe you are alluding to in your
question. Here is the funny thing, though: radiation pressure has nothing to
do with what happens in the Crooke's radiometer. It is not nearly sensitive
enough to observe radiation pressure, it is rather a thermal effect as
explained in the Wikepedia article I have linked to. Radiation pressure is
real, though, and the more sensitive
Nichols radiometer
can observe it.
![]() QUESTION:
QUESTION:
If we have a car driving at a fixed distance (e.g. 100 km), does it cost more energy to reach the destination at 100 km/hr versus 50 km/hr?
![]() ANSWER:
ANSWER:
Certainly. The air drag on something moving through air is
approximately proportional to the speed squared, so the 100 km/hr car has 4 times
the air drag to overcome. Of course, you do not use 4 times as much fuel
because there are lots of other energy losses which do not depend on
velocity, but you do use a significant amount more fuel.
![]() QUESTION:
QUESTION:
I'm a young aeronautical student and I'm doing a project on small, basic fixed-wing aircraft. I need to include some explanation of how lift is generated. My teacher has vaguely mentioned the Bernoulli theory once or twice. However after some research, I found that the Bernoulli explanation is outdated. I've found other more accepted theories, only which are too complex for both my understanding and academic level. Could you provide a more accurate but relatively simplified explanation of lift?
![]() ANSWER:
ANSWER:
I wouldn't say "the Bernoulli explanation is outdated," it just
isn't the whole explanation. Basically, Newton's third law is responsible
for much of the lift in flightâthe air coming off the trailing edge of the
wing is deflected down which means the wing exerted a downward force on it
which means it exerted an upward force on the wing. Books about flying
usually refer to this as "angle of attack." A more complete explanation may
be found in an
earlier answer. I can also recommend a book, Stick and Rudder by
Wolfgang Langewiesche.
![]() QUESTION:
QUESTION:
I am a writer involved in the creation of exhibitry for the Telus Spark science museum in Calgary, Alberta. We're building a new gallery about electricity.
We have an exhibit about the problem of so-called Vampire Power--the constant sipping of electrical energy by home appliances on standby mode.
I'm just a writer, not a physicist, but I have posited that many of our energy conservation problems are not actually problems during the winter months, when all the homes in the city of Calgary are being heated. My reasoning is that all of the electrical energy consumed by everything from coffee makers to the charger for your mobile phone to the TV just end up as waste heat, anyway. And that heat will be that much less heat your furnace (or baseboard heater) has to put out to keep your house warm. So this waste energy is not really wasted at all.
Now, I guess that for lightbulbs and televisions and other things emitting light as part of their function, you want to be sure that your curtains are closed so that light energy is not escaping out of the windows and into the streets, where it ends up as heat outdoors, and not in your house where you want it.
And of course, in summer, when these same houses are air-conditioned, the waste heat from these appliances is counterproductive, and should be reduced as much as possible.
The designers and project administrators are skeptical of my reasoning. They're saying that a TV is a less efficient way (energetically) to produce heat than an electric baseboard heater. But I say it doesn't matter, because all the energy ends up as heat anyway. Even the sound from your TV will bounce off the objects in the room, heating them up.
Is there a flaw in my reasoning?
![]() ANSWER:
ANSWER:
Let me start out by saying that you are certainly correct, all
electrical power eventually ends up as heat. That said, I think that
suggesting that the wasted power should not be worried about is misguided
for the following reason. The "vampire power" used by the standby mode of
many appliances and electronics is really rather low, probably normally a
few watts. Such a power source for heating your home would probably only
account for a temperature increase of way less than one degree. But, the
thermostat connected to your heating system is really not sensitive enough
for there to be any difference at all which would result in lower energy
consumption by your heating system. In other words, with or without the
vampire heat, your heating energy use will be the same. On the other hand,
there are thousands of other homes also consuming a few wasted watts of
power. If they all stopped there would be kilowatts of power not being used
but nobody's heating bill would be changed. This is only the result of my
thinking about your question a bit before answering it, I have not seen any
similar conclusions.
![]() QUESTION:
QUESTION:
Suppose a container is partially filled with a liquid. A small sphere made of a material whose density is less than the liquid is in equilibrium inside the liquid with the help of a thread such that one end of the thread is tied to the sphere and the other end to the bottom of the container. the whole apparatus is kept on a weighing machine. if the thread is cut, then will the reading of the weighing machine change?
Since the tension in the thread is an internal force, the reading should not change.
However the free body diagram suggests that the reading should change.
![]() ANSWER:
ANSWER:
When you refer to "âŚthe free body diagramâŚ", you must specify
the body. Solving problems like this are most often easiest if you make a
clever choice of body. I would choose the body as the
container+liquid+ball+thread (taken as weightless, probably); in that case
the only downward force is the weight of all three and the only upward force
is the scale, so the scale reads the total weight with no reference to
whether the thread is connected to the ball or not. You can make this
problem difficult by focusing on a different body, maybe the container, but if you
draw all your free-body diagrams correctly and apply Newton's third law, you
still get the same answer that the the scale reads the total weight. To the
left I have shown all the forces on each of the bodies: red is the tension in
the string which is also the force the string exerts on the sphere and the
on the container; light blue is the force the container and fluid exert on
each other; black represents the weight of each; green is the buoyant force
which is the force of the fluid on the sphere and the force of the sphere on
the fluid; purple is the force the scale exerts on the container.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Suppose the sphere is accelerating upwards inside the fluid, under the influence of
the buoyant force. Now its acceleration is dependent upon the buoyant force, while the buoyant force is in turn dependent upon its acceleration. How do we precisely calculate these two quantities, at a particular instant of time?
![]() ANSWER:
ANSWER:
First of all, the buoyant force is not dependent on the
acceleration. As long as the sphere is fully submerged, the buoyant force (B)
is equal the the weight of the displaced fluid. But, you must also include
the drag force (D) which the fluid exerts on the sphere and that is
not simple to include. But, most fluids have sufficiently large viscosity
that the sphere will quickly come to its terminal velocity and move upward
with constant speed. When that happens B-D-W=0 where W is the
weight of the sphere. If you really want to pursue this farther, the
simplest approximation for the drag is that it is proportional to the speed
of the sphere, Stokes's
law. In that case, a=(B-W-Cv)/m where C is a
constant. If you were
to neglect drag altogether, which would be a poor approximation for any real
fluid, the acceleration would be uniform, a=(B-W)/m.
![]() QUESTION:
QUESTION:
I'm having a really hard time understanding something my professor asked me to think about today in my entry level physics class. How can someone ever tell if they are moving if they have no clues of the outside. (sound or sight) If I had a penny and threw it up it would just fall back down, so that would not work. I'm really stumped here!
![]() ANSWER:
ANSWER:
This is the heart of a profound physical and philosophical
concept. The laws of physics determine the outcome of any experiment you
might perform; for example, Newton's three laws of classical mechanics and
Maxwell's equations describing electromagnetism are laws of physics. Suppose
you have performed experiments to discover these laws in some particular
frame of reference and you convince yourself that they are laws which apply
and are reproducible for any mechanical or electromagnetic experiment you
can think of. Now you decide to redo all your experiments but in a frame of
reference which moves with a constant velocity relative to the original
frame; you discover a really remarkable thingâthe laws of physics are
identical in this new frame. You can then logically say that there is no
experiment you can perform to determine which of these frames is moving and
which is at rest. This is called the principle of relativity and frames in
which the laws of physics are true are called inertial frames of reference.
Any frame which moves with constant velocity relative to one inertial frame
is also an inertial frame. Essentially, there is no such thing as absolute
rest or absolute velocity. The laws of physics are not true in accelerating
(noninertial) frames.
Here is a little more information if you are interested: Newton's laws turn out to be not true for velocities comparable to the speed of light; at high speeds, however, the principle of relativity is still true provided that Newton's laws are corrected (theory of special relativity). Also, it turns out that the principle of relativity is true for all frames, not just inertial frames, provided that you introduce a new principle, the equivalence principle. The equivalence principle states that there is no experiment you can perform which can distinguish whether you are in a gravitational field with gravitational acceleration a or in a noninertial frame of reference with an acceleration a. The generalized principle of relativity and the equivalence principle form the basis of the theory of general relativity which is the modern theory of gravity.
![]() QUESTION:
QUESTION:
My question is this, If you are driving in a car (100km/h) and roll down
your window a vacuum is created in your car. but what if there is a 100km/h
tail wind. does the wind going the same direction cancel out the effect of
the vacuum?
![]() ANSWER:
ANSWER:
The reason air is drawn out through the open window is
Bernoulli's law, which states that when the velocity of a fluid increases
the pressure decreases. Therefore, the pressure outside the window (moving)
is lower than inside (not moving). This is easy to demonstrate by a smoker
inside the car and the smoke being drawn out the window. If there is a
tailwind with the same speed as the car, the air outside the car will not be
moving with respect to the car and there will therefore be no pressure
difference.
![]() QUESTION:
QUESTION:
Physics says that energy is always conserved in any form. My question is what happens to the energy contained in me if I die? In what form is it transformed?
![]() ANSWER:
ANSWER:
Actually, "physics says" that the energy of an isolated system
(no external forces doing work on it) is conserved. Or, you could say that
the energy of the entire universe is a constant. So, let's talk about what
energy there is in your body. Mostly, it is simply the mass of all the atoms
in your body, E=mc2 and this does not change because as
your body decays, all the atoms are indestructible. However, much of the
molecular structure of your body changes. I do not know that much detail
about microbes and organisms which hasten decay, but essentially they will
extract energy from fats and sugars and use it for their own purposes. I
assume that heat will also be a result of decay.
![]()
![]() QUESTION:
QUESTION:
I was recently at the Map and Government Library of the main library and stumbled upon a stereoscope map reader. When held over two accurately aligned aerial photographs of the hills and valleys of Gordon, Georgia, I can see one image of the trees and hills "popping up" as if they are 3-D. Both lenses are concave, and I was wondering how does the picture appear 3-D?
![]() ANSWER:
ANSWER:
First, we need a tutorial on how we see the world in 3-D.
Because we have two eyes (binocular vision), each eye sees a slightly
different image of the world because of
parallax. One of the
first things the brain of a newborn baby learns is how to interpret these
two images as a 3-D picture. If you had two cameras separated by the
distance between your eyes, the pictures would be slightly different. A
simple photograph, of course, contains only information from one perspective
and therefore lacks the 3-D quality. In the 19th century cameras
were designed with two lenses to form two images. If you then viewed one
image with one of your eyes and the other image with your other eye, you
could see the photograph as you would if you were looking at the original
object, i.e. in 3-D. The viewer is called a
stereoscope. The
purpose of the lenses is to allow you to view the very close photos with a
relaxed eyes.
![]() QUESTION:
QUESTION:
When Cavendish calculated the value of universal
gravitational constant he used mass of lead balls as reference. But how did
he know mass of the lead ball if he doest know the value of G?
![]() ANSWER:
ANSWER:
He could simply weigh them because we know W=mg. Since
you can also write W=mMearthG/Rearth2,
you can identify g=MearthG/Rearth2,
and g is easy to measure even if G is not.
![]() FOLLWOUP QUESTION:
FOLLWOUP QUESTION:
How did he build a weighing scale.
When weight is determined using a scale it should have been built w.r.t certain standard mass. But with out knowing value of G there is no way
 they had a standard mass. He could have weighed a 10kg mass as 1kg mass. So, how did he weight exact mass.
they had a standard mass. He could have weighed a 10kg mass as 1kg mass. So, how did he weight exact mass.
![]() ANSWER:
ANSWER:
The kilogram was officially defined in 1795 as the mass of 1
liter of water. The Cavendish experiment was performed in 1797-98. Even if
the kilogram were not defined, there were other mass definitions which
Cavendish could have used. As an example, let me consider the oldest
standard weight I could find reference to, the beqa (b) (shown in the figure) defined
about 5000 years ago as the mass of 200 grains of barley corn which is about
6.1 grams=6.1x10-3 kg. So if Cavendish had used the b as his mass
standard, he would have found G=6.67x10-11 kg2/(N∙m2)=6.67x10-11
[kg∙s2/m3]x[1 b/6.1x10-3 kg)=4.07x10-13
b∙s2/m3] (assuming that he used seconds and meters for
time and length). It is a different number but means exactly the same thing.
![]() QUESTION:
QUESTION:
I have a strange request.
I'm a nurse practitioner, I learn, like most people by seeing a picture or being shown the way something works. I don't know if you've heard of Frank-Starling curve related to the heart, it's the idea of volume or pressure on horizontal line and stroke volume or cardiac output
(CO) on vertical. The idea is more vol will help, too much will over distend and be less stroke volume or CO.
I have the idea of the spring with the weights on it to show this. But I really need something to exhibit this example.
![]() ANSWER:
ANSWER:
I hope I am not totally out of my depth here! I will attempt to
bring simple physics principles to bear on this question. I had never heard
of the Frank-Starling curve and did a little research to educate myself. The
curve basically shows, under various conditions, the relationship between
how much blood is loaded into the ventricle and how much of that blood is
then pumped out. Usually the absissa (x-axis, independent variable)
is something called
preload, but
the basics can be qualitatively understood by plotting volume of blood
filling the ventricle. In the figure to the left, focus on the curve labeled
B, Normal at rest. I interpret this as the result of the heart acting
as an elastic membrane and stretching as blood is added. As the membrane
stretches it behaves like a two-dimensional spring and the basic property of
a spring is approximated by Hooke's law which essentially says that the
force exerted by the spring is proportional to how much it is stretched.
Hence, adding more blood stretches the spring more and the more it stretches
the harder it pushes on the blood; therefore in a given time more blood will
be pumped out because of this greater force (pressure). This explains the
rise of these curves. Therefore, your idea of springs and weights is a good
one because elasticity is the key here, I think. Maybe even better would be
to take a couple of identical balloons and fill one with twice the air as
the other; then letting the air flow out for the same times, the fuller one
should blow out more air. Also, in times of stress or exercise, I have
learned that neurotransmitters are transmitted to the muscle cells in the
heart wall which results, via calcium ions, in stiffening the walls more so
that they exert even greater force (pressure) on the blood resulting in a
curve more like A, Normal during exercise. To demonstrate that, use
two different springs with different stiffness or use two different
balloons, one much harder to blow up than the other. Drugs can also be used
to try to adjust the shape of the curve, e.g. digoxin or calcium
channel blockers. Note that in curves C and D a point of diminishing returns
is reached actually causing the output to begin dropping with increased
input. I guess this could be likened to reaching an elastic limit like when
you stretch a spring too far and it will not go back to its unstretched
length.
![]() QUESTION:
QUESTION:
I've been wondering about the hazards of traveling at high speeds in
space for a while and the challenges it would bring for us in terms of
spaceship design. My main interest is interstellar travel and how meteors
might affect the safety of such an exercise. So if we had a spaceship that
would accelerate to let's say 7 percent c and we sent it along with some
colonists to Alpha Centauri and the ship while traveling 7 percent c hit a
meteor the size of a man's fist, how catastrophic would an impact of this
nature be to the spaceship?Let's say the meteor was 10cm across and was
comprised of iron.
![]() ANSWER:
ANSWER:
There is no way I can even begin to do a calculation here. It
would depend on the design of the space ship. Even if I had more details,
this would be more of an engineering problem than physics. You can use your
imagination, though. The shuttle Columbia was going 545 mph=11 m/s≈0.000004%
of c and a piece of foam insulation (much softer than iron) had
catastrophic results. You might be interested in another
recent answer.
![]() ADDED ANSWER:
ADDED ANSWER:
I estimate your meteor would have a kinetic energy of about 2x1017
J, about the same as 2,000 Nagasaki atomic bombs. Curtains for this space
ship!
.jpg)
![]() QUESTION:
QUESTION:
I was wondering if you could help me explain something that happen
whilst heating water using a bunsen burner the other day. I stopped heating
(turned the bunsen burner off) at 80 degrees, but the temperature of the
water (as read from a thermometer) continued to increase. This only lasted
for several minutes, but this is not what I had expected. Given that the
heat source was removed, I expected particles to begin to decrease in
kinetic energy, and therefore temperature decrease too. Am I correct in
thinking particles within water built up momentum during heating, meaning
they were still increasing kinetic energy and therefore temperature for a
short while after turning the bunsen burner off? This meaning the
thermometer increased in temperature too even though bunsen burner was off?
![]() ANSWER:
ANSWER:
Your speculation that the kinetic energies of the molecules
continued to increase because they were already increasing is wrongâenergy
change does not have "inertia". The
instant you stop adding energy (heating) the water, its temperature will
stop increasing. Therefore, something must have continued heating the water.
If you think about it, the bunsen burner, while the ultimate source of the
energy, is not what is heating the water; the bunsen burner is heating the
container and the container is heating the water. The container is much
hotter than the water when the bunsen burner is turned off and it will continue
heating the water until the two are in thermal equilibrium, at the same
temperature (ignoring the interaction with the air around them).
![]() QUESTION:
QUESTION:
Why do I WEIGH the same at the earths pole as I do at the equator ?
Given the earths radius 6378km and i'm doing 1600km/h and my MASS is 100kg thats about 3.1Nm/s of force trying to throw me off the ground.
YET
At the pole i still have 100kg MASS and the earths gravity hasn't changed ...whats the deal ?
![]() ANSWER:
ANSWER:
As anyone who follows my answers can tell you, I am very rigid
about what weight means. To me, my weight (on earth) is the force which the
earth exerts on me. A minority of text-book writers like to define weight to
be what a scale reads. There is one main reason why your weight is different
at the poles and equator: the earth is not a sphere but is slightly oblate
which means that you are closer to the center of the earth if you are at the
poles and so you are slightly heavier there. The figure to the left shows
equipotential surfaces for an oblate spheroid (much more oblate than earth)
and the ratio of the weights at the pole and the equator is 1.52/1.14=1.33.
There is an additional reason why a scale reads differently: because of the
earth's rotation, there is a centrifugal force at the equator which results
in a scale reading less than at the poles. If you take into account that the
earth is not really a uniform mass distribution, this can also affect the
local value of g. All of these are very small effects on earth. I
guess the bottom line to my answer is that you do not necessarily weigh the
same anywhere on the surface of the earth as anywhere else. Your mass is
always the same, though.
![]() QUESTION:
QUESTION:
As gas molecule come at rest at absolute zero temperature which is impossible to achieve and also kinetic energy depends on temperature then how is solid ice is formed
![]() ANSWER:
ANSWER:
Molecules in a solid are not at rest, they are vibrating like
masses on springs. As the gas cools, its molecules slow down and eventually
the speed is sufficiently slow that if one molecule collides with another
they will bind together. Eventually more and more bind together making the
solid.
![]() QUESTION:
QUESTION:
I intend to heat a sealed tank to 280 degrees fahrenheit to cook lumber. I would like to be able to keep the pressure at a contsant 40-50 psi inside the tank. I need to know how much the pressure will increase inside the tank as I add the heat. I don't want the tank to blow up on me while it's being heated. I plan on using heating elements inside the tank. If needed I will also add pressure to the tank to get to 40-50 psi.
![]() ANSWER:
ANSWER:
The operative principle here is the ideal gas law, PV=NRT
where P is absolute pressure, V is volume, N is
the amount of gas, T is absolute temperature, and R is
a constant. The pressure numbers you gave are, I assume, gauge pressure, the
amount above atmospheric pressure which is about P1=15 psi, so
your target absolute pressure range is P2=55-65
psi. The temperatures must be converted to kelvins (K), absolute
temperature: I will take room temperature T1=700F=294
K and T2=2800F=411 K. This is all we need to
know to find the final pressure assuming V, N, and R do
not change: P=P1(T2/T1)=15(411/294)=21
psi. This is well below your target pressure. Probably the easiest thing to
do is to increase the pressure before you heat it by pumping in
room-temperature air. Suppose you want a final pressure of about 60 psi (45
psi gauge pressure), then the room-temperature pressure you should start
with should be P1=60(T1/T2)=P1=60(294/411)=42.9
psi=27.9 psi gauge pressure.
All this assumes that your tank is strong enough to take these pressures and I cannot guarantee that. I strongly suggest that you be certain you have a pressure guage on the tank as well as a pressure relief valve which will keep the pressure from getting too high.
![]() QUESTION:
QUESTION:
When a string acting as a standing wave is plucked/oscillated at its fundamental frequency (like that of a guitar), is there a relationship between the amplitude of the string itself and the amplitude of the sound it makes. If so what exactly is it?
I know that the string will be a transverse wave while sound is a longitudinal wave, so im not sure how exactly to convert the amplitudes if there is a way to do so.
![]() ANSWER:
ANSWER:
Take a guitar string and connect it between two rigid points
(two granite walls, for example) and pluck it. You will hardly be able to
hear it at all. A guitar is a complex instrument and it is really the
vibration of the guitar itself and the air inside it that is mainly what you
hearâthe string excites the guitar and it acts like an amplifier. The
response of the guitar to the vibrating string depends on the quality of the
guitar or else there would be no reason to have some guitars much more
expensive than others. So there is no simple relationship which you seek
between the amplitude of the string and the amplitude of the of the
resulting sound. I would think, up to a point, you could roughly estimate
that the two were proportional. However, you also have to factor in that a
guitar string does not vibrate with only the fundamental frequency but also
includes all the overtones and the guitar will
respond differently to the different overtones.
![]() QUESTION:
QUESTION:
All the electrons in an atom keep moving (vibrating) year by year from where they get this much of energy?
And why the energy does not finishes like our energy finishes after some time?
![]() ANSWER:
ANSWER:
When you say
"âŚenergy
finishes after some timeâŚ"
I suppose you mean like you have to fill up your gas tank in order to keep
your car moving. The only reason you have to do that is because friction is
constantly taking energy away from your car so energy is being lost. But
electrons in atoms do not experience friction and, once they are given
energy in the first place, the energy will never go away. Imagine a mass
hanging on a spring and subject to no friction; once you start it
vibrating (give it some energy), it will never stop.
![]() QUESTION:
QUESTION:
Is higher frequency really more energy?
It is thought that higher frequency has more energy. However, the higher the frequency the smaller the wavelength. With that said, though the higher frequency is delivering more energy to a a given location, it is giving less total energy in a given area. A lower frequency is giving less energy to a given location, but more energy in an area. So the TOTAL energy of the wave would seem to be equal. Greater area(wavelength), lower frequency. Higher frequency, lower area(wavelength).
![]() ANSWER:
ANSWER:
I am afraid your thinking is muddled. Electromagnetic waves of a
given frequency are a collection of particles called photons; the smallest
amount of electromagnetic wave you may have is a single photon which will
correspond to a particular frequency. The energy E of a single photon
is proportional to its frequency f, E=hf where the
proportionality constant h is Planck's constant. So if 1000 red
photons hit a wall and 1000 blue photons hit a wall, the blue photons will
bring the most energy.
![]() QUESTION:
QUESTION:
I hope this question is stupid and is a very quick answer. If i have an object submerged in a tank of water, say a solid cylinder, obviously the pressure at the top of the cylinder will be less than the pressure at the bottom of the cylinder, due to the difference in depth between the two points (P=pgh). What I would like to know is how this difference in pressure exerts a force on the cylinder, and where? Is the force acting on the bottom of the cylinder, trying to push it to the surface? I just can't wrap my head around this at all.
![]() ANSWER:
ANSWER:
Sorry to disappoint you, but your question is not stupid. You
have discovered
Archimedes' principle. Since, as you note, the pressure at the bottom of
the object (pushing up) is greater than the pressure at the top of the
object (pushing down), there is a net push up. This force is called the
buoyant force. It may be shown that the buoyant force is equal to the weight
of the water displaced by the object. The buoyant force determines whether
an object floats (buoyant force greater than weight) or sinks (buoyant force
smaller than weight) and why swimming is sort of like flying.

![]() QUESTION:
QUESTION:
If a single seed can produce a huge tree then how can we say that the mass of the universe is constant?
![]() ANSWER:
ANSWER:
We can't say that the mass of the universe is constant; the
energy of the universe is constant. Every day, for example, the sun's mass
decreases because mass (hydrogen) is being turned into energy plus different
smaller mass (helium). In your example, the mass of the tree was not created
from nothing. The tree took water, carbon dioxide, and nutrients from the
soil and using energy from sunlight it built itself. All the mass and energy
are accounted for.
![]() QUESTION:
QUESTION:
I am a member of US Coast Guard Forces. I am trying to describe to people
how hard it is to find themâso
wear a life-jacket so we have more time.
I am looking for an 'apparent size' formula, i.e., supposing someone's head is 1 ft high, what is its apparent size to me, on a boat 200 ft away, looking for that person (who hopefully still has his head above water!)
200 ft is ~ 1/10th of a nautical mile and is a standard separation distance for search and rescue patterns to run at.
![]() ANSWER:
ANSWER:
The way astronomers determine relative sizes of objects in
telescopes is the angle subtended by the image of the object. The angle,
θ, in radians, is given by θ=s/R where s
is the size of the object and R is the distance away. So if someone's
head is 200 ft away, it will be smaller by a factor of 20 than if it were 10
ft away. But you are actually looking at the area of the head, and that is
proportional to the square of its size, so that area would appear to be 400
times smaller than if it were 10 ft away. Another way to put it is that at
200 ft a 1 ft diameter head would look like a 12/20=0.6 inch ball at 10 ft,
maybe like a grape 10 ft away.

![]() QUESTION:
QUESTION:
Regarding a atomic blast. What are what appears to be thin streamers on the outside of the mushroom cloud? They are some distance away from the cloud and go from the ground to the cloud itself.
![]() ANSWER:
ANSWER:
I assume you mean like shown to the left. These are the
contrails of rockets shot off just before the blast; their purpose is to
detect the shock wave from the explosion.
![]() QUESTION:
QUESTION:
I need a very brief explanation for Kindergarteners. (I just
want to use the right words; they can learn the details of what they mean
later.) In an amusement park ride in which long swings are spun around a
central pole, why do the swings rise up as the pole spins faster? (I assume
it's the same reason that a skirt rises up when the person wearing it
twirls.) Is it something to do with centrifugal force? Centripetal force?
Nothing I saw on the web about these forces seems to explain why the objects
rise, only why they move to the inside or outside of the orbit.
![]() ANSWER:
ANSWER:
For Kindergarteners, use of centrifugal force is probably best.
I guess the merry-go-rounds we had on playgrounds when I was a kid have been
deemed unsafe, but get your students to appreciate that the faster they are
spun on something akin to this, the harder it is to hang on. This is because
the centrifugal force which tries to push them off gets bigger as the
merry-go-round spins faster. Then you can just take a pendulum and
demonstrate that the harder you pull, the higher it rises. The little
diagram to the right shows the effect of the the centrifugal force F which will lift the pendulum bob higher as
it pulls harder.
![]() QUESTION:
QUESTION:
I have a question that been thats been unanswered from quite some time now. I even tried asking that to a person in NASA houston and he couldn't even understand. Hope you can help.
We know that space dust and debris keep on falling on earth. And I have read that its many tons a day. Considering mass of earth is increasing every day for millions of years now, how does it affect its revolution, speed and axis. Or does it even affect that.
![]() ANSWER:
ANSWER:
One estimate is that the earth gains 40,000 metric tons (4x107
kg) per year. So, in a million years that would be a gain of 4x1013
kg. The mass of the earth is 6x1024 kg. The moment of inertia
will be proportional to the mass times the square of the radius, so,
assuming the change in radius is negligible, the fractional change in moment
of inertia over a million years would be approximately 4x1013/6x1024≈10-9=10-7
%. Since angular momentum (moment of inertia times angular velocity) is
conserved, this would mean that the angular velocity would decrease by about
10-7 %, an increase in the length of a day of about (24 hr)(3600
s/hr)x10-9≈10-3
seconds in a million years!
![]() QUESTION:
QUESTION:
This might seem dumb, but i cannot understand the laws of thermodynamics applied to gravity.
If a moon orbits a planet in a stable orbit, it still pulls on the planet, and the planet pulls on the moon. This seems to generate heat (the heatsource on europa) and motion (tidalwaves on earth). How can this not violate the laws of thermodynamics?
![]() ANSWER:
ANSWER:
The first law of thermodynamics, which seems to be the crux of
your question, is nothing more than conservation of energy. Energy
conservation is true only for isolated systems, so let us think about a
single planet and a single moon isolated from everything else. In addition
to the simple central force of gravity, the two interact with each other via
tidal forces which result
from the sizes and relative masses of the two. Just what the effects of the
tidal forces are depends a lot on the relative sizes and distances of the
two, but, as you note, often appear to violate energy conservation. So,
let's look at that more closely. Soon after the moon was created, probably
by a cataclysmic collision with an asteroid, it was much closer to the earth
than today and it rotated on its axis at a much faster rate than it does
today (about 28 days, which is why it always shows the same side to us). The
tidal force caused what is called "tidal locking", the same side always
facing the earth. It would seem that this would represent a loss of energy
since it is not spinning as fast as it used to be, but as this happened, the
moon moved farther and farther away from the earth which represents an
increase in energy. So, the energy of the whole system stayed the same.
Today, the tidal effect is mainly due to the ocean tides on the earth and
now it is the earth which slows down its rotationâthe earth is losing
rotational kinetic energy and tending toward being tidally locked with the
moon. This is an extremely small effectâa day gets about 2 milliseconds
shorter during one century. But, just as was the case when the moon was
slowing down its rotation, the way energy is being conserved is by the moon
moving farther away, resulting in an increase in the earth-moon energy
keeping the total energy constant. If the tidal forces are great enough to
cause significant frictional heating because of the tidal force distortion
of the whole moon (your Europa example), energy is lost because some of the
heat is radiated into space. So the first law would be violated, but you
would expect that since some energy is escaping from the planet-moon system.
You can see that your error was to assume a "stable orbit".
![]() QUESTION:
QUESTION:
This might seem dumb, but i cannot understand the laws of thermodynamics applied to gravity.
If a moon orbits a planet in a stable orbit, it still pulls on the planet, and the planet pulls on the moon. This seems to generate heat (the heatsource on europa) and motion (tidalwaves on earth). How can this not violate the laws of thermodynamics?
![]() ANSWER:
ANSWER:
The first law of thermodynamics, which seems to be the crux of
your question, is nothing more than conservation of energy. Energy
conservation is true only for isolated systems, so let us think about a
single planet and a single moon isolated from everything else. In addition
to the simple central force of gravity, the two interact with each other via
tidal forces which result
from the sizes and relative masses of the two. Just what the effects of the
tidal forces are depends a lot on the relative sizes and distances of the
two, but, as you note, often appear to violate energy conservation. So,
let's look at that more closely. Soon after the moon was created, probably
by a cataclysmic collision with an asteroid, it was much closer to the earth
than today and it rotated on its axis at a much faster rate than it does
today (about 28 days, which is why it always shows the same side to us). The
tidal force caused what is called "tidal locking", the same side always
facing the earth. It would seem that this would represent a loss of energy
since it is not spinning as fast as it used to be, but as this happened, the
moon moved farther and farther away from the earth which represents an
increase in energy. So, the energy of the whole system stayed the same.
Today, the tidal effect is mainly due to the ocean tides on the earth and
now it is the earth which slows down its rotationâthe earth is losing
rotational kinetic energy and tending toward being tidally locked with the
moon. This is an extremely small effectâa day gets about 2 milliseconds
shorter during one century. But, just as was the case when the moon was
slowing down its rotation, the way energy is being conserved is by the moon
moving farther away, resulting in an increase in the earth-moon energy
keeping the total energy constant. If the tidal forces are great enough to
cause significant frictional heating because of the tidal force distortion
of the whole moon (your Europa example), energy is lost because some of the
heat is radiated into space. So the first law would be violated, but you
would expect that since some energy is escaping from the planet-moon system.
You can see that your error was to assume a "stable orbit".
![]() QUESTION:
QUESTION:
A while back my friend and I were playing computer games my room together. We noticed that it was getting very hot in the room and I said "just think how hot it would be if we didn't have efficient CPU coolers!" He responded, "It would actually be cooler in here if we didn't have efficient coolers because more heat would be in the CPU and less would be in the room."
My question is this, would the overall heat in a room occupied by gaming computers be higher with less efficient CPU coolers or would it be higher with more efficient CPU coolers?
![]() ANSWER:
ANSWER:
The CPU generates a certain amouint of power in the form of
heat. You want to get that away from the CPU so you install some kind of
cooler. The simplest would be just fins thermally coupled to the chip to
radiate the heat away faster due to increased effective surface area. In the
long run, either of these will end up heating the environment at the same
rate because both are generating the same power, it is just that the
equilibrium temperature of the chip or chip+radiator will be different. The
next simplest cooler would be a fan; but a fan itself consumes power and so
it adds to the total power dumped into the room. This would come from the
heating of the fan motor. Or, you could have some kind of refrigerator;
again, this would add more heat to the room than the power generated by the
CPU. A refrigerator extracts heat from one place and dumps heat in another.
Because of thermodynamics, the heat dumped is always greater than the heat
extracted. For example, you should not cool your kitchen by opening the door
of your refrigerator because the coils at the back put more heat into the
room than the cooler takes out. Finally, if you have some kind of liquid
cooling and dump its heat somewhere outside the room, the overall effect
would be to heat the room less.

![]() QUESTION:
QUESTION:
I'm a non-scientist researching the issue of the relative efficiency of water transportation versus land and air transportation. The studies I consult all indicate that bulk cargo transportation by water is far more efficient than land or air transportation, but they stop short of getting into the physics of why this is so. Something to do with friction, I imagine--but exactly what?
![]() ANSWER:
ANSWER:
I am sure there are lots of considerations. Since you mention
friction, let's run with that. I will compare ground with water
transportation. Imagine a truck or a train, completely empty. For it to
drive at a constant speed the engine must provide a certain power, energy
delivered per unit time; the reason that it cannot just move forward without
an engine is that there is friction of various kindsâin the axels, in the
rolling of the wheels, and air drag. The drag depends only on your speed, so
if we agree to go a certain speed, this friction can be ignored. The rest of
the friction is determined by the weight of the train or truck. Now, suppose
you load the train or truck with cargo, say 10 times the weight of the empty
train or truck. Friction (other than drag) will increase by a factor of 11
because friction is proportional to the total weight. So you need almost 11
times more power to maintain the constant speed. Now think about a ship. All
the friction is drag, air drag and water drag. These now depend on speed but
there is no friction which depends (directly) on the weight. If you add 10
times the weight as we did before, the ship will go down deeper in the
water; this will increase the water drag somewhat, but it will certainly not
be 10 times bigger as was the case for ground transport. Roughly speaking,
the drag will be proportional to the cross sectional area of the ship in the
water and I would be surprised if that doubled when loading a ship.
![]() QUESTION:
QUESTION:
I looked up how our astronauts breathe on the ISS; splitting water molecules into gaseous hydrogen and oxygen (H2 and O2). So my question is: how much water would natural processes have to had split for there to be as much oxygen that is present in our current atmosphere?
I assume that's a tough one to answer without engineers etc. I just wish there was already an answer available.
![]() ANSWER:
ANSWER:
This is not particularly "tough" to estimate. The total mass of
the atmosphere is about 5x1018 kg and about 1/5 of that is
oxygen; so there is about 1018 kg of oxygen in the atmosphere.
About 90% of the mass of water is oxygen, so the total amount of water you
would have to split would be about 0.9x1018 kg. I believe that
the origin of our atmospheric oxygen is from plants (cyanobacteria, to be
precise), though, where photosynthesis turns carbon dioxide and water into carbohydrates and oxygen.
![]() QUESTION:
QUESTION:
What is the change in velocity of the earth's rotation if a person (myself) who weighs 60 kg were to stand on something about a foot tall.
Ps this is not a homework question, I'm just a curious teen who's never taken physics. Also it's the middle of the summer for me in
New Orleans.
![]() ANSWER:
ANSWER:
The glib answer to this question would be, for all intents and
purposes, the change in rotation would be zero. It is a good opportunity
to talk about the physics involved and to estimate how small small is here. The moment of inertia of the earth is about Ie=8x1037
kg∙m2. Your moment of inertia if you are on the earth's
surface is about Iy=60x(6.4x106)2=2.5x1015 kg∙m2. The moment of the
earth plus you is I=Ie+Iy≈Ie=8x1037.
If you increase your distance by the amount 0.3 m, about 1 ft, your moment
of inertia increases to Iy+ΔI=60x(6.4x106+0.3)2=Iy(1+4.7x10-8)2≈2.5x1015(1+2x4.7x10-8)=2.5x1015+ΔI
and so ΔI=9.4x10-8 kg∙m2. So you and the earth
start with I=8x1037
and end with I+ΔI=
![]() QUESTION:
QUESTION:
If I lift a book for thirty minutes I feel tired. Physics says that
I did no work but it also says that if energy is lost some amount of work has to be done (though it may result in net zero work). Why do we feel tired without performing "work in the language of physics"
![]() ANSWER:
ANSWER:
In the example of simply holding up a weight in an outstretched hand,
physics would say no work is being done because the force on the weight is not acting over a distance; you and I both know, however, that sugar is being burned to provide the energy necessary to hold this weight stationary. What is going on there, as I understand it, is that the muscle fibers in your arm are continually slipping and retensioning thereby doing lots of little parcels of work to hold your arm steady.
![]() QUESTION:
QUESTION:
My friend believes there is the energy potential in a small rock to run a city for days. Is this theory correct?
![]() ANSWER:
ANSWER:
If you could find a way to change all the mass of that stone into energy you could get an amazing amount of energy. For example, suppose the mass were 100 grams=0.1 kg. Then the energy there is
mc2=0.1x(3x108)2 which is about 1016 J. Suppose you spread this out for a week; then the power would be
(1016 Joules)/[7 day(24 hour/day)(3600 second/hour)]=16.5x109
Watts=16.5 GW. This is about twice a large as the largest nuclear power plant in the world.
Unfortunately, the most efficient way to generate large amounts of power
(nuclear fusion, the energy of the sun and the hydrogen bomb) is only 1%
efficient.
![]() QUESTION:
QUESTION:
Is the energy needed to increase the temperature by 5 degrees, for example, the same energy needed to decrease the temperature of the same matter by 5 degrees?![]() ANSWER:
ANSWER:
I think you mean "the same energy
released to decrease the temperature"; you do not add energy to decrease temperature.
The answer to your question is that it depends on how you heat and cool. An
example of where it would not be the same is if you heat a gas allowing it
to expand at a constant pressure and then cool it keeping its volume
constant, the energy you put in would be more than the energy you got out.
![]() QUESTION:
QUESTION:
What is mass?![]() ANSWER:
ANSWER:
There two kinds of mass. Inertial mass is the property an
object has which resists acceleration when a force is applied; the harder it
is to accelerate something, the more inertial mass it has. Gravitational
mass is the property an object has which allows it to feel and create
gravitational forces; for example, the more gravitational mass an object has
the greater the force it will feel due to the earth's gravityâthe more it
will weigh. It turns out that the two masses are actually identical; this
fact is one of the cornerstones of the theory of general relativity.
![]() QUESTION:
QUESTION:
when a drop of water is dropped on to a hot iron plate why does it become spherical before evaporating?
![]() ANSWER:
ANSWER:
Any place where the water touches the plate the water
will almost instantly vaporize. But the water must touch the plate for the
weight of the drop to be held up. The result of these two competing things
is that the water touches the plate only in a very small area. It is not
spherical, but close enough to look that way.
![]() QUESTION:
QUESTION:
Physics is my hobby, but, language is my education (MA).
I realized a while ago that there is no definition for motion beyond "when
something goes from point a to point b". There are archives of
"descriptions" of motion (e.g. Newton), but no "definition". After 3 years,
I have found a definition! So, what do I do? Journal article? Copyright?
Show up at some place and submit my idea? Please assume that what I am
saying is true. ![]() ANSWER:
ANSWER:
The reason that you cannot find an operational definition
is that there is none. There are generally two types of concepts in science,
quantitative and qualitative. If you are a "language guy" you must
understand that. Qualitative concepts are those which we understand in terms
of language, they are not quantitatively defined. Everyone understands that
motion is when something moves to some other location in some time. Asking
what the definition of motion is is like asking what the definition of wet
or large or speedy isâthere is none. For motion, though, there is an archaic
definition. When Newton stated his second law he wrote it as âThe alteration of motion is ever proportional to the motive force impressâd".
Today "alteration" is stated as "rate of change", "motion" is "linear
momentum" which is mass times velocity, and 'motive force" is simply
"force", so rate of change of momentum (d(mv)/dt) is
proportional to force. So, you might satisfy yourself that motion is mv
where m is operationally defined (kilogram, e.g.); v is
rate of change of position, a length divided by a time and both length
(meter, e.g.) and time (second, e.g.) are operationally
defined. Again I emphasize that this is archaic and motion today is
qualitative.
![]() QUESTION:
QUESTION:
I've been arguing with a friend about this, and I'm sure you've answered it before, but I spent about 30 minutes searching the web and I couldn't find anything! So to the question, if one were to make a "phone" out of a paper/styrofoam/tin cup connected to a string, would it work in space? I believe it would because the strong would act as a medium.![]() ANSWER:
ANSWER:
Yes and no. If you tapped on one cup that vibration would
be transmitted via the string to the other cup. But if what you had in mind
is speaking into one end and someone hearing on the other end, it would not
work because your voice is sound in the air which gets the cup vibrating and
there is no air.
![]() QUESTION:
QUESTION:
The definition of "electric current" I find in my school books is: "directed flow of electrons". The power stations here in my country use hydro power to make work some huge generators which create electricity, i.e directed flow of electrons. But their functioning is not based in obtaining electrons from something (not the water nor the metal), instead its function is to create some magnetic fields which seem to be essential in creating electric current.
My question: Is the above definition of electric current correct? If yes, where do the continuous flow of electrons come from? Are really magnetic fields a limitless source of electrons, if not, how do they generate limitless electricity?
![]() ANSWER:
ANSWER:
The electrons which flow in a wire were already there
before the current started. In materials which are conductors there are
electrons which are very easy to move around. Magnetic or electric fields
may be used to cause these "conduction electrons" to move. Electrons are not
being injected into the wire.

![]() QUESTION:
QUESTION:
Here's a question that I have been pondering. If a truck is driving on the freeway and a car pulls in closely behind the moving truck to take advantage of the draft created by the truck is there an energy cost to the truck or is having a car in it's wake energy neutral?
My gut feeling is that there would be a slight energy cost to the truck due to it's turbulence wake being interfered with.
![]()
 ANSWER:
ANSWER:
This, I discovered, is not a trivial question. For a
lengthy discussion, see
The Naked Scientists. Here is my take on it. There is no question that
the trailing car consumes less gas. The reason for this is not so much that
the truck is pulling the car but that the car experiences a much lower air
drag when drafting; the drag is approximately proportional to the square of
the velocity and the truck's wake is moving forward with the truck. What
seems to be controversial is the crux of your questionâis
there a cost to the truck? Some argue that the composite truck-car system
has less total air drag, others that there is a net cost to the truck which
need not (and almost certainly will not) equal the gain by the car. There is
certainly no conservation principle here because the new system has
different forces on it than the separate systems. My feeling it that there
is at least a small cost to the truck and I base this on an observation from
nature. Why do geese fly in a V? There is less overall air drag than if the
flock all flew individually. But periodically, the leader drops back and
another goose takes a turn at the front; must be because the leader has to
do more work.
![]() QUESTION:
QUESTION:
Has any human been more then 1,000,000,000 miles in space and returned?
![]() ANSWER:
ANSWER:
The farthest any human has been is the moon which is
about 240,000 miles from earth.
![]() QUESTION:
QUESTION:
My brother and I recently had a lively debate about the mechanics of temperature change within a glass of ice water (i.e. tap water sharing a glass with ice cubes). My brother remembers a Physics professor saying that the temperature of the (liquid) water within the glass won't change until the ice completely melts. Contrarily, I believe the temperature of the water within the glass begins changing immediately (after the liquid water has settled in the glass with the ice). Can you enlighten one (or both!) of us?
![]() ANSWER:
ANSWER:
Imagine doing the experiment in a well-insulated cup; a
styrofoam coffee cup would be a fair approximation. I just want to not worry
about the interaction with the rest of the environment. The tap water is
certainly warmer than the ice. What we know for sure is that if two objects
are in contact with each other, heat flows from the hotter to the colder.
So, heat flows from the water (cooling it) into the ice. This energy
absorbed by the ice is used to melt some of the ice meaning that some water
at 00C mixes with the already-present water making it cooler yet.
This continues until all the ice is melted (or all the ice and water is at 00C) and the whole system is now at a
considerably lower temperature than when you started. But, if you have ever
made and drunk a glass of ice water it should be obvious that your brother
is wrongâthe water is much colder than tap water shortly after the ice has
been added and long before all the ice has fully melted. What does not change is
the total energy inside the cup.
![]() QUESTION:
QUESTION:
If an ultra high energy cosmic ray with energy of 1020
eV were to strike an astronaut will that kill an astronaut?
![]() ANSWER:
ANSWER:
This is only about 6 J of energy. That is the energy
needed to lift 1 kg about 60 cm. And, it would probably not leave all its
energy in the astronaut. Certainly would not kill her.
![]() QUESTION:
QUESTION:
If an ultra high energy cosmic ray with energy of 1020
eV were to strike an astronaut will that kill an astronaut?
![]() ANSWER:
ANSWER:
This is only about 6 J of energy. That is the energy
needed to lift 1 kg about 60 cm. And, it would probably not leave all its
energy in the astronaut. Certainly would not kill her.
![]() QUESTION:
QUESTION:
We know, as we go deeper in a fluid the pressure increases and it's known that pressure is direct consequence of change in momentum of the fluid molecules, so can we conclude that as we go deeper in fluid the molecular velocity increases(as more is the velocity more is the force applied by collision or is my assumption wrong?
![]() ANSWER:
ANSWER:
The notion that pressure is related to molecular velocity
comes from the theory of ideal gases, and water is certainly not an ideal
gas. In a liquid, the pressure increases with depth because the deeper you
go, the more water there is above you, the weight of which is pushing down.
![]() QUESTION:
QUESTION:
For a statement to be a law it must be based on observations and
experiments. Newton, certainly didn't perform experiments to verify his universal law of gravitation.
Was it correct then to state it as a law?
![]() ANSWER:
ANSWER:
Newton may not have done the experiments, but his law was
the result of experiments done by others. Most important were
Kepler's three laws which were empirical summaries of a large body of
data on the motions of the planets. His law of gravitation, F=-MmG/r2,
provided a complete explanation of Kepler's laws. However, since the mass of
the sun was not known, only the product MG could be determined from
the data. A good
measurement of G was not done until more than 70 years after
Newton's death. Because gravity is such a weak force, this is a very
difficult measurement to make on a laboratory scale.

![]() QUESTION:
QUESTION:
I have recently begun learning how to play the electric guitar, and the other day my teacher was explaining to me how I can change between different pick ups on my guitar to get a different sound.
I am studying Year 11 Physics and have learnt about the harmonic series and I was wondering why the tone of my guitar changes when I change what pickup I'm using. Are there different harmonics and overtones that are accentuated by different pick ups?
![]() ANSWER:
ANSWER:
First, you might be interested in a
recent answer. I have shown the first few
possible ways a guitar string can vibrate. In an actual instrument, these
and many more are all happening at once in relative amplitudes determined,
in part, by how the instrument is played. Now, I presume that you have
several pickups placed in different places along the length of the string.
As you can see, the contribution from each overtone depends on where you
look at it and each is unique. One example would be if you put a pickup
right in the center of the string, none of the odd overtones would be
detected. Another example would be if you put the pickup 1/3 the length of
the string, the second, fifth, eighth, eleventh, etc. overtones would
not be detected. (I will let you see if you can figure out how I got that
series!). Basically, your intuition was right, different pickups pick up
different overtones.
![]() QUESTION:
QUESTION:
If a dome were on the moon which controlled temperature and
radiation inside. Would an Olympic sized swimming pool be able to be
swum in or would the water become airborne?
![]() ANSWER:
ANSWER:
There is still gravity on the moon, it is about 1/6 what
it is on earth. So, the water would definitely stay in the pool; a splash
would go much higher and farther than on earth, though. Swimming would be
pretty much the same as on earth, though, because, since you would be
lighter than the water in the same proportion, your buoyancy would be the
same. And, since most of swimming motion is horizontal, motion not affected
by gravity, it would be more or less the same as on earth. If you were to
swim down vertically, the pressure would increase about six times more
slowly since the pressure increase is proportional to the gravity.
![]() QUESTION:
QUESTION:
Using a hot plate as the sun, I am trying to use a magnifying lens to focus the radiant energy onto a thermometer. I measured the focal point length of the lens using white light at about 22 cm. When I try the experiment, there is no change in the thermometer. Why?
![]() ANSWER:
ANSWER:
The lens focuses visible light. Your hot
plate is mainly infrared light and the lens is not transparent to infrared
light, it is blocked. So your problem is that the hot plate is a very poor
replica of the sun because the sun is most intense in the visible part of
the spectrum.
![]() QUESTION:
QUESTION:
In an acoustic guitar, why does the timbre of a note change depending on where the string is plucked?
Is it to do with different wave lengths?
![]() ANSWER:
ANSWER:
For nonmusical readers, timbre refers to how a musical
note sounds. How can you tell the difference between a middle C on a piano,
a guitar, and trumpet? They all play the same "fundamental" note which has a
frequency of about 262 cycles per second. But, depending on the design of
the instrument and how it is played, other frequencies called overtones are
also present. It
is the relative mixture of these overtones which determine the timbre of the
instrument. A guitar is a relatively simple instrument in that its overtone
possibilities are all integer multiples of the fundamental. However, the
mixture of overtones may be controlled to some extent by the player by how
he plucks the string. Plucking it at the center, for example, emphasizes all
the even overtones, vibrations which have a maximum at the center of the
string (see the figure to the left). A more lengthy discussion can be found
here.

![]() QUESTION:
QUESTION:
Using real-world estimates for the coefficient of friction between his feet and the ground, how fast could the Flash run a quarter-mile? Assume that the limiting factor for his acceleration is the force parallel to the ground that his feet can apply.
![]() ANSWER:
ANSWER:
Suppose he is running on a dry asphalt road with
rubber-sole shoes. Then the coefficient of static friction is approximately
μ≈0.8. The maximum force of friction on level ground would be fmax≈μN=μmg≈8m
where m is his mass. So, his acceleration would be a=fmax/m=8
m/s2. A quarter mile is about 400 m, so assuming uniform
acceleration the appropriate kinematic equation would be 400=Đ
at2=4t2,
so t=10 s.
![]() QUESTION:
QUESTION:
Why is it that hot objects such as lightbulb filaments emit light while cold objects such as ourselves emit no light at all?
![]() ANSWER:
ANSWER:
Well, let's first define "light" as any electromagnetic
radiation, not just the visible spectrum. All objects radiate light and the
wavelengths they predominantly radiate depends on temperature. A human body
has a temperature around 300 K (800F) and a tungsten filament has
a temperature of around 3000 K (50000F). The picture to the right
shows the radiation for both of these temperatures; also note the visible
spectrum indicated by the colored vertical bands near 0.7 microns. At 3000
K, the radiation is most intense in the region of visible light; at 300 K
there is almost no intensity of visible light and the spectrum is most
intense around 10 microns which is in the "invisible" infrared spectrum.
Night vision goggles are sensitive to infrared radiation and enable you to
see "cold" objects in dark situations.
![]() QUESTION:
QUESTION:
I understand that acceleration due to gravity decreases with distance, specifically by the inverse square law. That being said, what is the maximum distance for which one can use 9.81 m/s2 as g for Earth?
![]() ANSWER:
ANSWER:
That depends entirely on how accurate you want to be,
there is technically no place other than the surface of the earth where this
is the acceleration. Furthermore, the number 9.81 is simply an average
value; it varies over the surface of the earth due to local density
variations, rotation of the earth, influences of the moon's gravity,
altitude variation, etc. You need to ask something like "at what
altitude h from the surface is the value of g changed by X%?"
Then

![]() QUESTION:
QUESTION:
In a good fireplace the smoke goes up the chimney rather than out into the room even if the fire is not directly beneath the hole.What causes this draft and why is it better the taller chimney?Why is the draft better on a windy day? And why do chimneys puff?![]() ANSWER:
ANSWER:
The main reason that the smoke goes up the chimney is
that hot air rises. The hot air from the fireplace fills the chimney and
this rising air results in a lower pressure at the bottom of the chimney. So
all air and smoke at the bottom of the chimney is drawn upward. A taller
chimney is better because there is a larger volume of hot air resulting in a
lower pressure at the bottom; there is a limit, however, determined by
whether air higher up has cooled and by frictional drag considerations over
a longer distance. If a wind blows over the top of the chimney, Bernoulli's
equation tells us that the pressure is lowered there providing an even
greater lift of the air column; from what I have read, though, the hot air
rising is the most important consideration. I do not know what you mean by
"puff".
![]() QUESTION:
QUESTION:
If I am driving my car with a bowling ball in the trunk, does it take the same energy to accelerate the vehicle to a given speed at a given time if the ball is free to roll around as it would if it were fixed to the vehicle? I assume that the net energy use would be the same in both situations (same total vehicle mass), but the acceleration rates would be different - ie: the fixed ball would result in a constant acceleration to speed, while the rolling ball would result in a non-constant acceleration. If this is true, could I harness the energy of the ball's movement relative to the vehicle (using some sort of linear generator) without causing parasitic energy loss to the vehicle? ![]() ANSWER:
ANSWER:
As long as the ball and the car end up going the same
speed, the total energy to get them there is the same (neglecting frictional
and air drag forces). If you devise some way to take enegy away from the
ball, that energy ultimately must come from the engine.

![]() QUESTION:
QUESTION:
What would the yield of a 5000 ton iron slug
accelerated at 95% of C by say a bored Omnipotent be? Would it be enough to
mass scatter a planet?
![]() ANSWER:
ANSWER:
I get the strangest questions sometimes! So, 5000 metric
tons=5x106 kg. The kinetic energy would be K=E-mc2=mc2[(1/√(1-.952))-1]≈1024
J. The energy U required to totally disassemble a uniform mass M
of radius R is U=3GM2/(5R) where G=6.67x10-11
is the universal gravitational constant. So, taking the earth
as a "typical" planet, U=3∙6.67x10-11∙(6x1024)2/(5∙6.4x106)≈2x1032
J. So your god's slug is far short of supplying enough energy to totally
blast apart the earth.

![]() QUESTION:
QUESTION:
If I consider a
tube both end open and
dip one end in water
(like pipette in chemistry lab)
and close the other by
thumb, water remain
hanged in the tube. If we say it is because
the atmosphere that
pushes up on the water
in the tube is same as
that of remaining air in
tube pushing down on
the water. Won't the
water fall out due to its
own weight as the
upward and downward forces are the same?![]() ANSWER:
ANSWER:
As you lift the tube out of the water, the weight of the
water in the tube pulls it down and the volume of air between your thumb and
the top of the water in the tube increases. Because the volume increases,
the pressure decreases so that when the bottom end of the tube is pulled out
of the water the pressure at the top of the column of water is smaller than
atmospheric pressure at the bottom. Therefore, the water column has three
forces on it which are in equilibrium: its weight down, a force down due to
the pressure at the top, and a force up due to the pressure at the bottom.
Your error was in assuming that the pressure at the top of the column is
atmospheric.
![]() QUESTION:
QUESTION:
If an electron in an atom can only orbit in fixed orbitals at certain frequencies, how does a gas molecule increase its speed when heated. It implies that the gas pressure also would be allowed only at certain energy levels but the pressure seems to increase in a linear way and jump to fixed pressures when the molecule has attained enough energy.
![]() ANSWER:
ANSWER:
The question is, how can energy be added to a gas? Let's
think about a single molecule in the gas. It has, essentially, two kinds of
energyâinternal energy which are allowed states of the molecule and are
quantized, that is restricted to certain discrete values, and the kinetic
energy associated with the molecule's motion as a whole as it hurtles across
the room. This kinetic energy is not quantized. So, when you heat up a gas
you are adding to its kinetic energy for normal temperatures. You have to
get to extremely high temperatures before you start excite atomic states.
You might be interested in why internal states are quantized and kinetic
energy is not. In quantum mechanics, systems which are bound (like electrons
in atoms) are quantized whereas systems which are not bound (like your
freely moving molecule) are not.
Bernoulli's equation is, essentially, just
conservation of energy for an ideal fluid; water is not an ideal
fluid, but close enough for this to be a pretty good approximation. However,
you will be asking this moving fluid to do work on your generator which will
take energy away and slow the water down. So, maybe it is useful to
calculate the energy which this moving water has. The quantities in the
equation are energy per unit volume of the water, so E= ρghV where E is the energy
contained by a volume V of the water. The power P (not to be
confused with pressure), is the rate at which the moving water is delivering
energy, P=dE/dt=ρgh(dV/dt).
If the cross section of your pipe is A, then dV/dt=Av
so P=ρghAv.
Here is an example: taking h=5 m with
v=10 m/s as above, using ρ=1000 kg/m3, and assuming a
pipe with a diameter of A=1 m2, P=5x105
W=500 kW. You could not get any more power than that from this water.
![]() QUESTION:
QUESTION:
Generally, we are trying to determine how much electricity will be generated by falling water . With that in mind, an engineering group has proposed a project whereby they place one of their machines inside a tube. We have all of the electrical equations worked out from the movement of the blades inside the machine -- the question for the Physicist is this: what is the speed of the water if it falls 5M or 10M or 20M? If the diameter of the pipe is an important variable, the answer is that we can make the mouth of the pipe as wide as we want: 5M, 10M, 20M etc. Bottom line, we want to achieve a water speed of at least 6 meters/second.
![]() ANSWER:
ANSWER:
You have not given me any details about the source of
this water. This sounds like a classic Bernoulli's equation problem in
elementary physics where you have a deep reservoir and there is a hole at a
depth h in the dam; what is the speed with which the water squirts
out? This hole could be your pipe and the cross section of the pipe does not
matter as long as its diameter is small compared to h. Bernoulli's
equation states that Đ
ρv2+ρgy+P=constant
where
ρ is
the density of the fluid, P is the pressure, v is the speed of
the fluid, y is the vertical position, and g=9.8 m/s2≈10
m/s2 is the acceleration due to gravity. In your case, I would
choose y=0 at the bottom of the dam where your pipe is, so y=h
at the surface; the velocity at the surface of the lake is
approximately zero and the velocity in the pipe is v; the pressure at
the top and the bottom is the same, atmospheric pressure PA.
So, Bernoulli's equation is Đ
ρv2+ρg∙0+PA=Đ
ρ∙02+ρgh+PA
or, Đ
ρv2=ρgh, or v=√(2gh).
Interestingly, this is exactly the speed the water would have if you just
dropped it off the top of the dam. For example, at a depth of 5 m the speed
should be about 10 m/s before you put your machine in it.

![]() QUESTION:
QUESTION:
I was watching Babylon 5 and in there there was a description of an Earth Alliance space ship weapon. The weapon was a gun that has two very conductive parts on both sides and a conductive armature in the middle and electricity somehow launches the projectile. The gun is 60 meters long, has two barrels with each capable of firing two shots per second simultaneously. The projectile is 930 kg in mass (1.7 m long 20 cm in diameter) to a velocity of 41.5 km/s. The barrel of this electric gun is 60 meters long. Is this kind of gun physically possible to build?
![]() ANSWER:
ANSWER:
I always like to look first at the energetics when
answering questions like this. Assuming that the acceleration of the
projectile is uniform, I find that the time it would take to traverse the
barrel is 0.029 s and the average acceleration is 1.4x106 m/s2.
Thus, the average force on the projectile would be F=ma=1.4x106x930=1.3x109
N=280,000,000 lb. I do not think you could have a projectile which would not
be destroyed by such a force. But, suppose the projectile could withstand
this force; the energy which you would have to give it would be E=Đ
mv2=8x1011
J. Delivering this energy in 0.029 s would require a power input of P=8x1011
You might be interested in similar earlier questions I have answered.
![]() QUESTION:
QUESTION:
Would it be possible to suspend an electron via electrostatic levitation in
a uniform magnetic field? And if the voltage was decreased enough so that
the electrostatic force on the electron was lower than the force due to the
electron's weight would the electron then experience a 'fall' due to
gravity?
I'm asking this because I'm wondering if placing a positron in a uniform magnetic field (in a vacuum) and lowering the voltage to a very small value so that the electrostatic force is lower than the weight would cause a positron to also experience a 'fall'. And if it did experience a fall it could be ascertained whether it would fall upwards or downwards.
I'm 17 years old and in the UK about to study physics at university in september and was just curious about this since one of our topics this year was electrical phenomena and we talked about millikan's oil drop experiment which featured a similar sort of suspension when the electrostatic force and force due to gravity were balanced.
It's a thought I had when wondering if antimatter was affected by gravity the same way matter is.
![]() ANSWER:
ANSWER:
It is always nice to see young folks asking interesting
questions. First, I need to correct one thing: everywhere you refer to a
"magnetic field" you should say "electric field"; a magnetic field exerts no
force on a charge at rest which is what you want to observe, Đ° la
Millikan. Now, it is known to extraordinary precision that the inertial mass
of a positron is equal to the inertial mass of an electron. By inertial mass
I mean the ratio of the force you apply to it divided by its acceleration,
in other words its resistance to being accelerated. (A more correct way,
relativistically, to say this would be that they have equal momenta for
equal speeds.) I believe it is true that nobody has ever "weighed" a
positron by measuring the force it experiences in a gravitational field.
But, if the gravitational mass were different from the inertial mass, this
would fly in the face of the theory of general relativity. But, let's talk
about the feasibility of your experiment. The mass of an electron is about
10-30 kg so its weight would be about 10-29 N (taking
g≈10 m/s2). The electron charge is about 1.6x10-19
C and so the electric field required to levitate an electron would be 10-29/1.6x10-19≈6x10-11
V/m. Suppose we use a parallel plate capacitor to create this field. The
charge density σ on a plate with field E is about σ=ε0E≈10-11x6x10-11=6x10-22
C/m2 which would correspond to an electron density on the plates
of about 6x10-22/1.6x10-19≈0.004
electrons/m2! This would correspond to about one electron for
every 250 square meters! That would not give a very uniform field would it?
There is no such thing as a uniform surface charge density because charges
in nature do not comprise a continuous fluid; so really tiny uniform fields
are not possible. I did all that just for the fun of it, but there is an
even more serious considerationâthe earth itself has an electric field near
the surface of typically 100 V/m pointing down, so an electron would be
repelled upward. To do your experiment you would have to get rid of that
field and I do not believe that it would be possible to be assured that you
could make the residual field much less than your
6x10-11 V/m. Back to the drawing board! Keep asking those hard
and interesting questions, though, and good luck with your university
studies.
![]() ADDED
NOTE:
ADDED
NOTE:
A
recent article discusses a new proposal to compare matter and antimatter
weights.
![]() QUESTION:
QUESTION:
What is the size of an image as a function of its constant velocity ? i.e. what is the percentage increase of the image of a square travelling at 1 m/s towards a fixed camera? Is there some equation to calculate this?
![]() ANSWER:
ANSWER:
Since you do not give any details about the camera, I assume
it has a fixed focal length f. I will call the size of the object
L, the size of the image h, and the distance from the camera to
the object R. You wish to relate the rate of change of h, u=dh/dt,
to the rate of change of R, dR/dt=-v where v is
the speed the object is approaching the camera; note that if the
object is approaching the camera, R is decreasing, i.e. dR/dt<0.
(If you do not know calculus, you will not understand my work here but you
will end up with a formula for the rate at which h changes.) Because
of the geometry of the situation (shown to the left) we can write L/R=h/f
or h=Lf/R. Differentiating, dh/dt=-Lf(dR/dt)/R2
or u=Lfv/R2. This is the rate at which h
is changing. Suppose that f=5 cm=0.05 m, v=1 m/s, L=10
cm=0.1 m, and R=2 m; then h=0.05x0.1/2=0.0025 m=2.5 mm and
the image is growing at the rate of u=1.25 mm/s. After 1 s, the
object has moved 1 m and so now h=0.05x0.1/1=0.005 m=5 mm and is now
increasing at the rate of 5 mm/s. So, you see, the rate the image increases
in size depends not only on v but also on how far away the object is
(R) and how far the image is from the lens (f). If you need to
know what h is as a function of t, you need to also know where
the object was at some earlier time which I will call t=0; then R0=R(t=0)
and so R(t)=R0-vt. Finally, we can
write h(t)=Lf/R(t)=Lf/(R0-vt).
For the example above and choosing R0=2 m, the graph on
the right shows the image size as the object approaches the camera; note
that both the size and the rate of growth approach infinity as R
approaches zero (t approaches 2 s).
![]() QUESTION:
QUESTION:
Without having wings, how does a helicopter turn in air?
![]() ANSWER:
ANSWER:
First of all, a helicopter does have wings. The rotor is
shaped like a wing and moves through the air by spinning thereby creating
lift. Imagine the path of the overhead rotor as a disk. The rotor is
connected to a plate called the swashplate (the thing between the rotor and
the fuselage in the picture) which can be tilted relative to the main shaft
to the motor and which causes the disk of the rotor to tilt relative to the
horizontal plane. Tilt it forward and the helicopter goes forward, to the
right and it goes right, etc. The swashplate is controlled by a
joystick in the cockpit called the cyclic. The tail rotor is also used in
turns, controlling yaw (rotation about a vertical axis); yaw is controlled
with foot pedals.
![]() QUESTION:
QUESTION:
We have a metal ruler 1 yard in length. If held in exact balance center then "pinged" it causes vibrations. nothing new there BUT at exact equal distances to either side there is a point at which it appears that the vibrations stop (a calm spot) for about 1 inch then the vibrations start again and continue to the end. We've tested and the vibrations don't stop, they are just a much smaller wave length. What is is this "calm spot" phenomenon? What causes it? Does it happen with earthquakes too?
Really geeked out about this! Way cool!
![]() ANSWER:
ANSWER:


You are exciting standing waves when you "ping" the stick. These are waves
which bounce back and forth from the ends of the stick and, for special
wavelengths, are just right to to resonate like a guitar string or an organ
pipe. The various wavelengths for which resonance occurs are called the
modes of oscillation. For a stick clamped at the middle, the lowest mode,
called the fundamental, has approximately 1/4 of a wavelength on either side
of the center as shown by the upper part of the figure above. A point with
zero amplitude, the center for the fundamental, is called a node and points
with maximum amplitude, the ends for the fundamental, are called antinodes.
What you are seeing is the next mode, called the first overtone, which has
approximately 3/4 of a wavelength on either side; this mode has three nodes
and four antinodes. To the right are animations for a stick clamped
at the end but they are exactly what your stick is doing on one half. Here
the nodes are near the darkest blue. Earthquakes are traveling waves and
therefore do not have nodes.
![]() QUESTION:
QUESTION:
If you have two permanent cylindrical magnets (the kind with a hole in the center) and you stack them with poles opposite on a pencil, the top magnet will "float" above the bottom magnet. Energy is being expended to keep the magnet "up" the pencil. Where is the energy coming from? The bottom magnet will be pushing down with an equal but opposite force, but that does not cancel the energy needed to float the top magnet as far as I can see.
![]() ANSWER:
ANSWER:
I am afraid you do not understand energy. The lower magnet
exerts a force on the upper magnet. The force holds it there in equilibrium,
it does not require energy to hold it there. It is no different from saying
that if one of the magnets were hanging from a string, where does the energy
to hold it there come from? Or, if one of the magnets were sitting on a
table top, where does the energy to hold it there come from?
![]() QUESTION:
QUESTION:
During a discussion with my 6th grade class about the Law of Inertia and space travel, a student asked: "If a spacecraft leaves a solar system, for example Voyager 1, will its velocity increase due to the lack of gravity from the sun." Fairly certain the answer is no; however, it did spark a rather interesting debate. Can you explain?
![]() ANSWER:
ANSWER:
Perhaps the key is to note that "leaves the solar system"
does not mean that there is no longer any gravity from the sun.
Rather there is a boundary where the solar wind, particles like protons and
electrons, stops; this is called the heliopause and has been definitely
observed by the Voyager 1 spacecraft as shown in the graph to the right.
This shows the amount of solar wind the Voyager detected as it moved during
the months of 2011-2. In September 2012 it dropped to near zero. This is
where we define the edge of the solar system to be and it is about 50
Astronomical Units (AU) from the sun; the earth is one AU from the sun. But
the gravity from the whole solar system is still present and the craft will
continue slowing down, but ever so slightly since as you get farther away
from a mass the gravity gets weaker. This craft has enough speed that, if it
never encountered any other mass it would keep going forever. I did a rough
calculation and found that the acceleration of Voyager is about a=-0.01
mi/hr2 which means that it loses about 1/100 mph per hour; but
the speed is about 40,000 mph, so I think we could agree that it is moving
with an almost constant speed. As it gets farther away, the acceleration
will get even smaller (physicists call slowing down negative acceleration,
not deceleration). Until it gets close to something else, like some other
star, it will keep going with an almost constant speed. When it does
approach another star it will begin speeding up. Your students should
appreciate that the only thing which can change the speed of something is a
force, a push or a pull.
![]() QUESTION:
QUESTION:
why does the ground frost go deeper when the surface begins to
thaw?
![]() ANSWER:
ANSWER:
The way you frame this question is that frost has gone to
certain depth before the thaw and then goes deeper because of the
thaw. In fact, there is what is called a
frost front, the line between frozen and unfrozen soil, which moves
slowly downward if the air temperature is below freezing. When the air
temperature goes above freezing, the top thaws but the frost front
continues moving down for a while because there is still a frozen region
above it which prevents it from getting the information that the air has
warmed. So, the thaw does not cause the frost to deeper, it is just
continuing what it was already doing. Eventually the thawing will reach the
frost front and all the soil will be thawed; in some arctic and antarctic
regions, the thaw will never reach all the way to the frost line and
permafrost results.

![]() QUESTION:
QUESTION:
I am building a cold frame to keep veggies alive in the winter. It will be 3' x 6' with two "doors" (called lights) each 3' x 3' that will be hinged to the frame. The frame probably weighs about 10 - 15 lbs. The doors will be quite lightweight, possibly only 3lbs each. I wanted to use magnets to keep the doors closed at night or when I am not venting the cold frame. We often get very windy days with 40mph wind speeds and gusts to 60 mph. From what I've read, magnets have different "pull force" properties. I'd like a way to figure out what pull force the magnet for each door needs to have to withstand the winds we get. Please don't tell me to just hook the doors closed -- shockingly, it appears magnets are a more cost effective solution.
![]() ANSWER:
ANSWER:
I must say that I cannot believe that you could not buy a
couple of simple hooks/latches for under $5, but I will do a rough
calculation for you to estimate the force you would need to apply at the
edge of the doors to hold it down in a 60 mph=26.8 m/s wind. When a fluid
moves with some speed v across a surface, the pressure is lower than
if it were not moving; this is how an airplane wing works and why cigarette
smoke is drawn out the cracked window of a car. To estimate the effect,
Bernoulli's equation is used: Đ
ρv2+ρgh+P=constant,
where ρ is the density of the
fluid (ρair≈1 kg/m3), P is the pressure,
g is the acceleration due to gravity, and h is the height
relative to some chosen h=0. For your situation both surfaces are at
essentially the same height so PA=P+Đ
ρv2
where the pressure inside your frame is atmospheric pressure (PA)
and the velocity inside is zero. So, PA-P=ΔP=Đ
ρv2=Đ
∙1∙26.82=359
N/m2=7.5 lb/ft2. This would be the pressure trying to
lift the door. So the total force on each door would be F=AΔP=9∙7.5=67.5
lb where A=3∙3 ft2=9 ft2 is the area of the
door. But, this is not the answer since we want to keep it from swinging
about the hinges, not lifting into the air. So, assuming that the force is
distributed uniformly over the whole area, you may take the whole force to
act in the middle, 1.5 ft from the hinges, so the torque which is exerted is
1.5∙67.5≈100 ft∙lb. But, the weight of the door also exerts a torque, but
opposite the torque due to the wind (the weight tries to hold it down)
-3x1.5=-4.5 ft∙lb. So, the net torque on the door about the hinges is about
95 ft∙lb. To hold the door closed, one needs to exert a torque equal and
opposite to this. To do this, it would be wisest to apply the force at the
edge opposite the hinges to get the maximum torque for the force. The
required force from your magnets would then be F=95/3=32 lb. Note
that this is just an estimate. Fluid dynamics in the real world can be very
complex. Also note that, if my calculations are anywhere close to correct,
you should probably be sure the whole thing is attached to the ground or the
side of your house since the total force on the whole thing would be
67.6+67.5-3-3-15=114 lb, enough to blow the whole thing away in a 60 mph
wind! Also, once the door just barely opens, the wind will get under it and
simply blow it up, Bernoulli no longer makes any difference.

![]() QUESTION:
QUESTION:
Galileo was punished by the Church for teaching that the sun is stationary and the earth moves around it.His opponents held the view that the earth is stationary and the sun moves around it.If the absolute motion has no meaning, are the two viewpoints not equally correct or equally wrong? i.e, By the concept of relative motion can't we say both?if so, then why do we usually say that earth goes round the sun,and the other way round?
![]() ANSWER:
ANSWER:
If the sun and earth were both just moving with constant
velocity and not interacting in any way, you would have a point. However,
because of their gravitational interaction and the fact that the mass of the
sun is hugely bigger than the mass of the earth, there is no way you can
sensibly argue that the sun orbits the earth. Each exerts a gravitational
force on the other (equal and opposite) but because the sun is so massive,
the force has almost no effect on it. If the earth were not orbiting but
simply released from rest, it would fall into the sun. There would be no
question which object had the greater accelerationâit would be obvious to
any observer that it was the smaller mass, the larger mass practically
unaffected. So, if any frames are accelerating, they are not equivalent to
those not accelerating. What you call "the
concept of relative motion" applies only to unaccelerated frames.

![]() QUESTION:
QUESTION:
If a dogs bark measures approximately 60-80 decibel, how much will it reduce traveling in air (average 20 Celsius) over 500 meter.
Could you please brake down the formula for me so I can calculate other distances.
![]() ANSWER:
ANSWER:
You should first read an
earlier answer for a detailed
explanation of what a decibel (dB) is. The main reason for loss of sound
intensity I (measured in watts per square meter, W/m2) is
that the sound waves spread as they get farther away so the energy per
second (power) striking your ear gets smaller. The intensity falls off like
1/R2 where R is the distance from the source. You
do not specify the distance from the dog that the 60-80 dB level is
measured, so I will arbitrarily put it at 1 m. Therefore the ratio of
intensities at 500 and 1 m would be I500/I1=1/5002
or I500=4x10-6I1. But,
the catch is that dB is a measure of the level L (a logarithmic
scale), not the intensity. So we need the equations to convert between L
and I. These are L=10∙log10(I/10-12)
and I=10-12∙10(L/10) where I is
in W/m2. So, as an example I will choose L=70 dB, so I1=10-12∙10(70/10)=10-5
W/m2 and I500=4x10-6∙10-5=4x10-11
W/m2. Finally, we find what the dB level of I500
is: L500=10∙log10(4x10-11/10-12)=10∙log10(40)=16
dB. I believe that this will the main source of quieting with distance, not
any absorption of the sound by the air. Wind can also have an effect on the
intensity if it is across the direction the sound travels to reach you. By
the way, when the intensity reaches 10-12 W/m2,
it will be below the "threshold of hearing" and you will no longer hear it;
that corresponds to 0 dB.
![]() QUESTION:
QUESTION:
Let's say that we started mining for metals and such somewhere other than earth. What if any would the effects of large scale increase (and I mean really really big) in planet mass be? Also what would happen to the other planets we were robbing of minerals as their mass decreased?
![]() ANSWER:
ANSWER:
As long as the mass of the orbiting body is much less than
the mass of the orbited body, the orbital motion is independent of the mass
of the orbiting body. So, the length of the year would be unchanged.
However, increasing the mass and radius of the planet would increase its
moment of inertia, so its rotational speed would decrease and the day would
get longer. Keep in mind, though, that a huge amount of stuff would have to
be added for any real difference to occur.

![]() QUESTION:
QUESTION:
I am trying to determine the buoyancy of a 10 kg polyethylene tray (density = 0.95 g/cm3=950
kg/m3) that is used in lobster pounds to hold lobsters. The tray holds 60 kg of lobster, and fills up with water up to the lid (which floats at the top of the water). The volume of the tray is 0.1223 m3. The lobsters are held in seawater (density = 1026 kg/m3). So, my question is how much air is required to be placed in cavities in the lid to keep the tray floating at the top of the water?
![]() ANSWER:
ANSWER:
I will take the "volume of the tray" to be the inside volume,
that is the volume occupied by lobsters and water. The density of a lobster
is sure to vary from animal to animal, but it certainly must be larger than
the water since the creatures dwell on the bottom. I actually found a
measurment of a lobster's density to be 1187 kg/m3, so I will use
that as an approximation for all lobsters. So, the volume occupied by 60 kg
of lobsters is Vlobsters=60/1187=0.0505 m3. So,
the volume of water needed to fill up the tray is Vwater=0.1223-0.0505=0.0718
m3; so the mass of the water is Mwater=1026x0.0718=73.7
kg. The volume of the polyethylene is Vpoly=10/950=0.0105 m3.
So, the total mass is 60+10+73.7=143.7 kg and the total volume is
0.1223+0.0105=0.1328 m3. The density of the full tray is then
ρ=143.7/0.1328=1082 kg/m3; since this is greater than the
density of the water (1026 kg/m3), it will sink, hence presumably
the point of this question. In order for it to "just" float, volume must be
increased until the density is equal to 1026 kg/m3, i.e.
1026=143.7/V or V=0.1401 m3; so, the volume of the
air should be Vair=0.1401-0.1328=0.0073 m3=7300
cm3. This would be a volume of a cube about 20 cm on a side. I
guess I would increase that by at least 50% as a safety factor. (Note that I
have neglected the density of the air which is about 1 kg/m3.)
![]() QUESTION:
QUESTION:
Why are loops provided for transporting oil/water for longer distances?
![]() ANSWER:
ANSWER:
When the temperature of the pipe changes it changes length.
In the figure to the left, the pipe will expand if you heat it up and
contract if you cool it down. If it were just a straight pipe, the resulting
forces on the pipe along its length could be large enough to cause it to
buckle and fail. Inserting loops allows the length changes to be taken up by
the size of the loop as shown.

![]() QUESTION:
QUESTION:
I was playing a game known as ''Fallout 3'' and in the game there are laser weapons. The laser weapons are powered by a marshmallow sized microfusion cells that are basically miniature nuclear reactors that fuses hydrogen atoms. In the game they produce enough power to turn a 500 kilogram bear into ash in one second. So could a reactor that small produce enough power for the gun and how energy much would a marshmallow sized blob of fused hydrogen produce? A normal microfusion cell in the game has enough energy to fire 24 of these shots. So would it be possible in any way for these laser weapons to be able to be this powerful with an energy source like the microfusion cell?
![]() ANSWER:
ANSWER:
I have no way to estimate the "power
to turn a 500 kilogram bear into ash in one second". I am sure you realize
that, with today's technology, the possibility of there being such a power
supply is zilch. Let's just do a few estimates to show how hard this is. One
gram of hydrogen fuel (deuterium + tritium), if fully fused into
helium+neutrons, releases something on the order of 300 GJ of energy; so, if
released in 24 one second pulses, each pulse would be about 10 GW. That is
probably way more than your bear burning would need, so let's say 100 MW
would do it; so, we would need about 10-2 g of fuel. I calculate
that to confine that amount of gas in a volume of 10-5 m3
(about 1 in3) would require a pressure of about 5,000,000
atmospheres! That, in itself, should be enough to convince you that this
machine could probably never be possible. If you need more convincing,
consider shielding: 80% of the energy produced is in the kinetic energy of
neutrons. How are you going to harvest that energy in such a small volume
and how are you going to protect yourself from the huge neutron flux? And
surely there needs to be some sort of mechanism to control the process and
convert the energy into usable electrical energy to power the laser; all
that is supposed to fit into 1 in3? This truly is a fantasy game
with no connection to reality!

![]() QUESTION:
QUESTION:
I just watched a nature document about the largest snake that ever lived on Earth that was the Titanoboa that could exert a pressure of 400 pounds per square inch and that lived in the water mostly. So my question is that could a Titanoboa destroy a submarine by coiling around it with the pressure of 400 pounds per square inch assuming that the submarine is small enough for the 48 foot snake to coil around it?
![]() ANSWER:
ANSWER:
The pressure under water increases by about 0.44 psi/ft. To
get to 400 psi, therefore, a submarine must go to a depth of 400/0.44=909
ft. WWII U-boats had collapse depths of 660-920 ft. Modern submarines have
collapse depths of around 2400 ft. So, it depends on the submarine, but most
modern ones could withstand 400 psi. The only proviso is that they are
designed to have the pressure uniformly distributed over the whole surface,
not a narrow band where a snake would squeeze; a very localized pressure
could cause a structural failure at a lower pressure.

![]() QUESTION:
QUESTION:
I came across
this just now.
It implies a balloon full of air weighs more than the same balloon empty. That doesn't feel right to me as an inflated balloon is surely buoyant by the amount of air it contains. i.e. The extra weight of the air is cancelled out by the buoyancy. The site above is a respected organisation and I would be surprised if is recommending an experiment based on a false assumption. However, I cannot see how the instructions they give could possibly be used to determine the density of air.
![]() ANSWER:
ANSWER:
You are right, the experiment ignores the buoyant force on
the balloon; if the density of the air in the balloon were identical to the
density of the air outside the balloon, the experiment would fail to find
any weight of air. However, the pressure inside the balloon is greater than
the pressure outside and therefore the density of the air inside is larger
than normal atmospheric density. The experiment then measures the difference
between the mass inside the balloon and the mass of an equal volume of air
at atmospheric pressure. This would still be a reasonable order-of-magnitude
measurement of the density of air. A more accurate experiment would be to
measure the pressure to which the balloon was inflated; with that
information you could do a better measurement of the air density.
![]() QUESTION:
QUESTION:
What should be the temperature of a gas molecule if it needs to escape out of earth's gravitational pull suppose if we take the case of oxygen at what temperature its average velocity will be enough to escape earth's gravitational pull?
![]() ANSWER:
ANSWER:
Temperature of a gas is
a statistical quantity, no single gas molecule has a temperature. A gas of a
particular temperature has a distribution of speeds called the
Maxwell-Boltzmann distribution which contains all possible speeds. The
figure to the left shows this distribution for N2 for several
temperatures. The escape velocity from the surface of the earth is about
11,000 m/s, so you can see that a heavy molecule like nitrogen has almost no
molecules going that fast at normal temperatures (300 K), or even if T=1000
K. The picture to the right compares the distribution of speeds for N2
with that for H2, about 14 times lighter. You see that the most
likely speed of H2 is about 4 times faster than N2.
Comparing with the figure to the left, 300 K hydrogen gas would have a most
probable speed of more than 1200 m/s. Although there are still very few with
speeds higher than 11,000 m/s, there are still a few which escape.
Eventually, as the slower molecules speed up to fill in the distribution,
they would essentially all leak out of the atmosphere. That is the reason
why there is almost no hydrogen or helium in the atmosphere. Most hydrogen
on earth is locked up in water and other molecules, but since helium is
inert, the only source of it is from underground, usually as a byproduct of
natural gas wells. The form of the Maxwell-Boltzmann distribution is given
by 4π[m/(2πkT)]3/2v2exp[-mv2/(2kT)].
![]() QUESTION:
QUESTION:
Assume we're in a very large hollow sphere. (let's say r = 1 light year).
Then we take a very powerful laser with extremely low diffraction and we fire it while effectuating a full rotation with it.
Wouldn't the laser point travel faster than light on the inside surface of the sphere?
Or does it fall as into the immaterial category and is exempted from the rule?
![]() ANSWER:
ANSWER:
You do not need such an extreme condition to do what you
want. The distance to the moon is about R=3.8x108 m, so if
you swept your laser beam across the surface of the moon the speed of the
spot would be equal to the speed of light c=3x108 m/s if c=Rω
where ω is the angular velocity you are rotating the laser. So,
ω=3x108/3.8x108=0.79 radians/second=450
per secondâreally easy to do. But that spot is not anything, really, because
the spot a second from now will not be "made of" the same photons that it is
made of right now. The most important thing is that there is no way that
this spot could be made to carry information from one point on its path to
another. And you are right, it has no mass, but even massless light cannot
travel faster than the speed of light.

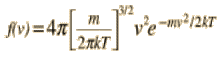
![]() QUESTION:
QUESTION:
is there any transfer of kinetic energy between two objects which have same mass and moving with same velocity and they collide with each other and the collision is elastic ? if it is not then why the molecules of the gas have different velocity
![]() ANSWER:
ANSWER:
You seem to have the idea that distribution of kinetic
energies is a result of collisions between molecules. Even if the molecules
were point particles and never collided, they would not be monoenergetic.
The reason for the Maxwell-Boltzmann distribution of speeds is explained
well at the
hyperphysics web site. The answer to your question is that if two
particles with equal mass and equal speed collide elastically, no kinetic
energy is transferred.
![]() QUESTION:
QUESTION:
None has ever seen the atom or nucleus inside it because it really very very very small then how the dimension of it is known I mean how do we know that atom is of the radius of 10^-10m and nucleus is of 10^-15m
![]() ANSWER:
ANSWER:
The size of an atom has been known for a long time, since the
early 19th century. Avagadro's number is NA≈6x1023
atoms/mole and tells you how many atoms there in a mole of a substance and
density is easily measured. For example, carbon has an atomic number of 12
so a mole has a mass of 12 grams. The density of carbon is about 2 g/cm3,
so one mole of carbon occupies a volume of about 12/2=6 cm3.
Therefore the volume occupied by one carbon atom is V≈6/6x1023=10-23
cm3, so the size (diameter) of a carbon atom is about 3√10-23≈2x10-8
cm=2x10-10 m. Of course, today individual atoms can be "imaged",
just not in the usual optical way; see an earlier
answer. The size of a nucleus was not determined until about 100 years
later, the early 20th century. Early experiments of Rutherford
scattering of alpha particles could be understood if all the mass of the
atom (except for the electrons) was a point at the center of the atom.
Eventually the experiments were able to find departures from this model and
the size of the nucleus could be inferred. You can also do diffraction of
particle-wave beams to determine the size; an example of how this can be
done with a beam of elastically-scattered protons is given in an
earlier answer.

![]() QUESTION:
QUESTION:
How fast a person would have to move to be completely invisible to our eyes? Like Goku from Dragon Ball.
![]() ANSWER:
ANSWER:
Well, I never heard of Goku. I guess I am not up on Japanese
anime! The only way for him to be invisible would be for the visible light
coming from him being Doppler shifted out of the visible range which is
wavelengths about 390-700 nm. I will first do one-dimensional calculations,
he is coming directly at you or going directly away. The appropriate
equation is λ'/λ=√[(1-β)/(1+β)] where λ' is the observed wavelength, λ
is the laser wavelength, and β is the ratio of the velocity
v of Goku relative to the speed of light c, β=v/c;
β>0 is for Goku moving toward you. When he is coming
toward you, β>0 and so he must be going fast enough that 700 nm
light is shifted to 390 nm light (blue shift). I find then that βtoward=0.53.
Similarly, when he is moving away from you, β<0 and so he must
be going fast enough that 390 nm light is shifted to 700 nm light (red
shift). I find then that βaway=-0.53. So, he needs to
be moving with a speed of about half the speed of light.
If he is not moving directly in a line to or from you, the situation is a little more complicated. The more general expression for the Doppler shift is λ'/λ=(1+βcosθ)/√(1-β2) where θ is the angle between his path and your line of sight. (Note that when θ=00, this reduces to the equation above.) When θ=900 he is directly in front of you and so λ'/λ=1/√(1-β2), always a red shift because 1/√(1-β2) is always greater than 1 so λ'>λ. Solving, βtransverse=0.83.
One more thing: he will be emitting other frequencies beside visible. For example, he will be emitting infrared radiation which will be doppler-shifted into the visible when he is moving toward you. I have ignored this possibility and assumed that he only emits visible light. After all, he is just a made up character anyway, right?!
![]() QUESTION:
QUESTION:
What is the force that causes you to fall over when a moving bus comes to an immediate stop? I'm having an argument with my teacher over what the answer is, it would be great if you could explain!
![]() ANSWER:
ANSWER:
When the bus is stopping, it is accelerating and so it is a
noninertial frame. That means that Newton's laws are not valid if you are
riding inside the bus. But, if we watch you from the bus stop, Newton's laws
do apply and we conclude that if you move with the bus, there must be a
force which is causing you to accelerate also. Friction provides a force
which, except under extreme circumstances, accelerates your feet along with
the bus; but, unless you are holding on to something, there is nothing to
provide a force on your upper body which therefore tends to keep going
forward without accelerating. All this says that the reason you fall forward
is not due to any force, rather it is due to lack of a force. There is,
though, another way to look at this problem. If you are in an accelerating
frame, like the bus, you can force Newton's laws to be true by adding fictitious
forces. The best known example of a fictitious force is the
centrifugal force in a rotating (and therefore
accelerating) frame. In the bus which has an acceleration a you can
invent a fictitious force Ffictitious on any
mass m in the bus, Ffictitious=-ma;
if you do that, Newton's laws become true inside the bus and the force Ffictitious
may be thought of as being the force which provides your acceleration.
Note that the acceleration is opposite the direction of the bus when it is
stopping, and so the fictitious force is forward as you know if you have
fallen over in a stopping bus. When the bus is speeding up you tend to fall
backwards. Since there are two answers here, depending on how you choose to
view the problem, so maybe you and your teacher are
both right!
![]() QUESTION:
QUESTION:
How fast must one move away from a typical light bulb so that it Doppler shifts into microwave radiation and cooks him/her?
![]() ANSWER:
ANSWER:
The expression for relativistic Doppler shift is δ≡fobserved/fsource=√[(1+β)/(1-β)]
where β is the ratio of
the relative speed of the source and observer to the speed of light. Taking
fsource≈600 THz=6x1014 Hz and
fobserved≈2.5 GHz=2.5x109 Hz, I find
δ≈4.2x10-6. Now, the
Doppler equation may be rewritten as
β=-[(1-δ2)/(1+δ2)]≈-(1-δ2)2≈-(1-2δ2)=-0.999999999966,
pretty fast! I used binomial expansion, (1+x)n≈1+nx+âŚ
if x<<1, a couple of times to approximate.
![]() QUESTION:
QUESTION:
At what speed does a pitching machine need to be set on in order for a ball to travel 39 feet and cross homeplate at 32 miles an hour?
![]() ANSWER:
ANSWER:
If there were no air friction and the ball crossed the plate
at the same elevation that it left the machine, the answer would be 32 mph.
A ball pitched that slowly would not lose much speed in the roughly one
second it takes to get to the plate. Using the estimates of air drag I used
in earlier answers, I
found that perhaps 1-2 mph will be lost, so you could set your machine at
about 33-34 mph.
![]() QUESTION:
QUESTION:
Would it be possible to build a spacecraft that would propel itself by creating magnetic fields and those magnetic fields would repel each other causing the spacecraft to move?
![]() ANSWER:
ANSWER:
Look at my little spacecraft to the left here. I have created
your repelling magnetic fields by a couple of bar magnets. They exert equal
and opposite forces on each other (Newton's third law). Therefore they exert
equal and opposite forces on the front and back of the spacecraft. Therefore
the net force on the spacecraft is zero. A general rule of thumb is that the
sum of all internal forces on a system must equal zero.
![]() QUESTION:
QUESTION:
I'm doing a science fair project that compares wattage of bulbs vs. heat output and light intensity. I want show that more efficient bulbs covert energy into light and not heat. I was going to put different kinds of 60 watts light bulbs in a Styrofoam container and measure the heat difference in 5 minutes. Can you show me a example ,using units, how to calculate the light intensity or lumens?
![]() ANSWER:
ANSWER:
So, you want to be quantitative in your project? You need to
be sure you understand the definitions of all the things you are working
with:
-
A Watt (W) a measure of power. Power is the rate of use of energy. 1 W=1 J/s (Joules per second) meaning one J of energy is consumed (work done) per second.
-
A Joule is the work done when you push with a force of 1 N (Newton) over a distance of 1 m (meter).
-
A Newton is the force you must apply to a 1 kg (kilogram) object to cause an acceleration of 1 m/s2.
-
A lumen is a unit of intensity which depends on the wavelength of the light. Since you are dealing with white light, I would recommend that you do not try to express your light intensity in lumens; it is very complicated to calculate. Rather, you should simply state the brightness of your light bulb in Watts; a 100 W light bulb, for example, you may find to have only 20 W of radiated visible light as I will explain below.
Now, I have recently answered a question about R-value of insulation; I would recommend that you read that first. The most important thing you should take from that answer is that the rate of heat flow (dQ/dt=Pheat) out of your box is equal to the temperature difference (Tin-Tout=ΔT) between inside and outside of the box, Pheat=KΔT where K is some constant (ΔT should be measured in 0C). From my earlier answer, you will see that K=1/[(R-value)∙A] but you do not really need to know that.
What you need to do is calibrate your box by measuring K. To do this, you will need a heater which radiates a negligible amount of light whose power P0 you need to know; usually this will be written on the heater itself somewhere, for example P0=200 W. If not, you will have to measure the current (in A) and voltage (in V, probably about 110 V) and multiply them together to get the power in W. Leave the heater in the box until the temperature stops rising and call the temperature difference ΔT0. Now, K=P0/ΔT0âyour box is now calibrated. Now put in a light bulb and leave it there until the temperature stops changing and you have a measurement of ΔT; now you know that the power Pheat which that light bulb puts into heat is Pheat=KΔT. Now, the amount of light brightness is Plight=P-Pheat where P is the rated power of the light bulb.
Here is a made-up example. You use a 200 W heater to calibrate and find a steady-state temperature difference of 20 0C, so K=200/20=10 W/0C. Now, you put a 60 W incandescent light bulb in and measure a steady-state temperature difference of 5 0C. Then Pheat=KΔT=(10 W/0C)x(5 0C)=50 W. Then Plight=P-Pheat=60-50=10 W. So, this bulb would be about (10/60)x100%≈17% efficient. This kind of calculation is not usually called efficiency in this context, rather source luminous efficacy. You might want to look at the discussion on Wikepedia of efficiency and efficicacy. Since you likely do not have instruments to measure visible light flux in lumens, this is probably the best approach for you. You will be able to make the point, I think, that the fraction of energy put into heat by incandescent bulbs is much higher than for compact flourescent and LED sources.
![]() QUESTION:
QUESTION:
Let's assume I have a magnet that can lift 100 tons. And I attach the magnet in a chain and attach the chain into roof for a system to magnetically lift items and then drop them to other places. Would the chain have to be able to take the 100 ton load or would the magnet take the 100 ton load because after all it is the one keeping the lifted item up?
![]() ANSWER:
ANSWER:
The magnet itself holds up the 100 ton weight. The chain
holds up the 100 ton weight plus the weight of the magnet itself. The roof
holds up the 100 ton weight plus the weight of the magnet plus the weight of
the chain.

![]() QUESTION:
QUESTION:
how is a shock wave generated by a supersonic jet?
![]() ANSWER:
ANSWER:
The animation to the left shows an animation of a source of
sound moving to the right with the speed of sound. The expanding blue
circles show the crests of waves emitted when the souce was at the center of
each circle. Notice that all of these are tangent at the source and that
therefore these waves pile up as you can see by the leading very bright
edge. That is the sonic boom.
![]() QUESTION:
QUESTION:
Recently, I was riding my bike and failed to notice a long, wide patch of black ice on the bike path ahead. My speed was "leisurely" (12-15 mph). After about 2-3 seconds on the ice, I could feel my bike slipping then falling to the right. I fell on the right side of my body, my hip and right arm taking on the brunt of the impact, but continued to glide forward (along with the bike) for another 3-4 seconds. I expected my body to be quite sore the days to follow since it felt like a very hard fall, but it was not the case. My question is, Could the icy surface have allowed my body (and the bike's) forward motion to decelerate relatively gradually, rather than come to a harsh stop, therefore lessening the force of impact and, consequently, damage to my body?
![]() ANSWER:
ANSWER:
What hurts us? Force. If you had just been standing still on
your bike and fallen over, when you hit the ground you would feel the force
of the ground stopping you in a very short time. The ground is hard and this
force will cause you to stop quickly, that is with a large acceleration, so
it will hurt because F=ma and if a is big, F is big.
However, you are not going very fast when you hit the ground, so that
reduces the acceleration during the time you are stopping. All in all, not
much pain from just toppling over. On the other hand, if you are moving and
fall over, you still experience the same force perpendicular to the ground
that you did when you were at rest and fell, but now there is a force due to
the friction between you and the ground and that force is parallel to the
ground. As in the earlier case, the time it takes you to stop determines the
force you feel and, in sliding on ice, you lengthened the time thereby
lessening the force. In other words, the fall was about equivalent to simply
toppling over from rest. (Another danger of falling not on ice is that the
force will exert a torque on your body which will tend to get you tumbling
which could lead to more injury.)
![]() QUESTION:
QUESTION:
When 2 or more musical instruments are playing the same note at the same time, presumably it often happens that the multiple sound waves from the different instruments are out of phase with each other. Therefore, more oscillations per second would reach our ears. If this is so, why then do we not perceive the resultant waveform as having a higher pitch or frequency?
![]() ANSWER:
ANSWER:
From two different instruments there will be no interference effects for many reasons. One is that the two have different timbres;
there is a whole bunch of different frequencies which play and mixture of
frequencies differs from instrument to instrumentâotherwise all instruments
playing a given note would sound the same. See an
earlier answer for more detail.
If you had two sources, each with a single frequency, then if they arrived
at a point out of phase, they would cancel, not double the frequency.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Thank you very much! I'm still a little confused, and here's why: When I was in school we had a computer class and the teacher showed us how musical tones were produced with the old Apple computer, by playing a series of repeated "clicks" with a likewise repeated pause between clicks. The longer the pause between clicks, the lower the pitch of the perceived tone. So in my mind, perhaps incorrectly, I am likening those clicks to the cycle of the sound wave for a particular musical tone. If you have 2 flutes playing the same note, and they are out of phase, you would hear more cycles per second, but you don't hear a higher pitch, the way you would if your computer was making more clicks per second, and I still don't get why. I'm sorry! Are you saying that it's because the flutes aren't perfectly matched? What if you played 2 recordings of the same flute, exactly half a cycle out of phase. Would you raise the audible pitch to twice the frequency in that case? I suspect not, given what you said before, but I don't understand why.
![]() ANSWER:
ANSWER:
The important physical principle that applies is the
superposition principle: if there are two waves passing through the same
location, the net disturbance of the two is their sum. You are right, if you
had one click generator at 1000 clicks per second and a second at 1000
clicks per second but delayed by 0.0005 seconds, you would hear 2000 clicks
per second. But, a musical instrument is not a series of clicks, rather it
is a very complex continuous wave pattern; a particular note on a flute is
shown to the left. Any wave, no matter how complex, may be represented as a
sum of sinesoidal waves of different wavelengths, so whatever I can
demonstrate for a single sine wave will be applicable to any complex wave.
Of course, it would be impossible to have two flutes do this experiment, but
suppose that you took a recording of a flute and played it through two
different speakers which had been wired to play exactly out of phase. The
figure shows a sine wave (black) and a negative sine wave (red) and their
sum (blue). This is called completely destructive interference, no sound at
all.
Finally, and this is a technicality you may wish to just ignore, your example of the delayed tick generator is not really 1800 out of phase. As I said above, any wave form, even clicks, can be represented by a sum of sine and cosine waves so 1800 out of phase means upside down, not shifted; only for a simple sine wave or cosine wave are shifted and upside down the same.
![]() QUESTION:
QUESTION:
Why do water and mirrors reflect light to form imgaes but not surfaces like wood or concrete?
![]() ANSWER:
ANSWER:
Because the surfaces of nonreflective materials are not
smooth enough.
![]() QUESTION:
QUESTION:
I have created a hot box made from 2 inches of polyisocyanurate. It measures 17 inches by 17 inches on the inside. I heated up the inside to 140 degrees farenheit and I measured the change in tempature for 30 minutes. The final tempature was 102 degrees farenheit. The outside temp was 67 Fahrenheit and the room was large enough that the system did not change the room temperature.
The rated value of the insulation is R 13.1. How do I calculate the experimental R-value? I have tried using both Q = m c delta T and Newton's second law of cooling ... and I cant seem to get a number that makes sense. Can you help?
![]() ANSWER:
ANSWER:
I have a suspicion that something is wrong either with your data or
with my understanding of the setup. I will tell you what I did. R-value
is defined as R-value≡|Tin-Tout|/[(dQ/dt)/A]
where dQ/dt is the rate of heat flowing through the
insulation, A is the area (assuming that the rate through it is the
same everywhere), and |Tin-Tout|
is the temperature difference between the inside of the box and the
outside. In the US R-value is stated in units ft2∙0F∙h/BTU,
but I prefer to work in SI units (where the notation RSI is often
used instead of R-value) so the answer will be in m2∙K/W;
in the end we can easily convert one into the other, R-value=5.68
RSI. There is an approximation you make that should be thought about;
since you make only one time measurement, 30 minutes=1800 s, you only
measure an average dQ/dt over that time interval, call it ΔQ/Δt.
Accordingly, an average temperature should be used, (T1in+T2in)/2.
I first convert your numbers to SI units, T2in=102
0F=312 K, T2in=140 0F=333
K, Tout=67 0F=293 K, 17 in=0.432 m (so A=6x0.4322=1.12
m2). The density of air is about 1.2 kg/m3 and the
volume is 0.4323=0.081 m3, so the mass of the air is
m=0.097 kg. Now, I calculate ΔQ=mC(T1in-T2in)=1460
J where C≈720 J/(kg∙K) is the specific heat. You can also calculate
the heat transfer by assuming that air is a diatomic ideal gas, ΔQ=(5/2)nR(T1in-T2in)
where n is the number of moles and R is the universal gas
constant and get about the same answer for ΔQ. Finally, using |((T1in+T2in)/2)-Tout|=29.5
K, RSI=29.5/[(1460/1800)/1.12]=40.7 m2∙K/W. This results
in R-value=231 ft2∙0F∙h/BTU, obviously wrong.
Trying to understand this discrepancy, I decided to look more carefully at the behavior of the changing temperature. Without going into the details (but you can find them here), it may be shown that T(t)=Tout+(T1in-Tout)e-βt=67+73e-0.007t where β=[5.68A/R-value]/[(5/2)nR]; I have used your value of 13.1 ft2∙0F∙h/BTU for R-value. The result is shown by the red curve in the figure. As you can see, the expected behavior is that the temperature should reach 67 0F in about 10 minutes. Using the value I deduced from your data, 231 ft2∙0F∙h/BTU, the blue curve results.
I would be happy if someone could find an error in my analysis, but I have checked and rechecked it and found nothing wrong. Regarding your experiment, I believe that it would be good to take data at much smaller time intervals so that you can see the exponential behavior of the temperature. Also, the equations here are all steady-state situations and a likely place where your measurement could have gone awry is that much of the heat lost from the air ended up heating up the insulation, not actually conducting through it into the exterior. I would suggest that you try to redo the experiment where you hold the temperature at 140 0F for a good long time so that you are sure that the steady-state conduction of the heat is occuring, then start the experiment.
![]() ADDED
COMMENT:
ADDED
COMMENT:
It just occurred to me that there is another possible source of error.
How did you heat up the air in the box? If you had some sort of electrical
heating element and just turned it off and left it inside the box, this will
be a serious source of error since it will be significantly hotter than 1400
and will continue to add heat to the air after you turn it off.

![]() QUESTION:
QUESTION:
My question pertains to the periodic table of elements. Why is tungsten represented with the letter W? I am assuming that the letter W was the first letter of the person's name who discovered the element- is this correct?
![]() ANSWER:
ANSWER:
The word tungsten comes from the Swedish, tung sten=heavy
stone. The symbol W comes from the word wolfram which comes from the mineral
wolframite which is the ore which is the principle type of tungsten ore. The
word wolframite comes from the words wolf rahm=wolf soot or wolf
cream because wolframite interfered with the smelting of tin and was said to
"devour" the tin (like a wolf)! Since both tungsten and wolfram come from
the Swedish, you might wonder why it was not given the symbol T. It turns
out that a mineral Sheelite was called tungsten in Sweden and so they chose
to call it wolfram to avoid confusion. Credit for discovery of the element
goes to two Spanish brothers, Jose and Fausto Elhuyar, who isolated it from
an acid made from wolframite in 1783.
![]() QUESTION:
QUESTION:
Why transverse waves cannot travel in air and interior of liquids even though they can travel in solids where particles are strongly packed together?
![]() ANSWER:
ANSWER:
A wave requires that there be restoring forces between atoms
of the medium. For longitudinal waves to happen, there must be such
restoring forces with atoms along the direction the wave is traveling; this
can happen with solids, liquids, or gases and essentially the waves are
pressure waves. For transverse waves, there must be restoring forces
perpendicular to the direction of the wave velocity (often called "shear
forces") and liquids and gases cannot support such shear.

![]() QUESTION:
QUESTION:
Hi! I was playing a video game called "Mass Effect 2" and in the game a
drill instructor gives a lesson about the main gun of a Mount Everest
class dreadnought that is the first dreadnought class made by largest
human government in ME universe known as Systems Alliance. The main gun
is a rail gun that accelerates one 20kg ferrous slug to 4025 km/s and it
takes 5 seconds to charge. The slug impacts with kinetic energy of
162006250000000 joules which is 38,7 kt of tnt. The main gun is 800
meters long and built into the superstructure of 888 meter long
dreadnought that has mass of at least one milloin tons. Would there be
any problems of having our future warships operating in space equipped
with this kind of weapon and does this design sound feasible? And in the
game's lore it is stated that an impact from this weapon levels entire
cityblocks. Would this projectile moving at 4025km\s be able to level a
cityblock in a metropolitan area because the Turians (a species in Mass
Effect) fired these slugs to human cities on the colony of Shanxi
leveling a cityblock clean of even the sturdiest skyscrapers
![]() ANSWER:
ANSWER:
Gamers and sci-fiers have asked questions like this before.
That is good, to think about the physics and how it might affect the
practicability of these kinds of weapons in the real world. You might also
be interested in a couple of earlier answers regarding the game
Halo and the movie Eraser.
Your numbers are right, the kinetic energy of a 20 kg mass traveling at a speed
around 4x106 m/s is about 1.6x1014 J.
(The speed is just a little above 1% the speed of light, so classical
calculations should be ok.) As I noted in the Eraser answer, the energy of
the atomic bomb dropped on Nagasaki was about 1014 J, so this
should answer your question about whether or not there is adequate energy to
demolish a city blockâeasily!
-
It takes 5 s to charge, so let's see what the required power input would be: P=E/t=1.6x1014/5≈3x1013 W=30 TW. The average power consumption of the entire earth is 15 TW. Where are you going to get this kind of power in the middle of empty space? Maybe you can just carry hundreds of atomic bombs with you?
-
And, let's talk about the launch. If the acceleration over the 800 m is uniform, it would take about 4x10-4 s resulting in an acceleration of 1010 m/s2. That means that the force necessary to give this acceleration to a 20 kg mass is 2x1011 N≈45 billion pounds. Do you think an iron slug could withstand such a force?
Given the time of acceleration, what is the power delivered to the slug? P=E/t=1.6x1014/4x10-4 s≈4x1017 W.
Unlike the previous two answers, recoil for this gun should not be a serious problem. If the mass of the ship is a million metric tons, 109 kg, the recoil velocity should only be about 20x4x106/109=8 cm/s.
I think you would agree that this device would be totally unworkable in the real world.
![]() ADDED
COMMENT:
ADDED
COMMENT:
In my comment above stating that recoil would not be a
problem, I have to take that back. Even though 8 cm/s is not very fast, that
speed is acquired in a very short time, 4x10-4 s, so the
acceleration of the ship is very large, a=0.08/4x10-4=200
m/s2 which is approximately 20g, quite a jolt!
![]() QUESTION:
QUESTION:
When two objects with mass are placed together, do they actually ever touch or is there a space between the objects on a microscopic level?
![]() ANSWER:
ANSWER:
It gets tricky to define what you mean by "touch". When you
get to a microscopic level, there is no way to actually define what the
surface is, it is fuzzy rather than sharp. The surface is comprised of the
outer electrons of the atoms and these are charged; hence they repel each
other and since the electric repulsion gets greater as the electrons get
closer, you might think of the upper object "floating" above the lower. It
is actually something called the "electron
degeneracy pressure", the Pauli exclusion principle which prevents
electrons from occupying the same quantum state, which keep the electrons
apart.
![]() QUESTION:
QUESTION:
How many particles do the particle accelerators at most accelerate when they are running experiments? One, ten, hundreds or thousands?
![]() ANSWER:
ANSWER:
When I was doing experiments some years ago, typical beam
currents were on the order of a few nanoamperes. Usually, these were protons
which each have a charge of 1.6x10-19 C. So, suppose the beam
current is 16 nA=16x10-9 C/s; then the number current is [16x10-9
C/s]/[1.6x10-19 C/proton]=1011 protons/second, about
100 billion. At the LHC in Europe, the intensity is much larger, on the
order of 4x1018 protons/s which would correspond to an average
current of about 0.6 A. The high number intensities are vital because the
events physicists are looking for are extremely improbable. The LHC is a
pulsed machine, its beam is a series of very short pulses. So, the
instantaneous current during a pulse is much larger than the average
current.
![]() QUESTION:
QUESTION:
Given a airplane at speed 600 knots, whose track at its closest point passes by one at 15 kilometers away (elevation angle not important,) what are the formulas that would describe the shape of the decibel readings over time? (which are something like 25 25 40 40 40 38 36 34 30
25 25, with 25 dbA being the background.)
![]() ANSWER:
ANSWER:
I will call the distance of closest approach (15 km) d,
the speed (600 knot=0.309 km/s) v, the distance between the plane and
observer r, and choose t=0 to be the time of closest approach.
Assuming that the sound from the plane is isotropic (a relatively poor
assumption), the intensity of the sound is proportional to 1/r2=1/(d2+v2t2),
so I(t)=C/(d2+v2t2);
note that this is not dB but something like watts/m2. I is
an absolute intensity (power/unit area), dB levels measure relative levels
on a logarithmic scale. I will call
the maximum intensity I0=C/d2 and
the dB level relative to the maximum is given by LdB=10∙log10(I/I0)=10∙log10(d2/(d2+v2t2)).
The graph to the right shows the plot for your numbers.
![]() QUESTION:
QUESTION:
How can time exist in space if time is a man made tool we created to monitor the revolution of our earth around our own star? Once you left this solar system time would have no concept. you wouldn't be able to monitor it would you?
How can Einsteins theory of relativity be real if time doesn't exist in space. He says that (earth time) passes slower for an object travelling at the speed of light through space, but how can you monitor that on a clock (still on earth time) in space where time doesn't exist?
Our sun is not the centre of our galaxy, it's not even the centre of our universe so the way we control time would not make a difference at any other point in space, An object travelling at the speed of light would still be in the same moment as us but there watch wouldn't be correct as the time it showed would be useless to there point in space.
![]() ANSWER:
ANSWER:
You are totally off base here. Measurement of time has
nothing whatever to do with the motion of the earth. You may think of it
that way and ancient man certainly thought of it that way, but today the
second is defined in terms of an atomic clock which would tick at the same
rate anywhere in the universe. The official definition of the second is: "The second is the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom."
If I have an atomic clock and you have an identical atomic clock which you
take on a high-speed trip away from and back to me, when you return we will
find that your clock ticked fewer times than mine. (See the
twin paradox.)
![]() QUESTION:
QUESTION:
I have a question, when you drop a solid sphere of aluminum into a bucket of water sitting on the ground. The buoyant force equals the weight of the water displaced, which is less than the weight of the sphere, so it sinks to the bottom. If you take the bucket with you on an elevator that accelerates upward, the apparent weight of the water increases and the buoyant force on the sphere increases, too. Could the acceleration of the elevator be great enough to make the sphere pop up out of the bucket of water?
![]() ANSWER:
ANSWER:
The easiest way to understand this problem is to use the
equivalence principle which says, briefly, that there is no way you can
distinguish between being in a uniformly accelerated frame and being in a
uniform gravitational field. Your case is a little more complicated since
you are in an accelerated frame which is in a gravitational field. But the
equivalence principle says that if you elevator has an acceleration a,
all experiments you might do would have the same results as if you were not
accelerating but in a field whose acceleration was g+a. But, if you
were in a gravitational field with acceleration g+a, the weight of
the displaced water would be Mw(g+a) and the weight
of the aluminum would be Ma(g+a) where Ma
and Mw are the masses of the aluminum and displaced water,
respectively. In other words, the weight and buoyant force increase
proportionately so that the buoyant force would always be smaller than the
weight.
![]() QUESTION:
QUESTION:
If I wear earmuffs that lower the noise by 20 decibels and then put on earplugs that lower the noise by another 20 decibels will this all combine to 40db noise reduction?
![]() ANSWER:
ANSWER:
The relative decibel level L is determined by the ratio of
the power levels of two different levels: L=10∙log10(P1/P0).
This can be written as P1=10L/10P0.
In your case, I will say that P1>P2>P3
and the relative dB levels are 20 dB for P1
and P2 and 20 dB for
P2 and P3. So, P1=1020/2P2=100P2
and P2=1020/2P3=100P3.
If you combine these you find that P1=10,000P3=1040/10P3.
So, the answer to your question is yes, 40 dB is the relative decibel level
for P3 and P1.
![]() QUESTION:
QUESTION:
Need to scale a physical object up in size, either double or quadruple. It's a circular acrylic plate, with multiple weights attached around it's edge, to lower the resonant frequency to a specific frequency, 32hz.
The plate is 16â in diameter, the weights around it's edge add up to 1.05 kg. It needs to be scaled to 32â or 64â. It will scale in diameter but not thickness, which will remain 1/8â for all diameters.
If the size is doubled to 32â, along with doubling the weights around the edge to 2.1 kg, will the resonant frequency be lowered to the same frequency as the 16â plate with 1.05 kg weights?
If not, how does this scale? How far off approximately will the resonant frequency be from 32hz?
Same question for scaling to 64â with 4.2 kg weights around the edge.
![]() ANSWER:
ANSWER:
Doing a precise calculation like this is impossible without
more details about where the weights are placed. Even then it is extremely
complicated and beyond the scope of my site to do; a circular disc
calculation always involves Bessel functions, neither simple nor intuitive.
However, I know that your scaling will not work the way you expect; I will
show you how I reached that conclusion. To make sure you understand
oscillating systems, let's start by considering a coil spring attached to a
mass m; the stiffness of the spring is characterized by a quantity
called the spring constant k; if it takes a force of F to
stretch the spring a distance D, then k=F/D. The
frequency of oscillation of this mass on this spring turns out to be f=(1/2π)√(k/m).
So, you see, the mass on a spring behaves the way you wantâif you double
both the spring constant and the mass, the frequency is unchanged. Now, you
can think of your disc like a spring: if you hang weights around the
circumference it will warp down from the center. The more weight you hang,
the more it will warp, just like a coil spring stretches in proportion to
the force. As an approximation, since I cannot do a disc, I figured a leaf
spring would be the next best thing. So, I found a
calculator
on the web which calculates the stiffness (spring constant) of a leaf
spring. I found that if you double the length of any given leaf spring, you
decrease the spring constant by a factor of 8. So, if you had a leaf spring,
doubled its length, and doubled its mass, the frequency f' would be
f'=f√[(k'/m')/(k/m)]=f√[((k/8)/(2m))/(k/m))]=32/4=8
Hz. For a leaf spring you have to decrease the mass 8 times to keep
the frequency constant. Your disc is not a leaf spring, but it is more
similar to that than to a coil spring. Now, if you think about it, it should
be intuitive that you have to decrease the mass: a bigger disc will be
easier to bend (smaller k) and putting more load (bigger m) on
it will make the frequency (which depends on the ratio k/m)
far from the original frequency. I haven't told you how scaling works for
your specific system, but I hope I have pointed you in the right direction.
If the weights can be fairly easily varied, trial and error (known as
"tuning" here) might be your best bet.

![]() QUESTION:
QUESTION:
my teacher had me specifically look up the answer to this question but really not understand any other answer what these other sites are giving me. any help? " in addition to the molecular to-and-fro vibration assoicated with temperature, some molecules can absorb large amounts of energy in the form of internal vibrations and rotations in the atoms making up the molecules. would you expect materials composed of such molecules to have a high or a low specific heat?"
![]() ANSWER:
ANSWER:
I want to keep it fairly simple, so let us consider only monatomic (single
atoms like He or Ar) and diatonic molecules (two atoms, like O2
or H2). I will also talk only about CV,
specific heat at constant volume. The specific heat at constant pressure,
CP, is simply related to it by CP=CV+R
where R is the universal gas constant. Also, this discussion is only
applicable to ideal gases and many real gases are well approximated as ideal
gases, at least for understanding specific heat qualitatively. Specific heat
is the amount of temperature increase resulting from a certain amount of
energy added to the gas. Temperature is a measure of the energy content of
the gas, so adding energy to a monatomic gas increases the average kinetic
energy per molecule Đ
mv2=Đ
m(vx2+vy2+vz2).
It is said that a point mass has three degrees of freedom (called
translational), x, y, and z, three ways to accept the
energy as it turns out. There is a famous theorem called equipartition of
energy which says that each degree of freedom accepts 1/f of the
energy added where f is the number of degrees of freedom for the
molecule. Then, it may be shown that CV=3(Đ
R); in
other words each degree of freedom contributes Đ
R to CV.
This can be generalized to higher degrees of freedom so that CV=f(Đ
R).
Now let us think about a diatomic molecule, visualize a dumbbell. A rotating
dumbbell has energy, so a diatomic molecule has another way to accept
energy. It can also vibrate, so there is another way it can accept energy.
These are additional degrees of freedom, so the specific heat must increase.
However, there is an important proviso due to quantum mechanicsâto excite a
rotational or vibrational state in a molecule requires some minimum energy
and so, at very low temperatures, only translational degrees of freedom will
be available. But as the temperature increases, first rotational and then at
higher temperatures vibrational degrees of freedom can start taking the
added energy. Hence the specific heat is dependent of temperature as shown
to the right for a diatomic gas (note that ĈV=CV/R).
Let's see if we can understand this (refer to the figure at the left above).
The dumbbell can not rotate about its own axis, only about an axis
perpendicular to the line connecting the two atoms, but there are two such
axes as shown by the red diagram; so, there are two degrees of freedom
because of rotation. As shown by the graph of the specific heat, it starts
out at 3R/2 but when the temperature gets high enough the two
rotational degrees of freedom begin to contribute giving 5R/2 as
expected. As the temperature gets higher yet we see two more degrees of
freedom apparently contributing because the specific heat increases to 7R/2;
this is due to the molecule now being able to vibrate. But, this is a puzzle
because there is only one degree of vibrational freedom, the molecule can
only vibrate along its own axis. The reason is kind of technical: the
vibrational energy has both potential and kinetic parts and each behaves
like a degree of freedom. If you think this is complicated, imagine how it
goes with more complex molecules!

![]() QUESTION:
QUESTION:
the question is "why does dust fly off when a hanging carpet is beaten with a stick?" Now some people answer it is due to inertia some say it is due to inertia and newton's third law. I think it is due to inertia and Newton's third law because when we hit the carpet the dust particles also jump in the in the direction in which we hit it. If it is inertia only then it must jump in opposite direction. So please clear the confusion.
![]() ANSWER:
ANSWER:
The reason that the dust is on the rug in the first place is
that there is an adhesive force between the dust and the fibers of the
fabric. When you strike the rug with the stick, many of the fibers are
caused to have an acceleration. If a fiber accelerates, the dust attached to
it must accelerate and that acceleration can only be provided by the force
adhering it to the fiber; but that force is not big enough and so the dust
separates and is then subject to air currents which carry it away. In that
sense, I guess that inertia would be the explanation, but I fail to see why
this means it "must jump in the opposite direction". Further, I do not see
what Newton's third law has to do with anything here. The only force on the
dust is the force due to the fiber and the dust exerts an equal and opposite
force on the fiber; but the fiber, being so relatively massive, is almost
totally unaffected by the force from the dust.
![]() QUESTION:
QUESTION:
Suppose that the Death Star was stationary and aiming its laser at a relatively small moving space craft, like a Space Shuttle, and there was enough distance between them so the Death Star had to lead the shot. Would another space craft flying by at close to the speed of light see the laser miss while the people in the Death Star would see a hit, since the speed of light is constant, and the shot will travel faster according to the observers in the craft flying by, and will reach the intended target location before that Space Shuttle gets there?
![]() ANSWER:
ANSWER:
You make a contradictory statement: "since
the speed of light is constant, and the shot will travel faster according to
the observers in the craft flying by". If the speed is constant, how can it
travel faster? In fact, all observers will agree that the shuttle will be
hit. Two observers cannot disagree on an event which happens in one frame;
they can only disagree on things like "where" and "when" the event happened.
![]() QUESTION:
QUESTION:
I just watched a documentary about the history of nuclear weapons and it said that 100 megatons is the maximum ''practical'' yield for a nuke because if it gets bigger than that, the fireball will be larger than thickness of the majority of the atmosphere and therefore most of the effect of the nuke will escape to space making bombs larger than 100 megatons redundant as an idea. Can you confirm this?
![]() ANSWER:
ANSWER:
No, I cannot confirm this because it does not make sense to
me. The fireball of the largest bomb ever detonated, 50 Mt, had a radius of
about 2.3 km. I estimate that a bomb with twice that energy would have a
radius about 3√2=1.26 times bigger, 2.9 km. Airplanes fly at an
altitude of about 30,000 ft=9.1 km and there is certainly enough atmosphere
there for an airplane to fly. And, even if most of the atmosphere was gone
at 3 km, why would that imply that "most
of the effectâŚwill escape to space"? The blast also does a lot of damage
beyond the fireball at ground level which would increase with the yield of
the bomb, and that is where you want to do damage. It is my impression that
the reasons for not developing larger bombs are tactical: the heavier the
bomb, the more difficult it is to deliver it.
![]() QUESTION:
QUESTION:
We have a kitchen table that is extremely heavy and we know of no way to
weigh it. If I put one leg on a scale, it reads 143.2 lbs. I'm thinking
we can't simply multiply that number by four because it seems it may
register some of the weight from at least part of the other three
quarters.
![]() ANSWER:
ANSWER:
Get a 2x4 which will span the two legs at one end and weigh
it; call that weight w. Put the 2x4 under the legs at one end and the
scale under that; the scale will read W1. Move the 2x4 and
scale to the legs at the other end; the scale will read W2.
The weight of your table is W=W1+W2-2w.
If your table is symmetrical, you will find W1 to be about
the same as W2.
![]() QUESTION:
QUESTION:
I work with autoclaves, my question is what would happen if a person got trapped in an pressure vessel and the autoclave was pressured to 3 pounds (this is the normal pressure value after the door is locked)?
![]() ANSWER:
ANSWER:
For the benefit of readers who do not know what an autoclave
is, it is a sterilizing chamber using high-temperature steam (~1200C)
at high pressures. Pressure is measured in pounds per square inch (PSI) and
atmospheric pressure is about 14.7 PSI. So, I assume your 3 pounds is 3 PSI
above atmospheric, called the gauge pressure. So the added pressure would be
about 20% above normal. When you go under water, about 30 ft, you experience
about 100% above normal, double the normal atmospheric pressure, and you
know you can do that with no ill effect. So, essentially what would happen
in your scenario is that you might feel a little pressure in your eardrums
but not much else.
![]() QUESTION:
QUESTION:
If electrical currents are charged particles, then electricity must be composed of matter (obvious.....I think) if that were the case, then our thoughts, dreams, etc, are simply a result of charged neurons interacting within our synapses through electrical currents.
So, I suppose my question is, if our are thoughts are confined to ourselves or do they hold a place within the whole concept of time and space.
![]() ANSWER:
ANSWER:
Certainly, brain activity involves electric currents.
Electric currents create electromagnetic fields which can be detected
outside of you, so brain activity is not "confined to ourselves."
Neuroscience researchers routinely sense these fields with detectors outside
the subjects. If you are suggesting a possible explanation for ESP, I sure
would not bank on it. As far as we know, our brains are good at creating
very weak fields but not at detecting very weak fields. Also, there is
presently no known way of actually interpreting the thoughts which caused
those fields.

![]() QUESTION:
QUESTION:
From a physicist's point of view do you ever see us using antimatter as an energy source and are there any ways to even theoretically to create antimatter in adequate quantities? Is antimatter power really just a theoretical thing that won't get any practical use in your opinion?
![]() ANSWER:
ANSWER:
So, you have to ask yourself where you are going to get this
antimatter. You have to make it because there is never any appreciabale
amount just sitting around. You can be sure that it would cost you more
energy to create it than you would get from annihilating it.
![]() QUESTION:
QUESTION:
why do we say that materials in our world are mostly empty space
![]() ANSWER:
ANSWER:
The simplest way to think about atoms is to have little
electrons in orbits around the nucleus. The nucleus is extremely small
compared to the size of the atoms and electrons have a tiny mass compared to
the nucleus. Therefore, like you would say that the solar system is composed
mostly of empty space, you would say that the atom is composed of mostly
empty space. The reality is, though, that the elctrons are really smeared
out over the whole volume of the atom, they are like a cloud rather than
like little planets, so the atoms are not really empty space.
![]() QUESTION:
QUESTION:
There is a demonstration where a person is put in a trashbag and the air vacuumed out. The person can't move their arms. Is this because of the pressure difference between the inside and outside of the bag, or because of the large surface area of the bag allows them to feel more pressure?
![]() ANSWER:
ANSWER:
There are two things going on here. First, it is like being
tied up, the bag restrains you. If you were shrink-wrapped you would also
not be able to move. But, the trash bag is bigger than you so it would not
be "tied up" by it because it would be like a loop rope which was 5 feet in
diameter. However, when the air in the bag is removed, the atmospheric
pressure on the outside holds the bag tightly to you and it becomes just
like shrink-wrapping. Here is a
you-tube video (you
can find lots of others).
![]() QUESTION:
QUESTION:
My physics teacher has taught us that people who are going to travel in an aeroplane should empty ink from their pens as if ink is filled at high pressure at the ground level, it will leak out when the plane flies in the low pressure. But the plane is air-tight. How can low pressure act from outside the walls of the plane? Also, does the density of the ink changes when we carry to low-pressure region?
![]() ANSWER:
ANSWER:
The inside of an airliner is pressurized, but not to
sea-level atmospheric pressure. The pressure is typically about the same as
the pressure at an altitude of 2100 m, approximately 80% of sea-level
pressure. Ink is mostly water and water is essentially incompressible, so
the density does not change.
![]() QUESTION:
QUESTION:
I was curious to know how the kinetic energy a water balloon endures when free falling affects the radius of it's splatter.
![]() ANSWER:
ANSWER:
So, you are wondering what the radius of the splatter depends
on and how? Of course, to do an accurate calculation would be neigh on
impossible. I will just do a very rough approximation and then you
can do an experiment and see if it makes any sense. At the instant that the
water baloon hits the ground its kinetic energy is K=Đ
MV2=Mgh
where M is the mass of the water balloon, V is the speed it is
going, h is the height from which it was dropped, and g is the
acceleration due to gravity. Suppose that most of the energy of the water
ends up as kinetic energy of the droplets in the splash and that the splash
is made up of N drops all the same size, mass m and speed v
each. Then the kinetic energy of the splash is Đ
Nmv2=Đ
Mv2=Mgh.
In other words, the speed of each drop is the same speed as the balloon had.
Therefore the speed of each drop of the splash is v=√(2gh).
Now, the radius of the splash will surely be proportional to the speed of
the drops, R~√h (read "R is proportional to the square
root of h"). So my prediction is, for example, that if you drop it
from 8 m the splash will be about twice the size as if you drop it from 2 m.
This, as I said, is very rough. If you try to check it, let me know. (In
answer to your question, the kinetic energy does not "endure" since
eventually everything comes to rest. When I assume that the kinetic energy
is approximately conserved in the splash, I am talking about immediately
after the balloon hits.)
![]() QUESTION:
QUESTION:
if i put a half of Hollow tube insid the water(and the other half is in the
air) and drop to it a coin - it will sink.
now if i put from the top of the tube a coin that fit the Diameter of the
tube and water cant pass this coin what will happen?
![]() ANSWER:
ANSWER:
When the coin first touches the water, there will be its own
weight Mg down acting down on it, the atmospheric pressure force PAA
acting down on it (A is its area), and the atmospheric pressure force
PAA of the surface of the water acting up on it.
Hence the net force will be Mg down and it begins to sink. However,
after it has sunk to a depth D the pressure up from the water has
increased by an amount ρgD where ρ is the density of the
water. So now, Ma=-Mg-PAA+(PAA+ρgDA),
or a=-g+ρgDA/M. If the water caused no drag on the coin as it
fell (obviously not correct), the coin would oscillate about the equilibrium
depth De=M/(ρA) with simple harmonic
motion. In the real world, there would be some drag forces and the coin
would eventually come to rest at De.
![]() QUESTION:
QUESTION:
i'm trying to understand black body radiation, i've heard that "every object at a finite temperature radiates light" and my question is, why is it specified 'finite temperature'? isn't that kind of redundant? is there any object that has infinite temperature?
![]() ANSWER:
ANSWER:
Often "finite" is incorrectly used to mean "nonzero"; I would
say that is the case here. Temperature is a measure of average energy per
particle, so, to a first approximation there is no upper limit to
temperature. However, there is not an inifinite amount of energy in the
entire universe, so the temperature does have an upper limit depending on
how much energy the universe contains.
![]() QUESTION::
QUESTION::
You have devoted your professional life to Physics and have known or worked with some very bright people. I wondered what you think sets some (Telsa, Newton, Einstein, et al) apart?
Just being smart is not enough as there are many smart folks out there. I've knew a few @ Florida that scored 1600 of 1600 on SAT & a few @ P&G over the years.
Is it how they think about things, imagination as Einstein said, or what? Wondered what you thought.
![]() ANSWER:
ANSWER:
Have you read the book
Outliers by Malcolm Gladwell? It presents examples of what I consider to be an important component of successâserendipity of circumstances. Here is how this may have helped Einstein and Newton:
-
Newton was at Cambridge when it was closed down because of the Great Plague in 1665. He went to the family home and had two years for private study during which he laid the foundations of his theories of gravity and optics and his invention of the calculus.
-
Einstein was not able to get an academic position and his position at the Swiss Patent Office was so trivial to him that he had plenty of time to develop special relativity, photoelectric theory, and get a good start on general relativity (see his recent biography by Walter Isaacson).
Getting a 1600 on the SAT is no indicator at all, in my opinion. Both Einstein and Newton were famously very undistinguished students. Being in the right place at the right time and having an obsessive curiosity and posessing the willingness and imagination to think in new directions are much more important in my opinion.
![]() QUESTION:
QUESTION:
I've read about space habitat concepts for a while and I've ran into an interesting concept. The concept I've ran into is the McKendree Cylinder which is basically an O'Neill Cylinder made of carbon nanotubes. The O'Neill cylinder made of steel would be 32km long and 6km in diamter. The McKendree Cylinder would be 4600 km long and 460km in diameter. And the maximum length for MvKendree Cylinder is 10000km and diameter of 1000km. So McKendree one could be built a lot bigger than O'Neill one because the carbon nanotubes have greater endurance. But a habitat of thousands of km's seems to be really big when compared to what we can build from other materials. And as I recall we don't have any ways to produce Carbon Nanotubes in large quantities. Is it theoretically possible to build a habitat 10000km long and 1000 wide put of carbon nanotubes. And is the McKendree cylinder more of a theoretical design than a practical design that actually could be built?
![]() ANSWER:
ANSWER:
I presume that the issue is more a strength issue than
anything else. To illustrate how the strength of the material and its mass
determine the size the habitat can be, consider a rotating string of beads,
each of mass m. The rotation rate must be such that a=v2/R=g
where v is the tangential speed of each bead. Therefore each bead
must experience a force F=mg. This force can only come from the two
strings attaching each bead to its nearest neighbors and, from my drawing to
the left, F=mg=2Tsinθ. But, we will imagine many, many
beads on this string and we will call the distance between them d; so
we can make the small angle approximation that sinθ≈θ=d/R.
Solving for T, T=mgR/(2d). Now imagine that the beads
are atoms; d will be about the same for steel or carbon, g is
just a constant, msteel≈5mcarbon,
and the
Young's modulus of carbon nanotubes is about 5 times bigger than steel,
Tsteel≈Tcarbon/5.
So, Rcarbon/Rsteel≈(Tcarbon/Tsteel)/(mcarbon/msteel)≈25.
Your numbers are Rcarbon/Rsteel≈460/6=77;
I would have to say that my calculation is pretty good given that I have
made very rough estimates and I am not an engineer! I do not know what
considerations would limit the length of the habitat. (Of course, neither of
these models is presently practical to actually build, so call them
theoretical if you like. However, there is certainly no problem building
them if resources and manufacturing capabilities were available.)
![]() QUESTION:
QUESTION:
I want to run a 7.5kw generator for eight hours. I do know it takes 15hp to run a 7.5kw generator.
But I want to use weight to do it. Like a grand father clock. How much weight would I need to use if the weight could drop 6ft. ? I would like the equation or equations so I could choose to use more distance or use more weight to make this work for my application.
![]() ANSWER:
ANSWER:
So, what is 15 hp in SI units? 15 hp=11.2 kW; this makes
sense since some of the power is lost to things like friction. Your falling
weight must generate 1.12x104 J/s. If a mass m in kg falls
with some constant speed v, the power generated will be P=mgv
where g=9.8 m/s2 is the acceleration due to gravity. Now,
you stipulate that the time must be 8 hr=2.88x104 s, so if it
falls h meters in 8 hr, the speed would be v=h/2.88x104=3.47x10-5h.
So, P=mh∙9.8∙3.47x10-5=1.12x104=mh∙3.4x10-4;
so, your sought equation is mh=3.29x107 kg∙m. So, for h=2
m (approximately 6 ft), m=1.65x107 kg≈16,000
tons. You might want to rethink your plan! If you want to include the time
as a variable (in other words, wind your "grandfather's clock" more
frequently), the equation would be mh/t=1,140 kg∙m/s. (You
will need some kind of governor to regulate the speed and some gearing
system to ensure that the translational speed of the mass creates the right
rpm for the generator design.) I am afraid that a falling weight is not a
very good choice of power source for this application.
![]() QUESTION:
QUESTION:
Assume a small box, filled with small molecules, e.g.
hydrogen. The box is placed in a vastly larger box filled with bigger
molecules, e.g nitrogen. Pressure and temperature are equal at start. I
punch a tiny hole in the small box, so tiny only hydrogen molecules can
pass it. In the small box the molecules are whizzing around and some
molecules will leave the box through that small hole into the vast
space, so the chances of returning into the small box are near to zero.
Will there be a near vacuŃm in the small box after some time? If not,
why?
![]() ANSWER:
ANSWER:
This is, I believe, the same as the small box being permeable
to H2 but not N2; all that is different is the time it
would take to reach equilibrium. Equilibrium would be when the rate of H2
leaking out would equal the rate leaking back in. I believe the temperatures
in and out would remain the same but the pressure outside would get greater
as H2 leaked into the larger volume while the pressure in the
smaller volume would get smaller. It seems to me that equilibrium would be
reached when the number of hydrogen molecules per unit volume was the same
inside as outside. That would correspond approximately ("âŚvastly largerâŚ")
to a pressure reduction of a factor of Vsmall box/Vlarge
box for the small box.
![]() QUESTION:
QUESTION:
The other day I was having people over for dinner .
Among them was a physicist and a chemist .
The physicist talked about a puzzle he learned in school.
It goes like this .
He said : How high can one suck up water in a vertical pipe.
The pipe can be as long as you want and the diameter does not play a role .
We did not know : he then answered : you can only suck it up ( not pump it up ) 10 meters .
He talked about creating a vacuum and the difference in pressure at top op the pipe and below .
He also used a formula something like this roo ( the greek letter r ) times g times h .
roo being the density , g 9,81 m/sec . and h being the height.
At 10 meters he came out at Zero I believe.
What is your opinion on this matter .
Is it like that and can you explain this a little better than our company .
![]() ANSWER:
ANSWER:
Here is the situation: A long tube of cross section A
is stuck into a reservoir of water. The pressure at the top of the tube is
Ptop and you can adjust this pressure. The pressure at the
bottom of the tube is Pbottom and it is equal to
atmospheric pressure which is approximately 105 N/m2.
The water rises in the tube to some height h. The density of the
water is ρ=103 kg/m3, the acceleration due to gravity
is approximately g≈10 m/s2, and the volume of the water in
the tube is V=Ah, so the weight of the water is W=ρgV≈104Ah.
The force due to pressure is the pressure times the area, so there is a
force up on the bottom of Fbottom=105A
and a force down on the top of Ftop=PtopA;
there is also a force down on the column of water of its own weight W.
Since the column is in equilibrium, Fbottom-W-Ftop=0=105A-104Ah-PtopA,
so 105-104h-Ptop=0. If the
top is open to the atmosphere, Ptop=105 and so
h=0; the water will not rise in the tube at all. The best a pump
which is "sucking" can do is to make the pressure at the top zero, so, in
that case, h=105/104=10 m.
I think you should think of the column as being pushed up by the atmospheric pressure, not "sucked" up by the vacuum.

![]() QUESTION:
QUESTION:
the book i am reading says, "while walking on ice, one should take
small steps to avoid slipping because small steps ensure smaller
friction". Is the statement true? I think that yes, we should walk with
small steps but because they ensure larger friction because of larger
normal reaction. Is the book or i am right?
![]() ANSWER:
ANSWER:
The coefficient of static friction is larger than the
coefficient of kinetic friction. When you walk, static friction provides the
forward force to accelerate you forward. However, if you try to accelerate
forward too quickly on ice, the required friction will become too large for
static friction to be the situation and you will slip. Therefore, you want
to walk such that each step requires less friction than usual so that you do
not slip on the icier surface where the coefficient of static friction is
smaller than usual. Your book is right.
![]() QUESTION::
QUESTION::
I have searched for an answer to this question in vain.
A dropped large ball, with a small ball on top, will bounce and transfer the upwards momentum into the small ball, launching the small ball very high into the air. (As far as I understand this, I saw a demo).
Ignoring air resistance for now, how heavy would the large ball have to be, to launch a one kilogram weight into orbit, and what would the height of the drop have to be?
As an example, a 100 tonne ball dropped from 10 metres, with a 1kg ball on top, does a bounce, what is the velocity result for that?
How does the elasticity of the ball affect it? (eg, a large metal ball or weight might just impact the ground).
![]() ANSWER:
ANSWER:
This problem is fully explained and worked out at
this link. The final result, if the mass of the big ball is much bigger
than the mass of the little ball, is that the speed the little ball rebounds
is given by v≈3√(2gh) where h is the height from which it was
dropped. This means that the masses really do not matter. The height to
which the smaller ball bounces is 9 times the height from which it was
dropped. It is assumed that all collisions are perfectly elastic. The speed
required for a near earth orbit is about 8x103 m/s, so h=v2/(18g)=3.6x106
m! To put this in perspective, the radius of the earth is about 6.4x106
m, so h is about half this. This is a really rough calculation because g
will be considerably smaller (by a factor of about 0.4) at this altitude.
Even if you did make this work, the ball goes straight up and you need it to
go horizontally to go into orbit. I think it is not a very practical idea!
![]() QUESTION:
QUESTION:
Lightening rods used to protect the buildings, are made to be pointed . Is there any scientific reason behind that ?..... what is that if it is so?...........why these protecting rods are not made round or of some other shape ?
![]() ANSWER:
ANSWER:
Surprisingly (to me), this is a question not fully
understood. What is known for sure is that the primary purpose of the
lightning rod is to provide the electric current of a lightning strike with
a low-resistance path to the ground; that is its main function. The
reasoning for having a sharp point is, presumably, to help prevent a
lightning strike. A thundercloud carries a large negative charge; the
resulting strong electric field induces positive charge on the ground and
objects on the ground. But, when the lightning rod becomes charged, the
density of charge near the point becomes large and so there is a very strong
electric field around the point. This field is so strong that it can
actually ionize air molecules nearby and the resulting electrons go to the
point and ultimately to the earth and the positive ions go up to the cloud;
this is called
corona discharge. So the cloud becomes less negative and the ground and
all on it becomes less positive, resulting is a weaker field and lower
chance of lightning. Well, that is the reasoning but, as I stated at the
start, actual data supporting this are sparse or nonexistent. Certainly
corona discharge happens but whether it makes a significant difference in as
huge a system as a thundercloud is not clear.
![]() QUESTION:
QUESTION:
What role does the force of friction play in the movement of a cycle....?? I have learnt that the friction acts in the forward direction on the rear wheel and backward direction on the front wheel.How can it be...?? I think I am missing a broader link to why a wheel actually rotates.
![]() ANSWER:
ANSWER:
In this discussion I will ignore all friction except that
which occurs due to the contact of the wheels with the road. The two kinds
of friction we normally learn about in elementary physics courses are static
and kinetic friction. Kinetic friction is the frictional force between two
surfaces which are sliding on each other; it is kinetic friction which stops
a box sliding across the floor. Static friction is the force between two
surfaces which are not sliding on each other; it is static friction which
keeps your bike from skidding when turning a corner. A third contact
friction force is called rolling friction; this is not terribly important
for a bike but is the force which will eventually stop you if you coast on
level ground and you are most aware of it if your tires are
under-inflatedâharder to pedal. Rolling friction on both wheels will always
point backwards. First think about a bike which is not skidding. If you go
in a straight path on level ground without pedaling, only rolling friction
stops you and neither kinetic nor static friction are in play. Now suppose
you start pedaling to accelerate forward. Think about what your back wheel
"wants to do"; if the road were icy, the wheel would spin and the force
which keeps it from spinning on a dry road is static friction. The road will
exert a forward force on the wheel to keep it from spinning. A force is
required to accelerate anything and this static friction force is what
accelerates your bike forward. The friction on the front wheel is just the
rolling friction backwards. Finally, suppose you brake: if both brakes are
applied gently enough that you do not skid, static friction on both front
and rear wheels will point backward; if both wheels skid during braking,
kinetic friction on both front and rear wheels will point backward. You
probably know that if you apply the brakes so that they are not quite
skidding, you will stop in a shorter distance than if you skid. When you
round a curve, both wheels have a static friction force which points
perpendicular to your direction and toward the curve's center because you
are accelerating when you move in a circle even if you are going with
constant speed. More detail on
rolling friction and on
bicycle turning can be found
in earlier answers.
![]() QUESTION:
QUESTION:
This is a question that relates indirectly to my profession. I am a
chiropractor , a colleague of mine has found a way to initiate a muscle
relaxation response by treating individual muscle attachments a certain
way. He explains his theory by using the example of a bowstring. He says
that when one pulls the string on a bowstring to shoot an arrow the
tension of the string attachments onto the bow diminishes cause the two
ends are approached. Somehow I have my doubts about that. I know the
direction of tension changes, but does the tension decrease ? Is there a
way this can be measured and whats your opinion on this matter.
![]() ANSWER:
ANSWER:
First, look at the bow not drawn, shown to the left. There is
a tension in the string, T1. The bow pulls up on the
string at the top with a force T1 and down on the string
at the bottom with a force T1. (It is a common student
mistake to say that if the bow pulls up at the top with force T1
and down on the bottom with T1, the tension in the string
is 2T1. This is wrong.) I think we can agree that if the
string is shortened, as in the middle picture, the tension will
increase and so the force the bow will exert top and bottom, vertically will
increase. So, a flexed bow will exert a greater force vertically on the
string, T2 at both ends. Now, if the bow drawn by pulling
on the original string with a force F such that the bow is the same
shape as in the middle picture, each end of the string will also have a
horizontal force F/2 as shown in the right figure and the vertical
components (T2) will remain the same. In the drawing, T2
and F/2 are the forces the bow end exert on the string, and T3
is the force which the string exerts on the bow end; Newton's third law says
these must be equal and opposite, so the string has a tension T3=√[(F/2)2+T22].
Clearly T3>T2>T1,
so you are right, the tension increases when you draw the bow.
Finally, anybody who has ever drawn a bow knows that the farther you draw it
the harder it gets to draw it farther; in this sense, the bow is like a
spring where to pull it a little requires little force, but to pull it a lot
requires larger force.
![]() QUESTION:
QUESTION:
I know that visible light has much more energy than microwaves but how is it that microwaves can heat food while visible light can't? Not even gamma rays (which we wouldn't want to use for our food anyway) can heat thing like microwaves.
![]() ANSWER:
ANSWER:
First, it is not energy that matters, rather power, the rate
at which energy is delivered to what you are trying to heat. While it is
true that a visible-light photon has more energy than a microwave photon (E=hf),
you cannot make a statement about total energy without knowing how many
photons of each you have. So, if you concentrate light from the sun to a
spot you can burn paper. But, there must also be something going on beyond
power, something about how the radiation interacts with what you want to
heat. For example, even very intense light will not greatly heat up a sheet
of glass because almost none of the light will be absorbed, thereby giving
its energy to the glass. Microwave radiation is just the right frequency to
excite vibrations of water molecules, so many of the impinging photons
are absorbed and give their energy to the foodâheating it.

![]() QUESTION:
QUESTION:
So i'm building a big aquarium for a friend who is a performing mermaid. The tank is going to be built on a trailer for easy transport. the framing will be steel. My question is what formula do i need to determine what thickness acrylic i'll need to make the tank strong but as light as possible. If i'm building a 6 ft. by 4ft by 4ft tank.
A: Hw do you determine p.s.i. for water in a container by volume. (pressure exerted on the walls)
B: what formula do i use to plug in gallons, p.s.i., etc..
C: what can i use to determine the min. thickness of acrylic i'll need.
![]() ANSWER:
ANSWER:
The gauge pressure P (pressure above atmospheric) at a
depth D in a fluid with weight density ρ is
P=Dρ. The density of water is ρ=0.0361 lb/in3, so the
P=0
PSI at the top of the tank, P=(0.0361 lb/in3)x(48 in)=
1.73 PSI at the bottom, and P=(0.0361 lb/in3)xD in
general (D in inches). Since atmospheric pressure is about 14.7 PSI,
the pressure in a tank of this depth is relatively small. So, the answer to
your question A is that the pressure does not depend on the volume at all,
only on the depth; you could have a tank 4 ft deep and a mile on the sides
and the pressure would be just the same as yours. You could also calculate
the total force on a side of width W; that force is Đ
WD2ρ,
but that number is not very necessary for you since the force is uniformly
distributed across W. For example, the force on each 4x4 side would
be about 2000 lb and on each 4x6 side would be about 3000 lb. There is also
a torque on each side about the top edge of each side of WD3ρ/3
(which tries to rip the side away with the top edge as the pivot). Those
torques are about 32,000 in∙lb=2660 ft∙lb and 48,000 in∙lb=3990 ft∙lb for
the short and long sides. Your questions B and C are engineering questions,
not physics, but there is certainly no formula in which you would plug in
either a volume or a pressure to get a thickness of the plastic because, as
I showed above, only the depth matters. You can probably check with an
aquarium supply place how thick your plastic needs to be for a depth of 4
ft. I found
one
site which recommends 3/4 in thick for a 30 in depth; the purpose of
this is to prevent bowing of the acrylic which would be mainly a horizontal
bulge, not to hold back the water from breaking the plastic. Some bulging
may be acceptable to you to save costs. Looking at the numbers above,
though, I think an important concern for you is the strength of the
framingâthose edges have to hold a lot of force and torque. You might also
think about the force on the bottom of the tank which will be about 6000 lb.
![]() QUESTION:
QUESTION:
If 100 kg person was standing on an imaginary platform in space
(feet toward the sun) the same distance as the earth and not in orbit
around the sun, how much would they weigh?
![]() ANSWER:
ANSWER:
The force F on a mass m by a mass M
where the two are separated by a distance R is given by Newton's
universal law of gravitation, F=MmG/R2 where G=6.67x10-11
Nm2/kg2. Putting in m=102 kg, M=2x1030
kg, and R=1.5x1011 m, I find F=0.59 N=0.133 lb.
This would mean that near the equator the "weight" of a 100 kg man would be
roughly 980.59 N at midnight and 979.41 N at noon (not taking into account
the moon which would probably have a larger contribution than the sun).
![]() QUESTION:
QUESTION:
Is the âsuperpositionâ of multiple waves simply a way of thinking about multiple waves (i.e. there is no new wave, only the original ones which can be dealt with/thought of as if they were a single wave), or is a single (new) wave created by these multiple waves? And if the latter is the case (i.e. it is a new wave), then is this new wave âsuperimposedâ upon the originals (i.e. the original waves remain, but another one--their superposition--is added âaboveâ them), or would the original waves âcombineâ (e.g. two waves would become one, and the original two would no longer remain)?
![]() ANSWER:
ANSWER:
The question you ask is all semantics. The superposition
principle simply states that, at any point in space and at any time, the net
wave displacement is the sum of all displacements of all waves. It makes no
difference whether you want to call that displacement one wave or many. The
superposition principle is the result of the fact that the wave equation is
a linear equation and therefore if A(x,y,z,t) and
B(x,y,z,t) are separately solutions to some wave equation,
then A+B is also a solution.
![]() QUESTION:
QUESTION:
What happens to all of the light photons that enter your eyes each day?
![]() ANSWER:
ANSWER:
They are absorbed by molecules in your eye and give their
energy to performing the necessary chemistry on the molecules which absorb
them to send electrical impulses to your brain for processing into images.
![]() QUESTION:
QUESTION:
You can stand on an empty soda can and it will support your weight. But touch a pencil point gently to the side, and the can will crumple. I'm trying to find out why.
![]() ANSWER:
ANSWER:
Imagine the can to be made up of many thin sticks, as
pictured to the left; I will suppose there are 100 sticks and your weight is
100 lb. Each stick must therefore hold up 1 lb. If the stick is perfectly
straight, it is able to support 1 lb but if it gets the slightest "kink" in
it, it will not and will quickly fold. But that stick is actually attached
to the sticks on either side of it, so if it folds it will drag its
neighbors with it and they will drag their neighbors and the whole can will
fail.
![]() QUESTION:
QUESTION:
I really don't understand why there are assumptions made in physics....if those assumptions are neglected then practical physics doesn't come into play??....while we study the change in acceleration due to gravity with height we consider earth to be a homogeneous sphere but while studying the variation of g with shape we consider earth to be elliptical which is the actual shape...which means that the first case is wrong if the assumption is neglected?
![]() ANSWER:
ANSWER:
Almost any problem in physics (or any science, for that
matter) requires making judicious approximations. Physics is straightforward
only for the simplest of cases and to solve any real-world problem usually
you decide what factors contribute in a minor enough way that their effects
may be neglected. You mention gravity, so let's use a projectile launched
from earth. What must we take into account if we want to do the problem
exactly?
-
The earth is not a perfect sphere, as you note, so you must measure the distribution of the mass of the earth relative to its center of mass and then find the acceleration of gravity at each point both on the surface and above it.
-
The earth is not an inertial frame, it is rotating, so you must take into account the (fictitious) centrifugal and Coriolis forces. Similarly, the earth goes around the sun in an eliptical path, so the fictitious forces associated with that acceleration must be taken into account.
-
The moon exerts a gravitational force which we should include; after all, the effects of this force are evident from observing tides. The sun also exerts a gravitational force, as does every other object in the universe.
-
The projectile is flying through the air, so we must take air friction into account which, to complicate matters, depends on the velocity of the projectile. Also, if there happens to be a wind, this will exert a force on the projectile.
If we were interested, for example, in the flight of a baseball after it was hit, we would be foolish to take all the things listed above into account. You would never learn how physics works unless you can see for that problem that nonuniformity of the earth, nonsphericity of the earth, the moon, the sun, and the earth's rotation would make almost no noticable difference if you just ignored them altogether. The only thing you might want to worry about is air friction; after all, you could never have a curve ball without air friction. But, even air friction is usually neglected in most introductory physics problems because it just makes understanding projectile motion too difficult if you are just starting to learn physics. If you are interested, however, in calculating precisely the orbit of a satellite (a different kind of projectile) you would certainly need to know the gravitational field more precisely than you need to know it for a baseball.
![]() QUESTION:
QUESTION:
I understand where time comes from to an extent. Days-revolution of
the earth, year- orbit around the sun, seconds- duration of
9,192,631,770 cycles of microwave light absorbed or emitted by the
hyperfine transition of caesium-133 atoms in their ground state
undisturbed by external fields. I understand that we might not be able
to travel at the speed of light. But the hadron collider moves particles
at 99.999994% (something like that) the speed of light. If they were to
use a caesium-133 molecule would the the time of decay change or would
that be an external field being in the collider?
![]() ANSWER:
ANSWER:
Nobody understands what time is. However, we can
operationally define what one unit of time is. You have given a couple of
examples of operational definitions of units of time. Since Einstein came up
with the theory of special relativity, we now underatand that how fast time
proceeds depends on who measures it. The atomic clock you refer to is not
really a good example since it is the frequency of the radiation, not the
decay time. But, if you did happen to have a 133Cs clock going at
0.99999994c, it would keep time fine in its own rest frame but you
would measure it to run slow by a factor of 1/√(1-0.999999942)=2887.
In other words, when the atomic clock ticked off 1 s, your clock would read
2887 s=48 min.

![]() QUESTION:
QUESTION:
I'm doing book research on the Triangle Shirtwaist Factory
fire, a huge fire in the early part of the last century in which many
women jumped or either fell out of a factory window from 100 feet up. I
encountered one statistic that said they hit the ground with a force of
around 11,400 pounds. This seems like way too much force to me, given
that they probably only weight 125 lbs or so. I've tried looking up easy
formulas to verify this online, but I haven't come up with anything
definitive. It seems like the variables which I can plug into an
equation are weight (I'm assuming an average of 55 kg); height (100
feet) and gravity (9.8 meters/sec squared) The site
http://hyperphysics.phy-astr.gsu.edu/hbase/flobi.html provides
boxes to plug in numbers, and they also ask for "distance traveled after
impact". This is one variable I don't know. The women (none of whom
survived the jump impact) were landing on concrete, which is of course
pretty immobile. I typed in ".01 meters" for distance traveled after
impact. ??? The site gives me a number of 1,794,870 newtons. Is it
possible to convert this into kilograms?
![]() ANSWER:
ANSWER:
The reason you are having problems is that it is impossible
to calculate the force just by knowing how high they jumped from, in other
words, how fast they were going when they hit. The calculation you did is one
way to estimate the force, by knowing how far the victim moved before
stopping. Of course, this is not really possible to get exactly because it
would depend on how the person hit the ground. For example, hitting head or
feet first, a reasonable estimate of a stopping distance would be half the
body height (about 1 m); or hitting spread eagle, probably more like 10
cm=0.1 m. Putting these into the hyperphysics calculator, the numbers are
about 16,000 N (corresponding to about 1600 kg or 3600 lb) and 160,000 N
(corresponding to about 16,000 kg or 36,000 lb), respectively. These are of
the same order of magnitude as the 11,400 lb estimate your other reference came up
with. In your case, you have to think about more than how much the ground
deforms, but also how the body will deform. These forces are rough estimates
of the average force.
The way I usually look at this kind of problem is to try to estimate the force from the time of collision. From 30 m (roughly 100 ft) the speed at the ground would be about 24 m/s. The time to travel about 1 m to stop (again, about half body height) would be about 1/12 s. Then, instead of using kinetic energy to calculate the force as the hyperphysics calculator did, use Newton's second law which says that F=mv/t=(55 kg)x(24 m/s)/(1/12 s)≈16,000 N where F is the average force during impact. This is the same answer as above, which it should be since it is the same physics. If there had been a big airbag at the bottom which would increase the collision time to 1/2 s, the force would have been more like 270 N≈61 lb, probably nobody would have died.
![]() QUESTION:
QUESTION:
Here is the setup:
You have a larger container with 2L of water in it, and above that you have a smaller container with an airtight piston/plunger inside it. A counterweight attached to the piston. The upper (smaller) container is attached to the lower (larger) container via a pipe.
The question:
How much would the counterweight need to weigh, to pull the piston up and fill the smaller container with water?
Assumptions:
- The piston weighs nothing and has no friction.
- 1L of water weighs 1kg
My best guess would be that the counterweight needs to weigh 1kg? Is this correct?
(If not, what would it be, and why?)
(It seems simple enough, but there might be something I don't know about, that I'm not factoring in?)
![]() ANSWER:
ANSWER:
Why have I waited so long to answer this question? Something
about the picture bothered me and I could not put my finger on it. I kept
coming back to the picture and kept being bothered. I think I now understand
the problem. The pipe between the two containers plays a crucial role. If
the pipe is the same size as the upper container, you get one answer, the
one you want―1 kg is the unknown mass. But suppose that the pipe is very
tiny; in that case only a tiny mass would be needed because the bottom of
the upper container would hold up most of the weight of the water. Let me do
the case where there is no pipe, you just have a hollow tube of cross
section A into which the piston if fitted and which is immersed in
the water. When you have lifted the piston until half the water (1 kg) is in
the tube above the surface of the water in the reservoir and a height h
above the surface, the forces on the water plus the piston are: the weight
of the water down, W=-ρghA=-1000ghA=-g; the force of the
atmospheric pressure Pa=105 N/m2 up
on the bottom of the column,
Fbottom=PaA;
the force of the atmospheric pressure down on the top of the piston, Ftop=-PaA;
and the tension in the string, necessarily equal to the unknown weight Mg.
Therefore PaA-PaA+Mg-g=0 or M=1 kg. Keep in mind that there is an important constraint
on the geometry of the tube: if the tube is so narrow that h>10.2 m,
no weight will be able to lift it higher and the piston will separate from
the water and there will be a vacuum between the piston and the upper
surface of the water. You can see this because if the pressure at the top is
zero, ρghA=PaA,
h=Pa/ρg=105/(9.8x103)=10.2
m; this is just a water barometer.
![]() QUESTION:
QUESTION:
I have been debating this for years and have read many online forums. My question regards solar heat and how it is conducted into water.
I have a large swimming pool. My current solar cover is silvery with round bubbles underside. The silvery material supposed holds heat better and warms up the water better, as well as preventing evaporation, dirt in the pool etc... I now need to replace the cover which has worked reasonably well for 6 years, but I always thought it doesn't help heat the pool much.
My thought is that diamond shaped air bubbles on the underside will have a greater surface area for transmitting heat into the water. But I cannot get a good answer on what color the material should be. These covers come in silvery, clear, dark blue and light blue. I thought dark blue would absorb more heat, but others say clear helps magnify the sun's rays and produce more heat. Still others say light blue is best, others say the silver. The benefits of these covers are multiple. They definitely do keep heat in overnight, stop evaporation, and keep pools cleaner. But I really want a cover that will help heat up the pool during the day if no one is swimming yet. So what is best? Diamond bubbles or circular? Clear or dark blue, or silver as I currently have?
![]() ANSWER:
ANSWER:
My knee-jerk reaction is to agree with you that the best
choice would be a dark color. However, there are many variables and you
could get tricked. To get heat into the water is the main concern for you,
not necessarily how much heat gets absorbed in the cover itself. A little
search resulted in
some
data which, if accurate, I think tells the story. Evidently, the most
important thing which determines heat transmitted to the water (heating
power) is how thick the cover is. This makes sense since the thicker the
cover, the more absorbed energy it can hold and therefore the more energy is
avaiable for heating the pool. So choose any color you like best, anything
else would be fine tuning at best. I suspect bubble shape is pretty
irrelevant too.
![]() QUESTION:
QUESTION:
Is it possible to make carbon monoxide (carbon MONoxide, NOT dioxide) into a liquid?
![]() ANSWER:
ANSWER:
Try as I might, I could not find a phase diagram of CO.
However, the
Wikepedia entry for CO lists a triple point and critical point, so one
can be confident that liquid and solid phases exist and a rough phase
diagram can be drawn. The data are
T=-205.1
°C,
P=0.15
atm for the triple point and
T=-140.3
°C,
P=34.5
atm for the critical point.
I have sketched an approximate qualitative phase diagram to the left. For
comparison, I have also shown, on the right, the phase diagram for CO2.
If you want to make CO vapor into a liquid at atmospheric pressure you would
need to cool it to about -170 0C; to solidify it, you would have
to go down to around -200 0C. (Wikepedia lists the boiling point
as -192.5 0C and the freezing point as -205 0C, so my
rough phase diagram isn't too bad.) Note the very large differences between
the two: the triple point and critical point for CO are both much lower in
pressure and temperature than for CO2.

![]() QUESTION:
QUESTION:
how much negative charge do I accumulate by touching the earth?
Here is how I (tried) to answer this question:
The Earth carries a negative electric charge of roughly 500 thousand Coulombs (according to different sources I've seen). If I touch the Earth I should therefore pick up some of this electric charge (through conduction) and become negative charged. Assuming the earth can modeled as a conducting sphere with radius 6371 km and me as a conducting sphere with radius 1 m, around how much negative charge would I accumulate? The reason I ask is because I'm trying to prove to myself that grounding does indeed render a charged object neutral (i.e. transfers all the object's charge to the Earth). Using the well known equation for two connected conducting spheres with different radii (see Example 3-13 on page 115 in David Cheng's "Field and Wave Electromagnetics, 2nd Ed."), I calculate 0.0785 C, which is way too big and must be wrong.
![]() ANSWER:
ANSWER:
There is an old joke in physics the punchline of which is
"consider a spherical cow". I like the spirit of your question, but your
approximations are killing you, I think. But, I cannot quarrel with the
earth being approximated as a sphere and approximating yourself as a sphere
is probably ok too. The problem is the assumption that you and the earth are
conductors. If you take your number for net charge you will find that the
surface charge density is about 1 nC/m2. If your answer were
anywhere near right, you would have to get all the charge from around 108
m2 in your vicinity. But it is not free to move around, either on
the ground or in you. Although you are standing in an electric field, caused
by the earth's net charge, on the order of 150 V/m, this field cannot cause
any significant electric charge to flow onto you because you are not a good
conductor.
![]() QUESTION:
QUESTION:
I am a physician on an internet mailing list.
Someone asked why it is easier to push fluid into thick skin using a thin 1cc tuberculin syringe (6 cm long for one cc of fluid) compared to pushing that one cc through the same size needle but from a wider bore 3 cc syringe (1cc is marked off along only 2 cm of distance along the hub).
My theory was that one could develop more pounds per sq cm of pressure using the thinner bore plunger than the same pressure expanded over the wider area of the 3cc syringe. I thought the difference between the two was based on the square of the radius of the syringes.
Others argued for something called Poiseuille's equation which described flow through a tube based on the fourth power of the radius.
![]() ANSWER:
ANSWER:
Poiseuille's equation gives the pressure drop ΔP along a tube
of length L and radius R due to the viscosity μ of the
fluid, ΔP=8μLQ/(πR4), where Q is the
flow rate. Although I did not do a calculation, common sense tells me that,
since the tubes are not long, the fluid is probably not very viscous, and
the flow rate is very small, that the pressure drop for the 6 or 2 cm is
negligibly small. Your suggestion is the correct one. If you exert equal
forces on the two with your thumb, the resulting gauge pressure in the
thinner syringe will be 9 times greater.
![]() QUESTION:
QUESTION:
Convection, conduction and radiation with respect to heat loss in the human body. If 2 equally dressed, equally insulated and body surface area and BMI candidates are sitting in rooms with no air movement, at an ambient temperature of 40 degrees, with the difference that one subjects' room is at nearly 100 percent humidity and the other subject's room is at 35% humidity. Is the saturation of the air and loss of heat by the first subject a function of conductive heat loss? I understand that movement of heat in a liquid or gas state is convection, but would not the high humidity increase the conductive principle of heat loss (and a reason that cold and damp is very uncomfortable)? Or is that still a principle of convection, the gradiant differences in air and body causing a convective heat transfer.... I believe the humidity adds a conductive component... Am I misunderstanding?
![]() ANSWER:
ANSWER:
Heat loss by conduction of a gas is always very small
compared to convection and radiation. However, here we are talking about
organisms, not just blocks of something or other, and we have evolved to
cool ourselves by evaporative cooling (sweating) which is really important.
Since evaporation occurs at a lower rate when the air is humid, humidity
plays an important role. Still, you are interested in whether conductivity
of air (small though it may be) depends on humidity. The answer is yes, but
the effect happens to be exactly opposite of what you expect―conductivity
decreases as humidity increases as shown on the graph at the right.
![]() QUESTION:
QUESTION:
If a rogue planet the same size as Earth was about to hit us, would there be a period of weightlessness here before impact from the gravity of the rogue planet?
![]() ANSWER:
ANSWER:
By "same size" I assume you mean same mass and radius. You
would not be exactly weightless unless you were at the exact point of
initial impact and then only at the instant when you were crushed. The net
gravitational force on you could be calculated fairly easily just by adding
the two vector forces for any configuration of the two planets; it would be
tedious, though. I will do two simple examples. The gravitational force on
you (your weight) is given by W=MmG/R2 where M
is the mass of the earth, m is your mass, R is the radius of
the earth, and G is the universal gravitation constant. I will call
the distance between the centers of the two planets r and assume that
the collision is "head on", that is,
the rogue planet's center is moving directly toward the center of the
earth. Then it is pretty easy to see that if you are standing at the point
of impact, the force F on you is F=W(1-(R2/(r-R)2));
note that the collision occurs when r=2R and F=0 as I
stated at the beginning of the answer. If you were standing on the opposite
side of the earth, F=W(1+(R2/(r+R)2));
now, when r=2R, F=10W/9. The graph to the right
shows the force you would feel on the impact side (black) and opposite side
(red) as functions of r. Note that when r is very large,
F≈W.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
What if a rogue planet 2X the mass of Earth was about to collide, would the oceans be pulled from their beds before impact?
![]() ANSWER:
ANSWER:
I have added a curve for the near side case you ask about. As
you can see, there is a time before impact (when r=2R) when
the force goes negative. That means the net force is pointing toward the
other planet, not earth, so anything on the earth's surface near the impact
point, including the oceans, will "fall up".
![]() QUESTION:
QUESTION:
Am failing to understand a logic of nuclear reactor. (The
questioner refers to this
link.)
There have been 11 nuclear accidents till now. Considering they occurred during a cumulated total of 14000 reactor years of operation (which i dont understand), how would 15000 nuclear reactors cause an accident every month? Please help understand this.. Am getting so confused an restless here!
![]() ANSWER:
ANSWER:
The rate at which major accidents have occurred since
reactors have been being built is R=11/1.4x104=7.8x10-4
accidents/reactor/year. If you have N reactors, then the rate at
which accidents will occur for those N is NR=1.5x104x7.8x10-4=11.79
accidents/year≈1 accident/month.
![]() QUESTION:
QUESTION:
For a story I'm writing I have a space station about 500 meters long with a diameter of about 100 meters. How does one figure out how fast the station has to rotate (correct term?) around it's long axis so that it has 1 Gravity around the circumference inside?
![]() ANSWER:
ANSWER:
If you move in a circle of radius R with speed v,
there must be a force on you of F=mv2/R where m
is your mass; this force is directed toward the center of the circle. On
your space station, the force would be provided by the walls and you want
that force to be equal to your weight on earth which is W=mg, g=9.8
m/s2 being the acceleration due to gravity. So, that means you
want v=√(gR)=√(50x9.8)=22.1 m/s. The circumference of the
space station is 2πR=314.2 m, so the time to complete one revolution
would be 314.2/22.1=14.2 s; so the rate of rotation would be 1/14.2=0.07
revolutions per second or 4.2 RPM.
![]() QUESTION:
QUESTION:
Astronomy:Astrology :: Physics:Nucleonics ?
![]() ANSWER:
ANSWER:
It took me a minute to realize that this is one of those
SAT-style analogy questions, "astronomy is to astrology as physics is to
nucleonics?" The answer is that this is false because nucleonics (variably
the study of nuclear energy, or of nucleons or nuclei, or nuclear phenomena)
is a real science and astrology is certainly not. A better analogy would be
astronomy:astrology::physics:psychics.
![]() QUESTION:
QUESTION:
an object is thrown vertically upward on earth with the speed of light . will it leave earth ? My teacher said that it will travel vertically with decreasing c ( gravity ) and reach zero at one point and fall back earth with increasing speed until it reaches earth with the initial speed c , is he right ? Nd what will be the object's route after it starts moving, straight or performing elliptical orbit ?
![]() ANSWER:
ANSWER:
First of all, site groundrules forbid questions assuming an
object can move with the speed of light. But, since your question is a
little more substantive, I will modify it slightly so that your object may
go any speed less than the speed light, say 99.999999% the speed of light.
The fact is that any object with a speed greater than or equal to the
escape velocity will never fall back down.
The escape velocity from the surface of the earth is only about 11 km/s≈7
mi/s. Your teacher is wrong. The shape of its trajectory if its initial
speed is greater than the excape velocity depends on the direction it is
fired: a straight line if straight up, a hyperbola if shot nonvertically.
![]() QUESTION:
QUESTION:
I have a part (think like a round thick plastic cylinder- it actually is a safety device for heavy trucks that if the air shock system fails the bed of the truck rests on this cylinder).
Similar plastics are used in the part (a toughened with rubber nylon actually) on two exact tests with slight differences that my customer is saying should be NO DIFFERENCE- but I get a failure in one and not the other.
1rst test- 200 lb load at 4.00 feet drop- parts passed
2nd test - 220 lb load at 3.66 feet drop- parts failed
Now I know the "Force" is ~ the same...but could it be failure due to Kinetic Energy change (definition more dependent on mass?)?
![]() ANSWER:
ANSWER:
I have no idea what you mean by the force being the same, but
it is certainly the force which will determine whether the part fails or
not. Let's start with basics. When an object of mass m moving with
speed v strikes another object and stops, the average force F
to stop it was F=mv/t where t is the time it takes to
stop. Because of Newton's third law, if your load experiences a force F
up,
your part experiences an equal and opposite force of the same magnitude down and
it is that force which causes it to fail. The other thing you need to know
is how fast v an object is moving if dropped from a height h: v=√(2gh)
where g=32 ft/s2=9.8 m/s2 is the acceleration
due to gravity. Scientists prefer to work in metric (SI) units, so I will
need 200 lb (mass)=90.7 kg and 220 lb (mass)=99.8 kg. I calculate the
collision speed of the 200 lb load to be v200=4.88 m/s=16
ft/s and of the 220 lb load as v220=4.66 m/s=15.3 ft/s.
So, the average force over the part experiences over the collisions are F200=442.6/t200
and F220=465.1/t220; assuming the loads
both take the same time to stop, your results are not surprising because the
second test results in a larger force. For example, suppose the loads take
1/100 second to stop. F200=442.6/0.01=44,260
N=9,950 lb and F220=465.1/0.01=46,510
N=10,456 lb. If you cause the collision time to be longer (for example by
putting a piece of rubber on top of your part) you can greatly reduce the
force on the part during collision.
![]() NOTE
ADDED, CORRECTION:
NOTE
ADDED, CORRECTION:
I made a mistake above. When the load is stopping, there are
two forces on it, F and its own weight mg, so mv/t=F-mg,
not just F. So F=mv/t+mg. The corrected values
above are F200=442.6/t200+888.9
and F220=465.1/t220+978.0.
In the example where t=0.01 s, F200=45,149 N=10,150
lb and F220=47,488 N=10,676 lb. The conclusion that the
220 lb load results in a larger force on the part is unchanged.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I did made a mistake when I say "force": the customer has the 200 pound weight dropped from a 4 foot height with the end result of 800 foot lbs of energy in one test and in the other test it is 220 lb weight x 3.66 feet in the other test- 800 foot lbs of energy (805 actually).
Are you saying using this kind of "math" for failure analysis is flawed?
![]() ANSWER:
ANSWER:
The calculation of "energy delivered" is certainly correct
and, indeed, in this case, approximately equal amounts of energy (weight x
height is correct for energy here) have been delivered. But, physicists (and
probably engineers too) tend to think of force as what matters in breaking
something. After all, some of the energy goes into things other than breaking
the part―heat, sound, deformation or damage to load, etc.―but the
force I calculate is certainly applied to the part. In addition, the forces
differ by 5.2% whereas the energies differ by only 0.6%. And, perhaps most
important, you have definitively shown that the analysis method must be flawed
because you actually did the experiment (testing is what science is all
about!) and showed it to be wrong. Maybe the best test would be to put the
part in a hydraulic press and measure the force required to make the part
fail.
![]() QUESTION:
QUESTION:
Yesterday, while traveling on the train, I observed a fly come trough the door, it hovered in the centre of the ile and did not touch the inner cabin of the train. The train began to move and the fly continued to hover exactly where it was, it did not seem to struggle with maintaining the same momentum as the train, it just simply hovered. Can anyone explain to me why the fly was able to maintain the same speed as the train without having direct contact with the cabin?
![]() ANSWER:
ANSWER:
The fly is hovering in the air. The air moves forward with
the train. However, when the train accelerates forward, you feel like you
are being pushed backwards and have to adjust slightly to keep where you
are. The fly also will have to make a little adjustment to keep from
drifting backward.
![]() QUESTION:
QUESTION:
Pertaining to the asteroid that recently exploded over Russia, a television "news" station claimed the asteroid exploded with the same force of 20 atomic bombs... now I understand this space rock did quite some damage, but was it's demise really equivalent to the combined exploding force of 20 nuclear warheads?
![]() ANSWER:
ANSWER:
Well, its mass was about m≈1.1x107 kg and
its speed was about v≈1.8x104 m/s, so its kinetic energy
was about E≈Đ
mv2≈18x1014 J. The energy
of the Nagasaki atomic bomb was about 1014 J, so 20 is about
right. However, its energy was not all released at once and it is estimated
that the energy of the main explosion was about 4x1014 J, about 4 Nagasaki bombs.
![]() QUESTION:
QUESTION:
Suppose I built a tubesat (personal hobby sat) and sent it to 193 miles above the earth into orbit. Inside this sat would be a single shot co2 based "air gun" which would fire a single microchip based package approximately the size of a stick of gum into deeper space, hopefully propelling it forever outward. My estimates of package size and air gun capabilities lead me to believe I can shoot the package at as much as 1400 fps or so, thus around 1000mph at launch...
My question is - will it work? Can I "shoot" a tiny package out into space from near earth orbit in this fashion?
![]() ANSWER:
ANSWER:
The escape velocity from a near-earth orbit is approximately
25,000 mph. The speed of a satellite in near-earth orbit is about 18,000
mph. So, the maximum speed of your package is about 19,000 mph. Looks like
it will not escape.
![]() QUESTION:
QUESTION:
How do objects (specifically spacecrafts) accelerate in the near vacuum of space? What do they push off of in order to accelerate?
![]() ANSWER:
ANSWER:
That is not how a rocket works, it does not "push against"
something. Imagine yourself standing on very slippery ice holding a very
heavy rock. If you throw the rock, you recoil in the opposite direction. You
do not recoil because the rocks pushes on the air; the same thing would
happen if there were no air.
![]() QUESTION:
QUESTION:
I will be filling a pressure vessel (a soda keg) with old, flat tennis balls, then pressuring the vessel to ~30+ psi. The goal is to re-pressurize the old balls so they bounce "like new" (I'm told new unopened tennis ball cans are pressurized to ~17 psi). I believe this will be possible because the rubber membranes of the balls under their felt covers are permeable (to air).
The vessel has a gauge to allow monitoring of the internal pressure. My question is ... as air molecules are forced across the rubber membranes of the balls, would you expect the vessel's pressure reading to remain constant, or would you expect it to drop?
![]() ANSWER:
ANSWER:
Suppose the pressure is not so large that the balls are
crushed, they maintain their size. When you first pressurize the volume
around the balls, the pressure outside the balls is greater than inside
which, as you suggest, will cause the air to seep into the balls until
the pressure is equalized. The ideal gas equation is PV=CNT where
P is pressure, V is volume, C is some constant, N
is the amount of gas, and T is the temperature. The volume of
the gas outside the balls (which is where you measure pressure) does not
change and I will assume that the temperature does not change. But, the
amount of gas in that volume gets smaller. Therefore the pressure must
get smaller. Incidentally, you will not really be getting the equivalent
of "virgin" tennis balls. The "fuzz", probably all worn off, plays an
important role in the aerodynamics of a tennis ball just as dimples on a
golf ball do.
![]() QUESTION:
QUESTION:
My questions pertains to the gravitational constant. I'm a theoretical
physicist, so I don't need an obvious answer, and I know the
gravitational force equation works well enough to use but you have more
experience than me so... Shouldn't a universally correct gravity
equation not have a gravitational constant derived from earth? Are we
missing something universally basic about gravity? Even Einstein's
equations use an earth based gravitational constant as part of the
definition. This seems very flawed to me... perhaps you could help me
here?
![]() ANSWER:
ANSWER:
If there is something which we believe to be a universal
constant, we measure it; we are here so we measure it here. But the
question you ask could be asked of any constant. How do we know that
Planck's constant is the same everywhere (and "everywhen") in the
universe? Once we have the value measured here, and we can measure most
accurately here, we look elsewhere for evidence that physical constants
may vary over distance or time. As far as I know, no evidence has been
found for inconstancy of fundamental constants, but it has been looked
for.
![]() QUESTION:
QUESTION:
Solve an argument for us please: My friend says that Sound is not part of the Electromagnetic Spectrum and I say it is. I CAN NOT find an answer anywhere on the Internet. What I find is that anything below radio waves in the frequency spectrum is just ignored. Why doesn't the EM Spectrum start at 0hz? If the audio spectrum is ~20hz-20khz then WHEN/WHERE does the EM spectrum start? Wikipedia "Radio Waves" says that radio frequencies can get as low as 3khz. That is an audio frequency, right? So, I'm just looking for a "break point" at which audio becomes radio. And at what point do audio waves become part of the EM spectrum? Is it a definition problem?
![]() ANSWER:
ANSWER:
Sorry to be the bearer of bad news, but sound is not an
electromagnetic wave. What the wave is is determined not by frequency,
but by "what is waving". Sound is a wave which travels in some medium,
for example air. If there is no medium between you and a source of
sound, you will not hear it. Electromagnetic waves are composed of
electric and magnetic fields which are "waving" and can travel through a
vacuum unlike any other wave. See an
earlier answer. Another difference
is that sound is a longitudinal wave (the air vibrates parallel to the
direction the sound is going) and EM waves are transverse (the electric
and magnetic fields vibrate perpendicular to the direction the wave is
going).
![]() QUESTION:
QUESTION:
What would happen if we were to compress a gas's atoms so tightly that they could no longer flow freely to be a gas would it change forms into a solid?
![]() ANSWER:
ANSWER:
It depends on what the gas is. Each material has its own phase diagram which shows what happens as pressure and temperature are changed.
As an example, the figure to the right shows the phase diagram for
water. You can see that at temperatures above about 00C
increasing the pressure on a gas at constant temperature (which is what
you would do to "compress
a gas's atoms"), you create a liquid (called a phase change) If you have
temperatures below
00C and very low pressures, you
can have water in a vapor state and, if you increase the pressure, you
will cause a phase change to solid water (ice).
![]() QUESTION:
QUESTION:
A planet was discovered, Gliese 581g, that is 20 light years from Earth. This planet is the right size and distance from its' sun to have liquid water on the surface and therefore life. How long would it take to reach this planet traveling at 18,000 mph, the approximate speed at which our rockets can can currently travel?
![]() ANSWER:
ANSWER:
20 ly is about 1.2x1014 mi, so t=1.2x1014/1.8x104=6.7x109
hr=760,000 yr.
![]()
![]() QUESTION:
QUESTION:
Is it true that a Wave Train travels at 1/2 the speed of its constituent waves? If so, why? I mean, say a storm in the Gulf of Alaska stirs up some seas. We might see, some distance away, that individual swell waves are moving at 30 knots, but from a bird's eye view, we would see that the area of disturbance expands toward Hawaii at only 15 knots. If this is true, is it only true of transverse waves. Is there such a thing as a longitudinal wave train?
![]() ANSWER:
ANSWER:
What you are talking about is that wave packets or wave
trains are composed of more than one wavelength and there is dispersion,
i.e. different wavelengths travel with different velocities in
the medium; this is known as dispersion and is the reason that a prism
breaks white light into a spectrum of colors. There are, as you note,
two kinds of velocity. The velocity of the waves themselves is called
the phase velocity and the velocity of the wave packets is called group
velocity. For water waves the result is that the group velocity is half
the phase velocity. I did not know this; it is apparently true for water
surface waves in deep water. The little animation above is for just this
situation; the green dots travel with the packets (group velocity) and
the red dots travel twice as fast with the waves (phase velocity).
Everything I have said applies just as well to longitudinal waves.

![]() QUESTION:
QUESTION:
I'm looking for a generator to produce 100% of my current electrical usage and my usage rate is 1,400 kw/h im seeking to find what volt generator i need to buy . would a 50 kw generator be too much or to little?
![]() ANSWER:
ANSWER:
Well, you have your units of electricity muddled, so let's
get that straight first. A watt (W) is a measure of the rate you
use energy, one joule (J) of energy per second. For example, a 1000 W
dryer uses 1000 J per second or 1 kW. The most common measure of energy
used is not the joule but the kilowatt hour (kW¡h), not kW/h as you
write. When you say your "usage rate
is 1,400 kw/h", you
must mean that you use 1400 kW¡h per month. Now, there are 24x30=720
hours per month, so your average power consumption is 1400 kW¡h/720 h,
about 2 kW. So, a 50 kW generator is probably overkill. On the other
hand, probably at least half of every day you use next to nothing, so a
better average is probably like 5 kW, still 10 times less than 50 kW.
But, what you really need to think about is your peak usage.
Energy hogs are typically anything which creates heat by getting a coil
hotâclothes dryers, electric ovens and stove tops, toasters, water
heaters, etc.âwhich are typically 1-3 kW each. Air conditioners
also use a lot of power, often 3-4 kW, so your usage is probably
seasonal. All things considered, something in the range of 10-20 kW
should do it.
![]() QUESTION:
QUESTION:
in the formula for HP (HP=TQ*RPM/5252) do you know where the constant 5252 comes from and what it represents?
![]() ANSWER:
ANSWER:
Horsepower is a measure of power, energy per unit time. The
units of torque (I assume TQ is torque) are force times distance
(e.g. ft¡lb or N¡m) which are also the units of energy and RPM
is revolutions/minute, which has the dimensions of 1/time, so your
formula for horsepower indeed has the units of power, essentially
energy/time. The trick is how to get it into the proper units. I am
guessing that torque is to be measured in ft¡lb. Now, 1 hp=550 ft¡lb/s
and TQ*RPM=ft¡lb¡rev¡min-1¡(2π/1 rev)¡(1
min/60 s)=0.10472 ft¡lb/s, so P=TQ*RPM/(550/0.10472)=TQ*RPM/5252.1
where P is power in hp, TQ is torque in ft¡lb, and RPM
is angular velocity in rev/min. So my guess that TQ is in ft¡lb
was right. So what the 5252 "represents" is what you must divide by to
get the wrong units (ft¡lb¡rev/min) into the right units (hp). [The
purpose of the (2π/rev) factor is that there are 2π
radians in one revolution.]
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
So if i'm understanding it right HP shows energy over time. What i was trying to understand is why HP matters. In my experiance with cars at the race track given as close to identical as posable cars, the one with more HP wins. Sometimes even if the other car had a signifigant torque advantage. With what you said this makes sense because in a given amount of time the car with more HP is inputting more energy in to the driveline than the car with less hp.
Or did i not understand that at all?
![]() ANSWER:
ANSWER:
You have it exactly right. What matters is the rate at which
energy is delivered to the car. You might also be interested in an
earlier answer in
which the power is part of the answer.

![]() QUESTION:
QUESTION:
If you shoot a bullet straight up into the air, its velocity at the very top of the trajectory is zero, even if only for an instant, as its upward velocity slows to nothing before becoming downward velocity. Downward vertical velocity then increases in the earthward direction . Would the velocity ever become dangerous if it landed on a living person? Is the weight of the bullet important? Does the atmosphere restrict the downward velocity?
![]() ANSWER:
ANSWER:
A falling bullet experiences a downward force of its own
weight and an upward force of air drag. The result of the air drag,
which increases with speed, is to have the falling object eventually
reach a maximum velocity called the terminal velocity which is
determined by its weight and its geometry (which is why you can jump out
of an airplane with a parachute). A .30 caliber bullet weighing about 10
grams has a terminal velocity of about 90 m/s (about 200 mph) and a .50
caliber bullet weighing about 42 grams has a terminal velocity of about
150 m/s (about 335 mph). A bullet traveling 60 m/s (about 130 mph) can
penetrate the skull so, yes, a falling bullet is dangerous. Dozens of
people are killed every year by celebratory gunfire.
![]() QUESTION:
QUESTION:
I'm trying to explain to student drivers how to avoid going into a skid during bad weather. A common rule of thumb is "skids happen when there is a change in speed or a change in direction."
Ok, so you are going up a hill at a steady 35 mph. When you reach that part of the incline when your automatic would normally downshift to get your rpm's up - you skid.
I know it has something to do with gravity's effect and you are actually accelerating in order to go same speed but somehow I can't seem to explain it right.
![]() ANSWER:
ANSWER:
The crucial point really is that the coefficient of static
friction is larger than the coefficient of sliding friction. That may be
too technical for your purposes, so let me explain. Static friction is
the frictional force which acts between two objects which in contact but
not sliding; for example, when a car is parked on a hill, the thing
which keeps it there is the frictional force between the tires and the
road and that is static friction. But, as the hill gets steeper, the
friction needed to keep the car from sliding gets bigger and,
eventually, there will not be enough friction and the car will slide
down the hill. But, what happens when the car just starts to
slide? Does the car start creeping slowly down the hill? No, as soon as
it "breaks away" it accelerates down the hill. The reason is that the
sliding friction is less than the static friction. The same is true when
the car is moving because the wheels are not slipping and therefore
static friction is operative. If you are moving with constant speed on a
straight, level road, almost no friction is needed to keep going. But,
when you accelerate you need more static friction from the tires (just
like you need more static friction on a steeper hill) and if you try to
accelerate too much your wheels will spin (just like the car will slide
down the hill). Or, if you brake you need more static friction from the
tires (just like you need more static friction on a steeper hill) and if
you try to brake too rapidly your wheels will skid (just like the car
will slide down the hill). You probably tell your students that they can
stop quicker if they do not slam on the brakes and skid; again, the
smaller sliding friction is why and that is why anti-lock brakes are
such a good safety feature. Turning a curve also requires static
friction because a turning car is actually accelerating even if the
speed is constant because the dirction of the velocity is changing; on a
very icy road where you can get almost no static friction, when you
steer into a curve nothing will happen and you will just skid straight
forward off the road. Your example about going up a slippery slope and
downshifting is more or the less the same as braking gently, trying to
get more static friction. Essentially, trying to keep a car going up the
hill at a constant speed is exactly the same as parking on the hillâthe
static friction required is the same and if the hill is slippery and
steep enough, you will be able to neither park nor go up with constant
speed. So, the downshifting has the same effect as accelerating, trying
to get more static friction. Even if you do not downshift, to keep going
up with constant speed would require that you give the car more gas than
on a level road.
![]() QUESTION::
QUESTION::
why is that during daytime when you turn on the headlights if your car the object ahead of you doesnt appearr to be brigther?
![]() ANSWER:
ANSWER:
Imagine you are sitting in a quiet room and whisper to the
person next to you. She can hear you. Now imagine that a jet airplane is
roaring right over your house. If you whisper, you will not be heard. The
headlights are a whisper compared to the intensity of sunlight.
![]() QUESTION:
QUESTION:
are
you a real physicist?
![]() ANSWER:
ANSWER:
No, I am an artificial physicist.
No, I am a virtual physicist.
No, I am an imaginary physicist.
![]() QUESTION:
QUESTION:
what
are the qualitative effects of thickness, tension and lenght on the
frequency of a vibrating string
![]() ANSWER:
ANSWER:
The frequency (f) of a vibrating string is determined by two
things, its length (L) and the speed of waves (v) in the
string. If the string is clamped at both ends (as in most stringed
instruments) then the frequency is f=v/(2L). The velocity is
determined by two things, the tension in the string (T) and its mass
density (m=m/L),
v=√[T/m].
So, finally, f=[1/(2L)]√[T/(m)].
That is quantitative and you asked for qualitative. Varying the three things
(tension, mass density, and length) separately while keeping the other two
constant results in:
- a shorter string has a higher pitch,
- a higher tension has a higher pitch, and
- a lower mass density has a higher pitch.
![]() QUESTION:
QUESTION:
why do meteors buen up when they fall through the
atmostphere while skydivers don't?
![]() ANSWER:
ANSWER:
Because meteors enter the atmosphere with very large velocities and
skydivers enter it with as much smaller speed, that of the airplane from
which they jump.
![]() QUESTION:
QUESTION:
Scene: A stationary spacecraft in deep space far from any
gravitational forces (planets, stars, etc). If it's engine(s) suddenly
went to full power, would crewmen/loose objects/etc. experience the
effects of acceleration (g forces), or would they accelerate at the same
rate as the spacecraft? If they do experience g's, would they be equal
to those experienced at ground level on Earth for the same level of
acceleration?
![]() ANSWER:
ANSWER:
Objects in the spacecraft would have to accelerate at the same rate and
would therefore have to feel an appropriate force accelerating them; this
force would be the ship itself or the seat they were sitting in, etc.
It is just the same as when you sit in an accelerating carâyou
feel you are being pushed into the back of the seat but what is really
happening is that the seat is pushing forward on you to provide your
acceleration. Since the human body is not designed to endure accelerations
much in excess of g, this is a compelling reason why space travel will never
be possible for single generations of humans. This is one of the reasons sci
fi movies where a spaceship accelerates from rest to near light speed in the
blink of an eye are fiction, not science.
![]() QUESTION:
QUESTION:
I was wondering about the chance of two balls bouncing
around a room colliding with each other? Would this chance increase if
one of the balls was stationary?
![]() ANSWER:
ANSWER:
The center of each ball must be in the same small volume, v, at a
given time; that volume is the volume of a sphere of radius twice the radius
of either ball. The probability of finding one ball in that volume is v/V
where V is the volume of the whole room (assuming the balls are
randomly moving around the volume of the room). If one of the balls is at
rest, it is at the center of v so the probability of its being in the
volume is 1 (100%). So the probability of a collision is v/V.
If both balls are moving, the probability of a collision is (v/V)2,
much smaller. For example, if v/V=0.001 then the probability
of a collision is 0.000001 if both are moving.
![]() QUESTION:
QUESTION:
Someone told me something really insane, but not having a
physics background, I could not refute them properly. If an object is
frozen, and be it that the atoms are still moving, why wouldn't the
atoms create a kinetic energy from their movement over a long period of
time and the object heat up and melt?
![]() ANSWER:
ANSWER:
Suppose the frozen object is well insulated so that no heat can enter or
leave. Then the temperature will remain constant (below 00C for
water). The average energy per molecule will remain constant because that is
what temperature measures. But, ice will not melt until it gets to 00C
and so it will not melt. Moving atoms do not "create" energy, they are
energy.
![]() QUESTION:
QUESTION:
Baseball related. I've heard conflicting answers and this question is prompted by the recent MLB homerun derby. When a player hits a pitch for a homerun does the speed of the pitch at all affect the distance? Will a fastball go further than a slower pitched ball? One camp contended yes, as although some energy was lost at contact with the bat there was still a transfer of energy from fastball to bat. The other camp said no, that the distance ball traveled had more to do with the strength of the hitter and the rotation of the ball than with the speed of the ball. Any light you can shed would be appreciated.
![]() ANSWER:
ANSWER:
Let's simplify the discussion by assuming a particular hitter, because
of the way he swings, can impart a set amount of impulse to the ball with
his swung bat. The definition of impulse is the average force on the ball
during the time it is contact with the bat times the time during which it is
contact. The pertinent physics principle here is Newton's second law which
may be stated as change in momentum (momentum is mass times velocity) equals
impulse. In words, this would mean that since it takes more impulse to "turn
around" a fastball, you are more likely to hit a homerun with a slower
pitch. Here is a numerical example: Suppose the average force is 400 lb over
1/100 of a second; this would result in an impulse of 4 lb s=17.8 N s
(physicists prefer metric units!) Now, the mass of a baseball is about 0.15
kg; the velocity of a fastball is about 100 mi/hr=45 m/s; the velocity of a
curveball is about 80 mi/hr=36 m/s. So, the incoming momentum for a fastball
is about 0.15 x (-45)=-6.75 kg m/s (the minus sign since the ball is coming
into the plate but I choose positive velocity (and impulse) to be away from
the plate) and the momentum after the impulse is 0.15v where v
is the velocity of the batted ball. So, momentum change is 0.15v-(-6.75)=0.15v+6.75
and, setting this equal to the impulse (17.8 N s), I find v=74
m/s=166 mi/hr. If you repeat this calculation for the curveball you will
find that v=84 m/s=188 mi/hr, faster. Of course, there are many
subtleties of baseball which this simple physics explanation does not
address and my assumption that a hitterr can impart only a certain amount of
impulse is obviously a rough approximation. Also, my guess for a typical
impulse may be not very realistic. Still, simple physics suggests a slower
pitch can be hit farther.
![]() QUESTION:
QUESTION:
Why, when a person jumps into a pool from a given height does the water "splash" higher then the initial height that the person jumped from? Assuming they jumped with a more vertical trajectory then horizontal.
![]() ANSWER:
ANSWER:
I guess I would reply "why not?" On what are you basing your
expectation? Lets look at a greatly oversimplified situation from the
perspective of energy conservation. Suppose that no energy were lost when
the person hits the water (of course, not correct but an extreme case). And
suppose that the entire splash is one blob of water 1/100 the mass of the
person. Now, the person starts out with an energy of MgH where M is
his mass and H is the height from which he jumps. Let's take M=100
kg, H=3 m, and g about 10 m/s2, so the energy is 3000
Joules. The blob will end with the same energy, so 3000=(100/100)x10xh where
h is the height to which the blob goes which you can see will be 300
m! Now, to make it more realistic, assume that the blob gets only 5% of the
person's energy instead of all of it. Then you would find h=15 m.
![]() QUESTION:
QUESTION:
I have a question regarding the flow of water from a fountain. How can the shape of the flow straight upward from a fountain be explained? Specifically, the stream goes straight up and then seems to widen as it gets higher, forming a Y-shape. Why does the water not flow upward in a perfectly straight column?
![]() ANSWER:
ANSWER:
You assume that all water comes out the spout with a speed straight up. But,
in fact, most "pieces" of the emergent water have small components of their
velocities which are horizontal. Then, over a large vertical distance the
stream will spread. Also there is a Bernoulli effect where the pressure is
lower at the surface of the fast-moving water.
![]() QUESTION:
QUESTION:
If you stopped an Earth satellite dead in its tracks, it would simply crash into the Earth.Why, then, donât the communications satellites that hover motionless above the same spot on Earth crash into the Earth?
![]() ANSWER:
ANSWER:
A communication satellite just appears to be standing still
because it stays exactly above a point on the equator. The point on the
equator goes around once every 24 hours and so does the communications
satellite. Here is a
cool site
where you can see the locations of the satellites. The ring of satellites
about 6 earth radii out are the communication satellites.
![]() QUESTION:
QUESTION:
I notice that sometimes there is no any or very weak sound while I open a new sealed bottle of carbonated water? But more frequently, that sound is very loud. Why is that happened, even it is the same type of water and the same manufacturer?
![]() ANSWER:
ANSWER:
Carbonated water is essentially water with carbon dioxide disolved in
it. When it is bottled the little bit of air in the top is at atmospheric
pressure. If everthing is the same as when it was bottled, when you open the
bottle there is little fizz. But, if you shake it up it causes the carbon
dioxide gas to go out of the water and into the little pocket of air at the
top of the bottle and the pressure in that air therefore increases because
there is more gas in the same volume. Now if you open it there is a fizz as
the gas escapes. Also, if you store it in the refrigerator it will tend to
fizz when you open it because cold water can hold less carbon dioxide than
warm water.
![]() QUESTION:
QUESTION:
It takes 23 hours 56 min & a few seconds for earth to complete one rotation.Take it as 23hrs & 57 min.So there is a loss of 3 min daily in the watch or clock.But our watches and clocks are of 24 hrs(or 12*2). So after 240 days ther is a loss of 12 hours ie, when it is 12 noon actually the watch or clock will show 12 midnight yesterday.It is not happening.Why is it so?
![]() ANSWER:
ANSWER:
It is because the earth also travels around the sun in its orbit. Hence,
the time for the sun to go from exactly overhead to that position again is
not the time it takes the earth to rotate once on its axis. The 3 minute
difference makes sense: [(3 min/day)/(24x60 min/day)]x[365
days/year]=0.76 days/year, about three fourths. That means we are in error
by about one quarter of a day at the end of one year. Hence, we need to
add one day every fourth year to make it all come out right. Since it is not
exactly 3/4 we do not add the extra day once each century.
![]() QUESTION:
QUESTION:
On the drive to pre-school this morning, my 4 & 1/2 year old
son asked me why it gets colder the higher we go on/above the earth,
when it is actually closer to the sun there.
![]() ANSWER:
ANSWER:
Well explaining this to a budding scientist who is so young will be a
challenge, but there are few things more important than encouraging children
to think and inquire and question. Important point number one is to get your
son to appreciate how far the sun is from the earth. It looks like it is up
there just out of reach, but the distance is 93,000,000 miles; to put this
in perspective, the earth has a diameter of about 8,000 miles and so it is
more than 11,000 earths stacked up to get to the sun. Now, how far is he
ever likely to go above the earth? Maybe 40,000 feet, about 8 miles, in a
commercial airplane. How does 8 miles compare with 93,000,000 miles? Pretty
insignificant, eh? Here is how insignificant: If we had a really powerful
electric heater 2000 feet (like half a mile) away we would feel some heat
but how much more would we feel if we moved closer by one breadth of a hair?
That is roughly equivalent to 8 miles compared to 93,000,000 miles.
Now, why is it colder as we go up? This is a little trickier for a four year old but the principle is the same which makes a refrigerator work, if a gas is expanded without any heat flowing into or out of it, it cools. At higher altitudes the air pressure is lower, the air is thinner (which is why it is very hard to breathe at the top of a very tall mountain, or why commercial airliners have to be pressurized). So, warm air near the earth rises and as it goes up it must expand because the pressure gets lower and very little heat goes into or out of it because air is a pretty poor conductor. So it cools.
![]() QUESTION:
QUESTION:
I've read that if an atomic nucleus was scaled up to the size of a period in size twelve font, the nearest orbiting electron would be 3m away. I've also heard that a nucleus the size of a baseball at 'home plate' would have its nearest electrons orbiting at 2nd base. Is there a specific ratio involved for 'size of nucleus': 'distance of electrons?'
![]() ANSWER:
ANSWER:
The nearest orbiting electron is not a very good yardstick to get a
feeling for nuclear sizes because it depends on what atom you are talking
about. Lead will have a much smaller "nearest orbit" than helium will. The
reason is that the electric force on the innermost electrons is much
stronger as the charge of the nucleus increases. What is more meaningful is
to compare the size of the nucleus with the size of the atom (which
quantifies the largest rather than smallest orbits). An atom has a
diameter on the order of 10-10 m whereas the nucleus has a
diameter on the order of 10-14 m. So the size ratio is ~1:10,000.
If the atom is the size of a football field (100 m) the nucleus is the size
of 100x10-4 m=1 cm, about the size of a gumball.
![]() QUESTION:
QUESTION:
A coworker and I have a disagreement over the law for the "Conservation of Matter".
We both agree on.... "Matter cannot be created or destroyed, only changed in form. The mass that was present before a chemical or physical change equals the mass that is present after the change"
But I add, "...except in a nuclear reaction." upon which he disagrees. Most online definitions seem to support his stance, although I have found some to support mine.
Who is right.
![]() ANSWER:
ANSWER:
Your "conservation of matter" is an antiquated idea. When you burn
something, let's say carbon, by combining it with oxygen, energy is
released. Where does this energy come from? The simple fact is that if you
were to weigh the carbon dioxide and compare that weight with the carbon and
oxygen you started with you would find less mass. Unfortunately, this is an
impossible experiment to do because chemistry is such an inefficient way of
producing energy that the mass change would be incredibly tiny. Suppose that
you get 1,000,000 joules of energy by burning a few pounds of coal; this
corresponds to a mass change of 106/(3x108)2
which is about 10-12 kg. This comes from E=mc2.
Imagine trying to measure this mass change if you burnt a few pounds of coal
to get this million joules of energy! In a way it was lucky because so much
of 18th and 19th century chemistry is based on this
conservation idea. In a nuclear reaction, as you note, the energy conversion
is much more efficient and masses change by measurable amounts, something
like 1%. So, the final accounting is: you are wrong once and right once and
your coworker is wrong twice. But, I would give you both a marginal pass on
the first because we learn this in chemistry courses and it is almost right.
![]() QUESTION:
QUESTION:
What do you think about the current work being done by the CERN? I think the Large Hadron Collider is a waste of money, when you consider that billions of people on the earth are living under the threaten of starving. Will the result of this experiment benifit our daily life?
![]() ANSWER:
ANSWER:
This is not an easy question. My own perspective is that what makes us human
is our quest for knowledge and understanding. And, if you make a little
study of the amount of money spent on science compared with the money needed
to feed the world's hungry, the fraction is very small. A society devoted
only to putting food on our tables, roofs over our heads, and clothes on our
backs is a society, in my opinion, not worth living in. When the space
programs were begun in the 50s and 60s many people said that it had no
relevance to everyday life, but it has spawned the whole current high tech
society we live in today providing employment for millions; because of
science we have myriad things never dreamed of a half century ago. While I
am sympathetic to the plight of the hungry, I suspect that if we stopped
spending money on science we would not shift all those resources to the
poor. A more appropriate question might be how limited resources for science
should be allocated among the many scientific endeavors wanting support.
![]() QUESTION:
QUESTION:
My question is very simple, but think as I might I cannot
figure it out! Why is the constant c in the famous equation E=mc2,
squared? If c is the speed of light which cannot be surpassed, then why
is it squared? Why not cubed or otherwise exponated?(sp. word?) Why is
it not to the first power as the entity itself? I have always wondered
this, maybe you could help me out.
![]() ANSWER:
ANSWER:
The question boils down to what we call dimensional analysis in
science. Every meaningful quantity in physics has dimensions which are
either mass (M), length (L) or time (T), or some combination of the three.
For example, a velocity, which is what c is, must have dimensions of
L/T (like miles/hour). Now, energy had dimensions of ML2/T2,
and mass, of course, has dimensions of M. The only way you can put M and L/T
together to get ML2/T2, is M(L/T)2 and
hence mc2 and not mc or mc3 or
any other combination. Another example is kinetic energy of a particle of
mass m moving with speed v,
Đ
mv2. There are ways to make energy from quantities
other than mass and velocity. For example energy may be written as a force
times a distance (this kind of energy is often called work) and force has
dimensions ML/T2, and distance is, of course, L, so together they
are ML2/T2. It's the old you can't compare apples and
oranges thing.
Incidentally, you can square the speed of light. The square is not a velocity and does not violate the fact that nothing can go faster. The speed of light is the largest possible velocity, not the largest possible number.
![]() QUESTION:
QUESTION:
According to Wikipedia, the universe is about 93 billion light years in diameter. If the earth were the size of a proton, how big would the universe be on this scale?
![]() ANSWER:
ANSWER:
A light year is about 1016 m, so the size of the universe
would be about 1027 m. The diameter of the earth is about 107
m and the size of a proton is about 10-15 m. Put it all together
and get reduced size of the universe=1027(10-15/107)=100,000
m.
![]() QUESTION:
QUESTION:
I teach 6th grade science and need some help on force/work/motion. Our textbook says that when I lift a book I am doing work as the force is applied in the direction of the motion. However, if I then carry that book across the room I am doing no work as the force continues to be vertical but the motion is horizontal. In terms of the definition of work this makes sense to me. However, I know my students will protest. How can I carry the book across the room and do no work on the book. It will seem counterintuitive to them. Can you help me explain this to 12 year olds? Am I doing work on my body, not the book? Isn't work being done to move the book across the room?
![]() ANSWER:
ANSWER:
The first thing you need to do is talk with your students about how
science works. It is very important, particularly in physics, that concepts
be well defined. And even though, sometimes, that definition may not jibe
with every day usage, there is usually a pretty good reason why it has been
defined the way it is. In the case of work done by a force on an object as
the object moves some distance, the definition, as you know, is the
distance times the component of the force along the distance. If
this were not the definition, then the whole concept of energy, so
enormously important to the whole structure of physics, would not be useful
at all. So, in carrying the book across the room with constant speed, indeed
no work is done.
I am not trying to beg the question here and now I will address the very valid concern you have. Let us just imagine an even simpler case, just holding the book in your hand with your arm stretched out from your body. Are you doing any work? What is needed to do work? Energy, right? Does it take any energy to hold the book there? It certainly does. Where does the energy come from? Essentially from last night's dinner and the oxygen you have recently breathed. Your muscles are doing work and the energy to do this work comes from chemical reactions in you body. I read about just this thing recently and it is very interesting. It turns out that all the little fibers in your muscles are constantly slipping and pulling back, so there really is a force being applied in the direction of the displacement. But the work is not being done on the book! The book remains at rest (or, if you are walking across the room, moving with constant speed), so it is not the recipient of this work. Remember, you can always identify work being done by energy changing, and the book moving at constant speed horizontally has constant energy.
![]() QUESTION:
QUESTION:
If you fold 3 sheets of paper -- each 8 x 11 inches. One is folded as an accordion. The second is folded as a triangular prism. The third is folded as a rectangular prism. If you stand these papers up (tall), place a piece of cardboard atop of each, and on that place a 500 gram weight, why does the accordian folded paper support the weight while the others do not?
This is a Science experiment that I want to do with my class who is studying structures. Therefore, could you please explain it in simple terms --childlike language? ie. weight dispersal is difficult for them to understand without a clear explanation.
![]() ANSWER:
ANSWER:
Try this: You have a very heavy table you wish to lift. You get ten
children and place them all around the table and they can lift it easily.
Now, you ask three children to do the same job and they cannot hold the
table up at all.
![]() QUESTION:
QUESTION:
I am having an argument with someone who insists that an untetherd balloon does NOT travel at the speed of the wind because of some wooly notion the movement relative to the Earths surface (even when not on it) requires an external force.
![]() ANSWER:
ANSWER:
There are all kinds of hair-splitting arguments you could make about the
preciseness of the balloon's being at rest relative to the air, but that
does not seem to be the heart of your question. For your purposes, a balloon
moves with the wind. This is why you cannot steer a balloon if it does not
have any propulsion other than the wind. I remember reading a book when I
was a boy in which they dragged a rope (touching the ground) to slow the
balloon down so that it could be steered. Movement relative to the earth's
surface requires a force only if you move through the air, but not if you
and the air are moving together.
![]() QUESTION:
QUESTION:
Iâm wondering whether or not a closed system like a terrarium with one plant seed in it would weigh more after the seed grew into a plant, my mind tells me that it canât because itâs a closed system, but then again there is a plant where there was not one before. Can we actually measure the weight of the "light" that has been converted into the plant?
![]() ANSWER:
ANSWER:
Energy must be added (in the form of light) to allow the plant to grow.
(Most seeds will germinate in the dark using the energy stored in the seed,
but this will quickly be exhausted.) Light provides the energy for the
chemistry which happens when the plant grows. The actual material (atoms)
used to make the plant can only come from material already in the terrariumâseed,
soil, water. The energy from the light gets converted into mass via E=mc2,
but that amount of mass is extraordinarily tiny, way smaller than you would
be able to measure.
![]() QUESTION:
QUESTION:
On a recent episode of Myth Busters I saw a demonstration of smething that I could not explain or understand. They basically took two phone books and wove the pages from each book into one another creating one larger book. At the end of each book steel plates were drilled and then steel cables were attached . It took two military tanks and 8,000 lbs of force to pull the two books apart! How do you explain that? There is no appreciable normal force applied to the books so what force was causing the resistance?
I am somewhat baffled by this and when someone first told me about it I didn't even believe it until I saw a video clip of it. can you explain it?
![]() ANSWER:
ANSWER:
As a physicist, I do not find this astonishing at all. There is just
about no limit to how big friction can be. For example, if you press the
palms of your hands together as hard as you can, you will be unable to slide
them. Try this experiment: rip out one page of the phone book and put it in
the middle sticking out some. You do not need to press very hard on the
phone book to not be able to pull the page out, it will tear first. To
understand this quantitatively is pretty hard because the maximum friction
force betwen two surfaces is propotional to how hard they are pressed
together (called the normal force) and I do not how to determine what the
normal force might be. It appears that the books in the experiment are taped
shut to keep them from flopping open, but this tape would put a modest
normal force on all the pages. Suppose that each surrface contributes a
frictional force of 1 lb (right order of magnitude from the one page
experiment) and there are 1000 pages per book and therefore 2000 surfaces,
then it would take 2000 lb, again the right order of magnitues.
![]() QUESTION:
QUESTION:
If Rayleigh scattering is inversely proportional to the fourth power of the wavelength, then why isn't the sky violet, or at least indigo?
![]() ANSWER:
ANSWER:
Actually, the sky is purple! Your eye, an imperfect instrument, is more
sensitive to blue than to purple.
![]() QUESTION:
QUESTION:
In a monoatomic gas, the mean velocities of the atoms is directly related to its temperature . When the gas is compressed by a very slow moving piston, the temperature raises. Within the kinetic theory of gases, what is the physical mechanim that makes the atoms increase their velocities?
![]() ANSWER:
ANSWER:
I assume we are talking about a gas which is insulated from its
environment, that is no heat flows in or out. When a gas is compressed, work
must be done on it. The work must increase the energy of the gas and the
only way to do that (for a monotonic ideal gas) is to increase the kinetic
energy of the molecules. If you want a mechanism, think of a piston moving
and colliding with the molecules and thereby increasing their kinetic
energies.
![]() QUESTION:
QUESTION:
Why is a metal door knob colder to touch then a wooden door knob?
![]() ANSWER:
ANSWER:
When your hand comes in contact with something, the more rapidly it
conducts heat away from your hand the colder it feels. Metal is a much
better heat conductor than wood.
![]() QUESTION:
QUESTION:
Consider two hollow spheres of equal size anchored under water. One is airtight. The other has an opening at its lowest point, but no water enters because the air pressure inside is equal to the water pressure at the opening. Will the open sphere have slightly less buoyancy because the pressurized air inside is more dense, or more buoyancy because the air pressure acting on all the upper surfaces exceeds the water pressure acting on the outside of those surfaces?
![]() ANSWER:
ANSWER:
The buoyant force is determined only by the amount of fluid displaced
(equal to the weight of that displaced fluid), so the buoyant force on each
will be the same. The weight of the pressurized sphere will be slightly
greater so its net upward force (buoyant force minus weight) will be
smaller.
![]() QUESTION:
QUESTION:
If a photovoltaic cell is energised by artificial light, can the cell output (KW) exceed the energy consumed by the light source?
![]() ANSWER:
ANSWER:
No. Three reasons:
- Photovoltaic cells are not 100% efficient.
- No light source is 100% efficient; for example a light bulb converts most of its energy to heat, not light.
- Energy conservation forbids that you can get more energy out of a closed system than you put in.
![]() QUESTION:
QUESTION:
My son and I got into an argument about the arm speed of baseball pitchers. He tried to tell me that in order for a pitcher to throw a ball 100 mph, that the release point of said pitcher's arm must be moving at least that speed (a little faster, in fact, to account for the weight of the ball and the resistance the ball would face before reaching the plate). I said it was preposterous to think that the pitcher's arm, at any point, could move that fast. Who is right and why?
![]() ANSWER:
ANSWER:
Your son is right. If your hand were going slower than the ball it would
not be in contact with the ball. When the ball is released it will never go
any faster than it is at that time in the horizontal direction, so how could
it have gotten going 100 mph if not by your hand?
![]() QUESTION:
QUESTION:
I'm a piping superintendant for a mechanical contractor and I have a pressure testing related question. I must pressure test (w/ air) the system at 660 psi. The pipe is 4" I.D. with a total developed length of 3,900 '. I have calculated the total cu/ft of air required at atmospheric pressure to be 340.27 cu/ft. How do I determine the amount of air that will be required in cu/ft at a pressure of 660 psi?
![]() ANSWER:
ANSWER:
660 PSI is about 44 times atmospheric pressure. So, providing the
temperature stays constant, you will need about 44 times more air to fill
the pipe at this pressure.
![]() QUESTION:
QUESTION:
Why does it take more energy to raise colder water by a degree ? I'm guessing that its because thermal conductivity rates vary with temperature.
eg
At 4 °C : the amount of energy required to warm one gram of air-free water from 3.5 °C to 4.5 °C at standard atmospheric pressure is about 4.204 J.
At 15 °C : the amount of energy required to warm one gram of air-free water from 14.5 °C to 15.5 °C at standard atmospheric pressure is about 4.1855 J.
![]() ANSWER:
ANSWER:
Conductivity is not the reason. The reason is that the
specific heat
of a material is a function of temperature.
![]() QUESTION:
QUESTION:
OK there is a question , the answer of which I cannot seem to fathom and it has always bugged me. What is the nature of probablity? Let me state this question with examples to show you what I am getting at. As I myself am at a loss at how to express the exact nature of this question any other way.
Lets say that you flip a quarter, nececcary assumptions being of course that you are flipping by hand and that by doing such you have perfectly random coin flipping ability. The first time you do you have a 50/50 chance of getting heads or tail. Now the more times you get the same result (lets say heads) will automatically make the next result more likely to be of the opposite result. Since it is unlikely to flip heads lets say 4 times in a row, it is even more unlikely to flip it 40 times in a row. So if you flip twice and get heads then it is less likely that you will get heads a third flip and even less so for a 4th, a 5th, etc. My question is that if I have just flipped three heads then what is the invisible force that makes the next flip more likely to be tails. what is its nature, and what negates it. For instance If I let a different person flip for me after the third heads result then will I be more likely to get a heads again since now it is a 50/50 chance. Or would the statistics be the same, since we would be flipping as a group. What about time. If I flipped three heads, and then waited 4 years before flipping again would I still be under the influence of the quarters that I flipped 4 years earlier? If not then why would 4 years be different than 4 seconds? or 4 milliseconds (If I could flip that fast). Is it the grouping of these events together that causes the probabability influence? What would happen if I decided to simply arbitrarily group random things into a structured pattern of my own making, then could I influence the outcome of future events. If not then why not? Another way to ask the question, could I make myself more likely to win at a coin flippiping contest if I flipped coins at home before the contest and waited until I flipped three or four heads in a row, then did nothing until the contest......would I be more likely to flip a tails, and If I chose tails before the contest then would I therefore be beating the odds? If not then why not?
![]() ANSWER:
ANSWER:
This violates the groundrule requiring concise, well-focused questions!
Furthermore it is not physics. Nevertheless, I will answer it because it is
such a pervasive misconception. The chance that a coin will come heads up is
50/50 every time you toss it. Asking what it will be this time is not the
same question as asking what is the probability of having 40 heads in a row.
I have known very smart people who cannot get over the feeling that if you
throw five heads in a row that a tails is somehow due to come up. If you
cannot get this, don't gamble!
![]() QUESTION:
QUESTION:
Why do people put their hands up during a rollercoaster ride?
![]() ANSWER:
ANSWER:
I do not think there is any physics involved here, just the "look, Ma,
no hands" principle.

![]() QUESTION:
QUESTION:
I took several photos from a window seat on the right side of a 2 engine propeller plane. The camera is an iphone. Why did the camera capture the blades of the plane as shown .Go to :
http://gallery.me.com/douglaskochel#100050
![]() ANSWER:
ANSWER:
I am not really sure, but I have an idea. A film camera exposes the
whole image at once whereas I presume that a digital camera reads its data
row-by-row. So when one row is read and recorded the propeller will be in a
different place then when later rows are read. Anybody reading this who has
a more informed idea, I would be glad to see it.
![]() ANSWER:
ANSWER:
Thanks to the reader who sent this in: "The iPhone is demonstrating the "rolling shutter" effect, see paper:
http://arxiv.org/PS_cache/cs/pdf/0503/0503076v1.pdf"
Scanning through the paper briefly, it seems that my answer was,
essentially, correct.
![]() ANSWER:
ANSWER:
Here are some more links:
http://www.youtube.com/watch?v=T055cp-JFUA
http://www.youtube.com/watch?v=Um3bGnSqLRY&feature=related
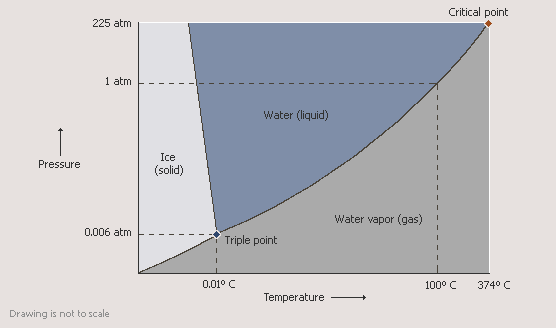
![]() QUESTION:
QUESTION:
I was wondering something about my pressure cooker. Obviously it requires energy, converting water into steam to create pressure to cook the food at higher temperatures than "normal" air pressure allows. If the food were submerged in the water totally, would I just be boiling my dinner and not getting any effects of the pressure? I was told you can't compress water, so any food sitting in water is not under extra pressure. In a pressurized environment, can water heat past 215 degrees F?
![]() ANSWER:
ANSWER:
The boiling point of water is determined by the pressure, is
approximately 2120 F at atmospheric pressure. I believe that
pressure cookers were invented because at high altitudes the pressure is
lower and so the lowered boiling point makes it take a long time to, say,
boil a potato. So a pressure cooker is tightly confined and when heated the
pressure increases causing the water in the pot to be have temperatures
higher than 2120 so things can cook more rapidly. You are
incorrect in assuming that, because water is (almost) incompressible, it is
"not under extra pressure". The pressure in both the water and the steam/air
above it are increased to the same value when the cooker is heated. To the
left is a phase diagram for water. Note that when the pressure is increased
beyond 1 atmosphere the boiling point (the temperature at which liquid and
vapor coesist) increases rapidly as the pressure is increased.
![]() QUESTION:
QUESTION:
I need a simple explanation on kilograms - newton conversion formula to explain to my nephew who is 11 years old.
![]() ANSWER:
ANSWER:
Technically, you cannot convert one to the other because they measure
different things: a newton (N) is a unit of force and a kilogram (kg) is a
unit of mass. Here is the rub, though: in contries where metric measures are
used, the kg is used to measure weight even though weight, the force which
the earth exerts on something, is not a mass. This, naturally, leads to
confusion when we first are learning about mass and force. If you take a 1
kg mass to the moon, it would weigh less than it does on the earth. So, to
make this clear we must carefully define force and weight as they relate to
mass. A force of one newton is that force which, when applied to a 1 kg mass
results in an acceleration of 1 m/s2. Now, an 11 year old
does not usually understand what acceleration is other than the qualitative
speeding up or slowing down. An object, starting from rest, with an
acceleration of 1 m/s2 has a speed of 1 m/s after 1 s, a speed of
2 m/s after 2 s, etc; it is the rate at which speed changes. (I guess
it is also helpful to know Newton's second law which says force is mass
times acceleration, so a 3 N force acting on a 3 kg mass also results in an
acceleration of 1 m/s.) Now, if you drop an object (regardless of its mass)
near the surface of the earth it will be observed to have an acceleration of
9.8 m/s2 so, the
force on it must equal its mass times 9.8. Therefore, e.g., a 10 kg mass
will have a weight of 98 N. At the market, what is measured is the weight of
the potatoes so when the scale reads 10 kg it means that the weight is 98 N.
That same scale would not read 10 kg on the moon for the same 10 kg of
potatoes.
![]() QUESTION:
QUESTION:
Hi, my sister and I were having a debate last night that I'm hoping you can settle for us. It seems to be a fairly rudimentary physics problem, but I'm hoping you'll tackle it.
It started when she claimed that the water coming out of a shower is falling at a slower rate near the ground than it is when it first comes out of the shower head. As evidence, she said that she couldn't rinse out her hair as effectively if she were sitting down in the shower than if she put her head right near the shower head...that the pressure isn't the same.
I said that was largely because the water just isn't as concentrated-- as it falls that 4-5 feet, it spreads out so the total force is less. Also, the angle of the shower head (probably not pointed straight down) contributes to the "spreading out".
That factor aside, she claimed the real reason was that gravity actually slows down the water as it falls. Air resistance (and terminal velocity) aside, her argument was that the water comes out of the shower head at a greater force than gravity, and once it's no longer under that pressure (having left the pipes and shower head), the speed actually backs off to meet the force of gravity.
I wasn't buying it. My simplified analogy is: if you were standing on the top of a building, pointed a gun straight down at the ground, and fired it, is the bullet travelling as fast when it hits the ground as when it first leaves the gun? Again, air resistance aside, I say yes-- it's travelling at least as fast...no way is it slowing down!
![]() ANSWER:
ANSWER:
I will address what I see as the main question, does the water slow
down, below. But let me make a few comments about your remarks. First, you
are right that the water spreads and so less water per second hits her head
if she is sitting down and this may very well be the main reason it is
slower to rinse. The argument that gravity slows the water down is totally
wrong unless the water is going up. But, your insistence in neglecting air
resistance throws out the whole possibility of the water slowing down since
that is the only thing which could do it. So let us discuss terminal
velocity. We know that if we drop something it will continue accelerating
until the force down (its weight) equals the force up (air resistance) at
which point it will fall with constant speed (terminal velocity). But what
if we don't drop it but rather throw it down with a speed larger than the
terminal velocity? Initially the air resistance will be larger than the
weight and so it will slow down but continue doing so until it slows down to
the terminal velocity. So, your contention that a bullet fired from the top
of a building will not slow down is wrong; it will if the initial velocity
is greater than the terminal velocity. So, how about the shower water? I
looked up the terminal velocity of a raindrop, which should be at least
comparable to the droplets from the shower: about 9 m/s. Now, the exit
velocity at the shower head will vary depending on the model and I could not
find any reference to actual speeds on the internet. So, I went outside and
turned on the hose with a spray nozzle attached to it and it appeared to go
maybe 20 feet high, about 7 meters; this would correspond to an initial
speed of about 15 m/s (just a rough estimate including an estimate of the
effect of air resistance). I think it is quite likely that the speed out of
the nozzle is greater than 9 m/s and so your sister is probably right but
definitely for the wrong reason. The reason her hair rinses better at the
top, though, is probably mainly for the reason you suggest which is
essentially greater flux, that is more water per second over her scalp, not
any reduction in speed.
![]() QUESTION:
QUESTION:
We currently use photons and electrons to send 1s and 0s to other places. Would neutrons work too? Could one send these neutrons to places where electrons or photons could not go? Like through the Earth? Google says there are portable neutron sources available. Are they strong enough and can they be modulated and detected at long distances?
![]() ANSWER:
ANSWER:
Neutrons have numerous things going against them:
- They are unstable outside a nucleus and beta decay after about 15 minutes.
- Although they do not interact electromagnetically, they do interact with nuclei via the strong force so their range, while longer than that of charged particles, is short and they would not pass through the earth, only go a few inches in.
- Because they have no charge, they are impossible to manipulate, steer, speed up, or slow down.
- They are difficult to detect, again because of their lack of charge.
![]() QUESTION:
QUESTION:
If it is true that there is no cold, only the absence of heat - my question is 'why'? As in why is there no heat, only the absence of cold?
![]() ANSWER:
ANSWER:
First of all, heat is energy transfer, not energy content. For example,
heat flows from a hot object to a cold one but you do not say that the hot
object has more heat than the cold one. It is important in science to
clearly distinguish between qualitative concepts and quantitative concepts.
Cold is an adjective, not a noun, and it is a qualitative concept which
refers to something with a relatively low temperature but it has no
quantitative meaning. Similarly, hot or warm are qualitative adjectives
which refer to something with a relatively high temperature. The temperature
of something is a quantitative measurement of how much internal energy the
object has. Temperature measures the average energy per constituent.
In a gas this is the average kinetic energy per molecule. So if one thing is
hot and another cold, the hot one has a higher average energy per atom. In
order to increase the temperature of something you have to add energy and
this is done by causing heat to flow to it.
![]() QUESTION:
QUESTION:
When my husband told me that the leak in our Westerbeke diesel was caused by capillary action and surface tension, I had no idea what he meant. I understand the concept of surface tension- the water molecules are more attracted to each other than a different subsstance. But I don't get the "adhesive" force. Is the water molecule on the top attracted to a charge coming from the wall of the tube? or hole in the paper towlel.
What gives.? I am a writer and trying to differentiate between the two for a metaphor.
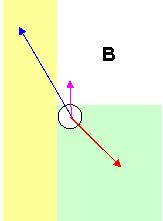
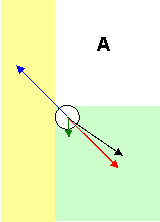
![]() ANSWER:
ANSWER:
Capillary action is the result of surface tension. The answer is a bit
involved, but I will try to spell it out below. I will try to keep it as
free from math and jargon as I can.
- Any two atoms or molecules will exert forces on each other. There is no general way you can summarize the details of this other than the forces are always electrical in nature. Put two oxygen molecules in proximity with each other and they will form an O2 molecule. Put many water molecules near each other (at not too high a temperature) and they will hold each other in a liquid because of attractive forces among them. Put a water molecule near a "glass molecule" (mainly SiO2) and the force of attraction will be greater than between two water molecules. The force between similar (different) molecules is referred to as cohesion (adhesion).
- Now, if you compare water molecules inside the liquid with those on the surface, those inside interact with more of their neighbors and therefore have a lower energy than those on the surface who interact with only about half as many. (An attractive interaction lowers energy; you can see this because two things which are stuck together can be pulled apart by adding energy, doing work, so it takes more energy to remove a molecule from the volume than from the surface.) A physical system will seek its lowest energy state, so the liquid (if isolated) will minimize the number on the surface, that is the surface area will be minimized. So a small volume of water will tend to become a sphere and a large body of water will tend to have a flat surface to achieve this. This tendency to have the surface push into its mimimum area is what surface tension is.
- But, what happens if the liquid is in contact with another material, say glass? Look at the figures to the right where I try to represent a molecule (circle) where the surface of the liquid meets the surface of the container. The molecule experiences a force down, its weight, (green); an average force due to all its water neighbors, down and to the right (black); and a force due to its interaction with the glass (blue). In figure A to the right I have chosen the force due to the glass to be exactly equal to the sum (red) of the weight and water forces. So all the forces add up to zero, the molecule is in equilibrium, and the surface will be perfectly flat; there is no meniscus and there would be no capillary action. But, suppose the glass force were a little bigger than the water+weight force. In that case the forces will not be balanced but instead there would be a net force (water+weight+glass) straight up (pink). This is the force which drags up the edges of the surface to make a concave meniscus and this upward force is what drags up the column of water in a thin tube, the capillary action. If the glass force were weaker than the water force, the force would have been down and we would have a convex meniscus curving down at the edges; this is what happens with mercury in glass and the capillary action is opposite, the surface is pushed down at the edges. You can read more in the Wikipedia article on capillary action.
- What happens is that the capillary force keeps pulling the water up but this means that more and more water has to be held up. Eventually, the edge of the meniscus will supply the same force as the weight of the water and it will stop rising. It is fairly easy to convince yourself that the height to which the water will rise in the tube is inversely proportional to the diameter of the tube. So if the capillary action causes a fluid to rise 1 cm in a 1 mm tube, the fluid will rise 10 cm in a 0.1 mm tube.
- A paper towel is just like a huge tangle of tiny, tiny worm holes and the water is drawn into them by capillary action.
![]() QUESTION:
QUESTION:
This has to do with the conservation of energy.
A spring is compressed and kept compressed by binding it with wire.
The whole assembly is tossed into an acid bath and is completely dissolved.
What happens to the potential energy stored in the spring?
![]() ANSWER:
ANSWER:
The potential energy has its origins at the atomic level. When you
compress a spring you cause the atoms to be more closely spaced than they
"want to be" and it takes work to scrunch them up like that, hence the
potential energy. When the spring atoms come apart, they start a little
closer to each other than they would if the spring were not compressed, so
they move a little faster when they leave and so the average kinetic energy
of all the atoms is a little larger than it would have been for the
uncompressed spring. The potential energy ends up as kinetic energy (thermal
energy).
![]() QUESTION:
QUESTION:
This has to do with the conservation of energy.
A spring is compressed and kept compressed by binding it with wire.
The whole assembly is tossed into an acid bath and is completely dissolved.
What happens to the potential energy stored in the spring?
![]() ANSWER:
ANSWER:
The potential energy has its origins at the atomic level. When you
compress a spring you cause the atoms to be more closely spaced than they
"want to be" and it takes work to scrunch them up like that, hence the
potential energy. When the spring atoms come apart, they start a little
closer to each other than they would if the spring were not compressed, so
they move a little faster when they leave and so the average kinetic energy
of all the atoms is a little larger than it would have been for the
uncompressed spring. The potential energy ends up as kinetic energy (thermal
energy).
![]() QUESTION:
QUESTION:
I have a question about why the shape of a window affects the
structure of the object it's in. For example, when Britain was producing
their commercial airplane "The Comet", they started tearing apart and
falling out of the sky over time. The engineers discovered that the
fuselage was getting cracks and tears due to the square-shaped windows
on the plane. I know that the cabin in the plane is pressurized so that
the passengers can breathe normally, and this extra pressure pushes on
the inside of the plane. But why does the air pressure cause cracks
around the square windows as opposed to the newer round windows? I heard
that it's because the corners of square windows act as some sort of
stress point or something, and over time they cause the cracks, but this
is where my understanding gets fuzzy. Can you please explain how those
square windows differ from the round windows of today, and how the
corners of the square windows caused the cracks/tears in the fuselage?
![]() ANSWER:
ANSWER:
The causes of the crashes of the
Comet was
actually a lot more complicated than you suggest. The main problem was an
underestimation of the importance of metal fatigue in the overall
engineering of an aircraft. It is like if you bend a paperclip back and
forth repeatedly, eventually it breaks; than is metal fatigue. Every time
the aircraft is pressurized it is like bending the paperclip. It is well
known that sharp corners are more vulnerable to failure under stress than
gentler curves; I have spent some time trying to think how to make this
plausible. I think a good analogy is the arch used in architecture. Compare
an arch to a "pointy arch" like an inverted V. The V will be able to hold
much less total weight because it will fail at its apex. The arch
distributes the load carrying over its whole length. Or, imagine that you
have a V-shaped object and a semicircular object of similar material and you
grasp the ends of each and try to break them; I think it is probably clear
that the V will break first, right at its apex, whereas the semicircle will
require much more force to break because no one part of it carries the brunt
of the force. Another example is in glass cutting. I have made many stained
glass windows and one of the things you learn early on is that it is almost
impossible to cut a sharp indentation into the glass without breaking it.
![]() QUESTION:
QUESTION:
I've been told that when a gas is cooled, it takes up less volume, and therefore its density increases.
I've also been told that a gas always fills its volume (i.e. a container).
These two ideas, however, seem to contradict one another. On the one hand, cooling a gas causes it to contract and decrease in volume, which would increase its density. However, on the other hand, a gas will always fill its volume, which means its volume doesn't change when cooled. Therefore, if the volume doesn't change when cooled since a gas will always fill its volume, then its density would not increase.
In other words, if a gas will always fill its volume, then cooling it would not increase its density since the gas always fills its volume and therefore remains at the same volume. In a closed container, if a gas expands to fill the volume of the container, then how could cooling the gas increase its density? How could a gas fill its container/volume on the one hand, but then on the other hand, when its cooled, decrease in volume and therefore increase in density? If a gas fills its container/volume, it wouldn't increase in density when cooled since it FILLS its volume. Therefore, since it fills its volume, the volume of the gas would remain constant. Therefore, since the volume of the gas would remain constant, its density would not increase when cooled.
So my question is, how could a gas increase in density when cooled if that same gas always fills the volume of the container it's in?
![]() ANSWER:
ANSWER:
That's a pretty long question which requires only a short answer. If the
amount of gas remains constant, the relation between pressure, volume, and
temperature is PV/T=constant. The situation you describe has a
constraint that volume remains a constant, so P/T=constant
which means that as the temperature goes down the pressure goes down; and,
the volume stays the same. So, if you cool a gas in a rigid container, the
density remains the same.
![]() QUESTION:
QUESTION:
If there is a yacht on a lake and it drops its anchor overboad. What happens to the water level in the lake. Apparently it falls. I have no idea why. Shouldn't it stay the same using common sense.
![]() ANSWER:
ANSWER:
This is a little complicated, so bear with me. First, you have to
understand Archimedes' principle which states that if you have an object in
a fluid, the fluid exerts an upward force on it and the magnitude of that
force (called the buoyant force) is equal to the weight of the fluid which
the object displaced. So, the boat plus anchor floating on the water have
displaced a volume of water whose weight is the same as the weight of the
boat plus anchor. Now, remove the anchor. Now the water is holding up only
the weight of the boat, so the water will have fallen equivalent to removing
water whose weight equals that of the anchor; but, the anchor is denser than
water, so the volume of the water of equal weight is bigger than the volume
of the anchor. Now, putting the anchor into the water, the water level will
go up equivalent to adding a volume of water equal to the volume of the
anchor. So the net effect has been a fall followed by a smaller rise, a net
fall.
![]() QUESTION:
QUESTION:
I took two cups of unequal size (one can hold a higher volume than the other), filled the largest one with water almost to the top, and left the other one empty. Then I took a twisted piece of paper towel and put one end in each cup. Capillary action caused water from one cup to go to the other and the other began to fill. My question is why did the empty cup only fill up until both cups were of equal height, rather than of equal volume.
![]() SIMILAR QUESTION:
SIMILAR QUESTION:
I've noticed that when steeping a cup of tea, the fluid will follow the string up and over the teacup lip and create a puddle around the cup, if I leave it steeping too long. What is this principle known as? I vaguely recall it from Jr. High, but am too old to remember it clearly and I can't manage to word the question properly to get a "Google" response to it.
![]() ANSWER:
ANSWER:
Capillary action uses the meniscus force to lift the water to the
highest point of your paper towel (string). Once it gets there, it can just flow
downhill. So, in essence, your piece of paper (string) just becomes a siphon.
![]() QUESTION:
QUESTION:
Why is the speed of sound slower in lead (25 degrees C) than fresh water when generally sound travels faster in solids than in liquids?
![]() ANSWER:
ANSWER:
The speed of sound is determined by two things, the elasticity of
the medium and the density
ρ
of the medium. How the elasticity is measured differs for liquids and
solids, for solids we use Young's modulus Y and for liquids the bulk
modulus B. So, the standard predictions are vwater=√(B/ρ)=√(2.2x109/1000)=1483
m/s and
vlead=√(Y/ρ)=√(16x109/11.3x103)=1190
m/s. The experimental numbers are 1493 m/s and 1158 m/s, respectively, in
pretty remarkable agreement with the predicted values. So, let's get
qualitative. Lead is not at all elastic. Can you imagine how a bell made out
of lead would sound? How well would a lead ball bounce off a hard floor?
Also lead is very dense, so that also drags down the speed down. So, we
should not really be surprised that the speed of sound is lower than in many
other solids.
![]() QUESTION:
QUESTION:
I understand that the power that a stream of moving water can generate or develop is proportional to the velocity of the water current, cubed. Can you explain where this comes from?
![]() ANSWER:
ANSWER:
I never saw this before, but I think I can figure it out. The power
P generated by a force F may be written as P=Fv where
v is the speed of the agent applying the force (the water here). Now,
if an object moves through a fluid, it experiences a drag force which, for
most cases of interest, is proportional to the square of the velocity,
F=Cv2. If the fluid exerts that force on the object moving
through it, then if it is the fluid that is moving instead of the object,
the force must be the same. Therefore, P=Cv3.
![]() QUESTION:
QUESTION:
enrico fermi once pointed out that a standerd lecture period [50 mint] is close to one micro centuery. how long is a micro centuery in minutes. and what is the percentage difference from fermi claim?
![]() ANSWER:
ANSWER:
Well, this isn't physics, but 1
μCentury=(100 yr)(365.25 days/yr)(24 hr/day)(60 min/hr)x10-6=52.6
min. Fermi was a real smart guy, particularly famous for "back of the
envelope" estimates.
![]() QUESTION:
QUESTION:
how does lightning conductor works during a thunder storm ?
![]() ANSWER:
ANSWER:
The basic idea is to provide a conducting path to take the current
from the lightning and send it to the ground. However, it also "attracts"
the lightening so that it hits the rod rather than the house. When a charged
cloud passes over, the objects under it become charged by induction. The rod
has a sharp point which means when the rod becomes charged, the electric
field near the tip becomes very strong and often strong enough to cause
electrons to stream into the air; this is called corona discharge (or St.
Elmo's fire if on the top of the mast of a ship). This charge density and
strong electric field then has the effect of directing a strike at the rod.
![]() QUESTION:
QUESTION:
This question came up in class and we went over it, but I still could not understand it. Assume the earth had sufficient nutrients and adequate water, no toxins present, uninterrupted growth, division every 20 minutes, and had e coli bacterium. How long would it take for this mass of bacterium to equal the weight of the earth? Is it possible?
![]() ANSWER:
ANSWER:
I think your teacher was trying to illustrate exponential growth. If
you have not had any calculus, you will not understand my answer. Anything
whose population changes in a way that is proportional to the population
itself gives rise to exponential growth or decay. So, dN/dt=cN
where N is the number at some time t, dN/dt is
the rate at which N is changing, and c is a constant of
proportionality. If c>0, N is increasing (growth); if c<0,
N is decreasing (decay). This should make sense to youâif
you double the number, you double the rate at which the number is growing.
The solution to this equation is N=N0ect
where N0 is the number at t=0. In our case we will
choose N0=1 (start with a single bacterium). What we know
is that if t=20 min, N=2, so 2=e20c. Solving
this, c=20/ln2 where ln is the natural logarithm. Now, denoting the
mass of one bacterium as m, we know that the mass M at any
time must be M=Nm=me20ct and if we let
M=Mearth, and solve for t we find t=20 ln(Mearth/m)/ln2.
I will let you do the math and look up the constants. I get a little less
than 2 days.
![]() QUESTION:
QUESTION:
First, take a large round, flat-bottomed container and pour in 3 inches or more of water. Sprinkle in about a quarter to a half teaspoon of sand. First stir the water at random and notice how the sand distributes itself in a random manner. Then, swirl the water around in the container with a spoon or other utensil in a continuous clock-wise or counter clock-wise motion for several seconds. Remove the stirrer. Why do the particles of sand aggregate in the center of the vortex? Since they are heavier than water (they sink), why aren't they spun to the sides of the container due to the negative centripetal force? Is this behavior similar for air and, for example, saw dust in industrial dust collectors?
![]() ANSWER:
ANSWER:
Seems it is not a trivial question. There is a ton of stuff
here, all of which I have not waded through.
![]() FOLLOWUP:
FOLLOWUP:
I followed up on the reference to "Einstein's Tea Leaves" and found
a very good
article.

![]() QUESTION:
QUESTION:
A friend claims that the inside of an LP record (or CD for that
matter) spins faster than the outside. I say this is impossible because
if it were true, the record/CD would tear itself apart. Who is right?
![]() ANSWER:
ANSWER:
LPs and CDs spin differently and therefore must be discussed
separately. First we need to clarify what "spin faster" means. Since a disk
is a rigid object, each point has the same angular velocity,
revolutions per minute (rpm) for example. Each point on any disk rotating at
100 rpm goes around 100 times per minute. However, if you look at the speed
of any point on the disk, the farther out you go the faster the point goes;
a point 4 inches from the axis will move with a speed twice as large as a
point 2 inches from the axis. An LP is sometimes referred to as a "33"
because it always spins with an angular velocity 33 1/3 rpm. The groove
moves past the needle slower and slower as the needle moves in during the
playing. So, if you were to microscopically look at what the groove looked
like for some note, that would look different depending where on the record
that note was recorded. CDs, on the other hand, are designed so that the
speed with which the data on the disk pass the laser reader is always the
same, so as the CD plays, the angular velocity is constantly adjusted to
keep the linear velocity of the data being read the same. The CD, unlike the
LP, reads from the middle out and as the laser moves out the angular
velocity decreases. So, clearly neither of you is right: inside and outside
spin the same, outside moves faster, CDs and LPs have different motions, and
nothing tears itself apart.
![]() QUESTION:
QUESTION:
Does a battery weigh more when full than discharged?
If not, then why is E= mc2 not relevant - assuming that discharging does some sort of work like emit light, heat or cause motion?
I googled this for an hour: I found about an equal # of YES/NO responses.
![]() ANSWER:
ANSWER:
I'll weigh in on this one (pun intended)! Yes, if you add energy to
anything you increase its mass. Let's get an idea of how much. The energy
stored in a 3.6 V lithium battery is about 104 J, so the
corresponding mass would be m=E/c2=104/(3x108)2≈10-13
kg. This is about 100,000 times smaller than the mass of a single dust
particle. Lots of luck trying to measure this mass change!
![]() QUESTION:
QUESTION:
I have been watching a lot of basketballgames lately and I have started to wonder:
Why does the net go up when scoring?
The ball goes down so I simply cant figure out why the net goes up. Can you help me?
![]() ANSWER:
ANSWER:
The unstretched net is a little smaller than the ball, so the ball
pulls it down when it goes through. But the net is attached to the rim and
so the net pulls the rim down. But, the rim is made of steel and therefore
acts like a spring; when the rim bounces back up it pulls the net up.
![]() QUESTION:
QUESTION:
How large or small is light year relative to our everyday life?
![]() ANSWER:
ANSWER:
A light year is the distance that light travels in one year. It is
almost incomprehensibly large compared to any lengths in your everyday life.
A light year is about 6x1012 miles. A spaceship traveling the speed of the
shuttle (about 20,000 mph) would require 34 thousand years to go one light
year.
![]() QUESTION:
QUESTION:
There is an urban myth, that if you put a can of liquid in a warm
woolly sock, soak the sock in water, and hang the sock in the summer
sun, the liquid gets colder. Is this true?
![]() ANSWER:
ANSWER:
This is no urban myth, this is a simple scientific fact. The sock
need not be warm. To understand this, take a wet towel and spin it rapidly
around for a few seconds. You will find that it gets very cold. That is
because it takes energy to evaporate a liquid and when the water evaporates
it extracts that energy from the water not yet evaporated. Most canteens are
covered with a fabric; the reason is that the fabric can be soaked and it
will keep the water inside cool even when the temperature is very hot. In
the desert water is sometimes carried in fabric bags which never dry out
until the bag is empty because the water slowly seeps out and evaporates.
There are also evaporative coolers which are very efficient air conditioners
if humidity is not an issue.
![]() QUESTION:
QUESTION:
The weight of a body is less when it is submerged in water, due to the upthrust.
But the weight of the water column above the body can be far more than the upthrust(weight of the displaced water).
So is it not that the weight of a body can increase when it is submerged in water?
![]() ANSWER:
ANSWER:
The weight of an object in a fluid is not less than its weight
anywhere elseâthe weight is the force
the earth exerts on something. However, there is an additional force when it
is in a fluid, the buoyant force (which you call "upthrust") which makes it
appear that the object has less weight. You do not understand the
nature of your "upthrust", however. When the object is completely submerged,
the water above the top pushes down on it as you suggest; but the water
under the object pushes up with an even greater force. It is the difference
of these two forces which is the buoyant force.
![]() QUESTION:
QUESTION:
My wife filled a metal thermos with soup (she says it was warm / room temp). She closed the lid tight and put it in the fridge. Next day, I take out of fridge and have trouble unscrewing top. As soon as I get it loose the lid pops up, soup explodes all over me and the counter, and it looks as if the soup is boiling for a few seconds. Actual temp is much cooler than I would have expected it to be for just being in the fridge.
![]() ANSWER:
ANSWER:
Here is what I think. The soup has some air above it. When sealed
the contents of the thermos are very hot. When they get cold, the pressure
in the air gets very much lower, so you have a partial vacuum inside the
thermosâthat is why you have trouble
opening it at first. But, when you finally get it cracked, outside air
rushes into the low pressure region thrusting out the soup all over the
place. I expect "âŚcooler than I would have expectedâŚ" is a misperception on
your part.
![]() QUESTION:
QUESTION:
I am an audio engineer and I have a question related to sound and
waveforms. What is the physical difference between a sound wave and an
electromagnetic wave? I understand that sound waves are mechanical
waves, and need a medium through which to travel, while electromagnetic
waves can exist in a vacuum. But what is the actual difference in energy
or physical makeup between the two? If I took an analog sine wave
oscillator with a frequency of say 440hz (which would be audible), and
sped it up to let's say, 1GHz, would I be generating a Microwave? Or is
there some physical difference between a sound wave and an
electromagnetic wave?
![]() ANSWER:
ANSWER:
Two things could hardly be more different than sound and light. The
only thing they have in common are that both are waves. In the case of
sound, the waves are longitudinal, that is, the stuff which is "waving" is
waving in the same direction as the wave is traveling; think of a hanging
slinky spring which has compression pulses moving in it. Sound needs a
medium in which to travel; since the molecules in the medium are what
transmit the wave, if you take away the medium, you necessarily take away
the wave. In the case of light, the waves are transverse, that is, the stuff
which is "waving" is waving perpendicular to the direction the wave is
traveling. What is waving in an electromagnetic wave is electric and
magnetic fields. Since the wave is not comprised of the medium through which
it might be moving, no medium is requiredâthe
wave can travel through empty space. You can read more detail about
electromagnetic waves in an
earlier answer.
Your 1 GHz sound wave is most certainly not a microwave, it is ultrasound.

transverse longitudinal
![]() QUESTION:
QUESTION:
11.2 km/s is the escape speed from Earth. Is it possible to escape from Earth at half this speed? Is it possible to escape from Earth at one quarter this speed?
![]() ANSWER:
ANSWER:
You need to understand what is meant by escape speed. It is the
minimum speed which you give an object at the earth's surface so that it
will never come back. Of course, you could escape with any speed, say 1
cm/year, but only if you keep pushing on it to keep it going; but that is
not what escape speed means.
![]() QUESTION:
QUESTION:
Hey! I was told that the human uterus can exert up to 400 n or 100 lbf of...force(?) when doing its uterus thing and pushing out a baby. I have no frame of reference for these numbers/units, and my wikipedia research provided me only with a lot of not-worth-the-mental-effort equations and definitions.
I'm just trying to put these facts in perspective. For example, is 100 lbf comparable to pushing a couch across the room? Lifting a small car? Doing 40 pushups? 600 pushups? Are any of these examples even remotely related to the units "n" or "lbf?"
I'm not seeking any kind of technical answer about how many calories explode when you exert 400 n of superpower to move a million-joule flavored kilogram 9 meters (by now you can see my level of physics expertise), just a simple "Oh 100 lbf, that's like X, which you are very familiar with and can relate to! What a neat thing to know about the uterus, we have all gained a new appreciation for its strength!"
![]() ANSWER:
ANSWER:
A small woman weighs about 100 lb; 100 lb is the force you would have to exert to hold her up. A 100 lb woman having a baby would exert a force with her uterus which would be the same force she would have to exert to do a pullup.
![]() QUESTION:
QUESTION:
If two quantities have different dimensions, can they be multiplied
or added? please support the answer with examples because i really can't
differentiate between the dimensions and the units !!
![]() ANSWER:
ANSWER:
First, let's be clear on what are meant by dimensions and units.
Dimensions are fundamental notions of three quantitiesâmass
(M), length (L), and time (T); units are the particular
operationally defined ways we measure the three dimensionsâthe kilogram (kg)
for M, the meter (m) for L, and the second (s) for T
are the so-called SI units, the ones scientists prefer. There are other
units for other quantities like force or energy or power, but all are
ultimately describable in terms of kg, m, and s. So, can two quantities with
different dimensions be added? Suppose we add 2 kg to 5 s; this would have
no meaning. It's the old "apples and oranges" thing, it just makes no sense.
On the other hand, we can multiply (or divide) things which have different
dimensions. For example, if a car goes 80 miles in 2 hours, its average
speed is (80 miles)/(2 hours)=40 mph; if a 2 kg object has an acceleration
of 3 m/s2, the net force on it is the product 6 kg∙m/s2
and the frequently occruing SI unit for force is given a name, the Newton
(N): 1 N=1 kg∙m/s2. Can you add things with the same dimensions
but different units? Yes, but the answer is usually not very useful. For
example, 1 ft + 1 m is the length of a foot and a meter, but that doesn't
say much; it would be better to convert to one or the other units before
adding, such as 1 ft=0.3048 m and so
1 ft + 1 m=1.3048 m. Also, it not a good idea to mix units when
multiplying quantities. For example, how far does a car going 50 mph go in 3
minute? The distance D=vt=(50 mi/hr)(3 min)=150 mi∙min/hr is pretty
meaningless because how far is a mi∙min/hr? Better to convert to the same
time units, for example 3 min=1/20 hr, so D=50x(1/20) mi=2.5 mi.
![]() QUESTION:
QUESTION:
if you have a rope the length of the equator around earth ,and then
you give the rope 3' feet slack ,how high would the rope rise above the
surface??
![]() ANSWER:
ANSWER:
I hope you don't think that the rope would spontaneously rise up if
it were longer than the circumference of the earth; you would have a
slightly slack rope laying on the ground. If you are asking the difference
in radii between one circle with a circumference C and another of
circumference C+δ, that is not
really physics. But, it is easy enough to do. If C is the
circumference of the earth, then C=2πR where R=6.4x106
m and
C+δ=2πR' where
R' is the radius of the circle your rope would make if δ=3
ft≈1 m. Then R'-R=δ/(2π)≈0.16 m. Notice that the answer is
independent of Râif the circumference of the earth were 1 m and the
rope were 2 m long, the height of the rope above the earth would still be
0.16 m!
![]() QUESTION:
QUESTION:
If you stand on a shrinking planet so that in effect you get closer
to its, your weight will increase. But if you instead burrow into the
planet you get closer to its center,your weight will decrease. Explain
please
![]() ANSWER:
ANSWER:
On or inside a sphere, the force depends only on the mass inside
you, not on that outside you; also, the force decreases as 1/r2
where r is the distance to the center. As the planet shrinks (mass
the same but radius smaller), the mass below you stays the same but the
distance gets smaller, so you get heavier. If you burrow, the mass inside
decreases proportional to r3 (the volume of a sphere is 4πr3/3)
so, the force changes like r3/r2=r
and therefore decreases as r decreases.
![]() QUESTION:
QUESTION:
We say that the moon has the gravitational force one sixth in
comparison to that of the earth. If the earth has held an atmosphere
with its gravitational force which is 480 kilometers high, why canât the
moon even hold an atmosphere one sixth of the height of the atmosphere
which the earth has, that is, 80 kilometers?
![]() ANSWER:
ANSWER:
Holding an atmosphere of a given composition and temperature by
gravity is an "all-or-nothing" thing. To understand, you have to first
understand escape velocity. If you throw something upwards it falls back;
throw it harder and it goes higher; throw it faster and faster, and
eventually you will reach a speed where it will never come back down. This
is called the escape velocity and it depends, of course, on how strong the
gravity is. So, the escape velocity from the moon is much less than the
escape velocity from the earth. Now, we need to talk about the speeds of
molecules in a gas. At a given temperature, there is a distribution of
velocities, called the Maxell-Boltzmann distribution, shown to the right.
The average speed is determined by temperature (the hotter, the faster) and
mass of the molecules (the lighter, the faster). So, as shown by the figure,
a few are always going very fast, maybe even greater than escape velocity.
So, suppose that some of the molecules have speeds greater than escape
velocity, perhaps the
Đ
% shown on the right in the diagram; then these will escape. But now the
distribution will not be correct, so it will readjust itself so some of the
molecules go faster; then these, in turn, escape also, and so on until all
molecules have escaped. On earth, helium and hydrogen have very high speeds
so that earth's gravity is not capable of holding helium and hydrogen in its
atmosphere and there is virtually none of these in the atmosphere. But
heavier molecules (N2, O2, CO2, etc.)
have such a tiny fraction above escape velocity that they do not escape (at
least at any rate that can be measured). But, on the moon, all gases would
behave like hydrogen and helium do on earth and all escape.
![]() QUESTION:
QUESTION:
Does the transfer of energy takes place when when we push a huge rock
with all our might?where does energy go which we spend? I thought that
the transfer of energy does not take place with respect to the wall,and
muscular energy is changed into heat energy.BUT MY TECHER IS SAYS When
we push huge rock and fail to move it,the energy spent in doing so is
absorbed by the rock.This energy is converted into potential energy of
configuration of the rock which results in its deformation.Ho wever,this
deformation is not visible on account of the huge size of the rock.
![]() ANSWER:
ANSWER:
I always hate to say that a teacher is wrong, but he is in this
case. If this were true, then if you pushed long enough you could observe a
change in the rock. Also, the surface the rock is on is pushing up with a
force equal to the rock's weight, a force much larger than you can exert,
and that does not result in any significant deformation. What is happening
here is discussed in an earlier
answer. Essentially it is a biological answer, not a physical one. The
way muscles work makes them consume energy even if they do no external work,
and that energy would presumably end up as heat.
![]() QUESTION:
QUESTION:
If we on earth measure time the way we do according to earth rotation etc .. Is there a different measurement of time in relation to the universe or is it all to do with rotation ? As the earth slows down would time slow down?
![]() ANSWER:
ANSWER:
Earth's rotation has not been the standard for time for over 300
years. If earth's rotation slowed down, time would not slow down. Time
is measured relative to a particular atomic vibration (atomic clock)
which is constant (as far as we know) anywhere in the universe. The rate
at which clocks click does, however, depend on the velocity of the
clock. This is time dilation in special relativity but not really
observable in everyday life.
![]() QUESTION:
QUESTION:
I am not a physicist and these questions should make it pretty clear.
Could you calculate the mass of Human? If so would you then be able to
put that in to the mass-energy equivalence and figure out how much
energy I am?
![]() ANSWER:
ANSWER:
Sure. Suppose your weight is 200 lb, then your mass is about M=90
kg. The speed of light is about c=3x108 m/s and so
E=Mc2=90x9x1016≈8x1018
J. To put this into perspective, the energy consumption of the whole
world in a year is about 1.85x1010 megawatt hours≈6.7x1019
J, so the energy could supply the whole world for a little more than one
month.
![]() QUESTION:
QUESTION:
I am considering getting a tattoo of the equation for Newton's First Law of Motion and want to make sure it is correct (for obvious reasons). I am in my forties and this would be my first because it is the first thing that really spoke to me. Basically, to keep moving and doing :)
![]() ANSWER:
ANSWER:
Newton's first law is not conveniently stated in an equation. Are
you committed to that?
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
So this what I had; does this make sense from physics standpoint? I read it as "in the absence of any external force, the acceleration is zero" which to means covers the meaning I want, which is "keep moving and you WILL keep moving, but sit still and you WILL keep sitting still". It is a reminder for me to stay active, adventurous and to keep moving..
![]() ANSWER:
ANSWER:
OK, how about the equation to the right? Here is what that
equation says: the rate at which momentum (p) changes is zero. If
this were Newton's second law there would be force F in place of
the zero. Momentum is mass times velocity, but the word momentum fits in
well with what you want to convey, I think. The equation says that if
the momentum is zero, it stays that way, if it is not, it stays that
way. Partly, Newton's first law is a special case of Newton's second law
(when there is no external force) and that aspect of it is often called
the law of inertia. The first law also has a deeper meaning, but that is
not relevant for what you want.
![]() QUESTION:
QUESTION:
Do you know why do golf balls have dimples? (does it make them more
aerodynamic and if so why?)
![]() ANSWER:
ANSWER:
I am The Physicist, I know everything! WellâŚmaybe
not everything. I do know why golf balls are dimpled and the reason is
also why tennis balls are fuzzy. Aerodynamics can be very complicated,
but I can explain it qualitatively. Air drag on a projectile is caused
mainly by the turbulent wake behind the object; the pressure is lower in
this turbulent region so there is more force on the front pushing back
than there is on the back pushing forward. As shown in the figure to the
left, if the air moves smoothly over the ball, the turbulent wake is
very broad. But, if you break up the boundary layer of air with some
kind of roughness on the surface, you get a much smaller turbulent wake
and therefore less drag, as shown in the figure to the right. It is
counterintuitive that a rough ball encounters less air drag than a
smooth one, but true.
![]() QUESTION:
QUESTION:
I know that 1u is equal to 1.6605x10^-27. Where does atomic mass come
from and why is it not the proton?
![]() ANSWER:
ANSWER:
When defining a unit of measurement (like u, the atomic mass unit),
one of the most important considerations is to have a readily available
standard for comparison. The atomic mass unit is defined to be 1/12 the
mass of a 12C atom where 12C is the isotope of
carbon with 6 protons and six neutrons. Carbon is a very abundant
element, easily obtainable. So, the atomic mass unit is 1/12 the mass of
12 g of 12C (1 mole) divided by Avagadro's number:
12/6.02214x1023/12=1.66054x10-24 g=1.66054x10-27
kg. The mass of a proton is much more inconvenient to measure.
![]() QUESTION:
QUESTION:
I am a writer and I am writing a science fiction novel with some events
taking place in a space station. My question is: Is it possible to have
a zone in the station that has gravity while another zone (rather
adjacent one) has zero gravity? This is important to me because although
the general plot of the story is fiction, the science part of it has to
be true to what we know so far to be possible.
![]() ANSWER:
ANSWER:
The only way we know to create "artificial gravity" is to be in an
accelerating frame. For example, an accelerating elevator in empty space
will appear to have a gravitational fieldâyou
could stand on the floor, would feel your "weight". A more practical way
to achieve acceleration is to move in a circle or radius R with
speed v. You would then experience an acceleration v2/R
which, if equal to earth's gravitational acceleration (9.8 m/s2),
would feel just like the gravity you were used to. You probably saw a
similar thing on the movie 2001: A Space Odyssey, where Dave
exercized on a spinning track. You could have an adjacent part of the
station which was not rotating. Gravity which just switches on, like on
the starship Enterprise on Star Trek, is not possible with
currently known physics.
![]() QUESTION:
QUESTION:
Which string of guitar produces highest pitch?
![]() ANSWER:
ANSWER:
That depends on how the instrument is tuned. A stringed instrument
is tuned by adjusting the tension in the strings. The speed of waves on
a string which has a mass density
μ kilograms per meter and tension T in Newtons is v=√(T/μ)
in meters per second. Since v=fλ where f is frequency
and λ is wavelength, f=(√(T/μ))/λ.
For a string like a guitar string, both ends are fixed so the length is
L and the fundamental pitch is that for which λ=2L, so
the frequency is f=(√(T/μ))/(2L).
So, there are three ways you can change the pitch:
-
Change T; this is what you do with tuning pegs.
-
Change μ; note that the lower-pitch strings are often thicker than the higher-pitch strings.
-
Change L; this is what you do when you press the string to the fret with your finger.
![]() QUESTION:
QUESTION:
What is difference between displacement amplitude and pressure amplitude and which has more direct influence on loudness of sound?
![]() ANSWER:
ANSWER:
Sound waves are longitudinal waves which means that the atoms in the
gas oscillate in the direction parallel to the direction the wave
travels. An average atom, if you watch it, vibrates back and forth. So
you can characterize the wave by specifying the frequency and maximum
value (amplitude) of this oscillating displacement. The loudness
(intensity) of the sound is proportional to the square of the amplitude.
The figure to the right indicates this displacement vibration with the
little red arrow. But, because all the atoms are vibrating like this,
the result is that at any time the atoms in some regions are more
tightly packed than if there were no sound and, in other regions, less
densely packed. Hence the pressure at any particular place changes with
the frequency of the sound. The intensity of the blue circles in the
figure indicate the pressure at any time. The amplitude of this pressure
oscillation is the maximum deviation from the pressure in the gas if
there were no sound. Again, the intensity is proportional to the square
of the amplitude of the pressure oscillations, but it is obviously a
different proportionality constant.
![]() QUESTION:
QUESTION:
why it is happen that when we look outside window of moving car ,nearby objects move faster and far off objects seems to be stationary
![]() ANSWER:
ANSWER:

![]() QUESTION:
QUESTION:
why is the filament of an incandescant bulb thin ?
![]() ANSWER:
ANSWER:
The power P dissipated in a tungsten wire, of length L
and diameter d, and for a voltage of 120 volts is approximately
P=2x1011 d2/L.
So, suppose you wanted a 100 watt lightbulb with a 1 cm=10-2
m length filament, then
d=2x10-6
m=2 microns; this is about ten times smaller than a human hair, so not
very practical. To be able to make it thicker you have to make it
longer. A typical filament is about 40 microns in diameter and so the
length would have to be about 3 meters long. So, how are you going to
fit such a long filament in a little light bulb? The photo shown to the
right shows you! Coil it. The thicker you make the filament, the longer
it has to be.

![]() QUESTION:
QUESTION:
why doesn't your head hurt when raindrops fall on your head despite
having an accelation of 9.8 m/s?
![]() ANSWER:
ANSWER:
The terminal velocity for a typical raindrop is only about 20 mph (9 m/s),
so it is not accelerating all the way down from the cloud. Also, when
the drop hits your head, it deforms, splatters, and spreads out, so much of
its energy goes into this, making it not hurt like a similar sized hail
stone would.
![]() QUESTION:
QUESTION:
If there is an absolute low temperature (absolute zero) is there such a thing as an absolute high temperature?
![]() ANSWER:
ANSWER:
Thinking of temperature as the average kinetic energy per particle,
the higher the temperature, the larger the speeds of the particles. But,
as velocities cannot exceed the light, there would seem to be an upper
limit. However, kinetic energy is not simply
Đ
mv2 and the energy can continue to increase even
though there eventually is negligible increase in velocity. Therefore,
there is no upper limit to the temperature a collection of particles may
have. However, there is not an inifinte amount of energy in the
universe, so the upper limit would be determined by the total energy in
the rest of the universe! That said, the question is not really quite so
simple. For a much more advanced discussion of this topic, see this
article.
![]() QUESTION:
QUESTION:
A chromatic musical instrument can be used to play any key, but does it
play them all equally well? In other words, will it sound better it
certain keys? (If you need a specific instrument, lets say a simple
Helmholtz resonator, such as an ocarina.) I have read a lot about
formants, the harmonic series and fundamental notes. I know that
individual notes will have slightly varying timbres (harmonic series).
But will the fundamental note have the richest harmonics?
![]() ANSWER:
ANSWER:
I guess, first of all, we should say that "sound better" is a
subjective thing. The physics of musical instruments is a field unto
itself and I certainly cannot cover it in a concise answer which is the
modus operandi of this site. A few things are worth pointing out,
though. First, terminology: the fundamental frequency is the lowest
frequency present in the note, other frequencies present are called
overtones, sometimes overtones are harmonics which are integer multiples
of the fundamental frequency. Why does the same note played on a piano
and a violin sound so different? It is determined by the timbre of the
note played on each instrument and this is, essentially, the relative
amplitudes of the fundamental and all the overtones produced by the
instrument. The amazing thing is that many musical sounds which your
brain perceives as some note, contains much more of the overtones than
of the fundamental, the frequency of the note which your brain is
hearing. In fact, if you remove the fundamental entirely from the
spectrum, your brain still will "hear" the note as the fundamental. That
is why tiny speakers which cannot put out, say f=20 Hz, bass
frquencies still sound like they have bass response. Some instruments
produce overtones which are just slightly sharper or flatter than the
corresponding harmonics, again affecting the timbre. As an example I
show the Fourier analysis for three notes played on a bassoon. Note that
at the lowest frequency, f=98 Hz, the fundamental is less loud
than most of the overtones. It gets more complicated still if you
consider time; if you look at the relative loudnesses of all the
overtones, they change from when the note begins (say plucking a string)
and when it ends (string stops vibrating).
![]() QUESTION:
QUESTION:
I would like to know why wet sand is used for the zeer pot? Is it possible to use other material instead, for example, just simply water ?
![]() ANSWER:
ANSWER:
A zeer pot is essentially an evaporative refrigerator. The cooling
results from evaporation of water. The faster the water evaporates, the
cooler food in the inner pot is kept. If you just filled the space
between with water, it would evaporate slowly because there would be
only a small surface from which it could evaporate. Putting in sand, the
water wets the sand and there is a large amount of surface area from
which water can evaporate much more quickly.
![]() QUESTION:
QUESTION:
How did the value of G=6*10^-11 derived???
or
How did Newton got the value of the constant G?
![]() ANSWER:
ANSWER:
G is a fundamental constant of nature, it cannot be derived. Newton
did not get the value of G, the best he could do was get the
product GM where M is the mass of the sun. He shows that
GM=4π2a3/T2
where a is the semimajor axis of the orbit of a planet and
T is the period. This is a derivation of Kepler's third law and
is the real triumph of Newton. It was 70 years after Newton's death that
the first measurement of G was made by
Cavendish.
You can also get MearthG=R2g
where Mearth is the mass of the earth, R is
the radius of the earth, and g=9.8 m/s2; so Newton
could have found the ratio Mearth/M without
knowing G.
![]() QUESTION:
QUESTION:
If we leave earth we would need a time scale not based off of the rotation of the earth. What would this time scale likely be and how would it progress?
![]() ANSWER:
ANSWER:
The unit of time is not at all based on the motion of the earth or
the solar system. Rather it is based on something called an
atomic clock.
See the definition of the
second. Just take an atomic clock with you when you leave earth.
![]() QUESTION:
QUESTION:
I have made an argument with a friend over the following,
A steel ball bearing was held just below a surface of a tank of water and released. He argued that at the instant of release, the acceleration was 9.81m/s2. His reason was there was no upthrust as the ball bearing had not moved yet. I disagreed. My argument was there was upthrust as it was in the water, be it moving or not. Hence the starting acceleration was less than 9.81m/s2.
![]() ANSWER:
ANSWER:
You need to ask what the forces on the ball bearing are. There is
its own weight, straight down. There is a drag force which is usually
taken to be proportional to some power of the velocity and is, at least
to a good approximation, zero if the ball is not moving; even if the
fluid were very viscous, like honey for example, the initial downward
acceleration would be g to a good approximation, but almost
immediately terminal velocity would be achieved and it would move with
constant velocity. This is what your friend has in mind, I believe.
However, there is an additional force, the buoyant force which is
upward. Therefore, the initial acceleration when v=0 would be
less than g even if the drag force were exactly zero. You should
avoid qualitative terms like "upthrust" and think about forces on the
ball bearing.
![]() QUESTION:
QUESTION:
Why does air friction increase as an object is falling? Say a ball is falling from a very high position. We know that its acceleration at first is 10 m/s. But after some time it will decelerate until it is moving with a constant velocity. Why is this so? I know that air friction is the reason but why does the friction increase? The surface area of the falling object remains constant but why the opposing frictional force increases?
![]() ANSWER:
ANSWER:
Think about the pressure in a box containing a gas with temperature
T. It is well known that the pressure on any side of inside of
the box is proportional to T. But the temperature is just
proportional to the average kinetic energy per molecule, so the force on
the wall is proportional to the square of the average speed of the
molecules. When an object is falling, it is being hit by air molecules,
and the faster it falls, the faster it sees those molecules colliding
with it. So, it is sort of like seeing the effective air temperature
getting bigger in the frame of the object, hence a bigger pressure and
force.
![]() QUESTION:
QUESTION:
Hello, I am a U.S. Navy Diver and my buddies and I like to sit around and talk about the physics relating to our job. One scenario that has come up is regarding the straw in the glass of water trick where you place your finger over the top of the straw creating a suction or vacuum and then are able to lift the water yada yada. My question is that if you can replicate the scenario to be large enough for a man to swim up the straw could he? and if so what would happen when he reached the vacuum at the top of the straw. We were thinking that if you dipped a large tube in to a swimming pool, capped off the top and then lifted the tube 20 or so feet in the air and left just enough of the tube (2 ft) in the pool could a man swim up the tube? If he could what depth would his depth gage read at the mouth of the tube and apon ascent up the tube so forth. Also, I believe there is a vacuum of space at the very top of the tube. What would happen if the man got all the way up the tube and tried to take a breath?
scenario to be large enough for a man to swim up the straw could he? and if so what would happen when he reached the vacuum at the top of the straw. We were thinking that if you dipped a large tube in to a swimming pool, capped off the top and then lifted the tube 20 or so feet in the air and left just enough of the tube (2 ft) in the pool could a man swim up the tube? If he could what depth would his depth gage read at the mouth of the tube and apon ascent up the tube so forth. Also, I believe there is a vacuum of space at the very top of the tube. What would happen if the man got all the way up the tube and tried to take a breath?
![]() ANSWER:
ANSWER:
The pressure at the surface of the uncontained water is atmospheric
(PA) and the deeper (d) down you go, the
greater the pressure (P) becomes because of the weight of the
water above you, P=PA+ρgd
where ρ is the mass density of water and g is the
acceleration due to gravity (so ρg is the weight density). Now,
the pressure at the top of the contained water is zero, and the pressure
you feel in the tube will therefore decrease as you go up to some height
h, P=PA-ρgh.
When h is about 10 m (where the top surface is) the pressure
in the water (and therefore on you) is zero and this would be just like
being ejected into space from the space station, very uncomfortable to
say the least. You would not have to go very high up the tube before
feeling very uncomfortable. You would, however, experience the same
buoyancy in the tube because this does not depend on the pressure, just
the pressure gradient which is the same everywhere in the water. If your
head popped out the top surface in the tube, there would be no breathing
since there is no air, but you would be unconscious and likely dead by
then anyway. (To get a vacuum at the top and a top surface, your tube
must be longer than 10.3 m, about 34 ft.)
![]() QUESTION:
QUESTION:
What caused Felix' Baumgartner to go into a flat spin? I thought at that altitude he was in space and there was no atmosphere. Someone told me it was an effect of gravity but I just don't see that way as I think about it.
![]() ANSWER:
ANSWER:
If there were "no atmosphere", his helium balloon would not
have gotten there in the first place. Although the density of the air up
there is way less than at sea level, there is still some.
![]() QUESTION:
QUESTION:
Why the energy corresponding to the most probable speed is not the most probable energy?
![]() ANSWER:
ANSWER:
What is the most probable speed? If the distribution of
speeds is N(v)dv, then the most probable speed is the
location of the greatest maximum of this function determined by setting dN/dv=0
and solving for the maximum which I will call v1. Now,
what is the distribution of E=Đ
mv2?
N(v)dv=N(√(2E/m))(dv/dE)dE≡N'(E)dE,
so N'(E)=N(√(2E/m))(dv/dE)
and the solutions to dN'/dE=0 do not necessarly lead to the same values of v
as the solutions of dN/dv=0 do; I will call the speed of the
most probable energy v2. I will do one simple example.
Suppose N(v)=cv2exp(-cv2)
where c is a constant with units s2/m2 (see the
graph to the right). Then dN/dv=0=2c¡exp(-cv2)[v-cv3]
which has three solutions (for positive v), v=∞
(minimum), v=0 (minimum), and v=v1=1/√c
(maximum). Now, I will leave it to you to show that N'(E)=cE1/2¡exp(-2cE/m))/(21/2m3/2).
Then dN'/dE=0=[Đ
E-1/2â(2c/m)E1/2]exp(-2cE/m),
with two solutions, E=∞ (minimum), and E=m/4c
(maximum); so, Đ
mv22=m/4c and
v2=1/√(2c)≠v1.

![]() QUESTION:
QUESTION:
If light in earths atmosphere goes a little slower than light in a vacum, then how come when you turn on a light or laser pointer you don't hear a sonic boom?
![]() ANSWER:
ANSWER:
A sonic boom occurs when a source of sound (airplane, for
example, or bull whip) moves through a medium faster than the speed of sound
in that medium. A light source (photons) is not a source of sound. There is a similar situation when a charged particle
moves through a medium faster than light moves through that mediumâI
guess you might call it an optic boom. This phenomenon is called Čerenkov
radiation and happens often in water-moderated nuclear reactors which
exhibit a blue glow because electrons (β radiation) go faster than the speed
of light in water; that blue light is your optic boom, actually billions of
booms from billions of electrons.
![]() QUESTION:
QUESTION:
If i'm riding at 100mph how much pressure in lbs is exerted onto the bridge of my nose by my glasses? Is there a sliding scale conversion i can keep in mind as i'm riding?
![]() ANSWER:
ANSWER:
There is a very handy approximate formula for the force F
on an object of area A in a wind of speed v, F≈ŃAv2;
this formula must use SI units, v in m/s, A in m2,
and F in N. I will convert your numbers to SI, do the calculation,
then convert back. For the speed, v=100 mph=45 m/s; I will estimate
your glasses to have an area of two lenses, each about 2.5"x2.5"=6.25 in2=0.004
m2, so A=0.008 m2. So, I find the force is F≈4
N=0.9 lb. So, something like a pound of force will be applied over the area
the glasses frame touches you. Notice that the force is proportional to the
square of the speed, so if you go half the speed (50 mph) you will only
experience Ń the force. The scale you should keep in mind is that the force
increases like the square of the speed.
![]() QUESTION:
QUESTION:
How tall can a steel cylinder be before it collapses under its own weight?
![]() ANSWER:
ANSWER:
There is a classic estimate by Victor Weisskopf of the
maximum height a mountain can be which you can see
here.
The height h must be smaller than the height where the material down
low would start to melt. This inequality is given by h<E/(Ampg)
where E is the energy per molecule necessary to melt the material, A
is the molecular weight, mp is the mass of a proton, and
g is the acceleration due to gravity. For your steel cylinder I used
the latent heat of fusion of iron (A=56) to calculate E=2.5x10-20
J/molecule. Then you find h<30,000 m. Keep in mind that this is just
a rough estimate; a more accurate calculation would have to be done by an
engineer. Also, this assumes you can build it on something which can support
it and that would not be possible since rock requires less energy to melt
(4.8x10-20 J/molecule, according to the
article referenced above) than iron.
![]() QUESTION:
QUESTION:
Is there a direct relationship between sound level (Decibels), Frequency and Intensity of Sound Wave?
![]() ANSWER:
ANSWER:
A decibel (dB) is a relative measurement of sound loudness,
not an absolute measure. The definition of the decibel level L of a sound
with intensity I relative to another intensity I0
is L=10¡log10(I/I0). Usually I0
is chosen to be the intensity of the threshold of hearing 10-12
W/m2. Technically, the threshold of hearing is dependent on
the frequency, but for most applications the reference level is simply
chosen as 10-12 so that L=10¡log10(I/10-12)
if I is measured in W/m2. Thus, for I=10-12
W/m2, L=0 dB. It is important to note that, like the
Richter scale for earthquakes, dB is a log scale, so an increase of 1 dB is
an increase of a factor of 10 in intensity; for example, 5 dB has an
intensity 100 times bigger than 3 dB.
![]() QUESTION:
QUESTION:
If all objects are attracted by the force of
Gravity to the center of the earth, why aren't air moloculesd sucked
down to the floor?
![]() ANSWER:
ANSWER:
They are, but they don't
just go there and stay. Since the molecules are flying around with
large velocities because of their temperature, they don't all just lie
on the floor. However, there are more near the floor than there are
near the ceiling. And, the higher you go, the fewer and fewer there are
and eventually there are none—space. If there were no gravity at
all, the air would all eventually leak out into space.
![]() QUESTION:
QUESTION:
Are all isotopes of iron magnetic or has nobody
ever performed experiments upon the isolated isotopes to find out?
![]() ANSWER:
ANSWER:
Ferromagnetism is an
atomic, not nuclear, effect and all isotopes of iron are ferromagnetic.
![]() QUESTION:
QUESTION:
If heat causes most materials to expand, why do
certain clothes shrink when put in the dryer?
![]() ANSWER:
ANSWER:
Obviously, shrinkage has
nothing to do with thermal expansion since the clothes do not return to
their original size when they cool down. So, we are really out of the
realm of physics. What happens is that cotton contains quite a lot of
cellulose and celluose is very good at soaking up water. But if the
water is removed very quickly, the cellulose fibers become considerably
shorter than they were, causing the whole garment to become smaller. It
is usually possible, by rewetting the garment, stretching it, and
drying it slowly, to reverse shrinkage.
![]() QUESTION:
QUESTION:
why gravitational effects are ignored when
considering motion of electrons in electric fields
![]() ANSWER:
ANSWER:
Because gravitational
forces are insignificantly tiny compared to electric forces. Example:
an electron a distance of any distance r from a proton.
Gravitational force is Fg=MpMeG/r2
and electrostatic force is Fe=ke2/r2.
Hence Fg/Fe=MpMeG/ke2=1.7x10-27x9x10-31x6.67x10-11/(9x109x(1.6x10-16)2)=4.4x10-46.
![]() QUESTION:
QUESTION:
Just a quick question, Im a biologist and no virtually nothing of physics. There is currently a lot of debate here in the UK on the efficacy of homeopathic "medicines". According to homeopathists a 1M solution serially diluted 10^-50 (i.e. more than Avagadros constant) in water will somehow inprint a memory of the diluted molecule in the water.
The pro homeopath lobby are trying to explain this with Quantum mechanics, is there any scientific basis for this?
an example:
"From what I've read I think that Werner Heisenberg's theory of energy-time indeterminacy and Erwin SchrŃdinger's thoughts on there being many indeterminate states possible until a conscious observation is made are the most fitting regarding homeopathic efficacy.
These try to address the curious "tunneling" of electrons into unexpected areas of space, and the "wave function" of particles which are said to "collapse" into a specific state due to the act of being observed."
In my opinion, this kind of statement is total nonsense. There is no basis in physics or chemistry to support the claims of homeopathy that somehow water molecules have a "memory" of previously dissolved chemicals. And, if it were so, what about all the other substances which must have been previously dissolved in the history of the water?
![]() QUESTION:
QUESTION:
the pressure at the bottom of earth's atmosphere is about 100,000 N/m squared. this means there is a force of 100,000N acting on every square meter of area! your body has about 1.5 square meters of surface.why arent you crushed by the atmosphere?
Because we evolved in this environment and therefore there is a balancing pressure from inside. Every cell has an internal pressure of approximately one atmosphere. Think of a bottle which you have put a cork inâwhy doesn't it get crushed?
![]() QUESTION:
QUESTION:
A submarine rises to the ocean's surface to take on passengers and the sinks back underwater. How can I expain how this works to my 10 year old daughter.
A submarine has balast tanks. They start out filled with air. Now, sea water is permitted to flow into the tanks and it is just like a boat springing a leak, so it sinks. However, the air which was in these tanks is not allowed to escape, rather it is pumped into small tanks under high pressure. When the submarine wants to come back up, the air is pumped back into the tanks pushing the water back out into the ocean.
![]() QUESTION:
QUESTION:
I want to give my students a relative understanding of the size of an atom. If a bowling ball were enlarged to the size of the entire earth, (and its atoms enlarged proportionately), how big would just one of its atoms be? the size of a house? a beach ball?
The radius of a bowling ball is about 0.1 m and the radius of the earth is about 6x106 m. So the magnification is about 6x107. The radius of an atom is about 1 Đ=10-10 m, so the magnified atom would have a radius of about 6x107x10-10 m=6x10-3 m=6 mm, about a quarter of an inch. Now, take it a step farther: magnify the whole atom to the size of the earth, magnification now an additional 6x106/6x10-3=109. So the net magnification is now 6x107x109=6x1016. The radius of the atomic nucleus is about 5x10-15 m, so if the atom is the size of the earth, the nucleus has a radius of 6x1016x5x10-15 m=300 m. Atoms are small, nuclei are really small!
![]() QUESTION:
QUESTION:
The other day I was thinking about energy...and this led to a little wonder!
When we drop an object we hear a sound - this is generally considered as kinetic energy transforming into sound energy, correct?
Well, what I was wondering was why does it become sound energy? What in the history of the universe/physics determined that kinetic energy will become sound energy when there is a collision? Why doesn't it become heat energy for example, or light energy?
When two objects collide, kinetic energy is not conserved, that is, it does not remain constant. However, energy as a whole in an isolated system must be conserved, lost kinetic energy must show up somewhere. Where it shows up depends on the nature of the system but it can go to heat, sound (as you note), or, in rare cases, light. But, just because you hear it does not mean that sound is the only mechanism going on. In fact, even if the sound is very loud, the energy carried away by sound is usually a very small fraction of the total kinetic energy loss. In nearly all collisions of macroscopic objects, most of the energy is carried away as heat.
![]()
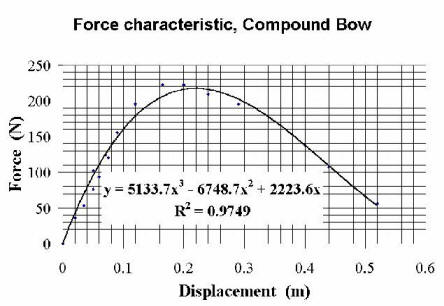 QUESTION:
QUESTION:
Please settle an argument for me. I have tried to convince my wife that a compound bow cannot deliver more force to an arrow than one exerts upon it when pulling it back. My point is that regardless of the pulley system involved of the compound bow, the force imparted upon the arrow by the bow string cannot exceed the force imparted by the archer upon the bow string when pulling it back.
My understanding is that the advantage of the compound bow is something called "let-off". The bow is designed in such a way that the force you must apply at a particular pull distance first increases and then decreases. (A conventional bow has force increasing the more the bow is pulled.) This allows you to be more relaxed and have longer time to aim. But, because the force applied in the middle was large, the energy stored in the bow can still be very large. The figure shows the force as a function of pull distance. You are correct, though, the force you exert on the string at each position will be the same as the force the string exerts on the arrow at each position after release.
![]() QUESTION:
QUESTION:
Can the radiation from CAT scans penetrate walls? I had my pocketbook in
a room adjacent to the room where my CAT scan was performed. I had a
metal water container in my pocketbook. Is it possible for the radiation
to have penetrated the wall and permanently ruined my container/water
bottle making it permanently radioactive?
CT scans are nothing more than glorified x-rays. I am sure that the walls are probably shielded to keep the x-rays in the room where the scan is done. But that is beside the point because x-rays do not make anything radioactive, permanently or temporarily. If your purse and water bottle had been in the room with you they would not have become radioactive. The only reason for shielding is to protect people; excessive exposure to x-rays can cause damage to living tissue. That is why technicians leave the room when an x-ray machine is on. For the patient, who is there for a one-shot deal, it is no reason for concern, but for personnel around all day every day, it is.
![]() QUESTION:
QUESTION:
Do spirits have any mass ?
The density of alcohol is 0.79 gm/mL.
![]() QUESTION:
QUESTION: 
My question is: why does light bend when it slows down? I'm currently a
physics student at UC Santa Barbara (2nd year) and so I know that light
has a finite speed, and it slows down when it enters another medium, and
if it enters another medium at an angle other than perpendicular it
bends (refracts). I know about angle of incidence and all that, I just
don't understand why light has to bend because it slows down? As I
understand it light can be thought as a quanta of energy, an
infinitesimal wave packet (maybe that's where I'm wrong?) So why does it
need to bend just because it is slowing down in an angled medium? I've
often heard the analogy of a car: if it hits glass angled downward from
left to right then the upper left tire hits the glass first and slows
down while the right wheel remains faster and therefore bends it
"upwards". But light packets don't have a discernible "thickness" where
one part hits before another (I don't think!) so that analogy breaks
down for me! Sorry for rambling, I'm just confused.
Refraction is geometric optics and thinking of photons is definitely not the way to best understand it. You should think in terms of wavesâwave fronts and rays. I found a nice description (based on Huygen's principle) on the web. Refer to the picture on the right.
- Wavefront 1 reaches A.
- Wavefront from A starts to spread out.
- When incident wavefront reaches B, secondary wavelet from A has travelled a shorter distance to reach D.
- It gives a new wavefront 2.
- As a result the wave path bends towards the normal.
![]() QUESTION:
QUESTION:
Is their a maximum tempeture or can heat be infinite. If their is an abslute cold why can't there be an absolute heat. If heat causes aomic particles to accelerate is it possible for heat to cause matter to go beyond e=mc^2.
There is a speed limit for particles (the speed of light), but there is no energy limit. And, since the temperature is defined to be the average energy per particle in the object, there is no upper limit to temperature. Of course, as energy per particle increases, molecules and atoms disintegrate into nuclei and electrons (a plasma) and then nuclei start interacting with other and transmuting and so forth, so the identity of what it is you have may change, but there is no upper limit on the total energy of a system.
![]() QUESTION:
QUESTION:
If your in a n elevator that is falling, you should jump in the air right before it hits the bottom to survive. Why or why not ?
It will make practically no difference, you're dead either way. Suppose you fall from about 20 stories, about 100 m. The speed the elevator would hit the ground would be about 70 m/s (about 154 mph). How high can you jump? Maybe 1 m? The corresponding speed would be about 4 m/s. If you jumped an instant before rock bottom you would end up hitting the ground with a speed of only 66 m/s (about 150 mph).
![]() QUESTION:
QUESTION:
I seem to have a paradox. Suppose we have 2 independent waves of amplitude A and energy E and in phase and travelling in the same direction coming from 2 lasers which are wired together. If we combine these 2 waves, by superposition, we will get a resultant wave with the same frequency and wavelength and amplitude 2A. Since the power of a wave is proportional to the amplitude squared and the frequency of all these waves are the same, the energy of the resultant wave should be 4E. However, by conservation of energy, the energy of the resultant wave should be 2E. Doesn't this violate the conservation of energy? Can't we get free energy?
![]() ANSWER:
ANSWER:
Well, this is the second time I have answered this questionâI
had to delete the first answer because it was flat-out wrong. Maybe I'll
get it right this time. I have talked to a half dozen physicists, one of
whom is an expert in laser spectroscopy and also does extensive computer
simulations of electromagnetic wave phenomena. There are a few facets of
the answer to the question, but the most important overview comment is
that it turns out that the question technically violates my groundrule
discouraging "questions
based on unphysical assumptions".
Of course, I am not criticizing the questioner on this point inasmuch as
it took me 3 weeks to decide that this was at the heart of why I was
having so much trouble answering what seemed like such a straightforward
question. I will try to address the facets of the answer with a bulleted
list:
-
The question is posed as if we are looking at electromagnetic waves which are one-dimensional, like the idealized wave on a string. Physics texts do this all the time; so does Ask the Physicistâjust look at an earlier answer where I even show a nice picture of such a wave.
-
Now, we need to make sure we know what is meant by "the power of a wave is proportional to the amplitude squared" as the questioner states. This is almost right but it is the power flux, which is energy/time/area which is the integrated rate of energy flowing per square meter. Through zero area the power flux would be infinite because the area would be zero, so the whole amplitude squared thing would be of no physical consequence.
-
The bottom line, however, is that there is no such thing as a one-dimensional electromagnetic wave. Even if there were, we would not be able to satisfy the conditions of the question, putting two identical waves on top of each other, as I will argue below.
-
The light from a laser is, over the cross section of the beam, approximately a plane wave, that is the wave fronts are disks. This is a good approximation only away from the edges of the beam, so we will only use the center portion in our imagined experiment.
-
Now we come to the piиce de rКsistance. It is not possible to take the beams from two lasers, which are exactly alike in frequency and geometry, and put them together with their wave vectors parallel and perfectly in phase. (My laser expert agrees with this statement). You cannot shine the second laser through the first, for example. You might think you could do this with mirrors somehow, but those mirrors steering one beam will inevitably get in the way of the other beam. So the best you can do is have them almost the way you stipulate, coming together with the wave fronts almost parallel. Now there will indeed be places where the intensity over some small area is twice as large as the sum of the two laser intensities, but this does not violate energy conservation because there will be other places where there is zero intensity. If you integrate over the whole area which includes the intersection of the two beams, you get all the energy which came from the two lasers, no more, no less. In essence, you have the double-slit experiment.
-
Another word for energy/time/area is intensity and there is no such thing as conservation of intensity. A much more mundane example would be a lens: here we take a beam of light and focus it to a small spot hundreds of times more intense than the incident beam and do not worry about what that tells us about energy conservation.
-
One colleague advised me to tell you to just think of the two beams as being comprised of photons, each with a certain amount of energy and each indestructable, so energy has to be conserved. Of course, we both knew we wouldn't be getting any "free energy" anyway, didn't we?
![]() QUESTION:
QUESTION:
I am a artist currently studying in London! I was going to make some work about the Sun, more specifically the sunset. I did some calculations and tried to work out the difference in sunset times if you were on the ground and to each other floor in a building. Working with the measurement of one floor being 10ft I worked out the time, PER INCH, the sunsets are 0.05625 seconds in difference. I was wondering if you could confirm or replace this figure as correct.
![]() ANSWER:
ANSWER:
Here is the way I worked it out. Let R be the radius of the earth
(R=6.4x106 m) and h be the height above the
surface from which you observe the sunset. The sun will set over the
horizon which is the point where you would draw a tangent from your
observation point. Since the tangent to the surface is perpendicular to
the radius drawn to that point, a right triangle is formed as shown in
the picture to the right. For the angle A in that triangle we can
write
cosA=R/(R+h)=(1+h/R)-1. If
h is much less than R we can approximate (1+h/R)-1≈(1-h/R).
Also, the angle A will be very small in which case you can
approximate cosA≈1-(A2/2).
Therefore, A≈√(2h/R); the angle A in these
equations has to be expressed in radians. To find the time T
associated with this angle, change A to revolutions by dividing
it by 2π (e.g. if the angle is 900=π/2,
this is Ń of a revolution); then divide the revolutions by 24 to get
hours and that by 3600 to get seconds. If I do all this I get T≈7.7√h.
So, for example, if you view the sunset from 100 m above the surface, it
will occur 77 s later than if viewed from the surface, more than a
minute. You cannot really specify the time difference per inch, as you
do, because the time is not a linear function of the height. If you ask
the average change per inch over the first 100 m, you get about 0.02
s/inch, in the same ballpark as your calculation. The graph shows a
calculation of the time differences for heights up to 1000 m, the height
of a modest mountain. I guess my calculations are really only right on
the equator if the earth's axis were not tilted, but I don't think you
want to worry about that kind of detail and neither do I!
![]() QUESTION:
QUESTION:
What is the difference between a "principle" and a "law" i n physics?
Why do we have "Archimede's Principle" and "Newtow's Law"?
I could never understand when one uses one or the other....
![]() ANSWER:
ANSWER:
Philosophy of physics may have very precise definitions of terms like
these, but I think it can be ambiguous in physics. Here is my take on
it. A physical law is a statement of an experimental measurement which
is correct as accurately as you can measure it and for any condition
under which it can be experimentally observed. Newton's second law is a
very good example; it states that an object's acceleration is
proportional to the net force on it and inversely proportional to its
mass. The only way to find this out is to measure the acceleration while
you vary the force and mass. Archimedes' principle, however, does not
require that you go to a laboratory and measure the buoyant force, you
can derive it using Newtonian mechanics. Sometimes, laws are misnamed
from this perspective. Hooke's law, which states that the force a spring
exerts on an object connected to it is proportional to its stretch (or
compression) and opposite the stretch (or compression), is only
approximately true and over only a limited range of stretches.
![]() QUESTION:
QUESTION:
It has been many years since I took math and physics. Can you please show me the total solution of this formula. I would have to go back to my college physics class to solve:
RCF = 1.12r [(RPM/1000)squared] where r is 83mm and RCF is 2500g.
I no longer know how to handle the [(RPM/1000)squared.] I know there are calculators to do this but I want to see the soluton.
![]() ANSWER:
ANSWER:
I have never seen this particular equation before (not surprising, since
the units are unphysics-like) but, after a little searching I found that
RCF must be relative centrifugal force. So, this must be
something centrifuge guys use. As I have often noted, centrifugal force
is a fictitious force, no such thing. It is a force invented to make
Newton's laws work for an accelerating system like a centrifuge; if you
are in a centrifuge, you feel like there is a force pushing you outward
but there isn't really. But, for this system it is pretty easy because
the centrifugal force is equal and opposite the real force, the
centripetal force, which is holding you in circular motion. The
magnitude of the centripetal force (and therefore of the centrifugal
force) is given by a very well-known equation, F=mrω2
where m is the mass in kg, r the radius of the circle
in meters, and
ω
is the angular velocity in s-1. I believe that RCF is F/mg,
the times greater than the weight of the object that the centripetal
force is, a dimensionless quantity, where g=9.8 m/s2
is the acceleration due to gravity. So, we have RCF=(rω2/g)
but only if all the units are expressed as given above. So, it is now
just the tedium of converting: r in mm to r in m requires
us to multiply by 10-3 and
ω expressed in rev/min/1000 requires that we multiply by
[(1 min/60 s)x(2π radians/1 rev)x1000]2
and so, RCF=(rω2/9.8)x10-3x[(1
min/60 s)x(2π radians/1 rev)x1000]2=1.119
rω2
where r is expressed in mm and
ω is expressed in rev/(1000 min).
Since this works out so beautifully, I am confused by your factor of
g on your value of RCF; RCF should be a dimensionless quantity and
so I might assume that 2500g=2500x9.8=24,500. Or maybe the g is
stuck on to indicate that the force would be 2500 times greater than the
weight on earth; that would be more likely because that is what RCF is.
So, let's take the second assumption, that RCF=2500=1.119x83xω2=92.9and
so
ω=√(2500/92.9)=5.19
rev/1000 min=519 RPM. Rereading your question, I think you were just
interested in the last couple of sentences, but I had to be sure I knew
where this came from before I tried to get a number from it.
![]() QUESTION:
QUESTION:
if you have an indestructible box and fill it with enough water such that if the water were frozen its volume would exceed the interior space of the box, what would happen? would the water freeze until the space was filled, leaving some liquid? would the water freeze completely with the ice being more dense?
![]() ANSWER:
ANSWER:
Well, site ground rules forbid "indestructible" boxes since there is no such
thing. Still, I will answer your question because you could make a very
strong box. The problem with your question is that it assumes that "ice"
is just one thing, the solid form of water. In fact, there are many
different kinds (phases) of ice depending on the temperature and
pressure. In your case, as you tried to freeze the water, its tendency
to expand would greatly increase the pressure. You can see a
P-T phase diagram
for water on Wikepedia. As you see, there is no simple answer to your
question.
![]() QUESTION:
QUESTION: 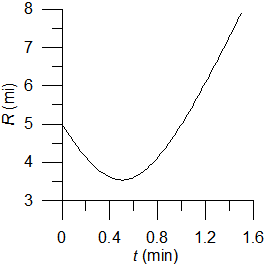
I am an air traffic controller and last night we got into the following discussion which has two sides of beliefs and no side budges. Two planes at the same altitude have to be 5 miles apart. We have a tool that places a 5 mile circle around a plane to give us a visual reference with the location of the plane being the center point. If a plane that has this circle is heading south (180 degrees) and a second plane is on the 5 mile circle to the east of the plane heading west (270 degrees) at the exact same speed. Will these planes ever get closer then 5 miles? One side argues using pythagorean theorem that they will. If each plane moves 2.5 miles they will get to be withinn approx 3.5 miles. The other side argues that the center of the circle continues to move with the plane and therefore you will maintain your 5 miles.
![]() ANSWER:
ANSWER:
The easiest way to see this problem is to view the situation from one
plane or the other. Let the plane going south be labelled S and the
plane going west be labelled W. Suppose the speed of each plane is v.
As seen by S, W is going northwest with a speed u=v√2.
The two components of this velocity are ux=-v
and uy=v. I have chosen the y-axis to be north
and the x-axis to be east; the origin, x=y=0, is at plane S. The
coordinates of plane W (relative to plane S) are then x=5-vt,
y=vt where t is the time since W was due east of S. We can
now calculate the distance R between the two as a function of
t: R=√(x2+y2)=√((5-vt)2+(vt)2).
A little algebra leads to R=5√[1+((2v2t2-10vt)/25)].
So, you see, the whole thing boils down to whether the quantity 2v2t2-10vt
ever becomes negative, in which case R will be less than 5
miles. Noting that both v (speed) and t (time) are always
positive numbers, when vt is between 0 and 5, R is less
than 5 miles. For example, if v=300 mph, the distance will be
less than 5 miles until time t=(5 mi)/(300 mi/hr)=1/60 hr=1
minute. The closest the two planes will get will be at t=Đ
min
when R=3.54 mi. Shown to the right is a graph illustrating this
specific numerical example. (Actually, the argument for each of the two
moving 2.5 miles works very well and is correct.)
![]() QUESTION:
QUESTION:
Theoretically, how many human hairs would be needed to lift an elephant?
![]() ANSWER:
ANSWER:
A typical elephant weighs about 10,000 lb. A healthy human hair can hold
about 3 oz=0.1875 lb. Therefore, N=
10,000/0.1875≈53,000.
![]() QUESTION:
QUESTION:
Can an atom retain information about any other atom it was bonded with in the past if even for a very short time after that bond is broken?
![]() ANSWER:
ANSWER:
Well, every chemical reaction has a time profile and the reaction
products might not end up in their ground states, so some time will
elapse before you have the reaction products in their ground states.
These times, are very short, like microseconds or nanoseconds or
picoseconds. If you are asking me in a subtle way what I think of
homeopathy, I think it is a crock.
![]() QUESTION:
QUESTION:
while watching a kid deliver flyers, he delivered one home then crossed the street to deliver to the home across the street. I wondered whether it would be better to deliver the 20 homes on one side first, then cross the street and deliver all on the other side. Does it take longer by crossing the street every time or should he deliver one side of the street then cross the street and deliver on the other side.
If you can explain how to do the math as well I would be most grateful.
![]() ANSWER:
ANSWER:
Well, this is not really physics, is it? Anyhow, it is a nice little
mental exercise. The bottom line is that it depends on how wide the
street is and how closely spaced the houses are. Call the length of the
street L and the width W. The houses are equally spaced
and directly across the street from each other and there are N of
them. For simplicity I will assume the kid delivers to one house,
crosses the street and delivers 2, crosses the street and delivers 2,
etc. He could zig-zag and deliver one at a time before crossing, but
that makes the geometry too complicated for the quick and dirty answer.
So, call x1 your way, up one side and back the other:
x1=2L+W. The kid's way is x2
and (I will let you draw a picture and figure this out) x2=L+NW=(2L+W)+((N-1)W-L)=x1+((N-1)W-L).
So, x2-x1=(N-1)W-L.
For your way to be shortest, x2-x1>0,
so L<(N-1)W, or, W>L/(N-1);
but, L/(N-1)=D where D is the distance
between houses, so your way is shortest if the street is wider than the
distance between houses. That is the solution to your problem for the
simplest street crossing pattern. But, there is probably a more
important considerationâhe
probably did not want to end up where he started if he had more than
just your street to do.
![]() QUESTION:
QUESTION:
If I have a 150 long cable attached to two poles (100 feet high), and there is a 25 foot sag, how far apart do the poles have to be?
![]() ANSWER:
ANSWER:
This is a classic problem in the calculus of variations. The shape the
curve takes is called a catenary and the equation is y=k(cosh(x/k)-cosh(a/k))
where a is the distance from each suspension point to the center
(essentially what you are asking for) and k is a constant
determined by the conditions (length of the cable, 150 ft, and the
amount of sag, 25 ft). Also, cosh is a mathematical function called the
hyperbolic cosine. When I put in your conditions, I find that k=100 ft
and a=69.3 ft. Hence, the answer to your question is 2x69.3=138.6
ft. (Incidentally, there is a second equation you need which relates
k and a to the length L of the cable,
Đ
L=ksinh(a/k).
Here sinh is the hyperbolic sine.) If I graph y, I get the
picture below.
![]() QUESTION:
QUESTION:
Ignoring relativity and just using Newtonian physics, how much energy would it take to move a 1000 metric ton space ship 10 light years in 10 days? Assume constant acceleration and ignore deceleration. (The ship will just make a "fly by" at some distant star 10 light years away without bothering to try and stop.) I'm sure the amount of energy needed will be enormous, so please try to describe the amount of energy in a way that people can grasp.
![]() ANSWER:
ANSWER:
I usually ignore questions with faster-than-light assumptions but (i)
the question stipulates that I calculate the answer classically, without
relativity, and (ii) the questioner made a donation and I guess I
have my price! Simple kinematics, assuming the space ship starts at
rest, are x=Đ
at2
and v=at; using the x and t given by the questioner, I find that
a=2.5x105 m/s2 (which is more than a 20,000
times gâkinda crushing to any passengers) and v=2.2x1011 m/s
(nearly 1000 times faster than the speed of light). So, it passes the
distant star with a kinetic energy of T=Đ
mv2≈2.4x1028
J. The entire US consumes about 1020 J/year, so the
(fictional) spaceship would require the entire energy consumption of the
US for about a quarter of a billion years.
![]() QUESTION:
QUESTION:
ItŇs not clear to me why atoms with even particles (C and N, for example) donŇt have spin values. More precisely, why hydrogen (spin 1/2) loses this property after a neutron is "added" into its nucleus (deuterium)?
![]() ANSWER:
ANSWER:
Spin values of particles are intrinsic and they are not changed by
interactions with other particles. Neither the neutron nor the proton
"loses" its spin when they bind together; the spin of a deuteron is 1,
that is the two
Đ
spins couple to make 1. However, Đ
and Đ
could also couple to 0; this
does not imply that those spins are not there, it is just that they are
aligned oppositely (think of one going clockwise, the other
counterclockwise). This is what usually happens in heavier nucleiâpairs
of protons and pairs of neutrons couple to 0. All nuclei with even
numbers of protons and neutrons (called even-even nuclei) have zero
spin; 12C66 and 16O88
are both spin zero nuclei. However, odd-A nuclei never have zero spin
since there is always one unpaired nucleon; for example, 13C
has a spin of Đ
. The same thing happens with the electrons in the atom:
electrons, also with spin Đ
, pair to zero, so both C and O have zero
spin of electrons. 14N77 is an odd-odd
nucleus and has, like the deuteron, a spin of 1. One more detail: the
intrinsic spins are not the only kinds of "spin" a system of particles
can have. In a bound system like a nucleus or an atom, each particle
also has "orbital spin" which results from its motion in the atom or
nucleus. So, a nucleus with one unpaired particle might have a spin of
7/2 resulting from coupling of its intrinsic spin of Đ
and its orbital
spin of 3.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
itŇs still not clear to me why deuterium do not ressonate into NMR
spectrometer, once it has spin value +1. I thought that only atoms with
spin 0 (by coupling of opposite spin values) were "invisible" to NMR.
![]() ANSWER:
ANSWER:
NMR has a radio frequency perfectly tuned to "flip" the spin of a proton
(from ms=Đ
to
ms=-Đ
)
in a particular magnetic field. This tuning is such that the photon's
energy is the same as the energy necessary to cause that energy
difference and that energy difference is determined by the magnitude of
the magnetic field and by the magnetic moment of the proton. The
magnetic moment of the deuteron and the resulting energy differences of
its ms substates simply do not match the frequency for
protons.
![]() QUESTION:
QUESTION:
When one looks at a reflexion of an object on a mirror, hee sees the object in "3D". But if one looks at a photograph of the same object, it does not appear in "3D". So what is the difference between the light comming from a mirror and the light comming from a photograph, that let our brain add a deepness to a seen object?
![]() ANSWER:
ANSWER:
Because you are looking at the image with two eyes and so you see two
slightly different perspectives; your brain interprets this information
as three dimensional. The camera has only one "eye" and hence does not
carry the three dimensional information. When you look at the
photograph, you are only looking at part of the information you receive
when you look at the actual mirror. If you close one eye and look in the
mirror you will see only a two dimensional image. (But you must remain
still, because you can get three dimensional information, via
parallax, to your brain by moving your eye around.)
![]() QUESTION:
QUESTION: 
I wear glasses to see distant objects clearly, when I don't wear my glasses distant objects look blurry. My glasses broke and left me unable to see my television clearly, so I came up with an idea, if I hold a mirror close to my face and tilted towards the television I should be able to see the television clearly. To my surprise this was not the case, the television still looks blurry in the mirror even though the mirror was close enough to be seen clearly. Normally with my glasses on the television would have appeared clearly in the mirror. Assuming the image of the television is a perfect representation of the television itself why does it still look blurry even though the mirror reflecting the image is close to my face?
![]() ANSWER:
ANSWER:
The reason is very simple. A mirror forms an image which is just as far
behind the mirror as the object is in front of the mirror. Your eye
attempts to look at the image, not the mirror, and your eye is
unable to focus on that distant image.
![]() QUESTION:
QUESTION:
If You Were To Fall In A Hole Through The Center Of The Earth, How Long Would It Take You To Land In Beijing?
![]() ANSWER:
ANSWER:
If the earth is modeled as a uniform sphere (same density throughout its
volume), it turns out that a particle of mass m behaves as if it were on
a spring with spring constant k=mMG/R3 where
M is the mass of the earth, G is Newton's universal constant
of gravitation, and R is the radius of the earth. Putting in the
numbers and using
![]() QUESTION:
QUESTION:
If all of the elementary particles in the atoms of the sun (you can assume pure hydrogen for simplicity if you like) were to condense in on themselves such that all electrons, protons and neutrons were in intimate contact with one another, how large would the sun be? What would its (approximate) density be? How would this compare to the density of a novaed star? I know this reads like a textbook question, but I'm an engineer and I cant think of any less-textbooky way of asking.
![]() ANSWER:
ANSWER:
What you are describing, essentially, is a neutron star. It results from
gravitational collapsed of an exhausted star. The density is comparable
to that of a nucleus, about 2x1017 kg/m3.
![]() QUESTION:
QUESTION: 
Can we literally see an atom given today's technology ?
![]() ANSWER:
ANSWER:
Depends on what you mean by "see". If you mean seeing light from the
atom forming an image of it in a microscope, like we observe bacteria
for example, then no. The reason is that an atom is much smaller than
the wavelength of visible light and geometrical optics does not allow
that. But individual atoms can be imaged with electron microscopes or
things called atomic force microscopes and scanning tunneling
microscopes. Google those to see how they work. Atoms can be manipulated
too. The picture shows a famous IBM image of individual atoms pushed
around to spell IBM.
![]() QUESTION:
QUESTION:
Two trains 200 km apart are moving at a relative speed of 50 km/h. A fly takes off from one train, flying straight to the other one at the speed of 75 km/h, touches and flies back to the first train. How far will the fly have gone when the trains collide?
![]() ANSWER:
ANSWER:
I suppose this might be somebody's homework, but I have waited long enough
that the homework was probably due long ago! It takes the trains 4 hours
to collide. Something going 75 km/hr will travel 300 km in that time.
![]() QUESTION:
QUESTION:
I saw the experiment by an Astronaut in which bits of salt or sugar clumped together while in a bag of water, thus showing gravitational attraction. Made me wonder why we do not see similar occurances on Earth. Eg. Why doesn't a grain of sand on a pier migrate toward an aircraft carrier while docked?
![]() ANSWER:
ANSWER:
You must have misunderstood what that experiment was trying to
demonstrate. Gravity is an incredibly weak force. For example, the mass
of a grain of salt is about 10-7 kg, so two such grains
separated by 1 mm=10-3 m would be about F=10-7x10-7x6.67x10-11/(10-3)2
![]() QUESTION:
QUESTION:
my question is regarding the dimensions. physical quantities do have dimension in the form [ LMT ] but what is this actually?
![]() ANSWER:
ANSWER:
Once you have
operational definitions of length [L] (distance between two points in
space), time [T] ("distance" between two events at the same point in space),
and mass [M] (inertia, resistance to being accelerated), every other
physical thing you might measure or observe may be expressed in terms of
these three. These are usually called dimensions but are not the same things
as when we talk about three dimensions, e.g.; each of the "three
dimensions" are length. Sometimes we talk about space-time or
four-dimensional space which adds time to three dimensions. Scientists
usually prefer units in the SI system to measure [L], meters (m); [M],
kilograms (kg); and [T], seconds (s). Some examples are
-
area: [L2] m2
-
volume: [L3] m3
-
speed: [L/T] m/s
-
force: [ML/T2] kg m/s2 (called a newton, N)
-
energy: [ML2/T2] kg m2/s2=N m (called a joule, J)
-
power: [ML2/T3] kg m2/s3=J/s (called a watt, W)
Dimensional analysis is often useful in checking calculations. Supposed you derived that the energy of something was E=5mv3 where m is mass and v is speed. Then the dimensions of the left side are [ML2/T2] and the right side are [ML3/T3]. Since these are not the same, your derivation must have been wrong.
![]()
 QUESTION:
QUESTION:
here's my question which I read in an article from the early days of space flight:
A manned spacecraft is circling the moon at an altitude of 100 miles above the surface, and the astronaut on board noted the "angle of depression of the horizon was 23.8 degrees. With this known data, the astronaut was able to determine the radius (or diameter) of the moon. I drew a diagram of the moon and the orbiting spacecraft with the known height of craft above the moon and the depression angle of 23.8 degrees. Thinking that this would be a simple case of similar triangles, etc. I found that I could not determine the radius of the moon from the given data
![]() ANSWER:
ANSWER:
The figure to
the right shows what you need. The angle A in this figure is, you will
agree, your 23.80. You can see that cos23.80=R/(R+100).
Solving, I find R=1076 mi, pretty close to the known radius of 1079 mi.
![]() QUESTION:
QUESTION:
hey man,
we had a discussion at the bar and we were not sure about this.
here it goes.
when you knock on a vacuum? like, u have a trunk with a vacuum inside.
what will be the sound. is it A. none at all? B. like a solid piece of wood?( in the case of a trunk ) c. something else
It may not be the greatest of questions but i'd apprieciate any answer.
![]() ANSWER:
ANSWER:
What sound
does something make when you "excite" it? Something has to move to make a
sound. The classic example would be a guitar string. If you just had a
string stretched between two nails in a concrete floor, you would barely be
able to hear it when plucked. Now, if you connect the string to a flexible
piece of wood (like with the bridge of a guitar), the vibrations of the
string will be transferred to the wood which will also start vibrating in
some complex fashion (like the head of a drum makes sound). You may now be
able to hear it a little better. Now put a volume of air behind the wood
(that is, make a guitar). Now the whole volume of air will start vibrating
which will amplify the sound made by the vibrating wood which is amplifying
the vibrating string. There is a lot more to a guitar than a plucked string.
If you now close up the hole and pump out that vibrating air, you will still
be able to hear the guitar but it will not be nearly as loud (or as pretty)
without that vibrating chamber of air.
![]() QUESTION:
QUESTION: 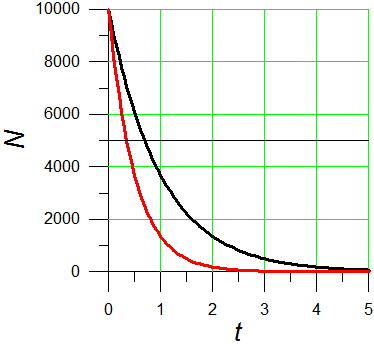
I have a question on Law of Decay.I never heard of it before and I am quite confused with the question asked.Its about a radioactive material that is known to decay at a rate proportional to the amount present. What does the mass of the material initially,got to do with the time taken for example,5 hours, and after this hours ,the material has lost some percentage of its mass.Can you try explain to me what's this whole thing about and how do I even get to start??
![]() ANSWER:
ANSWER:
This is very
fundamental and can apply either to decay or growth. The idea is that the
rate of decay or growth is proportional to the population. Does it make
sense? Suppose we have 10,000 radioactive nuclei and we measure that they
are decaying at a rate of 50 per second; it is then perfectly reasonable to
assume that if we had 20,000 instead, we would see 100 per second decaying.
It simply reflects the situation that it is equally probable for any of the
population to decay in the next 5 seconds, for example. It also applies to
many growth problems. For example, if you have 10,000 bacteria and they are
growing at the rate of 50 per second, the rate of growth of 20,000 of them
would be 100 per second. The general way to write this down (I assume you
know some calculus?) is dN/dt=
![]() QUESTION:
QUESTION:
Why
are massless photons stopped by paper while a neutrino (with mass),
easily passes through the earth?
![]() ANSWER:
ANSWER:
A photon
interacts strongly with electric charges of which all matter is composed.
Neutrinos do not.
![]() QUESTION:
QUESTION:
Heat recovery ventilators are becoming very popular as homeowners weatherize their homes. They are simple units that intake air from outside, exhaust stale air from inside. Heat is transferred from the exhaust air to the intake air through a plenum of aluminum. All very simple so far.
Except, they work too well! They can take 0 deg F outside air, 70 degree exhaust air and instead of warming the intake air to 35 deg, like most of us would expect, they warm it to 50 degrees!
How do they do this?! Does the answer lie in the fact that 70 deg F contains more than twice the energy of 35 deg air?
(NB: No heat pumps, freon, electrical resistance, etc. are involved)
![]() ANSWER:
ANSWER:
Suppose that
you mixed equal amounts of 00 air and 700 air. Then,
you are right, you would expect to get 350 air. But, suppose that
you could take the heat out of 700 air such that you cooled it
down to 00 and then took that heat and put it into an equal
amount of 00 air. You would end up with 700 fresh air
coming in and 00 stale air going out and have violated no laws of
physics
![]() QUESTION:
QUESTION:
This question was mentioned to me a long time ago by a physicist who I think was just trying to mess with my head - a task at which he succeeded.
One of the simplest ways of measuring the circumference of a circle that many children are taught is rolling out the circle; and this is basically the starting point of my question.
 To make my question clear, I feel I have to describe the process :
Take a wheel or circle; draw a radius on it from the center to the edge; position the circle on a flat surface or number line so that the radius points straight down at a known point; roll the circle along the line until the radius is again pointing straight down at a second point and mark it; the distance between the two points is the circumference of the circle.
Now draw another circle on the first that is half the size of the original.
If you repeat the original procedure of measuring the circumference of the larger circle, the smaller circle also starts and ends at the same position despite travelling a larger distance than it's own circumference?
Why can't I get my head around this?
I hope this doesn't count as a maths question - it was originally put to me by a physicist...
To make my question clear, I feel I have to describe the process :
Take a wheel or circle; draw a radius on it from the center to the edge; position the circle on a flat surface or number line so that the radius points straight down at a known point; roll the circle along the line until the radius is again pointing straight down at a second point and mark it; the distance between the two points is the circumference of the circle.
Now draw another circle on the first that is half the size of the original.
If you repeat the original procedure of measuring the circumference of the larger circle, the smaller circle also starts and ends at the same position despite travelling a larger distance than it's own circumference?
Why can't I get my head around this?
I hope this doesn't count as a maths question - it was originally put to me by a physicist...
![]() ANSWER:
ANSWER:
The small circle is not rolling on the dashed line, it is slipping on it. At any given time the whole circle is rotating around the point of contact
of the big circle with the ground, that is, the point of contact is at rest (that is what rolling without slipping
means). Therefore, a point a distance s above the point of contact is moving forward with a speed
vs/R where v is the forward speed of the center, and
R is the radius of the big circle. The bottom of the small circle is going forward with speed
v/2 and the dashed line is at rest.
![]() QUESTION:
QUESTION:
If work is defined as force x distance then if you are pushing against an immovable object, no work is being done. Nevertheless, you are expending energy as you are pushing. It seems to me that there is some kind of paradox here--you are losing energy but you are not doing any work. Can you explain?
![]() ANSWER:
ANSWER:
Physics would say no work is being done because the force is not acting over a distance; you and I both know, however, that sugar is being burned to provide the energy necessary to
push on this stationary object. What is going on here, as I understand it, is that the muscle fibers in your arm are continually slipping and retensioning thereby doing lots of little parcels of work to hold your arm steady.
![]() QUESTION:
QUESTION:
although you can't see an atoms through a microscope, at some point a clump of atoms is large enough to see as a dot through the microscope. What determines when the clump of atoms is big enough to be seen?
![]() ANSWER:
ANSWER:
The best optical microscope can resolve objects as small as about 0.2
![]() QUESTION:
QUESTION:
Please settle a bar room argument. 1. An ice cube is floating in a bowl of water: how does the water level change as the ice melts? 2. An ice cube containing the same amount of water as before but this time also containing an air bubble is floated: what happens to the water level as the ice melts and how does this level differ from the change before? 3. The same ice cube as in 1 but this time with a nail (or some heavy object) embedded in it is sunk; what happens to the level of water as the ice melts and how does this level differ from the previous 2 cases?
![]() ANSWER:
ANSWER:
Case #1 is a classic problem. Archimedes' principle states that the
buoyant force equals the weight of the displaced water. Since the ice just
turns into water, it exactly fills the void it originally created and the
water level stays the same. Note that it should be clear that the density of
ice is less than water since it floats. Case #3 is essentially to hold the
ice totally submerged until it melts. But since the melted ice has a smaller
volume than the unmelted ice, the water level will go down. Case #2 is
essentially the same as case #1 because the buoyant force must still hold up
the weight of the ice so the weight of the displaced water is still equal to
the weight of the ice; so, when the ice melts it is water of that same
volume. I have assumed that the weight of the air in the bubble is
negligible.
![]() QUESTION:
QUESTION:
My husband and I are having a disagreement on the energy used to air dry laundry indoors.
He argues that it is less energy efficient than, or at least the same as. running the gas dryer, to air dry laundry indoors in winter because then the house heating system has to work harder to convert the water molecules in the clothes to liquid and gas.
I don't have a good answer for him, but it just seems counter-intuitive. It seems like the air drying clothes are at the same temperature as the surrounding air, and don't need heat to "wam up" the water in the clothes. It also seems like the water in the clothes would evaporate due to the dry air (some mumbo jumpo about liquid/vapor equilibrium), not because of heat energy being transferred to the molecules. He doesn't deny that air drying provides moisture to the room, his argument is that the energy required to evaporate the water ultimately comes from the furnace so we might as well run the humidifier and the gas dryer.
What do you think?![]() ANSWER:
ANSWER:
Your husband is not going to like this, but he is dead wrong. You could
turn your furnace off and your clothes would dry just about as fast.
Certainly air drying clothes takes energy from the environment, but the
amount is trivial compared with how much your furnace needs to put out to
keep your home warm. Believe me, your furnace will never notice. Yesterday
it was about 35 degrees at my house and I hung out clothes which dried in
about 2 hours. Clothes dryers are among the biggest energy hogs of all our
appliances because so much of the energy goes out the exhaust or heats up
the dryer drum or just leaks away in some other way. When I started hanging
out my clothes instead of putting them in the dryer my electric bills went
down about $20 per month. Here is another thing (ok, this is kinda off the
wall!): if you dry your clothes in the house it will humidify your house
which makes it feel warmer so you can actually turn the furnace down!
![]() QUESTION:
QUESTION:
Consider this scenario - there's a room full of mirrors
(for argument's sake let's say all surfaces in the room are 100%
reflective). There is a single light source in the ceiling which is
sending photons bouncing back and forth off the mirrors. If the light
source is switched off one assumes the room will go dark. Why is this
the case though? Why don't the photons already emitted from the light
source continue to be reflected around the room ad infinitum (i.e. why
doesn't the room stay bright)? Why would shutting off the light source
affect photons that have already been emitted?
![]() ANSWER:
ANSWER:
There is no such thing as a perfect mirror. If there were,
you had better not leave the light on too long since the light will
continue to increase because there is no loss. When you turn it off,
the light would remain bouncing around. Suppose that the mirrors were
99.99% efficient, far better than the best mirror, and the walls were 3
m apart. Then in one millisecond (10-3 s=0.001 s), the
intensity of the light would be reduced to about 1/22,000 of its
original intensity! So the real world can impose pretty big constraints
on ideal situations we can dream up.
![]() QUESTION:
QUESTION:
two walls stand opposite each other. The length between
them is L. one of the walls is moving toward the other at velocity V a
bird sits on that wall starts to fly back and forth at velocity 2V how
far will the bird travel before it gets crushed (assume the bird has no
dimension and that only when the walls meet will the bird be crushed)
![]() ANSWER:
ANSWER:
This is a trick question, much easier than it seems. The
walls will smash together at the time T=L/v and during
that time the bird will fly a distance S=2vT=2L. OK,
I will admit it—I spent some time trying to compute the infinite series
before I figured this out! But it was kind of cool because I was able
to use simple logic to find that the infinite series from n=1 to n=∞ of
(1/3)n is 1/2 which I could not do mathematically because I
am not very good at evaluating infinite series.
![]() QUESTION:
QUESTION:
Thank you in being available for this type of thing. I
chat at physorg and I learn alot, but there are some cranks who state
things of opinion as fact. Please laugh at this question! A member of
physorg is adament that the neutron is the force carrier for gravity.
Myself and 2 or 3 others are trying to explain why and how that can't
be and why the graviton fits with our current knowledge, but he
continues to claim he is correct. Could you please come up with one
statement of why this is impossible so that I can quote it to him.
There must be a perfectly clear answer that even he has to recognize as
fact, yes?
![]() ANSWER:
ANSWER:
The current theory of gravity, general relativity,
attributes the gravitational force to geometric effects, the warping of
space-time by the presence of mass. There is no successful theory of
quantum gravity, that is the field has not been successfully quantized
thereby allowing identification of the "force carrier". There is no
such thing as a graviton, it is only a qualitative idea at this time.
So, your nemesis thinks maybe the neutron is the graviton, right? Here
is what is wrong with that:
- To the best of our knowledge, the gravitational force propogates with the speed of light. The neutron, being a particle with mass, cannot travel the speed of light. In fact neutrons, having no charge, are quite difficult to accelerate and are usually relatively slow in nature.
- The neutron is not a stable particle unless it is bound inside a nucleus; a free neutron has a lifetime on the order of 15 minutes at which time it will decay into a proton, and electron, and an antineutrino. This would not be very good for communication of the gravitational force between, say, the sun and Jupitor would it?
- Forces which have carriers with mass, for example the strong nuclear interaction with mesons as field quanta, are very short ranged. Gravity is a long-range interaction like electromagnetism, that is it falls off like 1/r2. The force carrier for electromagnetism is the photon which is massless and one would therefore expect the graviton to be massless.
![]() QUESTION:
QUESTION:
Does a kernel of popped popcorn have the same number of
calories as it had before it was popped? Do not consider that it is
fried in butter, or that tiny particles of the popcorn fly off when it
is popped. My friend suggests that it uses energy (calories!) in the
popping process, I believe it simply is releasing energy it has
received in the heating process, which cause moisture in the kernel to
turn to steam, expanding, and creating the "popping". Do total calories
remain the same before and after?
![]() ANSWER:
ANSWER:
The first thing we should acknowledge is that what
"cooking" does is change the chemical composition of whatever you are
cooking, and changing the chemistry inevitably changes the caloric
content. That said, let's examine what happens when you "cook" popcorn.
The water inside the kernel becomes superheated and the hull cannot
contain the increased pressure and the kernel explodes. When this
happens the starch contained in the kernel expands rapidly which is
what the popcorn is. The rapid expansion causes cooling which tends to
keep the starch from undergoing a chemical change, and therefore
popping corn is, to a large extent, not really cooking. So, in my
judgment, you are correct: the caloric content is not much changed by
the popping.
![]() QUESTION:
QUESTION:
Somewhat technical question,
so I don't know if it breaks the ground rules. I work in MRI and have
had some QM courses a long, long time ago. But this continues to puzzle
me. I don't mind at all looking it up in the QM books if only I knew
what to look under. Could you provide a reference or the correct
"topic" I could read up on? A charged spin-1/2 particle has a
gyromagnetic ratio.
For example, a proton has a QM spin-magnetic moment. When it is placed
in a constant and uniform magnetic field its magentic moment will be at
an angle (about 54.7 degrees) to the direction of the applied uniform
magentic field and it will precess around the direction of this
applied, external field.
The proton will radiate as it precesses in the magnetic field. This can
be detected by pickup coils. For example, this is how an MRI system
works. (But I am interested in a single particle case, not in an
ensemble of particles.)
Question: Where does the energy come from to drive the precession and
the associated radiating process as the particle precesses?
If from the magnetic field, then wouldn't this "drain", say, a
permanent magnet (system of magnets) generateing the magnetic field?
That doesn't seem right (but maybe).... Being in a uniform magentic
field, the gradient of B would be zero. So I guess there wouldn't be
any net translational force on the particle. I think this is because
there would not be any difference in energy between being at p1=(x, y,
z) and being at p2=(x+dx, y+dy, z+dz) so no net force to translate the
particle from p1 to p2. So does the particle just sit there radiating
as it precesses? That doesn't seem right. If it radiates it should be
loosing energy and going into a lower energy state. But there doesn't
seem to be a lower energy state to go into? Or, for every "bit" of
energy radiated it must be getting that amount of energy from someplace
else, but where/how? That is what is confussing to me.
If the magnetic field were not uniform I could see that the particle
would translate into a lower energy state and would convert some of the
potential energy into kinetic energy and radiation energy. But in a
constant uniform magnetic field?
![]() ANSWER: {this
answer is not complete yet, I have to go to a concert!}
ANSWER: {this
answer is not complete yet, I have to go to a concert!}
Your question is closer to
breaking groundrules for not being concise and well-focused than being
too technical. However, I will answer it because it is interesting. If
you work with MRI, I am afraid I must tell you that you do not really
understand what is going on. If a classical magnetic moment is placed
in a uniform magnetic field it will align with the field. That is what
it wants to do. If it is a quantum mechanical particle (that is it has
a spin angular momentum) it cannot align with the field because the
component of the total angular momentum (which is J=ħ√[3/4])
along the field direction may be only ±½ħ. That
is where your angle comes from, cos(54.7)=½/√[3/4]. It is not
really correct to say that the proton precesses; it is more correct to
say that it is equally probable to be at any azimuthal angle and so
many texts describe this situation as precession. Go ahead and think of
it as precession, but it certainly does not radiate energy. Note that
the moment is "up", that is 54.70 relative to the field
direction. Its other state, 54.70 relative to the opposite
direction ("down") is at a higher energy because it takes work to take
the "up" aligned moment and turn it to a "down" moment. Let us say that
it takes an energy E (which depends on the field strength) to
flip the moment from up to down. In an MRI what happens now is that we
shine in some electromagnetic radiation. If the radiation is of just
the right frequency, that is f=E/h, there will be a high
likelihood that the radiation will be absorbed resonantly (hence the
"R" in MRI, magnetic resonance imaging). This absorption is what is
detected in MRI. This is a very simplified overview, but it gives the
basic physics principles. The details of how the whole imaging process
is very much more complicated because of the problem of locating where
the absorption is taking place.
![]() QUESTION:
QUESTION:
If there were a civilization
on a planet orbiting Alpha Centauri 4.37 light years away, how big
would the diameter of their radio telescope have to be to clearly
receive a TV signal from Earth? I asked the people at SETI the same
question once and never got an answer.
![]() ANSWER:
ANSWER:
OK, I will take a stab at
this. But, I am not an engineer and do not really know for sure how
much information one must receive to be able to put together a tv
picture. I will assume that, since the wave nature of the radio waves
carries the information, we will need at least one million photons per
cycle of the wave. My thinking is more in line with AM radio waves
where there is one constant frequency of carrier waves and the
information is carried by the amplitude of the wave; I realize that
this is not really what tv is but it should give an order of magnitude
estimate. The typical power of a tv station is about 100 kW=105
J/s. The energy of a single photon is hf=6.6x10-34x108=6.6x10-26
J/photon so for our power source we have N=105/6.6x10-26=1.5x1030
photons per second. The frequency of a tv station is about 100 MHz= 108
s-1. To get 106 photons per cycle we therefore
need 106x108=1014 photons per second.
4.7 ly=4.4x1016 m so the intensity (in photons/second/square
meter) at Alpha Centauri will be about 1.5x1030/[4p(4.4x1016)2]=6x10-5
photons/s/m2. We therefore need an area of 1014/6x10-5=1.7x1018
m2. That is about an 800,000 mile square. This hinges mainly
on my assumption of needing 106 photons per cycle of the
wave which might be wrong by several orders of magnitude.
![]() QUESTION:
QUESTION:
Is there any relationship
between a sine wave and the bell shaped curve used in statistics? They
look similar. Is there a reason for this or is it just a coincidence? I
suppose a mathematician could come up with a formula to describe the
relationship. However, would such a formula have any significance? (It
just occurred to me I'm asking the same question twice. If such a
formula lacks significance that implies any relationship between the
two curves is just coincidence.)
![]() ANSWER:
ANSWER:
You have been looking over
too restricted range if you think that a bell-shaped curve and a
sinesoidal function have similar shapes. To the left is a comparison
between the two. Once you get away from the central maximum of the
bell-shaped curve there is no relationship between the two. There is no
mathematical relationship between the two functions however you could
make a bell-shaped curve by adding an infinite number of sinesoidal
curves with appropriate weights; this is called a fourier transform
representation of a gaussian function (another name for a bell-shaped
curve).
![]() QUESTION:
QUESTION:
How would i calculate the
number of grains of sand on Earth ???
![]() ANSWER:
ANSWER:
There is, of course, no way
to calculate it. You could estimate it, however. I am not a geologist,
so I really don't know how much sand there is in the world but it must
be a lot. I will take a wild guess that there is enough sand to cover
the entire earth to a depth of 10 cm =10-1 m (there is
probably more than that). The surface area of the earth is about 5 x 1014
m2 (from A=4pR2)
so the total volume of sand is about 5 x 1013 m3.
Now, I will guess that a typical grain of sand would have a diameter of
maybe 0.1 mm=10-4 m so the volume of a typical grain of sand
would be about 10-12 m3. So the number of grains
of sand would be the ratio of the volumes (volume of sand/volume of one
unit of sand), about 5 x 1026, quite a lot! This is
comparable to about how many atoms there are in your pencil.
![]() QUESTION:
QUESTION:
I have learned that we all
will inhale (at least once in our lives) the very same atoms as our
ancestors from thousands of years ago. If this is true, does this mean
that our bodies atoms are bound to this Earth and remain here
permanently after we die. Does our atmosphere and (or) gravity restrict
our atoms (after death) to the Earth, or can our atoms find their way
off the Earth into space and possibly to other worlds? I ask these
questions for spiritual reasons and out of true scientific curiosity.
![]() ANSWER:
ANSWER:
Suppose that we assume that
the atmosphere gets completely mixed up by weather patterns after a
relatively short time, say a year; this essentially means that a
molecule here today is equally likely to be anywhere else in the world
in a year. Now, I calculated the volume of the atmosphere assuming it
to be 20 km thick; that would include most of the molecules. Now, I
assumed a typical human breath is about 1 liter; then I find that the
number of lungs full of air there are in the atmosphere is roughly
1.5x1021. Next I roughly estimate the number molecules in
one lung full of air to be about 3x1022. So, if I take one
breath and redistribute the air over the whole atmosphere, I will find
about 20 molecules of that air in any other breath. So, very roughly
speaking, each breath you take will have 20 molecules of the last
breath John Kennedy took before he died. But, we might more likely be
interested in the number of molecules over a lifetime; taking Leonardo
da Vinci, who lived to age 67 as an example, the number of breaths
breathed in his lifetime was about 7x108 (I assumed about
20 breaths/minute), so every breath you take will contain about 1.4x1010
molecules (that is about 14 billion) that were breathed by da Vinci!
Keep in mind that my calculations are very rough but they should give a
good approximation of orders of magnitude.
Your second question is not really related. Gravity does a good job of keeping most molecules in the atmosphere confined to this world. However, there are virtually no hydrogen molecules or helium atoms in the atmosphere because they have escaped into space. Helium is recovered as a byproduct of natural gas, having been confined underground where it cannot escape. The reason for this is that temperature is a measure of the average kinetic energy of the molecules and lighter molecules have much higher speeds than say oxygen or nitrogen at the same temperature. The speeds are large enough that the fastest have a velocity larger than the escape velocity and fly off into space. For the same reason, the moon has no atmosphere because the escape velocity is much lower and all the gas escapes.
![]() QUESTION:
QUESTION:
My question starts with fundamental laws: gravity, electromagnetism, etc. As I understand it, these are the forces with the capacity to exert work on the physical world. I'm curious whether the work that biological systems produce are the product of fundamental forces, and if not, whether physics defines the source of the force that produces work in biology.
![]() ANSWER:
ANSWER:
Biology is essentially applied chemistry and chemistry is essentially
applied atomic and molecular physics. The four fundamental forces (gravity,
electromagnetic, nuclear, and weak) are the only ones we know in nature.
Biology, at root, is mainly electromagnetism because that is the force which
governs interactions among atoms and molecules. The other three forces play
little role in biology.
![]() QUESTION:
QUESTION:
When we say we consumed electricity at home ?
what actually we consume Voltage,current or energy of the charge flowing ?
![]() ANSWER:
ANSWER:
You pay for energy and that is what you should think about consuming.
The electric bill is billed at some rate per kilowatt-hour. A watt is a
joule per second, so 1 kW-hr=1000 J hr/s (3600 s/hr)=3,600,000 J.
![]() ADDED QUESTION:
ADDED QUESTION:
why were these scientist so smart and at such a young age? It seems like the best of them were Jewish/Germans, e.g. Einstein and Oppenheimer .
![]() ANSWER:
ANSWER:
Well, one reason that young guys have an advantage if we are talking about revolutionary breakthroughs is that they are not so brainwashed with the status quo. Why Jews and Germans? Because, in the 19th century these cultures respected and rewarded intellectual activity, including science, unlike the antiscience and antiintellectual bozos today (read Tea Party).
Bohr was Danish, Fermi was Italian, Yukawa was Japanese, Rutherford was from
New Zealand, Feynman was American, so Germany did not have a monopoly.
![]() QUESTION:
QUESTION:
Why is the speed of sound slower in lead (25 degrees C) than fresh water when generally sound travels faster in solids than in liquids?
![]() ANSWER:
ANSWER:
The speed of sound is determined by two things, the elasticity of
the medium and the density
![]() QUESTION:
QUESTION:
If I could detonate a firework inside a contained vacuum void of any other mass objects (simulating the big bag) and watched (over time) would I see the particles eventually attract to each other? Would the results of this sort of experiment prove gravity exists in every particle ever created?
![]() ANSWER:
ANSWER:
No. The gravitational attraction is very, very small between
the little pieces of your firecracker. So the speeds the pieces had when it blew
up would have exceeded the escape velocities from their neighbors and they
would continue moving apart forever. Escape velocity is the speed
something must have to escape from the gravity of something
else; e.g. the escape velocity from the surface of the earth is about 7 miles per
second, but this is for a much stronger gravitational force. Just to give
you another example where the mass involved is still much larger than your
masses but much smaller than the mass of the earth, the escape velocity from
the surface of a baseball is about 8 cm/hr.
![]() QUESTION:
QUESTION:
am a member of a group of
people with an interest in space & the universe. We have been
having a debate that is no closer to being solved than when it first
arose. This is topic being debated: If an alien race were to live on a
planet several light years away from Earth, we know that Earth would
look like a star in their night sky. We also know that the light they
saw would've left Earth many many years ago; perhaps even when the
dinosaurs lived. If they were to have a telescope SO powerful that it
could zoom in on the living animals on the surface of Earth, would they
be zooming in to see the animals of present-day Earth? Or, would they
be looking at the dinosaurs? I would VERY much appreciate if you could
help us in finally putting this debate to rest.
![]() ANSWER:
ANSWER:
To see something, your eye
(or telescope) must detect light which was emitted from that object (or
reflected from it). So, when you look at a friend who is 100 m away,
you are not seeing him as he is right now but how he was 100/3 x 108=3.3
x 10-7s ago. 1/3 of a millisecond is a quite measurable
time. Now suppose you are on a planet which is 100 light years from
earth. When you see the earth you are seeing as it was 100 years ago
because a light year is the distance light travels in a year. The moon
is 1.3 light seconds from the earth and the sun is 8.3 light minutes
from the earth. So, when you see the moon you are seeing it as it was
1.3 seconds ago. If the sun were to blow up right now, you would not
know it for 8.3 minutes.
![]() QUESTION:
QUESTION:
why do bats and owls have
good night vision compare to humans?
![]() ANSWER:
ANSWER:
You have probably heard the
phrase "blind as a bat"; well, bats are not really blind but their
eyesight is not very good. The way they "see" using sound waves like
radar: they emit ultrasound which then bounces off things in their
environment and they are able to navigate by hearing the echos. They
might as well be blind. Owls, however, have very good night eyesight.
There are several things about their eyes which give them good night
vision:
- Their eyes are quite large,
- the iris can open very far to let in more light,
- the eye is cylincrical rather than spherical which allows the retina to be larger,
- the retina is packed with a great many "rods", cells most sensitive to low-level light (cones, the other type of vision cell, allow color vision), and
- the back of the retina is reflective which means that light which does not interact with the rods on its way in gets another chance.
Most animals have better night vision than we do because of the reflective layer called the tapetum lucidum which we do not have. That is the reason that the eyes of many animals at night tend to shine when light is shined at them--it is reflected back.
![]() QUESTION:
QUESTION:
Why does a diamond glitter
so much?
![]() ANSWER:
ANSWER:
In a nutshell, it is because
diamond has a very high index of refraction, 2.42. For reference, the
indices of refraction of glass and water are about 1.5 and 1.3
respectively. What this means is that light travels much more slowly in
diamond than in air and the result of this is that it is very much bent
when it goes from air to diamond or vice versa. It also has the
effect that much of the light which enters the diamond does not go
through but is reflected back (due to something called total internal
reflection, also the way that fiber optics works). This effect can be
accentuated by cutting the diamond cleverly and that is the purpose of
the facets. Therefore, the "glittering" is because most of the light
which strikes it bounces back toward you.
![]() QUESTION:
QUESTION:
I read about Cerenkov
radiation and the "blue glow" that it causes. Is this glow always blue?
If not, does it depend on what the medium is (water, oil, etc.) or what
the particle traveling faster than light is?
![]() ANSWER:
ANSWER:
The intensity of the radiation is
proportional to the frequency. Therefore, the higher the frequency
(shorter the wavelength) the more intense the radiation (the spectrum
is continuous, not of a single wavelength). Therefore, it turns out
that most of the "light" is in the ultraviolet spectrum. You would
therefore think that Cerenkov radiation should look purple, but the eye
is more sensitive to blue so that is what we perceive. For the same
reason (sensitivity of the eye) the sky is blue and not purple.
![]() QUESTION:
QUESTION:
I'm currently in an argument
with a few friends, some of which are in engineering whether gravity
and the idea's surrounding it are covered as the Theory of Gravity or
the Law of Gravity.
I've been lead to believe that it is the Theory of Gravity and as such
it is concidered a law merely because it has been around for so long.
However, it is still JUST A THEORY.
Now if I'm wrong I'll recant and apologise to them.
So, is it the Theory of Gravity or the Law of Gravity. And do you have
any links or references that I could use to either prove or disprove it
either way?
![]() ANSWER:
ANSWER:
I would say that it depends
on how you define a law and a theory. Here are my definitions: a law is
a mathematical statement describing how something is
whereas a theory is an explanation of why something is.
Now, I assume that you are referring to Newton's universal law of
gravitation, namely F=-Gm1m2/r2.
This is an empirical law that tells you the force which two objects
exert on each other because of the gravitationsl attraction; it says
nothing about what the origin of this force is, that is why do two
objects which have mass attract each other. I would therefore say that
this is not a theory of gravity, it is a law of physics. On the other
hand, the theory of general relativity explains why two masses attract
each other (because the presence of mass "warps" the space around it}
and therefore is the operative theory of gravity. I should point out
that either a law or a theory might be applicable only in special
circumstances; for example, Newton's three laws of motion are
applicable in everyday life but when you try to extend them to very
large speeds or very small distances, they become inapplicable.
![]() QUESTION:
QUESTION:
I know that the length of an
organ pipe (as well as the speed of sound in air) determines the
frequency of sound produced within it. Does the diameter of the pipe
have any effect on the sound produced?
![]() ANSWER:
ANSWER:
What the length determines is the
fundamental frequency, but no musical instrument contains just the
fundamental. each note played by each instrument also contains what are
called overtones, other frequencies, usually simple multiples of the
fundamental. The relative intensities of the many frequencies produced
is called the timbre and it is what allows you to tell the difference
between an A played on a violin or an organ or a trumpet etc.
Geometrical properties of organ pipes other than its length determine
its timbre; design of organ pipes has evolved from trial and error and,
as such, is more an art than a science.
![]() QUESTION:
QUESTION:
What happens to all the
light photons that enter your eyes?
![]() ANSWER:
ANSWER:
For the most part, they vanish giving their
energy to heat or chemical reactions which initiate nerve impulses
which your brain detects and interprets.
![]() QUESTION:
QUESTION:
My family is astounded with
long thin projections of ice that form regularly and randomly on top of
ice cubes since I began placing the ice cube trays in the freezer door.
Even when the door is unopened from the time the trays are filled until
the time the ice is well hardened, the needle like spears that usually
slant in various directions at about a 45 degree angle, still form.
Some of these projections reach a length of about an inch. On some
cubes there are large fat lumps that raise up somewhat like a low
volcano. The trays are stacked one on top of the other and the cubes in
the bottom one does not, of course, have these curious growths. Can you
explain how this happens?I
![]() ANSWER: (Thanks
to Professor Craig
Wiegert)
ANSWER: (Thanks
to Professor Craig
Wiegert)
I've also witnessed this phenomenon.
(Unfortunately, automatic ice
makers seem to be largely immune to this curiosity, so it's been
several
years.) The creation of these ice spikes has to do with the fact that
the ice cube freezes from the outside in. The top surface starts to
"crust over" first, with the ice growing outward from the edges of the
cube (in the same way that lakes freeze over in colder climes).
Meanwhile, the sides and bottom of the cube also start to freeze.
Because ice is less dense than water, the growing "skin" of ice starts
to crowd out the unfrozen water at the center of the cube. The water
has nowhere to go but up. If the top surface of the cube is mostly
frozen except for a thin spot in the middle, the water will be pushed
out of that opening to form a bump. When the conditions are right, the
"bump" will instead become an ice tube (freezing from the outside in,
remember) and the water will be able to rise even higher. The end
result is the ice spike.
Better descriptions, with lots of nice photos, movies, and some
experimental results, are available at:
http://www.its.caltech.edu/~atomic/snowcrystals/icespikes/icespikes.htm
and
http://www.physics.utoronto.ca/~smorris/edl/icespikes/icespikes.html
The best example I ever saw was in my family's backyard birdbath when
we
lived in Oregon. A cold front had swept through overnight, and the next
morning we found an ice spike at least 4 inches tall protruding from
the
center of the basin. There's probably a picture tucked away somewhere
in a family photo album...
![]() QUESTION:
QUESTION:
According the Law of
Conservation of Mass (or matter), matter is neither created nor
destroyed, it simply changes form. So, when a baby is gestating, where
do the atoms that make up that fetus come from? My thought is that the
matter is coming from two sources: the sperm and egg to begin with, and
from the food that the mother is ingesting to nourish the fetus. (And I
suppose the air she is breathing contributes to the nourishment of the
fetus.) Would that be correct? I figure that's where new plants come
from....they pull atoms of nourishment from the ground and that helps
build the plant itself.
![]() ANSWER:
ANSWER:
First of all, there is no such thing as
conservation of mass. Energy is what is conserved and matter is a kind
of energy (you know, E=mc2). The idea of
conservation of mass is a 19th century concept and comes from chemistry
where it is generally assumed that if you have a certain mass of
hydrogen and the appropriate mass of oxygen and if they combine to form
water, the mass of the water will equal the sum of the masses of
hydrogen and oxygen. However, if you could make an accurate enough
measurement, you would find that the water had a little less mass than
the hydrogen plus oxygen (because you must put energy in to break the
water apart and it shows up as mass in the end). That said, the forces
holding molecules together are incredibly weak and so the change of
mass in chemical reactions is incredibly small, so, for all intents and
purposes, mass is conserved. And therefore, you are right that the
mother supplies all the mass (after conception). And, yes, plants get
their mass for growth from the ground and the air.
![]() QUESTION:
QUESTION:
Given the length of a column
of air in a musical instrument changes the frequency of the note
(shorter column, higher pitch), I assumed that this was why adding
water to a wineglass changed its frequency when made to "sing".
However, on reflection, adding more water to a wineglass lowers the
pitch. Given adding more water decreased the length of the column of
air, this can't be the correct explanation (shorter column of are
should increase the frequency).
Moreover, I've done the same "experiment" with the wineglass submerged
to the same depth as it was previously filled (ie., water is at the
same height on the outside, as it was previously on the inside). The
pitch was the same in both cases.
I've also noted that the same volume of water at a higher temperature
increases the pitch of the note. My question is what is the correct
explanation for the change of pitch of a "singing" wineglass? (I think
that is must be something to do with the damping effect of the water in
direct contact with the glass. This makes sense given at a higher temp,
the density of the water is lower, therefore the absorption of sound
energy is less for the same height of water in contact with the glass.
Less absorption, less change in frequency.)
![]() ANSWER:
ANSWER:
The reason is that it is not the air column
but rather the glass which is resonating. Think of a mass on a spring:
if you increase the mass (inertia) you decrease the frequency and I
think that is what you are doing by adding water, increasing inertia
against vibration. In that light, it is not surprising that you get the
same frequency whether the water is inside or outside the glass
(although I would not expect them to be precisely the same). The
temperature effect may simply be that you are changing the elasticity
(spring constant) of the glass by changing the temperature; try heating
the glass without adding water.
![]() QUESTION:
QUESTION:
I am a 16 year old student
currently enrolled in Physics at my high school. I was given an extra
credit assignment in which I have to figure out all the steps to
convert meters per second to miles per hour. I need to know every
single step in completing the conversion. I have done research, and
have found nothing that has helped me out. Thank you for your time.
![]() ANSWER:
ANSWER:
The trick to unit conversion is to
repeatedly multiply by 1.0 (we can always do that, right?) until the
units are what we want. Since I will not do your homework for you (it
violates the groundrules of this site!), I will work out an analogous
problem. Suppose that I want to convert a pressure expressed in pounds
per square inch (psi) to the more "scientific" expression of newtons per square meter. For
a concrete example, let's do 14.7 psi which is about atmospheric
pressure:
14.7 (lb/in2)x(1 in/ 2.54 cm)2x(100 cm/1 m)2x(1 N/.225 lb)=1.01x105 N/m2.
![]() QUESTION:
QUESTION:
I was just wondering, could
the principle of superposition of waves be used to muffle or even
silence a noise projecting from a sound source? So, perhaps if a source
of sound was project a particular frequency, and i places another
source of the same frequency and ampilitude in another position, say
half a wavelength behind, could the original noise be silenced?
![]() ANSWER:
ANSWER:
Yes. In fact, that is how noise-cancelling
headphones work--the external sounds are captured by a microphone,
flipped, and added back to the incoming sounds. Then you hear only
(almost) the sounds being sent to the headphones, music, talk, etc.
Pilots often use this device so that the hear only other crew members,
ground controllers, etc. The answer to your second question is
also yes but you must also take care that the two speakers are in
phase. This kind of destructive interference is responsible for "dead
spots" in concert halls.
![]() QUESTION:
QUESTION:
I've
heard of this experiment: Two parallel mirrors are set up and a laser
is fired perpendicularly between them. It is then possible to view the
beam of laser light (maybe with some dust or smoke between the mirrors)
falling towards the earth with an acceleration of -9.8 m/s/s. Is this
possible? If so, has this ever been performed?
![]() ANSWER:
ANSWER:
It is true that light will
fall with an acceleration of 9.8 m/s2 (but retaining a
constant speed, that is the vertical component of the velocity would
increase), so in principle your device would work. But, think about the
scale of things. If the mirrors were 3 m apart, it would take 10-8
s for the light to go from one to the other. In this time the light
would "fall" 9.8 x (10-8)2/2 m which is about 5 x
10-15 m, about the size of a nucleus! I reckon (gt2/2)
that it would take about a hundredth of a second to fall 1 mm, right?
But in this time, light travels 3 x 108 x 10-2 =
3,000,000 m, a million reflections in our device. But no real mirror is
completely reflective; an amazingly good mirror would be 99.9%
reflective, but a million reflections would leave you with about 10-435
(.9991,000,000) of the initial intensity! Clearly, this
seems to be an impossible experiment and I very much doubt that any
variation of it has been done.
![]() QUESTION:
QUESTION:
I teach Science in Oconee County, Georgia. In class one
day we were discussing the Northern Lights and they are "cosmic
radiation" that is being burned up in our atmosphere at the poles due
to the high concentration of magetism from the earth's magnetic field.
I had two questions, wondering if you guys might be able to help me
answer the questions:
- I wanted to make sure I was correct in the cause for the northern and southern lights.
- I had a student ask, why we couldn't use large magnets or even the magnetic north/south pole to stop large scale radiation type attacks, ie. whether it be a nuclear war, an atomic bomb, or even to help clean up something like the leak at the Russian nuclear plant?
![]() ANSWER:
ANSWER:
Referring to northern lights as
"radiation...being burned up" is inaccurate. Here is a brief
explanation: There is a constant stream of electrons and protons which
come from the sun called the "solar wind". (During times of intense
sunspot activity the intensity of these particles increases.) If the
earth did not have a magnetic field, these particles would simply plow
through the earth's atmosphere (ionizing and exciting atoms as they
went) and then hit the ground where they would lose all their energy.
But, because the earth is like a giant bar magnet, these incoming
charged particles get deflected and their tendency, because of the
nature of the magnetic force, is to spiral around the magnetic field
lines toward the poles. Hence, there is a concentration of these
charged particles around the poles (which is why the aurora phenomena
are usually very far north or south) and as they follow the field lines
down, they strike the upper atmosphere. When these energetic particles
hit the air, they ionize (knock off an electron or two) the atoms along
the way and when these ions recombine with electrons, light is
emmitted--hence the "lights" part of the phenomenon. So,
you see, it is not really a case of radiation being "cleaned up" at
all. The cases you refer to are nuclear radiation and there the most
damaging radiation is usually gamma radiation which is very energetic
electromagnetic radiation (like x-rays but even more energetic); since
gamma rays have no electric charge, they are totally unaffected by
magnetic fields.
![]() QUESTION:
QUESTION:
Is the statement correct: "Today the temperature is 40
degrees Celsius and yesterday it was 20 degrees Celsius so it is twice
as hot today as it was yesterday"
![]() ANSWER:
ANSWER:
Although "as hot" is a qualitative
statement, physicists would say certainly not. It is the Kelvin
temperature which determines the energy content of something, and the
Kelvin temperature is 273 degrees below the Celcius temperature. Thus
the two temperatures would be 313oK and 293oK.
Maybe you could say that 40oK is twice as hot as 20oK
![]() QUESTION:
QUESTION:
im a senior citizen who completed a short senior course on
physics so maybe this is stupid.
l. is a photon also an electron?
2. does an electron ever break down into another particle and are all
electrons charged?
![]() ANSWER:
ANSWER:
1. No. A photon is light, it has no mass and
no electric charge; an electron has both.
2. No, an electron is a stable particle. It is possible to collide
electrons with other particles and create new particles which do not
include any electrons.
![]() QUESTION:
QUESTION:
I may be wrong, but it seems to me that a freezer full of
cold food is colder than the same freezer att he same temperature but
filled with air. Is one actually a few degrees colder than the other?
![]() ANSWER:
ANSWER:
"Colder" and "at the same temperature" are
contradictory. Colder means at a lower temperature.
![]() QUESTION:
QUESTION:
Imagine a lightsource (i.e
Flashlight) located someplace incredibly far away from me, the space
between the lightsource and myself is empty and there is nothing else
in the universe. Once I turned the light on, would I eventually get to
see the light no matter how small the source is, or would the light
"wear out" at some point?
![]() ANSWER:
ANSWER:
It certainly never "wears
out". But whether or not you can detect it depends on how intense it
is, how far away it is, and the nature of the source. The simplest
source to think about is a point source the intensity of which falls
off like 1/r2. Eventually, we will be far
enough away that the intensity becomes so small that we must think of
the light as photons instead of waves. The intensity will then be very
few photons per second per square meter. In principle, though, as long
as you made a very big detector capable of detecting a single photon
and waited long enough, you would eventually see one. If you used a
laser instead of a point source, the light would not fall off strongly
with distance and, provided that your detector intercepted the beam,
you would easily be able to detect it. However, no laser is really
perfectly collimated and the comments for the point source would be
applicable to some extent for large distances.
![]() QUESTION:
QUESTION:
Is there an upper limit as
to how hot ordinary matter can get? Since temperature is really the
average energy of the particles of matter, it would appear that
eventually the average speed of the particles would approach the speed
of light. Since nothing can go faster than light, what happens to super
enegetic particles when more and more engery is applied to them? Do
they get more massive? If so, at what temperature do these relavistic
effects become significant?
![]() ANSWER:
ANSWER:
Although there is an upper limit to the
speed a particle can have, there is no limit to how much kinetic energy
it may have (because kinetic energy is not mv2/2 in
relativity). For example, a particle with speed 0.9999 of the speed of
light has ten times the kinetic energy as a particle with speed 0.999
the speed of light (only 0.1% slower).
![]() QUESTION:
QUESTION:
I'm wondering how much
slower light travels in non-vacuum environments, i.e. air, water, etc.
Maybe you have a chart comparing the medium that the light is
travelling in to speed in whatever unit, say % of c.
![]() ANSWER:
ANSWER:
There is a well known physical constant
called index of refraction, n. It is defined as n=c/v
where v is the speed in the medium. Some typical indices of
refraction are air: 1.0003; water: 1.333; flint glass: 1.66; diamond:
2.42.
![]() QUESTION:
QUESTION:
why don't a roof collapse
from atmospheric pressure
![]() ANSWER:
ANSWER:
Because the pressure also pushes up from the
underside.
![]() QUESTION:
QUESTION:
My 7 year old daughter has a
"simple" physics question, but I want to give her a precise answer in
terms she can understand. I am hoping you can help. Here it is: At sea
level, would a soccer ball which is completely deflated (and collapsed)
have a greater or lesser weight (as measured on a standard scale) than
one filled with helium? My supposition is that the scale weight goes
down when filled with helium, even though the overall mass is increased
by the helium itself. Is this correct? That's a concept she can't
understand and I want to explain it if possible.
![]() ANSWER:
ANSWER:
Your question has an ambiguity in it: you
ask about the weight "as
measured on a standard scale". However, a standard scale does not
necessarily measure the weight of an object sitting on it, it measures
the force you push down on it with. So, a 10 pound weight on the scale
and on which you are pulling up with a force of 4 pounds will only
"weigh" 6 pounds according to the scale. So, let me address the
question in two parts.
- Which has more weight, the empty ball or the full ball? Obviously, the full ball since it has the weight of the ball plus the weight of whatever it is filled with.
- Which will have the greater apparent weight as measured by the scale? Here a new force, the buoyant force, comes into play. When you put an object into a fluid (air is a fluid) there is an upward force on it which is equal to the weight of the displaced fluid. Since you are dealing with a 7 year old, just give her a simple example of a buoyant force: e.g. a soccer ball filled with air on the bottom of a swimming pool pops to the top because of the buoyant force; the buoyant force on the soccer ball in air is just less than in water because water is more dense than air. So, assuming that the helium is at a pressure (close to atmospheric) not too high, there will be an upward buoyant force (equal in magnitude to the weight of an equal volume of air) greater than the weight of the added helium, and so the apparent weight will be less than the empty ball.
![]() QUESTION:
QUESTION:
The other day I was watching
a child play with one of those funfair baloons, filled with (what i
think is) hellium. Often children let go these ballons, and they just
keep on rising and rising...
My question is: how high will such a ballon rise, assuming minimal wind
(i.e. if the ballon rose approx. vertically)?
What if the ballon had hidrogen instead of hellium? Is it different?
![]() ANSWER:
ANSWER:
The reason the balloon rises is the same
reason wood floats. When an object is in a fluid (like air or water) it
experiences an upward force (called the buoyant force) equal in
magnitude to the weight of the fluid which it displaces; this is called
Archimedes' principle. So the balloon has two forces on it, its own
weight down and the buoyant force up. If the weight of the air
displaced by the balloon is greater than the weight of the balloon,
there is a net force pushing up which will push the baloon up. This
will be the case if the balloon is filled with helium but not if it is
filled with water, for example. Now, the air in our atmosphere has, as
you probably know, the property that it gets less and less dense as you
go higher and higher; for example, it is quite hard to get enough air
on top of Mt. Everest and airplanes which fly at more that a few
thousand feet must be pressurized. For this reason, the buoyant force
gets smaller and smaller as the balloon rises until, eventually, it is
the same as the balloon's weight and it will stop rising. I have
ignored, in my explanation, the fact that the balloon will get larger
as it goes higher because the pressure of the gas inside stays about
the same while the pressure of the air on the outside gets smaller; I
think the important thing to appreciate is the Archimedes' principle
thing. This is the principle which lets "lighter than air" craft (hot
air balloons, blimps, etc.) fly.
![]() QUESTION:
QUESTION:
why does "fire" behave the way it does in space? why
does it not "go up" like fire on earth, but instead look like a sphere
or something? also, he says that he's heard it's more "dangerous"
[sic] [unpredictable?] in space and never goes out? is any of
that latter claim true?
![]() ANSWER:
ANSWER:
This is a good question and you can find it discussed
many places on the web. Two are
Wonderquest and
Scientific American. I will add my two cents' worth: How could a
flame go up if there is no direction identifiable as up? If all
directions are equivalent, then a physical phenomenon like a flame
would of necessity be spherically symmetric like the space. Regarding
the "never goes out" part, a flame is just a chemical reaction and if
either the fuel or the oxygen runs out, the flame will stop. Regarding
"dangerous", on earth the "updraft" of the flame allows oxygen to be
"sucked in" at the point of combustion making for more efficient
burning, so that would likely be a more dangerous situation. I believe
that something burns more quickly in gravity for this reason.
![]() QUESTION:
QUESTION:
If you skimmed a one
molecule thick layer of water off the surface of the earth's oceans how
much water would you have?
![]() ANSWER:
ANSWER:
The surface area of the earth is about 200 million square
miles and about 70% is water, so 140 million square miles; that is
about 3.6x1014 m2. The diameter of a water
molecule is about 3 angstroms=3x10-10 m. So the volume is
11x104 m3 which is about 30 million gallons. It
would fit in a cube of about 50 yards on a side.
![]() QUESTION:
QUESTION:
Why is parking a car in a
measured space easier while reversing than when moving forwad?
![]() ANSWER:
ANSWER:
I don't know if this is really physics; more common sense. It
is because you steer with your front wheels. If you steer your front
end into a parking space, the rear end is left outside and there is no
way to get it in. If you steer so that your rear end goes in first (you
have to go in reverse to do this) then your front end is left outside
but now you can steer it in.
![]() QUESTION:
QUESTION:
What causes light bulbs to
glow? Is it the gas inside? Do different kinds of bulbs
contain different gases? Like neon gas in neon light bulbs.
![]() ANSWER:
ANSWER:
Usually when we refer to "light bulbs" we are talking about
"incandescent" lights. Here electric current is passed through a very
thin filament (wire) and it becomes white hot; that is the source of
the light. The bulb is filled with an inert gas so that the wire will
not burn as it would in air. There is a disadvantage to this kind of
light, however--only a small fraction of the energy it uses is
converted to light, only about 10%; most of the rest of the energy
becomes heat. "Flourescent" lights are much more efficient. These
devices have a mercury vapor inside them which is caused by a very high
voltage across the ends of the tube to emit radiation; unfortunately,
most of this radiation is in the ultraviolet region which is not
visible. To remedy this, the tube is coated with a material called a
phosphor. When ultraviolet radiation strikes the phosphor, it is
absorbed and reemitted as visible light. (You may have seen a "black
light" which makes some clothing, posters, etc. glow; it is an
ultraviolet light and the the glowing things are phosphors.) If you
fill the tube with other gasses it will often glow with visible colors
without a phosphor, e.g. neon will glow orange.
![]() QUESTION:
QUESTION:
While helping my daughter in grade 5 with a wind power project I was
wondering how to measure in a simple way the wind speed of the fan. We
thought to try the approach where you suspend a ping pong ball from a
thread. A table exists which relates angle of swing to wind speed.
However I was wondering about the physics of it.
If you have a ping pong ball suspended from a 30 cm thread and the ping pong ball weights 0.0027 KG then if a wind blows the string at an angle of 30 degrees from the vertical, then what would be the wind speed. What formula would you use if you ignore the aerodynamic effects of the wind going around the ball etc. I am helping Raeann with her wind power project. So we have a room fan that we use to drive a wind turbine (propeller hooked to a motor). It would be nice to measure the wind speed of the fan. It is expensive to buy a real anemometer so people on the net have published a table that relates ping pong ball angle to wind speed. However I was interested if you could calculate this. So the force downwards is mg for the ping pong ball. The tension onthe thread would have a downward force and a sideward force component. The sideways force would have to be matched by the pressure of the wind. Wind pressure would include the density of air and the cross section area of the ping pong ball I would imagine. Also there is the potential energy of the ball lifting up so many meters would be matched by the kinetic energy of the ball. So any thoughts. [Questioner also included data which came from http://marsville.enoreo.on.ca/mission/challenges/anemometer.htm .
Angle
kph
90 0.00
85 9.30
80 13.20
75 16.30 
70 19.00
65 21.60
60 24.00
55 26.40
50 29.00
45 31.50
40 34.40
35 37.60
30 41.50
25 46.20
20 52.30 .]
![]() ANSWER:
ANSWER:
If you plot your data, angle as a function of wind speed, it
will not be particularly enlightening. Before plotting anything you
should think about the physics. This is the simple pendulum problem
except with a horizontal force which keeps the ball at a particular
angle. I will not do the details which you can get in any elementary
physics text; I will give the results. Let us call the (horizontal)
force of the wind on the ball F, the (vertical) weight of the
ball W, and the tension (along the string) in the string T,
and the angle the string makes with the horizontal q. Then, solving this
problem we find that T=W/sinq and F=Tcosq =Wcosq /sinq . To understand the
physics, therefore, you should plot F as a function of cosq /sinq . I have done
this in the plot on the right. The black crosses are the data, the red
line is a fit. In essence, what you find by fitting the data is that
this is almost a perfect parabola, that is the force is proportional to
the wind speed squared.
If you want to now calculate the force of the wind on the ball, it is approximately F=W 0.001 v2 where v is the speed of the wind in km/hr. Once you know the force, you can deduce the angle q =arctan[W/F]=arctan[1000/v2]. For example, if v=24, q = arctan[1.74]=60.1 degrees, in pretty good agreement with the data above. It is interesting that the length of the string is irrelevant; also, you do not need to know the weight of the ball as long as you have the quoted data. Probably more useful to you would be the inverse of this equation, v=[1000/tan q ]1/2 ; for example, if the angle is 30 degrees, v=41.6 km/hr.
For common wind speeds on things about the size of ping pong balls, wind resistance is roughly proportional to speed squared. This is not always the case and it can also be proportional to the wind speed or to some combination of linear and quadratic.
So now you understand things. Perhaps the simplest thing to do is just take the given data as the "calibration" of your instrument and then, having measured the angle, interpolate.
![]() QUESTION:
QUESTION:
My husband and I may get divorced over this question! We both
have our positions, so maybe you can help us out. It's extremely
cold here in Calgary, about -20 celcius, and this came up on the way
home after starting up a very cold car. When starting the car,
after the temperature gage starts to indicate that the engine is
warming up, my husband cranks the heat full blast. It's my
position that if he were to keep it at a low setting, the air coming
out of the vent would be warmer, just not as much of it. If we
select the high setting, the temperature coming out of the vent will be
cooler. I think this is because it is forced air, and cold air is
being added to warm air from the engine that is not so warm yet,
thereby diluting it. Once the engine has warmed up enough, the
effect of the forced air created by cranking the heat is irrelevant
because the engine is very hot (meaning that the temperature of the air
coming out of the vent is the same at any setting, once the engine is
hot). He says that the setting of the fan does not change the
temperature coming out of the vents at the same engine temperature.
Which one of us is right????
![]() ANSWER:
ANSWER:
Well, it depends on what you want. If you want the air to be
as warm as possible coming in, you are likely right. On the other hand,
what you probably really want is to maximize the rate at which your car
is heating up and, in that case, your husband is likely right. I say
"likely" for the following reasons. Heat will be transferred from the
heating coils to the air passing over them at some rate and that rate
may or may not depend on the rate at which air is flowing over
them. One possible scenario is that the rate is about the same
regardless of whether the fan is high or low, i.e. maybe the
same amount of heat per second is achieved with either fast or slow air
flow; in this scenario, the air from the slower fan will be warmer than
from the faster fan but each will warm the car up in the same amount of
time because each carries the same number of calories or BTU or
whatever per second. It is my guess that your husband is right if you
want to heat the car up as soon as possible since I would guess that
fast air blowing across the heater coils would take the heat away
faster from the coils.
But, as is often the case in science, there is nothing to take the place of a measurement and that might be what you have to do to get a definitive answer. Let us make up what an experiment might measure so you can see how you could definitively do a measurement. The first thing you need to know is that the energy contained in a gas is proportional to its absolute temperature, i.e. E=a(T+273) where a is some constant, E is the energy, and T is the celcius temperature; the 273 is to convert T to absolute temperature (-273 C is absolute zero). Suppose that the temperature of your air is 15 and your husband's is 5. Then, the same volume of air contains energy in the ratio Ewife/Ehusband=288/278=1.036 (you are winning so far!) But, the volumes of air are not the same--your husband's method moves, let's say, twice as much air, so Ewife/Ehusband=1.036/2=0.518, your method now losing out by nearly a factor of two. This is not definitive since it depends on the relative temperatures and air flow volumes. I expect, as I said above, that the way to warm up the car the fastest is your husband's.
![]() QUESTION:
QUESTION: 
We know that in the case of earthquake waves, P longitudenal waves can
pass through the liquid core but S transverse waves cannot - why is
that?
![]() ANSWER:
ANSWER:
For a longitudinal wave to traverse a medium, the medium must
be compressible. This is how sound travels through air or water
or steel. The medium is displaced in a direction parallel to the
direction the wave is moving and does that by compressing closer to
gether. For a transverse wave to traverse a medium, the medium
must have a shear elasticity; I am not sure that
this is the right wording but if the medium is displaced in a direction
perpendicular to the direction the wave moves, it must "spring
back". A solid does this, a liquid or a gas does
not. Representations of the two types of waves are shown at
the right. The S wave could not exist if there were not a
restoring force in a vertical direction in the figure. The P
wave, however, has a natural restoring force because the pressure
increase in the regions of compression push the material back.
I am not sure that
this is the right wording but if the medium is displaced in a direction
perpendicular to the direction the wave moves, it must "spring
back". A solid does this, a liquid or a gas does
not. Representations of the two types of waves are shown at
the right. The S wave could not exist if there were not a
restoring force in a vertical direction in the figure. The P
wave, however, has a natural restoring force because the pressure
increase in the regions of compression push the material back.
![]() QUESTION:
QUESTION:
I have a question that i really want to know the answer to. I'm
hoping you can help. Sometime when you're watching tv or driving
on the road and you look at cars it appears that the rims of the cars
are actually rotating in a backwards motion. Why does this happen?
![]() ANSWER
ANSWER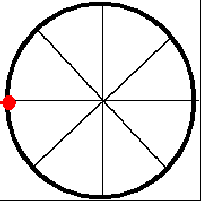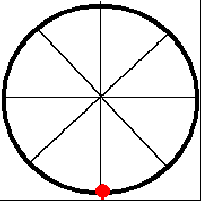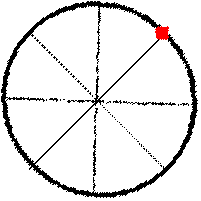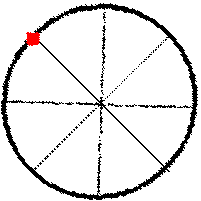 :
:
If it happens on the road, I don't really know why; I have
never seen that. I can tell you why it happens in movies and
TV. The classic example is a wagon wheel in a cowboy movie.
The key to understanding is to recognize that a movie is a series of
still photographs in a sequence of time. Imagine a spinning wheel
with two of the spokes labeled A and B such that if you watch one place
you will see A there first and then, some time t0
later you see B at the same place; so t0 is the time
it takes the wheel to rotate the angle equal to the angle between two
spokes. Now suppose that you are taking a movie of this spinning
wheel and the time between frames is some time t; then, if t=t0
each frame would have all the spokes in the same position so the wheel
in the movie would appear to not be rotating! [An example is
shown to the right: here the wheel rotates as you can see from the red
dot on the rim of the wheel, but it does not appear to be if you don't
watch the red dot.] If t were a little more than t0,
the wheel in the movie would appear to be going in the correct
direction, but slowly; if t were a little less than t0,
the wheel in the movie would appear to be going backwards. There
you have it.
You can get a similar effect in "real life" if you view something with a strobe light; some light sources have a normally imperceptible flicker (often 60 cycles per second like the line voltage powering them) which can cause the source to be a strobe.
![]() QUESTION:
QUESTION:
Do raindrops spherical or of the classical raindrop shape?
And what make it shape that way? How can somebody see the shape of
raindrops? Is there a simple experiment I can do to verify it? Will
raindrops from clouds higher in the sky larger/smaller than those from
lower clouds?
![]() ANSWER:
ANSWER:
Shown to the right is a picture I stole from a site
which explains this all very nicely. Raindrops smaller than about
1 mm in radius remain spherical and, as the size gets bigger, they tend
toward a shape like a hamburger bun (called "oblate"). (The
numbers shown are the radii of spherical drops which have the same
masses as the ones shown.) To imagine the shape for each case
drawn here, imagine rotating the the shape about a vertical axis
passing through the center. What is happening, of course, is that
the drop sees air rushing "up" which tends to flatten it out. All
these are assuming that the drops are falling in still air. It is
interesting that for very large drops, which would be on the order of
one centimeter across if spherical, a little parachute actually forms
which then breaks like a bubble and results in smaller drops. I
believe that there is no easy way to correlate size with altitude since
other factors will determine it. In any case, raindrops never
have the classic teardrop shape. Verification would probably
require high speed photography; the shapes are equilibrium shapes after
terminal velocity has been reached, so you couldn't just look at drops
falling a few feet.
![]() QUESTION:
QUESTION:
Given the laws of attraction, what (force?) is it that keeps
electrons from "falling" into or colliding with the atomic nucleus?
![]() ANSWER:
ANSWER:
You are actually asking the wrong question. An
identical question in many ways is 'what keeps the moon from falling
into or colliding with the earth?' In both cases we have a light
object orbiting a heavy object; they are able to do this because the
attractive force (gravity in one case, electrical force in the other)
keeps them in orbit. Newton understood this orbiting phenomenon
qualitatively by imagining throwing a rock off the top of a mountain:
- Just throw it and it falls to the valley below.
- Throw it harder and it goes much farther before it hits the ground.
- Throw it harder and it passes over the horizon before it hits the ground, so you never see it hit.
- Throw it harder and it keeps "falling" but never hits the ground and goes all the way around the world and comes back and hits you in the back!
So, what do I mean that you have asked the wrong question? An electron which accelerates (as a circling electron does because the direction of its velocity is always changing) radiates energy away. This is how the antenna at a radio station works--electrons are accelerated back and forth in the antenna. Therefore, an electron in a circular orbit should radiate its energy away and spiral into the nucleus as it loses energy. This does not happen and that is the puzzle. It was solved by the discovery of quantum mechanics back in the early 20th century; it was found that certain special orbits (quantum states of the system) are stable and do not radiate their energy away.
![]() QUESTION:
QUESTION:
I have a question that has been bothering me. It came about
when my teaher at my high school was lecturing about Albert Michelson
and his speed of light experiment. How did he control the rate of
rotation of his eight-sided mirrors. Without the help of computers what
machine did he use to keep the speed constant as well as measuring the
time it took for the mirrors to make one rotation.
![]() ANSWER:
ANSWER:
I was not able to find anything about the details of
Michelson's experiments. He apparently did it once around 1870
and again with greater accuracy around 1920. What I can tell you,
however, is that regulating the speed of a rotating motor was within
the realm of 19th century technology; there are things
called "governors" which mechanically sense changes in speed and feed
back to the motor to keep it going at a constant rate. Governors
were used way back in the era of steam engines running mills in
England. Regarding measuring the rate, that is a really simple
matter if you are certain that the speed remains constant: just count
the number of revolutions in a minute; at the high rates probably
involved in these experiments, this would still be relatively
simple--just have a cam on the axel which actuates a counter. So
the short answer to your question is that computers aren't needed for
this level of technology.
![]() QUESTION:
QUESTION:
How does aluminum foil work? If you wrap food in
aluminim foil, does it keep it warm? Does aluminum foill conduct
heat? Why doesn't it get hot when you put it in the oven?
![]() ANSWER:
ANSWER:
Aluminum is an excellent conductor of heat. Therefore,
it would be a poor choice for wrapping something to keep it hot.
And, it does get hot when you put it in the oven. It soon will
reach the temperature of the air in the oven. So, you ask, why
don't you get burned when you pick up a piece of foil you have just
removed from the oven? The internal energy which something at a
particular temperature has is proportional to its volume and the rate
at which the energy is radiated away is proportional to its surface
area; so hot foil has little energy (because of its small volume) and
it loses it very quickly (because of its large surface area). If
you took a block of aluminum from a hot oven it would be unwise to
touch it for several minutes.
![]() QUESTION:
QUESTION:
If 2 combined materials that are carbon dated to be from the
year 1300 AD, and it is found that 60% of the material was from the
year 1500 AD, can the date of the other 40% of the material be
approximately calculated?
![]() ANSWER:
ANSWER:
Well, I am certainly not an expert but I understand how
carbon dating is done. I can give you an answer in theory.
Someone who actually does it would have to judge whether it would be
practical in practice. Also I am going to take a somewhat
different perspective (from your actual question) because it lends
itself to a clearer explanation: rather than consider what I would
consider an erroneous dating, the details of which I do not know, I
will assume that we have two materials, one of known age and one of
unknown age whose relative amounts are also known, and that we simply
take a measurement of the radioactivity of the source. I am not
going to go through the derivation of the formula I derived to answer
this question for myself. If you are really interested, send
another question. What I find is:
tB=tA-(1/l)ln[(N0A/N0B)((R exp{ltA})/(lN0A)-1)]
where tB and tA are the ages of the two materials, N0A and N0B are the number of 14C atoms at the "creation" of each of the two materials, l is the decay constant of 14C (about 1.2x10-4 yr-1, corresponding to a half life of about 5700 yr), and R is the current rate of radioactivity coming from the source. (ln[] is natural logarithm, exp{} is exponential function.) Everything on the right side of the equation should be known:
- If we know the total amount of the sample and the relative amounts of the two materials then we can infer N0A and N0B (assuming, of course, that carbon dating works).
- We know tA.
- We measure R.
Here is an example: tA=1000 yr, N0A=1011, N0B=2x1011, R=3.07x107 yr-1 (corresponding to about one decay per second), then tB=2023 yr. That does not explicitly answer your question, but it shows that the answer to your question is a definite yes in theory. If you know abundances of both and age of one then you can infer age of the other from the observed radioactivity.
![]() QUESTION:
QUESTION:
When the sun is in the sky, it is too bright to look directly
at, but at sunset we are able to look directly at it. Why is this so?
![]() ANSWER:
ANSWER:
When light passes through our atmosphere, molecules of air
and particles of dust and smoke scatter the light. The picture at
the right shows light coming straight down through the atmosphere at
midday and light coming through the atmosphere at sunset. As you
can see, the light at sunset has much more atmosphere to pass
through. Therefore, a much larger amount of the light from the
sun is scattered out of the original beam of light at sunset so it is
much less intense and therefore easier to look at. Incidentally,
this is also the reason the sky is blue. As you know, the sunset
is very red. The reason for this is that the atmosphere scatters
blue light much more efficiently than red light so more blue gets
removed by scattering. When you look at a point in the sky you
are really seeing light from the sun which has scattered from that
point and you see blue predominantly. If there were no
atmosphere, the sky would be black even in the middle of the day; you
may have seen pictures taken on the moon where the sky is black when
the sun is in the lunar sky.
![]() QUESTION:
QUESTION:
Exactly how does a megaphone "magnify" sound?

![]() ANSWER:
ANSWER:
It does not magnify the sound. Rather it focuses the
sound. It is very much like the reflector in the headlight of an
automobile where light which would have gone straight up is reflected
to go straight ahead instead. In the picture above, the star
represents the source of sound and the heavy black lines the sides of
the megaphone. All the sound "rays" which are red would not have
been there if the megaphone had not been there. Instead they
would have gone along the dashed black lines.
![]() QUESTION:
QUESTION:
My students swear to me that when they did their science fair
projects last year in middle school they "proved" that hot water will
freeze faster than cold water. This doesn't make sense to me so we are
experimenting tomorrow to analyze what factors may contribute to their
theory. In the meantime, is that true? If so, why?
![]() ANSWER:
ANSWER:
This is the perennial question for scientists from
laymen! Alas, it has no clear and simple answer since it depends
very much on the conditions under which an experiment is
performed. In a nutshell, here is the important concept: if
evaporation from the hot water plays an important role, it is possible
and even likely that the hot water will freeze faster. What is
well known is that evaporation results in cooling. Another way to
put this is that it takes energy to cause a transition from liquid
phase to a gas phase. An easy way to demonstrate this is to take
a damp rag and swing it vigorously around your head; it gets really
cold. So I will give you two scenarios, one in which the hot will
likely freeze first and one in which the cold will certainly freeze
first.
- Suppose we have two wooden buckets each containing a gallon of water, one hot and one cold. The cold one must not be so cold that it is just about to freeze; imagine one room temperature (~700F) and the other hot tap water (~1600F). The buckets, being wood, are pretty good insulators, so most of the conductive/convective cooling comes from contact with the very cold air by the surfaces. But the hot water has an advantage: in addition to its conductive/convective cooling it has (greater) evaporative cooling, so it is likely to "catch up" with the cooler bucket before the cooler bucket freezes. Now we have two buckets of water at the same temperature, but there is now less water in the originally hot bucket because some of it evaporated away. Starting with two buckets of water one with a gallon and one with less, and having the rate of energy leaving each bucket about the same, the one with less water will cool faster and therefore freeze first!
- Suppose we have two one gallon sealed glass bottles filled with water, one hot and one cold. Because they are sealed, evaporation cannot play a significant role so each will cool at about the same rate, so the one that started cold will certainly freeze first.
Because of the subtleties here, this is not a good experiment for novice scientists! There are too many variables in terms of how energy gets in and out of the system and even in terms of parts of the system escaping. The important things to teach your kids are
- A certain amount of heat (energy) added will result in a certain increase of temperature in a certain amount of stuff (specific heat),
- a certain amount of heat is required to change a certain amount of a solid into a liquid (latent heat of fusion), and
- a certain amount of heat is required to change a certain amount of a liquid into a gas (latent heat of evaporation)
To read more about this topic, go to the MadSci Network and search on "freeze water hot" with the AND choice. That page, a much bigger one than ours, has received at least 46 queries like yours!
![]() QUESTION:
QUESTION:
Im a lower sixth student studying physics in the UK [2 yrs
before uni] and have a question:
Gravity pulls air particles towards it, and the further away from the
earth the particle is the weaker the pull of gravity, hence the higher
you go the thinner the air. Why then, is the ozone layer there? Just
because O3 is heavier than both O2 AND N2, the molecules making up the
greatest percentage or air, it should be pulled right down close to the
earth because by F=ma it will have a stronger force, or does the
pressure of the air at sea level hold it up.
Also, another point of argument this question stems from is am i right
in thinking that as you leave the atmosphere and go into space,
pressure drops off rather than there suddenly being no pressure as u
exit the outer layer of the atmnosphere because there are stary
particles etc.
![]() ANSWER:
ANSWER:
The first thing we need to discuss is why the atmosphere gets
thinner as you go up. It is most definitely not because, as you
believe, that gravity gets weaker as you go up. It is true that
gravity gets weaker, but by a very small amount over the distance where
there is any appreciable atmosphere (which could be anything from like
200 km to 1000 km depending on what you mean by "appreciable").
For example, if the acceleration of gravity is 9.8 m/s2 at
the earth's surface, it will be about 9.2 m/s2 at an
altitude of 200 km. The ozone layer is in the region 20-30 km of
altitude where the gravitational acceleration would be about 9.7 m/s2.
As you probably know, in the ocean as you go deeper and deeper down the
pressure gets greater and greater. The reason for this is that
the weight of all the water above has to be held up. But the
water does not get "thinner" as you go up--why not? Because water
is, for all intents and purposes, an incompressible fluid--no matter
how big the pressure, the volume of 1 kg of water stays almost the
same. Air, which is also a fluid, is far from what we would call
incompressible. The air inside your bicycle tire is at a
relatively high pressure and if you let it out it will occupy a much
bigger volume. Therefore, if you view yourself as being at the
bottom of a 200 km deep sea of air, the atmospheric pressure you
experience is due to the weight of all the air above you. Just
like in the ocean, if you go up the pressure will decrease but this
will now result also in the air being less compressed, i.e.
less dense. So that is why the air gets thinner as you go up.
Now, why are the ozone molecules in the atmosphere mostly up high? First let's ask why they are formed up there. The density is much lower high up in the atmosphere, but there are still a lot of O2 molecules--just not as many per cubic meter as there are here at the surface of the earth. But there is almost nothing above them, so they see all the radiation which is striking the earth from outer space, in particular they see pretty intense ultraviolet (UV) radiation from the sun. When UV strikes an O2 molecule, the energy is about right to dissociate it into two O atoms. These float around until eventually the O atom will find an O2 molecule and the two will combine to form your ozone molecule O3. That's how the ozone gets there and the reason the same thing doesn't happen at lower altitudes is that much of the UV has been absorbed or reduced as it plows down into the atmosphere; of course it does happen at lower altitudes, but just not enough to create a significant amount of ozone.
Finally, why doesn't the ozone get "pulled down close to the earth" as you suggest? Does the water at the surface of a lake fall down to the bottom? This only happens by convection, for example if the water at the surface is colder than the rest of the water in the lake it will be more dense and therefore sink to the bottom. (Of course, that is why the water at the bottom of a lake is generally colder.) The same idea applies to the atmosphere--convection causes cold air to sink and warm air to rise. This convection is the origin of all our planet's weather. However, in the region where the ozone exists (called the stratosphere), the air gets warmer as you get higher so all the air is already "where it wants to be" so there is very little convection and the ozone stays put.
Your last question is about how the density falls off. Yes, it is smooth and gradual and in fact there is no place in the universe where the pressure is zero. In intergalactic space there are still a few atoms per cubic meter.
I hope that I have helped you understand this process. A very good web site to learn more about the atmosphere is http://daac.gsfc.nasa.gov/CAMPAIGN_DOCS/ATM_CHEM/ozone_atmosphere.html.
![]() QUESTION:
QUESTION:
Am I correct in assuming that water at 4 degrees centigrade is more
dense that water at say 5 or 6 degres centigrade. The change in density
is negligible between the two, but yet theoretically existant?
![]() ANSWER:
ANSWER:
You are completely correct. Water, in fact, has its largest
density at 4 C. Most materials expand as you heat them up and
therefore, since the volume increases while the mass stays the same, the
density decreases. This is true for water only above 4 C.
The bizarre thing is that water also expands as you cool it below 4 C.
This simple fact has profound effects on the nature of our world which
has so much water in it. In the winter the environment causes the
water in a lake to cool down, first near the surface which is in contact
with the cold air. The layer of water at the surface cools and
gets denser and therefore sinks to the bottom. This continues
happening until all the water in the lake is 4 C. Now, as the
water near the surface cools further it becomes less dense so it floats
(stays at the top) until it reaches 0 C at which point it freezes and
becomes ice. This is why ice floats in water. For most
materials (take solid iron in molten iron, for example) the solid sinks.
If water behaved like this, a lake would freeze from the bottom up.
You would not be able to ice skate until the entire lake was solid!
So you see, these tiny changes in density are not, as you assert,
negligible. Also, it has nothing to do with "theoretically"; this
is an experimental fact, not a theoretical hypothesis.
![]() QUESTION:
QUESTION:
Why does the flame of a candle blow out in a wind or a
breath? What exactly is the explanation of this?
![]() ANSWER:
ANSWER:
I must admit that I stole this answer from another web site,
but I'm not into reinventing wheels! Fire is an autocatalytic
oxidation process, which cannot go on if you disperse the zone where
the reaction happens, i.e. the flame. In other words, when you
blow on the candle you rapidly dilute the contents of the fire, which
makes the amount of heat per unit of volume not sufficient for the
chain reaction of burning to continue. Consider also that the flame
"feeds" off vaporized paraffin, and if you blow it away the flame has
nothing to burn. Third factor is cooling, which is (again) associated
with dilution. As a result the flame goes out.
![]() QUESTION:
QUESTION:
My brother and I are currently having a discussion
(argument) about whether or not the water in a solar collector can
freeze if the air temperature does not go below 32 degrees Fahrenheit.
He argues, and I have read on websites, that this is possible because
solar collectors are near perfect blackbody radiators and are
transferring their heat into a cold dark night sky. I argue that this
would be true if there was no intervening atmosphere and the heat
radiated into cold dark space. But no matter how ‘perfect’ a blackbody
absorber/radiator the solar collector is it is radiating its heat into
an atmosphere at some temperature. If the collector did get cooler than
the atmosphere then heat would transfer from the atmosphere back into
the collector to establish equilibrium.
![]() ANSWER:
ANSWER:
I do not know much about solar collectors. But, what I
do know for certain is that water freezes at 32F! Regardless of
what the other conditions are, if the water gets down to 32F it will
freeze. I presume that the water is contained in some pipe, maybe
a copper tube painted black? Then, I presume the question is
whether the copper can be colder than the surrounding air by virtue of
radiating energy away. Of course it can--but, it depends
on how fast the energy is being radiated away. If the tube
becomes colder than the air, then energy will flow from the air to the
tube via conduction and convection. So it is all a balance
problem--the warmer the tube the greater the rate of radiation;
however, the greater the temperature difference between the tube and
the air around it, the greater the rate of conduction from the air back
to the tube. I strongly suspect that you are right for most
conditions you might have--that is, I expect the air to carry
energy back to the tube just as fast as it radiates away.
In thinking about this problem, I have found it is instructive to do a few rough calculations to get a feeling for the numbers we are talking about. I emphasize that these are just rough estimates to get the idea of what we are dealing with.
- First, let's calculate a typical energy radiation rate for a black body. To do this you need to know Stephan's law which states that, for a black body, the energy radiated per unit time per unit area of an object with temperature (in degrees Kelvin) T is sT4 where s=5.67 x 10-8 joules/m2/s/(0K)4. (A joule/s is a watt.) So, suppose we have a cube 1 cm on a side whose surface area is thus 6 cm2 near the freezing point of water of 2730K. Then I calculate that the rate of energy radiation is about 180 joules/s=180 watts. Frankly, I was a little surprised at how large this number is. What it means, as I will show next, is that if this were all that was going on, the water in your collector would freeze very quickly.
- So, let's now estimate energy change it takes to change the temperature. To do this, I will calculate how much energy it takes to change the temperature of 1 cm3 of water (which has a mass of 1 gram=10-3 kg) by one degree Kelvin (same as one degree Celsius). The heat (in joules) you must remove in order to lower the temperature of a mass m by an amount DT is given by mCDT where C is a constant called the specific heat. For water C=4186 joules/kg/oK, so I calculate that the heat needed to cool the gram of water by 1 degree is about 4.2 joules. It loses (at the rate of 180 watts) this amount of energy in about 0.02 seconds! This is why frost can form at air temperatures above freezing and why your brother is worried about your solar collector. Even if we are dealing with something far from being a perfect black body, the rate of energy radiation would still be on the order of a few watts so the time to lower the temperature to freezing would be on the order of no more than a few seconds.
- Assuming that radiation is the only thing happening, the water will quickly go down to freezing temperature. Now, as more heat is removed, the water will start turning into ice. About 300 joules must be removed to freeze a gram of water, so another few seconds should do it.
- So, why doesn't this just happen all the time? For one thing, there are things all over the place which are also radiating at about the same rate and the black body absorbs any of this radiation which falls on it. Furthermore, the air, by conduction and convection, will, if warmer than the water, carry heat to it. This is a complicated problem (because air generally transfers heat mainly by convection which is very complicated) which does not lend itself well to rough calculations. However, you can get an idea of expected rate of energy transfer by conduction by imagining the water to be enclosed in copper container. So, imagine our cubic centimeter of water enclosed in a copper box 1 mm thick and suppose that the temperature of the water (and inside of box) is one degree colder than the temperature of the air (and outside of box). The rate at which energy is conducted is given by kADT/Dx where A is the area (6 cm2), DT is the temperature difference, Dx is the thickness (1 mm), and k is the thermal conductivity (397 for copper). Doing this, I find that about 240 watts of power flow into the water, more than it is radiating but close. Now the problem reduces to whether the air can carry heat to the outside of the copper fast enough to maintain this temperature difference. It certainly cannot do it by conduction because the thermal conductivity k for air is very small (0.0234). But, I believe that under normal circumstances convection, along with other radiation being absorbed by the box, will be able to warm the outside of the box fast enough to keep the energy loss by radiation balanced.
So, where has all this led us? Your brother is certainly right--this could happen. The proof is that it is well known that frost can form when air temperatures are above freezing. (Actually, I believe that evaporative cooling also contributes to this phenomenon.) However, I earnestly believe that you are right in all but particularly extreme situations. If the air temperature is within a degree or two of the freezing temperature, you should probably consider the possibility that it might freeze.
![]() QUESTION:
QUESTION:
In my Physics class we are doing a project on making our own
hot air balloon which only flies from 2 ordinary birthday candles. How
would I make something like this?
![]() ANSWER:
ANSWER:
Since the net force up (i.e. the buoyant force minus
the weight) will be depend on the buoyant force on the balloon, you
want to make the balloon as big as you can to make the lift big.
On the other hand, as you make the balloon bigger, the total weight
will inevitibly get bigger (the material in the balloon weighs
something), so this says make the balloon smaller! So, what is
the ratio of the volume to the area? Assuming that it is
something like a sphere, this ratio is (4pr3/3)/(4pr2)=r/3.
So you have a net gain in overall force up as you increase the size of
the balloon. However, the last variable is the heating device, in
your case pretty puny! So, there is obviously no way you could
keep hot a huge balloon full of air because heat would escape as fast
as you could put it in. So, here is my advice to you: make the
payload (which is just what you need to hold the candles) as light as
you possibly can. Then find a material from which to construct
your balloon (essentially just a bag open at the bottom) from the
lightest material you can. Then experiment with different size
bags until the whole thing lifts off the ground. Good luck!
![]() QUESTION:
QUESTION:
Im a lower sixth student studying physics in the UK [2 yrs
before uni] and have a question:
Gravity pulls air particles towards it, and the further away from the
earth the particle is the weaker the pull of gravity, hence the higher
you go the thinner the air. Why then, is the ozone layer there? Just
because O3 is heavier than both O2 AND N2, the molecules making up the
greatest percentage or air, it should be pulled right down close to the
earth because by F=ma it will have a stronger force, or does the
pressure of the air at sea level hold it up.
Also, another point of argument this question stems from is am i right
in thinking that as you leave the atmosphere and go into space,
pressure drops off rather than there suddenly being no pressure as u
exit the outer layer of the atmnosphere because there are stary
particles etc.
![]() ANSWER:
ANSWER:
The first thing we need to discuss is why the atmosphere gets
thinner as you go up. It is most definitely not because, as you
believe, that gravity gets weaker as you go up. It is true that
gravity gets weaker, but by a very small amount over the distance where
there is any appreciable atmosphere (which could be anything from like
200 km to 1000 km depending on what you mean by "appreciable").
For example, if the acceleration of gravity is 9.8 m/s2 at
the earth's surface, it will be about 9.2 m/s2 at an
altitude of 200 km. The ozone layer is in the region 20-30 km of
altitude where the gravitational acceleration would be about 9.7 m/s2.
As you probably know, in the ocean as you go deeper and deeper down the
pressure gets greater and greater. The reason for this is that
the weight of all the water above has to be held up. But the
water does not get "thinner" as you go up--why not? Because water
is, for all intents and purposes, an incompressible fluid--no matter
how big the pressure, the volume of 1 kg of water stays almost the
same. Air, which is also a fluid, is far from what we would call
incompressible. The air inside your bicycle tire is at a
relatively high pressure and if you let it out it will occupy a much
bigger volume. Therefore, if you view yourself as being at the
bottom of a 200 km deep sea of air, the atmospheric pressure you
experience is due to the weight of all the air above you. Just
like in the ocean, if you go up the pressure will decrease but this
will now result also in the air being less compressed, i.e.
less dense. So that is why the air gets thinner as you go up.
Now, why are the ozone molecules in the atmosphere mostly up high? First let's ask why they are formed up there. The density is much lower high up in the atmosphere, but there are still a lot of O2 molecules--just not as many per cubic meter as there are here at the surface of the earth. But there is almost nothing above them, so they see all the radiation which is striking the earth from outer space, in particular they see pretty intense ultraviolet (UV) radiation from the sun. When UV strikes an O2 molecule, the energy is about right to dissociate it into two O atoms. These float around until eventually the O atom will find an O2 molecule and the two will combine to form your ozone molecule O3. That's how the ozone gets there and the reason the same thing doesn't happen at lower altitudes is that much of the UV has been absorbed or reduced as it plows down into the atmosphere; of course it does happen at lower altitudes, but just not enough to create a significant amount of ozone.
Finally, why doesn't the ozone get "pulled down close to the earth" as you suggest? Does the water at the surface of a lake fall down to the bottom? This only happens by convection, for example if the water at the surface is colder than the rest of the water in the lake it will be more dense and therefore sink to the bottom. (Of course, that is why the water at the bottom of a lake is generally colder.) The same idea applies to the atmosphere--convection causes cold air to sink and warm air to rise. This convection is the origin of all our planet's weather. However, in the region where the ozone exists (called the stratosphere), the air gets warmer as you get higher so all the air is already "where it wants to be" so there is very little convection and the ozone stays put.
Your last question is about how the density falls off. Yes, it is smooth and gradual and in fact there is no place in the universe where the pressure is zero. In intergalactic space there are still a few atoms per cubic meter.
I hope that I have helped you understand this process. A very good web site to learn more about the atmosphere is http://daac.gsfc.nasa.gov/CAMPAIGN_DOCS/ATM_CHEM/ozone_atmosphere.html.
![]() QUESTION:
QUESTION:
Am I correct in assuming that water at 4 degrees centigrade is more
dense that water at say 5 or 6 degres centigrade. The change in density
is negligible between the two, but yet theoretically existant?
![]() ANSWER:
ANSWER:
You are completely correct. Water, in fact, has its largest
density at 4 C. Most materials expand as you heat them up and
therefore, since the volume increases while the mass stays the same, the
density decreases. This is true for water only above 4 C.
The bizarre thing is that water also expands as you cool it below 4 C.
This simple fact has profound effects on the nature of our world which
has so much water in it. In the winter the environment causes the
water in a lake to cool down, first near the surface which is in contact
with the cold air. The layer of water at the surface cools and
gets denser and therefore sinks to the bottom. This continues
happening until all the water in the lake is 4 C. Now, as the
water near the surface cools further it becomes less dense so it floats
(stays at the top) until it reaches 0 C at which point it freezes and
becomes ice. This is why ice floats in water. For most
materials (take solid iron in molten iron, for example) the solid sinks.
If water behaved like this, a lake would freeze from the bottom up.
You would not be able to ice skate until the entire lake was solid!
So you see, these tiny changes in density are not, as you assert,
negligible. Also, it has nothing to do with "theoretically"; this
is an experimental fact, not a theoretical hypothesis.
![]() QUESTION:
QUESTION:
Why does the flame of a candle blow out in a wind or a
breath? What exactly is the explanation of this?
![]() ANSWER:
ANSWER:
I must admit that I stole this answer from another web site,
but I'm not into reinventing wheels! Fire is an autocatalytic
oxidation process, which cannot go on if you disperse the zone where
the reaction happens, i.e. the flame. In other words, when you
blow on the candle you rapidly dilute the contents of the fire, which
makes the amount of heat per unit of volume not sufficient for the
chain reaction of burning to continue. Consider also that the flame
"feeds" off vaporized paraffin, and if you blow it away the flame has
nothing to burn. Third factor is cooling, which is (again) associated
with dilution. As a result the flame goes out.
![]() QUESTION:
QUESTION:
I need to know which element has a symbol which does not
relate to its name, eg: Copper = Cu = Derived from latin name Sulpher =
S = First letter
![]() ANSWER:
ANSWER:
To the best
of my knowledge, no element which has been officially named by the
international agency responsible for naming ( IUPAC ) has a symbol
which has no relation to either the actual name or to its name in
another (usually classical) language (e.g. Ag for argentum which
is Latin for silver). Many of the names are in honor of famous
scientists (Einsteinium, Curium, etc.) and many are named for
places where they were first discovered (Ytterbium, Erbium, Yttrium, e.g.,
are all named for a village in Sweden called Ytterby). There are a
number elements for which agreement upon their names has not been
reached, so perhaps these are what you are looking for. They have been
given temporary names and symbols. For more information you may go to
the website Weblements, http://chemserv.bc.edu/web_elements/web-elements-home.html,
and links in that site. For information on the naming issues, see http://www.webelements.com/webelements/properties/text/definitions/name.html.
![]() QUESTION:
QUESTION:
As I understand it, osmosis does not require any energy to
occur; it is passive. If a passive process can move water in an upward
direction against gravity....then the osmosed water would then have
potential energy...correct? If you can't create or destroy energy, you
can only change it from one form to another....and it took no energy to
give the water potential energy....what was the energy which had to be
converted to the potential energy the water now has? Also, where
is the entropy in that conversion? Thanks, Brett
![]() ANSWER:
ANSWER:
First a disclaimer: I don't have any expertise here! I
did a little research, though. First of all, let's define what
osmosis is: essentially a membrane lets water pass through but does not
allow cer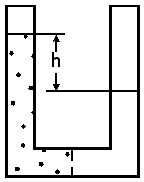 tain
molecules dissolved in the water through. The classic
example illustrating what happens is a U-shaped tube with water in it
and a permeable membrane across the tube at the bottom. Water may
pass through the membrane unimpeded and therefore, if there is just
water in the tube, the level of fluid in each side is the same.
However, if you put, for example, some salt in one side, water will
flow through from the pure water side to the salty side raising the
level of the salty side and lowering the level of the pure water
side. This system, as you note, has more gravitational potential
energy than before the water flowed, so the question is: where did this
energy come from? The solute behaves like an ideal gas and moves
around in the solvent with some average velocity. The solute
molecules are therefore colliding with the membrane transferring
momentum and energy to it and the net result is a pressure differential
across it. This pressure difference is what causes the
water to flow preferentially in one direction and the flow will
continue until the pressure difference is the same as the hydrostatic
pressure due to the weight of the upper column of water. The work
(energy) to increase the potential energy came from the kinetic energy
of the solute molecules which must therefore have slowed down (that is,
this "solute gas" must have cooled down in the process).
tain
molecules dissolved in the water through. The classic
example illustrating what happens is a U-shaped tube with water in it
and a permeable membrane across the tube at the bottom. Water may
pass through the membrane unimpeded and therefore, if there is just
water in the tube, the level of fluid in each side is the same.
However, if you put, for example, some salt in one side, water will
flow through from the pure water side to the salty side raising the
level of the salty side and lowering the level of the pure water
side. This system, as you note, has more gravitational potential
energy than before the water flowed, so the question is: where did this
energy come from? The solute behaves like an ideal gas and moves
around in the solvent with some average velocity. The solute
molecules are therefore colliding with the membrane transferring
momentum and energy to it and the net result is a pressure differential
across it. This pressure difference is what causes the
water to flow preferentially in one direction and the flow will
continue until the pressure difference is the same as the hydrostatic
pressure due to the weight of the upper column of water. The work
(energy) to increase the potential energy came from the kinetic energy
of the solute molecules which must therefore have slowed down (that is,
this "solute gas" must have cooled down in the process).
You state that "osmosis does not require any energy". What this means is that no external agent does any work; that doesn't mean no work was done. As you can see, the total energy of the system has stayed the same because the potential energy increased and the kinetic energy decreased.
Finally, with regard to entropy, the second law of thermodynamics states, in one incarnation, that "as two interacting macroscopic systems approach equilibrium, the changes in the system variables will be such that the entropy of the combined system increases." So, the entropy of the system increases.
The website where I learned about osmosis is http://members.tripod.com/~urila/
![]() QUESTION:
QUESTION:
My high school physics teacher told our class one day that
when we bounced a ball off of the floor, that eventually at some
instant the atoms of the ball could arrange themselves perfectly so
that they all miss the atoms of the floor and therefore fall straight
through. I wanted so badly to argue, but seeing as how I was puny 12th
grader and my grade depended on my mouth I decided otherwise. So my
question would be, is there any logic what-so-ever in that statement???
![]() ANSWER:
ANSWER:
I suspect
that your teacher was trying to provide a dramatic example of the
notion that, as you know, most of the volume of an atom is "empty
space". The positively charged nucleus of an atom has a radius on
the order of 10-15 meters while the atom itself is of the
order of 10-10 meters but almost all of the mass of the atom
is in the nucleus; the electrons, which occupy the "empty space" have a
mass which is about 4000 times smaller than the mass of the
nucleus. However, his statement that the ball could pass through
the floor because of an accidental alignment of the atoms is, in fact,
incorrect. The reason for this is that the "empty space" in
atoms, while containing almost no mass, carries half the electrical
charge of the atoms and the negative electric charge on the outside of
the atoms in the floor exerts a repulsive force on the negative charge
of the atoms in the ball.
To understand what is going on, imagine one atom slowly approaching another single atom. Although introductory courses in chemistry or physics usually have you visualize the electrons in little "planetary" orbits around the nucleus, a much more accurate picture is that the electrons form a "cloud" of negative charge around the nucleus. Thus the two clouds repel each other and the incident atom "bounces back". If the incident atom has a high enough velocity the clouds may penetrate each other and then the attractive force of the nucleus may be seen and a molecule might form. If the incident energy is higher still, the two may simply pass through each other. The velocities where the two might pass through each other (maybe something like a tenth the speed of light, 30,000,000 meters per second!) is far higher than any ball is likely to have and at such energies neither the ball nor the floor would remain in tact. So, you see, the force which makes the ball bounce back (or simply holds up the ball's weight if the ball is just sitting on the floor) is electrical in origin and that force would not go away if the atoms happened to "line up" as your teacher suggests.
There is one more subtle possibility which your teacher may have been trying to illustrate; it is called "tunneling" and is an effect of quantum physics. In classical physics if an object is confined by forces to move in a region of space it is called a "bound" particle and cannot escape. Even if there is some nearby region of space where it would not be bound it still can't get there. In quantum mechanics, however, there is a probability that it could be found outside the bound region and so if you watch long enough it might just magically pop out there! In fact George Gamow showed back in the 30's that tunneling is the proper explanation for radioactive alpha-particle decay in heavy nuclei. I suspect that the probability of the ball tunneling through the floor would be so small that you could wait for several times the age of the universe to expect it to happen!