![]() QUESTION:
QUESTION:
I have an old fashion balance scale, center fulcrum and two dishes on either side of equal weight. If I place two weights on either side and the weights are nearly the same, the heavier side dips slightly, if the difference between the weights are large, the heavier side dips much more. I do not understand why this is so. Logic says that if there is any difference at all, the heavier side should continue to drop until it reaches a barrier to the fall no matter what the difference in the weight.
I asked a physics instructor and he did not have the answer either.
![]() ANSWER:
ANSWER:
I have received this question before and, alas, I have not found
the answer. I have asked readers to suggest answers but nobody ever has.
See an earlier answer.
![]() ADDED
ANSWER:
ADDED
ANSWER:
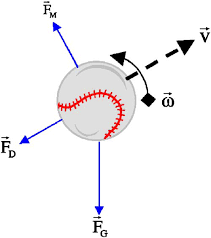
I have found the answer. The center of mass
⊗ of the scale
itself must be below the fulcrum (suspension point). Then, as shown
above, if the beam is off horizontal for the empty scale or equal
weights in each pan, there will be a restoring torque to force a balance
only for the horizontal beam.
![]() QUESTION:
QUESTION:
I made a statement to somebody that a plane hitting a building was the same as if the building hit the plane at exactly the same speed,the plane now stationary. The results would be the same. In other words, if a man with large hands slapped my hand at 50 mph, it would be same as me slapping his hand at 50 mph.....its interchangable.....the other person said, no, the mass of the building and hand would have different results...
![]() ANSWER:
ANSWER:
Either you or your friend could be right depending on what you
mean by "different results". Let me try to set up a simple example to
demonstrate why.
-
Imagine we have a 2 lb ball of putty moving with a speed of 5 mph striking and sticking to a 18 lb bowling ball at rest; the time it takes to collide is 0.1 s. After the collision, the two move together with a speed of v1. To find v1, use momentum conservation: 2x5=(18+2)v1, v1=0.5 mph.
-
Next, imagine we have a 18 lb bowling ball moving with a speed of 5 mph striking and sticking to a 2 lb ball of putty at rest; the time it takes to collide is 0.1 s. After the collision, the two move together with a speed of v2. To find v2, use momentum conservation: 18x5=(18+2)v2, v2=4.5 mph.
So, you see that the two scenarios have different speeds after the colliision. But, suppose that you were the putty ball. During the collision you feel a force and the force is what is going to hurt you. Do you get hurt as badly, not as badly, or equally as badly during the collision? What determines the force you feel is the acceleration you experience during the collision, how quickly your velocity changes, which is your final velocity minus your initial velocity divided by the time of the collision.
-
For the putty ball moving initially, (vfinal-vinitial)/t=(0.5-5)/0.1=-45 mph/s.
-
For the bowling ball moving initially, (vfinal-vinitial)/t=(0-4.5)/0.1=-45 mph/s.
You could go through through the exact same process to find that the bowling ball experienced exactly the same force regardless of who moved initially. A physicist would say that you were right, but the ambiguity of your statement means that the other guy could split hairs. As far as physics is concerned, the only thing which matters is the relative velocities of the two before the collision. If the putty ball were moving 105 mph and the bowling ball were moving 100 mph in the same direction, the result of the collision which matters (the force) would be the same.
![]() QUESTION:
QUESTION:
My question is about the maximum tension experienced by a bow string. I'm
specifically concerned with a traditional or recurve bow NOT a compound bow
with pullies. I want to know the max tension compared to the draw weight so
I have an idea how strong to make my strings. So here's the scenario, what's
the maximum tension in the string for a recurve with a 70 lbs draw weight
and a physical weight of 25 oz? I'm assuming the maximum tension is when
it's at brace (not full draw), right after the arrow leaves. I think this
because not only does the string have to oppose the restoring force of the
bow limbs but it also has to stop the momentum of the limbs that isn't
transferred to the arrow.
![]() ANSWER:
ANSWER:
To compute the tension I would need to know the geometry of the bow. I can
tell you that the tension will be at the maximum draw for a simple bow, not
where the arrow leaves the string.
![]() REPLY:
REPLY:
The bow is 64 inches long and the string is about 4-5 inches shorter than the bow. It Is braced at 6 inches and has tips that are 3 inches recurved behind the handle. Its draw length is 28 inches and has an elipitcal/circular tiller shape at full draw.
![]() ANSWER:
ANSWER:
(An incorrect answer was posted earlier. This is a reposting, correct
now, I hope!)
When researching the physics of archery I discovered that this can be a
very complicated problem requiring very sophisticated numerical
calculations on computers if you want precision descriptions of all the
details. You, however, require only a rough calculation for estimating
the strength of the string. I can do that and it is more appropriate for
the spirit of this site‚ÄĒto solve problems with simple physics
concepts. This problem requires facility with trigonometry,
understanding of Hooke's law, and application of Newton's first law. The
simple model I will use was one used before the advent of computers; the
bow is modeled as two straight rods (purple) the ends of which move on a
circle as the string (red) is drawn. With this simple model, most of the
details of your bow are not necessary. When the string is braced
(undrawn) there is a certain tension in the string and this tension will
increase as the bow is drawn. So, the maximum will be at the maximum
draw. The figure shows, roughly to scale, the situation. Using simple
trigonometry (law of cosines), I find β=59.60.
The point where the draw weight W is being applied must be in
equilibrium, W-2Tcosβ=0; solving, T=69.2
lb. I think that your concern about the string having to "stop the
momentum of the limbs" is misplaced because bows tend to be quite
elastic so that nearly all the energy imparted to the bow by drawing it
is imparted to the arrow and the limbs will end nearly at rest. Not so
if you draw and release without an arrow, though; what I have read is
that in that situation you are more likely to break your bow than the
string. I am working on a general solution which I will later add here
but thought I would post the part of the solution which answers your
question regarding the tension in the string.
![]() GENERALIZED
SOLUTION:
GENERALIZED
SOLUTION:
To get a better understanding of this problem it is worthwhile to
find an analytical solution for the tension as a function of draw
distance. My research showed me that a traditional or recurve bow
behaves, to an excellent approximation, like a simple spring
(Hooke's law), the draw weight being proportional to the draw distance,
i.e. W≈kx where x is the distance the
string is drawn and k is the spring constant. In this case, since W=70 lb when x=28
in, k=2.5 lb/in. Using the law of cosines, cosβ=(L2+(x+d)2-R2)/(2L(x+d)).
Again, the point where the force W is applied
is in equilibrium so W-2Tcosβ=0 or T(x)=kx/(2cosβ).
Now, note that in the limit where x → 0, β → 900
and cosβ → x/L. Therefore T(0)=kL/2.
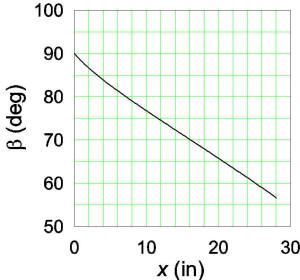
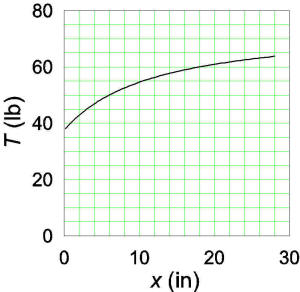
Using your numbers, T(0)=37.5 lb and the angle and tension for
all points are plotted below. At full draw, β=560
and T=64 lb. It was interesting to me that in order for the
calculated values to be correct at zero draw, very precise relative values of
R and L
had to be used because otherwise the expression for cosβ would not be 0 exactly when x=0. The value was
R=30.59411708 inches for L=30.
![]() QUESTION:
QUESTION:
Suppose a block is moving with constant velocity towards right on a frictionless surface and during its motion another block of slightly smaller mass lands on top of it from a negligible height.
I argue that the lower block will eventually start moving to the left and upper block will end up moving towards right provided that there is friction between the blocks but not between lower block and ground . My friends can't accept my reasoning. Am I wrong? Please help!
![]() ANSWER:
ANSWER:
I hate to tell you, but you are wrong. This is actually a simple
momentum conservation problem. Call the masses of the upper and lower
blocks m and M, respectively. Before they come
together the momentum is Mv where v is the incoming
speed of M. When the masses come in contact they will slide on
each other but, because there is friction, they will eventually stop
sliding and both will move with a velocity u; the linear momentum will
now be (M+m)u. Conserving momentum, u=[M/(M+m)]v.
They both end up going with speed u and move to the right.
You can also determine the time it takes for the sliding to stop. m will feel a frictional force to the right of magnitude f=μmg and M will feel a frictional force to the left of magnitude f=μmg (Newton's third law). So, choosing +x to the right, the acceleration of m is a=μg and the acceleration of M is A=-μg(m/M). The velocities as a function of t are vm=μgt and vM=v-μgt(m/M); we are interested in the time when vm=vM, so solving for t, t=Mv/[μg(M+m)]. If you substitute this back into vm or vM, you will find the same value we found for u above: vm=vM=u=[M/(M+m)]v.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
If the block of mass M is not too long, i.e., the total distance that the upper block can slide is less that the distance it could move in your calculated time " t" , wouldn't the two blocks get separated?
![]() ANSWER:
ANSWER:
Well, of course the block has to be big enough, otherwise m
will drop down on the frictionless surface. It would be a good exercize
for a student to calculate how far the block would slide for some
μ. And then, if this is greater than the size of the bottom
block, how fast will each be moving after separating.
![]() QUESTION:
QUESTION:
I do not want a theoretical answer, but has any experimentalist ever put a very sensitive weight balance below a vacuum chamber before and after vacuating it? Does it get lighter or... heavier? I do not have a sensitive balance nor a vacuum chamber.
The reason I ask is that it would say something about the density, or absence of density, of the vacuum.
If I understand pressure correctly, the scale would read a smaller weight value, due to less gas being in the column of air directly above it, but there might also be new physics there, if it is not the case. I simply do not know.
![]() ANSWER:
ANSWER:
You do not want a "theoretical answer" but you clearly do not understand
the physics so I am obliged to give you one anyway. Let us assume the
simplest possible "weight balance" so that I do not have to worry that
it might operate differently in a vacuum. Envision just a simple string
with a tiny butcher's scale which will measure the tension in the string
and then hang an unknown weight of mass M and volume V
from the string. Besides the string, there are two forces on the object
being weighed, its weight Mg and the buoyant force B=ρVg
where ρ is the density of air (about 1 kg/m3 at
atmospheric pressure) and g=9.8 m/s2 is the
acceleration due to gravity. The scale will read W=Mg-B, an
incorrect measure of the weight. Putting the whole device in a vacuum
will change B to zero because the air is gone, so W=Mg,
the correct weight. To get an idea of how important this is, consider
weighing a solid block of iron whose mass is 1 kg. The density of iron
is ρiron=7870 kg=M/V, so the
volume of the block is V=1/7870=1.27x10-4 m3.
So, the true weight is W=9.8 N and the measured weight in air
is (9.8-1.27x10-4) N=9.7999 N, an error of 0.0013%. However,
there are certainly examples where the effect of buoyancy would be very
important. For example, consider an air-filled balloon. I did a rough
calculation and estimated that the volume of an inflated balloon is
about 5x10-3 m3 so it contains about 5x10-3
kg of air; the mass of an uninflated balloon is about 5 gm=5x10-3
kg, so the total weight of the inflated balloon is about 9.8x10-2
N. But if you weighed it in air you would only measure half that amount.
Your question, has anybody ever actually observed this, is a no brainer:
since the existence of a buoyant force has been known and understood for
well over 2000 years (Archimedes' principle), anyone wanting to make an
extremely accurate measurement of a mass would either correct for it or
eliminate it.
![]() QUESTION:
QUESTION:
Several years ago, I was caught in a massive windstorm in a skyscraper. I was on the 54th floor (approx. 756 feet from street level, full building height is 909 feet) , pulling cable, and I stopped for a break. I left a cable pulling string hanging from the ceiling (48 inches free hanging length) in the office, with a 1/4 lb weight attached, and when the storm hit, the weight began swinging like a pendulum. The arc was 16 inches (eyeballing it), and traversing the length of the arc took about 1 second. How can I calculate how far (full arc) the skyscraper was moving by observing what the pendulum in the building was doing?
![]() ANSWER:
ANSWER:
A 48" pendulum has a period of about 2.2 s, the time to swing over the
arc and back. Since you were estimating, the pendulum was swinging with
about the period it would if the building were not moving at all. I
would conclude that either the pendulum got swinging somehow and the
building was not perceptibly moving or that the period of the building's
motion was about the same. If the building was swinging with a period
significantly different from 2 s, the pendulum would be swinging with
that same period; that is called a driven oscillator.
![]() QUESTION:
QUESTION:
Let's say you have three 20-foot putts. Same stimp meter (pace on the green). Let's say in all cases, the green is flat after the hole. I.e. don't worry about things like the ball running away or anything.
-
Putt 1 travels flat and then shortly before the hole, it rises 6 inches.
-
Putt 2 has an rise of 6 inches right after you hit it, and then travels flat to the hole the rest of the way.
-
Putt 3 rises 6 inches gently from the ball to the hole at a constant angle.
Do you hit all three putts the same initial speed? Follow up question : What if you have the same 20 foot putt but halfway to the hole the ground rises 8 inches, and then drops 2 inches and then flattens out the rest of the way to the hole. . .same speed?
![]() ANSWER:
ANSWER:
Refer to the figure.
If there were no friction, it would make no difference how the rise
occurred, only the amount of rise. In that case vhole=√(vputt2-2gh).
However, there is friction which will slow the ball further and the
frictional force on a slope (f=μmgcosθ) will
be different than on level ground (f=μmg); here μ
is the coefficient of friction (essentially, I believe, what is
measured by the "stimp meter"), m is the mass of the ball, and
g is the acceleration due to gravity. Since the frictional
force is smaller on the slope, you might think that less energy is lost
to friction on the slope. But, what matters is not the force but its
product with the distance s over which it acts, specifically
the work done by friction is Wf=-fs where
the negative sign indicates that the friction takes energy away from the
ball. When the ball is moving forward along along the segment L2,
the distance it travels is s=L2/cosθ
and so the work done is Wf=fs=(μmgcosθ)(L2/cosθ)=μmgL2,
exactly the same as if the slope was not there. The total work done by
friction, regardless of the path, is Wf=μmgL.
The final velocity is then
vhole=√[vputt2-2g(h+μL)].
![]() QUESTION:
QUESTION:
I'm coordinating a piece of action for a tvc (tv ad), which requires me to build a rig to raise an actor 3 m off the ground, as if he is being taken away by aliens! It's been a long time since school for me, however I feel that there would be a formula that would assist me in calculating how much counterweight is required on a pulley system with 2:1 MA to raise an 80kg actor 3m in 1.5 seconds?
Are you able to clarify the principals to be used in calculating this problem?
This is definitely not homework!
![]() ANSWER:
ANSWER:
The actor will experience an accelleration a such that he moves a
distance y in a time t: y=½at2
, so for this case a=2y/t2=2x3/(1.5)=2.7
m/s2. Choosing the man plus pulley above him as the body
(assuming the mass of the pulley is negligible), Newton's second law is
2T-mg=ma or T=½m(g+a)=½x80x(9.8+2.7)=500
N where g=9.8 m/s2 is the acceleration due to
gravity. Finally sum forces for the weight Mg which has the
same magnitude of acceleration as the actor: Mg-T=Ma, so
M=T/(g-a)=500/(9.8-2.7)=70.4 kg. You may want to keep in
mind that the speed of the actor at the end of the 1.5 s is v=at=2.7x1.5=4.05
m/s; if the weight is stopped after the 1.5 s, he will continue moving
upwards until he has risen another h=½v2/g=0.84
m and then fall back.
![]() QUESTION:
QUESTION:
I've been trying to figure out how to weigh my boat on its trailer, and it seemed to me that putting a scale under each of the two wheels and the tongue and adding the three weights together might not yield a correct result, but your
table weight answer, makes me think maybe it could be.
![]() ANSWER:
ANSWER:
Assuming that you do not have three scales which could be all engaged at
once, lifting one wheel at a time will introduce errors. Refer to the figure above
(noting that I have made the boat on the trailer invisible!): I have
notated 2S as the distance between the wheels, L the
distance from the axle to the tongue support, q the distance
from the ground to the center of mass (COM
©) of the boat plus trailer, d
the distance of COM forward of the axle, and W the weight of
the boat plus trailer. The normal forces Ni
are the forces up on each of the three points of contact; if an ideal
scale of zero thickness were placed under a wheel, the magnitude of the
appropriate normal force is what it would read and N1+N2+N3=W. I have also assumed that the
COM is centered laterally. The geometry and algebra are a bit tedious,
so I give only final answers. In each case I imagine lifting one point
of contact by the angle θ and then measuring the normal
force which I will call N'i. N'3
is the easiest since it does not depend on θ, N'3=Wd/L.
The other two are, by symmetry, the same: N'1=N'2=½W[1-(d/L)-(½q/S)tanθ].
If you now compute the sum, N'1+N'2+N'3≡W'=W[1-(q/S)tanθ].
So your measurement of the weight will be wrong. As an example, suppose
that S=3 ft and q=5 ft and you lift a wheel h=4
in=1/3 ft off the ground; then tanθ=(1/3)/(2x3)=1/18 and
the measured weight will be W(1-(5/3)/18)=0.91W,
nearly a 10% error. The culprit here is that the center of gravity is so
far off the ground. To get a more accurate measurement, block the
opposite wheel so that it is also h above the ground (the
tongue support does not need to be blocked); you only have to do this
once since N1=N2 and N3
does not depend on its height.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Also, in your
table weight example, wouldn't elevating one end of the table with a 2x4 and putting a scale beneath it shift (rotate) the table's weight (CoG) somewhat toward its other end and lessen the measured weight of the weighed end, and error be particularly noticeable if the span of the table is short and the scale is several inches high? If I could remember my trig I could pose this question more intelligently, but the extreme, if hypothetical, case would be if the table end were elevated all the way to vertical, where it would weigh nothing.
![]() ANSWER:
ANSWER:
Congratulations, you have caught one of The Physicist's rare
errors! I must admit that I was thinking small angle here and that is
the only case where it is a good approximation to say that elevating one
end of the table does not change the normal force. And, again, I did not
really appreciate the importance of the fact that the COM is not
colinear with the other two forces until I started puzzling over your
boat trailer question. You can see an example of a case where this is
not an issue in an earlier question about a
boat dock. The correct
answer to the
table weight
example would be W'=W[1-(q/S)tanθ].
(I have changed the notation and assumptions from original problem just
to make the solution more concise. In particular, I have assumed that
the COM is a distance q above the floor and equidistant from
the ends and sides; I have neglected the weight w of the 2x4,
and ¬ĹW=W1=W2; S
is the length of the table.) So, if q=3 ft, S=10 ft,
and h=1/3 ft (COM above floor), W'=W[1-(3/10)(1/3)/10]=0.91W.
![]() QUESTION:
QUESTION:
I would like to know the formula to calculate the final speed of a
mass sliding down a steep slope and hitting a less steep slope to the bottom.
Obviously I cannot calculate the speed on each slope separately and
add them. Here are the numbers.
-
First slope : 1.721 Meter high, 35 degrees, friction coefficient 0.14.
-
Second slope : 2.536 Meter high, 25 degrees, friction coefficient 0.14.
Obviously the final speed will not be the total of both speeds, so how do I add the speed of the first slope to the second slope to obtain final velocity?
![]() ANSWER:
ANSWER:
Well, I started to work this out and found that the length of the two
runs are exactly 3 m and 6 m. I therefore surmise that this is
homework and this site is not for homework help.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Hahaha, thank you for answering. At 51, I am surely not going back to school :) In fact the lenght I gave you are not precisely the one I will use for the slides. I want to understand the way to make the right calculations because the first incline has to be steeper to reduce the overall length of the slide. I am a conceptor mostly in transportation but this project is for a waterpark.
![]() ANSWER:
ANSWER:
It is easiest to do this using energy concepts. Total energy of a mass
m moving with speed v and at a height h above
some arbitrarily chosen h=0 level is E=½mv2+mgh;
g=9.8 m/s2 is the acceleration due to gravity. For a
given system the energy is conserved (the same everywhere) as long as
there is no agent adding or subtracting energy from the system. If there
were no friction in your slides, energy would be conserved. so, if you
chose h=0 at the bottom and started from the top with v=0,
the initial energy would be E1=mgh and the
final energy would be E2=½mv2;
setting them equal and solving for v, v=√(2gh);
note that the mass does not matter. In your case, v=√(2x9.8x(1.721+2.536))=9.13
m/s.
Alas, there is friction and the frictional force f for a mass m sliding on an incline θ is f=μmgcosθ. The amount which a force changes the energy if it acts over a distance s is called the work done and the work done by friction is Wf=-μmgs·cosθ; the minus sign indicates that friction takes energy away from the system. Now, instead of writing E2=E1, we write E2=E1+W—the energy you end up with equals the energy you started with plus what you added (negative for the case of friction).
Now we can address your specific case. ½mv2=mgh-μmgs1cosθ1-μmgs2cosθ2=9.8x[(1.721+2.536)-0.14(3cos350+6cos250)]=31.6 m2/s2. Solving for the velocity, v=7.95 m/s.
The formula you seek if you are doing a slide with two different slopes is v=√{2g[h-μ(s1cosθ1+s2cosθ2)]}.
![]() QUESTION:
QUESTION:
I was asked by my son if you get more speed on a flat (fixed slope) skate ramp or a curved ramp (1/4 pipe) of equal height (12ft). I think the flat ramp would result in greater speed as there is no change in energy force and the fixed straight ramp is constant, the 1/4 pipe is vertical and needs to change direction to horizontal resulting in directional change and loss of energy
![]() ANSWER:
ANSWER:
Your reference to "change in energy
force" has no meaning in physics. If friction is neglected, the only
thing which matters is the vertical distance fallen and so the speed at
the bottom would be identically the same regardless of the shape of the
ramp. Refer to the figures on the left. Without friction, the speed at
the bottom is v=√(2gh) where h is the
height. Including friction complicates things.
-
The ramp is easiest to do: the three forces on the skater are his weight mg, the normal force N, and the frictional force f. The magnitude of the frictional force is f=μN where μ is the coefficient of friction. Newton's equations are ΣFy=N-mgcosφ=0 and ΣFx=mgsinφ-μN=ma; the solutions are N=mgcosφ and a=g(sinφ-μcosφ). Now, notice that the acceleration depends on the angle of the incline which means that the speed at the bottom will also depend on the angle, the steeper the faster. Therefore it is not really fair to compare the flat ramp with the quarter pipe because the quarter pipe will always have its horizontal distance equal to its vertical fall. So the only fair comparison is for the flat ramp to have φ=450. In that case, a=g(1-μ)/√2. I calculate that the speed at the bottom is vflat_ramp=√(2gh(1-μ)).
-
For the quarter pipe, the situation is much harder to calculate because the normal force gets larger as the skater falls thereby increasing the friction. Newton's equations are ΣFx=mgcosθ-μN=ma and ΣFy=N-mgsinθ=mv2/R where a is the tangential acceleration and R is the radius of the pipe. I have no idea how to solve these because they are coupled, second-order, nonlinear differential equations. I am guessing that there is not a closed-form analytical solution and the equations would have to be solved numerically. For this case, though, we are interested in cases where the friction is low, μ<<1. We can calculate the velocity v as a function of θ for the no-friction case, μ=0 and then use that v to approximate the normal force as a function of theta and use that to find the energy lost to friction: v(θ)≈√(2gRsinθ), N≈3mgsinθ, f≈3μmgsinθ. Using these, I find v¼pipe≈√(2gh(1-3μ)).
So, to do a numerical example, R=h=12 ft, μ=0.1, g=32 ft/s2, vflat_ramp=26.3 ft/s, v¼pipe≈23.2 ft/s. (v=27.7 ft/s for zero friction.)
![]() ADDED
COMMENT:
ADDED
COMMENT:
The person who suggested approximating the velocity as the zero-friction
velocity for the ¼ pipe performed numerical solutions for the
differential equations.
His post: "Out of curiosity, I simulated the setup. With μ=0.001 and
m=R=g=1 I got E=0.99701, in agreement with your result.
μ=0.01 leads to
E=0.9704. Even with μ=0.1, the approximation is not bad:
E=0.732.
The mass stops at the center for μ>0.60. Tested with 100, 200 and 500 steps: The critical value is somewhere between 0.603 and 0.605. There is no obvious mathematical constant in that range."
Interpreting, his E is the calculated value of the kinetic energy divided by mgh. For this quantity, my approximation was [½mv2/(mgh)]=(1-3μ). Comparing the computed values with the approximated values: 0.99701≈0.997 for μ=0.001, 0.9704≈0.97 for μ=0.01, and 0.732≈0.7 for μ=0.1. Thanks to mfb for his interest and calculations!
![]() QUESTION:
QUESTION:
I was told that when a car is moving on a circular banked road. If the car reaches a very high velocity then it may move up the slope of the banked road! Is this possible and if so how?
![]() ANSWER:
ANSWER:
The
figure shows the car on the track. Three forces on it are the weight
W, the normal force N from the road, and the
frictional force f
from the road. Imagine that it is at rest so that all the forces are in
equilibrium: ΣFy=-W+Ncosθ-fsinθ=0
and ΣFx=Nsinθ-fcosθ=0.
The solutions are f=Wsinθ and N=Wcosθ. Now, if the car has some speed v, the car is still in
equilibrium in the y direction, but now has a centripetal acceleration
in the +x-direction of a=v2/R where R is
the radius of the track. So now, ΣFy=-W+Ncosθ-fsinθ=0
and ΣFx=Nsinθ-fcosθ=mv2/R.
Solving these equations, f=m(gsinθ-v2cosθ/R).
Now, notice that if v0=√(gRtanθ), f=0; at
this speed the car can go around the track even if it is perfectly
slippery. For speeds greater than v0, f will be
negative which means it must point down the slope. As the speed
increases beyond v0, the magnitude of the frictional
force will get bigger and bigger down the incline; but, there is a
maximum value which f can be, fmax=μN
where μ is the coefficient of static friction. The
corresponding velocity may be
shown to be vmax=‚ąö[gR(sinθ+μcosθ)/(cosθ-μsinθ)].
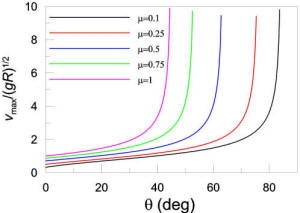 Not
every angle of incline or every μ will result in the car
slipping, however. Whenever (cosθ-μsinθ)]=0,
vmax=∞ and the car will not slip no matter how
fast it goes. For any given μ there will be a minimum angle θmin=tan-1(1/μ)
beyond which slipping will never occur; for example, for μ=0.5,
θmin=tan-1(2)=63.40.
The graph shows the behavior of vmax as a function
of angle for several values of μ.
Not
every angle of incline or every μ will result in the car
slipping, however. Whenever (cosθ-μsinθ)]=0,
vmax=∞ and the car will not slip no matter how
fast it goes. For any given μ there will be a minimum angle θmin=tan-1(1/μ)
beyond which slipping will never occur; for example, for μ=0.5,
θmin=tan-1(2)=63.40.
The graph shows the behavior of vmax as a function
of angle for several values of μ.
If you want a way to understand this qualitatively and you have worked with fictitious forces in accelerated frames, you can look in the frame of the car and there will be a centrifugal force pointing in the -x direction; this force will have a magnitude of mv2/R and, if it is greater than Nsinθ-fcosθ=N(sinθ-μcosθ) the car will move up the incline.

![]() QUESTION:
QUESTION:
There's an e-skate (electric skateboard) that I'm looking at that says it has 7 Nm of constant torque
and the radius of the wheel is 40 mm=0.04 m. How many seconds would it take to bring me (85 kg) to its top speed of 40 km/h? Their 4WD version says it has double torque, so 14 Nm. How long would that take to get to top speed? The e-skate is Mellow Drive. Other brands have lots of initial torque, but it drops as speed increases. Is this possible to calculate in the same way?
![]() ANSWER:
ANSWER:
The torque on the drive wheels will result in a frictional force between
the wheels and the road which drives the board forward. I am assuming
that that is the net torque to the two wheels, not the torque to each
wheel. So if the torque is 7
Nm, the force accelerating you is F=7/0.04=175 N. Ignoring all
friction, the
resulting acceleration would be a=175/85=2.1
m/s2. If the final velocity is v=40 km/hr=11.1 m/s,
the time is t=v/a=5.4 s. Now, is friction really
negligible? First consider the frictional force f from the
wheels which could be approximated as f=μmg where μ
is a coefficeint kinetic friction and mg=85x9.8=833 N. A
reasonable approximation for μ would be μ≈0.1;
with this μ the unpowered board would stop in about about 20
m if it had a speed of 2 m/s. The frictional force would then be about
83 N, not at all negligible. Redoing the calculations above for a net
force of 175-83=92 N, I find t=10.3 s. Finally we should talk
about air drag. The drag force D may be approximated (only in
SI units) as D≈¼Av2 where
A is the cross-sectional area you present to the wind, let's say
about A≈1 m2; so the biggest D gets
is about 30 N. Since most of the time spent is at lower speeds where
D is much smaller, I will not calculate the the time including
D (a much harder calculation because the force is not constant)
since all this is only a rough caclulation anyway; just think of 10 s as
a lower limit. You can, though, estimate the maximum speed if the torque
really did remain constant by finding the speed for which D=92
N: vmax≈√(4x92/1)≈19 m/s; this is
called the terminal velocity. For
constant torque, doubling it would result in a net force (again
neglecting D but including f) of 267 N and a time of
3.5 s. If you know how the
torque varies with speed, you could do a similar calculation but it
would be trickier because the force and therefore the acceleration would
change with time.
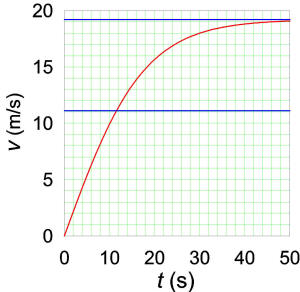
![]() ADDED
COMMENT:
ADDED
COMMENT:
Just for fun I added the air drag D for the two-wheel drive
case. I found that 11.1 m/s is reached in 11.5 s, only a very small
increase as I anticipated. The graph of v vs. t is
shown; you can see that the curve is nearly linear up to 11.1 m/s and
approaches 19.2 m/s at large times. The solutions are t=17.5·tanh-1(v/19.2)
and v=19.2·tanh(t/19.2). Don't take any of this
too seriously because of the numerous approximations I have made; I
would guess there would be about a 30-40% uncertainty—probably
5-15 s would give the experimental time. If you get one of these, let me
know how long it actually takes.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Someone said the mechanical power needed to ride at 40 kmh was 1900 KW. Is that true?
![]() ANSWER:
ANSWER:
The power P delivered by a torque τ at
angular velocity ω is given by P=τω.
In your case τ=7 N·m and ω=v/r=11.1/0.04=278
s-1, so P=1943 W, not kW.
![]() QUESTION:
QUESTION:
Hello, I'm looking for a physics expert to help me with a problem. We were learning Simple Harmonic Motion in our class today and I was struck with curiosity when my professor showed us a ball rolling without slipping on a turntable. The motion that the ball took surprised me because I never imagined that it would move in that fashion. I then started to wonder if it was possible to describe the ball motion in terms of (x,y) for a function of time. I talked to my professor about this problem and it had him stumped. Can you please help me out with this problem and explain in detail how you got your solution.
Here’s the full question I’m proposing and all the conditions:
A spherical ball of mass ‚Äúm‚ÄĚ, moment of inertia ‚ÄúI‚ÄĚ about any axis through its center, and radius ‚Äúa‚ÄĚ, rolls without slipping and without dissipation on a horizontal turntable (of radius ‚Äúr‚ÄĚ) describe the balls motion in terms of (x,y) for a function of time.
**The turntable is rotating about the vertical z-axis at a constant unspecified angular velocity.
**Radius and mass of the turntable and the ball are unspecified.
![]() ANSWER:
ANSWER:
I was unfamiliar with this problem, but it is interesting. Although the
path of the ball depends on the initial conditions, apparently if you
just set it on the turntable it will
move in a circle
which is at rest in the laboratory frame. I will tell you at the outset
that this is a quite advanced classical mechanics problem and is well
beyond the purposes of this site. However, it was interesting enough to
me that I did a little research to try to get a feeling for how it can
be approached. I will not provide details, but they can be found in a
1979 article in American Journal of
Physics. I do not know your level, but if you are a high school
student, the math is probably beyond your grasp, all the vector
calculus. As you can see from the article, trying to write the solution
in Cartesian coordinates, as you have specified, is not the way to go.
Using the vectors r and ω
as the author does implies using cylindrical polar coordinates (r,
θ, z).
![]() QUESTION:
QUESTION:
Ok so I am in AP Physics 1 and we are learning about Circular Motion. When
I was doing a problem I noticed a problem in which a car is set at a
constant speed and it asks what the free body diagram looks like at the top
of the hill. As I'm doing multiple questions I think about what the free body
diagram would look like just after passing the top of the hill so not at the
top but not fully down the hill. I tried to do the trick where you set it to
an x and y plane but there is no force inwards from the Normal Force and
then of course there's the Weight Force.... If a more skilled Physcisist could
help me it would help so much in furthering my understanding in physics.
![]() COMMENT:
COMMENT:
This student and I had a spirited debate about what constitutes homework
or tutoring help, forbidden on Ask the Physicist. His argument
was "…the
question I brought to your attention does not exsist…" because he
could not find it in a book somewhere and therefore not classifiable as
homework; that, of course, is nonsense because this is a very standard
question. Nevertheless, since he is so avid to learn, I am going to
answer it!
![]() ANSWER:
ANSWER:
The question is kind of ambiguous because it refers to
constant speed; but if the car is to maintain constant speed down the
hill, there will have to be some drag friction. If a constant speed
v is maintained, the free body diagram is shown on the left. I will
choose a coordinate system with +y pointing along the direction
opposite the normal force and +x tangent to the circle and
pointing downhill. The car is inequilibrium in the x direction and has
an acceleration of magnitude v2/R in the
positive y direction. Newton's laws are ΣFx=0=mgsinθ-f
and ΣFy=mv2/R=mgcosθ-N.
The solutions are simply obtained: f=mgsinθ
and N=m[gcosθ-v2/R].
An interesting result is that when θ=cos-1(v2/(gR)),
N=0 and the car will leave the road.
Another possible case is that there is no friction and the car has speed
v
at the top of the hill; the car will therefore speed up as it goes down
the hill. Using energy conservation it is easy to show that its speed
when at angle
θ is v'2=v2+2gR(1-cosθ)
and so the centripetal acceleration is ay=v2/R+2g(1-cosθ).
Notice that there will also be a tangential acceleration, ax,
an unknown at this stage. Now the equations to solve are ΣFx=max=mgsinθ
and ΣFy=m(v2/R+2g(1-cosθ))=mgcosθ-N.
The solutions are ax=gsinθ
and N=m(v2/R+g(2-3cosθ)).
Again, there will be an angle for which N=0 which is where the car would
leave the road, the determination of which I will leave to my AP
student.
![]() QUESTION:
QUESTION:
Say you have a conveyor belt with constant speed v. I put a bottle on the belt suddenly.
How do I know that it would not tip and whether there is a critical speed for the conveyor belt so tipping would never happen?
![]() ANSWER:
ANSWER:
I believe that it depends only on the geometry of the bottle and on the
coefficient of kinetic friction μ between the bottle
and the belt. In the figure, H is the position of the center of
mass ⊗ of the
bottle above the base and R is the radius of the base. When the
bottle touches the belt there will be a frictional force f
in the same direction as the velocity of the belt which will cause an
acceleration of the bottle to bring it up to the belt speed. But, as you
note, the bottle might tip over because of the torques it experiences
due to the forces on it. Because the bottle is trying to tip, the normal
force on the bottle should be expressed as two different forces
N1 and N2
acting on the leading and trailing edges of the base. Since the bottle
is accelerating, it is imperative to calculate the torques about the
center of mass of the bottle. The bottle is in equilibrium in the
vertical direction so N1+N2=mg.
The frictional force is f=μ(N1+N2)=μmg.
The torques will sum to zero if the bottle is not tipping, 0=fH+RN1-RN2.
Now, if the bottle is just about to tip over, N1=0
and so the torque equation becomes 0=fH-RN2=μmgH-Rmg
or μmax=R/H; this is the
maximum that the coefficient of friction could without the bottle
tipping. The result does not depend on either m or v.
For example, if R=3 cm and H=6 cm, then μ≤0.5.
![]() ADDED
NOTE:
ADDED
NOTE:
The normal force could have been handled differently by having a single
force N acting a distance d from the leading edge of the base of the
bottle. Then when d=2R the bottle would be about to
tip. You would get the same result as above.
![]() QUESTION:
QUESTION:
I am standing on a scale on carriage that is going down the slope without friction. The slope angle is
theta. What will the scale show in two cases:
-
The carriage is shaped in a way that the scale is horizontal with respect to ground (that is is a special edge shaped carriage)
-
The carriage is regular so the the scale is not paralleled to the ground.
I am trying to understand how a special wedge or insoles in ski show would effect weight felt by a person. In case 1 I think the answer should be mg(1-(sin(theta)^2)) but I am not sure.
In case 2. I have no idea. I think scales can misfunction if the slope is too strong.
![]() ANSWER:
ANSWER:
Before doing either case, imagine that we choose the man and the
carriage as the body to look at. It is the standard introductory physics
problem of something sliding down a frictionless incline. The principle
result is that the acceleration of the man and the carriage are the same
and have a magnitude a=gsinθ down the
slope.
-
The figure on the left shows the forces on the man standing on the horizontal scale. There is his own weight, mg and the scale exerts a normal force N vertically up; the scale will read N. The contact between the man and the scale cannot be frictionless or else the man would not accelerate along with the carriage, so there is also a frictional force f. Newton's equations for the man are ma=mgsinθ=-Nsinθ+fcosθ+mgsinθ and 0=Ncosθ-fsinθ-mgsinθ. Solving, I find N=mgcos2θ and f=mgsinθcosθ.
-
The figure on the right shows the man on the scale parallel to the incline. Now no friction is needed and the scale, again, will read N but N will be different. Newton's equations are 0=-mgcosθ+N and ma=mgsinθ, just the same as the classic object on the frictionless incline. So the scale reads N=mgcosθ.
The graph compares the two cases.
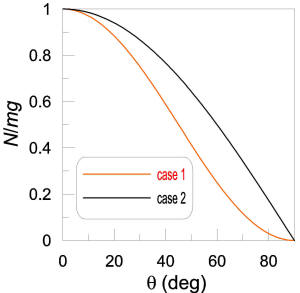
![]() QUESTION:
QUESTION:
If two people are carrying a canoe parallel to the ground, how much weight are they each carrying? would it be half of the weight of the canoe, more than half, or less than half?
![]() ANSWER:
ANSWER:
It all depends on two things—where the center of gravity is
and where the two people exert their forces. In the figure the weight
W of the canoe acts at the center of gravity
and the two people exert forces F1
and F2 at distances at distances
d1 and d2 from the center of
gravity. The two people must hold up all the weight between them, so
F1+F2=W. The canoe is not
rotating about its center of gravity so the net torque must be zero, so
F1d1=F2d2.
Solving, F1=W[d2/(d1+d2)]
and F2=W[d1/(d1+d2)].
If d1=d2, each holds up half the
weight.
![]() QUESTION:
QUESTION:
I'm shopping for a pole chainsaw and trying to figure how heavy a 7 lbs saw at the end of a 8' pole would "feel", at about a 45 degree angle.
![]() ANSWER:
ANSWER:
It depends on how you hold it and where the center of gravity is. Refer
to the figure. The weight W acts at the center
of gravity which I have chosen to be at a diatance c from your
right hand. The position of your left hand I have denoted as being a
distance d from your right hand. For simplicity I have assumed
that you will exert a force L with your left
hand perpendicular to the pole; your right hand exerts a force with
horizontal and vertical components H and
V respectively. You specify 45°, so
the horizontal and vertical components of L
are equal and of magnitude L/√2. The two equations for
translational equilibrium are ΣFvertical=0=-W+L/√2+V
and ΣFhorizontal=0=-L/√2+H.
These may be simplified to H=L/√2 and V=W-H.
There are three unknowns and only two equations, so we need a third
equation; the sum of torques must also be zero. Summing torques about
the right hand, Στ=dL-cW/√2=0 or L=cW/(d√2).
Therefore, H=cW/(2d) and V=W[1-cW/(2d)].
For example, suppose W=7 lb, d=3 ft, c=4 ft:
I find L=6.6 lb, H=4.7 lb, V=2.3 lb. The
force R exerted by your right hand is R=√(V2+H2)=5.2
lb. The key to easy handling is to choose the saw with the smallest
c which will minimize the torque you must exert.
![]() QUESTION:
QUESTION:
How does a torque applied to a wheel cause translational motion? Please don't say the ground pushes on the wheel.
The wheel is stationary at the road surface. From my understanding friction creates a torque equal to the driving torque so where does the net accelerating force come from and where does it act? If you could explain with a free body diagram showing all the forces present that would greatly enhance my understanding.
![]() ANSWER:
ANSWER:
If you are asking someone to explain something you do not understand,
don't tell them what not to say! You have, in essence, asked me to not
answer your question because it is the friction which accelerates your
car forward. Let me see if I can explain it to you. Suppose you have a
car with its brakes on at rest on a road. You get behind the car and
push as hard as you can but, alas, it will not budge. What force is
preventing it from moving? The road exerts a static frictional force on
the car, even though it is "stationary"; then, clearly, you cannot say
that the road cannot push a surface in contact with it just because the
surfaces are not sliding on each other. Suppose that there were no
friction between the tire and the road and the car was at rest. No
matter how hard you push your engine which, through the transmission and
various linkages, exerts a torque on the wheels, you would go nowhere,
the torque just spinning the wheels. But, if there is friction, the
wheel, at the point of contact with the road, would exert a force on the
road (opposite the direction you want to go). But Newton's third law
tells you that if the wheel exerts a force on the road, the road exerts
an equal and opposite (forward) force on the wheel. That is the force
which accelerates that car forward.
![]() QUESTION:
QUESTION:
A steel pole weighing 1000kgs and is 9 metres long what would the weight of the pole be on the end if I tried to lift it from the end?
![]() ANSWER:
ANSWER:
First, let's get one thing clear—the weight of something is the
force which the earth exerts on it and never changes. Also, technically
a kilogram is a unit of mass but I will treat it as a weight since many
countries do. What you want, I believe, is the force you need to exert
to lift it.
It is not really clear what it means to lift "from the end". Two
scenarios suggest themselves to me:
-
Lift it from one end while the other end rests on the ground
In order for the rod to be just barely lifted off the floor at one end, the torque due to F must be equal in magnitude to the torque due to W=1000, 9xF=4.5x1000=4500 or F=500 kg. The floor holds up the other half of the weight.
-
Grab onto one end and lift the whole rod keeping it horizontal.
It is impossible to lift it horizontally using only a force at the end because you could not exert enough torque to keep the rod from rotating due to the torque caused by the weight. You might try to do it by using two hands, one at the end pushing down and the other some distance d from the end pushing up. In that case (see the figure above), summing the torques about the end you find that Fup=4500/d; for example, choosing d=20 cm=0.2 m, Fup=22,500 kg. You can also find Fdown by summing all forces to zero, Fup-W-Fdown=0=22,500-1000-Fdown or Fdown=21,500 kg.

![]() QUESTION:
QUESTION:
According to third law of motion a bird sitting on a tree branch cannot fly due to reaction then how does it fly?
![]() ANSWER:
ANSWER:
Why would you think that? The so-called reaction force is exerted down
on the branch, not on the bird. Let's dissect the physics of this bird.
The eagle on the left is sitting on a branch. There are two forces on
him—his weight W and the force
the branch exerts up on him F. These forces
are equal and opposite because of Newton's first law. But, what
about the reaction partner of F, the equal and
opposite Newton's third law partner? That force is the force which the
eagle exerts down on the branch and is not a force on the eagle
(which is why I did not even draw it in the force diagram of the eagle).
The picture on the right shows the eagle just as he is lifitng off. Now
there is an additional force L due to the lift
generated by the flapping wings. Since L+F>W, the eagle is no
longer in equilibrium and will accelerate upward. As soon as the talons
leave the branch, F disappears.
![]() QUESTION:
QUESTION:
This past weekend I was in Vermont and was walking down a relatively steep gravelly road when I started gaining speed unintentionally and it seemed as thought my feet couldn't keep pace with the top half of my body. I kept accelerating for about 20-25 paces and saw a tree looming in front of me when I fell down flat.
Is there a name for what happened and is there
 anyway I could have stopped it once it began? I ask because this happened to me once before in almost the same conditions years ago and, at the time, I ended up with 2 missing front teeth, a black eye, and bruises/cuts on both forearms.
anyway I could have stopped it once it began? I ask because this happened to me once before in almost the same conditions years ago and, at the time, I ended up with 2 missing front teeth, a black eye, and bruises/cuts on both forearms.
![]() ANSWER:
ANSWER:
I have had this happen to me and know the helpless feeling of not being
able to stop running. The red arrow in the picture represents your
weight, acting at your center of gravity somewhere in your trunk. This
force exerts a torque about your leading foot which tends to rotate you
in a clockwise direction. Imagine that this runner were not running but
just standing still. The only way to keep from falling forward (rotating
about that leading food) would be to exert an opposite torque and this
could only be done by your foot/ankle; but the requisite muscles are not
strong enough to exert the necessary torque. Think about it—if
you were just standing on level ground, how far could you lean forward
without falling forward? Not very far! And it is even worse if you are
running because you have a forward momentum which also is tending to
topple you forward if you try to stop. All that I can think of that you
can do to avoid a fall is to try to slow enough that you can get
yourself more vertical so that your center of gravity is vertically
above your feet. If the hill is not too long, you can keep running until
you get to the bottom, but you will be speeding up the whole way.
![]() QUESTION:
QUESTION:
How many g forces will a driver experience accelerating from 0 to 200 mph
in 1/4 mile, straight line acceleration.
![]() ANSWER:
ANSWER:
No homework. But there are lots of advertisers on this page which will help
with homework.
![]() FOLLOWUP:
FOLLOWUP:
This is not homework.
It happens to come from one of the
country's top 100 trial lawyers who would have gone to medical school
instead if he had the math ability to figure this out myself.
Of course, I have lost two trials in 28 years and my time goes for $650 an h)p8
I will just have an associate do it for me tomorrow--if it is still of any concern.
This is the first time that I have ever used one of these "Ask Jeeves" sites and will be the last.
And my new Vette has a g force display so if I really wanted to know I would have gotten in and fkoored it instead of relying on some bottom feeder like you.

![]() ANSWER:
ANSWER:
Wow! I am so excited to get a question from one of the country's top 100
trial lawyers. I am so honored, even though I am just a tiny "bottom
feeder" in the presence of such a paragon. Sorry for the sarcasm, dear
readers, but this is a good opportunity for me to emphasize that one of
the important things about Ask The Physicist is that it is not a
homework help or tutoring site. I feel very strongly about this because,
having been a teacher for 40 years, I feel strongly that students should
do their own work and the internet gives too many opportunities for
"cheating" in that regard. I reject what I judge to be homework
questions and, inevitably, I occasionally make a mistake. If you think
my ethical stand on this issue makes me the scum of the earth, so be it.
When I do make a mistake, I usually answer the question and I will do
that here. The equations of motion for uniform acceleration for the
object starting at rest are v=at and d=½at2
where, in this case, v=200 mph=89.4 m/s and d=¼
mile=402 m. The time can be eliminated using the first equation, t=89.4/a
and substituting into the second equation, 402=½a(89.4/a)2=3996/a
or a=9.94 m/s2. The acceleration due to gravity
is 9.8 m/s2 and so this is just about 1 g of acceleration,
a=1.01g. I figure that anyone who charges $650/hour
for his services can afford to send a little of that my way!
![]() QUESTION:
QUESTION:
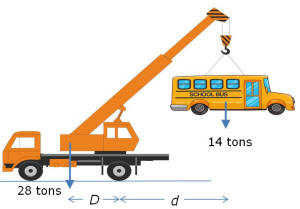
From the physics theories and calculation, how does a crane fall of a bridge when trying to pull out a bus from the water? (crane = 28 ton, bus = 14 ton)
![]() ANSWER:
ANSWER:
It's all about the torques. In the figure, if the crane tips over it
will rotate about the rear wheel. When this is just about to happen the
front wheel has zero normal force from the road on it. At this time, the
road exerts a 42 ton force up on the rear wheels (they are holding up
all the weight). The weights each act at the center of gravity of the
crane and the bus. If I sum torques about the rear wheel, they must
equal zero, that is 28D=14d or d/D=2.
So, if d is greater than 2D, the whole system will
rotate about the rear wheels and topple off the bridge.
![]() QUESTION:
QUESTION:
If you had two point masses m1 and m2 in space separated by a distance d, how long would it take for them to collide under gravity alone? I'd imagine it's a changing force/acceleration, so some calculus must be involved.
![]() ANSWER:
ANSWER:
I have solved this problem many times before but always for specific
masses and distances. To avoid the calculus you refer to, the trick is
to use Kepler's laws for planetary motion. You can find references on the
FAQ page. The one you
might find most useful is this
link. You will see that
the relevant time to collision is t=T/2=√(πμa3/K)
where μ=m1m2/(m1+m2)
is the reduced mass, a=d/2, and K=Gm1m2.
Therefore, t=√[πd3/(8G(m1+m2)].
![]() QUESTION:
QUESTION:
A tire rolling on a level surface at a linear speed of 10 MPH rolls on to a conveyor belt which is also moving at 10 MPH in the same direction. How will the tire's speed change? Will it be 20 Mph? 10 MPH? Will it's rotation stop?
Reverse?
![]() ANSWER:
ANSWER:
This problem is a little trickier than I had anticipated. On the other
hand, the final answer is much simpler than I had anticipated. Shown in
the figure to the left is (top) the situation when the rolling tire
first touches the conveyer belt. It is rolling without sliding so the
point of contact with the floor is at rest, the center is moving forward
with a speed v (your 10 mph), and the top is moving forward
with speed 2v; the belt is moving forward also with speed v.
I find this problem much easier to do if I transform into a coordinate
system which is moving with speed v to the right; in that
coordinate system the belt (upper surface) and tire are both at rest and
the top and bottom edges of the tire have speeds v as shown.
Before getting into the hard part, there is a special case which we can
get out of the way first: if there is no friction the tire will continue
on its merry way unchanged, both its speed and its angular velocity
unchanged because there are no net forces or torques on it.
Now,
as soon as it gets on the belt there will be a frictional force
f trying to accelerate it to the right so it will
start sliding along the belt (at rest in the frame we are using). The
frictional force will be f=μmg where μ is the
coefficient of kinetic friction, m is the mass of the tire, and
g is the acceleration due to gravity. Call v' the
speed which the center acquires in some time t. Then Newton's
second law for translational motion is mΔv=μmgt=mv',
so v'=μgt.
There
will also be a torque τ=fr=μmgr which acts opposite the
direction the tire is rotating. There will come a time when the bottom
edge of the tire will be at rest relative to the belt because of this
torque. At that instant, we can transform back into the original
coordinate system and the tire will be moving forward with speed
v+v'. Newton's second law for rotational motion is ΔL=τt=-(μmgr)(v'/μg)=-mv'r.
where L is the angular momentum of the system. The angular
momentum is the angular momentum about the center of mass plus the
angular momentum of the center of mass. L1=Iω1+0=Iv/r
where I is the moment of inertia about the center of mass;
L2=Iω2+mrv'=(v'/r)(I+mr2).
Therefore, (v'/r)(I+mr2)-Iv/r=-mv'r
or, v'=Iv/(I+2mr2). This is
surprisingly simple, particularly surprising that it does not depend on
μ. However, the time to stop sliding does depend on μ,
t=v'/μg; the slipperier the surface, the longer it
takes to stop slipping, as expected.
Finally
we need to transform back into the original coordinate system by simply
adding v as shown in the final figure. As an example, suppose
we model the tire as a uniform cylinder of mass m and moment of
inertial I=½mr2; then v'=v/5,
or in your case, 2 mph, so the tire is rolling without slipping with a
speed of 12 mph.
![]() ADDED
NOTE:
ADDED
NOTE:
Note that the new angular velocity of the tire is ω'=v'/r
only a small fraction of the original value of ω=v/r.
This drop in angular velocity can be clearly seen in a
Mythbusters
episode showing a car driving onto a ramp from a moving truck, a
very similar situation to the conveyor belt problem in this question.
![]() QUESTION:
QUESTION:
I was wondering if, when an object enters earth's atmosphere from space, does it experience a lateral force as it enters the atmosphere? In other words, does it suddenly get "pushed" sideways due the earth's rotation?
![]() ANSWER:
ANSWER:
This had never occurred to me, but certainly the meteorite will be
deflected because of the "wind" of the rotating atmosphere. But, how big
an effect is this? The average speed of a meteorite is about 17 km/s;
and I calculate the speed of the "wind" to be about 0.47 km/s at the
equator. So, even if the meteorite acquired all of the speed of the
atmosphere, it will still be trivially small compared to the vertical
speed. Another way to look at it is to look at the drag forces the
meteorite experiences when it encounters the atmosphere; these are proportional
to the squares of the speeds, so the ratio of the horizontal force to the
vertical force will be about 0.472/172=0.0008. Compared to the force slowing down the vertical motion, the force
speeding up the horizontal motion is tiny.

![]() QUESTION:
QUESTION:
I have a question related to determining the force at impact.
Here's the question in two parts:
-
If a firefighter adds 45 pounds of gear to his overall weight, does it increase the impact force if he has no choice but to jump out a window and if so to what degree?
-
What is the effect on impact force of jumping out a second floor window vs. 3rd floor and above?
This actually isn't homework. I'm 54 years old and advising a charitable organization that provides safety systems to firefighters. One of the challenges they face is fire departments who don't have high rise buildings and feel they don't need the bailout systems. So I'm trying to figure out what the impact is for a firefighter forced to jump out a second story or third story window. This will help inform how they talk to prospective donors. If you could help me with that (understanding/identifying the increase in impact force from 1st to 2nd to 3rd floors and then up) it would be greatly appreciated. I've done a lot of googling around calculating impact and g forces, but its not making sense to me (I'm not being lazy, just not understanding).
![]() ANSWER:
ANSWER:
The "force at impact" depends, essentially, on the time to stop. If she
has a speed v, a mass m, and stops in a time t,
the average force F during the stopping time is given by
F=m(g+v/t) where g=32 ft/s2 is the acceleration due to
gravity. So, yes, if you increase the mass you increase the force
proportionally; I guess I would toss that extra 45 lb over before I
jumped! Regarding your second question, call the height of one floor
h. Jumping from the second floor would result in a speed of v2=√(2gh);
jumping from the third floor would result in a
speed of v3=2√(gh) which is
about 1.4 times larger than v2. In general, jumping
from the nth floor would result in a speed vn=√[2(n-1)gh].
Maybe some numerical examples would be useful to you. You prefer Imperial units, which makes things a little complicated. The quantity mg is the weight. I will take mg=160 lb and h=12 ft for my numerical calculations, so when I need the mass I will use 160 lb/32 ft/s2=5 lb·s2/ft. (The unit of mass in Imperial units is called the slug, 1 slug=1 lb·s2/ft.) The speeds from second and third floors will then be v2=27.7 ft/s=18.9 mph and v3=39.2 ft/s=26.7 mph; these speeds are independent of the mass. Finally we must approximate the times to stop. If she lands feet first, she could extend, as parachutists do, her stopping time by bending her knees into a squat; I will estimate the distance s she will travel while stopping as s=3 ft. The time may be shown to be t=2s/v so t2=2x3/27.7=0.22 s and t3=2x3/39.2=0.15 s. Finally, the average forces during impact are F2=160+5x27.7/0.22=790 lb and F3=160+5x39.2/0.15=1467 lb. These are approximately 5 and 9 times her weight (g-forces of about 5g and 9g).
![]() QUESTION:
QUESTION:
Well
I hope this doesn't seem off the wall but I want to know how much force
it would take to tip a 7.62 m tall,6.40 m wide and 22 ton Transformer over? It is for a story I'm doing about a comic book character.
![]() ANSWER:
ANSWER:
It depends on where and how the force F is
applied; if applied as shown in the diagram, it will be the smallest
possible.
I will assume that the center of gravity of the transformer is in the
geometrical center, so the weight W acts
there. When the force is just about to tip it over, all the force from
the floor, the normal force N and the
frictional force f, act on the edge opposite
where the force is applied. It will be in equilibrium, so you can easily
see that F=f and N=W. But, what you need is F
and to get it you need to sum the torques around the edge where N
and f act and sum to zero: Fh-Ww/2=0 or F=Ww/(2h).
Using your numbers, F=22x6.40/(2x7.62)=9.24 tons. If you want
the force in Newtons, assuming that the 22 ton mass is metric tons
(22,000 kg), F=9.8x9240=90,500 N.
![]() QUESTION:
QUESTION:
If you tow a boat from a tow path which is the best point to tie the rope onto the boat?
![]() ANSWER:
ANSWER:
The rope will exert a force on the boat, obviously. This force will tend
to do three things: exert a torque which will tend to rotate the boat
about a vertical axis through the center of gravity (you don't want
this), have a component along the bank which will pull it along the
canal (that is what you want), and have a component which will pull the
boat toward the shore (you don't want this). To minimize the tendency of
the boat to turn, attach the rope close to the center of gravity of the
boat. To minimize the tendency to drift (not turn) to the bank, make the
rope as long as possible so that most of its force will be exerted along
the bank. Some tiller will be needed to make small corrections, but
those should be minimal.![]() QUESTION:
QUESTION:
I am an avid sports fan and I have often wondered if the experts may be wrong about the myth of the rising fastball in the game of baseball. I played baseball for over 20 years and I can tell you that the ball does appear to rise when certain pitchers throw hard put a heavy backspin on the ball. I have been told that experts say it is nothing more than a visual trick your eyes play on you because a rising fastball is considered to be physically impossible. I can tell you first hand that a softball pitcher I know can throw a ball that rises after being thrown on a straight trajectory. I suspect the Magnus effect may have something to do with the anit-gravitational behavior of the ball. Do you think this could be what causes the ball to appear to rise as it travels, or is it just our perception?
![]() ANSWER:
ANSWER:
There is such a thing as a rising fastball, but it does not actually
rise; it simply falls more slowly than a nonspinning ball does. An
experienced hitter knows intuitively what a normal fastball does and
when presented with a rising fastball he will swear that it rose because
it actually fell less. Incidentally, by rise or fall, I am talking about
the direction of the acceleration. So a ball which is thrown at an angle
above the horizontal is obviously rising but it rises at a
 decreasing
rate of rise until it reaches the peak of its trajectory and then begins
back down; the rising fastball will actually rise farther. Then why do
we say it is a myth? It is easiest to understand by looking at a ball
thrown purely horizontally. Can spin cause the ball to actually go
upwards? To answer this, you need to think about all the forces on a
pitched ball. There is the weight, FG, which points
vertically down and causes the ball to accelerate downward (a
horizontally thrown 90 mph fastball falls about 4 feet on the way to the
plate); there is the drag FD which points opposite
the direction of flight and tends to slow the ball down (a
90 mph fastball
loses about 10 mph on the way to the plate); and there is the magnus
force FM which, for a ball with backspin ω
about a horizontal axis points perpendicular to the velocity and upward.
If the ball is moving horizontally the only way it could rise is for the
Magnus force to be larger than the weight. Measurements have been done
in wind tunnels and it is found that if the rotation is 1800 rpm, about
the most a pitcher could possibly put on it, the ball would have to be
going over 130 mph for the Magnus force to be equal to the weight. When
you say "thrown on a straight trajectory", you cannot mean it left his
hand horizontally because it would hit the ground before it got to the
plate; a fast pitch like that is impossible to accurately judge the
initial angle of the trajectory.
decreasing
rate of rise until it reaches the peak of its trajectory and then begins
back down; the rising fastball will actually rise farther. Then why do
we say it is a myth? It is easiest to understand by looking at a ball
thrown purely horizontally. Can spin cause the ball to actually go
upwards? To answer this, you need to think about all the forces on a
pitched ball. There is the weight, FG, which points
vertically down and causes the ball to accelerate downward (a
horizontally thrown 90 mph fastball falls about 4 feet on the way to the
plate); there is the drag FD which points opposite
the direction of flight and tends to slow the ball down (a
90 mph fastball
loses about 10 mph on the way to the plate); and there is the magnus
force FM which, for a ball with backspin ω
about a horizontal axis points perpendicular to the velocity and upward.
If the ball is moving horizontally the only way it could rise is for the
Magnus force to be larger than the weight. Measurements have been done
in wind tunnels and it is found that if the rotation is 1800 rpm, about
the most a pitcher could possibly put on it, the ball would have to be
going over 130 mph for the Magnus force to be equal to the weight. When
you say "thrown on a straight trajectory", you cannot mean it left his
hand horizontally because it would hit the ground before it got to the
plate; a fast pitch like that is impossible to accurately judge the
initial angle of the trajectory.
![]() QUESTION:
QUESTION:
In lifting an object to a higher level directly over its original location, the energy I expend increases potential energy. But, does some of the energy used in lifting it also go to accelerating it to higher rotational velocities as the circumference of its "orbit" increases as it is raised over its original position? Does this add kinetic energy and mass to the object whereas increasing potential energy does not?
![]() ANSWER:
ANSWER:
(Preface: all my calculations below assume that the height lifted is
much smaller than the radius of the earth. I also neglect the change in
the gravitational force over the distance the mass is lifted. Also, to
simplify things, all my calculations are at the equator.) Yes, work is
done to increase the kinetic energy. As viewed from an inertial frame,
watching the mass M get lifted to h, I estimate that
the kinetic energy changes by ΔK≈2hKinitial/R=MhRω2
where R=6.4x106 m is the radius of the earth and ω=7.3x10-5
s-1 is the angular velocity of the earth. For example,
lifting 1 kg a height of 1 m requires 0.03 J of work to increase the
kinetic energy. But wait a minute! Once we acknowledge that the earth is
rotating, we have to recognize that the mass, being in a circular orbit,
has a centripetal acceleration ac=Rω2
and therefore the net force on M is Mg-MRω2.
Therefore, the net work done is W≈(Mg-MRω2)h+MhRω2=Mgh.
![]() QUESTION:
QUESTION:
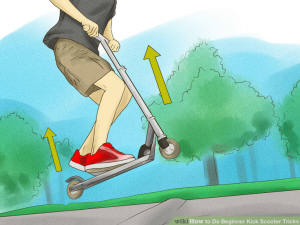
If I weigh 200lbs and am riding a kick scooter that weighs 14lbs, and I am riding at a speed of 10 mph and I jump the scooter off a curb, say 6 inches, what is the force in terms of pounds, that I am applying to the scooter as it lands?
![]() ANSWER:
ANSWER:
Usually it is not possible to answer this kind of question because what
is needed is to know how long the collision between you and the ground
lasted. In this case, though, we can estimate the time of this
collision. As you may know, paratroupers are trained to not land with
stiff legs, rather to bend at the knees during the landing; the purpose
is to prolong the landing time and this reduces the average force on the
legs during the landing. If a mass M hits the ground with some
speed V and stops in time t, the average force over
the time is F=W+MV/t where W is the weight,
200 lb; to convert the
weight to mass, divide by the acceleration due to gravity, g=32
ft/s2: M=W/g=(200 lb)/(32 ft/s2)=6.25
ft·lb/s2. The speed at impact can be determined
from V=√(2gh)=√[2x(32
ft/s2)x(½ ft)]=5.7 ft/s. If we approximate that
the distance S over which your legs bend on landing as S=1
ft, the time to stop is t=2S/V=(2x1 ft)/(5.7
ft/s)=0.35 s. So, finally, F=200 lb+(6.25
ft·lb/s2)(5.7 ft/s)/(0.35 s)=302 lb. This is
the force the scooter exerts on you which, by Newton's third law, is
equal the the force you exert on the scooter (but in opposite
direction). If you stop in ½ ft, the force would be 404 lb. Keep
in mind that this is a very approximate estimate of the average force.
![]() QUESTION:
QUESTION:
I am having a debate with my brother about climbing on an incline.
I understand the basics of climbing a hill on a diagonal. If you climb diagonally, you can avoid taking larger vertical steps at the cost of more horizontal movement. This makes each step take less energy while increasing the overall work and time needed.
However, it seems as though this rule does not work for stairs. Stairs do not allow for shorter vertical steps (you either make 100% progress on a step or 0%). Do I have this correct? Am I missing something?
![]() ANSWER:
ANSWER:
Slaloming up the incline will increase time spent but not increase work
done. This assumes no frictional forces are important, the only work you
do is the work lifting you. Since work done does not change but elapsed
time does, the average power you are generating going straight up is
greater than zigzaging. Going up steps, though, if you go across a step
you do no work, the only work done is lifting you to the next step. The
only way to get the equivalent lowered average power output as you do by
slaloming up the slope is to rest between steps.
![]() QUESTION:
QUESTION:
How strong would a man have to be to push a 16,000 lb bus on a flat surface?
![]() ANSWER:
ANSWER:
That depends on how much friction there is. And not just the friction on
the bus, but more importantly, the friction between the man's feet and
the ground. Newton's third law says that the force the man exerts on the
bus is equal and opposite the force which the bus exerts on the man (B
in the picture). Other forces on the man are his weight (W),
the friction the the road exerts on his feet (N),
and the force that the road exerts up on him (N).
If the bus is not moving, N=W and f=B, equilibrium.
The biggest that the frictional force can be without the man's feet slipping is
f=μN where μ is the coefficient of
static friction between shoe soles and road surface. A typical value of
μ for rubber on asphald, for example,
μ≈1, so the biggest f could be is
approximately his weight W;
this means that the largest force he could exert on the bus without
slipping would be
about equal to his weight. Taking W≈200 lb, if the
frictional force on the bus is taken to be zero, the bus would
accelerate forward with an acceleration of a=Bg/16000=200x32/16000=0.4
ft/s2 where g=32 ft/s2 is the
acceleration due to gravity; this means that after 10 s the bus would be
moving forward with a speed 4 ft/s. If there were a 100 lb frictional
force acting on the bus, the acceleration would only be a=0.2 ft/s2.
If there were a frictional force greater than 200 lb acting on the bus,
the man could not move it.
![]() QUESTION:
QUESTION:
I'm confused? One moment I'm reading about "inertial reference frames" and that "acceleration due to gravity" is unaffected by mass. This is followed up with examples such as the Bowling ball and feather. All good. Maths seems clear enough.
But then we start talking about a particular body/objects "acceleration due to gravity" at or near the surface of the Earth as being 9.8m/s2 which is calculated using the masses of earth and the "falling" body and Newton's Law. Similarly I read that if I go and stand on the moon the "acceleration due to gravity" will be different because the masses are different? Again seems to be clear.
What am I missing? How is it that the mass of two object does not affect the acceleration one moment but the accelerations of the moon and the earth on a body have differing values due in part (large part) to their mass?
![]() ANSWER:
ANSWER:
Look at the figure. Two masses, M and m, are separated
by a distance r. M exerts a force FmM
on m and m exerts a force FMm
on M; because of Newton's third law, these forces are equal and
opposite, FmM=-FMm.
Because of Newton's law of universal gravitation the forces have
magnitude FMn=FmM≡F=mMG/r2.
Then, using Newton's second law, each mass will have an acceleration
independent of its own mass of a=[mMG/r2]/m=MG/r2
and A=[mMG/r2]/M=mG/r2.
Note that I have been viewing this from outside the system; this frame
of reference is is called an inertial frame of reference. It is
important that we view the system from an inertial frame, because
otherwise Newton's laws are not correct.
So, what you have been taught is correct only if you view things from outside the two-body system. But what you have also probably been taught is that you measure this constant acceleration relative to the surface of the earth and that is technically incorrect because the earth is accelerating up to meet the falling mass and is therefore not an inertial frame. However, the earth's acceleration is extremely tiny, too small to measure. If M is much much larger than m, which is certainly the case for the earth and the moon, what you have been taught is, for all intents and purposes, correct.
![]() QUESTION:
QUESTION:
I am trying to explain to my brother why on a spinning wheel a point farther out is going faster than a point closer to axis, though the wheel is spinning at the same rpms. But he just cant figure it out. Could you give an explanation a 2 year old could understand?
PS My brother is 21.
![]() ANSWER:
ANSWER:
I could probably not convince a two-year old, but if your brother is
just a little smarter than one, I can probably convince him. The speed
of something is defined as the distance traveled divided by the time it takes to
travel that distance. For example, a car going around a circular race
track which has a total circumference of 2 miles takes 2 minutes to go
around once, its speed is (2 miles)/(2 minutes)=1 mile/minute=60 mph.
Suppose a wheel has an angular speed of 10 rpm and has a circumference
of 2 m. Then the distance a point on the rim will go in 1 minute is 20 m
because the wheel goes around 10 times; the speed of that point is
therefore 20 m/min. Now look at a point halfway from the axle to the
rim; it will move in a circle of circumference only 1 m so the distance
it travels in 1 min is only 10 m so its speed is therefore 10 m/min. In
a nutshell, a point near the center travels a shorter distance than a
point far from the center in the same time.
![]() QUESTION:
QUESTION:
Some car drivers reason that since tractor trailers have more tires, they
should be able to stop quicker. How much work does each car tire need to do
to stop it, compared with how much work each truck tire needs to do to stop
it? For ease of reference let's say a car is 4000 pounds and the truck is
80000 pounds while the speed involved is 65 miles per hour. Finally is the
work done proportional to the size difference of truck brakes versus car
brakes?
![]() ANSWER:
ANSWER:
I replied that this is not a homework
solving site.
![]() FOLLOWUP
QUESTION:
FOLLOWUP
QUESTION:
I didn't realize I had posed this in the form of a homework-ish question. I'm a 47yo truck driver, tired of hearing all the lame-@$$ rhetoric of the motoring public. Long, quiet, empty night highway helped me come at this from a different angle. Without too much detail, one truck wheel wrangles slightly more than a single car's worth of mass; is why trucks do NOT stop better despite having more wheels.
![]() ANSWER:
ANSWER:
I have never heard this but it is pretty nonsensical. How quickly any
vehicle can stop is determined by the maximum force which can be applied
by braking; if the coefficient of static friction between the tires and
the road is μ, the maximum force on a level surface
is μW. where W is the weight of the vehicle. The
distance s traveled will be determined by the work done by this
force, μWs, which will equal the initial kinetic
energy, ½Mv2=½(W/g)v2,
where M is the mass and g=32 ft/s2. So,
s=(1/(2μg)v2. So here is the
interesting thing: the distance traveled does not depend on the weight
of the vehicle, only by the initial speed and the condition of the road.
The force applied does depend on the weight and the force per wheel
would be 0.7x4000/4=700 lb for the car and 0.7x80000/18=3111 lb; but the
larger force is simply because of the larger weight and the only thing
which is important is the distance to stop. Of course, this also depends
on whether you have antilock brakes which let you get the maximum amount
of friction when you are just on the verge of skidding; if you lock the
brakes and you skid, you go farther before stopping. For your example,
v=65 mph=95 ft/s and μ is approximately 0.7 for
tires on a dry road, so s≈200 ft. I have neglected all
other forms of friction like rolling friction and air drag, but these
should be relatively unimportant. Bottom line—stopping distance
does not depend on number of tires nor on weight.

![]() QUESTION:
QUESTION:
I am a volunteer guide at South Foreland historic lighthouse in the UK. We have an optic weighing approximately 2 tons, floating in a close fitting trough containing only approx. 28 litres of mercury. What is the theory which enables this optic to float as it does not appear to fit within the basics of Archimedes principle.
![]() ANSWER:
ANSWER:
To float 2 metric tons (2000 kg) you must displace M=2000 kg of
mercury. The density of mercury is ρ=13,600 kg/m3,
so the volume you must displace is V=M/ρ=0.15 m3=150
l; this, I presume, is what is bothering you since only 28 l are used.
Suppose that the reservoir for the mercury is a cylinder of radius 1 m
and depth d; to contain 0.15 m3, the depth of the
container would have to be d=0.05 m=5 cm (estimating
π≈3). So, I will make a container 6 cm high for an
extra 20%, 180 l and I will buy that 180 l to fill it up. Now, let's
make the pedestal on which the lens sits be a solid cylinder of radius
99 cm so that when you put it into the reservoir there will be 1 cm gap
all around. So as you lower it into the reservoir, mercury will spill
out the top and you will be sure to capture it. When you have captured
150 l, the whole thing will be floating on the mercury. You return the
extra 150 l and have floated the lens with only 180-150=30 l. Of course,
in the real world you would only buy 30 l, put the pedestal into the
empty reservoir, and add mercury until it floats. (I realize that the
shape of the pedestal and reservoir are probably not full cylinders,
since you said "trough", but my simple example wouldn't be so simple
with more complicated volumes. The idea is the same, though.)
![]() QUESTION:
QUESTION:
Rod tied to a string tilts vertically but when it is rotated it becomes horizontal Why ???
Can't seem to find any answer
![]() ANSWER:
ANSWER:
The easiest way to see this is to introduce the (fictitious) centrifugal
forces shown in the figure above. As you can see, both exert a torque
about the suspension point which will tend to make the rod horizontal.
When the rod becomes horizontal, the forces are still there but no
longer exert torques.

![]() QUESTION:
QUESTION:
What is the effect of mass on torque? A wind turbine fan's blades are commonly very long to increase torque and to decrease speed.
How can I decrease speed using MASS? Or, can I increase torque, by increasing of mass, without increasing length of the blade? (without losing the energy.)
What is the formula applicable here?
![]() ANSWER:
ANSWER:
You are asking many questions here with no simple answers.
The simplest place to start is your first question: does the mass of the rotor have an effect on the torque on it? Typically, the turbine has three blades. I will just analyze a single one and the same arguments could be made for the other two. Call the length of the blade L and assume that the force on it due to the wind is approximately uniform along the length of the blade (the force on a tiny piece of the blade near the center is the same as the force on an identical tiny piece near the end). Then the total force F due to the wind will depend on the length of the blade, but the force per unit length, Φ=F/L will be more useful because it will depend only on how hard the wind is blowing. It is now pretty easy to show that the torque due to the wind is τwind=½ΦL2. So, the answer to your question is no, mass does not affect the torque; the torque depends only on how hard the wind is blowing and how long the blade is.
Your second question is how can you decrease speed by changing the mass M. If I model the blade as a uniform thin stick of length L, its moment of inertia is I=ML2/3. If it has an angular velocity ω1, its angular momentum is L1=Iω1=Mω1L2/3. If you increase the mass to M+m, the moment of inertia will increase to I'=(M+m)L2/3 and its angular velocity will change to ω2. But, the angular momentum will not be changed, Iω1=I'ω2; you can then solve this for the new angular velocity, ω2=(I/I')ω1=[M/(M+m)]ω1 which is smaller. However, the rotational kinetic energy E of the blade is now lower, E1=½Iω12 and E2=½I'ω22=½I{(M+m)/M}{[M/(M+m)]ω1}2 or E2=[M/(M+m)]E1. On the other hand, if you wanted to add mass but keep the energy the same, E2/E1=1=I'ω22/Iω12 or ω2=ω1√[M/(M+m)]; in this case, the angular momentum will have changed.
Your third question is moot since we have established that torque does not depend on mass.

![]() QUESTION:
QUESTION:
If I stood beside a small operating hovercraft with a sail built into the front of it and blew air into the sail with a leaf blower I know that the craft would move forward. Now the question.If I sat down on the hovercraft with the leaf blower in hand and we became one with the hovercraft and I then blew air into the sail would we move forward or would action and reaction of the leaf blower neutralize the forward motion?
![]() ANSWER:
ANSWER:
It is easiest to understand if you think first of using a stick
instead of a leaf blower. Standing on the ground and pushing with the
stick on the sail, there is an unbalanced force acting on your
hovercraft (the stick). Now, if you stand on the hovercraft, the stick
exerts a backward force on you (part of the hovercraft, now) and the
stick exerts a forward force on the hovercraft and these cancel out. Or,
if you like, the only forces which have any effect on a system are
external forces and by becoming part of the system what you do is no
longer an external force. The leaf blower is a little trickier, but I
believe even worse! The leaf blower will exert a backward force on you
(like a little jet engine) and the stream of air will exert a forward
force on the sail; but some of the force from the stream of air will be
diminished by the air slowing down on its way to sail because of
interaction with the still air. So, the net effect would be for the
whole hovercraft to move backwards; probably not noticible because of
friction and the smallness of the loss of power due to the still air.
![]() QUESTION:
QUESTION:
If basketball (A) weighs 1 lb and is tossed upward to goal (A) at a height
of 8 ft (5 ft above my daughter's head) and basketball B is 6lbs, At what
height should goal (B) be to generate the same force to toss?

![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Actually this is not homework, let me explain the situation. My daughter is 5 years old and playing Kindergarten basketball. Only one person on her team can toss the ball high enough to score, the ball weighs roughly 1 lb and the goal is roughly 8 ft high. I purchased a weight trainer ball that is exactly the same diameter as the regulation ball she uses but it's a 6 lb ball.
My theory is that I can build her a goal in the house that is not as tall but would require the same energy to make the basket. therefore making her stronger. And when it comes time to shoot the lighter ball in the taller goal, she shouldn't have any problems.
![]() ANSWER:
ANSWER:
For the 1 lb ball, the energy which must be supplied is 1x5=5 ft·lb,
assumning that she releases the ball at the level of the top of her
head. The 6 lb ball, if sent vertically with an energy input of 5 ft·lb,
will rise to a height of h=5/6=0.83 ft=10 inches above her head. All this
assumes that the ball is thrown straight up. Note that I have not really
answered your question because you asked for force and the energy input
depends both on force F and the distance s over which it is
applied. The energy input W could be written as W=Fs,
So, if you assume that she throws it the same way and pushes as hard as
she can, the force need not be known.
![]() QUESTION:
QUESTION:
I am trying to figure this out for a dear Uncle on Vancouver Island as a challenge. I have suffered a concussion so trying is difficult. He used to live in S. Wales and dropped stones done old coal shaft. He was a teacher.
Wonder if you could help me please.
"A stationary rock is allowed to drop down an 800 foot shaft. Without compensating for air resistance, how far does it fall during
the sixth second of its descent? This is the formula. Assume gravity value to be 32 feet per second per second.
Please set out your answer clearly showing your thought process, line by line. Use words as well as numbers.
I'm afraid your answer so far is incorrect.
If needed, the formula we used was S = ut + half gt2."
Thank you very much. I am in Gr 5!! I want to by a physicist.
![]() ANSWER:
ANSWER:
I will assume that this is not a homework problem (forbidden on
this site!); at least if it is you went to a lot of trouble to disguise
it! Your equation is right except since we will start the clock (t=0)
when you let go of the stone, u=0 because u in your
equation is the speed at t=0. Also this equation assumes that
S=0 at t=0 and that S increases in a downward
direction. So, at the end of 5 seconds (the beginning of the 6th
second) the position is S5=½x32x52=400
ft; at the end of 6 seconds the position is S6=½x32x62=576
ft. So the total distance traveled is 176 ft. I trust you will not
present this work to your uncle as your own.
![]() QUESTION:
QUESTION:
What would be the estimated terminal velocity be of a 4,300lb car falling from 30,000ft above sea level be?

![]() ANSWER:
ANSWER:
The terminal velocity, vt, does not depend
on the altitude from which you drop your car. This can be a very tricky
problem because vt does depend on the density of the
air which changes greatly from sea level to 30,000 ft. So to get a first
estimate, I will just assume sea level density everywhere. There is an
estimate for the drag force in sea level air which is good for a rough
estimate, FD=¼Av2
where A is the cross sectional area and v is the
speed. From this you can show that vt=2√(mg/A).
In SI units, m=4300 lb=1950 kg, g=9.8 m/s2,
and A≈2x4=8 m2 (estimating the car as 2 m wide
and 4 m long). Then vt≈100
m/s=224 mph.
I guess we should now ask whether we expect it to reach terminal velocity before it hits the ground. Actually, it will technically never really reach terminal velocity, only approach it—see an earlier answer. I will calculate how far it falls before it reaches 99% of vt. In the earlier answer, I show that the height from which you must drop it for it to reach terminal velocity with no air drag is hno drag=vt2/(2g), and the height from which you drop it for it to reach 99% of terminal velocity with air drag is hdrag=1.96vt2/g (derived from the expression v/vt=0.99=√[1-exp(-2gh/vt2)]. So, for your case, hno drag≈510 m and hdrag≈2000 m. At 2000 m (around 6000 ft) the air is about 85% the density of sea-level air, so I believe that my approximation assuming constant density is pretty good and the car would probably reach 99% of the terminal velocity by the time it hit the ground. To actually put in the change in density with altitude would make this a much more difficult problem.
![]() QUESTION:
QUESTION:
Does a round and square object, the same weight, fall the same?
![]() ANSWER:
ANSWER:
If air drag is negligible, like if you drop them from a few
feet, yes. If they fall fast enough for air drag to be important, they
will fall differently and, if they are about the same size, say a sphere
and a cube, the sphere will fall faster. That may be all you want, but I
will go on and explain in a bit more detail. The drag force FD
on an object may be approximated for every day objects, masses, and
speeds as FD=½CDρv2A
where ρ is the density of the air, v is the speed,
A
is the cross-sectional area presented to the onrushing air, and CD
is called the drag coefficient. CD depends only on
the shape of the object. CD≈0.5 for a sphere
and CD≈0.8 for a cube (falling with one face
to the wind). So, if their areas are about the same, the drag on the
sphere will be smaller and it will go faster. Of course if the sphere
area were ten times bigger than the cube area, that would be more
important than the somewhat smaller drag coefficient and the cube would
win.
![]() QUESTION:
QUESTION:
What happens gravitationally when the center of mass can no longer be considered a point but is instead an area? Specifically, suppose the Sun was to "explode" or supernova; ignoring the obvious destruction of the solar system, what would happen to the planetary orbit of Earth? I presume it would be roughly akin to letting go of the string at the end of which I have a ball spinning around me.
![]() ANSWER:
ANSWER:
The center of mass is always a point. If the sun were to
"explode", the center of center of mass would continue to be at the
center of where it was before the explosion. A star explodes
approximately isotropically, that is, material goes out at the same rate
in all directions. So, until the material reached the earth's orbit, the
orbit would be unchanged. But, as material gets outside the earth's
orbit, only the material inside would contribute to the force felt by
the earth (this is Gauss's law). So the earth would behave as if there
were a star of constantly decreasing mass at the original center of
mass.
![]() QUESTION:
QUESTION:
I bought a 400lb gun cabinet and need to pull it on a 2 wheel hand cart up
a 12ft ramp at about 35degrees to the horizontal How much load does 1 or 2
people have to carry and how much is borne by the wheel. I am trying to make
sure we can be comfortably safe!
![]() ANSWER:
ANSWER:
I could make a rough estimate but would need to know the dimensions of the
cabinet, if the center of gravity is near the geometrical center. I would
assume that the cabinet was parallel to the ramp when being pulled.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
It is 20X29X55. It would not be parallel to the ramp but about 20 degrees from the ramp (which is about 35 degrees to the ground (thus avoiding 4 steps).
![]() ANSWER:
ANSWER:
Since only an approximation can be reasonably done here, I will
essentially model the case as a uniform thin stick of length L
with weight W, normal force N
of the incline on the wheel, and a force F
which you exert on the upper end. In the diagram above, I have resolved
F into its components parallel (x)
and perpendicular (y) to the ramp. Next write the three
equations of equilibrium, x and y forces and the
torques; this will give you the force you need to apply
to move it up the ramp with constant speed.
ΣFx=0=Fx-Wsinθ
ΣFy=0=Fy+N-Wcosθ
Στ=0=½WLcos(θ+φ)-NLcos(φ).
I summed torques about the end where you are pulling. Putting in W=400 lb, θ=35º, and φ=20º, I find Fx=229 lb, Fy=206 lb, and N=122 lb. Note that you do not need to know the length L. The net force you have to exert is F=√[(Fx)2+(Fx)2]=308 lb. If someone were at the wheel pushing up the ramp with a force B, that would reduce both Fx and Fy. This would change the equations to
ΣFx=0=Fx-Wsinθ+B
ΣFy=0=Fy+N-Wcosθ
Στ=0=½WLcos(θ+φ)-NLcos(φ)+BLsin(φ).
For example, if B=100 lb, the solutions would be Fx=129 lb, Fy=169 lb, and N=159 lb; so your force would be F=213 lb.
![]() QUESTION:
QUESTION:
Would it be physically possible to create a parachute capable of delivering a main battle tank safely to a theatre of war?
Like how huge would it have to be?
![]() ANSWER:
ANSWER:
A reasonable estimate of the force F of air drag on an
object of mass m, speed v, and cross sectional area A is F=¼Av2;
this works only in SI units. The speed v when F=mg is called
the terminal velocity. I estimated a reasonable terminal velocity would
be the speed the tank would have if you dropped it from about 10 m,
v≈14 m/s. The mass of the
MBT-70 (KPz-70)
is about 4.5x104 kg. Putting it all together, I find that
A≈104 m2, a square about 100 m on a side or a
circle of radius about 30 m. You could do a more accurate calculation
but this gives you a reasonable estimate.
![]() QUESTION:
QUESTION:
When solving questions involving two identical springs being stretched to points A and B to create a total length and the natural length of the springs are given. What is a consistent way to calculate the amplitude?
Is it half of the length of AB subtract the natural length of the spring?
![]() ANSWER:
ANSWER:
I assume that the springs are in series—one attached to
the end of the other. Suppose that you exert some force F such
that the springs are stretched by a distance s. Then each
spring will be stretched by ½s. If k is
the common spring constant, F=½ks. Therefore
the two together behave like a single spring with spring constant ½k.
![]() QUESTION:
QUESTION:
In my AP Physics class, we have had a class-wide debate over a physics
problem for the last few days. The problem asked how much work it would take
to move a satellite that was orbiting Earth at a certain height to a greater
height. Some of us say that the work equals the change in potential energy,
while others say that the work is the change in the total mechanical energy.
The total energy method gives an answer of exactly half of the amount the
potential energy method gives. Who is right?
Both orbits are circular.
![]() ANSWER:
ANSWER:
Since the speeds in the two orbits are different, the kinetic
energies will be different, so the correct way to do this is
½mv22-mMG/r22=W+½mv12-mMG/r12.
Of course you will have to figure out what the velocities are in terms
of the radii, but that should be a piece of cake for AP students!
![]() QUESTION:
QUESTION:
A car is travelling 45 mph, with the road being at a 5-8% incline. How
long would it take a car to slow down without using breaks? This is not homework. I am a claims examiner that is trying to get some information as to the rate of speed in which a car decelerates.
![]() ANSWER:
ANSWER:
You are a claims examiner and you spell brakes "breaks"?! I could do this if I assumed no friction whatever, but it would not be predictive of the real world because there is plenty of friction acting on a moving car even without brakes applied. I could make a better estimate if you could tell me how far this particular car, starting at 45 mph, traveled on level ground with brakes not applied. Also, is the car in gear? In neutral? Engine running?
If there were absolutely no friction, the car would keep going until it had gone
vertically up a distance of about 20 m≈66 ft regardless of
the grade of the incline. For a 6% incline, the distance traveled by the
car would be about 1100 ft. In the real world it would be way less than
this.
![]() QUESTION:
QUESTION:
I knew that when a car which travels very fast and is brake very sudden, the
car will like "fly away". But is there any theory or principle or rule can
explain this?
![]() ANSWER:
ANSWER:
I do not know what "fly away" means.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
To explain, an illustration is made. Imagine a bicycle that travels
in very high velocity and it is braked suddenly and hardly, what will
happen. The bicycle will like "flying up" caused by the momentum. It is
also related to the principle of acceleration and deceleration.
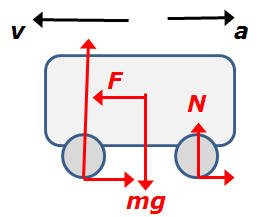
![]() ANSWER:
ANSWER:
OK, I get it now. Refer to the figure above. The easiest
way to do this is to introduce a
fictitious force. If
the car is accelerating with acceleration a (which points
opposite the velocity v when braking), Newton's first law will
be valid in the car frame if a force F=-ma acting at the center
of mass (COM) is introduced. The "real" forces on the car are a
normal forces up on each wheel by the road, the frictional forces
backwards on each wheel by the road, and the weight mg which
acts at the COM. In the drawing I have only labeled the weight, the
normal force on the rear wheel, and the fictitious force because those
are all you need to answer your question. If you wish, you could find
both normal forces and the sum of the two frictional forces in terms of
a; if all wheels were locked you could find the individual
frictional forces if you knew the coefficients of kinetic friction. Now,
I will sum torques τ about the point where the front wheel
touches the ground, Στ=mah+NL-mgs=0 where h
is the height of the center of mass above the ground, L is the
horizontal distace from the front axle to the COM, and s is the
horizontal distance between the wheels. You can now solve for N,
N=(mgs-mah)/L. Now think about N; if
N<0, the road would have to pull down on the back wheels to
hold the car from rotating forward about the front wheels. N
will be zero when the car is just about to "fly up"; therefore, if a>g(s/h),
the car will "fly up".
![]() QUESTION:
QUESTION:
Ships are often built on ways that slope down to a nearby body of water. often a ship is launched before most of its interior and superstructure have been installed and is completed when a float.
Is this done because the added weight would cause the ship to slide down the ways prematurely?

![]() ANSWER:
ANSWER:
Friction can be a tricky business, but the simplest behavior is
that the frictional force increases proportional to the weight. But the
force of the gravity trying to slide the weight down the slope is also
proportional to the weight. Therefore, doubling the weight of the ship
should not increase its tendency to slide down. Besides, if this were a
concern you could always temporarily block the path down the slope like
placing blocks in front of a vehicle on a slope to keep it from rolling.
I suspect the real reason is that the structure of the ramp is probably
not strong enough to support the full weight of the ship.

![]() QUESTION:
QUESTION:
I am doing an experiment on factors affecting the travel distance of a toy car from down a ramp and thought it would be a good idea to understand how a physicist thinks of things. My question is, how do you think weight of an object affects the distance it will travel after going down a ramp?
![]() ANSWER:
ANSWER:
The best discussion I have seen of the physics of pinewood derby
races is this
youtube video. You will see that what matters more than the added
weight is where you put it. (Thanks to my son Andy for pointing me to
this video; his son and my grandson Finn placed second in the Cub Scout
pinewood derby last year on the strength of the tips here!)
![]() QUESTION:
QUESTION:
What would happen if you threw a baseball at the speed of sound?
![]() ANSWER:
ANSWER:
At such a large speed, air drag has an enormous effect on ball.
To see the mathematical details see earlier answers for a
lacross ball
and a baseball. I
will make the same assumption that I did in those answers that the
amount by which the ball will fall will be very small compared to its
horizontal distance and the speed acquired in the vertical direction
will be very small compared to its horizontal speed. So I will ignore
the small effect which the vertical motion will have on the horizontal
motion. As discussed in the
earlier answer,
the horizontal distance x and speed v are given by
v=v0/(1+kt) and x=(v0/k)ln(1+kt)
where v0 is the initial velocity and k is a constant
determined by the mass, geometry, and initial velocity of the ball. For
v0=340 m/s (speed of sound) and a baseball
(mass=0.15 kg, diameter=0.075 m) these become v=340/(1+2.8t)
and x=121ln(1+2.8t) and are plotted below.
In one second the ball goes about 160 m and slows down to less than 100 m/s. During the same time, the ball will fall approximately 5 m and so, if launched horizontally from a height of 5 m will hit the ground in one second as shown below. Be sure to note the difference in horizontal and vertical scales; an insert shows the trajectory drawn to scale. The small distance fallen is the justification for my approximations above.
![]() QUESTION:
QUESTION:
Hi this may be a hard question but If I wanted to run 2200 gpm through a 2500 foot run with 50 feet of fall what size pvc pipe would this take?
This is all gravity.
![]() ANSWER:
ANSWER:
At first I just did a calculation with no corrections for
viscosity or drag. I found the velocity had to be about 17 m/s and the
diameter of a pvc pipe would have to be about 0.1 m≈4 in.
But then I worried about the fact that a pipe that long is likely to
have significant drag over its length. It is a pretty complicated
engineering calculation and I was unfamiliar with many of the
parameters. But I did find a
web
site which seems to have made it easy for me by including a
calculator. Frankly, I have no idea what the roughness coefficient is,
but it suggests a value of 150 for plastic. The result is below. As you
can see, to get a flow rate of about 2200 gpm would require a pipe with
diameter of about 10 in.
![]() QUESTION:
QUESTION:
If I place a liquid filled container on a scale and suspend a mass with greater density than the liquid within the liquid and then release the mass, will the scale register the full weight of the mass while the mass is in motion (falling) as compared to when the mass has settled on the bottom?
Will the scale read the same while the mass is accelerating as when it has achieved terminal velocity?
![]() ANSWER:
ANSWER:
Your second question indicates that you understand the answer
will be different depending on whether the falling mass is accelerating
or not. The figure shows that the weights of the fluid and the container
will act down on the scale. Now look at the falling object. In addition
to its weight there are two upward forces, the buoyant force
B and the drag force D;
these are both forces which the fluid exerts on the object. But Newton's
third law says if the fluid exerts a force on the object, the object
exerts an equal and opposite force on the fluid. Therefore the scale
will read Wf+Wc+B+D. If
the object is falling with constant speed, it is in equilibrium and so
B+D=Wo and the scale reads the total weight of
container, object, and fluid. If the object is accelerating down,
B+D<Wo and the scale reads less than the total weight of
container, object, and fluid. There is an
earlier question
similar to yours except the object is rising instead of
sinking.
QUESTION:
Have scientists done experiment on what is the value of gravity below the earth surface as depth increases? if done pl. provide chart g vs depth.
![]() ANSWER:
ANSWER:
The
deepest hole ever drilled is only about 12 km deep. I could
not find any reference to attempts to measure g at various depths
down
this hole. Since the radius is about 6.4x103 km, you would
only expect about a 0.2% variation over that distance. There are models
of the density of the earth, though, which have been determined by
observing waves transmitted through the earth during earthquakes or
nuclear bomb tests; these are believed to be a pretty good
representation of the radial density and can be used to calculate g.
The two figures above show the deduced density distribution and the
calculated g.
Usually in introductory physics classes we talk about the earth as having constant density, but as you can see, that is far from true—the core is much more dense than the mantles and crust. If it were true, g would decrease linearly to zero inside the earth. Instead, it increases slightly first to around 10 m/s2 and remains nearly constant until you are at a depth of around 2000 km. There is little likelihood that g will ever actually be measured deep inside the earth because the temperature increases greatly as you go deeper, already to near 200ºC at 12 km. However, if you have detailed information on density distribution, there is really no need to measure g.
![]() QUESTION:
QUESTION:
As part of our business we bag wrap passengers bags / suitcases prior to flying at the major UK airports.
We use and have used for many years a power pre stretch cast film —17 micron nano with a 300% capability.
Recent feedback from Heathrow airport suggests some of the passengers bags are sticking to the conveyer belts and are being miss-directed. I am being asked for the
'coefficient of friction' for the film we are using.
I have advised our supplier of this, they have sent through the data spec sheet but there is no mention of COF, on speaking with them they have never had this question raised before. Personally, I do not think this Is an issue with our film but more where customers themselves are wrapping their own bags with home use film. However, I need to provide proof that the film we are using does not have any adhesive properties.
My question is—would the COF affect this and how do I get the actual information on the film?
![]() ANSWER:
ANSWER:
The force of friction f depends on only two things:
what the surfaces which are sliding on each other are (conveyer material
and your plastic film) and the force N which presses the two
surfaces together; normally, on a level surface, the force N is
simply the weight of the object (suitcase in your case). There are two
kinds of COFs, kinetic and static. The kinetic coefficient, μk,
allows you to determine the frictional force on objects which are
sliding. In that case, f=μkN.
The static coefficient, μs, allows you to
determine how hard you have to push on the suitcase in order for it to
start sliding; in this case fmax=μsN
where fmax is the greatest frictional force you
can get. Since you are being asked to prove that it is not too "sticky",
it is the static, not the kinetic, coefficient which you need; measuring
μs is quite easy. The only problem is that μs
depends on the surfaces so you must have a piece of the material
from which the conveyer belts are made to make a measurement. Once you
have that, use it as an incline on which to place a wrapped suitcase.
Slowly increase the slope of the incline until the suitcase just begins
to slide. Your COF (μs) is equal to the tangent
of the angle of the incline which (see diagram above) is simply μs=H/L.
![]() QUESTION:
QUESTION:
A 1500lb 8'x8' box that is 3'6" tall is lifted at one of the four side so that the opposite side acts as a pivot on the ground (like a strong man flipping a giant tire in a a world strongest man competition). How much actual weight is being lifted? assuming that the weight distribution of the box is perfectly even.
![]() ANSWER:
ANSWER:
Well, that depends on how you lift it. Let's assume that you
lift it so that you cause it to rotate with uniform speed. One way that
you could accomplish this is to push in a direction perpendicular a line
drawn from where you are pushing and the edge on the box remaining on
the floor. Referring to the figure above, the equilibrium conditions are
N+Fcosθ-W=0, f-Fsinθ=0,
and ½LW-LFcosθ=½W-Fcosθ=0;
here F is the force you exert, W is the weight, N
is the force the floor exerts vertically, and f is the
frictional force exerted on the floor. Solving these I find that N=½W,
F=½W/cosθ, and f=½Wtanθ.
I suspect that the case you are interested in is when you first lift it
off the ground, θ=0. F=750 lb, half the total
weight. Note that this analysis is valid as long as the floor is not too
smooth, that is the box does not start sliding at some angle; the angle
is less than θ=tan-1(L/H)
because at that angle the center of gravity is directly over the pivot
side.
Of course there are lots of other ways you could
lift it which would be more efficient if your aim was to tip it over;
for example, you could start pushing horizontally once you got it off
the ground so that the floor would hold up all the weight rather than
half the weight. There is an
old answer very
similar to yours that you might be interested in.
One thing which occurs to me though is, since you know the car and
railroad crossing, why don't you just do the experiment and drive it
over the crossing?
f1+f1=C
for equilibrium of horizontal forces; N1+N2=W
for equilibrium of vertical forces; CH+L(N1-N2)=0
for equilibrium of torques about the red x. If you work this out, you find the normal forces
which are indicative of the weight the wheels support: N1=½(W-C(H/L))
and N2=½(W+C(H/L)). A few things to
note are: the outer wheel supports more weight, if C=0 (you are not turning), the inner
and outer wheels each support half the weight, at a high enough speed C will become so large
that N1=0 and if you go any faster you will tip over, and if the road cannot provide enough friction you
will skid before you will tip over. Now we come to your question. You first want the
maximum speed without tipping. Solving for v in the N1=0
equation gives vmax=√[RWL/(mH)]=√[RgL/H]
where g=9.8 m/s2=32 ft/s2
is the acceleration due to gravity. For example, suppose that R=7
ft, L=17 in=1.42 ft, H=30 in=2.5 ft. Then
vmax=√[7x32x1.42/(2.5)]=11.3 ft/s=7.7
mph. Be sure to note that the assumptions of a level
road (not banked) and wheels not slipping are used in my calculations.
Also be sure to note that W is the weight
of both box and trailer and 2L is the wheel base, not
the box width. One more thing is that you might not know how to
find the COG of the trailer plus box. If the COG of the trailer is Htrailer
above the ground (probably close to the axle) and the COG of the
box is Hbox above the ground, then H=(HboxxWbox+HtrailerxWtrailer)/W.
![]() QUESTION:
QUESTION:
I am an engineer working on the reconstruction of a traffic accident where it is alleged that a car traveling over a railroad crossing became airborne at a speed lower than the posted speed of the road. The information that I have available includes the type and make of the car and the geometry of the road. Nothing in the engineering literature that I can find addresses this issue. Despite the five quarters of physics that I took long ago, I am having trouble finding the information that I need to model this.
Any suggestions?
![]() ANSWER:
ANSWER:
This is sort of a classic introductory physics problem. The idea
is: when does an object lose contact with the surface on which it is
moving, usually taken to be a segment of a circle. I will do an
approximation that the shape is a circle and that the car is a point
mass. You can then generalize to your case from there or else give me
more information. In the sketch above, the radius of the circle is R,
the weight of the car is mg, the angle specifying the current
position of the car is θ, the force which is
causing the car to move with some constant speed v is F,
and the normal force of the road on the car is N. Note that
although the car has a constant speed, it has a centripetal acceleration
a=v2/R toward the center of the circle.
Applying Newton's laws, F-mgcosθ=0
and mgsinθ-N=mv2/R.
The first equation tells you what force you need to keep it moving at a
constant speed, F=mgcosθ which is really not of
interest to you; note that the force is in the direction of v
on the way up and opposite on the way down since the cosine changes sign
at 900. The second equation tells you what N is for
any position of the car, N=mgsinθ-mv2/R;
note that if N is negative it points toward the center but the
road cannot pull down, only push up, so the car could not stay on the
road at that speed and angle. What is really of interest is under what
conditions would N=0=gsinθ-v2/R
or v2=Rgsinθ; this would
tell you the speed (angle) at which a car with a particular angle
(speed) would leave the road. Note that it is independent of the mass.
Notice also that v2/Rg<1 because the sine
function cannot be larger than 1.0. For example, for what speed will the
car leave the road at 450 if gR=300 (m/s)2
(R≈30 m)? v=√(300x0.707)=14.6
m/s=32.7 mph. Or, at what angle will a car with speed 35 mph=15.6 m/s
leave the road?
θ=arcsin(15.62/300)=54.20.
![]() QUESTION:
QUESTION:
Say there is a cylinder on a ramp and the friction force from the ramp cancels out the parallel component of gravity. Therefore, the cylinder should be in linear equilibrium. However, from the reference point of the center axis of the cylinder, there is a net torque exerted by the friction force. Additionally, there is also a net torque exerted by the gravitational force from the reference point of the point of contact of the cylinder and the ramp. Therefore, it is not in rotational equilibrium and should start to rotate, correct? How is this possible, because if the cylinder starts to roll how can it also be in linear equilibrium?
![]() ANSWER:
ANSWER:
There is a simple answer to your question: the frictional force
is not equal to the component of the weight along the incline. Rather,
-f+mgsinθ=ma where θ is
the angle of the incline and a is the acceleration of the center of mass
down the incline.![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Thank you very much for your response. However, I think you may have misunderstood my question. I was asking what would happen in a case where the frictional force is set to cancel out the parallel component of weight. It seems as if the center of mass cannot move, but the cylinder needs to rotate. Therefore, it would appear as if the only outcome of this situation would be a cylinder rotating in place on a ramp, which does not seem possible. I think that the cylinder would have to roll down the ramp, but I can't see how this would be consistent with linear equilibrium.
![]() ANSWER:
ANSWER:
I did not misunderstand your question. You cannot simply adjust
the friction to be what you want it to be. You can, however, simulate
what you want to happen by wrapping a string around the cylinder and
pulling up on the string with a force mgsinθ
where
θ is the angle of the incline and m is the mass
of the cylinder; imagine that the incline is smooth (frictionless). Now
there will be a net torque about the center of mass of mgRsinθ=Iα
where I is the moment of inertia and
α is the angular acceleration of the cylinder. The
cylinder will spin in place. Your hand will have an acceleration of
a=mgR2sinθ/I; for a uniform
solid cylinder with I=½mR2,
a=2gsinθ.![]() ADDED
THOUGHT:
ADDED
THOUGHT:
If the coefficient of kinetic friction is exactly equal to
μk=tanθ,
the cylinder will slide down the incline with constant speed because the
frictional force will be f=μkN=(tanθ)(mgcosθ)=mgsinθ.
So, if you start it sliding and not rolling, it will begin spinning
about its center of mass because of the torque due to the friction and
have an angular acceleration α=fR/I; it will continue
sliding down the plane with constant speed, though.![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Thanks again but I am still a bit confused. It makes sense that the center of mass will move at a constant velocity while the cylinder is rolling, but how did it acquire that velocity in the first place if I start the cylinder at rest and not sliding as you wrote in the additional thought. In other words, what happens if the coefficient of static friction is equal to mgsinθ and the cylinder starts with no velocity of any kind?![]() ANSWER:
ANSWER:
If you start the cylinder
at rest on the incline and
μk=tanθ
(coefficient of static friction will be larger),
the cylinder will roll without slipping. If you solve the dynamics for
the cylinder rolling without slipping you will find that (see the figure
above) f=(mgsinθ)/3 and a=(2gsinθ)/3
where f is the frictional force and a is the
acceleration of the center of mass. Since f<mgsinθ,
if you simply let it go, it will roll without slipping. So, if you want
it to slide down with constant speed, you must give it a shove to start
it slipping.
![]() QUESTION:
QUESTION:
If I were to drop two round balls of different mass under water would they both fall to the bottom at the same velocity or would one reach the bottom first?
![]() ANSWER:
ANSWER:
The forces on a ball are its own weight mg down; the
buoyant force B up which would be equal in magnitude to the
weight of an equal volume of water; and the drag force f up
which would depend on the size the ball and its speed. The net force
F would be F=-mg+B+f; as the ball went faster and faster,
f would get bigger and bigger until eventually F=0 and
the ball would go down with a constant speed called the terminal
velocity. The larger the mass, the larger the terminal velocity. Without
specifying the the sizes of the balls, your question cannot be answered.
If they had identical sizes, the heavier ball would reach the bottom
first because it would have a larger terminal velocity. Of course, if
B>mg the ball would float!
![]() QUESTION:
QUESTION:
I'm trying to find a fast/easy way to test whether a sealed, consistently-dimensioned rectangular box is sufficiently "stable" for transport on a (small) 2-wheeled bicycle trailer. The box is pretty tall. If it's over-weighted and top-heavy, it'll flip the trailer around turns (which are sufficiently tight/quick). I figure there might be a quick, static "tip test" with a combination pull gauge, inclinometer and scale, but my math skills are primitive. Is there a simple way to ascertain whether, for a given object, a target stability threshold is met?
![]() ANSWER:
ANSWER:
There is an
earlier
answer about a bicycle making a turn. It would be helpful for you to
read that first. The easiest way
to do this problem of your trailer turning a curve is to introduce a fictitious
centrifugal force which I will call C, pointed
away from the center of the circle; the magnitude of this force will be mv2/R where
m is the mass of the box plus trailer, v
is its speed, and R is the radius of the curve. The picture to the right
shows all the forces on the box plus trailer: W is the weight and the green
x is the
center of gravity (COG) of the box plus trailer; f1 and f2 are the
frictional forces exerted by the road on the inside and outside wheels
respectively; N1 and N2 are the normal
forces exerted by the road on the inside and outside wheels respectively;
the center of gravity of the box plus trailer is a distance H above the road and the wheel base is
2L (with the center of gravity halfway between the wheels). Newton's
equations yield:
![]() ADDED
THOUGHT:
ADDED
THOUGHT:
When just about to tip, all the weight is on the outer wheel and so
N2=W
and f2=μN2=μW,
where
μ is the coefficient of static friction. If you work it out,
the minimum value the μ must have to keep the trailer from
skidding is μmin=L/H. For the
example worked out above, μmin=0.57. For
comparison, μ for rubber on dry asphalt is about
0.9, so the trailer would not skid.
![]() QUESTION:
QUESTION:
Will a heavier ball roll down a small slope faster than a lighter ball?
Or will a lighter ball roll down a small slope faster than a heavier ball?
![]() ANSWER:
ANSWER:
If both are solid balls of the same radius but of different masses, they
will take equal times if air drag is neglected as might be appropriate for a
"small slope". If they get going fast enough that air drag becomes
important, the heavier ball will win the race.
![]() QUESTION:
QUESTION:
Gasoline contains 40 megajoules of energy per kilogram and gasoline trucks have around a hundred tons of it. So how does a gasoline truck exploding not produce an explosion similar to a small nuke?
![]() ANSWER:
ANSWER:
Since it is always a little ambigous what is meant by a ton, I did my own
calculation using the volume of a tanker truck of about 10,000 gallons and
the density of gasoline of about 2.7 kg/gallon. I got the total energy
content of about 1012 J. The energy of the Nagasaki bomb, a small
bomb by today's standards, was about 1014 J, 100 times bigger.
Two things to consider are:
-
The bomb number represents total energy delivered whereas I would guess that likely less than half the energy content of the gasoline would actually be delivered.
-
The time over which the energy is delivered is likely much longer for the gasoline explosion than the nuclear explosion. As an example, just to illustrate the importance, suppose the bomb exploded in 1 ms=10-3 s and the tank in 1 s. Then the power delivered by each is 108 GW for the bomb and 103 GW for the tank. As a result the destructive power of the bomb would be much bigger.
![]() QUESTION:
QUESTION:
-
What exactly is momentum and how is it different from force?
-
I understand that p = mv and F = ma but they seem so similar in application that I haven't fully wrapped my head around it.
-
Additionally, what does it mean for something to have momentum in the first place, and why must it be conserved?
-
How does light have momentum if it, by nature, has 0 mass (I presume E =mc^2 comes into play somewhere here)?
-
Finally, what is the significance in the fact that light does have momentum (if it does)?
![]() ANSWER:
ANSWER:
You have lots of questions, really. I have rearranged your question to
delineate it into parts:
-
For your first question, just say that p=mv. My answer to #2 should clarify how force and linear momentum are related. Force and momentum have to be different because they are not even measured in the same units—momentum is mass*length/time and force is mass*length/time2.
-
What is acceleration? It is rate of change of velocity, a=(v2-v1)/t where t is the time to change speed from v1 to v2. So one could write that F=(mv2-mv1)/t=(p2-p1)/t; so force may be thought of as the rate of change of momentum. Newton actually stated his second law this way, not as F=ma. It is the second law which is a fundamental law of physics, momentum is just defined because of its simple and natural relationship to the second law.
-
It doesn't "mean" anything for something to have momentum, it is just a definition. However, consider the second law if there is no force acting; then F=0=(p2-p1)/t. In other words, p2=p1 which simply means that momentum does not change (is conserved). The condition for conservation of momentum of a system is that there be no external forces on it. For example; suppose you look at an isolated galaxy which has billions of stars in it all interacting with each other and there are negligible forces from the outside; if you sum up all the momenta of all the stars today and in 10 years from now, you would get the same answer even though the shape and orientation of the galaxy would change.
-
It turns out that if v is very large, comparable to the speed of light c, Newtonian mechanics is incorrect. (You could say that Newtonian mechanics is wrong but a superb approximation for low speeds.) If you say that p=mv it turns out that momentum is not conserved for an isolated system at very large speeds. However, since momentum conservation is such a powerful way to solve problems, we redefine momentum (in the theory of special relativity), to be p=mv/√(1-(v2/c2)), momentum is conserved again and we still have p≈mv for small v. It also turns out that, as a result of this new definition of p, we can write that E=√(p2c2+m2c4) where E is the energy of a particle of mass m. So if the particle is at rest, p=0 and E=mc2; if the particle has no mass, p=E/c.
-
No more significant than if a billiard ball has momentum—it just does.
I have deleted your question about angular momentum—it is off topic.
![]() QUESTION:
QUESTION:
I work in a high school where this question was posed by one of the pupils in a class I support. The question is this....
If you could attach a rope to a rocket, which would also be attached to earth, and sent it into space (out of our atmosphere) until the rope went taught and then cut the string. Would it stay in space or would it fall back to earth?
![]() ANSWER:
ANSWER:
This is one of those problems which I had fun with and I hope it will not be
too exhaustive an answer.
I will make the following assumptions:
-
the rocket always goes straight up;
-
the rocket stops moving vertically when the rope is taught;
-
the rope is cut the instant that the rocket stops;
-
fuel and the weight of the rope are not issues; and
-
the launch is from the equator. This makes things much simpler and I will briefly talk about a similar launch from some latitude at the end.
 My
view of this problem, therefore, is the same as if the rocket were on top
of a very long stick vertically straight up and the stick is suddenly
removed.
My
view of this problem, therefore, is the same as if the rocket were on top
of a very long stick vertically straight up and the stick is suddenly
removed.
The thing to appreciate is that even though the rocket goes straight up, it will have the same angular velocity ω as the earth so its speed will be ω(L+R) where L is the length of the rope and R is the radius of the earth. The angular velocity is ω=[(2π radians)/(24 hours)]x[(1 hour)/(3600 seconds)]=7.27x10-5 s-1. If L is just right, the rocket will assume an orbit like the geosynchronous communication satellites; this turns out to be if L=5.6R.
-
So, if the rope happens to be 5.6 times larger than the radius of the earth, the rocket will remain (apparently) stationary above its launch point; it is actually going in a circular orbit with a period of 24 hours. (The animation above illustrates this, although not to the correct scale.) For any other L the orbit will be an elipse with the center of the earth being at the focus. Visualize.
-
If L>5.6R, the starting point of the rocket will be the perigee (closest point to the earth) of its orbit. Visualize.
-
If L<5.6R, the starting point of the rocket will be the apogee (farthest point from the earth) of its orbit. Visualize.
-
For L<5.6R, though, there will be some critical distance L=Lc when the perigee of that orbit is exactly equal to R; in that case the orbit will just skim the surface of the earth. After some laborious algebra I found that Lc≈3.7R, about 2.2 earth radii inside the geosynchronous orbit. Visualize.
-
For L<Lc, the rocket will crash back into the earth but not where it was launched from because it is a projectile which has a horizontal speed greater than that of the earth's surface. Visualize.
-
Finally, if the horizontal speed of the rocket ω(L+R) is greater than or equal the escape ve=√[2MG/(R+L)], where M is the mass of the earth, the rocket will escape the earth and never come back. I calculated this to be when L=7.6R, two earth radii beyond the geosynchronous orbit. Visualize.
For any other latitude θ the speed of the satellite will be ω(L+R)sinθ. The resulting orbits, while all elliptical, are much more difficult to visualize and maybe we should save that for another day! However, the simplest launch of all would be from the north or south pole (θ=00 or 1800) because it acquires no horizontal velocity (ω(L+R)sinθ=0) where the rocket would fall straight back down regardless of how high it went.
![]() QUESTION:
QUESTION:
Will two objects traveling in the same direction ever collide? Assume the objects are on earth, unmanned and their mass, volume, weight, density and speed are the same. All variables that can come in to play should be assumed that they are equal, for example no hills, curves bumps and no change in surfaces to have any effect on the coefficient of friction. Just a question my wife and I were wondering about.
![]() ANSWER:
ANSWER:
I'm
not really sure what you are getting at here. If you are just wondering
whether two parallel lines ever intersect, the answer is no. But you seem to
want to know about material objects originally moving on parallel lines. To
make the situation simpler, let's just have the two objects, originally with
parallel velocities, move in otherwise empty space. If the original
velocities are equal and they are traveling side by side, they will
eventually collide because there is a gravitational attraction between them
which will eventually bring them together. However, if they are originally
side by side and traveling with unequal speeds, they would not collide if
their relative velocities were greater than the escape velocity. The escape
velocity for equal masses m originally separated by a distance
r is vescape=2√(mG/r) where G=6.67x10-11
N·m2/kg2 is the gravitational constant.
![]() QUESTION:
QUESTION:
A 400lb person jumps up 2-inches on earth. If same person jumps up on the
moon, how high would the jump be?
![]() ANSWER:
ANSWER:
I will assume that whatever the jumper does will add the same energy on both
earth and the moon. The gravitational potential energy U at the
highest point must be equal to that added by the jump, and U=mgh
where m is the mass (400 lb), h is the height (2 in on earth), and
g is the acceleration due to gravity (9.8 m/s2
on earth, 1.6 m/s2 on the moon). The mass is the same both
places, so hearthgearth=hmoongmoon. Solving,
hmoon=12.25 in.
![]() QUESTION:
QUESTION:
Hi, I was wondering what are the chances of survival from falling from the ninth floor of a building, going over the science of that how does surface affect the fall, body weight and trajectory. What is the difference from falling from a third story window as opposed to a higher up one?
![]() ANSWER:
ANSWER:
Someone else also asked this question; apparently it refers to a recent actual
incident of a student falling out a dorm room window about 85 ft≈26
m high; the student survived without serious injury. The second person also
wanted to know if I could estimate the force experienced on impact. First I
will calculate the speed he would hit the ground if there were no air drag.
The appropriate equations of motion are y(t)=26-½gt2. and
v(t)=gt where y(t) is the height above the ground
at time t, and g is
acceleration due to gravity which I will take to be g≈10
m/s2. The time when the ground (y=0) is reached is found
from the y equation, 0=26-5t2 or t=√(26/5)=2.3
s. Therefore v=10x2.3=23 m/s (about 51 mph). The terminal velocity of a falling
human is approximately 55 m/s, more than double the speed here, so the
effects of air drag are small and can be neglected for our purposes of
estimating. (If there is air drag, terminal velocity is the speed
which will eventually be reached when the drag becomes equal to the weight.)
Estimating the force this guy experienced when he hit the ground is a bit trickier, because what really matters is how quickly he stopped. Keep in mind that this is only a rough estimate because I do not know the exact nature of how the ground behaved when he hit it. The main principle is Newton's second law which may be stated as F=mΔv/Δt where m is the mass, Δt is the time to stop, Δv=23 m/s is the change in speed over that time, and F is the average force experienced over Δt. You can see that the shorter the time, the greater the force; he will be hurt a lot more falling on concrete than on a pile of mattresses. I was told that his weight was 156 lb which is m=71 kg and he fell onto about 2" of pine straw; that was probably over relatively soft earth which would have compressed a couple of more inches. So let's say he stopped over a distance of about 4"≈0.1 m. We can estimate the stopping time from the stopping distance by assuming that the decceleration is constant; without going into details, this results in the approximate time Δt≈0.01 s. Putting all that into the equation above for F, F≈71x23/0.01=163,000 N≈37,000 lb. This is a very large force, but keep in mind that if he hits flat it is spread out over his whole body, so we should really think about pressure; estimating his total area to be about 2 m2, I find that this results in a pressure of about 82,000 N/m2=12 lb/in2. That is still a pretty big force but you could certainly endure a force of 12 lb exerted over one square inch of your body pretty easily.
Another possibility is that the victim employed some variation of the technique parachuters use when hitting the ground, going feet first and using bending of the knees to lengthen the time of collision. Supposing that he has about 0.8 m of leg and body bending to apply, his stopping distance is about eight times as large which would result in in an eight times smaller average force, about 5,000 lb.
Falling from a third story window (about 32 feet, say) would result in a speed of about 14 m/s (31 mph) so the force would be reduced by a factor of a little less than a half.
![]() ADDED NOTE:
ADDED NOTE:
A rough estimate including air drag would have his speed at the ground be
about 21 m/s rather than 23 m/s as above. Given the rough estimates in all
these calculations, this 10% difference is indeed negligible.

![]() QUESTION:
QUESTION:
Gravity makes Earth orbit sun, Milky Way and Adromeda collide with each other,etc...
My question is, what can provide the necessary energy for a system like this for billions of years?
![]() ANSWER:
ANSWER:
The earth orbiting the sun has energy, but it takes zero energy to keep it
orbiting. The Milky Way and Andromeda galaxies have energy but no additional
energy is added as they move toward each other and eventually collide.
![]() QUESTION:
QUESTION:
It might look like a homework question, but it is not. Please help me. I have asked this question everywhere I could, but everybody seems to ignore it.
So, the problem is: Let us say we have two bodies A and B in contact with each other, with A lying at the back of B, and the system is on a friction-less horizontal surface. Let A have mass 5 kg and B 10 kg. Now let's say I apply a force of 45 N on A with my hand, then the system begins to accelerate at 3 m/s^2 and the net force on B by A is then 30 N, and B in reaction applies a net force of -30 N on A. Thus, the net force on A is 15 N. What I do not understand is why A is not applying a force of 45 N on B? If it is due to the reaction of B on A, how does A know in the first place that it is to exert a force of 30 N on B so that it receive a reaction of -30 N from B? Is not the reaction force of B on A some kind of a function of the action of A on B, and if it is, then how is the magnitude of the action of A on B is first determined? What is it that I do not understand about Newton's Third Law of Motion?
![]() ANSWER:
ANSWER:
OK, I will take your word for it that it is not homework. It is important to
be able to solve these kinds of problems. My method is to choose a body and
look only at that body. I choose first (as you did) to choose both masses as
the body, so M=15 kg and F=45 N and therefore a=F/M=3
m/s2. Next I choose B as the body. The only force on it is the
force which A exerts on it, FBA. Since we know that mB=10
kg and aB=3 m/s2, FBA=mBaB=30
N. Finally choose A as the body. Two forces act on A, F=45 N and the
force which B exerts on it, FAB=-FBA=-30
N; its mass is m5=5 kg and therefore a=(F+FAB)/m5=(45-30)/5=3
m/s2. The reason that there is not a 45 N force on B is because
your finger is not touching B, only A is touching B. The reason A "knows" to
exert a force on A is that it has no choice since A's acceleration and mass
are already fixed. Once you know the "reaction" force you automatically know
the "action" force because of Newton's third law, FAB=-FBA=-30
N for this problem. You could also have chosen A as the body before you
chose B as the body. Two forces act on A, F=45 N and the force which
B exerts on it, FAB. Its mass is m5=5 kg
and its acceleration is 3 m/s2; therefore (45+FAB)=m5a=15
N or FAB=15-45=-30 N.

![]() QUESTION:
QUESTION:
If I am running at average sprinting pace for an 17 year old male and
I jump off of a 80 meter drop, how far forward will I land from the jumping point? Assuming I am around 11 stone.
![]() ANSWER:
ANSWER:
80 m is pretty high, so you will be going very fast when you hit;
therefore, neglecting air drag might introduce significant error. But
air drag is pretty tricky to calculate and I will neglect it; the answer I
get will be somewhat bigger than what would really happen. I will take your
speed to correspond to running a 100 m dash in 15 s, about v ≈6.7
m/s. The equations of motion are x=6.7t and
y=-4.9t2
where x and y are the horizontal and ver tical positions
relative to the edge of the cliff and t is the time after jumping.
Solving the y equation for t when y=-80 m (the ground),
t=√(80/4.9)=4.04 s, so x=6.7x4.04=27.1 m. That is the answer
neglecting air drag. Note that it is independent of the mass m.
![]() QUESTION:
QUESTION:
What is the purpose of utilizing a percentage of body weight to determine how much weight to bench press/push/whatever? I know this seems like a fitness question and not a physics question, but what I am interested in is WHY weight would be used to determine how much one could (or should be able to) lift/push?
For example: A gym teacher wants to grade his students on their strength. He decides to use abililty to push a weighted sled across the floor as the measure. He wants to make the task equally difficult for every student in order to make the grading fair. So, he decides that each student will push 2x his/her body weight for 5 minutes and the grade will be based on how FAR the student is able to push.
So, Student A weighs 170 pounds and pushes 340 pounds (including the weight of the sled) for a total of 160 yards. Student B weighs 240 pounds and pushes 480 pounds (again, including the weight of the sled) for 80 yards. Student A pushed farther and gets a better grade, but Student B complains that he had to push much more weight so he should not get a worse grade.
Does Student B have a legitimate complaint or does his heavier weight contribute somehow to his ability to push that doesn't have anything to do with his strength? As in, does his weight help push the sled in some way?
Sorry, I don't know enough about physics to ask this question using proper physics terms like force, mass, etc. I hope you will still answer my question!
![]() ANSWER:
ANSWER:
I cannot comment on the rationale for correlating weight to strength. I can
certainly comment on the physics of your particular example of sled pushing.
I would first of all comment that this example is certainly not one solely
of strength because, since it is a timed activity, endurance as much as
strength is being tested; if one student, for example, were a heavy smoker,
he would likely become exhausted more easily. As a physicist, I would equate
"strength" with force. The specific example you give, though, seems to me to
be more related to energy (work done by the student) or power (rate of
energy delivered) than strength; purely in terms of strength, the heavier
student exerts more force. The force F which each student must exert
depends on the weight w he is pushing and the coefficient of friction
#956;
between the sled and the ground, F= μw.
The work W done in
pushing the sled a distance d is W=Fd= μwd.
The power generated if W
is delivered in a time t is P=W/t=μwd/t .
Both students have the same
μ
and
t , so WA/WB=PA/PB=dAwA/dBw
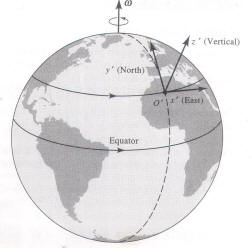
![]() QUESTION:
QUESTION:
the Coriolis effect..
on a freely falling body... is to east...?
motion of earth is towards east right.? so we must feel that falling body deflects to the west isn't it..???
![]() ANSWER:
ANSWER:
I cannot give the full derivation of the motion of a particle in a rotating
coordinate system, it is much too involved. I can give you the results,
though. The coordinate system we will use is the coordinate system (x',y',z')
shown to the right. The Coriolis force is given by 2mv'xω
where v' is
the velocity of m and
ω is the angular
velocity of the earth ( ≈ 7.3x10-5
s-1). Now, for a body dropped from some height h, the
direction of the velocity is in the negative z' direction, so the
direction of
v'xω
is east. This is not what
you would intuitively suspect (as you note), but it is true. An expression
for how far eastward it would drift before hitting the ground is x'=[( ω·cosλ)/3]√(8h3/g)
where λ is the latitude. For example, at the equator where λ=900,
and you drop it from 100 m, the deflection would be x'=2.2x10-2
m=2.2 cm.
![]() QUESTION:
QUESTION:
Two bodies A and B are at rest and in contact with each other. Now if some arrangements made body A exerts a pressure of 10 NEWTON on body B then according to NEWTON'S 3rd law of motion body B will also exert an equal force of 10 NEWTON in opposite direction so the resultant force should be zero, while practically we see that there will be a resultant force of 10 NEWTON acting on body b and if mass and other conditions of body B are such that it moves by applying 10 NEWTON force on it. Then it will start moving. HOW?
![]() ANSWER:
ANSWER:
You have this all confused. But, you are not alone! When doing this kind of
problem, you must choose a body to focus on; only forces on that body
affect its motion. So, if you are interested in what body B will do, you
look only at that body. The force which B exerts on A is not a force on B.
So, if B has a mass of, say, 2 kg and there are no other forces on B, it
will have an acceleration of aB=10/2=5 m/s2.
Since the 10 N force continues, A and B remain in contact, so aA
must also be 5 m/s2. One force on A is the 10 N force from B
which is in the opposite direction as the acceleration. But the net force on
A must surely be in the direction of the acceleration, so there must be some
other force (probably due to you pushing on A) on A which is bigger than 10
N and points in the direction of the acceleration. For example, if the mass
of A is 4 kg, F-10=4x5=20 N, so F=30 N. Finally, you could
look at A and B together as the body. In that case the forces they exert on
each other do cancel, the acceleration is 5 m/s2, and the total
mass is 6 N; therefore, there must be some external force (you again)
causing this 6 kg to have an acceleration of 5 m/s2: F=ma=6x5=30
N. All three ways of looking at this problem are consistent with each other.

![]() QUESTION:
QUESTION:
i love physics and this question i asked to my teacher and principal but they couldn't answer it so my question is about third law of motion "every reaction has an equal and opposite reaction" so when a truck moving with constant speed hits a stationary car so according to newton's 3rd law of motion truck shoud be stopped after collision because car applies equal force on truck which it have during collision.
![]() ANSWER:
ANSWER:
Why should it be stopped? Certainly the truck experiences the force which
the car exerts on it, but every force does not have the effect of stopping
the object which experiences a force. If you are running toward a fly which
is hovering at rest in your path, you feel the force of the fly but it does not
stop you.
![]() QUESTION:
QUESTION:
Supposing a weightless container is filled with water. I am sure the pressure at the bottom of liquid, P1 = atmospheric pressure + height of liquid x density of liquid x g = Patm + hdg, where Patm is atmospheric pressure and d is density of liquid. We can calculated this pressure as if liquid in region A and Region C does not exist.
But how about the the pressure at the base of the container, that is P2. Is P2 same as P1? For P2, do we need to consider the whole weight of the liquid, that is inclusive of the weight of water in region A and C?
![]() ANSWER:
ANSWER:
It depends on what the force on the bottom is. If the container is in
equilibrium, imagine it sitting on a table. The table would exert an upward
force equal to the weight W of all the water, so P2
would be W/Abottom where Abottom
is the area of the bottom of the container. This assumes that atmospheric
pressure is the same everywhere in the vicinity of the container; in other
words, I have ignored the buoyant force due to the air on the whole
container because it will surely be much smaller than W. ![]() FOLLOWUP
QUESTION:
FOLLOWUP
QUESTION:
Indeed the container is resting on the table. For P1, I use h x d x g. But for P2 you use W / Abottom, So can I say P1 not equal to P2 ?![]() ANSWER:
ANSWER:
Yes, but I have to admit that my answer was misleading in that I gave you
the gauge pressure, the pressure above atmospheric. So I should have said
that P2=Patm+W/Abottom.
There is no problem that P2 ≠ P1
because the force which the container exerts on the table is not P1Abottom.
Think about it—the
sides of your container exert a downward force on the bottom of the
container.

![]() QUESTION:
QUESTION:
Two of us disagree on part of a sol'n given by two people with Physics background, and I want to know if I am correct, or if I am missing something in the analysis of the problem...in case I have to explain it to a student.
Question concerning Forces/impulse..... 50kg person falling @15m/s is caught by superhero , and final velocity up is 10m/s.
Find change in velocity.
Find change in momentum .
It takes 0.1 sec to catch them.....ave Force is ?
answers are: vel = 25 m/s change in mom.. 1250 kg*m/s, and ave Force = 12,500 N.
Here's where we disagree: Person B says that 12,500 N is equiv. to 25 g ?????
They try to explain that 250 m/s^2 accel. corresponds to 25g.... I said it makes No sense at all, [ I know the accel. is 250, but that doesn't in any way imply a 25 g "equivalence" to me ]. They then went further to "prove" their point........Here is their argument...
500 N/g = 12500N / ( )g ..... I agree the ( ) = 25, but say there is No justification for the 500 N / g in the first place...... any ideas where it comes from , or how to justify that value ?
BTW I teach physics on and off at the HS level.... person B is an Engineer , I think
![]() ANSWER:
ANSWER:
Person B is wrong but has the right idea. (As you and your friend have
apparently done, I will approximate g ≈10
m/s2.)
We can agree that the acceleration is a=250 m/s2 and that
is undoubtedly 25g. Now, we need to write Newton's second law for the
person, -mg+F=ma=-500+F=12,500, so F=13,000 N. This is
the average force by the superhero on the person as she is stopped, so the answer that the
average force is 12,500 N is wrong. When one expresses a force as "gs of
force", this is a comparison of the force F to the weight of the
object mg, F(in gs)=F(in N)/mg=13,000/500=26
gs; this simply means that the force on the object is 26 times the
object's weight. So neither of you is completely right, but if there is any
money riding on this, your friend should be the winner because the only
error he made was to forget about the contribution of the weight to the
calculation of the force. I am hoping that superman knows enough physics to
make the time be at least 0.3 s so that Lois does not get badly hurt!
![]() QUESTION:
QUESTION:
I have something I have been wondering about.maybe you can answer. I recently drank a glass bottle of rootbeer and then set the empty bottle on the hood of my car that was slanted slightly (1980's model). Within seconds the empty bottle started to vibrate slightly and then"walked" down the hood of my car. The engine was turned off. I was trying to tell my girlfriend that it was from heat convection, but she disagreed. How can this happen? I did it a second time and the empty bottle did it again. Not my imagination.
![]() ANSWER:
ANSWER:
Here is what I think: The bottle probably had condensation (water) which was
fairly cool and the hood of your car was warm or even hot. The viscosity of
water depends quite sensitively on its temperature. If the water is heated
from 250C to 500C, for example, the
viscosity
decreases from about 890 to 547
μPa¬∑s which will result in a
much slipperier contact. (Think of a very heavy oil and a very light oil to
get an intuitive feeling for how viscosity would affect the frictional
force. Or, think of the old expression "…as slow as molasses in January…".)
![]() QUESTION:
QUESTION:
I don't know if you get this question alot, but a man standing on the ground is subjected to 2 forces. Gravity and normal reaction force. Do they form an action-reaction pair of forces?
![]() ANSWER:
ANSWER:
This is one of the most misunderstood aspects of Newton's laws. Let me state
Newton's third law for your man in a couple of ways:
-
The earth exerts a downward force on the man (his weight) and therefore the man exerts an upward force on the earth of the same magnitude as his weight.
-
The ground exerts an upward force on the man (the normal force) and therefore the man exerts a downward force on the ground of the same magnitude as his weight.
Both of these are correct statements of Newton's third law. Notice that the pairs of forces ("action-reaction") are never on the same object. The two forces you give are both on the same object (the man) and can therefore not be an "action-reaction" pair. So why are they equal and opposite? Because Newton's first law states that if the man is in equilibrium the sum of all forces on him must be zero; therefore the ground must exert an upward force to balance the weight. Your example has nothing to do with Newton's third law.
![]() QUESTION:
QUESTION:
Does a submarine have to work harder to travel at the same speed in deeper water?
![]() ANSWER:
ANSWER:
The drag
force in water is approximately proportional to the speed; it also
depends on the shape and on the viscosity of the water. As you go deeper
into the water, the pressure increases and the temperature decreases.
Viscosity only very weakly
depends on
pressure but increases significantly with temperature. After remaining
constant around 200C until a depth of about 200 m, temperature
rapidly decreases to about 40C at a depth of about 1000 m; the
viscosity, and therefore the drag,
nearly doubles at
that depth.
![]() QUESTION:
QUESTION:
if an object ( like a bullet ) is fired vertically at constant speed. Where does it land?
![]() ANSWER:
ANSWER:
This is a standard intermediate-level classical mechanics problem for
accelerated reference frames. All the mathematical background is much too
complicated to include here but the answer is that it lands a distance
d=4ωv03cosλ/(3g2)
west of where it was shot; here ω=7.27x10-5 s-1
is the angular velocity of the earth, v0 is the initial
velocity of the bullet, λ is the latitude where the gun is located,
and g=9.8 m/s2 is the acceleration due to gravity. This,
of course, neglects any air drag or wind corrections. For example, for λ=450
and v0=390 m/s (typical 9 mm muzzle speed), d≈60 m.
At the poles (λ=900), it goes up and comes back down
perfectly vertically.
![]() QUESTION:
QUESTION:
what is the cause of buoyancy.?
we faced many confusions about then we worked on it and did some experiments
and found an another reason which is satisfying all the conditions and
aspects...but we wanted to consult about it......
![]() ANSWER:
ANSWER:
The reason for buoyancy is simply that the force due to the fluid up on the
bottom of something is greater than the force of the fluid down on the top
because of the pressure difference.
![]() QUESTION:
QUESTION:
If I have two hoses a varying diameters such as a garden hose and a firehose that are vertical and approximately 20 feet long that are filled with the same amount of water and have the same size opening at the bottom, using just gravity, will water flow through each hose in the same amount of time?
This question came up during a recent visit with a customer. I sell feeding supplies for neonatal patients. The current product being used is a large bore tube compared to the smaller bore that my company sells. However the opening at the distal tip of the feeding tube is the same size for both. Again, using just gravity, shouldn't the speed at which formula flows through the distal end be the same since it bottlenecks there?
![]() ANSWER:
ANSWER:
Your first question ("…will
water flow through each hose in the same amount of time?") is ambiguous, so
let me answer the question by finding how the speed of the delivered formula
(labelled Vbottom in the figure) depends on the geometry.
The operative physics principal is Bernoulli's equation, P+–ÖρV2+ρgy=constant
where P is pressure, ρ is fluid density, y is the
height above some chosen reference level, and g=9.8 m/s2
is the acceleration due to gravity. In your case, P is atmospheric
pressure both at the top and at the bottom, I will choose y=0 at the
bottom so y=h at the top. Therefore Bernoulli's equation becomes Vtop2+2gh=Vbottom2
or Vbottom=√(2gh+Vtop2).
There are two ways that Vbottom
![]() QUESTION:
QUESTION:
I sent you $20 before I even
asked the question. This should tell you that I am very interested in the
answer. I am way passed school age. This is just for me.
This is a velocity question: The projectile is 25 inches long, 1/2 inch in diameter and weighs 1750 grains. Absolutely the most aerodynamic it can be. It will have a guidance system that will include a very small fin in the front and back. I know this is going to mess up the aerodynamics a bit but I am looking for an
answer as close as you can approximate.
How high would this "Arrow" need to be dropped in order to reach terminal velocity and just how fast is terminal velocity? What if the projectile weighed 3500 grains, would this change the velocity or would that only change the kinetic energy on impact? I know barometric pressure, humidity, crosswinds, temperature and the like will affect the speed. Just use an average day...which there aren't any...but something like neutral.
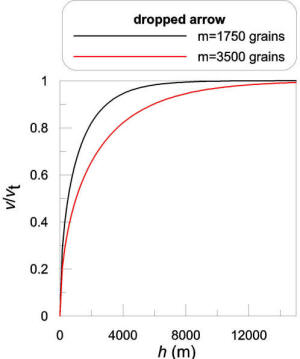 As I read that over, I realized I am asking what the fastest terminal velocity could be of the most aerodynamic object ever in free fall.
As I read that over, I realized I am asking what the fastest terminal velocity could be of the most aerodynamic object ever in free fall.
![]() ANSWER:
ANSWER:
It is ill-advised to make a donation before receiving an answer because if a
question makes no sense, I cannot answer it and have no means of returning
your money. In your case, there are some misconceptions and you need to
understand that the key word in your question is "approximate". All air-drag
questions can only have approximate solutions. Your main misconception is
that there is no such thing as "the most aerodynamic object ever". A
second misconception is that you will ever reach the terminal
velocity; the analytical solution to the problem has the terminal velocity
reached only after infinite time and I will use 99% of the terminal velocity
as having reached full speed. Since I have no information at all about the
detailed shape of the object, I will simply use a generic form for the air
drag F which can be assumed to be well approximated as a quadratic
function of velocity for this case, F=-cv2 where c
may be approximated as c≈—ėA, A being the cross
sectional area presented to the wind (the negative sign indicating that F
is opposite v). This approximate value of c is valid only if
SI units (meters, seconds, kilograms) are used.
Now, the solutions. I will not give full details since they are fairly
mathematical. Convert, first, to SI units: L=25"= 0.635 m, R=0.25"=0.00635
m, m1=1750 grain=0.1134
 kg, m2=3500
grain=0.2268 kg, A=πR2=1.267x10-4 m2,
F=(3.167x10-5 N)v2. To calculate the
terminal velocity vt, find when the drag force is equal to
the weight mg (g=9.8 m/s2): mg=cvt2,
vt=√(mg/c)=√(4mg/A); I find
vt1≈187 m/s and vt2≈265 m/s. The height
h from which you would have to drop these to achieve this speed with no
air drag is given by h=vt2/(2g), so h1no
drag=1780 m and h2no drag=3560 m. Now, if
air drag is included in the calculations, it can be shown (see any
intermediate-level classical mechanics text) that v/vt=√[1-exp(-2gh/vt2)].
Now, setting v/vt=0.99 and solving for h, I
find h1=6989 m and h2=14,034 m. I have
shown a graph with the velocity relative to the terminal velocity v/vt
as a function of the height h from which it was dropped. Keep in mind
that these calculations are approximations as explained above; I have tried
to give enough details so that you could vary the parameters if you like, in
particular the drag coefficient c and the ratio of v/vt.
kg, m2=3500
grain=0.2268 kg, A=πR2=1.267x10-4 m2,
F=(3.167x10-5 N)v2. To calculate the
terminal velocity vt, find when the drag force is equal to
the weight mg (g=9.8 m/s2): mg=cvt2,
vt=√(mg/c)=√(4mg/A); I find
vt1≈187 m/s and vt2≈265 m/s. The height
h from which you would have to drop these to achieve this speed with no
air drag is given by h=vt2/(2g), so h1no
drag=1780 m and h2no drag=3560 m. Now, if
air drag is included in the calculations, it can be shown (see any
intermediate-level classical mechanics text) that v/vt=√[1-exp(-2gh/vt2)].
Now, setting v/vt=0.99 and solving for h, I
find h1=6989 m and h2=14,034 m. I have
shown a graph with the velocity relative to the terminal velocity v/vt
as a function of the height h from which it was dropped. Keep in mind
that these calculations are approximations as explained above; I have tried
to give enough details so that you could vary the parameters if you like, in
particular the drag coefficient c and the ratio of v/vt.
![]() ADDED
COMMENTS:
ADDED
COMMENTS:
I came across a more detailed discussion of the drag forces for cylinders if
you are interested. You will be referring to the picture to the left above
for the following discussion. First, I need to discuss the definition of
c above more carefully. In more detail, c=–ÖρACd
where ρ is the density of air which is about 1.2 kg/m3 at
standard pressure and temperature and Cd is a number
(called the drag coefficient) which depends only on the geometry. Note that
for my calculations above the drag coefficient was Cd=—ėA/(–Öx1.2xA)=0.6.
The graphs above show that the drag coefficient depends on the ratio of L/d=L/(2R)
which has a value of 50 for your projectile. So, if your cylinder has a
blunt end,
Cd≈0.81
(c≈0.6xAx0.81=0.49¬∑A≈–ÖA)
and, for a rounded end,
Cd≈0.4
(c≈0.6xAx0.4=0.24¬∑A≈—ėA).
So, the calculation above is likely a good approximation to your
"… most
aerodynamic object…" My whole treatment of this problem, though, assumes
that c is a constant. However, as you can see above, c depends
on the air density and the air density depends on altitude. Surely at values
of h around 7 km or 14 km, the air density is much smaller than at
sea level and therefore c is much smaller and the terminal velocity
is much larger; this makes the problem considerably more difficult requiring
numerical solutions, beyond the scope of this web site.
![]() QUESTION:
QUESTION:
So if two cars were to hit each
other head on, what would be the best way to minimize danger? Would you slow
to a stop, go faster, or match the other cars speed? My sister says that you
would match the speed, because if you stopped you would absorb all of the
impact. My dad says you would stop because then the only force being put out
would be the other car.
![]() ANSWER:
ANSWER:
What hurts you is the force you feel. What determines the force you feel is
your acceleration, your rate of change of velocity during the collision. To
minimize acceleration, you should minimize the relative velocity between you
and the other car which means stopping would be best, but certainly any
braking before the collision will help. This assumes that the duration of
the actual collision does not depend on the relative speed which is probably
roughly true.
![]() QUESTION:
QUESTION:
I am interested in the effects of gravity on objects of the same mass in different configurations. Example:
Three long objects of the same mass, for the sake of example, three 6 foot 2x4 boards.
If I take two of the boards and lay them parallel, the gravitational attraction between them should be equal at all points.
However, if I arrange the three boards in a U shape, does the additional mass connecting the bottom of the two boards at the U cause the attraction to increase by only the amount of the additional mass (the third board), in other words, does the base of the U and the tips of the U retain the same gravitational attraction with regard to each other?
Or does the addition of the connecting mass at the base of the U change the attraction of the parallel boards and if so is it in decreasing effect along the parallel boards from the connected base to the tips of the U?
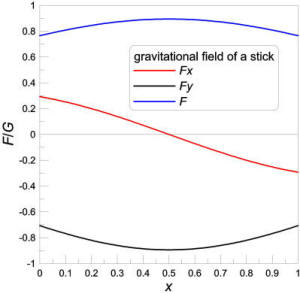
![]() ANSWER:
ANSWER:
First of all, it is not really clear what you mean when you say "…the
gravitational attraction between them should be equal at all points…"
The force felt by one little piece of mass on one board due to the other
board should be the same magnitude as the other board experiences; their
directions, however, will not be opposite each other except at the centers.
If we approximate your boards as thin sticks (pretty good since 2"<<72" and
4"<<72"), it is fairly easy to calculate the force experienced by a very
small piece of mass m in either board due to presence of the other
board for your parallel configuration; it is a little messy, so I will
not write it here. This force will have both an x-component and a
y-component. The graph to the left shows Fx and Fy
as well as the magnitude of the force, F=√(Fx2+Fy2)
for sticks of mass 1 kg, length 1 m, and separated by 1 m to illustrate; I
have chosen x=0 at the left end of the stick and x=1 at the
right end. I have normalized the forces to the gravitational constant G.
On the right you can see the forces on each stick at the ends and centers
(red shows the components). The addition of other masses, like your third
board, will not alter the forces between these two sticks but will certainly
alter the force felt by any mass on these sticks; I guess the answer to your
question is that the force which one board exerts on another is not changed
by adding more boards. Still, we are normally interested in the net
gravitational force on something, not just the force which one other object
of many exerts on it. (Incidentally, note that m will also experience
a force due to the rest of its own board.) You might be interested in an
earlier answer concerning gravitational
fields of cylinders
![]() QUESTION:
QUESTION:
Is tension a scalor or a vector
qunatity? While considering a rope why do we take into account its magnitude
and not direction? Plz clarify.
![]() ANSWER:
ANSWER:
Tension is the force which a rope or string exerts. Since it is a force, it
is a vector. Probably the reason you are confused is that, unlike most
unknown forces, you always know the direction of the tension force: it is
always in the same direction as the string and always pulls, never pushes.
So, when you solve a problem involving tension, the only unknown thing about
a tension force is its magnitude which is a scalar. So it might seem like
you are treating tension like a scalar, but you are not.

![]() QUESTION:
QUESTION:
This is a classic point of contention for pilots, and has recently come up again. I'd like to know your take on this. It seems more often than not, that the answer is the plane will take off. However, no one from that side of the argument addresses the force of the conveyer in the opposite direction canceling forward force from the engine thrust. I don't see how the aircraft could accelerate from a starting velocity of 0kts.
This question has grown men lobbing profanity-laced insults back and forth. The answers are generally not backed by aerodynamics or physics equations.
I am graduating from Embry-Riddle in August with a major in Aeronautics. I'm well past my aerodynamics class, so this is certainly not homework for me, but it is most interesting nonetheless. Without further delay, here is the question:
Imagine a 747 is sitting on a conveyor belt, as wide and long as a runway. The conveyor belt is designed to exactly match the speed of the wheels, moving in the opposite direction. Can the plane take off?
![]() ANSWER:
ANSWER:
My goodness, this is pretty basic physics and should not be a puzzle at a
school which has aviation as its main focus. In order for an airplane to
fly, lift must be generated. During takeoff, lift is almost entirely the
result of air passing over the wings and if the airplane is not moving
relative to the air, there is no lift. The engines, if you could point them
vertically, could provide lift and cause the airplane to "take off" if their
thrust were greater than the weight of the airplane. I looked up the maximum
thrust for a 747 and it is only a little greater than
—ė the weight. This is no
different than an airplane revving up its engines with the brakes locked. It
will certainly not be able to take off. Vertical takeoff planes like the
Harrier (pictured above) can do this, not conventional ones. A final
thought: if you had your 747 on the conveyer belt pointed into a very high
wind, it could take off, but since the takeoff speed of a 747 is around 180
mph, there are no such winds even in a hurricane.
![]() QUESTION:
QUESTION:
If im holding a box connected to a non stretching rope to my hand and i start accelerating upwards ( gravity pulls down ) How would i describe a tension in a string if my acceleration is increasing with time ( defined by some function ). This is not homework i swear. I just cant seem to equate all this.
![]() ANSWER:
ANSWER:
If the mass of the box is M and its acceleration is a, then
T-Mg=Ma (Newton's second law) so T=M(g+a).
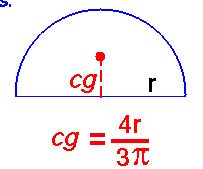
![]() QUESTION:
QUESTION:
If a circular disk has one half of heavier metal and other one of heavier metal. Would the centre of gravity and centre of mass different? Gravity is uniform. And in uniform gravity , does same mass bodies have their c.g and c.o.m equal?
![]() ANSWER:
ANSWER:
The center of mass and center of gravity are coincident if the gravitational
field is uniform (the same everywhere across the object). The center of mass
of a uniform half disk of radius R is a distance d=4R/(3π)
from the center of the straight edge diameter. If the mass density is ρ
and the thickness of the disk is t, the mass is M=ρtπR
![]() QUESTION:
QUESTION:
I have seen in your site these
questions about guns portrayed in
science fiction and you have done calculations for the recoil of these
things. So I have a question on how do I calculate the Gs that the recoil
causes? Let's use an example. If I have a ship with a mass of three million
tons and it has a six hundred meter long mass accelerator gun that fires a
twenty kilogram projectile at 2000km/s, how much recoil do I get from that?
![]() ANSWER:
ANSWER:
The speed, 2x106 m/s, is very small compared to c=3x108
m/s, so we can use classical mechanics and galilean kinematics. Assuming
that the projectile accelerates uniformly, 600=–Öat2
and
2x106=at; solving, a=3.3x109 m/s2
and t=6x10-4 s. The force on the projectile during the
6x10-4 seconds is F=20x3.3x109=6.6x1010
N. Newton's third law says that the ship (mass 3x106 metric
tons=3x109 kg) will experience an equal and opposite force during
this time, so aship=6.6x1010/3x109=22
m/s2=2.2g. The speed acquired by the ship is (20/3x109)x(2x106)=1.3
cm/s.
![]() QUESTION:
QUESTION:
Is there an equation that tells the period of rotation of pendulum with two masses placed at different distances from point of pivit?
![]() ANSWER:
ANSWER:
You must mean period of oscillation, not of rotation. The period of any
pendulum can only be approximated for small angle oscillations. Your problem
would have M1 a distance L1 from the
pivot and M2 a distance L2 from the
pivot. The moment of inertia of the pendulum is I=M1L12+M2L22.
It is a standard introductory calculation to show that the period T
of a pendulum is T=2π√[I/(MgL)]
where M is the total mass and L is the distance from the pivot
of the center of mass. In your case, M=(M1+M2)
and L=(M1L1+M2L2)/(M1+M2).
Putting it all together,
T=2π√[(M1L12+M2L22)/(g(M1L1+M2L2))].


![]() QUESTION:
QUESTION:
I have a question about the CoM on a rider and a bicycle.
The popular narrative or meme is that while riding a bike, with your hands on top of the bars, if you then move your hands to the 'drops' on road bike handlebars, that this lowers the CoM.
Personally, I do not believe it because we are talking about the riders shoulders and hands moving downward about 2-3".
![]() ANSWER:
ANSWER:
First of all, any drop at all of part of the mass of the object (even 2-3 inches) will result in a drop of the center of mass of the object. However, usually the drop is substantially more than just the distance from the top to the bottom of the handlebars because the cyclist also bends his arms at the elbows as shown in the figures above. Of course there is also the reduced air drag when in the lower position.
![]() QUESTION:
QUESTION:
I've seen the "battleship in a bathtub" physics illustration, in which we imagine a battleship in a bathtub just barely big enough to hold it (a one foot clearance on the sides and bottom). We are told that indeed the battleship will float with this seemingly minimum amount of water surrounding it. If this is true, how does that coincide with the fact that an object will float only if it displaces more than its own weight in water?
![]() ANSWER:
ANSWER:
Just because you cannot see the displaced water does not mean water has not been displaced to make room for the battleship. If the water in the tub were at the same level but the battleship missing, the volume occupied by the battleship would now be filled with water. Now, put the battleship in the tub and the displaced water will spill over the side of the tub.
![]() QUESTION:
QUESTION:
I am a state trooper here in NC. I was struck by a commercial full sized bus on December 24 2014. This bus was the size of a (trailways bus) . They pulled the recorder from the bus and determined the speed to be 69.5 mph. After impact my vehicle which was stationary in the road (hit from behind) traveled 180 feet after impact. Could you tell me how many g's that I endured. I was knocked unconscious.
![]() QUERY:
QUERY:
It is impossible to do more than a rough estimate with this information. I do need to know were you in gear or parking brake on so that you skidded rather than rolled?
![]() RESPONSE:
RESPONSE:
Photo of my 2007 Chevy Tahoe which
would have had about an extra 700 pounds of equipment. This was a 2 wheel
drive vehicle. Parking brake was off I believe. In reference to my question
about how many g's did I experiance in the accident. Struck from behind by
commercial bus. My Tahoe traveled 170 feet after impact. Final rest was on
rt grassy shoulder of roadway. I was hospitalized for 6 days at Duke
Hospital.
![]() ANSWER:
ANSWER:
First, be clear that what I can do is an order-of-magnitude calculation, making reasonable approximations. It should not be considered as an accurate calculation, for example something which would be used in a court of law. The bus would have a weight of about 28,000 lb≈12,700 kg and your Tahoe would have a mass of about 6000 lb≈2700 kg. Your car slid d=170 ft=52 m; the coefficient of sliding friction between rubber and dry asphalt I will take to be about μ≈0.65. First estimate the speed v which your car acquired in the collision: change in kinetic energy=work done by friction, –Ömv2=μmgd; solving this I find v≈26 m/s≈58 mph. Now, what is going to matter regarding the acceleration of the car (and you) is the time t which the collision lasted. Assuming that the acceleration was approximately constant over this time, a≈v/t≈26/t. To approximate t, use kinematics of uniform acceleration, s=–Öat2=–Öx(26/t)t2=13t where s is the distance the car moved during the collision which I will estimate from your picture to be the amount by which the car lost length during the collision, maybe about 10% of the approximate length of a Tahoe of about 5 m or about 0.5 m. So, t≈0.5/13≈0.038 s and so a≈26/0.038=421 m/s2≈421/9.8≈43 g. Again, keep in mind that there are lots of uncertainties, for example:
-
If the road were wet or much of the sliding was done in the grass, μ would have been smaller which would have resulted in the speed after the collision being slower which would have resulted in a smaller acceleration. If μ were only half as large, a≈33 g.
-
If the distance over the time of the collision were larger, the time would have been larger and the acceleration smaller. If s≈1 m, a≈22 g.
-
If both 1 and 2 are applied, a≈17 g.
In any case, you suffered quite an acceleration! Note that the folks on the bus experienced only about 2700/12,700=21% the acceleration you did.
![]() QUESTION:
QUESTION:
Is there a formula or equation something for vertical mass versus hortizontal mass. I work for a granite company, we have a forklift that's weight limit is 6,000 Lbs that is not a problem holding the slabs vertically however we have to place slabs horizontally on a flat table with suction cups. We bought a 7 foot boom to attach to the forklift. I just want an illustration of the inverse relationship of vertical and horizontal weight supported by physics.
![]() ANSWER:
ANSWER:
There is certainly not anything like horizontal and vertical mass. Mass is mass. What is going to matter to you for your problem is where the center of gravity (COG) of your load is and that will determine what the torque which will be exerted on the forklift; this torque will tell you whether you can lift the load without tipping the car. What you want not to happen is what is shown in the left-hand picture. I think that you can intuitively tell that the farther out the load is located, the likelier the forklift is to tip. The picture on the right shows how you need to think about the problem to plan for the car not to tip over the front wheels. What you need to know is where the COG of the car without the load is and where the COG of the load is; in the picture, these locations are where the little pinwheels are. The weight of the load is WL and its COG a distance DL from the front axle; the weight of the car is WC and its COG a distance DC from the front axle. The torque due to the load is TL=WLDL and the torque due to the car weight is TC=WCDC. As long as TC is greater than TL, the forklift will not tip over. Now you can see why things are different for a long slab loaded vertically and horizontally‚ÄĒsince the COG of a uniform slab is at its geometrical center, DL, and therefore TL, is much bigger for horizontal. Many cranes and forklifts have a lot of weight added toward the back to allow the load to have bigger torques; note in the figure that the COG of the car is near the rear implying added weight back there.
![]() QUESTION:
QUESTION:
From what I understand, when an elastic spring is stretched, the energy done to stretch it is stored as elastic potential energy in the spring. Also, there is a limit of proportionality where the spring will no longer go back to its original shape. Therefore, when I stretch a spring and the energy is stored, when I let go, the energy stored is transferred to kinetic energy when it goes back to its original shape. My question is, what happens to the stored energy in a spring when the spring has reached its limit of proportionality? The energy stored isn't transferred to kinetic energy as it doesn't go back to its original shape so where does it go?
![]() ANSWER:
ANSWER:
The spring is comprised of atoms which are bound together by molecular forces. You might think of each pair of atoms as being connected by tiny springs. When you stretch the spring, you are pulling pairs of atoms farther apart and each tiny stretch takes work and therefore stores energy. When you release it, each pair of stretched atoms pulls back to its original distance. But there are limits to how far you can stretch a bonded pair of atoms before the bond will be broken. The "lost" energy was used to break bonds between atoms. If you want to get more microscopic, just focus your attention on one pair of iron atoms, with total mass M. You pull them until they break apart; you have done some amound of work, call it W. But, you started with and ended with two atoms at rest, so what happened to the energy you put in? It turns out that if you had a sensitive enough scale you would find that the mass of the two separated atoms was no longer M but was slightly bigger, M+m. And, invoking Einstein's most famous equation, m=W/c2. No energy in a closed system is ever lost!
![]() QUESTION:
QUESTION:
You may have answered this before, but I could not find it by searching the site. Assume there are two objects in space separated by some relatively large distance. Assume object 1 to have the mass of the sun and object two the mass of a typical 100 meter iron asteroid. Assume the separation distance to be approximately 100 million kilometers. There is currently a fictional force preventing object 2 from accelerating towards object 1 and the relative velocity between the two objects in any other direction is zero. Now the fictional force disappears and object 2(asteroid) starts accelerating towards object 1(sun). I am wondering what the formula would be to determine the final velocity for object 2 as it impacts object 1. I know that object 1 has a gravitational acceleration that depends on the distance from it at 1/r–Ü but I am unsure how to put this formula together as both that number and the velocity are changing as r shrinks ‚Äď the velocity continues to climb as it gets closer due to the gravitational acceleration of the sun getting larger
![]() ANSWER:
ANSWER:
This is fairly easy using potential energy. The gravitational potential energy for a mass m whose center is a distance r from another mass M is U(r)=-MmG/r where G=6.67x10-11 N¬∑m2/kg2. The potential energy has been chosen so that U(0)=0 for r=∞. From the example you give, we can assume that M>>m and therefore M will remain at rest. You also need to know the radii of m and M, call them RM and Rm. So, the initial energy is E1=-MmG/r1 and the final energy is E2=-MmG/r2+–Ömv2 where r1=1011 m and r2=RM+Rm. You can do all the arithmetic if you like, but I am betting that an excellent approximation would be to take E1≈0 and Rm<<RM, so 0≈-MG/RM+–Öv2 or v≈√(2MG/RM). If you put in M and RM of the sun you find v≈6x105 m/s. This is also the escape velocity from the survace of the sun.
![]() QUESTION:
QUESTION:
If a Flea was dropped from the top of the eiffel tower what would happen to it?
![]() ANSWER:
ANSWER:
A flea has a very small terminal velocity which means that air drag force up on him will equal his own weight after he has achieved a very small speed. If the air were calm, he would drift slowly to the ground and arrive unhurt. If there were a wind, he might land blocks or miles from the base of the tower. Think of dropping a feather‚ÄĒsame idea.
![]() QUESTION:
QUESTION:
If everyone on Earth were to begin running due east at an appointed time, would the Earth slow in its rotation, even slightly? If so, would that reduction in speed be reversed once everyone ceased running (transferring their momentum back to the globe), or would the day have permanently become longer?
![]() ANSWER:
ANSWER:
Let's have a look at the numbers. Suppose that there are about 7 billion people with an average mass of 80 kg. The radius of the earth is about 6.4x106 m. So their moment of inertia is about MR2=7x109x80x(6.4x106)2=6.5x1024 kg¬∑m2. It would actually be quite a bit less than this because most of the earth's population resides at a distance less than 6.4x106 m from the axis of rotation, but let's just suppose everyone went down to the equator for this little game. If we approximate the earth to be a uniform sphere with mass of 6x1024 kg, its moment of inertia would be about 2MR2/5=2x6x1024x(6.4x106)2/5=9.8x1037 kg¬∑m2. The disparities are enormous and there would be no way you could ever notice any change. Let's look at an extreme case where everyone is running just as fast as the whole earth is moving and in the opposite direction (they would be running west). So, the initial angular momentum is the total moment of inertia 6.5x1024+9.8x1037 kg¬∑m2 times the initial angular velocity, 1 revolution/day. The final angular momentum would just be moment of inertia of the earth (all the people are no longer rotating) times the new angular velocity, call it ω. Then conserving angular momentum, (6.5x1024+9.8x1037)x1=9.8x1037ω or ω=1+6.5x1024/9.8x1037=(1+6.6x10-14) revolution/day. This means that the day would be longer by 0.0000000000066%. And, yes, in an idealized world where the people and the earth were the only things in the universe, the earth would speed back up again when everybody took a rest.
![]() QUESTION:
QUESTION:
Could an 8x12-inch sheet metal sign mounted on a 5-ft tall metal stanchion set in a 5-gal pail of concrete weighing 75 pounds be knocked over by a 30-mph gust of wind?
![]() ANSWER:
ANSWER:
Well, that would depend on things you have not told me, the geometry of the pail and also on the mass of the sign+stanchion. I can estimate the force on the sign due to the wind, call that F. This will result in a torque of 5F ft∙lb. I will work in SI units and then convert back to imperial units; A=96 in2=0.062 m2, v= 30 mph=13.4 m/s. The maximum force on the sign would be approximately F≈—ėAv2=—ėx0.062x13.42=2.78 N=0.625 lb. So now you can do a little experiment: push on the sign with a force of about 2/3 lb and see if it tips over. I suspect, if the base is broad enough, it will not tip over.

![]() QUESTION:
QUESTION:
I would like to know the measurements of each dimension of
a boat if the total weight of the boat were to carry 300 pounds. Also, we plan to make a canoe like shape so if you can help us know the measurements for that shape we would be very thankful.
![]() ANSWER:
ANSWER:
This is too vague. Lots of possible dimensions would do the trick. You also need to specify the weight of the boat, not just the load. The important thing is that the buoyant force must be equal to the weight of the boat plus load. The buoyant force is the weight of the water displaced by the floating boat. For example, if the boat itself weighs 100 lb, the boat must have the volume which 400 lb of water would occupy; the density of water is about 62.4 lb/ft3, so the volume of the boat would need to be 400/62.4=6.4 ft3. For example, suppose you model your canoe as a triangular prism as shown to the left where h=b and l=6 ft; its volume is –Öhbl=3h2=6.4, so h=1.5 ft. Of course, this would not be a good design since the surface of the water would be right at the gunnels of the canoe, just about to spill in; you would want to build in a safety factor by making the volume of the canoe quite a bit bigger than 6.4 ft3.
![]() QUESTION:
QUESTION:
My young son would like to know how fast something would have to move in order to defy gravity. Thanks! He's 10 and would like to become a physicist.
![]() ANSWER:
ANSWER:
The phrase "to defy gravity" does not really have any meaning. If you mean that if something goes fast enough you can make gravity go away, that does not happen. More likely you mean how fast does something have to be going to completely leave the earth and never come back, as in "everything which goes up must come down (except when it doesn't!)" This speed is called the escape velocity. The mathematical expression for escape velocity is ve=√(2MG/R) where M and R are the mass and the radius of the planet, respectively, and and G is Newton's universal constant of gravitation. This comes out to be about 7 m/s=25,000 mph for the earth. For a more detailed discussion (probably over the head of a 10 year old), see an earlier answer.
![]() QUESTION:
QUESTION:
Why does angular velocity act only the in case of circular motion?
I mean that if I see a car moving in a straight line(while I am in rest) still the angle subtended by the car at my eye changes (as the car approaches me) since theta is changing with time then there should be angular displacement, and accordingly angular velocity, shouldn't be?
![]() ANSWER:
ANSWER:
You are certainly right. You may describe the motion of any particle by specifying angular velocity relative to some axis; you must also express the velocity the object has radially away from (or toward) that axis to fully describe the situation. In the figure to the right, an axis has been chosen and the line from the axis to the car has a length r at this instant; the velocity v of the car has been resolved into radial (vr) and tangential (vθ) components. The rate at which r is changing is what vr is. The rate at which θ is changing is the angular velocity, ω=rvθ. If the car happened to be moving in a circle around the axis, vr=0.
![]() QUESTION:
QUESTION:
I have recently started flying quadcopters (QC) and on a forum I frequent, someone mentioned that by placing the battery of their QC on top of the frame rather than below it they felt that the QC quote "went from Buick to Porsche in responsiveness" Since I found this an interesting assertion I looked at the physics of the situation with my high school physics mentality and came up with this possible explanation. Note it is over 40 years since I left high school by the way, :-) and am just wondering what you think about my hypothesis and if you would care to venture your thoughts on the physics of this situation. My tongue in cheek explanation that accompanied the diagram read as "Correct me if I am wrong, it wouldn't be the first time. The quad pivots around point x and with the battery at the bottom in posn B the distance B is greater than the distance A which is the CG of a battery in posn A. Therefore to overcome the inertia of the posn B battery requires more force than overcoming the inertia of a battery in posn A. This makes the quad more responsive with the battery in posn A. Anyway that is my hypothesis but if I start believing my own BS then let me know"
![]() ANSWER:
ANSWER:
This is not quite as simple as I though it was going to be! I will give you the full-blown "physics talk" explanation. First, it will not have any effect on linear acceleration because all that determines that is the total mass of your QC and the force you can get from the propellers. However, moving the center of mass (COM) will have an effect on angular acceleration, the rate at which you can cause it to turn. The appropriate equation to understand this is Newton's second law in rotational form, torque τ equals the moment of inertia about the COM Icm times the angular acceleration α, τ=Icmα or α=τ/Icm. The torque due to each propeller is the force it exerts times the distance from C/L to the propeller shaft. The moment of inertia about the COM of the whole thing is what you need because the whole QC in flight will rotate about its COM. Everything depends on Icm, and the smaller you can make it, the greater angular acceleration you can get for a given torque. The farther away the battery is from the COM of the QC, the greater Icm will be. So to have the most responsive handling, you want to find the COM of the QC without its battery and put the COM of the battery right there. I am guessing that battery position A is closer to the COM of the QC without battery than battery position B is. If the mass of the battery is much less than the mass of the QC, the "Porsche‚Ķresponsiveness" is an illusion.
![]() QUERY:
QUERY:
It would be helpful if you could give me the relative masses of the QC without battery and the battery.
And also where the COM of the QC without the battery is located. I assume it is on the C/L, but how far from the airframe labeled on your diagram?
![]() REPLY:
REPLY:
The relative mass of the QC is 20 grams without the battery and 28 grams with the battery. The
COM of the QC without the battery is located on the C/L, but as to how far from the airframe labeled on my diagram I cannot answer. My whole hypothesis, for want of a better word is based on my assumption that if the left hand propeller is exerting an upward thrust and the right hand propeller a downwards thrust simultaneously, the the QC will rotate around point x.
![]() ANSWER:
ANSWER:
Your assumption, as I explained in the first answer, that it rotates
about x is not correct; it rotates about the COM wherever that is. It
may appear that it is rotating about another point because the overall
motion may be described as the sum of translational motion (along
a straight line) of the COM and rotational motion around
the COM. The mass you state cannot be correct since 20 gm is less than
an ounce; but this does not matter because to answer your question all I
need are the relative masses of the QC and the battery. As explained
above, the battery being a significant amount of the total mass (nearly
1/3), its placement will be important. So the whole key is that the
moment of inertia about the COM of the whole vehicle is lowest when the
two centers of mass are as close together as possible; this results in
the maximum angular acceleration for a given net torque.
![]() QUESTION:
QUESTION:
I'm a writer working on a nonfiction book that concerns climate and landscape, and am seeking help understanding a phenomenon I am hoping to explain to lay audiences in this book.
A hot air balloon pilot I interviewed described a near-crash. On a calm morning, this pilot took a family on a short flight over some meadows, not far from a geothermal plant. While preparing to land, the pilot's balloon was drawn uncontrollably towards the geothermal plant, where it was trapped in the column of hot air rising over the plant, like a ping pong ball over a hair drier. I am trying to understand what might have caused the balloon to be drawn towards this rising column of air. The pilot did not accidentally pass over the geothermal plant, but rather the balloon was uncontrollably sucked into the column from the side.
![]() ANSWER:
ANSWER:
This is a manifestation, I believe, of the Venturi effect which says, in essence, that the pressure in a fluid decreases as the velocity increases. It is just a special case of the Bernoulli equation, P+–Öρv2+ρgy=constant. In cases like this balloon, Bernoulli's equation will not give you precise results because it is valid only for incompressible ideal fluids which air certainly isn't. However, it is excellent for qualitatively understanding many things which happen in moving fluids. Examples of the Venturi effect abound. An airplane wing generates lift because air passes over the top faster than over the bottom resulting in a net upward pressure. A spinning baseball curves because the pressure on one side is greater than the other. A sheet of paper rises when you blow across the top (see picture). Although you do not see this so much any more, if smokers inside a moving car crack the window, the smoke will be drawn out by the lower pressure of the outside air rushing past. In the case of the balloon, the column of hot air is rising whereas the air around it is still, so objects near it will feel a force drawing them into the column.
![]() QUESTION:
QUESTION:
I came across a question in the back of the chapter that asked: "Because a smaller mass results in greater air resistance effects on a ski jumper, all other things being equal a lighter ski jumper flies farther than a heavier one."
According to the book the answer is true. My question is why?
![]() ANSWER:
ANSWER:
There are two forces on a ski jumper, his weight W and the force of air drag on him F. The weight is always a force which points vertically down and is proportional to the mass m. The air drag always points opposite the skier's velocity and depends only on the velocity magnitude, the properties of the air, and the shape of the skier, but not his mass. Shown in the figure are the force diagrams for the heavy (#1, leftmost) and light (#2) skiers when they are going up. (I have chosen an extreme case, the heavy skier about twice the mass of the light skier, to emphasize the difference. Everything else about the two is identical.) Each force results in an acceleration (shown as the green-dashed vectors) which result in net accelarations shown by the full-drawn green vectors. The lighter skier has a larger drag acceleration because the acceleration is F/m and both have accelerations due to their weights which are equal. But looking at the horizontal and vertical of the net acceleration, both are larger for the light skier‚ÄĒhe is losing forward speed faster and is accelerating toward the ground faster. Also shown in the figure are the force diagrams for the heavy (#3) and light (#4, rightmost) skier when they are going down. Now, the lighter skier still has a larger horizontal component of acceleration, he is slowing down faster, and his vertical component is perhaps just slightly smaller. I would conclude that your book is wrong, the heavy skier jumps farther. Consider the following experiment to demonstrate that the heavier will have a larger range using two balls of the same size, say a baseball and a baseball-sized nerf ball. Throw them each as hard as you can and projected at about the same angle; which would you expect to go farther? In fact, there is an analytical solution (approximation) for the range R of a projectile: R=[v02sin2θ/g)[1-(4v0sinθ/(3g))(C/m)] where v0 is the speed at launch, θ is the launch angle, and C is a constant which depends only on the size and shape of the projectile. Note that R gets larger as m gets larger.
You forgot about the air in the jar which weighs Z. I have answered
this kind of questions many times, usually we have birds in a box. It
all boils down to Newton's third law. Assume the jar is on a scale, fly
on the bottom. The scale reads X+Y+Z. Now suppose the fly
hovers or flies with constant velocity. To do that the air must exert an
upward force of Y on the fly; but that means the fly exerts a
downward force of Y on the air; but that would have to mean that
the air now exerts a downward force of Y+Z on the jar. So, again,
the scale reads X+Y+Z. Now suppose the fly has an upward acceleration a. To
do that, the air must exert an upward force of Y+(Y/g)a=Y(1+(a/g))
where g is the acceleration due to gravity; it then follows that
the scale will read X+Y(1+(a/g))+Z. Similarly,
if the fly has a downward acceleration of a, the scale will read
X+Y(1-(a/g))+Z.
If the fly is in free fall in the jar, the scale will read X+Z.
My answer ignores buoyancy of the fly and, when he is in free fall, air
drag. If we consider air drag, when the fly in free fall has reached
terminal velocity the scale will, again, read X+Y+Z.
We often think of putty balls colliding when we think of perfectly
inelastic collisions. The balls collide, squish together, and then stick
together. Think about squishing a putty ball‚ÄĒdoes it take any work? Of
course it does. Can you get that work back? Not a chance. What happened
to it? the ball got a little warmer. Or think of a colliding ball as a
spring. That makes sense because a rubber ball will compress and then,
when you quit pushing on it, go back to its original shape. So, you put
some energy into it. If it were an ideal ball-spring and you just let go
of it, it would oscillate from squished to stretched back and forth
forever. Does it do that? Of course not because it is not an ideal
ball-spring and that energy you put into it eventually (actually very
quickly) all disappears (becomes a bit of thermal energy in the ball).
So, even balls which do not stick together usually have some
inelasticity when they collide. But, when balls collide, what is the
force which does the squishing work? It is the force which one exerts on
the other and the other exerts on the one; Newton's third law tells you
that these have to be equal and opposite, so momentum is conserved even
if energy is not. Billiard balls are very good (and very stiff) springs
and collide almost elastically.
It would make more sense for your question to ask about either force, as
the original question did, or power, the rate
of delivering energy. If the mass is 104 metric tons, the
weight would be about F=108 N; that would be the force
you would need to exert to lift the submarine. If you were lifting at
the rate of v=10 m/s, the power P required would be about
P=F∙v=109 W=1 GW. A gigawatt is a typical
output for a nuclear power plant.

![]() QUESTION:
QUESTION:
I caught a fly in an empty jar and sealed it with lid. Container weighs X. Fly weighs Y. When the fly alights on the bottom, I assume the container now weighs X + Y. If the fly takes flight does the same hold true.
![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:
Hello, I am a junior in highschool, and I am currently studying about momentum in physics. I am a bit confused with the concept though. I get it is related to newton's laws and it is mostly used for collisions. I also learned this week about impulse and collisions and conservation of momentum.
So now my teacher explained that for momentum to be conserved the net force acting on an object must be 0. That's because Ft=deltap (so if f is 0 then change in momentum is 0 so it is conserved) Now we then took about inelastic collisions and that K.E is not conserved because some is changed to hear or other forms of energy. So I've also learned previously that deltaKE=Wnet so if there is change in KE there is work and therefore a force so how then is there a net force acting in inelastic collisions but still momentum is conserved ??
![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:
I just saw the question in your page about super powered people telekinetically lifting objects and how Newton's laws have something to say about that.
So that rose me a question about the thing. Lifting the submarine should require enormous amounts of energy, and this would naturally mean that a super powered individual who uses his or hers powers to lift an object such as a submarine would need to have some borderline magical energy production methods far surpassing anything biology gives to any creature.
So if we assume that the sub marine weighs ten thousand tons, how much energy would Magneto need to lift it at the speed of let's say ten meters per second? And how does that relate to energy consumption of a normal human, and would even a nuclear reactor be enough to produce the necessary energy for lifting the submarine?
![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:
I understand that, with a roughly spherical object, like the earth, the gravitational force tends to act on objects towards the centre of the sphere.
What would the direction of the force be with an object shaped like a cylinder? Also would the gravitational pull be greater on each end of the cylinder than at some point in the middle? (In which case I would guess that, in nature, any massive cylinder would collapse to form a sphere?)
![]() ANSWER:
ANSWER:
The gravitational field of a cylinder is pretty easy to calculate on its axis and very difficult to calculate elsewhere. At the center of each end of a cylinder of length L and radius R, the field g can be shown to be gend=[GM/(RL)][(2L/R)+–Ö-–Ö√(R2+L2)/R]. Let me first provide a qualitative argument that the field at the "poles" will be larger than at the "equator". At the equator, the contribution to the field from each piece of mass in one half will have a corresponding piece on the other side and their axial components will cancel out, leaving only the radial components. As long as L>R, there will be much less cancellation for fields at the "poles"; therefore, if the cylinder is not rigid, it will collapse to a sphere axially (from the poles). If L<R, this argument will work in the opposite way and you would expect the collapse to be radially in from the equator. Next, here is an approximate analytical solution for the case L>>R. The end fields can be approximated as gend≈3GM/(2R2). At the equator, Gauss's law may be used to show that gequator≈2GM/(LR). So gend/gequator≈3L/(2R)>>1. So, your expectation was right, but only if R<L. On the other hand, if R>>L, the field at the pole approaches the field at the center of a uniform disk which is zero by symmetry. So, whatever the field is at the equator, the force tends to collapse the cylinder radially (inward from the equator). The details of the calculations here are given in a separate page where I have also shown a rough sketch of the field for the L>R case.

![]() QUESTION:
QUESTION:
Built my kid a marshmallow shooter for a science project. Simple design. Main air chamber is 2" pvc
with a total length (including bend) of 32". It is then directed into a 3/4" inch
pvc pipe with 2 valves. The first valve (1) is the main shut off valve and inch or two from the 2" chamber. Then there is another
21" of 3/4" pvc into the 2nd valve (2). The barrel is 1/2" pvc and 24" long. We can fill the gun with 40 psi with both valves closed. We then open valve 1.
Pressure should drop a little, but not much. We then close 1 to preserve pressure and shoot marshmallows with almost 40 psi. They will go 40'. When we fill the tank with 40 psi with valve 1 open and valve 2 closed and shoot it, it'll shoot the marshmallow 100' or more. My question is:
why is releasing all the air at once shooting the marshmallows further? It's
driving me nuts. Is it the volume of gasses? How can I mathematically solve
this mystery?
![]() ANSWER:
ANSWER:
It is pretty easy to understand this qualitatively. As the
marshmallow moves down the barrel, the volume of the gas behind it increases
so the pressure decreases. Your first case (valve 1 closed) there is a
pretty big fractional increase in volume so, since PV is constant, a
pretty big decrease in the final pressure; in the second case (valve 1
open) there is a much smaller fractional increase in volume so there will be
a much smaller decrease in the final pressure. The average force felt by the
marshmallow over the length of the barrel will be bigger for the second
case.
Now, let's do it analytically. I will ignore the couple of inches between the main chamber and the first valve. The operative principle is that if temperature and amount of gas are unchanged, the product of the pressure and volume is a constant or, equivalently, Vinitial/Vfinal=Pfinal/Pinitial. An important thing to keep in mind is that 40 psi is the gauge pressure, the pressure above atmospheric pressure which is about 15 psi; so Pinitial=55 psi. The volume of each section is π(d/2)2L where d is the inner diameter of the pipe (a 3/4" pipe, e.g., specifies the diameter). So Vbarrel=4.7 in3, Vprimary=100 in3, Vsecondary=9.3 in3. In the first case Vinitial=Vsecondary=9.3 in3 and Vfinal=Vsecondary+Vbarrel=14 in3. Therefore Vinitial/Vfinal=0.66=Pfinal/Pinitial and, taking Pinitial=55 psi, Pfinal=36 psi and the corresponding gauge pressure is 21 psi; so the average gauge pressure during firing was (40+21)/2=30 psi. In the second case, Vfinal=Vsecondary+Vbarrel+Vprimary=114 in3 and Vinitial=Vsecondary+Vprimary=109.2 in3. Going through the same procedure as the first case, Pfinal=53 psi and the corresponding gauge pressure is 38 psi; so the average gauge pressure during firing was (38+40)/2=39 psi. This means the average force on the marshmallow was 81% greater for the second case; this means that the speed of the marshmallow is almost twice as great, so it is roughly in agreement with your measurements of a distance of 100' compared to 40'. I have not considered air drag during the flight after leaving the gun which will be fairly important for a marshmallow. Also, I have ignored friction between the marshmallow and the barrel; because of this and neglect of air drag, don't expect real good quantitative predictions of range.
![]() ADDED
NOTE:
ADDED
NOTE:
In the first case where you pressurize to 40 psi and then open
valve 1, the pressure will drop more than just a little as you expect. Vinitial/Vfinal=100/109.2=0.92,
so Pfinal=55x0.92=51 psi, so the final gauge pressure will
be about 36 psi, about a 10% drop.
![]() QUESTION:
QUESTION:
There's a weight standing equally on 2 legs, each of which is on a scale.
Each scale shows half the weight. If we disappear one of the legs (assume
it' stable and won't fall over.), the entire weight should transfer to the
remaining leg. Does it transfer instantly, or is there a time lag? If
there's a time lag, why? I say there's a time lag (but I can't explain why)
and my friend says it's instant.
![]() ANSWER:
ANSWER:
Generally, nature does not like discontinuities so you should always assume
first that "instantaneous" is not possible. That, indeed, is true for the
situation you describe. The two-leg scenario has some problems which
complicate things (like the center of mass is not directly over either scale
so removing a leg will result in a torque trying to tip the object over).
So, I will use a simpler problem, equivalent for your purposes. Imagine that
a weight sits on a scale. Now you place a second identical weight atop the
first. The information that the second weight has been added gets
transmitted at the speed of sound (in the first weight) to the scale. This
will still be a pretty short time, but not zero. I have ignored the time it
takes the scale to respond.

![]() QUESTION:
QUESTION:
Why is it that when my daughter spun the lazy Susan on our table, the salt shaker
went flying off?

![]() ANSWER:
ANSWER:
An object which is going in a circle requires a force to keep it
going in a circle. Imagine that you are spinning a stone attached to a
string in a horizontal circle. The force which keeps it going in a circle is
the string pulling on it. As you make it go around faster and faster, the
string has to pull harder and harder. Eventually the string can no longer
pull hard enough and breaks and the stone goes flying away. When the lazy
Susan is spinning the salt shaker is moving in a circle and therefore needs
a force to keep it going in a circle. The force which keeps it going in a
circle is friction between the lazy Susan and the shaker; if the lazy Susan
were very slippery, it would not be of much use. As it spins faster and
faster, you will need more and more friction but there is a limit to how
much friction you can get; think of trying to push a heavy box on the
floor‚ÄĒyou push harder and harder and eventually it will start moving. So, at
a high speed the shaker will fly off. Tell your daughter to not spin it so
fast! Or maybe she just likes to make it fly off. Good thing it wasn't a
glass of milk.
![]() QUESTION:
QUESTION:
When a gas is pressurized (in favorable conditions) it turns into liquid.
Further pressurizing it turns into solid. Now I exert larger pressure on
a uniform solid (form all directions). What will happen?
Also what will happen if I subject a fundamental particle to very large
pressure?
![]() ANSWER:
ANSWER:
Very large pressures can change the properties of the material
and new phases may occur (like water and ice are two different phases of H2O).
A particularly good example is water itself as shown in the figure to the
right; pressures up to about 10,000,000 atmospheres are shown in the graph
and numerous phases beyond ice/water/steam are seen at high pressures or
very low temperatures. For higher yet pressures, you need to look to stars.
If a star is massive enough it will, after going through a supernova stage,
collapse under the pressure of its own gravity to where electrons are pushed
into the protons and the whole star becomes a neutron star, essentially a
gigantic nucleus. If heavy enough, it will continue collapsing into a black
hole. What individual particles do depends on the pressure and they
essentially will retain their identities or undergo reactions with other
particles (as in the neutron star formation) or lose their identities (in a
black hole).
![]() QUESTION:
QUESTION:
An astronaut rotates in space an observes the universe rotating about them. How does the astronaut know whether the universe is rotating, or if it is their own motion causing that visual spin? Centripetal forces, of course, which will force blood into the fingertips which will surely be detectable in the astronauts frame of reference. Perhaps this suggests that there exists a universal state of rotational rest - detectable by measuring existence or absence of centripetal forces. Is there also a more general universal state of rest? A state that can be also measured and agreed on by any stationary or moving frame of reference? What do we already know about that has a velocity that can be measured and agreed on by all reference frames, even those with different relative velocity? What do we know of that, like zero, has an ultimate limit that cannot be exceeded? Could the speed of light actually be that universal rest frame?
![]() ANSWER:
ANSWER:
First of all, it is centrifugal force, not centripetal, which
causes blood to be pushed to extremities. But that is not important here.
There are two kinds of reference frames, inertial and noninertial. If you
are in an inertial frame of reference, Newton's laws of physics are true. A
noninertial frame is any frame which accelerates relative to any inertial
frame. Because Newton's laws are not valid for your rotating astronaut,
blood flows out to the fingertips even though there is nothing pushing it
out; that is why you will see centrifugal force referred to as a "fictitious"
force.
There is no preferred reference frame, no "absolute at rest."
![]() QUESTION:
QUESTION:
I am reading a scifi novel and in it gravity is simulated by constant thrust from the engines. If there is no inertia in space would not the spacecraft continue at that speed and therefore the gravity remain constant until the ship used thrusters to slow it down? In the novel, if the thrust is cut off the gravity is reduced. I can't get my head around it?
![]() ANSWER:
ANSWER:
When you are in a car which is accelerating you feel as if you
are being pushed back against the back of your seat; this is like a
horizontal "artificial gravity" and is the effect which causes the
artificial gravity when your spacecraft is burning its engines. When the car
stops accelerating and moves with constant velocity in a straight line, you
no longer feel that you are being pushed back; similarly in the spaceship
when you cut the engines. I have no idea what you mean that there is no
inertia in space. Inertia means resistant to change in velocity if acted on
by a force, so if the engines are not burning you feel weightless; gravity
is not "reduced", it disappears. It sounds like you think that you need to
push on the spacecraft to keep it going with a constant speed and nothing
could be further from the truth. Newton's first law (the law of inertia)
says that an object on which no net force acts will move in a straight line
with constant speed forever.
![]() QUESTION:
QUESTION:
If a gun is fired in space, how far/long will the bullet travel and how long will it spin? Why? Assumptions: 1) gun’s position is fixed relative to the earth; 2) gun’s barrel is rifled, thus the spin; 3) bullet travels in unobstructed straight line and it avoids being attracted to another body due to that body’s gravity.
In one of your earlier answers regarding the relative motion of a gun and bullet in space you say that the bullet would never stop traveling. I suppose that, in my question above, this also means that the bullet would spin forever as well?
This confuses me as it would seem to me that motion requires energy, which would eventually be depleted. What am I misunderstanding?
![]() ANSWER:
ANSWER:
I will first answer your last question. What you are
misunderstanding is Newton's first law which states that an object which
experiences no net force will move in a straight line with a constant speed;
also, a rigid body which experiences no net torque about its axis of
rotation through its center of mass will continue rotating with the same
rotational speed about that axis. With these you should understand the
answer to my previous answer and also why (your addition) it will spin
forever. The only proviso is that there is nowhere in the universe where
there is a perfect vacuum, always a few atoms around, and so there is always
a tiny amount of friction which would stop your bullet after maybe billions
of years. (Also, your supposition that "…it avoids being attracted to
another body due to that body’s gravity" cannot be literally true because
gravity is everywhere.
![]() QUESTION:
QUESTION:
This link is a video of anti gravity and
I want to know on how it really works?
![]() ANSWER:
ANSWER:
This one is pretty easy to debunk, I believe. The guy and all
the apparatus are upside down; the camera taking the video is also upside
down.
![]() QUESTION:
QUESTION:
If you have 2 plastic balls with the same outer surface but one is filled with water and the other one is empty and you released them, from rest, down the same slope, the ball with the water would accelerate more due to viscous flow right? If that is the case then would a ball that is fairly (but not completely) filled with sand accelerate faster than the empty ball and why? would there be a similar effect?
![]() ANSWER:
ANSWER:
There is no clear cut simple answer to this question. I prefer
to use energy conservation to look at problems like this. Let's first just
consider a hollow sphere and a solid sphere. If we have an object with mass
m, radius R, and moment of inertia (about center of
mass) I, it is easy to show that the speed of the object when it has
rolled down so that its vertical drop is h is given by
v=√[2mgh/(m+(I/R2))].
The moments of inertia are
Isolid=2mR2/5 and Ihollow=2mR2/3.
First note that the mass will cancel out, so
vsolid=√(10gh/7) and vhollow=√(6gh/5)<vsolid
and so the solid sphere is the winner.
Now, suppose a hollow sphere, mass m, radius R, moment of inertial I=2mR2/3 is filled with a fluid of mass M. (I assume that the spherical shell is very thin compared to the radius of the ball.) There are two extremes of what can happen, either the fluid does not rotate at all as the ball rolls (a superfluid) or else it begins rotating with the ball almost immediately (maybe molasses). In the first case, when the ball reaches the bottom its rotational kinetic energy will be all due to the rotating of the ball, its translational kinetic energy will be due to the both the ball and the fluid, and the potential energy at the beginning will be due to both:
–Ö(2mR2/3)(v2/R2)+–Ö(M+m)v2=(M+m)gh.
Solving, I find
v=√[2gh/(M+(5m/3))];
notice that if M=0, v=vhollow as it should,
so any nonzero M will result in losing to the hollow sphere. At the
other extreme, the fluid rotating rigidly the whole way, the energy
conservation equation will be
–Ö(2MR2/5)(v2/R2)+–Ö(2mR2/3)(v2/R2)+–Ö(M+m)v2=(M+m)gh.
Solving, I find
v=√[30(M+m)gh/(24M+25m)].
This can be compared with vhollow:
v/vhollow=√[(1+(M/m))/(1+(24M/25m))]
which is always greater than 1 (the denominator in the square root is
smaller than the numerator). Again, note that for M=0, v=vhollow.
Therefore the filled ball will always win if the fluid rotates.
Now, to your question. Water will be at neither of the extremes above. It will begin by not rotating, so in a race with a hollow ball, the hollow ball will jump off to a lead. After some elapsed time, all the water will be rotating with the ball containing it, so it will be now be gaining speed faster than the hollow ball and be catching up. Eventually, the water ball will catch up and pass the hollow ball; so, you see, which ball wins will depend on how long the race is. The way you state the sand part of the question is problematical "……fairly (but not completely) full…" is not very quantitative. Let's just say that it essentially fills the ball but is loosely enough packed so that it can slide over itself. In that case, the sand will act pretty much like a very viscous fluid and will get fully rotating with the ball more quickly than the water did. In both cases (water and sand), trying to do a analytical solution while the fluid is in the transition stage from not rotating to rotating is just about impossible; because of the effects of friction (viscosity, if you like), energy is not conserved during that time.
![]() QUESTION:
QUESTION:
If you were standing on a flat platform that was free falling from the sky let's say 12000 feet up and right before impact within a certain point, or say within 12 feet, and you jump vertically off the platform, what would happen to you? Would it decrease your speed and your impact or would it just delay you hitting the ground?
This question was asked to me by my friend and we both are very curious. We have a few thoughts on the outcome but aren't sure and we really want to know for sure. Hopefully you will be able to answer this for us thank you.
![]() ANSWER:
ANSWER:
I answered a similar question in an old
answer, jumping in a falling elevator. There is no way that jumping can
save you because the amount of upward speed you could give yourself is tiny
compared to your downward speed. What would happen depends on the mass of
the platform. If the platform had much less mass than you, most of your
effort would be to speed up the platform rather than slow you. If it were
much heavier than you, you would still only be able to reduce your downward
speed by about 3-4 m/s. Of course, if the platform were big enough it would
act like a parachute and you would not have to worry about a thing!

![]() QUESTION:
QUESTION:
I am building a customizable "cat highway" of wooden shelves in my living room. The issue I am having is figuring out how much holding force I need, rather than how much weight the actual shelf can support. I know the shelves are plenty strong enough. Now I need to have them fastened strongly enough to the wall. It would be easy, if all I had to consider was the maximum weight a shelf has to take, if all three cats were to lie on it at once. However, I also need to how much weight I have to budget for for impact force - both from a descending and an ascending cat.
As there isn't room for multiple cats to jump up or come down at one time, so only the weight of the heaviest cat (3.26587 kg) needs to be used for the calculations. Also, there will not be a height of more than 0.5 m from one shelf to another, nor a distance of more than 0.5 m between one shelf and another. I can't guarantee that they won't skip a shelf, so it might be safer to double the maximum distances just to be safe.
![]() ANSWER:
ANSWER:
Normally I answer such questions by "you cannot tell how much
force results if an object with some velocity drops onto something". The
reason is that the force depends on how quickly the object stops; that is
why it hurts more to drop on the floor than to drop on a mattress. In your
case, however, we can estimate the time the cat takes to stop because we can
estimate the length of its legs which is the distance over which it will
stop. You are probably not interested in the details, so I will give you the
final answer: assuming constant acceleration during the stopping period, the
force F necessary to stop a cat of mass m, falling from a
height h, and having legs of length ℓ may be approximated as F=mg(1+(h/ℓ)).
E.g., if h≈0.5 m and ℓ≈0.1 m, F≈6mg, six times
the weight of the cat.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Thank you for your answer!
I thought you might want to know that, unlike a lot of people, I AM actually interested in the details.
![]() ANSWER:
ANSWER:
OK, here goes: I will use a coordinate system with increasing
y vertically upward and y=0 at the landing shelf. The cat will
have acquired some velocity -v when his feet hit the shelf. Assuming
he stops after going a distance ℓ and accelerates uniformly, we have the two
kinematic equations 0=ℓ-vt+–Öat2 and 0=-v+at.
From the second equation t=v/a; so, from the first equation,
0=ℓ-v(v/a)+–Öa(v/a)2=ℓ-–Öv2/a
so a=–Öv2/ℓ. Now, as the cat is landing there are
two forces on him, his own weight mg down and the force F of
the shelf up, -mg+F and this must be equal, by Newton's second law,
to ma, so F=m(g+–Öv2/ℓ). This, by
Newton's third law, is the force which the cat exerts down on the shelf.
Finally, the speed if dropped from a height h is v=√(2gh),
so F=mg(1+(h/ℓ)).
![]() QUESTION:
QUESTION:
Imagine the inside of a spacecraft, in orbit, so astronauts experience weightlessness and things float with no friction etc (assume there is no atmosphere in the craft ...). A pencil is floating in mid-air inside the craft. An astronaut pushes (say flicks with a finger) the pencil on one of its very ends. This push will impart linear, rotational, or both types of motion to the previously stationary floating pencil? If the pencil should rotate, about what axis does it rotate and how is angular momentum conserved?
![]() ANSWER:
ANSWER:
There will be very small effects due to the fact that this is
not true "weightlessness" in that the spacecraft is accelerating in a
gravitational field and not of zero size. I take it that this kind of detail
is not what you are interested in, that I can simply answer your question
for the pencil being in empty space, initially at rest. I will suppose that
the pencil has mass m, moment of inertial I about its center
of mass which is a distance d from the end where a constant force
F is applied, perpendicular to d, for a very short time t.
Newton's second law for translational motion says that the impulse equals
the change in linear momentum, Ft=mv; after the impulse, the center
of mass will move in the direction that F was applied with speed
v=Ft/m. Newton's second law for rotational motion says that the angular
impulse equals the change in angular momentum, τt=Ftd=Iω; after the
impulse, the pencil will rotate around the center of mass with an angular
velocity ω=Ftd/I. A relationship between v and
ω can be written as ω=mvd/I. You can also write the total
energy of the pencil, the sum of translational and rotational kinetic
energies, as E=–Ömv2+–ÖIω2.
For example, if the pencil is modeled as a uniform stick of length
L, I=mL2/12 and d=L/2, so ω=mv(L/2)/(mL2/12)=6v/L
and E=3mv2/2; in this case, 2/3 of the kinetic
energy is due to the rotation. Also, the speed u of the end of the
pencil with respect to its center is u=Lω/2=3v. Regarding
angular momentum, Iω, it is conserved after the initial "flick"
because there are no torques on the pencil.

![]() QUESTION:
QUESTION:
In light of the recent deflated football scandal, is there a way to mathematically calculate the change in pressure as the temperature inside the ball changes? Would you assume the volume of the bladder inside the ball to change very little?
![]() ANSWER:
ANSWER:
Yes, the ideal gas law, PV/(NT)=constant where
P is pressure (not gauge pressure), V is the volume,
N is the amount of gas, and T is the absolute temperature.
Assuming that V and N remain constant, P/T=constant.
Let's do an example. Suppose that the ball is filled to a gauge pressure of
13 psi when the temperature is 700F. The absolute pressure is 13
plus atmospheric pressure 14.7 psi, P1=13+14.7=27.7 psi.
The temperature in kelvins (absolute) is 700F=294 K. Now suppose
we cool the football to 100F=261 K. Then, 27.7/294=P2/261,
P2=24.6 psi, and the resulting gauge pressure is
24.6-14.7=9.9 psi. I guess it is important to fill the ball at the
temperature at which it will be played.
![]() ADDED
NOTE:
ADDED
NOTE:
An article in the January 30
New York Times came to essentially the same conclusion as I did here. My
answer was posted on January 26. I was astounded to read in that article,
though, that initial calculations by physicists had applied the ideal
gas law using gauge pressure rather than absolute pressure! Shame on them!
![]() QUESTION:
QUESTION:
If a train is traveling at 60 m/s and a person runs and jumps off the rear of said train (opposite direction of travel) at 3 m/s. Which direction would the person travel?
Would they continue to move in the opposite direction of the train, move with the train at relative speed, or drop straight downward?
![]() ANSWER:
ANSWER:
Variations on this question are probably the most frequent
question I answer. I always say that you always have to specify velocity
relative to what. In your question, I take it that the velocity of the
train relative to the ground is 60 m/s and the velocity of the person
relative to the train is 3 m/s in the opposite direction as the train's
velocity. The velocity of the person relative to the ground is 57 m/s in the
direction of the train's velocity. An observer on the ground would see the
person with a horizontal velocity of 57 m/s regardless of whether he was on
the train or had jumped off the back. Once he is off the train he will begin
falling and hit the ground with both horizontal and vertical components of
his velocity. For example, if he starts at a height of 2 m above the ground,
his vertical component when he hits the ground will be about 6.3 m/s so his
total speed will be √(572+6.32)=57.3 m/s.
![]() QUESTION:
QUESTION:
If aluminium and copper pipes are of same length and diameter ... same magnet is dropped through them ...in copper it takes more time to come out of other end, i myself have done this... please answer why is it so?
![]() ANSWER:
ANSWER:
Aluminum has an electrical conductivity of about 3.5x108
Ω-1m-1 and copper has a value of about 6x108
Ω-1m-1. Therefore, at any speed, the magnet will
induce a larger current in the pipe for the more conductive copper.
![]() QUESTION:
QUESTION:
Newton's third law of motion states that, "To every action there is equal but opposite reaction". That means if i throw a ball on a wall it will bounce back but then what happens to mud, if i throw mud on a wall then
it does not it bounce back?
![]() ANSWER:
ANSWER:
The mud and wall still exert forces on each other during the
collision. The force which the wall exerts on the mud causes an acceleration
of the mud which has the effect of stopping it as per Newton's second law.

![]() QUESTION:
QUESTION:
Is there is any situation which fulfills the first condition of equilibrium but not second condition of equilibrium?
![]() ANSWER:
ANSWER:
Of course. Consider a uniform stick of which has opposite forces
on its ends, both perpendicular to the stick
![]() QUESTION:
QUESTION:
I understand the bullet leaving the gun at high velocity and bullet dropped from end of barrel at zero horizontal velocity hit the ground at the same time (assuming level ground etc.) but I have a different one. Two bullets leave the same barrel and we do not figure in anything other than level. One has twice as much mass as the other (so it needed more energy to get to the same velocity). So assuming they have the same shape and aerodynamics I think the air friction will act the same and they both hit the ground at the same time. But, others in my group think it doesn't seem right. What is the right answer?
![]() ANSWER:
ANSWER:
I do not understand your phrasing "…leave the same barrel and we
do not figure in anything other than level…" I will just assume that the two
bullets begin simultaneously at the same height with the same speed and in
the same direction. The force of air friction is determined by the shape of
the projectile, so each will experience the same force at any particular
speed. But the force F on the heavier bullet will result in a smaller
acceleration a than for the lighter bullet because of Newton's second
law, a=F/m. Therefore the lighter bullet will slow down faster
and hit the ground earlier. You can understand this intuitively with an
extreme example. Imagine a spherical balloon and a spherical cannonball of
the same size both projected horizontally at 100 mph. Which do you think
will hit the ground first?
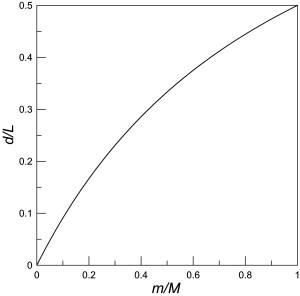
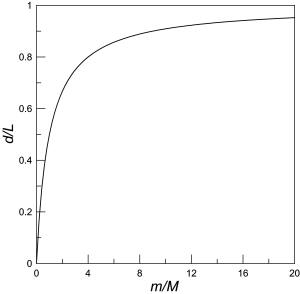
![]() QUESTION:
QUESTION:
I doing some work with model rockets and I am trying to understand more about the center of mass. Specifically what happens to the center of mass as more weight is added. I understand that the center of mass begins to move nearer to where the weight was added, but as I continue to add more weigh does the movement become larger or smaller? My observation is that it becomes larger, but I've read another document that suggest it should be come smaller. I'm having a difficult time finding other comments on the topic. I would appreciate any help you can provide. I'd like to understand if my observation is incorrect and if so - maybe understand why.
![]() ANSWER:
ANSWER:
Suppose the mass of the rocket before you start adding mass is
M and that the center of mass of the rocket is a distance L
away from where you will adding mass. If you start adding mass m, the
center of mass will move away from M and toward m such that it
will be a distance d from M. Then the equation for the center
of mass is d/L=(m/M)/[1+(m/M)].
The graph to the left is for no mass added (obviously, d=0) up to
m=M (d=L/2). To answer your question, note that as m
increases, the slope of the curve decreases, that is the rate of change of
position of the center of mass decreases. As m gets bigger and
bigger, the center of mass approaches d=L, and so clearly it will the
rate at which the position changes gets smaller. The graph on the right is
plotted up to m=10M so you can see this happen.
![]() QUESTION:
QUESTION:
I'm doing an assignment on helicopter flight, and I'm a little confused about the Bernoulli principle. He said that if a pipe is bigger at the beginning and smaller at the end, the fluid traveling through the end of the pipe would have a lower pressure.
This seems counter-intuitive. I would have thought that there would be more pressure on the fluid that's "squeezed in together". I don't think I fully understand the concept of pressure.
![]() ANSWER:
ANSWER:
Let's first write Bernoulli's equation, P+–Öρv2+ρgy=constant.
At any point in the fluid P is the pressure, ρ is the density,
v is the speed, g is acceleration due to gravity, and y
is the distance relative to some chosen reference point (above, y>0,
below y<0). Maybe it would help you to accept this if I tell you
that Bernoulli's equation is simply conservation of energy. Since To answer your question we can ignore the y part,
it is a horizontal pipe, P+–Öρv2=constant. You
should also understand that this equation is exactly true only under
idealized conditions:
-
An incompressible fluid (water is a very good approximation)
-
Laminar flow which means flowing smoothly, no turbulence
-
Irrotational which means there is never any local circulation like whirlpools.
-
There must be no viscosity or other kind or friction
What goes on around a helicopter blade satisfies none of these conditions! Nevertheless, Bernoulli's equation can be a very useful approximation to understand what is going on even if it is not exactly correct. The most important one for aerodynamics is that which you cite, that when v increases, P increases. I have struggled to come up with a way you could understand this intuitively, but don't seem to find a simple explanation. You should convince yourself that your intuition is wrong by doing some experiments. For example, notice that inside a moving car the smoke from a smoker is drawn through a cracked-open window because of the lower pressure outside where the velocity is higher. Or, do the old blowing on the piece of paper demonstration.
![]() QUESTION:
QUESTION:
I'm working on a story and I'm trying to give a correct scientific explanation I can as justification for the character's powers.
My questions are regarding speed and its various effects.
Considering a human of mass 60kg can move at the speed of 200 m/s to 300 m/s, and can accelerate and decelerate at the same rate as the acceleration of bullet fired at muzzle velocity (that is almost instantly)
-
What is the effect of drag at that speed on a human?
-
How much energy is required to gain this speed with the above mentioned acceleration and deceleration rate and weight moving for 50 meters?
-
What is the effect of G-force on the human?
-
How much kinetic energy will the human produce when moving at such speed?
-
Will the human be clearly visible (or observable) to another normal human, moving at such speed?
![]() ANSWER:
ANSWER:
This is really a ridiculously impossible scenario! I will assume
that v=250. I will not include all the details of the calculations.
-
You can estimate drag force as F≈—ėAv2 where A is the cross sectional area. If we take A≈2 m2, F≈3x104 N. With this force acting, the power (rate of energy loss) is about P=Fv=8x106 W=8000 kW. This would cause him to burn up, I would guess. I estimate that, if there were not some force to keep him moving, he would lose 90% of his speed in about 4 s.
-
He has an energy of –Ömv2=2x106 J. The acceleration and distance are irrelevant.
-
I took an M16 rifle as an example. The muzzle velocity is about 1000 m/s and the barrel length is about 50 cm, so I calculated that the acceleration would be about 106 m/s2, about 100,000 g. The maximum which the human body can withstand for short times is about 10 g. The time to accelerate the bullet would be about 10-3 s.
-
This makes no sense. The body has kinetic energy but does not produce it. Because of the drag, it loses kinetic energy to heat.
-
Your speeds are about the same as a commercial airliner, 500-600 mph, and there is certainly no problem seeing them.

![]() QUESTION:
QUESTION:
I am looking to find out at what speed an object (object 1) was traveling while hitting an other object (object 2) and pushing it straight ahead.
Object 1 was traveling straight, rubber wheels on asphalt (no skid marks), had a weight of 4500 lbs, and hit the object 2 with a weight of 3000 lbs at a 90 degree angle (side impact, rubber
sliding on dry asphalt). Object 2 was pushed 50 feet. I am looking for the formula to calculate
the speed of object 1 at impact. I know there are several factors involved and I do not need a exact number,
just an approximate but fairly close value.
![]() QUERY:
QUERY:
I take it that car 2 was at rest initially and that the two
remained in contact the whole time (since you said "pushed"). Also, that car 1 did not apply brakes.
![]() REPLY:
REPLY:
Yes that is correct - object 2 was at rest and object 1 did not apply
brakes.
![]() ANSWER:
ANSWER:
I prefer to work in SI units, so I will transform back to mph in
the end. The masses of the cars are about m1=4500 lb≈2040 kg and
m2=3000 lb≈1360 kg. The coefficient of kinetic friction for rubber
on dry asphalt is in the range 0.5-0.8, so I used μ=0.65. The
acceleration due to gravity is g=9.8 m/s2. The distance
pushed is d=50 ft≈15
m. The frictional force F acting on the two cars as they slide is due
only to the friction between the wheels of car 2 sliding on the
asphalt is F=μm2g=0.65x1360x9.8=8660 N. The work
done by this friction was W=-Fd=-8660x15=-130,000 J. This took away
the kinetic energy K the two vehicles had just after the collision,
so K=–Ö(m1+m2)v2,12=1700v2,12=130,000,
so v2,1=8.7 m/s≈20 mph; this is the speed the two cars had
immediately after impact. Finally, use momentum conservation to get the
speed of car 1 before the collision: m1v1=(m1+m2)v2,1=2040v1=3400x8.7=29,600
k∙m/s, and so v1=14.5 m/s≈32 mph.
![]() QUESTION:
QUESTION:
A motorcyclist strikes an automoble that turns directly in front of him. The motorcyclist had locked his brakes and was traveling at @ 30 to 35 mph when he struck the front left fender of the automobile and went over the top of his widnshield at approx. 5 feet. It the motorcylist weighs 210 lbs. how far would he have traveled before he struck the ground?
![]() ANSWER:
ANSWER:
There is no way to calculate this with the information you have
given me. All I can tell you is the absolute maximum distance he would go if
launched with a speed of about 30-35 mph at 450 angle to the
horizontal, about 25 meters. It would certainly be less than this since he
would lose some kinetic energy in the collision and would not be launched
with a speed as great as he came in with and he would likely be launched at
another angle.

![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I'm actually thinking that for me to clear a 5 foot windshield directly in front of me from a sitting position about 15 inches behind that windshield and from a sitting position my launch angle was very close if not more than 45 degrees. If that is the case, loss of kinetic energy is the only limiting factor to the distance I traveled before landing on my shoulder on the other side of the car. Is the loss of kinetic energy linear to the distance traveled? In other words if I lost 1/3 of my kinetic energy in the crash would the distance traveled be equal to 1/3 less distance? 25 meters is 82 feet minus 28 feet equals 54.
![]() ANSWER:
ANSWER:
OK, here is the full equation if you want to play around with
it: R=v2sin(2θ)/g where R is the
horizontal range in m, v the speed of launch in m/s, θ is the
launch angle, and g=9.8 m/s2 is the acceleration due to gravity;
this is for the projectile landing at the same level where it was launched
from, not really exactly true but of minimal consequence since we are only
doing a rough calculation. 30 mph=13.4 m/s, so you can put in any speed as
vm/s=0.45vmph.
For θ=450, R=v2/g. To answer your
question, the distance is not proportional to speed, rather to the square of
the speed. So, if you lost 1/3 of your speed (30 mph) in the collision your speed
in m/s would be v=20x0.45=9 m/s, so R=81/9.8=8.3 m≈27 ft. This is
more realistic, I believe, than 25 m which would be predicted for 35 mph.
![]() QUESTION:
QUESTION:
Most physics texts that I read state that a net torque tends to produce rotation - certainly true in case of a sphere rolling down an incline (friction produces the torque and this results in rotation). However, consider a particle of mass m in the XY reference frame, acted upon by a force F in a direction along the X axis producing an acceleration a = F/m. Let us assume that the mass m is located at (x= 0, y = y0) from the origin. Then there IS a net torque on the mass m (seen about an axis perpendicular to the XY plane passing through the origin) given by (y0) multiplied by F (angle being 90 deg). But mass m undergoes NO rotation! It simply translates in the direction of F. What's confusing for me - is there a definite criterion defining the situation when a net torque would produce rotation and when it would not.
![]() ANSWER:
ANSWER:
The example you stated is the simplest to understand because
this force is perpendicular to its moment arm and so the torque is τ=Fy0.
First of all, a point mass cannot, by definition, rotate about an axis
through itself. If you calculated the torque about an axis ay x=0,
y=y0, you would get zero torque and zero "rotation". I think
you are confusing yourself by saying that a torque causes a rotation. In
fact, a torque causes an angular acceleration about the axis, so you need to
ask whether your applied force causes an angular accleration. Angular
accleration a is related to the acceleration a by
α=at/R where R is the moment arm (y0
in your example)and at is the tangential acceleration, the
component of the acceleration a perpendicular to the moment arm. In your
notation, the acceleration is all tangential and so at=F/m.
Therefore, there is an angular acceleration α=F/(my0)
about the z axis at the instant you start your problem. Even if there
were no force and the mass were just moving with some velocity v in
the x direction right now, it would be considered to be rotating
about the z axis with an angular velocity ω=v/y0.
If you exerted some force which kept it moving in a circle of radius y0
with speed v (that would be a force which had no tangential
component, pointed toward the origin, and had a magnitude mv2/y0),
you would surely say that it was rotating around the origin, wouldn't you?
In general, whenever the velocity has a component perpendicular to the line
drawn to some axis, it has an angular velocity around that axis.
![]() QUESTION:
QUESTION:
From both my high school and university (albeit, introductory at university) physics courses, we've encountered the concept of escape velocity, as the velocity with which an unpowered mass must be accelerated to to escape the gravitational pull of a body.
We've also been given an extra piece of information about this, which is that the escape velocity is the speed at which an object will be accelerated to when it hits the surface of a body, falling from an infinitely far away point.
So here's my question - it seems then that if I sent an unpowered mass at the escape velocity of a body, then (assuming there were no other gravitational factors, etc), then when it reached the 'infinity far away point' it's velocity would equal zero. So, even though you could never reach that point - is that logic valid?
If so, doesn't that mean then that escape velocity is more of a measure of the velocity needed for an unpowered mass to reach x point far away? So then shouldn't it then, if I were to reach a point closer than one infinity far away, why wouldn't I be able to escape with a lesser velocity?
I suspect a flaw in my reasoning above, but I don't know what it is - any and all response would be greatly appreciated!!
![]() ANSWER:
ANSWER:
I am afraid I do not really get your point. But, escape velocity
is a concept somewhat divorced from reality because the universe is not
infinitely large and there are other things in it besides the earth and your
projectile. It is easy to see how the computation of (ideal) escape velocity
can be done. With nothing in the universe but the earth, the total energy of
the projectile at the earth's surface is –Ömv(r=Rearth)2-GMearthm/Rearth
where I have chosen potential energy to be zero at r=∞. Anywhere else
the energy would be –Ömv(r)2-GMearthm/r.
If we choose r=∞ and use energy conservation, –Ömv(Rearth)2-GMearthm/Rearth=–Ömv(∞)2
and the smallest velocity v(Rearth) could be is
called the escape velocity and corresponds to v(∞)=0, so vescape=√[2GMearth/Rearth].
If there were indeed nothing else in the universe and the universe were
infinitly large, this is the speed you would have to give something for it
to never come back. In the real world, interaction with other objects would
affect the speed necessary for the object to never come back, so you should
not think of escape velocity as that speed because escape velocity is well
defined but the speed to escape the real earth is not the same thing.
![]() QUESTION:
QUESTION:
We want to know if a a gun could and was traveling at the speed of light and it was fired would the bullet simply fire as normal or would the bullet refuse to leave the gun?
We have tryed to find a definitive answer elsewhere but can't seem to find one
![]() ANSWER:
ANSWER:
First of all, it is physically impossible for the gun to move
with the speed of light; see my faq
page to find out why. But, I think I can get to the crux of your question by
having your gun move at 99.9% the speed of light, v=0.999c.
Let us suppose the muzzle velocity of the gun were u=0.002c
(which is, incidentally, much faster than any real bullet would travel).
Now, classical physics would have a bystander see the bullet going with a
speed v+u=1.001c, faster than the speed of light. But we know
that this is not possible, so classical physics must be wrong. The correct
formula for velocity addition in
special relativity is (v+u)/[1+(uv/c2)]=1.001c/(1+0.999x0.002)=0.999004c,
just slightly faster than the gun. If you were moving along with the gun,
you would simply see the bullet go forward with a speed 0.002c. All
the above is if the bullet is fired in the direction the gun is traveling.
If you fire the gun backwards from its direction of travel, replace u
by -u and find that (v-u)/[1-(uv/c2)]=0.998996c,
slightly slower than the gun but moving in the same direction. If you were
moving along with the gun, you would simply see the bullet go backward with
a speed 0.002c.
![]() QUESTION:
QUESTION:
I am curious as to how a spoiler on a car somehow provides less wind resistance when driving. One would think that the more surface area against wind would cause more resistance which would slow down the car at a steady RPM.
I don't understand how adding another element that increases surface area would somehow decrease resistance. When I think about it, the less surface area against air flow, the less resistance there would be.
So my question is, do spoilers on cars really work? If they do, how?
I have always been curious about this and have never gotten a straight answer out of somebody that really understands how they work.

![]() ANSWER:
ANSWER:
Well, one might say that "nobody really understands how they
work"! I have "sort of"
answered this question before, but mostly dodged it. Here I will do a
little better, I hope! I can give you a good qualitative explanation but in
terms of being able to design one by just sitting down with some fundamental
equation like Bernoulli's equation, forget it. Fluid dynamics can be
deceptively simple or amazingly complex. To do serious aerodynamic design
requires extremely powerful computers and trial and error wind tunnel
experiments. The things we do to reduce air drag are often counterintuitive
compared to our expectations. With that prologue, let me give you a couple
of simple examples. Our expectations are that an object should be very
smooth and this is often the case, particularly if velocities are not too
large. Your expectation that the increasing area presented to the onrushing
air causes greater drag is reasonable and you will find many examples here
on AskThePhysicist.com where I approximate the drag force as being
proportional to the cross sectional area, e.g. Fdrag≈—ėAv2.
But there are many situations, particularly at high speeds, where this
expectation breaks down and the culprit is turbulence in the air. To
illustrate how turbulence affects drag and how smooth is sometimes not good,
consider a golf ball. Have you ever noticed that a golf ball has dimples?
The purpose of these dimples is to reduce air drag. As shown on the
left above, a smooth ball at a high velocity has a long turbulent volume
behind it; the pressure in this turbulent volume is lower than the pressure
on the front of the ball and this contributes to there being a large net
drag force. If golf balls were nice and somooth, they would die and fall
very much sooner than a dimpled golf ball does. The ball on the right shows
the effect of the dimples; the rough surface induces a layer of turbulence
which actually makes the ball "slipperier" which causes the flow around the
ball to come back together and reduces the volume of turbulence contributing
to drag. (The picture on the right, with most of the turbulence erased,
would be what the smooth ball would look like at low speeds.) The hairs on a
tennis ball serve the same purpose. One other
example is the net you sometimes see replacing the tailgate of a pickup
to reduce the drag the tailgate causes. This, it turns out, is a complete fraud. With
the tailgate closed a bubble of still air forms in the bed of the truck
which deflects the air smoothly over the rear of the truck. So, in your
case, the purpose of the spoiler, very similar to the golf ball dimples, is
to disrupt the smooth flow in such a way that the net effect is less
turbulence behind the vehicle. Incidentally, there is something called the
Reynolds number
which allows you to estimate whether or not turbulence is important.

![]() QUESTION:
QUESTION:
In many fictional works involving superpowered individuals there are people who can lift objects with their minds. Like an example is Magneto lifting a submarine with the magnetic fields he generates in the movie X-Men First Class. From what I remember from high school physics is that because of Newton's third law, all actions produce an equal counteraction. So wouldn't Magneto lifting a submarine with his powers lead to him being heavily attracted by the submarine and flying straight towards it like a bullet and then getting himself completely flattened into a pancake when he crashes with the submarine?
![]() ANSWER:
ANSWER:
You are absolutely right, if he exerts a force on the submarine,
the submarine exerts an equal and opposite force on him. Now, he is on some
kind of aircraft and holding on, so he would have to be superstrong to be
able to hold on since the force pulling him is greater than the weight of a
submarine. And whatever he is holding on to would have to be strong enough
that it could hold more than the weight of the submarine. And the aircraft
had better be able to carry the weight of a submarine. But, maybe his power
is in his left arm so the force would just rip his arm off. Pretty
preposterous, isn't it? Good thinking on your part.

![]() QUESTION:
QUESTION:
Imagine a tank full of water on top of a house with a drain pipe down to the ground. The higher the tank, the greater the velocity and force of water coming out of the end of the pipe. But does the tank drain any faster with greater height? You can't pull on water, so the water leaving the tank shouldn't care how high up the tank is, so the answer must be no. On the other hand, it does seem from actual experience that a bucket will be filled faster from the higher tank. I've even measured this! (Imagine this in a vacuum to bypass any air-pressure effects)
![]() ANSWER:
ANSWER:
The operative physical principle is Bernoulli's equation, P+–Öρv2+ρgy=constant.
Here, ρ is the density of the fluid, P is the pressure, v
is the speed of the fluid, and y is the elevation relative to some
y=0, all at any point in the fluid; g=9.8 m/s2
is the acceleration due to gravity. In your case, P is atmospheric
pressure both at the top and at the bottom (assuming the tank is not
sealed), I will assume y=0 at the bottom and y=h at the top
surface, the speeds at the bottom and top are vbottom and
vtop. Putting these into Bernoulli's equation and solving,
vbottom=√[2gh+vtop2].
Now, if the tank is much bigger than the pipe, usually the case, you can
approximate vtop≈0 and so vbottom≈√[2gh].
An interesting fact: this is exactly the speed the water would have if you
simply dropped it from a height h. (You do not have to imagine a
vacuum since the pressure is easily included and, as here, often the same
everywhere. If the tank were pressurized to a pressure greater than
atmospheric, the water would drain faster.)
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I see the math, but I remain puzzled for this reason: the water flow (in gpm, say) into the pipe (where it connects to the tank) is, obviously, the same as the flow at the bottom end of the pipe. Having constant gpm flow through a constant-diameter pipe necessarily means the water is passing through the entire pipe at the same velocity. So the velocity of the water that’s just entered the pipe must be the same as the velocity of the water that’s about to exit. But Bernoulli’s equation in the form you’ve given implies that the water is accelerating as it flows down the pipe. That would require more gpm out than what went in!
![]() ANSWER:
ANSWER:
No, I am assuming that the tank has water in it and the point I call
y=h in my answer is the top surface of the water in the tank which I subsequently approximate as a much larger area than the pipe.
You could, I guess, let y=h be the top of the pipe but then the
pressure there would not be atmospheric. Then you, as you suggest, would
have to say vtop=vbottom≡v; the
subscript top now means the top of the pipe. So, let's call the depth of the
water in the tank to be d and apply Bernoulli's equation to the tank
only: Ptop+–Öρv2+ρgh≈PA+ρg(d+h)
where I have again approximated the top surface of the tank to have zero
velocity. Then the pressure at the top of the pipe is Ptop≈PA+ρgd-–Öρv2.
Now apply Bernoulli's equation to the pipe: PA+ρgd-–Öρv2+–Öρv2+ρgh≈PA+–Öρv2
or –Öv2≈g(d+h) which you will see is the same
answer as above except h now means the bottom of the water in the
tank rather than the top of the water in the tank.
![]() ADDED
NOTES:
ADDED
NOTES:
Bernoulli's equation is only applicable for incompressible,
nonviscous fluids having laminar (nonturbulent) flow. It is a fairly good
approximation for gases with velocities small compared to the speed of
sound. It is a statement of conservation of energy.
![]() QUESTION:
QUESTION:
In a rotating frame of reference, do the Coriolis force and the centrifugal force act opposite to each other?
![]() ANSWER:
ANSWER:
Certainly not. The centrifugal force always points perpendicular
to the rotation axis. The centrifugal force always points in the direction
of vxω where ω is the angular
velocity and v is the velocity of the particle. It is possible
for the two to point in opposite directions, but not usual. An example where
they do point opposite is shown to the right. You might be interested in a
recent answer.
![]() QUESTION:
QUESTION:
I was trying to calculate the ideal performance of a bow. I wanted to relate the draw weight of a bow to the speed of the arrow after releasing it. And I couldn't do it. The things I have are arrow weight(300 gramms) and the draw weight peak(that means 27kg at 72cm). The draw weight works like this. At 72cm it's 27kg and at 0cm it's 0kg. It is a linear decrease in kg. 27kg at 72cm, 22.5kg at 60cm, 18.75kg at 50cm and so on. And now I wanted to calculate how fast the arrow will fly after shooting it. That means I would like to know how to calculate the speed of an object with a mass of 300g after 72cm of accelerating with a force of 27kg that linearly decreases over 72cm to 0kg. Could you please tell me the formula I need to use to calculate that? I realy would love the learn the way how I have to do it.
![]() ANSWER:
ANSWER:
If the force increases linearly with distance, it is behaving
like an ideal spring. The force F necessary to stretch a spring with
spring constant k a distance x is F=kx. Now, 27 kg is
not a force, it is a mass; but, if you mean that the force is the weight of
a 27 kg mass (which you doubtless must), then F=27x9.8=264.6 N. So,
since x=0.72 m, the spring constant of your bow is k=264.6/0.72=367.5
N/m. The potential energy of a spring stretched by x is –Ökx2=–Ö(367.5)(0.72)2=95.3
J. The kinetic energy of a mass m with a speed v is –Ömv2=–Ö(0.3)v2=0.15v2.
Ideally, all the potential energy of the bow is given to the kinetic energy
of the arrow, so v=√(95.3/0.15)=25.2 m/s≈56 mph. If the arrow is not
launched horizontally, there would be a small correction for change in
gravitational potential energy. I am not sure how good a model this is for a
real bow.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
The reason why I was asking is because I build bows and wanted to find out how good the efficiency of my bows are. And with your answer I found out that the weight of the arrows I mentioned to you and I was using in my own calculatoins was far too high. In the world of archery the arrows are measured in grains instead of grams but I forgot that and used 300 grams instead of 300 grains. So my calculations of the arrow speed were so low that I thought that I made a mistake in calculating. So I asked you. As the speed you calculated was very low too I started asking myself why and found out what mistake I made.
![]() ANSWER:
ANSWER:
300 gr=0.0194 kg, so –Ömv2=–Ö(0.0194)v2=0.0097v2,
so v=√(95.3/0.0097)=99.1
m/s≈125 mph. Incidentally, for easy unit conversion I recommend a free
little program called
Convert.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I understood your answer and started calculating bows to understand how efficient they work. I was very surprised when I calculated the efficiency of a compound bow(http://en.wikipedia.org/wiki/Compound_bow). The bow I used to make my calculations is a 2014 PSE Full Throttle from the Pro Series of PSE Archery (http://pse-archery.com/c/pro-series-compound-bows_full-throttle_full-throttle-black). The IBO-Bow Speed is measured with a speed chronograph with a bow with 70 pounds draw weight, 30 inches draw length and 350 grain arrow (http://www.archeryexchange.com/shopcontent.asp?type=amoibo). The speed measured is 362-370 fps.
The astonishing thing I found out that this compound bow has an efficiency of 110-120% compared to a perfect spring. How is this possible? Is it because of the special mechanical function of the cams(wheels) and the cables? Do these cams and cables use a special leverage provided by the cams to gain more power?
Here is a link to a pdf of a product review of several compound bows:
http://www.arrowtrademagazine.com/articles/july_14/July2014-FlagshipBowReport.pdf . On page 7 there is a draw force curve. And in the article they are talking about efficiency as well. But I don't realy understand what it means (dynamic efficiency and draw cycle efficiency).
![]() ANSWER:
ANSWER:
Actually, I have
previously answered a question about a compound bow which you might want
to look at to get a brief overview of its advantages. As you can see from
the draw force curve which you refer to (see left), the biggest advantage is
that you end up with a relatively small force even though you stored a large
amount of energy; this allows for conditions for more relaxed aiming and
easier steadying of the bow. You still have to put all the energy in which
you expect to get out. The important thing to understand is that the energy
stored in the bow is the area under the the force vs. pull curve. For
a simple spring, the force, kx, is a straight line and so the area
under it is the area of a triangle –Ö∙height∙base where the height is kx
and the base is x. The efficiency normally means the ratio of
energy out to energy in times 100. As best as I can tell, the draw cycle
efficiency is calculated by measuring force vs. distance pulling and
comparing with force vs. distance if you then slowly let it back
down. It seems to me that dynamical efficiency should compare measured
kinetic energies of the launched arrows which is the total energy extracted
from the bow, but that does not seem to be the case; I cannot find a clear
definition of dynamic efficiency. These differ only because of energy
losses, mainly due to friction. Suppose we had a linear bow with the same
draw (about 21"=1.75 ft) and which stored the same energy (78.3 ft∙lb); the
spring constant would 51.1 lb/ft and the force at maximum draw would be 89.5
lb. I have added the yellow curve to the graph from the paper you referred
to which is shown in the figure. Now each arrow from these two bows travels
the same distance while rubbing on the bow, so those rubbing frictional
forces are the same assuming similar materials and friction between the bow
and arrow. But the linear bow acquires a high speed much sooner than the
compound bow which means it is going much faster on average even though the
two end up at the same speed. But, the air drag is proportional to the
square of the velocity so the linear bow will likely lose more energy to air
drag during the launch than the compound bow. At least, that is my guess.
There can be miriad other reasons why the efficiencies differ due to details
like friction in the pulleys, different materials and designs, etc. I
must admit that I do not understand what actual and effective letoff are.
![]() QUESTION:
QUESTION:
What happens when you compress gas (for example carbondioxide) into a gas cylinder? I am thinking that as pressure increases, so does temperature (because of the increased kinetic energy of the gas molecules). But the 0th law of thermodynamics say that heat energy goes from an object of high temperature to an object of low temperature - so I am thinking that after a while the temperature of the gas will be the same as the room temperature?! Since pressure is constant in the cylinder, isn't the kinetic energy of the molecules? What happens with the gas as energy is transferred to the room? Am i misunderstanding something? I just can't seem to Get my head around this, so I am really hoping you can help med understand!
![]() ANSWER:
ANSWER:
When you say "…compress gas…into a gas cylinder…" I assume you
mean that you are adding gas to a cylinder with constant volume. All you
really need to know is the ideal gas law, PV=NRT where P is
pressure, V is volume, N is some measure of how much gas you
have, T is the absolute temperature, and R is just a constant
of proportionality. You need to make some approximations for a real-world
situation. If you add the gas really slowly and/or the cylinder has very
thin conductive walls, T will remain constant for the reason you
state‚ÄĒbecause the whole system will keep in thermal equilibrium with its
environment; this is called an isothermal process and as N increases,
P increases. The other extreme is that you take care to insulate the
cylinder and/or add the gas very quickly so no heat enters or leaves. In
this case, increasing N will increase the ratio P/T;
however, you do not have enough information to determine how P and
T independently change. If you are using some sort of pump, you will be
doing work on the system which will increase its temperature and therefore
the pressure has to increase also to keep P/T from decreasing.
Another way to add gas to the tank is to take another tank with much more
gas in it and connect the two of them together. Since the volume of the two
tanks and the total amount of gas in them is constant, the temperature of
the whole system will decrease. Again, pressure in your tank must change in
such a way that P/T increases and that could mean that P
would increase, decrease, or stay the same, depending on initial situations.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Thanks for the quick reply! I am still wondering though, is it possible for a compressed gas in a cylinder to have higher temperature than the room it is stored in over time? I am thinking comparing to coffee in a thermos after some hours will be the same temperature as its surroundings. Is the gas cylinder any different due to pressure inside the tank?
![]() ANSWER:
ANSWER:
Eventually the cylinder, room, and gas will all be at the same
temperature. If (see above) the temperature right after filling were higher
than the room temperature, it would cool down and the pressure would
decrease because now both V and N would be constant while the
gas cooled. Here is a numerical example: suppose that the room temperature
is 200C=293 K and the gas temperature is 400C=333 K
and the hot gas has a pressure of 4.0 Atm. Then, P/T=constant=4/333=Pfinal/293
or Pfinal=3.5
Atm.
![]() QUESTION:
QUESTION:
What is the effect of earth rotation on the human upright posture?
Please visit my website. I would
like to corroborate my hypothesis from a physics point of view.
![]() ANSWER:
ANSWER:
My original response, via email, was "The forces are negligibly small. I am quite certain that they are not
a factor in back pain." However, the questioner persisted.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Thank you for responding to my question regarding the effect of rotation on the upright posture. As you stated the effect is indeed subtle but it is there. The point of my work is that the human spine is much more sensitive to these forces than researches realize.
Did you solve the question of the effect of rotation on the standing posture and what was the result percentage please. Did you fiqure a formula for this and was it compatible with my rudimentry estimate of 30% percent anterior left torque and spinal differential findings of 8%?
![]() ANSWER:
ANSWER:
I cannot resist responding in some detail to this since it is so
wrong! What we need to understand is how to do physics in a rotating
(accelerating) frame of reference such as the earth. In such a frame, there
are real forces and fictitous forces. As the questioner correctly notes,
even though we call the fictitious forces fictitious, they can certainly be
felt by our bodies if they are large enough. The best known fictitious force is the centrifugal
force; this is what we feel trying to throw us off a rotating
merry-go-round. A person at rest on the earth's surface experiences a real
force called the weight which points toward the the center of the earth and
has a magnitude W=mg; a fictitious centrifugal force pointing
perpendicular to and away from the axis of rotation and has a magnitude Fcen=mrω2
where r is the distance from the axis and ω=7.3x10-5
radians/s is the angular velocity of the earth's rotation*; and whatever
force the floor exerts on the object to maintain equilibrium. If the person
is moving along the earth's surface, there is an additional fictitious force
called the Coriolis force which I will discuss later. I start with the
simplest situation which is someone standing on the equator. The first
figure is a view from the north pole; the earth rotates counterclockwise;
the man has a mass m=100 kg so his weight (red) is W=980 N;
the radius is r=Rearth=6.4x106 m, so the
centrifugal force (green and not to scale) is Fcen=100x6.4x106x(7.3x10-5)2=3.4
N; finally the force from the floor (black) is vertically upward and of
magnitude 980-3.4=976.6 N. Note that there is no net torque for a person at
the equator and the only effect is that there is approximately a 0.35%
reduction in apparent weight. Next let us examine a person at rest but at
some latitude, say 450 north as shown in the second figure above;
the color coding of the forces is the same as in the first figure. The
weight is the same, 980 N; the radius is r=Rearthsin450=4.5x106
and so Fcen=100x4.5x106x(7.3x10-5)2=2.4
N; Fcen has a radial component 2.4sin450=1.7
N which reduces the apparent weight (radial component of the floor force) by
that amount; Fcen has a tangential component
2.4cos450=1.7 N which results in a torque and is also the
magnitude of tangential component of the floor force. The torque tries to
rotate the person about his feet in a southerly direction (would be
northerly in the southern hemisphere) and has a magnitude of 1.7 N∙m,
estimating the center of gravity to be 1 m above the feet. To put this in
perspective, if the earth were not rotating the person would have to lean at
an angle of tan-1(2.4/980)=0.140 to have a comparable
torque about his feet; this angle is far smaller than leaning we do in
normal activities. Furthermore, since the direction we happen to be facing
is random, the average effect over time of these very tiny torques would be
zero.
Finally, there is another (fictitious) force which acts on objects on the rotating earth, the Coriolis force. This is the force responsible for the cyclonic motions of weather patterns. However, the object has to be moving and the direction of the force depends both on location and direction of the velocity. Its maximum possible magnitude is FCor=2mωv where v is the speed; its direction is always perpendicular to the velocity vector. The fastest the average person is likely to be moving is the speed of a passenger jet, about 500 mph≈220 m/s, so FCor=2x100x7.3x10-5x220=3.2 N. Again, this force is so small compared to other forces acting that its effect on physiololgy would be essentially zero.
*ω=(1 revolution/day)(2π radians/revolution)(1 day/24 hr)(1 hr/3600 s)=7.3x10-5 s-1
![]() QUESTION:
QUESTION:
If I was throwing a ball around with a friend on a torus-shaped space station which was rotating in order to simulate gravity, would I have to lead her? Alternatively: if I "dropped" the ball (i.e. let go of it) from, say, waist-high, would the ball land at my feet, or somewhere else?
(Assume that the torus is roughly 50m in diameter, neither
accelerating in space nor in terms of its rotation, and that we're using a
standard baseball.)
![]() ANSWER:
ANSWER:
My first inclination was to say that, assuming that the station
was big enough, it would be pretty much like playing catch on earth. The
reason for this guess was that I had worked out a similar problem for an
earlier answer. The question
there was if you were to jump straight up what would happen; this is
equivalent to throwing a ball straight up with some speed v. The
answer was that for sufficiently large R and small v, in
particular R>>v2/g, the time the ball was in the
air, the "height" it rose, and the time it took to "return" would all be
about the same as if you did the experiment on earth; also, the ball would
"land" back where you were. I believe that answers your question about
whether a dropped ball would land at your feet‚ÄĒit would (approximately). You
should be sure you understand that earlier answer. The leftmost figure above
reproduces the original figure for the ball thrown straight up. The other
two do not have all the vectors labeled, but you can tell by comparison what
they are. The components of v are shown by light blue vectors
and the red is just to aid me in adding the vectors v and
Rω. The second figure is if your partner is ahead of you (ahead
meaning in the direction of rotation). The third figure shows how you would
throw it if your partner were behind you. It is not at all clear to me where
you and your partner would be located when the ball "came back down" to the
ring (shown by green dots). Also, trying to do the problem analytically in
the nonrotating frame gets very messy. I am just interested, as are you, in
your situation‚ÄĒthrown baseballs in a 50 m ring rotating such that Rω2=g
where ω is the angular velocity in radians per second. So, I am going
to do the calculations in the rotating frame (where you and your partner are
at rest). This gets sort of tricky since we will have to introduce
fictitious forces to describe the motion of the ball; once you throw the
ball, there are no real forces on it. Now, maybe you throw the baseball
(mass about 0.15 kg) with a speed of 10 m/s≈22 mph. There are two fictitious
forces: the centrifugal force Fr=mRω2=mg
which points down for you and the Coriolis force FCor=2mωv=2mv√(g/R)
and points in a direction perpendicular to the vector v as
shown in the figure to the left. Now, let's calculate the magnitudes of
these forces. FCor=2x0.15x10x√(9.8/50)=1.3 N and Fr=0.15x9.8=1.5
N. The Coriolis force is not small compared to the centrifugal force and
therefore the ball will not behave at all as it would in a true uniform
gravitational field. You would go nuts trying to play catch on this space
station! The problem is that R=50 m is not much greater than v2/g=10.2
m. See the added thought below for a discussion of the dropped ball.
![]() ADDED
THOUGHT:
ADDED
THOUGHT:
When the ball is simply dropped from say h=1 m, the
Coriolis force is relatively small because the velocity is small for most of
the time of the fall. So, the deflection should be modest. I will try to
estimate the amount of deflection. The centrifugal force is mg and is
always radially out, choosing +y radially out, ay=-g+ayCor;
I will argue that the ball does not acquire enough speed for the Coriolis
force to have a significant radial component, so ayCor≈0,
and y≈h-–Ögt2, vy≈-gt.
So, the time to fall is approximately t≈√(2h/g)=0.45 s
and vy≈4.4 m/s. The Coriolis acceleration, if the velocity
is purely radial, points in the backward direction (to the left in my figure
above) and would have a maximum magnitude of about 2v√(g/R)≈3.9
m/s2. If the ball drops almost vertically the Coriolis
acceleration would be approximately ax≈2m√[(vx2+vy2)(g/R)]≈2mvy√(g/R)=2mgt√(g/R)=8.68t=dvx/dt;
therefore, integrating, vx≈4.34t2 and
x≈1.45t3.
So, at t=0.45 s, vx≈0.88 m/s and x≈0.13 m=13 cm.
![]() QUESTION:
QUESTION:
How does a GPS station work? I just learned about them and my teacher was a little unclear so I'm depending on you to hopefully give me a direct answer.
![]() ANSWER:
ANSWER:
Suppose that you were on a line and you wanted to know where you
were. If there were some point on that line and you knew where you were
relative to that point, then you would know where you are. Now suppose that
you were on a flat plane. Now you would need two other points the positions
of which you knew to figure out where you were relative to these points
(this is often called triangulation). Now suppose that you are just
somewhere in a three dimensional volume; it would follow that you would need
three points whose positions you knew to find out where you were in that
space. So, if you want to know where you are if you are at rest, you would
need to know the positions three points of reference at rest relative to you
and simple geometry would tell you where you were. The GPS system is a bunch
of satellites which are zooming around in their orbits and therefore,
because both they and possibly you also are moving, you also need to
synchronize all the clocks on the satellites with your clock; this
synchronization means that you need one more point because you now have four
unknowns you need to solve for, your three spacial positions and the data
necessary to find the exact time. The GPS receiver in your iphone or
whatever receives the data beamed from the four satellites and computes your
position to remarkably good accuracy.
![]() QUESTION:
QUESTION:
According to Newton's law of gravitation, gravitational force is inversely proportional to the distance between the center of mass of the bodies. So if i place my hands together, the distance between them is very less so the gravitational force should be very high but it is easier to separate them. How?
![]() ANSWER:
ANSWER:
First of all, the force is inversely proportional to the
square of the distance between the centers of mass. Because gravity is
nature's weakest force, it is tiny unless there is a very large amount of
mass. Let's estimate that the center of mass of your hands are separated by
1 cm=0.01 m and that the mass of each hand is about 0.25 kg (about –Ö lb).
The force each hand feels can be approximated as F=Gm1m2/r2=6.67x10-11x0.25x0.25/0.12=4.2x10-10
N≈10-10 lb. As a comparison, the gravitational force on each hand
by the earth (whose center is much farther away) is about 2.5 N.
![]() QUESTION:
QUESTION:
My son's friend asks: "why does a rolling object balance better than a stationary one?"
![]() ANSWER:
ANSWER:
I assume the friend is thinking about a bicycle which is, as we
all know, easier to stay up on if it is moving. The physics of a bicycle is
quite complicated, so I am not giving you the whole picture but rather one
aspect which will be understandable to a youngster. Any object which is
spinning has what is called angular momentum. Shown to the left is a
spinning wheel with its angular momentum vector shown. If the wheel were not
spinning, this vector would vanish. One of the most important laws in
physics is conservation of angluar momentum: if there are no torques on the
rotating object, its angular momentum will not change and that includes the
direction of the vector. So, if you are riding a bike straight down the
street, each wheel has a horizontal angular momentum pointing to the left.
If the bike starts to tip over, the angular momentum vector would try to
remain horizontal, keeping it from tipping. If you lean hard, there is now a
torque on the system and so the angular momentum will change but not
resulting in a fall but rather in a turn. You might want to get a toy
gyroscope to show the kids how angular momentum works.
![]() QUESTION:
QUESTION:
A tall tree cracks and falls. Can the resultant linear acceleration exceed the acceleration due to gravity?
![]() ANSWER:
ANSWER:
As the tree falls, it rotates about the point of contact with the ground
with some angular acceleration. Therefore, each point along the length of
the tree has a different acceleration which is perpendicular to the tree.
The falling tree is shown in the figure to the left. The weight mg
acts at the center of gravity a distance D from the rotation axis.
The tree has height L. An arbritrary distance up the tree is denoted
by x. The angle the tree makes with the vertical is θ. The net
torque τ on the tree is τ=mgDsinθ=Iα=Ia/x where
I is the moment of inertia of the tree about its pivot point, α
is the angular acceleration of the tree, and a is the
tangential acceleration of the point x. Therefore, a=mgxDsinθ/I.
Therefore, if mxDsinθ/I>1, a>g. Consider a
simple example modeling the tree as a long thin stick; then I=mL2/3
and D=L/2, so a=3gxsinθ/(2L). Take a
particular example, θ=600; then a=1.3gx/L
or any point with x>L/1.3 will have a>g.
![]() ADDED
NOTE:
ADDED
NOTE:
The discussion above refers to the tangential acceleration of a point
on the tree which is what I thought you were referring to. However, each
point at position x also has a centripetal acceleration, call it ac=v2/x=xω2.
You can get ω from energy conservation, mgD=–ÖIω2+mgDcosθ
and therefore ac=2mgxD(1-cosθ)/I.
So, the total acceleration is √(a2+ac2);
I will let you work that out. Modeling the tree as a uniform stick, I have
calculated the total acceleration for several values of x shown in
the graph to the right. For x=L/4, all angles have acceleration less
than g. For x=L/2, the center of mass, atotal>g
for angles greater than about 600. For x=L, atotal>g
for angles greater than about 350.

![]() QUESTION:
QUESTION:
I'm writing a fantasy novel and I just want to check my science.
In it there's a tower which is so tall that it is higher than the troposphere. There is a scene where someone smashes a window. My question is would the air all rush out due to unequal air pressure and when the air pressure settles would everyone feel the effects of explosive decompression or at least find it hard to breathe?
![]() ANSWER:
ANSWER:
Presumably, all your windows are sealed such that the inside is at
atmospheric pressure. "Higher than the troposphere" would imply the
stratosphere which is where commercial jets fly. As you doubtless know, the
pressure there is very low. The figure to the right shows that just above
the troposphere the pressure is only about 200 millibars, about 1/5 of
atmospheric pressure. There is not enough air there to keep you alive. You
may recall the crash of the private jet in 1999 which killed golfer Payne
Stewart. The plane lost pressure at an altitude of 11.9 km and everyone lost
consciousness; it flew on autopilot until it ran out of fuel and crashed.
Most certainly the air would be drawn (violently) out of your broken window.
Another thing you should think about is that you cannot simply pressurize
your entire tower to atmospheric pressure; you have to pressurize in layers
of a few hundred meters and isolated from each other. Otherwise you will
have the same strong pressure gradient with altitude as the atmosphere has!
![]() QUESTION:
QUESTION:
If I stick a pea on the out side of a cylinder that is rotating on a fixed axis at a constant speed, what are the forces being applied to the pea?
Is the pea under going acceleration? Even at a constant speed due to the angular changes.
![]() ANSWER:
ANSWER:
The pea is experiencing what is called uniform circular motion.
Its velocity is a vector tangent to the cylinder's surface. Although the
magnitude of the velocity (speed) is not changing, the direction of the
velocity is constantly changing. Therefore, since acceleration is rate of
change of velocity, there is an acceleration. This acceleration, called
centripetal acceleration, is a vector, points toward the axis of the
cylinder, and has a magnitude v2/R where v
is the speed of the surface of the cylinder (and therefore of the pea) and
R is the radius. A force must be applied toward the axis of magnitude
mv2/R where m is the mass of the pea. This
force is provided by whatever adhesive you used to stick the pea there. If
the adhesive is not strong enough, the pea will fly off. Of course there is
also the pea's weight pointing vertically down and, assuming the axis of
rotation is vertical, the adhesive must also exert a force upward to hold
the pea from falling due to its weight.
![]() QUESTION:
QUESTION:
What would happen if you were to take a satellite that's in orbit, put a giant ball of string on it, and slowly unwind the string letting the free end fall
to earth? Would it snap? What if it was made of a material that is extremely strong such as carbon nano tubes?
![]() ANSWER:
ANSWER:
Think about it. The ball of string is orbiting with you, has
your same speed, and seems to be "weightless" just like you. So you grab
onto the loose end and release the ball to fall and nothing happens, it just
orbits along with you! Sort of related to your question is the
space elevator
which might interest you.
![]() QUESTION:
QUESTION:
Why does mass not alter the acceleration in a vacuum. If a hammer falls to the earth faster than hammer falls to the moon, then mass does matter. Consider the opposite perspective. Earth falls to the hammer faster than the moon falls to the hammer. Am I wrong in my reasoning? I've asked a few of my physics teachers, but they said that my logic was flawed and you can't consider it that way without explaining why.
![]() ANSWER:
ANSWER:
You are completely misunderstanding the constance of
acceleration due to gravity, independent of mass. The statement assumes all
masses experience the same gravitational field (see
FAQ page). Obviously, because of Newton's
second law, the acceleration a due to any force F
depends on mass m, a=F/m. The "falling" of the moon or
earth to the hammer is negligibly small for all practical purposes. However,
you could calculate the initial acceleration of each. The force on the earth
or moon is F=MmG/R2 where M is the mass of
the earth (moon) and R is the radius of the earth (moon) (assuming
the hammer is close to the surface). So the initial acceleration of each
would be a=F/M=mG/R2 and therefore amoon/aearth=(Rearth/Rmoon)2.
So, the moon actually accelerates toward the hammer faster but it has
nothing to do with the mass as you can see, it is because the center of the
moon is much closer to the hammer than the center of the earth is. If you
were to place the hammer such that it was a distance Rearth
from the center of the moon, the earth and moon would have equal
accelerations. The earth and moon are responding to the gravitational field
of the hammer. So, you are wrong on all your statements and, guess what,
your physics teachers are right!
![]() QUESTION:
QUESTION:
Is it true that if you have two objects and nothing else you can't tell
which object is moving and which object is standing still? Does this mean that we don't know how fast earth is moving?
And there is no experiment we can conduct to see if we are moving or not?
![]() ANSWER:
ANSWER:
First, you have to understand the difference between inertial
and noninertial frames of reference. If Newton's first law is true where you
are, you are in an inertial frame of reference. (Newton's first law says
that if an object is at rest in your frame the sum of all forces on it is
zero.) Any other frame which moves with constant speed in a straight line
relative to your frame is also an inertial frame. Noninertial frames are any
frames which have an acceleration relative to an inertial frame. The
principle of relativity says that the laws of physics are exactly the same
in all inertial frames of reference. Since the laws of physics are what will
determine the result of any experiment you can do, it makes no sense to
refer to an object's being at rest unless with reference to something else.
Does this answer your question? Also, we do not know how fast the earth is
moving because that is a meaningless question unless we say, for example,
how fast is it moving relative to the sun, or how fast is it moving relative
to the center of the galaxy, etc.
![]() QUESTION:
QUESTION:
Why is a hard ball more likely than soft ball of equal mass and volume to break a glass window if they are thrown at the same speed?
![]() ANSWER:
ANSWER:
The average force F which an object exerts during a
collision is the change in momentum (Δp=mΔv) divided by the
time the collision took Δt. The soft ball has two things going for
it. First, because it is "squishy", the collision lasts longer, so Δtsoft>Δthard;
second, the soft ball is probably less elastic than the hard ball so that it
loses more energy in the collision and therefore bounces back with less
momentum resulting in Δpsoft<Δphard.
Therefore Δpsoft/Δtsoft<Δphard/Δthard
or Fsoft<Fhard.
![]() QUESTION:
QUESTION:
I have been attempting to teach myself chaos theory, however I have had trouble understanding it and how it is involved with different levels of quantum physics as well as relativity. I am also having trouble understanding the "three body problem", which seems to occur in many different physical systems.
I was hoping that you could help me to understand at least some of Chaos theory and how it connects to both quantum physics and relativity, and what exactly the "three body problem" is.
![]() ANSWER:
ANSWER:
I am sorry, but your question is too technical and too unfocused for the
purposes of this site. I can tell you something about the 3-body problem, though. If two bodies interact only with each other, for example the earth and the moon, you can write the orbits in simple analytic closed form. However, if there are three interacting bodies there is, in general, no closed-form solution. There are special cases where the 3-body problem can be solved, for example if one of the bodies is held fixed, but not in general.
If you google "three body problem" you will find more information. A
particularly interesting (and newsworthy) discussion may be read in
AAAS Science News. All these special cases are not chaotic because
they repeat in a periodic way. More general cases are not periodic and are
extraordinarily sensitive to initial conditions.

![]() QUESTION:
QUESTION:
I recently saw the movie Elysium. The most memorable thing was the space station. The station was a completely open system. Would the station's rotation keep its own atmosphere contained? How would a spacecraft land on a rotating ring like this? Would radiation levels just fry everyone and everything on it?
![]() ANSWER:
ANSWER:
The rotation causes an artificial gravity. If there were side
walls, you could certainly keep an atmosphere in there. For a detailed
discussion of how living there would be, see an
earlier answer. The way the
gravity works is that it is a centrifugal force (a
fictitious force) and you want the acceleration at the outer rim to be
equal to g=9.8 m/s2; the acceleration at the surface is
v2/R where v is the tangential speed at the
surface and R is the radius of the ring. So, v=√(g/R).
If we take, just as an example, R=1 kg=1000 m, then v≈0.1 m/s;
since the circumference is 2πR=6283 m, this means that the ring would
rotate about once every 63,000 s=1.7 days. I think you would agree that this
speed is very small, so a spacecraft would have no trouble landing on it
assuming that the spacecraft had gotten up to the same orbital speed. I do
not believe that the radiation level would necessarily "fry" everyone, but
it would be a concern for the long term and some kind of shielding would
have to be employed.
![]() QUESTION:
QUESTION:
according to newton law of motion "a body will move if a net force act on it" then why the earth moves around its axis?
![]() ANSWER:
ANSWER:
Whoa! You have Newton's first law all wrong. A body will move
with constant velocity if there are no forces on it. For
translational motion, this means that the body moves with constant speed in
a straight line; if you exert a force on the body, its velocity will change.
For rotational motion, this means that the body spins with constant speed in
a straight line; if you exert a torque on the body, its spinning speed will
change. The earth rotates on its axis with constant speed because there are
no torques on it.
![]() QUESTION:
QUESTION:
These are non-academic, practical questions regarding the physics of balance and weight shifting pertaining to a moveable kitchen island.
Q1: Will an 11 inch countertop overhang alone cause the island to tip?
Q2: If not, what amount of weight (lbs.) can be safely placed on the overhang before tipping?
Q3: Is there a formula I can use to calculate this?
Description:
I have a moveable kitchen island fabricated with locking casters. I wanted to place a quartz countertop over the island base with an additional 11 inch countertop overhang supported by steel beams extending from the island base. The total length of the countertop is 37 inches (26 inches on the island base plus 11 inches as the overhang).
Proposed dimensions of the island base with its portion of the quartz countertop:
W = 52.5 inches
L = 26 inches
H = 36.0 inches (34.5" base + 1.5" countertop which includes a 5/8 inch plywood sub-counter)
Total Weight of the Island Base with Its 26 Inch Portion of the Countertop = 298 lbs.
Proposed dimensions of the 11 inch overhang:
W = 52.5 inches
L = 11 inches length
H = 1.5 inches (2cm quartz plus 5/8 inch plywood sub-counter)
Total Weight of the 11 Inch Overhang Portion of the Countertop = 50 lbs.
The overhang is a key feature of the kitchen island for our household. The island is intended to serve multiple, mundane purposes in our very compact home: food prep, dining, and working on work projects / homework.
![]() ANSWER:
ANSWER:
I will assume that the center of gravity of the island without
the overhang is at the geometric center of the base and that the casters are
at the corners; also, that the center of gravity of the overhang is at its
geometrical center. The red vectors in the figure to the right are pertinent
forces for this problem, the 298 lb weight of the island acting at the
center of gravity (star), the 50 lb weight of the overhang acting at the
center of gravity (5.5" out), the force of the floor on the front casters (N2),
and the force of the floor acting on the rear wheels (N1).
(Ignore the force F for now.) Newton's first law stipulates
that the sum of all the forces must be zero, so N1+N2=348.
Also required for equilibrium is that the sum of torques about any axis must
be zero; choosing to sum the torques about the front casters, 26N1-298x13+50x5.5=0=26N1-3596
or N1=138 lb and so N2=210 lb. Now,
let's think about this answer: it tells you that this (unladen) island will
not tip over because there is still a lot of weight on the rear wheels. Now,
if you start adding weight to the overhang, eventually when you have added
enough weight, the force N1 will equal zero when it is
just about to tip over. So, add the force F at the outermost
edge of the overhang and find F when the island is just about to tip:
again summing torques about the front casters, -298x13+50x5.5+11F=0
or F=327 lb. This is the extreme situation‚ÄĒyou would have to put
twice this amount of weight, for example, halfway out the overhang to tip it
over. It looks to me that this will be safe for everyday use.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
The questioner sent an extremely lengthy recalculation of distances and weights. The only substantive changes were: weight of island without overhang,
W=414 lb; weight of overhang w=58 lb; distances of casters from sides
d=5.5"; distance of center of gravity from back side D=14".
![]() ANSWER:
ANSWER:
The relevant equations to redo the calculations for the unladen
island in the original
answer are
N1+N2=W+w and
(26-2d)N1-(26-D-d)W+(d+5.5)w=0.
I find N1=137 lb, so the unladen island will not
tip. For the second part of the calculation, adding the force F
such that N1=0, the relevant equation is
(11+d)F-(26-D-d)W+(d+5.5)w=0.
I find F=124 lb at the outer edge to tip the island. Again, a force of 248 lb in the center of the overhang would tip it. These forces are considerably smaller than the original calculation mainly because of the relocation of the casters closer to the center of gravity and, to a lesser extent, the moving forward of the center of gravity. Incidentally, it may seem that the vertical positon of the center of gravity would matter. It does not matter if the island does not tip; if it does begin to tip, it will tip faster if the center of gravity is higher, but not sooner. Since there is no chance that the island will tip sideways, the location of the center of gravity along the long edge is not relevant. Finally, if you are uncomfortable with the amount of weight to tip, I presume that you could add weight inside and near the back-bottom edge as a counter balance. For example, putting 100 lb at the back edge would increase F to 249 lb. (Anything you do which shifts the overall center of gravity closer to the back side will help stabilize against tipping.) You should also be aware that if you move it by pushing forward at the top of the back side, the resulting torque could tip it over, so be careful when moving it. I believe that if it were mine, I would look for a design modification which would move the front casters closer to the front.
![]() ADDED NOTE:
ADDED NOTE:
The questioner added some plans, one of which is shown to the left. Note
that there is a kick plate recessed by 2" all around. Presumably this plate
hides the casters and is very close to the floor. Therefore, as soon as the
island would start to tip, these would become the pivot point rather than
the caster itself which would make make it less vulnerable to tipping.
Essentially, in the calculations above you would reduce d by 2" to
d=3.5". This would result in a value of F=207 lb, quite an
improvement. You can see why I indicated above that moving the casters in by
5.5" was the main culprit in increasing "tippiness". (I am curious how, if
the kick plates hide the casters, you are able to lock them.)
![]() QUESTION::
QUESTION::
I'm trying to compare 2 measurements that denote impact. The
first measurement is as follows : a glass sheet can withstand a 25mm (diameter)
steel ball fired at 80 km's per hour. The second measurement is that another
sheet of glass can withstand a 277 gram steel ball dropped from 1 metre in
height with a back wind of 60 meters per second. I am trying to bring the second measurement to a
measurement comparable to the first measurement.
![]() ANSWER:
ANSWER:
The thing which will matter is the linear momentum (p=mv)
each ball brings to the glass. The reason is that you are interested in how
much force each glass can withstand and the force is the rate of change of
momentum. I assume that each ball will spend about the same amount of time
during the collision
and will exert its force over the same area (very nearly a point for a
sphere on a plane), so whichever ball has the most momentum when it hits the
glass will indicate the glass with the greatest strength. I took the mass
density ρ of steel as 8000 kg/m3. The volume of a sphere
is 4πR3/3, so m1=4ρπR13/3=4∙8000∙π∙0.01253/3=0.0654
kg. Since the speed is given, v1=80 km/hr=22 m/s, we can
immediately write the momentum for #1, p1=1.44 kg∙m/s.
Finding the speed of the second ball is a much more difficult problem. If it
were just falling, it would be trivial. But it is being pushed by the
downward wind which will make it speed up faster than just falling; so, it
is necessary to understand a little about air drag forces. For spheres of
normal speeds in air the force of friction is excellently approximated by
f=0.22D2u2 where D is the
diameter and u is the speed of the ball relative to the air.
From the density and mass, I find the radius to be 0.0434 m so D=0.0868
m. So, when the ball is first dropped, it has two forces pointing down, its
own weight mg=0.277∙9.8=2.71 N and the wind force 0.22∙0.08682602=5.97
N; the wind is more than twice the force as the weight. As it falls, it
speeds up and so the effect of the wind gets smaller. Newton's second law
for v2, if you care, is now of the form dv2/dt=g[1+((vw-v2)/vt)2]
where vt=√(mg/(0.22D22))
and vw is the speed of the wind. The solution to this
equation is v2=vw-vttan[tan-1(vw/vt)-(gt/vt)].
Putting in the numbers for this situation (vw=60 m/s, vt=40.5
m/s), the graph for the first 15 s, with and without wind, is shown to the
left. The behavior of this graph is interesting. The ball takes about 4 s to
reach a speed of 60 m/s; at that point the ball is at rest relative to the
air and so there is no air drag and the slope of the curve (which is
acceleration) is the same as the curve for no wind at all, as expected. Now,
if there were no wind it would take the ball about 0.45 s to fall 1 m and
the wind will surely get the ball there in a shorter time; therefore we are
really only interested in the first half second of the fall and this is
shown to the right. The acceleration over this time is very nearly uniform,
about a2=11/0.4=27.5 m/s2; since this is just
an estimate, I will do the calculation assuming uniform acceleration rather
than doing the exact calculation to find the velocity after 1 m. I find that
the time to reach 1 m is t=√(2/27.5)=0.27 s and so v2=at=7.4
m/s. Therefore, the momentum for #2 is p2=m2v2=0.277∙7.4=2.1
kg∙m/s. Ball #2 is the winner!
![]() ADDED
THOUGHTS:
ADDED
THOUGHTS:
In retrospect, I could have saved myself some work if I had
thought about the fact that in a time less than 0.45 s the acceleration
would be essentially constant and simply written 0.277a=2.71+5.97 ‚ÄĒ>
a=31.3 m/s2 which would give t=0.25 s and v2=7.9
m/s and p2=2.2 kg∙m/s. Secondly, I noticed that my solution for v2
was incorrect for speeds greater than 60 m/s, so I deleted that part of the
graph. To satisfy my own curiosity, I solved the problem for speeds greater
than 4 s. Because at later times the speed of the ball is greater than the
speed of the wind, the air drag force switches to up rather down so the
analytical solution to the problem becomes different, v2=vw+vttanh(g(t-4)/vt);
this corrected calculation is shown in blue.
The complete solution is now graphed to the left. At large times, the
solution approaches vt+vw as expected
since vt is the terminal velocity in still air.
![]() QUESTION:
QUESTION:
I have a question about the concept of angular momentum. Suppose a disc is attached to a pole and they're stationary in deep space. If we spin the disc, it's gonna have an angular momentum. Using the right thumb rule to determine the direction of which, does this mean the unit will start moving in said direction? Also, how does the spinning action produce a momentum perpendicular to the force we exerted to cause the spin?
![]() ANSWER:
ANSWER:
I am assuming the pole is attached axially, i.e. at the
center and perpendicular to the disk. Angular momentum is not a force and
therefore it will not cause the system to start moving. Also, it was not the
force you exerted which caused it to spin, it was the torque (see left), and
the direction of the torque τ is also given by the right hand rule such that the
angular momentum L points in the direction as the torque (see
right).
![]() QUESTION:
QUESTION:
I'm a young aeronautical student and I'm doing a project on small, basic fixed-wing aircraft. I need to include some explanation of how lift is generated. My teacher has vaguely mentioned the Bernoulli theory once or twice. However after some research, I found that the Bernoulli explanation is outdated. I've found other more accepted theories, only which are too complex for both my understanding and academic level. Could you provide a more accurate but relatively simplified explanation of lift?
![]() ANSWER:
ANSWER:
I wouldn't say "the Bernoulli explanation is outdated," it just
isn't the whole explanation. Basically, Newton's third law is responsible
for much of the lift in flight‚ÄĒthe air coming off the trailing edge of the
wing is deflected down which means the wing exerted a downward force on it
which means it exerted an upward force on the wing. Books about flying
usually refer to this as "angle of attack." A more complete explanation may
be found in an
earlier answer. I can also recommend a book, Stick and Rudder by
Wolfgang Langewiesche.
![]() QUESTION:
QUESTION:
If it was possible for every vehicle in the world to point East, and at perfect timing, all accelerate at the same time, surely the torque that is put down on the Earth would affect it's spinning energy?
![]() ANSWER:
ANSWER:
Yet another chance to demonstrate what a tiny speck we are in
this universe! There are about a billion, 109, vehicles in the
world. Suppose the average mass is 1000 kg (about 3000 lb) and the average
acceleration is about 5 m/s2 (half of g); so the average force
per vehicle is about 5000 N and the total force on the earth is therefore
5x1012 N. Suppose the average vehicle is at about 450
latitude, so the net torque is about τ=5x1012R/√2=2.3x1019
N∙m where R=6.4x106 m is the radius of the earth. The
angular acceleration is then given by α=τ/I where I
is the
moment of inertia of the earth, about 8x1037 kg∙m/s2.
So, α=2.3x1019/8x1037=3x10-19
radians/s2=5x10-18 revolutions/s2=4x10-8
revolutions/day2. If all your vehicles could maintain this
acceleration for a full minute, (certainly not possible), the length
of the day would shorten by 5x10-12 day=4x10-7 s.

![]() QUESTION:
QUESTION:
Can you explain the effect of rifling of the muzzle in rifles ?? I just know that the muzzling is done to impart spin to the bullet when it is fired ?? So, exactly how does the spin imparted to the bullet improves it's aiming accuracy or whatever it does ?
![]() ANSWER:
ANSWER:
An object, like the bullet, which is spinning about an axis
along its length has angular momentum. The angular momentum vector points
along the direction the bullet is flying. An important law in physics is the
conservation of angular momentum which says that the angular momentum of an
object never changes if there is no torque acting on it. So the angular
momentum will continue pointing along the path which means that the bullet
will not "tumble". It is the same principle which governs the spiral forward
pass in American football. Without spiraling, the tiniest asymetry in the
shape of the bullet will cause it to immediately start tumbling when it
leaves the barrel.
![]() QUESTION:
QUESTION:
With all the talk of new weapons using kinetic energy as the destructive force instead of traditional explosives; exactly how minimal could a warheads' mass be and what would its velocity need to be to create an "explosive" force of 5,000 lbs of high explosive?
![]() ANSWER:
ANSWER:
Funny, I have not heard "all the talk"! I did get one other
recent question similar to yours. Anyhow, I guess you want to compare the
kinetic energy of a projectile with the same energy as 5000 lb of TNT. 5000
lb is about 2.3 metric tons and the energy content of that amount of TNT is
about 1010 J. Since the kinetic energy of the projectile is –Ömv2,
there is no clear answer to your question because every mass would have a
different velocity to have the requisite amount of energy. The speed of a
near-earth satellite is about 8000 m/s and maybe such a satellite would be
used to launch your weapon, so let's use v=8000 m/s. Then, 1010=–Öm(8000)2
or m=313 kg=690 lb.
![]() QUESTION:
QUESTION:
I'm helping a middle school student with his physics homework. One of the concepts was mass and inertia and he told me that his teacher said they are equal and are synonyms. I was under the impression that they do not mean the same thing, that they are proportional. Could you clarify?
![]() ANSWER:
ANSWER:
Here is what the teacher was talking about: There are two kinds
of mass, inertial mass and gravitational mass. Inertial mass quantifies how
much an object resists changing its motion if a force acts on it.
Gravitational mass quantifies how much a gravitational force affects it and
how much it gravitationally affects other gravitational masses. It turns out
that the two are identical and there is really only one mass. This
equivalence is a prediction of the theory of general relativity and is also
the reason that all objects have the same gravitational acceleration.
Inertia is usually a qualitative term which describes how resistant an
object is to being accelerated, which is what inertial mass does
quantitatively. However, it is not so unusual to use inertia synonymously
with mass or inertial mass.
![]() QUESTION:
QUESTION:
My friend and I are having a discussion about centrifugal force and whether or not it exists, is real, and/or if it is present in daily life. Can you expand our knowledge and settle this dispute? We want to know everything about centrifugal force and if you can help us out that would be much appreciated.
![]() ANSWER:
ANSWER:
The important concept to understand here is that Newton's laws,
which describe motion, are not always true. For example, suppose that you
hang a simple pendulum from the roof of a car. When you are standing still
or driving down a straight road with constant speed, the pendulum hangs
straight down. The forces on the pendulum are its own weight, which points
straight down, and the tension in the string which pulls straight up.
This pendulum is in equilibrium here in the car and so Newton's first law
tells you that the sum of all the forces must add up to zero and so the
tension in the string must be equal to the weight of the pendulum bob. Now
suppose that you smoothly accelerate; you will find that the pendulum swings
toward the rear and hangs at some angle rather than straight down. You will
look at that pendulum and say, it is just hanging there at rest in the car
and so it must be in "equilibrium". On the other hand, there is no way the
(not parallel) forces of the weight and the tension can add up to zero.
Newton's first law is a false law in this car! If the first law is true, you
are in an inertial frame of reference. If it is false, you are in a
noninertial frame of reference. Generally, it is easy to identify a
noninertial frame‚ÄĒit accelerates relative to an inertial frame. A frame of
reference which is rotating is a noninertial frame because an object moving
on a curved path has an acceleration even if its speed is constant because
the direction of its velocity is always changing. It is shown in any
elementary physics text that the magnitude of this acceleration is a=mv2/R,
where m is its mass, v is its speed, and R is the
radius of the circle it is going around; the direction of the acceleration
vector is toward the center of the circle. The acceleration is called the
centripetal acceleration from the Latin verb peto which means
"I seek". The question is, is there any trick we can pull to force Newton's
laws to be true in a noninertial frame. The answer is yes; if you make up a
fictious force on any object of mass m which is Ffictitious=-ma
in the opposite direction as the acceleration, Newton's laws will work!
The centrifugal force is a fictitious force added so that you can
apply Newton's laws in rotating systems. (The Latin verb fugo means "I
flee".) To see examples of how fictitious forces work, see an earlier
question about
falling down in a bus which will link you to a question about a
car
rounding a curve and that will link to a
bicycle
leaning into a curve.
![]() QUESTION:
QUESTION:
Suppose a container is partially filled with a liquid. A small sphere made of a material whose density is less than the liquid is in equilibrium inside the liquid with the help of a thread such that one end of the thread is tied to the sphere and the other end to the bottom of the container. the whole apparatus is kept on a weighing machine. if the thread is cut, then will the reading of the weighing machine change?
Since the tension in the thread is an internal force, the reading should not change.
However the free body diagram suggests that the reading should change.
![]() ANSWER:
ANSWER:
When you refer to "…the free body diagram…", you must specify
the body. Solving problems like this are most often easiest if you make a
clever choice of body. I would choose the body as the
container+liquid+ball+thread (taken as weightless, probably); in that case
the only downward force is the weight of all three and the only upward force
is the scale, so the scale reads the total weight with no reference to
whether the thread is connected to the ball or not. You can make this
problem difficult by focusing on a different body, maybe the container, but if you
draw all your free-body diagrams correctly and apply Newton's third law, you
still get the same answer that the the scale reads the total weight. To the
left I have shown all the forces on each of the bodies: red is the tension in
the string which is also the force the string exerts on the sphere and the
on the container; light blue is the force the container and fluid exert on
each other; black represents the weight of each; green is the buoyant force
which is the force of the fluid on the sphere and the force of the sphere on
the fluid; purple is the force the scale exerts on the container.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Suppose the sphere is accelerating upwards inside the fluid, under the influence of
the buoyant force. Now its acceleration is dependent upon the buoyant force, while the buoyant force is in turn dependent upon its acceleration. How do we precisely calculate these two quantities, at a particular instant of time?
![]() ANSWER:
ANSWER:
First of all, the buoyant force is not dependent on the
acceleration. As long as the sphere is fully submerged, the buoyant force (B)
is equal the the weight of the displaced fluid. But, you must also include
the drag force (D) which the fluid exerts on the sphere and that is
not simple to include. But, most fluids have sufficiently large viscosity
that the sphere will quickly come to its terminal velocity and move upward
with constant speed. When that happens B-D-W=0 where W is the
weight of the sphere. If you really want to pursue this farther, the
simplest approximation for the drag is that it is proportional to the speed
of the sphere, Stokes's
law. In that case, a=(B-W-Cv)/m where C is a
constant. If you were
to neglect drag altogether, which would be a poor approximation for any real
fluid, the acceleration would be uniform, a=(B-W)/m.

![]() QUESTION:
QUESTION:
I recently saw an experiment on the popular show Mythbusters. The
experiment was: a truck moves in one direction at a constant velocity, carrying a canon facing the opposite direction. The canon then fires a football such that it will travel at the same speed at which the truck is going. Successfully performed by the Mythbusters team, the ball dropped straight down to the ground the moment it left the barrel, as theorized, to a remote observer. I wonder, since Earth rotates at about 470metres/s eastward at the equator, if a bullet is fired westward at the same speed but westward, will it drop like the football did? Although I highly doubt this is the case, my calculations so far prove it's theoretically plausible. Am I missing something? Please also elaborate if this is different from the truck-canon experiment.
![]() ANSWER:
ANSWER:
In the first example, both the canon and the truck were moving
relative to the ground and it was the ground relative to which the final
velocity was observed. So, the experiments are not equivalent unless the
rifle in the second example were moving east with a speed of 470 m/s. If the
rifle was at rest relative to the ground and the observer was not on the
ground but looking from space, she would observe the bullet drop straight
toward the center of the earth as the earth spun under it.
![]() QUESTION:
QUESTION:
I was discussing ballistics with someone the other day, and a thought came up about a detail that I am not 100% sure on.
With bullets designed to expand, generally speaking materials hardness and velocity determine that expansion. What I am wondering, is does the bullet's energy upon striking the target cause the expansion? Or is the expansion caused by the opposite forces imposed on the bullet by what it is striking? (Or would one say it is a combination thereof?)
![]() ANSWER:
ANSWER:
The thing to appreciate is that energy and force are not two
separate things. Everything you need to know about collisions is contained
in Newton's three laws. The idea of energy often makes problems easier to
solve or understand, but the first step in developing the formalism of
energy, called the work-energy theorem, is just Newton's second law "in
disguise". So, I will discuss the bullet collision both ways:
-
The bullet hits a wall and stops. What stops it? The force which the wall exerts on the bullet stops it. It begins expanding when it first touches the wall; a point off axis will start moving perpendicular to the direction of the bullet's velocity which has to mean that it is feeling forces from other parts of the bullet since that point is not touching the wall.
-
The bullet has kinetic energy when it hits the wall. After it stops, that energy is gone. Where did it go? Part of the energy went into doing the work necessary to "squish" the bullet and part was lost to internal friction intrinsic in squishing something soft but not elastic and ends up as thermal energy‚ÄĒthe squished bullet is hot.
![]() QUESTION:
QUESTION:
I am trying to help my son understand velocity, but find myself confused.
-
Person A drives in a circle. A physics website tells me this represents acceleration, a change in velocity, because his direction is constantly changing even though his speed may not be. Fair enough.
-
Person B takes a step forward and then a step backward to his original position. A different physics website tells me that this represents zero velocity, no acceleration, because he has not changed position.
But these answers seem contradictory, because person A, driving in a circle, will arrive at his original position at some point. In this respect, he is no different than person B, and could be considered zero velocity. Can't both of these examples be considered changes in velocity? I suppose it depends on the timeframe you use to measure the change in position (?). So the person driving in a continuous circle can be considered to not be accelerating in some cases? This makes no sense.
![]() ANSWER:
ANSWER:
The first example refers to the instantaneous velocity
and the instantaneous acceleration of person A; instantaneous refers
to an instant in time and both acceleration and velocity are continuously
changing. The second example refers to average velocity and
average acceleration. Average refers to the value of the quantity
averaged over some time period and the time period here is the time from
when he first stepped forward until he finished stepping back. Suppose that
was 10 s and the length of his step was 1 m; then the average velocity is
distance traveled divided by the time, 0/10=0 m/s and the average
acceleration was the change in velocity divided by the time, 0/10=0 m/s2.
Person A's average velocity and acceleration over exactly one time around
would also be zero.
![]() QUESTION:
QUESTION:
If two neutrons (just for the sake of ignoring charge) were separated from each other 1 light year, how long would it take for them to "touch" each other based on their gravitational attraction only? They are also in complete isolation from the rest of the universe.
![]() ANSWER:
ANSWER:
This is a very strange question. I have answered a nearly
identical question before but with much larger masses and smaller distances,
but the method is identical so I refer you
there. For your masses I calculate about 14x1018 years, about
a billion times the age of the universe. (I would also like to add that I do
not believe that this should be taken too seriously because no theory of
gravity has been accurately tested for either such large distances or such
small masses.)
![]() QUESTION:
QUESTION:
I am a fabricator and I currently have a task where I am attempting to create a braking system for downhill rapid propulsion (downhill racing).
Although the product exists, it is primitive and not fit for extreme measures, reliabilty, or convenience. There are many variables besides weight, drag coefficient, mass and gravitational acceleration. I would greatly appreciate your professional advice on creating a formula in which
I could create, change or gauge different systems for different masses. I have done much research and am increasingly frustrated yet interested.
I have come too some conclusions and have run many tests. I am using a polyester blend material for the canopy that is expansive and durable yet retractable, however. My cable system and my rapid cut down on drag are a problem. So my question is if
I weigh 160 pounds I am traveling at a speed between 30-60 miles per hour (we will say 45mph) at a down grade of 45% and i would like a slowing to 10 miles per hour between 40-50 feet from deployment. What would my initial area of my canopy be and what would the tensil strength of my cable need to be set at?
There are 3 points of contact for the cable system two high and one low.
![]() ANSWER:
ANSWER:
First, all air drag calculations are approximate and without
extremely complex computer simulations you can only do order-of-magnitude
calculations. Since you do not mention any sliding or rolling friction of
whatever is going down the incline, I will assume they are negligible. There
are, therefore, two forces on the mass, the gravitational force down the
incline mgsinθ and the drag of your "canopy" up the incline
which I will take as c2v2; here v
is the speed, m the mass, g the acceleration due to gravity,
θ the angle relative to the horizontal, and c2 is a
constant determined by the geometry of your canopy. A reasonable
approximation for c2 is c2≈—ėA
where A is the area presented to the direction of motion of the
canopy (only valid in SI units). Since I am a scientist, I will work
entirely in SI units here. Newton's second law, which governs the motion of
this system, is mdv/dt=-mgsinθ+—ėAv2
or dv/dt=gsinθ[1-(v2/vt2)]
where vt2=mgsinθ/c2=4mgsinθ/A;
vt is called the terminal velocity, the speed to which the
mass will slow as it goes forward. Solving the differential equation (this
is worked out in any intermediate-level classical mechanics book), the
following equation is found: v2=vt2(1-exp(-2gxsinθ/vt2)+v02exp(-2gxsinθ/vt2)
where x is the distance traveled and v0 was the
speed where x=0. That is everything you need since you know
everything except A. And you may want to use a fancier value for c2
more tailored to the details of your canopy. As an example, I will use
your numbers: m=160 lb=73 kg, v0=45 mph=20 m/s,
v=10 mph=4.5 m/s, x=45 ft=13.7 m, θ=450.
Putting these in, I find 20≈(2000/A)(1-exp(-0.094A))+400∙exp(-0.094A)
or A(0.05-exp(-0.094∙A))=5(1-exp(-0.094∙A)). Someone
more clever than I could probably solve this analytically for A, but
I will just solve it numerically by plotting the left and right sides of the
equation and finding the intersection (see inset figure on the left). I find
that A≈100 m2≈1000 ft2; this would be a square
about 30 ft on a side. (Since A is so large, one could have easily
solved this by simply neglecting the exponential functions, 0.05A≈5.)
Regarding the strength of the cables, since I do not have any details about
the design of the canopy, the best I can do is tell you the maximum force
the canopy would exert on the mass via the three cables. Since the
acceleration is -gsinθ+—ėAv2/m, the
greatest acceleration is when the velocity is greatest, when the braking
initiates. So, the force the cables must exert is -mgsinθ+—ėAv02
or -mgsinθ+c2v2. For
your specific example, this force would be about 9500 N≈2100 lb or roughly
700 lb/cable.
The figure on the right shows the solution I have come up with. Indeed it begins at 45 mph and drops to 10 mph at 45 ft. However, one might just as well say that the speed is also just about 10 mph at 25 ft, just not exactly. That is the problem with analytical solutions sometimes‚ÄĒthey demand exactness. To me this graph says that you could get away with a significantly smaller canopy and still qualitatively achieve your goal. I think I have done enough here setting stuff up and you could proceed and investigate how much things would change if you changed your speed at 45 ft to be 11 mph, e.g. And, don't forget, these are approximate solutions to be used as a rough guide.
![]() QUESTION:
QUESTION:
We can use the work-energy theorem in any inertial frame of reference.
When no external force is applied, and there is no change of height, the change in KE = -(Change in PE(spr)).
However, KE change depends upon the frame of reference and the extension of a spring does not depend upon frame's choice! HOW IS THIS POSSIBLE?
![]() ANSWER:
ANSWER:
The extension of the spring is the same in both frames, but the
work done by the spring is not because the same force acts over a different
distance in the moving frame. Forget potential energy and simply write ΔK=W
where W is the work done by any conservative external force, W=0∫XF(x)dx.
I have chosen the starting position as x=0; to keep the algebra
simple, I will also choose the starting velocity in this (x) frame to
be 0 and the final velocity to be V, so ΔK=–ÖMV2=W.
Suppose that it takes time t to reach the position X. Now,
suppose there is another reference frame (x') which has a speed U
in the +x direction and x'=0 at t=0 also. Then
x'=x-Ut and the initial velocity is U and the final velocity is
U-V in this frame, so ΔK'=–ÖM(V-U)2-–ÖMU2=–ÖMV2-MUV.
Finally, calculate the work done in the moving frame: W'=0∫X'F(x')dx'=0∫X-UtF(x-Ut)(dx-Udt)=W=0∫XF(x)dx-U0∫tF(t)dt.
The second integral is the impulse which is the change in momentum,
MV, so W'=0∫XF(x)dx-MUV=W-MUV.
Putting it all together, ΔK'=W'=–ÖMV2-MUV=W-MUV
or –ÖMV2=W.
![]() QUESTION:
QUESTION:
When Cavendish calculated the value of universal
gravitational constant he used mass of lead balls as reference. But how did
he know mass of the lead ball if he doest know the value of G?
![]() ANSWER:
ANSWER:
He could simply weigh them because we know W=mg. Since
you can also write W=mMearthG/Rearth2,
you can identify g=MearthG/Rearth2,
and g is easy to measure even if G is not.
![]() FOLLWOUP QUESTION:
FOLLWOUP QUESTION:
How did he build a weighing scale.
When weight is determined using a scale it should have been built w.r.t certain standard mass. But with out knowing value of G there is no way
 they had a standard mass. He could have weighed a 10kg mass as 1kg mass. So, how did he weight exact mass.
they had a standard mass. He could have weighed a 10kg mass as 1kg mass. So, how did he weight exact mass.
![]() ANSWER:
ANSWER:
The kilogram was officially defined in 1795 as the mass of 1
liter of water. The Cavendish experiment was performed in 1797-98. Even if
the kilogram were not defined, there were other mass definitions which
Cavendish could have used. As an example, let me consider the oldest
standard weight I could find reference to, the beqa (b) (shown in the figure) defined
about 5000 years ago as the mass of 200 grains of barley corn which is about
6.1 grams=6.1x10-3 kg. So if Cavendish had used the b as his mass
standard, he would have found G=6.67x10-11 kg2/(N∙m2)=6.67x10-11
[kg∙s2/m3]x[1 b/6.1x10-3 kg)=4.07x10-13
b∙s2/m3] (assuming that he used seconds and meters for
time and length). It is a different number but means exactly the same thing.
![]() QUESTION:
QUESTION:
A ball thrown upward has zero velocity at its highest point i.e no acceleration. The resultant of applied force and weight/gravity is also zero. Thus the body is at rest. Is it in equilibrium too? This is not a homework question. I and my friend are too confused.
![]() ANSWER:
ANSWER:
Right off the bat, your first sentence is incorrect.
Acceleration of something at rest is not necessarily zero. You cannot
determine whether an object is accelerating by knowing only its velocity
because acceleration is the way the velocity is changing which cannot be
known by simply knowing what the velocity is right now. In your example, the
ball is at rest right now but was moving upwards just before now and will be
moving down just after now. The ball has an acceleration which happens to be
9.8 m/s2; this means that one second before now it was moving
upwards with velocity 9.8 m/s and one second after now it will be moving
downward with velocity 9.8 m/s. It is not in equilibrium because Newton's
second law tells you that any object with a net force on it is not in
equilibrium; the only force (ignoring air drag) on the ball is its own
weight and this force is the source of its acceleration.
![]() QUESTION:
QUESTION:
Does mass affect kinetic energy?
![]() ANSWER:
ANSWER:
Of course. Classically the kinetic energy K=–Ömv2 where
m is mass and v is speed. Relativistically, K=E-m0c2
where c is the speed of light, m0 is the mass of
the object when not moving, the total energy E=√(p2c2+m02c4),
and the linear momentum p=m0v/√(1-v2/c2).
So, you see, mass appears all over the place. The momentum of a massless
particle, the photon, is p=E/c; its energy is all kinetic, and
K=E=pc
since a photon has momentum even though it has no mass.
![]() QUESTION:
QUESTION:
I am currently doing a research paper on the perfect free-kick, could you
find an equation that suits the following variables? The soccer ball is
kicked from the origin of a coordinate system with an unknown velocity such
that it passes through the points (x,y)=(9.15
m, 2.25 m) and (x,y)=(22.3 m, 2.22 m). How can I find the magnitude
and direction of the initial velocity? Just having an equation to help me work with would be very nice.
![]() ANSWER:
ANSWER:
The equations of motion for a projectile which has an initial
velocity with magnitude v0 and angle relative to the
horizontal θ are x=v0xt and y=v0yt-–Ögt2
where v0x=v0cosθ, v0y=v0sinθ,
t is the time, and g=9.8 m/s2. Solving the x-equation
for t, t=x/v0x; putting t into the
y-equation, y=(v0y/v0x)x-–Ög(x/v0x)2.
Since you have two (x,y) data points, you have two equations with two
unknowns, (v0x,v0y). The algebra is
tedious, but the result is that v0x=21.0 m/s and v0y=7.30
m/s; v0=22.2 m/s, θ=19.20. To check my
answer I drew the graph shown to the right (note the different x and y
scales); it looks like my solution passes pretty close to the data points.
![]() QUESTION:
QUESTION:
As when sudden brakes are applied during riding a fast moving bike the back wheel leaves the ground. Why? Also what must be the conditions for the wheel
to not leave ground and when bike semicirculy revolves?
![]() ANSWER:
ANSWER:
To the right is the "free-body diagram" showing the pertinent
forces if the back wheel has not left the ground. The weight mg acts
at the center of gravity of the bike+rider and each wheel has a normal force
(N) and frictional force (f) from the ground. The bike has an
acceleration a in the direction of the frictional forces, so f1+f2=ma.
The system is in equilibrium in the vertical direction, so N1+N2-mg=0.
The bike is also in rotational equilibrium so all the torques about any axis
must be zero; summing torques about the front axle, Rf1+Rf2+DN2-dmg=0
where R is the radius of the wheel, D is the distance between
axles, and d is the horizontal distance between the front axle and
the center of gravity. Now, suppose that the rear wheel is just about to
leave the ground; then N2=f2=0.
The three equations then become N1-mg=0, f1=ma, and Rf1-dmg=0.
Putting the second equation into the third and solving for the acceleration,
a=g(d/R); if you are slowing down any faster than this,
your rear wheel will lift off the ground and the bike will no longer be in
rotational equilibrium. If a is really big, you will keep rotating
until your center of gravity is forward of the front axle; then you will not
be able to stop the bike from rotating all the way over and crashing you on
the ground. This actually happened to me once when I was mountain biking
with my son and I broke a couple of ribs! I do not understand your second
question.
![]() QUESTION:
QUESTION:
My husband is employed as a school bus driver. He repeatedly tells the middle and HS students not to stand in the aisle until the bus comes to a complete stop. He tries to explain to them (without knowing the exact physics behind it) that if they're standing while the bus is moving at say 40 mph, and he has to stop short for some reason, they will not be able to stop their bodies from propelling forward. They never seem to "get it". How can he explain this from a physics point of view that they might better "get"?
![]() ANSWER:
ANSWER:
Are you kidding? You actually think a bunch of rowdy kids is
going to listen to a physics lecture on the bus? If you want a detailed
description of the physics of this exact situation, I have given it in an
earlier answer. Here is a
suggestion which will maybe work: take a tall box with little width, maybe 5
feet tall and 1x1 feet at the base. Have everyone in the bus sit down and
have one student stand the box in the center of the aisle when the bus is
moving at about 40 mph. Have your husband then stop abruptly (not so quickly
that the sitting students might hit their heads) and watch what happens to
the box. Better yet, get a mannequin to stand in the aisle. You could also
put a little cart with wheels in the aisle which would go zipping to the
front of the bus when it stopped. The physical principle is inertia: an
object in motion tends to stay in motion unless acted on by some force (like
if you were holding on to something).
![]() QUESTION:
QUESTION:
A person is standing on a platform. Below him is another person, not wearing a hard hat. The person on the platform drops a standard sized marble. Approximately how high would the platform have to be in order for a marble to cause trauma/injury?
![]() ANSWER:
ANSWER:
This is a little tricky because there is no such thing as a
"standard sized marble". I figured an average marble would have a diameter
of about 1 cm (R=0.5 cm=0.5x10-2 m) and a mass of about
M=1 g=10-3 kg. The second tricky part is that I do not know
how fast a marble needs to be going in order to penetrate the skull which is
how I would judge whether serious injury resulted. I do know that a bullet
which has roughly 10 times the mass of a marble will penetrate the skull at
a speed of about 60 m/s (about 130 mph). So, I would conclude that a marble
would have to be going quite a bit faster to penetrate the skull since it
would bring in a lot less momentum than a bullet with the same speed. So the
first question I will ask is what will be the speed if I drop it from a
height of h=5 miles (about 8000 m). Now, if you were just going to do
a simple introductory physics problem you would say "neglecting air
friction" the time to fall would be about t=√(2h/g)=√(16,000/10)=40
s and the speed at the ground would be about v=gt=10x40=400 m/s
(about 900 mph); I would guess that would do some serious damage! But wait!
It would be a really big mistake to say that air friction was negligible for
something going 900 mph. The drag on a falling object in air depends on how
fast it is going and can be approximated as F≈—ėAv2
(all quantities must be in SI units) where A=πR2≈2x10-5
m2 is the cross sectional area. When the drag is equal to the
weight, F=mg≈10-2 N, the marble will stop accelerating and
continue falling with the terminal velocity, vt=√(4mg/A)≈45
m/s (about 100 mph). So, since 45 m/s is much less than the 60 m/s necessary
for a bullet to penetrate the skull, I am guessing that no matter how high
you drop the marble from, it will not cause truly serious injury‚ÄĒit's going
to hurt though!
![]() QUESTION:
QUESTION:
Here is the scenario. I have a A volt motor that supplies B watt
to work. I connect the motor to a circular disc of R radius that is of M
mass and has a density of 1 unit. I want to use the motor to move a conveyor
belt of mass N. I will place an object of mass K on the conveyor belt. Is it
possible to find the velocity of which the object will be moving at given
the voltage? Or perhaps can we find the minimum about of voltage that is
needed to move the object. Assume that the efficiency of all the motor as
well as the whole thing is 100% and that frictional force and air resistance
can be neglected. You can add othervariables in either.
![]() ANSWER:
ANSWER:
This is an engineering problem, not physics.
However, it sounds to me like there is no answer if you have no frictional
losses because the motor will just keep adding energy to the system and
there is no loss.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
However, it should be able to work since the motor is attached to a conveyor belt, yes it will keep going but it will kep moving the conveyor belt only.
![]() ANSWER:
ANSWER:
If the motor is adding energy (B watts would mean B Joules of energy per second are being added) and there are no losses, where is that energy going? It will constantly accelerate the conveyer belt.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Is it possible to find the acceleration of the conveyor belt?
![]() ANSWER:
ANSWER:
Yes! Refer to the picture above. Suppose the mass and the
conveyor belt move with speed V; then the angular velocity of the
disc is ω=V/R. The moment of inertia of the disk is I=–ÖMR2.
The kinetic energy of the belt plus mass is KE1=–Ö(K+N)V2
and of the disc is KE2=–ÖIω2=—ėMV2,
so the total kinetic energy is KE=–Ö(–ÖM+K+N)V2.
The rate of change of the kinetic energy is equal to the power B,
B=(–ÖM+K+N)V(dV/dt)=(–ÖM+K+N)Va
where a is the acceleration. Solving, a=B/[(–ÖM+K+N)V]≡C/V.
Note that when V=0, a=∞; this just means that the motor cannot
deliver power unless it is actually spinning with some rate. But, as soon as
it gets moving it will have a very large acceleration which decreases as the
speed gets bigger and bigger. So, if you are really interested in such a
system, you will have to determine energy losses and probably also have a
motor with an adjustable power output. (Also, note that the voltage has
nothing to do with it, all you need is the power output.)
![]() QUESTION:
QUESTION:
If you have two weights, where one is 100 grams and the other is 200 grams and you use the same spring to create a pendulum with them (one at a time) why isn't the amplitude the double for the heavier weight?
(This is the result of an exercise we did, my personal curiosity, and my teacher's unwillingness to explain
because he says it's too complicated for our level.)
![]() ANSWER:
ANSWER:
I think you must surely mean a mass on a spring oscillating
vertically, not a pendulum. That is what I will assume. You have probably
not studied energy yet which is why your teacher did not want to get into
it. Energy methods are, by far, the easiest way to answer your question
which is what I will do. Two things you need to know: potential energy of a
spring which is stretched by an amount y is –Öky2
and gravitational potential energy of something a distance y above
where y=0 is mgy. Imagine taking a mass m and attaching
it to a spring with spring constant k which is unstretched and
holding it there for a moment. Where it is right now I will define to be
y=0 and so, since the spring is unstretched, the total energy of the
system is –Ök∙02+mg∙0=0;
the energy never changes. As it falls it speeds up for a while and then
slows down for a while (acquiring and then losing what is called kinetic
energy, energy by virtue of motion), finally stopping and going back up.
If it has fallen some distance A (for amplitude) before turning
around, the energy is now 0=–ÖkA2+mg(-A)
and so we find two solutions (it is a quadratic equation), A=0 (we
already knew it was at rest there) and A=√(2mg/k). So,
you see, the amplitude is proportional to the square root of the mass, not
the mass. (Incidentally, most folks would call the amplitude of this
oscillation to be –ÖA. I thought it would be clearer this way.)
![]() QUESTION:
QUESTION:
Is it possible to derive the formula for Kinetic Energy without using work? Or are they linked by definition?
![]() ANSWER:
ANSWER:
Well, I can tell you that you never have to utter the phrase
"work is defined as…" The work-energy theorem is merely the integral form of
Newton's second law. For simplicity, I will do this simple derivation in one
dimension. F=ma=m(dv/dt)=m(dv/dt)(dx/dx)=m(dv/dx)(dx/dt)=mvdv/dx.
Rearrange: Fdx=mvdv. Integrate:
![]() QUESTION:
QUESTION:
I came across your site while looking for the answer of a physics problem I would like to program in a Smartphone app.
A toy car is dragged from position A to B giving it an initial velocity (v=d/t). At point B the car is released where it travels in a straight line until the frictional force of the ground stops the toy car completely (position C). I would like to find a formula that relates the distance from B to C with the initial velocity provided from A to B.
![]() ANSWER:
ANSWER:
Of course, you have to know the frictional force f and
the mass m of the car in general. Assuming that the force is constant
all along the path B to C, the distance s can be written s=–Ömv2/f.
In most cases f is proportional to m so that you do not
need to know the mass. If you are on level ground, f=μmg where μ is called
the coefficient of friction and g=9.8 m/s2 is the
acceleration due to gravity (mg is the weight of the car). The
coefficient just is a parameter which is small if there is little friction.
So, finally you have s=v2/(2μg). If the car is on a
slope making an angle θ with the horizontal, s=v2/(2μg∙cosθ).
![]() QUESTION:
QUESTION:
Okay I have wondered this question for many years, and more over have
wondered how to ask it! So I think a scenario is best; when an object is
propelled forward or in any direction very rapidly, let's say for this case
a bullet out of a gun, does it advance through every speed in between it's
current speed, zero, and it's maximum velocity or does it simply "jump" from
zero to it's maximum velocity? And also the same for when it hits its
target, let's say a thick steel plate does it go from its current velocity
straight to zero, or is there some sort of slowing down in which it goes
through every speed in between?
![]() ANSWER:
ANSWER:
Fundamental to classical physics is Newton's second law. That
which changes the speed v of something is a force F, a push or
a pull. Further, the bigger the rate of change of speed (acceleration a),
the bigger the force‚ÄĒdouble the force and you double the acceleration. This
is often written as F=ma where m is the mass of the object. Suppose
that you shoot a bullet from a gun. The bullet starts with a speed v=0
and ends with speed v and this happens in some time t and so
the acceleration can be written as a=v/t. If, as you suggest, the
bullet "jumps" instantaneously to v, then t=0. But for t=0
the acceleration would be infinitely large which would imply that you had to
push on it with an infinite force. The same reasoning can be applied to
stopping the bullet. You know that the force propelling or stopping a bullet
in the real world is finite. It is a pretty good rule-of-thumb for everyday
occurances that there are no infinities or discontinuities (instantaneous
changes) in the universe.
![]() QUESTION:
QUESTION:
Please help a work related dispute. Can the weight of a patient in a wheelchair be calculated using f=Ma? Even if it's a guesstimate?
I thought, if m= F/a
Where a = V2-V1 / t Where V2 is the velocity of the chair (and porter?) and V1 is coming to a stop.
Would F be the mass of the porter multiplied by the common acceleration of chair and porter?
I'm guessing if I clock the speed of the porter I can calculate a.
![]() ANSWER:
ANSWER:
I guess that "porter" means the guy pushing the chair. You have
it all wrong, I am afraid. But, it is worth talking about for a bit. There
are three masses involved here, Mpatient, Mchair,
and Mporter. There is an acceleration a which we
can agree could be roughly measured by measuring times and distances.
Suppose we first look at all three and call the sum of their masses M.
Then M=Fall/a where Fall is the
force which is causing the collective mass to stop. If you neglect the
friction which would eventually stop the wheelchair with no porter, Fall
is the frictional force between the porter's feet and the floor; you do not
know that force. Suppose you focus your attention on the patient. Mpatient=Fpatient/a
where Fpatient
![]() QUESTION:
QUESTION:
I am writing a couple of SF novels that take place in significant part on a beanstalk station, i.e. a space elevator station located in geosynchronous orbit, and my question concerns the design. In my stories, the station is about a half mile wide with a shape similar to a hockey puck. The center third of the puck is attached to the elevator ribbon (both up to the counterweight and down to the planet of course) and fixed, therefore essentially in freefall.
My question concerns the outer section, which in my story spins in order to provide some g-force: is this a viable model? Some of my concerns are that the spin will create a gyroscopic effect as the station orbits around the Earth that will twist it off the ribbon or perhaps exert other forces on the hub that I'm not accounting for. One possible solution I thought of would be to split the outer section into two rings rotating in opposite directions to cancel out those effects.
Assuming some clever engineer works out the minor details of moving between the hub and the rotating section(s) is this design plausible? I like the science in my science fiction to be accurate and reasonable.
![]() ANSWER:
ANSWER:
I believe you are right to worry about the rotation causing
problems. If you just forget about the elevator and have a rotating "puck
station" in orbit, its axis will always point in the same direction in space
(conservation of angular momentum); so, if it were in a geosychronous orbit,
from earth it would appear to do a 3600 flip every day. I think that having a
counter-rotating ring would be a very good idea, the ring having the same
angular momentum (moment of inertia times angular velocity) as the main
station. If the station has a radius of about a quarter of a mile, about 400
m, the angular velocity ω needed to have an earth-like artificial
gravity (g=9.8 m/s2) at the edge would be ω=√(g/R)=0.16
radians/s=0.025 revolutions/s≈1.5 rpm.
![]() QUESTION:
QUESTION:
I need a very brief explanation for Kindergarteners. (I just
want to use the right words; they can learn the details of what they mean
later.) In an amusement park ride in which long swings are spun around a
central pole, why do the swings rise up as the pole spins faster? (I assume
it's the same reason that a skirt rises up when the person wearing it
twirls.) Is it something to do with centrifugal force? Centripetal force?
Nothing I saw on the web about these forces seems to explain why the objects
rise, only why they move to the inside or outside of the orbit.
![]() ANSWER:
ANSWER:
For Kindergarteners, use of centrifugal force is probably best.
I guess the merry-go-rounds we had on playgrounds when I was a kid have been
deemed unsafe, but get your students to appreciate that the faster they are
spun on something akin to this, the harder it is to hang on. This is because
the centrifugal force which tries to push them off gets bigger as the
merry-go-round spins faster. Then you can just take a pendulum and
demonstrate that the harder you pull, the higher it rises. The little
diagram to the right shows the effect of the the centrifugal force F which will lift the pendulum bob higher as
it pulls harder.
![]() QUESTION:
QUESTION:
I have a question that been thats been unanswered from quite some time now. I even tried asking that to a person in NASA houston and he couldn't even understand. Hope you can help.
We know that space dust and debris keep on falling on earth. And I have read that its many tons a day. Considering mass of earth is increasing every day for millions of years now, how does it affect its revolution, speed and axis. Or does it even affect that.
![]() ANSWER:
ANSWER:
One estimate is that the earth gains 40,000 metric tons (4x107
kg) per year. So, in a million years that would be a gain of 4x1013
kg. The mass of the earth is 6x1024 kg. The moment of inertia
will be proportional to the mass times the square of the radius, so,
assuming the change in radius is negligible, the fractional change in moment
of inertia over a million years would be approximately 4x1013/6x1024≈10-9=10-7
%. Since angular momentum (moment of inertia times angular velocity) is
conserved, this would mean that the angular velocity would decrease by about
10-7 %, an increase in the length of a day of about (24 hr)(3600
s/hr)x10-9≈10-3
seconds in a million years!
![]() QUESTION:
QUESTION:
I was explaining conservation of energy to my daughter when she was spinning on our office chair, and her rotational velocity increased as her moment of inertia decreased when she pulled her arms and legs toward the rotational axis. Is there an analogous example for linear motion, where the linear velocity increases as the mass decreases? I can't think of a real-world example of a body whose mass decreases (or increases).
![]() ANSWER:
ANSWER:
Actually, you were demonstrating conservation of angular
momentum, the product of the angular velocity and moment of inertia remains
constant for an isolated system. Energy is not conserved because rotational
energy is proportional to the product of the square of the angular velocity and moment of inertia.
But, you explained it correctly for your example. So, your question is if it
is possible for conservation linear momentum, the product of mass times
velocity, to result in a changed velocity due to a change of mass. You do
not usually see as many examples of this as for angular momentum because
rotating things change shape frequently whereas moving objects usually do
not have significant change of mass. The classic example is a conveyer belt
onto which mass is being dropped from a hopper. If you had a very long
frictionless conveyer belt with mass on it, it would have a certain linear
momentum. Now, if you start dropping mass on it, it will slow down.
Similarly, if you let mass drop off the end of the conveyer belt without
replacing it, it will speed up.
![]() QUESTION:
QUESTION:
How long does it take to stop a 7000 lbs vehicle at 45 mph? Time and distance please.
![]() ANSWER:
ANSWER:
You have not given me enough information, in particular what are
the wheels and the surface made of; surely you realize that a truck stopping
on ice will go much farther than a truck stopping on a dry road. I will work
it in general and then calculate it for a typical example. The quickest stop
you can affect is to apply the brakes hard enough that the wheels are just
about to start skidding; that is what anti-skid braking systems do.
Therefore the force F which is stopping you (on a level road) is the static
friction between the road and the wheels, F=μsW
where μs is the coefficient
of static friction between the wheels and the road, W=Mg is the
weight of the vehicle, M is the mass, and g=32 ft/s2
is the acceleration due to gravity. But, Newton's second law tells us that
also F=Ma where a is the acceleration of the vehicle.
Therefore, the acceleration is independent of the mass of the vehicle and
the acceleration is a=μsg.
Now that you have the acceleration you can write the equations of motion
for position x and velocity v as functions of time t:
x=v0t-–Öat2 and v=v0-at
where v0=45 mph=66 ft/s. Now, you need to specify
what μs is. For example, μs≈0.9 for rubber on
dry asphalt, so a≈0.9x32=28.8 ft/s2 and I find t≈66/28.8=2.3
s and x=66x2.3-–Öx28.8x2.32≈76 ft.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I'm trying to figure out if a traffic light at an intersection is timed too short for a heavier vehicle to stop in time. The speed limit is 45mph, the vehicle weighs ~7000 lbs (7200 empty w/driver) , there is a downward slope of which I'm trying to find out. Yes to dry pavement. What would you need to figure surface area of rubber/tire? And I need to time the light still. With all of the above information would you be able to calculate that?
![]() ANSWER:
ANSWER:
As I showed above, the weight is irrelevant. Of course, this is
an approximation as all friction calculations are, but a quite good one for
this situation. It is also important that my calculation is the shortest
time and minimum distance, what you would get by flooring the brake pedal
with anti-skid braking operating. If you do not have anti-skid braking and
you lock your wheels, it will take longer and go farther. Also, there is the
possibility that μs
could be different from 0.9 depending on local conditions (temperature,
surface condition, etc.). It is important to include the slope in the
calculation. If the slope is down as you say, the acceleration (I am
assuming you are not interested in the details) is a=32(μscosθ-sinθ)
where θ is the angle of the
slope; for example, if θ=200
and μs=0.9, a=32(0.9x0.94-0.34)=16.2 ft/s2,
quite a bit smaller than the value of 28.8 ft/s2
![]() QUESTION::
QUESTION::
Nothing can accelerate itself by applying force on itself. Besides, isolated forces do not exist and they exist in an action reaction pair.
These are the essence of Newton's third law. When an engine exerts force on a bike how can it accelerate the bike taking bike as a system in this argument? After all, a part is exerting force on another part , right?
![]() ANSWER:
ANSWER:
The engine exerts a torque on a wheel trying to make it spin. If
the bike were on ice, the wheel would spin, there would be no acceleration
and therefore there must have been zero net force on the bike+engine as you
surmise. However, if there is friction between the wheel and the ground, the
ground exerts a force on the wheel which is forward; this is the force which
drives the bike forward. Note that the wheel exerts a force backward on the
ground (Newton's third law) but the ground does not move because it is, effectively, infinitely
massive.
![]() QUESTION:
QUESTION:
When a bullet hits a door and gets embeded in it, no external force acts on the system of door and bullet but why is linear momentum not conserved and the angular momentum conserved? Can you give some examples where angular momentum is conserved but not linear? Can it be possible to have both linear and angular momentum conserved?
![]() ANSWER:
ANSWER:
I presume you are alluding to the classic introductory physics
problem of a bullet hitting a door mounted on frictionless hinges. Angular
momentum is conserved if there are no external torques, and since hinges
cannot exert a torque, it is. Linear momentum is conserved if there are no
external forces but the hinges exert a force on the door during the
collision time and so it is not. If the hinges were not there, the door and
the bullet would move forward and rotate about their center of mass
conserving both linear and angular momentum.
![]() QUESTION:
QUESTION:
What is the change in velocity of the earth's rotation if a person (myself) who weighs 60 kg were to stand on something about a foot tall.
Ps this is not a homework question, I'm just a curious teen who's never taken physics. Also it's the middle of the summer for me in
New Orleans.
![]() ANSWER:
ANSWER:
The glib answer to this question would be, for all intents and
purposes, the change in rotation would be zero. It is a good opportunity
to talk about the physics involved and to estimate how small small is here. The moment of inertia of the earth is about Ie=8x1037
kg∙m2. Your moment of inertia if you are on the earth's
surface is about Iy=60x(6.4x106)2=2.5x1015 kg∙m2. The moment of the
earth plus you is I=Ie+Iy≈Ie=8x1037.
If you increase your distance by the amount 0.3 m, about 1 ft, your moment
of inertia increases to Iy+ΔI=60x(6.4x106+0.3)2=Iy(1+4.7x10-8)2≈2.5x1015(1+2x4.7x10-8)=2.5x1015+ΔI
and so ΔI=9.4x10-8 kg∙m2. So you and the earth
start with I=8x1037
and end with I+ΔI=
![]() QUESTION:
QUESTION:
If an astronaut caught a ball in space, the ball would cause the astronaut to move backwards with the force the ball was moving at correct? then, as the astronaut is still moving backwards and throws the ball back where it came from, would the astronaut move even faster with the force of throwing the ball? or would their speed remain the same?![]() ANSWER:
ANSWER:
When she catches the ball, she exerts a force on it to
stop it (relative to her); the ball exerts an equal and opposite force on
her causing her (and the caught ball) to move in the direction the ball was
originally moving. When she throws it back, she must exert a force on it
opposite the direction she is moving; the ball exerts an equal and opposite force on her
causing her to move even faster in the direction she was moving. These are
examples of Newton's third law.
![]() QUESTION:
QUESTION:
What is mass?![]() ANSWER:
ANSWER:
There two kinds of mass. Inertial mass is the property an
object has which resists acceleration when a force is applied; the harder it
is to accelerate something, the more inertial mass it has. Gravitational
mass is the property an object has which allows it to feel and create
gravitational forces; for example, the more gravitational mass an object has
the greater the force it will feel due to the earth's gravity‚ÄĒthe more it
will weigh. It turns out that the two masses are actually identical; this
fact is one of the cornerstones of the theory of general relativity.
![]() QUESTION:
QUESTION:
My question is for a legal nature. I was recently in a head on collision. The crime scene analysis could not determine the speed of my vehicle but police reports indicated the other vehicle was doing 45+- mph. We were on a dirt road on impact. The vehicle going 45+- continued to travel 20 ft past impact pushing my vehicle back 40 ft. His vehicle is a 1 1/2 ton dodge ram and my vehicle was a 1 3/4 ton dodge caravan. What speed was my vehicle? This will be instrumental in a lawsuit currently being filed. Your help would be greatly appreciated. ![]() ANSWER:
ANSWER:
I am afraid that the speed cannot be determined from this
information for several reasons:
-
I do not know how much energy was lost in the collision.
-
I do not know whether the wheels were locked (brakes applied) or not.
-
I do not know the frictional forces which ultimately brought the vehicles to rest.
-
I believe the weight of the Dodge Ram is wrong. The Dodge Ram 1500 is referred to as 1–Ö tons because this is the maximum recommended load. An unladen Ram 1500 weighs more than 6000 lb; I found that the weight of the Caravan is about 1.75 tons, though.
![]() QUESTION:
QUESTION:
Friction opposes the relative motion between two surfaces. when a car travels on a circular path , how can the friction act sideways to provide necessary centripetal force. The friction should act backward relative to the motion of the car. the car doesn't tend to go sideways outward, then, how does friction act sideways?![]() ANSWER:
ANSWER:
There are two important classes of friction, kinetic
friction which occurs when two surfaces are sliding on each other and static
friction when they are not sliding. Kinetic friction is the one which
usually (but not always) acts opposite the direction of motion; an example
of kinetic friction acting in the direction of motion is a car which is
accelerating from rest and spinning its wheels‚ÄĒthe friction force on the
spinning wheels by the road is forward. Static friction can point in any
direction, depending on the situation. If a box is sitting at rest on an
incline, the frictional force points up the incline to keep it from sliding
down. If a car is moving but not skidding, the appropriate friction to think
about is the static friction between the wheels and the road. Think
about a very icy road; to drive around a curve at high speed is impossible
because there is no static friction and the car simply continues going
straight regardless of whether you turn the steering wheel or not.
![]() QUESTION:
QUESTION:
Gravitational potential energy is the term
that means the work done by the gravitational force to take an object to the gravitational field. Here the displacement is towards the force.So,it (Gravitational potential
energy) should be positive.But it is negative.Why?![]() ANSWER:
ANSWER:
You need to be a little more careful in how you define
potential energy. And, what is actually defined is the potential energy
difference between two points in space. The definition is ΔU=U(r')-U(r)=-
![]() QUESTION:
QUESTION:
ok, two stones. Both spherical and same mass and
density evenly spread in each stone. Set each about 1/2 the distance to the
moon. One leading the earth's orbit and one following the earth's orbit.
Both not moving relative to the earth, yet the same speed as the earth as it
moves around the sun. No tangent or orbital speed, the stones are starting
in freefall. Which gets to earth's surface first, neglecting
air drag.![]() ANSWER:
ANSWER:
Since you stipulate that the stones are not
orbiting, the stones are at rest with respect to the sun and the earth is
not. Therefore, the stone on the leading side of the orbiting earth will win
the race because the earth is moving toward it and away from the other when
the stones start dropping.![]() BETTER
ANSWER:
BETTER
ANSWER:
I see that I misread this question. I guess you meant there is no orbital
speed around the earth. To make this manageable at all I will neglect the
influence of the moon and assume a
spherically-symmetric mass distribution of the earth. In the figure
above, I show your two stones and the forces (blue arrows) on them. The
down-pointing forces are the from the sun (keeping them in orbit) and the
horizontal forces are the weights making them want to fall toward the earth.
The distances and forces are not drawn to scale; when the stones are about
30 earth radii away from the earth center (the moon is about 60 earth radii
away), the weight forces are about 2 times larger than the sun forces. The
big blue arrow shows the direction everyone is orbiting the sun. So, the
leading stone slows down its orbital speed and so will slightly fall toward
the sun as it falls toward the earth; the trailing
stone increases its orbital speed and so will slightly fall away from the
sun as it falls toward earth. These deflections are shown (probably quite
exaggerated) by the red arrows. Given the symmetry of the situation, I
would expect the two to be at the same distance from the center of the earth
at any given time‚ÄĒwhich is the
crux of your question, I think. To actually do this more quantitatively,
though, would be very hard because as the stones were deflected the weight
force would change direction now having a vertical component in the figure.
![]() QUESTION:
QUESTION:
I have a 10' long trailer I am using to haul a 4,000# symetrical object that is 6 ft in length. I was told to move it forward of the axle on the trailer to put some weight on the tongue for safety and better hauling. The maximum wt my pick up truck can hold on its hitch is 650#. I have tried to find equations for this on-line as it would be very useful for me to know how to adjust other loads as well. There are plenty of equations on-line that deal with finding the CG, but I can't find one that discusses how the weight on the tongue changes as the load is moved fore or aft of the axle. Trailer/towing experts just wing it. Do you know of an equation that would help me?![]() ANSWER:
ANSWER:
I will assume that the unladen trailer will have
approximately zero force on the hitch (which would mean that its center of
gravity (COG) is at the axle). You need to know where the COG of the load is; in your
specific case, you know that it is at the geometrical center (you said it is
symmetrical), 3' from either end. For loads not symmetrical, you need to
find it. I will call the distance between the axle and the hitch L.
Suppose that the COG is a distance x from the hitch. Then, the sum of
the torques about the axle must be zero, so Hx=W(L-x) where
H is the force (up) by the hitch and W is the weight (down) of the load.
Solving this, x=[W/(H+W)])L. For your case, with
H being 650 lb (although I cannot see why the maximum would be the
optimal) x=(4000/4650)L=0.86L. If your
trailer has more than one axle or its COG is not over the axel, I would need
more information like the geometry and weight of the trailer.

![]() QUESTION:
QUESTION:
Here's a question that I have been pondering. If a truck is driving on the freeway and a car pulls in closely behind the moving truck to take advantage of the draft created by the truck is there an energy cost to the truck or is having a car in it's wake energy neutral?
My gut feeling is that there would be a slight energy cost to the truck due to it's turbulence wake being interfered with.
![]()
 ANSWER:
ANSWER:
This, I discovered, is not a trivial question. For a
lengthy discussion, see
The Naked Scientists. Here is my take on it. There is no question that
the trailing car consumes less gas. The reason for this is not so much that
the truck is pulling the car but that the car experiences a much lower air
drag when drafting; the drag is approximately proportional to the square of
the velocity and the truck's wake is moving forward with the truck. What
seems to be controversial is the crux of your question‚ÄĒis
there a cost to the truck? Some argue that the composite truck-car system
has less total air drag, others that there is a net cost to the truck which
need not (and almost certainly will not) equal the gain by the car. There is
certainly no conservation principle here because the new system has
different forces on it than the separate systems. My feeling it that there
is at least a small cost to the truck and I base this on an observation from
nature. Why do geese fly in a V? There is less overall air drag than if the
flock all flew individually. But periodically, the leader drops back and
another goose takes a turn at the front; must be because the leader has to
do more work.
![]() QUESTION:
QUESTION:
A
friend asked me this and we disagreed with the answer.
If we put 25 kg of weight on top of 25 kg person, how much force would he
feel?
![]() ANSWER:
ANSWER:
Technically, a kilogram is not a weight but a mass. But,
since so many countries use it as a weight, I will do that for this problem.
The person feels the downward force of her own weight, 25 kg; the downward
force of the object pushing down on her, 25 kg; and the upward force of the
floor pushing up on her, 50 kg. The net force is zero because she is in
equilibrium.
![]() QUESTION:
QUESTION:
If an ultra high energy cosmic ray with energy of 1020
eV were to strike an astronaut will that kill an astronaut?
![]() ANSWER:
ANSWER:
This is only about 6 J of energy. That is the energy
needed to lift 1 kg about 60 cm. And, it would probably not leave all its
energy in the astronaut. Certainly would not kill her.
![]() QUESTION:
QUESTION:
If an ultra high energy cosmic ray with energy of 1020
eV were to strike an astronaut will that kill an astronaut?
![]() ANSWER:
ANSWER:
This is only about 6 J of energy. That is the energy
needed to lift 1 kg about 60 cm. And, it would probably not leave all its
energy in the astronaut. Certainly would not kill her.

![]() QUESTION:
QUESTION:
I have a question releated to weight/mass placement on a bar. My friend and I are weight lifters. We got into a discussion about the center of gravity on the bar. Here is the question. If we are using a 45 pound plate on each side and also have a 5 and 10 on each side. Each taking up the same space and the end of the bar is the same distance from the last weight and will not change. Does it change anything if the weights are not in the same order, from one side to the other? My friend says the side with the 45 pound plate close to the end is slightly heavier becuase the ratio has changed. I say nothing has changed becuase the weights on the bar are still taking up the same space. I believe it would only change if the distance to the end of the bar is changed, which it is not. I hope I explained this
well enough.![]() ANSWER:
ANSWER:
Assuming that the bar itself is uniform (has its center
of gravity (COG) at its geometrical center), the COG of the total barbell
depends on the location of the weights. Relative to the center of the bar,
the position of the center of gravity may be written as COG=(45x1+10x2+5x3-45x4-10x5-5x6)/120
where the xis are the distances of weights from the
center. Suppose that the weights are placed symmetrically (x1=x4, x2=x5, x3=x6);
then COG=0, the center of the bar. Now, suppose we interchange two of the
weights, exchange the 45 lb with the 10 lb on one side: COG=(45x2+10x1+5x3-45x4-10x5-5x6)/120=(45x1+10x2-45x2-10x1)/120=(35/120)(x1-x2);
since x1≠x2,
COG≠0, the barbell is no longer balanced. If that explanation is too
mathematical for you, try a more qualitative argument. Each weight W
a distance D from the center exerts a torque about the center and the
magnitude of that torque is WD. The net torque due to all weights
must be zero if the bar is to balance at its center. This means that the sum
of all the WDs on one side must be precisely equal to those on the
other if the barbell is to be balanced about its center. If you change the
Ds on only one side, the bar will not be balanced at its center.
(This qualitative argument is just the mathematical argument in words.) What
certainly does not change is the total weight.

![]() QUESTION:
QUESTION:
After watching the Bond classic YOU ONLY LIVE TWICE, I read that the scene where a craft in space overtakes a capsule ahead in the same orbit in order to "swallow" it, but would be impossible because it would have to be in a separate orbit. Then when it catches up, turn vertical and move upward. Why is it not possible for an object to accelerate in the same orbit as a slower object?
![]() ANSWER:
ANSWER:
If the two satellites were in the same orbit, they would
maintain the same separation. If they were in different but crossing orbits,
you could have them come together if properly synchronized; if you were to
observe this, say from the perspective of the "chased" satellite, it would
appear that the other satellite was coming at you from slightly above or
below. Finally, if the "chasing" satellite had rockets which he could point
in any direction with any thrust, he could move exactly on the same path as
the "chased" satellite but with a different speed.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I don't grasp the physical law that would prevent the "chasing" capsule to catch up in the same orbit (as we see in the movie) if its thrusters accelerate it.
![]() ANSWER:
ANSWER:
It is easiest if we just think about circular orbits;
near-earth orbits are nearly circular and I will consider only orbits whose
altitude is very small compared to the radius of the earth. With each orbit
there is one special speed v for an orbiting satellite where the
centripetal force equals the weight, mv2/R=mg or v=√(gR)
where g is the acceleration due to gravity, R is the radius of
the orbit (approximately Rearth), and m is the mass
of the satellite. If you are going faster or slower than that you will not
be in that circular orbit but some elliptical orbit which happens to cross
the circular orbit. But, let us just suppose that you are going a little
faster than v, say v+u where u<<v; you got there
by briefly firing your rockets out the rear tangent to the orbit. If you do
nothing else, you leave that orbit. However, the force necessary F to
keep you in that orbit would be m(v+u)2/R=F.
But part of F is the weight, so you can write F=mg+f where
f is what your rockets have to do. Therefore f=m(v+u)2/R-mg=m(v2+2vu+u2)/R-mg.
Now, mv2/R=mg from above and you can
neglect u2 because it will be very small compared to 2uv,
so f≈2muv√(g/R); you would have to point your
rockets away from the center of the earth so that this force would be down
but you would keep on that circular orbit going faster than other satellites
in that same orbit.
![]() QUESTION:
QUESTION:
For a statement to be a law it must be based on observations and
experiments. Newton, certainly didn't perform experiments to verify his universal law of gravitation.
Was it correct then to state it as a law?
![]() ANSWER:
ANSWER:
Newton may not have done the experiments, but his law was
the result of experiments done by others. Most important were
Kepler's three laws which were empirical summaries of a large body of
data on the motions of the planets. His law of gravitation, F=-MmG/r2,
provided a complete explanation of Kepler's laws. However, since the mass of
the sun was not known, only the product MG could be determined from
the data. A good
measurement of G was not done until more than 70 years after
Newton's death. Because gravity is such a weak force, this is a very
difficult measurement to make on a laboratory scale.
Basically, this is just a terminal velocity
problem. Suppose that we imagine just releasing a spherical balloon with
radius R, volume V=4πR3/3, cross sectional
area A=πR2, and mass m under water. The net
force upward would be F=ρgV-mg=4ρgπR3/3-mg
where ρ=1000 kg/m3 is the density of water and g=9.8
m/s2 is the acceleration due to gravity. The drag force can be
approximated as f=πv2R2ρCd/2
where the drag coefficient for a sphere is Cd=0.47 and
v is the speed of the balloon. So the net force is
Fnet=4ρgπR3/3-mg-πv2R2ρCd/2
and this is zero when v=vt, the terminal velocity, vt=√[(8gR/(3Cd))-2mg/(πR2ρCd))];
the second term in the square root is much smaller than the first because the mass of the
balloon is very small (about 0.04 kg if R=0.1 m and the air is at
atmospheric pressure) compared to the buoyant force. This is how fast a
balloon would rise in still water. So, that would be the speed the water
would have to be moving down for the balloon to stay in place. I did a rough
calculation for R=0.1 m and found vt≈2.4 m/s. These
estimates are all for the size of the pipe much greater than the size of the
balloon. Things get much more complicated if that is not the case, but you
would still be able to use the water flow to keep the balloon in place.![]() QUESTION:
QUESTION:
This question is in regards to flowing water and buoyancy. Lets say I have two connected reservoirs at different heights, therefore creating a pressure difference and fluid flow between them. There is a pump that refills the higher reservoir so the flow is constant, and there is a section of tubing that is vertical. If I were to put a buoyant object like a balloon in the vertical section of tubing with flow, could I keep it from floating to the top with enough flow? Basically can fluid flow in the opposite direction of the buoyancy force keep it from floating. I feel like it can but I am having trouble understanding why (seems like the only factor is density/displacement, maybe fluid flow increases drag?), just curious because my friend and I got into a random debate about it.
![]() ANSWER:
ANSWER:
Usually when we
think of buoyant forces we are thinking about fluid statics, all fluid at
rest. Your balloon in the tube will experience a buoyant force up and a
force down from its weight just as it would in a nonmoving fluid. If the
water is moving down, the balloon will also feel a downward force due to the
drag it experiences. What this drag force is will depend on the size of the
balloon, the size of the tube, and the speed of the water. It would be very
complicated to calculate, but I am sure there would be a correct speed for
any geometrical situation where the balloon would remain stationary. If that
is enough, you can stop reading here. If not, here is an example below:

![]() QUESTION:
QUESTION:
Using real-world estimates for the coefficient of friction between his feet and the ground, how fast could the Flash run a quarter-mile? Assume that the limiting factor for his acceleration is the force parallel to the ground that his feet can apply.
![]() ANSWER:
ANSWER:
Suppose he is running on a dry asphalt road with
rubber-sole shoes. Then the coefficient of static friction is approximately
μ≈0.8. The maximum force of friction on level ground would be fmax≈μN=μmg≈8m
where m is his mass. So, his acceleration would be a=fmax/m=8
m/s2. A quarter mile is about 400 m, so assuming uniform
acceleration the appropriate kinematic equation would be 400=–Öat2=4t2,
so t=10 s.
![]() QUESTION:
QUESTION:
I have a doubt about static friction and number of wheels.
As for elementary physics principles
1) static friction depends is mass times the coefficient of static friction
2) static friction does not depend on surface static friction is independent by the number of wheels.
... but it is hard to accept to me!
Let's suppose to design a cart to be pushed by a worker. The total weight (cart + content) is about 1000 kg.
The question is: as for the static friction it is better to use 4 or 6 wheels?
![]() ANSWER:
ANSWER:
If the cart is to be "pushed by a worker" it is not
static but rather kinetic friction which is in play unless all the wheels
are locked. And this is not friction due to the contact between the wheels
and the ground but friction due to the axles rubbing on the wheels. But,
let's talk about friction anyway because you seem to have a serious
misconception. First of all, the friction is proportional to the normal
force which presses the wheel to the road, not the mass. If there were one
wheel, the maximum static frictional force you could get before the cart
started slipping (call that fmax) would be the weight W times the
coefficient of static friction μs (on level ground), fmax=μsW.
If you had two wheels, each wheel would hold up half the weight so the
maximum static frictional force you could get from each wheel would
be μsW/2; but the total
force is still μsW. Things are more
complicated on a slope, but the conclusion is still that you do not gain an
advantage regarding traction by having more wheels. The reason big trucks,
for example, have many wheels is so that each wheel does not need to support
so much weight, not to get more traction.
![]() QUESTION:
QUESTION:
I understand that acceleration due to gravity decreases with distance, specifically by the inverse square law. That being said, what is the maximum distance for which one can use 9.81 m/s2 as g for Earth?
![]() ANSWER:
ANSWER:
That depends entirely on how accurate you want to be,
there is technically no place other than the surface of the earth where this
is the acceleration. Furthermore, the number 9.81 is simply an average
value; it varies over the surface of the earth due to local density
variations, rotation of the earth, influences of the moon's gravity,
altitude variation, etc. You need to ask something like "at what
altitude h from the surface is the value of g changed by X%?"
Then
![]() QUESTION:
QUESTION:
If I am driving my car with a bowling ball in the trunk, does it take the same energy to accelerate the vehicle to a given speed at a given time if the ball is free to roll around as it would if it were fixed to the vehicle? I assume that the net energy use would be the same in both situations (same total vehicle mass), but the acceleration rates would be different - ie: the fixed ball would result in a constant acceleration to speed, while the rolling ball would result in a non-constant acceleration. If this is true, could I harness the energy of the ball's movement relative to the vehicle (using some sort of linear generator) without causing parasitic energy loss to the vehicle? ![]() ANSWER:
ANSWER:
As long as the ball and the car end up going the same
speed, the total energy to get them there is the same (neglecting frictional
and air drag forces). If you devise some way to take enegy away from the
ball, that energy ultimately must come from the engine.
![]() QUESTION:
QUESTION:
Perhaps you can help solve a disagreement we have at work. The question being "Does a person's initial velocity during a jump equal their final velocity once the land?" My contention is "no" in that the jumper could theoretically produce any velocity on the way up, but downward would be limited to terminal velocity. Who's right?
![]() ANSWER:
ANSWER:
Technically, you are correct. If air drag is present,
energy is lost which results in the landing speed being less than the launch
speed. In practice, however, for a person jumping into the air the height
acquired is not high enough for this to be a measurable effect; that is,
this is an example where we can say, as we often do in an elementary physics
course, that air drag is negligible. A typical terminal velocity for a human
is about 120 mph≈54 m/s. If you jumped with this speed you go over 100 m
high, obviously not in the cards. I did a rough estimate assuming the
maximum height you could jump would be about 2 m; if the person drops from 2
m his speed at the ground would be about 6.32 m/s without drag, 6.30 m/s
with drag, a 0.3% difference. For comparison, dropping from 100 m the speeds
would be roughly 44.1 m/s and 37.1 m/s for no drag and drag,
respectively. It is good to be precisely correct as you are, but it is also
good to be able to make reasonable estimates in real-world situations.
![]() QUESTION:
QUESTION:
When a ball is thrown vertically upwards ignoring air resistance, and another ball is also thrown upwards with air resistance, the time taken is less for the ball with air resistance to reach max height. Why is this "because average acceleration/force is greater"? Wouldn't there be less acceleration/force because the air resistance cancels some out?
![]() ANSWER:
ANSWER:
The reason is that the ball with air resistance does not
go as high. The force on the ball without resistance is the weight of the
ball pointing in the downward direction; but the downward force is greater
for the ball with air resistance because the drag force is also pointing
down. Therefore the ball with resistance slows down faster so it stops more
quickly. Think of an extreme example: if you throw the ball upwards in honey
which has very great resistance, it stops almost immediately.
![]() QUESTION:
QUESTION:
Whenever we roll a ball or spin a quarter it will slow down and eventually stop, since energy cannot just dissapear where does it go?
![]() ANSWER:
ANSWER:
The kinetic energy is being taken away from the ball or
coin by friction. That energy shows up as thermal energy, the
ball/coin-table-air all get a little bit warmer. Also, since you can hear
the ball rolling and the coin spinning, some of the energy must be lost to
sound.
![]() QUESTION:
QUESTION:
Something
ridiculous I thought of, if the Moon suddenly stopped moving and began to
fall toward the Earth, how long would it take to impact? I'm stumped as to
how to calculate this, as the force on the Moon gradually increases as it
falls, and the Moon also pulls the Earth toward it, and the radius of each
object would have to be included.
I guess I am going to have to put questions like this one on the FAQ page. You should read the details of these earlier questions since I do not want to go over all the details again. It is tedious and uninstructive to try to do this kind of problem precisely. I, being a great advocate of "back of the envelope" estimates, use Kepler's laws to solve this kind of problem; I have found that a very excellent approximation to fall time can be found this way. I note that the mass of the moon is only about 1% of the mass of the earth, the period of the moon is about 28 days, and the moon's orbit is very nearly circular. The trick here is to use Kepler's third law and recognize that a vertical fall is equivalent to the very special orbit of a straight line which is an ellipse of semimajor axis half the length of the line. Kepler's third law tells us that (T2/T1)2=(R2/R1)3 where Ti is the period of orbit i and Ri is the semimajor axis of orbit i. Now, T1=28 and R2=R1/2 and so T2=T1/√8=9.9 days. But this is the time for this very eccentric orbit to complete a complete orbit, go back out to where it was dropped from; so, the time we want is half that time, 4.9 days.
But this is not what you really wanted since I have treated the earth and the moon as point masses. What you really want is when the two point masses are separated by a distance of the sum of the earth and moon radii, 6.4x106+1.7x104≈6.4x106 m. To see how much error this causes, I can use the equation for the velocity v at the position r=6.4x106 m if dropped from r=Rmoon-orbit=3.85x108 m which I derived in one of the earlier answers: v=√[2GM(1/6.4x106-1/3.85x108)]=1.1x104 m/s. It would continue speeding up if the collision did not happen, but even if it went with constant speed the time required would be about t=R/v=6.4x106/1.1x104=580 s=9.6 min. This is extremely small compared to the 4.9 day total time, so, to at least two significant figures, 4.9 days is the answer to your question.
An important part of doing physics, or any science, is knowing when to eliminate things which are of negligible importance!
![]() QUESTION:
QUESTION:
I'm a Science Olympiad coach trying to optimize the performance of our "Scrambler", a car which must be accelerated by only a falling mass.
Most competitors simply tie a weight to a string and route that string over a set of pulleys (using no mechanical advantage to convert the vertical falling acceleration horizontal.
…Read a whole lot more!
![]() ANSWER:
ANSWER:
Sorry, but if you read site groundrules you will see that "concise, well-focused questions" are required.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I was hoping you'd like the challenge of a motion/force problem that must span across several formula -- PE, KE, PEspring, velocity solved by
acceleration and distance only, etc. Something to sink your teeth into...
![]() ANSWER:
ANSWER:
It is really not that interesting to work the whole thing
out, but on second thought it is interesting to talk qualitatively and
generally about the questioner's proposal; so I will do that. I will
summarize the situation since I am sure none of you loyal readers will want
to read the whole original question. By using a falling mass M
attached to a car of mass m, it is wished to maximize the speed v
of the car for M having fallen through some some distance H.
The car moves only horizontally. The simplest thing to do is to have the two
simply attached by a string over a pulley. Then, using energy conservation,
0=–Ö(M+m)v2-MgH or v=√(2MgH/(M+m)).
What the questioner proposes is to hold the car at rest and insert a rubber
band in the string so that the falling weight stretches the rubber band
which has been carefully chosen to be just right that, when M has
fallen H, it has just come to rest and is held there. Now,
presumably, the rubber band has a potential energy of MgH. If the car
is now released, the rubber band will presumably contract back to its
original length giving its potential energy to the car, MgH=–Ömv2
or v=√(2MgH/m), a considerable improvement. My
suggestion would be to use a spring rather than a rubber band since a rubber
band has much more damping (energy loss due to internal friction) and
hysteresis (will not return to its original length). Since the rules fix
M and H, one obviously wants m to be as small as possible.
![]() QUESTION:
QUESTION:
Does acceleration have momentum?
In other words if you fire a rifle, does the highest velocity of the bullet occur as it exits the barrel or does the acceleration increase after it leaves the barrel?
![]() ANSWER:
ANSWER:
In terms of physics nomenclature, your first question has no
meaning. But your second question seems to clarify what you mean: if
something has an acceleration does it keep accelerating even if there are no
forces on it? The answer is an unequivocal no. The only thing which causes
acceleration is force and when the bullet exits the barrel of the gun the
force which was accelerating it disappears. If there were no new forces on
it, it would continue with the same velocity it had when it exited. There
are, however, two important forces on the bullet when it is outside the
gun‚ÄĒgravity and air drag. Gravity causes it to accelerate toward the ground
and air drag causes it to slow down.
![]() QUESTION:
QUESTION:
We have a metal ruler 1 yard in length. If held in exact balance center then "pinged" it causes vibrations. nothing new there BUT at exact equal distances to either side there is a point at which it appears that the vibrations stop (a calm spot) for about 1 inch then the vibrations start again and continue to the end. We've tested and the vibrations don't stop, they are just a much smaller wave length. What is is this "calm spot" phenomenon? What causes it? Does it happen with earthquakes too?
Really geeked out about this! Way cool!
![]() ANSWER:
ANSWER:


You are exciting standing waves when you "ping" the stick. These are waves
which bounce back and forth from the ends of the stick and, for special
wavelengths, are just right to to resonate like a guitar string or an organ
pipe. The various wavelengths for which resonance occurs are called the
modes of oscillation. For a stick clamped at the middle, the lowest mode,
called the fundamental, has approximately 1/4 of a wavelength on either side
of the center as shown by the upper part of the figure above. A point with
zero amplitude, the center for the fundamental, is called a node and points
with maximum amplitude, the ends for the fundamental, are called antinodes.
What you are seeing is the next mode, called the first overtone, which has
approximately 3/4 of a wavelength on either side; this mode has three nodes
and four antinodes. To the right are animations for a stick clamped
at the end but they are exactly what your stick is doing on one half. Here
the nodes are near the darkest blue. Earthquakes are traveling waves and
therefore do not have nodes.
![]() QUESTION:
QUESTION:
I've been reading about rotational space habitats for a while now and haven't found an answer to this question by googling. So how would a space habitat be rotated? By cogs? By propulsion systems?
![]() ANSWER:
ANSWER:
If you want to read more about the details of such habitats,
see my earlier answers (1 and
2). In answer to your question,
you would need thrusters to get the ring spinning and then to occasionally
correct minor changes, but once it was spinning, it would continue to spin
just the same forever if there were no external torques on it as would be
the case in empty space.
![]() QUESTION:
QUESTION:
The moon's gravity is one sixth that of the earth. Thus if you kicked a box with a force of 60 N across a frictionless floor on earth, the box would travel the same distance in 1 second as when the same box was placed on a frictionless floor on the moon and kicked with a force of 10 N. Am I wrong?
![]() ANSWER:
ANSWER:
You are wrong on both your conclusion and on your
"…kicked…with a force of…" premise. First the premise: you need to go the
FAQ and read the link
from the question about how much force does it take to make something move
with some speed. Just knowing the force you cannot know the resulting speed;
you need either how long the force was applied or over what distance it was
applied. Now, your question implies that you think it will be easier to get
the box on the moon moving with the same speed as a box on earth with that
speed. But, in fact, the box has the same mass on both the earth and moon
and you are not lifting it against gravity, so it is equally easy to move a
box horizontally on earth or the moon. It is six time harder to lift a box
on earth as on the moon. If there were friction, however, it would be harder
to move the box on earth than on the moon because the frictional force on
the moon would be six times smaller.
![]() QUESTION:
QUESTION:
If you have two permanent cylindrical magnets (the kind with a hole in the center) and you stack them with poles opposite on a pencil, the top magnet will "float" above the bottom magnet. Energy is being expended to keep the magnet "up" the pencil. Where is the energy coming from? The bottom magnet will be pushing down with an equal but opposite force, but that does not cancel the energy needed to float the top magnet as far as I can see.
![]() ANSWER:
ANSWER:
I am afraid you do not understand energy. The lower magnet
exerts a force on the upper magnet. The force holds it there in equilibrium,
it does not require energy to hold it there. It is no different from saying
that if one of the magnets were hanging from a string, where does the energy
to hold it there come from? Or, if one of the magnets were sitting on a
table top, where does the energy to hold it there come from?

![]() QUESTION:
QUESTION:
I read of "gravity assist" swingy-bys of Jupiter to speed a spacecraft up to reach the outer planets. As the spacecraft approaches Jupiter, it speeds up. But it retreats from Jupiter on a symmetric path (a hyperbola I think) and Jupiter will therefore slow the spacecraft down by the same amount on the outbound path. It appears there should be no net increase in speed, just a bending of the spacecraft path. But bending a spacecraft path also takes energy. So Jupiter is providing the energy in some manner though it is unclear to me how.
![]() ANSWER:
ANSWER:
The trick is that the planet, with much greater mass than the
spacecraft, is moving in its orbit and the boost comes from using the speed
of the planet to speed up the spacecraft. The figure shows the idealized
one-dimensional interaction with planet; because the mass of the spacecraft
is much less than the mass of the planet, the spacecraft picks up twice the
speed of the planet. For those who have studied elementary physics, this
should look vaguely familiar: a perfectly elastic collision between a BB at
rest and a bowling ball with speed U results in the BB going with
speed 2U and the bowling ball still going U. (Of course, this
is only approximately true if the mass of the BB is much smaller than
that of the bowling ball; the bowling ball will actually lose a very tiny
amount of its original speed.)
![]() QUESTION:
QUESTION:
My son is in 5th grade and he is supposed to be doing a Science Fair project and presenting in front of judges, some of which I have heard work at IBM. His teacher helped him set up an experiment where he rolled a car down an inclined plane 5 times adding more weight each time. Then he is to see if the car goes faster with more weight added. And then explain that due to research. I have read your other answers but I am so confused. Is gravity the only force working on the car to get down the incline? and if so does that mean that technically the car should always travel the same speed? Any help on where I can learn about this, or any information you may be able to help me with would be so greatly appreciated.
![]() ANSWER:
ANSWER:
The best place on my site to read is
this earlier answer.
There you will see that gravity is certainly not the only force acting on the car. Friction is very important. The normal kinds of friction, in axles, wheels,
etc. should, according to the simplest approximation, not affect the speed of the car‚ÄĒall masses should take the same time. That, as I explain in that post, is because all these forces are approximately proportional to the weight of the car and, of course, gravity is also proportional to the weight. The other kind of friction is air drag. The air drag is proportional to the speed of the car squared, so the faster the car goes the more air drag it has. You know that this is true because you have a very different experience if you stick your hand outside the window of a car going 10 mph and 80 mph. If air drag is important, the heavier car wins. I have said before that this is not really a very good experiment for a science fair because there are too many variables and approximations. Friction can be a very sticky thing in physics (pun intended!).
If he did not find the heaviest car the fastest, I do not know what to tell you except it is difficult to understand. If he did find the heaviest the fastest, here is how he could justify it: Two cars, each going the same speed down the ramp, have masses 1 kg and 2 kg. Since they are identical in all respects except mass, each experiences the same air drag frictional force, let’s call that Fdrag. Newton’s second law says that the acceleration adrag is equal to the force Fdrag divided by the mass m and so adrag=Fdrag/1 for the 1 kg mass and adrag=Fdrag/2 for the 2 kg mass. Here the acceleration is the rate of slowing down due to air drag (you might call that deceleration) and you see that the heavier car slows down less than the lighter car. All the other forces result in the same acceleration for each car since those forces are all proportional to the mass; maybe I should elaborate on that a little: Forces due to friction and gravity can be written Fother=Cm where C is some constant. And so aother=Fother/m=C which means that all accelerations should be the same, so only air drag gives advantage to the heavier car.
Finally one more example to illustrate: Drop two balls exactly the same size, one is a nerf ball (very light) and one is a lead ball (very heavy). If there were no air, both would fall to the ground in the same time. But you can easily show that the heavier one wins if there is air.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I'm still a little confused because his teacher is telling me it is not gravity that is pulling the truck down because it is a ramp and not falling and she says it is force and momentum moving the truck down the ramp. From what I have researched it looks to me like momentum is not really a force and only forces actually move objects? Also I think I understand that gravity is not the only force acting on the toy truck but it seems to be the only one pulling or pushing it downward and the frictional forces push upwards, opposite gravity?
![]() ANSWER:
ANSWER:
Your son's teacher has
this seriously wrong if she really said that it is not gravity pulling it
down the ramp. It most certainly is falling, it is just not falling straight
down. And you are right, momentum has nothing to do with its going down the
ramp; it has momentum but that is not what is causing it to go down the
ramp. So, I guess I will have to give you a complete primer on the motion of
an object on a ramp. I will draw some figures and use some equations but I
will try to give you as many words as I can to qualitatively explain; then
you can help your son create an explanation on his level. The basics are
that an object which has no net force on it moves with a constant velocity
(Newton's first law). To change the velocity (accelerate or decelerate) you
must push or pull on it (exert a force) (Newton's second law). In equation
form, Newton's second law may be stated F=ma where this says
force=mass times acceleration.
-
Let us first talk about the ideal case where there is no friction at all. The first picture shows the weight (gravity) as a red arrow. But you see, the weight actually does two things as indicated by the blue arrows‚ÄĒaccelerate the car down the ramp (smaller blue arrow) and push the car through the ramp (larger blue arrow). The car does accelerate down the track but it does not go through the ramp because the ramp pushes on the car with a force opposite the blue arrow, shown as a black arrow. So we can agree that the reason the car accelerates down the track is gravity. Now how does the acceleration depend on the weight of the car? If you have two cars and one has twice the weight of the other, the force (smaller blue arrow) down the ramp will be twice as big for the heavier one. On the other hand, Newton's second law says that the acceleration a of some weight (mass m) due to a given force F depends inversely on the weight a=F/m. So even if F is twice as big, because m is also twice as big, they both have the same acceleration! This means that if there is no friction of any kind, the weight of the car should make no difference.
Next let us add friction, the kind which results from one thing rubbing on another like wheels on axles, etc. The friction (shown as a purple arrow in the second figure) points up the ramp and so it tends to slow the car down. The important thing to know about these kinds of frictional forces is that they also depend on the weight of the car. If the car is twice as heavy, friction is twice as big. But if the friction depends on the weight, the acceleration will be the same just as it was for the weight force. Again, all cars should get to the bottom in just the same time again, it will just be a shorter time because the total force down the incline is smaller.
Finally, let us add in an air drag force (the green arrow in the third figure). Air drag is, as I explained in the original answer, a force which depends on two things‚ÄĒthe shape/size of the car and the speed of the car‚ÄĒbut not on the weight of the car. So air drag gives the heavier car the advantage because there is less slowing down due to the drag force.
![]() QUESTION:
QUESTION:
This question should be fairly quick. Are there any know situations were momentum isn't conserved? I would say no, as momentum is always conserved if you make your system big enough. The only time momentum appears to be not conserved is when you put restrictions on the size of your system, and don't account for the momentum transferred outside your system. When you include the system " outside" your system, momentum is in fact conserved.
![]() ANSWER:
ANSWER:
First, what you learn in first-year physics is that linear
momentum is conserved for an isolated system; an isolated system is
one for which there are no net external forces acting. This is actually a
result of Newton's third law which essentially states that the sum of all
internal forces in a system must equal zero. This works really well until
you get to electricity and magnetism where it is easy to find examples of
moving charges exerting electric and magnetic forces on each other which are
not equal and opposite (you can see an example in an
earlier answer). In that case you would say that such an isolated
system obeys neither Newton's third law nor momentum conservation. However,
looking deeper, we find that an electromagnetic field has energy, linear
momentum, and angular momentum content and, in the end, momentum
conservation, because of the momentum contained in the field, is still
conserved for an isolated system. Thus, Newton's third law is saved, but not
always in the simplistic "equal and opposite forces" language. Finally, if
linear momentum is p=mv, linear momentum is not
conserved in special relativity. But, physicists so revere momentum
conservation that in special relativity momentum is redefined so that it
will be conserved but still reduce to p=mv, for low
speeds: p≡γmv=mv/√[1-(v/c)2];
this then unifies energy E and linear momentum p into a single
entity which is conserved, the energy momentum 4-vector: E2-p2c2=m2c4.
Not as quick as you expected!
![]() QUESTION:
QUESTION:
What is the force that causes you to fall over when a moving bus comes to an immediate stop? I'm having an argument with my teacher over what the answer is, it would be great if you could explain!
![]() ANSWER:
ANSWER:
When the bus is stopping, it is accelerating and so it is a
noninertial frame. That means that Newton's laws are not valid if you are
riding inside the bus. But, if we watch you from the bus stop, Newton's laws
do apply and we conclude that if you move with the bus, there must be a
force which is causing you to accelerate also. Friction provides a force
which, except under extreme circumstances, accelerates your feet along with
the bus; but, unless you are holding on to something, there is nothing to
provide a force on your upper body which therefore tends to keep going
forward without accelerating. All this says that the reason you fall forward
is not due to any force, rather it is due to lack of a force. There is,
though, another way to look at this problem. If you are in an accelerating
frame, like the bus, you can force Newton's laws to be true by adding fictitious
forces. The best known example of a fictitious force is the
centrifugal force in a rotating (and therefore
accelerating) frame. In the bus which has an acceleration a you can
invent a fictitious force Ffictitious on any
mass m in the bus, Ffictitious=-ma;
if you do that, Newton's laws become true inside the bus and the force Ffictitious
may be thought of as being the force which provides your acceleration.
Note that the acceleration is opposite the direction of the bus when it is
stopping, and so the fictitious force is forward as you know if you have
fallen over in a stopping bus. When the bus is speeding up you tend to fall
backwards. Since there are two answers here, depending on how you choose to
view the problem, so maybe you and your teacher are
both right!
![]() QUESTION:
QUESTION:
if the earth had an orbit of 100,000 miles above the surface of the sun what would a person with a weight of 100 pounds weigh during the day and during the night and would there be any difference because of the gravitational pull from the sun.
![]() ANSWER:
ANSWER:
The radius of the sun is about 432,000 miles, so the radius
R
of the orbit would be R=532,000 mi=8.6x108 m. Since the
diameter of the earth, about 12.8x106 m, is small compared to the
radius of the orbit, there is only about a 0.1% change in the gravitational
attraction to the sun if you change the distance by one earth diameter. The
mass of the sun is M=2x1030 kg. The force of attraction of
the sun on the m=100 lb=45 kg person would be given by F=GMm/R2=6.67x10-11x2x1030x45/(8.6x108)2=8117
N=1825 lb, much bigger than the 100 lb force which the earth exerts on the
person. Now, to answer your question you need to define weight. I will
assume that we mean the net sum of all forces on the person so that Wday=1725
lb upwards and Wnight=1925 lb downward. Or, maybe you mean
what a scale on the floor would read (not actually what weight means) in
which case Wnight=1925 lb and Wday=0 lb.
These are really only noon and midnight weights since the forces due to the
earth and sun would not be parallel at other times.
![]() QUESTION:
QUESTION:
If a bullet was shot through a window of a moving train and was to come out on the other side of the train through a window. Would it come out through window 2 on the same the exact opposite side as window 1 or would it look as if the bullets direction was bended?
![]() ANSWER:
ANSWER:
If the bullet is shot straight at the train with some speed
V and the train is moving with some speed v, an observer on
the train sees the bullet moving with a speed V toward the opposite side and, at the
same time with a speed v toward the back of the train so that the bullet would
be traveling, as measured on the train, in a straight line across and
rearward with speed √(V2+v2)
![]() QUESTION:
QUESTION:
I've found the formula for gravitational attraction between two objects, but I can't quite "do the math" mainly because of the metric/english conversions...I want an answer that I can relate to in pounds or ounces, not dynes, ergs, or grams (I am aware of the distinction between mass and force) Here's my question:
I am driving my 18-wheeler truck which weighs 80,000 lb. fully loaded. I am driving due west at sunset, heading straight toward the sun which is about 93 million miles away. What is the 'tidal force' of attraction between my truck and the sun?
![]() ANSWER:
ANSWER:
I have the feeling that you want gravitational force, not
tidal force. Tidal force is the tendency for the
truck to be stretched because the gravitational force on the front of the
truck is a tiny bit larger than on the rear. The gravitational force is
computed by F=GMm/R2
where G=6.67x10-11 N∙m2/kg2,
M=2x1030 kg, m=8x104 lb=3.6x104
kg, and R=93x106 mi=1.5x1011 m. So I find F=213 N=48
lb. There is a very handy little free program called
Convert which
you can use to convert just about any units you might want to work in.
![]() QUESTION:
QUESTION:
Let's assume I have a magnet that can lift 100 tons. And I attach the magnet in a chain and attach the chain into roof for a system to magnetically lift items and then drop them to other places. Would the chain have to be able to take the 100 ton load or would the magnet take the 100 ton load because after all it is the one keeping the lifted item up?
![]() ANSWER:
ANSWER:
The magnet itself holds up the 100 ton weight. The chain
holds up the 100 ton weight plus the weight of the magnet itself. The roof
holds up the 100 ton weight plus the weight of the magnet plus the weight of
the chain.
![]() QUESTION:
QUESTION:
In 1973 a Physics instructor explained via math that the sidewalls of a regulation tire need not be present if the velocity of the vehicle was above a speed of 65+ mph. I tried to explain this to family members at Christmas and was scoffed at and then ridiculed. The Physic instructor had been let go from the GMC/Chevrolet plant several years before and he took the educational retraining route. His job was to change out instruments on GM cars running around a track and in excess of 100+ mph and his driver advised him that they had had a blow out and he needed to get out from under the dash and safety belted in at which time the slowed below the critical speed with the result that they did not crash but came close to it. Can you provide a link or the math to show that the speed is somewhere about 70+ miles and then the centripetal force will hold up the outer part of the tire. He did the math as part of educating us on acceleration, speed and force as it involved that part of the class curriculum.
The instructor was a good instructor in that he made the physics relevant to the real world if there is such a thing today and even at that time. Also this is why tires need sidewalls as they won't hold up in gravity and below a specific velocity.
![]() ANSWER:
ANSWER:
This is nonsense. If there is no air pressure to connect the tire to the axle, which would be the case if there were no sidewalls, what is going to hold up the weight of the car?
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
No not really if you get the tire up to speed as well as providing
forward momentum the circumference and the center point about which the
tire is rotating will hold the tire up even if there is a blow out as
the forward speed or acceleration is sufficient to hold it up will
prevent deflation aka collapse of the tire above a speed. Once the speed
or acceleration drops below a key critical the tire will start to
collapse and according to the GMC aka Physics instructor all hell broke
lose on the track and only the drivers expertise kept the ensuing
deceleration from causing him and driver problems. Once you reach
velocity the outer rim of the circle/sphere need not have anything to
hold it up if the instructors explanation and the math were correct.
Key elements:
-
Tires inflated to recommended PSI
-
Vehicle an experimental test GMC product running in excess of 100+ miles an hour.
-
According to the LAHC Physics instructor a knowledgeable and well trained driver at the wheel who on sensing the blow out got him out from under the dash and into the multi-point seat belt. Instructors job was instrument technician for the test bed aka the vehicle a GMC automobile with changeable instruments.
-
He was alive to prove it to the class with not sure what Physic concept/principal that escapes me.
![]() ANSWER:
ANSWER:
Well, maybe I misunderstand something here, but let's boil
this problem down to the simplest equivalent I can think of: imagine a tire
with sidewalls and just an axle which is supported by the sidewall, shown on
the left in my figure. Now, we would agree, I believe, that if the sidewall
suddenly disappeared, the axle would fall because there would be nothing
holding up that weight. How is that situation any different if the car is
moving? So, let's agree that "the
sidewalls…need not be present" is wrong because there has to be some
physical contact of the outer surface of the tire and the axle. So, my first
answer was a knee-jerk response to the notion that the sidewalls were not
needed.
![]() THE ANSWER
YOU WILL LIKE:
THE ANSWER
YOU WILL LIKE:
However, there is still a way that you might have a point. When the
blowout occurs, the pressure inside the tire is lost; this pressure is
typically 30 PSI=21,000 N/m2 above atmospheric pressure (which is
about 100,000 N/m2). If the car is sitting still, this loss of
pressure results in the wheel collapsing because the sidewalls alone are
insufficient to hold up the weight of the car unless the force due to the
pressure pushing on the outer part of the tire holds the sidewalls taut.
Now, imagine that you are driving with some speed V and viewing a
spinning tire from its axis, you see every point on the outer surface of the
wheel accelerating with an acceleration V2/R where
R is the radius of the tire. Therefore, every little piece of the tire
with mass m experiences a (fictitious) force (called the centrifugal
force) of mV2/R. That would be equivalent to there
being a pressure P exerted on that little piece of tire of P=mV2/(aR)
where a is the area of that little piece. But, every little piece
behaves like this, so it is equivalent to a pressure of P=MV2/(AR)
acting on the outer surface where M is the mass of the tire (assuming
the sidewalls are a small fraction) and A=2πRW is the area of
the outer surface and W is the tread width. So, if that pressure is
equal to 21,000 N/m2, it will be like the blowout never happened!
I took R≈16 in≈0.4 m, W≈12 in≈0.3 m, and M≈20 lb≈9 kg
and solved 21,000=MV2/(AR)=MV2/(2πR2W)
and found V=27 m/s=60 mph. (Incidentally, the "forward momentum" has
nothing to do with it.)
![]() QUESTION:
QUESTION:
which team wins in a tug of war: the team that pulls harder on the rope or the team that pushes harder against the ground.Can you explain please?
![]() ANSWER:
ANSWER:
Focus your attention on the guy in the red shirt. There are
two horizontal forces on him, the rope pulling to the left and the ground
pushing to the right. If he is not moving, these two forces must be of equal
magnitude. To win, he must accelerate to the right and so the ground must
exert a bigger force on him than the rope exerts on him. To complete the
answer, use Newton's third law which says that the force the rope (ground)
exerts on the man must be the equal and opposite to the force that the man
exerts on the rope (ground). So the winner must push harder on the ground.
![]() QUESTION:
QUESTION:
If a high jumper clears the bar, is it possible that the centre of mass of the body of the jumper passes below the bar? If so can you make me visualize the scenario by a video or image illustration or a vivid description? I think that the centre of mass can be below the bar during the jump, but it has come there after travelling above the bar.
![]() ANSWER:
ANSWER:
You can find dozens of pictures and videos on the internet. A
nice one is shown to the right here. The path under the bar of the center of
gravity of the jumper is shown. When the body is bent the center of gravity
is outside the body. Going over with the back down is called the Fosbury
flop after Dick Fosbury, the American high jumper who won the gold medal at
the 1968 Olympics.
![]() QUESTION:
QUESTION:
I want to know why does torque is able to do work. I Mean Torque vector always acts perpendicular to the surface therfore meaningthat angle between torque vector and angular displacement vector is always 90 degree. Whereby meaning work done by torque is always zero but it is obviously not so. I know how to derive that work expression but still I am wondering why is it so.
![]() ANSWER:
ANSWER:
You are mistaken, angle and torque vectors are not always
perpendicular. Shown in the figure to the right are the vector directions
relevant to your question. The angle through which this cylinder rotates,
θ, increases as the cylinder rotates counterclockwise as seen
from above; the vector direction is seen in the black vector θ
shown in the figure. If there is a force F
acting at a distance r from the
axis, the torque vector is given by the red vector
τ shown in the figure, τ=Fxr.
So, W=τ∙θ.
![]() QUESTION:
QUESTION:
In a system where I have a 1600mm beam with I=1,300,000kg-mm^2 rotating about an axis (shaft) at the far left end of the beam where it's initial position is resting at 0 degrees horizontal then rotating 180 degrees counterclockwise (from 3 o'clock to 9 o'clock) about the axis (shaft) at the end of the beam described above by way of a cable wrapped around a 12" diameter disc (disc attached to beam & shaft) where the cable runs out to the right tangentially at 6 o'clock horizontally over a pully wheel then down to a weight, say 300lbs, that will fall to apply enough torque to effect the rotation of the beam and accelerate it.
How do I account for role gravity plays in the falling weight keeping up with the rotation of the beam where the beam first has to overcome some amount of gravity to get from 3 o'clock to 12 o'clock but then gravity works in it's favor from 12 to 9.
My goal is to get a point at the end of the beam to hit a plate at about 100mph at the end of the rotation (9 o'clock).
![]() ANSWER:
ANSWER:
I am not certain that I understand exactly what the
configuration is and some of the numbers are missing (like mass of the disc)
or not fully specified (like the axis for the moment of inertia of the
beam). I will work it out in general and you can apply it to your situation.
The situation as I understand it, before and after, is shown to the right. I
will call the length of the beam L, its mass M1,
the radius of the disc R, its mass M2, the hanging
mass M3. I will assume the beam and disc are uniform so
that their moments of inertia are M1L2/3
and M2R2/2
respectively. I assume that the mass of the pulley is negligible and that
all friction can be ignored. In the final situation the beam and disc rotate
with angular velocity ω and the hanging mass has a speed v=Rω.
Note that the hanging mass has fallen a distance half the circumference of
the disc, πR. If you are interested only in how fast everything is
going at the end, you do not need to worry at all about what is going on at
any other time because this is a classic energy conservation problem and the
final energy is equal to the initial energy. I am not going to give you all
the details, I will just give the initial equation and its solution for the
end.
-
Energy conservation: 0=–Ö[(M1L2/3)+(M2R2/2)+M3R2]ω2-M3gπR
-
Solution for ω: ω=√{2M3gπR/[(M1L2/3)+(M2R2/2)+M3R2]}
Once you get ω, you can get the speed V of the end of the beam by calculating V=ωL.
If I take your numbers, M3=300 lb=136 kg, L=1.6 m, M1=1.52 kg (assuming the I you have given me is about an axis through the end of the beam), M2=0 (assuming it is small since you did not specify it), R=6"=0.15 m, and g=9.8 m/s2 (acceleration due to gravity), I find ω=17 s-1 so V=17x1.6=27 m/s=60 mph.
![]() ADDITIONAL
THOUGHT:
ADDITIONAL
THOUGHT:
You might think that you can increase the speed of the end of
the beam by increasing M3. However, there is an upper
limit. In the limit as M3‚ÄĒ‚Äļ∞,
ω‚ÄĒ‚Äļ√{2gπ/R}=20.3 s-1
giving V=72 mph. Assuming that the length of the beam is fixed, you
would have to decrease the radius of the disc to reach 100 mph.
![]() QUESTION:
QUESTION:
Orbiting astronauts are weightless because they are essentially in free-fall and don't "feel" Earth's gravitational force. Earth is orbiting the Sun and similarly Earth should not "feel" the Sun's gravity. However, the Sun has an effect on the ocean tides therefore it follows that the ocean water "feels" the Sun's gravity. Please explain.
![]() ANSWER:
ANSWER:
An astronaut is not weightless but she is in free fall and
therefore feels like she is. However, she is not aware of what are called
tidal forces because they are too small because she is relatively small; I
will try to clarify this. Let's take the case of the earth-moon interaction.
Because the moon's gravitational force falls off like 1/r2,
the forces felt on the earth are different at the side nearest to the moon,
farthest from the moon, and at the earth's center; this is shown in the
upper of the two figures to the left. The net effect, obtained by
subtracting the central gravitational force, is as shown in the lower
figure; that is why the tidal force raises the ocean level on both near and
far sides of the earth. The astronaut will also experience a tidal force but
since her size is so small compared to the size of the earth, she will not
feel the force try to stretch her; if you think about it, you will see that
the tidal force on an astronaut is greatest when she is standing on the
ground. When an object falls into a black hole, tidal forces become huge.
The above discussion contains nothing regarding how the moon and earth are
moving relative to each other so all the same arguments apply to tidal
forces the earth feels in the presence of the sun; these are, though, much
smaller since we are much farther from the sun.
![]() QUESTION:
QUESTION:
Conventional automobile steering produces a weight transfer from the inside wheels to those on the outside of the turn.
If, instead of deflecting the front wheels, one steers by turning the outside wheels faster than the inside wheels, will that also cause a weight transfer?
![]() ANSWER:
ANSWER:
There is an earlier
answer about a bicycle making a turn. It would be helpful for you to
read that first. I assume you want to understand why the weight is more
supported by the outside wheels, so I will try to show that. The easiest way
to do the problem of the car turning a curve is to introduce a fictitious
centrifugal force which I will call C, pointed
away from the center of the circle; the magnitude of this force will be
mv2/R where m is the mass of the car, v
is its speed, and R is the radius of the curve, although we do not
really need to know that to answer your question. The picture to the right
shows all the forces on the car: W is the weight and the green x is the
center of gravity; f1 and f2 are the
frictional forces exerted by the road on the inside and outside wheels
respectively; N1 and N2 are the normal
forces exerted by the road on the inside and outside wheels respectively;
the center of gravity is a distance H above the road and the wheel base is
2L (with the center of gravity halfway between the wheels). Newton's
equations yield:
-
f1+f1=C for equilibrium of horizontal forces;
-
N1+N2=W for equilibrium of vertical forces;
-
CH+L(N1-N2)=0 for equilibrium of torques about the red x.
If you work this out, you find the normal forces which are indicative of the weight the wheels support: N1=–Ö(W-C(H/L)) and N2=–Ö(W+C(H/L)). A few things to note are:
-
the outer wheels support more weight,
-
if C=0 (you are not turning), the inner and outer wheels each support half the weight,
-
at a high enough speed C will become so large that N1=0 and if you go any faster you will tip over, and
-
if the road cannot provide enough friction you will skid before you will tip over.
Now we come to your question. Regardless of how you cause the car to turn, the analysis done above will always be the same; the centrifugal force is trying to tip the car over and that is why the weight distribution shifts.
![]() QUESTION:
QUESTION:
If a gun was fired at the escape velocity of the Earth in a direction that it would not hit anything but not straightly up but instead more like in an angle of 45 degrees would the round still go to space? And if not what would the velocity needed be for a round that is fired at 45 degrees in to the sky be in order for the round to escape Earth?
![]() ANSWER:
ANSWER:
First, let's be clear that we are talking about an ideal
situation where we neglect the effects of air drag (which will slow the
projectile) or earth's rotation (which can add or subtract from the velocity
you give the projectile). The easiest way to get the value of the escape
velocity (ve) is to use energy conservation. Escape
velocity is that velocity which results in the projectile being at rest at
r=∞. Taking the potential energy U(r)=-GMm/r+C
to be zero at r=∞ (i.e., choose C=0), energy
conservation gives –Ömve2-GMm/R=0
where M and R are the mass and radius of the earth,
respectively; so, ve=√(2MG/R). You will
notice that this derivation has been done without any reference to the
direction of the velocity ve, so the direction
makes no difference.
![]() QUESTION:
QUESTION:
This is one of the most baffling physics questions so far. Suppose a cyclist is pedalling briskly, thus accelerating forward. He exerts force on the tyres, the tyres exert force on the ground, and the ground exerts a reaction force which accelerates the cyclist. Right? But now the cyclist applies brakes. Now he starts to retards. But since the tyres are still moving in the same direction, hence friction must also be acting in the same direction. Then which force is responsible for the retardation? I suppose the brakes cannot retard the 'cyclist and the cycle' system, since it is an internal force.
![]() ANSWER:
ANSWER:
There is nothing "baffling" here. You are right, all internal
forces should be ignored if you want to understand the motion of the
bicycle. The only external forces on the cycle and its rider are its own
weight, the normal force up from the road on the wheels, and the frictional
force between the road and the wheels. (I am neglecting internal friction
and air drag.) The first of these two add to zero (assuming a horizontal
road) and can be ignored for our purpose. If the acceleration is forward,
the friction if forward. If the acceleration is backward, the friction if
backward. The direction of the friction is not determined by the motion of
the wheels because the wheels are not slipping on the road (you hope) so
static friction, not kinetic friction, is responsible for the acceleration.
It is friction which speeds you up or slows you down.
![]() QUESTION:
QUESTION:
Consider a tug of war game. is the net work the ground on the two teams is negative, positive or zero?
![]() ANSWER:
ANSWER:
Just after one team has won, all players are moving. They
have a kinetic energy. Therefore positive work was done on the whole system
by friction with the ground. Once everyone stops moving, the net work done
on the system would have been zero.
![]() QUESTION:
QUESTION:
Trying to understand physics concepts is
an interest of mine. I was hoping you could shed some light to help my
understanding? The equation for Kinetic Energy: KE = 1/2 m v2.
I understand the value of velocity squared in that; the kinetic energy
of an object is proportional to its speed squared:double the speed,
quadruple the KE. But I am having trouble with why and what the 1/2
value is telling me about what is going on in the equation as to the
motion of mass and speed. It is pretty elementary stuff but if I want to
know about Energy, Work, Power and Heat I need to get the basics right.
![]() ANSWER:
ANSWER:
To do this on the simplest level, you need to know kinematics
for uniform acceleration [x=x0+v0t+–Öat2
and v=v0+at where the 0 subscripts denote the
position and velocity when t=0] and Newton's second law [F=ma].
Suppose that you have a constant force F that you exert on a mass
m over a distance s; the work done is W=Fs and work
changes the energy; that is, we say that the work done equals the energy
given to m. I will assume that m begins at rest and at the
origin, so x=s=–Öat2 and a=v/t; then
F=mv/t and s=–Ö(v/t)t2=–Övt.
Finally, W=Fs=(mv/t)(–Övt)=–Ömv2.
So, in the case of a constant force, the factor of –Ö comes from the –Öat2
part of the kinematic equation for position.
![]() EXTRA ANSWER:
EXTRA ANSWER:
If you know calculus, this is much simpler. Write dW=Fdx
and F=m(dv/dt) so W=0∫sFdx=0∫sm(dv/dt)dx=0∫vm(dx/dt)dv=0∫vmvdv=–Ömv2;
and this does not require F to be constant.
![]() QUESTION:
QUESTION:
why do we need to have a new expression for calculating the kinetic energy of a body that is in rotational as well as translational motion?
![]() ANSWER:
ANSWER:
Whether you do or not depends partly on how the object is
moving. For example, if the object is rolling on a surface without slipping,
it is instantaneously rotating about the point (or line) of contact and you
can write K=–ÖIω2 where I is the moment of
inertia about that axis; however, you could also show (using the parallel
axis theorem) that K=–ÖMvcm2+–ÖIcmωcm2
where vcm is the speed of the center of mass, ωcm
is the angular velocity about the center of mass (which is the same as
ω) and Icm is the moment of inertia
through the center of mass. For an object not rolling, K=–ÖMvcm2+–ÖIcmωcm2
is still the correct expression for kinetic energy at any instant but
you can no longer write the kinetic energy as pure rotation as you could for
the rolling object because there is no relationship between vcm
and ωcm.
![]() QUESTION:
QUESTION:
is work energy theorem valid in non inertial frames?
![]() ANSWER:
ANSWER:
The work-energy theorem says that the change in kinetic
energy of an object is equal to the work all forces do on it. Imagine that
you are in an accelerating rocket ship in empty space, a noninertial frame.
You have a ball in your hand and you let go of it. You observe this ball to
accelerate opposite the direction in which the ship is accelerating and therefore see its kinetic energy change. But, there are no
forces acting on it so no work is done. Another way you could come to this
conclusion is that the work-energy theorem is a result of Newton's laws and
Newton's laws are not valid in noninertial frames. You can, though, force
the work-energy theorem to be valid if you introduce fictitious forces, a
way to force Newton's laws to work in noninertial frames. (Centrifugal force
is an example of a fictitious force.) If you invent a
force on the objects of mass m in the accelerating (a)
rocket ship above of Ffictitious=-ma,
this force will appear to do the work equal to the change in kinetic energy.
![]() QUESTION:
QUESTION:
First, how much energy (in the most basic sense) does a car expend driving at a moderate speed for one mile. Next, how big would a spring have to be (roughly) to store the energy equivalent of what that car expended during that mile.
![]() ANSWER:
ANSWER:
I can only do a rough estimate. Suppose your car has an
internal combustion engine and gets 40 mpg. The energy content of 1 gallon
of gasoline is about 120 MJ, so you would use about 120/40=3 MJ of energy
per mile. But, a typical engine has only about 20% efficiency, so the energy
supplied to the car is only about 0.2x3=0.6 MJ=600,000 J. Now, you want to
store that much energy in a spring. For a spring, the energy stored is –Ökx2
where x is the amount by which it is compressed (or stretched) and
k is the spring constant which is determined by how stiff the spring is.
(The constant k can be measured by k=F/x where F
is the force you have to exert to stretch or compress it by x.)
Clearly, the bigger k is the less the spring will have to be
compressed to store a given amount of energy. The coil spring of a car, a
pretty stiff spring, has a typical spring constant of k≈25,000 N/m,
so to store 600,000 J of energy, 600,000≈–Ö∙25,000x2 or
x≈7 m! I do not see much possibility of having a spring powered car. You
probably had in mind a spiral spring like a watch spring, but to store that
much energy in any kind of spring is going to be impractical.
![]() FOLLOWUP QUESTIONS:
FOLLOWUP QUESTIONS:
Thanks for helping me with that.
I will admit that I'm still a little unclear about the answer though.
You are correct that I am wondering about a spring powered car but I definitely would not use a spiral spring. A compression spring would probably work best.
I don't understand your final answer. I am getting lost in the spring conversion formula. What does the final answer mean in layman's terms please?
![]() ANSWER:
ANSWER:
The spring would have to be compressed by 7 meters. That would mean that it would need to be at least twice that long, about 40 feet! You could use a stiffer spring
(see below) to get a smaller required compression, but imagine the force you would have to exert to compress it. Keep in mind that you would have to supply the energy to the spring in the first place, a lot of energy.
I know this spring is not going to work, but how much force would it
take to hold it compressed by 7 m? F=kx=25,000x7=175,000 N≈40,000
lb. Another issue is that as the spring unstretches, the force it exerts
gets smaller, so you would need to have some kind of governor mechanism
to deliver the energy smoothly.
![]() CONTINUED
CONTINUED
Also, there are two things that are working in favor of the feasibility of the spring car:
I know from researching that there are many other factors that affect the gas- to engine- to -transmission to -wheels to- road, etc cycle so that the total efficiency of the entire loop would be far less than 20%.
![]() ANSWER:
ANSWER:
This is taken care of by the fact that I have specified the
miles per gallon for the hypothetical car. The miles per gallon you get is
determined by how well you have minimized the effects other than engine
efficiency, mainly frictional effects. You asked for an estimate of the
energy which the car would use to keep going a constant speed, and this is
the best way I can think of doing that. Here is another way to estimate the
energy consumed: suppose that I push on the car to keep it going a constant
speed. I could probably do that with a force of about 100 lb≈445 N; one mile
is about 1600 m, so the work I do is the product of the force times the
distance and the work I do is the energy I use: W=445x1600≈712,000 J.
(Actually, I am pretty impressed by how close this is to my other estimate
of 600,000 J! It's just an accident that they are so close, but good that
they are of the same order of magnitude‚ÄĒit increases my confidence that the
energy consumed is pretty well approximated.)
![]() CONTINUED
CONTINUED
Despite my very basic and incomplete understanding of the formulas that give exact measurements for potential energy in springs and the potential energy available in compressed air it is obvious to me that if a car can run 300 miles off of a bottle of compressed air and a compressed air driven motor (these cars already exist and are in production in places like holland, india, etc) then a large spring perhaps three feet long and two feet around with a wire diameter of over half an inch could at least do the same.
Getting the potential energy out of the spring in a useful way to power the car is another ball of wax altogether though.
![]() ANSWER:
ANSWER:
If you want a 3 ft long spring, about 1 m, the most you could
probably compress it is about a half meter. To store 600,000 J of energy,
the equation would be 600,000=–Ökx2=–Ök(0.5)2=k/8,
and so the spring constant would be k=4,800,000 N/m. Then the force
to hold it at 0.5 m would be F=kx=2,400,000 N≈540,000
lb. If you were not faced with such enormous forces, like if you just wanted
to have a toy car go a few meters, you could certainly get the energy out of
the spring with a cleverly designed gear box; but the structural problems
you would face with forces of hundreds of thousands of pounds would be
insurmountable, I believe.
![]() QUESTION:
QUESTION:
In the case of a block that's dropped some vertical distance onto a spring,
it's reasonably easy to compute this value & to find the KE of the mass just before it hits the spring, hence the velocity.
What doesn't ever seem to be explained is what happens to the block's acceleration ("g" when it hits the spring). The motion of the block continues downward, but now the net force is Fnet = kx - Weight = ma, not Fnet = mg. This means that the acceleration continues to be positive as the block compresses the spring, but @ a slower rate. This also means that the velocity continues to increase until all the block's PE is converted to spring elastic energy (Eelastic). At maximum compression the block stops & motion ceases. Since the ideal spring is massless there are no losses due to friction, heat, sound, et. al.
Where does the Vmax occur? It's hard imagine for Vmax to happen @ the instant it stops? Is this process for the spring's resisting force linear?
![]() ANSWER:
ANSWER:
OK, suppose the speed when it hits the spring is v0.
Choosing +y to be up and y=0 at the end of the uncompressed
spring, may=-mg+k(-y). (Note that when the
spring is compressed its force is upward and y<0 so the force is in
the +y direction; this is why I write the force of the spring as k(-y).
Now, until y=-mg/k, the acceleration is negative (points down)
and the mass is still speeding up; below that point, the net force is
positive (points up) so the mass slows down. Therefore the greatest velocity
will be at y=-mg/k. Note that this position would be the
equilibrium position if you gently placed m on the spring. You could
also get this answer with energy conservation; using the same coordinate
system, E=–Ömv02=–Ömv2+–Öky2+mgy.
This can be rearranged to give v2=-(k/m)y2-2gy+v02;
if you differentiate this with respect to y and set equal to zero,
you find y=-mg/k for the maximum velocity position. At that
position you can solve for the speed, v=√[(mg2/k)+v02].
The key here is that you need to be very careful with the coordinate system and the signs of forces and potential energies. If you do not choose +y up, the potential energy will not be mgy (it would be -mgy). If you do not choose the unstretched spring as zero potential energy for the spring, –Öky2 will not be the potential energy.
![]() QUESTION:
QUESTION:
How long would it take for a 50lb solid steel sphere to sink a quarter mile through ordinary water?
![]() ANSWER:
ANSWER:
I will assume that the sphere quickly reaches terminal
velocity so that I can assume that it goes the whole half mile with that
constant speed. This should be an excellent approximation. The terminal
velocity may be written as vt=√[2mg/(ρACd)]
where m is the mass, g =9.8 m/s2 is the acceleration due to
gravity, ρ is the density of water (1000 kg/m3), A is the
cross sectional area of the sphere, and Cd is the drag
coefficient which is 0.47 for a sphere. There is one catch here, that this
is without buoyant force and the buoyant force in water is equal to the
weight of the displaced water which is not negligible here; when it comes
time to put in the mass I will put in an effective mass of the mass of the
steel sphere minus the mass of an equal volume of water. I will work in SI
units, so 50 lb=22.7 kg and 0.5 mi=805 m. The density of steel is 7850 kg/m3
so the volume occupied by 22.7 kg is V=22.7/7850=0.0289 m3;
the radius of a sphere with this volume (using V=4πR3/3)
is R=0.0884 m and so the area (using A=πR2)
is A=0.0245 m2. Finally, the effective mass would be m=22.7-1000x0.0289=19.8
kg. Putting all these into the equation for vt, I find
vt=5.81 m/s. The time an object going this speed takes to
travel 805 m is 805/5.81=139 s, 2 minutes and 19 seconds.
![]() QUESTION:
QUESTION:
A plumb bob is hung from the ceiling of a train compartment. If the train moves with an acceleration 'a' along a straight horizontal track, the string supporting the bob makes an angle with the normal to the ceiling whose tangent is 'a/g'. Suppose the train moves on an inclined straight track with uniform velocity. If the tangent of angle of the incline is 'a/g', the string again makes the same angle with the normal to the ceiling. Can a person sitting inside the compartment tell by looking at the plumb line whether the train is accelerated on a horizontal straight track or it is going on an incline with uniform velocity? If yes, how? If no, is there a method to do so?
![]() ANSWER:
ANSWER:
First you should carefully read an earlier answer on the
accelerated pendulum. (Actually, I see that you
are the person who asked that question!) To answer your question, you can't
tell by "looking" but you certainly can tell by measurements. For example,
in the accelerated problem the tension in the string is m√(g2+a2);
for the inclined track the tension is mg. Or, in the accelerated
problem you feel youself being pushed back with a force (fictitious) Ma,
but on the inclined track you feel yourself being pushed back with a force
(real) Mgsinθ=Mg[a/√(g2+a2)].
![]() QUESTION:
QUESTION:
what would happen if someone were to HOLD the gun and shoot it. The person would not be tethered to anything and would be floating freely in space. If that person is around 160Ibs and shot a High power rifle how fast would it project the wielder in the opposite direction? I know it wouldnt be as fast as the bullet because of the mass of the person but I'm curious to what extent they would be projected into space... if thats would even happen at all.
![]() ANSWER:
ANSWER:
First, read an earlier answer to a
question similar to yours. The concept you want to use here is momentum conservation.
Momentum is the product of mass times velocity and the total momentum of
a system must be the same before and after the gun has fired. The mass
of a 160 lb man plus his gun is about 75 kg, the mass of a typical bullet is
about 0.015 kg, and the muzzle velocity of a high-power rifle is about 250
m/s. So, since the momentum is zero before the rifle is fired, 0=75v-250x0.015=75v-3.75
or v=0.05 m/s which is about 10 ft/min.
![]() QUESTION:
QUESTION:
A rigid container filled with air is placed in vacuum. If a small hole is created on one side of the container, air leaks out and the container moves in the opposite direction. How would the container move if the situation were reversed, i.e. a rigid container of vacuum placed in air with a hole on one side of the container? I can't seem to apply Newton's 3rd law and momentum conservation to solve this convincingly.
![]() ANSWER:
ANSWER:
Let's just think of a cubical box with a hole in one face.
Any molecule which finds the hole will enter the cube, go to the opposite
face, collide with it, and rebound, thereby transferring some momentum to
the box. The box is now moving in the direction in which the molecule was
originally moving (I will call that the forward direction). The rebounding
molecule will either go back out the hole or hit inside the cube and bounce
back again. As long as the molecule stays inside the box, the net effect
will be zero but eventually it will find the hole and so the net effect will
be one collision moving the box in the forward direction. Now think of a
huge number of molecules entering the hole. At the beginning, more will be
coming in than going out so the net force on the box will be forward.
Eventually, there will be the same density of molecules inside and outside
the cube so the net force will become zero. Bottom line‚ÄĒthe cube moves in
the same direction as if air were being released from it. An intuitive way
to see this is to note that each entering molecule carries a momentum in the
forward direction, so that is the momentum available to be transferred to
the cube.
.jpg)
![]() QUESTION:
QUESTION:
I have a question about force on a lever. I am building a set of oars
for a whitewater raft. The industry is full of opinions but very few
physicists. We all agree that the force is greatest at the oar lock
(fulcrum) but nobody has any idea how much less force is present at the
neck (the narrow part just above the blade). If you will do this
one...here are the values. Using a 10' oar the fulcrum is at the 32-36"
mark and the neck is at the 90" mark. The blade occupies the remaining
30". We taper the oars knowing they don't need to be as strong away from
the fulcrum but nobody knows how much we can taper because we don't know
how much less force they need to withstand. The taper results in the
neck having anywhere from 65% to 80% of the wood on the shaft. I suspect
80% is overkill. Any thoughts.
![]() ANSWER:
ANSWER:
A disclaimer: I am not an engineer and an engineer would
probably be a better person to ask this question. When you are rowing, the
water exerts a force, call it F, on the blade of the oar. I am
thinking that the thing we should be thinking about is the torque which this
force exerts about the lock compared to the torque it exerts on the neck.
This force may be thought of as being 15" from the neck, approximately in
the middle of the blade; so the torque from the water force at the neck
would be 15F. The torque at the lock would be, assuming the lock is
35 inches from the handle, about 55"; so the torque from the water force at
the lock would be 55F. So the torque on the lock would about 55/15≈3.7
times bigger than the on the neck. Now we get into some pretty complicated
materials engineering, see this
link.
It turns out that the stress σ is inversely proportional to a
quantity Z called the section modulus. For a cylindrical shape of
radius R, the section modulus is Z=0.78R3.
So, I surmise that an estimate of how much smaller the neck would be than
the lock would be Rneck3/Rlock3≈1/3.7
or Rneck≈0.65Rlock, about 2/3 the
thickness.
![]() QUESTION:
QUESTION:
If I have a ramp that is 28 feet long, fixed at the upper end (shore) and weighs 400 lbs that has a 6 foot rise, how do I calculate the weight at the lower end (dock)? I am trying to determine how much floatation I need under the water end to support the weight of the ramp at that end. That rise varies during the course of the year from zero feet to a maximum of 7 feet.
![]() ANSWER:
ANSWER:
I am assuming that the ramp is a uniform plank, that is, that
its center of gravity is at its geometrical center (14'). Refer to the
picture on the left. Two equations must be satisfied for equilibrium, the
sum of all forces must equal zero and the sum of all torques about any axis
must be zero. The first condition gives us that F1+F2-400=0
and the second condition (summing torques about the center of the ramp)
gives us that F1-F2=0. Solving these two
equations, F1=F2=200 lb. Note that the
answer, 200 lb, is independent of the rise.
![]() QUESTION:
QUESTION:
Two dice are suspended in outer space with no visible forces acting on them. Their center of masses are 10 cm apart, and they each have an identical mass of .0033 kg. How long would it take for the force of gravity between them to cause them to touch? (We will assume they are volumeless for more ease in calculation).
![]() ANSWER:
ANSWER:
This seems a very difficult problem because the gravitational
force between them changes as they get closer and so it is not a case of
uniform acceleration. However, this is really just a special case of the
Kepler problem (the paths of particles experiencing 1/r2 forces) which I
have done in detail
before.
You can go over that in detail. For your case, K=Gm1m2=6.67x10-11x(3.3x10-3)2=7.26x10-16
N∙m2/kg2, the reduced mass is
μ=m1m2/(m1+m2)=0.0033/2=1.65x10-3
kg, and the semimajor axis
a=2.5
cm=2.5x10-2 m. Now, from the earlier
answer,
T=√(4πμa3/K)=5.98x104
s. The time you want is T/2=2.99x104 s. This is only 8.3
hours and seemed too short to me. To check if the time is reasonable, I
calculated the starting acceleration and assumed that the acceleration was
constant and each die had to go 5 cm; this time should be longer than the
correct time because the acceleration increases as the masses get closer.
The force on each die at the beginning is K/r2=7.26x10-16/0.052=3.04x10-13
N; so, the resulting initial acceleration is F/m=3.04x10-13/3.3x10-3=9.21x10-11
m/s2. So, assuming uniform acceleration, 0.05=–Öat2=4.61x10-11t2.
Solving, t=3.3x104 s. So, the answer above is, indeed,
reasonable.
![]() QUESTION:
QUESTION:
I have a question concerning a magnet suspended inside a copper tube. Does the copper tube accumulate the mass of the magnet? In other words, does the copper tube now weigh more with the magnet suspended in the middle? or is it partial weight because the magnet does fall inside, albeit slowly.
![]() ANSWER:
ANSWER:
First, some terminology. Weight is the force which the earth
exerts on something, so the weight of the copper tube is always the weight
of the copper tube. If a magnet falls through a copper tube, it induces
currents in the copper and these currents exert a force on the magnet which
tends to slow it down. In fact, the force becomes strong enough that the
magnet quickly reaches a terminal velocity‚ÄĒit falls with a constant speed.
That means that the tube is exerting an upward force on the magnet equal to
the weight of the magnet. But, Newton's third law says that if the tube
exerts a force on the magnet, the magnet exerts an equal and opposite force
on the tube. Therefore, if the tube is standing on a scale, the scale will
read the weight of the tube plus the weight of the magnet, but that does not
mean that the tube got heavier. It is just the same as if you put the tube
on the scale and pushed down on it with a force equal the weight of the
magnet; you would not say that the tube got heavier because you pushed on
it. A good demonstration of this can be seen at
this link.
![]() QUESTION:
QUESTION:
Suppose a constant force is acting on an particle, due to which the particle is accelerated. The the velocity of the particle is increasing at a constant rate. Now if I use the relation P=F.v, i get the power delivered to the particle different at different instants since the velocity is different at different instants. But it is difficult for me to digest that though the force applied is constant, the power goes on increasing. Am I thinking right?
![]() ANSWER:
ANSWER:
What is power? It is the rate of change of energy. In the
example you give, a constant force in one dimension, the energy at any
instant is –Ömv2. Just to illustrate, let's let m=2
kg, a=1 m/s2, and the mass begins at rest at t=0.
After the first second, E1=–Öx2x12=1 J; after
the second second, E2=–Öx2x22=4 J; after the
third second, E2=–Öx2x32=9 J; after the fourth
second, E2=–Öx2x42=16 J; etc. So, the
average power delivered over the first second is ΔE/Δt=(1-0)/1=1
W; the average power delivered over the second second is ΔE/Δt=(4-1)/1=3
W; the average power delivered over the third second is ΔE/Δt=(9-4)/1=5
W; the average power delivered over the fourth second is ΔE/Δt=(16-9)/1=7
W; etc. The reason you are not "thinking right" is that you deliver
more energy to a faster-moving object with a given force over a given time
because energy is proportional to the square of the speed. Another way to
look at it is that average energy delivered by a constant force F
acting over a distance Δx
is ΔE=FΔx but, in any
given time, the force acts over an ever-increasing distance adding an
ever-increasing amount of energy; of course, that is where your power
equation comes from, P=ΔE/Δt=FΔx/Δt=Fv.
![]() QUESTION:
QUESTION:
I've read about space habitat concepts for a while and I've ran into an interesting concept. The concept I've ran into is the McKendree Cylinder which is basically an O'Neill Cylinder made of carbon nanotubes. The O'Neill cylinder made of steel would be 32km long and 6km in diamter. The McKendree Cylinder would be 4600 km long and 460km in diameter. And the maximum length for MvKendree Cylinder is 10000km and diameter of 1000km. So McKendree one could be built a lot bigger than O'Neill one because the carbon nanotubes have greater endurance. But a habitat of thousands of km's seems to be really big when compared to what we can build from other materials. And as I recall we don't have any ways to produce Carbon Nanotubes in large quantities. Is it theoretically possible to build a habitat 10000km long and 1000 wide put of carbon nanotubes. And is the McKendree cylinder more of a theoretical design than a practical design that actually could be built?
![]() ANSWER:
ANSWER:
I presume that the issue is more a strength issue than
anything else. To illustrate how the strength of the material and its mass
determine the size the habitat can be, consider a rotating string of beads,
each of mass m. The rotation rate must be such that a=v2/R=g
where v is the tangential speed of each bead. Therefore each bead
must experience a force F=mg. This force can only come from the two
strings attaching each bead to its nearest neighbors and, from my drawing to
the left, F=mg=2Tsinθ. But, we will imagine many, many
beads on this string and we will call the distance between them d; so
we can make the small angle approximation that sinθ≈θ=d/R.
Solving for T, T=mgR/(2d). Now imagine that the beads
are atoms; d will be about the same for steel or carbon, g is
just a constant, msteel≈5mcarbon,
and the
Young's modulus of carbon nanotubes is about 5 times bigger than steel,
Tsteel≈Tcarbon/5.
So, Rcarbon/Rsteel≈(Tcarbon/Tsteel)/(mcarbon/msteel)≈25.
Your numbers are Rcarbon/Rsteel≈460/6=77;
I would have to say that my calculation is pretty good given that I have
made very rough estimates and I am not an engineer! I do not know what
considerations would limit the length of the habitat. (Of course, neither of
these models is presently practical to actually build, so call them
theoretical if you like. However, there is certainly no problem building
them if resources and manufacturing capabilities were available.)
![]() QUESTION:
QUESTION:
If I mounted a gun against a force gauge that measured in pounds and fired it in a vacuum and then fired it in my back yard would it read any different? How much of the recoil is actually produced by the gas pushing against the air in front of the muzzle or is it all newton thrust? There are people who claim that brakes on guns actually pull the gun forward counteracting newton force from acceleration which makes about as much sense to me as moving a boat by standing on the deck and pushing on the mast. Others who claim that part of recoil is from newton force and part is from the gas pushing against the air in front of the muzzle.
![]() ANSWER:
ANSWER:
This is a little tricky as are most problems which involve
air drag. First of all, look over an
earlier answer about the
recoil of an M4 carbine. To do my rough calculations, I will assume all the
data refer to a gun fired in vacuum; muzzle velocity of 940 m/s, bullet mass
m=0.004 kg, gun mass 2.77 kg, bullet diameter 45 mm. I will assume
that the acceleration along the length of the barrel (0.37 m) is uniform.
(Be sure that you realize that the muzzle velocity is the speed with
respect to the gun, not the ground.) So, the bullet starts at rest and
the equations which give its velocity and position at the end of the barrel
are 940=at and 0.37=–Öat2 where a is the
acceleration and t is the time to reach the end of the barrel.
Solving these two equations, I find that t=7.87x10-4 s and
a=1.2x106 m/s2. Using Newton's second law,
F=ma, we can now estimate the force experienced by the bullet during its
flight down the barrel as 0.004x1.2x106=4800 N=1079 lb. Now,
suppose that there is air in the barrel. As the bullet flies down the barrel
it will experience air drag which will be a force which will work against
the force propelling the bullet and therefore the muzzle velocity will be
smaller. As you will see from earlier
answers, a fairly good approximation for air drag force on an object
with cross sectional area A going with speed v is Fdrag≈—ėAv2.
For the 45 mm bullet, A≈1.59x10-3 m2, so taking the average speed to
be 940/2=470 m/s, I find Fdrag≈88 N=19.8 lb. This will be,
I believe, an underestimate because the bullet is not just plowing through
the air as it would outside the rifle but compressing the air in front of
it. Now the net force on the bullet is about 4800-88=4712 N. Now, the
average acceleration will be about 4712/0.004=1.178x106 m/s2,
slightly smaller; the corresponding time and muzzle velocity are t'=7.93x10-4
s and 934 m/s. In the earlier
example I found the bullet speed v and recoil velocity V
to be v=938.6 m/s and V=1.4 m/s; my (very rough) estimate for
including the effects of air are v=932.7 m/s and V=1.3 m/s.
There is slightly less recoil in air. The average force on the gun during
the firing time is the same as the force on the bullet (Newton's third law) ≈4800 N=1080 lb for vacuum, ≈4712
N=1059 lb including air. That sounds like a lot, but keep in mind that it
only lasts about 0.8 milliseconds. I have included a lot of details here, but you can
understand it qualitatively: because the bullet has to accelerate through
the air which causes drag, the muzzle velocity will be smaller so the recoil
velocity will be smaller as well.

![]() QUESTION:
QUESTION:
In Halo video game series there are Magnetic Accelerator Cannons on orbit around planets that can launch a 3000 ton magnetic projectile to 4% lightspeed. These cannons use the principle of the coil gun. These projectiles have a kinetic energy of 216000000000000000000 joules which translates to around 51.6 gigatons of tnt. So these cannons seem to have really unrealistic velocities for these projectiles. What would be the problems in developing these cannons to defend the human species from possible alien invaders? I know energy is one but I've heard that that if you were to accelerate a projectile to these kinds of speeds they would turn into plasma from the sheer amount of energy being transferred into them.
![]() ANSWER:
ANSWER:
I think you will get the picture of why this is a
preposterously impossible weapon if you read an earlier
answer. There the speed was much higher but the mass much smaller. Here
are the practical problems in a nutshell:
-
To accelerate it to this speed in a reasonable distance the force required would be so large as to totally disintegrate the projectile and the cannon for that matter.
-
Think about the recoil of the cannon. Unless its mass was much bigger than 3000 tons, much of the energy expended would be wasted, not to mention the disruption of the orbit. This would be a good reason to have it mounted on the ground rather than orbit.
-
Where are you going to get the necessary energy? I agree with your number for the kinetic energy of the projectile (–Ömv2 works fine for this relatively low speed and a ton here is a metric ton), ≈2.16x1020 J. Suppose it took one minute to get this much energy; then the power required would be 2.16x1020/60≈3.6x1018 W=3.6x109 GW. This is about 1,440,000 times greater than the current total power generated on earth of about 2500 GW. (Of course, that does not take into account the recoil energy of the cannon itself.)
-
Oh yeah, I almost forgot. There is no evidence whatever for alien bad guys.

![]() QUESTION:
QUESTION:
If I were to drop an empty wine bottle out of an airplane flying at say 35,000 feet above the ocean at 300 mph, would the bottle hit the surface of the water hard enough to break the bottle? I read somewhere something about terminal velocity being 120 mph, so would the resistance of the atmosphere slow the wine bottle to 120 mph by the time it made impact with the ocean? And would 120 mph be enough to shatter the wine bottle, or would it depend on how choppy the seas were versus a flat water surface?
![]() ANSWER:
ANSWER:
When I answer questions involving
air drag and terminal velocity, I
usually use the approximation that (in SI units) the force F of air
drag is F≈—ėAv2 where A is the area presented
to the wind and v is the speed. So, as something falls, the faster it
goes the greater the drag force on it so that, eventually, when the drag
equals the weight, the object will be in equilibrium and fall with constant
speed. Since the weight W is mg where m is the mass and
g=9.8 m/s2, the terminal velocity can be calculated: —ėAvterminal2≈mg
or vterminal≈2√(mg/A). So the
terminal velocity depends on the mass and size of the falling object and
your 120 mph is most likely not correct. Also, how it falls determines the
terminal velocity since it has a much bigger area falling broadside than
with the top or bottom pointing down. I figure that if it falls broadside
there will be a bigger pressure on the fat side than the neck which will
cause a net torque which will make it want to turn with its neck pointing
down; so I will assume that is how it falls . I happened to have an empty
wine bottle in my recycle bin which has a mass of about 0.5 kg and a
diameter of about 8 cm. When I calculate the terminal velocity I get vterminal≈63
m/s=140 mph. The 120 mph number you heard was probably a typical terminal
velocity of a human, and it is just coincidence that the wine bottle has a
terminal velocity close to that.
It is hard to say whether it would break or not. I think probably not. Suppose that it took 1 s to stop. Then the average force on the bottle would be F=ma=(0.5 kg x 63 m/s)/(1 s)=31.5 N≈7 lb which the bottle should be able to withstand. I know that they say that at high speeds hitting the water is like hitting a brick wall, but if the stopping time were 0.1 s the force would still only be about 70 lb.
(Who would have thought that I would find a picture of a falling wine bottle? You can find anything on the web!)
![]() QUESTION:
QUESTION:
This question is regarding Newton's cradles. Let's say a particular
one had 5 balls. We pull back 3 balls and let go. Now the other side
must rebound with 3 balls as well. This means that the middle ball must
carry on swinging. Does it ever theoretically stop for the briefest of
moments? What about in real life with compression and other factors?
![]() ANSWER:
ANSWER:
I presume you have read the recent
answer below. Usually, in collision problems, we ask what is going on
before the collision and after the collision, but not during the collision.
The details during the collision time depend on the details of the
interactions among the balls which we generally do not know. So in cases
like Newton's cradle, we approximate the collision to occur in zero time and
therefore approximate all accelerations to be instantaneous; this is clearly
not the case since it would require an infinite force to stop or start a
ball instantaneously. So, to be more realistic, we must, as you have done by
mentioning "compression", devise some model for the collisions. With steel
balls we could assume that each was a very stiff but perfectly elastic
spring which compressed during the collision. Then, assuming the collision
were perfectly elastic (again an approximation), the collisions would happen
in a very short but nonzero time. The two incoming balls would stop in a
short time because the middle ball would exert a large backward force on
them and the two outgoing balls initially at rest would get up to speed in a
very short time because the middle ball would exert a forward force on them.
Therefore, with this simple model, assuming all the balls are identical, the
middle ball would experience a zero net force during the collision time and
so it would proceed forward never changing its speed. I could imagine that
the middle ball might slow down slightly and then speed back up to its
original speed, but not stop. Even if the collisions were perfectly
inelastic, the middle ball (and all others) would move with speed 3/5 the
speed it came in with afterwards. Whatever happens, the middle ball would
certainly never be at rest.
![]() QUESTION:
QUESTION:
This one has bothered me since seeing it on TV the other evening. The device called Newton's Cradle, that executive metal ball swing toy found on many desks - I understand the basic principles of the conservation of motion, energy, etc. My mind can also wrap itself around the fact that when you raise and drop one ball, one ball on the opposite side responds by moving. What I don't understand though is why when you raise and drop two balls, TWO balls on the other side respond by moving. It would seem that to conserve energy/motion, the kinetic energy of the two balls that was raised would be transferred into the last ball and it would swing out twice as much as the two balls that started the motion. How do the two balls on the end "know" that it was two balls that started it? Can you please explain this?
![]() ANSWER:
ANSWER:
Be clear that the approximation to use is that the collisions
are elastic, both energy and momentum must be conserved; for steel balls,
this is a pretty good approximation. OK, let's assume that two balls come in
with speed v1 and one ball goes out with speed v2.
Conserving momentum, 2mv1=mv2 or v2=2v1.
Now, look at energy: E1=–Ö(2mv12)=mv12
and E2=–Ömv22=–Öm(2v1)2=2mv12.
Energy is not conserved, mv12≠2mv12.
You can actually prove if that a mass M comes in, only if the mass
going out is M will both energy and momentum be conserved. Here is
the proof:
-
momentum: MV=mv => v=(MV/m)
-
energy: –ÖMV2=–Ömv2=–Öm(MV/m)2 => M=M2/m => m=M
-
since m=M, v=V from momentum.
Nature "knows"! You can't fool Mother Nature.
![]() QUESTION::
QUESTION::
I have searched for an answer to this question in vain.
A dropped large ball, with a small ball on top, will bounce and transfer the upwards momentum into the small ball, launching the small ball very high into the air. (As far as I understand this, I saw a demo).
Ignoring air resistance for now, how heavy would the large ball have to be, to launch a one kilogram weight into orbit, and what would the height of the drop have to be?
As an example, a 100 tonne ball dropped from 10 metres, with a 1kg ball on top, does a bounce, what is the velocity result for that?
How does the elasticity of the ball affect it? (eg, a large metal ball or weight might just impact the ground).
![]() ANSWER:
ANSWER:
This problem is fully explained and worked out at
this link. The final result, if the mass of the big ball is much bigger
than the mass of the little ball, is that the speed the little ball rebounds
is given by v≈3√(2gh) where h is the height from which it was
dropped. This means that the masses really do not matter. The height to
which the smaller ball bounces is 9 times the height from which it was
dropped. It is assumed that all collisions are perfectly elastic. The speed
required for a near earth orbit is about 8x103 m/s, so h=v2/(18g)=3.6x106
m! To put this in perspective, the radius of the earth is about 6.4x106
m, so h is about half this. This is a really rough calculation because g
will be considerably smaller (by a factor of about 0.4) at this altitude.
Even if you did make this work, the ball goes straight up and you need it to
go horizontally to go into orbit. I think it is not a very practical idea!
![]() QUESTION:
QUESTION:
What role does the force of friction play in the movement of a cycle....?? I have learnt that the friction acts in the forward direction on the rear wheel and backward direction on the front wheel.How can it be...?? I think I am missing a broader link to why a wheel actually rotates.
![]() ANSWER:
ANSWER:
In this discussion I will ignore all friction except that
which occurs due to the contact of the wheels with the road. The two kinds
of friction we normally learn about in elementary physics courses are static
and kinetic friction. Kinetic friction is the frictional force between two
surfaces which are sliding on each other; it is kinetic friction which stops
a box sliding across the floor. Static friction is the force between two
surfaces which are not sliding on each other; it is static friction which
keeps your bike from skidding when turning a corner. A third contact
friction force is called rolling friction; this is not terribly important
for a bike but is the force which will eventually stop you if you coast on
level ground and you are most aware of it if your tires are
under-inflated‚ÄĒharder to pedal. Rolling friction on both wheels will always
point backwards. First think about a bike which is not skidding. If you go
in a straight path on level ground without pedaling, only rolling friction
stops you and neither kinetic nor static friction are in play. Now suppose
you start pedaling to accelerate forward. Think about what your back wheel
"wants to do"; if the road were icy, the wheel would spin and the force
which keeps it from spinning on a dry road is static friction. The road will
exert a forward force on the wheel to keep it from spinning. A force is
required to accelerate anything and this static friction force is what
accelerates your bike forward. The friction on the front wheel is just the
rolling friction backwards. Finally, suppose you brake: if both brakes are
applied gently enough that you do not skid, static friction on both front
and rear wheels will point backward; if both wheels skid during braking,
kinetic friction on both front and rear wheels will point backward. You
probably know that if you apply the brakes so that they are not quite
skidding, you will stop in a shorter distance than if you skid. When you
round a curve, both wheels have a static friction force which points
perpendicular to your direction and toward the curve's center because you
are accelerating when you move in a circle even if you are going with
constant speed. More detail on
rolling friction and on
bicycle turning can be found
in earlier answers.
![]() QUESTION:
QUESTION:
I had asked you a question and you had answered it. To illustrate your point, you had quoted an example that a pendulum hanging from the ceiling of a car moving with a uniform acceleration makes an angle with the vertical. Now we have been taught in our course as well. We have also learnt that tangent of the angle is equal to a/g. My question is that will that pendulum exhibit uniform oscillations if it is displaced from its normal position?
![]() ANSWER:
ANSWER:
I presume that by "its normal position" you mean its new
equilibrium position off the vertical. The answer to your question is that
it will exhibit oscillations about this position; the period, though, will
not be given by T≈2π√(L/g) but rather by T'≈2π√[L/√(g2+a2)].
This is most easily understood by introducing a fictitious force ma
opposite the direction of the acceleration. Now you can see that the force
exerting a torque on this pendulum has a magnitude of m√(g2+a2)
rather than mg as in the unaccelerated pendulum. So it is just like
the usual pendulum analysis with a somewhat larger acceleration due to
gravity.
![]() QUESTION:
QUESTION:
Are the equations of motion v = u + at, S = ut + 0.5at^2 , and v^2 = u^2 + 2aS applicable if a particle travels at a speed close to that of light? I think that they are applicable, and only F =ma is not, but my friend says that those 3 equations are also not. Who is right?
![]() ANSWER:
ANSWER:
Your friend is right. These are the classical equations for
uniform acceleration, and uniform acceleration is not possible in the theory
of special relativity for a constant force. Constant force, where F=dp/dt,
(which, incidentally, is the way Newton originally wrote his second law) can
be constant but does not result in constant acceleration. I have treated
this problem in detail in an
earlier answer; there I find that
v=(Ft/(m))/√[1+(Ft/(mc))2]
and
S=(mc2/F)(√[1+(Ft/(mc))2]-1)
(for your
u=0,
that is, the particle at rest at
t=0)
for constant force.
![]() QUESTION:
QUESTION:
This is a question about tractive effort of locomotives. I am a model railroader and we have been debating this situation for a while with no clear answer. If there is a locomotive on the track that has 4 driving wheels touching the rails, and the only change you make is to the number of wheels , now 6 driving wheels on the track, will tractive effort go up, stay the same or drop. The argument for staying the same is that each wheel now supports less weight, so tractive effort of each wheel would drop. The argument for tractive effort going up would be that there are more contact points on the rail, so it would pull more.
![]() ANSWER:
ANSWER:
What drives your train is the static friction between the
wheels and the track. The nature of static friction is that a maximum amount
of force may be achieved before the surfaces slip on each other. This force
Fmax is determined, to an excellent approximation in many
cases, by the nature of the surfaces (steel on steel for your case, I
presume) and how hard they are pressed together (called the normal force
N); Fmax=μN where μ is the coefficient
of static friction, a number determined by the materials. You will note that
this force does not depend on the area of contact. Essentially, adding
wheels adds surface area but, as you note, the force pressing the surfaces
together (namely the normal force which is determined by the weight) is
simply distributed over a larger area. So, the simplest first-order physics
answer is that the same maximum force from the wheels without slipping will
be achieved regardless of the number of wheels. Friction, though, can be a
tricky business and first-order physics does not always work for all
situations. For example, there are
instances where a car
tire can have greater "road hugging" (read increased friction) if the
road-tire contact area is increased. I believe in your case, though, since
the wheels and track are so little deformed by contact, that increasing the
number of wheels will not increase friction provided that the total
mass of the locomotive remains the same. Of course, if you are adding wheels
to an existing locomotive, you are adding mass so you will be increasing
Fmax. There is a very easy way to test this. Put the
locomotive (wheels not free to rotate) on a piece track which is attached to
a horizontal board. Gradually increase the angle of the board until the
train slides down. The tangent of the angle at which it starts to slide will
be equal to the coefficient of static friction. If increasing the number of
wheels does not increase the slip angle, there is no advantage.


![]() QUESTION:
QUESTION:
If a plane, while mid-flight, had an explosion from the wing or rear area, would the debris maintain the exact same momentum as the plane and go forward alongside it, would the debris go in front of the plane, or would the debris go behind the plane when the accident first happens? Me and two friends got on the topic after watching a movie dealing with a plane crash. One friend thinks debris would go in front, the other thinks the debris would maintain precise momentum with the plane, and I'm thinking it would go behind the plane. We'd really love for a physicist to clear up this question for us, thank you so much!
![]() ANSWER:
ANSWER:
What anything does is determined by the forces on it. A plane
flying in a straight horizontal line with constant speed has four main
forces acting on it: gravity (its own weight); lift which is the force which
counteracts the gravity to keep it flying level, drag caused by the air, and
the forward force exerted by the engines which counteracts the drag to keep
it from slowing down. If a piece of the plane suddenly separates from the
plane, it no longer has any foward force and it no longer has any
significant lift; so, it will start dropping vertically and slowing down
horizontally, falling down from and behind the plane. The falling is
generally more prounounced than the slowing down (gravity usually a greater
force than drag) so there would be a tendency for the piece to appear to
just drop straight down as seen from the plane. (Be sure to realize that the
forward velocity of the piece is approximately maintained so that someone on
the ground sees it moving forward with about the same speed as the plane.)
This is often seen in bombs dropped from a plane. On the left photograph the
drag on the bombs is small so they keep pace with the planes as they drop.
On the right, the bombs have little parachutes to increase drag and so they
fall behind the plane.
![]() QUESTION:
QUESTION:
If some object, at some distance far from the surface of the Earth, but much closer to the Earth than anything else (meaning everything else in the universe is negligible) is at rest initially but then begins accelerating towards the Earth due to gravity, how long will it take to get to the Earth?
I get that the acceleration is a=GM/r^2. And then you can write a as the second derivative of r which would make it a non-linear differential equation but I have no idea how to solve those really. I have taken a differential equations course but it was 3 years ago so I don't remember if we even solved non-linear ODE's ever.
![]() ANSWER:
ANSWER:
I have solved variations of this problem twice before,
one very recently regarding Coulomb's law
(simply another 1/r2 force) and
the other where the object
was falling into the sun instead of earth. You should read through these
first since I will skip a lot of the detail here. In the spirit of those two
answers, I will take you at your word that the object is "far from the
surface of the earth", that is, r>>Rearth. Hence, it is
just the Kepler problem with an orbit of eccentricity 1 and semimajor axis
a=r/2 and we need to find half the period T. Kepler's third
law states that T2=4π2a3/(GMearth).
Therefore, T/2=π√[r3/(8GMearth)].
For example, if r=100Rearth (which would mean at an
altitude of 99Rearth), T/2=9x105
s=250 hr.
You can always estimate how much error is made in this approximation (assuming the earth and objects are point objects going all the way to zero separation) by calculating the speed v the object arrives with at earth's surface. Energy conservation gives -GMearthm/r=–Ömv2-GMearthm/Rearth or v=√[2GM(1/Rearth-1/r)]. For the example I did, v=√[(198/100)GMearth/Rearth]=1.1x106 m/s. If the earth were a point mass, the object would continue speeding up. If it kept going into the earth at a constant speed, the time it would take to reach the center would be about 6 seconds, enormously shorter than the time to get to the surface, so the approximation is superb for r=100Rearth.
![]() QUESTION:
QUESTION:
i tried to find the time it would take for two charges to collide
under electrostatic force,realizing simple kinematics won't cut it,tired
to integrate but failed,how is the question done?and how does it differ
from gravitational force??
![]() QUERY:
QUERY:
You have to define what "collide" means. Since it is a 1/r2 force, if you use point charges the velocity will be infinite when they collide but they will do so in a finite time. Also, what are the initial conditions (velocities, positions), masses, charges.
![]() REPLY:
REPLY:
My initial question was the time it would take for a 1/r^2,to
collide,for example two bodies lets say 1g,and a charge of 1micro
coluomb,initial at rest attract each other,and collide,I can't use
simple kinematics to solve this question,what shall I do?
![]() QUERY:
QUERY:
How far apart are they?
![]() REPLY:
REPLY:
ok,for simplicity 1m apart,is there a general formula than can help?
![]() ANSWER:
ANSWER:
Whew! I finally have everything I need. This is the Kepler
problem, the same, as you suggest, as the solar system with gravity. You
may want to look at an
earlier answer similar to yours. It is very lengthy to work out the
whole problem in detail so I will refer you to a very good
lecture-note document from MIT; I will just give you some of the
necessary results to calculate what you want. First, a brief overview of
two of Kepler's laws:
-
Kepler's laws refer to problems where the force is of the form F=K/r2 where K is a constant and the force is attractive. So it could refer to either two masses or two opposite charges.
-
The first law states that bound planets move in ellipses with the sun at one focus. This is really only true if the sun is infinitely massive but the generalization still leads to an elliptical orbit for each body, both of which move around the center of mass of the two. Still, the semimajor axis a of the ellipse (which we will later need) in the center of mass system can be found for any orbit from the simple equation a=-K/(2E) where E is the energy of the system.
-
For your case, the particles move in a straight line toward each other and then turn around and return to their original positions. This is just the most elongated possible ellipse with an eccentricity of 1. Of course this would never really be possible in the real world since the particles would be going an infinite speed when they "collide". That means we really should do the problem relativistically which would greatly complicate the problem. Keep in mind that you are asking an unphysical question requiring point charges and infinite forces and velocities. But the answer below should be a good approximation of the time if they have some finite size small compared to their initial separation.
-
The third law relates the period of the orbit T to a: T2=4πμa3/K where μ=m1m2/(m1+m2) is the reduced mass. In the gravitational problem, K=Gm1m2 and in the electrostatic problem, K=keq1q2 where ke=9x109 N¬∑m2/C2.
For your case, the energy is given since the charges are initially at rest and separated by some distance S, so E=V(S)=keq1q2/S and so a=keq1q2/(2keq1q2/S)=S/2=0.5 m; the reduced mass in your case is μ=m1m2/(m1+m2)=10-3x10-3/(2x10-3)=0.5x10-3 kg; and K=kq1q2=9x109x10-6x10-6=9x10-3 N¬∑m2. Finally, the time it takes for a complete "orbit" (which would correspond to the particles returning to their original positions) would be T=√[4πμa3/K]=√[4π(0.5x10-3)(0.5)3/9x10-3]=0.3 s. But, the time you want is just half a period, T/2=0.15 s.
To help you visualize the orbits, the figure below shows the orbits for the two charges when the eccentricity is just less than 1; imagine the orbits getting flatter yet, approaching two straight lines.
![]() NOTE
ADDED:
NOTE
ADDED:
I got to wondering what the limits of doing this classically
are, that is, how good an approximation my calculation above would be for
some real system. This requires that I determine how close the two charges
would approach each other before their speed v became comparable to
the speed of light c. I will use the same notation as above and write
things classically. If released a distance S apart, then when they
reach a distance r apart energy conservation gives: keq1q2/S=keq1q2/r+–Öμv2
which results in v=√[(2ke|q1q2|/μ)(1/r-1/S)].
For the case in point, if I solve for r when v=c/10, a
reasonable upper limit for a classical calculation, I get r=4x10-8
m, about 100 times bigger than an atom. Alternatively, we could ask what the
velocity would be for a 1 mm separation, r=S/1000: v=√[(2ke|q1q2|/μ)(999/S)]=1.9x105
m/s=0.00063 c. In either case, I think we can conclude that the time
remaining to complete the half orbit will be extraordinarily small compared
to 0.15 s.
![]() QUESTION:
QUESTION:
does the terminal velocity in a parachutist's fall occurs two times?
one before opening the parachute
and one some time after opening the parachute Am i right?
![]() ANSWER:
ANSWER:
The terminal velocity is determined by (among other things)
the geometry of the falling object. In the simplest approximation, what
matters is the cross sectional area of the falling object. So, when the
parachute is opened, the area gets much bigger and the terminal velocity
gets much smaller. If the sky diver has achieved some larger terminal
velocity, she will slow down to the new terminal velocity. However, this
need not be the first time the terminal velocity changed. The sky diver can
orient in a ball or like a down pointing arrow and have a relatively large
terminal velocity or she can fall spread-eagle and slow down. So the
terminal velocity probably changed several times before the parachute was
opened.
![]() QUESTION:
QUESTION:
i am unable to understand a pulley problem
![]() ANSWER:
ANSWER:
This is a most peculiar problem! However, its solution ends
up being very easy to do (if not to visualize). I will assume that all
pulleys are massless and frictionless and that the string is massless and
unstretchable. I always tell my students when attacking this kind of problem
to "choose a body" upon which to focus and apply Newton's second law. There
are two obvious choices here, the left-side m which results in
-T+mg=maleft and the right-side m which results in
-2T+mg=maright. So, we have two equations and three
unknowns; the best you can do is to find the relation between the two
acclerations, 2aleft+aright=3g.
To generate a third equation, choose the left pulley which results in 2T-T=0=T.
So, the only result which works is aleft=aright=g,
both masses in free fall.
I was having a lot of trouble visualizing how this happens, so you I made
a little model and made a movie of it. To see it, go to the
Ask The
Physicist facebook page. (I know, it's not going to win an academy
award, but it satisfied my curiosity!) The two masses, with equal
accelerations, will move equal distances in equal times which then made it
pretty easy for me to make a little model on the floor with strings and
paint cans. Apparently the left pulley moves twice the distance the right
pulley moves in any given time.
![]() QUESTION:
QUESTION:
I've been trying to write a action sci-fi screenplay, but there is one problem that I can't get my head around.
During the climax, two characters fall from a 91 story building, with the first jumping off, and the second falling approximately 10 seconds later. The second character proceeds to catch up to the first, and they then brawl.
My question is, how much time would pass before they would hit the ground?
![]() ANSWER:
ANSWER:
There is a good reason you can't get your head around it:
the second character will not catch up to the first! I will give you a
little basic physics tutorial on possible scenarios. For purposes of
computation, I will assume that the height of your building is about 400 m
(about 13 ft/story) and I will approximate the acceleration due to gravity
to be g=10 m/s2.
-
First I will assume air drag is negligible, that they fall as if they are in a vacuum. Then the height y1 above the ground of character 1 is given by y1=400-5t2 where t is the time since he jumped. This tells us that when character 2 jumps, y1=400-500=-100 m; since y=0 is the ground, he has already hit the ground! The freefall time (the time when y1=0) from 400 m is about 8.9 seconds and the speed when he hits the ground will be about 89 m/s=200 mph.
-
So, maybe we just need to add some air drag. That certainly will be important for speeds on the order of 200 mph. When air drag is taken into account, you do not continue speeding up forever but eventually fall with some maximum constant speed called the terminal velocity; this happens when the air drag (up) is equal to your weight (down). If your mass is M, your weight is Mg or, with my approximation, 10M. Let's use M=100 kg (about 220 lb) so Mg=1000 N. A good approximation for air drag is F=—ėAv2 where A is the cross sectional area of the falling object and v is the speed. I will choose A=1 m2 so, if I set F=1000 and solve for v, I find a terminal velocity of vt=63 m/s=140 mph. The details of the math gets a little complicated here, so I will give you the results and spell out the details below for anybody interested. I find that the time that it takes to reach the ground now is about 10.8 seconds at which time the speed is about 59 m/s. So character 2 has less than a second to catch up to character 1, obviously impossible.
-
Finally, I should tell you that if the two characters are about identical, about the same size and weight, character 2 will never catch up with character 1 regardless of the height of the building. In the no-air-drag situation, both have the same acceleration and so their paths never cross. In the air-drag situation, both have the same terminal velocity so they will end up having that speed and separated by some constant distance. The only way to make it happen is to greatly change the cross sectional area of character 1, for example, give him a parachute!
I am guessing that, if you want to have any semblance of reality, you will want to rethink your climax!
![]() ADDED
DETAIL:
ADDED
DETAIL:
Vertical fall with quadratic air drag is a well-known
problem worked out in any intermediate classical mechanics textbook. The two
results which I used were v=vt√[1-exp(-2gh/vt2)]
and t=(vt/g)tanh-1(v/vt)
for an object dropped from height h.
![]() QUESTION:
QUESTION:
Was killing time on a slow day at work, and involved a coworker in the site. Some time later he ask a question, which might be up the physicist alley. Assuming we had a person seal in a vacuum with a piece of paper and a baseball, if he threw the baseball and then crumpled up the piece of paper and threw it. Would the paper fly as far as the baseball having no friction to affect it, or does gravity rule supreme and bring it to a halt just as well as it does outside a vacuum?
![]() ANSWER:
ANSWER:
Let's assume that you are throwing both as hard as you can
which means you exert equal forces on them. Also assume that you exert that
force over the same distance for each case which means you do the same
amount of work (force times distance) on each. That means that they have
equal kinetic energies when you release them. But, kinetic energy is –ÖMV2
where M is the mass and V is the speed. So, suppose the
baseball has a mass 100 times the sheet of paper; then, if they have equal
kinetic energies, the speed of the paper will be 10 times larger than the
baseball and therefore go 10 farther. Your last sentence makes no sense
because gravity does not "bring it to a halt", it is friction which does
that.
![]() QUESTION:
QUESTION:
Suppose a bullet is fired parallel to the ground, due to perpendicular direction of work done with respect to gravity, no work is done against it. Then why does not the bullet fall immediately to the ground as it does when it is not in motion? I have speculated that motion in in dimension reduces the effects of forces of other dimensions. Is there really such a thing in physics? If not, then what is the correct explanation?
![]() ANSWER:
ANSWER:
First, do not worry about what was happening to the bullet
while the gun was firing it; that is past history and has nothing to do with
what happens to the bullet after it leaves the gun. Newton's first and
second laws tell us that the only reason something will not move in a
straight line with constant speed (or be at rest which is a constant speed
of zero) is if there is a force acting on it. Further, the change in motion
the object experiences is in the direction which the force points. Normally
in elementary physics classes, we neglect the force of air drag (which is a
pretty poor approximation for a bullet) such that the only force is that due
to gravity which we call the weight of the object. So, all the bullet can do
is change its motion in the vertical position because that is the direction
that the weight points. So even though your bullet starts with no vertical
motion, it will fall just as it would if you simply dropped it. In other
words, it will take just the same time to drop to the ground whether you
fire it horizontally or simply drop it. In an
earlier answer, you can see
a strobe photograph where a ball launched horizontally and one dropped fall
vertically the same. In the real world, air drag is not negligible and is a
force which always points in the direction opposite the velocity. This
causes the bullet to slow down in the horizontal direction but to also speed
up more slowly vertically. The figure shows an example where the conditions
allow the whole range of scenerios to play out: because of the air drag, the
horizontal motion is eventually stopped and, because of the interplay
between weight and drag, the projectile ends up falling vertically with a
constant speed called the terminal velocity.
![]() QUESTION:
QUESTION:
I am in my powerful rocket. If my orbital speed around the sun was zero and I was the same distance from the sun as the Earth, and my rocket was firing at the exact velocity to hold my position to keep the rocket from from falling towards the sun but no greater, what would my 200 lb Earth body weigh on the rocket ship scales? I am guessing a bit less than 800 lbs. What do you say?
![]() QUESTION
TO QUESTIONER:
QUESTION
TO QUESTIONER:
What does that mean, "my orbital speed around the sun was zero"? If your speed is zero you are not orbiting. If you are at rest a distance of the earth's orbit from the sun, I would call that hovering. Then you have to calculate the sun's gravitational force on you to know your "weight".
![]() REPLY:
REPLY:
You are right, I did wish to know my weight when hovering,
![]() ANSWER:
ANSWER:
The force W which the sun exerts on you (aka your
"weight") is given by W=GMm/R2 where G=6.67x10-11
Nm2/kg2 is the universal constant of gravitation,
M=2x1030 kg is the mass of the sun, R=1.5x1011
m is the distance to the sun, and m=91 kg is the mass of a 200 lb
weight. If you do the arithmetic, the result is W=0.54 N=0.12 lb.
Quite a bit less than 800 lb! You might be interested in a
similar question where
the questioner wanted to know the time it would take the earth to fall
into the sun if it had no orbital speed.
![]() QUESTION:
QUESTION:
i have to know that why the mass of bob in a pendulum does not
affect the time of oscillation.....i think it should as the more massive
bob should have more potential energy when string is pulled for
10degrree but at the same time when its moving more air resistance would
also act on it. My book of physics says that the number of oscilllations does not affect the final answer of time period per each oscillation.
as we know that a pendulum should automatically stop moving after some time.
This means that if 100 oscillations are taken then the time per one oscillation should be decreased. I know im wrong as my physics book of GCSE says so but i want to know why im wrong and what part of my staement does not make sense
P.S : please use simple language or formulas(if u wanna use) as i wont be able to understand complex ones.
![]() ANSWER:
ANSWER:
Let's get straight what we are talking about. You refer to
air resistance and you note that the pendulum will eventually stop. Of
course, the main reason it stops is air resistance. Any air resistance is
assumed to be negligible in a treatment of the pendulum at your level (9th
grade), so imagine that there is none. Second, your book should tell you
that the pendulum only behaves in a simple way if the angle you start it at
is small; but even 300-400 is sufficiently small for
the standard treatment of the simple pendulum to be quite accurate. However,
your expectation that the air resistance will affect your measurement of the
period is wrong because, to an excellent approximation, the period does not
depend on the amplitude and so one period when you start and the amplitude
is, say, 200, will be almost exactly the same as one period when
the amplitude has decayed down to 50. Given your level of school,
I cannot give a very rigorous explanation for why the mass does not matter.
But, if you can understand resolving a vector into components and know
Newton's second law, that F=ma, then you should follow my
explanation. In the picture to the right you see the forces, mg
and T, which act on m. But we are interested in the
motion of m along its arc and neither T nor the
component of mg perpendicular to the arc can affect that
motion, so all that matters is the component of mg along the
arc which is mgsinθ and this is the force which causes the
mass to accelerate along the arc. So, applying Newton's second law for
motion along the arc, mgsinθ=ma; you will notice that m
cancels out so that a=gsinθ. Clearly the acceleration
will determine the motion along the arc and therefore the period will not
depend on m. But, of course, a real scientest tests his hypothesis.
Go to a park where there are swings and find a little boy and his father
both swinging; you will see that they both have the same period even though
they have very different masses. (Your argument about potential energy is
not valid because, although the potential energy at the top is, indeed,
proportional to m (U=mgh), the kinetic energy at the bottom is
also proportional to m (K=–Ömv2). So, again,
mass cancels out.) Finally, I should tell you what the period does depend
on: only on the length of the string and the acceleration due to gravity,
T=√(L/g)]/(2π). A pendulum clock will not keep good
time on the moon.
![]() QUESTION:
QUESTION:
Im trying to
figure out what speed a sphere weighing 4,506 lbs will attain on a 3 degree
grade from complete stop to 95 ft. [After communicating, it is a uniform sphere
of radius 4', rolls, does not slip.]
![]() ANSWER:
ANSWER:
The easiest way to solve this is conservation of energy.
Let's work in SI units, m=4506 lb=2044 kg, d=95'=29 m, and
R=4'=1.22 m. The energy at the top of the ramp is E1=mgh
where g=9.8m/s2, and h is the height above
the bottom which is h=dsin30=0.052d. The energy
at the bottom where the speed is v is E2=–Ömv2+–ÖIω2
where I=2mR2/5 is the moment of inertia and
ω=v/R is the angular velocity. Putting this all
together and solving for v, v=√(0.058gd)=4.07
m/s=13.4 ft/s=9.1 mi/hr. So, you see, the answer to your question does
not depend at all on either the mass or the radius of the sphere, R
and m cancel out as you can show for yourself.
![]() QUESTION:
QUESTION:
Figure skating - if you are doing a spin on ice and you leave your arms spread out it creates resistance, if you pull the in towards the body you create less resistance so you spin more easily. How do I express this with mathematical equation in physics?
[The questioner is a 13 year-old high school student with no physics
training.]

![]() ANSWER:
ANSWER:
While it is true that there is somewhat more air resistance
if your arms are outstretched, you are barking up the wrong tree if you
think this is the reason your spin speeds up when you pull your arms in.
The principle involved here is conservation of angular momentum which is
a topic usually covered late in an introductory physics course, so I
have to give you a little background here. For translational physics
(objects moving without spinning), Newton's second law is perhaps
paramount: the rate at which linear momentum changes is equal to the
force on the object. Linear momentum p is defined to be the mass
m of the object times its velocity v, p=mv. If an
object has no forces on it, the rate of change of linear momentum must
be zero which means that it never changes; this is called conservation
of linear momentum. For a single object, this means that it continues
moving in a straight line with constant speed because the mass will not
spontaneously change. In rotational physics, Newton's second law is
analogous to translational physics: the rate at which angular momentum
changes is equal to the torque on the object. Let's briefly discuss what
the quantities are in translational and rotational physics:
-
Force is what causes an object to accelerate, change its velocity. Torque is what causes an object to spin faster (called angular acceleration). Note that it is possible to exert a force on something without causing a torque, for example, pushing on a door where it is hinged does not open the door.
-
Linear momentum is p=mv. Angular momentum is L=Iω, the moment of inertia (see below) times the angular velocity (for example, revolutions per minute).
-
Mass is the resistance a body has to being accelerated; a one pound force exerted one second will cause a much bigger acceleration for a baseball than for a locomotive. Moment of inertia I is the resistance of a body has to being angularly accelerated (increased spinning speed). But, monent of inertia does not just depend on the mass of the body, it also depends on how that mass is distributed. In the case in point, the figure skater has a larger moment of inertia with her arms outstretched than not; the same torque applied to each will result in a smaller spin rate for the outstretched arms.
-
If you exert no force on an object, its linear momentum must remain constant. If you exert no torque on the object which is spinning, its angular momentum must remain constant.
Are there any torques on the skater who is spinning? Yes, there is the friction of the skates on the ice and the air drag on her body, and if she just does nothing she will eventually stop spinning. However, those torques are small (it would take a pretty long time for her to stop), so we can say that angular momentum is approximately conserved. Now, suppose that her moment of inertia with arms outstretched is Iout and with her arms pulled in is Iin=Iout/3, and that she is initially spinning with ωout=2 revolutions per second. Then apply momentum conservation:
-
Iinωin=Ioutωout
-
2Iin=Iinωout/3
-
ωout=6 revolutions per second.
That's the whole story. Because angular momentum is conserved, reducing the moment of inertia results in increasing the angular velocity.


![]() QUESTION:
QUESTION:
I teach a self defense course. I am
trying to explain to my students that a 230 grain bullet moving at 850
ft per sec not stop a 200 lbs person running at them at full speed. If i am correct or not could ypu please put it into terms that i could use.
![]() ANSWER:
ANSWER:
The concept you want to use here is momentum conservation.
Momentum is the product of mass times velocity and the total momentum of
a colliding system must be the same before and after the collision. The
one subtlety here is that if the momentum of a 2 lb mass moving
300 ft/s north is 600 lb·ft/s, then a 2 lb mass moving 300 ft/s south
has a momentum of -600 lb·ft/s. I will use lb to measure mass and ft/s
to measure velocity, so you have to
be sure you get all the units the same to make any sense: 230
grain=0.033 lb. You say "full speed" so I will use 30 ft/s to be the
person's velocity, which would correspond to a 10 second 100 yard dash.
So, the momentum before the bullet strikes (and lodges in) the man is
200x30-0.033x850=5972 lb·ft/s. (Notice the - sign on the momentum of the
bullet since it and the man are going in opposite directions.) After the
bullet lodges in the man the momentum is 200.033xV where V
is the velocity of the man (plus bullet) after he is hit. Setting the
momenta before and after equal and solving for V, V=5972/200.033=29.9
ft/s. So, you see, the man loses almost no velocity at all due to the
bullet. If you hit his head or his heart he might stop running but it is
certainly not the impact with the bullet which stops him. A qualitative
way to put this is that while the bullet has a speed about 30 times
greater than the man, it has a mass almost 7000 times smaller. Related
to that, when you see a movie in which a character is sent flying
backward by the impact of a bullet, it is total nonsense and will not
happen in real life.
![]() QUESTION:
QUESTION: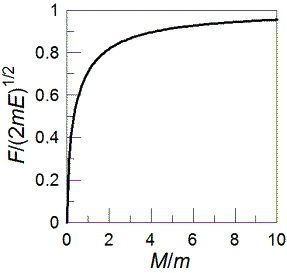
does the amount of force(i.e the amt. of RECOIL that a gun experience) require to hold a operating gun in position ,depends on the mass of it?
consider the following example - there are two persons A and B.A is having a 10 kg gun and B is having a 5 kg gun. Both guns are shooting the same type and number of bullets per second. Now ,which of the two persons would require to exert a greater force to hold the gun in position?
If the force require to hold both the guns in position is the same(which I think it is ),then is it not counterintuitive?? I mean ,imagine to exert the same force to the 50 kg gun and a 5 kg gun, to hold them in position??
![]() ANSWER:
ANSWER:
This problem is a little trickier than I expected. Here is
the way I approached the problem: imagine that there is nothing holding
a gun of mass M shooting a bullet of mass m. Then you can
use momentum conservation to find the relative speeds of the bullet,
v, and the gun, V, after being given an amount of energy
(from the gunpowder in the bullet) E; V=(m/M)v.
Usually, M>>m, so v>>V, so it might seem
that the lighter gun would go faster and be harder to stop; but the
catch is that it is easier to stop something with less mass, so it is
not really clear which is easiest to stop until we can write what the
speed V is. You might think I have already done that, but the
speed of the bullet v depends on the mass of the gun. To get rid
of v in my equation for V you need to introduce the
constant energy which gets given to the gun and the bullet, E=–Ömv2+–ÖMV2.
If you now solve this equation for v, substitute that into the
equation for V, you find V=√[(m/M)(2E/(m+M))].
Now, in order to stop this motion in a short time Δt you must
exert a force F=MV/Δt=√[(2mME/(m+M))]/Δt.
If you examine this, you will see that if M>>m, as is almost
always the case, F≈√[2mE]/Δt, independent of M.
For smaller gun masses where the bullet and gun have comparable masses,
I have plotted the force (divided by the constant √[2mE])
as a function of M/m. This is shown in the graph to the
right and you can see that it is easier to stop a lighter gun.
For the usual case where the gun is much more massive than the bullet, it is easy to see intuitively that force is independent of mass. In that case, the velocity of the bullet will be essentially the same for each case so v is not (to an excellent approximation) a function of M. So, V is inversely proportional to M and, since F is proportional to MV, F must be independent of M.
![]() NOTES
ADDED:
NOTES
ADDED:
It occurred to me that one could also define "recoil" as the
force necessary to stop the gun in a given distance Δx
(rather than in a given time Δt as above). Then the
magnitude of the work done by that force must be equal to the kinetic
energy the gun had, FΔx=–ÖMV2=–ÖM(m/M)(2E/(m+M))=E/(1+(M/m)).
In this case, it is clearly easier to stop a heavier gun.
So, how recoil is defined is important in discussing this question. A little research reveals that, indeed, gun enthusiasts do not think of perception of recoil as what they mean by recoil. Rather, there are several types of recoil which are used to quantify the effect. Recoil velocity is what I have called V; recoil energy is –ÖMV2; recoil momentum is MV; recoil impulse is the time it takes the gun to accelerate from rest to V, essentially the time the bullet is in the barrel (not what I call Δt). This is eminently sensible since each of these is unambiguously defined. Perception is rightly considered to be qualitative, dependent on the person firing the gun.
I also should note that my analyses above assume that perception begins when V has been acquired, but this is not really what happens because you actually start feeling the recoil at the instant the gun is fired. So you can ask what force you need to exert during the time the bullet is accelerating to hold the gun at rest; so, when the bullet exits the barrel, you experience no more force. Clearly this force is independent of M since the gun never moved. Now all bullets to which a constant energy E has been added exit with a velocity v=√(2E/m) because by holding the gun still you effectively make its mass infinite. Approximating that the acceleration, and therefore the force, is constant while the bullet is in the barrel, it is pretty easy to show that F=E/L where L is the length of the barrel. Again, there is no dependence on M. Of the three kinds of "recoil perception" I have defined, I think this last one makes the most sense.
![]() QUESTION::
QUESTION::
Newtons Law states that to every action there is an opposite and equal reaction. If a cue ball is stuck hard enough and strikes another ball, the other ball moves off with the same speed at which it is struck, while the cue ball stops dead. This is providing the cue and cue ball and struck ball are in a dead straight line. Does this mean that the cue ball has transfered all of its energy to the ball that moves off therefore not being able to follow on?
Have just found your site and find it very interesting and so give to you my thanks.

![]() ANSWER:
ANSWER:
This is an "action/reaction" example (Newton's third law)
only in an indirect sense: because the balls, when colliding, exert
equal and opposite forces on each other, their total momentum must not
change (be conserved). Billiard balls are very elastic and therefore, to
a good approximation, energy is conserved also. For the one-dimensional
case where one ball is initially at rest which you cite ("dead straight
line"), there are two equations to solve:
-
momentum conservation, m1v1=m1u1+m2u2, and
energy conservation, –Öm1v12=–Öm1u12+–Öm2u22,
where m1 is the mass of the incoming ball, m2 is the mass of the other (at rest) ball, v1 is the incoming speed, and u1 and u2 are the outgoing speeds. If you solve these, you get the speeds after the collision:
-
u1=v1(m1-m2)/(m1+m2)
-
u2=2m1v1/(m1+m2).
So, if m1=m2 (as for billiard balls), u1=0, u2=v1, as you note. And, certainly, as you also note, the first ball has transferred all its energy (and momentum) to the second ball. Since I have gone to the trouble of solving the problem generally, we might as well look at a couple of other special cases. Suppose that m1<<m2; this would be like colliding your cue ball with a granite wall. In that case u1≈-v1 and u2≈0, where ≈ means approximately equal; this is just what you would expect, the ball bounces back (that is what the - sign means) with the speed it went in and the wall stands still. Similarly suppose that m2<<m1; this would be like colliding your cue ball with a BB. In that case u1≈ v1 and u2≈2v1; so the cue ball never knew anything happened and the BB ends up going twice as fast as the cue ball.
Incidentally, for completeness, there is a second solution when you solve the two conservation equations, sometimes referred to as the "trivial" solution. You should expect two solutions because one of the equations is quadratic. The second solution is
-
u1=v1
-
u2=0.
This is called trivial because it would correspond to missing totally and you would certainly expect the energy and momentum to be conserved if the collision never happened.
![]() QUESTION:
QUESTION:
would it be possible to have a particle accelerator as an engine for a spaceship? Where by rerouting particles that are moving near the speed of light and making them collide with the back of the spacecraft would give the spacecraft a push in the back?
![]() ANSWER:
ANSWER:
You are essentially asking "if I, standing in my spaceship,
push on the front wall, will it go faster?" Whatever impulse you gain by
pushing forward with your hands will be cancelled by the frictional
force your feet exert backwards. Similarly, the impulse you get from the
push from the particles forward would be negated by the force necessary
to "reroute" them or to accelerate them in the first place. Anything you
do inside a closed system cannot change the momentum of that system. If
you were to fire the particles out the back like a rocket you could
propel the spaceship; this is the idea of
ion-drive
thrusters.
![]() QUESTION:
QUESTION:
could centrifugal force force actually be used to simulate gravity like in so many sci-fi stories?
one of my favorite sci-fi stories is the Ringworld by Larry Niven. The Ringworld of the title is a giant ring shaped structure the size of earth's orbit. It's centered on a star and has a habitable inside edge, gravity on this inside edge is simulated by the structure spinning fast enough to make objects feel as heavy as they would at 99.2% earth gravity.
If I were stood on a real structure like the Ringworld, and I jumped up in the air, would I fall back down or fly off into space?
![]() ANSWER:
ANSWER:
Yes, as long as the radius of the ring is large compared to
the size of the objects. In such a scenario, the centripetal
acceleration should be set equal to g, so g=Rω2
where ω is the angular velocity in radians per second. So, the
picture to the right shows the ring as viewed from outside. You now jump
straight up with a speed v. However, note that you also have a
tangential velocity of Rω so your actual velocity is √(v2+R2ω2).
So you see what will happen is that you will go in a straight line with
constant speed (because there are no forces on you) along that velocity
until you again strike the ring; it will seem that you jumped and came
back down. You can calculate the time you were in the air and how high
you went by doing some pretty straightforward geometry/trigonometry.
-
I find the two angles labeled θ above are the same so sinθ=v/√(v2+R2ω2) and cosθ=Rω/√(v2+R2ω2).
-
From these you can find the length of the chord (the length of your flight) C=2Rsinθ=2Rv/√(v2+R2ω2),
-
the height you go above the surface h=R(1-cosθ)=R(1-Rω/√(v2+R2ω2)), and
-
the time you are in the air T=C/√(v2+R2ω2)=2Rv/(v2+R2ω2).
Now, let's compare these with the time and height on earth. Remember that ω=√(g/R) and I will take R to be very large compared to compared to v2/g. So, now I find that
-
h=R(1-Rω/√(v2+R2ω2))=R(1-1/√(1+v2/(R2ω2))=R[1-(1+v2/(Rg))-–Ö]≈R[1-(1-–Öv2/(Rg)+‚Ķ]≈v2/(2g) and
-
T=2Rv/(v2+R2ω2)=2R/(v(1+R2ω2/v2))=2R/(v(1+Rg/v2))≈2v/g.
These two approximate results are just the same as for a projectile launched straight up on earth. Keep in mind, though, that R must be large. Also, you do not want to jump with a velocity which has a component parallel to the axis of rotation. If you are too close to the edge, you will miss the ring when you "fall back".
![]() QUESTION:
QUESTION:
Balancing a glass on knives how does it work?
The
video.
![]() ANSWER:
ANSWER:
It seems to me that they show you how to do it in the video.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
i'M
sorry I mean why does this happen? How come the three knives hold the glass?
![]() ANSWER:
ANSWER:
Examine each knife. Each has a force A up on
its handle from a glass; each has a force B up at the end of
its blade from one of the other three knives; each has a force C
down from the third knife; each knife has a force of its own weight
W down at the center of mass of the knife (where you could
balance it without any forces but the weight acting on it). On that knife,
the sum of the forces is zero, A+B-C-W=0. On that knife, the sum of
the torques about any axis is zero; for example, about the glass end the
where A is applied, B(d1+d2)-Cd1-Wd3=0.
These conditions are satisfied and the knives are all in equilibrium. There
is another interesting thing you can note: the force C on this
knife is the force one of its neighbors exerts down on it with the end of
its blade; but, by Newton's third law, the forces forces these two knives
exert on each other are equal and opposite. It follows, therefore, that
C=B since the knives are symmetrically arranged and all three must have
the same forces on them. You can also see that the three glasses must hold
up the total weight of the three knives, so 3A=3W, A=W.
If you solve for these forces you will find A=W
and C=B=W(d2/d3). Putting the
beer glass on top simply increases the forces B, C,
and A but the knives remain in equilibrium. Is this what you
were looking for?
![]() QUESTION:
QUESTION:
"A tube in the shape of a rectangle with rounded corners is placed in a vertical plane. You introduce two ball bearings at the upper right-hand corner. One travels by path AB and the other travels by path CD. Which will arrive first at the lower left-corner?"
My problem is with the velocity of the ball at the end of traveling down the first side, whether it be A or C. The problem states 'rounded corners'. Surely the ball does not come to a stop -i.e. zero velocity, as it turns the corner. So I would guess that there is a significant velocity after 'rounding' the corner and hence must be accounted for.
![]() ANSWER:
ANSWER:
This is a problem out of Halliday and Resnick, Chapter 3 on
kinematics. I have been assured that it not homework, rather someone
brushing up on introductory physics. I must admit that I am a little puzzled
by it because, although I can solve the problem analytically as a function
of the sides A and C and the angle θ which C makes with the
vertical, none of these is given; this means to me that there must be some
obvious qualitative reasoning for this picture which does not
require any details. In this picture, the ball going down C will have a much bigger acceleration than the ball going down A because it is steeper; since C is shorter, that ball will arrive at its turn earlier than the other ball. Also, because the first corner is lower along C than along A, the C ball will be going faster when it gets to its corner than the A ball will be. So, the C ball turns the corner earlier and with a higher speed. The C ball wins. That's the best I can do with qualitative reasoning. (I would be glad to have anybody write in with a better explanation.) However, my curiosity led me to solve the problem analytically so I could examine all the possibilities. I will not give the anaytical solutions for both of the two paths since they are a little messy, but they depend on A, C, and θ; click here to see these solutions. Plotted below are the times as a function of θ for 00-900. The case most closely resembling the given problem is where A=2C with θ≈300; The C ball is the clear winner as speculated above. One interesting thing to note is that when θ=450, the balls take the same time regardless of the lengths of the sides. This is easy to understand because both balls have identical accelerations of 0.707g the whole time. And, the ball starting on the steeper slope always wins the race, regardless of the lengths or the angle θ. Note also that as θ―>00 the time for A ―>∞, and as θ―>900 the time for C ―>∞. This is also easy to understand because a ball in a horizontal tube will not move at all.
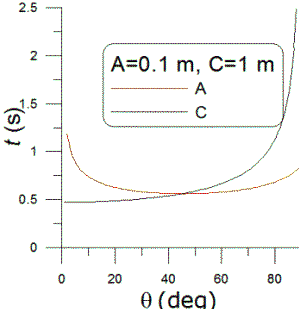
![]() QUESTION:
QUESTION:
how
fast will i fall down on the moon if i way 1000 pounds?
![]() ANSWER:
ANSWER:
Your weight is not relevant. The acceleration due to gravity at the
surface of the moon is about 1.6 m/s/s, so if I drop you, you will have a
speed of 1.6 m/s after one second, 3.2 m/s after 2 seconds, 4.8 m/s after 3
seconds, etc.
![]() QUESTION:
QUESTION:
I
have two friends that skydive. They got into an argument the other day
about how they felt some time after they jumped, once they reached
terminal velocity. One said he felt weightless, while the other said he
didn't feel weightless. My question is this, what should they feel at
terminal velocity? Should they feel 100% of their body weight? Does the
force from air resistance become a pseudo normal force? And, just for
fun, if they got crazy and jumped out of a plane with a large piece of
ply wood so that they were laying on the piece of wood which was falling
to the ground, would they feel their weight once they reached their new
terminal velocity?
![]() ANSWER:
ANSWER:
As my wife would say, there is no arguing with feelings. What it means
to be "weightless" in the usual vernacular is that there are either no
forces at all acting on you or else your weight is the only force on you but
you have an acceleration equal to the acceleration of gravity. If there were
no air at all your friends would be weightless as they fell; an astronaut in
orbit has a centripetal acceleration pointing toward the center of the earth
so, technically, he is free falling. It is important to bear in mind,
however, that this use of weightless is, strictly speaking, incorrect
because your weight is the force that the earth exerts on you and this does
not go away if you happen to be falling. Now, I would say that neither of
them should feel weightless by that definition because there is the weight
force down and the air resistance force up which are equal in magnitude at
terminal velocity so it is analogous to laying on the floor where the upward
force equal to your weight is the contact force with the floor. Do you feel
weightless when laying on the floor? I think you would not say so.
![]() QUESTION:
QUESTION:
Does a scale with a box that contains a flying bird register
the weight of both the box and the bird or just the box? Does relative
size of box and bird make a difference? Does it make a difference if the
box has perforations or no lid.(i.e., not a closed system). And is "how
closed the system is" a critical component to this problem.
![]() ANSWER:
ANSWER:
If the box is closed, the weight of the bird (assuming that it has no
vertical acceleration) will register. The reason is that the air exerts an
upward force on the bird equal to the bird's weight. So the bird, because of
Newton's third law, exerts an equal (to the bird's weight) downward force on
the air. So the forces on the air are its weight (likely to be negligible),
an upward force, and a downward force equal in magnitude to the bird's
weight; so, since the air is in equilibrium, the box exerts an upward force
equal to the weight of the air plus the weight of the bird. Therefore, again
because of Newton's third law, the air exerts a force down on the box which
includes the bird's weight. To a first approximation, all of the above still
applies even if the box is open, but things could get complicated in detail.
You might be interested in a
similar question I answered long ago about sand falling in an hourglass.
![]() QUESTION:
QUESTION:
What happens if I jump vertically on a moving bus? Will I
move back or will I stay in the same spot? And Why
![]() ANSWER:
ANSWER:
Physics is an experimental science and this would be an extremely easy
experiment for you to try. Even more impressive would be to jump straight up
in an airliner which has a speed of about 600 mi/hr which is almost 900
ft/s. So, if the plane were to move forward and you not, if you were in the
air for 0.2 s you would land about 180 feet behind where you jumped, obvious
nonsense! The reason you come back to where you jumped from is that you and
the plane both have the same forward velocity when you jump and it does not
just disappear when you are not in contact with the plane, you keep moving
forward with that same speed, just like the plane. An observer on the ground
would see you as moving in a parabolic path as you went by. Another example
is to look at WWII movies of bombers dropping bombs: the bombs all are
strung out (approximately) directly below the airplane. All this assumes
that the airplane (or bus) is traveling in a straight line with constant
speed.
![]() QUESTION:
QUESTION:
Does an object extremely far away from any other object has
inertia in space?
![]() ANSWER:
ANSWER:
Inertia is the property inherent of objects which cause them to resist
accelerating when pushed on by a force. It has nothing to do with the
environment. The object has no weight if in empty space.
![]() QUESTION:
QUESTION:
How do I determine the ideal weight of an object with a
given size to achieve maximum distance when put in motion? Example: I
know a baseball made of styrofoam or lead would not go very far when
thrown. An official baseball weight is 5 oz. If it were 4 oz or 6 oz
would it go as far of a greater distance when hit or thrown as the 5 oz
baseball?
![]() ANSWER:
ANSWER:
Take first the baseball and the styrofoam ball. The reason the baseball
goes farther is that air friction has a larger effect on the smaller mass.
In particular, the terminal velocity, that speed which an object will end up
having after a long time, is proportional to the square root of the mass.
Hence the greater the mass, the greater the range will be. The reason you
assume a lead ball will not go as far as the baseball is because you are
thinking that you cannot throw it as far; that is certainly true, but the
reason is that you do not have the strength to give it the same initial
velocity as the baseball. For a meaningful experiment each ball should be
projected with the same initial velocity; if that is done, the lead ball
will go farther than the baseball which will go farther than the styrofoam
ball.
![]() QUESTION:
QUESTION:
Is a juggler, while juggling three weights or any number really, lighter at all times than she would be if she merely carried the weight about her person? If so then by how much, when and why? If not then what does happen to their weight while they juggle at the various times they are and are not in contact with the juggled objects?
![]() ANSWER:
ANSWER:
First, I am a stickler for the use of the word weight. The juggler's
weight is the force by which the earth attracts him and so it is always the
same unless he overeats or goes on a diet. But, the apparent weight (what
would be read by a scale he is standing on) depends what is going on with
the balls. If all the balls are in the air at some time, his apparent weight
will be his actual weight. If he is simply holding one ball, the scale will
read his weight plus the ball's weight. If he is in the process of juggling
one of the balls, he is exerting an upward force which will be larger than
the weight of the ball (Newton's second law); but, because of Newton's third
law, we can conclude that the ball exerts an equal and opposite force on
him; and so the force read by the scale will be larger than the weight of
the ball plus juggler. An interesting and related problem is that of what
the apparent weight of an hourglass is, discussed in an
earlier answer.
![]() QUESTION:
QUESTION:
consider a space rocket in motion has ke=1/2 mv2. when the rocket accelerates to 2x its velocity, we would get 4x ke. would it really take 4x the amount of fuel to increase the velocity 2x? where is conservation in this example?
![]() ANSWER:
ANSWER:
First, talking about fuel is a little tricky because fuel has mass and
you have a more complicated rocket if its mass is changing. So let's talk
about a rocket whose total mass is much greater than the mass of the fuel or
else imagine an external agent pushing. Now, what is conserved in an
isolated system? The two important things are total energy and total linear
momentum. There is no such thing as conservation of velocity. To change
linear momentum which is mv, the mass times the velocity, you must
exert a force F over a time t and the change in momentum is
Ft. Ft is called the impulse. If you double the impulse, you
double the change in velocity if mass does not change. So push twice as hard
or twice as long and change the velocity twice as much. Now, if you want to
change the kinetic energy of the rocket, you must also push on it. But now
the conservation principle says that the change in the kinetic energy is
proportional to the work done one it. Work is Fx where F is
the force which acts for some distance x. So, if you double the
amount of work you double the change in kinetic energy, so you double the
change in v2 if mass is unchanged. If you start from rest
and do an amount of work W and end up with speed v, then if
you do 2W of work you will end up with only (√2)v
velocity. Burning twice the fuel will give twice the work (energy) so
the kinetic energy increases by a factor of two and the velocity increases
by a factor of
√2.
![]() QUESTION:
QUESTION:
Does adding mass to a toy car affect the force of gravity acting on the car, the acceleration of the car, or both as it rolls down a ramp? I want to do a lab in my middle school classroom where students investigate Newton's 2nd Law of motion by rolling a toy car down a ramp and measure the distance it rolls. They will use washers to increase the mass of the toy car. How would increasing the mass affect the distance the object rolls down the ramp? I found this lab on the Internet (without an answer key) and need to be sure that I'm right about what the outcome should be.
![]() ANSWER:
ANSWER:
Let's first talk about what the results should be according to
elementary physics. The force of gravity (called the weight) is proportional
to the mass. If you increase the mass by a factor of 2, the force impelling
it down the plane increases by a factor of 2. But, what does a force do? It
causes an acceleration in the direction of the force. But the acceleration
(from Newton's second law) is inversely proportional to the mass of an
object; this is called inertia, mass is the property of an object which
measures how resistant it is to an acceleration if you exert a force on it.
So, if you increase the mass by a certain factor you increase the force by
that factor and the net result is that the acceleration is unchanged! This
should be the lesson learned by doing this experiment. By the way, this is
the same idea as the old story of Galileo dropping a marble and a cannonball
from the leaning tower and finding them to hit the ground at the same time.
However, in the real world, there are other forces besides gravity, mainly
frictional forces, acting on the car and these can confuse the issue when
trying to do an experiment like you describe. As you will see when you look
over earlier answers to
just this question, sometimes the heavier car wins and sometimes the lighter
one wins; many details can make this experiment a mess! If I were you, I
would carefully do the experiment beforehand to make sure that it will teach
what you want it to!
![]() QUESTION:
QUESTION:
Is conservation of momentum proved practically if so what is the experiment?
![]() ANSWER:
ANSWER:
Actually, momentum conservation is more a definition than something you
verify. According to Newton's second law, the force equals the time rate of
change of something called momentum. If the momentum of a system is not
changing, it has, by definition, zero net force acting on it. In classical
mechanics, the momentum turns out to be mass times velocity. In relativity,
it is more complicated but still conserved for an isolated (no external
forces) system.
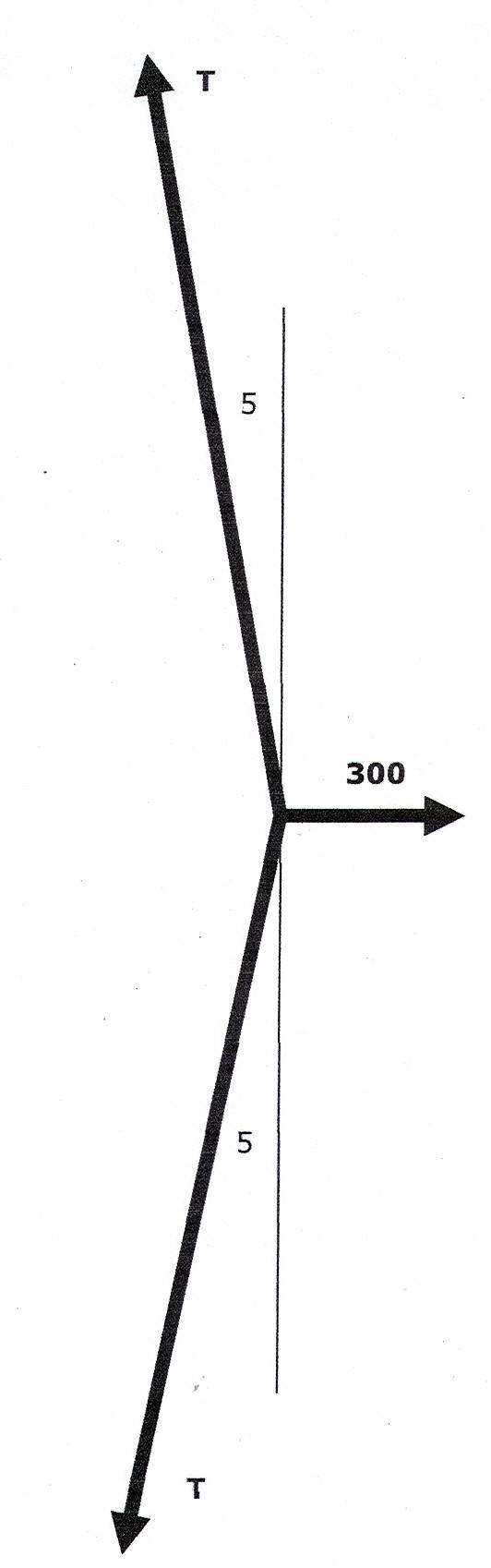
![]() QUESTION:
QUESTION:
Today on NPR's "Cartalk," someone called in a physics question. I would like to have a definite answer (very easy for you I'm sure). Here it is: A lady's car is stuck in the mud. She of course is alone with no phone and is a physicist. She ties a rope to her car bumper and a nearby tree. She then finds the mid-point of the rope and pushes with max effort which she estimates to be 300 Newtons. The car just begins to budge with the rope at about a 5 degree angle. With what force is the rope pulling on the car?
Ray, co-host of "Cartalk," said to find the sine of 5 degrees and then multiply by 300. Then he changed it to cosine of 5 degrees and multiply by 300. If any of these is right, I don't understand why. I've done vector problems before but they were simple Pythagorean probs (like, two ropes pull on an object at 90 degrees to each other--find the the single vector--easy).
![]() ANSWER:
ANSWER:
One of my favorite shows! Neither of the answers is right which is
surprising since Tom and Ray are both are MIT grads. Here is how you do the
problem: See the drawing (sorry for the quality) on the left. The point
where she is pulling is in equilibrium, so the vector sum of the three shown
vectors (her 300 lb pull and the tensions in the two halves of the rope)
must equal zero. The components perpendicular to her pull must add to zero,
so the tension (T) in each side of the rope is the same. This comes
from T1 cos 50-T2 cos 50=0,
so T1=T2=T. Similarly, the
components parallel to her pull must sum to zero, so 300-T sin 50-T
sin 50=0. So, T=300/2sin 50=1721 lb.
![]() QUESTION:
QUESTION:
If I secure 2 hemispheres in a vacuum (ie in space), then I bring it back to Earth at around sea level, what would be the strength of the hemishperes against being torn apart?
![]() ANSWER:
ANSWER:
I presume you mean how much force must be applied to pull them apart.
The geometry of the sphere makes a quantitative answer to your question
difficult (too mathematical) but I can give you an idea how big the force
would be. I will assume we have two "hemicubes", two halves of a hollow cube
which we put together. Atmospheric pressure is about 105 N/m2,
about 2100 lb/ft2. The forces pushing on the cube (or sphere)
depend on its size; imagine a 1 ft cube. The force holding it together, due
to the pressure on the two ends opposite the seam, would be 4200 pounds.
![]() QUESTION:
QUESTION:
picture a roof made made metal. stick a magnet to that roof. The magnet has weight naturally. so by keeping itself stuck to the roof it needs to oppose the force of gravity acting on it. It does so by exerting another force of attraction in the opposite direction, this force needs to be stronger than that of its own weight if it is to remain stuck to the roof.
This is where my question comes in: that force is work is it not. It is actively working to oppose its own weight. But its a permanent magnet and the amount of energy used to magnatise it compared to the amount it expends holding itself aloft is disproportional. I read that you do the work for the magnet when you pick it up to sick it to the roof and you'll need to do the same amount of work to pry it off again so in essence you have done the work for it and you have simply transferred it to a different potential state. But im sorry it does not make sense. There is a constant force opposing its attraction force to the roof. the force of gravity. This is in violation of newton, to apply a constant force you need a constant supply of energy. Where does the magnet derrive that energy from?
![]() ANSWER:
ANSWER:
You have this entirely wrong. First of all, the force necessary to hold the magnet to the roof must be exactly equal to the weight of the magnet. Second, the force holding it to the roof does no work because it does not act over a distance; if you used the magnet to move a nail across the table it would do work
on the nail. Finally, exerting a force does not require energy, only if the force does work.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
I am satisfied to a point with the answer but it still doesnt make sense If you look at it like this:
Take an ordinary object and attach it to a pully system. pull on the chord until the object meets the roof. now keep it there. since the object is not exerting its own force keeping it there you have to do that for it. in doing so over a period of time you will begin to tire as you are burning calories, expending enegry to keep that onbject aloft.
the magnet stuck to the metal roof is only kept there by the force it is applying to the roof. you said that force is not greater than its weight but just equal and opposite to gravity.
but what about an industrial magnet. you can easily support its weight on your hand, but put the magnet on your hand when resting on a metal plate it will crush your hand. I want to know how a magnet can apply a constant force and not "tire".
![]() ANSWER:
ANSWER:
Your question now verges on biology rather than physics. I do recording
for the blind and recently read a discussion regarding just what you are
asking, viz. how can you say I am not doing work when I hold a box
when I know energy is required to do so? The gist of the answer is that
muscles exert a force by individual fibers of the muscle continually
slipping and then recontracting, so for this special case the individual
componenets of the total force are all contiually pulling over a distance
and hence doing work. This is not the case for a mechanical system like your
magnet; or say you simply tied the rope in your pully to something (not a
muscle)‚ÄĒthe rope exerts the necessary
force and does not use any energy to do so. I do not see the relevance of
your "crush your hand" remarks. While your hand is being crushed the magnet
is moving so work is being done; when it is all crushed, no more work is
done.
![]() QUESTION:
QUESTION:
Hi, I'm reading Hal Clement's Mission of Gravity set on an oblate Jovian sized planet. The planet spins at 8 minutes per rev to create such squashed sphere. The main special thing about the planet is that the gravity at the equator is about 2 g and the gravity at the poles is a massive few hundred g. Now, the question is, is Hal Clement's physics right? Would there really be a gravity disparity on a planet like this? And if so, what creates it?
![]() ANSWER:
ANSWER:
The planet does not even have to be oblate for such an effect to take
place. The reason is the rotation. If you stand on a pole, you are not
rotating and so your apparent weight, the force the ground exerts up on you
is equal to your true weight (the force the planet exerts on you). If,
however, you are at the equator you are rotating around a circle of radius
R with speed V and so you have an acceleration equal to V2/R
pointed toward the center of the circle. The force causing this acceleration
must be however much of your weight is needed. Thus, from Newton's second
law, MV2/R=W-WA where W is
your true weight and WA is your apparent weight. Hence,
WA=W-MV2/R, much less than your true
weight if there is a large rotational speed. Eventually, as you decreased
the length of a "day", you would become "weightless". Be certain to note
that this effect is one of dynamics, not of a gravity disparity.
Incidentally, the true weight at the poles actually decreases as the planet
becomes more oblate. This can be deduced from imagining a "maximally oblate"
planet, a disk; because of symmetry, you would experience zero gravitational
force at the center of a disk.
![]() QUESTION:
QUESTION:
My friend and I are having a debate about a certain topic trying to come up with different theories of how the mechanics of this process works, yet with each theory we develop we get pulled deeper into the problem with more possibilities and factors affecting the issue.
The question is, if an average car, with ideal conditions, (ideal tire pressure, gear ratios, weight, driving conditions, weather) is traveling at a rate of 60 mph, are the tires moving faster than than the car itself. I argued that the rpms of the tire are moving at a rate faster than the car, (obviously) but since the wheel is attached to the car and the car is moving at a rate of 60 mph, the wheel too (not counting rpms) is moving at a rate of 60 mph where rubber meets road regardless the size of the tire. I do not understand his theory, but he claims, that with rpm's aside the tire in and of itself is moving faster than the car. I told him if you took a snap shot of the car moving at 60 mph, everything about the car is moving at 60 mph. To be able to figure out the exact speed of the tire as a seperate entity, you would HAVE to factor in its rpm. Please help me win this battle!
![]() ANSWER:
ANSWER:
Sorry, but you absolutely lose this battle! If the brakes are locked,
every point on the wheel will be moving forward with a velocity equal to the
velocity of the car. If the wheel is rolling, the point where "where
rubber meets road" is momentarily at rest. The very top of the wheel
is moving forward with a speed of twice the speed of the car. Points
on the front half of the tire are moving both down and forward (with speeds
and directions easily calculated) and those on the back half are moving both
up and forward. You cannot talk about the speed the tires are moving since
every point on the tire moves with a different speed. The best way to
visualize it is that every point on the tire is rotating about the "where
rubber meets road" point at any instant; the axel moves forward with speed
equal to the speed of the car.
![]() QUESTION:
QUESTION:
Can you provide a formula for the Earth's acceleration due to garvity and the speed of the Earth's rotation?
Would like to know how g = 9.81 m./sec sq. would change if the Earth had 16-hour days instead of 24.
![]() ANSWER:
ANSWER:
First, I must disabuse you of the notion that the acceleration due to
gravity would change. What happens is that your apparent weight changes
because you are accelerating in a circle. Your true weight is unchanged
since weight is simply the force with which the earth's gravity attracts
you. (The answer to your question depends on the latitude where you do the
experiment; for simplicity, I will do it for the equator where the effect is
largest.) From Newton's second law you may write N-mg=-m(2πR/T)2/R
where N is apparent weight, mg is true weight, R is
the radius of the earth, T is the period of rotation. Solving this, I
find N=mg(1-(2/T2)) if T is measured in
hours. Therefore the effect on apparent weight is about 200/T2
%. This is about a 0.35% effect for T=24 hours, a 0.78% effect for
T=16 hours. If the length of a day were less than about 1.4 hours, you
would leave the surface.
![]() QUESTION:
QUESTION:
Would you be able to verify the reasoning in the four simple paragraphs presented below and find a fault in them?
1. It is a generally accepted fact that in a head-on collision between two balls of equal mass moving with the same but opposite speeds, the two balls will rebound with equal but slower speeds. (R. Feynman, Lectures on Physics, Vol. 1, p. 10.7.)
2. If the above is true, then the following also must be true: When one of the balls in the above example is at rest, this ball must rebound with a slower speed after a collision with the moving ball of equal mass, while the moving ball comes to a perfectly ‚Äúdead‚ÄĚ stop.
3. Because the ball initially moving must come to a stop after the collision, the slower speed of the ball initially at rest must be used in the calculation of the total final momentum, making it smaller than the total initial momentum. Hence, the total momentum cannot be conserved in this type of collision.
4. Proof: The above outcome is confirmed by the fact that the total final energy cannot be conserved in the above collision. However, the only way that energy will not be conserved is if the speed of the ball initially at rest is slower than the speed of the ball initially moving, as the ball initially moving comes to a perfectly ‚Äúdead‚ÄĚ stop after the collision. In other words, the same slower speed of the ball initially at rest must be used in the calculation of both the total final energy and the total final momentum. Because both energy and momentum are the function of the same factors (the same masses and the same speeds), neither energy nor momentum can be conserved in the motions of the two balls, contradicting the law of conservation of momentum. Thus, we have mathematical proof that momentum cannot be conserved in all collisions.
![]() ANSWER:
ANSWER:
Statement #1 is far from true in general. This is true only for an
inelastic collision, one in which energy is lost in the collision. Statement
#2, the incoming ball being at rest after the collision, is true only for a
perfectly elastic collision (in which case the ball originally at rest exits
with the same speed as that of the incoming ball). Hence, since #2 is
incorrect, your "proof" fails. Linear momentum is always conserved in an
isolated system, i.e. a system which experiences no outside forces.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Thank you for responding to my query. However, I am not happy with your answer.
I thought the conditions in my query were clear. However, on the second thought, it is better to stipulate them. Here they are:
Conditions:
1. The two collisions described in paragraphs 1 and 2 are real collisions that could be performed in a laboratory. In these real-world collisions, energy is not conserved. Therefore, in order to avoid confusion, elastic collisions should not be considered or even mentioned in this case.
2. A made a survey among a dozen of reputable physicists, professors of physics and a well-known physics textbook whiter about the real collision in paragraph 2. The general consensus was that a glider initially moving on a frictionless air track in a laboratory will come to a perfect ‚Äúdead‚ÄĚ stop after colliding with a glider at rest of equal mass, as confirmed, according to them, by numerous already performed experiments.
Therefore, the assumption in paragraph 2 is that the ball initially moving would come to the above-mentioned perfect ‚Äėdead‚ÄĚ stop. What would then happen to the ball initially at rest?
You stated in your answer, that the ball initially moving would come to a stop only in a perfectly elastic collision, which do no exist in nature. This means that in a real collision, you assume that the ball initially moving will not come to a perfect "dead" stop. In what direction and at what speed will it move after the collision and what would happen to the ball initially at rest?
Your assumption contradicts the result of my survey. Indeed, what exactly would happen in a real head-on collision where energy is not conserved. Suppose the two balls are 2 kg each, and one moves initially at 2 m/s, while the other ball is at rest. What will be the speeds of the two balls after the collision? Once again, let's forget elastic collisions.
![]() ANSWER:
ANSWER:
Your conditions were crystal clear to me. All I said about condition #1
was that this is only true for an inelastic collision. I agree that real
world, macroscopic collisions will always result in energy loss. Your dozen
reputable physicists are either not competent or else they are telling you
what they think you want to hear‚ÄĒthe
stock answer for elastic collisions. It is only for elastic
collisions between identical particles, one initially at rest, that the
other is at rest after the collision. So how could those physicists be
wrong? Quite simply because the apparatus they describe is designed to have
a very low (not zero, since we agree that is not possible) energy loss when
the gliders collide and to have minimum friction (not frictionless as you
state). Hence the collision between gliders is so close to elastic that the
velocity of the incoming glider is so small that it is not noticable or is
stopped by the (nonzero) friction. I will present two situations to you to
try to convince you that condition #2 is flat-out incorrect if energy is
lost.
- Consider a perfectly inelastic collision, e.g. two balls of putty. In the head on collision, all kinetic energy is lost and the balls end up at rest, stuck together. If only one is moving before the collision, is it at rest after the collision? I think you must agree that it cannot be.
- My second example is a little more complicated. I will take your choice of 2 kg balls moving at a speed of 2 m/s toward each other. Then the energy before the collision is 2x(–Öx2x22)=8 J. Suppose that —ē of the energy is lost in the collision. Then after the collision the energy is 2 J. Therefore, 2x(–Öx2xv2)=2 J so v=1 m/s; each ball leaves the collision with a speed of 1 m/s. To find out how this same collision looks if one ball is at rest, I will not assume momentum conservation because you would object since you think you have disproved it. I will watch the original collision but while running alongside one of the balls, ok? Before the collision I see one ball at rest and the other approaching with speed 4 m/s. After the collision I see the struck ball moving (in the same direction as the other ball came in) with a speed of 3 m/s and the incoming ball moving (in the same direction) with a speed of 1 m/s. (Note that the same amount of energy, 6J, is lost in both scenarios.)
- If you redo the second example for 10% energy loss (0.8 J) you will find the speeds after the collision are about 3.9 m/s (for the struck one) and 0.1 m/s for the incoming one. For a 1% loss (0.08 J) they are about 3.99 m/s and 0.01 m/s
![]() QUESTION:
QUESTION:
I understand that "centrifugal" force is ficticious. Centripetal force is, however, a real force - but doesn't Newton's third law state that for every action there is an equal and opposite reaction? And wouldn't that reaction, in this case, be a "centrifugal" force? And, if the answer is that Newton's laws do not apply in a non inertial frame of reference, how are we permitted to use Newton's second law, F = ma (= v^2/r in this case), to quantify centripetal force?
![]() ANSWER:
ANSWER:
Anybody being introduced to Newton's laws often gets things confused.
Let us state Newton's third law carefully. If body A exerts a force on body
B, then body B exerts and equal and opposite force on body A. Consider the
earth going around the sun. The centripetal force is the force which the sun
exerts on the earth. This is the only force on the earth. Where is the so
called "reaction force"? Just read the law carefully and you will see that
the earth exerts a force on the sun which is equal and opposite to the force
the sun exerts on the earth. The "reaction force" is never on the
same body as the "action force". We are permitted to use F=ma because
what this equation means is: the total force on a body is equal to
the mass of that body times the acceleration of that body. The
force the sun exerts on the earth is the only force on the earth.
Let's take a look at what it means for there to be a "ficticious force". Suppose that you are in a car which is accelerating. What are all the forces on you? There is your weight, the force which the seat exerts up on you (equal and opposite your weight but having nothing to do with Newton's third law because they are both on you), and the force which the seat back exerts forward on you. Nothing mysterious, the seat back accelerates you forward. But suppose you want to do physics using the car as your reference frame. Then you are not accelerating (relative to the car) but the sum of the forces on you is not equal to zero; Newton's first law is not true in this reference frame. But, you insist on doing Newtonian mechanics in this frame. To do this you say, "hey, there is a force pushing me back in my seat". It feels that way but there is no such force. This added force is called a ficticious force added to make Newton's laws to be true in this accelerating system. If you are in a system which is spinning, imagine some carnival ride, you feel like you are being smashed back against the outside but what is really happening is that the outside is pushing in on you to provide your acceleration and you interpret that as your being pushed back. This is just like the car example in that there is no force pushing you outward, it just feels that way. And if you want to do physics using the spinning frame as your reference and using Newton's laws, you have to add a centrifugal force even though there is no such thing.
![]() QUESTION:
QUESTION:
how much does a lacrosse ball (2 inch diameter) slow down
(horizontal velocity only) if thrown at 80 mph from the instant it is
released until it reaches a point 10 meters away. Taking into account air
resistance.
![]() ANSWER:
ANSWER:
I prefer to work in metric units so 80 mph is about v0=35
m/s and the diameter is about D=6 cm=0.06 m. I will also need the
mass of a lacrosse ball which I looked up to be about m=0.15 kg. Now,
for a ball of this size traveling through air with this velocity, the air resistance force is
proportional to the square of the velocity. Therefore Newton's second law is
of the form -Cv2=ma=m(dv/dt)
where C is a constant which can be calculated approximately as C=0.22D2
for a sphere in air. Therefore we must solve the differential equation
(dv/dt)+0.00079v2=0. (I completely ignore
gravity because the ball starts with zero velocity in the vertical direction
and flies for only a very short time.) If you know differential equations,
then this is not particularly difficult to solve. I will do that later. For
starters, however, it is instructive to make a reasonable approximation and
see what we get. I am going to say that I expect, over so short a distance
as 10 m and starting with such a large initial velocity, that the
acceleration will not change much. So I will say that the acceleration at
the beginning, a0=-0.00079x352=-0.97 m/s2, does not
change much over the flight. So we have a uniform acceleration problem and
we can say x=v0t+–Öa0t2=10
and solve for t; I find that t=0.29 s. Finally, we can get the
estimated final velocity, v=v0+a0t=35-0.97x0.29=34.7
m/s. So the ball loses about 0.9% of its initial velocity.
For anyone interested in the exact solution of the differential equation, here it is. The solution to the equation is v=v0/(1+kt) where k=Cv0/m. And, x=(v0/k)ln(1+kt). Solving these I find that t=0.29 s and v=33.2 m/s. So, only about 5% of the velocity is lost.
![]() QUESTION:
QUESTION:
Suppose you hold a small ball in contact with, and directly over, the center of a large ball. If you then drop the small ball a short time after dropping the large ball, the small ball rebounds with surprising speed. To show the extreme case, ignore air resistance and suppose the large ball makes an elastic collision with the floor and then rebounds to make an elastic collision with the still-descending small ball. Just before the collision between the two balls, the large ball is moving upward with velocity and the small ball has velocity . (Do you see why?) Assume the large ball has a much greater mass than the small ball.
![]() ANSWER:
ANSWER:
I will not give all the details but, to understand this problem, you
need to understand one-dimensional elastic collisions between two masses.
There is a derivation in a
Wikepedia article. If a mass with speed v collides elastically
with a very much larger mass with speed V in the opposite direction
as the smaller mass, the smaller mass rebounds with a speed approximately
equal to v+2V. In the case you note, since the larger ball
rebounded from the floor elastically, both balls have about the same speed
when they collide, i.e. v=V, so the smaller ball rebounds with speed
3v.
![]() QUESTION:
QUESTION:
Based on Physics, is a 90 MPH Fastball Slower or Faster than a 95 MPH. At work we are trying to determine if the 95 MPH fastball loses energy faster than a 90 MPH fastball. Your answer is greatly appreciated.
![]() ANSWER:
ANSWER:
You are asking two questions; if a 95 mph ball loses energy faster than
a 90 mph fastball (it does) you cannot conclude that it "is faster" (by
which you mean, I presume, when it passes over the plate). For the details
of the following, see the earlier lacrosse
ball answer. Following the (exact) solution in that earlier answer, I
find that the 95 mph ball reaches the plate in 0.47 s and arrives at the
plate with a speed of about 80.8 mph. The 90 mph ball reaches the plate in
0.50 s and arrives at the plate with a speed of about 76.3 mph. So, each
loses about 14 mph with the faster ball losing a bit more. This surprised me
but I found another reference saying that something like 10 mph is what is
lost, so my calculations are reasonable. So they do not lose energy
significantly differently (the faster pitch lost more speed in a shorter
time so its average rate of change of speed was indeed bigger). (I used 3 inches for the diameter, 0.145 kg for the
mass, and 60'6" for the distance to the plate.) There is certainly no way that one could characterize a 95 mph
fastball as slower than a 90 mph fastball.
![]()
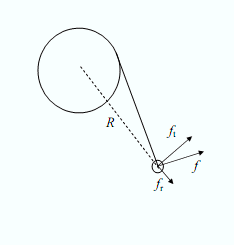
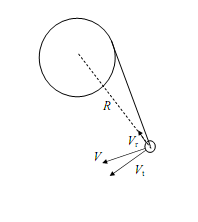
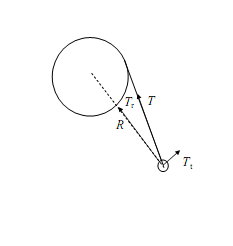 QUESTION:
QUESTION:
Consider centripetal force of a tetherball. This
would be provided by the tetherball's string. My physics teacher tells us
that since kinetic friction is orthogonal to centripetal force, it may be ignored in centripetal force's calculation. However, it is obvious that centripetal force depends on the ball's velocity: F=m(v squared)/r, and that velocity depends upon kinetic friction. So if the tetherball were to rub against the
ground, wouldn't it require are greater centripetal force?
![]() ANSWER:
ANSWER:
The tetherball is a particularly tricky example because of the thickness
of the pole. (First, ignore friction.) At any instant the ball is rotating
about the point where the rope is tangent to the pole and the ball is
moving perpendicular to the rope. But you would calculate centripetal
acceleration relative to the center of the pole. Therefore, the tension in
the rope is not the centripetal force, only its component Tr
along the radius R is (see first picture). Similarly, the centripetal
acceleration is not V2/R but Vt2/R
where Vt is the tangential component of the velocity (see
second picture). Finally, if there were friction present, it would
contribute to the centripetal force because the the frictional force will be
opposite the direction of the velocity and will therefore have a component
fr which is along R (see third picture). So, your
teacher is wrong because the velocity V is not perpendicular to the
centripetal force Tr-fr (compare all
three figures). On the other hand, you also are wrong because the reason is
not because the friction is changing the velocity of the ball (which, of
course, it is); note that all my arguments are made at an instant, not over
a time when the ball will slow down because of friction.
A couple of other things about the tetherball (without friction): Angular momentum is not conserved because there is an external torque (-TtR). Energy is conserved because there is no work being done by the tension (T and v are perpendicular).
![]() QUESTION:
QUESTION:
how much time will it take to travel down a 1000 ft , 30 degree ilcline with a 225 lb payload on a 200 lb soap box race car and if pay load was lighter would the time be shorter with lighter load?
Friction due to
the moving parts, like bearings, like the wheels rolling on the ground,
like wheels moving on axels, etc. Empirically, we find that this
kind of friction increases proportionally with how hard the moving parts
are pressed together and this, of course, is proportional to the total
weight of car plus rider. But, the force impelling the car down the hill
is also proportional to the total weight, so once again, the speed at
the bottom is independent of the load. There is something called the
coefficient of friction which tells you how much friction force there is
for a given force pressing the surfaces together. For example, if this
coefficient is 0.3 for a 100 lb box moving on a horizontal floor, you
would have to push with a 30 lb force to keep it moving with a constant
speed. If I take 0.3 to be your coefficient of friction, your speed at
the bottom would be about 26.8 m/s=60 mph. Since the acceleration is
about half what it was, the time is about twice as long, 22 s. For objects which
are going faster than a few mph, air drag becomes important. Air
friction depends on two things, the shape of the object and the speed it
is going. It does not depend on the mass of the object. Actually a
pretty good approximation to the magnitude of the force of air friction
is F≈—ėAv2 where A is the area presented
to the wind (this works only if F, v, and A are in SI
units). So, this force, which points up the incline just like the moving
parts friction, causes the car to slow down more. But, Newton's second
law says that a=F/m so that if F does not depend on
m, the acceleration (amount of slowing down due to this force)
gets smaller as m gets bigger. It gets a little complicated to
actually calculate the time and speed for this case, but the important
part is that this is the only place I can find where the weight of the
whole car makes a significant difference. So, the bottom line
is that if you go fast enough for air drag to be important (and I suspect
you do), the heavier of two otherwise identical cars should win.![]()
 ANSWER:
ANSWER:
I have dealt with this kind of question
before, but maybe it is time to
revisit the whole thing with one answer. First, consider the ideal situation
where there is no friction of any kind. Physicists do not like English
units, so I am going to convert everything to SI units: 1000 ft=305 m, 425
lb=193 kg. I assume that you do not want all the details of my calculations,
just the pertinent results. The time does not depend at all on what the mass
is (if friction plays no role). There is an acceleration down the incline
which is a=–Ög. I find
that the time to the bottom is about 11.2 s and the speed at the bottom is
about 54.9 m/s=123 mph. I assume you are not crazy enough to be in a soap
box car going that speed, so friction must play a role. There are two kinds
of friction you have to consider:
![]() QUESTION:
QUESTION:
Do you weigh more at the bottom or top of a large skyscraper?
Does the mass over your head count for more than the distance?
As an example, the tallest skyscraper currently is 828m tall and wieghs about 500,000 tons if it's empty, in Abu Dhabi.
Assuming that you weigh more at the bottom, how dense or large would the mass above your head have to be to make you weigh less?
![]() ANSWER:
ANSWER:
There are two effects you need to think about:
-
Because you are a different distance from the center of the earth when you are at the top, your weight is less. This turns out to be a 0.03% difference.
-
The gravitational force due to the mass of the skyscraper is really small. I just took all the mass to be at the center to check this. Then, if you are at bottom, the gravitational force from the skyscraper mass would about 0.000003% smaller than your weight at the top which would increase your (0.03% smaller) weight at the top and decrease your weight by that amount at the bottom. So, the effects of the skyscraper are negligible compared to other effects.
![]() QUESTION:
QUESTION:
My husband when riding his vintage motorcycle had an accident when negotiating a bend (200m radius) in the wet. it was found that the road surface only had friction coefficient of 0.3. What formula and other known parameters (like weight of bike, lean angle etc) can I use to determine what speed he could have safely negotiated the bend?
He was actually only doing about 40-43mph.
![]() ANSWER:
ANSWER:
I do not know where you got your coefficient of static friction
μs=0.3, but it can be only a rough estimate at best. I
find that rubber on wet concrete can have μs over the
range 0.45-0.75 and on wet asphalt over the range of 0.25-0.75. But, often
there is oil which was in the road which floats up when it rains and makes
it slipperier yet. I am assuming, since you didn't mention it, that the road
is not banked. In that case, the weight of the bike+rider and lean angle are
irrelevant. It is easy to calculate the minimum possible speed from Newton's
second law, μsmg=mv2/R, so v=√(μsgR).
Putting in your numbers I find v=24.3 m/s=54 mph. Evidently the
coefficient of friction was less than you assumed. "Discretion is the
better part of valor" (Shakespeare, Henry The Fourth, Part 1 Act 5,
scene 4); in other words, be very careful on wet roads!![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
The friction coefficient of 0.3 (equivalent to wet snow on tarmac) was obtained by pendulum testing in the wet to reflect the conditions at the time of the accident. You are correct in your assumption that the road was not banked. In fact the road comprises a slight adverse camber.
Given the low friction coefficient I am having great difficulty in understanding how the calculation can show that a motorcycle (at normal lean angle) can negotiate the bend at 54mph. I would not wish to attempt to negotiate that bend on the equivalent of wet snow at 54mph even in a car!
![]() ANSWER:
ANSWER:
This is a very standard calculation. I figure that at 54 mph it would take 13 s to traverse a 90 degree turn for this radius circle which does not seem unreasonable to be possible. Are you pretty sure of the 200 m number?
The key to this may well be the banking of the curve; if the road is banked wrong by 100,
I would calculate
v=15.1 m/s=34 mph, quite a significant difference.
![]() QUESTION:
QUESTION:
I am falling from a plane at terminal velocity. I have a ball in my hand. I throw it towards the ground. What happens? Does the ball accelerate away from me, or does it simply fall beside me? What about if it was a very heavy ball such as a cannon ball compared say to a baseball or a plastic 'WalMart' pool ball?
![]() ANSWER:
ANSWER:
Terminal velocity is determined by the geometry of the object, the
density of the fluid (air), and the mass of the object. The terminal
velocity in air for an object of mass m and cross sectional area A
can be roughly approximated by vt≈√(4mg/A)
(only in SI units). You and the ball have some terminal velocity together. When you depart
from the ball you both have different terminal velocities since the masses
and geometries have changed. Suppose it was a cannon ball. Then your net
mass gets smaller and your geometry does not change much, so you will have a
lower terminal velocity and slow down; the ball has a considerably smaller
cross sectional area than it did when it was "part of" you and therefore a
larger terminal velocity, so it will accelerate down until it reaches its
new terminal velocity. Suppose it was a styrofoam ball. Then neither your
net mass nor your geometry change much, so you will have about the same
terminal velocity and continue falling at about the same rate; the ball has
a considerably smaller mass than it did and therefore a smaller terminal
velocity, so it will experience an upward acceleration and slow down until
it reaches its new terminal velocity, you will overtake it and it will
appear to go up (but is actually just going down more slowly).
![]() QUESTION:
QUESTION:
My question has to do with traction and the movement of a wheel(a wheel alone). Traction is essential for its movement both linear and circular. But if we throw a wheel forward it rolls some meters and then it stops(and falls). Which force is responsible for the decrease in its velocity? Cause if traction is parallel to the ground facing backwards then linear movement 's negative accelleration is explained but not angular negative accelleration. If traction is parallel to the ground facing forward then angular negative accelleration is explained but not linear. If traction is zero then which force decreases both velocities linear and angular?
![]() ANSWER:
ANSWER:
One of the reasons I love doing Ask the Physicist is because
I often learn things I did not know or had never thought about. You would
think that a guy who has been teaching introductory physics courses for
nearly 50 years would find this question simple. But, indeed I was puzzled
by it because, as I have found by thinking about it and talking to some
friends, I wasn't thinking beyond the friction force (which questioner calls
traction) being simply the only force in the horizontal direction and
obviously stopping the forward motion after some distance. I never addressed
the angular acceleration of the wheel before. This answer will be
long-winded because that is what I do when I have learned something which
pleases me! What frictional forces are important to understand the rolling
of a wheel? Most introductory physics classes talk only about the contact
forces of static friction and kinetic friction. Kinetic friction is not
applicable to this problem because the wheel is
not slipping on the ground, and static friction might be important, but not
necessarily. If we have a round wheel rolling on a flat horizontal surface
(don't look at the figure yet!), there are three possible forces‚ÄĒthe weight which must
be vertical, pass through the center of mass, and (assuming it is a uniform
wheel) pass through the point of contact; the friction, which must be
parallel to the surface and pass through the point of contact; and the
normal force which must be perpendicular to the surface and pass through the
point of contact. If you now sum torques about the point of contact (as
noted by the questioner), there are none! So, there can be no angular
acceleration; if we have stipulated that the wheel does not slip, then there
can be no linear acceleration either and the wheel will roll forever and no
friction is required. But we all know better! A real wheel will eventually
slow down. The key is that there is no such thing as a perfectly round wheel
or a perfectly flat surface, one or both must be deformed. In that case, we
have to think about a new kind of friction called rolling friction, the
friction the wheel has because of the rolling. This is different from the
static friction, and static friction may still be present still to keep the
wheel from slipping.
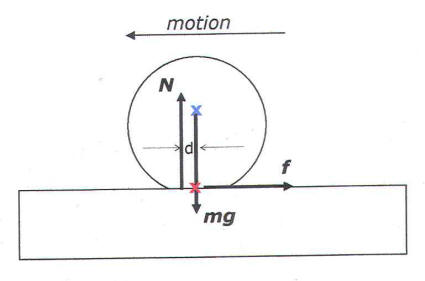 A perfectly round wheel cannot have rolling friction as
I showed above, it must deform which means that there is no longer a "point
(or line) of contact" but now an area of contact. Since the normal force is
only constrained to act somewhere where the two are in contact, it is now
possible (in fact inevitable) that this force will not act through the
center of mass of the wheel. That is the whole key to answering this
question. So, finally, the answer: refer to the figure where I have drawn
the forces mg, N, and f. The
weight is still constrained to be vertically down and pass through the
center of mass (blue cross). The normal force is constrained to be vertical
and act somewhere where the wheel and ground are in contact, drawn a
distance d to the left. The frictional force (which now includes both static
and rolling friction) is constrained to act at the surface and parallel to
it. I choose a coordinate system with x to the left and y up;
the axis (red cross) about which I will sum torques is at the ground
directly under the center of mass and positive torque results in an angular
acceleration which is positive when acceleration of the center of mass is
positive (counterclockwise around the axis). All is now straightforward: ΣFx=-f=ma,
ΣFy=N-mg=0, Στx=-Nd=Iα=Ia/L
where I is the moment of inertia about x
and L is the distance from x to
x. Finally, N=mg, a=-f/m,
and d=fI/(Lm2g).
A perfectly round wheel cannot have rolling friction as
I showed above, it must deform which means that there is no longer a "point
(or line) of contact" but now an area of contact. Since the normal force is
only constrained to act somewhere where the two are in contact, it is now
possible (in fact inevitable) that this force will not act through the
center of mass of the wheel. That is the whole key to answering this
question. So, finally, the answer: refer to the figure where I have drawn
the forces mg, N, and f. The
weight is still constrained to be vertically down and pass through the
center of mass (blue cross). The normal force is constrained to be vertical
and act somewhere where the wheel and ground are in contact, drawn a
distance d to the left. The frictional force (which now includes both static
and rolling friction) is constrained to act at the surface and parallel to
it. I choose a coordinate system with x to the left and y up;
the axis (red cross) about which I will sum torques is at the ground
directly under the center of mass and positive torque results in an angular
acceleration which is positive when acceleration of the center of mass is
positive (counterclockwise around the axis). All is now straightforward: ΣFx=-f=ma,
ΣFy=N-mg=0, Στx=-Nd=Iα=Ia/L
where I is the moment of inertia about x
and L is the distance from x to
x. Finally, N=mg, a=-f/m,
and d=fI/(Lm2g).
Finally, a couple of real-world provisos. Of course, N is really distributed over the whole area, but the dynamics can be done by assuming it effectively acts all at one point just like we assume the weight acts all at the center of mass. And, the rolling friction might not really act at the surface of contact since it arises from the deformation of the wheel and it might not be purely horizontal since it is not directly a force due to the contact with the floor. So, there are still some idealizations in my analysis, but there are always idealizations when dealing with friction. And, the problem could have been equally well done assuming the ground, not the wheel was being deformed. One could also have done the analysis by summing torques about the center of mass and using the parallel axis theorem Icm=I-mL2.
I would like to acknowledge a very useful discussion over pizza with friends and colleagues Edwards, Love, Meltzer, and Anderson.
![]() QUESTION:
QUESTION:
If I could detonate a firework inside a contained vacuum void of any other mass objects (simulating the big bag) and watched (over time) would I see the particles eventually attract to each other? Would the results of this sort of experiment prove gravity exists in every particle ever created?
![]() ANSWER:
ANSWER:
No. The gravitational attraction is very, very small between
the little pieces of your firecracker. So the speeds the pieces had when it blew
up would have exceeded the escape velocities from their neighbors and they
would continue moving apart forever. Escape velocity is the speed
something must have to escape from the gravity of something
else; e.g. the escape velocity from the surface of the earth is about 7 miles per
second, but this is for a much stronger gravitational force. Just to give
you another example where the mass involved is still much larger than your
masses but much smaller than the mass of the earth, the escape velocity from
the surface of a baseball is about 8 cm/hr.
![]() QUESTION:
QUESTION:
I am doing an experiment with dropping coffee filters. By changing the
mass (adding more filters) and keeping the distance the same (4 meters)
and recording the time it takes for the stack to hit the ground. By
doing this I find the velocity. Wouldn't there be an asymptote at 9.8,
for the velocity of the dropped object?
![]() ANSWER:
ANSWER:
Technically, you are not measuring the velocity, you are measuring
the average velocity. But, since coffee filters have such small mass, you
can probably assume that terminal velocity is reached almost immediately
after dropping. What you are studying is the fall of objects for which air
resistance is important. I do not know what you mean by the asymptote at
9.8, but it is certainly wrong because 9.8=g is the acceleration due
to gravity, it is not even a velocity. What you want is to find out how
velocity depends on mass. This will depend how the terminal velocity depends
on mass. Now, the force of air drag will depend on two things, the
geometrical size of the falling object (but all will be the same, so you
cannot study that) and the speed the thing is moving. Usually this force can
be parameterized by F=Cv2 where C is some
constant determined by the fluid (air) and the geometry, but not the mass.
So, the faster it falls the bigger this force is and when it gets as big as
the weight of the object it stops accelerating and falls with a constant
speed called the terminal velocity which you hope to be determining. So,
drag=weight when mg=Cv2 where m is the mass
and g=9.8 m/s2. Solving, v=√(mg/C);
so, if you make a graph of v vs. √m you should
get a straight line if indeed the force is a quadratic function of the
speed. And, from the slope, you could determine the constant C. If
you do not get a straight line from your data, try using
F=Cv; then if you plot v vs. m you will find a
straight line.
![]() QUESTION:
QUESTION:
We're having this physics discussion at work (in the medical field). One of my co-workers insists that if you took a pound of anything and spread it out evenly on a scale, it would weigh less than if you piled it up in the middle of the scale. He said that the density of the mass of whatever you piled on the scale, would increase the gravitational pull moreso than if the object being weighed was spread out evenly, like say mashed potatoes, for example. What do you say?
![]() ANSWER:
ANSWER:
The stock answer to this question is that weight is the force that
the earth exerts on a mass and that force is independent of how the mass is
distributed. But, that is not quite right and your question is clearly a
"hair-splitting" sort of question, so I will explain. The gravitational
force between two objects depends on how far apart they are‚ÄĒthe
farther apart, the smaller the force. The weight of something is determined
how far it "is" from the center of the earth. If you compare the mashed
potatoes spread out with the mashed potatoes heaped up, those heaped up are,
on average, farther away from the center of the earth by a few centimeters,
and therefore weigh less, not more. But, don't get too excited about
this‚ÄĒthe difference would be about one millionth of 1%, less than you could
ever hope to measure. You would get a much bigger difference if you weighed
the same thing upstairs and downstairs in your home, again something you
know from experience is, for all intents and purposes, the same. [Rereading
the question, let me address the density argument of your colleague. It is
true (again to a really small degree) that the weight of the potatoes on the
top of the heap will press down on those on the bottom and make the potatoes
slightly more dense. However, a scale does not measure density, it measures
mass and therefore two objects with different densities but equal masses
would weigh the same.]
![]() QUESTION:
QUESTION:
Why is it difficult to calculate the terminal velocity for a cat falling from a high roof top?
![]() ANSWER:
ANSWER:
I do not know what you mean "difficult to calculate". We can
estimate it pretty easily, but certainly not do it precisely. First of all,
any calculation having to do with air friction is going to have
approximations and assumptions. For something like a cat, roughly 2 kg (4.4
lb), falling, it is a very good approximation to say that the drag force is
proportional to the square of the velocity. It turns out that a fairly good
approximation for the force is F=—ėAv2
where A is the area the falling object presents to the onrushing wind
and v is the velocity (this is only for SI units). Since it depends
on A, it depends on how the cat orients itself: if in a ball he will
fall much faster than if all spread out. Suppose we take the area of a
falling cat to be about 20 cm x 40 cm=0.08 m2. Then the force
will be about 0.02v2. Now, the cat's weight is about mg=2x9.8≈20
N. When the force of air friction is equal to the weight force down, the cat
will fall with a constant velocity called the terminal velocity: 0.02vt2=20,
so vt=√(20/0.02)≈30 m/s=67 mph. If you google "terminal
velocity of a cat" you will find the number 60 mph, so my approximations
were evidently reasonable. There, now, that wasn't so difficult, was it?
![]() RELATED QUESTION:
RELATED QUESTION:
I was asked what the terminal velocity of an unladen sparrow is. I read that the average weight of a field sparrow is .5 ounces. Approximately 5 inches in size with a wingspan of 7.9inches. Lets say falling from 50ft?
![]() ANSWER:
ANSWER:
Look at the answer above. If the sparrow falls straight down with
wings stretched out, I would estimate his area to be
–Öx5x7.9=20 in2=0.013 m2. Following the same as for
the cat, but using m=0.5 oz=0.014 kg, I find vt≈6.6
m/s=15 mph=22 ft/s.
![]() QUESTION:
QUESTION:
I want to ask about weight shift in vehicle. Weight shift is a very common terminology among car enthusiast (but most of them not physicist or engineer, some might not even study science well). Magazine always comment an accessory will help in weight shift of the car, etc.
The common qualitative statements made by them in the use of weight shift are: (i) When a car turn, the weight shifts to outside wheels more; (ii) When a car accelerates, the weight shifts to the rear; (iii) when a car brakes, the weight shifts to the front.
The above is just some statements to clarify what I meant by the term "weight shift".
Here is my question: Is "weight shift" a misnomer, or an ill concept of physics (vehicle dynamics to be specify)? The weight of an object is determined by the gravitational pull, regardless of what motion the object is doing, so how can the weight of different sections of the car change during maneuver? I think if one was to say force acting on different sections of the car during maneuver is different, then it is correct; but to say the weight shifted during maneuver, I can't get it.
![]() ANSWER:
ANSWER:
Technically, weight shift is a misnomer, but it is not too bad
because it is a shift in apparent weight. Normally, we think of
weight as acting at the center of gravity of something, but if that something
is accelerating, it may appear to move elsewhere. I will try to explain. In
all three of your examples, the qualitative observations are essentially the
same. For the accelerating car, the "apparent weight" shifts toward the rear wheels, opposite the direction of the acceleration. For the braking
car, it is just the same as the accelerating car except that the direction
of the acceleration vector is toward the back, the "apparent weight" shifts
toward the front wheels, again opposite the direction of the
acceleration. For the car turning there is an acceleration also, this
time toward the center of the circle (called the centripetal acceleration)
and here the "apparent weight" shifts toward the outside wheels, again
opposite the direction of the acceleration. So, if I understand one of
these I will understand them all. In every case, the force which causes the
acceleration is the static friction between the tires and the road.
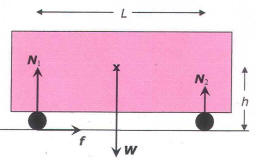 The
figure to the right shows a generic case. The center of gravity is at the
point marked x. The forces labeled are the weight W,
the force of the road up on the left tire N1, the
force of the road up on the right tire N2, and the
static friction force of the road on the tire f. If the car is
at rest or moving with constant speed, f=0, W=N1+N2,
and N1=N2; this assumes the center of
gravity is halfway between the wheels, but if the center of gravity were
moved to the left, we would have found that N1>N2.
The three scenarios you mention can all be represented by this figure. If
the car is accelerating, it is moving to the right and speeding up and the
left wheel is the rear wheel; here f=ma where m is the mass of
the car and a is its acceleration. If the car is braking, it is
moving to the left and slowing down and the left wheel is the front wheel;
again, it is the friction which causes the car to accelerate (slow down). If
the car is rounding a curve, the center of the curve is to the right, and
the left wheel is the outside wheel. We still have W=N1+N2,
but now the two forces N1 and N2 are not
equal. Since the car is not rotating about its center of gravity, if we sum
the torques about x it must sum to zero:(N1L/2)-(N2L/2)-fh=0,
so N1=N2+2fh/L. So,
N1>N2, it appears as if the
weight (center of gravity) has shifted toward the left. So, weight shift is
a pretty good name for it, I would say; apparent weight shift would have
sounded a bit pedantic for car buffs, don't you think? (By the way, I drew
the friction only on the left wheel but if there were friction on the right
wheel instead or in addition, the conclusions would all be the same because
the torques from the right wheel friction would have been the same sign as
the left.)
The
figure to the right shows a generic case. The center of gravity is at the
point marked x. The forces labeled are the weight W,
the force of the road up on the left tire N1, the
force of the road up on the right tire N2, and the
static friction force of the road on the tire f. If the car is
at rest or moving with constant speed, f=0, W=N1+N2,
and N1=N2; this assumes the center of
gravity is halfway between the wheels, but if the center of gravity were
moved to the left, we would have found that N1>N2.
The three scenarios you mention can all be represented by this figure. If
the car is accelerating, it is moving to the right and speeding up and the
left wheel is the rear wheel; here f=ma where m is the mass of
the car and a is its acceleration. If the car is braking, it is
moving to the left and slowing down and the left wheel is the front wheel;
again, it is the friction which causes the car to accelerate (slow down). If
the car is rounding a curve, the center of the curve is to the right, and
the left wheel is the outside wheel. We still have W=N1+N2,
but now the two forces N1 and N2 are not
equal. Since the car is not rotating about its center of gravity, if we sum
the torques about x it must sum to zero:(N1L/2)-(N2L/2)-fh=0,
so N1=N2+2fh/L. So,
N1>N2, it appears as if the
weight (center of gravity) has shifted toward the left. So, weight shift is
a pretty good name for it, I would say; apparent weight shift would have
sounded a bit pedantic for car buffs, don't you think? (By the way, I drew
the friction only on the left wheel but if there were friction on the right
wheel instead or in addition, the conclusions would all be the same because
the torques from the right wheel friction would have been the same sign as
the left.)
![]() QUESTION:
QUESTION:
Theoretically, if you were traveling through space in an object
e.g., a spaceship and going at an incredible speed in one direction what
would happen to you, inside, if it made an immediate 90 degree change in
direction? wouldyou smash against the inside of the craft?
![]() ANSWER:
ANSWER:
First of all, you cannot make
"an immediate 90 degree change in
direction". It would require an infinite force to stop your forward motion
simultaneous with an infinite force to start your sideways motion. So, you
have to say you make the turn through a curved path. As an example, I will
choose "an incredible speed" to be 104 m/s≈22,000
mph, just a little faster than the shuttle goes. Now, at that speed let's
make a 900 turn
around a curve of radius 1 km=103 m. Then the spaceship and
all its contents experience a centripetal acceleration of ac=v2/R=(104)2/103=105
m/s2. This is ten thousand times the acceleration due to gravity
which means that it would take a force of 10,000 times your weight to move
you in this circle. I would hate to see you after this maneuver, certainly
you would not be recognizable.

![]() QUESTION:
QUESTION:
My musical instrument has been broken during an air travel, but its container, a hard case with thick foam padding inside and outside is absolutely intact! how is this possible ?
![]() ANSWER:
ANSWER:
Suppose that it is dropped from a height of 3 m, about 10 ft. It
would hit the floor with a speed of about 8 m/s. Suppose the thickness of
the foam is 5 cm, about 2 in. Then the instrument would stop in a time of
about 0.013 s and would experience an acceleration of about 640 m/s2
which is about 64g where g is the acceleration due
to gravity. What this means is that, to stop your sitar in this short
distance would require an force of about 64 times bigger than its own
weight. Even dropping from 1 m would result in an acceleration of about 20g.
If the padding were well designed so that this force was distributed over
the whole surface of the instrument, it might survive, but probably one part
will take more than its share of the impact. So, the padding in your case
should be thought of as protecting the instrument from normal bumping and
jarring, not major drops.
![]() QUESTION:
QUESTION:
In strongman contests, the contestants pick up a
telephone pole at one end, push it upright and flip it over. The other end
of the telephone pole stays planted on the ground. Typically the telephone
poles weigh 300 lbs and are 30 feet long.
-
How would you calculate the actual weight of the pole being flipped at different points during the lift? For example, in the course of one flip we could say the pole travels in a 180 degree arc. The person is physically lifting for the first 90 degrees or less when gravity takes over. When the person picks it up off the ground it might be at 5 degrees, once it is over their head it could be at 30 degrees, once they take 2 steps forward it may be at 45 degrees, etc. - how do you calculate the actual weight of the pole along that arc at different points?
-
As the person walks forward to flip the pole over their arms remain over their head (i.e. in this example once they're at or past the 45 degree mark in the arc), but it seems the weight would lessen along a curve as the pole gets higher and gravity begins to assist? That is - the person (fulcrum?) might be moving in - say - 3 ft. increments as they walk forward to gain leverage to flip the pole over. How is the weight being lifted adjusted to account for that variable?
![]() ANSWER:
ANSWER:
First, some terminiology: the weight of the pole is 300 lb, that is
its actual weight. What you want, I believe, is the force you need to
exert to hold it at any given angle. This is a problem involving torques‚ÄĒyou
say that, in order to hold it at some angle, the torque you exert is equal
to the torque the weight exerts, a bit more to move it. (Torques are
calculated here about the point where the pole touches the ground.) The
torque due to the weight is easy, simply 300x15xcosθ=4500cosθ
ft-lb where θ is the angle the pole makes with the ground. The torque
you exert depends on where you push and the direction you push, an infinity
of possibilities. I have calculated for the two extreme possibilities: you
push vertically up or you push horizontally. For the vertical pushes I
assume that your hands are 7' above the ground; for the horizontal pushes I
assume that your hands are 5' above the ground. The graph above shows
vertical and horizontal forces you must exert vs. angle. Clearly, you
want to start your lift by exerting a vertical, not horizontal, force. When
you first lift it, you need to exert an upward force of 150 lb and when you
get to 13.50 your hands are at 7' and you can start moving
forward. When you get to a little more than 500, it starts to
become more advantageous to push horizontally, becoming much more
advantageous as you near the end. If you go real slowly, you will have to
exert a maximum force of about 500 lb, but when the force you need to exert
is small at the beginning you should push harder, thereby giving it some
added speed which will help it over the middle angles where the force is
maybe bigger than you can exert. Also, you will, through practice, learn to
shift smoothly from vertical to horizontal .
![]() QUESTION:
QUESTION:
A few days ago my friend & I were debating about how we could find the force with which a bullet of mass m and UNIFORM velocity v would hit a wall x m away. I said that the total energy would at the moment of impact would be equal to the kinetic energy of the bullet. So the total work done would be equal to the kinetic energy right at the moment of impact. So we could easily determine the kinetic energy by dividing the product of the mass and velocity by two. Then the result would be equal to the work done by the bullet. We could find the force by the formula W=fx. Please tell me if I am right.
![]() ANSWER:
ANSWER:
You are not right. You are right that the kinetic energy of the
bullet is lost. However, x which you define as the distance from the
wall to the gun, has nothing to do with it. Work is the force times the
distance over which it acts and the force is not acting all the way
across the room. What you might say is that if the bullet penetrates a distance
x into the wall then the average force may be written as F=(–Ömv2)/x.
But, that assumes that all the work done by the force results in
stopping the bullet, but some, much maybe, of that kinetic energy is
converted into heat and sound energy. (Incidentally, uniform velocity has
nothing to do with it, all that matters is how fast it is going when it hits
the wall.)
![]() QUESTION:
QUESTION:
I have struggled to get the simple explanation (non-mathematical form) for my troubling question from books. Still no luck.
Whts is force ? (as a concept)
What is the relationship between energy and force? I am not a physicist so could you please enlighten me and explain the concept in layman's term for me? Or with some analogy?
![]() ANSWER:
ANSWER:
A force is a push or a pull. It is one of those things you need to
have an intuitive feel for to begin doing physics. It is that which
causes an object to accelerate. In physics accelerate can mean two different
things, either change speed (speed up or slow down) or change direction.
Energy is a more subtle concept. To understand what energy is you need to
understand the concept of work. In physics, work is done by a force only if
the force is exerted over some distance. For example, if you push with a
force of 1000 pounds against an unmoveable wall, you do no work, but if you
push a box across the floor with a force of 10 pounds, you do work. When you
do work on an object you increase its energy. So, when you push the box
across the floor, it acquires what we call kinetic energy, energy by virtue
of motion, because it started at rest and ended up moving. If you use a
force to lift an object so that it starts out and ends up at rest, you have
still done work but now the energy you have given it is called potential
energy, energy by virtue of position. Different kinds of energy can
transform to others. For example, if you drop something its potential energy
is converted into kinetic energy as it falls.
![]() QUESTION:
QUESTION:
Is a golf ball going fastest after it leaves
the club head striking it, or is there still some accelertion as it
overcomes inertia?
![]() ANSWER:
ANSWER:
Nothing "overcomes inertia" on its own. Only a force causes an
acceleration and acceleration is what is meant by overcoming inertia. The
ball has its largest speed as it leaves the club because that force ends
then. When the ball is in flight, only two forces act on it‚ÄĒair
drag which always slows it down and gravity which slows it down on the way
up and speeds it up on the way down. But gravity can never speed the ball up
more on the way down than it slows it down on the way up.![]() FOLLOWUP
QUESTION:
FOLLOWUP
QUESTION:
Sorry I didn't do a better job asking the
question. My family and I are not looking to be told when peak
acceleration happens, we want to prove it mathematically. We have put
together a derivation to show that at its peak velocity a golf ball is
still in contact with the club head. Starting out with the length of the
drive we use the formula for projectile motion to find the peak velocity
of the ball. We work backward from there to derive all of our unknowns
but we run into trouble when we use the formula for uniform motion with
constant acceleration to calculate how far the ball and the club travel
during the time to accelerate. Because the distance the club travels is
expressed as S = u * t and the distance the ball travels is express as s
= u * t + a * t^2 / 2, there is always a few millimeters distance
between the ball and club when the ball reaches peak velocity.
![]() ANSWER:
ANSWER:
There is a difference between peak velocity and peak acceleration.
For example, a pendulum has its maximum velocity at the bottom when the
acceleration is zero. What you are doing is wrong because the acceleration
is not uniform as you assume. Let us, in accordance with my original answer,
focus only on the time during which the club is in contact with the ball;
the time after it leaves the club will always have a smaller velocity than
when it left the club. The graph to the right shows what the force which the
club exerts on the ball is likely to look like. The club first touches the
ball at t1
and the ball leaves the club at t2. The force over the
time of acceleration is not constant because the ball behaves like a spring.
When the force is biggest, the acceleration is biggest because of Newton's
second law, F=ma. However, the ball is speeding up over the whole
time interval and will therefore be going fastest at t2.
The area under the force curve is called the impulse and is equal to the
change in momentum of the ball which, because the ball starts at rest, is
mv where m is the mass and v is the speed at t2
of the ball. If you call Favg the average force on the
ball, then mv=Favg(t2-t1).
Putting in some numbers I found on the web, m=45 g, Favg=3000
lb, v=250 ft/s, I estimated that the time of contact is less than
half a millisecond.
![]() QUESTION:
QUESTION:
Ok, so I got into a big discussion today with my physics Honors teacher and he didn't even say who was right or wrong. The problem was that there is what you could consider a clothesline with a cable (for purpose of the problem the weight of the cable does not matter) and a weight is suspended exactly in the middle of the cable. The weight of the object was 25 N. The angle at which the cable meets the object/block is 30 degrees. What is the tension in the cable?
My theory behind this was that when you find the force tension it is for only half of the whole cable so you need to double the force tension and my teacher argued that y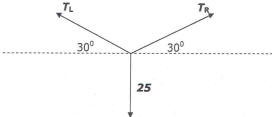 ou do not. So with this problem he said that the answer was 25 N of force tension and I said that it is 50 N of force tension. Who is right??
ou do not. So with this problem he said that the answer was 25 N of force tension and I said that it is 50 N of force tension. Who is right??
![]() ANSWER:
ANSWER:
I am sure that you will not be too surprised to find that your
teacher is right. Maybe this would be easiest for you if you do not think of
the tension in the cable but rather the tensions in the left and right
parts of the cable. If the angles of the two parts of the cable were
different, the tensions would be different. So, right away, the notion of
doubling the tension to account for the two halves is seen to be faulty
reasoning. If you call the two tensions TL and TR,
you can see that the horizontal components of the two tensions must be the
same: TLcos300-TRcos300=0,
so TL=TR=T. Similarly, the
vertical components of the two tensions must hold up the weight: TLsin300+TRsin300-25=0=T/2+T/2-25=T-25,
so T=25 N. This means that the tension in each side of the cable is
25 N and you could say, in this case, the tension in the cable is 25 N
everywhere.
![]() QUESTION:
QUESTION:
a body is moving with a velocity 'v' with
respect to (w.r.t.) a frame of reference s1.It bumps into a very heavy
object and comes to rest instantaneously,its kinetic energy(1/2*m*v^2)
as seen from the frame s1 is completely converted to thermal energy.Now
a man moving with a uniform velocity 'V' (in the direction of the body)
w.r.t. s1 observes the body , he notes that its initial kinetic energy
of the body is 1/2*m*(v+V)^2 and that after it rams into the heavy body
as 1/2*m*V^2 and concludes that the thermal energy produced is
m*v*V+1/2*m*V^2.Which of the two answers is correct?
![]() ANSWER:
ANSWER:
So, to answer your question we just need to find out how much the
kinetic energy changed as seen by both observers, right? Where you have gone
wrong is that you have not taken the energy of the wall into account and you
assume the wall has infinite mass. Of course, no wall has infinite mass but
if yours did, it would have, for the moving observer, infinite kinetic
energy both before and after the collision but those two infinities would
not be the same! What you need to do is assume the wall has a mass M
and the body has a mass m. So, your first observer sees a speed after
the collision (conserving momentum) of u=mv/(M+m) and a change
in kinetic energy of
ΔE=–Ö(M+m)u2-–Ömv2=–ÖmMv2/(M+m)
which is the energy converted into thermal energy. In your second scenario,
u=V+mv/(M+m) and
ΔE=–Ö(M+m)u2-(–Ömv2+–ÖMV2)=–ÖmMv2/(M+m),
exactly the same. You can also note that as M-‚Äļ∞,
ΔE-‚Äļ–Ömv2.
![]() QUESTION:
QUESTION:
gallile said that the force of gravity is the same on everything but the force of rubbing with the air molecule that change the speed of falling,so shouldnt 2 balls made from the same materiel but one is bigger than the other falling from the same heigth,the smaller touch the ground first cz her volum is smaller than the force of rubbing should be smaller than the big ball,but that is not the fact i dnt understand?
![]() ANSWER:
ANSWER:
First of all, Galileo never said the force of gravity is the same on
everything because the notions of force and gravity were not even conceived
before he was dead! Anyhow, that is not even true; the force of gravity is
greater for greater masses. What is the same is the acceleration due to
gravity, which Galileo supposedly demonstrated by showing that two objects
of different masses hit the ground simultaneously. This is only
approximately true because there is a force due to the air resistance as the
balls fall. Galileo did not take air resistance into account and balls of
different masses and sizes will not hit simultaneously. If you look at my
FAQ page you will find lots of discussion of problems involving air drag and
you will find that the force is proportional to velocity times the area
presented to the oncoming wind (approximately). If the two balls are made of
the same material, their masses are in the ratio (R1/R2)3
and their cross sectional areas are in the ratio (v1R1/v2R2)2.
As each ball falls, it initially is accelerating down but this acceleration
gets smaller as the speed increases because of the increasing air drag. Each
ball eventually falls fast enough that the air drag is equal to the weight
and falls with a constant speed called the terminal velocity. So, the weight
(mg) and the drag (—ėπR2v2)
are equal. Taking the ratio of the equations for the two balls, (R1/R2)3=(v1R1/v2R2)2
so v1=v2√(R1/R2).
Suppose that #1 is the smaller ball and R2=4R1;
then v1=–Öv2.
Since the smaller ball has the smaller terminal velocity, the larger (more
massive) ball will reach the ground first. So, in fact, your intuition was
wrong.
![]() QUESTION:
QUESTION:
how long does it take a 1 kg mass with an area of 1 square meter to get to terminal velocity when dropped. actually any size will work but i need the mass and area.
![]() ANSWER:
ANSWER:
Technically, it never reaches the terminal velocity but approaches
it. Also, you can only approximately do the calculation using an approximate
expression for the air drag force which I often use, F≈—ėAv2
where A is the area presented to the onrushing air and v
is the speed (and this is only true in SI units). I cannot tell from your
question whether you want a general solution for any mass (m) and
area or just for this specific problem. So, when I solve the problem for the
velocity as a function of time I get the solution v=√(g/c)tanh(t√(gc))
where g is the acceleration due to gravity (9.8 m/s2),
c=—ėA/m, and tanh is the hyperbolic tangent function. For
your specific problem, v=6.26tanh(1.57t), so the terminal
velocity is 6.26 m/s because tanh(∞)=1. The graph of this is shown to the
right; as you can see, the terminal velocity is reached, for all intents and
purposes, by about 1.5-2 seconds. Sorry if this is more technical than you
wanted; oh, and the tanh is defined as tanh(x)=[(ex-e-x)/(ex+e-x)].
![]() QUESTION:
QUESTION:
if a planet were suddenly stopped in its circular orbit ,show that it would fail into the sun in time (T into sq.rt. of 2 divided by 8) where T is time period of revolution.
In that idealized situation, you are right, you
land where you went up; gravity acts only in the direction straight down
and therefore there is no horizontal acceleration and you land where you
jumped. Now, suppose the earth is round but not
rotating on its axis. When the man jumps, he has a velocity with two
components, one away from the center of the earth and one equal to the
train's velocity. The component parallel to the train will not change
during the flight because there is no force in that direction. But, as
he gets farther away, he covers less angular distance than the train so
that when he finally gets back down the train has traveled farther and
he lands behind it. Finally, the real situation where the earth is
rotating. Now where the man lands depends also on the direction in which
the train is moving. If the train is in the northern hemisphere and is moving north, the man will not only
land behind but also east of the train; in the southern hemisphere he
will land west of the train. This is called the Coriolis force and
results from the fact that the coordinate system is rotating. Overall, you win the debate with your brother
because, although only under ideal conditions does the man land where he
launched, gravity has nothing to do with it. Your bullet on the train
idea is an entirely different thing since the bullet which just drops
was not fired vertically.
![]() ANSWER:
ANSWER:
Kepler's third law states that the square of the period of an orbit
T is proportional to the cube of the length of the semimajor axis
A, T2/A3=constant. For a circle, the
semimajor axis is the radius. For a straight line, the semimajor axis is
half the length. So, T2/A3=T'2/(A/2)3
or T'=T/√8.
![]() QUESTION:
QUESTION:
two massive particles m1 and m2 are released from a large distance.what are the speeds of particles when distance between them is 'r'?
![]() ANSWER:
ANSWER:
The total energy of the system is zero and the total linear momentum
is zero. When they are a distance r apart, energy conservation and
momentum conservation give the equations
–Öm1v12+–Öm2v22
-(Gm1m2/r)=0 and m1v1-m2v2=0.
If you solve these you will find that v1=m2√[G/(r(m1+m2))]
and v2=m1√[G/(r(m1+m2))]
![]() QUESTION:
QUESTION:
ok!
Suppose we have to masses m attached to a line of length 2r rotating around their cm. Lets further suppose that there is a mechanism of some kind that when activated lets the line extend in length for example 2 times longer.
The masses of the line and the mechanism are supposed to be very small compared to the masses m and the masses m are point masses so their individual rotations can be ignored.
Initially the masses have speed v, so:
total angular momemtum J = 2mvr
total kinetic energy K = mv^2
after the line is allowed to become 2 times longer then, because of the conservation of angular angular momentum, the velocities of the rotating masses will be v/2 (J=2mvr= 2m*v/2*2r).
But now the kinetic energy is 1/4*mv^2
So where did the energy go?
![]() ANSWER:
ANSWER:
Suppose we model your mechanism as a thread which connects the two
masses which are beads which can slide frictionlessly on a long rotating
rod. The two are each a distance r from the rotation axis, as you
suggest, and have a speed v. Now, cut the thread. Each bead starts
moving out the rod and both angular momentum and energy are conserved
because there are no external torques or forces doing work. When each gets
to a distance 2r from the rotation axis, it has a tangential
component of its velocity, as you suggest, of vt=v/2
as required by angular momentum conservation. But, each also has a radial
velocity; you can easily find the radial velocity
vr from energy conservation: E1=mv2=E2=2x–Öm(vt2+vr2)=m(—ėv2+vr2)
so vr=(v/2)√3.
Finally, to be sure we reproduce the problem you are interested in, we must
stop those beads from sliding out, maybe just put a couple of little hooks
to "catch" them when they get to 2r. The little hooks had to do work
to stop the beads and that is where the energy went.
![]() QUESTION:
QUESTION:
Why is it that if you blow a spider suspended by her web she floats out but then when this pendulum swings back it stops when the web is vertical and doesn't swing back and forth? Is it due to the air friction as it comes back to equilibrium or perhaps the dynamic structure of the web strand that absorbs energy that would have made the web swing back and forth?
![]() ANSWER:
ANSWER:
It is caused by air drag. This is called a damped oscillator. If
there were no air, the spider would swing back and forth with constant
amplitude, just like a clock pendulum (apart from the little friction from
bending the thread she hangs from. A spider has so little mass that her
terminal velocity is very small‚ÄĒdrop
her off the roof and she will not get hurt because she quickly comes to some
constant velocity because the air drag, which can be approximated as being
proportional to her speed, quickly becomes equal to her weight. If the air
drag is not too big, the pendulum will swing back and forth with ever
decreasing amplitude; this is called underdamped. For larger drag, as in the
case of your spider, she never crosses over the equilibrium and just slowly
approaches the bottom of her swing; this is called overdamping. There is a
third possibility called critically damped, but it is qualitatively just
like overdamping, so let's not go there. There is a neat
web site (pun
intended) where you can play with the damping for a mass on a spring, not a
pendulum, but the idea is the same. (The constants there are k is a
measure of the stiffness of the spring, m is the mass, and b
is a measure of how big the drag is.) Two examples from that applet are
shown below. The first might be a pea on a thread where it swings back and
forth a few times before stopping. The second case is your spider whose
swing just dies away.
![]() QUESTION:
QUESTION:
I am a lineman and a intriguing question has been brought to my attention and would love some help. How high would a wooden pole weighing approximately 1500 pounds need to be dropped in order to crush a steel toed boot with a crush rating of 2500 pounds?
![]() ANSWER:
ANSWER:
Usually I trash such questions (see my
FAQ page). However in this case you
tell me the force which the toe can withstand (which I will call F=2500
lb) and the weight of the pole (which I will call W=1500 lb). We have
to make one approximation, that the force is constant over the time it takes
to crush it and you will also need to know how much the toe crushes (I will
call that S). I will not bore you with the details, but I find that,
if H is the height from which it is dropped, H/S=(F/W)-1.
For your numbers, H/S=0.67; that is pretty small. For example, if the toe
crushes by S=3", dropping the pole from H=2" would be enough
to crush it. I would avoid dropping such a thing on my toes.
![]() QUESTION:
QUESTION:
Recently, I was involved in a 4-car pileup on the freeway. The roads were dry, and I was traveling at 40-45 mph in a 2003 Honda Accord
(gross weight: 4300 lbs) when the car in front of me, at about 1 car length
away, started braking. I braked and stopped 3-5 feet behind the car in
front of me before the guy behind me rear-ended me.
The CHP officer claims that I caused the accident by making an unsafe lane
change. The guy behind me was driving a 2005 Toyota Sequoia (gross weight:
6500 lbs.) at 30-35 mph and he was roughly 1-1.5 car lengths behind me when
I got in front of him. I argued that if I could come to a complete & safe
stop going up to 10 mph faster than him, then there's no reason why he
couldn't stop in time. The CHP officer says that since his car has more
mass, he needed more room to stop. I think the difference in speed should
account for the difference in mass. So, who's right?
![]() ANSWER:
ANSWER:
I cannot judge on this. If you made an unsafe lane change, I think
you will not gain much by arguing. Certainly 1-1.5 car lengths is too small
for the speeds you were going. To first approximation, though, if you are
getting maximum braking (just barely not skidding) or if you are skidding,
the distance to stop does not depend on mass, just the initial velocity (and reaction
time).![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Would you mind explaining why distance to stop doesn't depend on mass, just velocity, if you are getting maximum braking?
![]() ANSWER:
ANSWER:
The force of friction if you are just about to skid on a level road
is F=μsmg
where m is mass, g is acceleration due to gravity (9.8 m/s2
or 32 ft/s2), and μs is a constant (called
coefficient of static friction) determined by the surfaces (let's say rubber
on dry asphalt). But, Newton's second law says F=ma where a is
the acceleration. Therefore, ma=μsmg
and so m cancels out and the acceleration (which determines how
far you go) is independent of m: a=μsg.
It is easy to show that the distance you go before stopping is s=–Öv02/(μsg)
where v0 is the speed when you start braking. I find that,
taking μs≈0.6, s≈110 ft for 45 mph and 70 ft
for 35 mph. These are the absolute minimum (which you can approximate if you
have antilock brakes) and assuming zero reaction time (which is impossible).
Also, if the vehicle locks the wheels and skids, you go farther yet because
the physics is all the same except the coefficient of friction is smaller if
the surfaces slide.
![]() QUESTION:
QUESTION:
ma+kx=0 →(A) is an equation which represents mass spring system. It is a linear equation of second order. If I want to make it non-linear I make it like ma+kx+k1(x^3)=0, i.e. I add another term k1(x^3). Why can‚Äôt I add k1(x^2) to (A) to make it non-linear?
![]() ANSWER:
ANSWER:
Because the force would be repulsive when x<0, that is, it
would not be a restoring force. Your equation for the spring is essentially
F=-kx. For F to be a restoring force, it must be an odd
function of x.
![]() QUESTION:
QUESTION:
Suppose we have Bob the astronaut sitting without a space suit in a
spaceship full of air on a mission to Mars. Bob is very fond of balloons
and is holding on to a nice, big, red helium balloon via a piece of
string. Bob is sitting facing the front of the spaceship. Mission
Control decides to slowly accelerate the spaceship. In which direction
will the balloon move relative to Bob? Why?
![]() ANSWER:
ANSWER:
I do not like this question because the reason a helium balloon
floats is that the buoyant force, which floats it, arises because the
pressure in the air is bigger underneath the balloon than above it; on a
mission in empty space, the pressure everywhere in the cabin is the same
and so the balloon would not go up! Let's just have Bob ride in an
accelerating car right here on earth. There are three forces on the
balloon, its weight W, the buoyant force B,
and the tension in the string T. B and
T are both vertical, and so, for the balloon to have an
acceleration in the direction of the acceleration a of the
car, T must have a horizontal component in the direction
of a. All this is shown in the figure to the right.
Therefore the balloon will move backward opposite the direction of the
acceleration. In the spaceship where there would be no buoyant force and
no weight, the balloon would appear to accelerate backwards until the
string was straight and "horizontal".![]() "ENHANCED"
ANSWER:
"ENHANCED"
ANSWER:
It has been pointed out to me (again, thanks to Michael Weissman at
Ask the Van) that my answer would be correct only if there
were no air in the spacecraft. What I failed to think about was that if
there is air in the cabin, forward acceleration will cause the pressure
at the rear of the cabin to be greater than at the front; therefore
there would be a buoyant force on the balloon from back to front. So, if
the mass of the balloon is less than the mass of an equal volume of air,
the direction the balloon would move would be forward, not rearward. If
you are familiar with the equivalence principle, it is even easier to
understand. The equivalence principle states that there is no experiment
you can perform which can distinguish between an accelerated frame and
being in an unaccelerated frame in a uniform gravitational field with
the same accelerateion (due to gravity). So, if the acceleration of the
ship were g, the balloon would have to behave just the same as it
would on earth except forward now would play the role of up on earth, so
the balloon would go forward just like the balloon on earth would go up.
(My example of the car on earth, above, would also have a "pseudo
buoyant force" in the direction of a, so both this force
and the horizontal component of the tension would be in the direction of
a meaning that the balloon would always go the opposite
direction of a here on earth.)
![]() QUESTION:
QUESTION:.jpg)
I'm a big fan of SpaceX and space in general. So as you may know the
Dragon Spacecraft is performing maneuvers to dock with the station. At
this moment I'm watching the Dragon orbiting about 2 miles directly
below the ISS. My question is: how can the spacecraft hold its position
below the station when it should need to be going faster given that it's
closer to the earth. Or is the difference so small that the effects of
orbital decay are not even noticeable until many orbits later?
![]() ANSWER:
ANSWER:
Kepler's third law says that the ratio of the periods of two orbits
is equal to the square root of the ratio of the cubes of their radii:
T1/T2=(R1/R2)3/2.
Suppose that R1=R2+δ,
then
T1/T2=(1+(δ/R2))3/2≈1+3δ/(2R2)
where I have used the binomial expansion to approximate the root because
certainly
δ/R2
is very small. Now, put in some numbers: the radius of the orbit is
about 4000 miles and
δ is 2 miles, so T1/T2=1+6/8000=1.00075.
This means that if T2 is 90 minutes, T1
is 90 minutes + 4 seconds. So, your last statement wraps it up pretty
well.
![]() QUESTION:
QUESTION:
Would you give an example of how centripetal force (if I am correct in
thinking and not confusing centrifugal force) helps keep the lacrosse
ball from falling out of the net when cradling (semi circular motion)
the ball. She is in 7th grade and used the example of the water bucket
spinning Ina circle to explain to her friends why it works, but I would
like a more thorough explanation.
![]() ANSWER:
ANSWER:
I will try to make this comprehensible to a bright 7th grader.
Newton's second law says that what a force does is cause an object to
accelerate. In everyday life, accelerate means speed up or slow down,
but in physics it can also mean that the velocity changes direction
without speeding up or slowing down. So, when something moves in a
circular path, even with constant speed, there has to be some force
present. Here is one example. Consider the International Space Station
which moves in a circle about 200 miles above the earth with an
approximately constant speed of about 18,000 mph. So it is accelerating
because it is moving in a circle, always changing its direction. What is
the force which causes that acceleration? It is simply the only force it
experiences, its own weight which is a force which points toward the
center of the earth. A force which causes a change in direction is
called a centripetal force and must have a magnitude of mv2/r
where m is the mass, v is the velocity, and r is
the radius of the circle. Now, a more down-to-earth example. If you have
a ball of mass m attached to a string of length r and you
wish to swing it over your head, when it passes over the top of the
circle it has two forces acting on it, its weight and the tension in the
string, both downward forces. If it is going very fast, the tension in
the string will be very big, maybe big enough that the string would
break because the string was not strong enough. As it goes slower and
slower, the required centripetal force gets smaller and smaller so the
tension also must get smaller because the weight cannot change.
Eventually you will be able to go over the top with the tension in the
string zero, that is the string is not needed at that instant. But, that
is the smallest speed you can go because if you try to go slower, the
weight will be bigger that the centripetal force needed and so the
string will go slack and the ball will fall out of its circular path. If
you had used a stick instead of a string attached to the ball, you could
go through as slowly as you wished because, unlike a string, a stick can
push. There is no such thing as a centrifugal force, it is called a
fictitious force and is added to make Newton's laws work in an
accelerating reference frame. E.g., if you are sitting in a car
speeding up, for example, you would swear that there is a force pushing
you back but there isn't; you feel the back of the seat pushing you
forward to accelerate you and your brain interprets this as being pushed
back against the seat. See cartoon at the right.
![]() QUESTION:
QUESTION:
I am a professional juggler. One of the patterns I juggle has balls thrown to two different heights. The right hand throws across to the left and vice versa. Basically I know that the balls thrown from the right hand reach their peak in the same amount of time as the balls thrown from the left take to peak and fall down again (to be caught by the right at the same level as they were thrown).
When I learned this juggling pattern I was still in school and I remember using Newton's laws to work out that the ball thrown from the right hand peaks at exactly 4 times the height of the ball thrown from the left. (If you google this, a ball dropped from 4m will fall to the ground in 9ms and a ball dropped from 1m will fall to the ground in 4.5ms)
Please tell me how I worked out the relative heights using Newton's formulas and my knowledge of the relative time the balls take in the air! (If you need to see an example, you can google it, it's a standard juggling pattern known as "triple singles" because of the triple spins thrown if you juggle it with clubs.)
![]() ANSWER:
ANSWER:
This requires only that you know the equations of motion for uniform
acceleration because the ball has a constant acceleration of g=-9.8
m/s2 when in flight (the minus sign meaning it is speeding up if
falling, slowing down if rising. These equations are y=v0t-–Ögt2
and v=v0-gt where v is the velocity at time
t and y is the height (at time t) above where it was
thrown (at time t=0) with velocity v0. So, we have
one pair of equations for the ball that goes higher (I will call it #1) and
another pair for the other ball (#2):
y1=v01t-–Ögt2
and v1=v01-gt and
y2=v02t-–Ögt2
and v2=v02-gt.
Suppose #1 goes to a height h1 before coming back. The
time t to reach h1 is found by knowing that v1=0
at that time, so t=v01/g. Put that time into the
equation for y1 and find h1=–Öv012/g.
Now, you tell me that you want #2 to make the full trip up and down in the
same time; that means that it will make the trip up in half that time, t=–Öv01/g.
If you now put this time into the equation for y2 (which
we would call h2 at this time), you will find that h2=⅛v012/g=—ėh1.
Of practical interest to the juggler is that you must give #1 twice the
initial velocity of #2 to achieve the desired heights.
![]() QUESTION:
QUESTION:
consider a water wheel with mass of 600kg, rotating @ 18 RPM, wheel diameter is 3 meters and the diameter of its axle is 0.1 meter.
the wheel is fed with 10 liters of water per second from the top, causing it to rotate and eventually releasing the water at the bottom (3 meters lower).
Neglecting efficiency losses due to friction, air drag etc..., the available energy from the water should be MGH: 10 x 9.8 x 3 = 294 joules. However, considering the wheel's diameter, its mass and its RPM, the wheel's kinetic energy (1/2 x moment of inertia x angular velocity squared) is 1200 joules.
Where did the extra joules of energy come from?
Secondly, the diameter of the axle is only 0.1 meter so this hypothetical wheel has a mechanical advantage of 30 (MA= radius wheel / radius axle). Does this mean the initial energy of water is magnified 30 times at the axle? If not so, then what has been magnified 30 times?
![]() ANSWER:
ANSWER:
Your analysis is taking the wrong approach on several counts. First,
what you calculate as "available energy from the water" is available
power from the water, J/s=watts. How much of that energy ends up being
delivered to the wheel depends on the design of the wheel. To the right
we see water entering the wheel at some speed; if it leaves the wheel at
the same speed (which would happen if the circumference of the wheel
were moving at the same speed as the incoming water for the wheel I use
to illustrate), then your wheel is getting all that energy. If that were
the case, then this wheel would be losing energy at the same rate to
frictional forces (plus any work you were extracting from the wheel,
maybe to grind grain or something). You do not say where you got the
moment of inertia to calculate the kinetic energy of the wheel, but I
figure that the biggest it could be, if all the mass were at the
circumference (I=MR2), would be about 5400 kg m2
which, using 18 rpm=1.9 s-1, would give an energy of about
9700 J, quite a bit bigger than your 1200 J. If you were able to deliver
294 J/s to the wheel, it would take about 4 seconds to get to 1200 J if
there were no friction.
The bottom line is that a discrepancy between power being delivered to
something and the energy it has is not a discrepancy at all since they
are different things. Regarding your second question, it is force which
is magnified 30 times; this is simply a lever.![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
The formula I used for calculating the moment of inertia was 1/2 x mass x radius^2 = 1/2 x 600 x 1.5^2 = 675 kg-m^2.
Is it possible to harness the available kinetic energy to do work? i.e can this energy be used to do more work (output) than what the original input by the water allowed (10 liters/second)?
secondly, if force was magnified 30 times at the axle, is this magnification useful in terms of driving machinery such as water pumps, generators etc...? i.e can the original power of the water be used to drive a more powerful machine?
![]() ANSWER:
ANSWER:
First, note that I misread your original question and used 3 m as
the radius, not the diameter. So, note that the water leaves the wheel
halfway to the water below, so the available power is only 147 watts.
The moment of inertia you used was for a uniform cylinder or disk and I
would guess that the real moment of inertia is somewhere between our two
answers (mine corrected to 1350 kg m2). You can never get more
energy from a system than has been put into it. If you find a way to
start using this kinetic energy, the wheel will slow down. You can think
of the wheel as an energy storage device, having acquired that energy
from the water. So, you could use that energy but it would quickly be
used up. This is the principle of a
flywheel on a
mechanical device where you get it spinning when you have energy to
store and then later use the energy.
![]() QUESTION:
QUESTION:
I've recently been having a heated debate over a scenario composed of very basic principles of physics, and I was wondering if you could help us figure this out. Both of us have presented different arguments, and neither of us can agree with the other. We have found very few relevant webpages, however, after scanning through some of your Q&As, we found one that I will mention. So here it is: If a man is on top of a moving object moving at a constant velocity x (in a vacuum, where air resistance is ignored) and he jumps straight up, will he land in the same position he jumped from, assuming that he doesn't flail his legs? I personally believe that he will, because first off, when released from the friction of the train, the man will still have the momentum of velocity x, and without air resistance will continue to go that velocity until gravity brings him back down. However, my brother believes that gravity will deter the motion of the man in some way that he will land off the mark.
The other example that we found is the bullet on the train example. If a bullet is fired at a speed equivalent to that of the train's from the back of the train then relative to the ground , the bullet is at a standstill and will fall straight down. I think that this example supports my answer, but we are not sure. Could you please provide an answer?
![]() ANSWER:
ANSWER:
You have really not given me enough information. Is this happening
on the earth? Or is it some idealized "flat" earth where the train is
traveling in a straight line and gravity is always pointing in the same
direction (perpendicular to the path of the train)? This (flat earth) is
the scenario usually portrayed in textbooks because it is usually an
excellent approximation.
![]() QUESTION:
QUESTION:
I was watching the TV show, The Universe, the episode about alien planets. It talked about how planets and their stars revolve around their common center of mass and/or gravity, I forget which one. How does that work when you have more than one planet? Because, as we know, all of our planets do not revolved with the sun in a straight line. So where is the octuple fulcrum that creates the revolutions of our sun and the planets? And how did it occur? Please give me
the most detailed answer you can, as well as fact checks with my question.
![]() ANSWER:
ANSWER:
For simplicity, suppose the solar system is isolated, the forces it
experiences from the rest of the galaxy or the rest of the universe are
negligible; this is an excellent approximation over times long compared
to times associated with the motion of the planets. You can compute the
center of mass of the whole solar system just about as easily as for two
bodies. Since you say you want "the most
detailed answer" I can give, I will do the details. For anybody reading
the answer, you can just skip the math and read the narrative and
understand things qualitatively. Suppose we choose some point in space
as the origin of our coordinate system; each body in the solar system
has a vector position Ri in this system and a
mass Mi. Then the position of the center of mass is
defined to be Rcom=ΣMiRi/ΣMi
where the symbol
Σ means to sum over all the objects. For example, the
term ΣMi
is the mass of the whole solar system which I will call M.
Notice, for example, that if the mass of the sun is much greater than
all the other masses, the position of the center of mass is
approximately the position of the sun. Now I am going to find the
velocity and acceleration of the center of mass by differentiating with
respect to time once and twice respectively: Mvcom=M(dRcom/dt)=ΣMi(dRi/dt)=ΣMivi
and
Macom=M(dvcom/dt)=ΣMi(dvi/dt)=ΣMiai
where vi is the velocity of the ith
object and ai is its acceleration. Now, we can
apply Newton's second law to the acceleration equation:
Macom=ΣMiai=ΣFi
where Fi is the net force felt by the ith
object which is simply Σj≠iFij
where Fij is the force on the ith
particle due to the presence of the jth particle and this sum
runs over j but not the term j=i because an object does not exert a
force on itself. So,
Macom=ΣΣj≠iFij.
But now look at the double sum: for every term Fij
there is also a term in the sum Fji and Fij=-Fji
because of Newton's third law (the force of the ith on the jth
is equal and opposite of the force of the jth on the ith).
So, finally we have acom=0, the center of mass
moves with constant velocity and if we happen to have chosen a
coordinate system at rest with the center of mass, the center of mass
never moves. In other words, the whole solar system, no matter how
complicated its motion, orbits around the center of mass. If the total
solar system experiences a force F from the rest of the
universe, the only difference is that the center of mass now has an
acceleration acom=F/M; but
you can still say that the solar system orbits around its center of
mass, it is just that the center of mass is now "orbiting" around some
other point. Maybe that is more detail than you really wanted, but it is
a standard derivation in any introductory physics course. The bottom
line: any system of interacting objects orbits around its collective
center of mass.
![]() QUESTION:
QUESTION:
My friend and I had a drunken argument. I would like independent council to weigh in (there's $300 on the line)
I was given a unique bottle opener by a friend who is a brewer for craft brewery in the northeast. It is a flat piece of wood with a smooth screw embedded in one end ( think ______T_ )
Its measurements in 1/16ths of inches are as follows:
88 long. screw centered 11 from one end. side of screw to end is 9 short side. 75 long side screw lip is 4 from bar bottle cap is 4 high 17 across.
The argument is as follows.
Person A: There is less force required to open the bottle pressing down with the cap positioned _________XXXT___ (between the screw and the user)
Person B: There is less force required to open the bottle pulling up with the cap postioned __________TXXX .
With my horrible description of the problem. Can you prove either arguement successfully?
![]() ANSWER:
ANSWER:
I have redrawn your attempt to picture this to make it clearer. The
picture to the right shows the two situations with person A below and
person B above. To answer the question I will compute the force which
the nail exerts on the bottle top for equal forces by the user.
Whichever of these is the biggest is the winner. Doing this is a simple
first-semester physics statics problems, most easily done by summing the
torques in each case about the point on the bottle cap just opposite the
nail; that point is a distance R from the end where F
is applied for person B and a distance R-2d for person
A. I find that the nail exerts a force of A=F[(R/d)-2]
for A and a force of B=F(R/d) for B;
B is the winner of the bet. For your numbers, d=17/16" and R=(77+17)/16"=94/16",
so R/d=5.53 and the ratio of the forces is B/A=5.53/3.53=1.57,
making option B 57% bigger, quite definitive. (If a $300 bet is really
on the line, don't forget to reward The Physicist!)
![]() QUESTION:
QUESTION:
If I am towing a vehicle from a standing start is there an equation for calculating the amount of force I would be using for example if I tow a vehicle that weighs twelve tonnes because it has wheels and is therefore not a "dead weight" how do I work out how much force I would be exerting on the tow rope/towing vehicle and also how would I factor in different gradients as it would obviously require greater force on an upslope. This came up in my workplace where our towrope are rated to three tonnes and I was trying to explain that it does not mean you could not tow a vehicle over that weight.
![]() ANSWER:
ANSWER:
This is a good question to illuminate elementary Newtonian
physics. Your referring to "dead weight" really has no meaning in physics,
but you apparently mean that the object can move with little friction. So,
let's assume there is no friction; this is, of course, never true, but it
puts an upper limit to anything I do. On level ground, any force will move
the vehicle if there is no friction. What matters is how quickly you start
it moving, in other words what the acceleration is. For example, suppose you
have a 4 lb fish hanging on a 5 lb test line; if you pull it up slowly you
will land it, but if you try to jerk it up really fast the line will break.
The physical principle in play here is Newton's second law, F=ma
where F is the force, m is the mass, and a is the
acceleration of m due to F. So, in your case, m=12
t=12,000 kg; the maximum force you can apply is 3 t=29,420 N because the 3 t
rating means that it can hold up a 3 t mass which has a weight of 3000x9.8
N. So the maximum acceleration is amax=29,420/12,000=2.45
m/s2=5.5 mph/s. This means that if you speed up to 5.5 mph in one
second, the rope will almost break. Of course, there will be friction and so
to be safe I would recommend a factor of roughly two, an acceleration of
about 3 mph/s would probably be safe. Here is an equation you can use (which
does not include any safety factor): amax=22(MT/MV)
mph/s where MV is the mass of the vehicle, and MT
is the mass rating of the towrope. If you are trying to tow up a hill which
makes an angle θ with the horizontal, you need to apply a factor of
sinθ to the equation above, amax=22(MT/MV)sinθ,
because some of the vehicle's weight is now directed down the hill instead
of straight down. If the grade is 300, for example, sinθ=–Ö.
![]() SIMILAR QUESTION:
SIMILAR QUESTION:
watching a tv commercial showing how mighty a pickup truck is-it's
towing the space shuttle, which weighs (according to the announcer), 292,000 lb (146 tons). Now I know that it's not as if the pickup is lifting 146 tons-I figure the load on the little pin hooking the shuttle to the pickup will be (initially) 146 tons times the coefficient of friction for the tarmac upon which both vehicles are riding-am I right?
![]() ANSWER:
ANSWER:
First, read the question and answer preceding yours. Assuming
there is negligible friction in the bearings of the carriage for the
shuttle, it is not hard to get the shuttle moving with a small acceleration.
In the other question, though, the numbers were much smaller than in your
case where there is what appears to be a steel towing bar which would far
exceed the strength of a tow rope to tow things with weights of several tons
rather than several hundred. So, with such a strong "tow rope" you might
think that you could have as big an acceleration as you like. For example,
if the breaking strength of the pin (probably the weakest link) were 100
tons, my little formula above would say that you could have an acceleration
up to about 22x(100/146)≈15 mph/s (0 to 60 in 4 seconds)! This will
obviously not happen. There are two considerations you need to think about.
First, the force which provides the acceleration is actually the static
friction between the truck wheels and the road; the biggest this force can
be is f=μW where μ is the coefficient of static friction and
W is the weight of the truck. For rubber on dry concrete, μ≈0.7
and the weight of a Toyota Tundra pickup is about 3 tons, so f=3x0.7≈2
tons; so, the maximum acceleration is only about 0.3 mph/s. The second
consideration is how rapidly the truck can deliver the energy needed to move
the load, in other words its power rating of about 300 hp. I calculate that
the maximum acceleration with a 146 ton load would be about 4 mph/s. So, it
appears that the main limiting factor on the acceleration is the possibility
of the tires spinning. Keep in mind that these are all just rough estimates,
but they give the general picture.
![]() QUESTION:
QUESTION:
Why when a cyclist is turning round a bend, he tends to lean inwards with the bike?
![]() ANSWER:
ANSWER:
The picture at the right shows the forces (real and fictitious) on
the cyclist. (I copied this from the Wikepedia article on bicycle
dynamics.) The circle represents the center of mass of the system. Since
he is moving in a circle of radius r and with speed v, he
experiences a centripetal acceleration ac=v2/r
to the left. The forces on him are his own weight mg, the normal
force N up from the road, and the frictional force Ff
which is the force providing the acceleration. If you want to apply
Newton's second law in the frame of reference of the cyclist, which is
not an inertial frame, you must add the fictitious centrifugal force -mac
as shown in the figure. Note that if he were not leaning, there would be
an unbalanced torque about the point where the tire touches the ground,
τ=mLv2/r where L is the distance to the
center of mass, which would cause him to rotate clockwise, that is to
fall over. When he leans, though, the weight also exerts a torque, so
the two torques can balance if the angle is just right: mgLsinθ=mLv2cosθ/r,
or θ=tan-1(v2/rg).
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION: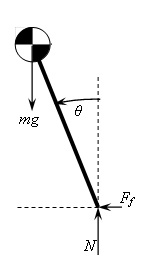
Can it be explained without invoking the fictitious force because it may be too technical? Can I say the bike has a tendency to move in a tangential direction to the bend, this causes the bike to topple outward, so leaning inward will prevent the bike from toppling?
![]() ANSWER:
ANSWER:
You can say "the bike has a tendency
to move in a tangential direction to the bend, this causes the bike to
topple outward" but that does not explain why it "topples outward", does
it? You certainly can do this problem using Newtonian mechanics without
introducing the centrifugal force, but you must calculate any torques
about the center of mass, nowhere else will work. The new figure looks
just the same but with the centrifugal force removed. Now, the sum of
all the vertically directed forces must add to zero, -mg+N=0
which tells you that N=mg. And, the sum of all the horizontally
directed forces must equal mass times acceleration, Ff=mv2/r.
So, given m, v, and r, you now know all the forces.
But you still need to know the angle of lean for the cyclist to not
topple over. This is achieved by summing all torques (about the center
of mass) and setting it equal to zero (so that it does not start to
rotate in the plane of the page),
Στ=0=NLsinθ-FfLcosθ=mgLsinθ-(mv2L/r)cosθ.
And so, solving for θ, we get the same answer as above, θ=tan-1(v2/rg).

![]() QUESTION:
QUESTION:
Is it the orbital velocity of an object that enters the earth's atmosphere that causes that object to typically burn up and disentigrate? Could you, in theory, freefall
 from the International Space Station safely if you had zero orbital velocity?
from the International Space Station safely if you had zero orbital velocity?
![]() ANSWER:
ANSWER:
It is certainly high speed through the air which causes an object to
get hot. The effect of high speeds on the body and the effectiveness of
space suits in protecting it at high speeds will be tested in
a jump from about 23 miles any day now. Felix Baumgartner is
expected to exceed sound speed before his parachute opens. However, the
altitude of the space station is about 250 miles and I suspect that
falling from that height through almost no atmosphere would give the
jumper too much speed when he encountered the atmosphere to be able to
survive.
![]() RELATED
QUESTION:
RELATED
QUESTION:
I have a question about Felix Baumgartner and his skydive attempt. How
is it possible for him to break the speed of sound in his jump? My
thinking is that objects reach a terminal velocity - jumping from a
higher distance from earth would therefore not make any more difference
in the maximum velocity. Also, I heard that he won't be able to breathe
for a certain period of time. Is that because of how fast he's going, or
because of the atmospheric conditions at such a distance from earth?
![]() ANSWER:
ANSWER:
The reason there is a terminal velocity is that the air drag on a
moving object increases approximately like the speed squared (if you go
twice as fast, you experience four times the drag). But what the
terminal speed is depends on how much air there is and at high
altitudes, there is almost no air. There is some terminal speed, but it
is much bigger than it is at lower altitudes. The terminal velocity is
inversely proportional to the density, 1/√ρ;
the density of air at 23 miles is less than 1/100 that at sea level, so
the terminal velocity is ten times bigger. The speed of sound, though,
also changes with altitude; it is about 740 mph at sea level and about
670 mph at 20 miles up. I do not really know what your question about "won't
be able to breathe" means. If he did not have his "space suit" he would
certainly not be able to breathe until he got down to an altitude around
5 miles up (just not enough air).
![]() QUESTION:
QUESTION:
Consider two satellites in orbit around earth following each other in the very same orbital path, but say 2000 km apart. And consider that they be connected together by a very thin string. Here is the question:
Can this string be gently pulled until it makes an absolutely straight line? Or will it follow the so-called curvature of space that is supposed to exist around earth, between the two satellites’ positions?
![]() ANSWER:
ANSWER:
This is a tricky question with lots of possible secenarios
for what might happen for various conditions.
-
First, suppose the string is not a string but a rigid stick but of negligible mass which we miraculously make appear between the two satellites happily orbiting in a circular orbit, one following the other. Now, we no longer have two satellites but one instead. One of the laws of classical physics says that if you want to know how a rigid body behaves under the influence of external forces, find the net force on the body and the center of mass of the body will move as if it were a point mass experiencing that force. Now, the center of mass of the pair is below the orbit they are in and therefore this single satellite is moving too slowly to move in a circular orbit and the center of mass will change to moving in an elliptical orbit.
-
What if you put a string of negligible mass between them in a straight line? Since it has no mass, it experiences no force and everything will behave like it was not there.
-
Now, if you connect them with a string which has mass, it also experiences gravity and each piece of string is really wanting to be at a larger orbit so, I believe, the tendency will be for the string to curve to fit the circular orbit of the two heavier satellites. This is an approximation assuming the string has a much smaller mass than the satellites. In reality, the string will exert forces on the satellites and alter their orbits.
-
Under your "gently pulled" secenario, the string would pull gently also on you and the other satellite thereby altering both orbits.
![]() QUESTION:
QUESTION:
My question is about tension: what exactly is it? Now, I know how
tension is defined, but my problem comes when trying to reason it out
with force diagrams or drawings. Take this classic example: There is a
tug-of-war match going on between 2 contestants. One contestant pulls to
the right with a force of 300 N. The other pulls to the left with a
force of 300 N. What is the tension in the rope? Now, I know the tension
in the string is 300 N just by definition/recognition...but why? The
example proposes a situation in which the net force is zero, so there is
no acceleration of the rope. The "force of tension" resists the pull
from the contestant on the right with 300 N, and the same goes for the
contestant on the left. So, if we represent these forces of tension with
vectors, they would both be pointing toward the "midpoint" of the rope.
That being said, why don't these tension vectors add to make 600 N net
force? Or conversely, why don't these vector forces subtract to make a 0
N net force. Also a side note: In a lot of classical mechanics problems,
we always see problems involving "massless" ropes. What exactly does
that mean and why do we need to define a rope as "massless" in order to
carry out problems involving strings/ropes?
![]() ANSWER:
ANSWER:
The tension is nothing more than the force which a rope
exerts on something it is tied to. Tension has some important properties. It
is always tangent to the rope and a rope can never push, it only pulls. Of
course, ropes are never massless in the real world, but we can often
approximate them as if they were if they were if their mass is much less
than everything else. I can see that your main problem is that you have not
been properly instructed on how to attack these simple statics problems. The
first thing you have to do is to choose a body on which to focus and
look only at that; you are attempting to look at the rope and both men all
at once.
-
Let me start with a simpler example, a 1 kg mass hanging from the ceiling on a massless rope. (I will use 10 m/s2 to approximate acceleration due to gravity). So, I will choose a body, the 1 kg mass. What are all the forces on it? Its own weight, 10 N straight down and the force which the rope exerts up. That force by the rope is the tension. Pretty simple, the tension at the bottom of the rope must be 10 N.
-
Now I will choose a different body, the 1 kg mass plus half the rope. What are all the forces on the body? The weight of the body, still 10 N, and the force which the upper half of the rope exerts on the body (at the point where the upper and lower halves of the rope touch). The unknown force again must be 10 N and so the tension in the middle of the rope is 10 N.
-
Now I will choose the 1 kg mass and the whole rope as the body. What are all the forces on it? The weight of the body, still 10 N, and the force which the ceiling exerts up on the top end of the rope. So now we find that the ceiling must exert an upward force of 10 N on the top of the rope. But, Newton's third law says that if the ceiling exerts a force on the rope, the rope exerts an equal and opposite force on the ceiling. So, once again we find the tension in the rope, now at the top, is 10 N. (This is very much like your tug-o-war problem if you think about it: the weight pulls down on the rope with a force of 10 N and the ceiling pulls up on the rope with a force of 10 N, but the tension in the rope, I have just shown, is 10 N everywhere, not 20 N.)
Next, do the same problem but now let the mass of the rope be 1 kg also, clearly not even approximately massless.
-
So, I will choose a body, the 1 kg mass. What are all the forces on it? Its own weight, 10 N straight down and the force which the rope exerts up. That force by the rope is the tension. Pretty simple, the tension at the bottom of the rope must be 10 N.
-
Now I will choose a different body, the 1 kg mass plus half the rope. What are all the forces on the body? The weight of the body, now 15 N, and the force which the upper half of the rope exerts on the body (at the point where the upper and lower halves of the rope touch). The unknown force must now be 15 N and so the tension in the middle of the rope is 15 N.
-
Now I will choose the 1 kg mass and the whole rope as the body. What are all the forces on it? The weight of the body, now 20 N, and the force which the ceiling exerts up on the top end of the rope. So now we find that the ceiling must exert an upward force of 20 N on the top of the rope. But, Newton's third law says that if the ceiling exerts a force on the rope, the rope exerts an equal and opposite force on the ceiling. So, now we find the tension in the rope at the top is 20 N.
Finally, let's do your tug-o-war problem. Part of your confusion is saying that each man exerts a force of 300 N. It is much better to simply say that it is a tie right now so the men must be exerting equal forces in magnitude.
-
I will choose man #1 as the body. What are all the (horizontal) forces on the man? The rope pulls him with an unknown force and some other force must pull him in the opposite direction so that he remains in equilibrium; that other force is simply the friction between his feet and the ground which we will take to be 300 N. Therefore the tension at end #1 will be 300 N. Of course, since the rope exerts a force of 300 N on the man, the man must be exerting a 300 N force on the rope as was originally stated in the problem, but that is not a force on the chosen body.
-
I will next choose man #2 as the body. What are all the (horizontal) forces on the man? The rope pulls him with an unknown force and some other force must pull him in the opposite direction so that he remains in equilibrium; that other force is simply the friction between his feet and the ground which we will take to be 300 N. Therefore the tension at end #2 will be 300 N.
-
I will choose man #1 plus half the rope as the body. What are all the (horizontal) forces on the body? The friction pulls one direction with 300 N and the #2 half or the rope pulls on the #1 half of the rope with the same force, so the tension in the middle of the rope is 300 N.
-
Suppose we choose both men plus the rope as the body. Then friction pulls to the left with 300 N and to the right with 300 N and the rope can be totally ignored because it does not exert any net force on the body being an internal force.
![]() FOLLOWUP
QUESTION:
FOLLOWUP
QUESTION:
I see where I got confused. I didn't understand how to apply Newton's
3rd Law to the problem. So the force of the man on the rope (his pull on the
rope) is an action-reaction pair with the force of the rope on the man
(tension)? Also, do we always consider action-reaction pairs as forces that
"cancel" each other out or sum to zero? Lastly, if the forces of friction
between their feet and the ground are the ones that add up to a zero net
force, what would happen to the tension in the case that one man was able to
exert a greater force of friction in one direction? How could we calculate
the tension in the rope then?
![]() ANSWER:
ANSWER:
Yes, Newton's third law states that if A exerts a force on
B, B exerts an equal and opposite force on A. There is never an occasion
to add the action and reaction forces because they are forces on different
things. They do sum to zero, but that means nothing because one is on the
man and one is on the rope, so why would you add them? If the men pull with
different forces, the system is no longer in equilibrium and accelerates in
the direction of the net force. But still, the tension in the rope is the
same throughout its length. Here is how that goes, using Newton's second law
(N2) (it is a bit more complicated). In the picture, the man on the left in
the blue shirt has a frictional force of 400 N to the left and the man on
the right in the red shirt has a frictional force 300 N to the right. Each
man has a mass of 100 kg and the rope is massless.
-
First, choose both men plus the rope as the body. All the forces are 400 N to the left and 300 N to the right, so the net force is -400+300=-100 N to the left. N2 says this is the mass of the body (200 kg) times the acceleration a, so -100=200a and a=-0.5 m/s2. The acceleration of both men will be 0.5 m/s2 to the left.
-
Next, choose the left man as the body. All the forces are 400 to the left and the force the rope exerts on the blue shirt man, call it Tblue. Now N2 says that Tblue-400=100a=-50 so Tblue=350 N.
-
Next, choose the right man as the body. All the forces are 300 to the right and the force the rope exerts on the red shirt man, call it Tred. Now N2 says that -Tred+300=100a=-50 so Tred=350 N.
So, the tension in the rope is still the same everywhere (you could do the above exercise of choosing one man plus half the rope to show that it is also 350 N in the middle) and, for this problem, it turns out to be just the average of the pulls at each end.

![]() QUESTION:
QUESTION:
My co-workers and I have been in a very heated discussion. They tell me I am wrong and my theory is stupid. Will a bullet fired (perfectly horizontal) and a bullet dropped hit the ground at the same time? My answer is yes, because gravity is constant.
![]() ANSWER:
ANSWER:
One picture is worth a thousand words. The figure to the
right is an actual strobed photograph of a ball (red) launched horizontally
and another (yellow) dropped. If the red ball had been going faster, both
would still have moved together in their vertical positions. The reason is
that each starts with the same vertical velocity (zero) and experience the
same acceleration in that direction (32 ft/s/s). Because a bullet has such a
high velocity, air drag will have a significant effect on it but this will
affect its motion in the horizontal direction, almost not at all in the
vertical direction. This is not a "theory", it is an experimental fact as
the photograph shows.

![]() QUESTION:
QUESTION:
I am a writer putting together a science fiction screenplay. Those who know me say I have an attention to detail--to a fault. There is one particular element I would like to be as accurate as possible. I'm hoping you might be able to help me.
Here is the scenario: A spacecraft leaves earth on course to the moon. In order to create an Earth-like gravity inside the ship; the ship accelerates at a constant rate exerting a force on the occupants equal to one G. Half way through the trip the craft will flip, then decelerate for the remainder of the journey. This would give the same sensation of false gravity to the occupants of the craft.
So here is the question: If this were possible; how long would it take to actually reach the moon?
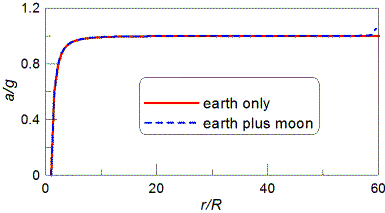
![]() ANSWER:
ANSWER:
Since you are such a stickler for detail, I will give you
detail, probably far more than you want! Your scheme of having an
acceleration with "constant rate" would work in empty space but not between
the earth and the moon because the force causing the acceleration is not the
only force on you, the earth's and moon's gravity are also acting. As you go
away from the earth the earths gravity gets smaller like 1/r2
where r is the distance from the earth's center, and the moon's gets
bigger as you get closer. So, it becomes a complicated problem as to how
much force must be applied to keep the acceleration just right for where you
are. The picture to the right shows you in your rocket ship. Let's call your
mass M. Then there are two forces on you, your weight W
down and the force the scale you are standing on exerts on you, F.
W gets smaller as you get farther and farther away and you
want F to always be what your weight would be on the earth's surface,
Mg. So, Newton's second law says that F-W=Ma=Mg-W where a
is the acceleration you must have. Note that, for the time being, I am
ignoring the moon; that would just complicate things and its force is much
smaller than the earth's, at least for the first half of the trip. I want
you to understand the complication caused by the fact that W changes
as you go farther away. Now, how does W change? W=MMEG/r2=Mg(R/r)2
Where R is the radius of the earth and ME is
the mass of the earth. We can now solve for the acceleration the spacecraft
would have to have: a=g(1-(R/r)2). I have
plotted this in red on the graph above. (The distance to the moon is about
60 earth radii.) Note that for most of the trip the acceleration is just
about g. I also calculated the effect the moon would have, blue
dashed line, and, except for the very end of the trip, it is pretty
negligible. Now that we have taken care of the always-important details, we
can try to answer your question. To calculate the time exactly would be very
complicated, but, since the required acceleration is g for almost the
whole trip, it looks like we can get a real good approximation by just
assuming a=g for the first half and a=-g for the second half;
your perceived weight (F) will just decrease from twice its usual
value when you take off to about normal when you get to about 5 earth radii
in altitude. The symmetry of the situation is such that I need only
calculate the time for the first half of the trip and double it. The
appropriate equation to use is r=r0+v0t+–Öat2
where
r0=R is where you start and v0=0
is the speed you start with. Halfway to the moon is about r=30R=R+–Öat2
and so, putting in the numbers, I find t≈1.69 hours and so the time
to the moon would be about 3.4 hours. You can also calculate the maximum
speed you would have to be about 140,000 mph halfway.
![]() QUESTION:
QUESTION:
Lets say you have a tennis ball machine. The tennis balls must travel though a 5ft tube before leaving the machine. Lets say that the machine is spitting out 60 balls a second at 50 mph. The machine is on a swivel and a person changes the position of the machine by moving the 5ft tube left and right by pushing or pulling with his or her hand. If the speed of the balls were increased to 500 mph would it be harder for the person to move the tube? And if so why?
![]() ANSWER:
ANSWER:
This question is very similar to one I answered a long time
ago. If you are interested in the mathematical details, you can
link there. Here is the old question: Suppose that a mass m is
tied to a string of length R0 and is going in a circle
with angular velocity
ω0. Now, the string breaks. A force which has no radial
component (the direction of the force is always perpendicular to the line
drawn from the original axis of rotation to the mass) is applied to keep the
mass's angular velocity constant; what is the force? How is this like your
question? As your ball travels down the tube, assuming the barrel has no
friction, the tube exerts a force like the one described above if the tube
rotates with constant angular speed. How is it different from your question?
The original question has the ball at rest in the radial direction at the
beginning but your ball starts out with some radial velocity (your 50 or 500
mph). The earlier solution has two constants a and b which
will be different for your problem. Suppose we call the initial ball
velocity v0; then where the earlier solution says "…where
a and b are constants to be determined…"
we will get different values because dr/dt=v0
instead of zero at t=0. If you really care and are good at math, you
can find the new values of the constants yourself, but I suspect you just
want an answer. The answer for the force the tube exerts on the ball (which
is the force you must exert on the tube) as a function of time turns out to
be F(t)=2mω02[R0sinh(ω0t)+ω0v0cosh(ω0t)].
(Don't lose heart, this will get much less technical soon; it is just that I
want to include details for my many readers who like the math!) To finally
answer your question, I need to put in some numbers. Since physicists do not
like English units, I will use comparable metric system units:
-
I will choose ω0=1 s-1. This corresponds to about 500 sweep of your gun in one second.
-
The two velocities I will use are v0=20 m/s (about 45 mph) and v0=200 m/s (about 450 mph).
-
The tube length will be 2 m (about 6 ft).
-
I will use R0=0, that is, the bullet is launched from the point where the gun is pivoted; hence F(t)=2mω03v0cosh(ω0t).
-
I will choose m=0.5 kg, a little heavy for a tennis ball, but it really doesn't matter because I am just interested in the relative forces for the two v0 values.
-
As you stipulated, I will choose 60 s-1 as the rate that the balls are launched, but first of all I will just look at what happens for a single ball.
-
Note that the slower ball (20 m/s) will take 0.1 s to reach the end of the tube and the faster ball 0.01 s
So, putting this in, we get F(t)=v0cosh(t). Now, the hyperbolic cosine function (cosh) at t=0 is 1, at t=0.1 is 1.005, and at t=0.01 is 1.0001. This is what I meant when I said things would get simpler. For all intents and purposes the force is a constant because the cosh does not vary significantly for the time the ball is in the tube. So, finally, F≈v0. The force you have to exert while a single fast ball is in the tube is 200 N; the force you have to exert while a single slow ball is in the tube is 20 N. But, that is not the whole story because there may be more than one ball in the tube. The distance between fast balls is (200 m/s)/(60 s-1)=3.3 m, so there is only one ball at a time in the tube. But, the distance between slow balls is (20 m/s)/(60 s-1)=1/3 m so there are 6 balls in the tube at a time. The final answer: you need a force of 200 N for the fast ball gun, 120 N for the slow ball gun, the fast ball gun is harder to rotate.
![]() NOTE
ADDED:
NOTE
ADDED:
While the fast ball is in the tube, the required force is 200 N, but
there is only a ball in the tube (4/3)/2=2/3 of the time; so the average
force over many balls is more like 133 N, still bigger than for the small
balls but not so much bigger. It also occurs to me that for the real-world
application we should be thinking of the torque we have to apply which
changes as a ball moves down the tube; oh well, I'm getting tired of this
problem!
![]() QUESTION:
QUESTION:
Assume there is a buoy in the ocean, anchored to the ocean floor. If the tide is low, there is little to no pressure on the chain holding the buoy to the floor. When the tide is high (the depth of the water = the length of the chain) the chain is completely taut, so let's say the pressure on the chain is X. But what if there is a storm and the water level rises over the buoy. Is the pressure on the chain still X or is it greater than X? Does the pressure continue to increase as the water level rises or does it stop at X?
In other words: does buoyancy increase as you dive deeper or does it have a set value?
![]() ANSWER:
ANSWER:
(We do not talk about "pressure" in the chain, rather the
force by the chain on what it is attached to, usually called tension;
pressure is force per unit area.) The buoyant force is equal to the weight
of the displaced fluid. To make things clear, let's choose a specific
example. Suppose the buoy has a density which is 1/10 the density of water.
Then, if untethered, it will float with 1/10 its volume submerged so the
buoyant force just counteracts the weight. Now, at low tide, attach a chain
to the ocean floor which is straight but slack. As the tide rises, more and
more of the buoy is under the surface. For example, when half the volume of
the buoy is submerged the buoyant force is 5 times the weight of the buoy.
So all the forces on the buoy are the weight W down, the tension T in the chain
down, and the buoyant force B=5W up: B-W-T=0=5W-W-T=4W-T,
so T=4W. Suppose the water keeps rising until the buoy is
totally submerged so the buoyant force is now 10W; so now T=9W. Now,
if the water keeps rising, the same amount of the buoy is always submerged
and so the tension stops increasing no matter how deep the water becomes.
(Although we think of water as incompressible, at extreme depths the density
does get a tiny bit bigger so the buoyant force at the bottom of the ocean
will be a tiny bit bigger, but a trivially small difference.)
![]() QUESTION:
QUESTION:
Why do rifles not slightly fire high? The split second a bullet explodes
the recoil force should start to spin the gun slightly so that the
muzzle lifts up. This is because the recoil action of the gun is not
directed at the center of gravity of the gun but above it. (I just
checked my rifle and the center of gravity is almost a inch below the
center of the barrel).
![]() ANSWER:
ANSWER:
You are certainly right, an unrestrained rifle would both
recoil backwards and acquire an angular velocity about the center of mass.
However, and I will not do any calculations here, because the rifle has such
a large mass compared to the bullet, I am confident that the angle through
which the rifle would rotate during the extremely short time the bullet is
in the barrel would be trivially small. Even so, the sight mechanism is
always adjusted for a certain distance and the effect you site would be
included in the calibrations of the sight if it were not totally negligible.
![]() NOTE
ADDED:
NOTE
ADDED:
The following occurs to me: the angular momentum of the bullet plus gun
before firing is zero and must be zero afterwards. The bullet is confined to
move along the barrel and the center of mass (of the bullet plus gun) does
not move significantly during the time the bullet is in the barrel.
Therefore, I do not expect the gun to acquire an angular velocity until the
bullet leaves. Again, this is contingent on the bullet having much less mass
than the gun.
![]() QUESTION:
QUESTION:
If you have two objects with exactly the same volume and surface area, and if you
apply an equal force on both of them, the one with less mass will have a greater acceleration. This is because F=ma. But, if you do this experiment in any fluid, which one will go farther? The surface areas are the same so neither will have a greater form drag. But because acceleration due to force, the object with less mass will slow down much more than the other It is also known that the drag acting on an object is directly proportional to the square of its speed. So, even if the object with less mass has a greater acceleration in the beginning, it will slow down much more than the one with greater mass. So which one will travel farther?
![]() NOTE
ADDED:
NOTE
ADDED:
After several communications, the question is this: If the same force
F acts on both objects for the same time and then stops, which object
goes farther? There is no gravity, so this is a one-dimensional problem.
Both objects start at rest. This is one of those quite technical answers
although, without understanding all the math, you can see the qualitative
behavior. This is going to be a lengthy answer, so maybe you just
might want to skip it!
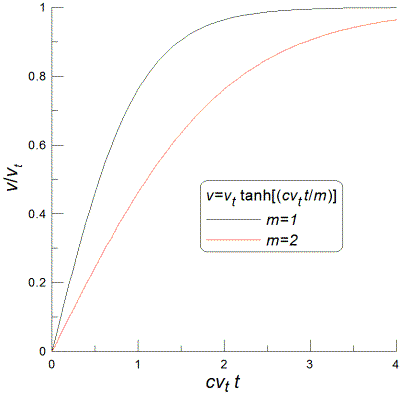
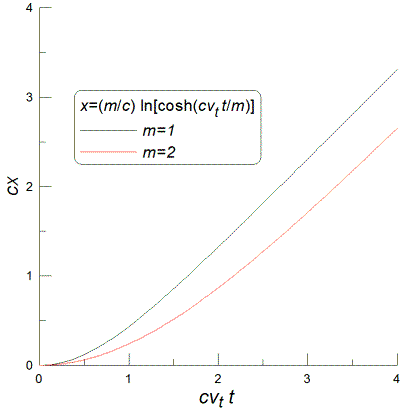
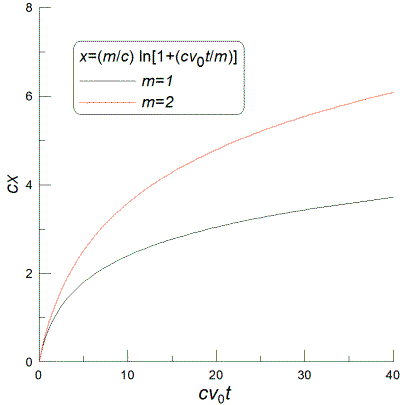
![]() ANSWER
(CORRECTED, 11/11/12):
ANSWER
(CORRECTED, 11/11/12):
I will assume that the drag force is given by Fdrag=-cv2
where c is the same for both objects (as stipulated by the
questioner).
-
For the first part of the problem, Newton's second law is mdv/dt=F-cv2. At large times the velocity will become essentially equal to a constant because F≈cv2; this speed is called the terminal velocity vt=√(F/c). Without going into any detail the solution is v=vt tanh[(cvtt/m)]. This is plotted on the first figure above; the larger the mass, the longer it takes to reach the terminal velocity so, as noted by the questioner, the lighter mass will go farther in a given time. To get the position as a function of time, we need to solve v=dx/dt=vt tanh[(cvtt/m)]; the solution is x=(m/c) ln[cosh(cvtt/m)]. This is plotted in the second figure above; the smaller mass goes farther but after a long enough time, the two keep a constant distance apart.
-
For the second part of the problem, Newton's second law is mdv/dt=-cv2. Now, the velocity will begin with a speed v0 which is the speed at the end of the time interval in the first part. Without going into any detail the solution is v=v0/[1+(cv0t/m)]. This is plotted on the third figure above; the smaller mass clearly loses velocity more quickly as expected. To get the position as a function of time, we need to solve v=dx/dt=v0/[1+(cv0t/m)]; the solution is x=(m/c) ln[1+(cv0t/m)]. This is plotted in the fourth figure above; if the two start with equal speeds at the same place (which they do not), the larger mass would always be ahead of the smaller mass. However, there is a curious result if the drag force is of the form -cv2‚ÄĒbecause the position is logarithmic, the objects never stop moving so the question "which one will travel farther?" has no answer, each will go infinitely far. The "fix" for this situation is that the nature of the drag force changes for very low velocities and is better described as Fdrag=-bv which results in a solution like x=D(1-e-bt/m) which does have the maximum range of D for large t. I am not going to make this a three-step problem because at large enough times the velocities become so small that we might as well consider the objects to have stopped, knowing that they will certainly stop due to the changed nature of the drag.
-
To solve this problem analytically from here is probably not the most illuminating thing to do. I am going to just calculate a few numerical examples where I will choose
-
F=1 N, c=1 N·s2/m2, vt=1 m/s.
-
For the first part of the problem I will choose two different times, t1=0.5 s and t1=10 s; the first will be before terminal velocity is reached, the second has terminal velocity nearly reached by all.
-
For the second part of the problem I will choose a time such that v=0.001 m/s; these times turn out to be approximately equal numerically to the 1000m for my choice of parameters, e.g. it takes t≈1000 s for a 1 kg mass to reach v=0.001 m/s regardless of initial velocity.
-
I will calculate for three masses, 1 kg, 2 kg, and 5 kg.
-
The results are shown in the following table:
| m (kg) | t1 (s) | v (m/s) | x1 (m) | t2 (s) | x2 (m) | x1+x2 (m) |
| 1 | 0.5 | 0.462 | 0.120 | 1000 | 4.796 | 4.916 |
| 1 | 10 | 1 | 9.307 | 1000 | 6.909 | 16.216 |
| 2 | 0.5 | 0.245 | 0.062 | 2000 | 11.011 | 11.073 |
| 2 | 10 | 1 | 8.614 | 2000 | 13.818 | 22.432 |
| 5 | 0.5 | 0.0997 | 0.025 | 5000 | 23.061 | 23.086 |
| 5 | 10 | 0.964 | 6.625 | 5000 | 34.361 | 40.986 |
My earlier answer had an error, namely the time it takes to reach v=1 mm/s is not t≈m but rather t≈1000m. Now the answer to the question seems to clearly be that the more massive object goes farthest. Plotting the three cases for different masses below (choosing a t1 large enough that all masses have the terminal velocity), it is clear that at long enough times the largest mass will always be the farthest ahead at any given time. This conclusion is independent of the values of c or vt.
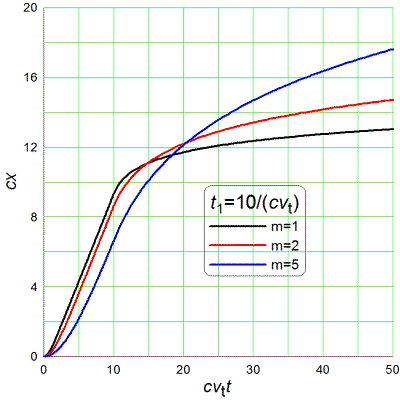
![]() ALTERNATIVE
SOLUTION:
ALTERNATIVE
SOLUTION:
An alternative solution, with F=-bv, is presented below. For a linear drag force it is shown
that the total distance traveled is independent of mass.
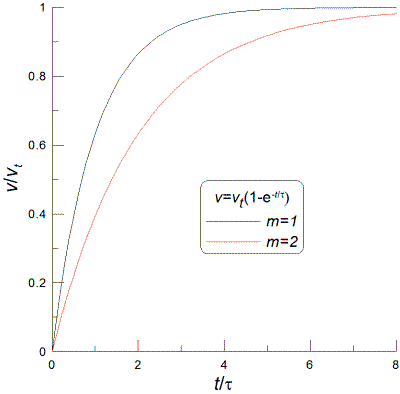
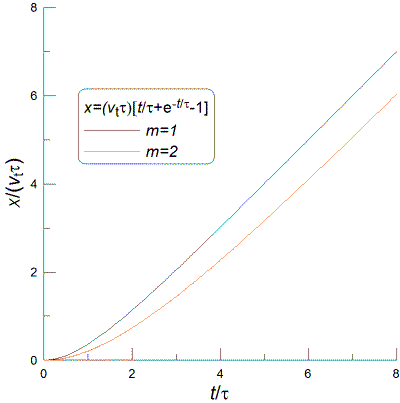
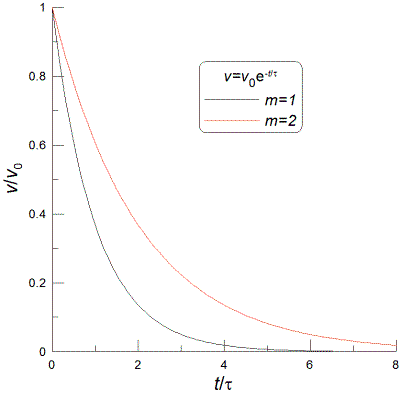
![]() ANSWER:
ANSWER:
I will assume that the drag force is given by Fdrag=-bv
where b is the same for both objects (as stipulated by the
questioner).
-
For the first part of the problem, Newton's second law is mdv/dt=F-bv. At large times the velocity will become essentially equal to a constant because F≈bv; this speed is called the terminal velocity vt=(F/b). Without going into any detail the solution is v=vt (1-e-t/τ) where τ=m/b is the characteristic time. This is plotted on the first figure above; the larger the mass, the longer it takes to reach the terminal velocity so, as noted by the questioner, the lighter mass will go farther in a given time. To get the position as a function of time, we need to solve v=vt (1-e-t/τ); the solution is x=vt[t-τ(1-e-t/τ)]. This is plotted in the second figure above; the smaller mass goes farther but after a long enough time, the two keep a constant distance apart.
-
For the second part of the problem, Newton's second law is mdv/dt=-bv. Now, the velocity will begin with a speed v0 which is the speed at the end of the time interval in the first part. Without going into any detail the solution is v=v0e-t/τ. This is plotted on the third figure above; the smaller mass clearly loses velocity more quickly as expected. To get the position as a function of time, we need to solve v=dx/dt=v0e-t/τ; the solution is x=v0τ(1-e-t/τ). This is plotted in the fourth figure above; if the two start with equal speeds at the same place (which they do not), the larger mass would always be ahead of the smaller mass. Here, unlike the quadratic drag case, the objects reach a maximum distance and so we do not need to make approximations regarding how far each goes. It now turns out that the problem can be done analytically quite easily. The maximum distance for the second part of the problem is for t=∞, so x2=v0τ with v0=vt(1-e-t/τ) where t is the time in the first part until the force is stopped. Now, x1=vt[t-τ(1-e-t/τ)] and so x1+x2=vt[t-τ(1-e-t/τ)]+vtτ(1-e-t/τ)=vtt. The distance traveled is independent of the mass.
![]() QUESTION:
QUESTION:
I am teaching a high school physics class and we are using the range
equation for projectile motion. Why isn't there two angles that would
work each time for this equation? The author only has us solving for one
angle but wouldn't there always be two angles that would work for the
same range?
![]() ANSWER:
ANSWER:
The range equation, R=2v02sinθcosθ/g
is not usually used to solve for the angles. However, given R and
v0, you could solve for θ. A little manipulation leads
to cos4θ-cos2θ+R2g2/(4v04)=0
which is a quadratic equation in cos2θ; there are
therefore two solutions for cos2θ and two positive
solutions for θ as you have correctly deduced. Note that if R2g2/v04>1
there are no real solutions.
![]() QUESTION:
QUESTION:
If you drop an egg and it crashes, it breaks.
If the egg is dropped and there is a platform going down below the egg, at the same speed as the egg, very slowly decreasing speed, until they touch (while falling), will the egg break?
![]() ANSWER:
ANSWER:
By making the platform move just a little slower than the egg
you are achieving the same thing as if you were to carefully put the egg on
a stationary surface‚ÄĒcausing the force between the two to be small. What causes
an egg to break? When it collides with the floor, the floor exerts a force
on it to cause it to stop. The more quickly the egg stops, the greater the
force it must experience. Of course, if the force gets too big, that is if
it has to stop too quickly, the shell will not be strong enough to withstand
it. To keep the egg from breaking, you may cause the time of the collision
to be longer. For example, drop it on a pillow and the egg will not break
because it takes longer to stop and so it experiences a smaller force. But,
there is another way to get a smaller force‚ÄĒif the egg is moving more slowly,
it does not to have such a large velocity change to stop. This is what
happens when you place the egg on a table and that is what happens if the
table is moving down with just a little less speed than the egg.

![]() QUESTION:
QUESTION:
Please settle a debate in my family: would it be possible for a human being to execute a one-armed iron cross on the still rings (gymnastics)?
![]() ANSWER:
ANSWER:
Technically possible, physically probably impossible. The
physics is that the torque exerted by your hand grasping the ring would have
to be equal and opposite the torque exerted by your weight. Let's say the
ring has a thickness of 5 cm (about 2"), the distance from your hand to your
center of mass is 1 m, and your weight is 650 N ( about 150 lb). Then the
torque due to your weight is (Tw=1 m)x(650 N)=650 N·m.
Your hand has a moment arm of 2.5 cm=0.025 m, so the torque your hand exerts
must be Th=650 N·m=Fhx0.025 where Fh
is the force your hand exerts on the ring, so Fh=650/0.025=26,000
N=5845 lb. Your gripping hand would have to exert a force of nearly 6000 lb
on the ring to keep you from rotating about your hand. I think that even if
you were strong enough to grip it tightly enough for there to be a 6000 lb
force, that force would rip ths skin off your hand or perhaps the squeeze
would break bones in your hand.
![]() QUESTION:
QUESTION:
When you put a candle on a spinning turntable, why does the flame point inwards?
![]() ANSWER:
ANSWER:
You can find a good explanation at
Big Site of Amazing Facts. The answer is very similar to an
earlier answer of mine.

![]() QUESTION:
QUESTION:
I teach Jr. High science. I have a question that I need help with when explaining it to some of my SPED students.
If you were playing football on the moon, would it be as hard to stop a 150 kg lineman as it would be on the Earth?
![]() ANSWER:
ANSWER:
I would say that it would be easier to lift him but just as
hard to stop his forward motion. On the moon you weigh less; the 100 kg man
would weigh about 330 lb, but because gravity is about 6 times weaker on the
moon, he would only weigh about 55 lb. But to stop him, you are not stopping
his weight, you are stopping his mass and his mass is still 150 kg. You need
to impress on your students the difference between weight and mass. Weight
is how hard gravity pulls on a mass but mass is a measure of inertia, how
hard it is to stop something from moving (or to start it moving).
(The following is probably too abstract for your students, but I include it for completeness. The force which stops the advancing runner is actually the friction between your feet and the ground. For example, if you were standing on very slippery ice it would be much harder to stop him. The friction between you and the ground is proportional to your weight, so you have less friction on the moon resulting in less ability to stop the runner.)
![]() QUESTION:
QUESTION:
Hello, my teacher and I had a bit of a bicker. A man is driving a truck
and is on the highway going 70 MPH. Another driver is going 70 miles per
hour with the same truck. They hit each other and my teacher believes it
will be as if the truck hit a stationary object at 140 MPH, and I said
and argued that it would still be as if it hit a stationery object at 70
MPH. Who is right? I saw Mythbusters (The Discovery TV show) do test on
it and that is how I got my answer.
![]() ANSWER:
ANSWER:
The problem is that the situation is not fully enough
described‚ÄĒ"‚Ķas if the truck hit‚Ķ" is not defined, what does that mean? The
important idea here is Newton's second law, F=m(Δv/Δt)
where F is the average force experienced by mass m during the
time Δt which the collision lasted and Δv is the change
in velocity during that time. Also useful is conservation of momentum for a
collision (which is actually just Newton's second law in disguise); momentum
is the product of mass times velocity and the sum of all the momentum
after the collision must equal the sum of all the momentum before the
collision. I
will give you two scenarios:
-
The collisions are perfectly inelastic (which means colliding objects stick together) and the "stationary object" is a wall of essentially infinite mass (like a really thick stone wall or a really big tree). This means that all objects come to rest after the collision. The force experienced by anything depends on how long the collision lasted, so we need to stipulate that the collisions last the same time. For this scenario, the force felt by the 140 mph truck would be twice as large as the force felt by the 70 mph truck. This is a situation where you are right.
-
 The collisions are perfectly inelastic and the
"stationary object" is the other truck. Again, assume that the
collisions last the same time. In this situation, the trucks are not at
rest after the collision if one truck is parked before the collision.
You can (neglecting any friction) easily calculate their speeds after
the collision using momentum conservation: 140M=2Mv, so
v=70. But, note that the change in speed for either truck for either
collision is 70 mph, so this is a situation where your teacher is right.
The collisions are perfectly inelastic and the
"stationary object" is the other truck. Again, assume that the
collisions last the same time. In this situation, the trucks are not at
rest after the collision if one truck is parked before the collision.
You can (neglecting any friction) easily calculate their speeds after
the collision using momentum conservation: 140M=2Mv, so
v=70. But, note that the change in speed for either truck for either
collision is 70 mph, so this is a situation where your teacher is right.
Remember, in science you can only argue intelligently if the subject of the argument is well-defined!
![]() QUESTION:
QUESTION:
The earth orbits around the sun because it has angular momentum. If we stopped the earth in orbit and then let it fall straight towards the sun, how long would it take to reach the sun in seconds?
![]() ANSWER:
ANSWER:
The questioner sent me a bunch of data about the masses of
the sun and earth, the radius of the earth's orbit, and Newton's universal
constant of gravitation. But, you do not need any of that stuff‚ÄĒall you need
to know is
Kepler's first and third laws and the fact that the period of earth's
(approximately circular) orbit is one year.
-
Kepler's first law states that the orbit of a planet is an ellipse with a semimajor axis a and with the sun at one focus of the ellipse. A circular orbit has a semimajor axis equal to the radius of the circle, so a1=RE where RE is the radius of the earth's orbit; the eccentricity of a circle is 0. The other extreme is an ellipse with eccentricity 1 which is a straight line from the sun to the earth and so the semimajor axis for a "dropped earth" is a2=RE/2. Of course, this is not an orbit you will actually see in nature because there is no such thing as a point mass and the speed of the earth when the two point masses coincide would be infinite, but if we can cleverly deduce the period of this orbit, one-half that period will be the answer to your question.
Kepler's third law states that the square of the period T of an orbit is proportional to the cube of its semimajor axis, so T12/T22=a13/a23=RE3/(RE/2)3=8. So, T2=T1/√8=0.354 years. So, the time to go half a period is 0.177 years=64.6 days. I will let you put that into seconds.
I am not sure I would say that the earth orbits the sun is because it has angular momentum. True, it has angular momentum, but the reason is that the sun exerts a force on it. Technically the straight line path is an orbit, but it has no angular momentum.
![]() QUESTION:
QUESTION:
I am curious about something that I just read in
an earth science book about the shape of the Earth. Since the polar
circumference is less than the equatorial circumference, the Earth is
an oblate spheroid. The authors attribute this shape to centrifugal
force caused by the Earth's acceleration. However, I thought that
centrifugal force was not a real force, but was instead due to a mass's
inertia resisting the acceleration. Am I misunderstanding the concept?
Thanks for helping me resolve this conundrum.
![]() ANSWER:
ANSWER:
(This is sort of a
long-winded answer, but I want to have an explanation of centrifugal
and fictitious forces I can later refer to.) Centrifugal force is what
we call a fictitious force. In an accelerating system, Newton's laws
are not true. For example, if you are inside a big rotating drum you
feel a force pushing you into the wall, right? Well, actually you do
not; what you feel is the wall pushing you toward the axis of the drum.
Your brain is trained mostly in nonaccelerating systems (moving with
constant velocity) and so it wants to use Newton's first law which says
that if an object is at rest the forces on it must add to zero; to make
Newton's first law true (you are at rest in your system which is
accelerating), your brain invents a force equal and opposite the
centripetal force. This is called the centrifugal force and it does not
really exist. A fictitious force is one we invent to force Newton's
laws to be true in an accelerating system. Just because it does not
exist does not mean that we cannot do physics with Newton's laws using
it. If the accelerating system is a centrifuge, it works, doesn't it?
The heaviest stuff is "pushed out" by the centrifugal force is true
even if centrifugal force is just something we made up to make
calculations easier. The rotating fluid earth is a little complicated,
but I think that it is pretty intuitive: a ball of putty (or pizza
dough) made to rotate faster and faster will stretch out into a pancake
and you can say it is the centrifugal force which is causing it. A
simpler case of "centrifugal stretching" is the following. A spring is
attached to a nail at one end and a mass at the other. If you make it
rotate about the nail, the spring will stretch out just the right
amount so that the force of the spring will provide the necessary
centripetal force. But if you make it go faster, a larger force will be
required and so the spring will have to stretch more to do that. That
example is easy to see without centrifugal force, but if you view it
from the perspective of the rotating mass, you will say the centrifugal
force pushes you out.
![]() QUESTION:
QUESTION:
In a newton's cradle(which has usually 8 bobs or balls)if i let 5 balls bang on the other 3 balls then after collision 5 balls would move on the other side.Why 5 balls are moving and not three balls?
Both energy (–ÖΣmv2) and linear momentum (Σmv) must be conserved where Σm is the mass. Suppose that 5 come in and 3 go out. Then momentum conservation says 3m0u=5m0v (where v is the speed of the balls coming in, u is the speed of the 3 balls going out, and m0 is the mass of one ball). So, u=(5/3)v. So now, the energy of the incoming balls is –Ö(5m)v2=2.5v2 and the energy of the outgoing balls is –Ö(3m)u2=–Ö(3m)((5/3)v)2=4.17v2; so energy would not be conserved. The only way to have both energy and momentum conserved is to have the same number of balls going out as went in.
![]() QUESTION:
QUESTION:
Two balloons that have the same weight and volume are filled with equal amounts of helium. One is rigid and the other is free to expand as the pressure outside decreases. When released, which will rise higher? Why?
On each balloon there are two forces‚ÄĒits weight (which makes it want to fall) and the buoyant force on it (which makes it want to rise). The weights are the same and never change. The buoyant force is proportional to the volume, so whichever has the greater volume has the greater buoyant force. The expanding balloon wins.
![]() QUESTION:
QUESTION:
In case one I accelerate an apple to one mph. It requires x amount of work to accelerate the apple by one mph.
Next I accelerate the same apple by another one mph. This requires the same amount of energy as in the first example, ie the energy necessary to accelerate one kg by one mph.
Thus I have expended twice as much energy to accelerate from one mph to two mph. But the apple now has 4 times as much energy.
I would so much appreciate an explanation in laymen's terms. I must be really stupid. I just cannot see the logic.
No, you're not stupid; it is a little subtle. Energy is not what we call an invariant quantity, that is the kinetic energy something has depends on the frame from which you observe it. What your thought experiment does is shift frames for the second acceleration; you have put yourself in a frame where the object starts at rest. When you do this, you move into a frame where the apple is at rest, that is has zero energy. Therefore, your second experiment is nothing more than a repeat of your first experiment. If you calculate the work you have to do in the original rest frame to accelerate the object from speed v to speed 2v you will find W=–Öm(3v2) which then leads to the correct total energy and work of –Öm(4v2).
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
This is what I have trouble understanding. Assuming no friction or wind force, etc. it requires x amount of fuel to accelerate a car by 1 mph, and x amount of fuel for each additional 1 mph. Thus change in velocity is directly proportional to energy input. But change in kinetic energy is proportional to the square of change in velocity. Energy input should equal the change in kinetic energy of the car, but apparently does not. I know there is a basic flaw in that reasoning, but where is it?
It does not take the same amount of fuel to accelerate the second 1 mph. It is a little tricky to talk about a car where it is actually the force of friction of the tires which push the car forward to accelerate it. That is were the work is done on the car, a forward force F which is constant if you are accelerating at a constant rate. Now, if the car starts at rest and increases its speed at a constant rate to speed v, how far, d, has it gone? Well, simple kinematics tell us that d=–Ö(F/m)t2 and v=(F/m)t, so d=–Ö(F/m)[mv/F]2=[–Ömv2]/F. Therefore, the work F does to bring it to v is W=Fd=–Ömv2. Now, let's calculate the work F must do to increase the speed from v to 2v. The new distance traveled, d', is d'=vt+–Ö(F/m)t2 with 2v=v+(F/m)t => v=(F/m)t; note that the time the force acts is the same but the distance over which it pushes is larger, so more work is being done. If you do the algebra here (put t=mv/F into the d' equation), you will find d'=3d. It takes three times the energy to increase the speed by another 1 mph in your example. I suspect you are still bothered! And I think I can say why. If you burn fuel at a constant rate you will not accelerate at a constant rate; to accelerate at a constant rate you have to increase the rate at which you burn fuel as you go along. If you burn fuel at a constant rate, the time for the second 1 mph gain will be longer than for the first 1 mph; and guess how much‚ÄĒexactly 3 times longer! (I always go that extra mile for folks nice enough to make a donation!)
![]() QUESTION:
QUESTION:
if a water-filled container's weight with an object in it is equal to
the container plus the buoyant force on the object if it has not sunk,
Why then does the buoyant force point opposite to the direction of the
weight of the container? Would you then not subtract the buoyant force
from the weight of the container to get the total weight?
Aha, you make the classic mistake made by thousands of physics students going before you‚ÄĒyou are not focusing on one body at a time. Let me run through the various possible scenarios here and see if you understand.
- Look at the object. What are the forces on it? Its weight w down and a force b which the water exerts on it, up. (We call b the buoyant force.) Newton's first law (N1) requires b-w=0, so b=w.
- Look at the container and water. What are the forces on them? Their weight W down, a force N from the scale they are sitting on, up, and a force f which the object exerts on the water. Newton's third law tells us that f=b and points down. N1 now tells us N-W-f=0=N-W-w, and so N=W+w. There is the answer to your question‚ÄĒthe scale reads the total weight. But let's look at another possibility.
- Look at the container and water and object all together. The forces are the weight, W+w down, and the force of the scale N up. The buoyant force does not come into it at all because the forces the water and object exert on each other are internal forces and cancel out (or, b-f=0). So N1 tells you that N=W+w. Again, there is your answer‚ÄĒthe scale reads the total weight.
![]() QUESTION:
QUESTION:
Tie an object such as a pencil eraser to a string. Use the
string to swing the object around your head at a constant speed. Can the
object be swung so that the string is parallel to the horizontal, flat,
and even floor on which you stand?
No. The reason is that the object must in equilibrium in the vertical direction since it has no vertical component of its velocity (or acceleration), so the forces in the vertical direction must add to zero. One force in the vertical direction is the weight, straight down. There must be another force which points up and is equal in magnitude to the weight; this can only be the vertical component of the tension in the string and a horizontal string has no vertical component of its tension.
![]() QUESTION:
QUESTION:
a co-worker of mine was describing a time where he threw a box weighing about one hundred pounds out of a window on the eighth floor of a building. In an effort to dramatize the story a little, he wanted to express to us how forceful the impact was of the box on the ground below. he mentioned what I considered to be a rather dubious rule-of-thumb: an object's weight doubles for every foot it falls. At home in the evening I relayed the story to my roommates, and we discussed how unlikely it was that this was true--just for being such a simple, neat multiplier. Our subsequent research on the internet (involving many formulas, calculators and conversion charts) seemed to (roughly) confirm his statement. Being poor physicists, we are open to believing the calculations, but, perhaps as good scientists, we continue to doubt. Can you help? As a general rule-of-thumb, does his statement hold any water: does an object's "weight" double for every foot it falls?
I must have written this a hundred times‚ÄĒthe weight of something is the force that the earth pulls on it. The weight of the box is the same no matter where it is dropped from (unless the height is not small compared to the size of the earth). So, what might he be trying to say? Suppose we ask how much force would be needed to stop the box in a distance of, say, one foot. The work to stop an object with an energy of 500 ft-lb is equal to 500 ft-lb; so, to stop a 1 lb box which has an energy of 500 ft-lb, you would have to exert a 500 lb force to stop it in a distance of 1 ft (work is force times distance). To acquire this energy, it would have to be dropped from 500 ft up; the energy something has at the ground is proportional to how high you drop it from, so it has twice as much energy than if you had dropped it from 250 ft. Clearly, the energy does not double with every foot, so I don't know what he means about doubling every foot of fall. With every foot of fall a 1 lb box increases its energy by 1 ft-lb.
![]() QUESTION:
QUESTION:
I am in the 8th grade. I am doing a project for my science class on the physics of arm motion in swimming. Can you give me some information? I get extra credit if I get information from a professional.
I do not quite know what you want. Here is something: what is it that pushes you forward? Is it your arm? No, it is the water that pushes you forward. Here is how it works. When you move your arm backwards under the water toward your feet, you are pushing on the water, pushing it backwards. Newton's third law says that if one object (hand) exerts a force on a second object (water), the second object (water) exerts an equal and opposite force on the first object (hand). Therefore, the water pushes you forward.
![]() QUESTION:
QUESTION:
This question may sound trivial, but please bear with me. Assume a
person is standing on Earth and is going to be hit by a very large
object. Let's say there was a large object (with a large mass) and it
started accelerating towards you from a foot away at a rate of about 1
foot/second. The mass of the object is such that the gravitational force
between the person and the huge object is negligible compared to the
gravitational force of Earth. If the acceleration is extremely small,
will the huge mass of the object coming in contact with the person be
enough to send the person flying?
The acceleration is irrelevant, it is the speed at the instant it hits you that matters. "Send the person flying" is not a very quantitative statement. Let's just talk about your speed after the collision. Let your mass be 100 kg (about 220 lb) and you are hit by a freight train with a hugely bigger mass. Two extremes:
-
Perfectly inelastic, you "stick" to the locomotive so your speed is equal to the speed of the train, v. The collision will happen in a relatively short time, call it t. Your average acceleration is then v/t so the force you experience is mv/t. If v=0.1 m/s and the time of collision is 0.1 s, you would experience a force of about 100 N, about 22 lb. No big deal. But, as v gets bigger or t gets smaller the force gets bigger.
-
The other extreme is a perfectly elastic collision where you are moving on your own after the collision (and have done so conserving energy). In this case your final speed will be about twice the speed of the train, 2v. So the force over the collision time will be about twice as large.
The bottom line of my answer is that if you are hit by a big thing going very slowly you will probably not get hurt badly.
![]() QUESTION:
QUESTION:
My question is about fluid dynamics.
What is the relationship between the drag coeffient and the reynolds number? Based on my research I've been able to establish that for low reynolds numbers (which is what I'm interested in) the relationship is inversely proportional and defined as:
Cd=24/Re
This took some research on my part! The Reynold's number is Re=ρvL/μ where ρ is fluid density, v is speed of an object relative to the fluid, L is a length characteristic of the situation, and μ is the viscosity of the fluid. Drag coefficient is CD= 2FD/(ρv2A) where A is the area presented normal to the flow and FD is the drag force. To relate these, we must choose a specific example, typically a sphere at relatively low velocity for which the drag force may be written as FD=6πμRv and the characteristic length is the diameter, L=2R. Putting in that A=πR2, simple algebra leads to ReCD=24.
![]() QUESTION:
QUESTION:
Could you explain why the driver of a car must keep her foot on the
accelerator to maintain a constant speed and therefore why energy is
needed to maintain the cars speed??
Wouldn't it be great if we could have a car which had no energy loss? Unfortunately, the world has forces which we cannot avoid which take energy away from something moving along. These fall into the category of frictional forces: a spinning wheel has friction in its bearings which will eventually cause it to stop; an object moving thought the air has air resistance which will eventually stop it as it moves along; the tires are not perfectly elastic and as they roll they are being continually deformed and undeformed and energy is lost. Without all these forces, we could accelerate up to speed and disengage the engine from the wheels and turn it off and just cruise. However, one can work hard to minimize these forces in the design of cars; making the cars aerodyamic, reducing the weight, and other tricks can minimize the energy we lose.


![]() QUESTION:
QUESTION:
Do you know why do golf balls have dimples? (does it make them more aerodynamic and if so why?)
![]() ANSWER:
ANSWER:
I am The Physicist, I know everything! Well…maybe
not everything. I do know why golf balls are dimpled and the reason is
also why tennis balls are fuzzy. Aerodynamics can be very complicated,
but I can explain it qualitatively. Air drag on a projectile is caused
mainly by the turbulent wake behind the object; the pressure is lower in
this turbulent region so there is more force on the front pushing back
than there is on the back pushing forward. As shown in the figure to the
left, if the air moves smoothly over the ball, the turbulent wake is
very broad. But, if you break up the boundary layer of air with some
kind of roughness on the surface, you get a much smaller turbulent wake
and therefore less drag, as shown in the figure to the right. It is
counterintuitive that a rough ball encounters less air drag than a
smooth one, but true.
![]() QUESTION:
QUESTION:
I dont completely understand newton's third law of motion.. It says every action, there is an equal and opposite reaction, but when we apply force to a book, why doesnt the book apply the same force to us? And why are we able to push the book wherever we want, if, according to third law of motion, book should also have an equal reaction force?
The book does exert an equal and opposite force on you. So, why does the book move and you do not? There are several reasons. First, you have much more mass than the book does and so your force on the book has a much bigger effect than its force on you (Newton's second law, a=F/m). Second, there is friction between you and the floor which can be much bigger than the force the book exerts on you, so you do not move; but the friction between the book and the table is normally less than the force you apply to it, so it does move. Imagine that the book is nailed to the table and you are standing on a floor which is very slippery ice. Now, when you push on the book, it will be you who moves. Or, if you and the book were in empty space and you threw it (by exerting a force on it), you would recoil (with a much slower speed) because of the book's force on you.
![]() QUESTION:
QUESTION:

An old type car antenna, often called whip aerial , moves back and forth when the car is moving but when you speed up it seem to oscillate in figure 8 motion. Why is that?
Vibrating systems have different modes of vibration. The prettiest example I could find is some of the modes of a drum, shown above. A real drum will have all its infinite modes going on simultaneously but some will play a more important role than others depending on how the drum is excited. The leftmost one above is called the fundamental and would be the primary one if the drum were struck right in the center; the center of the drum in this case is called an antinode, a place which has maximum amplitude. The right-most one above is another higher mode which, you will note, has the center of the drum not moving; this is called a node and would probably not contribute much if the drum were struck in the center. Your antenna, when just going back and forth, is mainly in its fundamental mode. But when you go a different speed you are doing the equivalent of striking the drumhead somewhere other than its center and exciting a higher mode.
![]() ANSWER ADDED LATER:
ANSWER ADDED LATER:
I found modes of a beam which should be analogous to your specific
problem. Is the second mode similar to your "figure eight"?


![]() QUESTION:
QUESTION:
A friend of mine and I have an argument over what is a faster sport tennis or badminton. The criteria is how fast it would take to serve a tennis ball/shuttlecock from one side of an olympic sized tennis/badminton court to the player waiting on the other side assuming that both are standing on the out of bounds line. We are assuming ideal conditions and that the players in both cases are equally strong and fast.
![]() ANSWER:
ANSWER:
You may not realize it, but your question is mostly about air drag on
projectiles. I seem to get more questions about air drag than just about
anything else except maybe variations of the twin paradox. Maybe that is
because it is perhaps the most important phenomenon mostly swept under
the rug in most elementary physics courses. There are several instances
of earlier questions involving
baseballs and
lacrosse balls
which are very similar to this one. For
high speed projectiles, air drag is very important; e.g., a 100 mph
baseball loses about 10 mph by the time it crosses the plate.
Approximations have to be made to quantify the situation you are
interested in, but I feel the results I will present are pretty close to
what happens on the court. (The following is probably way more detail
than you want, but I put it here for anybody who might be interested.)
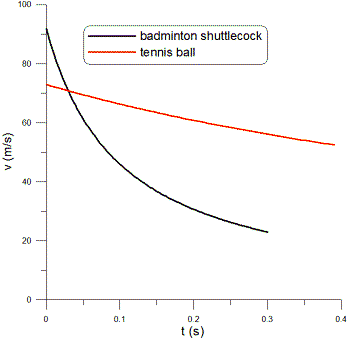
The approximations are:
-
I neglect gravity because the times involved are are sufficiently short that the ball/shuttlecock will not fall far or very much change its vertical speed.
-
I assume that the drag is proportional to the square of the speed‚ÄĒtwice the speed, four times the force of drag. This is an excellent approximation for these speeds, these objects.
-
The form of the force I use is F≈—ėAv2 where A is the cross sectional area presented to the wind. Here A=πR2 where R is the radius of the ball or the outer circle of the feathers. This probably slightly overestimates the force for the tennis ball (whose "hairs" have the function of decreasing the drag) and underestimates it for the shuttlecock (whose "feathers" are designed to increase drag).
-
Data for tennis:
-
v0=73 m/s=163 mph
-
R=0.032 m=1.26 in
-
m=0.057 kg=2 oz
-
back line to back line distance: 24 m
-
-
Data for badminton:
-
v0=92 m/s=206 mph
-
R=0.025 m=1 in
-
m=0.005 kg=0.18 oz
-
back line to back line distance: 13.4 m
-
I used the fastest recorded serves for the velocity off the racquets, v0. If you integrate F=ma, you get the following solutions: v=v0/(1+kt) and x=(v0/k)ln(1+kt) where k=—ėAv0/m. Here are the results:
-
The tennis ball takes 0.39 s to travel the distance, arrives with a speed of 62 m/s (139 mph), a loss of 11 m/s (24 mph).
-
The badminton shuttlecock takes 0.30 s to travel the distance, arrives with a speed of 25 m/s (56 mph), a loss 67 m/s (150 mph).
I will leave it to you to argue about what these numbers tell you about which "is the fastest sport". The shuttlecock starts off the fastest because is has a smaller mass and can therefore have a larger acceleration from the force from the racquet. But it slows down very rapidly mainly because of its small mass. The graph shows the speeds as functions of time.
![]() QUESTION:
QUESTION:
A rollerblader leans into a turn as he moves in a circle. The net torque about any point in the rollerblader must be zero if the rollerblader is not to fall over. If the torque is computed about his center of gravity, then the torque caused by the normal force of the ground up on his wheeels is balanced by the torque due to the centripetal force of static friction of the ground on his wheels. If these torques are computed about the contact point of the wheels on the ground, however, there seems to be a non-zero, net torque due to his weight since the normal and static friction forces act through the contact point and would not contribute to the torque about this point. The moment of inertia of the wheels negligable. How can there (seemingly) be a net torque about the contact point and none about the cg?
P.S. I submitted this question to the "Mad Scientists Network" and the engineer who answered it said there was an outward, "righting" force that acts through the cg. He did not state the nature of this force but it sounded suspiciously like he was thinking of centrifugal force. This didn't seem right to me. I want to know how a physicist would explain this.
![]() ANSWER:
ANSWER:
Hey, guess what: the engineer got it right! He just didn't give you a
complete enough explanation, and you deserve one! Ask the Physicist
goes where other Q&A sites only dream to go! Enough silliness, here it
is. Newton's laws are not valid in accelerating frames of reference and
you are attempting to apply Newton's first law (N1) (the sum of all
torques equal zero is the rotational equivalent of N1) to the skater who
is accelerating because he is moving in a circle. If he were not
accelerating, i.e. moving in a straight line and leaned over he
would fall. The best way to deal with accelerating systems like
this is to do a trick which inserts forces which do not exist to force
Newton's laws to be true; these are called fictitious forces. In this
case you must add a fictitious force which points away from the center
of the circle, acts at the cg, and has a magnitude equal to the
centripetal force; this is called the centrifugal (Latin root center
fleeing, fugo is I flee) force. Then everything works out and he is
in "equilibrium" in his accelerating frame.
![]() QUESTION:
QUESTION:
I just recently had an argument with an engineering friend of mine and was hoping you could help settle it as we tend to end up at an impasse when it comes to disagreements like this.
The argument involves human body falling at terminal velocity and landing back first on various materials.
He is of the opinion that landing on cement will ultimately cause less damage to the body than landing on soft loosely packed soil. He bases this on the idea that the speed of sound through something as dense as cement is faster than the speed of sound moving through something as dense as flesh and that this somehow imparts a greater ability to absorb an impact and therefore will do less damage to the body than loosely packed soil.
I am of the opinion that the soil is able to shift its position under pressure and able to be compacted into a denser form than its current state and that this allows it to better absorb the impact (than concrete would) which reduces the damage done to the object hitting it.
He argues that this is only the case in low speed impacts and that in a high speed impact at terminal velocity the concrete would be the better material to land on.
So, which material would you expect to do the least amount of damage to an object with roughly the same density as water that hits it at terminal velocity and why?
![]() ANSWER:
ANSWER:
That is just about the craziest thing I ever heard! What hurts you when you
stop is the force you feel. If you feel a large force, you are hurt; if
the force you feel is small, you shrug it off. So the trick is to
minimize the force. One way to write Newton's second law is that
mΔv=Ft
where m is the mass,
Δv is
the change in speed, F is the average force, and t is the
time during which F acts. (The physics way to say this is that the change in
momentum is equal to the impulse, mv being momentum and Ft being
impulse.) So, letting your mass be about 100 kg and your terminal
velocity be about 50 m/s, F=5000/t. Clearly, the bigger
you make the collision time t, the smaller F will be. If
you hit concrete you stop very quickly, say a hundreth of a second, so
the force you feel is 500,000 Newtons, about 112,000 pounds. If you
could make the collision last 1 second, for example by landing in a
swimming pool full of shredded foam rubber, the force would be 5000
Newtons, about 1100 pounds, which you would probably survive.
![]() QUESTION:
QUESTION:
If your riding a motorcycle, going 55 miles per hour, and it is 75 degrees outside, what is the temperature of the air that you feel on your skin? I ride a motorcycle and I know that there is a formula but I just don't know what it is and I hope that you have the answer.
![]() ANSWER:
ANSWER:
You must be referring to the wind chill index which attempts to
quantify how cold it feels at a certain temperature and wind speed. I
find that it is not defined for the situation you want‚ÄĒ
750F
just never feels cold, I guess. It is only defined for temperatures
between -450 and 450. Read all about it at
NWS.
![]() QUESTION:
QUESTION:
if you shoot a gun towards the back of the train and the bullet goes 2000 miles and hour in a train thats going 2000 miles does the bullet stop? what would happen?
![]() ANSWER:
ANSWER:
For questions like this I always start with "…you
must specify the velocity relative to what…" You would see the bullet
travel toward the back of the train with a speed of 2000 mph but
somebody standing by the side of the tracks would see the bullet
standing still.
![]() QUESTION:
QUESTION:
I am a 8th grade physical science teacher and I want to be sure about my understanding of action/reaction forces before explaining it to my students.
My students recently completed a ‚Äėballoon rocket activity‚Äô where they calculated speed and identified and described the action/ reactions forces involved. Here are my two possible explanations. Which one is correct?
#1 action force-the air in the balloon exerts a force on the air in the room as it is released, reaction force-the air in the room pushes on the air coming out of the balloon causing motion
#2 action force-balloon pushes on the air in the balloon (forcing it out), reaction force-the air in the balloon pushes back on the balloon causing motion.
I do understand that action/reaction forces involve two objects and do not cancel. I tried to relate the balloon’s behavior to that of a rocket when launched to space.
![]() ANSWER:
ANSWER:
The balloon would work perfectly well in a vacuum. Hence, the room air
has nothing to do with it. Your #2 is the correct view. The balloon
pushes the air and the air pushes with an equal and opposite force on
the balloon. When you say that they "do not cancel", that means that
they do not cancel if you look at one body or another. But if you look
at the two or more bodies as a whole, all the Newton's third law forces
do cancel out. That is why when an artillery shell explodes the center
of mass continues moving in a parabola even as the pieces fly apart. It
is particularly important not to consider any pair of equal and opposite
forces to be due to Newton's third law. For example, my weight is a
force 200 lb down and the floor exerts a force up on me equal to 200 lb.
These are due to Newton's first law, not the third; you seem to
understand that when you say the forces "involve two objects". Any two
forces on an object which are equal and opposite cannot be Newton's
third law forces. For me on the floor, the floor exerts a force up on me
and I exert an equal and opposite down on the floor‚ÄĒthat
is Newton's third law.
![]() QUESTION:
QUESTION:
Alright - hopefully you can help me clear up my issue with this concept. I made up this question for some students and I understand how the math works, but why it does is beyond me - hope you can help!
A man who jumps straight up with an initial velocity of 3.70 m/s (enough a person with a 2.36 m reach to jump and touch the rim on a 10 ft hoop: 3.05m high) will travel up the 3.05 m. Easy math, easy understanding. What is hard to understand is how if that man was to run horizontally with that same speed (3.70 m/s) how he would also be able to reach that same height? This is PE=KE stuff and also easy, just hard to believe. Do you have a way you could better explain this? It just seems even in a perfect world with no wasted energy that some of the energy would not be enough compared to just jumping straight up. Instead of all of the velocity being concentrated in one direction (up), its broken into 2 components going up and out. I know energy does not have vectors, but it still baffles me - thanks!
![]() ANSWER:
ANSWER:
The problem, I think, is that PE=KE simply does not get it except for
the simplest problems. The way to view it is (PE+KE)before=(PE+KE)after.
So, choosing the ground as PE=0, the first problem has PEbefore=0
and PEafter=mgh=9.8mh,
KEbefore=–Öm(3.7)2=6.85m
and KEafter=0, so 6.85m+0=0+9.8mh or h=0.70
m; add to that your 2.36 m reach and you get 3.06 m. In your second
(more puzzling to you) problem, you still need to get to h=0.70
m, but you start with a horizontal component of your velocity vx=3.7
m/s. But to go up, you must give yourself a vertical component of your
velocity of vy. When you get to the top you do not
have zero kinetic energy, but the kinetic energy due to your horizontal
velocity (which never changes). So the way to set it up is KEbefore=–Öm[(3.7)2+vy2],
KEafter=–Öm(3.7)2, PEbefore=0, PEafter=(9.8)(0.70)m.
If you put this all together, you will find that you need a (suprise!)
vertical component of velocity of vy=3.7 m/s.
![]() FOLLOWUP QUESTION:
FOLLOWUP QUESTION:
Alright I left a crucial part out of my last question about the vertical jumping velocity and the horizontal running velocity. The velocity that the man jumps vertically with 3.7 m/s allows him to reach up to the 3.05 m rim. The second man runs horizontally - grabs a rope (pendulum) - and this should take him up to the same height given his same reach. The first problem you can do like you said with the potential and kinetic energies or constant acceleration formulas. The second I can do as well. I'm ok on the math, i just don't know how that could be? The first man is directing all of his energy in one direction while the second man is grabbing a rope which would take him both vertically AND horizontally. How can the same velocity get that man to travel the same vertical height but in the second case - a further distance?
![]() ANSWER:
ANSWER:
The method is still the same. But now he starts with a velocity of 3.7
m/s and ends (at the top of the swing) with zero velocity. So, applying
(PE+KE)before=(PE+KE)after, (0+–Öm(3.7)2)=(9.8mh+0).
Note that this looks just like your first problem‚ÄĒit starts out with all
kinetic and ends up with all potential energy. The shape of the path is
irrelevant, i.e., if it starts at the ground with some speed and ends up
somewhere else at rest, then it makes no difference how it got there.
Don't worry about the "further distance" because no energy is lost or
gained by the horizontal motion.
![]() QUESTION:
QUESTION:
You have a long rope. You tide it into a tree and go walking around the world. When you come back to the tree from the other side. You push the rope tight and untide it from the tree and and tide the ropes together. Is this possible, or will it float.
![]() ANSWER:
ANSWER:
Sorry, this could not possibly work with a real rope. For one thing, the
rope would sag under its own weight before you got to the horizon from
the tree. But, just suppose you had this rope in a circle a few meters
above the ground and all the way around the world. Look at a small piece
of the rope and see if it is in equilibrium. There is its own weight,
straight down, and the tension in the rope pulling left and down and
right and down. No forces up, so how could that little piece of the rope
be in equilibrium?
![]() QUESTION:
QUESTION:
If you stopped an Earth satellite dead in its tracks, it would simply crash into Earth. Why, then, don't the communications satellites that "hover motionless" above the same spot on Earth crash into Earth?
![]() ANSWER:
ANSWER:
Because they only appear to hover motionless. Don't forget, the earth is
spinning around once every 24 hours. The period of a communication
satellite is 24 hours, it is not standing still.
![]() QUESTION:
QUESTION:
it's a question the answer to which I wish to use as an analog when I make (always free) talks to citizen (and other) groups regarding homelessness; and specifically in response to the complaint by some in the audience that the homeless need to just pick themselves up by their own bootstraps and stop being a burden on society. I keep trying to explain to them that once one has fallen all the way down (as opposed to just tipping over a little, or even falling to one's knees; and especially once they've slipped so through certain kinds of society's cracks), it actually takes more effort to get back up again than it took to knock the person down. (And, trust me, it does.)
[The Physicist: The questioner wishes to compare the energy
necessary to tip over a cylinder of radius R whose center of
gravity is a distance h above the floor to the energy required to
lift it back up.] What is the amount of
energy needed to tip it over from vertical to horizontal compared with
(versus) the amount of energy needed to pick/tip it back up and make it
vertical again? I'm looking for a ratio.
![]() ANSWER:
ANSWER:
To tip it over, you have to move the center of gravity (COG) so it is above
the point on the floor where the cylinder touches the floor; to do this
you must raise the COG a distance
h[√(1+(R/h)2)-1]. The work necessary to
do this is Wfall=mgh[√(1+(R/h)2)-1].
If R is much smaller than h, this may be approximated as
Wfall≈–Ömgh(R/h)2. The
work necessary to lift it back up is Wlift=mg(h-R).
Again, if R is much smaller than h, Wlift≈mgh.
So, the ratio is Wlift/Wfall≈2(h/R)2.
For example, if h=5R, Wlift/Wfall≈50;
it takes 50 times the work to lift as to push over!
![]() QUESTION:
QUESTION:
Does an object immediately start to lose speed once an unbalanced force stops acting on it? For example, does a baseball achieve its highest speed at the exact moment it leaves the pitcher's hand and then begin to slow down due to air resistance or is there a period of time after it leaves the pitcher's hand when it might actually pick up speed before beginning to slow?
![]() ANSWER:
ANSWER:
You have to look at all the forces in a given problem. The mass will
always respond instantaneously to whatever forces are on it at the
moment. After a pitched ball leaves the pitcher's hand, the hand has
nothing to do with what happens thereafter. The important forces on it
are its own weight (gravity) straight down, and whatever air drag does
to it. Air drag is
pretty significant on a baseball‚ÄĒa
95 mph fastball loses about 10-15 mph by the time (about –Ö second) it
gets to the plate. So the instant it leaves the pitcher's hand, it
starts speeding up in the down direction (due to weight) and slowing
down in the direction it is moving. The air drag always slows it down,
the gravity can either speed it up or slow it down depending on whether
it is moving up (slows it) or down (speeds it). The net effect is
usually to slow it because the pitcher has to loft the ball a bit for it
to reach the strike zone high enough, so there is little net change in
the vertical component of the velocity. Of course, the preceeding does
not apply if you are interested in a breaking (curve, slider, etc.)
ball. In that case there will be air friction forces not strictly
opposite the direction of the velocity; I believe that a curve ball will
sometime "break" at the last moment due to a downward force due to the
spin on the ball which adds to gravity and makes the ball fall faster
than it would just because of gravity.
![]() QUESTION:
QUESTION:
Why does a rugby
ball dropped vertically from the ground with it's long axis at an angle
to the ground bounce backwards? What provides the force in the
horizontal direction and in which way does it act?Plus if the Contact
force on the ball is resolved and it does not pass through the ball's
centre of mass in which way will the centre of mass of the ball move and
how does this motion relate to the line of action of the contact force ?
![]() ANSWER:
ANSWER: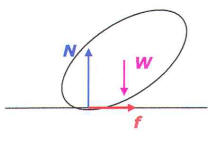
You are certainly right, if there were no force with a horizontal
component, the ball would have to rebound straight back up although with
some spin about the center of mass. However, what you refer to as the
"contact force" has two components, normally called the normal force and
the frictional force. If the surface were frictionless, the ball would
come straight back up. But there is friction, a horizontal force, and
the direction it points in is the direction which the ball will
accelerate while there is contact. If there were no friction (f
in the picture), the normal force (N) would exert a torque
about the center of mass which would make the ball rotate clockwise. So,
the ball would want to slide to the left during the collision and so the
friction will point to the right and that is the horizontal direction
the ball will move after bouncing. The center of mass will accelerate in
the direction of the sum of all three forces on it (including the weight
W). The torque about the center of mass will determine how
the ball rotates after bouncing:
-
if N+f passes through the center of mass, it will not rotate;
-
if N+f passes above the center of mass, it will rotate clockwise;
-
if N+f passes below the center of mass, it will rotate counterclockwise.
When I bounce an American football (I don't have a rugby ball), I find it goes clockwise.
![]() QUESTION:
QUESTION:
How much force does it take to move a 3600 lb object?
![]() ANSWER:
ANSWER:
Again we have that question "how much force does it take…"
when there is no answer. Suppose the object were on a very smooth level
surface (virtually firctionless). Then it would take maybe 1/10 oz of
force to get it moving 1 ft/s if you pushed for a second. But suppose
the object were on a rough surface. It might take a million pounds of
force just to break it away from the friction. Suppose that the object
were welded to the floor. Then maybe it would take a trillion tons of
force to get it moving. The only sensible question you can ask without
giving more information (and a definition of what is meant by "to move")
is how much force does it take to lift a 3600 lb object? That would be
3600 lb.
![]() QUESTION:
QUESTION:
I know that the full Law of Conservation of Energy can be shown as:
"KE{gained} + PE{gained} = KE{lost} + PE{lost} + (F{friction} * {distance})"
The "F{f}d" part is equal to the energy lost/gained by thermal energy due to friction. This would suggest that thermal energy due to friction is equal to the force of friction times the distance. However, I cannot find anyone that says this, or even backs this up! Most of the answers I find (of which their are very few) are differential calculus equations, none of which agree with each other. What is the actual formula, and why isn't it "F{f}d?"
![]() ANSWER:
ANSWER:
First, that is not at all how I would write the energy equation. I
prefer E2=E1+W where E2
is the energy at the end, E1 is the energy at the
beginning, and W is the work done by all external agents. When I
write E this means the sum of kinetic energy and potential
energy. All external agents mean all forces for which we have not
introduced a potential energy function. I tell my students this is easy
to remember because it says "what you end up with is what you started
with plus what you added". If the external agent is friction, the work
it does is negative because it takes energy away. This is not what you
should call "Law of Conservation of
Energy" because energy is not conserved but changes by W. So,
the work done by friction is W=-Fd. The law of energy
conservation states that the energy of an isolated system never
changes. So, where did the energy which friction "took away" go if we
imagine doing the whole experiment in some enclosed box to isolate it
from the rest of the universe? Friction must be converting some of the
energy we started with into some other form of energy (not showing up as
obvious kinetic or potential energy), as you correctly feel. Most of the
energy will end up as thermal energy, everything gets hotter. Also, a
sliding object makes noise and sound waves carry energy. Thermal energy
and sound waves are just microscopically another form of kinetic energy.
![]() QUESTION:
QUESTION: 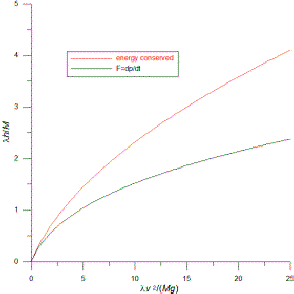
Consider a ball with mass M attached to a very long cord with linear density
λ. If you calculate the ball's maximum height when you throw the ball up with initial velocity
v, using F = dp / dt, F = - (M +
λy) g, and p = (M +
λy) dy / dt, you will obtain something different of what you obtain trying to calculate the maximum height using conservation of energy. How energy is dissipated in this case?
The cord is straight below M and it is longer than the maximum height.
In the beginning of the movement, only the ball moves, and the cord is on the ground. As the ball goes up, it pulls the cord.
[I have changed your notation slightly.]
![]() MY FIRST (INCORRECT!) ANSWER:
MY FIRST (INCORRECT!) ANSWER:
Let's first do energy conservation. Energy is conserved because the only
force on the ball + cord is gravity. (There is also the force of the
table on the stationary part of the string, but it does no work. E1=–ÖMv2,
E2=Mgh+λhg(–Öh)=Mgh+–Öλgh2
where h is the maximum value of y. Setting
E1=E2,
you must solve the quadratic equation –Öλgh2+Mgh-–ÖMv2=0.
You get two solutions, one for which h<0 which is discarded. The
final solution is h=(M/λ)(-1+√{1+[λv2/(Mg)]}).
As a check, if
λ=0 this may be shown to be h=v2/(2g),
the well-known answer for no hanging cord. Now, you say you solved it by
solving F=dp/dt? I
was unable to do so. I can get the differential equation for Newton's
second law, but it is a nonlinear, second-order differential equation:
0=(M+λy)(g+d2y/dt2)+λ(dy/dt)2.
Maybe I could solve this if I brushed up on differential equations, but
I am not willing to do that!
![]() MY SECOND ANSWER:
MY SECOND ANSWER:
The questioner, Emilio Matos of Brazil, sent me his solution solving
the
F=dp/dt equation. He was much more clever
than I and achieved a solution of h=(M/λ)(-1+(3√{1+[3λv2/(2Mg)]}).
A copy of his solution (in Portuguese) is
attached; note his slightly
different notation: h for y, m for λ, v0
for v, hmax for h. The graph shown above
compares the correct solution with my incorrect solution assuming energy
conservation; the correct solution has a much lower maximum height
indicating substantial loss of energy. My statement that "the
only force on the ball + cord is gravity" is incorrect because the mass
is increasing. In order for the "next piece" of cord to be moved from
rest to moving up, a force must be exerted on it; that means that the
next piece of cord exerts a downward force on the end of the moving cord
which does negative work on the system. This is most easily
seen by imagining a mass m sliding on a horizontal frictionless surface
(avoiding the complication of gravity) with speed v and picking up a mass dm at rest. An impulse
of Fdt=dp=(m+dm)(v+dv)-mv=vdm+mdv
must be delivered to dm to speed it up, and so m
experiences an impulse which slows it down. Of course, this is nothing
more than F=dp/dt, but with a focus on the
nature of F. In the case of interest, there is the additional
force of gravity; the important thing to realize is that this force is
not the only force because if it were the acceleration would simply be -g
which it clearly is not. Hence, energy is not conserved. Incidentally,
the correct solution for h also reduces to
h=v2/(2g) for a weightless cord showing that,
just because an answer reduces to a known result in a particular limit,
the answer is not necessarily correct! Now that we understand the
problem, I am not going through the calculations necessary to use
energy to solve this problem (by calculating the work done by F)
because it would simply go over the same ground already covered by Mr.
Matos' solution.
![]() QUESTION:
QUESTION:
if a bullet was travelling at 823meters per sec and hit an object that stopped it dead how much force per square cm would be exerted onto the target?
![]() ANSWER:
ANSWER:
Here is the
question which I get in one form or another which indicates how poorly
understood the concept of force is! First, you want to ask what the force
exerted by the bullet is, not the force per cm2. If you were able
to get the force, you could divide that by the cross sectional area of the
bullet to find the effective force per unit area; but you cannot get the
force because it depends on how quickly the bullet stops. If you mean by
"stopped it dead" that it stops instantaneously, then the force would be
infinite. The average force is the change in momentum (mass times velocity)
divided by the time to stop. So, you need also the mass of the bullet.
Suppose the bullet had a mass 0.02 kg, then the change in momentum
(0.02x823) is about 16 kg m/s. If it stops in 0.01 s the average force is
1600 N=360 lb, if it stops in 0.001 s the average force is 16,000 N=3600 lb.
![]() QUESTION:
QUESTION:
My teacher did a demonstration in class where there was a mass of 1 kg suspended by a string above it and then he attached a string below the mass. For the first demonstration, he pulled quickly to show that a rapid acceleration on the string below the mass would break that string. For the second demonstration, he showed that if you gradually accelerate the pulling of the string below, the string holding the mass would break instead. Could you please explain why this is the case, including the interaction between the two tensions between the strings? I understand that a greater acceleration means a greater force, but I have difficulty understanding why the gradual pull breaks the upper string and what "breaking the tension of the string" means.
![]() ANSWER:
ANSWER:
If you pull
up gradually with a force F and the mass M is at rest, then
the forces on the mass are its weight, -Mg, the lower string, -Tlower,
and the upper string Tupper=F. Newton's first law states that 0=F-Mg-Tlower.
So, the tension in the upper string is greater than the tension in the
lower, F=Mg+Tlower. So, as you gradually increase F, the tension
in the upper string will reach the breaking point first. I assume that in
the second case, the lower string starts out slack and the mass is pulled
upward by the upper string. When the lower string suddenly gets taught,
there is suddenly a very large acceleration in the downward direction which
can only be provided by the lower string. Therefore, there is suddenly a
large tension in the lower string which exceeds the breaking strength and
breaks it.
![]() QUESTION:
QUESTION:
I had a question regarding relativity. If I'm not mistaken, the principle of relativity states that different reference frames are essentially equivalent in that you can't discern a "stationary" reference frame from a "moving" one (that basically there is no such thing as absolute position). So, i was considering a collision of two objects, one of which is much more massive than the other (say, a train and a person). From an observer relative to the person, the train is approaching at a certain speed (say, 5 mph). if the train were to crash into the person, the result would be very bloody and cause severe damage to the person. If, however, this were viewed by an observer moving alongside the train, it would appear as if the person simply walked into the train at 5 mph, and would emerge damaged, but not severely harmed. How is it that this doesn't contradict the principle of relativity? An event's result seems to depend on a "stationary" reference frame (that either the person or the train is moving), when according to relativity the result should be the same regardless of the observer's frame of reference.
![]() ANSWER:
ANSWER:
I'm sorry,
but your assumption that the 5 mph train will be a violent accident is
simply wrong. If you are hit by a 5 mph train you will suffer the same
injuries as if you run into a train at a speed of 5 mph. Think about it‚ÄĒas
the train approached you could simply grab on to the front and start moving
with it. It would hurt a little bit, but no more than if you ran real hard
into the train at rest. If the train were going 100 mph, it would kill you,
but if you were launched at 100 mph into the train, you would die with
similar injuries.
![]() QUESTION:
QUESTION:
If all inertial frames of reference are equivalent, and there is no way to identify which of two objects which are becoming further apart is moving, how is it possible to determine which of two objects is accelerating? For example, how do we know that a train is accelerating away from a platform, and not vice-versa, if it is impossible to determine which is moving when the train is traveling at a constant velocity?
If all inertial frames of reference are equivalent, and there is no way to identify which of two objects which are becoming further apart is moving, how is it possible to determine which of two objects is accelerating? For example, how do we know that a train is accelerating away from a platform, and not vice-versa, if it is impossible to determine which is moving when the train is traveling at a constant velocity?
![]() ANSWER:
ANSWER:
One way you
can identify an inertial frame is if Newton's first law is true (an object
at rest or moving with constant velocity has zero net force on it). For
example, sitting at the train station there is a pendulum bob hanging
straight down; the earth is pulling straight down with a force (called the
weight) and the string is pulling straight up with a force which may be
measured to have the same magnitude as the weight. Now, if somebody is
accelerating in a train going by and also has a pendulum, it will not hang
straight down but at an angle. But there are still only two forces on that
pendulum bob, the weight straight down and the string not straight up. So,
if you are in the train's frame of reference, you conclude that Newton's
first law is not true.
![]() QUESTION:
QUESTION:
why do paratroopers roll on landing
![]() ANSWER:
ANSWER:
When you hit
the ground, the ground exerts a force up on you to stop you. The force which
it exerts depends on how long the collision lasts. This is a result of
Newton's second law which says that F=mΔv/Δt
where m is your mass, Δv is your change in speed, and Δt is
the time to stop. You have no control over your mass or the speed you hit
the ground, but you can make Δt longer and rolling is one trick for
doing that. The longer you can make your collision with the ground last, the
less it will hurt. Also, just jumping off a table, for example, it is more
painful if you hold your legs straight than if you bend them while stopping.
![]() QUESTION:
QUESTION:
In a projectile motion, which has a farther range (neglecting air resistance, or in a vacuum) fired from a catapult with constant force and same angle of flight, a paper(crumpled) or a rock? Knowing that the paper's mass is less than the rock, I thought that the paper would have a farther range since mass is inversely proportional to acceleration; but my teacher says otherwise, that they would have the same range. Who is correct?
![]() ANSWER:
ANSWER:
The problem is not specified completely, so either of you could be right.
Think about it: if the (constant) force acted on the rock for 5 minutes but
on the paper for 1 second, the rock would go way farther. You can go one of
two ways‚ÄĒspecify the time the force
acts on each or the distance over which the force acts on each.
-
If the forces exerted on both are the same and the time which the force acts for each is the same, then you are right and your reasoning is right. Your reasoning is right because the acceleration of the less massive paper is larger and if the times of acceleration are the same, it ends up going faster; the ratio of the velocities will be given by v1/v2=m2/m1. If the rock is 4 times more massive than the paper, it will have —ė the initial velocity of the paper.
-
However, if the catapult exerts equal forces over the same distance (the distance of the arc of the arm, presumably), the paper will still have a larger initial velocity than the rock. But it will not be because of acceleration being different since the two will spend different times experiencing the force. Here each acquires the same kinetic energy because equal work was done on them. In this case, the paper still goes faster but the ratio of velocities is v1/v2=√(m2/m1). If the rock is 4 times more massive than the paper, it will have –Ö the initial velocity of the paper.
The second scenario is likeliest to be a description of a catapult. A very light stone will get launched in a much shorter time than a very heavy stone and both will experience the force over the same distance. In all fairness to your teacher, he was trying to illustrate that, without air drag, two projectiles with identical initial conditions will go over identical paths. This requires stipulating equal initial velocities, though, not equal forces.
![]() QUESTION:
QUESTION:
My son has a question that I can't seem to find an answer to researching on the web. WHAT FORCE IS BEHIND A GOLF BALL WHEN HIT ON THE MOON? I appreciate your time on answering this for my son. I think it has something to do with Velocity, but not sure!
![]() ANSWER:
ANSWER:
I think there is some confusion about what force is here. Here are all the
forces a golf ball experiences here on earth:
-
The club, traveling with some speed, hits the ball and exerts a contact force on it for a very short time but it is a very big force and it results in the ball acquiring a very large velocity. As soon as the ball leaves the club, there is no force "keeping it moving". If there were no other forces, it would keep going forever with the speed with which it left the club.
-
Once it is started, gravity pulls down on it which is the force which eventually does bring the ball back to the ground.
-
As it flies through the air, it experiences air drag which can be very complicated. Essentially, it is a force trying to slow it down and the bigger the speed is the bigger this force is.
-
If it happens to be spinning, the air drag can act asymmetrically so that the ball curves. This is what is called a hook or a slice in golf (depending whether it curves left or right, respectively, for a right-handed golfer).
-
Of course, when it hits the ground, it experiences forces from the ground which ultimately bring it to rest.
What is different on the moon?
-
If the club is the same club with the same speed, there is no difference for this force. Therefore, the ball launches just the same as on earth.
-
The moon is much smaller than the earth and the result is that the gravity on the moon is much weaker. Therefore, this force (trying to pull the ball back down) is much smaller and the ball will go a lot farther.
-
Since there is no air on the moon, there is no drag and this also results in the ball going much farther.
-
The ball will not curve on the moon, regardless of how much spin it has.
-
When it hits the ground, things are about the same as on earth except that all the forces are smaller, again because of gravity being smaller, so the ball rolls farther before it stops (also because it is going much faster when it hits the ground than it would have been on earth).
![]() QUESTION:
QUESTION:
Why was work done defined as Force x Displacement? Is there a sound reason or was it simply derived from the work energy theorem?
![]() ANSWER:
ANSWER:
Work was not defined as Fd, it arises naturally from Newton's second
law (the source of essentially all classical mechanics). You start with
Newton's second law, F=ma, rewrite it as F=m(dv/dt),
use the chain rule F=m(dv/dx)(dx/dt)=mv(dv/dx),
rearrange mvdv=Fdx. On the right of this equation is
work done if m moves the small distance dx; on the left is what turns
out to be how much the kinetic energy changes when that work is done. If you
integrate this you get
Δ(–Ömv2)=FΔx=W.
Maybe this was too much detail for you.
![]() QUESTION:
QUESTION:
If 225 pounds falls 24 inches straight down to the ground, propelled only by the force of gravity, what is the force of impact?
![]() ALMOST
SIMULTANEOUS QUESTION:
ALMOST
SIMULTANEOUS QUESTION:
what is the striking force of an object that weighs 300lb falling from a height of 3 feet
![]() ANSWER:
ANSWER:
My God, will I never stop getting this question?
It depends entirely on the details of the collision. In essence, what
you need to know is how long did it take for the weight to stop? If you had
checked the FAQ page you would have
found an answer. There is no such thing as "striking force".
![]() QUESTION:
QUESTION:
You and a child half your height lean out over the edge of a pool at the same angle. If you both let go simultaneously, who will tip over faster and hit the water first? Or will they hit at the same time?
![]() ANSWER:
ANSWER:
The child will hit the water first. To understand why, model a person as
a stick of height L and mass M. Newton's second law says Iα=(MgLsinθ)/2
where I is the moment of inertia about the end of the stick, α
is the angular acceleration, θ is the angle the person makes with the
vertical, and g is the acceleration due to gravity. The right side is
the torque exerted on the falling object and angular acceleration measures
how quickly the rate of falling is increasing. So, whoever has the biggest
α hits first. The moment of inertia needed is I=ML2/3,
so solving for α, α=[(MgLsinθ)/2]/[ML2/3]=3gsinθ/(2L).
So, mass does not matter and the larger L is the smaller α is.
To convince yourself that this is reasonable, imagine a race to fall over
between a matchstick and a 100 ft high chimney.
![]() QUESTION:
QUESTION:
I fly alots of transatlantic flights and a friend of mine in discussion have a disagreement.
Here's the problem- If I am flying in a plane at 60,000 feet and he is flying in a plane at 20,000 feet and our airspeeds are 400 mph.
Who covers more ground faster the higher aircraft or the lower aircraft?
I contend the higher aircraft will have a higher ground speed than the lower aircraft even though they are both travelling at the same speed of 400 mph. I believe the further you are away from the earth the distance you travel in a straight line is lengthened by the curvature of a sphere. Whose right?
![]() ANSWER:
ANSWER:
I think it is a good idea to define "ground speed". Let's say it is the
speed of the plane's shadow as measured by somebody on the ground. Then if
you have a speed v and are a distance h above the earth's surface, the ground speed vg
can be shown to be vg=v(R/(R+h)) where R
is the radius of the earth. Alas, you are wrong! (By the way, I do not know
what you mean "travel in a straight" line because if you fly at some
altitude you are flying in a circular path.) To make this plausible,
consider the following: two planes, each with speed 400 mph, one at altitude
1000 ft, the other at altitude 100,000 miles and both are keeping their
altitudes constant; which will go all the way around the world first?
Because the altitudes of your example are so small compared to the radius of
the earth, there is practically no difference. I calculate the ground speeds
to be 398.9 for the higher plane and 399.6 for the lower. [If you care, here
is the proof. The ground speed and the plane both have the same angular
velocity which is essentially the rate you are going around the circle, for
example 1 revolution per month is the angular velocity of the moon around
the earth, 1 revolution per day is the angular velocity of the earth on its
axis, 1 revolution per year is the angular velocity of the earth around the
sun. If angular velocity is measured in radians per second, then the angular
velocity is v/r where r is the radius
of the circle v is going. Then, vg/R=v/(R+h).]
![]() QUESTION:
QUESTION:
My students hear all the time that there is ZERO G. I tell them that astronauts are free falling, like someone jumping out of an airplane. But I hear professionals say zero G all the time and the kids are confused. How do explain that gravity exists everywhere, and then they hear of zero g on the space station ?
![]() ANSWER:
ANSWER:
First, let me say that your example (which I have not included here) is
not a good one. Let me attempt to give an answer to the question regarding
zero-g (sometimes referred to as weightlessness). Those terminologies are,
strictly speaking, incorrect. What is your weight? It is the force which the
earth exerts on you. It is not what is measured by a scale; a scale measures
the force you exert on it, not the force the earth exerts on you. Of course,
in every day life the force which you exert on the scale happens to equal
your weight, but if you are in an elevator accelerating up the scale will
read more than your weight. If you are in an elevator free falling down, the
scale reads zero but your weight is still the same. If you say zero-g you
imply that the gravitational field is zero but that is certainly not true
anywhere near the earth (except at that point where the earth's and moon's
gravity cancel). I presume that you have taught your students about
centripetal acceleration. Anything which moves in a circle of radius R
with speed v has an acceleration toward the center of the circle of
v2/R. A satellite in a circular orbit has just the
right speed such that this acceleration is equal to g so, as you
correctly state, it is the same as the free falling elevator‚ÄĒyou
feel like there is no gravity. All this is standard physics.
Here is another perspective: Einstein's principle of equivalence states that there is no experiment you can do to distinguish whether you are in a gravitational field or in an accelerated frame of reference (that is, the freely falling elevator and having zero gravity are physically indistinguishable from inside). So, if it looks like a duck and quacks like a duck, we might as well call it a duck!
(One final note: Note that I have ignored the tiny correction that if you are orbiting with your feet "down" your feet have a slightly different acceleration from your head.)
![]() QUESTION:
QUESTION:
if an object is falling at a
fixed rate of 500 feet per minute, what g-force will that object
experience upon impact on the earth's surface. If possible include the
formula so other rates could be used, since I would also like to
calculate the g-force for the forward motion at different velocities.
FYI: this is an attempt at calculating the best combination of
conditions for an off-airport landing in un-inviting terrain by an
aircraft experiencing complete power loss.
![]() QUESTION:
QUESTION:
I fell down the stairs two
years ago and am still wondering what effect the impact might have had
on my brain. I fell head-first from the top to the bottom, and hit the
wall where it meets the small landing at the bottom - with my head. My
body kind of crumpled to my left. I fell 11 steps of normal height,
with my body turning head first, without touching the wall or railing.
The landing at the bottom is about 3 feet from the stairs to a plaster
wall. The impact was at the top of my head. Please let me know the
fall's velocity and force of impact of my head - and if you can, how my
brain would have moved inside my skull after the impact.
![]() ANSWER:
ANSWER:
Both of these questions are
unanswerable because the force is proportional to the acceleration,
that is the time rate of change of velocity. So knowing the velocity
when an object hits and the fact that it is at rest afterward gives you
the change in velocity but you cannot compute the rate of change of
velocity without a time. So, if an object changes its speed by 500
ft/min =2.54 m/s, its mass is 100 kg, and it stops in 0.5 s, the
average acceleration is 2.54/0.5=5.08 m/s2 and the average
force experienced is ma=100x5.08=508 N=114 lb. Since the weight
of 100 kg is about 220 lb, the force of the ground must be 114+220=334
lb. So the force you would feel is larger than your weight by
334/220=1.5, so you would feel a 1.5 g-force. This is an example, but
if either of these questioners really wants an answer, more data are
needed.
![]() QUESTION:
QUESTION:
I don't understand Newton's
Third Law. If it is true then surely, for example, it is impossible to
move your hand through a table since the reaction will always equal the
weight.
![]() ANSWER:
ANSWER:
Newton's third law (N3) says
that if one object exerts a force on another, the other exerts an equal
and opposite force on the one. Many students misunderstand this law as
you demonstrate in your example. Instead of talking about a hand, let
us assume there is a book on the table. Are there any forces on the
book? Yes, there is its own weight straight down (let's call that force
W) and maybe the table, which touches the book, also
exerts a force on the book (let's call that force T). Since
the book is not accelerating, the total force on it must be zero (that
is Newton's first law, N1) and so T must be a force straight up
which is of the same magnitude as W. These forces are equal and
opposite because of N3, right? WRONG, WRONG, WRONG! These
forces are equal and opposite because of N1 and they have absolutely
nothing to do with N3. They cannot be a N3 pair because both are on the
same body (book) and N3 addresses forces on different bodies. So, what
is the N3 (reaction) force which pairs with the force T? Since T
is the force the table exerts on the book, N3 tells us
that the book exerts a force down on the table which has
the same magnitude as T. And, what is the N3 (reaction) force
which pairs with the force W? Since W is the force the
earth exerts on the book, N3 tells us that the book
exerts a force up on the earth which has the same magnitude as W.
That's right, the book exerts a force on the whole earth. N3 can never
cause something not to move because the relevant forces are on
different objects.
![]() QUESTION:
QUESTION:
An acquaintance and I are
having a heated discussion relating to the 1960 jump from 103,000 ft
from a gondola by Joe Kittinger. According to several reports,
Kittinger reached speeds over 600 MPH after he jumped. Since I can't
prove that he did, I'm no physicist, he believes he must be correct.
How can I determine the speeds that were reached in this jump?
![]() ANSWER:
ANSWER:
In principle, this is a
simple free fall problem. In practice, we need to worry about air
resistance since that becomes important in real life at high speeds.
However, there is very little air above about 60,000 feet, so let's
assume that there is no air resistance and see how far he has to fall
to reach a speed of 600 mi/hr and if it is less than about 40,000 feet
he probably achieved that speed. The acceleration due to gravity is
about 21.8 mi/hr/s; that is a freely falling object will gain about
21.8 miles/hour as each second clicks by. One pertinent physics
equation is v=at where v is the speed (assuming
we start from rest), a is the acceleration, and t is
the time. So, putting 600 in for v and 21.8 in for a we
can solve for t: t=27.5 s; in other words, after about
a half a minute the object will be going 600 mi/hr. The second
pertinent equation is s=½at2 where s
is the distance traveled in time t. Solving for s I
find s=12,000 ft, that is he will have a speed of 600 mi/hr
when he is at about 90,000 ft, still far above where there is
signficant air. (Incidentally, in the second calculation I used a=32
ft/s/s so the units would come out right, viz. feet.) So, I
would say that yes, he must have gone at least 600 mi/hr. I did a
little research and saw 714 mi/hr quoted as the highest speed he
achieved. Once he starts encountering significant amounts of air he
will begin slowing down.
![]() FOLLOWUP
QUESTION:
FOLLOWUP
QUESTION:
This is a follow-up, and didn't know if I should post it
online or not, since you've already answered it. But, the person with
whom I'm having this discussion still insists you're answer is wrong.
He fancies himself smarter than a nuclear-physicist, I guess, and, by
his calculations , the top speed that Kittinger could have reached is
350 mph. Here is his argument and his calculations, referring to your
response.
"That's just a repeat of what the other professor said, and in both cases they conveniently ignore drag. If you're going to ignore drag then ignore it and the guy keeps falling at increasing speed. Why stop accelerating at the point that corresponds to what the claims are? When you plug the drag variables into NASA's algorithm Kittinger doesn't get to 614mph. The professors don't bother to verify that the air is too thin to have any effect. Tell the college professor's to go to the Chemical Engineer's Handbook and look up Fluid and Particle Dynamics. In there is a table that describes the activity of bodies in free fall through a fluid. When they're going slow, they are stable. As they increase in speed they first start to tumble erratically, then they start spinning about their axis of least inertia. The tumbling starts somewhere around Mach 0.4 and the spinning around Mach 0.6 That's the flat spin the story eludes to, and the college professors ignore. If he fell at 614mph he's at Mach 0.9 and is in a flat spin. The big problem is all the contradictory statements that are attributed to Kittinger. He the first supersonic skydiver. He gets to an estimated 614 mph or 714. He has no sense of speed, yet he knows he keeps accelerating after the drag chute opens. That chute opens at 13 secs, or 16 secs or at 96000 feet. First of all drag doesn't work like a break. A body sitting still has no drag. As it speeds up drag increases and keeps increasing until the force propeling the object and the force of drag are equal. Then the object stops accelerating and moves at constant speed as long as force and drag stay the same. Drag is related to Velocity(speed) by the drag equation. D = 0.5 x Cp x p x A x V^2 So as long as you keep the Cp,p, & A the same, there is one value for drag for every value of speed (V) I'm not going into all the other crap, but the force pulling Kittinger down and causing him to speed up is gravitiy working on his weight. At roughly 300 lbs it takes 300 lbs of drag to stop him from accelerating. He's the shape of a brick, roughly half as wide as long and 1/3 thick as long. The Cp of a brick is 2.1. We use that to compute air flows through our tunnel kilns at the brickyard. The density of the air is about 0.00004 slugs/cuft. He is exposing about 15 sqft of area to the "wind". So if we plug in all those numbers in the Drag equation and solve for V(speed), he stops accelerating at 690 fps or 470mph. I'd say the air is thick enough to make a difference. But that doesn't take into account the drag on the small parachute he deployed to keep himself from going into that flat spin. It's 6' in diameter that's 28.26 sqft of area. The Cp for a round chute is 1.5. So as long as the drag on the chute and the drag on Kittinger doesn't total 300 lbs or more he is still accelerating. At 13 secs the total drag is 254lbs and his speed is 283 mph. He'll accelerate for less than a second more and get to about 290 mph. At 16 seconds the total drag is 384 lbs, so he'll decelerate from 347 mph with a pretty good jerk. I have no idea where or why the 96000 ft comes from, so I'm going to ignore it. He supposedly used a timer to deploy the chute. The speed of sound is around 660mph and tumbling would start somewhere around Mach 0.4 which is 0.4 x 660 = 264mph. That's damn close to the 13 sec mark. We'll never know based on the info available, but I don't think he got over 300-350mph."
Here are
the facts, as presented in an article at http://www.centennialofflight.gov/essay/Explorers_Record_Setters_and_Daredevils/Kittinger/EX31.htm
1. Kittinger jumped from 102,800 ft.
2. His weight is approximately 300 lbs.
3. He was falling in a backward orientation
4. After falling for 13 secs, a small chute, 6 ft. in diameter, opened.
5. He feel for 4 min. and 36 secs more bringing him to 17,500 ft.
![]() ANSWER:
ANSWER:
Your friend certainly makes
some quite good points, although he is maybe a bit overemotional and
maybe a little hostile to us college professors. It is true that we
often simplify problems to get to the core of a problem. So let me be a
little more careful and go over the calculation of your friend the way
I would do it since some of the numbers he quotes are undocumented and
some of them (in particular slugs/ft3) are completely
incomprehensible to a modern physicist! Your friend must be an
engineer. His equation is quite correct, that is the terminal velocity
is given by v=[(2mg)/(rACp)]1/2
. Now it is easy to see how disputes can arise because the answer, of
course, depends the choice of constants some of which are not easy to
estimate (for example, I would say approximating the man as a brick is
what some nutty college professor might do). The density of the air at
100,000 ft is about 1/100 the density at sea level and, since the
density at sea level is about 1.3 kg/m3, I will take r=1.3x10-2
kg/m3. I searched the web for tables of drag coefficients
and found that a
parachutist has Cd=1-1.4 (not 2.1 as your friend
assumed); I will use 1.2. The cross sectional area also requires a
rough estimate since it depends on whether he is falling, for example,
feet first or is falling "belly flop" orientation. I will assume the
latter so as to get as small a speed as possible and I will estimate
the area as about A=2 m x 0.5 m=1 m2 (your friend
uses 15 ft2, about 1.4 m2). Using m=136
kg (300 lb) and g =9.8 m/s2, we are ready to estimate v;
I get v=413 m/s= 924 mi/hr.
But, there is important information which you did not tell me the first time through--the opening of the small chute. So now the cross sectional area is about 2.5 m2 and the drag coefficient is about 1.42 (I model it as an open hemisphere into the wind). So now I get a reduced terminal velocity of v=240 m/s= 537 mi/hr.
Now I have the terminal velocities, what happens in our specific example? The space is too limited here to put in all the details, but I have assumed a constant density for the first 4000 m (about 12,000) of fall. I went back to an intermediate mechanics book to find the dynamic analysis of the falling body with quadratic velocity dependent drag force and I could apply (knowing the terminal velocities from above) the analysis to this specific problem. In the first 13 seconds I find that he falls about 1000 m and ends up with a speed of 130 m/s (291 mi/hr). Then, after he has fallen 3000 m more he will have a speed of 208 m/s (465 mi/hr). But he is still accelerating but now the air gets denser so his acceleration decreases even more; nevertheless, as he falls, since he is still fairly far below terminal velocity (240 m/s) he will end up going faster than 465 mi/hr.
So who is right here? Well, your friend is right in that we will never know based on information we have. I can easily imagine that I have made a factor of two error in the density, the area, or the drag coefficient (and so could your friend); increasing all by a factor of two would reduce the terminal velocity by almost 2/3 which is the difference between 600 mi/hr and 200 mi/hr. The results are too sensitive to modest changes in the parameters.
![]() QUESTION:
QUESTION:
Let's say I have a metal rod
about a half an inch thick and 300,000 kilometers long. Then say I give
one end of said rod a mighty whack with a hammer, propelling it forward
by one inch in a mere fraction of a second. My questions is, wouldn't
the impact of my hammer cause the other end of the rod to move forward
one inch just as rapidly as the end where I whacked it? And would this
violate Einstein's law that states that nothing can move faster than
"C"? Or would the far end of the rod have to wait one second after my
whacking my end before moving forward by one inch?
![]() ANSWER:
ANSWER:
Have you thought about the
implications of your question? I figure the mass of the rod would be
about 1010 kg. Suppose that you exert a constant force such
that after 0.1 s it is moving with a speed of about 0.5 m/s; it would
have moved about an inch in this time. The force is the change in
momentum divided by the elapsed time so, roughly speaking, the required
force is about 1012 N. Where are you going to get such a
force? Anyhow, to the meat of your question: no, the other end would
not start moving instantaneously. It could not begin moving until at
least one second later than your end started moving for the reason you
state: no information can travel faster than c. In reality, it
would be much longer than one second because your "mighty whack" will
compress the rod and this compression will move with the speed of sound
in the metal and this compression is what travels to the other end to
move it.
![]() QUESTION:
QUESTION:
Hi I'm a 52 year old high
school teacher and this is a problem I could not solve in the new
curriculum. Here it is, word for word:
A red ball is stationary on a billiard table OABC. It is then struck by a white ball of equal mass and equal radius with velocity u( -2i + 11j ) where i and j are unit vectors along OA and OC respectively. After impact the red and white balls have velocities parallel to vectors -3i + 4j, 2i + 4j respectively. Prove that the coefficient of restitution between the two balls is 1/2.
![]() ANSWER:
ANSWER:
First, allow me a little
rant! It is utterly ridiculous that this problem is part of a high
school curriculum. Coefficient of restitution (COR) is one of the least
important concepts in classical mechanics. Furthermore, it is nearly
always defined in terms of a one-dimensional collision which the
collision in your problem is not, so it looks like the problem writer
is trying to confuse the reader (which I consider to be poor
educational method). Furthermore, I find that I do not get 1/2 for the
coefficient of restitution when I work the problem. I will outline the
solution to the problem and give my results. You can reconstruct the
solution and see if I have made any errors. First, the COR e is related
to the energy loss Q in the collision by Q=½mv2(1-e2)
where m=m1m2/(m1+m2)
(reduced mass) and v is the incident velocity (if one of the
two particles is at rest as it is here). It makes no difference what
the actual masses are since they are equal, so I shall choose m1=m2=1
kg such that Q=31.25(1-e2) J. (I have used v2=125
m2/s2 as given in the problem.) Now, just
calculate Q to get e. The information given about the recoiling
velocities is their directions, not their magnitudes; to get the speeds
you must do momentum conservation. The red ball moves at an angle of
53.10 above the negative x axis and the white ball
moves at an angle of 63.40 above the positive x
axis. Conserving momentum in x and y directions I now
find the speeds of the red and white balls: vr=7.5
m/s and vw=5.59 m/s. Hence the energy after the
collision is 43.75 J and before the collision 62.5 J, so Q=18.75
J. Solving now for COR: 18.75=31.25(1-e2), e=0.63, not ½.
There is actually another way you can do it: if you work in the center of mass system it essentially looks like a one-dimensional collision since the two particles after the collision move colinearly apart with speeds of 3.54 m/s each so that the speed of separation is 7.08 m/s and the speed of approach before the collision is 11.18 m/s. The COR is defined as the ratio of the speed of separation over the speed of approach which works out to, you guessed it, e=0.63! Now I have more confidence in my solution.
![]() QUESTION:
QUESTION:
Real life question: Tire pressure on
and off the car: I am getting a new tire for my car. While it's on the
rack, they check the pressure and it's a perfect 32 psi. They put the
tire on my car, then lower the 3000 pound car back down on it, and say
see ya' later. I say,"Shouldn't you check the pressure while the weight
of the 3000 pound car is down on it?" "Nah", they say, it doesn't
change. That doesn't make sense to me. I actually asked this question to
my brother who is a ultra-high vacuum physicist at Sandia Labs, and he
didn't know. I also asked this question at the famous Cartalk.com forum
and got laughed out of it.
![]() ANSWER:
ANSWER:
Here is the basic physics, the ideal
gas law: PV=NRT where P is pressure, V
is volume, T is absolute temperature, N is the amount of
gas, and R is a constant of nature. Let's assume that T
stays the same when the car is lowered off the rack. Now, presumably the
volume of the gas in the tire decreases a little bit; therefore, the
pressure must increase a little bit to keep the product PV equal
to the constant NRT. However, the volume changes by a very small
amount compared to the total volume of the tire, so for all intents and
purposes (but not exactly) "it doesn't change".
![]() QUESTION:
QUESTION:
I am a librarian assisting a
library patron. The patron says at one time he had a book that gave him
a formula to compute the weight of an object. If you put an object,
such as a car, on a tire or ball or something that is pressurized, and
you know the PSI, you can measure the size of the point of contact with
the ground (the flat surface of the tire on the ground) and calculate
the weight of the object.
![]() ANSWER:
ANSWER:
Consider a piston of cross
sectional area A, vertical, which has a pressure P
under it and a weight W sitting on it and everything is in
equilbrium; for simplicity, neglect the weight of the piston itself or
imagine it to have been absorbed into W. We must not forget
that there is an atmospheric pressure Pa pushing
down on the cylinder. Then Newton's first law specifies that the sum of
all the forces must add to zero, and so PA-W-PaA=0
(pressure time area equals force) so W=(P-Pa)A. But
(P-Pa) is what is called the guage pressure, it is
the pressure which most pressure guages read, the amount over (or
under) atmospheric pressure. So 30 psi means, usually, 30+14.7 psi
since Pa=14.7 psi. This seems to me to be
equivalent to your question. Let's check it for reasonableness: suppose
a car has each of its four tires in contact with the ground by an area
of 6"x4" and the tire (guage) pressure is 30 psi. Then the weight of
that car would be 6x4x4x30=2880 lb which is about what cars weigh.
![]() QUESTION:
QUESTION: 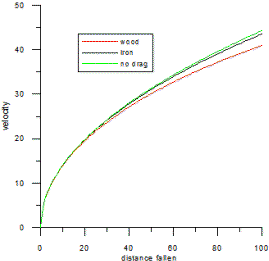
A metal weighing 10kg and wood also weighing
10kg are both dropped from a building which would hit the ground first?
If they are of the same shape,which would hit the ground first?
![]() ANSWER:
ANSWER:
If air drag is negligible, they would hit the ground simultaneously. If
air drag is a factor, then the one with the larger density will hit first. A
good approximation to air drag force is F=—ėAv2
where A is the cross sectional area presented to the wind and v
is the speed; this equation is only true if SI units are used. The one
having the larger density will have the smaller volume and therefore the
smaller A; hence, at any given v the denser will have the
smaller air drag force. The question, then, is how high does the building
have to be in order for air drag to be important. I assume the two are
spheres, the density of the metal is 8000 kg/m3 (near iron), and
the density of the wood is 800 kg/m3 (near oak). You can find the
terminal velocity of each by finding the speed at which the drag force
equals the weight. Without any details, I find the terminal velocities of
the metal and wood balls are 167 and 78 m/s respectively. The plot at the
right compares the velocities of the oak and iron balls after they have
fallen a given distance and also shows how each would move if there were no
air drag. As you can see, even dropping from 100 m neither ball is anywhere
near terminal velocity and neither velocity is much reduced from free fall.
If you drop the balls from less than about 30 m, they will, for all intents
and purposes, hit simultaneously.
![]() QUESTION:
QUESTION: 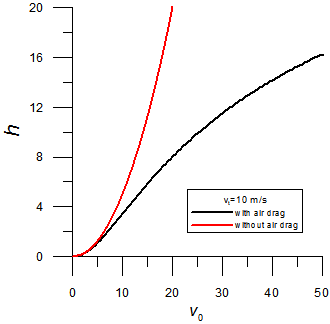
There are numerous problems connected with air drag acting on the falling object. What if it acts on the object thrown up with a given initial speed v(0) and has a given terminal velocity of v(term)? What height would an object rise to?
![]() ANSWER:
ANSWER:
This is a standard problem, and if the object is such that we can
approximate a drag force of the form F=-cv2, the solution
is h=(vt2/(2g))ln(1+(v0/vt)2).
The graph to the right shows heights achieved for various initial velocities
if the terminal velocity is 10 m/s compared to the case of no air drag.
![]() QUESTION:
QUESTION:
Here is the scenario: a pool ball is traveling at certain pace with an enormous amount of spin on it. Once it hits the rail at about a 45 degree angle is it possible for it to shoot off of the rail and travel faster than it was going before when it was on it's way to the rail?
![]() ANSWER:
ANSWER:
It does not even need to have "an enormous amount of spin", a modest
amount will probably do it. The ball, coming into the rail, has
translational kinetic energy and rotational kinetic energy. The friction
between the ball and the rail can transfer some of the rotational energy to
kinetic energy, so after the collision it will have a higher speed and a
smaller spin.
![]() QUESTION:
QUESTION:
Why do I go faster than my lighter weight friends when on a bike? I have noticed this downhill, but also on flats, I'm pedaling less. Assuming we both have top of the line bikes (we do). I thought things fell at the same rate regardless of mass. I think momentum and friction have something to do with this, but can you remind me of the principles involved here?
![]() ANSWER:
ANSWER:
If it were not for air drag, everybody should be pretty much equivalent.
However, the air drag F depends mainly on the cross sectional area
A presented to the wind and the speed v; a useful approximation I
often use in these answers is F

![]() QUESTION:
QUESTION:
I have just started a new job and have been asked to do a presentation on the ABS (Avalanche Bag system). Upon reading about the product they kept quoting that the system works on the "Law of Inverse Particles." I figure ok, it's a Law, it should be fairly simple to research, but when I started typing it into search engines I am getting no feedback on this Law at all. So my question is does this Law even exits? If so is there maybe another name that it goes by? If it does exist who created it? Any help that you can off me on this topic will be very much appreciated, in the mean time I'll keep on checking books, sites and asking old teachers!
![]() ANSWER:
ANSWER:
I have never heard of the law of inverse particles. However, just
looking over how this thing is supposed to work, it just looks like
Archimedes' Principle to me. Archimedes' principle says that when an object
is placed in a fluid it experiences an upward force, called the buoyant
force, which is equal to the magnitude of the weight of the displaced fluid.
Hence, if the object has a density less than the density of the fluid, it
will float, if it is greater it will sink. I am guessing that the snow in an
avalanche acts much like a fluid and, if you can significantly decrease your
overall density, you will "float" on the surface, much like a cork floats on
water. The way you decrease your density is to increase your volume with the
inflated airbags. Why they invent this screwy name for this escapes me, must
be an effective marketing technique.
![]() QUESTION:
QUESTION:
As a gas bubble rises in a column of liquid, it expands due to the decrease in pressure from the liquid above it. Intuition tells me that the diameter of the bubble will increase at a decreasing rate; but is that true? Does the bubble's diameter increase at a decreasing rate over time, does it increase linearly with time, or does it expand at an increasing rate?
![]() ANSWER:
ANSWER:
Assuming temperature stays constant, volume is inversely proportional to
the pressure. Since the pressure increases linearly with depth, the volume
of the bubble will decrease linearly with depth. But the volume is
proportional to the cube of the radius, so the radius does not decrease
linearly with the depth. I have derived the following equation to
approximate how the radius R varies with the depth d: R/R0=3
![]() QUESTION:
QUESTION:
I need you to settle an argument between my wife and I.
We are traveling down the road at 60 mph. My wife throws a piece of balled up gum out the window. When it hits the ground, my wife thinks it will roll backwards. This is not possible and I know it will roll forward at a speed less than 60 mph due to friction.
Who is right?
![]() ANSWER:
ANSWER:
You are
![]() QUESTION:
QUESTION:
Since kinetic energy = 1/2 mv^2, it follows that, for a given mass, a doubling of velocity requires a quadrupling of energy.
It seems to be certain then, that 2 joules are required to accelerate a 1 kg mass from zero to one meter per second in one second (ie accel=1m/s2)
Change in kinetic energy is equal to work. W1=
–Öx1x12-–Öx1x02=–Ö J, not 2 J.Now, according to the KE formula, to further accelerate the mass to 2 meters per second requires an additional 6 joules... because at that velocity, the energy now possessed by the mass is 8 joules - 4 times higher than when it was moving at 1m/s.
W2=–Öx1x22-–Öx1x12=3/2 J, not 6 J.
Here is my question: (in the form of a thought experiment) Scenario: I am in space Let's suppose I use 2 joules of energy to accelerate the mass to 1m/sec, relative to me. A spaceship, passing by with velocity 1m/sec and going in the same direction as the mass, has a second person onboard who intercepts that mass. (Because it's and the ship's speed are equal, the mass is effectively at rest with respect to the ship. Now let that person - on the moving train - apply 2 joules of energy to again accelerate the mass to 1 m/sec relative to HIM. So the actual velocity of the mass is now 2m/sec, relative to the first observer (me) (Assume same direction...) So, between us, only 4 joules of energy have been required to get the mass to 2 m/sec instead of the 8 implied by the KE equation. I have no difficulty in grasping that energy goes up as the square of velocity, but for the life of me, I cannot understand why both observers cannot use 2 joules of energy to effect an increase of 1 m/sec each Surely, what is true for one must be true for the other... ? (ie. that it only requires 2 joules to effect an increase in velocity of 1m/sec, relative to that frame) I have posted this on a Physics Forum and the only responses I have gotten allude to the fact I am getting it all messed up by changing the frame of reference and hence, the numbers won't add up. They say KE is not frame invariant and I can understand that - but no-one can explain where my logic is wrong... Can you possibly enlighten me ?
![]() ANSWER:
ANSWER:
You have made some errors in your preliminary calculations above which I
have corrected. Those who told you that kinetic energy is different in
different frames are certainly on the mark. But, I will show that the work
done in one frame is also not the same, that is, if you do W Joules
of work, somebody moving relative to you will see you do a different amount
of work, that is, the energy expended is not something everybody will agree
on. I am going to set up a scenario which I hope will show you where you
have gone wrong. The ship goes by with a speed of 1 m/s and the guy on the
ship exerts a 2 N force on a 1 kg mass, initially at rest in the ship, for 1 s. The acceleration is
therefore F/m=2 m/s2. The distance (in the ship)
the mass travels is x=
![]() QUESTION:
QUESTION:
I noticed in a textbook that 'g' varies directly with distance inside the Earth's radius but is inversely proportional to it outside. I understand the reason for the latter but would like to know more about the former - thanks! Please keep it simple.
![]() ANSWER:
ANSWER:
Here is as simple as I can make it: First, the assumption must made that
the mass of the earth is uniformly distributed, that is, the density is
constant everywhere. This is roughly true on a large scale. Second, you must
know that Newton's universal law of gravitation says that the force of
gravity from a spherical object is proportional to the mass M of the object
you are being attracted to and inversely proportional to r2
where r is the distance to the center of the sphere. [You erred when
you said g is inversely proportional to r, it is r2.]
Third, there is one more thing you need to know, called Gauss's law which
states that only the mass inside where you are attracts you, the mass
outside of r
exerts no gravitational force on you. So, as long as you are outside, F~Mtotal/r2;
but, if you are inside, only part of Mtotal, Mpartial,
exerts the force on you, F~Mpartial/r2.
But, think about it for a minute: Mpartial is proportional to
the volume of the smaller interior sphere and that is proportional to r3
(V=(4/3)
![]() QUESTION:
QUESTION:
When you face a wall, place your toes against it, and try to rise up on the balls of your feet, why can't you?
![]() ANSWER:
ANSWER:
When you stand up straight, your center of gravity is above a point
between your heel and toes and you do not tip over because there is no net
torque which would tip you over. When you go up on your toes and are unable
to lean forward, your center of gravity now exerts a torque about your toes
which rotates your body backward. Try standing on your toes when you are not
against the wall; in order to remain standing you will find that you must
lean forward so that your center of gravity will be directly over your toes.
![]() QUESTION:
QUESTION:
I was doing some water sports and was wearing a wet suit and a 50N (50 Newtowns) rated buoyancy aid. I weigh 93Kg. Cliff jumping into the sea, after resurfacing I bobbed gently on the surface with no swimming effort.
Later wearing same equipment on fresh water river, fell of a kayak and promptly sank! To get to and stay on surface I had to swim or actively tread water. The question is what value N rated buoyancy would I need to "bob gently" in fresh water?
![]() ANSWER:
ANSWER:
You do not weigh 93 kg, your mass is 93 kg and your weight is 93x9.8=911
N. Suppose that you just float with your head above water in salt water.
Then the buoyant force the water is exerting up is 911-50=861 N. Archimedes'
principle says that this is the weight of the displaced water, and let's say
salt water has a density of 1030 kg/m3; so, the volume of your
body less head must be 861/(1030x9.8)=0.085 m3. So, the buoyancy
you can expect in fresh water if just your head is up is 0.085x1000x9.8=836
N because the density of fresh water is 1000 kg/m3. So, to have
identical buoyancy to the salt water situation, you need an additional 25 N
(861-836) buoyancy.
![]() QUESTION:
QUESTION:
If a man was to be proportionately increased in size, would it be more difficult for him to perform a pull-up? All his body percents are exactly the same including his muscle, fat, ability, ect. The pull-up bar is also high enough that his feet would not touch the ground in either situation.
![]() ANSWER:
ANSWER:
Scaling of biological organisms has been a topic of interest for a long
time. I think Leonardo de Vinci was the first to think about it. Anyhow, I
think the answer to your question is that it would be harder to do a pullup.
Here is why: The weight of something is proportional to the cube of its
dimensions. So, if you doubled all the dimensions of a man, his weight would
increase eightfold. But, the strength of bones or muscles is dependent on
their cross sectional areas, a bone or muscle doubled in size would have
about four times the strength.
![]() QUESTION:
QUESTION:
I've been told that when a gas is cooled, it takes up less volume, and therefore its density increases.
I've also been told that a gas always fills its volume (i.e. a container).
These two ideas, however, seem to contradict one another. On the one hand, cooling a gas causes it to contract and decrease in volume, which would increase its density. However, on the other hand, a gas will always fill its volume, which means its volume doesn't change when cooled. Therefore, if the volume doesn't change when cooled since a gas will always fill its volume, then its density would not increase.
In other words, if a gas will always fill its volume, then cooling it would not increase its density since the gas always fills its volume and therefore remains at the same volume. In a closed container, if a gas expands to fill the volume of the container, then how could cooling the gas increase its density? How could a gas fill its container/volume on the one hand, but then on the other hand, when its cooled, decrease in volume and therefore increase in density? If a gas fills its container/volume, it wouldn't increase in density when cooled since it FILLS its volume. Therefore, since it fills its volume, the volume of the gas would remain constant. Therefore, since the volume of the gas would remain constant, its density would not increase when cooled.
So my question is, how could a gas increase in density when cooled if that same gas always fills the volume of the container it's in?
![]() ANSWER:
ANSWER:
That's a pretty long question which requires only a short answer. If the
amount of gas remains constant, the relation between pressure, volume, and
temperature is PV/T=constant. The situation you describe has a
constraint that volume remains a constant, so P/T=constant
which means that as the temperature goes down the pressure goes down; and,
the volume stays the same. So, if you cool a gas in a rigid container, the
density remains the same.
![]() QUESTION:
QUESTION:
how much time will it take to travel down a 1000 ft , 30 degree ilcline with a 225 lb payload on a 200 lb soap box race car and if pay load was lighter would the time be shorter with lighter load?
![]()
 ANSWER:
ANSWER:
I have dealt with this kind of question
before, but maybe it is time to
revisit the whole thing with one answer. First, consider the ideal situation
where there is no friction of any kind. Physicists do not like English
units, so I am going to convert everything to SI units: 1000 ft=305 m, 425
lb=193 kg. I assume that you do not want all the details of my calculations,
just the pertinent results. The time does not depend at all on what the mass
is (if friction plays no role). There is an acceleration down the incline
which is a=
-
Friction due to the moving parts, like bearings, like the wheels rolling on the ground, like wheels moving on axels, etc. Empirically, we find that this kind of friction increases proportionally with how hard the moving parts are pressed together and this, of course, is proportional to the total weight of car plus rider. But, the force impelling the car down the hill is also proportional to the total weight, so once again, the speed at the bottom is independent of the load. There is something called the coefficient of friction which tells you how much friction force there is for a given force pressing the surfaces together. For example, if this coefficient is 0.3 for a 100 lb box moving on a horizontal floor, you would have to push with a 30 lb force to keep it moving with a constant speed. If I take 0.3 to be your coefficient of friction, your speed at the bottom would be about 26.8 m/s=60 mph. Since the acceleration is about half what it was, the time is about twice as long, 22 s.
-
For objects which are going faster than a few mph, air drag becomes important. Air friction depends on two things, the shape of the object and the speed it is going. It does not depend on the mass of the object. Actually a pretty good approximation to the magnitude of the force of air friction is F≈—ėAv2 where A is the area presented to the wind (this works only if F, v, and A are in SI units). So, this force, which points up the incline just like the moving parts friction, causes the car to slow down more. But, Newton's second law says that a=F/m so that if F does not depend on m, the acceleration (amount of slowing down due to this force) gets smaller as m gets bigger. It gets a little complicated to actually calculate the time and speed for this case, but the important part is that this is the only place I can find where the weight of the whole car makes a significant difference.
So, the bottom line is that if you go fast enough for air drag to be important (and I suspect you do), the heavier of two otherwise identical cars should win.
![]() QUESTION:
QUESTION:
Just like a ball when hits a wall it bounces back, why dont people bounce back in the same way, when opposite force is exerted on them by the wall (as in case of ball)??
![]() ANSWER:
ANSWER:
It is because of elasticity. When two objects collide, how they move
after the collision is determined by what happens to energy after the
collision. If you drop a superball on the floor it rebounds almost as high
as from where it was dropped; if you drop a putty ball, it does not. When
the superball hits the floor, it compresses but it compresses like a spring
which "stores" the energy. So the energy of the moving ball is moved into
the energy of the spring. The spring now decompresses and gives the energy
back to the motion of the ball and it flies back into the air. It obviously
did not give all the ball's energy back since the ball did not quite
rebound to where it was dropped from; the little bit of energy lost shows up
as heat and sound. The putty ball also compresses when it hits but it bears
no resemblance to a spring because after you compress it (which takes
energy), it does not decompress and give energy back. Here, the energy of the
ball's motion is used to compress the putty ball and that energy shows up as
heat and sound entirely. The superball (neglecting the little amount of
energy lost) is referred to as an elastic collision and the putty ball is a
perfectly inelastic collision.
![]() QUESTION:
QUESTION:
I am falling from a plane at terminal velocity. I have a ball in my hand. I throw it towards the ground. What happens? Does the ball accelerate away from me, or does it simply fall beside me? What about if it was a very heavy ball such as a cannon ball compared say to a baseball or a plastic 'WalMart' pool ball?
![]() ANSWER:
ANSWER:
Terminal velocity is determined by the geometry of the object, the
density of the fluid (air), and the mass of the object. The terminal
velocity in air for an object of mass m and cross sectional area A
can be roughly approximated by vt
![]() QUESTION:
QUESTION:
My question has to do with traction and the movement of a wheel(a wheel alone). Traction is essential for its movement both linear and circular. But if we throw a wheel forward it rolls some meters and then it stops(and falls). Which force is responsible for the decrease in its velocity? Cause if traction is parallel to the ground facing backwards then linear movement 's negative accelleration is explained but not angular negative accelleration. If traction is parallel to the ground facing forward then angular negative accelleration is explained but not linear. If traction is zero then which force decreases both velocities linear and angular?
![]() ANSWER:
ANSWER:
One of the reasons I love doing Ask the Physicist is because
I often learn things I did not know or had never thought about. You would
think that a guy who has been teaching introductory physics courses for
nearly 50 years would find this question simple. But, indeed I was puzzled
by it because, as I have found by thinking about it and talking to some
friends, I wasn't thinking beyond the friction force (which questioner calls
traction) being simply the only force in the horizontal direction and
obviously stopping the forward motion after some distance. I never addressed
the angular acceleration of the wheel before. This answer will be
long-winded because that is what I do when I have learned something which
pleases me! What frictional forces are important to understand the rolling
of a wheel? Most introductory physics classes talk only about the contact
forces of static friction and kinetic friction. Kinetic friction is not
applicable to this problem because the wheel is not slipping on the ground,
and static friction might
be important, but not necessarily. If we have a round wheel rolling on a
flat horizontal surface (don't look at the figure yet!), there are three
possible forces
 A perfectly round wheel cannot have rolling friction as
I showed above, it must deform which means that there is no longer a "point
(or line) of contact" but now an area of contact. Since the normal force is
only constrained to act somewhere where the two are in contact, it is now
possible (in fact inevitable) that this force will not act through the
center of mass of the wheel. That is the whole key to answering this
question. So, finally, the answer: refer to the figure where I have drawn
the forces mg, N, and f. The
weight is still constrained to be vertically down and pass through the
center of mass (blue cross). The normal force is constrained to be vertical
and act somewhere where the wheel and ground are in contact, drawn a
distance d to the left. The frictional force (which now includes both static
and rolling friction) is constrained to act at the surface and parallel to
it. I choose a coordinate system with x to the left and y up;
the axis (red cross) about which I will sum torques is at the ground
directly under the center of mass and positive torque results in an angular
acceleration which is positive when acceleration of the center of mass is
positive (counterclockwise around the axis). All is now straightforward: ΣFx=-f=ma,
ΣFy=N-mg=0, Στx=-Nd=Iα=Ia/L
where I is the moment of inertia about x
and L is the distance from x to
x. Finally, N=mg, a=-f/m,
and d=fI/(Lm2g).
A perfectly round wheel cannot have rolling friction as
I showed above, it must deform which means that there is no longer a "point
(or line) of contact" but now an area of contact. Since the normal force is
only constrained to act somewhere where the two are in contact, it is now
possible (in fact inevitable) that this force will not act through the
center of mass of the wheel. That is the whole key to answering this
question. So, finally, the answer: refer to the figure where I have drawn
the forces mg, N, and f. The
weight is still constrained to be vertically down and pass through the
center of mass (blue cross). The normal force is constrained to be vertical
and act somewhere where the wheel and ground are in contact, drawn a
distance d to the left. The frictional force (which now includes both static
and rolling friction) is constrained to act at the surface and parallel to
it. I choose a coordinate system with x to the left and y up;
the axis (red cross) about which I will sum torques is at the ground
directly under the center of mass and positive torque results in an angular
acceleration which is positive when acceleration of the center of mass is
positive (counterclockwise around the axis). All is now straightforward: ΣFx=-f=ma,
ΣFy=N-mg=0, Στx=-Nd=Iα=Ia/L
where I is the moment of inertia about x
and L is the distance from x to
x. Finally, N=mg, a=-f/m,
and d=fI/(Lm2g).
Finally, a couple of real-world provisos. Of course, N is really distributed over the whole area, but the dynamics can be done by assuming it effectively acts all at one point just like we assume the weight acts all at the center of mass. And, the rolling friction might not really act at the surface of contact since it arises from the deformation of the wheel and it might not be purely horizontal since it is not directly a force due to the contact with the floor. So, there are still some idealizations in my analysis, but there are always idealizations when dealing with friction. And, the problem could have been equally well done assuming the ground, not the wheel was being deformed. One could also have done the analysis by summing torques about the center of mass and using the parallel axis theorem Icm=I-mL2.
I would like to acknowledge a very useful discussion over pizza with friends and colleagues Edwards, Love, Meltzer, and Anderson.
![]() QUESTION:
QUESTION:
A fly is hovering in a car. the car is going 45 MPH with the windows up. the car hits a solid object and suddenly stops. Does the fly hit the front window, the back window, or nothing at all?
![]() ANSWER:
ANSWER:
This is tricky. The stock answer would be that the fly would smash
into the front windshield just like you would if you weren't wearing your
seat belt. But, the fly is actually hovering with respect to the air, and so
whatever happens to the air will be what happens to the fly. The air does
not all smash into the windshield but more or less stays just where it is
relative to the car. The reason for this is that air is a collection of
molecules most of which are already going much faster relative to the car
than the car is relative to the ground. An average air molecule is going
about 1200 mph. Think of half of them going (relative to the road) toward
the back with speed like 1155 mph and half going toward the front with speed
like 1245 mph, so their average is still 1200. When the car stops, the fly
sees no significant change and just continues hovering where he is. He has
such a small mass that he does not have enough inertia to overcome the air
drag he would be experiencing and hit the windshield.
![]() QUESTION:
QUESTION:
How many Newtons are exerted when a 300 lb. man falls 3 ft.?
![]() ANSWER:
ANSWER:
Read faq page.
This question has no answer.
![]() QUESTION:
QUESTION:
We are working to produce a safety harness and the strap material we are using has a maximum Newton rating - we were trying to get an idea of what Newton rating would be needed to support a 300 lb. man if he fell 3 ft. Being hunters (tree stand safety harness) - perhaps we are wording the question incorrectly. Can you clarify your response?
![]() ANSWER:
ANSWER:
What matters is how long it takes the falling guy to stop. The mass
of a 300 lb guy is about 130 kg, the acceleration of gravity is 10 m/s2,
and so the weight of the guy is about 1300 N. You need that strong a strap
just to hang him there at rest. If he falls 3 ft (about 1 m) he will be
going about 4.5 m/s. So, let's call F the force needed to stop him
and t the time it takes him to stop; I reckon that F
![]() QUESTION:
QUESTION:
what is the upward force in pounds on the bottom of an empty
basin caused by a groundwater depth of 8 feet above the tank bottom? The
basin has a base of 300 square feet. What is the formula? This
is in regards to not emptying a tank fully for repair as the upward
force may displace it from its resting place.
![]() ANSWER:
ANSWER:
The key here is to find the pressure at a depth d (8 ft in
your case) below the surface of a liquid of density
![]() QUESTION:
QUESTION:
Please can you explain what
happens to the energy released by the shattering of a glass on a hard
surface? We are told that the energy on Earth has remained constant
since the formation of the planet so what is the fate of the energy
produced by this event?
![]() ANSWER:
ANSWER:
What makes you think energy
is released? Why does a piece of glass not just spontaneously break?
The fact is, you must put energy into the glass to make it break. If
you drop it, it has kinetic energy when it hits and then the surface
does work on it by exerting forces on it. So the question should be
what happened to the energy which got put into the glass to break it.
It takes work (energy) to break molecular bonds which were holding the
glass together before it broke; there goes some of the input energy. It
makes a big crash; there goes some more of the energy (sound). It will
heat up a little bit; there goes some more of the energy.
![]() QUESTION:
QUESTION:
I am revising some
poorly-written curriculum materials for my Integrated Technology class,
and have stumbled upon this paragraph:
"Energy can not be seen since, unlike matter, it has no mass. However,
it can be measured, sensed, or otherwise detected. For example, we
cannot actually see the energy of a light bulb traveling through air,
but we can see its illumination reflected from this laboratory manual
or the walls of this room."
While there is some correct information here, the statement that energy
can't be seen strikes me as wrong. It seems to me the issues are: 1) We
can only see energy in the visible portion of the spectrum and 2) it
must be directed toward our eye for us to see it. The fact that light
is not matter doesn't, in fact, matter. In fact, I would say that we
can't see matter without (visible light) energy.
Is my assessment correct (the explanation, as written, is wrong or at
least misleading), or can you illuminate me on this subject?
![]() ANSWER:
ANSWER:
It is most unsettling to a
physicist to read garbage like this! Energy is, simply stated, the
ability to do work. It comes in all forms, not just electromagnetic
(light). A moving car has energy due to its motion (kinetic). A falling
skydiver has energy by virtue of his altitude (potential). A cup of hot
soup has energy by virtue of its temperature (heat). A bottle of
gasoline has chemical energy stored which can, as you know, be
exploited. To speak about "seeing" energy is ludicrous; can you see a
moving car, a falling skydiver, a cup of soup, a beam of light? It is
also inaccurate to say that energy does not have mass; as we know from
the theory of relativity, mass is energy‚ÄĒyou know, E=mc2!
![]() QUESTION:
QUESTION:
A sky-diver is falling
toward earth. A tunnel has been previously excavated completly through
the earth at exactly the location of the skydiver's landing. He
continues his dive through the tunnel without touching the sides of the
tunnel. I believe that Newton would have had him stop at the earth's
core. Where would Einstein have him stop?
![]() ANSWER:
ANSWER:
First, since this is clearly an idealized
problem, let us neglect air friction (which is, of course, not
negligible because the skydiver has a terminal speed before he hits the
ground). Until he enters the tunnel he is accelerating with a constant
acceleration down. When he enters the tunnel, he experiences less and
less force as he goes deeper because there is less and less of the
earth pulling on him (all of the earth outside him exerts no force)
until finally at the center he has zero force on him but he has his
highest velocity of the whole trip since he has been speeding up the
whole time. Now as he moves away from the center he slows down. When he
reemerges at the other end of the tunnel he has exactly the same speed
as he had when he entered it. He continues until he reaches the
altitude from which he originally jumped at which point he turns around
and begins the process all over again. Newton an Einstein would both
agree on this. If air friction were included, he would not go as far
and if he happened to stop at the center of the earth, he would stay
there forever. If the air friction were included the general solution
to the problem would be that he would oscillate back and forth going
less far each time until he finally stopped in the center. There is an
interesting aspect of this problem: when the skydiver is inside the
tunnel, he moves exactly like he were a mass on an ideal spring.
![]() QUESTION:
QUESTION:
if their is a truck full of
birds and the birds are sitting at the bottom of a trailer ,does it
weigh the same as if all the birds are flying?
![]() ANSWER:
ANSWER:
There is more than one answer to this
question. Let us assume that the birds are hovering or moving with
constant velocities. In that case, each bird stays in flight because
the air exerts a force up on him equal to the bird's weight; but
Newton's third law requires that the bird therefore exerts an equal
downward force on the air. Therefore the net weight of the whole truck
is unchanged. All forces internal to a system cancel out in the
calculation of the net force on that system because of Newton's third
law. Another possibility would be if the birds have an acceleration
with a vertical component; the simplest example is that all the birds
are in freefall inside (probably not what you had in mind by "flying")
in which case the birds would not contribute to the weight (neglecting
any air friction or buoyancy). A similar question was
answered earlier which might interest you.
![]() QUESTION:
QUESTION:
If I shoot a modern arrow
straight up into the air with a bow that exerts 75 lbs of thrust does
the arrow travel to the top of it's flight in the same amount of time
that it takes to fall back to earth?
![]() ANSWER:
ANSWER:
A freshman physics class would say yes but
that is if you neglect air friction. On the way up the arrow has two
forces on it: its weight down and the air friction also down. On the
way down it also has two forces on it: its weight down and the air
friction up. The problem is complicated somewhat by the fact that the
air friction force depends on velocity, so it is not possible, without
stipulations on the initial speed and the details of the air friction
to determine which will be quicker, up or down, but since the forces on
them are definitely different if there is any air friction at all, the
times will definitely differ.
![]() QUESTION:
QUESTION:
Is it possible for a
helicopter to hover above the Earth and have the Earth move under as it
rotates so that the helicopter would "travel" around the Earth in 24
hours?
![]() ANSWER:
ANSWER:
Inasmuch as the earth drags its atmosphere
with it, the helicopter would have to travel at a speed much larger
than helicopters go relative to the air to remain in the same position
in space as you stipulate. So, no it is not possible.
![]() QUESTION:
QUESTION:
Does a hockey puck reach
it's maximum velocity at the last instant of contact with the hockey
stick, or is there such a thing as (for lack of the proper terminology)
'residual acceleration' I have considered this at great length..
>From what I know in physics if there is no longer force being
applied to the puck there should not be any accelertion after the
contact....
Almost a logical deduction.. however seeing replays and it's almost an
instinct telling me that I might be wrong.. It doesn't feel like the
stick is travelling at a the same velocity as the puck is.. 100mph
shots and all.. Perception maybe different than reality.. anyway, if I
am wrong and there the puck continues to accelerate for a short
distance after leaving the stick,. it's because of the flex in the
stick, the energy transfered into the puck has not fully caused it to
accelerate.. possibly like the flex in a golf ball..
![]() ANSWER:
ANSWER:
A short answer to your long
question: The puck cannot continue to accelerate (gain speed) after it
leaves the stick. In the physics sense, it does accelerate but with a
negative acceleration, that is it slows down.
![]() QUESTION:
QUESTION:
My question regards a
discrepancy between answers I get when I work a problem using two
different approaches. This problem was given to me several years ago,
and although I got the right answer then, I was told that I could have
also used a different approach. I have tried several times since to do
this problem the other way, but have had no luck. The problem is this:
if a pole of length L is stood on end and released, if the initial
velocity is neglegible, what is the final velocity of a point at the
end of the pole when it hits the ground. I believe I originally solved
this problem using the concept of the potential energy being converted
to kinetic energy (mgL=(1/2)mv2), getting an answer of
v=(2(g)(L))^(1/2). I am now trying to solve it using calculus by
integrating the equation v2=2ad over all da from 0 to 9.81m/s2 (where d
is the arc length of the falling pole), and taking the square root of
both sides. When I do this I end up with an answer of v=((
PI)(g)(L))^(1/2). What am I doing wrong?
![]() ANSWER:
ANSWER:
Neither of your methods is correct. The
second method, using v2=2ad is wrong because
this equation is valid only if the point has uniform acceleration which
it does not. The first method is incorrect because you treat the
stick as a point mass at the end of the stick falling straight down
which is not what is happening. The only way to solve this problem in
closed form is to use energy conservation as you have tried to do;
however, you must use rotational dynamics to do this. So the potential
energy at the beginning is mgL/2 because the center of mass of
the body is located halfway up the stick; the kinetic energy when the
stick hits the ground is Iw2/2 where
I is the moment of inertia of a the stick about its end
(which is ML2/3 for a uniform stick of mass M
and length L) and w is the angular velocity of the stick (which
is v/L if v is the speed of the point at the
end). If you now equate the energies before and after and do the
algebra, you will find v=(3gL)1/2.
![]() QUESTION:
QUESTION:
I am teaching physics at a
Kansas high school, and my students and I were debating over a problem.
The problem is as follows:
Two 20-N boxes are placed on both ends of an ideal rope. The rope is
then passed over two pulleys fixed on each of the two edges of a fixed
table, so that one 20-N box hangs on one pulley, and the other 20-N box
hangs on the other pulley (the rope being continuous over the two
pulleys).
We have been debating over the value of the tension in the rope,
whether it's 20 N or 40 N. Half of the class agrees with me that the
tension is going to be 20 N, but I cannot convince the rest of the
class that the tension is not 40 N, but rather, 20 N. (Or is it me
who's wrong?)
![]() ANSWER:
ANSWER:
Breathe easy--you are right! The tension in
this rope is 20 N. The tension at a point in a rope is defined as the
force which it exerts on what it is attached to. So you need to focus
on one box or the other. You now say, what are all the forces on that
box? One is its own weight which we know to be 20 N vertically down.
Another is the force which the rope exerts on it; technically we know
neither the magnitude nor direction of this force, but it is called the
tension in the rope at the point of attachment. There are no other
forces on the box. Since it is in equlibrium, all (both) forces must
add to zero, so the tension is 20 N straight up. And, for a rope of
negligible mass the tension must be the same everywhere on the rope;
otherwise if you inserted a tiny mass in the rope and the tension were
different on one side than the other, the tiny mass would not be in
equilibrium.
![]() QUESTION:
QUESTION:
If you were to drop an ice
cube and a shot glass from 4 feet up, which would land and break first?
Why?
![]() QUESTION:
QUESTION:
My question to you involves
the feather and bowling ball freefall experiement in a vacuum. Now I
understand that by removing the factors of air resistance that you free
up the feather to fall much faster than it normally would. But the part
I'm having trouble with is that they do indeed fall, gravity is
obviously still involved and the ball still outweighs the feather many
times over. In fact the term "weight" is defined by the amount of force
gravity exerts on an object's mass. (not totally clueless, I just look
like I am) So by that term should not the ball fall much more quickly
since gravity has that much influence on it?
![]() ANSWER:
ANSWER:
Since these two questions are so similar, I
will answer them with one answer. Ignoring or removing air friction
results in all falling objects as having the same vertical
acceleration, 9.8 m/s/s; that is the speed of any freely falling object
increases by 9.8 m/s as each second ticks by. Hence, the ice cube and
the shot glass and the feather and the bowling ball will all hit
simultaneously. To understand the "why" you need to know two things:
- Newton's second law states that the acceleration of an object is proportional to the force it experiences and inversely proportional to its mass; if we define a unit of force to be that which causes one kilogram to have an acceleration of 1 m/s/s, then a=F/m if F is in Newtons.
- An object's weight, the force which the earth exerts on it, is proportional to its mass. So we can write that W=mg where, for now, g is just some constant; if we measure the weight in Newtons and the mass in kilograms, then we find (by simply measuring) that g=9.8 m/s/s.
Putting these two things together for the case where the force in Newton's second law is the weight of an object, then a=W/m=mg/m=g. Note that m cancels out; this is the key to understanding. Although the weight is proportional to the mass, the inertia (resistance to acceleration) is also proportional to the mass, so all objects have the same acceleration.
![]() QUESTION:
QUESTION:
I am writing in the interest
of hopefully resolving a question which had arisen in my workplace. One
gentleman poses the hypothetical situation of a motionless tank sitting
on solid ice which he describes as "very slick and smooth - so much so
that if one were to toss a penny across the surface then it would glide
on endlessly." He posits that the tank is then started and attempts to
move forward. His position is that the tank will not be able to move as
the treads would simply spin on the ice. His detractor posits that the
treads are moved by the wheels inside the treads and that this would be
able to propel the tank forward. So, would this tank be able to move
forward or not? If so, what propertys of physics would make it be able
to move and, if not, why would this tank not be able to move forward?
The gentleman's scenario also posits that there is no friction between
the tank treads and the ice. Is it realistic, physically speaking, to
posit these two surfaces touching and no friction existing between them?
![]() ANSWER:
ANSWER:
How genteel you are! The gentleman who says
that the tank will not move forward if the ice is perfectly
frictionless is correct. It is the force of friction which accelerates
the tank forward, not the force which the wheels exert on the treads;
if the wheels exert a force on the treads, then Newton's third law says
the treads exert an equal and opposite force on the wheels so the two
cancell each other out. No it is not possible to have a perfectly
frictionless surface; it is possible to get a good enough
approximation, however, to do an experiment which should convince the
second gentleman.
![]() QUESTION:
QUESTION:
I recently heard that if you
shoot a bullet straight out with one hand and drop a bullet to the
ground from the same height with the other hand then both bullets will
hit the ground at the same time. Is this true and why. It would seem
that the bullet being shot would have much more energy behind it abd
take longer to expend that energy and hit the ground.
![]() ANSWER:
ANSWER:
This is what happens
assuming that there is no air friction (which is actually a pretty poor
approximation for something going as fast as a bullet). But, if there
were no air, they would hit simultaneously. The reason is that they
both move identically in the vertical direction, that is they both have
the same acceleration vertically whereas the one shot moves with
constant speed horizontally. So, imagine having a horizontal spotlight
which cast a shadow of the shot bullet on a screen, a way of looking
separately at its vertically motion. The shadow would move in exactly
the same way as the dropped bullet.
![]() QUESTION:
QUESTION:
If you were to drop two
equal boxes of equal dimensions built with the same material and you
filled one with ping pong balls and the other with bricks. You than
proceded to drop them both simaltaneously out of an airplane at 2000
feet. Which one would hit the ground first and why?
![]() ANSWER:
ANSWER:
In an elementary physics course you are
taught that all objects have the same acceleration, so from that
perspective the motion of the two boxes would be identical and they
would therefore hit the ground simultaneously. However, in the real
world there is air friction which is normally neglected when you first
learn about free fall. However, air friction is not negligible
particularly if speeds get very large. So, as you stipulate, the
geometries of the two objects are the same, they will both have equal
air friction for a given speed. However, when the air friction force
equals the weight of the object, it will stop accelerating and fall at
constant speed; therefore the lighter box will stop accelerating sooner
and therefore hit the ground later.
![]() QUESTION:
QUESTION:
I always wondered about this
question and was hoping you can shed some light on it for me.
I noticed on Star Trek, they have gravity on their spaceships. I know
this is a sci-fi program and realize its all fictional based on some
scientific facts. But, I always wondered , why can't we put gravity on
the spacestation we have orbiting our planet now?
I know we have simulated 0 gravity on earth. Why can't gravity be
simulated on a spacestation in space?
![]() ANSWER:
ANSWER:
The only way we know to "simulate gravity"
is to be in an accelerating frame of reference. If you are in a frame
accelerating down with an acceleration of 9.8 m/s2 near the
earth (e.g. a freely falling elevator) you will feel weightless. That
is why you are weightless in the space station because it is in free
fall, just like the elevator but it is a free falling projectile. To
create "gravity" you would have to have a local acceleration of 9.8 m/s2;
the way to do this is to have a very large donut shaped space station
(say maybe a few hundred meters across) which is rotating with the
right speed so that you could walk around the inside of the outer
surface feeling as if there were gravity.
![]() QUESTION:
QUESTION: 
The discussion is if there
was such a thing as a indoor wakeboard training facility would the
hydro dynamics be such that if water speed was equal in the following
scenarios could equal amounts of 'big air' be obtained.
- A 200# wake boarder is being towed behind a boat at a distance of 60' at 20 mph. The wake height is 24" high and has a 45 degree angle on the outside of the wake. The wake boarder has sufficient skill to cut in from outside the wake and obtain a height of 36" and travel 20'. Rope mounting height is 36" above water level.
- The same 200# wake boarder is in a wave pool capable of creating the same water conditions as being towed behind a boat at a distance of 60' at 20 mph. Same wake characteristics and same skill level from the same wake boarder. Will the Wake boarder be able to obtain the same height and distance as he would behind a boat? Same rope, rope height same everything.
Some of us say yes some say no. Some are of the opinion that forward momentum generated by the boat would enable greater distances to be obtained. Others say that the height and distance would be equal because it is the speed of the water going by and the ability to generate speed perpendicular to the direction of the water that provides the speed to obtain height and distance.
![]() ANSWER:
ANSWER:
You are going to have the water going by in
#2 with the same speed as the boat in #1--good. You are going to have a
wake with the same characteristics (same height and motion relative to
the wakeboarder)--good, although I am not convinced that it would be
easy to actually do this since the wake shape has to be essentially at
rest relative to the wakeboarder whereas the water per se is not. What
you do not talk about is the air. In #1 there is a significant wind in
the face of the wakeboarder so you better have a big fan for #2. I
believe that air friction will play a very important role after he
lifts off, that is he will essentially fly like a ski jumper. I think
that if you don't forget the air, it will be a pretty good simulation.
Incidentally, the boat has nothing to do with the mechanics of
the wakeboarder because they are not in contact so the boat cannot
exert any forces on him. Whatever happens to the wakeboarder depends
only on his interactions with water, air, and rope (and, of course
gravity).
![]() QUESTION:
QUESTION:
if you shot a bullet
directly up, when it came back down would its speed be the same as when
it left the gun or does terminal velocity prevent that.
![]() ANSWER:
ANSWER:
If there were no air friction, the speed
would be the same. But there is significant air friction which takes
kinetic energy away from the bullet, so it is going more slowly when it
hits the ground. Incidentally, because the earth is rotating, the
bullet would not hit precisely at the point from where it was fired
straight up.
![]() QUESTION:
QUESTION:
Usually when I get bored, I spin my chair. First I take a
spin with my legs in. When I strech my legs out, the speed decreases,
which is abvious because of the laws of the centrifugal force. The
weird think, though, is when I retract my legs again, the speed
INcreases after it has decreased. I asked my scince teacher about this
conundrum, and her suggestion was that perhaps I retracted my feet fast
enough to give my spin energy enough to spin faster. To me that just
doesn't seem right.
![]() ANSWER:
ANSWER:
First of all, there is no such thing as "the
laws of the centrifugal force", so though it may be obvious to you that
you slow down, it should not be! What you are experiencing here is
conservation of angular momentum. Angular momentum is the product of
the angular velocity (for example, the number of revolutions per
second) and the moment of inertia the object has relative to the axis
about which it is rotating. Moment of inertia is essentially a measure
of how far away, on average, the mass of the object is from the axis of
rotation. So, when your legs are in your moment of inertia is smaller
than when your legs are out. The angular momentum of an object remains
constant (is conserved) if there are no external torques on the system.
You and the chair spinning can be approximated as having no torque,
although there is some due to friction which will eventually, as you
know, cause your angular momentum to vanish (because you stop
spinning). But, over the short term, your angular momentum stays about
the same, so if you put your legs out your angular velocity must
decrease and if you pull them in, it must increase. This is the same
principle dancers and skaters use to increase their spin rate by
pulling in their arms.
![]() QUESTION:
QUESTION:
I was just wondering why when you rub two items together
(like your hand on carpet for example) heat is generated? Where does
that energy come from?
![]() ANSWER:
ANSWER:
It comes from you. When you cause the two
surfaces to move against each other you do work (a force acting over a
distance) and work adds energy to a system, in this case heat energy.
![]() QUESTION:
QUESTION:
A recently published book on baseball pitching claims that
an arm/hand assembly travelling at 31 mph will allow for a ball to be
released at 95 mph. The author's contention is that, because of the law
of conservation of momentum, the larger mass of the arm travelling at
31 mph will transfer momentum to the smaller mass of the ball, thus
causing it to accelerate to 95 mph in order to satisfy that law.
It is my contention that there can be no transfer of momentum unless
there is a sudden decrease in velocity of the carrier due to an
external force being applied, thus allowing the carrier to "give up"
it's momentum to the unconstrained object (the ball).
I proposed this question. What event has occurred from a point 1
millionth of a second prior to ball release and a second point 1
millionth of a second after release that causes momentum to be
transferred?
The masses of the arm and ball have not changed. Therefore, the only
variable in the momentum equation to change is velocity. If the
velocity is reduced by internal means, muscular relaxation, the
momentum will be not be transferred to the ball but dissipated within
the body. There is no external force, like a brick wall to stop the
arm, therefore there can be no transfer of momentum to the ball.
Am I correct here? Any help would be greatly appreciated.
![]() ANSWER:
ANSWER:
I feel quite certain that the speed of the
part of the "arm/hand assembly" (as you call it) which is in contact
with the ball is moving with the same speed as the ball when it is
released. It is totally fallacious to talk about the speed of the
"arm/hand assembly" because each part is moving with a different speed:
- the shoulder has a small speed due to motion forward of the body
- the elbow has a speed which is the vector sum of the velocity of the shoulder and the velocity of the elbow due to its rotation about the shoulder
- the wrist has a speed which is the vector sum of the velocity of the elbow and the velocity of the wrist due to its rotation about the elbow
- the hand (and ball) has a speed which is the vector sum of the velocity of the wrist and the velocity of the hand due to its rotation about the wrist
So, you see, it is not so simple.
![]() QUESTION:
QUESTION:
What would the effect on the
perceived gravitational pull of our planet if the rotation (or spin) of
the planet was increased by a factor of 4? I would assume that the
increased momentum at the outer edges would cause items on the surface
to experience a lower gravitational pull. Unfortunately, I can not
locate any equations to summarize this. Can you lend any assistance?
![]() ANSWER:
ANSWER:
The answer to your question
depends on where you are. The effect would be zero at the poles and
maximized at the equator. I will work it out for the equator. The first
thing you need to do is calculate your acceleration. Since you are
moving in a circle, your acceleration is v2/R=(2pR/T)2/R=4pR/T2=4x3.14x6.4x106/(3600x24/4)=0.17
m/s2; here v is the speed of something on the
equator, R is the radius of the earth, and T is the
period ("length of day" which you stipulate to be 24/4=6 hours). This
is the centripetal acceleration and the direction is toward the center
of the earth. The sum of all forces on you must add up to your mass (m)
times this acceleration. The forces on you are your own weight mg=9.8m
(down) and the force that the ground exerts up on you, call
it N. So we have N-9.8m=-0.17m, or N=9.63m.
The force N is the force by which you perceive how
heavy you feel, so you feel about 1.7% lighter than if the earth were
not rotating; if you were standing on a scale, which measures the force
you exert on it, not your weight, it would read 1.7% smaller than your
actual weight mg.
![]() QUESTION:
QUESTION:
Why do keepers of the famous
clock Big Ben in London add or remove coins from the bottom of the
pendulum to speed up or slow down the clock if the mass of pendulum has
nothing to do with the pendulum's period?
![]() ANSWER:
ANSWER:
Because Big Ben's pendulum is not a simple
pendulum, that is it is not a point mass attached to a massless string.
It is what is often referred to as a "physical pendulum" and its period
is determined by its moment of inertia and the moment of inertia
depends on how much mass there is and where it is.
![]() QUESTION:
QUESTION:
Hi, quick question, a few
friends and I had a little debate the other day. Basically the premise
of the debate was that if humans somehow started to dump all our
garbage into space the mass of the earth would be affected enough to
somehow affect earth's orbit. Their contention was that everything is
produced by the earth as in what humans make from it therefore if we
started jettisoning it into space it would affect earth's mass to alter
its orbit however miniscule. I saw something really wrong with this, in
my view there are many variables not being taken into account here that
affect earth's mass and its relation to the sun and its orbit and that
garbage is too small a variable or another counteracting variable would
negate any effect it could have if it was sent into space. Yes a little
bit of a weird topic lol, but any insight would be appreciated.
![]() ANSWER:
ANSWER:
If the earth's mass suddenly decreased by
half, the period of the orbit (one year) would be totally unaffected.
The period of the orbit of a satellite is independent of its mass if
the sun's mass is very large compared to the earth's mass (2x1030
kg vs. 6x1024 kg, a ratio of about 3/1,000,000). To
be exact, it is the reduced mass of the system which matters; that
would be msunmearth/(msun
+mearth), but, since msun>>mearth,
the reduced mass is incredibly close to mearth, and
the dependence of the orbit on the mass is completely negligible.
Technically, however, your friends are right that a change of mass will
affect the orbit; it is just that for even a huge change in mass (a
large fraction of the earth's total mass) the effect would be so small
as to be unmeasurable.
Another problem to consider is the possible disruption of the earth's orbit because of how the mass was ejected. For example, in the extreme case where you jettison half the earth's mass into space with some velocity the remaining half would recoil with the same velocity which would certainly seriously alter the orbit. But if you jettisoned a million tons, the earth's recoil would be negligible.
![]() QUESTION:
QUESTION:
what would happen if a small
hole was drilled right through Earth, that is from one side to another
going through the Earth's core, and I so happen to drop an object into
that hole, would the object fall right through, fall towards the middle
and stay there, or result in a ping pong effect? (Given that the
posibillty of creating such a hole is possible, without a catastrophic
event happening)
![]() ANSWER:
ANSWER:
This is a classic introductory physics
problem. The object will speed up until it gets to the center and slow
down until it gets to the hole opening at the other side, will then
start speeding up back toward the center, etc. If the earth is
modeled as having uniform mass density (which is only roughly
accurate), the motion of the object will be what we call simple
harmonic motion, that is it will behave exactly as if it were attached
to a giant spring.
![]() QUESTION:
QUESTION:
In physics class we performed an experiment called projectiles launshed
at an angle (to the horizontal). Now we made a setup where we let a
marble shoot away with the help of an elastic band. We then measured
the distance the marble travelled when letting it shoot from different
angles, 20, 30, 40,45, 50, 60, 70 degrees. I would appretiate some
theory concerning this experiment because I thaught that the marble
would reach the longest distance from the angle 45 but the distance of
the angles 40, 45 and 50 were very similar....would you please explain
to me a little about what a "fair test" is and what factors do
actually affect the range of this elastic band.
![]() ANSWER:
ANSWER: 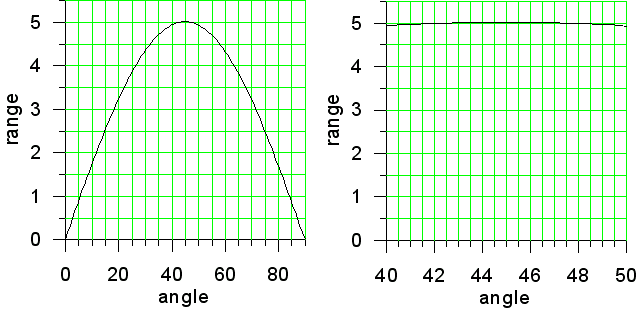
Well, an elastic band is not a terribly good energy source
because it tends to get "fatigued" with repeated use so it will not
produce reproducible results. But, even if you were using a
better launcher, say a good steel spring, your results would not be
surprising. The expression for the range of a projectile is R=v2sin(2q)/g where v
is the speed at launch, g is the acceleration due to gravity,
and q is the angle of
launch. To the right I have plotted the range as a function of
the angle for an experiment where the maximum range is 5 m. The
maximum is at 450. But the thing to note is how slowly
the range is changing when you are at angles close to 450;
the right-most graph is the same as the other graph except that it is
plotted only over the range 40-500. As you can see,
any angle in this range will give about the same value for the range--5
m.
![]() QUESTION:
QUESTION:
If action & reaction are always equal in magitude & opposite in
direction, why don't they always cancel one another & leave no net
force to accelerating a body?
![]() ANSWER:
ANSWER:
Newton's third law states that if one object exerts a force
on a second, the second exerts an equal and opposite force on the
first. Therefore, the "action/reaction" forces are never exerted
on one body. If you select a body to study, its motion is
determined only by the forces exerted on it, not by forces exerted by
it. Students often make mistakes with this "action/reaction"
thing because they tend to identify any pair of equal and opposite
forces as being an "action/reaction" pair. For example, a 1 lb
book sitting on a horizontal table has two forces on it, its 1 lb.
weight pointing down and a force of 1 lb which the table exerts up on
it (usually called the normal force); these have nothing to do with
Newton's third law but are equal and opposite because the book is in
equilibrium and the force the table exerts is therefore required to be
1 lb up. If we now look at the table, the book exerts a 1 lb
force down on it because of Newton's third law; the "action/reaction"
pair is the force the table exerts on the book and the force which the
book exerts on the table. Lots of novice physics students want to
say that the weight of the book is the 1 lb force down on the
table--this is totally false since this is a force on the book, not the
table.
![]() QUESTION:
QUESTION:
I am having trouble understanding torque. What is it? A
force? A tendency? Something else? Also, how does it differ from
inertia? Does it not resist circular motion? I am very
mathematical, so maybe an explanation and/or derivation of the formula
t=Fd could help me.
![]() ANSWER:
ANSWER:
It is difficult to come up with an answer since you ask a
question, "...how does it differ from inertia?" which indicates that
you know very little about rotational physics! I will try, but
you must first understand translational physics, where everything may
be treated as a point mass. In this arena, you might very well
ask "...what is force and how does it differ from inertia?"
- Inertia, which is called mass (m), is the property which measures how resistant something is to being accelerated (a) if it is pushed or pulled; the amount of push or pull, called force (F), measures how effective the push or pull is at causing acceleration. All this is stated, of course, by Newton's second law, F=ma.
In rotational physics the whole scenario sounds very much the same:
- Inertia, which is called moment of inertia (I), is the property which measures how resistant something is to having an angular acceleration (a) about some axis; that "thing" which causes the angular acceleration, called torque (t), measures how effective the "thing" is at causing acceleration. All this is stated, of course, by Newton's second law in rotational form, t=Ia.
For translational physics, the only thing which determines inertia is how much stuff (mass) there is; for rotational physics, inertia is determined by how much stuff there is but also how it is distributed: an object with most of its mass near its axel is much easier to get spinning than is an object with equal mass but much of it far from its axel. For translational physics, the force is determined only by hard we push; for rotational physics, torque is determined by how hard we push but also where we push and the direction in which we push. For example, suppose you want to open a door and you push as hard as you can but you push at the hinged end of the door; the door doesn't open, does it? This is because the torque increases as you increase the "moment arm", the distance from the rotation axis to where the force is applied (your t=Fd equation). Actually, your equation is a bit too simplified to completely understand torque. If you have an open door and push at the edge of the door which is opposite the hinges but you push straight toward the hinges, you do not close the door even though F and d are both big. It is really only the component of the force Fp which is perpendicular to d which contributes to the torque, so t=Fpd.
![]() QUESTION:
QUESTION:
Okay, I have a stick of mass M and length L held so that it makes and
angle theta with respect to the floor. The stick is not hinged on
the floor, and the contact between the end of the stick and the floor
is frictionless. I release the stick and it falls to the
floor. How do I find the horizontal distance the left end (the
end on the floor) travels during the fall? And with what speed
does the right end (the end initially in the air) hit the floor?
![]() ANSWER:
ANSWER:
This is easier than you think. Since there are no
forces which have horizontal components, the center of mass of the
stick must fall straight down. The distance the end will move is (L/2)(1-cosq). The second
question (not quite so easy!) should be addressed by energy
conservation. At the time the stick is released, it has only
potential energy E1=Mg(L/2)sinq . Just before it
hits, the speed of the end will be v and the speed of the
center of mass will be v/2. The energy, purely kinetic,
will be the kinetic energy of the center of mass plus the kinetic
energy about the center of mass: E2=(1/2)M(v/2)2+(1/2)Iw2=(1/8)Mv2+(1/2)(ML2/12)[(v/2)/(L/2)]2=Mv2/6.
Equating E1 and E2 now gives v=[3gLsinq ]1/2.
![]() QUESTION:
QUESTION:
I have been curious about this problem for some time. If a solid
ball of mass m and radius r is resting on a block of mass M and a
horizontal force is applied to the block, how would I find the maximum
value of the force F that moves the block without causing the ball to
slide. This assumes there is friction between the block and the
ball, but not between the ground and the block. I think F acting
on the ball has to equal the force due to friction between the two
objects, but I'm not sure if, when finding this frictional force, you
consider the mass to be m+M or just m. And I feel like I'm
leaving something out. Thanks!
![]() ANSWER:
ANSWER:
This is a tricky problem. We know the ball has a
frictional force forward on it given by f=mmg if the ball is about to
slip. Therefore, the center of mass of the ball has a forward
acceleration of am=mg.
However,
this is not the forward acceleration of the block. So now
consider the sum of torques about the center of mass of the
ball. This must equal the angular acceleration of the ball about
its center of mass times the moment of inertia of the ball about its
center of mass: t=fr=mmgr=(2mr(2mr2/5)(at/r)
where at is the acceleration of the rim of the ball with
respect to the center of mass of the ball. Therefore at=5mg/2. Now, since
the center of mass itself has an acceleration, then the acceleration of
the point of contact between the ball and the block as measured in the
laboratory is at-am=aM=3mg/2.; I have
called this aM because it is also the acceleration
of M since the ball is not slipping. So, finally, F-f=F-mmg=M(3mg/2), so F=mg(m+3M/2).
Note that the ball exerts a force on the block of magnitude f
backwards because of Newton's third law.
Note that I have used a theorem of classical mechanics: The sum of torques about the center of mass of a rigid body is equal to Ia even if the center of mass is accelerating.
![]() QUESTION:
QUESTION:
The extremes
of "perfectly elastic" and "perfectly inelastic" collisions are
somewhat confusing as most books show something between the
extremes. For instance, a billard ball that hits the billard
table's side bumper and moves away with the same constant velocity that
it approached with would have 0 change in the ball's momentum, because:
mass of ball * (+velocity) = (mass of ball) *(-velocity), hence net =
0, assuming only x component direction. Kinetic energy is conserved,
but momentum is not? s the way to think about this collision, or
think of a small object (the ball) colliding with a much larger object
(the table). Just seems "fuzzy"?
![]() ANSWER:
ANSWER:
Well, perfectly elastic simply means that kinetic energy is
conserved. Perfectly inelastic is a little more subtle since it
is defined as all the kinetic energy in the center of mass system as
disappearing in the collision; it is easy to recognize, though, since
it corresponds to the interacting particles being stuck together
afterwards.
The billiard ball collision you cite you have incorrectly analyzed. There is not zero change in linear momentum of the ball because linear momentum is a vector. The change is a vector away from the bumper with magnitude 2mv. The momentum of the ball is not conserved because there is an external agent which delivers an impulse (force x time) to it; that agent, of course, is the bumper. If you want to see momentum and energy both conserved, you must look at some isolated system: imagine the pool table to rest on a frictionless floor so that the system is the ball plus (the much more massive) table; then the table would recoil a tiny amount and the ball would have slightly less speed after the collision such that energy and momentum would both be conserved. In the limit that the mass of the table approaches infinity, the ball would have the same speed after the collision as before but the momentum of table would be nonzero after the collision even though it would be at rest! This is because zero x infinity need not be either zero or infinity. This assures momentum is conserved. Of course, there is no such thing as infinite mass and the real world has the table essentially at rest after the collision.
![]() QUESTION:
QUESTION:
My question is rather simple, but has created much
controversey among my friends and I. When I am at an amusement park, I
often wonder... Which part of the rollercoaster goes faster? The front,
or the back? I immediately come to the conclusion that the
rollercoaster MUST be going the same speed, in the front and the back.
My friends disagree with me, and say that the back is going faster. I'm
pretty sure that this is untrue. Could you explain the reason our
confusion, and give a brief answer.
![]() ANSWER
ANSWER
For a roller coaster, every car moves with the same
speed. The reason is that all the cars are constrained to move on
the track. If they were not constrained to move on the track,
however, one part of the train could easily move with a different speed
from another. Imagine, for example, that the train rotated around
the front car which was standing still (except for its rotational
motion); then each car, as you moved toward the other end, would be
moving faster than the one before. When I was a kid we used to
play "crack the whip" when ice skating: a long line of kids would skate
across a pond and the kid at one end would essentially stop and the
kids near the other end would get a very exciting and fast ride!
![]() QUESTION:
QUESTION:
At science centers, you can usually find the activity with
the bicycle wheel and a spinning chair? Can you explain the gyroscopic
precession principles involved with that activity and what makes you
spin when you change the angle of the bicycle wheel? Also, can you
please explain that using simple language...most websites I have
visited about this question are difficult for a layman to understand.
![]() ANSWER:
ANSWER:
Precession is not an issue here; rather, conservation of
angular momentum must
be appreciated. Imagine that you are holding a spinning wheel
with its axel pointing vertically and that you are standing on a
turntable which can rotate without significant friction. Although
there are external forces on you (your weight, the weight of the wheel,
and the force the table exerts up), none of these forces exerts any
torque on you and the wheel. The total angular momentum of a system
which has no external torques on it must never change which is what it
means to say that the angular momentum is conserved. Angular
momentum is a vector quantity. If you look down on the spinning
wheel and it is spinning counterclockwise, it has an angular momentum
vector which points up and has a magnitude which I will call L.
You are not spinning and have an angular momentum, therefore,
of zero. Therefore the total angular momentum of you + the wheel
is L upward and this is what it must always be. Now you
flip the wheel over so that the angular momentum of the wheel is L
downward, so the angular momentum of the wheel has changed by an
amount of 2L downward. But, the total angular momentum
cannot change so an angular momentum of 2L upward must pop up
somewhere; the only part of the system which can get angular momentum
is you, so you must start spinning such that your angular momentum is 2L
upward which means, since up means counterclockwise as seen from
above, you will spin counterclockwise as seen from above. Here is
a movie.
must
be appreciated. Imagine that you are holding a spinning wheel
with its axel pointing vertically and that you are standing on a
turntable which can rotate without significant friction. Although
there are external forces on you (your weight, the weight of the wheel,
and the force the table exerts up), none of these forces exerts any
torque on you and the wheel. The total angular momentum of a system
which has no external torques on it must never change which is what it
means to say that the angular momentum is conserved. Angular
momentum is a vector quantity. If you look down on the spinning
wheel and it is spinning counterclockwise, it has an angular momentum
vector which points up and has a magnitude which I will call L.
You are not spinning and have an angular momentum, therefore,
of zero. Therefore the total angular momentum of you + the wheel
is L upward and this is what it must always be. Now you
flip the wheel over so that the angular momentum of the wheel is L
downward, so the angular momentum of the wheel has changed by an
amount of 2L downward. But, the total angular momentum
cannot change so an angular momentum of 2L upward must pop up
somewhere; the only part of the system which can get angular momentum
is you, so you must start spinning such that your angular momentum is 2L
upward which means, since up means counterclockwise as seen from
above, you will spin counterclockwise as seen from above. Here is
a movie.
Incidentally, if you care, conservation of angular momentum is simply a consequence of Newton's first law in its rotational form. In translational form, Newton's first law says that, if there are no external forces on a system, the linear momentum will be conserved; in rotational form it is that, if there are no external torques on a system, the angular momentum will be conserved.
![]() QUESTION:
QUESTION:
I want to ask a few questions about "coefficient of friction"
1.Apart from experimentally determine the coefficient of friction
between two surfaces, is there any theotical way to do it? For example,
if we know the structure of the two materials, can we then proceed to
calculate the coefficent of friction, and if we can, how? What factors
(temperature, charge on the sufaces, etc.) are involved in the
calculation?
2.If we know the coefficient of friction between, say, surface A and
surface B and name if x, that between surface B and surface C be y, can
we then say that the coefficient of friction between A and C would be
at maximum x+y? Similarly can we say it be at least the minimum of
(x,y,abolute(x-y))?
3.In my textbook it tells me that coefficient of static friction
between two clean steel surfaces is approximately 0.6 and the
coresponding value of kinetic friction is still 0.6, which means the
value differ very little, the same is true for telflon, which in my
book it says both value are 0.04, however for lubricated steel
surfaces, the values for static and kinetic friction are 0.09 and 0.05,
which is nearly a double, the coefficient of static and kinetic
friction between two glass surfaces is 0.9-1.0 and 0.4, which is once
again nearly a double. What makes the difference between them? Is there
any pair of surface that has a great difference between coefficient of
static and kinetic friction?
Lasly is there any reference you would recommend me about this
topic?
Thanks very much for answering my questions.
![]() ANSWER:
ANSWER:
Ah, such an innocent-sounding question! Every freshman
physics student learns about the very simple idea of a coeffiecient of
friction, the proportionality constant between the magnitude of a
frictional force and the normal force (how hard the surfaces are
pressed together). And that there are two types, static and
kinetic, and that they are so easy to understand. But here is the
catch: f=mN is a statement of an
approximate experimental fact, not a law of physics. You cannot
derive it from known laws, you cannot deduce it from first
principles. Surprisingly, friction is fairly poorly
understood. I have gone to the website
for the Tribology (study of interacting surfaces) Laboratory at the
University of Florida and find the following statement: "When two
bodies are in contact and relative motion, a finite force is required
to maintain this motion, the friction force . A coefficient of friction
is calculated by dividing the friction force by the normal force. To
date, despite considerable efforts, there is no model capable of
predicting friction coefficients from first principles. Thus, careful
and proven experimental techniques represent the most sophisticated and
reliable technique for investigating, designing, and assessing the
tribological worthiness of new materials." The most famous
example of a large difference between static and kinetic friction is
the violin bow; here the instrument is excited by the bow repeatedly slipping/sticking
on the string. The two links I have given here would be good
places to start your research. Do a google search on "theory of
friction"; much of what you find will be quite technical.
![]() QUESTION:
QUESTION:
About that "moving molecules" question--let's say we had a
glass of water. The water molecules would have the "tendency" to form
hydrogen bonds with each other. Wouldn't we need a constant input of
energy to break these bonds and keep the water in a liquid state? If
so, where does this energy come from? Is it, for the most part,
radiation?
![]() ANSWER:
ANSWER:
The answer is pretty much the same as the one just
below. Yes, the water molecules want to bond to other water
molecules and that is exactly what happens when the water freezes to
ice. But they do not bond to each other if you have liquid water
above 00C because the kinetic energy which an average
molecule has is greater than the energy which is necessary to break the
bond. It is kind of like saying: suppose we have two heavy balls
which each are moving very fast in opposite directions and we decide to
tie them together with a little rubber band; the rubber band would just
break. However, if you take the kinetic energy away from the water
molecules (i.e. cool the water down) then eventually they will
bond together. Just as below, there is no need to "keep"
everything moving; Newton's first law takes care of that.
Incidentally, radiation has absolutely nothing to do with anything here.
![]() QUESTION:
QUESTION:
Can you explain to me what exactly KEEPS molecules moving?
With no energy being added, they should just eventually stop, shouldn't
they? Where does this energy that keeps them moving come from? In the
end, does it all come down to radiation from the sun?
![]() ANSWER:
ANSWER:
You have fallen into one of the most common traps regarding
misunderstanding how the universe works. Newton's first law
states that an object which experiences no net force will continue to
move with constant speed in a straight line. What this means is
that if something is moving and nothing is pushing or pulling on it,
then you do not have to do anything to keep it moving. In terms
of energy, if something has a certain amount of energy, then it will
retain that energy until some external agent changes it; this is called
conservation of energy. I am not sure what you have in mind with
your question, but probably the molecules moving around in a gas.
As you probably know, the temperature of a gas is a measure of the
average kinetic energy per molecule. If the gas is in thermal
equilibrium with the walls, then when a molecule hits the wall it
rebounds (on the average) with the same kinetic energy it had
beforehand. You don't have to do anything to keep it
moving. Incidentally, if Newton's first law were not true we
would never have sent probes to the distant planets like Saturn and
Jupiter or even the close ones like Mars and Venus. The reason is
that if we had to KEEP the probe moving by burning an engine the whole
way we could never carry enough fuel. What actually happens is
that we burn up almost all the fuel escaping the earth and acquiring a
high speed and then we just turn off the engines and coast the rest of
the way.
![]() QUESTION:
QUESTION:
I heard speeding up (gradually stepping more on gas pedal)
while driving on a long, sharp curve was better (safer) than slowing
down (gently braking). Is this true?
![]() ANSWER:
ANSWER:
Let us assume that the main safety concern in turning a curve
is the possibility of skidding. My answer will address that
concern. There are lots of other issues that could affect
"safety" such as whether you have better control while accelerating a
front-wheel or rear-wheel drive car, or whether you have a four-wheel
drive car, or the fact that braking occurs on all four wheels but
acceleration uses (usually) only two, etc. These are
engineering issues which I don't want to get into. In the safe
use of a car, the force of static friction between the road and
the wheels provides the force to brake the car, accelerate the car, or
move a car around a curve. The fact that it is static friction
confuses some people since the car is obviously not static.  However, if
all is well, the tires are at all times at rest where they touch the
road. An important feature of static friction is that there is a
limit to how much you can get; for example, if a heavy box is sitting
on the floor, you can push gently and it won't move, push harder and it
won't move, push harder still and it won't move...but eventually it
will "break away" and start sliding across the room. This is what
happens when you slam on your brakes and start to skid, "peel out" when
accelerating, or break into a skid when turning a curve too fast.
When you go around a curve, the static friction from your tires must
provide a force equal to mv2/R where m
and v are the mass and speed of the car (this could be smaller
for a banked curve) and R is the radius of the curve. Let
us assume that you are going through with the fastest speed possible so
that if you went any faster you would skid. This force is labeled
'turn' in the two pictures above which show the forces on the
"footprint" of a tire on the road; this 'turn' force is pointing toward
the center of the circle about which the car is turning. The two
pictures show what happens if you either accelerate or brake: an
additional force is required and the sum of the two, labeled 'net', is
bigger than the static friction can give and you will go into a
skid. Therefore, if you fear you might be approaching a curve
going too fast, you should do your slowing down before you
start the curve, don't try to do it while you are negotiating the
curve.
However, if
all is well, the tires are at all times at rest where they touch the
road. An important feature of static friction is that there is a
limit to how much you can get; for example, if a heavy box is sitting
on the floor, you can push gently and it won't move, push harder and it
won't move, push harder still and it won't move...but eventually it
will "break away" and start sliding across the room. This is what
happens when you slam on your brakes and start to skid, "peel out" when
accelerating, or break into a skid when turning a curve too fast.
When you go around a curve, the static friction from your tires must
provide a force equal to mv2/R where m
and v are the mass and speed of the car (this could be smaller
for a banked curve) and R is the radius of the curve. Let
us assume that you are going through with the fastest speed possible so
that if you went any faster you would skid. This force is labeled
'turn' in the two pictures above which show the forces on the
"footprint" of a tire on the road; this 'turn' force is pointing toward
the center of the circle about which the car is turning. The two
pictures show what happens if you either accelerate or brake: an
additional force is required and the sum of the two, labeled 'net', is
bigger than the static friction can give and you will go into a
skid. Therefore, if you fear you might be approaching a curve
going too fast, you should do your slowing down before you
start the curve, don't try to do it while you are negotiating the
curve.
![]() QUESTION:
QUESTION:
If there is a ball that is traveling on a vertical axis at
2m/s and hits a 45 degree angle, it will then travel at 2m/s to the
left. Now lets say that before the collision the ball and the angle
were traveling to the left at 3m/s relative to the planet Venus (or
whatever). After the ball collides with the angle it's total velocity,
relative to venus will be 5m/s to the left. Before the collision,
relative to Venus, the ball was traveling at 3.8m (I used the
pythagorean theorm with 2m/s and 3m/s). How is it that the ball has
increased velocity relative to Venus without any energy being added to
the system. The angle should only redirect the velocity. If the ball
hit any kind of angle that was fixed in space relative to Venus there
would be no way to change the velocity from 3.8 to 5. How is this
possible?
![]() ANSWER:
ANSWER:
I can answer your question, but you have made it far harder
than it need be. Furthermore, I am not sure that you have gotten
the velocity of the ball after the collision right for the second
scenario, but it doesn't really matter since we can look at a much
easier example (easier because it is a one-dimensional collision,
whereas yours is two-dimensional) and learn where this mysterious added
energy comes from. Suppose we have a ball which collides
elastically with a stationary wall; if the ball comes in with speed v
to the right, then it rebounds (to the left) with speed v
also--energy is conserved.  Now, if the
wall is moving toward the ball (to the left) with speed u, the
velocity of the ball after the collision will be v'=v+2u to
the left and the velocity of the wall will still be u'=u to
the left. How did I get these speeds after the
collision? Well, these are the speeds only if the wall has an
infinite mass. We get the results by conserving linear momentum
and kinetic energy for a collision of a ball of mass m and a
wall of mass M and then let M approach infinity.
So they are approximate solutions to the real problem if M is
enormously bigger than m which is what you are presumably
assuming. But these solutions cannot be exactly true because no
wall is really infinitely massive. But, if it were, it would have
an infinite amount of energy before the collision if it were moving; it
then loses the amount of energy which the ball gains, but if you
subtract a finite number from infinity you still get infinity. So
it sort of looks like energy materialized from nowhere but it really
comes from the infinite energy which the wall has! So, basically,
any energy which the ball gains must come from the wall.
Now, if the
wall is moving toward the ball (to the left) with speed u, the
velocity of the ball after the collision will be v'=v+2u to
the left and the velocity of the wall will still be u'=u to
the left. How did I get these speeds after the
collision? Well, these are the speeds only if the wall has an
infinite mass. We get the results by conserving linear momentum
and kinetic energy for a collision of a ball of mass m and a
wall of mass M and then let M approach infinity.
So they are approximate solutions to the real problem if M is
enormously bigger than m which is what you are presumably
assuming. But these solutions cannot be exactly true because no
wall is really infinitely massive. But, if it were, it would have
an infinite amount of energy before the collision if it were moving; it
then loses the amount of energy which the ball gains, but if you
subtract a finite number from infinity you still get infinity. So
it sort of looks like energy materialized from nowhere but it really
comes from the infinite energy which the wall has! So, basically,
any energy which the ball gains must come from the wall.
Incidentally,
the general solutions to the problem if M is not infinite are
v'=[(m-M)v-2Mu]/(m+M)
u'=[(m-M)u+2mv]/(m+M)
which you can show are approximately v'=-(v+2u)
and u'=-u for very large M, that is M>>m.
(The minus signs denote that they are both traveling to the left.)
![]() QUESTION:
QUESTION:
I have a question regarding Kinetic Frictional Force. The
magnitude of the kinetic frictional force is equal to the coefficient
of kinetic friction multiplied by the value of the normal force;
therefore, there is no dependence on surface area. Based on that, I was
wondering if it were fair to say that tire companies that advertise
that wider tires "grip the road" better than average size tires (made
of identicle material), are deceiving consumers? Since wider tires cost
considerably more, I was just wondering if they were misleading the
public or if there were other forces/laws that apply to this scenario
that do involve surface area.
![]() ANSWER:
ANSWER:
This is not an easy question you have asked! I did a
little research and here a few particularly enlightening answers to
this question which I have found (stolen!) on the web:
- "In
general, most of the responses were speculative, and centered on
factors such as the nature of the tire-road surface interface, heat
dissipation, tire deformation and elasticity, stability, and a myriad
of other environmental and engineering constraints. The 'best' answer
suggested that the tire problem did not fall under the standard Coulomb
(dry) friction parameters, thus using tires as an example was comparing
apples to oranges.
"Indeed, further digging supports the latter statement. According to Engineering Mechanics: Vol. 1, Statics (2nd ed), JL Meriam and LG Kraige, Wiley and Sons: New York, 1986, the coefficient of ROLLING RESISTANCE, while analogous to the coefficient of static or kinetic friction, is really an entirely different beast. It would be most difficult to describe fully without a free body diagram, but is a function of many factors, including, but not limited to: road and tire deformation and the resultant pressure over the area of contact, elastic and plastic properties of the mating materials, wheel radius, speed of travel, and roughness of the surfaces. Meriam and Kraige state, '... depends on many factors which are difficult to quantify, so that a comprehensive theory of rolling resistance is not available.'" (Plagiarized from Biomch-L Newsgroup)
- "This
is a good question and one which is commonly asked by students when
friction is discussed. It is true that wider tires commonly have better
traction. The main reason why this is so does not relate to contact
patch, however, but to composition. Soft compound tires are required to
be wider in order for the side-wall to support the weight of the car.
softer tires have a larger coefficient of friction, therefore better
traction. A narrow, soft tire would not be strong enough, nor would it
last very long. Wear in a tire is related to contact patch. Harder
compound tires wear much longer, and can be narrower. They do, however
have a lower coefficient of friction, therefore less traction. Among
tires of the same type and composition, here is no appreciable
difference in 'traction' with different widths. Wider tires, assuming
all other factors are equal, commonly have stiffer side-walls and
experience less roll. This gives better cornering performance."
(Plagiarized from physlink.com)
- "Now let's look at what happens at the tire-to-road interface. In a perfect physic's laboratory world, one usually asserts that the friction force (i.e., the braking force) between two objects is a function of two things: the coefficient of friction at the interface, and the normal force. (Muddying the waters more than a little bit is the fact that this is only true for two "smooth" surfaces sliding against each other. It doesn't take into account that rubber is relatively malleable, and tends to fill the small nooks and crannies in a roadway, thereby changing the nature of the "braking" problem into one containing both frictional and shearing-type forces. This turns out to be a VERY difficult complication. Worse, the vulcanized forms of rubber used in most automotive tires has rather weird coefficient properties that don't behave nice and linearly. But I digress...)" (Plagiarized from datsuns.com)
You can find a lot more by going to Google and searching on friction AND "surface area" AND tires.
![]() QUESTION:
QUESTION:
My physics students and I are debating which principle better
explains why airplanes and helicopters are able to fly - is it Newton's
3rd law or Bernoulli's principle? Also, if a helicopter is stationary
and you have a scale with enough capacity, can you measure its weight
while it levitates above the scale? Can an airplane do this if it were
able to levitate?
![]() ANSWER:
ANSWER:
Indeed, both are important in the design of a wing or a
helicopter propeller, but Bernoulli's principle is the more important
one (that is, normally the pressure difference due to the difference in
velocity of air over the top and bottom of a wing provides most of the
lift). Newton's third law (N-3) also plays a role for the
following reason: Because of the shape of the wing, the air which came
straight in before it encounters the wing leaves the wing with a
downward component of its velocity; the wing must therefore have
exerted a downward force on the air so, because of N-3, the air must
have exerted an upward force on the wing. The balance between the
two types of lift can be altered by changing the "angle of attack", the
angle which the wing makes with the direction of flight. If the
angle of attack becomes bigger, the air is thrust more in the downward
direction than otherwise, so N-3 becomes relatively more
important. (Although, changing the angle of attack also increases
the Bernoulli effect because the speed of the air over the top will be
greater relative to over the bottom when the wing is tilted.) I
would guess that sustained level flight with the airplane upside down
(which is possible) would depend primarily on N-3 and therefore require
a rather large angle of attack. Incidentally, there is a limit to
how much lift you can gain by increasing angle of attack; eventually,
air on the upper of the surface of the wing will be unable to flow
smoothly, will become turbulent, and all the Bernoulli lift will be
lost. This is called a stall. I have had some flying
lessons where stalls were purposely caused and I can assure you, the
plane begins falling like a rock which shows that N-3 alone will not
keep the plane in the air!
The answer to your second question is no. If you are standing under a helicopter which is hovering, you experience the downward force of the air which is thrust down. However, this force is nowhere near the downward force of the whole weight of the helicopter. If you were able to "gather" all this downward wind and if the wind lost no energy coming down from the helicopter, the net force down would still be much smaller than the weight of the helicopter. This again emphasizes that the role played by N-3 is relatively small.
![]() QUESTION:
QUESTION:
We recently had an unfortunate incident in Chicago where
scaffolding fell from the John Hancock Building and killed three people
who were in their vehicles. This led to a barroom discussion on what
could kill a pedestrian if it was dropped off the Empire State
Building. Some are of the opinion that something as small as a penny
could do the job. Others say it would have to be something the size of
a rock.
![]() ANSWER:
ANSWER:
This is a great question, but it does not (which is the case
for most "real-world" questions) have a simple answer. I think
that there are essentially four things you need to understand in order
to discuss the problem--force, pressure, acceleration due to gravity,
and terminal velocity.
- You probably know all about acceleration due to gravity. If there were no air friction then all objects would have a constant acceleration down of approximately 10 m/s/s. What this means is that when you drop something from rest, it will have a speed down of 10 m/s after 1 second, 20 m/s after 2 seconds, 30 m/s after 3 seconds, etc. I will not burden you with any equations but will assume that you will trust me to calculate for myself and tell you the answer of how fast something will be going after having fallen some distance or some time! Obviously, this will be necessary to us later.
- In the real world, there is air friction and this can seriously affect the acceleration due to gravity. Because the air friction depends on how fast something is moving (for example, imagine the force of the wind on your hand sticking out the window of a car going 20 and a car going 80), it turns out that instead of accelerating forever, a falling object eventually reaches some terminal velocity and then falls with constant speed after that. How big that terminal velocity is depends on lots of things, but very much on the size and shape of the object. Some examples: a parachute causes the terminal velocity to be so low (but only when open!) that you can safely jump out of an airplane with it; an ant could jump off the empire state building and experience no injury; in fact, cats have fallen out of apartment windows 40 stories up and survived; a dust particle has a terminal velocity so close to zero that it will stay in the air for years because of drafts pushing it back up every time it starts to fall.
- Of course, you know what force is qualitatively. Quantitatively force is mass times acceleration. So, for example, if you want to stop a 1000 kg (about 2000 lb) car going 10 m/s (about 20 mi/hr) in one second, its acceleration would have to be 10 m/s/s; the force you would have to exert is 1000x10=10,000 newtons (about 2500 lb).
I'll come back to pressure later. So, let's drop a penny off the empire state building and neglect air friction. I would guess that the height is something like 100 stories x 3 m/story=300 m. The speed it would acquire would be about 80 m/s. Now, it hits your head which must stop it before it enters the brain, maybe 5 mm inside. So, I figure that it must stop in about .0001 seconds which means that it must have an acceleration of 800,000 m/s/s! If we estimate the mass of the penny to be 1 gram=1/1000 kg, them mass times acceleration is about 800 newtons (200 lb). So your head must exert an upward force of 200 lb on the penny and the penny, therefore, will exert a force of 200 lb down on your head! So the question is, could your head withstand such a force? Yes and no. Imagine a penny laying on your head and a 200 lb man standing on it. This would quite likely not cause your skull to be crushed. On the other hand, imagine a penny standing on its edge and a 200 lb man standing on it. In all likelihood, his weight would drive the penny through your skull. So, if the penny hit you flat side, you would probably survive. If it hit you edgewise, you might not. If you now factor in air friction, the penny would be going slower, maybe only half as fast; so in the final analysis, I would say you have a fair chance of surviving a penny strike. Something much more massive than a penny, say baseball, would almost certainly do you in since the force is proportional to the mass and the final speed would be about the same.
- Finally, why is the penny more dangerous on its edge than on its side? Because in the former case the whole force is spread over a much smaller area of your head than in the latter. Force per unit area is called pressure, and pressure on your skull is more indicative of strength against breaking than force is. A sharp dagger dropped from the second story of a building would have no problem getting through your skull because the force is all applied over essentially a point so the pressure is almost infinite.
![]() QUESTION:
QUESTION:
We know that when a ball is thrown it is being affected by
air resistance, lighter balls will then have a short range (as a ballon
does), heavier balls, due to its mass, will have smaller initial
velocity and thus have a short range also. So I'm going to investigate
which texture (density) of ball will have the longest range. However, I
have encountered a few problem.
1. Should I assume my hand exert constant force or constant power?
2. In deducing the equation for the range, I came across with the
following equation:
1/R * LN(1-(bR/mvCOS(z)))=bTAN(z)/mg - (b^2)/(v(m^2)COS(z))
where R is the range, m is the mass of the ball, z is the angle of
projection, b is the resisive parameter (I assume air resistance to be
bv), and g the gravitational acceleration. But I'm not able to
solve for R, can you help me solve that?
![]() ANSWER:
ANSWER:
You have several serious misconceptions here which you should
surely straighten out by doing more reading and research. The
trajectory of a projectile is determined solely by its initial
velocity, the constant you refer to as b, and, if b is
not zero, the mass. Your statement that "heavier balls, due to
its mass, will have smaller initial velocity" is wrong. Initial
velocity is whatever you give it. So you make a mistake to think
of your hand as having anything at all to do with the problem. I
am not saying that mass has nothing to do with the problem, but it
enters only in a subtle way as you will see below; if there were no air
friction, the trajectories of all objects with identical initial
conditions are identical. But mass is not the only thing which
determines what the effects of air resistance will be. For
example, a parachute surely has much more mass than a BB but encounters
enormously more air resistance. If you want to do an experiment
comparing trajectories of different things, you will need to figure out
how to give those things all the same initial conditions (particularly
speed and direction at the beginning). Once your hand or whatever
is no longer in contact with the thing, your hand or whatever is
irrelevant.
So, you found a formula and you want me to solve it! First of all, there is an error in your formula (you are missing one minus sign). The correct formula is ln(1-x)/x=-[1+(bv/(mg cos(z)))] where x=(bR)/(mv cos(z)). I should tell you that this is a well studied problem and is standard in almost all intermediate level classical mechanics textbooks, so you will find this formula in just about any classical mechanics textbook. It is, alas, what is called a transcendental equation, that is one which cannot be solved in closed form. That doesn't mean you can't solve it for a specific case (specific b, m, z, v), you just have to do it approximately or numerically. Since R is the only thing you are varying for a specific case you could, for example, program a computer to keep computing the left side of the equation until it was close enough (say within 1%) to the right side of the equation. Or, you can solve it graphically. Since your formula is of the form
ln(1-x)=-Cx
where C is just some constant and x is proportional to R. So, if you plot both ln(1-x) and -Cx vs. x, where they cross will be the x corresponding to the R you seek. An example, for C=2 is graphed to the left.
Finally, there is an elegant way to approach the problem if x is very small. By small I mean small compared to one; notice that x cannot be bigger than or equal to 1 because ln(0) is negative infinity and logs of negative numbers do not exist (for your purposes). In that case you may approximate ln(1-x) as the first few terms of a power series expansion, -x+x2/2-x3/3. Using this you can show that you may approximate R=(2v2 sin(z) cos(z)/g)[1-(4bv sin(z))/(3mg)]. This is a formula which you can evaluate directly, but don't forget that it is approximately correct only for (bR)/(mv cos(z)) small.
An excellent reference for this topic is Mechanics by Keith Symon published by Addison-Wesley but many other texts will cover it also.
![]() QUESTION:
QUESTION:
I have recently being investigating, damping of a rigid
pendulum? I used the equation y1=y0e-kt
(the -kt is to the power of e, y0 is the initial amplitude
and y1 is the final amplitude). I damped the pendulum using
different areas of card and timed how long 5 oscillations took. I would
like to know how I would justify using 5 swngs and not 10 for example?
I had to draw a graph of Area against k. I found that T(period) is
independent of area. However, I would like to find out if I could
expand this investigation to obtain more results. Also, is it true that
a simple pendulum is an approximation of simple harmonic motion? and
does s.h.m only occur when there is a small amplitude?
![]() QUESTION TO THE
QUESTIONER:
QUESTION TO THE
QUESTIONER:
Please clarify what you mean by area.
![]() REPLY:
REPLY:
We used card to dampen the ruler, by place it at right angles
to the plane of oscillation. To vary the damping, I varied the
area(centimetres squared) of card.
![]() ANSWER:
ANSWER:
OK, so the picture I have is that you used a ruler as a
pendulum and you attached cards of varying areas to the end and
perpendicular to the direction of swing to induce varying air
friction. Let me first answer your last question: as you state
correctly, a pendulum is not an example of simple harmonic motion, one
characteristic of which is that the period is independent of the
amplitude. However, to a very good approximation it is SHM if the
amplitude is not too large. For a pendulum, amplitude is the
maximum angle through which it swings. How large is too
large? That depends on how accurately you measure things.
My guess is that you are using a stopwatch or maybe just the second
hand of a clock to
 measure times; you would probably find constant
periods for your pendulum up to maybe as large as 400.
In fact it would be an interesting extension of your study to measure
period as a function of amplitude: measure the period for amplitudes of
say 100 to as big as you can get (if your ruler is mounted
so that you can have amplitudes bigger than 900 you could go
all the way up to almost 1800.) If you then plot your
data you should find a straight horizontal line up to some maximum
angle and then it should go up.
measure times; you would probably find constant
periods for your pendulum up to maybe as large as 400.
In fact it would be an interesting extension of your study to measure
period as a function of amplitude: measure the period for amplitudes of
say 100 to as big as you can get (if your ruler is mounted
so that you can have amplitudes bigger than 900 you could go
all the way up to almost 1800.) If you then plot your
data you should find a straight horizontal line up to some maximum
angle and then it should go up.
Now, we come to the crux of your
experiment which, as I see it, is to observe the effect of damping on
the motion. So you measured the time of five oscillations and
found that you got the same answer for all dampings. This is a
good start. What you have shown is that different small
oscillation pendula with different damping (that is different k because
that is what you vary by changing the card area) all have the same
periods. In fact, that is what you are supposed to find if you
study the theory of the damped oscillator which predicts that you get
exactly the same oscillatory motion except that the amplitude decreases
exponentially as a function of time. The graph to the left shows
what theory predicts. You see that the damped oscillator has
exactly the same period as the undamped one. So you have verified
that aspect of the theory. However, what you need to do now are
some measurements of the amplitude as a function of time and see if it
really is exponential. The way you would do that is to measure
the angle of the pendulum each time it reaches the amplitude (when you
release it, one half period later, one half period later, etc).
This is a little trickier measurement since you would have to tape an
angle scale to the wall or something like that. What would be
really cool is if you could take a video of it and then make the
measurements on the tv or computer screen. If the theory is
right, then you should get a series of points which can be plotted vs.
time (one half period per point) which fall off like the blue lines
above. And, the data for different damping should now look different
with the larger cards falling faster than the smaller cards. Now,
finally, if you are good at math, you should be able to extract the
constants k for each card so you can see how k depends on area.
The easiest way to do this is to plot your data on semilog graph paper
(or plot the logarithm of amplitude vs. time); if the data are
truly exponential, you should get a straight line and k is essentially
the slope of that line.
Incidentally, when measuring these amplitudes it would be a good idea to use a very long pendulum so that the period becomes much bigger because it would be easier to measure because it would go slowly longer near the end of each swing; and you could tape a more accurate (that is bigger) angle scale to the wall which would be easier to read.
![]() QUESTION:
QUESTION:
Hi!
I'm involved in a "science problem of the week" contest. The idea is to
research each question, making contact with anyone who might be of
help. Perhaps you could assist me with this latest question?
Thanks!
Consider the following scenario...
In this situation, a person sits in a seat and pulls down on a rope. As
a result, the seat and the person in it rise up. If the seat and
a man together weigh 180 pounds, with how much force must the man pull
down on the rope in order to raise himself and the seat up with a
constant speed?
![]() ANSWER:
ANSWER:
This is a
classic problem often appearing in textbooks. Shown in the figure
above is the picture from Serway's text Physics for Scientists and
Engineers (I'm probably violating some copyright by reproducing
it!) So I will refer to the boy and swing instead of your man and
seat since that is the picture I found. Since the boy and swing
are to move up with constant velocity, this is a Newton's first law
problem, i.e. the sum of all forces on anything you choose to
look at must add up to zero. The easiest thing to look at is the
boy+swing. The forces on the boy and swing are its 180 lb. weight
(down), the tension of the rope tied to the swing (up),
and the tension of the rope the boy is pulling on (up).
But the ropes tied to the swing and on which the boy is pulling are the
same rope so they have the same tension. Therefore, twice the
tension in the rope must equal 180 lb, so the tension in the rope is 90
lb. Technically, the problem has not yet been solved since what
is asked for is how hard the boy must pull down on the rope and we have
found how hard the rope pulls up on the boy; however, Newton's third
law tells us that these two forces must be equal and opposite, so the
final answer is 90 lb down.
![]() QUESTION:
QUESTION:
When placing an hourglass on a scale, will its mass increase,
decrease, or stay the same as the sand is falling?
![]() ANSWER:
ANSWER:
Here is a question with just layers and layers of
answers! I will address all the possibilities I can think of:
- First, let's just think of the problem purely classically (relativity is an issue as you will see below). Let us assume that the hourglass has nothing in it except sand (in particular, there is no air). During the time the sand is transferring from the upper to the lower chamber there is, at any time, a fraction of the sand falling and therefore not exerting any downward force on anything. Therefore, during the time the sand is falling there will be some fraction, say 1%, of the sand not being weighed, so the scale will read less at this time.
- Next let there be air in the hourglass. During the time when sand is falling the air will exert two upward forces on the sand, a frictional force and a buoyant force. If the air exerts an upward force on the sand, then Newton's third law stipulates that the sand exerts an equal but opposite force on the air which is part of the system being weighed, so the amount by which the weight is less will be smaller than if there is no air in the hourglass.
- A possibility related to part 2 of the answer is that, if the forces upward on the sand are not small compared with the weight of each sand particle (for example think of the particles of sand as being a very fine powder or think of the hourglass being filled with molasses), then the falling particles will quickly acquire a terminal velocity where the upward forces are exactly equal to the weight of the particles; in this case the hourglass system will always have the same weight as the sand falls.
- Another small effect is that the earth's gravitational field is not really uniform, that is the weight, which is just the force which the earth exerts on the sand, gets bigger like 1/r2 as r decreases where r is the distance to the center of the earth; it is weight, not mass, which the hourglass measures. Therefore the total weight when all the sand is in the bottom will be larger than when it was all in the top. This is a very small effect since the radius of the earth is about 6,400,000 m and the distance the sand falls is only something like 10 cm, so this effect will cause the weight to increase by an amount (I calculate) of about 3x10-6%!
- Now we come to relativistic effects. Einstein says E=mc2 where E is energy, m is mass, and c is the speed of light (about 3x108 m/s). Let's think about the energy of one grain of sand. At the top it has, relative to the bottom, a gravitational potential energy of mgh (where m is the mass of the grain of sand, h the distance it falls, and g the acceleration due to gravity) and no kinetic energy. Let us ignore effects like 2-4 above for purposes of clarity, so imagine an evacuated hourglass in a uniform gravitational field. As the sand falls its potential energy gets smaller and its kinetic energy gets larger, all the while keeping the total energy the same. When it hits the bottom, all of its energy is kinetic and equal in magnitude to mgh; but now it stops so this energy disappears. Or does it? No, energy is still conserved because the kinetic energy will be converted into heat and the sand+hourglass will warm up a bit. But, if we suppose that the whole system will then cool back down to the same temperature as its surroundings eventually, there has been a net loss of energy Mgh where M is the mass of all the sand. But a loss of total energy means a loss of total mass because E=mc2, so the change in mass is DM=Mgh/c2; if we again take the size of the hourglass (h) to be about 10 cm, I find DM/M=10-17 or about 10-15% change in mass!
In summary,
- #1 decreases the mass measured by something on the order of 1% while the sand is actually falling;
- #2 and #3 cause the effect in #1 to be smaller or zero;
- #4 increases the weight measured (but not the mass) by something on the order of 10-6% after the sand has fallen; and
- #5 decreases the mass by something on the order of 10-15% after the sand has fallen and cooled down.
This is probably way more than you wanted, but the answer you wanted should be in there somewhere! And, I had fun thinking about it!