QUESTION:
ANSWER:
QUESTION:
ANSWER: Wikepedia
definition of entanglement: "Quantum entanglement is
a physical phenomenon that occurs when pairs or groups of particles are
generated or interact in ways such that the quantum
state of
each particle cannot be described independently—instead, a quantum state may
be given for the system as a whole." This is custom-made for electrons in an
atom. The mathematical way of dealing with the Pauli exclusion principle in
a system is called antisymmetrization of the wave function. The result is
that you cannot label the electrons, all electrons are also part of all
other electrons in the system. The Z electrons in an atom are an
excellent example of an entangled group of particles, not just pairwise but
with all the other electrons.
QUESTION:
ANSWER:
QUESTION:
ANSWER:
f
is synonymous with energy E through the relation E=hf .
QUESTION:
ANSWER:
QUESTION:
ANSWER:
QUESTION:
ANSWER:
isolated system will
be conserved. Also because of the uncertainty principle, energy conservation
may be violated but only for very short times. Approximately, Δt ΔE <ħ
where ħ≈ 10-34 J∙s. So this means that the energy of a
system could increase by 10-34 J as long as it went back before 1
s had passed.
QUESTION:
ANSWER:
video animation
(it's in the Brief History… section,
Animation showing the wave-particle duality which illustrates the double slit for particles, waves,
particle-waves, and particle-waves where an observer determines the slit
through which slit the particle went through.
QUESTION:
ANSWER:
QUESTION: This might seem dumb, but i cannot understand the laws of thermodynamics applied to gravity.
If a moon orbits a planet in a stable orbit, it still pulls on the planet, and the planet pulls on the moon. This seems to generate heat (the heatsource on europa) and motion (tidalwaves on earth). How can this not violate the laws of thermodynamics?
ANSWER:
tidal forces which result
from the sizes and relative masses of the two. Just what the effects of the
tidal forces are depends a lot on the relative sizes and distances of the
two, but, as you note, often appear to violate energy conservation. So,
let's look at that more closely. Soon after the moon was created, probably
by a cataclysmic collision with an asteroid, it was much closer to the earth
than today and it rotated on its axis at a much faster rate than it does
today (about 28 days, which is why it always shows the same side to us). The
tidal force caused what is called "tidal locking", the same side always
facing the earth. It would seem that this would represent a loss of energy
since it is not spinning as fast as it used to be, but as this happened, the
moon moved farther and farther away from the earth which represents an
increase in energy. So, the energy of the whole system stayed the same.
Today, the tidal effect is mainly due to the ocean tides on the earth and
now it is the earth which slows down its rotation—the earth is losing
rotational kinetic energy and tending toward being tidally locked with the
moon. This is an extremely small effect—a day gets about 2 milliseconds
shorter during one century. But, just as was the case when the moon was
slowing down its rotation, the way energy is being conserved is by the moon
moving farther away, resulting in an increase in the earth-moon energy
keeping the total energy constant. If the tidal forces are great enough to
cause significant frictional heating because of the tidal force distortion
of the whole moon (your Europa example), energy is lost because some of the
heat is radiated into space. So the first law would be violated, but you
would expect that since some energy is escaping from the planet-moon system.
You can see that your error was to assume a "stable orbit".
QUESTION:
ANSWER:
QUESTION:
How is it possible to measure the the distance between an electron and a nucleus? I don't mean calculate, but measure. In other words, what is the operational definition of the Bohr radius?
ANSWER:
QUESTION::
ANSWER:
mc 2 )
of a hydrogen atom is about 1 GeV. Therefore, since you have added energy by
ionizing the atom, the atom is lighter by about 100x13.6/109 %≈10-6
%. Any molecular binding energy will be of the same
order-of-magnitude. The energy we get from chemistry comes from mass and it
is extremely inefficient. So, although E=mc 2 is at the
heart of things, you usually do not have to worry about mass changes in
molecular chemistry because they are so tiny. To do detailed calculations of
chemical reactions usually requires that you do things quantum mechanically
which requires a potential energy function. These calculations can be very
complex and approximate models are used to simulate the potential energies
of the molecular systems. Once you get beyond the simplest atoms and
molecules, the calculations can only be done numerically and approximately
on computers. An example of a potential energy function, the Morse
potential, for a diatomic molecule is shown in the figure to the left. The
form of this potential is V Morse =D e [1-exp(-(r-r e ))]2 ;
note that, for one of the atoms in the molecule, the force (slope of the
potential energy function) is repulsive for r<r e and
attractive for r>r e . This is expected since the molecule
has a nonzero size because of repulsion but is bound because of attraction.
A first approximation often used for bound molecules is a harmonic
oscillator potential (masses attached to a spring).
QUESTION:
It seems to me that bubble chambers provide information (e.g. particle position and momentum) that violates the Uncertainty Principle. Please explain why this is not so.
ANSWER:
x ~10-4
m and momentum information maybe accurate to Δp ~10-21
kg∙m/s. so Δx Δp ~10-25 kg∙m2 /s. The
uncertainity principle states that the product Δx Δp cannot
be smaller than approximately ћ~ 10-34 kg∙m2 /s.
The bubble chamber measurement is nowhere close to this.
QUESTION:
I am, for the most part, a biologist, but I always have found physics to be a curious subject and used to study it for a year or two. One of my questions that I hope you can answer involves quantum tunnelling. I am familiar with the basic concept of tunnelling; since quantum objects are "smeared" over an area, they have a small chance of spontaneously crossing a thin enough barrier.
What I am curious about, though, is to what extent this can occur. I have some heard people say that two protons, left to themselves for a long enough time, can spontaneously fuse into a deuteron. I have also heard that, given a long enough time, a car could quantum-tunnel out of its garage, an electron in my fingertip one second could instantly appear at Betelguese the next, or a rock could on incredible timescales behave like a liquid as atoms tunnel out of crystalline strucutres.
What I am curious is - is this actually possible? If my understanding is correct, particles can tunnel but only within a restricted area determined by its mass; an electron can go anywhere in a wide circle, a C60 fullerene may tunnel a distance about its own size, and a comparatively large structure like a virus cannot tunnel since the restricted area is less than its actual size. Could you please explain if it is theoretically possible for anything to teleport anywhere given enough time, or if my understanding is correct tunneling becomes impossible after a certain point?
ANSWER:
single,
concise, well-focused questions" but I will touch on a couple of aspects of
tunelling. To the right are shown probability distributions — the
first for lowest energy, the second a much higher energy — for
a mass on a spring (simple harmonic oscillator, SHO). Classically, when you
set the mass in motion, it oscillates between two points equidistant from
the equilibrium position; those points are shown by the red lines in the
figures. The faster you cause the mass to go (the higher its energy) the
greater the distance between the points (we say the greater the amplitude of
the oscillation) will be. These are called the turning points and if you ask
what the kinetic energy is beyond the turning points, you get a negative
value and since kinetic energy is positive definite all the time, this is
called the forbidden region. The probability distributions for the classical
cases are shown by the green lines and you note that it is most probable to
find the mass near the turning points because it is moving slowest there and
therefore spends most of its time there. The blue lines show the
probabilities for quantum mechanical calculations. If the energy gets very
high, the quantum calculation becomes, on average, much like the classical
calculation. But at low energies it is very different; the lowest energy
state, called the ground state, has the highest probability for the quantum
system in the center which is the lowest probability for the classical case.
But the most interesting thing is that the quantum calculations predict that
there is a probability that the mass will be in the forbidden region and
therefore it will spend part of its time there. You can never actually
observe the particle there but you can prove that it was there by observing
tunneling. Here is my proposed experiment. Looking at the ground state, the
amplitude is
x =±1;
suppose we design a spring so that it behaves normally as long as
x <1.5
but breaks when
x =1.5.
Then classically we will never see the spring break because the mass never
got there. But, quantum mechanics predicts that, if you wait long enough,
the spring will suddenly break and the mass will fly away. This is
tunneling. Perhaps the most famous example of tunneling is the theory of
alpha-particle decay of heavy elements. The graph to the left shows this
tunneling, showing the energy plotted as a function of the distance of the
alpha particle from the center of a nucleus in which it is bound. The gray
area is called the potential barrier the outline of which is simply the
potential energy of the alpha particle. To make this more intuitive, the
slope of the potential energy represents the force experienced by the
particle whose energy here is a little less than 10. Inside the surface of
the nucleus, the slope is very large from which we can conclude that the
particle is confined to move inside a radius of about 10 fm, and this would
be the classical turning point. However, this is a quantum mechanical
particle and its probability distribution penetrates into the forbidden
zone. But, at larger distances away the force on an alpha particle is very
different; because it and the nucleus are both positively charged, an alpha
particle outside to the right will be repelled which is what is represented
by the gradually decreasing height of the right side of the forbidden
region. Because of the nonzero probabilty in the barrier, it is possible to
leak out and it does —that
is, alpha decay does occur. But even in this microscopic case, lifetimes are
usually very long, millions of years or more.
Your other questions are mostly about
macroscopic things. The car is not like a single particle which might be
thought of as having a wave function and there is no single force on all the
pieces of the car so it becomes about impossible to even think about it.
Even if the car did behave like a single particle, it would be so classical
that any penetration into the forbidden region would be so small that you
would have to wait many universe ages for anything to happen if the car were
in its "in the garage ground state". Two protons are not going to fuse into
a deuteron because charge would not be conserved. An electron in your finger
will not appear somewhere far away; you are maybe confusing tunneling with
entanglement.
QUESTION:
A photon is created when an electron returns to its original energy state (I think). How/when does a photon die? Does it die? Does it run out of energy?
ANSWER:
If a photon encounters an atom like the one that
made it, the photon can excite the electron up to the higher state
again, thereby disappearing.
If it encounters an electron, the photon can
give the electron all its energy; this is called the photoelectric
effect.
If it encounters an electron, the photon can
scatter from the electron thereby losing part of its energy; this is
called the Compton effect.
If it has enough energy, it can interact with
the electric field of an atomic nucleus and spontaneously create an
electron-positron pair; this is called pair production.
The bottom line is that photons must find something
to interact with or else they will live (as far as we know) forever.
QUESTION:
I was wondering, since in quantum phisics observing a phenomenon can change the odds of this phenomenon to arise, how can a detector in a particle accelerator can be trusted? shouldn't it already vary the result simply by measuring them?
ANSWER:
that
particular particle to be 100% of what you measure. If, however, you
make many measurements then you can deduce the distribution of
probabilities. One measurement never gets you any useful information in
quantum mechanics. For example, suppose you want to measure the mass of a π0
meson. This particle decays into two photons, so, if you measure the enegies
of the two photons and add them, this is the rest-mass energy (E=mc 2 )
of the meson from which you can easily deduce the mass (m=E /c 2 ).
The graph to the right shows the results of many such measurements. Don't
worry about the units. The fact is that you might make one measurement which
gives you the mass and find that you get that m =0.026 units. You have
found that the meson you measured had that mass, but if you keep measuring
you will find that others have different masses; you have not caused all
mesons to have a mass of 0.026 units just because you determined one to have
that mass. You would be inclined to call the mass of the meson to be
approximately 0.020 units (the most probable value) with a distribution
determined by the rest of your data; the spread of these data, incidentally,
would tell you about how long this particle lives, on average, before
decaying into two photons. (Oh, by the way, any given meson has the whole
distribution of masses before you measure it; measuring it "puts it" at the
mass you measure. In other words, a particle does not have a definite mass
but a probability distribution of possible masses. Only if the particle is
stable (like an electron) does it have a definite mass.)
QUESTION:
Not, a physicist or even a student, simply a curious nurse. I was reading the papers explaining EPR and wanted to know if i was begining to understand this of if I am still way off.
When the question concerns "incompatible quantities" and that they should both have real values (but dont)... does this mean that the two arent relatable(mathmatically) or am i totally wrong?
ANSWER:
etc .) is associated with a mathematical
operator; an example would the position x of a particle on the x -axis
and I will call that operator X. To relate the operator with the
observable, we need to know the wave function of the particle, call it ψ (x ).
Then if it happens that Xψ (x )=x n ψ (x ),
then ψ (x ) is called an eigenfunction and x n
is called the eigenvalue which is what the position is if ψ (x )
is the wave function; ψ (x ) is denoted ψ n (x )
to distinguish it from other possible wave functions. If when you operate
X on ψ (x ) and do not get an eigenvalue equation, then the
particle simply does not have a well-defined position. In that case, the
best you can do is predict an average value you would find if you made many
measurements on a particle with wave function ψ (x ); this is
called the expectation value of x and I will not go into the detail
of how you do that. Now suppose that there is some other observable for the
same particle which we are interested in; an example would be the x -component
of the linear momentum p x where the operator would be
called P x and the corresponding eigenvalue equation would
be P x ψ (x )=p xn ψ (x ).
Finally, we come to the answer to your question: the operators X and
P x are said to be incompatible if XP x -P x X ≠0.
In fact, for the example I have chosen, X and
P x are incompatible:
XP x -P x X =iħ . This has a
well-known profound result, namely that the position and momentum of a
particle cannot be simultaneously known to arbitrary precision, AKA the
Heisenberg uncertainty principle.
QUESTION:
I've been studying Schrodinger's equation in one dimension as well as wave functions, and I came across the equation
Ae^i(kx-wt) which supposedly gives you the wave function. I know what all the quantities in this equation except for the "A" represent. I've heard that A has to do with boundary conditions, but I've also heard that A must be a complex number. Could you please tell me how to calculate what this A is supposed to be? Nothing I find on the internet or in books tells me how to find A.
ANSWER:
f (x,t ) is a solution, so is Af (x,t ) where A is an arbitrary constant.
That's mathematics. But, for the wave function to be physically meaningful,
we must require
- ∞ ∫ ∞
ψ*ψ dx =1 where ψ (x,t )=Af (x,t )A is called the normalization constant which, when evaluated from
the normalization integral, allows the interpretation that
ψ*ψ is the probability density.A must be zero. This is because it is
not a physical wave function since it extends over all space with constant
amplitude.
QUESTION:
When electron transitions between two energy levels it emits a light photon of energy E=h*v. But a photon is a light particle, i.e. it is localized in space. Such is wave packet is made up of many frequencies and not just one. Then how is E=h*v valid?
ANSWER:
E Δt ≈ħ or position/momentum Δx Δp x ≈ħ.
(These are actually inequalities, but this will do for my purposes.) As
you note, a photon really has a superposition of many frequencies and
therefore not a definite energy. The distribution of frequencies is
determined by the time it takes the photon to pass you, so if the photon is
very localized you will have a very large uncertainty in energy whereas if
it is very spread out, you will have a much better-defined energy. But, how
can this be if energy conservation is to hold? Doesn't the photon come from
the atom dropping from one atomic energy to another? The answer is no, the
energies of excited atomic states can not, contrary to what you might have
been taught, be precisely determined. The reason is simply that an excited
state has a lifetime and so to measure its energy you have only that time to
do so and therefore cannot determine its energy precisely. By contrast, the
ground state lives forever (Δt=∞ ) and it therefore has a well-defined
energy (ΔE= 0). Any
given photon has an energy equal to what the energy of the particular atom
that decayed had and if you measure many photons with great precision, you
will not get a perfectly sharp line no matter how good your instrument is
but rather observe a broadening of that line. This is called natural line
broadening. Typically, lines are quite narrow, on the order of ΔE /E ≈10-7 .
QUESTION:
I am really confused about what Heisenberg principle actually states...why cant the position and momentum can be measured together....cant we measure the position and momentum at any particular instant of time since physics can do anything???
ANSWER:
f . It turns out
that the momentum of the wave depends on f . The "position" of this
wave train is uncertain, you will admit because it has some length where it
exists. Now I said earlier that the wave has a frequency f , but in
reality, it has a well defined frequency only if the wave train is
infinitely long. If you want to write an expression for the finite wave, you
find that it is really made up of an infinite superposition of frequencies;
this is called a Fourier transform, decomposing some wave into simple
sinesoidal functions. The most important contributor is the momentum
corresponding to f , but there is a whole distribution of others. So,
you see that the wave has uncertainty in both position and momentum. As I
said above, infinite uncertainty in position will result in zero uncertainty
in momentum. Similarly, if you try to pin down the position by making the
wave train shorter and shorter, you find that the momentum distribution
becomes larger and larger.
QUESTION:
‘Electron can pass through two holes at the same time without splitting into two.’ I read it in a book, is it true? If so, explain it to me.. Please.
ANSWER:
earlier answer for more detail.
QUESTION:
I'm wondering what causes the fluctuations that happen in perfect vacuum in quantum physics?
Are they just an inherent part of the universe, or are there theories about what cause them?
ANSWER:
t and the amount by which energy
conservation is violated ΔE , then ΔE Δt≈ħ
must be true; here ħ≈ 10-34 J·s is the rationalized
Planck's constant. For example, suppose that an electron-positron pair at
rest suddenly pops into existence. The total energy of their rest masses is
about ΔE= 1 MeV=1.6x10-13 J, so
the time they may exist before disappearing again is Δt≈ħ /ΔE≈6x 10-22 s. I
guess this does not really answer your question because it tells you how
this can happen, not why it happens. Note that you must obey other
physical principles as well, for example two electrons cannot pop into
existence because it would violate charge conservation because suddenly net
electric charge would appear and there is no uncertainty principle for
electric charge.
QUESTION:
I've seen the Heisenberg Uncertainty Principle stated in various generalities. For example:
1) (most specific) You cannot measure the velocity of an electron without affecting its location (or vice versa).
ANSWER: #3 is certainly false. A simple example would be electric charge which
can be measured with accuracy without affecting the charge. #1 is certainly too
restricted since the HUP is not confined electrons; so, true but not
general. I guess that leaves #2. To my mind, however, it is better to state
it as follows. The more accurately you know linear momentum (which is the
mass times the velocity), the less accurately you can know position and
vice versa . So, if you know the position of something very well, you are
mostly ignorant of its velocity; but if you now measure that velocity so
that you know it very well, the position after the measurement will be
almost totally unknown. To make the HUP more general, we note that linear
momentum and position are conjugate variables . Conjugate variables are two
variables which, when one is measured the other is affected. There are many
pairs of conjugate variables in physics, the other best known pair is energy
and time. If a certain state in a system decays to the groundstate of the
system in a certain time, then the energy of that state cannot be measured
perfectly accurately, that is the state has an inherent width or
uncertainty. The ground state of a system may be measured exactly since it
lives for an infinite amount of time. Another example is in classical
physics, frequency and time. To measure the frequency very accurately you
must make your measurement over a long time. For example, if you listen to
only 1/10 of a cycle of a sound wave, you will hear not the tone associated
with its frequency but just a click, a mixture of many frequencies.
FOLLOWUP
QUESTION: I'm thinking of an inflated balloon sitting stationary on a table. I am certain that I can determine its momentum (zero) and yet still know its location. Also, if I open the balloon's knot, it will dance around randomly, making it more difficult to determine either its momentum or its location. I assume this is a misapplication of the principle (too general)?
ANSWER: The fact is that you cannot know
the momentum to be exactly zero. In fact, you could probably not even
measure it to be zero to one part in a thousand. The problem is that your
intuition is getting in the way of your understanding the HUP because you
are trying to apply it to a macroscopic object and it is completely
unnoticeable in that regime. To understand this, we have to get a little
more quantitative. The HUP states that the product of the uncertainties in
the momentum and position must be on the order of Planck's constant or
greater. Now, Planck's constant is on the order of 10-34 kg m2 /s2 .
So if your uncertainty in measuring momentum to be zero is 1/1,000,000 kg
m/s, then you can measure its position to an accuracy of 10-28 m!
If you work with elementary particles, however, the masses are so small (the
electron mass is like 10-30 kg) that momenta of even rapidly
moving particles are also small so the HUP becomes observable. For example,
suppose you have an electron going 100 m/s and so with momentum of about 10-28
kg m/s and you measure this to one part in a thousand, 10-3 x10-28 =10-31
kg m/s. Then you may not know its position more accurately than 10-3
m, a millimeter, which is a gigantic distance in the subatomic world (an
atom is like 10-10 m, a nucleus like 10-14 m).
QUESTION:
A few years ago it was not known whether neutrinos had mass. Then it was discovered that they can change types (electron - muon etc) and this was taken to imply that they MUST have mass. I don't understand this - why does the fact that they change types imply mass?
ANSWER:
QUESTION:
What are bosons and fermions?
ANSWER:
1/2, 3/2, 5/2… are ferminons; particles with spin 0, 1, 2… are bosons.
QUESTION:
I have two questions regarding rotational kinetic energy. I know that
rotational kinetic energy is defined as:
KE = 1/2 * I * w^2
Where KE is the rotational kinetic energy [in units of: joules;
kg*m^2/s^2], I is the Moment of inertial [in units of: kg* m^2], and w is
angular velocity [in units of: radians/sec^2 or 1/s^2] w^2 denotes angular velocity squared
so that the units check.
If (Electron or Nuclear) Spin is defined as J, with values equal to a half
integer * h/2pi, where h is Plank's constant [in units of: Joule *seconds
or kg*m^2/s],
#1, Is the rotational kinetic energy associated with Spin:
KE = 1/2 *J *w ? (so the units check).
Since V = w * R, where V is velocity, and R is the radius (or the Electron or
Nucleus), so w = V/R, and since the fastest possible speed is the speed of
light, c,
#2, Is the greatest possible rotational kinetic energy associated with Spin:
KE = 1/2 * J * c/R ? (so the units check).
ANSWER: J , the angular momentum is [√(J (J+1 ))]*h /(2π )J *h /(2π )
QUESTION:
is proton diffraction is possible?
ANSWER: 90 Zr plotted as a
function of the angle (in degrees) where the protons were observed.
Differential cross section is, essentially, the probability that the proton
(wave) will scatter (diffract) to some angle. This is very much like the
diffraction pattern you would observe for visible light striking a sphere—diffraction
maxima and minima. In fact, you can qualitatively understand this
diffraction pattern if you calculate the wavelength of the protons, λ=h /p ≈10-15
m, and approximate the positions of maxima by the double slit relation
nλ=d sinθ where we take d to be the diameter of the
nucleus. Taking the two consecutive maxima at 80 and 130 ,
λ=d (sin130 -sin80 )=0.08d =10-15 .
So, the diameter of the 90 Zr nucleus would be about 12.5x10-15
m=12.5 fm. As a check, the diameter of a nucleus with atomic weight A
is well approximated as d ≈2x1.25xA 1/3 fm, so for
A =90, d ≈11.2 fm, pretty good agreement for such a rough
calculation. The experiment was done at the Los Alamos Meson Physics
Facility (LAMPF).
QUESTION:
My 13 year old daughter is studying physics and has asked a question I have no idea how to answer so I am hoping you can help. She has been told at school the energy of a wave is proportional to the square of it's amplitude and therefore independent of frequency. However she told me she has also read that energy of a wave is given by E=hf (E is energy f is frequency h is Plank's constant) and so is proportional to frequency! She is utterly confused by this and asks which one is correct?
ANSWER: —quantum
mechanics. Light is both a wave and a particle (called a photon). If
you devise an experiment to prove that light is a wave (e.g. Young's
double slit
experiment), you will succeed. If you devise an experiment to prove that
light is a particle (e.g. the
photoelectric
effect ), you will succeed! Both energy statements in your question are
correct. But they are not really contradictory. The intensity of light is
the energy per unit time through an area, Joules/second/square
meter=Watts/meter2 . If you look at this as waves, this is
proportional to the amplitude squared. If you look at it as particles, this
is proportional to the number of photons passing through the area.
Therefore, red light of some intensity has more photons than blue light of
the same intensity because each "red photon" has less energy than each "blue
photon".
QUESTION:
I am trying to teach quantum physics for the first time. I am not sure what the link is between photoelectric effect and plancks constant or how to link it meaningfully for the students.
ANSWER: ΔE of the electrons
as a function of the frequency
ν W , to remove an electron from the metal, then the energy of the
electrons must be
ΔE=h ν -W h is the slope of the line. It just so happens that h
(the slope of the line) turns out to be Planck's constant, and that is
the link you seek.
QUESTION:
how vacuum fluctuation cause the formation of particle-antiparticle in vacuum?
QUESTION:
I read an article about quantum mechanics and it mentioned particles "popping into existence". Is the assumption that the particles are popping into existence from another invisible/unknown state of energy which exists, or is the claim that they are appearing out of "absolute nothingness" and violating the law of conservation of energy?
If the currently held belief is that the particles are actually appearing out of pure nothingness, how is it being proven that there is nothing there in the first place? I'm not a scientist obviously but I would have thought that absolute nothingness could not possibly change state into matter, and that there must be a real and invisible force already present which is temporarily changing state into those particles. Where the particles popping into existence even at absolute zero? Surely there must have been some energy somewhere !!!!
ANSWER:
ΔE Δt≈ħ, where ΔE is the amount by which
conservation is violated, Δt is the time the violation lasts, and
ħ≈ 6.6x10-13 keV-s where keV (kiloelectron volt) is a
unit of energy. The mass energy of an electron-positron pair is about
1000 keV, so if they are created out of nothing, they may exist for Δt≈ 6.6x10-16
s and then annihilate back to nothing. A proton-antiproton pair
has 2000 times more energy and so could last for only about Δt≈ 3.3x10-19
s So, there is no such thing as "pure nothingness" as you put it,
but you will never actually find anything there because anything which
"pops into existence" pops right back out in almost no time. Such
processes are called virtual pair production.
QUESTION:
ANSWER:
Е. The red lines are the energy states which you would get from solving
the Schrцdinger equation for this potential. But suppose that you did
not know what the potential energy function was for this system. Then
you could get a good first approximation by noting that the shape, near
the bottom, resembles a parabola which is the potential energy function
for a simple harmonic oscillator, V (x )=Ѕkx 2 .
It is a good first approximation for low-lying states. It is remarkable
how much you can learn about the dynamics of a diatomic molecule, for
example, by modeling it as a pair of masses attached together by a tiny
spring.
QUESTION:
In quantum mechanics how does the wave function of an observable relate
to the expected value of the observable?
ANSWER: the wave
function of an observable" you just want to say "the wave function
Ψ ". The wave function of the
system may or may not be an eigenfunction of the operator associated
with the observable you are interested in. For some observable z
whose associated operator is Z , then Zφ n =z n φ n
where z n is the nth eigenvalue and φ n
is the eigenfunction. Only unless
Ψ= φ n would
you say it is a wave function of the observable. The expectation value
of the observable z is defined as <z >≡<Ψ|Z|Ψ>=∫Ψ*ZΨ dτ
where Ψ* is the complex conjugate of Ψ and the
integral is over all space.
QUESTION:
Why the frequency of light does not change during the refraction of light?
ANSWER:
f
is composed of individual photons, each having energy E=hf .
QUESTION:
i was trying to explain the quantum double slit experiment to my friend and he wasn't buying it so i wanted to tell him about quantum entanglement to help him better understand the "spooky action at a distance" (as Einstein called it). Seeing as i am 14 and have only the most basic of the basic understandings of physics i was flabbergasted when, while telling him about the experiment where 1 electron is taken to Chicago and another is taken to saaaay THE ANDROMEDA GALAXY but are both in a quantum state (spinning up and down at the same time i think) and are kept in a box (so we cant see them). If when you look at the one in Chicago, it spins down the one in the Andromeda galaxy spins the opposite of the one you look at WITHOUT EVEN LOOKING AT that one. After trying to explain that to him he asked "how do you know its spinning up and down at the same time when the second you look at it, its spinning up OR down and furthermore I cannot see an electron so how can we even detect whether it is spinning up or down in the first place". I tried and tried to figure it out in my head but to no avail so i ask, can you you tell me what piece of equipment, while doing the quantum double slit experiment, measures and therefore causes the spooky result and also solve my query about how the physicists know that an electron is spinning up and down at the same time when the second they measure (WITH WHAT) it, it chooses to change to only one.
ANSWER: What makes your question difficult to
answer is that the quantum double slit experiment is not an example of
entanglement, rather an example of wave-particle duality; so you are
trying to convince your friend of something by using an inappropriate
example. I will briefly describe both:
In the double slit experiment, the
intensity of the light is turned down so low that only one photon at a
time passes through the slits. Lo and behold, a double slit pattern
appears on the screen and it appears one photon at a time. In other
words, the photon somehow passed through both slits, not one as you
would expect if the photon were a particle. But it is still a single
photon when you detect it, so how could it have gone through both slits?
Only if it were a wave when you needed to be. You get what you look for.
The piиce de rйsistance is that if you place a detector at one of
the slits to try to determine through which slit the photon passed, you
destroy the pattern on the screen! In an entanglement experiment you
create two electrons whose total spin is zero. However, it is a mixed
quantum system; so it is not simply one electron has spin up and the
other spin down, rather each has spin half up and half down. Now, if you
take one of them and measure its spin, the effect is that you "put" this
electron into the state you measure, say up; but, since the pair is a
single system, the total spin still has to be zero and so if you put one
into the up state, you are simultaneously putting the other into the
down state. It will be true even, as you specify, one is 2.5 million
light years away. You could have some alien measure the spin there and
send you his results but you wouldn't find out for 2.5 million years!
This experiment has actually been done here on earth where you can
actually find out the results before you die!
QUESTION:
I have a question regarding the uncertainty principle. Whether expressed in the position-momentum form or the energy-time form, I have seen the right-hand side of the inequality given in two slightly different ways. The first is "greater than or approximately equal to h-bar" and the second is "greater than or approximately equal to h-bar over two". In the second case, that would of course be h over 4*pi instead of h over 2*pi. The two different forms differ by a factor of 2. Could you please shed some light on this?
ANSWER: This question often comes up because, I believe, scientific statements
are generally expected to be precise and unambiguous. But, this is a
principle, not a law; it is not an equation, rather an inequality and an
approximate one at that. The root of the problem is that the notion of
"uncertainty" itself is a qualitative one. A precise quantative definition
depends on the specific situation. For example, what is the shape of the
wave packet which describes the position of a particular particle? Is it
gaussian, square, maybe half a sine wave? And, establishing that, what is to
be called uncertainty for that situation? Better, I think, to appreciate the
principle as a philosophical idea—there
are some things in nature that you simply cannot know with arbitrary
precision. The statements you see give you an idea of the order-of-magnitude
of how well some things can be known.
QUESTION:
how vacuum fluctuation cause the formation of particle-antiparticle in vacuum?
QUESTION:
I read an article about quantum mechanics and it mentioned particles "popping into existence". Is the assumption that the particles are popping into existence from another invisible/unknown state of energy which exists, or is the claim that they are appearing out of "absolute nothingness" and violating the law of conservation of energy?
If the currently held belief is that the particles are actually appearing out of pure nothingness, how is it being proven that there is nothing there in the first place? I'm not a scientist obviously but I would have thought that absolute nothingness could not possibly change state into matter, and that there must be a real and invisible force already present which is temporarily changing state into those particles. Where the particles popping into existence even at absolute zero? Surely there must have been some energy somewhere !!!!
ANSWER:
ΔE Δt≈ħ, where ΔE is the amount by which
conservation is violated, Δt is the time the violation lasts, and
ħ≈ 6.6x10-13 keV-s where keV (kiloelectron volt) is a
unit of energy. The mass energy of an electron-positron pair is about
1000 keV, so if they are created out of nothing, they may exist for Δt≈ 6.6x10-16
s and then annihilate back to nothing. A proton-antiproton pair
has 2000 times more energy and so could last for only about Δt≈ 3.3x10-19
s So, there is no such thing as "pure nothingness" as you put it,
but you will never actually find anything there because anything which
"pops into existence" pops right back out in almost no time. Such
processes are called virtual pair production.
QUESTION:
how were physicists able to determine that vanishingly tiny particles have the property of spin? is it really possible that the spin of such small objects is observable or is "spin" simply a term used to denote some sort of mathematical abstraction? is it correct to think of an electron "spinning" the way a top or frisbee does?
ANSWER: Nearly all experiments which detect spin are really detecting the
magnetic moment of something. The first experiment was the
Stern-Gerlach
experiment which took a beam of silver atoms and passed them through an
inhomogeneous (that is, not uniform) magnetic field. The idea is that a
magnetic dipole (like a tiny bar magnet) will experience a net force in
such a field. What was observed was that the beam split into two beams.
This implied that the atomic dipoles were half in a N up, S down
orientation and half in the other orientation. Any time you have a
charge distribution which has an angular momentum (the more general
physics term for spin), the result is a magnetic dipole moment. So, if
you observe something about magnetic moments, you are likely observing
something about angular momentum. In this case, the spin angular
momentum of the electron in silver may be either up or down because the
magnetic moment causes the beam to split in two, and from that it must
follow that the spin angular momentum quantum number is
Ѕ. Spin of elementary particles is very much like spin of macroscopic
objects like tops, that is it is what we call intrinsic angular
momentum, something which is intrinsic to the particle, not due to
its motion (like in an orbit around the nucleus, which gives rise to a
different kind of angular momentum called orbital angular momentum). On
the other hand, there are distinct differences between micro- and
macroscopic spin. In particular, you cannot explain it by using the
standard classical models; for example, if you take the electron to be a
solid sphere with its mass uniformly distributed and calculate the spin
using a reasonable size, the surface will be moving faster than the
speed of light. Also, unlike a top or frisbee, you cannot stop the spin
or speed it up. The origin of spin can be understood using relativistic
quantum mechanics where it appears naturally.
QUESTION:
is it correct (or at all meaningful) to say that Planck's constant is the quantum of momentum?
ANSWER: Planck's constant has the units of Joule-seconds, J s=kg m2 /s;
momentum has the units of mass times velocity, kg m/s. So it is not
momentum. Instead, the units of Planck's constant are the same as the
units for angular momentum which are also kg m2 /s. However,
it would be an oversimplification to say that "Planck's
constant is the quantum of [angular] momentum"; it sort of minimizes the
importance of h as a fundamental constant of nature. Planck's
constant was first used by Niels Bohr in this context (a unit of angular
momentum) in his model of the hydrogen atom. His model assumes that
allowed orbits correspond to angular momenta
Ln which are integral multiples
of
h /(2π ), Ln =nh /(2π )
where n is an integer greater than zero. It turns out that this,
although it worked in some respects, is not quite correct. We now know
that angular momentum is given by Ln ={√[n (n +1)]}h /(2π )
where n =0 is also allowed.
QUESTION:
Can you please break down Schrodingers equation for me? What each variable stands for and can you please explain to me the theory behind his equation. I'm just a curious English professor and I'm having a difficult time understanding the equation as well as Heisenberg's Uncertainty Principle equation. If you can put the breakdown in layman turns I will forever be grateful.
ANSWER: ц dinger
eqiation is what you had in mind. Link here.
QUESTION:
I have a question about Blackbody Radiation; I looked it up on Wikipedia but didn't quite understand it. What exactly is a Blackbody, and how can it theoretically emit infinite energy, and how is this related to Blackbody Radiation?
ANSWER: th
century the nature of BB radiation was well known and physicists were
trying to explain it. It turns out that classical physics predicted a
spectrum which contained an infinite amount of energy, obviously not
possible (that must be what you are referring to). This was referred to
as the "ultraviolet catastrophe" because the spectrum just got bigger
without bound for small wavelengths. The problem was finally solved by
Max Planck by proposing the first ever application of quantum physics.
QUESTION:
Can you please explain Uncertainty Principle with examples?
ANSWER: x )
and momentum (p=mv ) of a particle,
Δ p Δ x> ħ /2
where
Δq indicates uncertainty of q and
ħ is the rationalized Planck
constant, about 10-34 J-s. For example, if you have 1 kg ball
moving at a speed of 1 m/s,
and you are uncertain by 1%,
Δ p= 0.01
kg-m/s so you cannot know x to an accuracy better than 0.5x10-32
m; you can see why we never notice the uncertainty principle for
macroscopic objects. Another pair of conjugate variables are energy (E )
and time (t ), so,
Δ E Δ t> ħ /2.
The mass of an atom, ( E=mc 2 )
cannot be known precisely unless it is stable, that is if it lasts an
infinitely long time. Energies of excited states of atoms or nuclei are
not precisely knowable, they have inherent "widths" because they only
last a short time before decaying.
QUESTION:
Could you help me understand the concept that you can't measure a particle's speed and position at the same instant. It seems to me that this is a technical problem. We know that they have a speed and position at any instant so they are knowable, thought perhaps never to us, and therefore their future is determinable.
ANSWER:
can't measure a particle's speed and position at the same instant", it
is that you cannot know both to arbitrary precision . The uncertainty
principle says
m Δv Δ x ≈h /2π
where m is mass,
Δ v is uncertainty in
velocity, and
Δ x is uncertainty in
position, and h /2π ≈10-34 m2 -kg/s is the
rationalized Planck's constant. Let's take an example you could have
measured, say a BB with a mass 1 g=10-3 kg sitting on your desk
(supposedly at rest). You measure its postion to an accuracy of the
wavelength of visible light, 5x10-7 m (that would be a tour de
force measurement!) Then, how accurately do you know that it is truly at
rest?
Δv ≈h /2π /( m Δx )=10-34 /5x10-7 /10-3 =2x10-26
m/s, meaning it could have a velocity as big as this. So, we now test this
by waiting until we see it move one micron (10-6 m); it should
only take 10-6 /2x10-26 =5x1019 s=1.6
trillion years. That is about 10 thousand times the age of the universe! So,
you see, the uncertainty principle does not have any significant effect on
everyday life in our macroscopic world. That does not mean it is not true,
that means you cannot see it in everyday life. If you now look at electrons
(m ≈10-30 kg) inside atoms (Δ x ≈10-10
m), we have a very different story.
FOLLOWUP QUESTION:
I would like to have another go at my previous question about the uncertainty principle. I'm just an old farmer, long in the tooth and have just gotten interested in this physics stuff in the last ten or so years so let me present a thought experiment.
Say I shot a cue ball at a racked set of pool balls, once that ball is rolling there is a definite route each ball will take and the outcome will not be altered whether I know the forces involved or not. I can't predict the outcome since I can't possibly measure the exact forces
but that doesn't interfere with the outcome. Now I understand that by trying to measure particles, no matter how close I measure them, over the course of the life of a universe there will be drastic changes in any outcome I would predict. However, at the time of measuring,
isn't there already a prescribed path set in concrete based on Newtonian physics and if it were possible to know the forces involved and we had the technical ability could we not define that path. I realize there are probably other factors that would make that impossible such as particles popping into and out of existence but I
don't understand why not knowing the data makes the outcome any different. Isn't that why Einstein commented that god doesn't play with dice?
ANSWER: — everything
which will ever happen is already written. You can think of yourself as in
good company with Einstein since your world view, that Newtonian physics
rules and every particle right now has a specific position and speed, also
says that the universe is determinisitic. Forget free will!
QUESTION:
Please can you explain me or tell me something energy-time uncertainty principle and what is del E and del t in it?
ANSWER: —you
cannot simultaneously know the position and momentum of a particle to
arbitrary accuracy. However, there are other pairs of conjugate variables
for which the uncertainty principle occurs, two examples are angle/angular
momentum and energy/time. The energy/time uncertainty principle is a little
harder to get a grasp of, as you have found. There are two examples I can
think of which are examples of physical consequences of ΔE Δt ~h.
As you know, one
of the truths of classical physics is that the total energy of an
isolated system must be conserved. However, in quantum mechanics it is
perfectly ok for energy conservation to be violated, as long as you do
it for a very short time. So, suppose a photon with energy E is
suddenly emitted from a charged particle. This violates energy
conservation. But, if that photon disappears, gets reabsorbed or
absorbed by some other charged particle in a time on the order of Δt~h /E ,
that is ok. This gives rise to the so-called vacuum polarization where
particles pop into and out of existence even in completely empty space,
so we do not really think of a vacuum as containing nothing.
Another way to
look at ΔE Δt ~h is that to know an energy absolutely
perfectly, the measurement will take forever. So, the ground state of an
atom has a well defined energy because it never changes and is
"available" forever. So, apart from experimental uncertainties, you can
measure the energy of a stable atom perfectly accurately. However, the
excited state on an atom does not live forever, it decays and the decay
is characterized by a half life, τ Ѕ . Therefore, if you
measure the energy of such a state by measuring the energy of the
emitted photon, if you make many measurements you will find a spread of
energies ΔE=Γ~h /τ Ѕ . Because an excited atom
does not last forever, that energy state does not have a specific energy
and spectral lines are not really perfectly sharp. Very short-lived
states have very noticable widths. Measuring the widths of states is
often a more accurate way of measuring half lives.
QUESTION:
is proton diffraction is possible?
ANSWER: 90 Zr plotted as a
function of the angle (in degrees) where the protons were observed.
Differential cross section is, essentially, the probability that the proton
(wave) will scatter (diffract) to some angle. This is very much like the
diffraction pattern you would observe for visible light striking a sphere
—diffraction
maxima and minima. In fact, you can qualitatively understand this
diffraction pattern if you calculate the wavelength of the protons, λ=h /p ≈10-15
m, and approximate the positions of maxima by the double slit relation
nλ=d sinθ where we take d to be the diameter of the
nucleus. Taking the two consecutive maxima at 80 and 130 ,
λ=d (sin130 -sin80 )=0.08d =10-15 .
So, the diameter of the 90 Zr nucleus would be about 12.5x10-15
m=12.5 fm. As a check, the diameter of a nucleus with atomic weight A
is well approximated as d ≈2x1.25xA 1/3 fm, so for
A =90, d ≈11.2 fm, pretty good agreement for such a rough
calculation. The experiment was done at the Los Alamos Meson Physics
Facility (LAMPF).
QUESTION: how is it possible that
light can be both a particle and a wave! i need to know it's ruining my
whole life.
ANSWER: Ruining your whole life? How is it possible
that my tie can be both red and green? That is just the way it is. I
know that this is an unsatisfying answer, but science is based an
measurements (experiments) and if you study light and look for a wave,
you will find one but if you look for a particle you will find that
also. This is called the wave/particle duality and it is, essentially,
a statement of experimental fact. And you can do experiments which
unambiguously see both possibilities in the same experiment. The best
known example is to do a double
slit experiment with very low intensity. If the intensity is so
low that there is, say only 1 photon per minute passing through, then
it has to pass through one slit or the other, right? Wrong--you still
get an interference pattern. So, you say, light is therefore a wave,
not a particle. But, imagine that the screen detects the light using
the photoelectric
effect which cannot be understood unless you treat the light as a
collection of photons. This detector will work perfectly well in
displaying the interference pattern. This duality is not unique to
light: any particle will exhibit wave properties; e.g. that is
how an electron microscope works, by exploiting the wave properties of
electrons. Maybe I shouldn't have told you this since it may compound
your life-ruining distress! Wave/particle duality is a reality of
nature, that is all.
QUESTION: Do physicists believe that
the world is continuous or discrete? In other words, is there a
smallest distance a particle can travel and/or a smallest increment in
time?
ANSWER: This is an open question. Although nobody
has seen any evidence for the discreteness of space or time, many
serious theorists, particularly those working in quantum gravity,
believe that there does exist a distance which is the smallest possible
distance called the Planck length. This length is on the order of 10-35
m so it is not surprising that there is no experimental evidence for it
since this is 10-20 times the size of a proton! Similarly,
time is thought to have the smallest possible duration which is the
time it would take light to travel the Planck length, also very small.
QUESTION: Regarding the Stern-Gerlach
experiment of 1922 concerning space quantization, does this mean that
electrons come in two flavors, spin up and spin down?
ANSWER: Spin up and spin down have meaning only if
up and down have a meaning. Hence, you must first choose a coordinate
system in which to make measurements. When you do this, you may say
that electrons have two possible states, spin up and spin down.
However, a particular electron may be in a state which is a combination
of some probability of each. Quantum mechanics is weird!
QUESTION: Hi! Why doesnt an electron
emit radiation as it goes around the atom
is it not really accelerating?
Does the equal + and - charges make the dipole invisible.
ANSWER: This may be an unsatisfying answer, but it
doesn't because it doesn't! The problem is that our laws of classical
physics do not work at very small distances (or at very large speeds).
It turns out that an object must be described in terms of its "wave
function" which is, essentially, a statement of the probability of
finding it somewhere. When you do the calculations using the branch of
physics called quantum mechanics, the wave function is zero unless the
electron is in only certain states (including the ground state), so the
probability of finding it in a slightly less energetic orbit (as it
would tend toward if radiating energy away) is zero; hence, no
radiation. An alternative way to look at it is to say that the
electron should be thought of as a wave; it turns out that the
wavelength of the wave is exactly right to fit in the orbit so the wave
interferes constructively with itself (just like a vibrating guitar
string). However, for a different orbit, the wave each time around
"destroys" itself.
QUESTION: Does the Heisenberg
Uncertainty Principle say (a) that particles have a definate position
and momentum, but we are incapable of ever knowing them both
simultaneously or (b) that particles do not have a definate position
and momentum at all?
ANSWER: Technically, one may know one (position or
momentum) with perfect precision if we are totally ignorant of the
other. However, we can never be totally ignorant of either in practice
(for example, surely the particle in question is somewhere in the
universe). So, both your (a) and your (b) are correct, but (b) cannot
be by itself a statement of the principle because the degree to which
we can know one is determined by the degree to which we know the other.
QUESTION:
ANSWER: First, you don't want to consider a white light source since
it contains all wavelengths which considerably complicates the
problem. Understanding the double slit experiment hinges first on
something called Huygen's principle: every point on a wave front acts
like a new point source. Hence, when you put a narrow slit in
front of a source of light, it behaves like a line source and emits
cylindrical wavefronts. If there is another slit parallel to it,
the other slit is a source of waves in the same way. Now you have
to accept that when waves from the two sources hit some place in space (e.g.
a screen in front of them), the net result will be the simple sum of
the two waves. Hence, if the crests (wavefronts) of these two
waves arrive at that point simultaneously, the resulting waves will be
twice the amplitude of one source (bright), whereas if the crest of one
arrives at the same time as the trough of the other, they will cancel
and there will be no wave there (dark). A nice simulation may be
seen by clicking
here . Of course, with light this has nothing to do with
quantum mechanics--it is called the Young's double slit experiment and
has been known for 200 years. See also the answer to a previous question. When
quantum mechanics was beginning to be developed in the early 20th
century, the notion that things we traditionally think of as particles
might behave, under the right circumstances, like waves, was verified
using exactly the same ideas as the double-slit experiment.
"Embellish"
implies that I already know what you know and add to it! The
uncertainty principle states that, as an inescapable consequence of
quantum mechanics, there are certain pairs of observables (called
conjugate variables) which cannot both be known to arbitrary
precision. The best known pair is the momentum and position of a
particle. One may get the idea from the ideas of the slit
described above. Perhaps a small hole would be more instructive;
here Huygen's principle says that the hole, if very small, acts like a
point source so there are spherical wavefronts coming out of the
hole. But what does the hole try to do? The incoming waves
come straight into the mask but with a completely undetermined
position. The hole localizes the position of the wave but the
result is that the wave spreads out spherically so now we have almost
no determination of its direction (momentum is essentially equivalent
to velocity for our purposes here). So we start with no position
information and perfect direction information and end up the other way
around! If you make the hole larger, more of the light will go in
the forward direction coming through it (you will get a fuzzy image),
so there is always a compromise between knowledge of position and
velocity. This is a result of the wave nature of what you are
looking at and, when you start thinking of particles as waves, they
take on this uncertainty property as well. We never see particles
doing this in everyday life because the product of the uncertainties of
momentum and position is on the order of 10-34 kg m2 /s.
So, if you have a 1 kg ball whose uncertainty in position is 1 mm=10-3
m, you could (according to the uncertainty principle) measure its speed
as accurately as 10-31 m/s. Since it is absolutely
impossible to make such an accurate measurement, you would never notice
your inability to measure it perfectly.
QUESTION: Hello. I hope my question isn't too unfocused.
There is
a theory I've been trying to remember, but I can't get the details
right. I just remember it in a vague way. Hopefully you can help.
It's
about two particles (atoms?) with similar charges (?) (or identical in
some way, or perhaps connected and then broken into two pieces), so
that if something affects one of the particles, it will affect the
other particle. The theory is that this will be true no matter the
distance between the two particles: if one is here and the other is on
the other side of the galaxy, affecting the particle here will
INSTANTANEOUSLY affect the particle on the other side of the
galaxy.
Naturally,
this seems to contradict the limits of the speed of light, but it had
something to do with bending space and the seemingly instantaneous
affects of gravity. I think.
Anyway,
hopefully this sounds familiar to you. I'd appreciate any help you can
give on details about this theory (briefly is fine). Thanks very much.
ANSWER: What you are thinking about is often referred to as the EPR
(Einstein, Padolsky, Rosen) paradox or, in modern parlance, quantum
entanglement. The idea, roughly speaking is the following.
Attributes (things which can be measured) of physical systems in
quantum mechanics are often not definitive until you make a measurement
at which time your measurement actually places the object in the state
which has the attribute which you observe. I am going to make up
an example which, although frivolous, illustrates the paradox.
Suppose there is some particle and that particle can be either red or
green. Furthermore, suppose that if you have a pair of those
particles, one must be red and the other green--you can never have two
red or two green. So the attribute, that which the so-called
"state" of the system would describe, would be "red/green-ness".
The fundamental truth about quantum mechanics is that the state of a
system can be a mixture, that is a particle could be say 50% red and
50% green (strange as that may seem); so, for a pair of particles, if
one is 50% red and 50% green, so is the other. In practice what
this means is that if you have many such pairs and measured the color
of one of them, half the time you would see green, half red. You
are said to be, by virtue of the measurement (looking at it),
"collapsing the wave function", actually placing it in a pure red or
green state; but, since the pair must be one red and one green, you
must simultaneously place the other particle in the opposite
state. So the "faster than the speed of light" part comes in when
we let one of the particles go very far away before we look at the one
we keep at home. Then, instantaneously when we measure one the
other is determined even if it is on the other side of the galaxy!
There is
a very nice discussion of all this on the web at http://fergusmurray.members.beeb.net/Causality.html
QUESTION: What would the infrared frequency be, in microns, for the
temperature 86 degrees fahrenheit.What is the frequency
range, in microns, for low, middle, and far infrared.
ANSWER: For starters, frequency is not measured in microns since
frequency is number of vibrations per second and a micron is a unit of
length. I presume that you want to know the answers to your
questions as wavelengths in microns (1 micron =10-6 m, a
millionth of a meter).
Now,
regarding your question of what the wavelength is for an object at 860
F is: the fact is that objects radiate at all wavelengths, so we need
to discuss how the energy is distributed over all the
wavelengths. The details of the radiation depends on the
particular object which is radiating, but we can get a good idea of
what is going on by assuming the object is a perfect radiator and that
is called a blackbody. Blackbody radiation is extremely well
understood in physics and it was, in fact, the theoretical study of
blackbody radiation which gave quantum physics its birth. So, let
us find the wavelength at which the most energy is being radiated by a
blackbody. There is a handy equation which lets you find out at
which wavelength this maximum occurs: l =2900/T where l
is
the wavelength in microns and T is the temperature in degrees
Kelvin (the absolute temperature scale where zero degrees Kelvin,
absolute zero, is -273 degrees Celsius). 860 F is about
3030 K, so the most energy is being radiated at a wavelength
of 9.6 microns. A picture of the distribution of energy as a
function of wavelength is shown to the right.
The near
IR band contains energy in the range of wavelengths closest to the
visible, from approximately 0.750 to 1.3 microns . The intermediate
IR band (also called the middle IR band ) consists of
energy in the range 1.3 to 3.0 microns . The far IR band
extends from 2 to 14 microns .
QUESTION: How can one measure the molecular vibration of a body?
Is it using the electromagnetic radiation? If this is the way,
how would one measure the frequency of elec. waves, how would measure
something so fast in a terahertz or more? Molecular vibrations
are in terahertz, aren't these molecules (it's so fast) supposed to
produce so much heat, that the matter would simply melt?
ANSWER: The answer to this question requires that you understand a
little about quantum mechanics. When models of atoms and
molecules were first being devised, back around the end of the 19th
century, one of the most vexing problems was how to reconcile classical
electrodynamics with the possibility of having charges move around
inside an atom or molecule. The problem is that classical
electrodynamics says that an accelerating charge radiates its energy
away. As you probably know, the simplest approximately correct
model of an atom has electrons circling the nucleus of the atom.
But, something moving in a circle is constantly accelerating and so it
should quickly radiate away all its energy. However, this does
not happen for certain special states (which are said to be
quantized). That is just an unexpected fact of nature.
Where radiation from atoms comes from is when the atom in one allowed
state makes a change into an atom of a lower allowed state.
Electromagnetic radiation is "spit out" in order to conserve the energy
of the system. The same thing is true for molecules. If you
have a molecule which is vibrating, the energy of those vibrational
states are quantized and the molecule only radiates when it drops from
one state (having a large vibrational amplitude) to another state
(having a smaller vibrational amplitude). Therefore, if a
molecule is in its lowest possible vibrational state as would be normal
in, for example, O2 molecules moving around in the air, it
is vibrating with a large frequency but it does not radiate. The
only way to make it radiate is to excite the molecule to a higher state
and let it relax back down to the lowest state by emitting
electromagnetic radiation.
To answer
the question of how to measure the vibrations we must get a little more
quantitative. It turns out that the energy of a quantized
vibrator (visualize a diatomic molecule with a little spring attaching
one atom to the other) is given by En =(n +(1/2))hf
where n is an integer (0,1,2,3,...), h= 6.6x10-34
joule-s (known as Planck's constant), and f is the vibrational
frequency of the molecule. Now what you have to do is excite the
molecule from its lowest energy state (E0 =hf /2)
to its first excited state (E1 =3hf /2) and
observe the electromagnetic energy coming out and measure its frequency
which would be the same as the frequency of the oscillator. As a
concrete example, the frequency of radiation emitted by an excited CO
(carbon monoxide) molecule is 6.42x1013 Hz. The
corresponding radiation is in the infrared region of the spectrum and
has a wavelength of 4.7x10-6 m.
QUESTION: Dear Physicist, can you please tell me why photo current is
independent of frequency if intensity is kept constant. Arthur Beiser
on page 55 of his text perspectives of modern physics makes this
statement. This seems impossible because if intensity is defined as
power/metre squared then there must be few electrons emitted by higher
frequency light. I have been told that Beiser may be defining intensity
as flux of photons but on page 54 he quotes intensity in units of Watts
per metre squared. Please Help!!!
ANSWER: Suppose that the intensity I is energy/unit
time/unit area (the standard definition as you note). Then if dN/dt
is the rate at which photons are striking an area A
on the photocathode and hf is the energy/photon, we may
write dN/dt=IA/(hf). This just says photons/unit time/unit area=[energy/unit
time/unit area]/[energy/photon]. Now, clearly, the rate at which
electrons will be ejected/unit time from A will be proportional
to the number of photons striking A per unit time so it follows
that the current (which will be proportional to the number of electrons
ejected from A per unit time) will be proportional to dN/dt
and therefore inversely proportional to f and not independent
of it for a given I. Therefore you are right! The
photocurrent is independent of frequency if the photon flux remains
constant (some authors call this the photon intensity), but not if the
intensity remains constant.
When I first read the previous question I misread it and
therefore answered the wrong question! I leave my original answer
here in case anyone is interested in learning more about the
photoelectric effect The question
you ask was one of the pivotal questions which led to the development
of quantum physics around the beginning of the 20th century.
It is an excellent question and one which truly perplexed the best
minds in science at the time. It took Albert Einstein to come up
with the answer to this puzzle and his explanation later was recognized
with the Nobel Prize. Surprizingly, the citation for his Nobel
Prize did not mention the theory of relativity at all but did say
"especially for his discovery of the law of the photoelectric effect".
So your
question is basically "if the energy is present in that incident light
to knock out an electron, why do no electrons get knocked out?" I
will make the answer rather brief. This is a topic which you can
further research in just about any book on modern physics. The
answer is that light can only give up its energy in little increments
and those increments happen to be proporional to the frequency of the
light. The energy which light can give up in one little bundle is
E=hf where f is the frequency and h is called Planck's constant which
has a value of about 4x10-15 eV s (where s means seconds and
eV is the amount of energy an electron acquires if you let it
accelerate across 1 volt of potential difference). These little
"bundles of energy" are called photons. So suppose you have light
with a wavelength of 6000 Å (~orange light); its frequency is
about 0.5x1015 s-1 , so the energy of a photon
would be about 2 eV. Now, what do we need to knock out an
electron? In metals the electrons which are responsible for
electrical conduction are, for all intents and purposes, just freely
moving around inside the metal like a gas. But, when they come to
the surface, there is some barrier keeping them in like gas in a box;
if there weren't, then all the electrons would eventually just leave
the metal which we know does not happen. The amount of energy
necessary to remove one electron from the surface is called the work
function (a very poor name, by the way!) and the work functions for
most metals is around 2-5 eV. So, unless the photon has energy
greater than the work function the electron will not get removed from
the metal. You might wonder why two or more photons couldn't work
together to remove an electron. That is just a matter of
probability and, using even the most intense sources of radiation
available around 1900, there is a really small probability of two
photons interacting with the same electron at the "same time".
![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION: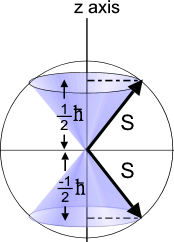
![]() ANSWER:
ANSWER:
![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER:![]() QUESTION:
QUESTION:![]() ANSWER:
ANSWER: 