Ask the Physicist!

QUESTION:
I know that we are taught that particles in solid objects or structures (atoms & molecules) are vibrating in a fixed position. Does this mean that the solid object itself is vibrating externally and/or macroscopically?

ANSWER:
For simplicity, let's just imagine that every atom is vibrating as if it were attached to a tiny spring. Each oscillator will have some frequency and amplitude. The frequencies are more or less fixed. But the amplitude of any given atom will change depending on temperature. At some constant temperature, all the oscilators are vibrating but they are normally vibrating in random directions, so there is no macroscopic behavior which you could observe which is associated with the vibrations. A given oscillator has an energy of ½kA² where k is some constant determinined by the stiffness of the spring and A is the amplitude of the vibration. The amplitude is determined by the temperature. Temperature is simply a measure of how much energy there is (called internal energy in thermodynamics) contained in the object. So a hot object will contain more energy than a cool object; more energy means bigger amplitudes, and therefore the object gets bigger. Thermal expansion is a macroscopic property caused by microscopic behavior, the amplitudes of vibration.

QUESTION:
How exactly do scintillation detectors manage to convert high-energy x-rays or gamma rays into visible light by excitation? I know that they work by atoms being excited by the high-energy electrons that are generated by the ionization of the atoms of the crystal but I still don't get how those high-energy electrons themselves can get away with just exciting/not ionizing other atoms in the crystal due to the fact that they themselves can carry thousands to even millions of electron volts of kinetic energy from the x-ray or gamma ray photons that they absorbed. Isn't that way too much energy for excitation?

ANSWER:
The idea of a scintillator is that the photons (Kev-MeV) ionize atoms, ejecting electrons into the material. But ionization energies are on the order of eV, so a single electron is likely to have only a small fraction of the total photon energy. So, as the photon plows through the crystal it creates hundreds or thousands of electrons. Ideally, the crystal should be thick enough to stop the photons but inevitably some will escape. But there are many slow electrons which have a relatively short range because of their low energies and these excite very few atoms which de-excite releasing photons mainly in the visible range. So each incoming photon, if it stays in the crystal, results in a large number of visible photons, the amplitude of which is proportional to the energy of the photon. It is easier to detect a pulse of light than an individual photon of high energy.

EMBELISHED ANSWER:
It has been a long time since I actually worked with scintillation detectors, and as I recalled I realized that my initial answer, although not technically incorrect, does not best describe how high-energy photons interact with the crystal. The photon interacts with electrons in two main ways:

The photoelectric effect is where a photon gives all its energy to one electron. If this happens we are lucky because the electron has all the energy but, being charged, it stops much more quickly and gives all its energy ultimately to many photons in the visible or near visible region which are easily detected as a pulse of light; this pulse of light is called the photopeak. If your experiment is spectroscopy, these photopeaks due to photons of several energies tell you the spectrum of gamma-rays.
But also the photons can simply scatter off an electron losing only part of their energy. The most they can lose is in a head-on collision (called backscatter) and so this will result in lower energy light pulses, i.e. at lower energy than the photopeak. The figure shows a spectrum of the decay of ¹³⁷Cs taken with a scintillator. The peak shown as a red line is the photopeak of the single gamma-ray of energy 0.667 MeV; the rapid rise of counts to the left of the photopeak is called the Compton edge, the largest possible energy of a Compton-scattered photon; the flat region is called the Compton plateau; the peak on that plateau is the backscatter peak, the lowest possible energy Compton-scattered photons. The sharp peak near zero is an x-ray resulting from internal conversion. The actual energy is very sharp and the compton edge is a sharp cutoff; the widths are due almost entirely to resolution of the detector. Also the gamma-ray photons have little probability of interacting with more than one electron, so most go through with no interaction at all (efficiency of the detector) or else interact once, contrary to what I implied in the original answer where I was thinking more about charged particle interactions.

The photoelectric effect is where a photon gives all its energy to one electron. If this happens we are lucky because the electron has all the energy but, being charged, it stops much more quickly and gives all its energy ultimately to many photons in the visible or near visible region which are easily detected as a pulse of light; this pulse of light is called the photopeak. If your experiment is spectroscopy, these photopeaks due to photons of several energies tell you the spectrum of gamma-rays.
But also the photons can simply scatter off an electron losing only part of their energy. The most they can lose is in a head-on collision (called backscatter) and so this will result in lower energy light pulses, i.e. at lower energy than the photopeak. The figure shows a spectrum of the decay of ¹³⁷Cs taken with a scintillator. The peak shown as a red line is the photopeak of the single gamma-ray of energy 0.667 MeV; the rapid rise of counts to the left of the photopeak is called the Compton edge, the largest possible energy of a Compton-scattered photon; the flat region is called the Compton plateau; the peak on that plateau is the backscatter peak, the lowest possible energy Compton-scattered photons. The sharp peak near zero is an x-ray resulting from internal conversion. The actual energy is very sharp and the compton edge is a sharp cutoff; the widths are due almost entirely to resolution of the detector. Also the gamma-ray photons have little probability of interacting with more than one electron, so most go through with no interaction at all (efficiency of the detector) or else interact once, contrary to what I implied in the original answer where I was thinking more about charged particle interactions.

QUESTION:
How exactly do scintillation detectors manage to convert high-energy x-rays or gamma rays into visible light by excitation? I know that they work by atoms being excited by the high-energy electrons that are generated by the ionization of the atoms of the crystal but I still don�t get how those high-energy electrons themselves can get away with just exciting/not ionizing other atoms in the crystal due to the fact that they themselves can carry thousands to even millions of electron volts of kinetic energy from the x-ray or gamma ray photons that they absorbed. Isn�t that way too much energy for excitation?

QUESTION:
I have a question that has been bothering my brain for a couple of years now.I am not a math person, therefore, I have a less than average understanding of physics. I've done a lot of Internet research on the subject but most things just seem subjective to me. They are stated like facts with no real explanation that satisfys me. This is the first result for asking a physicist so I will ask you first. So, time is defined by the radioactive decay of highly precise movement of the outer most electrons of ceasium atom. That is based on the rotation of earth and light in space... Which just seems absurd. I feel like we have progressed far enough as a species to have a much more accurate, objective, and universal time unit that doesn't rely on the earths orbit or an incredibly specific numbers of radioactive decay from a seemingly arbitrary element that has no basis on the reality of how time actually can be measured universally. It baffled me why we still use outdated and primitive units if time and calendars when we could have an objective time that doesn't care how awkward it makes telling time on earth for humans. A year is completely arbitrary to the universe. So how can we claim to understand physics when we don't even understand time properly? In my uneducated opinion I feel that time based in this way completely ruins math as a measurement of anything. It should be perfectly metric in it precision. 'metric time' so to speak which I know was a proposed theory before and laughed away annoyingly because it didn't fit within an earth year. A circle should be 100 degrees and geometric calculations should be based on that. Metric time metric geometry. Recalculating the metric system to be more easily accessible units. And hopefully a metric round number for the speed of light in the end. Just my opinion. Please help me know if I am just absurdly wrong worried about subjective vs objective units of measurement.

ANSWER:
This is not a "single, concise, well-focused question" as specified by site ground rules. It is very difficult to ferret out exactly what your point is but there is one thing you clearly do not understand. There is no such thing as universal time. If we find a clock which we are confident is sufficiently accurate, it will not run at the same rate at the top of a mountain as it does at sea level. If we take that clock and synchronize it with another and then take one of them on a trip, they will no longer be synchronized when the traveling clock returns. The relative the way time flows depends on its motion and the gravitational field it is in. But the rate at which time proceeds in any given frame of reference is the same for all clocks in that frame. In the twin paradox, for example, the traveling twin doesn't 'feel' like he is aging at a different rate, he 'feels' time passing just the same way as his earth-bound brother but their respective clocks will differ when they get back together. While it is true that we do not really understand what time is, we understand very well how it behaves.

Your other problem, apparently that some definitions of things like a meter, kilogram, kelvin, etc. seem arbitrary to you, are really pretty pointless because there is really no good reason other than it would please you to have 100 degrees in a circle. In fact the radian is a much more natural measure of angle than any other and the one used by physicists for most serious calculations. It is sometimes done that 'natural' units are used, for example define a system of units where the speed of light is 1, Planck's constant is 1, etc.; this might be useful for development of more compact equations for some physical laws but it would be difficult to understand physical laws intuitively if we choose 1 for two quantities in which, in the system of units we are used to, one is extraordinarily large and the other extraordinarily small. You also need to appreciate that, like all knowledge accumulations, physics is historical. Units of measurement need to be defined when they are discovered or understood or advanced. Sometimes such definitions or names take a long time to be revised; for example, only recently has the Coulomb (unit of charge) been not quantified by using the Ampere (the rate of charge flow) and instead by a the electric charge of certain number of electrons. Sometimes terminology becomes so entrenched that it never gets changed; for example, the electromotive force is not a force at all, rather a voltage. I really didn't mean to go into such a long disquisition, but sometimes I just go on and on!

QUESTION:
When I see an illustration of how a lens works, it shows light rays passing through the thinnest part [the edge] bending the most [toward a focal point], while those passing through the thickest bending least. The explanation seems to have something to do with the slowing through the medium, which I don't understand. Carried to the extreme, it would seem [A] light hitting, like, a one atom thick piece of the lens would be the most bent, or [B] light missing the lens would bend infinitely. Is "bending" a misleading term? Does this has anything to do with the weird wave/particle nature of quantum reality?

ANSWER:
Think of the lens as a stack of prisms of varying angles. For simplicity I will think of it as a stack of two triangles and a cube as shown in my figure, but for completeness think of very many very thin prisms of continuously changing angles. It is not misleading and has nothing to do with wave/particle duality, just classical refraction of light moving from one medium to another.

QUESTION:

Is gravity and gravitational force the same thing? I have seen the formula F= GmM/r^2 to calculate the gravitational force. I have an idea how Newton arrived at this formula (Kepler's observtions ?). Is this force F the same thing as for example somebody's weight? I have used m=70kg, M=mass of earth, G as the Gravitation constant and r=earth's radius. The result isn't anywhere near an average person's weight. Where am i wrong in my thinking? Also, I have read somewhere that the gravitational force between two bodies does NOT have an opposite force. However, we sometimes talk like this: if you are in balance, i.e. not falling,your weight pushes down on the earth, at the same time the earth pushes you up to lift you so you are stable. Is this not a contradiction with the first statement (NO opposite force)? I have spent days trying to clarify this on the internet, but it seems like the terms are not consistently used. I am so very, very confused.

ANSWER:
Maybe you are having trouble with units. Let me calculate with m=70 kg like you did, M=6x10²⁴ kg, r=6.4x10⁶ m, and G=6.67x10^-11N·m²/kg²: F=684 N=154 lb. If you live in a country where weights are measured in kilograms, the corresponding force is F/9.8=70 kg. That is nonsense where you say there is not an opposite force. Newton's third law says that if one object exerts another, then the other exerts an equal and opposite force on the one. For example, let's look at a 70 kg man standing on the ground; what are all the forces on him? The earth exerts a force on him down, his weight, W=684 N. The ground exerts a force on him upward, call it U. Since the man is at rest, so U=-W. These are equal and opposite forces but have nothing to do with Newton's third law; rather they are equal and opposite because of Newton's first law that the some of all forces on an object is zero if it is not accelerating. The third law always involves two separate objects; in this case, the earth exerts a force down on the man and the man exerts an equal and opposite force on the entire earth. The weight of the man is not a force on the earth as you state ("…your weight pushes down on the earth…"), it is a force on the man. Whenever you talk about equal and opposite forces referred to in Newton's third law, they always refer to two different objects.

QUESTION:
I was reading Seven Brief Lessons on Physics by Carlo Rovelli and that led me to look at the Standard Model of Particle Physics. The model explains 3 of the 4 forces that govern the universe, that is it does not explain gravity. Right before this part, I read about the general theory of relativity that says that gravity is actually the curvature of spacetime. My question is, how is gravity a "force" that needs to be explained, when it is actually the curvature of spacetime. To me, from general relativity it seems like gravity isn't an "interaction" between things its just how the structure of spacetime is. So, why do we need to explain it as a force?

ANSWER:
I once wondered this myself and I have gotten this question before and researched it a bit. What I discovered is that the very complicated mathematical framework of general relativity may certainly be viewed in the context of distorted spacetime, but that is not a unique visualization. The theory is also a field theory and therefore will have forces associated with it. In an earlier answer I discuss this. Also that answer links to the brief essay which is pretty easy to read which finally clarified this for me.

QUESTION:
Hurricanes in the Northern Hemisphere rotate counterclockwise due to the Coriolis Effect. We are at 5 degrees north and the water in our kitchen sink swirls clockwise while draining. What gives?

ANSWER:
The Coriolis force is too small to be observed in such a small system like your kitchen sink. The direction is determined by initial conditions (tiny currents you cannot see) or the geometry of the sink. This is particularly true for you because you are so close to the equator where the Coriolis force is zero.

QUESTION:
is 5kg down scalar or vector?

ANSWER:
This is a very strange question! In physics, the kilogram is a measure of mass, always a scalar quantity. Therefore, this is, in physics, a scalar and the appearance of the word 'down' is incorrect and meaningless. On the other hand, many countries use the kilogram as a unit of weight which is a vector which points toward the center of the earth; in that case it is a vector. But the magnitude of the weight of a 5 kilogram mass is 5x9.8=40 Newtons=11.02 pounds in physics.

QUESTION:
I am an aspiring sci-fi author, and I've written myself into a hole. I am not certain if Kepler's Laws of Planetary Motion and other gravitational physics questions are outside of your accepted questions, but here goes. I would like to have two planets (or one gas giant and some other class of celestial object) that both have the same year length, or a very similar year length. Essentially, the homeworld of a sapient species has the sun visible every day, but a large ring-system-bearing gas giant visible every night. From what I understand, this cannot happen with a moon and a parent gas giant, due to the moon's orbit placing the gas giant between the moon and the sun. I also believe that Kepler's laws do not allow for two objects with different distances to have the same period.

Is there some natural method that would allow for this configuration?

Could a planet-like object be in a gas giant's L1 (or possibly L4 or L5 for dusk/dawn visibility) Lagrangian point?

Could one of the two planets be "shepherded" by some other gravitational influence so that it matches the year of the other planet?

Could the smaller body be an escaped moon of the larger body and therefore it has the same momentum, and that momentum will decay over millions or billions of years?

Could a captured rogue planet have a speed that is unusual for its new parent star? A speed that would decay and normalize over millions or billions of years? I do not care how coincidental or extraordinarily unlikely the scenario needs to be, so long as it is a "natural" explanation. I do not want to resort to any high technology explanations such as "planetary engines" or "designer solar systems".

ANSWER:
Since the ground rules of the site require "single, concise, well-focused questions", I have not answered any of your questions which I have italicized. I have attached a picture showing the Lagrange points for a planet between L1 and L2. If your smaller planet were located at L1 and its rotational axis was perpendicular to the plane of the obit, the sun would shine all day and the larger planet would be visible all night. However, there is a serious problem for your scenario—L1, L2, and L3 all have unstable equilibrium in the radial direction although they are stable tangentially. The Webb telescope, recently placed at L2, does not just sit at that point but moves in a small orbit around it which is reasonably stable but needs occasional tweeks from small jets; the problem for you is that tweeking a whole planet would not be feasible. The L4 and L5 points are not strictly stable either but will not wander off but rather they will stay is orbits which will not be strictly periodic, more lissajou type patterns. Although not satisfying the desire to have all-day sun, all night other planet, they will be your best bet if you want to be perfectly scientifically accurate. You can learn more about this from the excellent Wikepedia article on Lagrange points or my earlier answer.

QUESTION:
Hello, I am in need of a way to find the coefficient drag force of a orange foam torus with a 10 in. (~25 cm) inside diameter, 1 ft. 2 in. (~36 cm) outside diameter,and 2-in. (~5 cm) thickness. for robotics I can not test said drag force so I am going the mathematical route would you know how I could find it using online resources that dont cost me I know that you can use a CFD but I am not expericended nor do I have time to find out how and information would be greatly appreciated

ANSWER:
You will never be able to get a very accurate number without highly powerful computer calculations. However, there is a pretty good approximation if the object is moving through air at approximately sea-level atmospheric pressure. It is surprisingly simple. One important proviso is that the calculation must be made in SI units, meters for length, seconds for time, kilograms for mass (which you will not need to use). So, it is F=¼Av² where F is the drag force (in Newtons), v is the speed (in m/s), and A (in m²) is the area presented to the onrushing air. (You will note that this is not a dimensionally correct equation; this is because the factor of ¼ is contains the other stuff like atmospheric pressure, density of dry air, etc.) For example, if your torus is moving in the direction of its axis, A=π[(0.36/2)²-(0.25/2)²]=0.053 m², so F=0.013v². Suppose v=3 m/s, then F=0.12 N=0.027 lb. If v=10 m/s, then F=1.3 N=0.29 lb. If it were moving perpendicular to the axis the area would be A=0.05x0.36=0.018 m².

QUESTION:
Why does frequency affect the energy of light waves, but not sound waves? Another way to ask the same question, Why is the energy of a sound wave only affected by its amplitude, not its frequency?

ANSWER:
As a matter of fact, the energy of electromagnetic wave is proportional to the square of the electric field at a particular point and time of the wave. What is generally referred to as the intensity is the energy averaged over some time interval. For a sinusoidal wave the average intensity I averaged over one complete wave is given by I=cε₀E_max²/2 where c is the speed of light, ε₀ is the permitivity of free space, and E_max is the maximum electric field; so, in classical electromagnetism, the intensity is just like any other wave. However, if classical electromagnetism is quantized (QED, quantum electrodynamics), it is found that the smallest possible enegy e of the quanta of the field (called a photon) is proportional to the frequency f of the wave to which it belongs, e=hf where f is Planck's constant. So if a red beam beam of light and a blue beam have the same E_max, and therefore the same intensity, there are more red photons than blue photons per cubic meter because a red photon has less energy.

QUESTION:
I want to understand how the speed of light really works. If i emited a beta particle travling at more than half the speed of light in one direction- lets say north - and emit another beta particle at more than half the speed of light at oposite direction - south -. How fast are they travling from each other? The comon answer would be that its lower than the speed of light, but lets say the particle travling north is emitting light toward the particle travling south. Would it catch up to it and hit it or will it never reach it? I suspect it wouldn't reach it due to the particles actually travling faster than the speed of light from each other.

ANSWER:
I want to start with your last sentence. "…the particles actually travling faster than the speed of light from each other." This is totally incorrect. In special relativity we learn that, if speeds are comparable to the speed of light, usual Galilean relativity is wrong and only approximately true at much slower speeds. Galilean relativity says, as you know, that if two cars are both traveling away from each other with speeds of 100 mph, then each sees the other moving away with speed 200 mph. Mathematically, we would write w=u+v where u and v are the speeds relative to the ground and w is the speed either sees the other going. However, this is simply wrong. In special relativity it should be expressed as

w=(u+v)/(1+uv/c²).

So, suppose u=v=0.8c where c is the speed of light. Then w=(1.6c)/(1+0.64)=0.98c. This, coupled with the knowledge that the speed of light is independent of the motion of the source and the receiver, means that the second particle will indeed be hit by the light emitted by the first. Note that if I had chosen u=v=0.0001c, approximately 67,000 mph,

w=2x67,000/(1.00000001)=134,000/1.000000001=133,999.9999 mph.

QUESTION:
I know you aren't an astrophysicist, but would you discuss why the planets move in elliptical orbits & not circular orbits? All the planets are experiencing the gravitational pull of the sun & of the other planets/moons. Certainly, most have had collisions with other bodies over the billions of yrs.

ANSWER:
The Kepler problem is completely understood for a two body attractive 1/r² force. If one body is much larger than the other, you will see elliptical orbits, a circle simply being an ellipse with eccentricity 0. The eccentricity is determined by the initial conditions, the velocity and position of the smaller object. The solution is exactly the same for masses more comperable but the coordinate system is the center of mass system. In reality, there is never a such a simple system and other objects exert gravitational forces on the original two so they don't move in perfect ellipses.

QUESTION:
If electron particles have mass, yet, being an elementary particle are a wave, when downloaded to a battery does the battery weight more after depletion and then filling? This may be related to the question: does a quantum wave have mass?

ANSWER:
A battery is not charged by adding electrons to it. It is charged by causing chemistry to happen which then is "unhappened" when the energy to perform the chemistry is withdrawn from the battery. For example, a AA battery, fully charged, has about 14,400 J (4 watt·hours) of stored energy. When it is fully used, it will have less mass because mass is a form of energy (E=mc²). So, the loss of mass m will be 14,400=m(3x10⁸)², or m=1.6x10^-13 kg.

QUESTION:
QUESTION:
This question is about the period of a simple pendulum. The period can be written as: T₀∝f(θ₀)√(L/g) I know that the function f(θ₀₎ is always equal to 2π, but what exactly is this function? How can I compute it? For instance, if I want to solve the question: "By what factor does T₀ change when θ₀ gets multiplied by 4?"

ANSWER:
Your assumption that f(θ₀) is always equal to 2π is wrong, it is only approximately true for small values of θ₀. Also, the period is a function of the starting angle, so it is better notated as T(θ₀) where T₀ would be T(θ₀=0)=2π√(L/g). For arbitrary values of T(θ₀) the solution becomes very difficult. If you are interested, I suggest the Wikepedia article on the simple pendulum. I have included a graph of a calculation using elliptic integrals; T/T₀ is your f/2π

QUESTION:
I wanna talk about concept so you know that newton's 2nd law said that netforce equal mass times acceration.but when I think about real life when you drop same mass from different height that mass hit the ground difference the higher one hit harder.but why If u calculate using newton's 2nd law u will get the same force because the gravity is the same. but when you using the change of monumentum to calculate this same problem the thing turn out to look right .So as you can see here i just lost so please help me I want to be a physicist.***from my understanding newton's 2nd law sis the same as change of moumentum***

ANSWER:
You are very confused. You seem to be asking about how to get the force which acted to stop the falling masses. It depends entirely on the nature of the ground. The mass m does not instantly stop but takes some time t to travel a distance d and has an acceleration of magnitude a. It hits the ground with a velocity -v₀. I will assume that both balls experience the same acceleration (and therefore the same force F from the ground) and that a is constant. First look at it using Newton's second law, F-mg=ma, so a=(F/m)-g

d=-v₀t+�at² and v=0=-v₀+at. So t=v₀/a and d=[-v₀²/a]+½[v₀²/a]=-�[v₀²/a]

Next, look at it from the perspective of rate of change of linear momentum, F-mg=Δp/Δt. But we know that Δp/Δt=ma, so this will result with the exact same equation a Newton's second law as you say, so you will get the same result for the depth as I have already done. The important takeaway for you is that the depth is proportional to the square of the speed with which the mass hits the ground.

QUESTION:
Please explain the concept of thrust with relation to space a vehicle with current technology. I am familiar with "for every action there is an equal and opposite reaction" but can't get my head around the concept of thrust in space. On the launch pad, the rocket engines push first against the ground (gravity) and finally escape Earth's gravitational pull. But what do they push against out in space?

ANSWER:
You idea of the propulsion coming from the wrong notion that the rocket is pushed forward by the exhaust pushing on the ground and then by its pushing against the air. This is totally wrong. You are correct that Newton's third law is important in understanding what is going on. Essentially the rocket must exert a force on the exhaust to eject it and the exhaust exerts an equal and opposite force on the rocket, propelling it. I suggest you read an earlier similar question and all the links you will find for a much more detailed discussion. Oh, and also this link might help.

QUESTION:
Why does gravity want to crush everything to the smallest possible point? Why can�t we solve gravity?

ANSWER:
You must keep in mind that when gravity is pulling stuff together there are other forces which can come into play. The classic example is a star. In star-forming regions of space dust and hydrogen gas have gravity pulling the whole mess of stuff together. When there is a gas which is being compressed (gravity is compressing the star-to-be in this case) the temperature and pressure of the gas increasea while the volume decreases. But pressure due to this heating is causing the gas to try to expand again. Eventually, if there is enough hydrogen, it will become hot enough that nuclear fusion will be ignited which will get it much hotter still; when that happens it settles down so the forces trying to collapse it further (gravity) and the forces trying to push it apart (pressure from heat) become equal and, voil�, a star is born! Billions of years later just about all the hydrogen is gone so the star starts cooling and therefore expanding. Several things can happen depending on the mass of the star. One thing that can happen, if the mass is large enough, is that the gravity wins the tug of war and the whole star collapses into a black hole which is indeed "the smallest possible point". I do not know what you mean by not solving gravity; the theory of general relativity is a quite good model of how gravity works but there are certainly a lot of things we do not know. Hard problems take time to get answers to!Why does gravity want to crush everything to the smallest possible point? Why can�t we solve gravity?

When I go bike riding with my friends. And if we start at the top of the hill coast to the bottom. The heavier cyclist will always be the fastest and first to the bottom. Why is that? It seems to contradict what I learned in high school physics about falling objects.

ANSWER:
If there were no friction at all, all would arrive at the same time, regardless of weight. But there is friction, so everyone will arrive at the bottom going more slowly than if there weren't. But most friction is proportional to the weight (strickly speaking to the mass), but the acceleration is proportional to the weight also so, in this case, all have the same acceleration down the incline and arrive simultaneously at the bottom; again, a tie. But there is one kind of friction which depends on the speed and that's air drag; drag force is proportional the speed squared and the geometry but not to the weight. So, at some particular speed all bikers (assuming roughly the same size) experience the same air drag but the heavier biker will have a smaller effect on her motion and arrive going faster than the others when she arrives. This can be easily understood by citing a simpler but analogous situation: Imagine dropping a bowling ball and a beach ball of the same size from a cliff�the bowling ball, being heavier, will hit the ground first.

Here is the math for those who care: Newton's second law says that F_net=ma where F_net is the net force on a mass m and a is the acceleration. F_net=mgsinθ-μmgsinθ-kv²=ma where g is the acceleration due to gravity, k is some constant for air drag, μ is some constant for other friction, v is the speed, and θ is the angle of incline of the hill. So, a=(1-μ)gsinθ-kv²/m. Note that I have chosen down the hill as the positive direction so that if m is speeding up down the hill, a is positive.

QUESTION:
The celestial ecliptic is at a right angle to the galactic ecliptic. Both rotate counter clockwise. So does the earth and Biological particles. Why does all advanced math operate in clockwise direction?

ANSWER:
Consider a clock. You look at it from the front and, duh, the hands rotate clockwise. Now, suppose it is a transparent clock and you watch it from behind. The same hands rotate counterclockwise! The terms, without the proper definition, are meaningless. When someone says the earth, the sun, all the planets, all the planets' orbits are almost all counterclockwise, she is not telling you from where you observing these rotations. It is true if you are observing the solar system from somewhere straight above our north pole. You could just as easily have decided to look from somewhere above the south pole and then everything would be going clockwise. "Advanced math" doesn't even use the clock terms; it defines where you are looking from and calls that positive. It gets more complicated if all the rotations are not in the same plane.

QUESTION:
if light is reflected of a mirror one would assume some of that energy would be put off as heat into the mirror even if it is a small percentage how does light still travel at the speed of light

ANSWER:
Some of the energy of the incoming light gets absorbed; no mirror is 100% reflective. Indeed, that energy removed mainly ends up as heat. But that energy will ultimately become infrared radiation; heat is energy flow and the energy can flow out as electromagnetic radiation or as convection in the air. Infrared is, indeed, light, just not visible light. So it travels with the speed of light, actually a tiny bit slower because it is not traveling in a vacuum.

QUESTION:
Why does everyone say that time machines are impossible while we have a cellphones? Is not a cellphone like a mini time machine. When taking a picture and looking at it later,it is like you are going back into time. Hopefully this answer can be answered, because I always get unsatisfying answers.

ANSWER:
Well, you might think watching a movie is the same as actually being there when the movie was made. The "when" here is the key to what physicists would call a time machine. The pyramids in Egypt are not a time machine because you cannot be there when they are being made, and if movies had been invented 3000 years ago and a film of their construction had been made, watching that film would not put you there. A time machine requires both a what and a when be experienced.

QUESTION:
I have a fluid dynamics question that seems fairly simple, but I haven't been able to find the answer from other sources. Does the rotational motion of water draining in a sink continue down the pipe? And do the bends in the drain pipe (the trap and subsequent turns) inhibit vorticle motion? For the rotation of water to continue past the drain, would one need a straight pipe?

ANSWER:
Put a glass of water on the table. Give it a good stir so that it is spinning around like a vortex and remove the spoon. As you watch it, the vortex will rather quickly go away and the water will become motionless. Why did this happen? For two reasons: First, the water is sliding on the inside surface of the glass and there is friction exerting a torque on the water causing it to slow down. Second, the water has some viscosity and, if you think of the volume of water to be thin concentric cylindrical shells each of which is rubbing its neighbors outside and inside, then the slowing of the outermost shell will be transmitted throughout the water, eventually stopping its rotational motion. Going through a bend, things get even worse because the friction will be trying to make the water have rotational motions not around the cylindrical axis.

QUESTION:
I just read that angular momentum is preserved. Suppose two arrows are shot and meet head to head in the air. Suppose that one or both of them was spinning. When they hit and fall to the Earth, wouldn't the spinning stop? Where would the angular momentum go?

ANSWER:
Like all conservation principles, conservation of angular momentum comes with provisions. Angular momentum is conserved if there is no net torque acting on the system. I don't understand why you have this pair of colliding and falling to the ground. Why not just have a spinning arrow which sticks in a target. Obviously the arrow which had angular momentum no longer does. The reason is that the friction between the arrow and target exerts a torque on the arrow opposite the direction it is spinning.

QUESTION:
How can Francium lose one proton and become Radon with the same mass number? Is such a nuclear reaction possible?

ANSWER:
As you probably know, the stability of a nucleus of a particular atomic number (Z) depends on the number of neutrons (N=A-Z) where A is the atomic weight. If a nucleus has too many neutrons it can decay by one neutron turning into a proton; it does this by β^--decay where the neutron emits an electron and a neutrino thereby changing its charge to positive. Even if it is a neutron outside of a nucleus it will decay like this�a neutron is not a stable particle outside of a nucleus. If the nucleus has too many protons, it can decay by a proton turning into a neutron. One way the proton can do this is by β⁺-decay emitting a positron (a positively charged electron, the electron's antiparticle) and a neutrino. But, there's a catch�the proton is a stable particle so to make a proton decay this way you need to supply some energy. Inside your Fr nucleus, the whole nucleus must provide this energy. It turns out, for Fr nuclei, that there is not enough energy available for β⁺-decay to occur. But, nature often finds a way! The nucleus 'grabs' one of the atomic electrons and gives it to a proton which then emits a neutrino and becomes a neutron; this is called electron capture. So A stays the same while Z decreases by 1.

QUESTION:
I hope this question does not bore you (it's a car collision question, but some things said at scene aren't adding up.) How fast would a 4,200lb vehicle need to be traveling to knock a 3,700lb vehicle 30ft, 40ft, 50ft? The 3,700lb vehicle is traveling on a perpendicular path when hit.

ANSWER:
There is nowhere near enough information to answer this question. And, in fact, only with a carefully set up experiment to answer it would all the information ever be available in the real world. I am, however, going to give a lengthy answer because I often often get questions like this and it would be helpful to me, to refer future such questions here.

The figure shows the two cars, their velocity vectors, and their masses just before the collision occurs. If the collision itself happens pretty quickly, we can approximate that linear momentum (mass times velocity) is the conserved, that is, remains the same before and after the collision. What makes this situation difficult is that linear momentum is a vector quantity because one car is going north and the other east. So to illustrate how to proceed, let's assume that the two cars stick together after the collision and each car is going 60 mph and we use your weights as mass. Then the eastern momentum before the collision is 60x4200=252,000 and the northern momentum is 60x3700=222,000. After the collision the two cars have a mass of 4200+3700=7900 and an unknown velocity which will call V; don't forget that this is a vector, so we need to get both the east and north parts of that vector. Now we use momentum conservation to get those:

V_E=252,000/7900=31.1 mph and V_N=222,000/7900=28.1 mph.

Then V=√(V_E²+V_N²)=41.9 mph and the direction is arctan(28.1/31.1)=42.1� north of east. So

this is the velocity immediately after the collision and the stuck-together cars start sliding in that direction with that speed. But, now they experience sliding friction which will slow the two until the eventually stop. So what you need to know is the coefficient of kinetic friction and you would calculate the distance to stop. For example, the coefficient of friction for rubber on dry concrete is about 0.85. Without any detail, I calculate the distance to be about D=70 ft.

Why is this not applicable to your problem? Because the two cars do not stick together. If they do not stick together the problem is much harder because there will now be 4 unknowns rather than 2. If all you do is momentum conservation you will still get only two equations so you will be unable to solve the problem. The problem we just did is called a perfectly inelastic collision, inelastic means that energy is lost in the collision and perfectly means this is the situation loses the most amount of energy possible. If the collision happens without losing any energy, it is called elastic; any collision between cars will not be perfectly elastic. The real problem is inelastic with the energy lost something less than the energy lost in a perfectly elastic collision.

Also, I have drawn my picture such that the collision happens about at the center of the struck car so that the two will not be rotating about their center of mass; if you hit near the back, for example, the two would spin as well as just slide, so the distance the two would slide would be smaller than 70 ft because some of the work done by friction would be used to stop the spinning.

Also, you do need to specify the condition of the road�an icy road, for example, would have a much smaller coefficient of friction resulting in the cars going much farther.

So, you see, this is a very complicated problem and there is not much hope of determining V₁ from D.

QUESTION:
We are visiting my son and daughter-in law for Thanksgiving. He has a wood-burning stove which has a little fan sitting on it. The fan has no battery or plug, but when the fire is lit, the fan starts up. He wanted to know how it works.

ANSWER:
Look at the picture of the fan. The base is triangular and above is an array of 'fins'. (I am not referring to the fins of the fan, rather the structure you can see behind the fan.) The bottom surface of the triangle is in contact with the stove so it is hot. The heat will conduct upwards and if the top and the bottom are all one piece the heat will flow upwards but because the fins have lots of surface area, they will radiate heat into the room. So the bottom of the whole thing will be hotter than the top. Now, it so happens that, if you have a situation like this, there will be a potential difference (voltage) between the top and bottom. Thermal gradients and electric potential gradients are related, so whenever there is a temperature difference there will also be a potential difference. So this potential difference is what drives the fan. In fact, there is a thin sheet of an insulator between the top and bottom parts which is not really needed but allows you the wire the fan with hidden wires; the purpose is probably to increase the temperature difference thereby increasing the voltage and therefore the fan speed. Wires connected to the top and bottom and then to the fan drives the fan.

QUESTION:
Hello, I am a middle school science teacher and we are learning about electricity and magnetism. We made a basic electromagnet by wrapping an iron nail in copper wire and connecting both ends of the wire to a battery and it worked fine. My question refers to the explanation of this demonstration. My understanding is that electricity is the flow of electrons through a substance. But in the case of this electromagnet, which atoms are these electrons coming from? First I thought the electrons originated from the zinc atoms within the battery, but then some explanations indicated that it was the outermost electrons from the copper that were flowing. Where do the electrons flowing through the wire come from?

ANSWER:
Two things need to be understood. First, the nature of a good conductor is that the outermost electrons are very weakly attached to their atoms. In fact, in a perfect detector the outermost electrons are moving around in the conductor just like gas molecules move around in the room, an 'electron gas'. But there is no net movement because all the electrons are moving around randomly. If you have a straw and blow into it you can cause there to be a net flow of air through the straw (a molecular current if you like). So you need to figure out how to 'blow' the electron gas through the wire. So secondly, that is where the battery comes in. As you know, a battery has two terminals called + and -. What this means is that the + terminal has a deficiency of electrons so there are a bunch of atoms missing their electrons so the overall charge of that terminal is positive. Similarly, the - terminal has a glut of electrons so there are a bunch of atoms with too many electrons so the overall charge of that terminal negative. So, we all know that like charges repel and different charges attract, right? Now connect a wire between the two terminals. What happens? The electrons in the 'electron gas' in the wire and near the negative terminal are going to be pushed away; similarly at the positive terminal the electron gas will be pulled in toward the positive terminal. Now we imagine a tiny man inside the battery whose job is to grab the electrons flowing into the battery at the positive terminal and carry them over to the negative terminal. Of course, there is no tiny man but there is some kind of chemistry going on which results in moving electrons from the positive to the negative terminal to keep the current flowing. Eventually all the molecules responsible for this chemistry use up all the right molecules to do this and the current stops so the battery needs to get recharged; kind of like the tiny man runs out of calories and needs to get some dinner to carry on.

Here is something you should appreciate also. The electrons in the current move very, very slowly. If you let the current flow until the battery is exhausted, an electron which started the negative terminal would probably not have made it to the positive terminal before the battery dies.

QUESTION:
Vehicle tyre balance beads. Do they work as counter balance inside a rotating tyre? I can't think of a mechanism which can overcome centrifugal force but, if you could enlighten me I would be greatful.

ANSWER:
I have spent a considerable amount of time on the internet trying to answer this. Some people (other than the manufacturers) swear by them. Many others swear that it is complete nonsense. One thing that makes sense to me is that you should not use plastic beads because of their lower density; stick to metal or ceramic. If you want to read a lengthy discussion by physicists, see this Physics Forums thread.

QUESTION:
why does current produces magnetic field?

ANSWER:
Why does a charge produce an electric field? Sometimes you just need to accept certain facts as "just the way nature is". An electric charge creates only an electric field when it is at rest and both electric and magnetic fields when it is moving�this is just a fact determined by experiments. "Why" is not an appropriate question. There is a partial answer, however: these two fields are really both the same thing, different aspects of the electromagnetic field.

QUESTION:
If Apohphis approaches Earth closer than the communication satellites orbit, would it possibly destroy many of them, causing trillions of pieces of debris to fly off rendering that orbital level virtually useless and make leaving Earth nearly impossible for future space flights due to the dangerous debris field?

ANSWER:
Let's try to get some idea of how dense the orbiting fragments would be. The mass of Apohphis is about M=7x10¹⁰ kg. To start, let's suppose we are able to reduce it to a powder which covers the entire sphere of the earth as a uniform spherical shell at some distance R with some thickness t (as you would require to block outgoing space flights). So the volume of this shell would be approximately V=4πR²t and the density is ρ=M/V=5.6x10⁹/(tR²) kg/m³. Therefore t=5.6x10⁹/R². Suppose that we choose R=5R_e=3.2x10⁷ m (about 1.4 R_e inside geosyncronous orbits) where R_e is the radius of the earth . Then t=5.5x10^-6 m. Now, of course, this would be nothing to worry about but let's now condensed this total mass into 100 kg chunks separated uniformly over the area 4πR². I find that each chunk would occupy about 1.8x10⁷ m² which would mean the average spacing would be about 1.3 km. But, of course you could never expect to be able to "destroy" the asteroid in such a way that would have fragments cover the entire surface of the surface of the earth, so the answer is that you could not ever do what you suggest.

QUESTION:
I�m trying to understand how early in the uranium decay chain protons appear to go from thorium -234 to protactinium-234 to uranium-234, since the beta radiation that causes the two transitions only eject electrons � so where do the new protons come from to go from atomic weight 90 to 92. I can�t find an explanation anywhere on the internet

ANSWER:
You have to ask yourself where these electrons come from. β^--decay is essentially the the decay of a neutron. The neutron emits an electron and a neutrino leaving behind a proton because electric charge must be conserved. Two decays adds two protons, hence the atomic number number (not weight) increases by 2; atomic weight 234 stays the same.

QUESTION:
Consider an object like an A4 sheet, without any potential of light reflecting,I mean Zero, and it's not transparent, so light can't pass through. Now imagine that I'm holding it in front of you.so obviously you can't see what I'm holding, because it doesn't reflect any light, and you cant see the behind of the object either, because it's not transparent. So my question is "What you gonna see in that area, where the object is?" I know it wouldn't be a black area, because it should be a black thing to see a black thing,or should be nothing at all(Like Space), but there is a thing, and its not black.

ANSWER:
There is a constraint on questions in the ground rules of my site which states that I do not usually answer questions "�based on unphysical assumptions." Your question is about an object which neither reflects nor transmits any light. Why is that "unphysical"? Because every object not at absolute zero temperature (which is everything) is constantly radiating energy. Just because it might happen to be radiating almost entirely outside the visible spectrum, it is still radiating. You specify that it neither reflects nor transmits, so it must be absorbing all the energy which strikes it. Where does that energy go? It goes to heat, so the object will just get hotter and hotter without bound if it does not radiate. What happens in the real world is that if the object is originally cooler (warmer) than its environment, it will absorb more (less) energy than it radiates until it comes into thermal equilibrium with its environment; when in thermal equilibrium it will be radiating and absorbing at equal rates. A radiation spectrum for some object at room temperature is shown in the figure. Note that there is essentially no radiation with wavelength less than 3 microns; your eye can only see visible light between 0.4 and 0.7 microns.

QUESTION:
I've just watched a Brian Cox documentary about gravity. He states that if information enters a black hole it can re-emerge imprinted in radiation and is not destroyed. What do physicists mean by "information"?

ANSWER:
This is a very difficult question, not one which can be answered concisely and accurately at the layman's level. The definition comes from advanced mathematics concepts, more than physics. To be frank, I do not really have a good understanding myself. If you want to delve into it more deeply, I would suggest this link. I could have dodged this question because, as stated on the site, I do not do astronomy/astrophysics/cosmology and "information" arises mostly in the cosmology of black holes. It was, for decades, assumed that nothing can escape a black hole if inside the event horizon, so therefore information would be lost too. Then Stephen Hawking found a way that something actually could escape a black hole, Hawking radiation. Since a black holes form and behave following the laws of physics and anything which escapes violates the laws of physics, this situation is called the Information Paradox.

QUESTION:
Although physics tells us that there are no solids (according to my understanding) no one I know thinks of themselves and their world as basically immaterial. Do we actually live in a universe made of forces or am I misunderstanding the nature of materiality?

ANSWER:
Where did you get the idea that there are no solids? There is a whole branch of physics called solid-state physics.

FOLLOWUP QUESTION:
I got the idea that there are no actual solids from several places. One is the makeup of the atom which is reportedly almost entirely empty of solid matter. Another is the statement that the amount of solid matter in a human is equal to one grain of lead dust which I read in Symmetry magazine from the US Dept of Energy. So if atoms contain almost no solid matter then wouldn't the rigid formations they often assume also be nearly devoid of solid matter?

ANSWER:
When you talk about "solid matter" you evidently are thinking about homogeneous matter where no matter how small of piece you cut off, it will have the same density as any other piece of the same matter. There is no such thing, but you would be hard pressed to be able to get small enough a piece to prove it. The notion of "solid matter" is vague and not particularly useful. Until you get down to the atomic level of size, you would get what is called a solid. It is totally untrue that atoms are mostly empty space. It is true that almost all of the mass of the atom is in the nucleus, but that doesn't mean the rest of the atom is empty. The first successful model of the atom, by Niels Bohr, had electrons in well defined orbits around the much more massive nucleus. Subsequently quantum mechanics was developed which is necessary to properly describe atomic structure and spectra. The more modern picture of the atom is that the electrons lose their individual identites and the previous discrete orbits are now described by a wave function which can be described as a probability function representing the likelyhood of finding an electron with a given set of quantum numbers at any point in the volume of the atom. So that outer part of the atom is not "�almost entirely empty�" but, rather, is entirely full! The part of your question regarding the DOE magazine statement comparing a tiny amount of the "�solid matter in a human�" is most likely comparing the mass of all the nuclei in your body, imagining them to be all put together in a single volume which would be very small but, for all intents and purposes, having almost all the mass in your body. In other words, the article is essentially calling "nuclear matter" what you call "solid matter". The nuclear density is about ρ=2x10¹⁷ kg/m³ so for a M=100 kg person this would occupy a volume of about V=M/ρ=5x10^-16 m³and this would correspond to a size of about 10^-5 m which would be about the size of a dust particle.

Probably the the one thing in the universe which is closest to what you think of as "solid matter" is a neutron star, the remnant of a burnt out star not quite heavy enough to become a black hole. Approximately entirely made up of neutrons, a giant nucleus!

FOLLOWUP QUESTION:
If possible I would love to take this one more step. Full disclosure is that for almost a decade I have been fascinated by the 'empty atom' issue and you furthered my understanding of what I often see referred to as the electron cloud. And while it's certainly true that the presence of the electron cloud or wave function means the atom is not empty, neither does it mean that the atom is full in the sense of how most non physicists see the world. To illustrate what I mean, I'd like to go back to what John Dalton expected would be eventually found to be the composition of the atom. I've read that he posited they would be found to be "solid, massy, hard, impenetrable, movable particles". Now he of course lived long before Thompson, Rutherford and Bohr, et al but my point is that most people today still share his belief about the basic nature of things. Most of us assume their bodies and the things around them are, at base, made up of things more substantial than wave functions or clouds of electrons. Even Bohr wrote, in what sounds like astonishment, "Everything we call real is made up of things that cannot possibly be regarded as real." I added the "possibly" because I speak Swedish which is very similar to Danish so I know how Scandinavians understate things. ;) So I guess my basic question is what is the nature of the human body? I asked an Oregon high school science teacher and after thinking it over his answer was, "We are areas of space filled with fields, created by and inhabited by (fundamentally) size-less particles."

ANSWER:
Every thing in the universe, not just the body, consists of energy in various forms. There is mass (E=mc²) which consists of fundamental particles, there is the motion of mass (kinetic energy), there are the force fields which are the interactions among particles (fields have energy densities). Even what we think of as a vacuum is not really a vacuum since particle-antiparticle pairs are constantly popping into and out of existence for short times; quantum mechanics, perhaps our most successful though not the best understood theory, allows energy to fluctuate within constraints (uncertainty principle.)

In response to your comment "�how most non physicists see the world.": I don't get this. Non physicists see only the macro world and perceive that "things" like a block of lead or a block of aluminum seem uniform so that must be the way matter "is". Just because extranuclear space has a different density than nuclear space does not mean that it is not "full". Do you think of a block of aluminum to be less "full" than a block of lead?

FOLLOWUP QUESTION:
How is the situation of humans living their lives assuming that they are solid, or semi-solid, creatures made out of physical 'stuff'different from the situation in pre Copernican times when everyone was walking around on a flat earth at the center of the universe?

ANSWER:
It seems to me that there is no comparison between these two misunderstandings. A clear understanding of what "physical stuff" is is not nearly as central to our lives nor ever likely to be. The realms of relativity and quantum physics are outside the experience of everyday life because most of us have never experienced speeds comperable to light speed nor stuff as small as atoms. Knowing what stuff really is can, in my opinion, never have the impact on the everyman's world comparable to knowing an untruth about the environment which he does perceive.

QUESTION:
I'm in the middle of a debate with my son and hoping you might be able to assess us but totally fine if you can't. So my son showed me a video about Elon Musk if he had put one of his twin on his space ship and one travelled at the speed of light for 5 years and then 5 years back. He would be 10 and the twin that stayed on earth would ve 23. Though I understand ok there physical age might be different how is it possible for the physical, mental and body's age be different. I don't understand or think that possible our body's don't stop developing regardless of where we are do they, how is that even possible.

ANSWER:
First, special relativity shows that it is impossible for anything with mass to travel at the speed of light. But, I can still answer your question but just with the traveling twin traveling 99% the speed of light. The main thing you are missing is that you are assuming that all clocks in the universe run at the same rate; in fact, if you have two identical clocks they do not run at the same rate if one is on earth and the other is moving relative to the earth. Now, to get quantitative, there are three things you need to know about special relativity:

The speed of light in a vacuum is always the same speed no matter how its source moves or how the observer is moving. (If you have trouble accepting this, read an earlier answer and the links therein.)
Moving clocks run slower than clocks at rest; this is called time dilation. (If you have trouble accepting this, consider an earlier answer about the light clock. HINT: This is true because of the constancy of the speed of light.)
Moving lengths are shorter than lengths at rest; this is called length contraction.

I am assuming you do not want any of the algebra which will let us calculate our example, a trip to a star 5 light years (LY) away by a space ship having a speed 99% the speed of light and back. So the earth-bound twin sees his brother speeding away on the path of this 5 LY distance. But the traveling twin sees the 5 LY distance moving with the speed 99% of light speed, so he sees the distance he has to go to be 0.705 LY because of length contraction; if you are interested, the factor of contraction is √(1-0.99²). Therefore the total distance he travels is L=1.41 LY with a speed of v=0.99 LY/yr, so the time of the jouney T=L/v=1.41/0.99=1.42 yr. So, while his brother (along with all clocks on earth) aged 10 years, he (along with all clocks on the space ship) aged only 1.42 years.

All this, I am sure, seems counterintuitive to you. But what is intuition? It's what you expect to happen based on your experience. But, what experience do you have with things traveling with speeds comparable to light speeds (186,000 miles per second)? But I assure you that both length contraction and time dilation have been measured and verified to great accuracies.

QUESTION:
when an object has a force applied to it does that mean that the object on top of it has the same force?

ANSWER:
If you exert a force on an object, that force is on that object, no other. The way you solve such problems is to choose something to look at and find all the forces on that object, similarly on othe objects in the system. I have drawn a figure to illustrate your problem. A force F pushes on box A which sits on a frictionless floor; a box B sits atop box A and there is sufficient friction that box B moves along with A as it accelerates to the right. What are all the forces on A?

the force F,
the normal force N_BA which box B exerts down on it,
the weight W_A of the box A,
the normal force which the floor exerts up on it, and
the frictional force f_BA which B exerts on A.

Now apply Newton's 1^st and 2^nd laws:

F-f_BA=m_Aa where a is the acceletation of A (and also B) and m_A is A's mass.

N_FA-N_BA-W_A=0.

We now have two equations with four unknowns (F, W_A, m_A are presumably given). But we still have to do the same analysis for box B. What are the forces on box B?

B's weight W_B,
the normal force N_AB which A exerts up on B, and
the frictional force f_AB which A exerts to the right on B.

Now apply Newton's 1st and second laws:

f_AB=m_Ba

-W_B+N_AB=0.

We have now added two equations but also two more unknowns, f_ABand N_ABso we have four equations and six unknowns. But, wait a minute, Newton's 3^rd law tells us that N_AB=-N_BA and f_AB=-f_BA. So you now have six equations with six unknowns, so you can find all unknowns.

If there were no friction between A and B, B would just sit there until A has accelerated far enough that B would fall to the floor. If there were friction but not enough to keep the two moving together, B would have a smaller acceleration than A and eventually fall to the floor. So now you would now have seven unknowns (two accelerations instead of one) so you need a 7th equation; you would need to know the coefficient of kinetic friction μ which would give the additional equation f_AB=μN_AB.

QUESTION:
I wondered how U setup/arranged the differientials in your worked out ship/ball example. Not clear on the mathematics.

ANSWER:
I have copied the earlier Q&A below. Let me clarify my first answer first: There are two ways the question could be answered, the displacement of the ball as seen by an observer watching the boat go by and the actual path which the observer sees the ball take; the former is the blue line which is drawn straight line between the starting and ending locations of the ball, and the red line which is the path actually followed by the ball. My answer actually calculates the length of the blue line (the easy one) but not the length of the red path. But, as I stated, I got curious and then calculated the length of the red curve in the ADDED THOUGHT. This is what the current question is asking, for more clarification of the calculation of the red curve. Probably the main confusion of the questioner is where did the factor of 4 [√(1+4x²)]come from? Well, I must admit that I have no idea! When I saw this I thought "Why is there no g, no H, no v here?"

So let me now go into detail and redo the ADDED THOUGHT. The first step is pretty simple, an infinitesmal length of any 2-D path has x and y components dx and dy, so the length ds is √[(dx)²+(dy)²]. Next we factor out (dx)² and take it out of the square root, hence ds=dx√[1+(dy/dx)²]. This step is where the features of the shape of the path is brought in, so we need to write y(x) and differentiate it. But, this is simple projectile motion and y=H-�gt² and x=vt. (I have chosen the positive x-direction to be to the left in my figure.) Eliminating t between these two equations yields y(x)=H-�gx²/v² and dy/dx=-gx/v². The quantity to be integrated is ds=dx√(1+(g²/v⁴)x²)). Integrating, using Wolfram Alpha,

s=[ax√(1+a²x²)+sinh^-1(ax)]/(2a)+constant

where a=H/v². Now, evaluating the integral from x=0 to d where d is the distance traveled,

s=[ad√(1+a²d²)+sinh^-1(ad)]/(2a).

Finally putting in the values from the example in the original answer, H=4 m, d=4.5 m, v=5 m/s, I find s=6.27 m, about 4% longer than the displacement. In my original (incorrect) answer, s=9.19 m, about 34% larger than the displacement.

QUESTION:
A ball dropped from the top of the mast of a moving ship falls straight down parallel to the mast. But with the movement of the ship, it also falls down on an inclined LONGER path. In other words, it travels over two different distances at the same time. Which is the actual 'real' distance traveled?

ANSWER:
There is no such thing as "the actual 'real' distance traveled". The distance traveled in one frame of reference will be different than for another frame. For your question, if the ball is dropped from a mast of height H, it will travel a distance H in a time t where t=√(2H/g) where g=9.8 m/s² is the acceleration due to gravity. Now, look at the path of the ball from a dock the boat is passing; if the boat moves with a speed v, the distance the boat travels before the ball hits the deck is vt=v√(2H/g). The distance between the starting and ending points of its path (blue line) is √[(2v²H/g)+H²]. For example, if H=4 m and v=5 m/s, then t=0.9 s and the distance is 6.03 m. The path followed by the ball in the dock frame is a parabola (red line), so its length is the distance the ball has traveled; it is rather complicated mathematically to compute this distance.

ADDED THOUGHT:
I got curious and calculated the distance the ball actually traveled in the dock frame. You need to integrate ds=√[(dx)²+(dy)²]=[√(1+(dy/dx)²)]dx=[√(1+4x²)]dx from x=0 to x=vt. The result is s=�[2vt√(1+4v²t²)+sinh^-1(2vt)]; for the example above, s=9.19 m.

QUESTION:
suppose you are in a cave on a cold winter day and you have one blanket which is not large enough to wrap around you. should you put the blanket under you or over you to stay the warmest?

ANSWER:
I remember from my camping days I was told to always provide for a barrier of some sort between yourself and the ground, but it was never an either-or situation like you describe. But the physics would suggest that it is better to lay on your blanket than have it over you because heat can pass from you to the ground by conduction whereas heat passing from you to the air is slower because it does so by convection. What's the cave got to do with it?

QUESTION:
A ping pong ball is placed in a container of water. When the container is dropped, the ping pong ball will get launched to a great height. What maximum height can you reach with up to 2 liters of water?

ANSWER:
I have deleted much of your question because it violates the site ground rule that questions be "�single, concise, well-focused�" However, there is a very thorough video which discusses much of the physics and results of experiments. It is quite long and the narators have strong accents. But if you stick with it you will get what you need.

QUESTION:
When we heat the air inside a hot air ballon, the ballon rises. Does gravity afect the hot air differently because of the energy given to the air? And if gravity is the curvature of space-time, does giving energy to air by heating it, somehow affect the curvature of space-time?

ANSWER:
Let's just concentrate on the balloon. The presence of any mass or energy density affects the curvature of space-time. There is only one thing which causes the hot air balloon rise�Archimedes' principle, buoyancy. If the weight of a volume in a fluid is smaller than the same volume of that fluid, there will be an upward force on that volume which is greater than its own weight and it will therefore rise. The density of hot air is much smaller than the density of cool air so if the volume of the balloon of hot air is big enough it will rise. The reason that a helium balloon goes up is that its weight is smaller than the same volume of air.

QUESTION:
What I am trying to understand is the physics behind the following Guinness World Record. "Greatest height achieved launched from an airbag" In my own example i would like a 250kg person to jump/freefall say 10m into the airtube launching a 50kg person in the other end of the tube. Now if I understand basic physics: IF there was no loss of force in the transfer the impact velocity (should be 14m/s with a 10m fall) 14*5 (the weight diff 250/50) should be able to launch the person at 70m/s from the other end, 70m/s is very fast and there are probably many losses to take into account that would lessen the speed, however with that 70m/s a person would easily rise some 100 + m high. (or so I think). This obv. does not happen. The G-force of this acceleration from 0-70 in say, err 0.2 sec, should exert some 35G's (perhaps killing the person). How should I think?

ANSWER:
We will never be able to use simple physics to get a reasonable model. But we can look at it to see how predictions based on introductory physics ideas work and see how badly they might fail.

First, let's look at energy in the problem. I will approximate g≈10 m/s² and assume that air drag is negligible. If we assume that energy is conserved it is pretty easy because the system is at rest at the beginning and the end, so the initial potential energy is
U_i=MgH=250x10x10=2.5x10⁴ J
and the final potential energy is
U_f=mgh=50x10xh=500h J.
Now, if energy is to be conserved, U_i=U_f, so h=50 m. Since he only went up 22 m, we can say that approximately half of the total energy of the system was lost.

Now we can estimate the average forces felt by everyone during as they either stopped or launched. The relation between velocity and height is v=√(2gh), so the velocity of the 250 kg guys was v₂₅₀=14.1 m/s when they hit the hit the bag; and the velocity of the 50 kg guy as he launched was v₅₀=21 m/s. The video looks like maybe those guys went down by at most 2 m and the elapsed time at constant acceleration a to go a distance d is

t=2d/(v_f+v_i)

where v_f and v_iare the final and initial velocities, respectively. I find t₂₅₀=0.28 s and t₅₀=0.19 s. Since we know that for constant acceleration from or to v=0 is given a=v/t,

a₂₅₀=14.1/0.28=50 m/s²=5g

and

a₅₀=21/0.19=111 m/s²=11g.

Five G over 0.28 seconds is probably quite doable, but eleven over 0.19 seconds might hurt! I couldn't get a good view of the launched guy's launch, so maybe d was larger than 2m. I did notice, though, that he was laying flat on his back so the force which would be about 50x111=5550 N (1236 lb) would be spread over a large area; so, taking his area to be about 1 m², and the average pressure would be about 5550 N/m² (only about 0.8 PSI).

Now we can estimate the average forces felt by everyone during as they either stopped or launched. The relation between velocity and height is v=√(2gh), so the velocity of the 250 kg guys was v₂₅₀=14.1 m/s when they hit the hit the bag; and the velocity of the 50 kg guy as he launched was v₅₀=21 m/s. The video looks like maybe those guys went down at most 2 m and the elapsed time at constant acceleration a to go a distance d is

t=2d/(v_f+v_i)

where v_f and v_iare the final and initial velocities, respectively. I find t₂₅₀=0.28 s and t₅₀=0.19 s. Since we know that for constant acceleration from or to v=0 is given a=v/t,

a₂₅₀=14.1/0.28=50 m/s²=5g

and

a₅₀=21/0.19=111 m/s²=11g.

Five G over 0.28 seconds is probably quite doable, but eleven over 0.19 might hurt. I couldn't get a good view of the launched guy's launch, so maybe d was larger than 2m.

QUESTION:
If you could drill a hole 1 inch in area to the center of the earth and let the atmosphere fill it what would teh pressure be at teh bottom,at teh center of the earth? would the air remain gaseous or would it become a liquid or solid? I did the math and came up with roughly 775x sea level pressure but that assumed 1 m^3 or air weights roughly 2.75Lbs. i assume that as the air compresses there would be more air molecules in the hole than would be at standard pressure so it would have greater pressure im assuming the hole is lined with som esupre material so it doesnt collapse on itself

ANSWER:
After nearly 20 years and thousands of questions answered, it would not be surprising to find that I could not remember all of them. I knew that I had answered a question demonstrating that the density of the earth was not uniform and I was searching for that when I came upon a previously answered question almost identical to yours and worked out in detail!

QUESTION:
What are inertial frames?

ANSWER:
An inertial frame is a frame of reference in which Newton's first law is true. Once you have found one inertial frame you have found them all: Any frame of reference which has a constant velocity relative to an inertial frame is also an inertial frame; any frame which accelerates relative to any inertial frame is not.

QUESTION:
in the equation E=MC2 I don't understand c2...c2 is impossible...nothing can travel faster than light and this equation has it doubled....please explain

ANSWER:
First of all what you write as C2 is C² and this is not 2 times C but rather C times C. And furthermore, even if a 2 times C happened to appear in some equation it would necessarily mean that something were moving with that speed, it would just happen to have the value for the speed of light and the factor of 2 appearing in the same equation. Also, if this were 2C in this equation it would not be dimensionally correct. For more detail, see an earlier answer.

QUESTION:
My question is in regard to the speed of light, and the possibility of anything traveling faster than light. If a space based laser is mounted on a variable speed rotating platform and then activated, allowing the beam to travel for 1 hour. During this hour, the platform begins to rotate and is accelerated to ~10000 rpm. If the speed of light is 186000 miles per second, the light would have straight line traveled ~66,960,000 miles from the source at the 1 hour mark. If the laser is rotating @ 10,000 rpm, and light doesn't bend, that would mean the furthest end would be moving at 4,207,220,882 miles every .006 seconds, which is much faster than light speed?

ANSWER:
You make your question far too convoluted. You are essentially asking if the spot of light projected on a distant screen by a rotating laser can be going faster than the speed of light. The answer is yes, but you asked if anything can go faster than c and the spot of light is not "anything". See an earlier answer where your laser rotating at 1 rev/s will sweep across the moon at a speed of about 10c!

QUESTION:
Can you please explain the derivation for E=mc^2

ANSWER:
See an earlier answer.

QUESTION:
if potential energy depends upon height then according to Earth we all are attracted by the center of the Earth then, the height should be considered between the object and center of the Earth then, the potential energy is always present. It can never be zero. Then the kinetic energy will not be independent. It always depends on gravity. The object on the ground has potential energy, as the distance is calculated between the earth's center and the object. If the object moves it will have a displacement so kinetic energy takes place but it also has potential energy as the distance between the object and the earth's center is not reduced. so my conclusion is kinetic energy depends on gravity and potential energy. Is this right?

ANSWER:
You make the same mistake many make, that potential energy is meaningful on its own. Instead, since an integration is used to define potential energy, it is always arbitrary to within an additive constant. Therefore only the potential energy difference is a meaningful quantity. The result is that you are free to choose the zero of the potential to be anywhere you like. Usually when we do mechanics problems close to the surface where the potential energy function may be excellently approximated to V(r)=mgr where r is the distance above wherever you choose V=0. For example, if you choose the ground to be zero, then V(h)=mgh where (h) is the altitude; however, if you choose V=0 at h=H, where H is some fixed height above ground, the potential energy will be V(h)=mg(h-H). So, you see, if h is above H, V will be positive, but it will be negative between H and the ground. Until you understand this, it is pointless to talk about kinetic energy. If you go very far off the ground you will find that gravity gets smaller, it falls off like 1/r² where r is the distance from the center of the earth; in that situation it is customary to choose V(r=∞)=0 and V is negative everywhere.

QUESTION:
Why are there difficulties in integrating general relativity and quantum physics?

ANSWER:
See three earlier answers, genrel1, genrel2, genrel3.

QUESTION:
In your Jetpack answer, you said that if they could maintain a 1 m/s speed velocity they would escape. Wouldn�t you need at least a 9.9 m/s squared acceleration to get escape velocity Assuming you started at sea level?

ANSWER:
You misunderstood my answer or you misunderstand escape velocity. Escape velocity is the minimum velocity you must have at some particular distance r from the center of a large sphere (like the earth) of mass M in order to never return to that sphere. If I guarantee that I will continue pushing the object at some constant speed, it will never come back. But escape velocity refers to an object which, after the first push, is not being pushed by anybody. Note that if you launch something from the distance to the moon, its escape velocity will be much smaller than from closer to the surface of the earth because the gravity is weaker

QUESTION:
If a person was on a transatlantic flight going from East to West at say 500mph and they ran down the aisle of the plane from tail towards the nose at say 5mph would they be travelling at 505mph?

ANSWER:
Whenever I get a question like this I always tell the questioner that whenever you ask about a velocity your question should include "�relative to something." In your case your velocity relative to the airplane is 5 mph, your velocity relative to the earth is 505 mph.

QUESTION:
Why are there difficulties in integrating general relativity and quantum physics?

ANSWER:
See three earlier answers, genrel1, genrel2, genrel3.

QUESTION:
When Coulomb derived the equation for force between two charges, there is a proportionality constant, 'k' which turns out to be proportional to 1/epsilon. My question is, how was it determined that this is so? Using Gauss's law doesn't answer my question, since Gauss seems to use Coulomb's law to derive Gauss's law. I looked everywhere for an answer to this but all textbooks just put the epsilon (permittivity) term in there, without stating how this was known.

ANSWER:
Coulomb didn't derive his law. Like all laws of physics, he was stating an experimental fact in mathematical form. Doing experiments he discovered that the magnitude of the force between two point charges, q and Q, and separated by a distance r was proportional the the product qQ and inversely proportional to r². To me, that is Coulomb's law�a statement of an experimental fact. Now, how is this law useful in electromagnetic theory? Only if it is an equation, so we just stick a constant in there. But to measure that constant you would need to have a system of units by which you measure the relevant quantities�electric charge, distance, and force. If Coulomb were the first person to do electrostatics experiments, he would have had the priveledge of defining the unit of charge. Force and distance were already defined, the Newton (1 N is the net force to cause a 1 kg object to have an acceleration of 1 m/s²) and the meter, respectively. But he wasn't and the Coulomb* had already been defined in terms of the Ampere which was determined by measuring the force between two current-carrying parallel wires. So he just needed to get two equal charges (which he presumably knew how to do) and seperate them by some distance he could measure. Measuring the force on each would then give the constant, k=Fr²/q²=9x10⁹ Nm²/C². So, the force between two 1 C charges separated by 1 m is 9x10⁹! You may be sure that Coulomb was working with charges much less than a Coulomb. That this may be written as k=1/(4πε₀) is just an alternate way of writing the proportionality constant; it turns out all the math in electromagnetic theory turns out to be much more compactly and neatly stated if k is rewritten this way. (A hint why this may be so is that 4πr² is the area of a sphere centered on a point charge.)

*The Coulomb has recently been redefined as the magnitude of the charge of 6.241509�10¹⁸ electrons.

QUESTION:
A space rocket needs a velocity of 7.9 km/s to reach space. Is it in any way possible to reach space with a lower velocity like let's say 4 km/s if there is a constant lifting velocity of 4 km/s? Or would the 4km/s object stop moving upwards at one point even if it had enough fuel to go for a long long time? A scifi show I watch had jetpacks at similar speeds and I was just wondering if a jetpack going straight up at 4km/s for let's say 200 seconds could reach the height of 800 km?

ANSWER:
"�to reach space�" really has no quantitative meaning because there is no specific place where space begins. It seems that you are not talking about escape velocity because that is about 11.2 km/s for earth. At any rate, think about for a moment: If you had sufficient fuel so you could make your "space rocket" go with a constant speed of 1 inch/second, there would be absolutely no limit to how far you could go. See a recent answer. Your jetpack question can't be answered because I would not have enough information: Does it go at a constant speed of 4 km/s or is it given a speed of 4 km/s at the ground and goes up as a projectile? Also, at that speed air drag would not be negligible.

QUESTION:
I have a tank that holds 2167 gallons of 60F water in an insulated room. My question is how much cooling will this uninsulated tank provide to the room?

ANSWER:
I don't know all the information I need, namely the volume and temperature of the air in the room. But I can show you how to do the problem. However, I need to work in SI units, so you will too. All variables subscripted with a refer to air and those with w refer to water :

T_a temperature, V_a volume, M_a mass, ρ_a density, C_a specific heat, all for the air;
T_w temperature, V_w volume, M_w mass, ρ_w density, C_w specific heat, all for the water;

A few things of to keep in mind:

For air there are two kinds of specific heat, constant volume and constant pressure; I will be using constant volume.
The mass is the density times the volume, M=ρV.
The numbers I will use later when I calculate are
- T_w=60�F=289K,[T_a=100�F=311K]
- V_w=2167 gallons=8.2 m³,[V_a=125 m³]
- C_w=4181 J/kg�K, C_a=718 J/kg�K
- ρ_w=1000 kg/m³, ρ_a=1.2 kg/m³
- M_w=ρ_wV_w=8.2x10³, [M_a=ρ_aV_a=150 kg]
The numbers in square brackets are numbers I used but the questioner did not give.

Now, the physics. The thermodynamic energy in Joules may be written as U=MCT. If something causes the energy to change, the change in energy is ΔU=MCΔT where ΔT=T_final-T_initialis the change in temperature. In our case, the temperature of the water will increase and the temperature of the air will decrease. So ΔU will be positive for the water, negative for the air. But, this is a closed system so the total change in energy must be zero, whatever the air lost the water gained: M_aC_a(T-T_a)+M_wC_w(T-T_w)=0 where T is the final temperature. Now we just solve for T to find out how well the cool water will cool down the air. I find:

T=[M_aC_aT_a+M_wC_wT_w]/[M_aC_a+M_wC_w].

Solving, I find that T=289.1 K. The water has hardly warmed up at all and the room has cooled down a lot. The air has a much smaller mass and much smaller specific heat so it doesn't take much temperature change in the water to cool the air.

QUESTION:
When calculating gravitational effects on a large scale, do physicists take account of the time it takes for gravity to cross large distances? For example, the milky way has a radius of about 50,000 light years, so the gravitational effect on the most distant stars from the center is a result of the mass on average of stars 50,000 years in the past, when the stars had more mass due to the fact that they are constantly converting mass into energy.

ANSWER:
The lifetimes of stars are billions of years and their final masses are not all that far from what they started with, so the mass loss in 50,000 years is a proverbial "drop in the bucket".

QUESTION:
I understand about escape velocity ( and it being about ballistic flight ) but have often pondered this: If I fly vertically up at the north pole with a constant acceleration, can I escape the pull of the Earth WITHOUT reaching escape velocity? Even say at 1 ms^-2? I assume I have "unlimited" fuel.

ANSWER:
If you can maintain that acceleration you will certainly escape. In fact, if you reach the escape velocity for some altitude at that altitude you can turn your engines off. (Escape velocity gets smaller as altitude increases but your speed is increasing, so eventually they will be equal.) In fact, if you can maintain some constant speed, say 1 m/s, you will escape; and when you get to the altitude where the escape velocity is 1 m/s, you can turn off your engines and keep moving forever. Oh, by the way, you don't need to go to the north pole, it will work anywhere.

QUESTION:
I had a couple of questions regarding magnetic flux that I was hoping you could help me with. Firstly, I was wondering if a 2D non-closed surface has magnetic flux if it is placed in a uniform magnetic field??, and what should be the area of that 2d non closed surface? Secondly, I was curious to know whether a 1D straight line has magnetic flux if it is placed in a uniform magnetic field.

ANSWER:
I will give you a few examples which show non-closed surfaces which demonstrate how flux is calculated.

A flat plane with area A and a field B normal to the surface, Φ=BA.
A flat plane with area A and a field B which makes an angle θ with the normal to the plane, [Φ=BAcosθ].
A flat plane with area A and a field parallel to the surface, Φ=0 because the field never passes through the area.
A hollow hemisphere of radius R with the base open and the field normal to the area of the base (parallel to the axis of symmetry). See the diagram. This is a much harder one! The flux through the tiny area dA is dΦ=BdAcosθ. The lower-case d indicates a tiny (infinitesimal) quantity. If you know integral calculus you could add up all the infinitesimals over the entire surface and you would find Φ=πR²B. If you are clever you can do this much more cleverly and easily. Every field line which contributes to the flux through the curved surface also passes through the area of the base and perpendicular to the base, so the flux through the base is simply Φ=BA as in example #1, and the area of that circle is πR².

The answer to your second qustion is no because a straight line cannot define an area through which the field could pass. If you took that line and bent it so that it closed, there would be flux through it.

QUESTION:
How would I convert 24 frames per second to reflect mph? By that I mean, how fast would a moving object have to go to animate a still images on their surface?

ANSWER:
I do not understand the question.

FOLLOW UP QUESTION:
I�m asking how fast a train would have to be going in order to animate a series of still images placed along each car. This is based on how movies are made. I�d like to know if it is possible to animate a series of murals on the side of a bullet train. I�m just not sure how to reflect frames/second in mph in order to calculate it myself.

ANSWER:
It depends on the width of your frames. suppose your frames are a width W ft/frame wide and the speed of the train is V ft/s; I will convert V to mi/hr later. Then the number of frames passing you per second is V/W ( ft/s)(frames/ft)=V/W frames/second=24. For example, suppose W=10 ft; then, V=240 ft/s=164 mi/hr. You would probably prefer V in mi/hr, so V/W (mi/hr)(1 hr/3600 s)(5280 ft/1 mi)(frames/ft), so 1.467�V/W=24 frames/s (where V is mph).

QUESTION:
Assuming that the gravitational acceleration is constant and equal, in magnitude, to the acceleration of gravity at the surface of the earth, how far would light deflect from a straight line path as it travels one earth diameter, 1.28x10⁷m.

ANSWER:
This is really a difficult problem because to do it accurately, you would have to use general relativity, beyond the scope of this site. But there is a semiclassical way to get an estimate of the answer you seek. So, brace yourself, this is going to be one of my long-winded answers which result from a question which I never had thought about very deeply. So we'll touch on classical kinematics, special and general relativity, and a little history of physics.

So, there are two ways to attack this problem because of what is called the equivalence principle, a cornerstone in general relativity, which states: If you are in a gravitational field, in our case a uniform field with acceleration g, there is no experiment you can perform in a frame of reference which has an acceleration of magnitude g which will be different from being in the field. The diagram shows an elevator acclerating upward with acceleration a=g and a beam of light (velocity c₁) entering perpendicular to the acceleration. So someone on the elevator would see the light bend down as shown by the red curve. If this were the path of some particle, say a proton, it would be pretty easy. It would be a parabola, at some other time it would have velocity c₂ with components c_x and c_y where c_x=c₁ and c_y=-gt. (Be sure to note that c is the speed of the proton here, not the speed of light.) Also note that c₂>c₁ because c_x is constant throughout but c_y is constantly increasing. This is just first-semester introductory physics. I will come back to this, but we need to emphasize that this is not the same for light because although the speed of the particle with mass increases, the speed of the light must stay the same, c₁=c₂. So the path will not be a parabola. However, because the speed is so big, the field so small, and the distance relatively short, a parabolic path should give us a pretty good order-of-magnitude estimate. Things are simplified by the fact that in Newtonian mechanics the acceleration is independent of the mass. Now, the time for the light to traverse the distance L is t=L/c and the distance fallen in that time is �gt². Therefore, y=-�gL²/c²; for your numbers I find y≈-8.9x10^-3 m, a little less than a centimeter.

We have assumed that the photon follows the same parabolic path as all of the particles with mass, but, as explained above, they do not because c must not change as the photon "falls" because of special relativity. Its energy will change though as the y-component of c increases, resulting in a blue shift as the photon as it moves in the same direction as the field, gaining energy. For these reasons we have to expect that our estimate for deflection will be too small.

Now a little history. When Einstein first proposed this deflection of light it was essentially the same approximation I have made here. The British astronomer Eddington decided that he could look for gravitational bending of photons passing close to the sun during a total eclipse. His measurements disagreed with Einstein's approximation by about a factor of about 2. Einstein eventually was able to use a more complete general relativity to get this factor of 2. Knowing this, my calculation to answer your question should be doubled, y=-gt²≈-0.018 m, about 2 cm; this corresponds of a deflection of about 0.3x10^-3 arcseconds. This looked sort of large to me, but when I compared it to Eddington's result for the deflection for the star whose light just grazed the the surface of the sun, 1.75 arcseconds, it didn't seem too big.

QUESTION:
I read that F=-dU/dr is the relation between a conservative force and potential energy. Now when I put the value of gravitational force in this equation and integrate it both side with respect to dr. Then the expression for potential energy comes out positive where as I know that gravitational potential energy expression has a negative sign in front of it... I am unable to figure out what's wrong with my approach and why the sign doesn't come out right.

ANSWER:
You have to be very careful with signs in problems like this. So look at the figure. I have drawn two masses, m and M, and the force which m feels has a magnitude of mMG/r²; but the r component of F is -mMG/r² because the vector F is pointing in the opposite direction as the vector r. So now the equation you are asking about becomes

mMG/r²dr=dU/dr or dU=mMGr^-2dr.

Now, I am going to choose the zero of potential energy to be at r=∞, U(∞)=0 and integrate from r=r to ∞.

U(∞)-(U(r)=mMG[(-1)(∞^-1-r^-1) or U(r)=-mMG/r.

Well, waddaya know, you got it right! You are apparently thinking that potential energy must always be positive. In fact, the potential energy is arbitray within any arbitrary constant; this is because we get at it via integration, and an indefinite integral always has an arbitrary additive constant. The only thing which actually matters is the potential energy difference between two points. Be sure to note that I chose U(∞)=0 because I knew that would give me the simplest form of U. I could have chosen any other r=r₀ (except r=0 since the force is infinite there) for the point of zero potential energy, but it would have been messier; that would have had U positive for r>r₀and negative for r<r₀.

QUESTION: In the �Laws Of Motion� chapter, under gravitation, specifically �Free Fall� I have a query. When do we assume u to be 0 and when do we assume v to be 0? For example, when an object is dropped from a height. Is v=0? is u=0? Or if an object is thrown vertically upwards. Sometimes I see the solution stating that u=0 or v=0 because "obviously" but I can�t seem to figure it when to assume which to be 0, and when I need to find the value.

ANSWER:
(After a query to the questioner, u is the initial velocity and v is the final velocity.) It makes no difference how you label the the variables in the problem. Usually when you start solving a problem, you choose a time when you call t=0 and you choose where where you choose y=0 and x=0. So if you drop it when t=0 and x=0, y=h, the initial velocity is 0; the final velocity is the velocity where ever the problem ends. For example, if you want to know with what the velocity the object hits the ground, that would be the final velocity. I will give you a few other examples: (In all cases, the final velocity can be the velocity at any time other than t=0, depending what the problem is.)

If you throw it up from the ground (y=0 at t=0) with some velocity, that is the initial velocity which will be positive.
If you throw it down it up from the some height h (y=h at t=0) with some velocity, that is the initial velocity which will be negative.
If you throw it up from the some height h (y=h at t=0) with some velocity, that is the initial velocity which will be positive.

QUESTION
On a globe, we should see the horizon beneath our feet but we don�t; we see it at eyelevel. And all foreground objects should appear above the horizon, but they appear below the horizon. What�s going on?

ANSWER:
I don't understand your first sentence at all. By definition, the horizon is the point where you can no longer see the surface of the globe. It depends on how far your eye is from the surface. If your eyes are 5 feet off the ground, your horizon is different from a pilot's at an altitude 30,000 ft. My little sketch shows that the horizon is the tangent to your line of sight. It had been noted that sailing ships did not just appear to get smaller and smaller as they sailed away; instead at some point they simply seemed to be sinking away. This is also shown in the picture.

QUESTION
Some friends and I have a disagreement and cannot seem to find the answer: when one twists a swing, it raises the person on the swing. Would the rope/chain be considered a simple machine? What is the physics behind twisting a swing and letting it raise you (and ultimately spin you)? I know it�s random, but it has turned into quite a disagreement!

ANSWER:
I think everybody wins here. There is not really an accepted definition of a simple machine. Roughly as simple machine may be viewed as a machine with few if any moving parts. One type of simple machine has an external agent which adds energy to an object but you can get all that energy back; this is called an ideal simple machine, one which has no friction to cause energy loss. For example, consider a frictionless incline making an angle θ with the horizontal where you exert a force F on an object with weight W, F=Wsinθ pushing it a distance D and raising it Dsinθ; so the force you would have applied to lift it straight up would have been W, much larger than your effort. However, the work to push it up the ramp (Wsinθ�D) was the same as you would have done if you had lifted it straight up (Dsinθ�W). Also, if you release it you will accelerate back to the bottom but now have kinetic energy (�mv², where m=W/g is mass and g is the accereration due to gravity); this will be equal to Dsinθ because the energy can be retrieved.

Now, in your case, the machine is the swing and it satisfies characteristic properties of a simple machines�the force which the agent exerts to twist it is clearly less than the weight of the person on the swing, it has few or no moving parts, energy you put in can be recoverred (although with friction losses). And I would say that it if a screw is a simple machine so is a twisted swing. It will certainly not be an ideal simple machine because there will be friction involved in twisting and untwisting of the ropes. It is also a bit complicated by the fact that the first half turn raises the seat much more than subsequent turns do. So now the agent does work turning it, say turns, by exerting a torque FRθ if he does his pushing a distance R from the spinning axis (complicated by the fact F is bigger for the first half turn). After the agent stops turning the swing it has risen a distance h above the starting point with potential energy mgh; so now as it spins down it finally gets to the bottom where it has some kinetic energy, all rotational, which will be less than mgh depending on the loss to friction. So, because there is no agreed-upon definition of a "simple machine" and the idea of such a classification is really archaic, you are all arguing about something of no consequence!

QUESTION
When I cut, let's say a plastic packaging, with my scissors, what happens on molecular, atomic and subatomic level with all the protons, electrons and neutrons as the force of the scissors cuts the plastic?

ANSWER:
Nothing happens at the subatomic level because the energies holding nuclei together are far larger than energies you provide by your scissors. Everything which is disrupted is electromagnetic by nature. You are breaking bonds holding the plastic together, bonds of molecules with neighboring molecules; bonds holding the molecules themselves together; and, inevitably, some atoms will become ionized as electrons become separated from atoms.

QUESTION
In the case of Twin Paradox of Special Relativity, we say the travelling twin, twin A, will age slower. But one twin's travel is relative to the other, isn't it? Meaning, if we assume that twin A is travelling in positive x-direction, then the case that twin A is stationary and twin B is travelling in negative x-direction should also give the same result, shouldn't it ? So, my question is whose clock is it that's actually going to run slower ? Because from twin A's observation, twin B is in motion hence his clock should run slower relative to twin A. But from twin B's observation, twin A is in motion and hence his clock should run slower relative to twin B. So which twin aged and which didn't ?

ANSWER:
In this problem, there are two frames of reference which matter, the rest frame of the stay-at-home twin/earth/destination and the rest frame of the traveling twin. In a nutshell the traveling twin arrives younger than his brother because in his frame the distance between the earth and destination is shorter than that distance for the earth-bound twin because of length contraction. You should look at my earlier answer to the twin paradox for more detail.

QUESTION
Is every particle in the universe exerting a gravitational effect on every single particle in the universe? - If the universe was completely empty except for two protons.. No matter where those protons were, and assuming enough time exists in the universe, would they eventually orbit each other? - If so, say one proton magically jumped a centimeter to the "left". How long would that change take to affect the other proton? Is this a speed of light thing, or does the change happen instantaneoulsy?

ANSWER:
You are thinking only of gravity. But there are other forces between two protons; their electric charges exert repulsive forces on them and those forces are totally abdominant in their interaction. Gravity is the weakest of all nature's forces and the only reason that you are aware of gravitational forces is that you live in an environment close to a huge hunk of mass (earth!). In fact, I am not aware of any measurements of gravitational forces between elementary particles. So for all intents and purposes, electrostatics are the only forces acting on the two and they will never orbit each other, just fly apart.

QUESTION
Approximately how much water must be displaced to bring a 900 pound object to the surface if the object displaces 10 cubic feet of sea water? I know the answer is 4.0625 cubic feet. My question is what if the question doesn't give you the objects displacement amount, like in this case what if it didn't say the object displaces 10 cubic feet. How do I determine how much the object actually displaces? Lets say its a boat motor its not perfectly cubed to measure easily.

ANSWER:
I find this problem to be poorly worded. In fact I find it to be incorrect (why 4.0625 cubic feet?) and not very instructive. So let me start this problem all over. We have an object which is completely submerged in the water and has a weight of 900 lb. Now, suppose that we want to keep it submerged and just remain at some constant depth going neither up nor down. What do we have to do? Easy: Just exert an upward force of 900 lb on the object and it will be in equilibrium ala Newton's first law. Where does that force come from? The water exerts an upward force on anything in it which is called the buoyant force. Archimedes tells up that the buoyant force is equal (in magnitude) to the weight of the displaced water. The density of sea water is 65 lb/ft³, so the volume of displaced water must be 900/65=13.85 ft³. If the volume displaced is 4.0625 ft³ this object will sink. So now I don't know what you are after here; in your first sentence you ask "�how much water must be displaced�if the object displaces 10 cubic feet of�water?" Duh�10 cubic feet! This will only give you a buoyant force of 650 lb and the object will sink. Any object which has a weight of 900 lb and is floating you may be sure is displacing 13.85 ft³ of sea water. That, of course, does not mean that that is what the volume of the object is because some of it will be above the surface of the water.

QUESTION
If time is a dimension of space, why is it not measured in meters?? Are all dimensions in string theory measured in meters?

ANSWER:
Actually, it is a dimension in 4 dimensional space-time. Usually when plotted on a graph it is plotted as ct where c is the speed of light. Likewise, when the 4-D formulation is worked out. This quantity does have the dimensions of length. I am not a fan of string theory.

QUESTION
I'm curious as to why only moving charges produce magnetic fields, while static charges do not. Additionally, since electrons possess an intrinsic magnetic property due to their spin, shouldn't static charges also create magnetic fields?

ANSWER:
Well, that's just the way nature is. I know that is a smug-sounding answer, but experiments verify that this is the case. On the other hand, as you suggest, electrons do, indeed, behave like tiny bar magnets, i.e., they have a magnetic moment. If you like, think of the electron being a tiny charged sphere which is spinning; just don't take that classical picture too seriously. Usually a bunch of excess electrons on an object have their moments, which are incredibly small anyway, pointing in random directions and adding to zero; so you can assume that object to have some net charge and no magnetic field.

QUESTION
Can ultraviolet rays break apart the bonds of Carbon Dioxide?

ANSWER:
I find, from a website, that the total dissociation energy of CO₂ is about 0.5x010⁸ J/mole. Converting that to electron volts per molecule I find E=0.5x10⁷ eV/molecule. The energy range of UV radiation is about 3-124 eV/photon, so it isn't even close to being able to break apart the molecule.

QUESTION
A rod hinged at one end is released from the horizontal position as shown in the figure. When it becomes vertical its lower half separates without exerting any reaction at the breaking point. Then find the maximum angle 'θ' in degrees made by the hinged upper half with the vertical. Many answers on the internet do not consider mass to be broken into half as well. They only consider length to be broken into half. Hence, I believe the answer should be different.

ANSWER:
This looks suspiciously like a homework problem. So I won't work it out but I will answer your question. The answer to a problem like this does not depend at all on what the mass is. The potential and kinetic energies are always proportional to whatever the mass is, e.g. �[ML²/3]ω²-MgL/2, whereas the potential energy is proportional to L while the kinetic energy is proportional to L², so changing L changes one differently than the other.

QUESTION
I have a new gas oven. All of my recipes are in Celsius. So I bought an oven thermometer that shows Celsius readings. I knew that gas mark 6 correlates to an electric oven temperature of 200, so I was expecting this to be the reading on the thermometer. However it never got any higher than 160. Is this because of the different types of heat or should it have read 200?

ANSWER:
I had never heard of gas mark as a temperature scale. However, when I looked it up in Wikepedia, here is what I got:

All F temperatures have been rounded to the nearest 5 degrees. But I do not understand your question. Is your new oven calibrated in gas marks? That is, if you want 200 C do you set your oven to 6 gas marks? If the answer is yes and you set the oven temperature to gas mark 6 and you only measure it as 160 C, your new oven will need to be calibrated.

QUESTION
I have a simple question that I would like answered. I am a person who is retired and studying physics for fun. I want to correctly calculate this equation that uses Coulomb's constant.

m= 9x10⁹ N�m²/C²/(3x10⁸ m/s)²

I have rounded the questioner's numbers (8.99 to 9 and 299,792,458 to 3x10⁸) to simplify the discussion.

Chat GPT says the answer should be m~9.98 x 10^-36 kg I don't get this answer when I try to calculate it manually. Culombs constant has many dimensions and I am confused by that.

ANSWER:
Dimensional analysis can be confusing. It appears that this equation has m=k/c² where m is some mass, k is Coulomb's constant, and c is the speed of light in vacuum. Four of the SI base units appear in this equation, mass (M), length (L), time (T), and electric current (I). Note that electric charge is not a base unit unit, electric current is; a Coulomb is one Ampere�second. My capital letters here are to specify dimensions, not SI units. A Newton has dimension ML/T², so the dimensions of the right side of the equation are (ML/T²)(L²)/(IT)²/(L/T)²=(ML/T²)/I². If, indeed, m is meant to be mass, this equation is not dimensionally correct, rather m=10^-7 N/A². We all learn first to think of only three base units, M, L, and T and that anything can be measured in terms of these. But, there are seven base units and none can be expressed in terms of only the first three.

QUESTION
Hi. Is there an affordable instrument available that will allow me to precisely measure the wavelength of whatever oil paint colors I might mix? My goal is to be able to mix up two separate colors in the exact mathematical ratio as the frequencies of two separate musical notes. Of course I will also need to be able to measure sound frequencies of those notes, as well.

ANSWER:
None of your oils have anything close to a single wavelength. If you measure the spectrum of wavelengths you might be able to find the most intense part of the spectrum; but it is not really meaningful other than in a qualitative sense. Also, the spectrum of anything depends on the way it is illuminated. The same is true of musical notes, made by a musical instrument. A musical instrument creates a discrete spectrum of the lowest vibration (called the fundamental) and its harmonics which depend on the instrument design, often integer multiples or half multiples of the fundamental. Different instruments have different relative intensities of the fundamentals which is why you can tell the difference between a piano and a saxaphone playing the same note.

QUESTION
I was discussing the one-way speed of light problem with a friend of mine who is invested in it being almost infinite coming to us and half c going out. I had never heard of it so in the beginning it seemed silly until I started looking into it. I got it that we can't use watches to measure to get to the speed, because the Act of separating them will desynchronise them. (don't we know the mechanics of this good enough to correct for it?) I know that a bunch of highly intelligent Physicists tried and as far as I understood failed to prove c = c. Can we prove C is not infinite in one way? I came up with an experiment but am sure it can�t be that easy. If we have two points in Orbit (for example the ISS and the moon) can�t we send a beam of light and an object with finite but high and observable speed at the same time and measure at the arrival of the light and the object how long they are apart and repeat the other way? If we find the same difference the speed of light would be constant if not it would depend if it is coming in or going out. I�d like to call it the Beam Bean experiment for Mister Bean lands after the light. Your help is very much appreciated!

ANSWER:
I would judge your question to violate the site ground rule requiring "single, concise, well-focused questions". So I will not try to understand your idea for an experiment nor debate whether this is a possibility (that the speed of light is infinite or nearly so in one direction). I will state that it is a nonsensical supposition in my opinion. One of the the postulates of the theory of special relativity is that the speed of light in vacuum is a universal constant of nature; the result any measurement of c will be totally independent of the motion of the observer or the source; this has been verified by numerous experiments and with that assumption the speed at the first leg of the trip could be close to infinite. I appreciate that the most common way to measure speed, a round trip, depends on the constancy of c, but much of physics, which beautifully describes nature, would be wrong if c were not a universal constant.

QUESTION
This is a scenario that I have been having an office debate about for a while between quite a few people. We can�t seem to find a real answer online and we are all very interested in the physics behind it. If a car is traveling at 60 mph on a highway and a tow truck with a ramp is traveling at 55 mph, if the car maintains his/her foot on the pedal and hits the ramp of the tow truck, will it fly off the front of the tow truck? Separately, what if it was the same scenario except the tow truck is traveling at 40mph instead ? We�re assuming the ramp is extremely close to the ground. What would happen in the case that the angle of the ramp is 15 degrees, 30 degrees, and 45 degrees. Please neglect any form of friction caused from the wheels hitting the ramp. We are assuming the ramp is flush with the road.

ANSWER:
This is a really fun question, but let me make a couple of comments first. You ask me to ignore friction but friction, as you will see, is required to understand the problem. The other thing is that you say you are "�very interested in the physics�" In that case, you should not start with a whole bunch of scenarios, but start by understanding a simplified special case which you can understand without having all the various relative speeds and angles to complicate things. In an earlier answer I solved the problem for a cylinder (wheel of your car) rolling with velocity v on level ground encountering a horizontal belt (surface of your ramp) also moving with velocity v. This has all been worked out in the earlier answer and, as you will see, the result is that the wheel will pick up a little velocity but not enough to "�fly off the front of the tow truck." There will be a little velocity relative to the truck/ramp but you will lose some speed going up the ramp which would you require to accelerate or brake depending on details, but you could easily stop once you were fully on. Also, you can actually see this happen in an old MythBusters episode.

I will post this. I think that the earlier answer contains all the interesting physics necessary to understand the situation(s) you describe. I will mess around a bit with different relative speeds and maybe angles, and if I get anything interesting I will post it and let you know.

ADDED COMMENTS:
So, I have worked out the situation for the car approaching the tow truck with a larger speed than the speed of the truck. I have pretty much followed the same path as I did with equal speeds. A cylinder of mass m and radius r, rolling on a level surface at a linear speed of v, rolls on to a conveyor belt which is moving at a speed u<v in the same direction as the cylinder.

Shown in the first figure is the situation when the rolling cylinder first touches the conveyer belt. It is rolling without sliding so the point of contact with the floor is at rest, the center is moving forward with a speed v and the top is moving forward with speed 2v; the belt is moving forward also with speed u<v.

I find this problem much easier to do if I transform into a coordinate system which is moving with speed v to the right; in that coordinate system the belt has a velocity (u-v), i.e., a magnitude (v-u) and direction to the left. The cylinder is at rest and rotating; the top and bottom edges of the cylinder have speeds v as shown in the second figure. Note that the cylinder is rotating in a clockwise direction.

Now, as soon as it gets on the belt there will be a frictional force f trying to accelerate it to the right so it will start sliding along the belt (moving to the left with speed v-u in the frame we are using). The frictional force will be f=μmg where μ is the coefficient of kinetic friction, m is the mass of the cylinder, and g is the acceleration due to gravity. Call v' the speed which the center acquires in some time t. Then Newton's second law for translational motion is mΔv=μmgt=mv', so v'=μgt. This is shown in the third figure.

There will also be a torque τ=fr=μmgr which acts opposite the direction the cylinder is rotating. There will come a time when the bottom edge of the cylinder will be at rest relative to the belt because of this torque; therefore, the point of contact will be moving to the left with speed v-u. We are particularly interested in the time when the cylinder stops slipping as shown in the fourth figure. Newton's second law for rotational motion is ΔL=τt=-(μmgr)(v'/μg)=-mv'r where L is the angular momentum of the system. For the initial angular momentum, L₁=Iω₁=Iv/r because the initial angular velocity is ω₁=v/r, and where I is the moment of inertia about the center of mass. The angular momentum of the system at the time the the sliding stops is a bit trickier. The axis of rotation about which the cylinder is rotating is at the bottom of the cylinder; but that axis has a speed of v-u, so we must momentarily jump into a frame where that point is at rest to determine the speed of the center of mass around that axis�that speed is v'+v-u. The moment of inertia about that axis is I'=I+mr² (parallel axis theorem). Finally, L₂=[(v'+v-u)/r)](I+mr²). Therefore, [(v'+v-u)/r](I+mr²)-Iv/r=-mv'r or, v'=(u(I+mr²)-vmr²)/(I+2mr²). {Note, if u=v this gives the result of the earlier answer.} The time to stop sliding depends on μ, t=v'/μg; the slipperier the surface, the longer it takes to stop slipping, as expected.

Finally we need to transform back into the original coordinate system by simply adding v as shown in the final figure; the new velocity is v+v'=(v+u)(I+mr²)/(I+2mr²). As an example, suppose we model the cylinder as a uniform cylinder of mass m and moment of inertial I=�mr²; then v'=(3/5)(v+u). So the case you asked about, v=60, u=55, the speed increase of the car, if you approximate that the ramp is horizontal, is 5x3/5=3 mph.

One addition here: The algebra, of which I show few details, is quite tedious. I grew frustrated and resorted to Wolfram Alpha which did it in a jiffy!

QUESTION
Why same charges repel and unlike charges attract each other's?

ANSWER:
This question is very difficult to answer and is similar to the same kind of question about gravity. Because of the similarity of gravitational and electromagnetic I will also discuss gravity. Be aware that these often can be thought of as philosophic questions; I will first discuss how these topics would be discussed before the 20^th century. For gravity we know that masses attract each other. You might ask "why?", just like you asked about the forces between electric charges. But, it is simply the way nature is and, in some sense, a pointless question because we can observe it happening. The moon is held in its orbit because the earth is pulling on it. Next you can find out, by doing experiments, more details about this mysterious force. For point masses or spherically symmetric masses find that the force F is proportional to the product of the masses m and M and inversely proportional to the square of the distance r between them, F=-GMm/r² where G is just a proportionality constant and the negative denotes an attractive force. Once you know what the force between two point masses you can calculate just about anything regarding forces between any mass distributions.

Now let's turn to your question. First, what is the most obvious difference between gravity and electromagnetism? There are two different kinds of electric charge but only one kind of mass. Ignoring that for right now, we know that any charge will exert a force on another charge. We now proceed to study experimentally the electric force. We find that sometimes the force we observe is repulsive, sometimes attractive, but we find that its magnitude is proportional to the product of the point two charges q and Q and inversely proportional to r², F=�kqQ/r² where k is a proportionality constant and the plus/minus sign denotes repulsive/attractive; this is why I say that the two forces are analogous. We now need to do an additional experiment�what determines repulsive/attractive? We quickly find that two like charges repel and two differing charges attract. Do you understand why, at least before the 20^th century, this is a meaningless question. The answer is simply that this is the way nature is.

I should briefly talk about G and k, the proportionality constants. What they are depends on how we choose to measure things. Physicists usually prefer the SI system of units, length in meters (m), mass in kilograms (kg), charge in Coulombs (C), time in seconds (s), force in Newtons (N=kg�m/s2). So G has units N�m²/kg² and k has units N�m²/C². These must be measured experimentally.

But work in the 20^th century has led to a little deeper understanding of "why". During the second decade of the 20^th century Einstein developed the theory of general relativity which is essentially an update to Newtonian gravity but incorporating the theory of special relativity into classical Newtonian mechanics. The take away of GR is that the reason masses attract each other is that mass warps space-time. So there is an answer to why, but next you are going to ask me why mass warps space-time and we're back in the "why loop"! During the middle decades of the 20^th century the final piece of electromagnetic theory (arguably the best and best understood theories of all physics) was added; the fields needed to be properly quantized. The photon became to be understood as the "messenger" of the forces among charges. The theory is called quantum electrodynamics (QED) and the answer to your question emerges naturally. To my mind, QED is a better answer to the 'why question' for charges than GR is for mass. Maybe this is because it is so hard to visualize deformed space-time or maybe because no one has successfully quantized the gravitational field. Long answer to a short question!

QUESTION
When a tree limb hangs over the road it must take a lot of energy to hold it up. Where does the energy come from? My arm gets tired after a very short time held out

ANSWER:
I get this question fairly frequently. There is an excellent web page explaining why the tree does not get tired but you do.

QUESTION
If a car travels 70 mph. And a bullet travels 100 mph. If you shoot a bullet forward direction from a moving car, what is the speed of bullet now with respect to the person standing on the road?

ANSWER:
This sounds like homework.

FOLLOWUP:
No. I am not in school, I am working in an office and all employees are on two sides. Half of us think bullets go 170 and half 70. But none of us can explain why with full satisfaction. If you want me to further prove this is the office, let me know. But I would really appreciate it if you answer.

PS I am on side at 70 mph.

ANSWER:
If the bullet were had a speed of 70 relative to the observer on the side of the road, she would see the bullet and the car both going along side by side at 70 mph. If that were the case, you wouldn't even have to stick the gun out the window to fire it forward; you could just fire it straight toward the windshield and it would just drop straight down. So you should know intuitively that could not be the answer. So, the winner is 170. But let's talk about how physics treats this problem. This is a classic problem in Galilean relativity. The equation for relative velocities (usually called the velocity addition formula GAF) in Galilean relativity is V_AB=V_AC+V_CB where the notation is that V_XY is the velocity of X relative to Y. In your case, in words, A is the bullet, B is the ground, and C is the car: V_{bullet,ground}=V_bullet,car+V_car,ground=100+70=170 mph. That answers your question.

Suppose you had asked what the speed relative to the ground was if the bullet was fired backwards. What you need to know is V_bullet,car=-V_car,bullet=-100 mph. This is because the GAF is a vector equation and, in one dimension, you need to specify whether a velocity is positive or negative where I have chosen the positive direction to be the direction of the car. So the answer in this case is V_{bullet,ground}=-100+70=-30 mph. What if the bullet had a speed of 70 mph backwards? V_{bullet,ground}=-70+70=0 mph. The bullet would be seen by the observer on the ground to drop straight down! An old MythBusters episode demonstrates this beautifully.

BONUS ADVANCED ANSWER:
I noted earlier that the GAF is a vector equation, V_AB=V_AC+V_CB; examples have been one-dimensional. But suppose that we shoot the rifle straight out the window perpendicular to the the velocity of the car. The diagram shows the velocity vector of the car relative to the ground pointing to the right and the velocity of the bullet relative to the car pointing up. Their sum is shown as V_{bullet,ground}. The magnitude of this vector is V_{bullet,ground}=√(100²+70²)=122.1 mph in a direction θ=tan^-1(100/70)=55�.

QUESTION:
I'm converting a bus into a tiny home and want to power it with clean energy sources. I was recently thinking about capturing power with windmills while driving, but understand that drag may be an issue and take more power (and cost in fuel) than it generates. I was wondering if placement couldn't alleviate this in some way. Like placing the fan in front of the vehicle, or channeling the wind into the windmill like a ram scoop on a muscle car?

ANSWER:
There is a nice way the first and second laws of thermodynamics can be stated: You can't get something for nothing, you can't even break even. You can be sure that the increase in gasoline consumption will represent significantly larger energy consumption than the energy that your windmill will store; think of all the energy losses to friction in the windmill, generator, and engine. And, burning more gasoline will be detrimental to the environment. The only way a windmill will be a good idea is if you park with your engine turned off in a good wind. When you are driving, put it away. Another idea you might want to investigate is putting solar panels on your roof.

QUESTION:
I have a 0.2kg mass attached to a vertical spring with k=10. Using Newton's 1st law I want to find how far the spring will stretch until the system is at rest. So, kx=mg, and x = 0.2 meters. The elastic potential energy of the spring is now 1/2*k*y^2 or 0.2 Joules. But, if I see how much gravitational potential energy the mass lost by moving down 0.2 meters it comes to 0.39 Joules - almost double the PE of the spring. The system is ideal with no friction. How did the mass lose 0.39 joules but the spring only gained 0.20 joules. This seems to violate the law of conservation of energy. Any ideas on the discrepancy?

ANSWER:
When is conservation of energy applicable? If no external forces do work on the system. How did your mass get from the unstretched position to the equilibrium position? You couldn't have just let go of it because then it would have just flown past the equilibrium position and continued oscillating. You had to do work on it, you had to place it in the equilibrium position! Here is how you should do any energy problem:

The energy equation is E₂=E₁+W where E₁₍₂₎=U₁₍₂₎+K₁₍₂₎ is the initial(final) energy, U₁₍₂₎ is the initial(final) potential energy, K₁₍₂₎ is the initial(final) kinetic energy, and W is the work done by external forces.
When I was teaching I used to tell my students that this is easy to remember�what you end with is what you started with plus what you added. Keep in mind that work can be either positive or negative, depending if you put energy in or take it out. Friction, for example, will normally be negative work because it takes energy away from a system.
In your case, choosing y=0 as the unstretched spring position of m and positive y direction vertically upward you find that �ky²+mgy=W. Note that I have only included the potential energies because my goal is to find the value(s) of y where the mass is at rest.
First, what happens if you just let it go? That's what you did. You get a quadratic equation which will have two solutions, �ky²+mgy=0 which has solutions y=0 and y=-2mg/k; it oscilates between 0 and -2mg/k being at rest at the ends where it changes directions.
For what you really wanted to know, you have done the right thing* and found that the equilibrium position is y=-mg/k=-0.2 m. (I am using g≈10 m/s² for convenience as you apparently did.)
Now if you want to know how much work it took to move it from the unstretched position to here you simply use �ky²+mgy=W=-0.2 J. The negative sign makes sense because you have to hold it back as you lower it so that it ends up at rest at the equilibrium position.

*�except you have not been careful with signs. If you choose y=0 and +y up, anything below y=0 will be a negative gravitational potential energy.

QUESTION:
My name is Shane, I am a 100% Disabled United States Marine; I am trying to understand an aspect of physics that doesn�t make sense to me. I hope my service and sacrifice for this country merits a moment of your time. I was hoping someone would be willing to help me with my conundrum. In 1633, Galileo was forced to recant his heliocentric model of the universe. It was not until 1687, when Sir Isaac Newton released his model of gravity that it became commonly accepted that the Earth was not at the center of the universe. The problem I see is that, in 1676, when the Danish astronomer Ole Roemer measure the �universal speed of light,� humans were still using a Geocentric model of the universe. The reason why Ole Romer called it a �universal speed of light� is because he would have been burned alive for heresy if he said the speed of light didn�t have a universal constant speed. The problem I see, is that the entire subject of physics is based on a universal constant speed of light, but the idea for a universal constant speed is based entirely on religious superstition and not scientific evidence. Humans have only measured the speed of light from a single curvature of spacetime on Earth. If light cannot escape a black hole, then the speed of light has reached 0 m/s, meaning that somewhere in the universe, light does not have a universal constant speed. The observation that can be made from this is that gravity effects the speed of light. I know that the physics community tries to ignore this fact by calling it time dilation, but it is impossible to truly grasp time dilation unless you understand that light does not have a universal constant speed. Everything in physics that can�t be explained can be explained by a variable speed of light. Here are two major things in physics easily explained; I can explain much more than this. The reason why the universe seems to be expanding faster is because as the gravitational bodies move further away from the center of the universe, there is less gravity acting on the light, so the light is traveling faster, allowing humans to make observations of the universe faster. If it took a billion years for light to travel from the stars billions of years ago, then as the light travels faster, it only takes a million years for the light to be observable from Earth now. The universe isn�t expanding faster, light is traveling faster, allowing humans to make observations of the changes to the universe faster but from a single curvature of spacetime on Earth. The reason that light is both a particle and a wave is because when light is a particle it has been trapped in the third dimension and transformed into useable energy. When light is a wave, you are watching the 4th dimensional effects of the interaction between light and gravity. I went through and made all the adjustments to physics so that it finally makes sense using the assumption that light has a variable speed. I am looking for someone to help me revitalize the subject of physics and to look at my mathematics. I created a formula for calculating a variable speed limit for light based on the gravitational pull of planetary bodies. I replaced the variable of �c� in Einstein�s formula of e=mc^2 with my formula for a variable speed limit. I was hoping you would be interested in looking at my model of reality, it is much more complete than the current model.

ANSWER:
First, let me call your attention to a couple of ground rules of this site: "Please...submit single, concise, well-focused questions" and "I do not wish to nor do I have the time to critique your personal theory of the universe!" Your 'question' adheres to neither of these. I am only offering a few observations about your question out of respect for your "service and sacrifice".

Your history is a bit inaccurate. But, before we get to physics, I would recommend that you look at history with an appreciation of the speed of communications in the 17th century. Major advances and events would take weeks or months or even years to become "commonly accepted" and therefore the time of acceptance is a fuzzy concept. In my view, it was firmly established that the solar system was heliocentric when Kepler published his first two laws in 1609, based on decades of careful and accurate observations of planetary motion by Brahe; this predates Galileo's persecution by the Catholic Church by 24 years. I have no idea whether Galileo was aware of Kepler's laws.
I find no reference anywhere that Roemer's attempts to measure the speed of light by comparing measurements at different longitudes of eclipses of the moons of Jupiter made any reference to the "universal speed of light". Nor am I aware of the church's insistence that the speed is a universal constant; thus I doubt your suggestion that Roemer "would have been burned alive" for saying so. In fact, the very idea that the speed of light in vacuum is a fundamental constant was not accepted until the early 20th century when the theory of special relativity was published by Einstein, certainly not "based entirely on religious superstition". (I may be wrong about the church's having an interest in the constancy of the speed of light, but that is not really an issue for me because the church is not really an authority on such things. It is certainly a non-issue to me what the church's opinion is.)
Let's talk about light and black holes. I guess I should ask why you even believe that black holes exist and that light can't escape. Only general relativity predicts their existence and the constancy of the speed of light is an irreplaceable component of that theory. But the crux is your statement that the speed of light will go to zero. You do not say anything about quantum physics, but it is easier to understand the light's captivity if we think about photons, the quanta of light, whose energy is E=hf where h is Planck's constant and f is the frequency of the light wave of which this photon is a member. Imagine a photon near the black hole moving away from it. As it moves forward it does not lose energy by losing speed as you suggest or as a baseball would, it loses energy by having its frequency decrease (red shift). Where does that energy go? It goes to increase the mass of the black hole so that eventually that photon is gone and the black hole has increased its mass by Δm=hf/c².
The rest of your theory I will not try to debunk. Let me just say that all of the physics which depends on the constancy of the speed of light has explained a huge amount of measurements of things not just close to the earth, but things near the outer limits of the observable universe. Attempts have also been made to see if the fundamental constants differ elsewhere, i.e. in the past, all to no avail.

QUESTION:
Can a pebble or any small hard rigid object lying on road can be flicked by the tyre of a moving vehicle. And if then What is the physics behind it? In what manner the pebble or object moves?

ANSWER:
The most common way for this to happen is if a stone gets stuck in the tread of the tire. If there is a stone stuck in the tread you could get it out if you pull on it hard enough, so if there is a force big enough, the tire will not be able to hold on to it and it will fly away. An important thing to understand about a wheel which is rolling without slipping is that the place where the wheel touches the road is at rest. So at any instant of time, every point on the wheel is rotating about the point where the wheel touches the road. My figure shows a wheel which is rolling to the left and I have imagined two stones (red triangles) which are distances (orange) from the axis of rotation such that the smaller distance is half the larger distance The velocities (green) of the stones are perpendicular to their orange lines and the farther stone has a speed twice that of the closer stone. Each stone, at this instant, has a centripetal acceleration v²/R meaning that the farther away stone will have twice the acceleration as the nearer one; since the force F necessary to keep the stone moving in its circle is F=ma, twice as large a force will be required to hold it there. So eventually, for most stones, the force will become bigger than the tread can hold and fly off.

QUESTION:
Do photons have momentum? In the energy-momentum relation: E^2=(mc^2)^2+(pc)2 In case of photons, the equation simplifies to: E=pc. As p=γmv, has mass in it and photons have 0 rest mass. But in many places, I have heard that photons, indeed have momentum.But how?

ANSWER:
The derivation of the relativistic linear momentum you quote is valid only for particles which have mass. For your question you need to find an alternate expression for the energy of a photon, one that comes from QED (quantum electrodynamics) field theory. You probably know it, it is the equation which relates the energy to the frequency f of photon, E=hf where h is Planck's constant. Thus you find p=hf/c.

QUESTION:
So basically, photons are massless objects. If they are massless, how do they possess energy and what equation is used to calculate the energy?

ANSWER:
I get this question or some variant of it often. And it is not surprising because we are taught that energy is E=�mv² and E=mc². But it turns out that �mv² is only an approximation which is no longer accurate at very high speeds. And E=mc² is often misunderstood; it is what is called the rest mass energy, the energy which a mass m possesses by virtue of its mass when at rest. Since the photon is never at rest, this is clearly not applicable to photons. It turns out that the energy of a photon is given by hf where h is Planck's constant and f is the frequency of the light waves of which the photon is one of many photons. Photons also have a linear momentum of hf/c.

QUESTION:
Max Planck is credited with introducing the idea of a quantum of energy. Apparently, this came out of his equation E=hv. Of course (h) is Planck�s constant, and (v) is the wavelength of the radiation being used. (v) is continuous. Something continuous multiplied by a constant is still continuous. How does this lead to the idea of quanta? What am I missing here?

ANSWER:
Be careful when you say "of course"! What you assumed you saw as a vee (v) was actually a Greek letter nu (ν); and ν is not wavelength, it is frequency. So let's avoid confusion and denote frequency as f, E=hf. Planck's work does not stipulate that any old photon you see has a quantized energy. Indeed the energy of a photon can be anything you like. Essentially Planck imagined the radiated energy from something comes from the numerous oscillating atoms or molecules or whatever. Any particular oscillator of a particular frequency was thought to be able to be any energy at all and you change the energy of an oscillator by changing its amplitude. But if you do a calculation assuming a very large ensemble of oscillators, each with a continuous spectrum of possible energies, it turns out to radiate an infinite amount of energy! Planck found that if you had oscillators of frequency f and energies not continuous but quantized: hf, 2hf, 3hf, 4hf� data of the spectra of the radiation could be fitted well with a particular choice of the constant h (of course Planck didn't know Planck's constant!); it's like if you said that if you had a mass hanging on a spring it could oscillate with an amplitude of 1 cm, 2 cm, 3 cm, 4 cm� but not with an amplitude of 3.7 cm! The energies of the tiny oscillators were what is quantized, not the photons they emitted. What is generally quantized is the energy of a system of particles which are all bound together.

QUESTION:
My dad and I were debating whether a shuttle crashing to earth would exert force on the occupants. He said no because in freefall you are weightless. I wondered however if the force of the acceleration of the fall added to the speed the shuttle already had as it entered the atmosphere would make a difference. Ah, the joys of science fiction spurred physics debates lol. Would you settle the debate for us? If you have a corroborating equation you would make these two nerds even happier. Thank you. Not for school, I am 57 and Dad is 79.

ANSWER:
First, let's consider the simplest possible approximation�air drag is negligible. In that case the shuttle and all its occupants would indeed be in free fall and your dad is right. (I will come back to this free-fall situation later). However, air does exert a large force on the shuttle, so its acceleration is not simply due to gravity (which always points straight down), it is also due to a drag force which points in the opposite direction as the velocity. This is all shown in the first figure. At the instant of the situation in that figure, the acceleration of the shuttle is in the direction of the net force on it, shown in green; so the acceleration in the vertical is smaller than g and the acceleration in the horizontal is to the left. The nature of the drag force is that it gets larger as the speed increases; so what will happen eventually is that the horizontal force will approach zero (fall straight down) and the vertical force will equal the weight. At that time the shuttle will fall straight down with a constant speed called the terminal velocity.

Next we should address the forces which the occupants will experience. The occupants, of course, do not experience air drag. But they are in an accelerating frame of reference, the frame being the shuttle and all its contents. Why does that matter? Because Newton's laws, which are what we use to solve problems like this, are not true in accelerating frames. But there is a very easy way to make them applicable�insert a force (which does not actually exist) which points in the opposite direction of the acceleration of the frame of reference; this is called a fictitious force. So now look at the second figure where I show the situation if an astronaut is in the shuttle and it is falling but air drag has been neglected. There is only one real force as we look from the outside so he has a downward acceleration of g. But we want to know what he feels, not what we see; since he is in a frame which is accelerating down with acceleration a=g, he will experience straight up with magnitude F=ma=mg. Thus the net force he feels is zero which we already knew.

Finally we look at the situation in the first figure but for the astronaut (the third figure). The weight vector is mg, where m is the mass of the astronaut, and he is in a reference frame which has an acceleration a (green) as in the first figure. Now the fictitious force F is ma in the direction opposite a. The net thing which he feels is the sum of the weight and the fictious force as shown. So he will feel (components of F) a downward force which is smaller than his weight and a force to the right which is even smaller, in magnitude, than his weight.

One thing I haven't considered is possible rotational motion. Since you say "crashing to earth" it seems likely that it would be tumbling and spinning. That would involve rotating frames of reference which involve other kinds of acceleration. It would get too complicated for the expected level of this site and I will leave that for another day. By the way, centrifugal force is a fictitious force.

QUESTION:
i havent learned physics yet in school but im reading those beginner Science articles on space/time. (im an artist and i dont like math but this is really really cool) everybody draws gravity as pressing down on a like a mesh surface, is time there too? if i had to draw it itd be like two lines both being stretched down with how dense the planets are. like a really dense planet would press down a LOT on the weird gravity mesh, it would also stretch out time a lot and make everything slow. so the farther you got away from the gravity, the faster time would get cuz its not being stretched. like how astronauts get younger in space (theyre father away from the earths gravity) also, if theres two planets making pressing down on this weird space/time mesh, could you pinch them together to make a really long distance take very little time? like by connecting these two points you could go reallllyyy far in like a few minutes. cuz gravity/time/space are all connected i think.

ANSWER:
The first thing we should get straight is that your "mesh" gravity demo (I usually call this the "trampoline" model) is a very simple cartoon to illustrate how the theory of general relativity "explains" gravity. Here space is a two-dimensional space and the presence of mass in this space (which itself has to be in a gravitational field so the mass will actually warp the space) causes it to warp. It is impossible to draw a four-dimensional picture showing the warping of that four-dimensional space/time by the presence of mass. But, you obviously get the concept that time as well as three dimensions of space are all interdependent and affected by the presence of mass. Since you have studied no physics, it would be pointless for me to try to go any farther than that in explaining the theory of general relativity. I admire your curiosity in pursuing those science popularization articles. Now, you are an artist, so you are perfectly free, if you have a feeling for concepts but little mathematics, to express your visions of how you might make art which is inspired by these concepts!

QUESTION:
People are worried that Earth is slowly loosing its moon, because Earth will go crazy. Mercury and Venus don't have moons and their orbits and rotations are stable. What gives?

ANSWER:
Funny, I have never met a single person who is "�worried that Earth is slowly loosing [sic] its moon�". Do you know the rate at which this is happening? 1.5 inches per year! So tell all those worried people to stop worrying. There will be no noticable change for hundreds of generations. Why do you think "�Earth will go crazy"? And what does that mean, anyway? If you are interested in why the moon is receding rather than coming closer, see an earlier answer. There is also a nice video which explains that the moon will never actually leave the earth.

QUESTION:
My assumtion: Things that get too hot eventually glow. Question: Does coolder matter have some way of binding photons? If so, What force weakeneds within matter that it's grip on those escaping photons when the matter heats up the the point of glowing and emiting light? I do get that light is always shinning through different spectra, is it just the rapidly vibrating hotter matter that speeds up the wave form of an emited photon?

ANSWER:
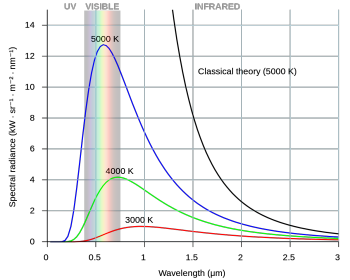
Everything radiates regardless of its temperature. Most objects are pretty well described as black bodies. Also see a earlier answer of mine. The intensity of the radiation as a function of the wavelength of the radiation is shown in the figure for three temperatures. At 5000 K, approximately the temperature of the surface of the sun, the most ratiation is in our visible range; this is a wonderful example of evolution, showing that we evolved such that our eyes are most sensitive to the wavelengths which illuminate our world. As the temperature gets cooler, the peak shifts toward longer (redder) wavelengths; At 3000 K, roughly room temperature, nearly all the radiation is in the infrared part of the spectrum where our eyes cannot detect it but infrared cameras and glasses can. You are right that as you increase temperature the radiation in the visible region will become intense enough to see it. But your idea that all those emitted photons have been sitting around waiting to be radiated is totally wrong. Photons are created when electric charges are accelerated. The electrons in the atoms are vibrating about and get created at the time of emission.

QUESTION:
What does it mean when 'if a charge is taken through a potential difference'?

ANSWER:
It means that the charge moves in a volume where there is an electric field. It means that work is done (positive or negative) on the charge as it moves from one point to another; the work done is independent of the path between the two points.

QUESTION:
How is it that half the surface of a sphere [the Moon] can be illuminated with the same intensity of sunlight rather than a gradient?

ANSWER:
I don't understand the question.

REPLY:
A computer-generated lambertian model illuminated with collimated light (as from the sun) contrasted with the illumination of the moon:

ANSWER:
It turns out that the reason is quite simple: The moon is not well-described as Lambertian surface for numerous reasons. A good explanation can be seen at this link.

QUESTION:
We now know that protons and neutrons are comprised of 3 quarks. Is there any reason to believe that is it? Quarks are the most basic so called 'building blocks' of particles or...., is it possible quarks are comprised of some other as of yet undiscovered particles and so on and so on...?

ANSWER:
It is generally believed that, like electrons, quarks are indivisible particles; no self-respecting scientist would insist that it is not possible that they have some underlying structure. But, the notion that protons are comprised simply of 3 quarks is a big simplification. See an earlier answer for a discussion of this.

QUESTION:
Hi, as I was surfing the internet I became interested in the concept of renormalization and found something related to it's history quite interesting. Renormalization is usually credited to three men, Richard Feymann (the famous one), Julian Schwinger and Shin'ichirō Tomonaga, they even received the Nobel, Tomonaga seems to have published his first paper about renormalization in 1943, in japanese (https://academic.oup.com/ptp/article/1/2/27/1877120?login=false). Is there some reason he is not given a pioneering role in places like wikipedia and physics books? I thought the discovery was made almost simultaneous, but he just was obstructed by war and language barrier. As I'm not expert in the subject at hand, does the first Tomonaga paper lacks something that makes it not a renormalization paper?

ANSWER:
I do not understand what is bothering you so much. All received three were awarded the Nobel Prize in Physics 1965 for their contributions to quantum electrodynamics; you can't get any better recognition than that. The Wikepedia article on renormalization credits all three along with Kramer, Bethe, and Dyson for making important contributions to renormalization theory (Tomonaga has the most references).

QUESTION:
Hopefull I�m not breaking ground rules. Related to climat change which I beleive is real.. but the recent finding of a hiker lost on a gkazier 4 decades ago seems to say the glazier is at the same point it was at 40 years ago�. So assuming glazier are not normall ever growing and they seem to ebb snd flow(is this right). Then this particular glazier seems to be at the same point it was at 40 years ago� how does this knowledge fit in to the obvious climate changes we seem to be experiencing?

ANSWER:
I do not see how you can glean any information from his being found. First, since he was lost and never found, we have no idea where he was when he died. Second, there is a reason why glaciers are called "rivers of ice"�they are always moving. So you neither know where this hiker died nor where that location has moved to over the intervening time.

QUESTION:
Distance between 2 planets (A & B) is 10 light years. One spaceship (1) leaves planet A and travels to planet B at an average velocity of 0.25c. A second spaceship (2) leaves planet A 20 years later and travels to planet B at an average velocity of 0.5c. Do they arrive at planet B at the same time?

ANSWER:
It depends on whose clocks you used. Let's first use clocks on planet A: It obviously takes a time T₁=40 years for #1 and T₂=20 years for #2, so, as observed by A, they arrive simultaneously. Now, #1 would measure, because of length contraction, the distance between A and B to be L'₁=L₁√(1-0.25²)=9.68 ly; similarly, #2 would measure that distance to be L'₂=L₂√(1-0.5²)=8.7 ly. The corresponding times (T=L/v) would be T'₁=38.7 yr and T'₂=17.3 yr. Now we need to find the speed of #2 relative to #1; [v₂₁=0.5c+0.125c]/[1+(0.5x0.25]=0.286c. We can now calculate how long it takes for #2 to catch up with #1, (L₂/2)/v₂₁=16.9 years; but it takes #1 T'₁/2=19.4 years to arrive at B, so #2 arrives at B 2.5 years earlier than #1. What is simultaneous in one frame is not necessarily simultaneous in another.

QUESTION:
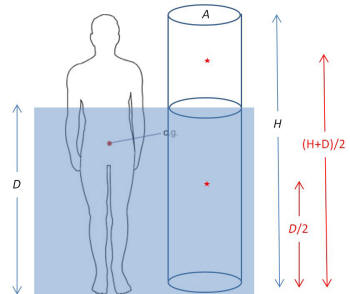
Hello, I am very interested in how standing, walking etc in a pool affects the location your standing center of gravity - normally just in front of S1-S2. My gut feeling is that it raises is a tiny bit, but I'm not at all sure. Do you have the answer?

ANSWER:
There is, of course, no exact answer to this question�bodies are different, distribution of mass is highly nonuniform, the depth of the water matters, etc. Center of gravity (cog) is different than center of mass (com) because com depends on how mass is distributed whereas cog depends on how apparent weight is distributed. Because there is a buoyant force on the body in the water, his apparent weight of that section is less. The figure shows a man of height H standing in water of a depth D. I was a little surprised to find for the man not in water, as the questioner implies, that the cog is near his waist, about H/2; then I realized that the heaviest bones (legs and pelvis) are below the waist so this was reasonable. Being in the middle like this suggested that the mass is fairly uniformly distributed so I chose to model the man by a uniform cylinder of mass M and volume V=AH; this is a very rough estimate but is the best I can do and it will give an order-of-magnitude of how far the cog will move upward. Before the water is added the cog of the cylinder is at H/2 and the total weight is Mg where g=9.8 m/s² is the acceleration due to gravity. The total weight is Mg=ρ_manVg, where ρ_man=985 kg/m³ is a typical mass density for a man*. Now let's add the water. The apparent weight of the submerged part of the cylinder is W₁=(ρ_water-ρ_man)DAg and the cog is y₁=D/2 above the bottom because the mass is assumed to be uniformly distributed. The weight of the unsubmerged volume is W₂=ρ_man(H-D)Ag and its position is at y₂=(H+D)/2. So we can now write the position of the new cog, y_cog=(W₁y₁+W₂y₂)/(W₁+W₂). The density of water is 997 kg/m3, so y_cog=[6D²+493(H²-D²]/[12D+985(H-D)]. As a numerical example I will look at an H=2 m tall person standing in water of depth D=1.3 m; this would be roughly the scale which is in the figure I have drawn. Doing the arithmetic I find that y_cog=1.63 m. This is just barely below the cog of the unsubmerged portion of the cylinder or man which is at 1.65 m. Note that this is by no means a "tiny bit" as you speculated. The reason for this is easy to understand�because the density of water and the density of the man are so close to each other, the effective mass of the submerged mass is very nearly zero.

*As a touchpoint, a 200 lb man has a mass of about 90 kg, so V=90/985=0.1 m³. Since V=AH where A is the area of our model cylinder, A=V/H=0.05 m².

QUESTION:
When light moves upward against gravity it red-shifts (and blue shifts if it were relected back down). Let's say that the shift is causes blue visible light to actually go red. How does this work in a photonic sense. Do blue photons turn into red photons? If so, what has happened to the energy, did it disappear? Energy can't just disappear, photons have no mass, so it hasn't become potential energy, where did the energy go?

ANSWER:
When you throw a ball straight up in the air it slows down, eventually stops, and falls back down. In physics terms, the ball loses kinetic energy on the way up and gains it on the way down. Usually we "invent" a potential energy function and consider it the result of work done by the gravitational force, negative work going up, positive work falling down. In this case the ball's lost (gained) energy is gained (lost) by the by the gravitational field. In the case of a photon, again energy of the photon is lost on the way up and gained on the way down. Again, the energy which is lost is gained by the field and vice versa. A photon cannot slow down or speed up because that is a law of nature; its energy is given by E=hf where h is Planck's constant and f is the frequency of the corresponding electromagnetic field of which the photon is a "member". Thus the red/blue shifts. To make this a little more concrete, you probably know that light cannot escape from a black hole so as it moves away it eventually disappears altogether; so the field has gained all the energy of that photon and this results in the source of the field, the black hole, increasing its mass by the amount Δm=hf/c².

QUESTION:
Hi, my question centres around the motorcycle community and that �loud pipes saves lives�. For context if you are not a biker, the premise is that if your bike is very loud, you are more likely to be heard by cars/drivers sooner and therefore reducing your risk of them not seeing you and crashing into you. The counter argument to this is, as the exhausts are at the rear of the bike the sound is lost out of the back and therefore they won�t hear you until you have reached or gone past the car. This then is further argued that for this to apply you will need to be travelling faster than the speed of sound. I believe the Doppler effect sits in this somewhere too but I�m not knowledgeable enough to know. So my question is; Can a motorcycle travelling down a road at Xmph be heard by a vehicle ahead of it and at what distance does the vehicle ahead begin to hear the motorcycle? I realise there are a number of variables that would need to be factored in to make here, (noise inside the car, speed travelling, etc., but I guess that�s why I�m asking the question

ANSWER:
I found a website where this question was addressed scientifically, not just somebody's opinion. I could do no better. The bottom line is that loud pipes do not save lives. I might add that loud pipes do annoy people who value a quiet environment! I might also add to that gasoline leaf blowers, lawn mowers, loud cars, etc.

QUESTION:
If I were travelling at 100mph in a sealed unit ie a train with no air movement and I dropped a cricket ball from directly above a cross marked on the floor, would the ball hit the cross? As the drop is approx. 8 feet would the result be the same if the sealed unit/train was 100 feet tall. I maintain the once the ball has left my hand it no longer has direct contact with the movement force and it would very slowly loose forward momentum as while the contained air is still moving at 100mph it would not have the density/power/whatever to overcome the weight of the cricket ball and it's forward momentum would gradually decrease. I ask this as someone says that no matter from what height the ball was dropped the forward momentum world remain exactly 100mph and therefore hit the cross. I am 72 and back when I was at school we did not do this sort of maths(?).

ANSWER:
This is interesting because it is such a common gedanken used to demonstrate the Galilean relativity of two-dimensional kinematics. But never is it discussed what the conditions are for it to be absolutely true. Since the speeds involved are all much less than the speed of light, I answer this question considering only Newtonian classical mechanics. The answer, as I will show for the real world, is no, even from 8'. The conditions are:

The experiment must be performed in an inertial frame of reference. That is, the frame of reference must not be accelerating and we are assuming that the frame is the train itself.
The experiment must be performed in a uniform gravitational field. The direction and magnitude of the gravitational force must be constant in magnitude every everywhere.

These are well approximated in the real world as long as the distances aren't too large. First, referring to #1, the train is on the surface of the earth which is a sphere so the train is moving with some speed v in a circle which has the radius of the earth R so it has a centripetal acceleration v²/R. But, it is really more complicated than that because this circular train track is attached to the earth and the earth is rotating on its axis. I won't go any farther, but we could also say that the earth is revolving around the sun, the sun is revolving around the center of the galaxy, etc. ad nauseum. The point is that the frame of the train is not an inertial frame; it is an excellent approximation for most everyday situations.

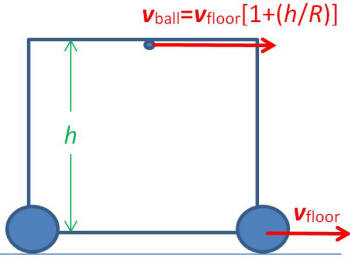Next I will give examples of how these two accelerating frames (circular track and rotating earth) can affect where the dropped ball lands. I have drawn a figure which shows the train car and the ball on the ceiling, the car being h meters above the floor. But, if the car is traversing a circle, the ceiling is moving faster than the floor as shown in the figure by a factor of (1+(h/R). The ball will take some time to fall and during that time the floor will move forward a distance v_floort and the ball v_floort(1+(h/R)) so the ball lands v_floorth/R farther forward than the X initially under it. Of course for a normal train car h/R is an incredibly small number and you would be hard-pressed to observe it. But if you dropped it from an altitude of R, the ball would go twice as far as the X on the floor. A much larger effect, though, is from the rotation of the earth and is called the Coriolis force. It is beyond the scope of this site to get into this force, but the effect turns out to be that the falling ball will be deflected in an easterly direction by the amount d=(ωcosφ/3)√[8h³/g] where φ is the latitude where the ball is dropped, ω is the angular velocity of the earth's rotation (7.27x10^-5 s^-1), and g is the acceleration due to gravity (9.8 m/s²). If you do the calculation for h=100 m, φ=45� you find that d=1.55x10^-2 m=1.55 cm. Compare this with the deflection of the ball dropping from 100 m and the train going 100 mph=0.028 m/s, d=0.2 mm.

The central part of your question, "�I maintain�gradually decrease." is totally wrong. You, on the train, see the ball with zero horizontal velocity falling in perfectly still air. An observer outside sees the ball with some initial horizontal speed the same as the horizontal speed of the air. Air drag will have an effect on the falling ball, increasing the fall time.

Finally, condition #2 that the experiment must be conducted in a uniform gravitational field. This is an exellent approximation near the surface, but going away from the earth the field decreases like 1/r². I haven't thought about the impact this would have the falling ball experiment, but I think I have adequately shown that the "falling on the X" part is wrong, so I will save that for another day!

QUESTION:
In photoelectric effect, why do we deal with "maximum" kinetic energy?

ANSWER:
When a photon strikes the surface of metal it may interact with an electron in the metal. Suppose that an energy W is required to remove an electron from the surface. Then, if a photon of energy E interacts with an electron on the surface, the electron is ejected with a kinetic energy K and the electron will have a kinetic energy K=E-(E'+W) where E' is the energy which the photon has after the interaction. Now, suppose that the photon gives all its energy to the electron, E'=0, and this will be the largest possible kinetic energy the electron to have, K_max=E-W.

QUESTION:
Hello!! I have a question that is related to space but deals mostly with the physics of orbital mechanics and free fall objects. If you were to have a space station that maintains a constant altitude above a planet or stellar body, would you still have gravity? Would that gravity be the same as the gravity on the surface of the body or would it be a portion of that gravity?

ANSWER:
Gravity is a force field which is caused by the presence of mass. Because it is a very weak force, a very large amount of mass is necessary for us to be able to perceive its presence. It is a field which, if caused by a massive spherical object (planet, star, etc.), decreases as you get farther away. Isaac Newton first discovered the force F on an object of mass m, a distance r from the center of a spherical object of mass M and radius R is F=GMm/r²where G is a constant. If d is the altitude, d=r-R, so r=(R+d) and F=GMm/(R+d)². I suppose that answers your questions�yes, you "would you still have gravity"; no, gravity would not "�be the same as the gravity on the surface�" because it decreases like 1/r². There is, however, an important thing to keep in mind�although there is gravity there, you would not feel it because when in orbit you are in free fall as gravity provides the centripetal force to keep you in orbit. Discussions of astronauts being "weightless" when in orbit are inaccurate�they still have weight but don't feel it.

QUESTION:
This is a question that goes (I suppose) to the fundamental nature of things and for which you may think me the village simpleton. But I'll give it a go. Let's assume a single free photon traveling across the universe at x frequency. What force, what principle, what property keeps the photon locked in its cycle of crest to trough to crest again? What pulls it back to center? Why can not it simply "break free" of this cycle and fly off in a static state to parts unknown. In other words, why? Why does energy vibrate at all?

ANSWER:
The answers to your questions require some pretty serious math/physics to answer rigorously. But I will do my best to try to give you a more qualitative overview. The most important thing to keep in mind is that trying to think of quantum phenomena in terms of classical phenomena is unreliable and nothing more than a means of trying to understand in terms of our everyday experience. You have some problems with classical physics as well, so let's start there.

"Why does energy vibrate?" Energy is not a thing, it is a property which things have. One kind of energy is kinetic energy, the energy of motion. If an object is moving in a straight line, or spinning, or vibrating it has kinetic energy; unless something interacts to take some or all of that energy away, it will never go away�that's called conservation of energy. In fact, the reason energy is useful in physics is that physicists have defined it so that it will obey a conservation law for any "isolated" system. The energy of the entire universe never changes.
"�what�keeps the photon locked in its cycle [?]�" Think of a vibrating guitar string: It will vibrate forever because of energy conservation, right? Of course not, because it is not an isolated system. It is vibrating in air and as it moves through the air the pushes on the string opposite the direction the string is moving, slowing it down just like a wind will push on you. Where did that energy go? The air, if you had a very sensitive way to measure its temperature, would warm up just a tiny bit. Another way the energy gets lost (from the string) is that the string is attached to the bridge which is attached to the body, so the string gives up some of its energy to the whole guitar as it starts vibrating too. But that vibration sends out sound waves which flow away carrying more of the enrgy with them. If you just stretched the string across two nails on a rod it would vibrate much longer and you would hardly be able to hear it because because energy is not "leaking" to the guitar.

Now, back to the photon. The first thing is that it is not a particle or a wave, it is a particle and a wave. This, particle/wave duality, is hard to swallow since there is no really good analogy in classical physics. If you look for a particle, you will find a particle; if you look for a wave, you will find a wave. Just like an ideal guitar string, it needs nothing to keep it in its state. A photon is the tiniest amount of a ray of light that can exist. It has energy which is proportional to the frequency of the light which it is part of. You just get confused if, as you have done, you try to think of it vibrating with that frequency. If it is in empty space and nothing interacts with it, energy conservation just keeps it moving along with a certain kinetic energy and linear momentum (also a conserved quantity). It has no "static state" and cannot "break out" without violating energy conservation. However, if it happened to encounter an electron it would interact with it and some of its energy might be given to the electron.

QUESTION:
I have a question about defining types of heat transfer. Me and a friend got into a debate about wether the so called "radiant" heat in the concrete floor that has heated fluid pipes running through it, is in fact radiant or convection type. Since the temperature of the air in the room is heated by this method i say it was convection occuring. But its always called "radiant" heat when we have heated slab floors. Is the heat emitted from this slab in the form of radiant waves then, or is the parcel of air itself in contact with the slab heated and then convects outward via the air itself? What type of heat are we talking about here?

ANSWER:
Both play a role in heating the room. If no air were in the room, the ceiling and walls would eventually warm up because of the radiant energy from the floor. But if there is air in the room, the radiant energy would heat up the air but not uniformly so currents of air, convection, would occur.

QUESTION:
I have a 3.7V and 600mah battery, which has a big bms that can handle a high current before rendering a short circuit, but now I have 2 3.7V and 600mah batteries, the problem is their bms can't hand alot of current like the last one, and my device shuts off when i try it on. so can't I connect these 2 batteries in parallel with the bms of the first battery, so the device doesn't turn off, and it gets a better battery life time?

ANSWER:
I don't know anything about battery management systems (bls) but I do know DC circuits, so I will take a shot at your question. For illustration, let's say that your first battery can handle a current of 3 A and the other two can handle 1 A; suppose your device draws 3 A. If they all have the same the same internal resistance and you connect them, each will have 1 A flowing through them and two of the three are right at the limit before they shut off. If, however, the two have a resistance smaller than that of the third, they would need to have more than 1 A and, I presume, the bms would shut them down.

QUESTION:
This is a question about sound. If you were to increase the temperature of a medium without allowing the volume (of the medium) to change, how would this affect soundwaves that travel through it? I've tried researching this but most of the answers I get refer to how the change in temperature changes the density of the medium, which is not what I am interested in. I want to know what happens if you prevent the density from changing. I know such an increase in temperature would increase the pressure, but I don't know if that would make the sound louder or change it at all.

ANSWER:
This question depends a lot on the situation you have�is it a gas or liquid or solid? What is it made of? What is its molecular structure? But you are lucky if you want to consider a gas which is well described by the ideal gas law, PV=NRT. Volume V is constant, N measures the amount of gas, also constant, T is absolute temperature (your variable), and R=8.31 J/mol�K is the universal gas constant. The sound has a frequency which will not change but the speed v will so the wavelength of the sound will change. It turns out that the speed depends only on the temperature and what the gas is. I will not go through the whole derivation because it requires a lot of facility with thermodynamic theory, but I will give you the final result:

v=√[γRT/M]

where M is the molecular mass of the gas and γ is the adiabadic index, the ratio of the specific heat at constant pressure to the specific heat at constant volume, C_P/C_V. For example, for air, γ=1.4 and M=0.029 kg/mole, so v=20.03√T. Don't forget that T must be the absolute temperature, K. I get v=347 m/s at T=300 K.

QUESTION:
The Bohr model correctly interpreted the atomic spectra of the hydrogen atom and predicted that the excited atom would emit a photon whose energy is equal to the energy difference between two specific levels in the atom.... After that, quantum mechanics appeared and the Schr�dinger equation for the hydrogen atom was solved Bohr model becomes incorrect (or inaccurate, or incomplete) From the Schr�dinger equation, we learned that the electron does not revolve in a specific orbit around the nucleus, but its distance from the nucleus is a potential, that is, it is not a specific orbit. The question is here: How is the energy of the photon emitted from the atom (a specific energy that is responsible for the distinctive atomic spectrum) equal to the energy difference between two orbits, even though the energy of each orbit is indefinite?? For example, the energy of the primary orbital in the hydrogen atom, according to Bohr = 13.6 ev And the energy of the second orbit = 3.4 ev, so the difference = 10.2 ev But in the Schr�dinger equation, the electron in the first level can take energy greater or less than 13.6. It is true that the average energy in the Earth's orbit is equal to this value, but there are possibilities for it to be greater than even twice this value or less, so how is the difference between the two levels always constant = 10.2. This is proven practically and experimentally through the atomic spectrum of the hydrogen atom.

ANSWER:
You have many misconceptions. The Bohr model is semiclassical and in most respects just plain wrong. Nevertheless, it played a very important roll in the development of modern physics. Just to list a few errors:

Electrons are not simply particles.
The electrons do not move in circular orbits.
The orbital energies are not determined by quantizing the angular momentum of the orbit.
The values of the angular moment are wrong. For example, the ground state has zero angular momentum so to think it as an orbit is dead wrong.
All states are assumed to be stable so their decay to lower states is not explained.
It is empirical and makes sense only in that it reproduces experimental spectra.

You have a problem with energies. The zero of the electric potential of a point charge is chosen to be infinitely far away. This is sort of standard of atomic or nuclear physics. The energy of the ground state is E=-13.6 eV. Negative energy means the electron is bound, so 13.6 eV is the ionization energy, the energy you must expend to free an electron in this state. In quantum mechanics we find that the electron is not a particle but simultaneously a particle and a wave (wave-particle duality). The solution of the Schr�dinger equation for the hydrogen atom yields not some orbit for an electron, but a function (wave function) which is interpreted as a probability distribution; for example, for a small volume ΔV=ΔxΔyΔz at some point (x,y,z) where the wave function is Ψ(x,y,z), Ψ² is the probability of finding the electron in that volume. But the solution has a definite energy (eigenvalue) for each state, not an indeterminate energy as you seem to think. Finally, quantum mechanics gives us the uncertainty principle: certain pairs of observable quantities can't be known to arbitrary accuracy. The pair of interest to us is energy and time�the better you know time, the less well you know the energy. The ground state of lives forever and so its energy is exactly -13.6 eV; but the excited states have definite lifetimes so their energies are uncertain. In principle, if you measure the energy of a line in the hydrogen spectrum you would find that it has a spread, the shorter the lifetime the larger the spread. This spread is very small and also often swamped by other effects: most spectra come from tubes where the atoms are moving very rapidly and you get a spread due to Doppler shifts of atoms moving toward or away from you. I have no idea what you are talking about regarding the earth's orbit.

QUESTION:
We have an above-ground pool that contains roughly 8400 gal of water. It's dimensions are 25ft long x 16ft wide x 52 inches deep. Our question: Is it possible to hook a garden hose to the bottom drain outlet of the pool, and get the water to rise up to the level of the pool edge (52") and then drain back down into the pool, *without the aid of a pump*?

ANSWER:
I was following everything in your question until I got to "�and then drain back down into the pool�". I am going to assume that you want to connect the hose at the level of the bottom of the pool and fill the pool that way and that is what I will answer. The key is that if the pressure of the hose is less than the pressure at the bottom of the pool when it is full, it will not fill. The typical water pressure in a household is in the range of 40-80 psi, so I wall assume yours is 60 psi as an example. The pressure at the surface of your pool when it is full is atmospheric pressure, 14.7 psi. As you go down into the water the pressure increases at a rate of 0.0371 psi per inch. So the pressure at the bottom of your filled pool is 14.7+52x0.0371=19.3 psi. This is smaller than 60 psi so you can fill your pool this way. On the other hand, why would you want to? It would probably be faster to fill it from the top because the rate of flow through the hose is bound to decrease as the back pressure on it gets larger as the pool fills.

QUESTION:
Suppose a compression spring is placed between two nearby identical bodies in space. The stiffness and natural length of the spring are accurately known. The gravitational attraction between the bodies then compresses the spring slightly, and the compressed length allows the bodies� rest mass to be estimated. The spring�s compressed length should be the same for an observer moving at high speed at right angles to the spring, so the mass should be seen to be the same as before. But using SR the observer knows this observed mass exceeds its rest mass. The rest mass would be less than the mass measured in its rest frame. So how is this consistent with invariant rest mass?

ANSWER:
The answer is simple. The spring constant is not invariant, it depends on your frame of reference. Related to this is the realization that force is not really a useful concept in special relativity.

QUESTION:
Suppose a rocket flies at high speed toward a stationary laser and carries equipment to measure the frequency of the laser�s light. The speed of the rocket is known and hence so is the non-relativistic Doppler shift. After allowing for this shift the measured frequency of the light should be slightly blue shifted. This is because the time rate of the atoms in the rocket will be slightly reduced due to its high speed, so in comparison the frequency of the laser�s atoms will be higher.

ANSWER:
You are making this too difficult. To calculate the frequency of the radiation observed on the rocket you only need to know the frequency in the laser's rest frame; the way the radiation was created is irrelevant. And I do not know why you ever mention the non-relativistic Doppler shift because it is incorrect for electromagnetic radiation. The correct Doppler shift equation is λ_rocket/λ_laser=√[(1+β)/(1-β)] where where β=v/c, v the relative speed and c the speed of light; this equation has β>0 for the rocket and the laser moving away from each other. In your case β<0. For example, if β=-0.7, λ_rocket/λ_laser=0.42, blue shift.

QUESTION:
The double slit experiment using a series of particles raises a question: Why does the electron or photon gun not shoot straight? Assuming the gun is positioned between the two slits, it should just hit the same point on the barrier every time. CRT�s had accurate electron guns, why not an accurate gun for this experiment? Can you describe the nature of the trajectory variance? Cyclical, random or something else?

ANSWER:
You miss the whole point of double-slit diffraction. Diffraction happens for waves but a "pure" particle (if there were such a thing) does not diffract. Any elementary particle, e.g., electrons and photons, are both particle and wave�if you look for a wave you will find a wave, if you look for a particle you will find a particle. This is called wave-particle duality. If you look for wave behavior of electrons you need to look for diffraction.

The rule-of-thumb for whether diffraction is important is that the slit or obstruction not be much larger than the wavelength of the wave. E.g., the wavelength of light in the middle of the visible spectrum is about 5x10^-7 m; the slits in a good diffraction grating are spaced by about 5x10^-6 m and the diffraction is easily seen. But what if the slits had been one meter apart? In that case you would be hard put to see any diffraction and the photons could be carefully shot straight into the gap. There would be single-slit diffraction from the two slits, but let's just say they were each a centimeter wide; if you looked really hard you might find a little fuzziness of the shadows of the edges of the slits which would be diffraction.

Now let's turn to diffraction of electrons. The wavelength of an electron accelerated by a voltage of 1 kV (which has a speed of about 1/10 the speed of light) is about 4x10^-11 m. So your slits would need to be not too much bigger than that. But you would not be able to fabricate slits that close together because t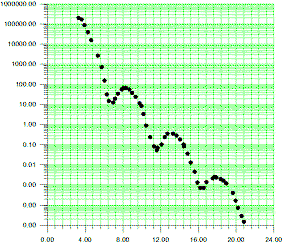he size on an atom is about 10^-10 m! So the pictures you see in text books of electrons and a double slit are a fraud! No such slits exist. But that slight-of-hand is just to get students understand one wave in terms of some other wave you already understand without going into all the technical details of how you can really do it. There is no doubt that electrons behave as waves. The first experiment to observe electron diffraction was the Davison-Germer experiment; they directed an electron beam onto an iron crystal, using the regular spacing of the iron atoms as a kind of diffraction grating. So, protons, having much larger mass than electrons, have much smaller wavelengths. An earlier answer showed the results for 800 MeV protons scattering from a ⁹⁰Zr nucleus. Protons of this energy have momenta of about 10^-15 m, so to see diffraction you need a target not too much larger than that size; the size of nuclei is about this size. The results are shown in the graph which shows the intensity of the proton diffracted from the nucleus. For more detail, read the answer linked to here.

This now answers your question about CRT electrons not having any problem hitting a small dot on the screen�the dot is really huge compared to the electron wavelength.

QUESTION:
How does touch work from a physical perspective? From a biological perspective we know that mechanoreceptors carry impulses along nerves to the central nervous system. For examples when my fingers touch the keyboard of my laptop the mechanical pressure is converted into electrical signals sent to my brain and I feel the keyboard. From a physical perspective one might argue that we never touch anything. The cloud of electrons buzzing around the atomic nuclei comprising the atoms of my fingertips interacts with the the electrons of the keyboard, virtual photons convey the information of the electromagnetic field, but there is no touching involved. The electrons do not �touch� each other. Though there is no touch involved perhaps we might say that electrons �feel� forces (and accumulate energies from them) whenever there are electromagnetic fields. My question is: What is going on at the atomic level when we touch something? How does the interaction between the electromagnetic fields of my electrons and the electrons of the keyboard turn into an electrical current strong enough for my brain to detect it?

ANSWER:
I have recently answered a question which touched on the microscopic origin of contact forces. It turns out that the contact force is mainly due to a quantum effect, not to electromagnetic forces between atoms on the surfaces. Wikepedia states that "�in quantum mechanics the Pauli exclusion principle (PEP) states that two or more identical particles with half-integer spins (i.e. fermions) cannot occupy the same quantum state within a quantum system simultaneously�". In other words, when two objects get close enough, the wave functions of atoms on the surfaces begin to overlap and the electrons in the atoms begin to be approaching the same state and atoms on both surfaces stop getting closer to avoid violating PEP. It isn't really a force but the effect is the same�the surfaces push away from each other. The result will be a compression just below the surfaces which will then be detected by the nerves but, not being a biologist, I couldn't give you any useful explanation how the nerves work. Regarding whether the objects actually "touch" requires, at atomic distances, a definition of what we mean by touch. I would say that if wave functions of atoms overlap that they are touching.

QUESTION:
I am confused and need help on understanding forces acting on a car when it is moving uniformly on a level road. When a car is moving uniformly (say forward) on a level road, what is the direction of friction acting on it? Some say it is to the left, because some textbooks would describe the above situation as a having a driving force pointing forward, and friction pointing backward. But then I also have read some online posts, saying that the so-called "driving force" is actually friction. So the friction should point forward. Also, I came across with something called "rolling resistance". But I am not sure how I could include it in my understanding. While this question may seem simple, it really confused me a lot because I am not sure how much textbook situations deviate from real life.

ANSWER:
When you say "�the friction�" you imply that there is only one frictional force acting on the car. In the case of a car going with constant speed on a straight road, there are three important kinds of friction acting:

The tires are constantly getting slightly deformed at the bottom and deforming them requires a force. This is called rolling friction and is what is mainly responsible, at low speeds, why, if nothing is pushing the car, it will roll to a stop eventually. The road exerts a force on the tire and the tire exerts an equal force on the road. (Newton's third law.) This force acts backwards.
A second force is static friction which causes your "driving force" to impart a forward force on the tire. The mechanics of your car causes there to be a torque on your wheels which tries to cause them to rotate counterclockwise (as seen from the side). In fact, if the road were frictionless (icy, for example) the tire would spin and not cause the car to move forward. This static friction also keeps your car from slipping if the road curves; in that case, the static friction will have a component in the direction you are going and a component toward the center of the curve you are negotiating.
Finally there is air drag which exerts a force on the car opposite its velocity. It becomes more important as the speed increases, increasing quadratically (e.g. 3 times more speed gives 9 times more drag.)

You might wonder why static friction could drive the car forward�the car is certainly not static. But where the "rubber meets the road" is certainly static.

I hope this clears it up for you.

QUESTION:
I am in high school and I conducted an experiment that involved a parallel spring systems, mass and vertical displacement. The system had an equivalent spring constant of around 80N/m. I noticed that a 200g mass produces close to 0 displacement, but the difference in displacement in between 1000g and 1200g is close around 2-3cm. So why does the increase from 0-200g so insignificant compared to the increase from 1000g-2000g. According to hooke's law shouldnt this similar increase in force result in the same displacement?

ANSWER:
The problem here is that Hooke's law is not really a law, it is an approximation which works very well in some situations and not for all situations. For example, suppose you hung a 1 metric ton mass (1000 kg), a 9800 N weight, from your spring; would you expect it to stretch 122.5 m? Springs in the real world are approximately linear for a limited range of applied forces. If I were you, I would make more measurements by adding masses in 200 g (m=0.2 kg) increments making careful measurements of the stretch and then plot the stretch as a function of the weight (W=mg); this should yield for small masses the slope of the line is smaller than 80 N/m for small W but becomes 80 N/m. It might also be interesting to then take weights off to see if it traces back on the stretching data; if it doesn't, that is called hysteresis.

QUESTION:
A motorcycle has to move with a constant speed on an over-bridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point. What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge? My Trouble:- I found the answer in internet saying the Normal force acting on motorcycle will be zero. But I am not getting this part that Why and How will the Normal force be zero? Isn't Normal force a repulsive (electrostatic) force between atoms of two bodies in contact, then why will it be zero!?

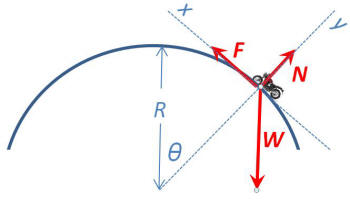
ANSWER:
First of all, it is not at all helpful to think of the microscopic origins of normal forces in classical mechanics problems like this one. Also, almost every physics book you will read will say that it is the result of electromagnetic forces, but this is incorrect; the origin of this force is mainly due to quantum effects�the Pauli exclusion principle�as first shown by Freeman Dyson. All we need to say is that when two objects are in contact with each other there are forces that each exerts on the other which, by Newton's third law, are equal and opposite. As is often done with vectors, it is convenient to resolve this force into two components, the force tangent to the surface of contact (usually called the frictional force F) and the normal component (usually called the normal force N). See my figure. So the motorcycle in this problem has two forces acting on it, its weight W and the contact force which has components F and N. There is zero acceleration in the x-direction so

F-Wsinθ=0,

F=mgsinθ.

There is a centripetal acceleration in the negative y-direction, a_y=-v²/R

-mv²/R=N-Wcosθ,

N=m(gcosθ-v²/R).

Some things to note:

Both N and F are functions of θ.
F is positive on the way up but negative (braking) on the way down. It is zero at the top.
N is always positive.
If gcosθ-v²/R≤0, N becomes zero or negative; for a motorcycle, N can't be negative because this particular contact force can only push, not pull. This does not mean that the normal force can never pull down. What if the road were made of iron and the motorcycle carried a very powerful magnet? Also, roller coasters are not just rolling on wheels but have to have a mechanism such that if you were to stop at the top of an inside loop-the-loop you would not crash to the ground. What does it mean if N=0? It means that the motorcycle is no longer on the road; once N=0 the only force acting on the motorcycle is its own weight and so it becomes a projectile; F will disappear also so its speed will no longer remain constant; this happens all the time in a motocross race.
For a given angle where N=0, what is the speed v? v=√(Rgcosθ). That speed is greatest when when θ=0�. So we finally come up with the answer to your question, v_max=√(Rg).

QUESTION:
I'm finding there are 2 seemingly contradictory concepts when it comes to air pressure and temperature. The first is that when temperature rises, it increase the pressure of the air because the molecules move more quickly causing them to hit the walls of their container more forcefully and more often. The second is that colder air has more pressure because the molecules come closer together, making it more dense which results in it having higher pressure.

ANSWER:
The problem is that you are looking too narrowly. There are other variables besides pressure P and temperature T. We should start with the simplest behavior of a gas, the ideal gas law, PV=NT where V is the volume of the gas and N is some measure of the amount of that gas. Usually, if we want to find the relation between two of these four variables, we hold the other two constant. If we do that for P and T we obviously find that pressure increases linearly with temperature, P∝T, your first "concept," but it should have been modified by "�if N and V are held constant�". It is now clear that your second "concept" cannot also be true under the same proviso. So let's hold just N constant (don't add any new air to V); so now P∝T/V. So your second "concept" is true only if the rate which T decreases is smaller than the rate at which V decreases; in other words, the pressure will increase in a cooling gas if the volume is sufficiently compressed.

QUESTION:
We are working on a gravity energy system. How much electrical output (kWs) can we expect from a 50,000 lbs weight, falling at a rate of 6 inches per second, and what the kWs would be if the same 50.000 lbs was falling at a velocity of 1 foot per second?

ANSWER:
First, let me be a bit of a scold. A Watt is a unit of power, energy per unit time, whereas a Watt-second is a unit of energy, force times distance. You give me enough information to tell you the power but not the energy where I would have to know the time the weight fell. Also, a Watt is a Joule per second (J/s) or a Newton-meter per second (N�m/s); but you use Imperial units (inches, pounds) so I will have to first convert these to SI units. End of scold! The mass of 50,000 lb is m=22,680 kg, so the weight is 22,680x9.8=2.22x10⁵ N; 1 ft=0.305 m. So, since it falls 0.305 m in 1 s, the energy per second is 2.22x10⁵x0.305=67.8 kW. So, you could get this much power for however long as it fell. If it falls for 100 ft, you would deliver this power for 100 seconds, a little less than 2 minutes. Of course if you correct for friction losses it would be less than that. But more importantly, I hope you have a cheap and easy source to pull it back to the top.

QUESTION:
I was asked this question many years ago and passed it on without results: A30 foot wooden freestanding pole on a concrete platform is leaning 10 degrees from vertical and held in place by a wire. The wire breaks, how many seconds does it take for the pole to fall to the horizontal ground? Don�t loose sleep over it. Greetings from Klaus a 87 yr old forgetful physicist

ANSWER:
This is basically the simple (physical) pendulum problem where Newton's second law results in d²θ/dt² ∝ -sinθ. But you will recall that this differential equation can only be approximately solved for θ<<1 and the solution is the simple harmonic oscillator. When you and I were students solutions of the large-angle simple pendulum were very tedious employing power series or sometimes obscure special functions. Today one could write a simple computer program to solve the equation numerically pretty easily.

QUESTION:
If Entangled particles separated over great distances act simultaneously, then the "force" binding them must act faster than light speed? If a particle was on earth and entangled with a particle in the sun (for example) then interacting with the earth based particle would generate an immediate effect on the sun based particle. But if the force / energy that binds the two moved at the speed of light, then it would take 8 minutes for one to impact another, so does this force move faster than light speed? And how does this reconcile with Einstein?

ANSWER:
You at least partially understand why Einstein referred to entanglement as "spooky action at a distance". The particles need not be bound and there is no "force" which is somehow keeping track of the other particle. The entangled particles have been prepared so that they are, in essence, a single quantum system. Although we would feel that there was something "communicating" between the two particles, it has been proven that whatever it is cannot be used to send information.

QUESTION:
Why do 2 spheres hung by a light string with the same mass but different charges (+ve) make the same vertical inclination with the string?

ANSWER:
Because of Newton's third law: If object A exerts a force on object B, then object B exerts an equal and opposite force on object A.

QUESTION:
In a rigid body like a coin, if an impulse is given along its centre of mass then we calculate the change in momentum by multiplying mass and velocity change of the body.then energy is it kinetic energy due to velocity of its centre of mass. but if impulse of same magnitude is applied not along the centre of mass then we get both linear and angular velocity. But linear velocity is same as in the first case. But if we observe the energy then we get both linear kinetic energy and angular kinetic energy. How is this possible? How can we get extra energy without giving more impulse to the rigid body?

ANSWER:
This is a little tricky because, as you state, an impulse of J causes an increase in kinetic energy, so if you apply J anywhere on the body you should get the same increase in kinetic energy. (I am assuming no external forces here so we need not worry about potential inergy.) So, if I apply a force, the direction of the vector passing through the center of mass of a rigid body of mass m, I can write J=mv_cmwhere v_cm is the velocity of the center of mass. So the energy resulting from the impulse is E=�mv_cm². In this situation, all energy goes into translational energy. But if we exert J elsewhere, it now also exerts a torque about the center of mass which causes the object to also acquire a rotational kinetic energy. Now, J=mv'_cm+Iω/d where ω is the angular velocity about the center of mass, I is the moment of inertial about the center of mass, and d is the moment arm of the torque about the center of mass. I believe this answers your question because clearly v_cm>v'_cm so the translational energy gets smaller. A very useful theorem of classical mechanics is that the kinetic energy of a rigid body is equal to the kinetic energy of the center of mass plus the kinetic energy about the center of mass, so in this case, �mv_cm²=�mv'_cm²+�Iω².

QUESTION:
is there an equation that could define the oscillatory motion of a screw as it rolls down a ramp

ANSWER:
See an earlier answer.

QUESTION:
Hi, I was in my house the other day at night when I noticed a bizarre light effect coming through a window sun blind. Looking across from the hill I live on are street lamps. When the light of these shined through the netting I was perceiving what I could only determine to be an interference pattern. A point of light was split into 3 definite points. It didn't matter how far from the netting I was and if I moved my head side to side the pattern did not change, the spacing remained specific. I will be happy to send a video of the phenomena.

ANSWER:
The questioner, at my request, sent a video and a picture illustrating grid size. I have taken a screen shot of the pattern. The pattern certainly looks like a diffraction pattern. But, on closer inspection, there are some issues. The first thing that comes to mind is that a streetlight is normally white light and seeing a diffraction pattern from white light is not the familiar pattern of bright and dark spots because the pattern for a particular grating depends on the wavelength of the light so all the wavelengths from that white light would overlap. On the other hand, some street lights are sodium-vapor lamps and sodium has two very close very bright lines (the sodium D-lines) with wavelengths a little less than 600 nm=0.6 μ (microns); this wavelength has a color which is yellow-orange, and so is the pattern we are examining. Now, looking at the the grid-size picture, I would estimate that the holes are on the order of a quarter of a millimeter, 0.25 mm=250 μ, with a spacing of about 0.5 mm=500 μ. There is a general rule of thumb that for diffraction to be significant the sizes of the diffracting object should not be big compared to the wavelength of the light, and this grid has features almost three orders of magnitude bigger than the wavelength of the light if it is from a sodium lamp. If it is not a sodium lamp, I have no idea why it is the color it is. So I have no definitive answer to the question. My best guess is that the pattern is simply the pattern of light passing through the mesh, essentially just the projection of the mesh pattern and that the source is a sodium lamp.

ADDED THOUGHT:
I was just proofing this answer before I posted it. The question included "�A point of light was split into 3 definite points. It didn't matter how far from the netting I was�". If this was the case, it is definitely not diffraction which would spread as you moved farther away. It was worth doing all the work, though, because it illustrates how scientists try to see all the angles of a problem, not just jump to a quick conclusion.FOLLOWUP QUESTION:
Thanks for taking the time to do a thought experiment on this puzzling phenomena. I would like to challenge the concept that it is the grid mesh projecting through. If this was the case, then depending on the angle the grid should move, my hand is not steady in the video, but the grid pattern does not move. As the camera pans surely the pattern should move respectively and the central bright spot would get split as a fibres moved across it? The same pattern is present on both white and yellow sources. Could it possibly be a diffraction through the actual strands if they are translucent nylon, similar to a rainbow diffraction through a water droplet? I have attached another image I noticed a couple of days ago, this shows a window from a long distance away reflecting sunlight through the mesh. We can see a splitting of the light into its constituent colours. Hopefully this adds some useful information? ANSWER:
First, a little correction: The "rainbow" phenomenon is refraction, not diffraction; that, in fact, may be the best clue yet to the final answer to your question. Let me argue one more time against diffraction. I think I have done about as exhaustive an analysis as I can, given what I have. Maybe if I had a piece of the material and could do experiments on it I could learn more. One question: The pattern�is it ON the mesh itself? Or can the light be projected on a screen of some sort? If it is something just on the mesh, it is not diffraction. If you have adequate intensity and could get it to project onto a screen, the pattern would spread more as the screen got farther from the mesh. Just to get a better grasp of how the diffraction can be expected to look we can compare the spacings W of the between maxima or minima for a double slit diffraction pattern, W=λL/d (see my figure), where λ is the wavelength of the light, ~0.4-0.7 μ for visible light. This is just a rough approximation to spacing we would expect, but one which an excellent order-of-magnitude estimate of spacings in any multiple appatures array. First, it depends on how far away you put a screen; If L is 2 m away, the spacing is twice what it is when L=1 m. Taking a typical visible wavelength to be 0.5 μ, W=0.5x1/500=1 mm at L=1 m. Somewhat to surprise, this is not at odds with your observation. But it is not definitive because the spots must get farther apart as you move away from the mesh. If you find that the spacing remains the same, relative to the grid, regardless of the distance you are from the grid, it is not diffraction. I do like your idea that perhaps refractions of the light passing through translucent fibers is responsible. So I guess I still stick with my original conclusion about what we are seeing.

QUESTION:
Let we have the result of a physical measurment like this: "Experiments have Dirac�s number at 1.00115965221 with an uncertainty of about 4 in the last digit" Is this gives any interval that we could say certainly Dirac's number is within it? I mean exact certainty like 3<π<4. If so what is smallest such an interval?

ANSWER:
The answer to your question hangs on what you mean by "about 4". Normally we would say what your question says but without the 'about' which would be denoted by 1.00115965221(4) or 1.00115965221�0.00000000004. But the "about" indicates that there is uncertainty in the uncertainty, and I don't really know how to notate that.

QUESTION:
Does it require more nuclei to fuse the heavier elements and is it the reason for why the heavier elements are more rare?. For example it takes 4 hydrogen nuclei to make one helium nuclei so it takes more helium nuclei to create the next element.

ANSWER:
It is not fruitful to think of fusion as how many nuclei are fused to make a particular nucleus because there are so many ways any element could be made by fusion reactions. For example, you could make ¹²C by fusing two ⁶Li or three⁴He. What needs to be considered is the energetics of fusion, can you make a new nucleus by fusing lighter nuclei? At the beginning of the existence of the universe there was almost nothing but hydrogen, a little helium, maybe a bit of lithium. Now, if enough of these primordial elements become bound by gravity, they will eventually collapse to the point where fusion ignites and you have a star. Why do stars shine and get very hot? Because fusion results in huge amounts of energy being released as it happens. As the star gets older and older the average nucleus is getting heavier and heavier. But now there is a "barrier" for this process to continue forever until you have one giant nucleus: it turns out that when you reach iron, fusion happens only if you add energy, that is it is no longer a source of energy when heavier nuclei fuse. So the earliest stars had almost no elements in them heavier than iron. Then why are there elements heavier than iron in the universe? It is because when the a star is near the end of its life it ends with a terrific bang called a nova which creates an enormous energy which forces fusion to continue as the star is exploding creating many new elements. After the nova, all the debris along with hydrogen clouds coalesce and make new stars and those stars have heavier stuff like lead and gold and silver etc. in them. This is why Carl Sagan liked to say "We are all made of star dust".

QUESTION:
Why is Chernobyl still a toxic wasteland and Heroshima and Nagasaki populated and safe today?

ANSWER:
An atomic bomb and a reactor meltdown are very different events. A bomb carries a relatively small amount of fissile materials. For example, Fat Man, the Nagasaki bomb had about 14 lb. of plutonium-239; about 2 lb. actually fissioned in the explosion. Since long-lived radioactive isotopes from the bomb come from those two pounds, there is not really all that much. Furthermore, that bomb was detonated at 1650 feet altitude, the radioactive fission products would have been spread over a pretty large area. Most of the casualties were due to burns, pressure burst, flying debris, collapsing walls and roofs, etc.; only those in a relatively small area directly under the explosion were injured of killed because of direct radiation (gamma rays, x rays, neutrons).

A large nuclear reactor like at Chernobyl has a core of about 100 metric tons of uranium when first installed and as that uranium is used up it is converted to many radioactive isotopes, both short-lived and long-lived, which are still confined in the cylinders the core is composed of and highly radioactive. At Chernobyl a combination of human error, design faults, and mechanical failures caused the core to overheat, the resulting steam at too high a pressure to be contained, and the steam containment exploded sending out huge amounts of radioactive steam to escape. Since the water also cools the core, the core overheated, burned, and melted and the explosions spread all the nuclear waste over the adjacent land. A whole different order-of-magnitude from a bomb.

ANSWER:
It is not fruitful to think of fusion as how many nuclei are fused to make a particular nucleus because there are so many ways any element could be made by fusion reactions. For example, you could make ¹²C by fusing two ⁶Li or three⁴He. What needs to be considered is the energetics of fusion, can you make a new nucleus by fusing lighter nuclei? At the beginning of the existence of the universe there was almost nothing but hydrogen, a little helium, maybe a bit of lithium. Now, if enough of these primordial elements become bound by gravity, they will eventually collapse to the point where fusion ignites and you have a star. Why do stars shine and get very hot? Because fusion results in huge amounts of energy being released as it happens. As the star gets older and older the average nucleus is getting heavier and heavier. But now there is a "barrier" for this process to continue forever until you have one giant nucleus: it turns out that when you reach iron, fusion happens only if you add energy, that is it is no longer a source of energy when heavier nuclei fuse. So the earliest stars had almost no elements in them heavier than iron. Then why are there elements heavier than iron in the universe? It is because when the a star is near the end of its life it ends with a terrific bang called a nova which creates an enormous energy which forces fusion to continue as the star is exploding creating many new elements. After the nova, all the debris along with hydrogen clouds coalesce and make new stars and those stars have heavier stuff like lead and gold and silver etc. in them. This why Carl Sagan liked to say "We are all made of star dust".

QUESTION:
Why is Chernobyl still a toxic wasteland and Heroshima and Nagasaki populated and safe today?

A large nuclear reactor like at Chernobyl has a core of about 100 metric tons of uranium when first installed and as that uranium is used up it is converted to many radioactive isotopes, both short-lived and long-lived, which are still confined in the cylinders the core is composed of and highly radioactive. At Chernobyl a combination of human error, design faults, and mechanical failures caused the core to overheat, the resulting steam at too high a pressure to be contained, and the steam containment exploded sending out huge amounts of radioactive steam to escape. Since the water also cools the core, the core overheated, burnt, and melted and the explosions spread all the nuclear waste over the adjacent land. A whole different order-of-magnitude from a bomb.

QUESTION:
I have a fairly simple question (for you) regarding tangental and cebtripital force acceleration. Assuming a pendulum with a rigid shaft 44" long weighing 60gms with a mass of 300gms on the end (44" from pivot) how would I calculate the effect of adding [say] 2" on the opposite end (weighting 100gms) on speed of the swinging pendulum. What would that weight or force be called? Radial accelerator? I'm not even sure I am asking this correctly.

ANSWER:It is not as simple as you might think, but just a little messy algebra-wise, not hard conceptionally if you know basic classical mechanics including rotational motion which I will assume that you do. I will assume that the shaft is uniform and thin, the other two masses are point masses, and the friction is negligible, so energy must be conserved. (See my notation on my figure.) The pendulum is lifted to some angle θ and released from rest. I will choose the level of zero potential energy to be the bottom end of the stick when it is vertical. When released there is no kinetic energy T, only potential energy V₁:

E₁=V₁=[m₂L₂+m₁(L₂-L₁)+m₃(L₂/2)](1-cosθ)g.

When it has rotated down to the vertical position where the angular velocity ω will be largest, it has both kinetic energy T and potential energy V₂:

V₂=[m₁(L₂-L₁)+ �m₃L₂)]g

T=�Iω²

where ω is the angular velocity and I is the moment of inertia:

I=[m₂L₂²+m₁(L₂-L₁)²+m₃L₂²/3].

So we may now solve for ω=√{2(V₁-V₂)/I}.

I will now look at your particular case. Unfortunately you mixed your units and I always prefer to work in SI units, so I will choose θ=60� so cosθ=0.5 and use SI units:

m₁=0.1 kg (or m₁=0), L₁=2"=0.051 m, m₂=0.3 kg, L₂=44"=1.12 m, and m₃=0.06 kg, and g=9.8 m/s².

First the pendulum without m₁:

V₁=1.81 J

V₂=0.33 J

I=0.40 kg�m²

ω=2.72 s^-1 (radians/second)

Since the velocity u a distance R from the axis of rotation is u=Rω, u of m₂ is u₂=1.12x2.72=3.05 m/s=6.82 mph.

Second, add m₁:

V'₁=2.33 J

V'₂=1.05 J

I'=0.44 kg�m²

ω'=2.08 s^-1 (radians/second)

u₂'=1.12x2.41=2.70 m/s=6.04 mph.

So the effect of adding m₁ has been to decrease the speed of the pendulum. Increasing the moment of inertia decreases the speed but the increased potential energy difference (V₁-V₂) increases it more. Regarding your question "What would that weight or force be called? Radial accelerator?", the force of the 100 gram weight isn't called anything�it is an added weight to the system, an added force, an added torque, an addition to the moment of inertia of the system. It would be wrong to call it an accelerator because its effect here is to slow it down.

QUESTION:
I have a question about and relativity. I have recently discovered a planet that is exactly the same as Earth but it orbits its star at twice the rate that Earth does. There is an advanced rate there that I want to talk to. I know that there will be a delay as the message travels but will there also be problems owing to differing experiences of time because of relativity? What if instead of "orbits its star" I meant "rotates on its axis"?

ANSWER:
Your question is a little strange. What does "exactly the same" mean? Twice the rate could occur in many ways determined by the mass of the star and the distance of the planet from the star; furthermore, it the earth had a mass twice as big as it does, it would orbit the sun with the same rate as it does now. But none of that matters since you are asking me to assess the relativity effects on time. In order to for relativity to have any significant effects (except for the most demandingly accurate time measurements, such as required for GPS), the quanty v/c must be not much smaller than 1; here v is the speed the planet is moving (relative to the star, let's say) and c is the speed of light. v=3x10⁴ m/s and c=3x10⁸ m/s, so v/c=10^-4. Relativity has a negiligible effect for almost all situations involving planetary motions.

QUESTION:
I was wondering in a typical graph that shows the x,y,z electric and magnetic components of an oscillating electromagnetic wave where the y and z axes are used to describe the behavior of the electric and magnetic fields, is it representing the strength of the fields at any given distance/time along the wave (x,t) or is it showing how far the fields extend into space along their axis? or both?

ANSWER:
The former, i.e. the relative magnitudes of electric fields and magnetic fields at the instant when the graph was drawn; the wave, as it has been drawn, is moving in the +x direction. However, the relative magnitudes of the electric and magnetic fields is meaningless because they are measured in different SI units (electric field in Volts/meter or Newtons/Coulomb, magnetic field in Teslas). Using SI units, the electric field is much larger than the magnetic field. Regarding the information the graph gives about spacial properties of the fields, only directional information is meaningful; e.g., the electric field is perpendicular to the magnetic field and lies in the (y,x) plane.

QUESTION:
Today my wife placed two identical jars in our microwave. Both were open and filled with the same amount of water at the same temperature. The jars were placed directly across from one another, approximately halfway to the edge of the rotating glass plate. One jar began to actively boil, while the other jar did not. About 30 seconds later the water in the non-boiling jar burst explosively into a full boil. She shut off the microwave and had to wipe down the entire inside. What could possibly explain this unexpected result?

ANSWER:
Water at atmospheric pressure normally boils at 100�C. But to boil, bubbles of water vapor must form; these bubbles normally form in existing tiny air bubbles or around microscopically small impurities in the water and are called nucleation points. Water with few nucleation points can get hotter than 100�C and is called superheated water. Superheated water is quite unstable so when one bubble of vapor starts to form it expands very rapidly and the result looks like an explosion like your wife witnessed.

QUESTION:
What kind of equipment would I theoretically need to build a time machine? I'm writing a novel based on the subject.

ANSWER:
A DeLorean, a flux capacitor, and a Mr. Fusion. I hope you get the joke here; if not, google Back to the Future, a trilogy of movies. I hope that you don't think I am ridiculing you, but there is no good physics answer: the current laws of physics forbid backward time travel but you can travel forward in time by taking an extremely long, very fast trip returning to the place you started from (the twin paradox). But you are writing a novel and can let your imagination run wild!

QUESTION:
I once saw in a science museum, experiment. They had a piece of thin metal that connected to some kind of permanent magnet, and the metal became red hot, and fell awa, when it became red hot. The metal was touching the magnet. I was wondering if you could have two of those magnets,real big, attract to each other almost all the way. Then have two pieces of thin metal become red hot, and you could then separate the magnets. The exhibit did this over and over, all day.

ANSWER:
The magnet holding up the metal is not a permanent magnet but an electromagnet which creates not a constant magnetic field but a constantly changing (AC) field. Varying magnetic fields induce varying electric fields. The alternating electric fields causes an electric current in the thin metal and that current causes resistive heating in the metal, just like AC currents in your toaster heats up the wires. The reason that the cool metal is held up is that it is probably a ferromagnetic material which becomes magnetized in an external magnetic field and therefore is attracted to the magnet. But this magnetization will not happen at a temperature above some temperature called the Curie temperature. For iron this temperature is about 770 �C so the hot metal will drop.

QUESTION:
I was wondering if you went deep in the ocean, where there is a lot of pressure due to the water, if you took a open container down with you and closed it (air tight) would it still have the same pressure inside? And if you took it to the surface would it still contain that pressure?

ANSWER:
I never thought about it, but I cannot think why not. For example, suppose you take the open container (full of water) to the bottom of the Mariana trench where the pressure is more than 1000 times atmospheric pressure; the pressure inside and outside the container is now 1000 atmospheres. Now close the container and bring it up to put the surface. There would be a gauge pressure of about 999 atmosphers pushing out. It had better be a pretty strong container!

QUESTION:
How to calculate the downward force at the weight 2, in grams, not inch grams and (not torque).

ANSWER:
Your question has lots of problems. Is the system in equilibrium? If so there needs to be some other force present to keep it in equilibrium, so where would that force be applied? You ask "what is the force from the weight at this angle" What weight? What angle? Force on what by what? The pivot is not at the center. Is the line connecting the two masses to be considered weightless?

REPLY:

Do not want equalibriam, I want to know what the downward force is under the 78 grams as if I had a scale under it. What I calculate is not what the value I physically measured. The angle is 90 degrees, parallel to earths gravity. Consider the pivot point is at the centre of the 2 weights. (Not the way you drew it. I will use the numbers on your figure.) The Force is from the heavier weight 78 gms. (No it isn't. Yes, the 78 gm weight does exert a downward force on the line equal to its weight, but that force is not what your scale will read.) The line connected to the 2 weights is neglectable; I have calculated the line and know has very little affect on the system.

ANSWER:
You can't have it both ways. If you put a scale under it, the scale holds it in equilibrium and is therefore another force on the seesaw. If you simply have it as you have drawn it at rest and let it go it will have an angular acceleration (even though it is at rest at that instant); it is therefore a little trickier to calculate.I will show each way:

Equilibrium (with scale)

The net torque must be zero: 9.7x24+10.7x(F-78)=0, so F=(834.6-232.8)/10.7=56.2 grams
Nonequlibrium (free to rotate)

This is a little trickier so I will switch to SI units (kg, m, s) shown in green; N is Newtons (kg�m/s²). There is a net torque about your pivot which is τ=0.76x0.27-0.24x0.25=0.145 N�m. Note that I have chosen clockwise to be positive. A torque causes an angular acceleration α=τ/I where I is the moment of inertia about the axis about which τ is calculated. Since the moment of inertia of a point mass m a distance r from the axis is mr², the moment of inertia is I=0.0245x0.25²+0.0775x0.27²=0.0072 kg�m² so α=20.2 s^-2. The linear acceleration is a=rα=0.27x20.2=5.5 m/s2, about half gravitational acceleration. Now, you are interested in the forces on your 78 gram mass. There are two forces, the weight of 0.76 N pointing down and the force F which the bar exerts up; Using Newton's second law, 0.76 -F=0.0775x5.5=0.33 N=33.7 gram (force). If there were a massless scale attached to the bat, this is what it would read at the instant you released it.

QUESTION:
If photons of light are massless (without mass) why are they constrained from escaping a black hole's intense gravity?

ANSWER:
In classical physics an object which is in a gravitational field is affected only if it has mass. But, general relativity tells us that massless particles do indeed see gravitational fields. Very massive stars and galaxies bend the paths of passing photons; this is called gravitational lensing and was first observed more than 100 years ago. Now, think of throwing a ball straight up giving it an initial energy of �mv²; because of gravity it loses its energy as it goes up and, at some height it will have lost all its kinetic energy. Now, consider a photon in a very strong gravitational field. As the photon moves away from the object causing this field (black hole, for example), it loses energy just like the ball did. But, unlike the ball, it cannot lose energy by slowing down because the speed of light must always be a constant c. The energy of a photon is given by E=hf where f is the frequency of the light and h is Planck's constant. Since we can write f=c/λ where λ is the wavelength, so the photon loses energy by increasing its wavelength. (This is called the gravitational red shift.) So now, if the field is strong enough the photon will lose all its energy and simply be gone. But its energy is not gone and contributes to the growth of the mass of the black hole.

QUESTION:
Consider sitting in an airliner traveling between cities. If a parakeet is free inside the plane and lets go of, lets say, the seat, and wants to simply fly inside the plane�will the parakeet have to begin flying faster and faster to remain inside the aircraft unattached? What happens?

ANSWER:
The bird flies relative to the air inside the airplane. The inside air is at rest relative to the airplane. The airplane is not accelerating. Therefore it maies no difference whether the airplane is going 600 milea per hour or sitting at rest at the airport; the way that the bird flies is identical in both situations.

QUESTION:
I'm thinking electromagnetic waves and their propagation, and I'm having trouble seeing how energy is transferred. In the analogy with a string, I know that there is a tension on the string enabled by the bonds between the atoms of the string. I know how energy can be stored and transferred through these bond interactions. Back in the electromagnetic field, what is it about the field in one point of space that allows it to transfer energy to the next point in space? Referring to the analogy, what is the analog for tension or atomic bonds in the electromagnetic field? I feel certain that what I'm asking for is either a facet of the speed of light, or perhaps vacuum permittivity, but I'm having a difficult time fitting those concepts into my understanding.

ANSWER:
Think about the electric field at some point where the light is passing by. It is capable of exerting a force on a charge which might be there. The charge will acquire kinetic energy as it is accelerated by the field. Therefore the light must carry energy. Another way to look at it is that light may be thought of as photons which have energy which they can transfer to something else.

QUESTION:
I am a tennis pro, and have been a tennis stringer for over 40yrs. I always have had the idea that Sound (Musical Notes) maybe more accurate then the pull weight measured by the pound or kilo, on a stringing machine, when stringing a racquet. Is this feasible? I have strung a racquet by using a guitar tuner to insure every string plucked when pulled, hits the same note and then clamped. Am I way off base and the physics/math of weight vs sound, behind this is wrong?

ANSWER:
The frequency f ("musicsl note") of a vibrating string depends on three things: the tension T in the string, its length L, aad its mass density μ. Mass density might be measured as ounces per inch which depends on the string you chose. The equation is f=[√(T/μ)]/(2L). From all that I read, the strings should all have the same tension. But the strings are not all the same length, so they would not have the same frequency (note). So yes, you are "way off base"!

QUESTION:
Can increase in pressure inside a hollow semi circular sphere or a paraboloid or other half cut closed figure cause it to produce lift?

ANSWER:
No. Why would you think that? There is one way it could happen, but only with a decrease of the pressure of the air inside the container: If the weight of the container and the air in it were smaller than an equal volume of the air outside (normal atmospheric pressure); this is just Archimedes' principle. The reason a helium balloon rises is because its weight is less than the weight of air which it displaces.

QUESTION:
I have a question about time. Time on earth moves at one rate. Satellites in orbit operate in a slightly different time and have to be updated to maintain accuracy. If I travelled to Mars to live what would be the time difference between the people on earth and the people on Mars? Would people age differently on the different planet.

ANSWER:
The difference between rates of clocks on Mars and clocks on earth would be negligibly different. Satellites, particularly those used by GPS, need extraordinarly accurate time synchronism because the sighals (EM waves) it deals with are moving so fast that a tiny error in time could give rise to a large error in distance.

QUESTION:
THE MOTION OF THE STARS AND PLANETS IS A PUSH AND PULL OF ENERGIES. THE STARS GREAT GRAVITY KEEPS THE PLANETS IN ORBIT AROUND THEM. MY QUESTION IS ABOUT THE TWO FORCES THAT EITHER KEEP THE PLANETS TRAPPED IN THE STARS GRAVITY WELL OR ALLOW THEM AS IN AN EXPANDING UNIVERSE TO OOPOSE THAT GRAVITY BY THEIR "CENTRIFICAL" FORCE AND EITHER ESCAPE THE STARS GRAVITY OR SUCCOMB TO IT AND EVENTUALLY HAVE THEIR ORBITS DECAY GIVEN THAT THE LIFE OF THE STAR IS LONG ENOUGH? HYPOTHETICALLY DO NOT ALL PLANETS ORBITS DECAY AND SUCCOMB TO THIS? IF NOT, WHAT FORCE KEEPS THE PLANETS IN THEIR ORBITS OTHER THAN THEIR ELLIPSES, THE CONSTANT INWARD THEN OUTWARD DISTANCE FROM THE STAR, WHAT FORCE ACTS ON THE PLANET KEEPING THEM FROM EVENTUALLY GOING TO THE SUN?

ANSWER:
It seems as if you have not studied physics much; that's ok, I can give you an overview and point you in the right direction for further study on your part. We must first ask what forces act on planets. There is no such thing as a centrifugal force, it is what is called a fictitious force because it is simply something we make up in certain circumstances where Newton's laws do not work. Perhaps you are thinking of the accelerating universe expansion caused by "dark energy" when you refer "EXPANDING UNIVERSE�'CENTRIFICAL' FORCE." That is unmeasurably small. Therefore, there is no "PUSH AND PULL" tug of war going on, it is only pull, i.e. gravity. The problem you are wrestling with, understanding planetary morion and generally called the Kepler problem, was solved about 350 years ago by Isaac Newton. Essentially what he found is that any body moving around a much heavier body moves in a stable periodic orbit (does not decay and does not change its shape), not "EVENTUALLY GOING TO THE SUN". I urge you do learn about Kepler's laws and the solution of the Kepler problem.

QUESTION:
I am a medical student currently studying the cardiovascular system and I am having difficulty in understanding how a pressure drop is created inside blood vessels. My question is: in a laminar constant flow where the pipe contains a viscous liquid what creates the pressure drop along the pipe between point A and point B assuming they are on the same level? In other words, how does friction lower the pressure? Does it decrease the rate of collisions between the liquid molecules? If yes, how does it do that? If no, is there another parameter that contributes to pressure apart from the rate of collisions?

ANSWER:
I presume that you are familiar with Poiseuille�s law,

R=ΔP�4πr⁴/(8ηL),

where a fluid with viscosity η is flowing through a tube (artery?) of length L and radius r, R is the rate of fluid flow, ΔP is the pressure drop over L. Now, I see a real problem with your question: you state that there is a pressure drop "created" and you try to understand this microscopically. Since we are talking about cardio, let's just say that, if the blood if moving, something has to be pushing it. Let's go back to the heart; the heart is a pump and muscles in this amazing pump are exerting a force on the artery we are looking at. The force is distributed over the whole area of the artery so there is a pressure at that end. After the blood has moved a certain distance L we will find a lower pressure; why? Because the viscosity is just friction and exerts a backward force over the whole volume. If it were an ideal fluid with no viscosity, the pressure would be the same on either end. Now I have sketched a cartoon of what is happening: There is some force (left red vector) which is pushing the fluid ahead of it and, some distance down the pipe, there would necessarily be an analogous force (right red vector) pushing the fluid in front of it (if viscosity were zero). But, because there is viscosity, there is a drag force which lessens the pushing force as you move along the fluid flow; I have represented this by the center red vector as the net effect on the pushing force across this length of pipe. Adding this net drag force to the right red vector results in the right-pointing green vector which means the pressure on the right end must be smaller than on the left. We normally think of friction as slowing something down, but because we assume this to be an incompressible fluid, this is not possible for a fluid. When I am presented with an equation, in this case Poiseuille�s law, I like to ask if it makes sense. Assuming that I change one variable while holding the others constant:

If you increase viscosity, flow rate decreases�honey flows more slowly than water;
if you increase the length the rate decrease or the pressure drop increases;
if you increase the radius of the pipe, the flow rate increases or the pressure drop decreases.

This all makes sense.

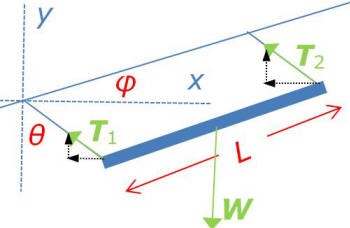
QUESTION:
If a rigid rod is suspended at its ends from 2 strings of equal length but hung at a slope (approx. 15-degrees from horizontal), will the strings hang vertically (plumb) or at an angle?

ANSWER:
I assume that you will have the strings attached to the slope a distance L apart (see the diagram); if they weren't, it would not be possible for them to be plumb. Now, we want to find when the rod will be in equilibrium. That means that the sum of all forces on the rod must add to zero (Newton's first law). So I have drawn the diagram showing the strings making an angle θ with the vertical (y), and the angle the slope makes with the horizontal (x) is φ. There are just three forces, the weight W, the tensions of the strings on the rod T₁ and T₂; also I have shown the horizontal and vertical components of the tensions (black). I assume that the rod has uniform mass distribution so that the weight acts at the center of the rod. If the tensions were big enough, the rod could be in equilibrium in the vertical direction because the weight is down and the vertical tension components are up. But in the horizontal direction the only forces are the x components of the tensions and they both point in the negative x direction; therefore it cannot be in equilibrium. So we conclude that the strings must be plumb (θ=0). We can also conclude that the tensions must be equal be equal because there must be no net torque on the rod. Also, T=W/2 to satisfy translational equilibrium.

QUESTION:
When making a large roll of paper, does the surface temperature of the roll change as its wound up. Does it change as it is unwound (rate of paper coming off roll is constant, so core of roll spins faster as roll gets smaller. I always wanted to know the physics behind this when printing newspapers for 25 years! ~Shawn (The Boston Globe)

ANSWER:
The paper should certainly heat up. The reason is that friction is present. Imagine taking a sheet of paper and hanging it from one edge (#0 in the figure) You now pull it out to position #1 and release it. Gravity will pull it back and, perhaps it will swing down like a pendulum. It will either swing back to #0 or even keep moving until it gets to #2; but it certainly will not go as far to the right as it was dropped from. Similarly when it swings back to the left again to #3 it will not go as far as it did to #2. Eventually it will stop at #0 again. To start this pendulum you needed to do work, so you endowed the paper with some energy. But, after all was said and done, the energy you gave it is gone. Imagine this happening inside a large sealed box so we can think of our paper pendulum as an isolated system; then one of the most important laws of physics is conservation of energy, the total energy of an isolated system never changes, should apply. So where did the energy you added go? Heat! The paper and the air in the box will become slightly heated. There are two main ways that friction works. Probably the most important one is the air drag slowing it down as it moves through the air; but this does not seem like it would be important for paper going onto or off of the roll since in that case the motion is not perpendicular to the surface, rather the motion slices through the air. The other way is that the paper is not perfectly elastic, some of the energy you put in is lost just by bending the paper which would heat it; think of a thin sheet of a soft metal which, if you bend it back and forth a few times, you can feel that it is getting hotter. So, if you were pump all the air out of the box, it would still stop swinging eventually but probably quite a bit more slowly.

QUESTION:
If two objects are moving away from each other at half the speed of light, then are they each travelling at the speed of light relative to each other? And is that possible?

ANSWER:
No that is not possible because velocities do not add the way you expect them to if the speeds are large. In your world, if two cars are moving with speeds u and v in opposite directions, you would say that v'=u+v where v' is the speed which v is going relative to u; this is called Galilean relativity. But for objects moving with speeds comparable with c, the speed of light, the correct expression is v'=(u+v)/[1+(uv/c²)]. In your question, u=v=0.5c and you will find that v'=0.8c. See an earlier answer. Note that, if the speeds of the objects are much smaller than c, uv/c²≈0 and you get the familiar answer.

QUESTION:
How are the mass of the moon and earth related to the moons orbit?

ANSWER:
I will only give the results for circular orbits. In general, the period T of the orbit is T=2π√[R³/(G(M+m)] where M and m are the masses of the earth and moon, respectively, G=6.67x10^-11�m³�kg⁻¹�s⁻² is the gravitational constant, and R is the radius of the orbit. If m<<M, this may be approximated as T=2π√[R³/(GM)]; this is Kepler's third law, the square of the period of a circular orbit is proportional to the cube of its radius T²∝R³.

QUESTION:
This one has been bordering me for over 2 decades : What would be the reading on a spring balance if 2 equal in magnitude but opposite forces are applying on it ?

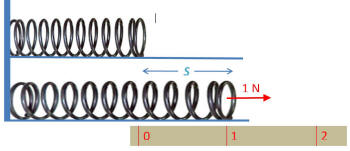
ANSWER:
If we are going to use a spring balance, let's first calibrate it. Take a spring, lay it on a table, and attach it to the wall as shown on the figure. Next, exert many forces on the end to stretch it and mark on a scale the forces corresponding to what you have pulled with. Since we assume that this is an ideal spring the distance it is pulled (S) is proportional to the force exerted The proportionality constant, usually denoted as k, is called the spring constant: F=ks. For example, if S=10 cm in my figure, k=1/0.1=10 N/m. So I have taylored my example to your question and the scale at this stretch tells us that you are pulling to the right with a force of 1 N. Note that the spring is in equilibrium because it is at rest, so Newton's first law must apply (the sum of all the forces must equal zero). Vertical forces are the spring's weight down and the force upward of the table which must be equal to each other in magnitude. Wait a minute! Is there anything other than you which might be exerting a horizontal force on the spring? Of course, since the spring is attached to the wall, it must exert a force of magnitude 1 N to the left. That is what you asked about.

QUESTION:
Is there a similar doppler-like shift in sound frequency if the sound source and receiver are stationary relative to each other but the air is moving at high speed across both. A rocket team I am mentoring is doing this experiment on their rocket with a buzzer and microphones above and below the buzzer, then recording the frequency of the buzzer during flight.

ANSWER:
This is no different from the source and observer both moving with the same velocity through still air for which there is no Doppler shift.

QUESTION:
I am writing a sci-fi novel and have a question related to the physics of astronomical bodies. I know quite a bit of physics but wanted to double check something. I wanted to know if a "cracked" moon would retain a gravitational pull? Now by "cracked", imagine the planet (moon in this case, orbiting a gas giant)in its past was "destroyed" by a super weapon that fractured its hemispheres apart. I figure if the hhemispheres were still close enough they would rejoin into a sphere... but I like the aesthetic of a ruined world. Also this is a moon orbiting a gas giant so I figure some parts would be flung out due to the forces. So could this body still hold a gravitational pull (even if weak) in the broken state?

ANSWER:
Strange that you are talking about a "moon", since that usually means something orbiting a planet; smaller things orbiting the star are ususally called asteroids or dwarf planets; I will assume that this halved object is not orbiting some other larger object, just the gas giant. When the "super weapon" broke up your moon it was probably a very violent event where each half would have gone flying away with likely enough speed to escape each other. In that case they would just end up in a new orbit around the star and interact only slightly with each other. Another possibility is that the two would end up in orbit around their center of mass and the center of mass would orbit around the star the same way the whole moon did before its destruction. I find that the second scenario would be unlikely because they would have flown directly away from each other and, if they are not going fast enough to escape from each other, they will eventually come back and crash into each other. The crash would not be gentle and would not result in the original sphere simply returning. Now, to your question. There is nothing magic about a sphere and if you have two hemispheres each of them would have a gravitational field half the strength of the two of them. Any object, regardless of its shape, has a gravitational field. Near a nonspherical object the strength of the field depends on where, precisely, where you measure it; but if you look at the field far away from it the field will be very close to that of the whole sphere. The force F on a point (or spherical) mass m due to another (point or spherical) mass M a distance R away is given by F=MmG/R².

QUESTION:
A common golf practice putting aid consists of a 9-foot green mat that rises 5 inches in the final 1 foot, to a standard sized golf hole. Balls putted to the hole from any distance away that reach the lip of the hole but do not go in, will roll back down the small hill and return to a point well beyond the starting point of the putt, often rolling beyond the 9-foot length of the mat. Thinking of the conservation of mass and energy, can you explain how the ball can return to a point beyond its point of origin? It seems like it would need more energy on the return trip than was imparted upon the ball initially in order to do this.

ANSWER:
You are forgetting that the ball begins its journey with considerable kinetic energy. So it would have to lose quite a lot of energy to friction to not get beyond the starting point. If it lost no energy to friction it would be moving with the same speed you hit it with when it got back to the same place it started.

I'm a little disturbed by your reference to "�the conservation of mass and energy�" because there is no such thing as conservation of mass, mass being a form of energy. You should just think of conservation of energy. Many times in physics the mass of a system increases or decreases or disappears altogether.

QUESTION:
What does it mean that a black hole rips time? Does time stop or not work or changes in a black hole?

ANSWER:
Because of time dilation, the closer something gets to the black hole, the more slowly time runs. At the event horizon, inside of which nothing, even light, can escape, time stops. So, from the perspective of someone outside the black hole watching something falling into the black hole, it simply stops. However, we certainly know that it does continue into the black hole. Nobody, I believe, knows what the laws of physics inside the the event horizon and what time does. Of course, since nothing can get out of a black hole, we can never do a direct measurement of what is going on inside. So hypotheses can be tested using only indirect evidence.

I will remind you that, as stated on the site, I normally do not do astronomy/astrophysics/cosmology. I would urge you to find an astronomy site which will answer your question (again a couple of recommendations on the site).

QUESTION:
I was watching videos on some strange properties of mercury, and its ability to generate electromagnetic fields(EMF) when having electricity applied to it. I was wondering if EMF's have any effect, or reaction with gravity? For example, if a car was hypothetically inside a EMF stronger than the one it is in on earth, then would that cause the car to be less effected by the earth's gravity? My hypothesis is if an object is inside a considerably stronger EMF than its surrounding environment, then that object behaves as if gravity is like water to a HydroFin. If you could clarify the relation between gravity and EMF's, and tell me if my hypothesis holds any water I would greatly appreciate it

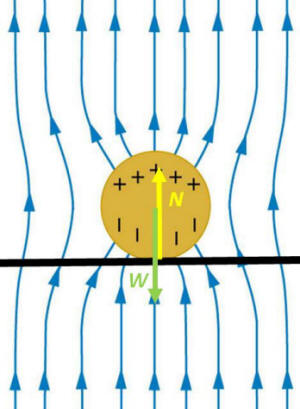
ANSWER:
Your question is very confusing.

First, it is usual notation in physics that EMF is an acronym for electromagnetic force, not field; this itself is an anachronism because it is a voltage (potential difference), not a force!
Secondly, "�having electricity applied to it�" is ambiguous; I will take that to mean that a current is caused to flow through it. Interestingly, it does not appear that you ever talk about this again
Third, electromagnetic field is broad and not fully specified, so I shall assume you mean an electric field.
Fourth, your entire sentence "My hypothesis is�HyfroFin." makes no sense, so I will ignore it.

The crux of what your question is, as I see it, the sentence "For example�gravity." What you want to know is, essentially, if you put a car into a strong electric field, will it be "less effected by�gravity?" I will use a conducting sphere to represent your car because that will still convey the same ideas but allow me to draw an easy to understand figure. First, ignore the blue lines; there is no electric field yet. Your car sits on the road (black line) and is not moving. The earth exerts a force (green arrow) W down on your car and is called the weight. The car is in equilibrium because the road exerts an upward force (yellow arrow) N on the car which is of the same magnitude as the weight; N is what you would measure if the car were sitting on a scale. You can't change the weight but you could exert another upward force on the car which would make it seem to have less weight because N would get smaller. So you want to exert an additional upward force by putting it in a strong electric field. I will put it in a uniform electric field. (A uniform field is one which has the same strength everywhere and points in the same direction everywhere; if your car weren't there all the blue arrows would be parallel and equally spaced.) Now, what happens to the car when you turn on the field? Because it is made of metal which is a conductor, electrons in the car experience a force opposite the field direction and positive charges are left behind where the electrons migrated from . This charge distribution on the surface of the car now creates an electric field of its own and the blue arrows in the figure are the vector sum of the original uniform field and the field created by the car. The positive charges on the top of the car experience a force upward but the negative charges on the bottom experience a force downward and so the net result of adding the electric field is zero. So your hypothesis that the field will counter the gravity is not correct.

QUESTION:
Hi, i am an out of school adult, electronics engineer, good understanding of phisics, however my question: We know like charged objects repel, we can determine how strong the repelingness is, however HOW IS THE MOTIVE FORCE IMPARTED TO MOVE THE OBJECTS APPART? THERE IS A COMMUNICATION A 'FIELD' WHAT IS THE REPELINGNESS CONSTRUCTED OF AND HOW DOES IT WORK?

ANSWER:
Classical electricity and magnetism (E&M) is an empirical field theory, based on experiments. A simpler field theory is Newtonian gravity; here we find that any two masses will attract each other. We imagine that masses are the source of gravitational fields but also masses feel gravitational fields. If one mass m is near another mass M, it feels a force at all places around it, a vector, so the force field is essentially a vector specification for every point in space, a "continuous table" which can be expressed as a function; for example, if the masses are point masses, the force M exerts on m is F_Mm=u₀Mmk/r²where u₀ is a dimensionless vector of magnitude u₀=1 which points from m to M, and r is the distance between the masses, and k is just some constant; similarly, the force m exerts on M is F_mM=-u₀Mmk/r²; you probably know this Newton' universal law of gravitation. But we want something which is more general than specific to a particular situation. So, if we divide out m for example, F_Mm/m=u₀Mmk/r²≡G_M; this is called the gravitational field due to M and may be thought of as the way that M alters the space around it and also lets you know the force any point mass nearby feels due to its presence.

So now you have had your tutorial in fields and we can move on to talk about E&M. The electric field is pretty much the same as the gravitational field except the masses are replaced by electric charges and k is obviously not the same (I will call it k'), E_Q=u₀Qk'/r² for point charges. A big difference from gravitational theory is that while there is only one kind of mass, there are two kinds of charge, so the possibility of repulsive as well as attractive forces exists. As you no doubt know, opposites attract, sames repel.

So far I haven't probably told you anything you didn't already know. I surmise, from the capitalization you have used, that you don't want to know about the field but what is actually happening that you can get your teeth into. It turns out that force fields can be quantized, which in the case of E&M, means that electric waves (light, radio, etc.) may be thought of as streams of tiny "pieces" of the wave called photons; for a particular frequency wave all photons have the same energy. If you now fully flesh out E&M into the quantized field theory (quantum electrodynamics, QED), photons may be interpreted as the "messengers" of the field. Think of an electric charge as being surrounded by photons, the density of which gets smaller as you get farther away. A nearby charge, with its own "cloud" of photons, interacts with the other charge via these photons; there is your mechanism you seek! The complete theory of E&M, including QED, is generally considered the most complete theory we have in physics. Also, you can't directly observe this photon cloud because the photons are called "virtual", popping into and out of existence. Incidentally, nobody has been successful in quantizing the gravitational field, but if it were the "field messenger" analogous to the photon for E&M would be called the graviton.

QUESTION:
Equivalence principle. I understand that if I'm in an elevator in deep space and it starts accelerating upwards at 9.8 m/s^2, if I drop a ball I would see it move to the floor the same as it would on Earth. If the elevator continues to accelerate and I drop the ball again I would see the ball move to the floor but in a much shorter period of time and so this wouldn't match what happens on Earth. Does this mean the equivalence principle only applies to that initial period when the elevator starts accelerating?

ANSWER:
The equivalence principle states that you cannot tell whether you are in a frame accelerating relative to an inertial frame or in an inertial frame with a gravitational field. The principle does not depend at all on what the current speed of the accelerating frame is, only its acceleration. So, for example, if you have an acceleration of 29 m/s², no experiment you perform will be different than if you were in a gravitational field with g=29 m/s²; even if you have a speed of a million miles per hour, your acceleration is not changing.

QUESTION:
The Wright brothers invented controlled flight. In the years since, we have gone from a fabric covered frame to synthetics and carbon composites and the exploration of space. Einstein and others came up with the physics that developed atomic energy, both bad and good. Since the mid 1940's what has physics come up with, a material, process, better mouse trap, that has made life better? Are not all these creations in technology the results of garage experiment, engineers, both mechanical and chemical, and inventors looking for a better way? What have physicists been doing for the last 80 years, other than smashing things together in accelerators to make pretty pictures?

ANSWER:
Wow, you seem to have quite an axe to grind! First, let me address the "philosophical" issue. One of the things which makes us human is that we are curious, always seeking better understanding of our world, in fact the whole universe. Even though new discoveries, to people like you, seem pointless because they seem to have no application you can use in your everyday life, they often pan out in the end. So I will enumerate just a few examples

So, one of the most important components of modern technology was created by physicists. Can you imagine modern life without transisters? Sure, engineers collaborated after the discovery by miniturizing but without physics your mobile phone would be absolutely impossible.
How about lasers? Guess who you can thank for lasers�that's right physicists. They are everywhere, scanners in grocery stores, the little clip-on-your-finger blood oxygen sensors, surveyers instruments, etc.
Had a CT scan or MRI lately? Physicists invented them.
Computers? When I was in college I had a summer job in the company where research and development for making components for nuclear submarines was done. They had a computer in a room with an area of probably about 10 yards by 30 yards made using vacuum tubes; it had far less computing power than the iPhone I have in my pocket. Who first built computers? Need I really ask?

I hope you get the idea.

ADDED THOUGHT:
By the way, fundamental "discoveries" are never found by inventors' garage experiments any more. These "discoveries" are extensions of what is already known�a better mouse trap but not the fundamental idea of a mouse trap.

QUESTION:
In nuclear physics we talk about bombardment of a nucleus with neutrons. Can the same be done with protons? A neutron can decay into an proton (after in average 9 minutes). At the moment of this change, a "travelling neutron" might change into a proton before it hits the nucleus. What happens then?

ANSWER:
Protons are much easier to use to study nuclear structure than neutrons. Because protons have electric charge they can be accelerated and steered using magnitic and electric fields. Neutrons have no charge and therefore you need to get them from nuclear decay or from reactions of other particles with nuclei, for example bombarding a nucleus with protons and look for neutrons coming out. Protons are much easier than neutrons to detect making protons (or other charged particles) more useful for experiments. Regarding your second question, if a neutron decays before interacting with the target, it makes no difference since it is neutrons which the experiment is designed to observe and unwanted protons would be very small compared to the flux of neutrons.

QUESTION:
If time slows as we approach the speed of light, and stops at the speed of light. And photons are particles of light, then surely from the photon�s perspective, they are all still inside the Big Bang. They have not started expanding with the universe, which is travelling slower than the speed of light. Because photons only travel at the speed of light. Which implies that all photons we interact with, are still connected together inside the Big Bang. Does this not explain some of the mysteries of quantum physics we are trying to solve?

ANSWER:
Photons do not have a "perspective". It is pointless to talk about how things look from a photon because, being a stable particle, it has nothing "aboard". You can read about this issue in an earlier answer.

QUESTION:
I have a pot I bought from Goodwill. One of those gorgeous well balanced copper bottom pots. When I got it home and I put it on my electric stove top and boil water, for example, that the pot shakes and shakes and shakes while it�s preparing to boil and boiling water. Turns out the pot has kind of a point in the center of it so It�s not a flat bottom pot. Heres my question. I�ve always wanted to know is why the heat from my electric stove top makes my pot shaken, shake shake. If I did not watch the pot, it would possibly fall off the stove top because the hotter the element is the more it shakes and jiggles. Why does it do this to my pot of water?

ANSWER:
You must have one of those glass surface ranges. So the pot never has its whole bottom on the surface. If it were sitting with its center of gravity exactly above the "point" it would be called unstable equilibrium. The tiniest bit off and it is not any longer in equlibrium and it topples over until something stops it, in your case the bottom edge of your pan hits the stove top. (Think about trying to balance a pencil on its point.) But it is still very close to equilibrium so it takes a very small force to cause it to rock back toward equilibrium but, again, it won't stay there and will drop to some other point on the bottom edge, etc., etc. Heating up something very hot causes all sorts of things to happen�the metal expands and warps a tiny bit more in one place or another causing the position of the center of gravity to move around; as the water heats it convects around or starts bubbling up in one place and not another; as the pot rocks, the water sloshes around a little. All these things keep changing and causing the pot to shake around

QUESTION:
I have a question about gravitational waves. What happens to a gravitational wave if it encounters a massive object? If a gravitational wave, created, perhaps, by two black holes colliding with each other, reaches some massive object and passes through it, does this cause the object to move? And if it does move, does it, in turn, create further gravitational waves? Does it strengthen the original wave such that it lasts longer? I guess another way of putting it is, would a gravitational wave from two colliding black holes be more or less likely to reach the earth if it passed through other planets on the way? I assume the effect would be very small, but would there be any effect at all?

ANSWER:
I normally do not answer questions on astronomy/astrophysics/cosmology as stated on the site. But, I will take a stab at this one. I think we can assume that the superposition principle applies to gravitational waves, so any gravitational waves passing the same point in space would simply add. It has taken many decades of many physicists trying for gravitational waves to be actually observed. And, if any mass accelerates it will create gravitational waves. So let's consider Jupiter, a quite large mass which is accelerating constantly because of its orbital motion. The gravitational waves predicted are undetectably small. It takes a catastrophic event like the merging of two black holes to make detectable waves. Even though they are large distances from us, we still can detect them although their intensity decreases quadratically with the distance they have traveled. These waves are enormously bigger than any they might encounter, so the addition of others makes no detectable difference.

QUESTION:
What would happen if fermions had no spin? Would this violate the Pauli exclusion principle?

ANSWER:
They would not be fermions would they? Then the Pauli exclusion principle would not apply to them. And, atoms could not exist, nuclei could not exist, stars could not exist—our universe as we know it could not exist.

QUESTION:
If I look at the polar plot of the Klein-Nishina differential cross section with respect to solid angle for Compton scattering, it appears that for high-energy photons, forward scattering dominates. That is, the scattering angles are near zero, and the energy transfer to the electron is low. But then I look at the differential cross section for recoil electrons with respect to their energy vs. recoil energy and I see that the most highest probability for scattering an electron into a particular energy occurs at the Compton edge (i.e. a photon-scattering angle of ~ 180 deg). These two things seem contrary to one another. Clearly I am missing some basic concept.

ANSWER:
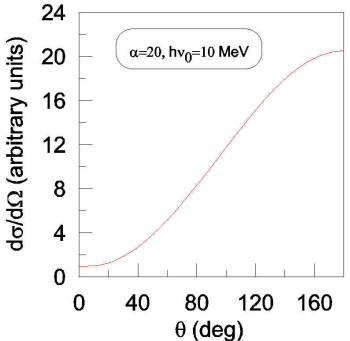You should read the details of this issue in the discussion on Physics Forums. I urge you to download the book (Evans) referred to in the Physics Forums discussion. I will use results from the book and discussion to give you my "quick and dirty" explanation of the energy dependence of dσ/dT where T is the electron kinetic energy. Suppose that the angle which the electron recoils is φ then the differential cross section is dσ/dΩ' where dΩ'=2πsinφdφ. (Note that Evans notates the cross section as _eσ.) In the book it is shown (eq. 4.5) that (dσ/dφ)=2πsinφ(dσ/dΩ') which is the angular distribution of the differential cross section. Now, cleverly, the chain rule is applied (eq. 5.1): dσ/dφ=(dσ/dT)(dT/dφ). Finally one can show (eq 5.2) that

dσ/dT=(dσ/dΩ)[2π/(α²m₀c²]{[(1+α)²-α²cos²φ]/[(1+α)²-α)(2+α))cos²φ]}².

Here α=hν₀/m₀c² where hν₀ is the energy of the incident photon and m₀c² is the rest mass energy of the electron. Be sure to note that (dσ/dΩ) is a function of θ; I have looked up reference D12 of the Evans book and gotten the equation for (dσ/dΩ) and plotted it for hν₀=10 MeV; your intuition was right: the cross section for electrons scattering is largest when the photon scatters to 180�. There will be, at each angle φ, an energy spectrum and that is what [dσ/dT](α,θ,φ) gives you. Now the spectrum you are interested in is the spectrum of all electrons so you integrate over θ and φ. The resulting spectrum you will see cannot be be larger than hν₀ because that is all the energy the photons brings in and, since the photon will not be totally absorbed, the highest energy electrons will be a little less than that. I guess that wasn't so "quick"!

QUESTION:
I am an Indian,I came across a section from my religious scripture that States. "When atoms move to cover space, this is called time, and time is measured according to the amount of space covered by atoms [Srimad Bhagavatam 3.11. 3-4]. It is generally accepted that when time stands still (although impossible), there is no movement of anything. This also confirms that the movement of atoms is time" can you answer the validity of this?

ANSWER:
We know, from the successful theories of special and general relativity, that time and space are not independent things, that they are coupled to each other such that different observers have different observations regarding the values of space and time in their own frames. Your has statement some validity in that it recognizes that time and space are in some way related. The statement that "�the movement of atoms is [my emphasis] time�", however, is vague and its meaning not operationally defined. I have heard some of our best cosmologists state that if only we really understood what time is we would understand the universe much better than we do.

QUESTION:
Recently I've been thinking about alternative explanations to the double-slit experiment and there is one idea that I can't debunk. Accelerating and decelerating electrons creates an electromagnetic field that can later affect the movement of electrons. So is it possible that the double slit experiment doesn't prove electrons are waves but was rather caused by an electromagnetic field that affected the movement of electrons?

ANSWER:
What electrons are you thinking about? So, we arrange the situation so that only one electron per second goes through the slit(s) and there are no other electrons to be affected by the presence of the incident electron (.e.g., make the slits out of an insulating material). You will still find the same double slit diffraction pattern. Further, you will observe only one electron at a time striking the detector screen. I think you should not waste your time trying to disprove wave-particle duality; the number of measurements and experiments which prove it are beyond number.

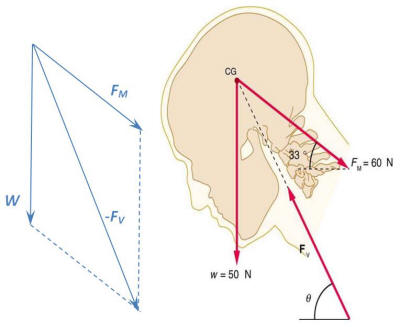
QUESTION:
As a massage therapist, I often see images of a head hanging lower and lower, labeled with the increased weight at each degree of tilt. Now the head only weighs so much and it's hard to believe that a couple vertabrae add all the kilograms. So what is really being said?

ANSWER:
When I first started to research this I was appalled at how badly the analyses were from a physics standpoint. First of all, you, unlike almost anybody, are correct in saying that the head has a weight, period. The weight of something is a force which points toward the center of the earth and is the force which the earth exerts on it. So the fact that 90% of articles say the weight of the head increases as we lean forward is nonsense. I have lifted a generic diagram of what happens when you lean forward. A simplified model of what the forces on your head are its weight W, the force F_M due to a muscle attached to the vertebra behind your head, and a force F_V due to the top vertebra pushing up. Now, the head is in equilibrium so the sum of these three forces must equal zero; another way to say this is that the sum F_M+Wmust equal the negative of F_V which is why I have labeled the sum on the diagram to the left as -F_V.

-F_Vis also the force which the head exerts on the vertebra . This force is what is usually called the weight of the head and is clearly larger than the weight. When you are standing straight up F_M=0 so F_V =-W. Note also that all forces have been assumed to pass throught the center of gravity so that we do not need to think about torques.

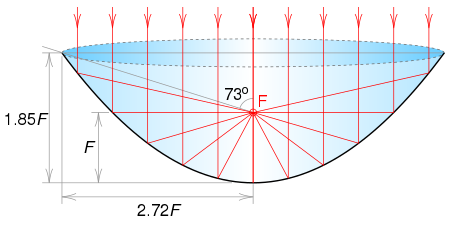
QUESTION:
Would it be possible for someone to construct a funnel or cornucopia shaped object with a polished mirror surface that directed all light incident to any surface to reflect down to a point like a fiber optic cable?

ANSWER:
Probably the closest you could come to doing this is a parabolic mirror which focuses all light from distances much greater than its focal length to a single point. Reflection telescopes are parabolic and have have the advantage over lens telescopes because they have neither chromatic nor spherical aberations.

QUESTION:
If you take a flat piece of black metal, say iron, it is not emitting light/photons at that moment. If anything it could said that it is absorbing them. If you then pass a powerful electrical current through the piece of metal it can then become so bright that you cannot look at it. Is the brightness being seen truly being caused by the sudden release of photons? If so how is the current passing through the iron generating photons?

ANSWER:
Every object is constantly emitting photons. If that object is in thermal equilibrium with its environment, the rate at which it emits energy is equal to the rate at which it absorbs energy. Even if the object is cool, say room temperature or a little above, it emits photons. That is how night-vision goggles work, "seeing" infrared radiation. If you now pass a current through this bar it heats up because of resistive heating (just like your toaster) and it is now hotter than its environment and it emits more photons than it absorbs and, because it is much hotter, it emits photons which are in the visible spectrum, red.

QUESTION:
Hi, is there any work being done on wavelengths/wave forms being helical in structure? The more I look at wavelengths, the more it seems counterintuitive to me that they exist in on a flat plane, and that, surely they must have at least some level of 'spin' or some level of helical movement? I am just wondering if any work has been done in this area, or if it has been 100% proven that they move within a flat plane.

ANSWER:
I commend you for thinking, great intuitive leap! You are absolutely correct, the waves which are first taught in a physics class are what are linearly polarized, or said to have linear polarization. For an electromagnetic wave, a linearly polarized wave always has the electric field perpendicular to the direction the wave is moving and always in a single plane in which the line of travel is entirely contained. In situations where that plane is rotating about the line of travel is when you get the "helical" behavior you have been speculating about; this is called circular polarization. The little animation shows how the electric field (little red arrow) varies; note that the electric field in this polarization has two components which are 90� (� of a wavelength) out of phase with each other. If you want to learn more about polarization, see the Wikepedia article. You ask whether there is "�any work being done�". No, all this has been well understood for about 200 years!

QUESTION:
I have an assignment for my year 11 physics but I accidently made the experiment I conducted for it much harder to understand then it should be. The original prac was simply attatching different coloured paper around 4 beakers and recording the change in temperature in a heat box using heat lamps. This was simple to explain and I did a shorter practise assignment on it. In the experiment we have though we instead decided to change the colour of the water, and heat it up with the sun. We can't retake the prac but I cannot find a formula that works for the expected relationship, neither do I understand what any of it even means.

I was able to get an AI to create a fomula:

ΔT = (P � t) / (M � C � AF) where:

P = solar radiation (1361 W/m2)
t = time (600 seconds or 10 minutes)
m = mass of dyed water (300 g)
C = specific heat capacity of water (4.184 J/g�C)
AF = absorption factor (let's assume it is 0.5)

But this formula doesn't take into consideration the outside temperature, and I don't understand what is actually happening.

ANSWER:
The first thing I want to emphasize is that physics is not formulas. Yes, equations are the way we approach physics problems, but if you think physics is getting a "formula" and plugging numbers into it to get an answer, then you will never really know how to understand nature. Let's take a look at the formula which the AI gave you. Does it make sense? What causes the temperature to change? Some of the light entering the beakers is absorbed which means that the energy heats up the water. So the more light which is absorbed (large absorption factor) the more the temperature will change; but the A-not-so-brilliant-I has put AF in the denominator which means large AF results in small ΔT, blatantly wrong! Also an exercise worth doing when determining whether an equation is possibly correct is to do a dimensional analysis�are the dimensions the same on each side of the equation? I will do this analysis in terms of units rather than dimensions which makes it easier here. Left side of the equation has units of temperature (K); K is for Kelvin, the unit for temperature in SI units. Look at the right side: P has W/m²=(J/s)/m², t has units of seconds (s), M is kg, C is J/(kg�K), AF is m^-1. Putting them all together, [(J/s)(s)/(m²)]/[(kg)(J/(kg�K)(m^-1)]=K/m; so the equation is almost dimensionally correct. The culprit here is the AF; perhaps your AI bot did not use the usual definition of absorption fraction, maybe simply the fraction not getting through (i.e. 50% if AF=0.5), but to put it in the denominator still is wrong because this would say that twice as much energy is absorbed as comes in! But now I think I see the problem. If we take AF to be a fraction or percentage, the dimensions of the right side are now K/m², still different from the left (K). I think that AF should be changed to A times F where A is the area the light is shining on and F is the fraction of the light energy absorbed and both A and F should be moved to the numerator:

ΔT=P�t�F�A/(M�C)

and this will be dimensionally correct. The outside temperature does not enter because we assume that the water is at that temperature to start and all we care about is the change in temperature. Also, I have used Kelvin temperatures but all we want is change in T and ΔT is the same for �C and K. Let me try to see if this gives anything at all like we would expect just guessing A and F:

P=1361 W/m²

t=300 s

F=0.5

M=0.3 kg

A=100 cm²x(1 m/100 cm)²=10^-2 m²

C=(4.184 J/g�C)x(1000 g�K/1 kg)=4.184x10³ J/kg�K

I find ΔT=1.63 �C which seems reasonable.

But, what does your assignment ask for? It asks only what the temperature is after 10 minutes, it does not ask you to have an equation. But I hope that you have learned something about how you should approach understanding the meaning of an equation. I had to spend quite a bit of time on your question because you started me with an equation where there were some clear errors and also a serious misunderstanding of what you had (AF rather than A�F). I hope that you now "�understand what is actually happening�".

QUESTION:
I just went bowling and was able to roll a 14 Pound ball at 23.36MPH. I was just wondering how many pounds of force was needed to reach that speed? I threw out my back and arm in the process but it was totally worth it.

ANSWER:
If you had bothered to look in the faq page you would not have to ask this question. And, how in the world did you ascertain the speed so accurately? The answer is that it is impossible to answer this question because there is not enough information. As one quick example, suppose we view you pushing on the ball with a force F₁ for 0.1 seconds; it would require a force of approximately F₁=148 lb to achieve the ball's speed of 23.36 mph. Now, if you instead push for 0.2 seconds, it would require a force of approximately F₂=74 lb to achieve the ball's speed. Two different forces would result in the same speed! If you want to have more detail, go to the faq page and follow the link there.

QUESTION:
Hello, I am a motorcycle rider and an argument that comes up repeatedly in the community is regarding the effects of sheer winds pushing a motorcycle to the left or right. Obviously, wind pushes a motorcycle,but the issue in questions is whether solid wheels like that on a Harley Fatboy "catch" more wind than that of a wheel with spokes. I've always been of the understanding that a spoked wheel spinning at the same rpm's would essentially be the same as a solid wheel and there is no real difference to the rider on the motorcycle. Are you able to explain this and which is correct?

ANSWER:
I feel quite certain that the force of a cross wind on a solid wheel would be larger than on a spoked wheel, spinning or not; for a wind to exert a force on something the wind must push on it and, whether the wheel is spinning or not, it has a much smaller area for the wind to actually hit. There is a fair amount of research which has been done on bicycles rather than motorcycles, but the emphasis seems to be mainly on the effect on drag forces along the direction of the velocity rather than laterally. I think that strong opinions are based on perception of the rider who has ridden cycles with both kinds of wheels and perceives no difference. For example, a rider is likely to think that the two wheel contributions are the same because the force of a cross wind on the rider and the rest of the cycle (red arrow in figure) is probably much larger than the difference between spoked and solid wheels, making any difference difficult to feel. Similarly, the force tending to tip the cycle over (as opposed to the tendency to push it laterally) is relatively smaller for the wheels (green arrows) than for the rider and the rest of the cycle (red arrow) because, the red arrow is much higher off the ground and much larger than the green arrows and therefore exerts a much larger tipping torque.; again this lessens the ability to percieve a difference in the two types of wheels.

QUESTION:
I cannot find the answer to this question anywhere. Consider 1kg rock traveling through space at a constant velocity. It has a constant amount of kinetic energy. If it comes near a large planet and gets caught in its gravitational field, and eventually hits the surface of the planet, its velocity will increase as it approaches the planet, thereby increasing its kinetic energy. How can we reconcile this with the first law of thermodynamics, namely energy can neither be created or destroyed but only transferred from one place to another. Where does this new energy come from? Gravity is a field, not energy.

ANSWER:
You misunderstand conservation of energy. Only the energy of an isolated system is conserved. In your example, the rock was originally isolated and so its energy was conserved, i.e. it moved with constant velocity in a straight line. However, when it encountered the planet, it was no longer an isolated system. It experienced a force (the gravity of the planet) which did work on it and increased its kinetic energy. Incidentally, a gravitational field is energy, it has an energy density.

QUESTION:
I am new student of diagnostic imaging - ultrasound and have a question regarding the acoustic variables. As per the information that I collected I came to an understanding that the particle motion is the distance covered or displacement of the particle. However my Professor was disagreeing with this and says that particle motion is not the distance. Could you please help me to clarify this?

ANSWER:
There is no way I can know the jargon used in your specialized field. "Particle motion" could be one or more quantities--frequency and amplitude for example. But what particles are being described?

FOLLOWUP QUESTION:
So basically, we are learning about sound waves and its properties and its appplication in ultrasound imaging. The lecture was regarding the acoustic variables and were having discussion on "particle motion" as the sound travels through the medium. As per what I read, the particle motion is because of the oscillations in the particles of the medium as sound travels through it and it is distance and can be measured in cms, etc. However our instructor said that particle motion is not particle displacement and hence distance is not an acoustic variable. I am not really convinced by his explanation and was seeking some advice on this.

ANSWER:
Again I emphasize that I am not an expert in ultrasound symantics and you would be much better advised to talk with your instructor to find out what he/she means. Generally, in acoustics, we do not pay much attention to what the particles in the medium are doing. We know they are moving around in some way but we are more interested in the wave itself.

What are the properties of the wave which you are using for imaging, for example.

The three most important variables are its velocity v in the medium (made up of molecules which presumably are your "particles"), the wavelength λ of the wave, and the frequency f; these three are related, v=λf.
Also important in understanding the wave is its amplitude which is a measure of how "loud" the sound is.
A fifth important variable is the phase of the wave, important if interference of more than one wave is considered.

What is the motion of the particles which underlie the sound wave?

Sound waves are known to be longitudinal, i.e. the particle motion is oscillatory parallel to the direction of the velocity of the wave.
Being oscillatory, the each particle moves about fixed point in space, it does not move with the wave; so "displacement" and "velocity" of the particle depends on the time and their time-averaged values are zero. This may be the reason your instructor does not like your choice of displacement to be part of particle motion.
The individual particles vibrate with a frequency which is the same as the frequency of the wave and with an amplitude which is proportional to whatever you observe the amplitude of the wave to be.

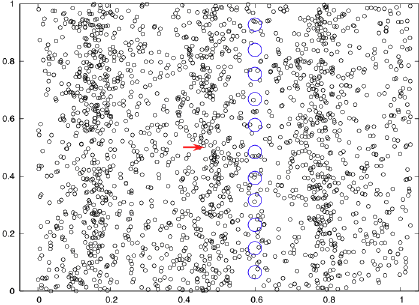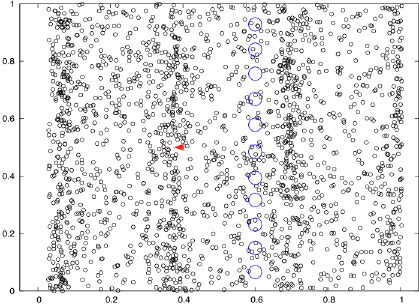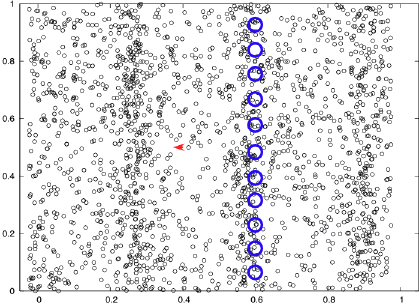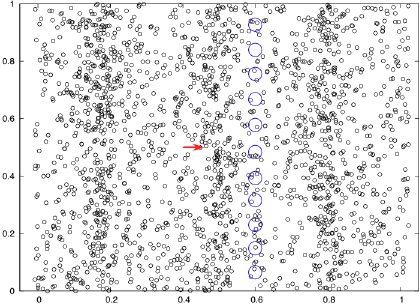
The animation illustrates the particle motion. The little red arrow tracks the longitudinal oscillatory motion of a single particle. Watching the open circles shows them getting more and then less densly populated which indicates that sound may be more macroscopically viewed as regions of high and low pressure which propogate in the direction the waves are traveling.

I hope that this helps you. Anyway, it is the best I am going to be able to do!

QUESTION:
in a scene from Apollo 13, astronaut Ken Mattingly and engineer John Aarons are seeking to help the crew of the Apollo 13 transfer the remaining power from a battery on the LEM to a battery on the Command Module to which the 3 astronauts had returned after the had used the LEM as a "lifeboat"...how can that be done? Especially when the LEM battery has less "juice" than the battery on the Command Module? No doubt an umbilicus would be attached from one battery to the other-would the power simply flow spontaneously from one battery the other? And however they were caused this to occur, wouldn't the current flow from the battery with MORE power to the one with less? How can the power be "coaxed" from the weaker battery to the stronger?I

ANSWER:
There is a nice article on the web which addresses your question.

QUESTION:
I am a freelance writer, and I am trying to build a scenario, only if it is theoretically possible. Here it goes. In the movie Interstellar, which I know is likely more film than proven science, there is a planet in which time passes slower than time on earth because of its proximity to a massive black hole. So every hour on Planet A equals ten or so years on Earth. I have found some theories and answers online that all suggest this is possible, time dilation, relatively stuff. What I am trying to understand is can the opposite be true? Is it possible with specific conditions that a planet could exist in which time moves faster than it does on Earth. For instance, on Earth one year is 365 days. Could there be a scenario in which for every year on Earth, 20 or 50 years passes on Planet B? I have tried to find this answer online, and by asking people who have a better understanding of this subject matter than I do, but I haven't gotten close to sniffing this.

ANSWER:
First, Interstellar has received many accolades for the accuracy of the physics. At the beginning of the production they hired Kip Thorne, a renoun theoretical astrophysicist and Nobel laureate as an advisor; he kept a very tight rein on maintaining good science, forbidding, for example, faster-than-light-speed of space ships. A picture is worth 1000 words! Look at the graph I have included. This graph illustrates the rate at which clocks in circular orbits run faster than a clock on the surface. Both time dilation due to velocity (red curve) and gravitational time dilation due to earth's gravity (green curve) as well as the net time rate change (blue curve). The clock considering only special relativity (speed) runs slower but the effect is zero infinitely far away. The clock considering only general relativity (gravity) runs faster and is fast as it can get infinitely far away. Infinitely far away the clock will run faster at a rate of about 700x10^-12 second for each second on earth's surface; that is the fastest you can get a clock to go compared to earth. One year on earth would be shorter by 0.022 seconds than the distant clock. What you want is not possible.

QUESTION:
I would appreciate it if you could explain how a screw/conical shaped object moves down an inclined surface. I understand that it may have to do with circular motion of some sort, but in real life, I have noticed that it seems to oscillate, with its oscillations increasing as it rolls down in some scenarios, I'm just curious as to what concepts are involved in this!

ANSWER:
A cone on an inclined plane can be very easy to describe, pretty easy to describe but just qualitatively, or really hard to describe. If there is no friction between the cone and the plane and it starts from rest, it will slide straight down the incline just like a cube or ball would with no friction; thats the easy one. If the cone can roll only without slipping (infinite friction), it will not go down the incline at all but oscillate like a pendulum as illustrated in the figure; this is the easy situation to understand qualitatively. It could be described analytically because there are only two variables, the angle of swing of this pendulum, and the rotational angle about the axis of the cylinder, but it would not be easy; also, it would likely require require small angle approximations as in the simple pendulum. If the cone can slip and roll, the problem is much too difficult for the purposes of this site. I can imagine it slipping and rolling, as you have observed, and having an oscillating behavior. For more detail, try this link.

QUESTION:
let's assume that a race is taking place between the speed of light and a person with a stick. The stick is as long as the earth-sun distance, and it needs a millimeter to touch the earth. My position is in the sun. The goal of the race is for one of these contestants to touch the earth. So the contestant with the stick only needs to touch the stick for the stick to touch the earth. Which of the contestants will win?

ANSWER:
Your question is very much like a similar earlier question. The answer is that the light would touch the earth before the stick, long before. When you push your end of the stick to move it forward 1 mm, the other end does not instantaneously move. The information that you have moved your end moves down the stick atom by atom with the speed of sound in whatever the material you have made the stick of. The speed of sound is far slower than the speed of light. Besides, the mass of such a stick would be so enormous that it would take an enormous force to provide the necessary acceleration to move it forward in a relatively short time.

QUESTION:
Why can't energy just be seen as a measure of change? It seems to me that if something changes then there must be a compensatory change somewhere else. Consider the case of a mass at a elevation of 3m above the earth. What we call its potential energy is both a measure of the amount of change that occurred to raise the mass and a measure of how much chage will occur if it is released. Its kinetic energy is at each moment as it falls is a measure of how much change has occurred. More mass moved more change; moving faster more change happening. Thus, kinetic energy as a measure of change would involve both mass and velocity as it does. When it hits the ground and stops that a change that needs to be compensated for. The earth is deformed, i.e., other things moved, i.e., had an increase in their kinetic energy although this would probably be measured as an increase in heat. The object would also be hotter, as its own atoms would have be jolted into motion, so actually just kinetic energy, i.e., change in motion. There would probably me some sound energy also just kinetic energy of air molecules, etc. Isn't this all just different ways of measuring different changes in different parts of a system? I have seen answers to this question. All in the negative, but they are unconvincing. Mostly they say something like, "No, energy is ... " or something really unhelpful like, "Everything is energy"

ANSWER:
Your question is qualitative. Science is primarily quantitative. I think you hit on well-thought out ideas but they are qualitative ideas and that may be useful for understanding things conceptually, but not for putting you in the position to study nature quantitatively. One of physics' most important laws is that the total energy of an isolated system never changes; indeed, when energy is not conserved, i.e. changing, that is important to measure and understand why. But you are not really going to appreciate that if you think that energy is "...just...a measure of change" are you? Science requires clear quantitative definitions of the variables which you can measure to test whether your laws and hypotheses are true or not. And I might ask what is the mass energy of a particle, you know, E=mc², got to do with change? Or, how can the energy density of a constant electric field be understood "just" in terms of change?

QUESTION:
If I am trying to find what length is needed for a pendulum for it to complete one back and one forward motion to the beats per second of a song, how would I do that?

ANSWER:
A simple pendulum is defined to be a point mass M attached to a massless string of length L. The period T of such a pendulum is approximately T=2π√(L/g) where g is the acceleration due to gravity which has a value of 9.8 m/s² (if L is in meters) or 32 ft/s² (if L is in feet). All times are in seconds (s). Therefore L=T²g/(4π²); putting in the values for g and pi, L=0.248T² m or L=0.811T² ft. For example, suppose that T=2 s; then L=3.24 ft=38.9 inches.

All this comes with a couple of provisos though. First, there are no such things as point masses or massless strings; this should be pretty easy to ignore as long as the size of the mass is much smaller than the length of the string. Second, you will note that I used the word approximately when describing the equation for T. It turns out that when deriving this equation you find that the differential equation you need to solve does not have a closed form solution, you have to make the approximation that the maximum angle of swing is small, for your purposes you should probably keep the angle of swing (from vertical) to be less than 30� for the formulae to work well. By the way, note that the equation for T does not depend on either the mass or the amplitude; for larger angles this is not the case.

QUESTION:
In the twins paradox, twin A travels away at nearly the speed of light and, some time later, returns at nearly the speed of light. Twin A has aged less than twin B. However, since velocity is relative, twin A sees twin B travel away and then return, so twin B should have aged less than twin A. Obviously both can't be right. The difference is that twin A accelerated. Did the rate of aging actually only reduce during the periods of acceleration, i.e. while twin A was subject to a force? If so, is this related to the slowing of time while subject to a gravitational force?

ANSWER:
The twin paradox is not a paradox at all; it is easily understood. It has nothing to do with the acceleration or gravity. What you are missing is length contraction. The trip is to some distant star and back. The distance between this star, as measured by the earthbound twin, is D. But the traveling twin sees that distance to be D√[1-(v/c)²] because of length contraction. I urge you to go to my faq page where you can find a link to my discussion of the twin paradox.

QUESTION:
My question in regard to the photoelectric effect. All electromagnetic waves travel at the speed of light, yet their frequencies can change. There's something here I'm not getting.

ANSWER:
I don't see how this relates to the photoelectric effect. Perhaps you are thinking about the Compton effect where a photon scatters from an electron and its frequency after the collision is smaller than before the collision? If the light has some frequency f then the energy of one photon is E=hf where h is Planck's constant. And, although a photon has no mass, its linear momentum is p=hf/c where c is the speed of light. Now, let's think classically for a moment. Suppose one ball collides with another which is at rest; after the collision the incoming ball will be going more slowly than before the collision, that is, both its linear momentum and its energy are smaller. The same is true for a photon colliding with an electron and its energy and momentum are both smaller and the only way that can happen is if it has a lower frequency. It is hard to swallow, at first, that something can change its momentum without changing its speed, but if it has no mass, it may be hard to imagine it has any momentum at all! But, that's the way it is in special relativity.

QUESTION:
My question in regard to the photoelectric effect. All electromagnetic waves travel at the speed of light, yet their frequencies can change. There's something here I'm not getting.

QUESTION:
I had a little fun question. I was watching an old Shrek commercial and he threw donkey into space. Donkey weighs 400 lbs mind you. How strong would Shrek have to be and the force needed to do that?

ANSWER:
So, I attached a picture from the video showing Donkey just as he stopped and began to fall back down. Let's make a guess that he is at a distance 10 earth radii (R₀) from the center of the earth (i.e., at an altitude of 9R₀). The potential energy U of mass m at a distance r from the center of the earth is U=-MmG/r where M is the mass of the earth and G is the universal gravitational constant. The donkey's total energy at the instant that Shrek releases him is his potential energy plus kinetic energy, E₁=-MmG/R₀+�mv², where v is the speed of Donkey; at the peak of his trajectory his energy is E₂=-MmG/(10R₀). If we neglect friction as he passes through the atmosphere, the energies must eqal each other; so if we equate them and put in all the data we would need, M, m, G, and R₀, we can solve for the velocity. You are probably not interested in all the arithmetic, so I will skip it and give you the answer, v=7500 m/s=17,000 mph. Now you can find the kinetic energy to be 5.1x10⁹ J=1400 kilowatt-hours. If Shrek exerts an average force over, let's estimate, about 6 ft, the force would be about 2.55x10⁹ N=4.6x10¹¹ lb. Even if Donkey were made from the strongest material known to mankind, there is no way he could survive this force!.

QUESTION:
How much wind force would be required to move an air cargo container measuring 6'x6'x6', with an empty weight of 138 pounds sitting on a bed of rollers, ball bearings or casters? Is it less than would be required if sitting on the ground?

ANSWER:
So, it depends on the material it is made from, what the "ground" is like, and how good the the rollers are. I will assume that the ground is very hard and horizontal. If you were doing the pushing other than the wind, there would be two things you could ask: how hard must you push to get it moving and then how hard to keep it moving at a constant speed. In a situation like this (horizontal) the force of friction (f) is proportional to the weight (W), f=μW where μ is called the coefficient of 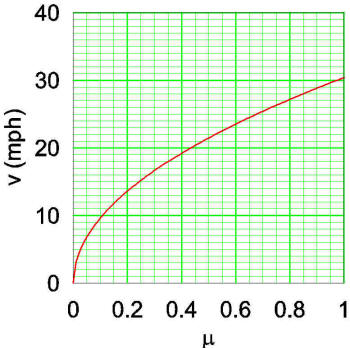friction; if μ is a small number it will be easy to move, if large it will be hard. There are two kinds of μ, static and kinetic, which give you the force for starting or keeping at a constant speed, respectively; μ_static>μ_kinetic. That takes care of the sliding part; now we have to address the speed of the wind and how much force it exerts on something. There is a very useful way to estimate this force �Av² where A is the area presented to the wind in m², F is in Newtons (N), and v is the wind speed in m/s. Since this is in SI units, I will have to convert to your Imperial units to SI units, W=138 lb=614 N, A=36 ft² =3.34 m². So now, the push must be equal to the frictional force, 614μ=3.34v² or v=√(184μ) m/s=30.4√μ mph. We could now try some examples:

wood sliding on concrete, μ=0.62, v=24 mph
steel sliding on steel, μ=0.8, v=27 mph
nylon casters on concrete, μ=0.04, v=6.1 mph

I have included a graph of speeds as a function of coefficient of friction.

QUESTION:
What are the physics principles of throwing boiling water in extreme cold and instantly becomes cloud (no snow i guess).

ANSWER:
See this article and this video.

QUESTION:
OK, maybe a stupid question, but it doesn't leave me alone: If you are in a room where all walls are mirrors and the only light source inside the room is a flashlight you are holding, then shouldn't the room stay perfectly lit, when you turn the flashlight off? ...at least for a decent amount of time, as all the photons keep bouncing around and only slowly get absorbed (by the mirrors' imperfections and your own body, including your eyes)? Intuitively, I assume the room goes pitch black immediately, as you turn off the light, but I do not know why.

ANSWER:
The reason is that the light goes so fast and loses a tiny bit of light with each reflections but there are so many that the light decays very fast. To see some numerical details worked out, go to an earlier answer.

QUESTION:
Can we see further around the Earth due to spacetime curvature from gravity? Because the equations for how far our visible horizon is and my own personal experience, don't quite seem to mesh.

ANSWER:
The curvature would be incredibly small, far to observe using your "�own personal experience�. I don't know what your experience is but it is probably due to the assumption that the earth is a perfect sphere which is which it certainly is not, particularly over small distances.

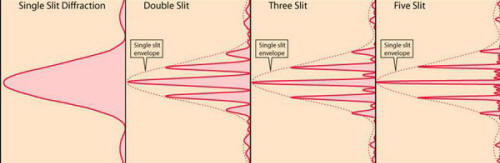
QUESTION:
Our class was discussing the observer effect in the triple-slit experiment. I understand it pretty well up until the observer effect comes into play. If no one is observing the outcome, how do you know it's not doing the same thing as when you're observing? This reminds me of the 'if a tree falls in the woods, and no one is there to hear it' riddle. It's not really a riddle as it surely does make a sound be no one was there to hear it.

ANSWER:
The "observer" is not just someone standing around watching the experiment. What it means is that you set up some kind of measurement apparatus to determine through which slit the particle passed. That measurement will destroy the interference pattern.

QUESTION:
Is it possible to entangle more than two particles? Is there a limit?

ANSWER:
Not only is it possible, it has been done. In principle, there is no limit.

QUESTION:
Quick physics question! If the sun starts to die could it be restarted with a trillion nuclear bombs? I know it�s impossible to make a trillion nuclear bombs, but if it were possible and the sun was dying.. what would happen if we tossed said bombs into the sun? Would the sun explode or will it reignite

ANSWER:
The reason a star dies is that it runs out of fuel, mainly hydrogen and some helium; so unless you can add enough hydrogen to make a new sun, you cannot kickstart it somehow because there is nothing left to restart. One H bomb contains about 300 kg of hydrogen. One trillion is 10¹², so a trillion bombs would add about 3x10¹⁴ kg of hydrogen. The mass of the sun, mostly hydrogen, is about 2x10³⁰ kg. The bombs have 16 orders of magnitude less mass than the sun; so tiny are the bombs that the sun would not even notice.

QUESTION:
I have an odd question I can't stop thinking about; I'd love some help, and I'm doing everything I can to find an answer to this, including sending messages to multiple people that may carry the ability to help me. No this is not a botted message, I'm writing this in person I assure you. taking c as the speed of light. Now, considering an Object moving away from me to my right at 60% of c, if it emits a light towards me that light will travel towards me at 100% of c itself. Now the light being emitted towards me has a relative velocity of 160% of c to the object it's emitting the light from. Now let us name the previous object in question object D, and let us take another object; object B and say it's moving away from me to my left at 60% of c. Now the light being emitted from object D is traveling at c relative to me, and 60% of c relative to object B, and the light is also traveling towards object B, and we can safely assume it's bound to reach object B at some point. This is from my perspective as an observer (which we shall state as an observer on object A) at rest relative to objects B and D. Now as Special Relativity states, as long as an object is moving at a constant velocity it's safe to assume in relation to another object that it very well may be at rest and the other object may be moving. Knowing Special Relativity doesn't constrain relative speed if we shift our frame of reference to object B, we observe object A moving away from the speed of light from object B but we do not observe object D or any light emitted from it as it is moving away from us faster than the speed of light (I'm going to assume it's possible because of relative speeds), however considering out frame of reference from object A, we clearly saw light from object D reach object B, here lies my confusion. What is actually happening? Do I lack a good understanding of special relativity hence I give rise to faulty and stupid questions? I'm eagerly waiting for a response, please let me know.

ANSWER:
This question should really be thrown out because it is neither concise nor well-focused as stipulated in the site ground rules. However, I can address it concisely so I will answer it. Yes, you do "�lack a good understanding of special relativity�"; the speed of light in vacuum is the same for all observers. You should see an earlier answer discussing velocity addition in special relativity. Using v'=(u+v)/[1+(uv/c²)] for your first situation, v=c and u=0.6c, v'=1.6c/(1+0.6)=c; both observers see the same speed of the light.

QUESTION:
I am attempting to figure out the pressure or impact the following would exert. Picture a square plate (filter plate), 48" X 48", 2" Thick, 125lb... These plates are, hanging, supported by two top-mounted angle iron bars. The plate supports have rollers at each end and the plates while hanging can be slid for cleaning. The Question: If one of that support (hanging the plate) would fail, and the plate would swing (one holder still intact) approximately 2 ft. and strike an object; what impact pressure and strike force would be applied? Summary: Square plate, appx. 125lbs. swinging appx. 4 ft., what would the impact be when the plate strikes an object?

ANSWER:
I am not sure that I get the picture from your description. Seems like the plate rotates about a horizontal axis along one edge and swings until it is vertical as shown edgewise in my sketch. Is this right? I will proceed assuming that this is right. What I can do, assuming that there is negligible friction of the pivot and the plate, is calculate the angular velocity of the plate when it is vertical, how fast it is rotating. However, I should warn you that it is impossible to answer your question because the answer depends on the nature of the collision between the plate and whatever it is colliding with. Let me give you a couple of examples to demonstrate that your question cannot be answered without a lot more information. Pressure is the force divided by area. So if a small object is struck and experiences some force F, it will experience a larger pressure than a large object experiencing the same force would. Also, note that the speed of the plate close to the pivot but gets larger farther away from the pivot; therefore, the pressure during colliosion increases as you get farther from the pivot. Now, how do you compute the force? When the plate hits some object, the object experiences some average force which is equal to the change in the linear momentum Δmv (its mass m times its speed v) divided by the time t the collision acted, F=Δmv/t. To illustrate, imagine two balls, each having a mass m, one hard like a billiard ball and another which is very squishy. When the plate strikes the billiard ball, the ball will take off almost immediately, in a very short time, so the average force over that time will very large. When the plate strikes the squishy ball, they will remain in contact far longer so the average force will be much smaller. This also is why if you fall onto concrete you get hurt much more than if you fall onto a mattress. Given the fact that to answer your question, even approximately, is impossible without more information, I will stop now.

FOLLOWUP QUESTION:
Let me give you just a little more information if I may; Here's the problem I have a worker standing on a work platform, cleaning, and spraying "Filter Plates", these are plates on a large Water Treatment Filter Press. The plates are "hung" by two top-mounted hangers. They are in line with each other, and cascade, pressed to squeeze out water and contaminants; about 20 plates on the unit. Concern: If (and it has happened) one of the plate "Hanging Brackets" breaks, get's loosen the plate may lose its hanging capability, not completely fall since the other hanger is intact, but Swing Out and possibly strike the worker while they are on the work platform.

REPLY:
So, we have a uniform 4x4 square hanging down vertically from supports approximately at the two corners at the top. One corner fails and the square rotates about a horizontal axis through one corner and normal to the plate? Keep in mind that, as I explained in the original answer, it is not possible to simply associate a force with some moving object, you must have information about what it hits and how. Therefore you can only expect an order-of-magnitude approximate calculation making assumptions about the collision time and the angle the square has rotated through before hitting the worker. Your picture shows the square to have not yet rotated through 45^� and the corner hitting the worker approximately in his trunk. Are those approximately true? Would it matter if I did my approximate calculation assuming 45^� where the square would have its greatest speed?

FOLLOWUP QUESTION:
Subsequent exchanges with the questioner brought up the following important point: The rotating stops on its own by the time it reaches the bottom where, without friction, it would be moving the fastest. This means that friction plays a very important role in this problem. So I have concluded that the best approach is more qualitative.

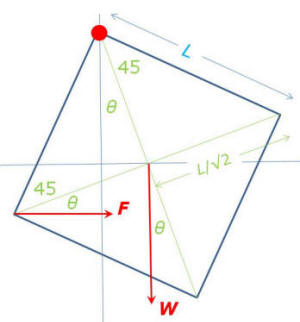
ANSWER:
The figure shows the plate swinging from one support only. L=4 ft and W=125 lb are the size and weight of the square. The angle θ denotes how far the plate plate has rotated from its initial position, 45�; when θ=0� the center of the plate is directly below the suspension point. The length of a diagonal of the square is 2L/√2 and the weight acts at the center of the square (assuming uniform mass distribution). I am interested in what horizontal force (shown as F in the figure) must be applied to hold the plate from rotating. I am ignoring friction for now. Summing torques to zero about the pivot point I find that F=W[sin(θ)/sin(θ+45�)/√2]. The graph shows F plotted as a function of θ; the required force is modest, 62.5 lb at the largest, and less than 40 lb at smaller angles where striking a worker is more likely. Furthermore, if it were moving at smaller angles it would be going slowly because of the frictional force; also the frictional torque would be opposing the torque due to the weight and reduce the necessary force F needed to bring the system into equilibrium. If it is going slowly and the torque necessary to stop it is rather small, I would conclude that a worker could rather easly just reach up and grab it to stop it. My only reservation would be that the suspension point at the pivot is not designed to be a pivot and might not always behave the same; if the friction were such that it would pass the equilbrium position with a significant velocity, it could be more dangerous.

QUESTION:
Holding a car FOB against your head will increase its effective range. For example, if you are trying to lock/ unlock your car from a distance and the FOB battery isn't strong enough to make a strong enough signal to reach your car, you can hold your car key against your head... which extends the effective distance of the FOB by several/ dozens of yards, and may allow you to then lock unlock your car if you are just out of your FOB's range. There are many websites which document this. I know it sounds crazy, but it's real. What is your opinion regarding how this trick amplifies the FOB signal?

ANSWER:
It is not my "opinion", it definitely works and the reason is very well understood. The explanation is fairly long and technical and involves the wavelength of the beam from the FOB, the size of your body, the size of your head, resonance, and the dipolar property of water molecules. There is a pretty clear yet entertaining video which you can watch at this llink.

QUESTION:
Hello, this is to settle an argument between my brother and I and we can't find an answer, so I hope you can help us. There are two soda cans cold out of the fridge, both at the same temperature and sitting in the same environment (say on a coffee table). One can has been opened and the other remains sealed. Does the can that has not been opened warm faster because its still sealed and under pressure.

ANSWER:
Let me first address how heat is transmitted to and through the interior of the unopened can. We generally think of heat transfer as occuring via three ways: radiation, conduction, and convection.

The can has two surfaces, the bottom and side, where heat may be conducted through the aluminum directly to the soda; the third surface, the top, has aluminum in contact with the gas at the top through which which heat may be conducted to the surface of the soda. The rate (R) of heat transfer through a medium of thickness t with a temperature difference ΔT is proportional to ΔT
and inversely proportional to t, R=σΔT/t, where σ is the conductivity; clearly, since the conductivity of the gas is much smaller than for the aluminum and its thickness much larger, much less heat is conducted through the top.
Now, the soda near the inner surface is warmer than it is inside, so now the heat could conduct into the cooler volume. But, in a fluid, heat is much more efficiently distributed via convection, currents in the fluid. Similarly, heat through the gas at the top of the can will occur much more efficiently by convection.
I don't believe that radiation plays a particularly important role in the heating of the soda.

So, now, what changes when the top is opened? As you noted, the pressure in the gas will decrease meaning a smaller density and therefore a smaller conductivity. But, convection will play the major role in the gas and I believe that the gas will quickly equilibrate with the outside air; then, the temperature at the top surface of the soda will be the same as outside air. Also, the soda in the open can will be losing its carbonation, but since there is only about 0.04 oz of CO₂ in a 12 oz soda, I would expect no significant changes in the properties of the soda as it loses the CO₂.

So, I expect the open can to warm up faster. But, I am not absolutely positive and suspect that there will not be a big difference. Here is what I would do: get an instant read thermometer and put it in the open can; then wait until the soda gets to about � of the room temperature and quickly open the closed can and measure the temperature. If you do this experiment, please let me know the result!

QUESTION:
My question is: assuming space was a perfect vacuum, (for simplification purposes) as light travels through it, and then slows down (however minutely)by entering a planet's atmosphere, once it passes through the amosphere and re-enters a vacuum, does it resume (accelerate to) its original speed or does it remain at the slower speed caused by the atmosphere?

ANSWER:
In any medium light has a speed v, a frequency f, and a wavelength λ. The energy of any single photon is E=hf where h is Planck's constant; also, v, λ, and f are related by v=λf. The energy of any photon cannot change, so f remains constant regardless of v. Therefore when the light moves from the atmosphere to a vacuum, its wavelength increases so that v=c where c is the speed of light in a vacuum.

QUESTION:
Calculate the kinetic energy of a 5,000 kg meteoroid traveling at 11.2 km s-1. If it were to impact the surface of Earth at this velocity, what would be the equivalent strength of the explosion using the units of Tons of TNT?

ANSWER:
The speed is very small compared to the speed of light (c=3x108 m/s), so classical mechanics can be used. The kinetic energy is K=�mv²=3.14x10¹¹ J. 1 Joule (J) is 2.39x10^-10tons of tnt, so the energy released is 3.14x10¹¹x2.39x10^-10=75 tons of tnt.

QUESTION:
I watched the "trip to infinity" doc on netflix and there was a part that said if you put an apple in a box, that apple will eventually decompose but the trapped energy will eventually create something else. Can the same concept be applied to humans and rebirth? Is our body just energy that takes another shape eventually after we die?

ANSWER:
Assuming you have a box where nothing can go in or out, you would have an isolated system consisting of the apple and whatever air is inside. If there are no bacteria present there would be no mechanism for decomposition. Even so, the water in the apple would evaporate out, eventually drying the apple. One apparent energy transfer would be in the form of heat and it would warm up inside. But, the heat can't escape. When the water evaporates, some chemistry might happen inside the apple releasing heat energy and changing the composition of what is left of the apple. Etc., etc., etc. But you can be sure that the apple will not eventually become a mouse or a peach or even a new apple. Putting you in the box would eventually result in the same fate as the apple, but you can be sure that rebirth is not in the cards. Of course, there is no such thing as a perfect isolating box and heat, the main result of the apple's demise, would eventually leak out and radiate away until the inside and outside of the box were in thermal equilibrium.

QUESTION:
In general science class years ago I learned that when a balloon is inflated and the stem released, the pressure of the air in the balloon pressing against the front side opposite the stem is greater than the ambient air pressure in front of the balloon and since the pressure at the stem is being released, the balloon moves toward the lower pressure area ahead of it. This is not hard to understand for a balloon or rocket. However, I don't understand how this principle works in a jet engine. Since the forward end of a jet (particularly a ram jet) is open also, what is the interior pressure pushing against to move the jet forward?

ANSWER:
Frankly, I do not particularly like this way to explain rocket propulsion. It is much more easily explained using Newton's third law, if object A exerts a force on object B, object B exerts an equal and opposite force on object B. Think of each molecule of the ejected gas: for it to get propelled out, the engine must exert a backward force on it; therefore this molecule of the gas exerts an equal force on the engine but in the forward direction. I suggest that you read two earier answers, (1) and (2): The first discusses rockets and such, the second has a discussion on how a jet engine works.

QUESTION:
I have read somewhere that only the Earth below, not the Earth above, exerts a gravitational force on a deeply buried piece of matter. What does this statement mean? We know all masses exert gravitational force on each other. Then why upper part of earth does not exert gravitational force on deeply buried objects below?

ANSWER:
First, for this statement to be true, the earth must be a sphere and spherically symmetric. (Spherically symmetric means that, at a particular distanc from the center of the earth, the density is the same regardless of the direction of that radius vector. So, for example, if you are 100 miles toward the north pole, the south pole, or the equator, the density is the same at all three of those positions.) Consider first a tiny piece of mass right at the center of the earth. you should intuitively see that it will experience no force because for every little piece of mass inside the earth exerting a force on the centered mass there is mass on the other side of the earth which exerts a force of the same magnitude pointing in the opposite direction, so the force due to these two "earth above" pieces of the earth cancel to zero. Similarly every other piece of the earth has a partner exerting an equal and opposite force on the centered mass. (This has nothing to do with Newton's third law!) The net force on a small piece of the earth's mass anywhere but the center is considerably harder to calculate and beyond the scope of this site. The result however is that the net force on any small piece of earth is equal to the force which a point mass equal to the mass of the "earth below" located at the center of the earth. To learn more about details, learn about Gauss's Law.

QUESTION:
From the perspective of light (hypothetically), how much time passes approximately for it to get from andromeda to us, 2.54 million light years away. I know the obvious answer (2.54 million years) but I am wondering whether time dilation due to velocity occurs, and whether the distance from any gravity(Mass) has any additional time dilating effects.

ANSWER:
The length of time that anything happens depends on the observer. Yes, the earth will see the light from Andromeda arriving after a trip of 2.54 million years. But, something moving relative to the earth will see it take some different time. For example, suppose there is a space ship moving from the earth toward Andromeda with a speed 80% the speed of light. An observer on the ship will see the distance from earth to Andromeda to be shrunken, 2.54x√(1-0.8²)=1.52 million light years and therefore the light takes1.52x10⁶ years to make the trip in his frame. If you are asking (as many have) how long it takes in the photon's frame of reference, a photon has n perspective because it cannot have any kind of clock it carries. See earlier an answer and an earlier yet answer linked to.

QUESTION:
If you have a house and it's 32F outside, do you really save on heating fuel if you set your thermostat on 68 instead of 72? I hear them suggesting that all the time but what I recall from HS physics class is that if the furnace turns on at 4 degrees below the setting it's going to take x-btu to raise it that 4 degree range regardless.

ANSWER:
You recall wrong. Fewer BTU are required to increase temperature 4� starting at 50� than starting from 60� because heat leaks out of the house faster at higher temperatures. So let me try to convince you that you consume less fuel if you keep your thermostat at a low temperature. Here is my scenario: when I awaken in the morning when the temperature is 32� outside the temperature is 60� inside because that is what I set my thermostat to when I go to sleep. Now I turn my thermostat to 68�, it will take a certain amount of energy to raise the inside temperature to the set temperature; however, if I set it to 72�, it will take more energy to raise it to 72� because it has to raise it to 68� on the way. In order to hold the temperature to any constant value the furnace must replace the energy which is leaking from the house, through walls, ceilings, floors, doors, windows, etc. It turns out that the rate that heat conducts through a barrier is proportional to the temperature difference across the barrier. Therefore, the heat leaks out of the house faster if the inside temperature is 72� than it does when it is 68�; therefore, more heat from your furnace is required for the 72� thermostat setting.

QUESTION:
Am I right in assuming the diagram they normally use to illustrate how mass bends spacetime, usually depicted as a sheet with bowling ball in the middle of it, which creates a cone like depression in the sheet representing the curvature of spacetime created by mass that draws in other objects is completely oversimplified and inaccurate because no matter what direction an object is approaching a planet from, it is drawn into the gravity, so the curvature must be a sphere around the planet rather than a cone like depression underneath it ? I have never taken physics so please excuse ignorance if I am completely wrong.

ANSWER:
See the FAQ page. Search for "trampoline model".

QUESTION:
So if I bowl a 14lb ball at a speed of 24mph, how much would the force weight be when the ball impacts on the pins. I was talking with a friend about this while bowling and I was telling him that the force and the impact would be much greater then bowling it at like 1mph and hitting you. I just don't know how to calculate it.

ANSWER:
It is very cumberson to do physics using imperial units, so I will switch to SI (metric) units and switch back later. A 14 lb ball has a mass of about 6.4 kg; 24 mph is about 10.7 m/s; 1 mph is about 4.5 m/s; we will also want the mass of a bowling pin, about 1.5 kg and the mass of 200 lb man, about 91 kg. I will first consider the bowling ball colliding elastically and head-on (both traveling in the same direction as the incoming ball) with the pin first. With no extra detail here, I find that after the collision the bowling ball has a speed of about 6.64 m/s (14.9 mph) and the pin has a speed of about 17.3 m/s (39 mph). How did this happen? During some time t the two were in contact exerting equal and opposite forces on each other, the ball slowing down and the pin speeding up. The average force experienced by each has a magnitude I will call F. Over the time t the change in momentum (mass times velocity) of the pin (which is (17.3x1.5-0)=26 kg�m/s is equal to Ft which is called the impulse. So the force of the ball on the pin is F=26/t. I don't know what the time of the collision is but I know it is small; let's just say that it's on the order of a hundreth of a second, t=0.01 s. Then =0.26/0.01=2600 N=585 lb. Now consider the ball hitting the gut of the 200 lb=91 kg man. This is not an elastic collision because I would assume that the ball and man will remain stuck together after both are going with the same velocity which would be about [4.5x6.4/(91+6.4)]v=0.3 m/s. Again, I do not know how long the collision took but it is a lot longer than a hundreth of a second, let's estimate that t=0.5 s. Now the impulse is 0.5F=0.3x91=27.3 kg�m/s, so F=27.3/0.5=54.6 N=12.3 lb. The bottom line is that the force of the ball on the pin, 585 lb, is much larger than the force, 54.6 lb, of the slower ball on the man, mainly because the duration of the collision is so much shorter for the ball-pin collision.

QUESTION:
So i'm having a bit of a heated scientific discussion with a pal the minute. My question is if you threw (not dropped) a light object and a heavy object with the same force in the direction of the gravitational pull, which object would express more acceleration if there is any difference?

ANSWER:
During the time you are exerting the force F (presumably straight down) on each object, the total force on it would be mg+F where m is the mass of the object and g is the acceleration due to gravity; mg is the weight. Newton's second law says that the net force is equal to mass times acceleration, so the acceleration a is a=g+F/m. So, while the force acts, the heavier mass has the smaller acceleration. Once the force stops when it leaves your hand the accelerations become identical, g, regardless of the fact that they may have different speeds when released. All this ignores air drag.

QUESTION:
as a mechanically-biased person but untrained physicist, who has an interest in all things scientific, one thing has been puzzling me lately. When particle physicists talk of manipulating particles (say, in the LHC, or discussing entanglement, or even in the slit experiment) - how do they isloate just one or two particles? And what might the particles be? Even a single photon must involve alot of physical process just to catch it and use it. How do they do the 'nitty gritty' 'hands-on' stuff? I guess it's a mechanical and not a theoretical concern that I'm having trouble with!

ANSWER:
I will talk first about photons. Every time one excited atom decays to a lower-energy state, one photon comes out. The same is true of an excited nucleus. Exciting atoms and looking at their spectra is 19th century physics. It is often done by passing an electric current throught a gas; the electrons excite the atoms of the gas which emits photons and detectors see them, one by one. But wait a minute, where do the electrons come from. It turns out that electrons are very easy to get: simply take a tungsten filiment and heat it up until it glows red or white. Electrons stream off the filament and electric and magnetic fields can manipulate them. Heavier things need what are called sources to strip electrons off of atoms and the ionized atoms again can be manipulated with EM fields. Often those ions (simply protons if the ionized atoms are hydrogen) are accelerated and "shot" at a target, often a thin foil or container of a gas. Then they pass through the tartet and some interact with the target atoms and they may bounce out having been scattered by the target atoms. The scattered particles are then detected, one by one.

QUESTION:
The wave solution to the Photoelectric effect. Hi there. I was recently examining the relationship between the work function of a material and its threshold wavelength. It was clear to me that the relationship is expressed as: (λW)² = c/2 Where λ is the threshold wavelength, W is the work function in Evs, and c is the speed of light. However, I am unable to find the name of this solution online. Do know what this relationship is called, and a link that explains it?

ANSWER:
The equation you are asking me the name of cannot be any meaningful equation at all because it is not dimensionally correct. The work function has dimensions of energy which would be mass�(length/time)²=M�L²/T², so the left side of your equation has dimensions (L�(M�L²/T²))²=M²�L⁶/T⁴ and the right side is just a speed L/T. The fundamental equation you seek for the photoelectric effect is that the work function, the minimum energy required to remove one electron from the surface, is equal to the energy of a photon of frequency f which is Plank's constant h times f, W=hf. If you would rather use the wavelength λ than f, note that λf=c, so W=hc/λ. I am not aware of any name this equation has. Once you have defined what W is, the only physics is Einstein's postulate that the energy of a photon is hf.

QUESTION:
According to a video game, a 20kg iron bullet traveling at 1.3% the speed of light will impact a surface with the force of a 38 kiloton bomb when sent through the vacuum of space. But is it true?

ANSWER:
First, it is not force but energy delivered that you want to talk about. What is the energy delivered by this "bullet"? We can use Newtonian physics to detrmine the answer because this speed is very small compared to the speed of light. So the speed of the bullet is v=0.013x3x10⁸=3.9x10⁶ m/s. So the energy E can be written as E=�mv²=1.52x10¹⁴ J where m=20 kg is the mass of the bullet. Now, 1 Joule (J) is 2.39x10^-13 kilotons of tnt, so E=1.52x10¹⁴x2.39x10^-13=36.4 kiloton. This is pretty close to 38 and video game guys may have used a slightly larger value of the conversion factor.

QUESTION:
I am wanting to build a greenhouse/garden with a big water tank buried underground. I would like to add a spigot at slightly above ground level where I can attach a hose or fill a bucket. Would the pressure from gravity on the top of the water in the tank be enough to push water out of a pipe say half a meter above the top of the tank? Let�s say a 40 mm pipe.

ANSWER:
Absolutely not! What you refer to as "pressure from gravity" is actually pressure from the atmosphere and atmospheric pressure is virtually the same at the hose as it is at the tank. If you want to have the tank buried you will need a pump pull up the water. If all you generally need is a bucketfull, just get a hand pump like farm houses all used to use to bring up water from a well.

QUESTION:
Would less energy be required to launch a spacecraft by having in take off like a plane, using a runway/ramp? Using retractable/eject-able wings for lift seems like you would conserve energy, as opposed to launching straight up (fighting gravity without benefit of atmospheric lift provided by wings). A pilot buddy of mine said the energy used would be the same, regardless of method used.

ANSWER:
I expect that lift from wings would be trivially small compared with the force needed to accelerate up to orbital speed. Also, because of energy lost to air drag, it is required that the rocket get out of the asmosphere as quickly as possible. Also, because most rockets big enough to put significant payloads into space would be much heavier than any airplane, there would be an enormous engineering problem to get wings big enough and strong enough to provide lift just to keep it from falling, let alone rising. And, I think your buddy is wrong. Space rockets get up to high speeds very rapidly and the energy loss due to air drag would be significant.

QUESTION:
Does an electric car with a direct drive DC motor use any energy to stay stationary on a hill? The car has a "hold mode" which prevents the car from moving downhill when stopped.

ANSWER:
I am pretty sure if the ignition (do they call it that for electric vehicles?) is on that some energy is being used by various electric devices (radio, fan, AC, lights, etc.) but that probably all comes from the battery as opposed to the motor itself.

QUESTION:
Comparing gas combustion vehicles to electric vehicles, if a Camry/Accord weighs 3300 lbs and maybe add 100 lbs for gasoline and if an electric battery weighs 1000 lbs making an electric vehicle weigh about 4300 lbs, what is joules per mile to move a gasoline combustion car vs joules per mile to move and electric vehicle? Electric vehicles weighing so much more I just can't see how they are more energy efficient. Am I missing something. Also wouldn't you agree that electric vehicles are by and large powered by hydrocarbons?

ANSWER:
Yes, you are missing something. Electric and internal combustion engines have very different efficiencies. Electric motors can have efficiencies up to about 85% whereas internal combustion engines are more like 40% efficient. This means that an internal combustion engine wastes approximately 4 times as much energy to heat than its electric counterpart (60%/15%). A reasonable estimate of how much of the energy is lost because of the weight to keep a car running at a constant speed would be that the amount would be proportional to the weight; so the case you give would be that the internal combustion car would waste about 0.77 (3300/4300) that of the electric car due to frictional forces for similarly designed cars.

So there is no question that the electric car would be the hands-down winner in a Joule/mile comparison. However, this is only part of the story. To make a complete inventory is a much more complicated issue. As you note, most electricity is still generated using hydrocarbon sources�oil, natural gas, and coal; as time goes on, this will change to more renewable sources. Also, the energy used to manufacture the batteries and transport them to the vehicle is not negligible. Also, transporting gasoline to the consumers is responsible for carbon emissions whereas transporting the electric power is not.

QUESTION:
Is there any way we can measure surface tension of liquids at a school laboratory or our home (in other words, without any special equipment)?

ANSWER:
First I want to apologize to the questioner for taking so long to answer this question; when I first researched finding a way I was unsuccessful and put it aside for the time being, just returning it to today. Today I found an excellent article giving three ways using only easily available equipment.

QUESTION:
I'm writing a book where at one point my main character, in a single pilot private airplane, falls from the sky before she catches herself. I need to know how many G forces would affect her as she falls. I have a few numbers but I'm not sure what to do with them! Her plane weighs about 7500 lbs. She falls for 45 seconds. The average commercial plane weighs about 530000 lbs and receives between 6-12 G forces as it falls. How many G forces does my small aircraft receive?

ANSWER:
I find your question very puzzling. Let's think about the falling airplanes. If you drop an airplane it will begin to fall with the acceleration due to gravity g which is about g=32 ft/s² which means that during each second it falls, it speeds up by an amount 32 ft/s. If that airplane's weight is the only force on it, it experiences zero G force; it's like someone in an elevator where the cable has snapped and that person feels "weightless". But the weight is not the only force on the plane, there is also an air-drag force upwards; so, when the plane has acquired some downward speed it has an acceleration less than g so the net force on the plane is a little bigger than zero G force. Since the drag force gets bigger as the speed down gets bigger, eventually the plane will be falling with some constant speed called the terminal velocity. Now someone on the plane will feel a G force of exactly 1.0 G. So I have no idea how that 6-12 G for a falling airplane could be right unless the plane was in a rapid spin as well as falling so that the forces on the wings could very well exceed their weight resulting on forces bigger than 1.0 G. Also the magnitude of the air drag depends on the orientation of the plane�a plane falling nose down would have a much smaller air drag at some particular speed than one falling belly down. So, I don't know what you are hoping to achieve in your book, but getting a huge force on a passenger in a plane dropping out of the sky is not going to happen. Since you indicate that she manages to get the plane to stop falling at some point, she might experience a large G force during that time since that would require her achieving a very large acceleration upwards during the maneuver to stop her fall.

QUESTION:
Is Galileo law of free fall true?

ANSWER:
It is true only if air drag is neglected. If there were no air it would be exactly true. Imagine dropping a golf ball and a sheet of paper; they obviously do not experience the same accelerations as they fall to the ground.

QUESTION:
Will Rotational inertia increase as a gymnast moves from an extended position to a tucked position?

ANSWER:
No, rotational inertia (usually called moment of inertia, I, decreases as mass of the object is moved closer to the axis of rotation. (See the question immediately following yours.) Since the angular momentum (moment of inertia times angular speed, ω) is approximately conserved in this situation�Iω=constant�reducing I will cause ω to increase.

QUESTION:
We see that ice skaters spin faster then they draw in their arms. What happens if then simultaneously draw one arm in while extending the other? Would this negate the effect? Obviously the center or gravity would shift, but assuming this was compensated for would there be any change in rotational speed?

ANSWER:
The wording of your question is confusing. She starts spinning with her arms out. One thing she can do is pull both in which causes her to spin faster. If she only pulls one arm in she will also spin faster but not as fast as when she pulls in both. Ignoring friction, if she puts both arms back out she will slow down to the spin speed at the beginning. The physics reason is that if an object is spinning about its axis you can speed it up by making its moment of inertia smaller; if the object is spinning about its axis you can slow it down by making its moment of inertia larger. The moment of inertia is a quantity which measures how close the mass of the object is to the axis of rotation; if the skater could pull in not just her arms but suck her whole body in so that it is all say 5 cm in diameter it would spin enormously fast! I have seen skaters begin the spin with one leg extended out which gives even more spin as she moves the mass of arms and that leg in closer to the rotation axis.

QUESTION:
I have gotten into knife sharpening lately, which has Got me thinking about steels� structure. Can steel, in theory, get as Sharp as one molecule at the edge? Can some steels, in theory, get sharper than others, Because of different structual grits?

ANSWER:
I am not going to get into the steel issues because knife and sword making and its sharpening is almost an art form. Also, you have to ask what the knife is for; generally judged the sharpest is one with a 10� bevel on the edge. But you are probably interested in the limits. I have read that a diamond can be sharpened to the degree where the edge is about 1 nm (10^-9 m) wide; the diameter of an atom is about 0.2 nm, so the edge is around 5 atoms wide. Obsidian, favored for arrowheads, can be about 3 nm wide, about 15 atoms.

QUESTION:
My understanding is if I drop an object, the object is stationary and it the earth that rises to meet it @ 9.8 meters sec squared. It is very difficult for me to visualize why the earth can appear to remain stationary while it continues to expand.

ANSWER:
I don't know where you got your "understanding", but it is totally wrong. The object accelerates toward the center of the earth (vertically) at g=9.8 m/s² and the earth remains at rest. If you want to get really picky, you could say that the object accelerates downward with an acceleration ^g=9.8 m/s² and the earth accelerates upward with an acceleration a tiny bit larger than zero. Here is how it goes: Newton's third law states that if the earth exerts a force on the object of magnitude W (the weight which has the magnitude mg where m is the mass of the object), then the object exerts an equal and opposite force on the earth. Newton's second law says that the acceleration of an object is equal to the force it experiences divided by its mass. So, call the mass of the earth M and its acceleration A; then the acceleration of the earth is A=mg/M and the acceleration of the object is a=g. The mass of the earth is M=6x10²⁴ kg so, for an object with mass 1 kg the earth's acceleration is A=1x9.8/6x10²⁴=1.63x10^-24 m/s², essentially zero!

QUESTION:
I'd like to know if solid objects move through the different gases (hydrogen, methane, oxygen etc) differently. I'm 51 yes old and this isn't my homework but I asked this same question multiple different ways and the internet so far has yielded no answers of any real relevance.

ANSWER:
When an object moves through a gas it experiences a drag force F in addition to any other forces which might be acting (e.g., gravity). The force, which acts opposite the object's velocity v, is given approximately by F=�ρv²CA where ρ is the density of the gas, v is the speed, C is a constant which depends on the shape, and A is the effective cross-sectional area the object presents to the onrushing gas. For example, for a sphere of radius R, C=�, A=πR², so F=�πR²ρv². Clearly, the density of the different gasses will be different for a given pressure and temperature of the gas. So the answer to your question is "yes".

QUESTION:
I have been atempting to find a formula that calculates the mass of a planet that dose not rely on acceleration due to gravity OR a formula that dose not rely on planitary mass to calculate acceleration due to gravity, and in both situations densty is not known. i have noticed that if i find a formula that completes this calculation then the answer can then be used to determine the others value. I have found the formula M = 4π²r³/gt² But to my understanding the value of (g) is acceleration due to gravity so cannot be the formula i am looking for, in an ideal answer the formula is one that could be applied to a foregn planet and insted relys on values visualy obtained; orbital period, orbital radius, planitary diamiter, planitary volume in any number or order of visualy obtained values. If the above formula is not the one i am looking for can you include the correct one please?

ANSWER:
You have run upon the problem which Newton had to struggle with�it is not possible to find the mass of a spherical gravitational source without knowing the magnitude of the force between two point (or spherically symmetric) masses. Newton's guess for the force between two point (or spherically symmetric) masses, M and m, separated by a distance R, was that the magnitude of the force F is proportional to Mm/R², or F=GMm/R² where G is the proportionality constant. Just knowing this results in completely deriving Kepler's laws of planetary motion, but you could not find any masses without knowing the proportionality constant G. Newton made a lucky guess that if the average density of the earth was between 5 and 6 times the density of water and g=9.8 m/s², then G=(6.7�0.6)x10^-11 m³�kg^-1�s^-2; this is extremely close to the modern value G=(6.67430�0.00015)x10^-11 m³�kg^-1�s^-2. (See more detail here.) This should help you with your dilemma. At the surface of a planet of mass M and radius R the weight of a particle of m is W=mg. But the weight of a particle is the force which the planet exerts on it, i.e., mg=GMm/R²or M=gR²/G.

Laws of physics generally take the form of proportionalities. To see if they are valid laws one must make the proportionality become an equation by introducing a proportionality constant. To determine if this is a correct law, one must determine the constant by doing an experiment.

QUESTION:
In one of the Superman movies, Superman saves a plane from crashing by holding it by the nose and lowering it to the ground, in the show The Boys, a character named Homelander refuses to save a plane full of people because he claims it's impossible to save the plane without destroying it. Do you think it would be possible for a person with superpowers to hold a plane by its landing gear to slow the plane down and lower it to the ground? Yeah I'm arguing with somebody on facebook about this, I think it would be possible, they're calling me names and saying I don't understand physics, so I googled "ask a physicist" and here I am. Hope you can answer my question and I hope you enjoy thinking about it.

ANSWER:
To see a clip of what is being described here, link here.

The site ground rules specify that questions based on unphysical assumptions (superpowers?) are not answered. In this case I feel that some discussion is warranted. One of my biggest problems with Superman is, what does he do for propulsion? In order to stop or start or turn there needs to be a force on him. He can't exert a force on himself. And if he pushes hard enough to stop the plane in midair he would have to exert a huge force but Newton's third law would stipulate that the plane would exert an equal and opposite force on him; because his mass is tiny compared to the mass of the airplane, the plane would have a tiny change in its speed whereas Superman would be pushed off with an enormous speed opposite the direction he is pushing. Also, the "skin" of an airplane is relatively thin and pushing with a huge force over a small area would punch right through it. No matter how strong he is, there is no way this is in any way possible without violating the laws of physics. Of course, if you say it is possible because superpowers permit laws of physics to be violated, then it is possible; but if that were the case, the discussion would be inappropriate for a physics site.

The stuff I have been talking about is discussed in more detail than my answer on this link.

QUESTION:
I hope you can help with a slightly random one. I happened an article about the recent Nobel Prize-winning work done by Alain Aspect, John Clauser and Anton Zeilinger concerning entangled quantum states. Full disclosure, I am not an academic or even remotely versed in your world. But, as a layperson (I'm creative in advertising) it certainly caught my imagination and got me thinking. My question relates to the experiment's use of lab-grown diamonds over natural ones. I understand their research has untold implications and possibilities, but for myself (and my wandering creative mind), it got me thinking more deeply around the "what ifs" involving the emotional value people could put on having a pair of entangled diamonds. For decades, natural diamonds have been the symbol of true love, but what if lab-grown diamonds could tell a greater love story, based on the idea that only they can talk to each other and feel each other's vibrations? Knowing this, my burning question centres around - Whether entanglement is exclusive to lab-grown diamonds vs mined ones. And do the pair of diamonds need to be made at the same time? What makes them suitable for entanglement? This is what we are hoping to find out in the simplest of terms. I'm looking into this as part of a pro-active passion project. It's a story I feel worthy of telling and I'd value any assistance or guidance. When considering the true value of lab-grown diamonds, it's not about the price or rarity, but more about the emotional worth to people. And if entanglement can only happen between the lab-grown variety over mined ones, then it's a story that could radically change people's opinions and actions when buying them.

ANSWER:
As I have admitted before, I am not an authority on entanglement. However, I believe that I can answer your question quickly. Every crystal has some flaws, either presence of impurity atoms or dislocations of the crystral structure itself; no diamond is 100% pure carbon atoms. The presence of certain impurities in a crystal often determine its color. It turns out that a particular impurity, nitrogen, in a diamond is a particularly useful candidate for studying entanglement; called nitrogen vacancies (NV), two NVs can be entangled and are quite stable. This is what is being entangled in the experiments you cite, not two diamonds. My guess is that lab-grown diamonds are used in these experiments because the impurities can be controlled during the growth process. Your idea was lovely and romantic, and I am sorry to have to shoot it down!

QUESTION:
This is an odd one recently I saw a graphic saying that the Ocean on Titan could be 100KM deep and have a 20KM ice sheet. What my question is, is what would the pressure do to water a 100KM deep? I know from my crude calucations that 1km is 100bar on earth so that means the pressure could be 10000 bar or about 90,000PSI. Would some sort of fusion occur or would any heat be generated at that depth at all?

ANSWER:
It really isn't clear what the oceans are composed of�water, methane, ammonia, mixtures, etc.�but you have made some other miscalculations so let's just do the necessary calculations for water as an example to understand how to do it. First of all, you have apparently used the acceleration due to gravity to be about 10 m/s², just like on earth. But, the actual value of g on the surface of Titan is only about 1.35 m/s², much lower. Since the depth you want to calculate, 120 km, is very small compared to the radius of Titan, about 2600 km, I will assume that g=1.35 m/s² is constant. (It will actually get smaller as you go deeper.) Water is nearly incompressible so I will approximate its density ρ=10³kg/m³ to remain constant. Also, because the density of ice is approximately the same as water, I will just calculate the pressure at a depth d from the surface of the ice as if it were water also. Finally we can write P=P₀+ρgh where P₀ is atmospheric pressure at the surface, about 1.47x10⁵ N/m². So, P=1.62x10⁸ N/m²=1.62x10⁸ Pa=1620 bar=23,500 PSI. The phase diagram shown shows that for the water to not freeze at high pressures it must be at a temperature greater than 0� C up to about 10⁷ Pa. At about 2x10⁸ Pa, about where I have estimated the pressure to be 120 km down, it could remain liquid down to about -50� C. If there is liquid water, there would have to be some heating mechanism�vulcanism, radioactivity, tidal force friction, etc. I don't believe the pressure itself would cause any heat and certainly not fusion.

QUESTION:
The no-communication theorem seems to forbid faster than light communication between entangled things (particles seems to specific here). 'Setting' the quantum state destroys the entanglement. There are however now ways to "gently measure" the superposition state without destroying it. This would appear to permit a scheme where faster than light communication is possible without violating the "no-communication" theorem. Take an entangled pair and send one to the moon, use gentle measurement to verify the particle on the moon is still in superposition, and measure the one on earth. The timing of the collapse of the 'moon' particle can contain information. We don't care what the collapsed state is, just the timing of it. With several particles we can use a 'Morse' code to send long and short intervals between superposition collapse. Is this an experiment worth doing?

ANSWER:
DISCLAIMER: I am by no means no expert in the subtleties of entanglement and had never heard of "gentle measurements" until receiving this question. I have done some quick researching on this and my answer is a quick impression and should not be judged as a fact!

I read a brief description of the experiment which was done. "The "gentle measurement" was performed on a single superconducting qubit, not on a particle entangled with another. It seems unlikely to me that this method could be applied to an entangled pair of particles without destroying the entanglement.

QUESTION:
How we can calculate the number of photons comming out of a light bulb? Is there any equation? Can we use the same equation with x-ray to know the total number of photons per x-ray?

ANSWER:
If a lightbulb were monochromatic it would be pretty easy to estimate this; the reason is that white light has a whole spectrum of different wavelengths and the energy of a photon of a particular color depends on the wavelength. Another issue is that, depending on the kind of light bulb you use, there will be a great many photons not in the visible range; if it is a light bulb you are interested in, you are probably mostly interested in the visible light. The way that light is measured is very complicated, even convoluted at times. In an earlier answer I have written one of my longest ever answers, addressing how light intensity units are defined; near the end of that answer I estimate the flux of visible light of sunlight to be roughly 4.4x10¹² (photons/s/m²). This may serve as an order-of-magnitude rough estimate of the number you seek because the amount of sunlight falling on one square meter would probably be comparable to the light from a 100 W light bulb. The number of photons would depend on the type of bulb. An incandescent bulb has many photons outside visible whereas an LED bulb has many fewer. This can be seen in the figure showing spectra of LED, incandescent, and CFL bulbs compared to sunlight at earth's surface. Note that the LED has very little of its spectrum outside the visible region whereas the intensity of an incandescent bulb is still rising at the red end meaning much of the radiation is in the form of heat.

Regarding x-radiation, at least for medical x-rays, you could probably do a reasonable estimate for a particular machine because the dominant parts of the spectrum are discrete peaks as shown in the second figure.

QUESTION:
My understanding is Uranium and its daughter elements naturally shed mass as they change from one element to the next. Is this change effecting the gravity of the earth no matter how slight?

ANSWER:
Lots of nuclear reactions result in a loss of mass. But, mass being a form of energy, the released energy is not lost but exists in forms other than mass. It could be heat, light, kinetic energy of ejected particles, etc. Most of this energy does not leave the earth, so the total energy density (which determines the gravity, not just mass) of the earth is essentially unchanged. Indeed, energy lost from the earth, some photons for example, will result in a tiny (and I mean unmeasurably tiny) change in the earth's gravity.

QUESTION:
Let's say you're driving a car 70 mph with all the windows closed. There's a fly buzzing around your head, and then you hit a telephone pole. Obviously we know that everything in the car will hit the windshield due to the momentum, but what happens to the fly? Does he hit the windshield too or does he remain in the middle in the air?

ANSWER:
Let's talk about what happens to the air. All the molecules are moving around with speeds mostly much more than than the speed of the car. When the car hits, there is a tendency for the molecules move forward but they don't all smash into the windshield; rather, there is a tendency for the pressure in air to become very slightly higher closer to the front of the car. The fly does not witness any appreciable difference in the air, which is the environment he encounters, and will fly around happily.

Actually, a more interesting question is what if there is a helium balloon in the car. It will move to the backwards instead of forward, experiencing a buoyant force backwards because of the gradient of air pressure.

QUESTION:
You're standing 3 feet from a mirror looking at yourself. Perceptually, you're seeing your body 6 feet away (3 feet to the mirror and the reflection is another 3 feet), but how far is your actual vision traveling? If you look at the mirror frame, that image is 3 feet away, but when you're looking at your reflection, does the vision travel 6 feet because the image has to travel to the mirror 3 feet and then to your eye 3 feet? Another way to ask is if you shine a flashlight into the mirror from 3ft, then the light has to travel 3 feet to the mirror and 3 ft back to your eye, so 6'.. is this correct?

ANSWER:
This is a matter of semantics. It actually makes no sense to talk about how far your vision travels. Your vision doesn't travel. This is a virtual image so it is not actually where you would deduce it to be. If you want to know how the light travels, that is 6 ft. If you want to know where the image is, that is also 6 ft.

QUESTION:
Two spacecrafts tethered together; one heavier than the other tumbling through space, where the heavier one gets an intermittent push, and its momentum of no more than 10 N per day over a year; what would its maximum velocity be? Or would it keep on accelerating after no further energy is applied to the system?Two spacecrafts tethered together; one heavier than the other tumbling through space, where the heavier one gets an intermittent push, and its momentum of no more than 10 N per day over a year; what would its maximum velocity be? Or would it keep on accelerating after no further energy is applied to the system?

ANSWER:
This question is problematical on several levels. First, by "tumbling through space" I presume that you mean that they are rotating about the center of mass of the pair with the tether taut. In that case, the system will have both translational and rotational energy and momentum. You have specified that the force is applied to the heavier one, not the center of mass of the system, so the result will be that part of the enegy you add will change the translation energy (�(m+M)v²) and part to the rotational energy (�Iω²). Similarly for linear and angular momenta. When no forces are being applied, the system will have some constant energy shared by the two. But if you continue adding energy you will certainly continue speeding the pair up without limit for a long while; eventually you will have to treat the system relativistically when speeds become comparable to the speed of light. What will absolutely not happen is that it would "�keep on accelerating after no further energy is applied to the system�" This is simply Newton's first law. If you want to get more detailed, you would have to specify not only the only force but the time during which it was applied (force times time=impulse) and work done (force times distance applied).

QUESTION:
In several online references to earthquake magnitudes, e.g Wikipedia states that the energy released is proportional to the 3/2 power of the shaking amplitude. I'm puzzled by this, as in all other wave phenomena I know about e.g Alternating Current, light, sound etc the power is proportional to the square of the wave amplitude?

ANSWER:
In all the examples you cite the waves are monochormatic, they have a single wave length and frequency. But, an earthquake is a spectrum of many frequencies and even defining what you mean by amplitude is tricky. I am not very well versed in geophysics, but I would assume that the 3/2 is not derived from first principles but rather is approximately determined empirically from measurements.

QUESTION:
Assume you travel at a percentage of lightspeed and return in say one year of travel and everyone has aged say 25 years to your one year. If you listen to a radio broadcast from your point of origin what will you hear?

ANSWER:
It will be different on the way out than the way back. Although the example in a previous answer has `every person on earth having aged 8 years more than you, not 25, the discussion in that answer will let you get the idea of what to expect.

QUESTION:
Can two strings connected at the top (like an upside Y design) pick up double the amount of weight (equal amount of weight at the end of each string) rather than just one string alone?

ANSWER:
The figure shows the forces I want to talk about. Focus your attention first on the knot where the three strings meet. There are three forces on the knot, T₁, T₂, and T₃. Assuming the weight is uniform, the tensions in strings 2 and 3 are the same; I will call that tension just T. Also shown are the components of 2 and 3, x being horizontal and y vertical. Also, because of symmetry, the x-components of 2 and 3 cancel each other out. So we can write that T₁-T_2y-T_3x=0=T₁-2Tcosθ, or T=T₁/(2cosθ). Next, focus your attetion on the block which has three forces on it, its weight W and the two strings attached to it but in the opposite direction as they pull on the knot (I have just drawn the components here.) Again, the x-components cancel out and we have W-2Tcosθ=0. Putting both results together we find that T₁=W, the same result as if you were lifting it with one string. Actually, it is much easier to look at all the forces on the block plus the knot; that way anything between the two is irrelevant. You will always find that to lift something your must exert an upward force equal to its weight.

QUESTION:
I don't do homework anymore. Not at 75 years old. But I do like learning physics. Please explain how matter can be solid given that like charges repel and electrons make up the outer clouds (I almost said shells - showing my age) of atoms. Shouldn't atoms repel each other thus making solids impossible?

ANSWER:
Because the atom has a positively charged nucleus, it has zero net charge. So if two atoms are not actually "touching" they will not exert forces on each other. If they get close enough to each other the electron clouds will start to overlap and interact with each other. The result is often that the atoms will actually attract each other. Oxygen and hydrogen actually mostly occur in pairs. You often learn, in a qualitative sense, that atoms share their electrons with their nearest neighbors; that is not surprising because some of the electrons in one atom can be closer to the nucleus of the other atom.

QUESTION:
If entangled particles are like two coins spinning on the desk in front of me, and I slap my hand down on one of the spinning coins and then read that it landed on heads, did the other coin stop spinning instantly, without me touching it, and did it land on tails? I'm obviously a layman trying make sense of all of the various explanations I see on the internet.

ANSWER:
I like the analogy of a coin with two possible "states", heads up or tails up, to illustrate a spin � particle which has two possible states, spin up or spin down. And we could imagine the spinning coin as having equal probabilities of heads or tails like an electron could have equal probabilities of up or down. Suppose that you and I each had an electron and each of prepared the electron's state to be a mixed up/down state. Then if I measure mine and it turns out to be down, yours doesn't instantly become up. Why not? Because these two electrons are not entangled since they have been independently prepared. Similarly, your two coins are not entangled and when you measure yours it could be either up or down with equal probabilities.

QUESTION:
How much electricity is required to move a 5,000 pound EV up a 20 degree incline

ANSWER:
What you really want is not "how much electricity" but "how much energy from the battery". Also, telling me the incline does not tell me how far up you go, i.e., how far up the road do you go at a 20� incline. Suppose you go along the road for 1 mile. Then I calculate that energy supplied if there were no friction would be 1.22x10⁷ J=3.4 kw�hr. I have assumed that you go a constant speed. Due to friction this would be maybe about 10% bigger.

QUESTION:
If I have two syringes connected by a 10,000 km tube filled with liquid. Syringe A is open/full. Syringe B is closed/empty. I press down syringe A causing syringe B to open/fill up. Would there be any latency between the time A is pressed, and when B fills up? There is no air in the system, and the tube isn't flexible.

ANSWER:
When you press you create a compression in the fluid at A; this compression travels at the speed (v) of sound in the liquid to B. So the time it takes 10⁷v. If the fluid is water which has approximately v=1500 m/s, the time is about 1.5x10⁴ s=41.7 hours.

QUESTION:
Does the pressure of gas in a sphere follow an inverse cube law based on the principle that the change in volume is a cube of the radius?

ANSWER:
Certainly the pressure in a sphere is inversely proportional to R³ if temperature and amount of gas remain constant. But, who cares? Radius of a sphere is not what you would call a thermodynamic variable the way volume is.

QUESTION:
My question is that if the moon doesn't have an atmosphere which means it doesn't have a pressure too how the apollo 11 astronauts spacesuit didn't explode? Based on boyle's law?

ANSWER:
What matters is the net pressure on the space suit. Although there is zero pressure outside the suit, there will be approximately atmospheric pressure P_A inside. The same suit on earth could have P_A outside and 2P_A inside and not explode.

QUESTION:
Please explain how opposite processes, fission and fusion, both release energy. It seems to me that fusion would need energy input to fuse atoms, yet it releases energy.

ANSWER:
See an earlier answer.

QUESTION:
I read the Rama series by Arthur C. Clark and I have a question. There is a circular 'ocean' that is held in place by the centripetal force of a revolving cylindrical spaceship. One bank of the ocean is level with the fluid the other bank is 50 ft high. A character studying the spaceship states that the 50 ft is to contain the ocean while the ship accelerates and therefor they can calculate a maximum acceleration of the ship. Is this possible? How would they do it?

ANSWER:
This is a fairly easy problem as long as you used some reasonable approximations. I will assume that the depth of the ocean (d) is very small compared to the radius of the cylinder (R) so that the centripetal acceleration (a_c)is approximately equal at all depths, a_c=Rω², where ω is the angular velocity. I have done a bit of research and found some pertinent information:

R=8,000 m,
The ship is 50,000 m, long,
the "ocean" is a belt L=10,000 m wide located at the center of the ship,
the bank is h=500 m high (not 50 ft),
ω=0.25 rpm=0.026 s^-1; therefore, Rω²=a_c=5.48 m/s², a little more than �g.
I could find no information about d but it needs to be small compared to R as noted above.

The first figure shows a schematic sketch of the ocean. I am going to focus on a small slice, indicated in red, in doing my analysis. Whatever happens here will be the same as any other slice I focus on. The acceleration of the whole ship will be to the right; you can imagine that the water would want to be pushed toward the left and we want to ultimately want to find what the maximum acceleration is if the 500 m bank is to contain the water.

The second figure shows my slice of the ocean when the ship has some acceleration a to the right. In this figure, the axis of the cylinder is straight up 8,000 m above the bottom of the ocean. It is very important to note that x- and y-axes have very different scales; I do this for clarity since angles get small. The surface of the water will be, as drawn, a flat plane with an incline angle θ. I know this because the acceleration is uniform in both x and y directions. If a=0 the surface will be where the green dotted line is. I will now analyze the problem by focusing on a tiny piece of the water of mass m on the surface; any location will work because of the uniform accelerations. I am going to do this problem from inside the ship; as you know, in an accelerating frame of reference Newton's laws are not correct but you can force them to be true by inventing fictitious forces; the fictitious forces here are -ma and -ma_c shown in yellow as well as the net fictitious force. Of course there is also a real force (not drawn) on m, the force by the surrounding water on it, and it must be equal and opposite the net fictitious force because we have made this a statics problem. So the fact that the net fictitious force is normal to the surface is not an accident, it is a necessity; fluids can exert only normal forces at their surfaces, not tangential. Now by simple geometry we can determine the angle θ to be θ=tan^-1(a/a_c). We can now do the case in point to find the maximum acceleration, a_max=a_ctan(θ_max)=5.48x(500/5000)=0.548 m/s² and θ_max=5.71�. (Note, however, that slowing down is also an acceleration; in that case a would point backwards and the water would spill off to the right. To slow down you would have to turn the the ship around first.)

Finally, a few comments on the above analysis:

I have drawn the second figure so that d=h=500 m. Everything I did above was right if d≥h.
If d<h the water eventually, as acceleration increases, will no longer extend all the way to the right hand shore.
With d≥h=500 m the surface always goes below the a=0 plane exactly halfway between the two shores. This is because all the water going to the left half must leave the right half.

QUESTION:
I'm a physics student who just had a few questions and I would really appreciate it if you could answer them for me: I was studying granular materials and how if you fill up a bottle with rice and then insert a stick or spoon into it, then at a certain level of immersion, you can pick up the whole bottle using the spoon. I know that all of this relates to the compact density of the granular material but what do you think are other things I should focus on to better understand this topic? Do you suggest that I talk about any other physical properties of granular materials to understand this phenomenon (like dilatancy or shear force, if so then how are these concepts linked with the topic?)? I also would love to know what you think are the parameters of this experiment (of lifting up bottles of rice by immersing a stick or a spoon to a certain depth). What are the things that are being assumed when explaining this phenomenon? What things will cause the experiment to not work? Like is there anything we should take care of (like moisture content of granular materials or the shear force being applied to them)? Are there any equations I should acquaint myself with?

ANSWER:
Your question violates the site ground rule requiring "...single, concise, well-focused questions..." Still, I will make some suggestions on data you should consider taking. If you are a student, it is probably better to approach this problem empirically rather getting into theoretical analysis too deeply. I would choose one material, rice for example, and think about what variables might come into play. What you can most easily measure is the depth at which you can first lift the container, i.e. the upward force is equal to the weight of the container plus grains. Some variables affecting this are the height of the container, the cross-sectional area of the container, the shape of the container, the surface area of the "stick", the material the stick is made of, the shape of the stick, etc. And I would keep it simple, cylindrical containers, sticks with only vertical surfaces (circular or square or rectangular crossections). I would try to use containers which were much lighter than the granular material. This would give you a lot of data and graphing it might yield interesting results. You might now try the same process with a different matrial, e.g. dry sand. To tell the truth, I really do not know much at all about this kind of physics but I do know that analysis of these kinds of problems usually involves computer simulations, not first-principle physics. In fact I cannot actually envision being able to lift a container of rice like this; perhaps using a bottle, as you have done, with a neck is required and my suggestion of an open topped cylinder is impossible. Good luck!

QUESTION:
I have a question about gravity So as we know gravity is significantly less on high mountains or tall buildings and increases as we lose height. My question is that if we have 2 objects with the same volume and mass, 1 falls on a mountain and one falls on a beach ( note that they are released from the same height based on the surface they shall fall on ) Will they both reach the ground at the same time or will their speeds be different?

ANSWER:
If you neglect air drag, the one on the mountain will experience a smaller weight force and will therefore have a smaller acceleration. It will therefore arrive at the ground later and with a smaller velocity. But air drag might very well not be negligible. On the mountain top the air density is less dense than at sea level and therefore the air drag will be smaller. Now it is a more ccomplicated problem. If, in addition to your stipulation of equal masses and volumes we stipulate the same shapes, the time it would take to reach the bottom would depend on the height of the mountain and the height of the fall. (I have assumed that the height of the fall is small enough that one can approximate that the change of air density and the gravitational force are negligible.)

QUESTION:
If a fly was the bottom of the cylinder that weights 100 n. And then the fly flies around the open cylinder what is the weight of the clyinder is less than 100 or equal to 100n

ANSWER:
Also important is the weight of the air in the cylinder. The weight of the cylinder is always equal to 100 N; the question is: if the cylinder (and fly at rest) are sitting on a scale, what does the scale read when the fly flies? See an earlier answer.

chis question has no answer because heat is defined as the flow of energy, not an amount of energy. For a detailed discussion of thermodynamic terminolgy, see an earlier answer.

QUESTION:
It seems evident that global warming is driving more moisture into the atmosphere. Is it possible that moisture is escaping to low-earth orbit, never to return?

ANSWER:
The velocity necessary to achieve near-earth orbit is about 18,000 mph. The most probable speed of a water molecule at 120�F is about 1220 mph. Escape velocity from the earth is about 25,000 mph. I don't think you need to worry too much about water molecules escaping from earth.

QUESTION:
I've seen that a recent AI analysis of particle collider data suggests that a proton has an extra charm and anti charm quirks, if this analysis proves to be a discovery above sigma 5, could it help explain dark matter? I just haven't seen anyone talk about this, thanks in advance

ANSWER:
Why would you think this would have anything to do with dark matter? The mass of the proton is known to high accuracy so these data would only alter the model for the internal structure of a proton, not its mass. No change in mass means no solution to the unknown extra mass supposedly implying dark matter.

QUESTION:
let's say a bag of rice was dumped from a flying plane, and you knew every conditions that would act on each grain. Every gust of wind, complete topographical information, the position of each grain of rice, exact gravity force, everything. If you had unlimited resources, computing power, time etc. Would it be able to calculate where every grain of rice would end up?

ANSWER:
These are some pretty severe suppositions you are placing. And you did not include effects on the grains due to their shapes. Let's start with a single grain. In principle this is a classical mechanics problem, solvable. But there are some serious problems with what will surely be a major contributor to the problem, air drag; there are quite good approximations for the air drag force, but they are not exact. For that reason, you could only predict approximately where any particular grain would land. If there are many grains, there will be interactions among them. These interactions would be mainly due to disruptions in the air flow due to the motion of the grains themselves; and if two grains collide, it would be virtually impossible to predict the velocity of each after the collision. Maybe most important is that the motion of the air is chaotic, not predictable for any particular position at any predictable time. I could envision the positions being predictable if the experiment were performed in a perfect vacuum and care was taken in dumping them that they be far enough apart that they never suffer a collision.

QUESTION:
If I were in London England and launched a drone with 6 hours of battery and set it to hoover perfectly still, when the battery died would the drone land in London or America?

ANSWER:
What you need to understand is that your drone is rotating around the earth's axis just like anything "at rest" is. When you set it up to hover over London it is already moving right along with London. The drone flies relative to the air, so if you set it up when the air is still and if later a wind starts blowing, the drone will move with the wind; but it will certainly not get blown as far as America is from London in six hours.

QUESTION:
We're having a lively debate at work regarding best driving practices for fuel economy, ad we've finally settled into two camps on one specific topic; what to do when approaching a hill. Group 1 believes that the driver should always coast on downslopes and never touch the gas. Their reasoning being to cash in on all the free momentum you can get. The 2nd group of us dissent and claim that's exactly when you should accelerate, with the rationale of using gravity as a catalyst for a more fuel efficient fuel burn. Is there a clear cut answer to this; and if not, what's a good way to think about the problem?

ANSWER:
As you go down the hill do you suppose you use more fuel when coasting or accelerating? It seems to me the answer is obvious. Suppose the hill is 1 mile long and the accelerating car consumes 0.1 gallons of gas and the coasting car consumes 0.05 gallons; for that leg of your trip the coasting has 20 mpg and the accelerating has 10 mpg. If your car is a hybrid you will consume no gas and the energy you gain by speeding up will be saved in the batteries so this mile was free when computing mpg. I'm afraid that "using gravity as a catalyst for a more fuel efficient fuel burn" means nothing to me.

QUESTION:
When radiation passes through a GM-tube the gas inside is ionised. How come that a GM-tube is reusable if the atoms in the gas change. They lose electrons, so those atoms wouldn't be able to absorb the energy of the radiation the same as gas that hasn't already been ionised. So wouldn't the gas that can be ionised eventually run out?

ANSWER:
These tubes are filled with a noble gas, helium, neon, argon, etc. Many atoms (let's say N) become ionized as the radiation passes through the gas. But they don't stay ionized because the we now have N free electrons and N positive ions and they recombine because the Coulomb force attracts electrons to to the ions.

QUESTION:
I am out of high school and looking to strengthen my understanding of physics, this question has been bugging me. For third law, it states that every action force has an equal or opposite reaction. How does third law apply to rockets? Everyone tells me that it is the act of throwing something or the opposite reaction force that propels the rocket or the balloon, but I think they are all wrong it is not because of the releasing of the fluid, I think it is the net force within the system of the rocket ship or the balloon that pushes it up. Am I correct?

ANSWER:
I suggest that you read a recent answer on jet ski propulsion. This addresses the issues about rocket propulsion. Your explanation for rocket propulsion is wrong. Newton's third law is indeed the correct explanation.

FOLLOWUP QUESTION:
So I read the dialogue/conversation(chat?) about the seadoo and the "friend" and yes you are completely right (obviously) about how the seadoo would still acccelerate even on air, it's just a different medium. The breakdown of the engine makes complete sense to me aswell, and 100% third law applies, from the impeller being attached to the boat or the body of the vessel and the impeler is forcing out water to the nozzel, so impeller pushe water out water has interaction with impeller impeller is pushed by water in opposite direction voila movement. But from the little information I gathered, it seems rocket engines are different. They are like mini explosions that are contained, and I understand third law is still applied when in earth atmosphere and stratosphere the air will cause drag from it interacting with the vessel but third law doesn't make sense in space which has no air ( their are particles in space like neutrinos traveling understandablly but rockets don't push off of that light sails do.) the point is with the seadoo it is interacting with the water medium and in the other example the air medium to traverse. But in space I think third law does not apply, due to their being a vacuum. But yeah on earth it makes sense, the thrust has to overcome the force air has on the rocket or the drag, so Newtons third applies to earth but I don't think for space.

ANSWER:
A jet engine draws air from the atmosphere and adds kinetic energy (speeds it up using a fan driven by fuel carried in the airplane) to the air which it ejects out the back; the reason that this will not work in space is that there is no air to draw in, NOT because the jet needs air to "push against". The same principle applies to the jet ski motor but water is the propellant, not air; the air has nothing to do with why the jet ski works outside of the water (be sure to note that the question of the 'friend' states "�with a source of incoming water for the water pump inside it�"). It would work just as well in space as long as you fed it water; similarly, a jet engine would work just fine in space as long as you provided it with air. A rocket engine works on exactly the same principle as a jet engine except that the fuel itself is both the impeller and the impelled. Something gives kinetic energy to the molecules (your little explosions); that something is chemistry. But each molecule which is going faster than it originally was, has experienced a force accelerating it out the nozzle and therefore the exiting molecule exerts an equal force back on the rocket ship.

Alas, I believe that one of the most used and least understood principles in physics is action/reaction to describe Newton's third law. Those words should be discarded and the statement of the law should be "If object A exerts a force on object B, object B exerts an equal and opposite force on object A".

QUESTION:
My question is, why is it that fission occurs when a neutron and a 235Uranium collide?

ANSWER:
Any decay mode of a nucleus which can occur (is not forbidden by conservation rules and is exothermic) will happen with some probability. Many nuclei are unstable to β decay and many heavy nuclei can decay by α decay. α decay is just a very asymetric fission. In fact, ²³⁵U undergoes spontaneous fission without any neutrons at all, but its half life is about 3.5x10¹⁷ years; so the rate of spontaneous fission is about 14 fissions/gram/day. However, if you can find a way to add energy to the nucleus you can greatly increase the probability for fission to occur. If you want to have a picture of what is happening we can use a semiclassical model of the nucleus which is very successful, the liquid drop model. ²³⁵U is not spherical but shaped like an American football (prolate); when you strike it with a neutron or the neutron is absorbed, the resulting nucleus is highly excited which means, for a prolate liquid drop, that it is simultaneously rotating and vibrating. If it rotates fast enough the centrifugal force stretches it which, is sufficiently stretched, causes a neck to form which then makes fission likely. See the figure for a cartoon of the fission. The liquid drop model was developed by Aage Bohr, James Rainwater, and Ben Mottelson who received a Nobel Prize for their work.

QUESTION:
If I measure my velocity in relation to light, can I determine if I am stationary or in motion? Since light is measured as the same speed (in a vacuum) by all observers? I.e. I can calculate my speed as x% of the speed of light letting me know if my "spaceship" is stationary or moving with respect to that light?

ANSWER:
I cannot understand how you can measure your speed relative to something which will always be seen by you as moving at the same speed regardless of your speed. No matter what your speed is relative to the some other object (e.g., like the ground if you are in a car), the light you see will always have the same speed relative to you.

QUESTION:
Since acceleration is a change in speed or direction, And moving in a circle at constant speed is therefore accelerating; And since continued acceleration requires an external force, Isn't any point on a spinning object in space accelerating forever without an external force ? For example, I understand that accelerating a rocket in space to v, the rocket will continue at v until it encounters a large object. But spinning the rocket and then letting it go, what keeps the rotation going indefinitely, since any point on the rocket is accelerating due to the spin ?

ANSWER:
For your first question, let's consider you standing on the spinning earth. Are there any forces on you? Of course there are�the gravitational force (your weight) W, the normal force N of the ground, and a frictional force f with the ground, as shown on the figure. So you, standing somewhere in the US northwest, experience these three forces drawn in red; I have also drawn the components parallel and perpendicular to the earth's rotation axis. You are also moving in the circle shown in yellow. So the force providing the centripetal force is the vector sum of all three components perpendicular to the axis.

For the second part of your question, why does the rocket moving with velocity v continue moving with the same velocity if there are no external forces on it? Because of Newton's first law which may be stated that the linear momentum (mass times velocity) is conserved (remains constant) if there are no external forces. If the rocket is spinning, why does it continue to spin? Also because of Newton's first law which, in this case, may be stated that the angular momentum (moment of inertia times angular velocity) is conserved (remains constant) if there are no external torques. And the force which causes each point to continually accelerate is just the force which holds the whole rocket together, electrical forces between the atoms.

QUESTION:
I have thought about F=ma and p=mv but I am missing something and it's driving me crazy. This actually has a practical application for people like me. If you skydive (90 kg person), you accelerate at 9.8 m/s² for approximately 3-5 seconds (estimate) before you reach terminal velocity of about 120 mph (54 m/s). The force required for slowing down is the deceleration that occurs when you open your chute. (At least that is how I think of the issue). So the amount of force to slow down to a velocity of 8 mph is much greater while in free fall than the force required to slow down to a velocity of 8 mph (3.6 m/s) while at a terminal velocity of 120 mph. Right?

ANSWER:
I think your problem is that you are assuming that there is some constant force acting which slows you down from 120 to 8 mph after the chute opens. In fact, the force which slows you down and causes you to reach some terminal velocity (120 mph without open chute, 8 mph with) is air drag force which depends on both the object's speed and its cross sectional area A. A good approximation of the drag force near sea level is �Av²; this approximation is only true if you work in SI units (metric) which is why I converted your speeds to m/s in your question. So, when you jump out of the plane there is no drag but as you accelerate down because of your weight (mass times g, mg) you go faster and the drag force will get bigger and bigger until it is approximately equal to weight down and you will stop accelerating, �Av²=mg. This lets you write an expression for the terminal velocity, v=√(4mg/A). With your numbers, 54²=4x9.8x90/A so the effective area is 1.2 m². Now the chute opens and the area gets much bigger which means that you are now going much faster than the terminal velocity so you will slow down; 3.6²=4x9.8x90/A or A=272 m². Before you open your chute you can speed up by orienting your body straight down (smaller area) and slow down by falling spread-eagle.

QUESTION:
When fusion or fission happens, the nuclear particles lose mass, how?

ANSWER:
If you consider one nucleus for fission or two for fusion and imagine them as each isolated systems, the total energy of each isolated system must remain the same. Don't forget, mass is energy, E=mc^2. So, if mass is lost, as you point out, some energy of the system is now missing. If that is the case, then the missing mass energy shows up as kinetic energy of the final parts of the system.

QUESTION:
Does a 'sea doo' have to be sitting in water in order for it to accelerate? This ignores the fact that it needs a water intake. In other words, if the sea doo was suspended over the water, with a source of incoming water for the water pump inside it, would it still accelerate through the air, without sitting in the lake, and having the outgoing water stream hitting the surrounding water in the lake, in order to provide forward movement at the usual speed?

ANSWER:
Hmm...are you the 'friend' whose question I recently answered?! If so, are you angry to be wrong? The answer to your question is that the sea doo would definitely accelerate; it is simply a jet engine which uses water rather than air for propulsion. If you read carefully my earlier answer, you will see that the propulsion is not due to the ejected water pushing on the water outside but rather due to the ejected water pushing backwards on the impeller blade and therefore on the whole craft.

QUESTION:
I am curious as to what happens when you crack a whip, but specifically regarding how much heat is liberated when it reaches supersonic speed. Let's say for example that I crack a whip while surrounded by a highly flammable substance in the air. Would the heat released be enough to ignite this substance and create a fireball?

ANSWER:
The end of the whip has a very small mass and therefore its kinetic energy is pretty small even though it is moving very fast. The little research I have done leads me to suspect most of the energy goes into the shock wave, not heat. If you want to get a lot of details about the physics of bull whips, go to this link and scroll down to April Jennifer Choi; be sure to watch the video there too. I have included a high-speed camera picture of the shock wave.

QUESTION:
I have been having an argument with a 'friend' for 3 years now about how seadoo thrust works. He says that the water must hit something in order to move the vessel forward. I believe that it is basic mass * velocity = force.

ANSWER:
Your friend is wrong. I would guess that his opinion stems from that old issue about how a rocket works: the exiting hot gas must push against the atmosphere to move the rocket. Therefore rockets do not work in empty space, right? WRONG! Of course, you are completely wrong when you say that the force is equal to the product of the mass and the velocity. Mass (kg) times velocity (m/s) does not even have the dimensions of force (kg�m/s²). The figure shows a diagram of the jet. The engine is not in the figure but is spinning the drive shaft 8. Attached to the shaft is a propeller, referred to as the impeller 10. As it spins it exerts a force on the water which pushes water out the nozzle in a stream B. The water pushed out is now replaced by drawing water in from the outside through a hole in the bottom of the boat (on the left in the diagram). Now comes the physics of the whole thing: Newton's third law says that if the impeller exerts a force on the water, the water exerts an equal and opposite force on the impeller. But the impeller is attached to the boat, so the force on the impeller is a force on the boat which pushes it to the left. (I have deleted the second question about the water and the wall because it makes no sense; resistance is not defined.)

QUESTION:
Spinning metal shafts power our world as in generators, automobiles, etc. My question is does the very atomic or molecular center of a shaft also spin or does it remain still.

ANSWER:
First of all, you cannot apply the concepts of classical mechanics at a microscopic (atomic) level. The notion of the exact point of the axis of rotation being remaining at rest assumes that the rotating object has a uniform mass distribution; at the atomic level it is not uniform at all. Also, in classical mechanics you can talk about a point which occupies zero volume and has no rotational degree of freedom and an atom satisfies neither of those conditions.

QUESTION:
Re: speed of gravitational waves. Why is it said to be the same as the speed of light? The speed of light =1/root(eu) where e is the vacuum permittivity and u is the vacuum permeability. e is an electric field parameter and u is a magnetic field parameter, both of which affect photons. Why would electric and magnetic parameters affect the speed of gravitational waves? It doesn't make any sense.

ANSWER:
We do not have a theory of quantum gravity, and therefore the graviton, which would play the same role for gravity as photons play for electromagnetism ("messenger" of the field), is merely a speculation. However, it is believed that a graviton would have to be massless and therefore would travel at the speed of light. Actually, there is a quite good measurement of the speed of gravity which comes from the gravity wave measurements at the LIGO/Virgo gravitational wave detectors. Most events detecting gravitational waves are from collisions and merging of two black holes, and therefore we do not detect any electromagnetic radiation since light cannot escape a black hole. Rarely, though, gravitational waves from a collision of two neutron stars is observed. In 2017 such a collision was observed and 1.7 s later a gamma ray burst was observed; this implies that the speeds of light and gravity differ by less than one part in 10¹⁵! The 1.7 s difference can be attributed to the fact that photons are affected by interaction with the interstellar medium (not a perfect vacuum) thus slowing them ever so slightly.

FOLLOWUP QUESTION:
The Physicist said: "However, it is believed that a graviton would have to be massless and therefore would travel at the speed of light." this is what I don't get. why would EM parameters affect the speed of gravity. Here is my suggestion: Early after the big bang, the four forces are thought to have been united. I suspect that when gravity and EM were united, they shared a parameter that determined the speed of all of their waves. i.e., they were the same, 300,000 km/s. So speeds of grav waves and EM waves share a common origin and it is not correct to say gave waves are governed by EM.

ANSWER:
Since I state on the site that I do not do astronomy/astrophysics/cosmology, I will not comment on your hypothesis about the big bang and unified forces at the time. However, gravity and electromagnetism are already linked and I will briefly explain how. The theory of special relativity had its origin purely in electromagnetism�the speed of light is independent of the motion of the source or the observer. And, although Einstein stated it as a postulate, that fact is already a consequence of the transformation properties of the waves which emerge from Maxwell's equations, perhaps the best understood of all field theories. Having formulated special relativity, Einstein next turned to extend it to have a broader application, the theory of general relativity. Of course, general relativity is the best theory we have of gravity, and since it is evolved from special relativity which evolved from electromagnetism, we can say that gravity has its roots in electromagnetic theory. Gravity must then obey all the findings of special relativity, in particular that the speed of anything must not exceed the speed of light and a massless particle must travel at the speed of light.

QUESTION:
leaving aside for the moment what relativity theopry says, do you know of any experiment that has been performed to show that pure energy can gravitate?

ANSWER:
What is "pure energy"? This has no meaning in physics, energy is energy. And by "gravitate" do you mean responds to a gravitational field? So, I will choose light as your "pure energy". It is an experimental fact that light is bent when passing through a gravitational field, so it "gravitates".

QUESTION:
my book says, "friction helps in transferring the motion from one body to another". I am not getting this. can you please explain this.

ANSWER:
Here is just one example of many I might think of. There are two wheels side by side; one is rotating with some speed as shown in the upper half of the figure, the other is not rotating. We now move the rotating wheel so that it eventually touches the unrotating wheel. If there were no friction between the two wheels, the rotating wheel would keep rotating and the unrotating wheel would stay stationary. But if there is friction, the stationary wheel would feel a torque due the frictional force from the rotating wheel. This torque would cause the the stationary wheel to speed up; Newton's third law would tell you that the rotating wheel would feel a frictional force in the opposite direction which would cause it to slow down. Some of the motion of one wheel has been transferred to the other by friction. If the two wheels were identical, they would eventually stop slipping would and the wheels would rotate with the same speeds but in opposite directions.

QUESTION:
Is alternating current the same principle as reverse polarity?

ANSWER:
Neither one of these is a "principle" but they are related to each other. Alternating current refers to a current which is changing direction; to change the direction you need to change the polarity of the electric potential which is driving the current.

QUESTION:
William Herschel's rainbow experiment discovered infrared rays. Looking at the results of the experiment, we see infrared rays hotter than visible red light and red hotter than blue light. Why? The wavelength of infrared is longer than red light and the wavelength of red is longer than blue. Additionally astronomers tell us red stars are cooler than blue ones.

ANSWER:
A single photon has an energy proportional to its frequency and therefore inversely proportional to its wavelength. So blue photons have more energy than red photons; this explains why red stars are cooler than blue stars. So your question is why Herschel found higher temperatures at the red end of the spectrum than the blue. The main explanation was, because he used a prism to create the spectrum of sunlight, and the prism has an index of refraction which is a function of the wavelength. That is what causes different colors to bend by different angles. But it is not a linear function of wavelength, rather the curve shown in the figure. Note that the short-wavelength (blue) index of refraction changes much more rapidly than at long-wavelengths (red). Therefore the blue portion of the spectrum is much more spread out than the red and therefore the thermometer for blue measures a smaller fraction of the total blue spectrum than the thermometer for read measures for the red part.

QUESTION:
I have seen many years ago a nasa invented patent which i will present to you in a link, which was supposed to propel itself by using double pendulum method. Im asking of you to check it, whether its false or true. https://youtu.be/6A_cEZCXBIc I hired a specialist in blender to make this animation, based on my memory, because i couldnt find it.

ANSWER:
Sorry, I can make no sense of this. What I can tell you is that no isolated object can propel itself. If there are no external forces on an object its linear momentum (mass times velocity) must remain constant.

QUESTION:
Say I had an extremely bright flashlight, one impossibly bright for our current technology, and I shone it into space. If I were to then move that light a bit, would I be able to see, in real time, the ray of light bend as it catches up? Or would it be instant? This is specifically referring to the stratosphere

ANSWER:
Brightness has nothing to do with it�since there is air and dust up through the stratosphere there would be some scattering allowing you to see the beam for any intensity. The question is whether you could see a bend. The stratosphere is approximately between 10 km and 30 km. How long does it take the light to travel 30 km? t=3x10⁴/3x10⁸=10^-4 s. Now, suppose you move the light through θ=10�=0.175 rad in T=0.1 s; if the transmission were instantaneous the beam at R=30 km would move with a speed of V=3x10⁴x0.175/0.1=5.25x10⁴m/s so it would go a distance of D=5.25x10³ m. The light beam is not (as you state) a straight line but lags the straight line a bit. All this is shown in the figure where blue is for straight line travel (instantaneous) and red for actual (but not to scale as we shall see!) path. But the actual beam at 30 km will lag the instantenous beam by t=10^-4 s which means that the actual distance traveled in 0.1 s is D-d=V(T-t)=5.25x10⁴(0.1-10^-4)=5.25x(10³-1)=5.245x10³. So (D-d)/D=0.999; so d is far smaller than sketched in the figure, only 0.1% of D. I suggest that it would be virtually impossible to visually detect any curvature of the beam.

QUESTION:
Why do we always see the same stars in the sky as the ancients did? As if we are ment to be traveling through space... wouldn't we see different stars and certainly wouldn't Polaris at least not be the same centre point?

ANSWER:
It mostly has to do with the enormous distances to stars from earth. I looked up some data: the speed of a typical star in our galaxy is about 8x10⁵ km/hr which is about 10^-3c where c is the speed of light and the radius of the Milky Way galaxy is about 5x10⁴ ly (light years). So I will choose as a likely distance to a star in our sky 1000 ly and a reasonable speed perpendicular to our line of sight of 10^-3 c. In one year the star will move 0.001 ly. I have sketched this in the figure (obviously not drawn to scale); the angle θ is 10^-6 radians, about 0.0001�. In 1000 years it will only have moved about 0.1�, measureable but not even noticeable. So to see significant changes to constellations you really need to wait hundreds of thousands of years. Also of interest is that the earth has a precession of its axis with a period of about 26,000 years. This does not result in any change of relative positions of stars but rather moves them around; in about 12,000 years Vega will be the north star, not Polaris. Polaris (and everything else) would have moved about 40� in the sky.

QUESTION:
I have a very mundane question. I have a job pushing wheelchairs up driveways and ramps, and also walking wheelchairs down ramps and driveways. So I'm interested in the force needed to do that based on the incline of the ramp or driveway. Assume that a wheelchair has solid rubber tires that don't deform much. Assume also that the combined weight of the person and wheelchair is 400 pounds. How much force would be needed to push the person and chair

On a flat surface with no incline
Up an incline of 5 degrees
Up an incline of 10 degrees
Any other combinations of weight and incline that you might find interesting or instructive.
Also, would the force going in the reverse direction (walking the wheelchair down the driveway instead of up) be the same.

ANSWER:
I will solve the problem in general, then I can apply that to all your questions. In the diagram I show all the forces on the wheelchair plus occupant:

W, the net weight; I also show the components of W along and normal to the incline, respectively;
N the normal force which the incline exerts on the chair; this is the force which the incline exerts to keep the chair from falling through it.
f, the frictional force impeding the motion; this can be approximated as f=μN where μ is a constant. After searching around I found that μ can be approximated by a small number of about 0.02.
P is the force which the lady (that's you!) pushes to keep the wheelchair moving with a constant speed.

All forces must add up to zero; we achieve this summing separately x and y forces:

N-W_y=0=N-Wcosθ or N=Wcosθ, and
P-W_x-f=0=P-Wsinθ-Wμcosθ, or P=W(sinθ+μcosθ).

Now I can answer your questions:

No incline means θ=0, so P=400x0.02=8 lb.
For θ=5, P=400(0.0872+0.0199)=42.8 lb.
For θ=10, P=400(0.174+0.0197)=77.5 lb.
Note in #5 that going down the incline the friction helps you; going up you have to push against it.
For going down the incline, θ is negative, so the equation for P (which is now a pull rather than a push) is P=W(-sin|θ|+μcos|θ|).
So for θ=5, P=400(-0.0872+0.0199)=-26.9 lb.

QUESTION:
I understand why the twin paradox works in theory, but if man had the means to produce all the requisite energy to propel a spaceship at any acceleration for any duration of time , could a twin physically leave earth in a space craft and come back 50 years later noticeably different in age from his/her twin? Or would the amount of acceleration required to obtain the necessary relative speeds be to much for a human to bear?

ANSWER:
You are certainly right, the usual discussion of the twin paradox assumes that all accelerations are essentially instantenous which would make the necessary force infinite. Because we evolved in an environment where the gravitational acceleration is about g=10 m/s² we cannot endure accelerations much larger than that. The largest a normal healthy person can endure is about 9 times g and that only for a few seconds before blacking out. So if you could maintain a constant acceleration of g would be ideal, but slow; just to get to c/2, for example (in the traveling twin's frame) would take about 6 months. You might be interested in this web page.

QUESTION:
I have to settle a friendly bet. My friend says if gravity was ever instantly nullified for the entire planet Earth, that people and anything not bolted down would instantly begin to fly off into space. I disagree, because there are other forces at work like inertia, friction, air pressure, etc that I believe would need to be overcome before everything simply went into freefall. I realize that what he describes would eventually happen as those forces reconcile naturally...but how quickly would that happen?

ANSWER:
Sorry, your friend wins this bet. Everyone on earth is moving in a circle as the earth rotates on its axis. We are in uniform circular motion which requires a force toward the axis to keep moving in the circle. This force is the component of your weight toward the axis of rotation, shown as W_r in my figure. If your weight W disappears, so does W_r and you will continue moving in a straight line in an easterly direction tangential to the surface. Being tangential to the surface, you would be rising as you moved; but the earth would be rotating beneath you so you would perceive your path as approximately straight up. Since the air is moving essentially with the rotating earth, it would not much impede your departure. Inertia is not a force. Friction from what? You are essentially moving with the air, so no effects due to air drag or air pressure would retard your departure.

QUESTION:
In Einstein's famous equation E= MC², has anyone ever demonstrated the reversibility of the equation; I.e M= E/C²; the transmutation of pure energy into newly created matter? I'm a scientist and this simple question has stumped both myself and my peers.

ANSWER:
"Pure energy" has no meaning. I can give you a couple of examples of energy being converted into mass. The first is called pair production. A photon (a quantum of light, electromagnetic energy) has no mass but has an energy E=hf where h is Planck's constant and f is the frequency of the photon. If the energy of the photon is large enough, it can (and does) turn into an electron and its antiparticle the positron, each with mass m_e. A photon will not do this on its own, but can be triggered to do it by an intense electric field, for example close to a nucleus of an atom. Another way that we can turn energy into mass is to break apart some nucleus. A simple gedanken is to break a nucleus into two pieces and pull them away from each other so the two pieces end up very far apart. Because we know that nuclei exist, those two pieces must begin our experiment being very attracted to each other; so to bring them very far apart from each other requires that we do positive work (that which increases energy) on them. If you now weigh the two pieces and compare them with the weight of the original nucleus, you will find more mass than you started, energy to mass.

QUESTION:
I am not a student...Brain storming. Q:in a 100' dia. X 50' high tank with a 10' dia. X 52' high cylinder attached in center,standing straight up (water tight). Fill lg. tank with water. How much pressure is exerted per square inch on inner cylinder at the bottom first few feet?

ANSWER:
The pressure in a fluid at depth d is P=P_a+ρgd where P_a is atmospheric pressure, g is the acceleration due to gravity, and ρ is the density of the fluid. This will also be the pressure on your smaller cylinder at this depth.

QUESTION:
I'm just writing a sci-fi story and am a little pedantic about details. My question is: if my space craft is launching from the Martian surface will my occupants and their unsecured things inside the space craft experience weightlessness like we see on space stations like the ISS at some point?

ANSWER:
During the launch they will not experience "weightlessness" because there is a net force upwards to accelerate the craft and all its occupants upwards. As soon as the engines are turned off, though, they are in free fall and will experience "weightlessness". Be sure to understand that if you define (as I do) weight to be the force of gravity on something, they are not really weightless but only feel like they are. Once they are far away from Mars, the gravitational force will be small enough that you may say they are approximately truly weightless.

QUESTION:
Is force the only thing that can make something move? And secondly, what makes something accelerate? Is it when energy changes form?

ANSWER:
Newton's first law says that an object in motion with constant velocity will continue like that until acted upon a force; forces change the motion of an object, but no force is required to keep it moving. Newton's second law says that forces change the motion of a particle, accelerates it. Your last sentence does not mean anything to me.

QUESTION:
So, kinematics is the about motion, disregarding the forces, like a(t) = dv/dt. What do you call "non-kinematics", when forces are included? Would you call uniform circular motion "kinematics" if what causes the centripetal force is not specified?

ANSWER:
Kinematics is the description of motion without any reference to the cause of the motion. If you attribute Newton's second law as being the cause of any particular motion, it is called dynamics. If you say that an object moves in a circle R with constant speed v and has an accelleration with constant magnitude a=v²/R which always points toward the center of the circle, that is kinematics.

QUESTION:
My question could be a simple questions, but still I was not able to get a proper explanation for it from the people I asked. If an ascending balloon in the air is carrying a box and the box is released, why does the box move slighlty upward before going down?

ANSWER:
I think you will understand better if I exaggerate the situation a bit. Instead of a balloon drifting lazily upward, the box is being carried upward by a rocket ascending with a speed of 1000 mph. Surely you realize that the box is moving upward with a speed of 1000 mph. And if you now release the box, it would not simply immediately be at rest! It will be going upward with a speed of 1000 mph, but would begin slowing down immediately because of the downward force on the weight of the box.

QUESTION:
Hi, a question from a home brewer. A constant heat source is applied to a container of water. Is the rate of boil off constant or does it vary as the volume of boiling water decreases?

ANSWER:
Once all the water comes to the boiling point, all the energy being added (heat) goes into the water*, a certain amount energy will result in a certain amount water evaporation. So the rate should not depend on the volume of water.

*I assume that radiation losses from the container and the surface of the water are negligible.

QUESTION:
It's been proven that time passes faster on the mountain top than on the lowland. Does this speed of the passage of time continue to decrease if it is monitored below the earth's surface toward the earth's core?

ANSWER:
The stronger the gravitational field, the more slowly time passes. If you move from the surface of the earth toward the center, the gravitational field decreases and becomes zero at the center. Therefore the clock inside the volume will run faster than one on the surface.

QUESTION:
How is sound 'carried on the wind' when it itself is a frequency?

ANSWER:
Your question does not make sense to me. I do not see what "�itself is a frequency�" means and what that might have to do with sound being "�carried on the wind�" Sound is a wave which is distubances which propogates through the air, maybe even one particular frequency but not necessarily. If there is no wind, you would measure the sound to have some speed, say v_s. If there happened to be a wind of speed v_w and blowing in the same direction as the sound is moving, you would measure the speed of the sound to be v_s+v_w . So I guess you would say that the wind is carrying the sound at a speed faster than the sound would travel with no wind.

QUESTION:
Can elementary particles be created or destroyed. The impression I am under based on the confusing answers I've found regarding this question is that as far as we can tell, they cannot. Which makes sense, because my understanding of our understanding of the subject at hand is that Elementary particles (Fermions/Bosons) cannot be created from nothing or destroyed into nothing. I get that with annihilation, fusion/fission, vaporization, and plenty more I didn't list or am unaware of basically result in the conversion and recycling of particles, but that doesn't mean, to me at least, they can be destroyed.

ANSWER:
Your understanding of the words created or destroyed is not what physicists would say those words mean. You are missing the fundamental principle here. Any closed system must have its total energy conserved, not conservation of particle kind. If two protons collide with sufficent energy they may both disappear but not into nothing. The energy they had (including mass energy, of course) must show up as some kind of energy so there has been no loss of total energy. So the collision might result in several particles which are not protons. So I would say that the protons have been destroyed and some other kind of particles have been created. But you would say that the protons have not been destroyed and the other particles have not been created. Your definitions is too restrictive to be useful in physics. But, using your definitions, no particle can be either created nor destroyed.

QUESTION:
My intuition may be wrong here... I get the feeling that I've sat in front of electric out door heaters which are really warm, you can feel the heat on your skin, even if there is a breeze. An outdoor LPG heater I guess is warmer on a still day but on a breezy day. What's going on here? Or am I just plain mistaken?

ANSWER:
There are three ways we generally have heat transfer:

Conduction where heat flows through a solid.
Convection where heat is carried by currents in fluids.
Radiation where heat is radiated away from something hot.

In your case, only #3 is a significant contributor to the heat you feel. The wind has almost nothing to do with it.

QUESTION:
What is the significance of the Dipole moment in electrostatics? No one simply multiplies the distance between charges and the magnitude of the charge without a reason.

ANSWER:
What is the significance of a monopole (a single charge) in electrostatics? Well they exist in nature and so we might want to understand what the electric field of a charge will be; it turns out, as you doubtless know, to fall off like 1/r² where r is the distance you are from the charge. But, there are two kinds of electric charge, positive and negative we usually label them. And since pairs of equal electric charges often happen in nature (for example a hydrogen atom), we might like to know what the field of a dipole looks like. It turns out that because there is zero net charge in a dipole, at far distances from the hydrogen atom you will see no field at all or at least you can surmise that it falls off faster than 1/r². In fact it falls off approximately like 1/r³ and it is not spherically symmetric like a point charge field is. If you think about it, all molecules and solids are held together by attractive forces between electrons and protons. So thinking of molecules requires thinking about dipoles.

QUESTION:
If a boxer was to throw a punch wearing 12 oz gloves and then throw the same punch wearing 16 oz gloves which one would have the most impact force/damage? (...not...homework, just a debate between friends who have no one with the intelligence to settle the debate.)

ANSWER:
A little research on my part found that the only differences are the weight of the glove and the amount of padding. The 12 oz gloves are what are normally used in matches, the 16 oz are for training and sparring. The reason they are used in sparring is that the extra padding will prevent hurting the other guy as much when you throw your best punch.

QUESTION:
As energy could be converted to mass, if the einstein's equation is applied, then the equivalent mass will be produced. Then the neighbouring planet will gets gravitational potential energy, so after this proces, we created even more energy than before? If it's correct, what's the extra energy from?

ANSWER:
I am assuming that at the beginning of the experiment you have a planet and some energy density hanging around somewhere nearby. To make things simple I will assume that the energy density of the energy hanging around is spherical and uniform; then I find a way to convert the energy into mass which is also spherical and uniform. So now you are saying that the energy arising in the planet-mass system is different from what was in the planet-energy system because of the gravitational interaction between the two masses. But here is what you are missing: not only mass causes gravity, but any energy density causes gravity. In my example there is no difference between the energy contained in the whole systems because all the fields are exactly what they were before the energy to mass conversion. Believe me, in any closed system (interacting with nothing else) the total energy remains constant.

QUESTION:
I am a criminologist so this is out of my area but I need this information: As I understand it, entanglement occurs when a particle pair is divided and then separated Such as a photon. If they had to be together and they became entangled in would not the maximum distance they can never be effectively tested such a test were to be developed would be within the speed of light distance over a given time.

ANSWER:
You have sort of hit on why Einstein called it "spooky action at a distance"! What entanglement is is two particles, two electrons or two photons, for example, which have wave functions which are mixed. (Wave functions essentially tell you something about the particles.) The most common experiment is to prepare the system so that the two electrons have zero net spin. In classical physics this could only occur if one spins clockwise and the other counterclockwise, so these would not be "entangled". But in quantum physics a wave function need not be "pure" and you could get zero net spin if both particles were 50-50 clockwise-counterclockwise and we would say that they are entangled. Some time later, and it could be as long as you like, you make a measurement to determine the spin of one of the two and determine that it is spinning counterclockwise; instantaneously the wave function of the other would become pure clockwise. What a measurement does it to "collapse" the wave function and put the particle into a "pure" state. And the catch here is the word instantaneously means just that so any worries about waiting for the second particle to "get the message" that her partner has been determined to be in a pure state are not relevant. In principle you could wait years to make your measurement and then determine the immediate result on the other; you would have to do some very careful timing of the measurement of the far gone particle but you would find that it happened at the same time as your measurement.

QUESTION:
I have a question regarding light and mirrors. I have been taught that light consists of all colors and that things that appear to be white are only white because they reflect all light. This has me confused because there's another thing that i know of which also reflects all light, mirrors. Why is it then that mirrors create a perfect mirror image whereas a white piece of paper is only the colour white?

ANSWER:
Because a mirror has a very smooth reflective surface and therefor the law of reflection, that a ray of light reflects at the same angle relative to the normal with which it came in, and therefore an image will be formed. A piece of paper is rough and any ray of light which strikes it will reflect out at a random angle.

QUESTION:
This question comes from my 11 year-old, who thinks about this stuff while falling asleep. Some objects, like dry wood, float because they are less dense than water. Water is heavy. Is there some depth where the weight of the water column above an object would keep it submerged, even though the object is less dense than water. If the less dense object would rise regardless of the depth, why doesn't the weight of all the water above keep it down?

ANSWER:
As you go deeper and deeper the pressure in the water gets larger and larger. Suppose that you have a cube of wood. So, the force down on the top of the wood is enormous so you might think this would certainly hold it down. However, if you go a little bit deeper to the bottom of the cube you find the pressure is a little bit bigger than at the top, so the force up on the wood is a little bit bigger than the force down at the top.

QUESTION:
Witch falls faster a bowling ball or a tennis ball

ANSWER:
In a vacuum, both fall the same. In air the force F due to air drag, which points upward if the ball is falling, may be approximated as �Av² where A is the area presented to the onrushing air and v is the speed. The net force on a falling ball is mg (the weight of the ball) down plus the drag force, �Av²-mg=maso the acceleration is a=[�Av²/m]-g. Putting in the size and mass of the two balls I find that the drag accelerations are a_tennis=0.015v² and a_bowling=0.0013v². The drag causes more than 10 times the acceleration on the tennis ball which will therefore fall more slowly than the bowling ball.

QUESTION:
Momentum is always conserved, whenever I hear a statement that momentum is not conserved, it is usually because the system being evaluated is not big enough to account for all the momentum. With that said, I often hear statements that momentum is not conserved in General Relativity, but if you account for the momentum in the field, momentum is conserved. maybe not in the mechanical mass x velocity aspect, but if you account for all the momentum, including field momentum it appears to all be accounted for. So, with all that said, why do you read / hear statements about how General Relativity does not conserve momentum? Is it because they are only viewing the mechanical mass x velocity momentum? And not taking into accounting for the momentum in the gravitational field?

ANSWER:
Details regarding general relativity are beyond the scope of this site; I often answer broad questions on that subject, the general principles (principle of relativity, spacetime, equivalence principle, etc.) Let me tell you what I do know about linear momentum and then I will point you to a link where you can learn more about your question.

In Newtonian mechanics, a vector quantity equal to the rest mass m times the velocity v is found to be constant for isolated systems; d(mv)/dt=dp/dt=F_ext. The quantity F_ext is the net sum of all forces acting on the system from the outside; similarly, p is the vector sum of all linear momenta of all the pieces of the system. This equation is just a different way of writing Newton's second law, so you may think of linear momentum conservation as a clever trick, not some new physical law.

In classical electricity and magnetism, you are right: if you want to see familiar conservation princlples you must consider the energy, linear momentum, and angular momentum content of the fields.

In special relativity, if you define linear momentum as rest mass times the velocity you find that it is not conserved for isolated systems. It turns out that you have to redefine linear momentum as γmv it is conserved where γ=1/√(1-(v²/c²)). I have discussed this here many times before and if you go to the faq page and search for momentum you will find several links. A more sophysticated way to view all this is in terms of 4-vectors where the energy-momentum vector has the (new) linear moment as the space-like components and energy as the time-like component.

Finally your question, what about general relativity? From my brief reading it seems to be a lot like electromagnetism�when a particle is bent by gravity, thereby changing its momentum, the field is also altered. General relativity is a very mathematical theory and so any discussion of details is likely to be beyond the purposes of this site. There is a good readable discussion at this link.

QUESTION:
I am sure you know that if you drop a hammer and a feather in a vacuum from an equal height, they will both hit the ground/floor at the same time. This I belive is because gravity exerts the same force on both objects but the feather has more air resistance to weight ratio. I drive trucks for a living so forgive me if this sounds dumb as I have no scientific training. My question is that once they are on the ground, why is the hammer harder to lift than the feather? I understand the hammer weighs more, but isn't weight just a consequence of the pull of gravity? The hammer weighed more when it was falling but was attracted to the earth's centre at the same rate as the feather (in a vacuum)

ANSWER:
Gravity does not exert the same force on each, it exerts a force (called its weight) which is proportional to the mass of each, w=mg for the feather and W=Mg on the hammer where g is the acceleration due to gravity. Now, Newton's second law tells us that if an object with a mass m (or M) experiences a force w (or W) it will experience an acceleration a=w/m=mg/m=g. (or A=W/M=Mg/M=g). So you see, with no other forces they will have the same acceleration which means they would speed up together thence hitting the ground simultaneously. In words, mass is a measure of the resistance to being accelerated by some force and weight is a force which is proportional to mass, then all masses fall with the same acceleration. In the real world there is air, and there is therefore air drag which is approximately proportional the the square of the speed and points upward, but it does not depend on the mass. Therefore the larger mass is less affected by the drag and wins the race as you know it must!

QUESTION:
Since all objects that have mass -the earth, a book etc. - cause a distortion of spacetime resulting in gravity, and E=mc2 tells us that mass and energy are the same thing, shouldn't energy cause a distortion of spacetime resulting in gravity?

ANSWER:
You are absolutely right! Spacetime is distorted by energy density.

QUESTION:
I'm a forensic scientist and feeling a bit out of my league here. I'm working on research to combat specific junk science ("grave dowsing"). I've published a blind study that showed the technique ineffective but one of the proponents continues to espouse what are clearly erroneous statements about a piezoelectric property of bone and oscillation of electromagnetic fields that he claims cause the divining rods to move. I've only seen one thing published about this, a really horrible article published out of the University of Lulea, Switzerland that had some overt and unforgivable errors in design. I think just a general understanding of simple physics make it obvious that even if bone had piezoelectric properties (which I very much doubt), that the electromagnetic field produced would be able to affect metal rods "1/2 mile away" as this instructor is telling students. I could do a bunch of experiments to disprove this but I think the answer is already there in physics and associated mathematics but I don't possess anything near the understanding of the mathematics to work the equations. My question, if you can forgive all the buildup, is whether you think I'm on the right track looking at the Lorentz force and Maxwell's equations. Would I be able to use those equations to figure the amount of charge that would have to be produced by a bone in order for it to move a metal rod even a meter away?

ANSWER:
Dowsing is a really tricky thing to try to analyze. There are some very bright people who thinks that dowsing for water works. And of course water is not going to exert a force on a willow branch or coat hanger. My feeling is that, like the old ouiga board, that the pushing of the stick is done by the dowser. And it is altogether likely that he does this unconsciously; these are often old codgers who have been doing this most of their lives and have experience. Another suggestion is that the some of the successes of water dowsers are that they are often working in areas where a drilled well anywhere in the vicinity would probably find water. So, now, what about the grave dowsers? I have found that bones do indeed have piezoelectric properties; it plays important roles in bone formation. It is not clear to me if it has to be a living bone, but just let us suppose that the weight of the ground above pushing down on the bone (a person in a coffin would not have any pressure being applied to his bones) creates a potential difference. The thing is that the net charge created is zero, the bone becomes positively charged on one side and negatively charged on the other; in that case, it looks like a parallel plate capacitor and nearly all the electric field would be from positive to negative, nearly all the field being confined to the bone. And, because it is dipolar, whatever field exists outside the bone would fall off very quickly (faster than the field of net charge which falls off like 1/r² with distance r); the field the dowsers think they can detect would fall off more like 1/r³. Add this to the fact that piezoelectric fields are very weak in the first place, I can see no possibility that they could be detected even by the most sensitive of instruments, let alone a piece of a coat hanger. Devotees are very serious about this, though, and it is a losing battle to try to convince them otherwise. Collect as much data regarding success/failure rates, do a good statistical analysis, and be happy with that.

Incidentally, statistical analysis is vital. The classic example is from several decades ago. For years it was presented as fact that clusters of cancer occur in communities where high voltage power lines crossed over, presumably due to the electric and magnetic fields associated with them. This was totally debunked by doing proper statistical analyses.

QUESTION:
If the angular and the linear velocity of a wheel at the point of contact to the road is equal to zero. Where does the velocity or the kinetic energy of the still moving car all go?

ANSWER:
It didn't "go" anywhere. There is no rule that anything which has kinetic energy must have all parts of itself moving with the same velocity. Those parts of the tire in contact with the road contribute nothing to the kinetic energy of the whole car. Perhaps it is a bit easier to understand with a WWII tank. The tread on the ground is at rest; the tread on top has to be going faster than the tank as a whole; all the wheels and gears are spinning and different parts are going up or down or forward or backward or in all other directions with different speeds. But, if you add up every single part's contribution to the kinetic energy of the whole tank, it will stay the same if the engine provides enough energy to overcome all the frictional forces present.

QUESTION:
Suppose you have two massless containers that are empty. They have no mass so there is no charge nor gravitational attraction between the containers. If we keep adding protons and neutrons into each container equally, a coulomb attraction from charge and a gravitational attraction due to gravity will develop. Initially, the coulomb force will far outweigh the gravitational force. However, as we continue to add protons and neutrons to the containers, the amount of mass collected will grow to the point where the macro size is large enough to no longer have much coulomb attraction. However, the gravitational attraction will grow. Is there a point where the attraction of charge will equal the attraction of gravity. Has this been investigated? And has this been achieved?

ANSWER:
I have held back thinking about how to answer this question for some time now. Only this morning did I realize that it is impossible. The reason is that if each container has a mass M and a charge Q, what determines the relative magnitude of the forces between the two containers due to gravity and to Coulomb forces is only going to depend on the ratio M/Q; but you propose to add equal amounts of charge and mass to each container so this ratio would never change!

There is also the problem of the interaction among the nucleons in the containers. You are essentially imagining creating super heavy nuclei and in any nucleus the mass is not equal to the sum of its parts. It would be impossible to determine the mass of systems of neutrons and protons in the numbers far above natuarally occuring nuclei

What I can do is calculate the ratio for two hypothectical point masses (M) and point charges (Q) separated by a distance R such that the attractive gravitational and repulsive Coulomb forces have equal magnitudes.

GM²/R²=kQ²/R²

M/Q=√(k/G)=√(9x10⁹/6.67x10^-11)=1.16x10¹⁰ kg/C.

QUESTION:
Let's say there is a container that contains water and an ice cube in floating in it. Some portion of ice is below the water (may be referred as bottom of ice) and some above (may be referred as top of ice). Now volume of only submerged portion of the ice is equal to the volume of the water displaced, isn't it? If so, where did the volume of melted upper portion of the ice that did not displace the water previously go? Should it not be added, hence increasing the total content of water? But that's not the case according to text books.

ANSWER:
The reason is that the ice does not have the same density (less than) as the water; that's why if floats. But, if it melts it become water and therefore has a density the same as the water. The fractional amount by which the density decreases is precisely equal to the amount by which the volume decreases.

QUESTION:
My question has to do with wind chill. I believe that I understand the basic mechanisms by which this works, but my question gets more convoluted. Thinking about how objects which fall into the earth's atmosphere from space will burn up due to the extreme heat of friction with the air, I am wondering if it is possible to say at what velocity would wind change from having a chilling effect to having a heating effect due to friction? My guess is that it would require wind speeds which would far surpass the point of being fatal to a human being, thus negating any specific concerns about wind chill as such, but who knows?

ANSWER:
First of all, you are extrapolating a qualitative quantity (essentially "how cold do you feel in a wind") into a region where it was never meant to be applied. You can find lots of details about wind chill in the Wikepedia article, but this article also states "Windchill temperature is defined only for temperatures at or below 10 �C (50 �F) and wind speeds above 4.8 kilometres per hour (3.0 mph)". The reason is that this effect of wind is to hasten temperture loss of the body due to the wind, and is most certainly not applicable to situations where the effect of wind is to increase, not decrease, temperature. In the summer time the main reason we feel hotter or cooler is the humidity. Instances where air drag has a nonnegligible effect of heating or cooling, these ideas do not apply. There is, in fact, no way to have a simple qualitative formula for the effect of speed on heating because it depends on the shape and size of the object and on the density of the air through which it is moving; the SST, for example had a "needle-shaped nose" to minimize heating at supersonic speeds and would have burnt up otherwise. The takeaway here is that qualitative quantities like this may play an important role in health and safety (e.g., high winds in cold weather can result in high probability of frostbite) and provide information helpful to deciding how to dress, for example, in different wind conditions.

QUESTION:
Hi. My question has to do with gravity. If you took two planets with the same mass, in an area of space without any other immediate gravitational influences, and put them just within each other's gravitation pull but not moving, would they collide, or would they orbit each other? If they would end up orbiting each other, why?

ANSWER:
As long as these planets are spherically symmetric (center of mass at the center, density only dependent on distance from the center), their centers will accelerate with equal accelerations until they collide. They could either stick together and come to rest or bounce off each other and each recoil with equal speeds in opposite directions. If they were not spherically symmetric, their centers of mass would certainly not be exterior the the planets, so their centers of mass would accelerate towards each other and they would still collide and therefore not orbit; if they stuck together, they would rotate about their total center of mass but have no translational kinetic energy.

QUESTION:
If two objects move parallel at the same speed light years away would the a person on one object be able to see the other object? This is assuming a similar starting position, my initial assumption would be no as any light from one object would fail to reach the position of the second object. Or would the two objects be able to observe each other but one would appear "behind" the first? I know its multiple questions but what would be the shift of the object if the second question is in the positive?

ANSWER:
Yes, the light from the trailing object would reach the leading object Y years after it was sent where Y is the number of light years between the two. You are not thinking about this problem using the principles of special relativity (SR). Perhaps the most important assumption of SR is the principle of relativity which asserts that the laws of physics are the same in all inertial frames of reference. An inertial frame is one which moves with constant velocity relative to another frame in which you know the laws of physics. In your case, since both objects are moving with constant speed in the same direction, they might as well be at rest.

QUESTION:
Is anyone trying to figure out how to tap into the energy that holds atoms together? I don't mean harnessing it to fuel our energy needs. I mean accessing it like we would a hard drive. It's the one thing that everything in the universe has in common and it's the one thing that connects us all. In it is knowledge beyond comprehension.

ANSWER:
So, the question you are asking is very vague. For example, what does "holds atoms together" mean?

Does it mean what holds atoms together in a macroscopic piece of matter?
Does it mean what holds the atom itself together?
Does it mean what holds the nucleus of an atom together?

And what does "accessing" mean? What we often think of when something is being held together is a force; in more advanced physics we usually express the presence of forces by introducing potential energy functions. So I am going to answer your question with a very broad brush; in essence, to "access" anything at the atomic level you need to ascertain, by doing experiments and interpreting the data, what the relevant potential energy functions are (or forces, if you like). And, guess what! That is what physicists and chemists have been doing for the past several hundred years. Condensed matter physicists address #1 above. Atomic and molecular physicists address #2. Nuclear and particle physicists address #3. In fact, thinkers from thousands of years ago, Greek philosophers for example, have been puzzling over these kinds of questions. So, is "anyone trying to figure out" answers to these questions? You bet! Thousands of men and women for thousands of years!

QUESTION:
Can air pressure be different inside the same container? I'm having a debate with my work. WE have a device (packer)that inflates like a long cylindrical ballon inside sewer pipes to install fiberglass patches. They are claiming that if our packer is at the end of the pipe and sticks out at all, that the air pressure inside the pipe, and contained, is less than the air pressure that is outside of the pipe and is bulging out because it is not contained (within the pipe). I say that the pressure is constant throughout the entire thing and there is no change in pressure inside vs outside the pipe because pressure has to be constant inside one container. Who is correct?

ANSWER:
So, lets assume that there is some pressure P inside the balloon and it has some volume V and that it is wholly inside the pipe. Now it comes to the end of the pipe and starts expanding outward since it no longer has the pipe to keep it to its previous cylindrical shape. If this happens pretty quickly the temperature will approximately stay the same. So the product of P and V will remain constant as it expands. The volume will increase so the pressure will decrease. During the time this expansion is happening, there will be a different pressure inside the pipe and outside but that will be for a very short time, the time it takes for the slightly lower pressure to equilibrate throughout the volume. If everything is static and in thermal equilibrium, the pressure will be the same everywhere.

QUESTION:
I have a question pertaining to sound. So, I was wondering how it is possible for me to hear someone facing away from me in say, an open field. Because I know for example, if in a closed space, the sound would bounce off the wall and come back to me, at least that's how I think it works. But if I'm able to hear someone facing away from me in an open field, Is sound more complicated than a directional wave, is it more spread out than I think?

ANSWER:
Usually in physics we think of wave sources in some simple geometric form. For example, if you think of sound as just like a laser for light as a narrow coherent beam of sound coming out of your mouth, only someone standing in front of you would be able to hear you, clearly not the case. If you think of it as a point source but radiating only forward, anybody in within a hemisphere in front of you would be able to hear you. But, as you note, this second simple model does not fit evidence from the real world, so it must also be incorrect. But if you think of it as a simple point source it would radiate in all directions. But that would say that I hear you just as loud whether in front of you or behind you; this also is not what we experience which is your voice is less loud if I am behind you rather than in front of you. However, we could account for the smaller amplitude from be due to the sound source being much more forward in the head/throat so sound emitted backwards gets attenuated passing through the head tissues and bones. The fact is that the source of a human voice is complicated; there is the larynx containing the vocal cords, the primary source of sound; but then there are also resonant cavities*, the mouth, nasal structures, sinuses, etc., which amplify and rebroadcast the sound.

*If you just had a guitar string simply stretched between two points in a room, you would be hardly able to hear it. The "box" of the guitar plays a vital role by resonating and amplifying the sound from the vibrating string.

QUESTION:
I've been thinking about the rising prevalence of coilguns, and an interesting puzzle came to my attention, which it is unfortunately beyond my limited "physics" ability to solve. Some context: Rifling in conventional kinetic firearms use grooves in the barrel to change some forward momentum into rotational energy, affording stability to the projectile. However, I want to try to achieve, with magnetism, an inverse effect - converting rotational energy (at least partially) into forward momentum, without any physical contact with the rotating entity in question. Assuming no constraints imposed by current technological progress: What forces, where, and when would be required to achieve such an effect? Feel free to go into any level of technical detail that you feel is necessary.

ANSWER:
You did not mention why this is of interest to you, so let's assume, since you mention guns, for purposes of an example, that you would like to take a rotating bullet-like object and convert its rotational kinetic energy into translational kinetic energy. Consider a solid cylinder with mass m, angular velocity ω, radius R, moment of inertia I=�mR². So, it will have a rotational energy K=�Iω² which we wish to convert 100% into translational kinetic energy K=�mv². If you do all the requisite algebra you will find that ω=(√2)(v/R). Suppose R=1 cm=10^-2 m, a very big bullet, and v=1000 m/s, a modest bullet speed; then I find that ω=1.4x10⁶ rpm. More than a million rpm means that this would not be a good way to get energy to launch a projectile.

QUESTION:
Baseball commentators often say a hard throwing pitcher is "providing the power". They are meaning the batter doesn't need to swing as hard as he would have to if the pitch was slower. I don't think that can be correct since the faster pitch will have more momentum in opposite direction of the force provided by the bat. What is the correct way of thinking about that?

ANSWER:
I believe that the best way to think about this is using impulse. The impulse is the average force F times the time Δt which the ball and bat are in contact, I=FΔt. Because of Newton's second law, F=Δp/Δt, I=Δp where Δp is the change of linear momentum. If the incoming pitch has a speed of v₁ and the outgoing ball has speed v₂, the change in momentum is m(v₂+v₁) where m is the mass of the ball, and therefore v₂=(I/m)-v₁. So you can see that the faster the pitch, the slower the speed of the hit ball if the batter exerts the same impulse to the ball. I suspect that the reason the commentators believe this is that a fast ball right down the middle, often called a mistake on the pitcher's part, probably yields the most home runs since it is the easiest for power hitters to hit; the reason is not that the ball is going faster, it is because it is going straighter. (All this assumes that the outgoing and incoming velocities are in exactly opposite directions to make my example a one-dimensional problem.)

QUESTION:
I want to demonstrate that NaCl solutions conduct electricity to my students and show this qualitatively and quantitatively. Is it possible to build a complete circuit as follows?
|--9 volt battery---NaCl solution---multimeter---LED/Daylight bulb---|
|---------------------------------------------<-----------------------------|

ANSWER:
Assuming that your multimeter can measure current as well as voltage this should work; if you are going to measure conductivity you need the current as a function of the concentration. Also, I would do the quantitative and qualitative experiments separately because LEDs are not ohmic and as you change the current you would change the voltage across the LED and therefore across the solution; you want to keep the voltage across the solution constant at 9 V when you are measuring the conductivity. Also, the resistance of the filament of an incandescent bulb changes as it heats up, so you should only use that when you are doing the the qualitative demonstration. Come to think of it, an incandescent bulb would probably be better because not all LEDs are dimmable so it might just turn off when you changed the solution or not change at all.

QUESTION:
Jupiter's moon Io is volcanically active due to the moon being squeezed by the gravity of Jupiter and the interactions with the other moons. Io is hot, where is that energy coming from? There is not supposed to be a 'free lunch' regarding energy, there has to be a cost in energy somewhere else. So what is the supplying the energy in Io. Gravity isn't an energy source, so what is the source of energy for Io?

ANSWER:
I usually do not answer questions about astronomy/astrophysics/cosmology, but will give this one a try. Why do you say that gravity "�isn't an energy source�"? It is one of the most important sources of energy there is; a ball dropped increases its kinetic energy as it falls because of the force of gravity doing work on it. In the case of Io, there is a large tidal force because of its gravitational interactions with Jupiter and other moons which are constantly squeezing and changing its shape. Imagine that you are squeezing and relaxing a rubber ball; the energy you are putting in will cause it to heat up. For a full-blown explanation, see the Wikepedia article on tidal heating.

QUESTION:
Why does certain object falls faster than others?

ANSWER:
If there is no air, all objects fall with the same acceleration. However, if the objects are falling in air, the air drag force affects some more than others, and they fall with different accelerations.

QUESTION:
Why light speed is a universal constant if gravity can bend space-time?

ANSWER:
In everyday life speed and velocity are synonymous. In physics velocity is a vector (specified by a magnitude and a direction) whereas speed is the magnitude of the velocity, a scalar. The speed of light is a universal constant, the velocity need not be. So a beam of light may be bent by gravity but still maintain a constant speed. It is like driving on a curvey road at a constant speed of 50 mph: your speed is a constant but your velocity is not.

QUESTION:
I have a weird question I'd like to ask. I was in the bomber ride, which consists of a long arm with a gondola seating 4 people at each end. The arm revolves forwards for a few times then backwards for a few more times, and the gondola also rotates 360� mid air. The arm is 120 feet high and revolves at a speed of 13 rpm, in which the passenger experiences 3.5 Gs according to Billy Danter's fun fair website. I vomited a little while the gondola was at the very top and rotating, but I cannot remember if we were going forwards or backwards. I apologize for the gross details, but I'm curious to know where my vomit had landed, as it did not splatter on me not on the next seat passenger.

ANSWER:
The picture of the ride is shown on the left. It rotates (13 rpm) about an axis in the center. If you want to see a video of this, click here. If you are at one of the outer ends of this thing, you will experience a "fictional" centrifugal force which is 3.5 times larger than your weight (I checked and this is correct). If you watch the video you will see that the gondola itself is also free to rotate about its own axis, but any centrifugal force due to that rotation is trivially small compared to the main centrifugal force and your own weight. The other picture shows the gondola at one end rotated to some angle and at the very top as specified by the questioner. The questioner vomits (I will assume straight out) and the vomit is labelled V and has a velocity in the direction of the yellow arrow. There are two forces, the orange vectors, on the vomit, its weight W down and the centrifugal force 3.5W up. The net force on the vomit is therefore about 2.5 times its weight and so it will appear to someone in the gondola someone in the gondola to follow a path roughly like the green-dashed line in the figure. So it is no surprise that it did not get on anybody.

QUESTION:
I have recently gotten into synthesizer and how they affect soundwaves. Can soundwaves really be a Sawtooth and triangle's waves? The sine wave is the only wave that seems possible to me.

ANSWER:
I don't know on what you base your belief that only sine waves are possible. In virtually all musical instruments the sounds produced are not pure sine waves; only electronic instruments are capable of creating simple sine waves. Imagine two instruments, say a violin and a piano, both play a middle C; do they sound just the same to you? Of course not; this qualitative difference is called timbre. The pitch of a tone is determined by its periodicity, the frequency with which the wave repeats its shape when passing; not only sine waves but any shape you can imagine could repeat itself over and over. Your brain hears the middle C as the same note from all instruments but hears differences as well. But, here is where you have gotten something right when you think of sine waves as being somehow special. Physicists and mathemeticians find sinesoidal waves to be very easy to work because they satisfy a very simple differential equation and because they form what is called a complete set of functions. As a result, any periodic function with frequency f may be described perfectly by a sum of sine and cosine functions with frequencies f, 2f, 3f, 4f� This is called a Fourier series representation of the wave. The sum is infinite, but normally only a few members are needed to give a good representation of the wave. The figure shows Fourier representations of a square wave for 1, 2, 3, and 4 terms in the series.

QUESTION:
What causes one person to float while another person only sinks? Is it the molecular make up of the water, the human, or a combination of both? I am very buoyant, I lay on the surface of water, even with a weight belt is hard for me to stay under water. My GrandMother floats like a large rock, straight to the bottom, she can't even swim with a life vest on. Why is that?

ANSWER:
The answer is pretty simple: if the density of the body (mass/volume) is less than the density of water (997 kg/m³) it will float, if more it will sink. The body is made up mainly of bone (~1900 kg/m³), fat (~914 kg/m³), and almost everything else (~1040 kg/m³). Approximately 14% of body mass is bone. So, only fat has a density less than water meaning the more fat you carry, the more buoyant you are likely to be. It is difficult to try to get more quantitative because the lungs occupy a not negligible fraction of the body volume and air density is ~1 kg/m³. Almost nobody with air in his/her lungs will sink like a stone. Your grandmother probably has very low body fat.

QUESTION:
Thank you for taking the time to read my question. I am seeking an explanation to my problem from some time now and I am very glad to have found your site. I'm an olympic wrestling strength and conditioning couch and I have my athletes practice an old isometric exercise called pushing the wall, to develop whole body strength and power. As I have gone thorough this exercise myself, after a year or so I have discovered that something interesting is happening and this is what I'm seeking an explanation for. As I push on the wall ( the push really comes from my back leg and the whole body but without whole body muscular tension), with the same pressure, without any other movement ( or an immovable surface) for let's say 30sec -1 min' when I slightly "push off" the wall ( I'm about 96 kg) and I mean gently, not with force, I find myself been thrown backward for 10-15 meters or more in some instances, by some kind of force..For the first few meters the force is very strong that I can't stop the movement myself. The momentum actually accelerates and it gets stronger as I keep been pushed backwards and my body keeps going backwards, after a while the momentum comes to a stop by itself, if I don't make an effort to stop it myself. Even if I put a slight pressure on the wall and push off very gently, the same effect takes place.

REPLY:
I have spent some trying to understanding how this could be. I keep coming back to your question but to no avail. If you still want me to try to figure this out, I would appreciate it if you would send me a video you mentioned.

FOLLOWUP #1:
Thank you so much for getting back to me. I really thought that my inquiry was weird enough for you to not consider it as true. For a while now I considered asking or talking with a physics professor about this and see if there is an explanation for this. You are the only person I thought to ask, and because I think this is a strange phenomena, I thought you might think it is fake and not bother taking it seriously. Because I think is indeed strange ( I call this force: "strange power"), I only think what other people might think about it and not even bother with it, as it seems that it is not a tangible physical thing or force, meaning that it seems that it isn't based on muscular force or physical exertion. As you see in the videos I really don't push hard at all.

ANSWER:
Let's look carefully at one of the videos you sent. I have inserted one frame showing you right after you have lost contact with the post; your body is clearly tending toward a sitting position. Your weight (one of the forces on you) acts at your center of gravity, clearly behind your feet. If you don't do something, you will fall on your ass because your weight exerts an unbalanced torque about your feet. To keep that from happening, you push forward with your feet on the floor and the floor pushes backwards on you; if the floor were extremely slippery, e.g. like ice, there would be nothing you could do to avoid going down. But, there being friction, you now have an unbalanced force on you which accelerates you backward. This, in itself, does not keep you from falling but it gives you time to straighten back up so that your weight no longer exerts any torque about your feet and you can now stop without falling. There is no "strange power" force here, just plain old Newtonian physics.

FOLLOWUP #2:
Thank you for examining that frame from the video. But, what is that, that is strongly moving my weight and acting on my center of gravity ( as you see in that frame) ? There is a strong power/force that is causing my position that you see in that frame, my center and body weight gets pushed backwards by that force and it keeps pushing me backwards while I step backwards trying to regain balance and stability. But, there is a strong force that strongly pushes me in that position, and keeps acting on me, when I only slightly push on the wall ( as you see in the videos). What is that force? and where is it coming from?..that is my question. What is that initial force or power that throws me backwards ( which is not the momentum caused by my center of gravity being behind my heals, there is a power that first pushes my weight and/or center of gravity in different positions thus creating a movement afterwards ). Take a look at my starting point. There are almost no external moving parts, that will logically/physically initiate a strong movement of my weight or center of gravity backwards and yet it happens. And also how can the other things that you see in the other videos be explained.

ANSWER:
I will answer your last question first. You sent four videos, each with 3 or 4 trials. In every trial, just before you lost contact with your hand, you swung your hips back so that your legs were angled backward so that your center of gravity (somewhere inside your chest) was behind your feet. There are no "�other things that you see in the other videos�" which need to be explained beyond this single frame and the little backward scurrying that follows.

I thought that my answer to your first followup question pretty clearly explained the whole thing without having to get into the details of the forces and torques I was talking about. But, it appears from your second question that you are not familiar with how forces are dealt with in physics. So I will give a little tutorial on the important points necessary to understand your situation. The most important thing to understand are Newton's three laws:

If an object is at rest or moving in a straight line with constant speed, the sum of all forces on it must add to zero.
If an object with mass M has net force F not equal to zero it will have an acceleration a=F/M in the direction of the net force.
If an object A experiences a force F from another object B, object B experiences a force of equal magnitude but in the opposite direction as F.

As an example, I will look at a case very similar to yours, a sprinter. The figure shows all the forces acting him, his weight W which is the force which the earth exerts vertically down on him, the normal force N which the ground exerts up on him, and the frictional force f which the ground exerts forward on him. Since he is not accelerating in the vertical direction, only forward, N must be equal in magnitude to W so that their sum is zero. The net force at this instant is f, a forward force which accelerates him in that direction. Most people will say that it is the muscles in his leg which propel him forward, but that is wrong; the muscles in his leg result in the foot pushing backward on the floor so, because of the third law, the floor pushes forward on him. (Most people would say that an engine is what drives a car forward, but it is actually friction between the tires and ground which causes the car to accelerate forward. You might be interested in an earlier answer.) There is still a subtlety regarding this situation which is important: suppose this sprinter encounters a patch of ice so that the friction becomes essentially zero. Now there is a net force on him which is zero. Does he simply glide across the ice and then resume running when he gets back to dry land? No, because his weight will cause his whole body to rotate about an axis passing through his feet and he will fall forward until his other foot or his knee hits the ground. (We say that W exerts a torque equal to W times the distance horizontally between the axis and the center of mass.)

So now your case. The next figure shows you a short time after you lost contact with the pole. You had to do something or else you would rotate because of the torque due to W and end up sitting on the ground*. Your brain can detect this situation and lifts your right leg and pushes on the floor with your left foot, causing a frictional force ("strange power"?!) pushing you backward and accelerating you. You will still be starting to rotate but note that your right foot will hit the floor less separated from the weight so your tendency to fall will be lessened due to the decreased torque. When that right food lands on the floor the left foot lifts and the roles of the two feet reverses. You keep backpedaling like this until, finally, your center of gravity is directly above your feet and you won't fall over.

*In one of your trials you failed to be able to stop the rotation and did, indeed, land on your ass. Notice your arms and lifted leg desperately trying to move your center of gravity farther relative to your right foot but it did not work! The reason was apparently that you dropped your hips too far when you launched.

If you just stood straight up with your center of gravity vertically above your feet, you would not feel the "strange power" when you lost contact with the pole. I know�I tried it.

FOLLOWUP #3:
I do understand what you are saying. Your last sentence was : "If you just stood straight up with your center of gravity vertically above your feet, you would not feel the "strange power" when you lost contact with the pole. I know�I tried it." Well, I tried it too, and again the "strange power" was pushing me off the wall..( strange power...is only a joke :) The upper body gets pushed by the force first and the feet follow. It looks like the feet are trying to catch up with the momentum of the upper body, but it doesn't feel that way because the force keeps pushing the upper body backwards not because of the momentum of the upper body going backwards. Again, it is the force, a very tangible force, from the slight push off the wall that keeps sending the body backwards and that creates the acceleration. The acceleration of movement doesn't come from trying to stay on my feet or to regain stability after the push off the wall. I know it looks like that but the feeling is not at all like that. This is how it is felt. Also sometimes the force goes down into the feet, making them move backwards, thus moving the whole body backwards, Anyway, maybe it is difficult to understand. It is something that has to be felt, and I have tried to explain it but maybe it is not clear in how I say it. Maybe the only explanation using physics is the one you are giving me. ( I was thinking more in terms of conservation of mechanical energy, potential energy stored in the mechanical bonds between atoms, stored elastic potential energy that changes into kinetic energy when it is released ) Here is a video of it, me standing upright. If you are insisting on the explanation of Newtonian laws at work here, I understand and I thank you for your time.

ANSWER:
Here are the first few seconds of one push. Your feet stay put but your body leans. By the time of the fifth picture your body feels like it is falling and your brain perceives you are falling. Your brain interprets that something is pushing you and screams to your body that it has to act fast, keep one foot planted and get the other foot back to try to stop the fall. And so forth as described in my answer.

FINAL FOLLOWUP:
Yeah, ok. I was sure you would say that. Your opinion makes sense when only watching, yet you seem to reject what I am trying to explain to you, that what you see is not what is actually happening, ..but you can have your opinion and thank you for that. It is great that you gave me your point of view, because now I know what other people might say and I know what to expect. If you would feel what I am talking about you would not have the same opinion. But it is perfectly ok. Thank you for your answer, thanks for trying.

MY COMMENT:
This is certainly not the first time I have had to end with "we'll just have to agree to disagree)!

QUESTION:
I built a spring loaded catapult which sent a practice golf ball a distance of 11.25 feet from a height of 2.66 ft at the horizontal (0 deggres) which I believe gives a velocity of 27.64 ft per sec, since free fall time is 0.407 sec. Then I launched the ball from a 28 deg angle and my assumption is that the initial velocity from any angle would now be 27.64 ft/sec, however the distance only came to 19.25 ft when I predicted it should go 23.8 ft. Working from the distance of 19.25 ft I get an initial velocity of 24.27 ft/sec. How come the initial velocity at another angle is different than the velocity when fired horizontally? I am doing this project in my high school Pre-Cal course of which I am the instructor.

ANSWER:
This will be a good lesson for your students. You are assuming that the usual kinematic equations for motion in a uniform gravitational field are exactly correct. But they are only approximations. In the real world there is air and air drag causes a force opposite the velocity vector which is approximately proportional to the square of the speed. So the mathematics are going to well beyond high school. Let's just consider the first case to discuss here since I can make rough calculations to estimate the effect of drag. I will not go into details, just give you the results of my scribbling. First you got a velocity 27.64 ft/s by dividing 11.25/0.407; this is only the horizontal component of the velocity because the ball would also acquire a downward vertical component of 0.407x32 ft/s=13.02 ft/s. The velocity when it hits the ground is √(13.02²+27.64²)=30.55 ft/s. But that is if you ignore air drag which will take velocity away as it flies. My rough calculations are that if the ball has a speed of about 30 ft/s the drag will exert a force of about 0.013 lb. This will cause an acceleration of about -4.3 ft/s² which would result in a loss of velocity over 0.407 s of about -1.75 ft/s. (What makes the math difficult is that, unlike uniform acceleration by gravity, the force on the ball changes with time.)

The lesson your students should learn is that it is important to ask yourself how good a description any "theoretical" model of a physical situation like projectile motion is. Your results were pretty good, but you were dealing with speeds of only about 20 mph; a driven golf ball can have speeds up to about 200 mph so the drag force they experience would like 100 times larger than at your speeds (proportional to v²). Predictions of the distance of a drive would not be close to how far the ball would actually go. Another example is a baseball; anyone having played outfield knows that a long fly ball ends falling almost straight down, not at the same angle it was launched. You can demonstrate this by throwing as hard as you can a crumpled sheet of paper; it will end up falling almost straight down having lost all its horizontal velocity.